Spot ignition of a wildland fire and its transition to propagation
Supan Wang A , Maria Thomsen B , Xinyan Huang C * and Carlos Fernandez-Pello D *
C * and Carlos Fernandez-Pello D *
A
B
C
D
Abstract
The prediction of the propagation of wildland fires is an important socio-technical problem. Wildland fires are often initiated by small spot ignition sources and then spread to larger burning areas.
Experiments are conducted for the spotting ignition of a forest surface fuel (pine needles) in a relatively large (up to 1 m2), horizontal laboratory bed, and the subsequent fire spread without wind. The spotting ignition sources are a cluster of steel particles, an ember and a small pilot flame.
Wildfire spread has an initial acceleration phase, with the growth of the burned area in the fuel bed following a power law dependence in time, almost independent of the ignition source. Comparison with previous larger-scale experiments and FARSITE modelling of the fire spread over similar fuel beds shows that the power function with time describes well the combined results of the initial wildfire growth and the transition to larger fire propagation for relatively long times.
The Rothermel equation under different environmental conditions may be extended to describe the initial accelerative growth of a spot fire. This work supports the modelling of fire propagation that currently is geared to a later time in the development of a wildfire.
Keywords: fire growth rate, fire spread model, hot-particle ignition, rate of spread, scale-up fire, spot fire, wildfire, Wildland–Urban-Interface fire.
Introduction
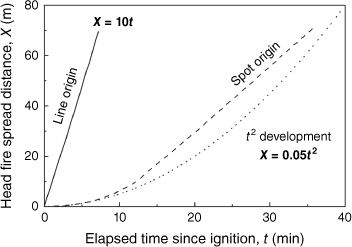
Wildland fires are becoming more frequent all around the world in a drier climate. Some of these fires may have catastrophic consequences with extensive damage to land, property, ecosystems, and lives (Liu et al. 2010; Ellis et al. 2022). It is expected that under the drier weather patterns related to the overall climate change, the problem will only become broader and worse. The development of a wildland fire can be separated into ignition, initial fire growth and a large-scale propagation. Most wildfires are ignited by a small spot (Fernandez-Pello 2017; Manzello et al. 2020) and initially spread with an increasing rate of spread (ROS) until they reach a linear spread (Fig. 1) (Johansen 1987).
Generally, wildland fires have been studied primarily with steady line fires after their initial development, and consequently, there is more data available for line fire model verification than for spot fires. Nevertheless, the growth of a wildfire from a point source or a line source shows very different growth characteristics and spread rates (Rothermel 1983, 1984; Lanoville and Schmidt 1985; Johansen 1987; Alexander et al. 1991; Wadhwani et al. 2023), as illustrated in Fig. 1. Rothermel (1984) showed that fires ignited by a point source tend to be less intense and of longer duration than those ignited with a line fire. Johansen (Johansen 1987) showed that line fires spread much faster than spot fires, so it takes several minutes for a point fire to reach ROS equilibrium. Lanoville and Schmidt (1985) reported ROS for line fires to be six times faster than for spot fires, and a similar trend was reported by Alexander et al. (1991). If the spot fire has a constant acceleration rate, its spread distance approximately satisfies the t-square law, also illustrated in Fig. 1.
Small ignition sources include clusters of hot metal sparks from power line interactions, heat from work (friction, grinding, welding) and other sources of incandescent particles from welding or fireworks processes (Babrauskas 2003; Wakelin 2010; Finney et al. 2013; Mikkelsen 2014; Ramljak et al. 2014; Fernandez-Pello 2017; Wang et al. 2017; Manzello et al. 2020). Once a wildfire starts spreading, fire spotting by firebrands becomes another potential mechanism for the ignition and spread of wildland fires by a small source. All these wildland fire ignition mechanisms have the common characteristic of a small and localised area of origin, with the subsequent spread of the fire to wider and larger areas.
The initial fire spread from a small source is three-dimensional and leaves a somewhat V pattern that is determined by the wind direction and its speed, the topography (buoyancy), the fuel characteristics (type of vegetation, moisture content, etc.), and the environmental conditions (temperature, humidity). Because of the three-dimensional characteristics of this type of propagating fire, its rate of spread has an initial acceleration phase leading to an equilibrium ROS when the fire reaches a size with an approximately linear fire front, referred to as a line fire. The initial acceleration phase is important because it may determine the characteristics of the fully developed wildfire and its ROS (Johansen 1987). Furthermore, in many cases, it is the only time when fire suppression could be effective (Albini 1984) because of the reduced fire intensity and speed.
In this work, we address the ignition and initial growth of a wildland fire from a small ignition source. Small ignition sources studied include a cluster of hot steel particles, glowing embers and a small flame. The fuel bed is a layer of pine needles in a lab setting. Our experiments report the ignition and initial growth of the fire with a burning area of up to 1 m2. The data are connected to large-scale data from different literatures (McAlpine and Wakimoto 1991; Cheney et al. 1993, 1998; Cheney and Gould 1995) and the transition to larger-scale wildfires is examined.
Experimental design
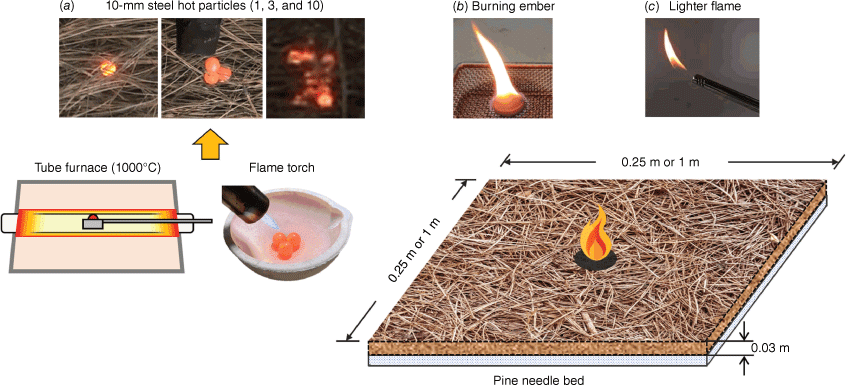
Experiments were conducted with different small ignition sources to observe their effects on the ignition and the subsequent fire growth of a representative forest fuel bed. The fuel bed was a layer of dead pine needles that were placed in two different horizontal flatbeds of 0.25 m × 0.25 m and 1.0 m × 1.0 m. The whole setup was contained in a large atrium without environmental wind. The pine needles were selected as a forest fuel bed that was dried in the sun. The depth and total fuel load of the fuel bed were 0.03 m and 0.7 kg m−2, respectively. The ambient temperature and relative humidity were, respectively, 22.6 ± 0.7°C and 48 ± 8%. In each test, the fuel moisture content was measured just before ignition and was 7.3 ± 0.3%.
In preliminary experiments, the ignition by spraying 375 tiny 2-mm particles (with energy equivalent to three 10-mm particles) was conducted, but only smouldering ignition occurred. As the particle size and wind speed increase, the chance of flaming ignition increases (Fernandez-Pello 2017; Manzello et al. 2020). To ensure a successful flaming ignition, we chose three strong ignition methods: lighter (pure flame), large hot metal particles, and embers (a combination of flaming and smouldering sources). The first experiment with the fuel bed of 0.25 m × 0.25 m was ignited by (a) one, three and ten steel particles with a particle temperature of 1,000°C and a particle diameter of 10 mm. These steel particles were heated in a crucible tube with the furnace until they reached 1,000°C and then dropped onto the fuel bed from a 10 cm height (Fig. 2).
The second experiment expanded the fuel bed to 1.0 m × 1.0 m. In addition to ignition by (a) hot metal particles, we added another two ignition sources: (b) a cylindrical wooden disk of 25 mm in diameter and 5 mm thickness that carries a stable flame and then dropped onto the fuel, and (c) a small lighter flame in contact with the fuel bed for 3 s, which can easily control the initial flaming ignition area. Among these three ignition methods, using metal particles will need a heating period of 3 min for particles to reach the preset temperature; the disk firebrand is heated in a metal mesh with a butane torch for about 15 s to ensure a stable flame that does not extinguish during the dropping process (Song et al. 2017; Zhang et al. 2023); and the lighter is the fastest to prepare and the most effortless to ignite fuel bed, as expected.
Photographs (or schematic) of the fuel bed and ignition sources are shown in Fig. 2. The ignition and fire growth processes were recorded with two video cameras (SONY Alpha 6400 and FDR-AX60) from a 45° front view and a side view. The evolution of the fire growth or burnt area was obtained by processing videos. For each scenario, tests were repeated at least twice, and a good test repeatability was found in terms of fire spread behaviours.
Ignition and initial fire spread
Fig. 3 shows a group of snapshots of the ignition and subsequent fire spread in the small pine needle fuel bed ignited by one, three and ten hot steel particles. Here, the 45° front view of the hot particle ignition and fire-spreading process is shown, and the recorded original video can be found in Supplementary Video S1. At time zero, the various numbers of hot particles were simultaneously dropped randomly onto the fuel bed, and generally, a stable burning flame was formed after 4 s. At the initial ignition stage, the larger ignition area was observed, as we increased the number of particles from 3 to 10. However, shortly after the initial ignition stage, the difference in flame coverage area and later fire spread among the three ignition sources gradually decreased.
Sequence of igniting pine needle by (a) one, (b) three and (c) ten hot particles with a particle temperature of 1,000°C and a particle diameter of 10 mm.

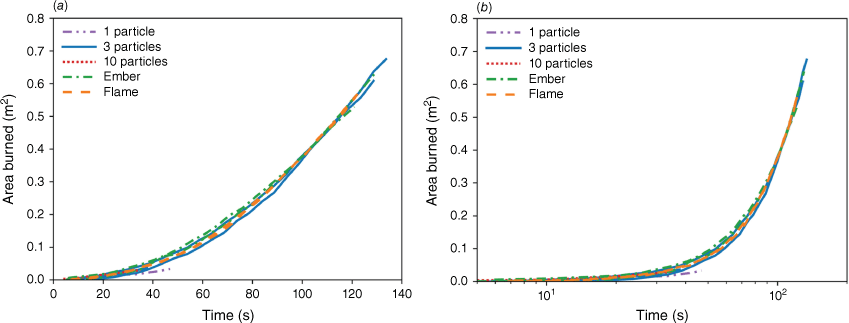
A sequence of images from the tests with the larger fuel bed, ignited by three hot steel particles, a burning ember, and a lighter flame, are shown in Fig. 4. Here, the 45° front view and side view of the fire-spreading process is shown, and the recorded original video can be found in Supplementary Video S2. For example, after three particles are dropped onto the fuel bed, the flaming ignition takes less than 5 s, and shortly after, the flame starts to spread radially outwards from the ignition location. If the time zero of three hot particles is postponed by 10 s, and the time frame of the firebrand is advanced by 5 s, there will be the same burned area (or ignition zone) at 30 s. This work focuses on the early-stage fire spread process after a stable flame occurs. Thus, the time zero for the fire phenomena in Fig. 4 and the measured burned area in Fig. 5a are adjusted based on the moment when all curves almost completely overlap.
Sequence of igniting pine needle bed (1.0 m × 1.0 m) by (a) hot particles, (b) ember, and (c) lighter flame.

Nevertheless, after the flame spread for about 30 s, both the quantities of the material ignited and the burned area were similar. In all cases, a circular burning area was observed as the flame propagated radially in all directions due to the uniform distribution of the pine needles and the absence of wind. Shortly after ignition, the flame spread began to accelerate gradually. It was observed that the burned areas merged with each other after about 100 s. From the measured burned area in Fig. 5a, it was also observed that the evolution of the flame spread area became the same when the burning area increased to about 0.4 m2. After a certain time (about 130 s), the flame spread approached bed edges, so only the data for the burning area below 0.70 m2 is considered, which is equivalent to a circle with a diameter of 0.94 m.
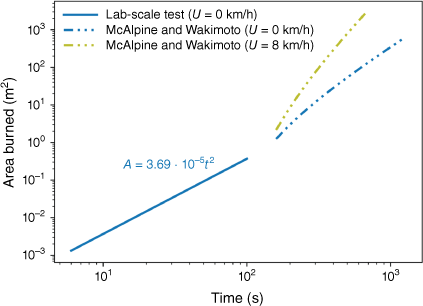
Fig. 5b includes more data of some repeating tests and replots them in a logarithmic scale. Overall, the difference caused by different ignition sources is comparable to the difference shown in repeating tests using the same ignition source. By using strong ignition sources, this work can focus on the early-stage fire spread process after the flame occurs. Thus, we conclude that except for the first few seconds after ignition, the rate of area burned follows a power law. Then, the average burned area Ab [m2] can be described by a t-square expression of time [s]:
where the fire intensity constant B = 3.7 × 10−5 depends weakly on the initial area of the source of the ignition. It is worth noting that this t-square growth is similar to that observed for structural fires (Hurley et al. 2016), and the fire would be considered slowly growing (Marchetti 2020).
Such a t-square fire growth can be derived when the radial rate of fire spread (ROS or Vf) is constant and the radius of the fire spreads radially over a uniform fuel bed (r = Vft). Then, the rate of circular area burned is given by:
In this work, the radial ROS is approximately 3.9 ± 0.2 mm/s for a horizontal flatbed without wind. This global average is also close to the direct measurement at different points of the expanding burning perimeter (or the leading edge of the fireline) from the video (see Fig. 6). Noticeably, in cases where the ignition uses one steel particle or ten steel particles in Figs 5 and 6b, the smaller burning duration (or area) is attributed to the smaller fuel bed in our previous work.
Measured radial ROS vs time: effect of (a) spread direction by three hot steel particles and (b) the spot ignition source, where the ROS value is the average of all repeating tests at a given time and all spread directions.
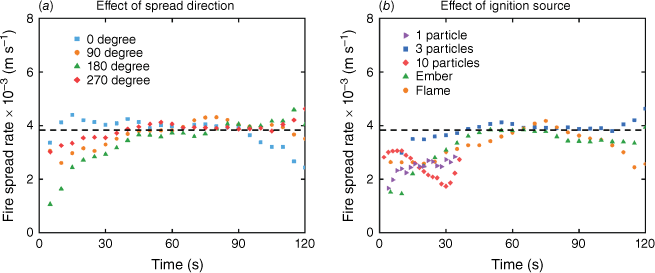
Note that the presence of a bed slope or wind would cause the fire to spread preferentially uphill or downwind. Also, the non-uniform fuel moisture would change the rate and pattern of fire spread. Then, their local ROS will not be the same in different directions but will form an ellipse or more complex burning patterns (Liu et al. 2014). Nevertheless, in terms of the burning area, it may still follow a power law with a different fitting coefficient at the early-stage ignition and fire spread period. These wildfire spread problems shall be further explored with larger-scale tests comprising complex fuel slopes or wind in future work.
Spread of the wildfire for a longer time
The experiments of McAlpine (1988) and McAlpine and Wakimoto (1991) provide information about the spread of a wildfire from a somewhat larger ignition source and over a longer spread time. Therefore, they can be used to extend the burning area evolution as shown in Fig. 5 to longer times. The data obtained by those authors are from experiments on the initial growth of wildland fire in a relatively large fuel bed, that were conducted with and without the influence of wind. Two different fuel beds, Ponderosa pine needles and Excelsior, were used. The data are divided into two zones: the accelerating phase of fire growth and the equilibrium phase of fire spread. This work only concentrates on quantifying the accelerating phase of fire growth. The data for the acceleration phase were used to develop correlations for the rate of flame spread of the form:
where t is the time elapsed since ignition, and A and B are constants and both related to the fuel characteristics and airflow conditions.
Following the analysis in McAlpine and Wakimoto (1991), these parameters can be determined as and , with α0, α1, β0, β1 and β2 representing numerical constants given by the authors. For the purpose of establishing comparisons with the current experiments, A and B were selected from the conditions with no forced flow, as A = 0.684 and B = 1.204, respectively. Additionally, results were also obtained considering a scenario with a forced air flow of 8 km h−1 imposed on the fire to observe the effect of this parameter on the correlation results. By considering that A and B are approximately constant, the rate of area burned also has an approximate power law dependence as:
It can, therefore, be inferred that the initial growth of a wildland fire from a small ignition source can be described by a power function of time.
From the results in Fig. 7, it can be concluded that the initial rate of growth of a wildfire can be predicted by a quadratic power function, although the slope seems to be dependent on the fuel bed characteristics. It should be noted that as the fire grows in size, the rate of wildfire growth is also characterised by a power function, even though ambient parameters, such as wind speed, start to have a bigger effect on the burned area. Similar results were also obtained by Cheney and co-workers (Cheney et al. 1993, 1998; Cheney and Gould 1995) in fire spread tests in grasslands in Australia, although the fires were ignited with a small line fire instead of a spot fire. The data in Fig. 7 and subsequent Fig. 9 are used to verify the trend rather than quantitative parameters of the quadratic power law between the area burned and time.
Combined average area burned for current lab-scale tests and large-scale tests (U presents wind speed) by McAlpine and Wakimoto (1991).
Extension by FARSITE to larger wildfire
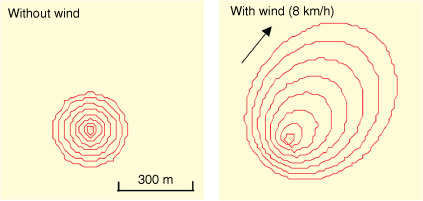
FARSITE is a computer model of wildland fire spread that is widely used to simulate fire growth. It is based on Rothermal’s wildfire ROS model (Rothermel 1984) under different environmental conditions (Finney 1995; Finney and Andrews 1999). Fig. 8 shows a typical FASITE simulation of wildfire spread with and without wind on a flat landscape with pine needles as the fuel bed.
A typical wildfire spread pattern simulated by FARSITE, where the time gap of each contour is 5 min.
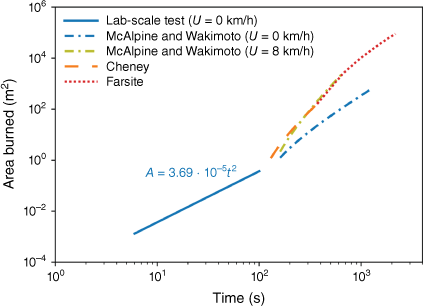
It has been applied here to simulate the growth of wildland fire from a point source (Thomsen et al. 2023), and to compare it with the experimental data in Fig. 5 and the reference data in Fig. 7. The results are presented in Fig. 9 on a logarithmic scale. It is seen that a power function with parameters that are dependent on the fuel bed and ambient characteristics is capable of predicting the initial growth of a wildland fire from a small ignition source. This finding may be useful in the applications of more complex computer models of wildland fire propagation that better describe a later time in the development of a wildfire (Thomsen et al. 2023). Herein, FARSITE mainly applies to the larger wildfire that is controlled by radiative heat transfer and does not apply to smaller or initial fire spread (Liu et al. 2021). For these smaller or initial fire spreads, the convective heat transport governed by buoyancy forces generated inside the flame is the dominant heat transfer process.
Combined average area burned for this work, McAlpine and Wakimoto (1991), Cheney et al. (1993), and FARSITE (Thomsen et al. 2023).
The results presented in Fig. 9 suggest that approximately a power function can describe the growth of a wildland fire under different environmental and fuel conditions. In this regard, an expression for the rate of fire spread (Rothermel 1983) from an empirical correlation of observed experimental data are:
where ξ is a non-dimensional ratio called propagating flux ratio, which relates the fire propagating rate generated under no-wind conditions and the heat release rate (HRR); ε represents a nondimensional parameter called effective heating number; ρb is the dry density of this type of fuel bed, Φw and Φs are dimensionless coefficients of the wind and slope effects, respectively; Qig is the heat required for ignition; and is the heat released intensity by the fire. Together with the present results, we may predict the initial growth of a wildland fire under different environmental, landscape and fuel conditions.
Combining Eqns 4 and 5, a more generalised expression can be obtained to predict the burning rate in the initial wildland fire growth for different environment and fuel bed conditions as presented below:
where the time exponent c is a function of the wind conditions. Under the conditions of a uniform fuel bed, no slope and no wind, the integral gives a quadratic dependence of the burned area with time. The model of Eqn 6 applies to the fire spread that is controlled by radiative heat transfer.
Therefore, we can conclude that the initial rate of growth of a wildfire can be predicted with a power function, although the power function seems to be dependent on the fuel bed characteristics. As the fire grows in size, the power function relation remains approximately valid, although other effects such as wind velocity and slope of the terrain, start becoming more relevant and can influence the rate of spread of the fire. These effects are reflected in some fire spread models, as shown in Fig. 9. After a certain time, the fire might transition into an equilibrium rate of spread, which is not described by the correlations proposed here. Moreover, the wildfire, especially large-scale fire, will be further affected by wind and slope, as described by Rothermel’s or other models available in the literature.
Conclusions
There are no data available to address the initial growth of wildland fire and the transition from spot ignition to wildland fire propagation. In this work, an experimental study of the ignition of surface pine needle beds by various small ignition sources is conducted. The data presented are extended to include the transition and subsequent fire spread behaviour under natural convection (no wind). The ignition sources considered as part of this work are a cluster of steel particles, an ember and a small pilot flame. The results show that the initial growth of the area of the fuel bed burned follows a quadratic power law dependence in time. Moreover, all burning patterns merge with each other at the burning rate of about 0.004 m2 s−1, which is almost independent of the spotting ignition source.
Furthermore, the initial growth experienced after ignition was compared and connected to the data obtained from different studies available in the literature, with and without wind effects. These results show a clear variation in terms of flow velocity, with higher rates of area burned when the fire is exposed to the wind. Relying on the well-known Rothermel expression for fire spread, the propagation of wildland fires can also be modelled as a series of ignition processes that allow the derivation of the burned area of the fire as a function of time, the relevant fuel and environmental conditions. This derivation may be useful in a more fundamental perspective, as well as the applications of more complex computer models of wildland fire propagation that currently are geared to a later time in the development of a wildfire.
Supplementary material
The original videos by different spotting ignition sources can be found in Supplementary Videos S1 and S2. The burned area from experiments and reference data can be found in Supplementary Data S1. Supplementary material is available online.
Data availability
The data that support this study will be shared upon reasonable request to the corresponding authors.
Conflicts of interest
The authors declare that there is no conflict of interest between each other. Dr Xinyan Huang is an Associate Editor of the Journal. To mitigate this potential conflict of interest he had no editor-level access to this manuscript during peer review.
Declaration of funding
Supan Wang thanks the support from the National Key R&D Program of China (No. 2023YFC3081600) and the National Natural Science Foundation of China (No. 52176113). Maria Thomsen thanks the support from Agencia Nacional de Investigación y Desarrollo vía proyecto SCIA/ANILLO ACT210052. Xinyan Huang is funded by the National Natural Science Foundation of China (No. 52322610).
Author contributions
Supan Wang: Investigation, Writing – Original Draft, Formal analysis, Resources; Maria Thomsen: Investigation, Writing – Original Draft, Formal analysis, Resources; Xinyan Huang: Investigation, Writing – Review & Editing, Methodology, Formal analysis; Carlos Fernandez-Pello: Conceptualisation, Methodology, Supervision, Writing – Review & Editing.
References
Albini FA (1984) Wildland Fires: Predicting the behavior of wildland fires—among nature’s most potent forces—can save lives, money, and natural resources. American Scientist 72, 590-597.
| Google Scholar |
Cheney NP, Gould JS (1995) Fire growth in grassland fuels. International Journal of Wildland Fire 5, 237-247.
| Crossref | Google Scholar |
Cheney NP, Gould JS, Catchpole WR (1993) The influence of fuel, weather and fire shape variables on fire-spread in grasslands. International Journal of Wildland Fire 3, 31-44.
| Crossref | Google Scholar |
Cheney NP, Gould JS, Catchpole WR (1998) Prediction of fire spread in grasslands. International Journal of Wildland Fire 8, 1-13.
| Crossref | Google Scholar |
Ellis TM, Bowman DMJS, Jain P, Flannigan MD, Williamson GJ (2022) Global increase in wildfire risk due to climate driven declines in fuel moisture. Global Change Biology 28, 1544-1559.
| Crossref | Google Scholar | PubMed |
Fernandez-Pello AC (2017) Wildland fire spot ignition by sparks and firebrands. Fire Safety Journal 91, 2-10.
| Crossref | Google Scholar |
Finney M (1995) FARSITE: a fire area simulator for fire managers. In ‘The Biswell Symposium: Fire issues and solutions in urban interface and Wildland ecosystems’, 15–17 February, Walnut Creek, CA. Gen. Tech. Rep. PSW-GTR-158. Pacific Southwest Research Station, Forest Service, U.S. Department of Agriculture, Albany, CA. pp. 55–56.
Finney MA, Andrews PL (1999) FARSITE—a program for fire growth simulation. Fire Management Notes 59, 13-15 Available at https://www.frames.gov/catalog/37280.
| Google Scholar |
Finney M, Cohen JD, McAllister SS, Jolly WM (2013) On the need for a theory of wildland fire spread. International Journal of Wildland Fire 22, 25-36.
| Crossref | Google Scholar |
Hurley MJ, Gottuk D, Hall JR, Harada K, Kuligowski E, Puchovsky M, Torero J, Watts JM, Wieczorek C (2016) ‘SFPE handbook of fire protection engineering’. 5th edn. (Springer) 10.1007/978-1-4939-2565-0
Liu Y, Stanturf J, Goodrick S (2010) Trends in global wildfire potential in a changing climate. Forest Ecology and Management 259, 685-697.
| Crossref | Google Scholar |
Liu N, Wu J, Chen H, Xie X, Zhang L, Yao B, Zhu J, Shan Y (2014) Effect of slope on spread of a linear flame front over a pine needle fuel bed: experiments and modelling. International Journal of Wildland Fire 23, 1087-1096.
| Crossref | Google Scholar |
Liu N, Lei J, Gao W, Chen H, Xie X (2021) Combustion dynamics of large-scale wildfires. Proceedings of the Combustion Institute 38, 157-198.
| Crossref | Google Scholar |
Manzello SL, Suzuki S, Gollner MJ, Fernandez-Pello AC (2020) Role of firebrand combustion in large outdoor fire spread. Progress in Energy and Combustion Science 76, 100801.
| Crossref | Google Scholar | PubMed |
Marchetti LJ (2020) Fire Dynamics Series: Fire Protection Fundamentals.PDHonline Course M282 (4 PDH). https://pdhonline.com/courses/m282/FireProtectionFundamentals.pdf
McAlpine RS (1988) The Acceleration of Point Source Fire to Equilibrium Spread. Master Dissertations, University of Montana, MT, USA. https://scholarworks.umt.edu/etd/1465.
McAlpine RS, Wakimoto RH (1991) The acceleration of fire from point source to equilibrium spread. Forest Science 37, 1314-1337.
| Google Scholar |
Mikkelsen K (2014) An Experimental Investigation of Ignition Propensity of Hot Work Processes in the Nuclear Industry. Master Dissertation, University of Waterloo, Canada. http://hdl.handle.net/10012/8396.
Ramljak I, Majstrović M, Sutlović E (2014) Statistical analysis of particles of conductor clashing. In ‘2014 IEEE International Energy Conference (ENERGYCON)’. Cavtat, Croatia. pp. 638–643. 10.1109/ENERGYCON.2014.6850494
Song J, Huang X, Liu N, Li H, Zhang L (2017) The wind effect on the transport and burning of firebrands. Fire Technology 53, 1555-1568.
| Crossref | Google Scholar |
Thomsen M, Fernandez-Pello AC, Williams FA (2023) On the growth of wildland fires from a small ignition source. Combustion Science and Technology 195, 3542-3556.
| Crossref | Google Scholar |
Wadhwani R, Sutherland D, Moinuddin K, Huang X (2023) Numerical simulation of two parallel merging wildfires. International Journal of Wildland Fire 32, 1726-1740.
| Crossref | Google Scholar |
Wakelin H (2010) Ignition Thresholds for Grassland Fuels and Implications for Activity Controls on Public Conservation Land in Canterbury. Master’s Dissertation, University of Canterbury, New Zealand. http://dx.doi.org/10.26021/1818.
Wang S, Huang X, Chen H, Liu N (2017) Interaction between flaming and smouldering in hot-particle ignition of forest fuels and effects of moisture and wind. International Journal of Wildland Fire 26, 71-81.
| Crossref | Google Scholar |
Zhang Z, Ding P, Wang S, Huang X (2023) Smouldering-to-flaming transition on wood induced by glowing char cracks and cross wind. Fuel 352, 129091.
| Crossref | Google Scholar |