Calculating fire danger of cured grasslands in temperate climates – the elements of the Grassland Fire Index (GLFI)
K.-P. Wittich A , C. Böttcher A * , P. Stammer A and M. Herbst AA Deutscher Wetterdienst (German Meteorological Service), Centre for Agrometeorological Research, Bundesallee 33, D-38116 Braunschweig, Germany.
International Journal of Wildland Fire 32(8) 1212-1225 https://doi.org/10.1071/WF22062
Submitted: 4 May 2022 Accepted: 25 June 2023 Published: 19 July 2023
Abstract
Increasing extreme weather events due to climate change require updated environmental monitoring and prediction systems in Germany.
The Grassland Fire Index (GLFI), developed by the German Meteorological Service ~15 years ago for temperate climates, was revised to improve fire-danger predictions during the fire season. Our paper gives insight into the new model version.
The former fire-behaviour core, i.e. Fosberg’s Fire Weather Index (FWI), is replaced by the standardised fire-reaction intensity, a different fuel-moisture of extinction term, and a replica of the fire-spread rate of the Canadian FFBP-System. A standardised ease-of-ignition index is added as a measure of ignition success. The fire module is supplied with diurnal dead-grass fuel-moisture calculations based on the water-budget and energy-balance concept.
The GLFI output is compared with diurnal fuel-moisture measurements and results of Wotton’s Grass-Fuel-Moisture model, Fosberg’s FWI, and Cheney’s rate of spread equation. The GLFI computes periods with a high fuel moisture more realistically, whereas it exceeds Cheney’s rate-of-fire spread systematically at lower wind speeds, which leads to higher danger ratings during calm-air conditions (as requested by users).
The GLFI estimates dead-fuel moisture and fire danger on open, horizontal topography according to the current scientific level. Model extensions are necessary to run the model on complex topography under varying greenness and occasional frost conditions.
Keywords: field and laboratory measurements, fire behaviour, fire intensity, fuel moisture, hourly fire-danger rating, ignition index, rate of spread, theoretical model.
Introduction
Characterised by 0.3–3 h time-lags, cured grasses belong to the light fuel types whose moisture content adapts quickly to variable meteorological conditions (Anderson 1990b; Catchpole et al. 2001; Marsden-Smedley and Catchpole 2001; Wotton 2009). After rain showers and dew-forming nights, short spells of fine and windy weather are sufficient to dry cured grasses out. When their moisture content falls below approximately 30% (dry-weight basis), they become readily ignitable (Albini 1976; Cheney and Sullivan 1997).
According to dry/wet-spell lengths analyses covering the years 1960–2010, western Central Europe (incl. Germany) showed no dominance of dry weather conditions in contrast to southern and eastern Europe (Zolina et al. 2013) and wildland-fire prone regions worldwide (Breinl et al. 2020). The temperate and semi-humid climate is the main reason why Germany was less vulnerable to wildfires in the past (see also Dawson and Goldsmith (2018) for the world map of annual number of wet days (≥0.1 mm/day)). Nevertheless, nation-wide climate-change analyses and projections using the Canadian Fire Weather Index show that weather conditions are becoming more favourable for wildfires (Deutscher Wetterdienst 2022).
In order to develop appropriate fire preparedness and response strategies for upcoming spells of fire weather, fire managers need weather-based wildfire-danger predictions. The term ‘fire danger’ used here follows the definition of NOAA-National Weather Service (2023), meaning ‘a subjective expression of an objective assessment of environmental (fuels and weather) factors which influence whether fires will start and how they might spread’.
Socioeconomic and environmental sectors benefit from grassland fire-danger ratings (e.g. Müller 1992). For example, fire-danger forecasts are relevant for the time management of cereal crop harvesting. To avoid crop fires caused by harvesting operations during the hot and dry midday hours (as a result of overheated machine parts or spark emissions), field work should be pre- or postponed to the cooler morning or evening hours when there is a lower fire danger. Similarly, high-speed grinding trains that are used for railroad track maintenance should defer their spark-emitting grinding operations to the dew-forming night hours or rainy days. Other restrictions apply to the operation of vintage steam train rides to prevent fires on embankments caused by ejected embers, and the conducting of firearm exercises by armed forces if the danger rating is high. Furthermore, economic damages due to careless lighting of fires by humans can be reduced by issuing public fire-weather forecasts through the electronic and classic media for days with high fire danger.
Due to this scope of applications, our updated fire-danger index for grass-covered areas in Germany should:
Respond to weather conditions throughout the diurnal cycle during the summer half-year;
Be easy enough to run in an operational mode for about 500 stations; and
Follow the current state of scientific knowledge.
The GLFI’s predecessor version
The GLFI’s predecessor (in operation since 2005, but unpublished) was based on Fosberg’s (1978) hourly Fire Weather Index (FWI) designed for regional climate conditions in the United States. The FWI includes Rothermel’s (1972) rate-of-spread component and an energy-release (flame-length) formula. Fuel moisture was estimated by the equilibrium value Feq in the range 0–30% (dry-weight basis, 30% representing the fibre-saturation point, FSP, and moisture of extinction, Fex). Thus, data input could be reduced to relative humidity, air temperature, and wind speed. For situations with variable weather (which are typical in Western Europe); however, we found that these three parameters are inadequate to capture the diurnal danger level correctly when the canopy is wet but screen-height relative humidity stays below 100%, resulting in Feq < 30% and FWI > 0 (scale: 0–100). To avoid misinterpretations caused by the FWI’s non-cumulative nature (no memory and time-lag effect), its Feq scheme was replaced by a dead-grass moisture model similar to that described below. Finally, the hourly FWI was combined with DWD’s dead-grass moisture index to get higher ratings under calm–dry weather conditions.
Materials and methods
The new version of the GLFI is an upgrade of the hybrid index above. In the following sections, we describe the current fuel-moisture core and the coupled fire-behaviour module that is similar to that used in the national fire-danger rating systems of the major wildfire countries – Australia (McArthur 1966; Matthews 2022), Canada (Forestry Canada Fire Danger Group 1992), and the United States (National Wildfire Coordinating Group 2002). An ad hoc crop-fire experiment, grass-moisture measurements and a comparison with Fosberg’s FWI and Wotton’s (2009) Grass-Fuel Moisture (GFM) model complete this article.
Model description
Formulas describing the energy balance and the water budget provide the basics for calculating the moisture content of a fully cured, dead grass canopy. The complex canopy structure is treated as a single layer following the so-called ‘big-leaf concept’ (Monteith 1965), which scales the vertical leaf-area density profile and energy-flux distribution down to a representative ‘source-sink’ fuel-bed level (thus avoiding more complex and time-consuming multi-layer modelling, e.g. Thompson (1981) and Matthews (2006)). Four processes of water exchange between the fuel bed and the ambient air are regarded: water-vapour ad- and desorption, absorption of intercepted rain and dew water and evaporation. Uptake of soil water by dead grass is excluded.
The model assumes that the terrain is covered by continuous grass fuel whose load and structure are invariable over space and time. Relief parameters, such as the surface azimuth and slope angle, are not considered, although they affect fire behaviour (Sharples 2009).
The GLFI uses an hourly time step to track the diurnal cycle of fire danger, which usually peaks in the afternoon when wind speed and gustiness are maximum and atmospheric humidity and fuel moisture are minimum (Beck et al. 2002; Lex and Wittich 2002), and to flag fire-prone nights when fuel moisture remains at a low level, e.g. during drought periods, prolonged heatwaves, and foehn events.
Fuel moisture descriptors
Fuel moisture content, F, is defined as the ratio of the mass of water contained in a fuel sample, mw, to its dry mass, md, obtained after oven drying at 105°C (National Wildfire Coordinating Group 2008; Matthews 2010):
where mt = mw + md is the total fuel loading, i.e. the mass of undried dead leaves per unit ground area (in kg m−2). The standard dry-mass value used in the GLFI is md = 0.65 kg m−2, which is in the range of typical grassland fuels (0.2–0.7 kg m−2, Anderson 1982; Forestry Canada Fire Danger Group 1992; Cruz et al. 2020) while tallgrass communities may reach maximum md values of up to 1.5 kg m−2 (Kidnie and Wotton 2015).
The mass of water in a fuel sample, mw, splits into external water, me, held on the leaf surface, and internal water, mi, enclosed in the cell cavities and walls, i.e. mw = me + mi. During rain and dew periods, external water accumulates on the leaves until the interception storage capacity, me,max, is reached, written as:
with ρw the density of water (=103 kg m−3) and a1,2 fuel-specific parameters proposed by Putuhena and Cordery (1996) for tussock grasses, i.e. a1 = 0.069 mm, a2 = 0.510 mm (kg m−2)−1 derived from laboratory rain experiments. Alternatively, me,max (in kg m−2) can be related to the leaf-area index, LAI (in m2 m−2), according to the empirical relationship of Menzel (1997), i.e.
with a = 1.2 for grassland (Vegas Galdos et al. 2012).
The maximum of internal water can be easily estimated using:
Dead grass maximum fuel moisture is in the range of Fmax = 200–450% (Couturier and Ripley 1973; de Groot et al. 2005). In the GLFI, the fuel-moisture maximum is set at 250% (Forestry Canada Fire Danger Group 1992; Wotton 2009).
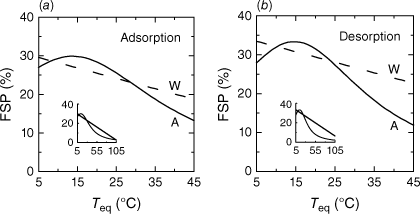
The mi-moisture regime is divided by the fibre-saturation point into two sub-regimes where internal water moves as free water (FSP < F < mi,max/md) and where it is bound to cell-wall structures and shows hygroscopic behaviour (0 < F ≤ FSP). The dynamic approach FSP = Feq,max ~ Feq(hi,sat,Ti) is used, where hi,sat is the intra-leaf relative humidity near saturation (=0.95), Ti the intra-leaf temperature, and Feq is evaluated by Anderson (1990a) under constant climate-chamber conditions at the end of ad-/desorption processes. Cheatgrass-based parameter settings (quadratic in T; see his table 3) hold for intra-leaf temperatures between 5 and 45°C, making the Feq-relationship suitable for operational use under a variety of atmospheric conditions. Fig. 1 shows a comparison between the FSPs of Anderson (1990a) and Van Wagner (1972), whose Feq formula (calibrated for reed grass at 26.7°C, with linear corrections over the range 15.6–48.9°C) was used by Wotton (2009) in his GFM model. The FSP profiles deviate from each other at the cold and warm ends of the temperature range. The insets demonstrate the robustness of both formulas to reproduce fictive drying-chamber conditions.
Fibre-saturation point (FSP) for different equilibrium temperatures and fixed relative humidity of 95% according to formulas provided by Van Wagner (1972) and Wotton (2009, dashed line marked by ‘W’) and Anderson (1990a, solid curve marked by ‘A’) using parameters for (a) adsorption and (b) desorption. The inlays show the hypothetical FSP(Teq) relationship with temperature extrapolated to the standard laboratory drying temperature of 105°C, where plant materials become kiln dry. Note that the range of validity of Feq-based FSP only extends to Teq ≅ 45°C, so the extreme range beyond this has to be interpreted with caution.
Energy balance of the grass layer
Moisture content of dead grass canopies depends on water-budget and energy-balance principles (Monteith 1965; Thompson 1981) that are interconnected via the latent heat-flux density λE (in W m−2):
with λ the latent heat of vaporisation of water (=2.5 × 106 J kg−1), E (in kg m−2 s−1) the mass flux of water vapour between the grass layer and the ambient air (positive upward), ρa the density of air (=1.2 kg m−3, subscript ‘a’ for air), qa (in kg kg−1) the specific humidity at screen height z (2 m), qsat(Ti) the temperature-dependent intra-leaf saturation value of q, and hi and Ti the intra-leaf fractional relative humidity and temperature (in K). Canopy and aerodynamic resistances, rc and ra (in s m−1), have to be overcome by water vapour along its diffusion path from the leaf’s cell structure to the canopy (i.e. big-leaf) surface, and from the canopy towards screen-height level.
The intra-leaf temperature is approximated by the canopy temperature, Tc (subscript c for canopy), as follows:
with Ta (in K) the air temperature at screen height, β a proportionality factor (0.4, suitable for model calibration) that coarsely represents the temperature and moisture conditions in the upper soil, Rnet,iso the isothermal net radiant flux density (in W m−2), ε the emissivity of the fuel bed (0.966, Sutherland 1986), σ the Stefan-Boltzmann constant (5.67 × 10−8 W m−2 K−4), cp the specific heat of air at constant pressure (1005 J kg−1 K−1), and ∂qsat(T)/∂T the derivative of qsat(T) taken at Ta. The isothermal net radiation reads:
with α the albedo (0.27), and L↓, S↓ the downwelling long- and shortwave radiation flux densities.
The aerodynamic resistance, ra, expresses the efficiency of turbulence on the vertical momentum and energy transfer between source-sink height z0 + d and screen height z, with d the displacement height and z0 the roughness length of the canopy. Both parameters depend on the height of the canopy, zc (in m), i.e. z0 ≈ 0.1 × zc and d ≈ 2/3 × zc (Campbell 1977; zc = 0.25 m used as default in the GLFI). The resistance (Choudhury et al. 1986) reads:
with κ (0.4) the von Karman constant, Rib the bulk-Richardson number, δ a stability-dependent exponent (−2.0 for Rib > 0, −0.75 for Rib < 0), and uz the wind speed (in m s−1) at screen height. The Rib number considers the effect of diabatic lapse rate:
where g is the acceleration due to gravity (9.81 m s−2).
In order to estimate the relative humidity at the liquid-vapour interface in the cavities of the grass leaves, hi, we use the approximation (e.g. Nelson 1983):
with heq the equilibrium humidity, M the molecular weight of water (18.015 kg mol−1), R* the universal gas constant (8.314 J mol−1 K−1), Teq the equilibrium leaf temperature (approximated by Tc), and Ψeq the water potential (in m2 s−2 = J kg−1) given by Gibbs free energy described by the numerical value equation:
with Feq approximated by mi/md, and c1,2 cheatgrass-specific constants according to Anderson (1990a), which take hysteresis between ad- and desorption into account. Cheatgrass can be found on nutrient-poor sandy soils in Germany and on coarsely granular structured or crushed-rock substrates along road sides and railway track beds.
In Eqn 5, both ra and hi include the canopy temperature. To avoid recursive iterations in Tc to fulfil the energy-balance equation, we estimate Tc for use in Eqns 8, 9 by the mean-value theorem:
with t the time (in s), Δt the hourly time step (=3600 s), and ∂Tc/∂Ta a temperature ratio set to 1.2 to allow for the larger diurnal amplitude at fuel-bed level compared to the smaller one at 2 m.
The internal canopy resistance rc is parameterised by:
with rc,res (10–40 s m−1) the residual vapour resistance at the wet end of internal moisture range where mi = mi,max, and rc,max the maximum resistance at the dry end where mi = 0. Here, we set rc,max = 4000 × (md,ref/md)a with a ≥ 1 and md,ref = 0.65 kg m−2 (see Thompson (1981) and Alfieri et al. (2008) for similar rc value range). Our rc,max approximation assumes that md is proportional to the evaporating leaf surface (or LAI), and the larger the leaf surface, the smaller the canopy resistance to water-vapour losses.
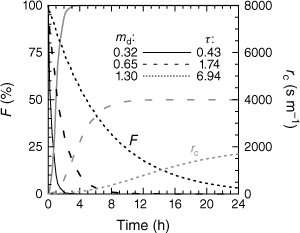
To demonstrate the interrelation between the temporal behaviour of fuel moisture and rc, the moisture exponent of Eqn 12 is replaced by the exponential drying relationship mi = mi,max × exp(−t/τ), using τ = (md/ρb)2/D the time-lag (in s) with ρb the bulk density arbitrarily set at 2.6 kg m−3 and D the diffusion coefficient of the order 1 × 10−5 m2 s−1. Fig. 2 exemplifies the temporal fuel-moisture curves for the three settings md = 0.325, 0.65 and 1.3 kg m−2, starting with Fmax = mi,max/md = 100% at time t = 0. The larger the fuel load, the slower the decrease of F due to higher time-lags. The rc profiles start with rc,ref = 10 s m−1, and at the end of drying they are at their maximum values between 8000 and 1000 s m−1.
Decreasing fuel moisture with time, F (black curves), and corresponding canopy resistance, rc (grey curves) for different fuel-bed characteristics md (in kg m−2) and τ (in h), see text; rc,max parameter: a = 1, canopy height: zc = {0.12, 0.25, 0.5} m for md = {0.325, 0.65, 1.3} kg m−2.
In the current version of the GLFI, the canopy resistance remains unaffected by the vapour-exchange direction in the hygroscopic moisture range, i.e. rc,des = rc,ads = rc. This is in line with Anderson (1990b) and Wotton (2009), who mentioned that the time-lags along opposite ad- and desorption pathways do not differ significantly for cheatgrass (τdes = 0.85 h, τads = 0.8 h), but contradictory to Luke and McArthur (1978), who state that desorption should proceed faster than adsorption, i.e. Edes > |Eads| and therefore rc,des ≠ rc,ads.
Water budget of grass fuels
Besides E (Eqn 4), the water-budget equation for the mass of leaf water per unit ground area, mw, includes the mass fluxes of precipitation and drainage, P and Dr (each in kg m−2 s−1), i.e.
with E split into the contributions of ex- and internal water, E = Ee + Ei. The rate of mass change of intercepted external water is calculated by:
with Ee > 0 for evaporation (Eqns 4, 5 with hi = 1 and 0 ≤ rc ≤ rc,res) and Ee < 0 for dewfall, which is a top-down vapour transfer process from ambient air to cool wet leaf surfaces (hi = 1 and rc = 0). As soon as me surpasses the interception capacity me,max because of rain- or dewfall, drainage occurs (Dr = me − me,max > 0, Dr = 0 otherwise).
As long as leaf surfaces are wet (me > 0), Ee is active but evaporation of internal water is inhibited (Ei = 0). Nevertheless, mi can increase up to mi,max as a result of water absorption according to:
with A the rate at which external water is transferred into internal water (in kg m−2 s−1). The process of absorption is assumed to be proportional to the difference between maximum and current intra-leaf water content. Because absorption depends on the physiological characteristics of leaves, a time-scale parameter, τabs (in s), is incorporated whereby:
Here, we assume τabs = 2–5 h. Laboratory water-absorption experiments by Liang et al. (2009) on three different species of fully grown turf grasses resulted in τabs ≅ 0.5–1 h, and McGechan and Pitt (1990) found τabs ≅ 15 h for grass swaths.
Wotton’s Grass Fuel Moisture (GFM) model
Wotton’s (2009) GFM model, developed as a supplement to the forest-floor related Fine Fuel Moisture Code (FFMC) of the Canadian Forest Fire Danger Rating System, is one of the most advanced mechanistic models concerning diurnal dead grass-moisture variability. It is adapted to fully cured, matted late-winter/early-spring grasses on open unshaded areas and uses hourly input data similar to ours, with the exception of longwave radiation. The theoretical framework of the GFM model complies with the FFMC, e.g. using e-folding response times to reach moisture equilibrium and using comparable structural forms of the Feq equation. Processes of energy and water transfer between fuel and atmosphere are thus a little more simplified compared with meteorological approaches described above.
Fire-behaviour prediction module
Besides fuel moisture, the following dynamic fire behavioural traits are included in the GLFI: rate of spread (ros), fire intensity, and an ease-of-ignition index.
Fire-spread rate
According to Forestry Canada Fire Danger Group (1992), rate of forward spread, ros (in m s−1), is given by:
with rosmax the maximum rate of spread at the end of the fire-growth phase, and b, c empirical coefficients, all three fitted to Australian grass fire data. Each parameter represents two types of fuel-bed characteristics, i.e. mat-forming grass in early spring which has been pressed down by recent winter snowpack, and standing (and better aerated) grass in the summer to autumn season (Table 1 for values currently implemented in the GLFI, but note that higher spread rates are observed in the field, e.g. 6.4 m s−1; see Noble (1991) and listings in Cheney et al. (1998) and Cruz et al. (2022)).
| Grass layer | rosmax (m s−1) | b | c | |
|---|---|---|---|---|
| Matted | 3.167 | 0.031 | 1.4 | |
| Standing | 4.167 | 0.035 | 1.7 |
In Eqn 17a, fF,u is a dimensionless wind-speed and fuel-moisture function that, as an alternative to the original Initial-Spread Index (ISI) of the Canadian Forest Fire Behaviour Prediction System (CFFBPS), is written as:
with F the fractional fuel moisture content, u10 the wind speed measured at 10 m (in m s−1), uc a wind speed normalisation factor (=5.5 m s−1), and c1 = 0.0581, c2 = 0.31 dimensionless parameters, which, in the range of u10 up to 10 m s−1, are fitted to the original ISI formula for fully cured grass (no ground slope) (see Forestry Canada Fire Danger Group 1992). High wind speeds and small fuel moistures result in rapid convergence towards rosmax via large fF,u.
Fig. 3 compares Eqn 17 with the original formula of the CFFBP-System (Forestry Canada Fire Danger Group 1992) and the findings of Cheney et al. (1998). As expected, at wind speeds up to u10 = 10 m s−1, there is no bias larger than 0.1 m s−1 between the original Canadian ros-version and our approximation (white and black circles). However, both formulas (CFFBPS and Eqn 17) overestimate Cheney’s ros-values by 0.5 m s−1 in the case of standing grass, still air, and low fuel moisture (F = 5%), and by 0.6 m s−1 at high wind speeds of 10 m s−1. At medium wind speeds of 5 m s−1, overrating is by about 0.15 m s−1. CFFBPS and Eqn 17 formulas reach their rosmax limit at about u10 = 17 m s−1 (not shown). At this u10 value, Cheney’s model provides nearly the same propagation speed, but continues to increase under the influence of gale-force winds. The curves plotted for F = 15% show smaller offsets at both ends of the wind speed range, whereas at moderate winds Cheney’s ros curve is underrated by up to 0.25 m s−1. At F = 25%, fires do not spread according to Cheney’s model (because of a ros-terminating Fex threshold) whereas both the CFFBPS- and Eqn 17-formulas provide an increase in ros from 0.03 to 0.25 m s−1 for rising u10 from 0 to 10 m s−1. A better conformity between the ros formulas is found for matted fuel beds.
Rate of spread (ros) as a function of 10 m wind speed based on the relationship of Cheney et al. (1998, solid line), Eqn 17 (black dots), and the original formula for fully cured grass provided by the Forestry Canada Fire Danger Group (1992, open circles). The curves represent (a) standing undisturbed grass and (b) matted and cut or grazed grass. Two moisture regimes are considered: dry (F = 5%) and medium (F = 15%). The F = 25% moisture regime is ignored because fires do not spread after Cheney et al. (1998) and are slower than 0.3 m s−1 for wind speeds up to u10 = 10 m s−1 (Forestry Canada Fire Danger Group (1992) and Eqn 17).
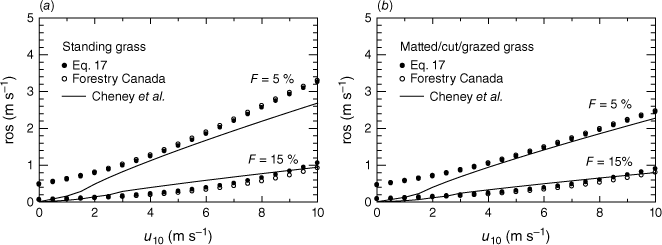
According to Cheney et al. (1998), no matter how low the fuel moisture is, the fire front does not propagate when mean wind speed zeros. In contrast, the CFFBP System and Eqn 17 provide rather high ros values (0.5–1 m s−1) if F ≤ 5% in still air (see Discussion).
Fuel moisture of extinction
The moisture of extinction, Fex, defines the moisture threshold above which fires will not spread (National Wildfire Coordinating Group 2002) or barely continue to burn (Wilson 1985), and, as a consequence, fuels will hardly ignite (Cheney 1981; Chuvieco et al. 2004; Dimitrakopoulos et al. 2010).
To estimate Fex, the rearranged form of Eqn 17 can be used assuming that ros = rosex at F = Fex, i.e.
Because rosex in the denominator disallows zeroing, we assume that rosex/rosmax is in the order of 10−3, i.e. fire line propagates over a distance of 11.4 and 15.0 m h−1 on matted and standing grass areas, respectively. In still air, Fex = 34% (45%) in standing (matted) grass and rises with increasing wind speed.
Fire intensity
Fire-reaction intensity, I, defined as the energy release per unit burning area at the front of a spreading fire (in W m−2, Sneeuwjagt and Frandsen 1977; Cheney 1990; Wilson 1990), is written as:
with Hfc the heat released from fuel combustion (14 000–19 000 kJ kg−1 for different grass species and moisture contents (Luke and McArthur 1978; Cheney and Sullivan 1997; Kidnie and Wotton 2015), ∂w/∂t (with a positive sign) the loss rate of fuel mass per unit ground area of the combustion zone, Δw (in kg m−2) the net weight of combustible fuel per unit ground area, and Δt (in s) the residence time. During the time increment Δt, the fire front with its rate of forward spread, ros (in m s−1), has passed the cross-frontal distance Δx (in m) represented by the horizontal flame depth that extends ‘from the leading edge of the flame front to the rear edge of the flaming area’ where combustion is still active (Alexander 1982). Thus, smouldering combustion behind the flaming area remains disregarded.
The net amount of fuel consumed by the fire depends on the moisture content as follows:
with Fex defined by Eqn 18, and Flow = 6% the setting below which combustion is nearly complete (Cheney 1981). Consequently, Δw ranges from 0 to md.
The GLFI is given by the dimensionless [0–1]-ratio:
Taking Δx/Δxmax = 1 leads to I/Imax = (Δw × ros)/(Δw × ros)max, being on par with the standardised form of Byram’s (1959) fireline intensity, IByr/IByr,max with IByr = I × Δx = Hfc × Δw × ros (in W m−1). Insertion of Eqns 17 and 20 shows that I/Imax is a function of wind speed, fuel dryness, and fuel-bed descriptors (Fig. 4).
Standardised fire intensity depending on fuel moisture for 10 m wind speeds of 0, 5, and 10 m s−1 (solid curves). Note that in the grey area fire-danger rating is uncertain (e.g. fire intensity in still air tends to zero when ros formula of Cheney et al. (1998) is used). The dashed line represents the fractional amount of combustible fuel. Fire-danger class boundaries are exemplarily set at a = 1/3 (see text).
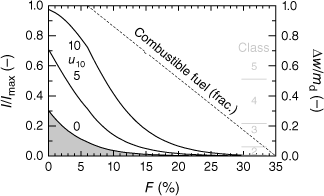
Besides individual settings of class boundaries, standardised intensities I/Imax can be easily transformed into a user-defined five-class danger rating, e.g. i = (1, …, 5) = 1 + int{5 × (I/Imax)a}, with a = 1 for a regular class range in I/Imax, and a < 1 for a non-linear one with small class ranges at small I/Imax ratios. Lower class boundaries are at I/Imax = {(i − 1)/5}1/a. A subjective placement of fire-danger classes on the I/Imax continuum can be done on the basis of prior grassland-fire reports published by environmental agencies or documented in the web and newspaper (NOAA-National Weather Service (2023)). Standardisation of fire intensity makes the GLFI a relative, dimensionless measure, which facilitates the comparison with other relative fire-danger indices such as the FWI.
Ease-of-ignition index
The dimensionless ease-of-ignition index Qig indicates the effectiveness of ignition agents releasing different amounts of energy to ignite dead grass at a given moisture content. The formula is based on the minimum energy required to dry out the fuel and raise its initial temperature to ignition temperature before combustion as a self-sustained exothermic reaction can start, i.e.
with λpi the heat of pre-ignition, Fup (44%) the threshold up to which a powerful ignition agent (e.g. a camp fire) is barely able to ignite moist dead grass, and Flow (6%) the lower moisture content up to which ignition agents such as small embers and hot particles (Cheney and Sullivan 1997) or minute smouldering firebrands (Cheney 1981) have a high chance of igniting dry grass and result in total fuel combustion.
Following Schroeder (1969), the λpi(F, Tc)-formula reads:
with λpi in kJ kg−1, Tig the fuel-specific ignition temperature set at 300°C, which is near 292°C found by von Deichmann (1958) for grass, Tc the initial fuel temperature (in °C), and F the fractional moisture content. It is evident that moister and cooler fuels require more energy to start flaming combustion than drier and warmer ones. Consequently, λpi rises with increasing F and decreasing Tc.
The Qig-function scales the ignition power into the range 0–1 (‘ignition unlikely’–‘ignition likely’), making Qig similar to the linear ‘ignition potential (IP)’ index proposed by Chuvieco et al. (2004). The Fup threshold given above is a result of extrapolating Chuvieco’s linear IP(F) function (defined between IP(0%) = 1.0 and IP(35%) = 0.2, see Discussion) towards IP = 0 giving Fup = 43.75%. A similar value is received based on data of a laboratory 30 s gas-flame ignition experiment (see Electronic Supplement) assuming Fup = Flow + Δpig × ({∂pig/∂F}F50)−1 = 6 + 1 × 38.4 = 44.4%, where pig is the fractional ignition probability and {∂pig/∂F}F50 is the slope of the curve pig(F) = {1 + exp(a + b × F)}−1 taken at the 50%-probability of success moisture for sustained ignitions, F50 = F(pig = 0.5) = −a/b.
Model testing: data acquisition
Comparative measurements were conducted at the DWD’s Agrometeorological Research Centre located in the northwestern outskirts of Braunschweig (λ = 10°26′55″E, ϕ = 52°17′35″N) in northern Germany to test the model performance. We confine our study to lysimetric fuel-moisture measurements and only one outdoor fire experiment because, with rare exceptions, it is illegal to light fires in Germany on the field scale.
Meteorological and fuel-moisture data
To calculate the energy balance and water budget of a grass layer throughout the diurnal cycle, the model needs hourly data consisting of dry and wet-bulb air temperature taken at 2 m standard screen-height level, wind speed at 2 and 10 m (standard anemometer level), down-welling short- and longwave radiation, and precipitation. These data were routinely measured by an automatic weather station installed over a short-grassed meadow in the climate garden of the research centre. With respect to sensor installation heights and sensor accuracies, the measurements fulfilled the WMO (World Meteorological Organization) standards for synoptic measuring networks as documented by WMO (2008).
Total weight of dead grass, mt, was measured gravimetrically at 15-min intervals covering measuring campaigns of 10 days in August 2009 and 4 weeks in September/October 2015 (see Figs 5 and 6). For this purpose, an electronic balance was used (accuracy: ±0.1 g), part of a self-manufactured mini-lysimeter installed in the upper soil of the climate garden (Wittich 2005). The tray consisted of a metal frame (dimension: l × w × h = 31.7 cm × 31.4 cm × 4.0 cm) with a wire mesh at its bottom that carried horizontally layered leaves of grass and allowed infiltrated rain water to drain off (discharge not recorded). The grass sample was covered by a coarse-meshed wire net to avoid leaf blow-out due to wind impact. The leaves were clipped 2–6 weeks before the start of the experiments and were stored in the laboratory in the meantime. At the end of the measuring period, the sample was oven-dried in the laboratory at 105°C for 24 h and re-weighed to obtain md and F(t).
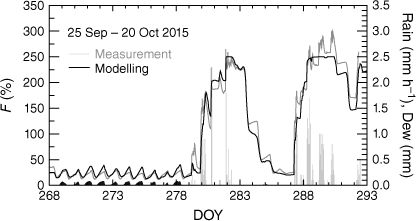
Moisture content of dead leaves of grass horizontally layered in the wire basket of the mini-lysimeter (grey curve), and analogue modelling (black curve). Vertical grey bars represent precipitation rate, black patches on the abscissa in the radiation nights represent dew events calculated by the model (Braunschweig, 25.9.–20.10.2015, DOY 268–293). Model performance measures: see text.
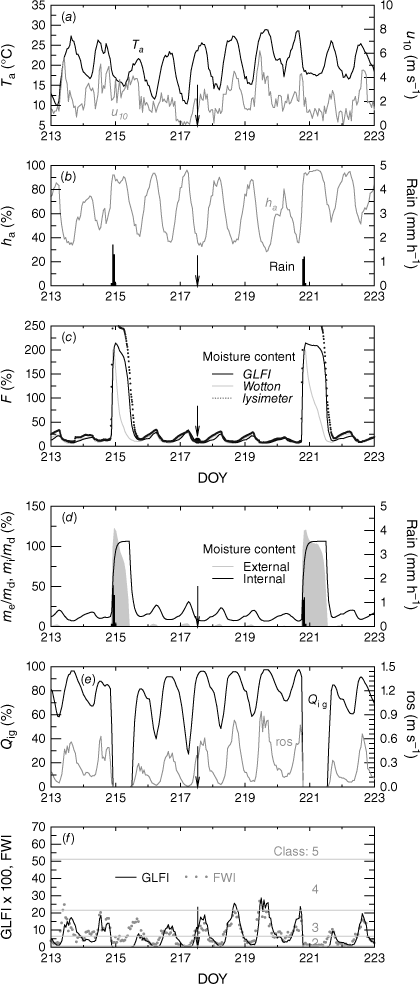
Hourly weather and fire conditions during the period of 1–11 August 2009 (DOY 213–DOY 223) at DWD-Braunschweig. Around noon on 5 August 2009 (DOY 217, 1240–1320 hours CET (Central European Time), indicated by a vertical arrow), two test fires were lit on a rye and an adjacent spring-barley plot. (a) Air temperature at standard measuring level 2 m, Ta, and wind speed at 10 m, u10. (b) Relative humidity at 2 m, ha, and rate of precipitation (bars). (c) Grass-moisture content, F, calculated by the GLFI (black curve) and Wotton’s GFM model (grey curve), compared with measurements (grain residues, solid circle; cured grass bed in the lysimeter, dotted curve). (d) Modelled internal moisture content (black curve) and external moisture content (grey areas with black bars for measured precipitation included), grey patches on the abscissa during rainless periods represent modelled dew events (me/md > 0). (e) Normalised ignition indicator, Qig, and rate of spread, ros. (f) Standardised intensity (line) with GLFI danger classes and Fosberg’s FWI (dots).
Outdoor flammability experiment
Experimental burning was conducted around midday of 5 August 2009 (DOY 217, 1240–1320 hours CET (Central European Time)) at the agricultural test site of the DWD station at Braunschweig. For this purpose, two freshly harvested test plots of rye and barley were selected. They were 12 × 33 m2 and 40 × 25 m2 in area and were covered with residues of clipped straw horizontally layered on standing stubbles (fuel height measured with a rule: about 0.25 m, number of replicates undocumented). The fuel load was estimated as 0.65 kg m−2, and the fuel moisture of both plots measured by oven-drying in the laboratory, was 10.7 and 10.9% (one sample per plot, respectively). The fire was lit by a gas lighter at different spots along the windward field edges. The rate of spread was estimated by measuring elapsed time when the flame front passed metal rods positioned at 5 m intervals in the main wind direction. At 1300 hours CET, under partially cloudy sky, the screen-level air temperature, relative humidity and global radiation were 23.7°C, 35.9%, and 678 W m−2, respectively, and wind speed was at an interim minimum of 1.1 m s−1 at 10 m. The measured or calculated time series of weather conditions (Fig. 6a, b), fuel moisture (Fig. 6c, d) and fire behaviour (Fig. 6e, f) extend over a 10-day period centred around the flammability experiment (marked by a vertical arrow). Burning duration of rye and barley plots was between 3 and 5 min and maximum flame height was estimated at 2–3 m.
Results
Fuel-moisture measurements and modelling
Field trials with the lysimeter were conducted in autumn 2015 (25 September–20 October 2015, DOY 268–293) under a broad spectrum of impacting weather conditions that resulted in an F-range between 12 and 250–300%. The upper value occurred during and after prolonged periods of rainfall (see Fig. 5), when seepage water probably stagnated in the densely packed tray containing horizontally layered blades of cured grass with an extreme fuel load of 1.2 kg m−2.
During rain-free days, grass moisture exhibits its typical diurnal oscillation: in the evening, water is taken up via adsorption, and at night, dew forms on the canopy surface as the result of strong radiative cooling. Simulated external dew water reached a maximum depth of 0.08 mm (me = 0.08 kg m−2) on the litter elements (indicated by black patches on the abscissa of Fig. 5), whereas atmospheric dewfall, totalled over negative E periods (not shown), accumulated to 0.28 mm, a magnitude in line with nocturnal dew amounts reported by Sudmeyer et al. (1994); see also Dawson and Goldsmith (2018) for the significance of dew in Central Europe. The discrepancy of 0.20 mm is due to the transfer of external dew into internal water, which keeps me at a low level. During daytime, especially under dry, sunny and windy weather conditions, the nocturnal dew film evaporated and the grass sample lost internal moisture via desorption, yielding diurnal cycles of litter moisture in the range of 12–40%. From DOY 279 onwards (6 October) heavy rainfall resulted in a sharp fuel-moisture increase up to the saturation limit of 250%. After the end of the rainy period (DOY = 282), it took about three dry days to return to the ignition-sensitive moisture range of below ∼35% (DOY = 285).
The fuel-moisture model was initialised on 1 January 2015, 0100 hours CET, with initial settings of F = 250% and Tc = Ta, and run under real atmospheric forcing with hourly time steps until 20 October 2015, covering the previous 4-week lysimeter-based fuel-moisture measuring period. Model performance measures show that our calculations are consistent with the observed drying and wetting periods of the dead grass sample, keeping the full moisture range (0–250%) in mind (mean fractional error MFE = n−1Σ|(oi − ci)/oi| = 16.7%; mean bias = 3.4%; modified coefficient of efficiency CEmod = 1 − {Σ|(oi − ci)|}/{Σ|(oi − oav)|} = 0.87, with oi and ci the observed and calculated variables, respectively, subscript av for average; CEmod > 0 indicates reliable model results whereasCEmod = 1 is the perfect fit; CEmod < 0 suggests a revision of the model according to Legates and McCabe (1999)).
Outdoor flammability experiment and comparison with GFM and FWI model
The following 10-day time series illustrate the weather conditions around the day of the experiment (5 August 2009, DOY 217), along with fuel-moisture outputs of the GLFI and Wotton’s GFM model, GLFI’s fire-behaviour elements, and Fosberg’s Fire Weather Index. The models were initiated on 1 January 2009, 0001 hours CET.
During the experiment, at 1240–1320 hours CET, the GLFI yielded a fuel moisture of 8.4% at 1300 hours CET, which is below the crop-residue moisture (10.8%, marked by a black circle in Fig. 6c) and the value measured by the grass-carrying mini-lysimeter (9.4%, dotted time series). The GLFI-based fuel-moisture time series is similar to the lysimeter measurement and the GFM modelling (6.5% at 1300 hours CET) for cured matted grass. The GFM model is well suited for comparison because some of its parameters (e.g. Fmax = 250%, zc = 0.3 m) are near those used in our experiment, but his md (=0.3 kg m−2) is half that of ours. To attenuate Wotton’s calculated daytime grass temperature, which was based on an empirical S↓- and u10-dependent formula, his Tc was cut off at Ta + 10°C when the difference Tc − Ta = 10°C was exceeded. Otherwise, land-surface temperatures of more than 40°C leading to very low fuel moistures of 3% would have been possible. A similar adjustment was necessary in the GLFI model using the me,max-relationship of Menzel (1997) instead of the one by Putuhena and Cordery (1996) to bring computed F(t) time series more in line with Wotton’s model results and lysimetric measurements during rain periods. A model comparison of GLFI- versus GFM outputs based on the 10-day time series results in an MFE of 23%. Main differences between both model runs occur during rain periods and at night mainly due to the slightly easier treatment of the nocturnal phase in the GFM model by setting Tc = Ta. Comparison with the lysimeter data of Fig. 6c provides Emod = 0.76 (GFLI) and Emod = 0.52 (GFM), so that both models are suitable to reproduce the main features of measured times series.
The Qig curve in Fig. 6e represents the range of ignition success of different agents (Qig = 0: fuel is too moist (F ≥ 44%) to be lit by a powerful agent, Qig = 1: fuel is dry enough (F ≤ 6%) to be lit by a broad spectrum of agents). As expected, the Qig time series is reversed to the diurnal fuel-moisture variation (Fig. 6c, d), reaching 96% at 1300 hours CET on the experimental day after starting at 27% around sunrise because of dew formation in the preceding night.
The calculated fire behaviour at noon on the experiment day was akin to the observed burning conditions: the modelled fire-line speed was 0.4 m s−1 and the observed speed was 0.5 m s−1 (about half of the wind speed at 10 m) (Fig. 6e). The GLFI classified the medium fire-weather conditions into danger class three (of five; Fig. 6f). Fosberg’s FWI was in a similar range, but showed higher values under moist (e.g. nocturnal) conditions (see DOY 215).
Discussion
The purpose of this study is to provide insight into some elements of the GLFI that predicts fire danger on a homogeneously cured grass layer in open flat terrain during dynamic weather situations. Because lighting crop and grass fires are generally banned by legal restrictions in Germany (with rare exceptions), our own validation measurements are confined to only two test fires. Therefore, the GLFI relies on theoretical standards (with experimental background) developed by international fire-meteorological communities.
Fuel moisture
Fuel moisture is a central parameter controlling fire behaviour and all its elements. To demonstrate the performance of our fuel-moisture model we compared the outcomes with (1) recordings of a mini-lysimeter and individual measurements taken during two test fires, and (2) the outcome of Wotton’s (2009) GFM model.
The GFM model, which originally was adapted to environmental conditions of Ontario/Canada, is integrated into the GLFI to provide additional background information for DWD’s advisory staff to verify the GLFI’s fuel moisture outcome. Two model modifications became necessary: (1) cutting off the canopy temperature in the GFM at Tc = Ta + 10°C when Tc exceeds the 10°C interval (leading to very low fuel moisture); and (2) preferring the more extreme me,max-relationship of Menzel (1997) in the GLFI to get fuel-moisture peaks during rain similar to those obtained by the GFM model. A striking feature in the GFM model is the rapid recovery rate of grass moisture after rainfall, even in nights when relative humidity exceeds 90%. In contrast, the GLFI keeps nocturnal fuel moisture at a high level as a consequence of dewfall or very low evaporation, resulting in longer periods of leaf wetness. For this reason, the energy-balance equation linked with the water-budget concept is a successful alternative to semi-empirical model assumptions regarding atmospheric water-exchange processes.
Ease-of-ignition index Qig
The Qig-index indicates the bandwidth of ignition agents with the capacity to light dead grass at a given moisture content (Qig → 1: broad spectrum of agents (e.g. sparks to campfires) is able to light relatively dry (F ≤ 6%) fuels; Qig → 0: only powerful agents are able to light relatively moist fuels (F ∼ 44%). Because λpi(F) is nearly linear, the fraction within the curly brackets of Eqn 22 can be approximated by (Fup − F)/(Fup − Flow). Consequently, Qig is comparable with the ignition potential (IP) index of Chuvieco et al. (2004), which is in the range between 1.0 and 0.2 for 0.0 ≤ F ≤ Fex (35%) and between 0.2 and 0 for Fex < F ≤ Fh-max (with Fh-max the local historical maximum).
Flammability tables included in Wright and Beall (1948/1968) confirm the lower and upper F limits of the Qig [=0–1] range. The tables show the efficiency of a spectrum of ignition agents (from cigarettes to large slash fires) to ignite the forest-duff top layer (grass not included) at different moisture ranges. The drier the fuel, the higher the ignition success, and the broader the spectrum of agents (with different heat-release rates) that are successful igniters.
Fuel moisture of extinction
Remodelling the Initial Spread Index equation allowed the transformation of the ros formula (Eqn 17) into an Fex approximation (Eqn 18), indicating that Fex (>c2 = 31%) increases with increasing u10 up to Fex ≈ 55% for standing grass. This is consistent with the assumption that, when wind tilts the flames forward, the pre-frontal zone receives more radiant energy necessary to dehydrate moister fuels to an ignitable level (see also Cheney et al. (1998) who preset Fex at 20% for u10 ≤ 2.8 m s−1, and 24% for u10 > 2.8 m s−1 resulting in ros = 0 m s−1 if F ≥ Fex).
According to Chuvieco et al. (2004), Fex also flags the limit where the likelihood of fire starting dramatically decreases. Similarly, Dimitrakopoulos et al. (2010) associated Fex with pig = 1%, resulting in Fex = 55%.
The dependency of Eqn 18 on fuel-bed descriptors is confirmed by Wilson (1985). His empirical estimate for Fex depends on the total surface area of fuel elements per unit ground area, S. When S is replaced by the leaf-area index, one gets Fex = 0.25 × ln(2 × LAI). For short to tall grass canopies characterised by LAIs of 2.5–5.5 m2 m−2, Fex amounts to 0.40–0.60, a range confirmed by Zhou et al. (2005) for live chaparral fuels (but caused by much more environmental factors and fuel-bed descriptors, incl. ground slope). Our Eqn 18 provides Fex values in a similar range, but fuel-bed parameters (Table 1) for standing grass result in smaller Fex values compared with matted/grazed grass when the same rosex/rosmax ratio is used for both canopy types.
Rate of forward spread
In the GLFI we use the rate-of-spread formula of the Canadian FFBP-System as a formal standard that, as a hybrid of double-exponential and power-law structures, is applicable to many other needle- and leaf-like fuel types. However, with regard to its double-exponential form in u10 and the inclusion of maximum propagation speed, rosmax, it differs from two principal forms of ros(u) functions: one describes a power-law profile, ros/rosmin = 1 + a × umfb, proposed by Rothermel (1972, with umf the mid-flame wind speed) and by Cheney et al. (1998, with u10 instead); and the other refers to an exponential profile, ros/rosmin = exp(c × u10), used in McArthur’s Mark 5 grassland meter (Noble et al. 1980). These two alternative forms include the no-wind rate of spread, rosmin, which, in the formulas of Rothermel (1972) and Cheney et al. (1998), is near zero, whereas the CFFBP-System and Eqn 17 provide spread rates of about 1 m s−1 in windless and extremely dry (F = 0%) situations.
Another peculiarity discussed by Beer (1993) is the discontinuity in the exponent b of the power-law function when mid-flame wind speed reaches umf = 2.5 m s−1 (or approx. 5 m s−1 if umf is logarithmically scaled up from zmf = 0.5 to z = 10 m standard level). A similar characteristic wind speed value can be found in the ros(u10) formula of the Canadian FFBP-System (i.e. uc = 5.5 m s−1 in Eqn 17), where the ros(u10) profile changes its curvature and starts to adapt to the rosmax plateau (see Cruz et al. (2022), fig. 6 at u10 = 20 km h−1). Cheney et al. (1998) fixed uc at 5 km h−1 (1.4 m s−1), i.e. at the minimum wind speed above which consistently heading fires are observed, associated with a change of the power-law exponent from 1 to 0.84. One of the quintessences of Beer’s (1993) discussion of the two principal ros(u) forms is that ‘neither a simple power-law nor an exponential’ function is able to describe the ‘true’ rate of fire spread so that we accept the double-exponential form.
Note that the rate-of-spread formula we use does not consider the direct influence of fuel load, fuel height, or fuel porosity, although the rosmax coefficients in Table 1 are the result of clearly different (i.e. matted vs standing) fuel-bed structures. A number of fire experiments published in the scientific literature, however, suggest the explicit inclusion of fuel-bed descriptors. For example, Davis (1949) proved on the basis of prairie test fires on dense (lightly grazed) and sparse (more heavily grazed) cured grasslands that the former advance more rapidly and with higher intensity. Similarly, Cheney et al. (1993) stated that fires in ‘natural undisturbed pastures spread 18% faster than fires in cut (or grazed) pastures’, but they added that ‘there was no evidence that fuel load had a direct influence on spread rate’ (p. 40). Field tests by Cruz et al. (2020) showed that fire fronts on unharvested cured wheat crops propagate more rapidly (ros ≈ 2 m s−1 when md = 0.53 kg m−2, zc = 0.73 m, ρb = 0.726 kg m−3) than fires on harvested crops (ros ≈ 1.5 m s−1, md = 0.21 kg m−2, zc = 0.29 m, ρb = 0.724 kg m−3). These findings tally closely with McArthur’s Australian Grassland Fire Danger Meter, which takes the fuel load into consideration, resulting in fire-spread rates that are twice as high when md has doubled (Noble et al. 1980). However, Cruz et al. (2018) found a positive correlation between md and ros only up to md = 0.3 kg m−2, and an inverse relationship beyond that value, giving an indication that ros is influenced by fuel-bed structure in a complex manner.
Fire intensity
Dry air masses increase the chance of human-related ignition on cured grass areas during calm periods of fine weather. This situation often arises when a high-pressure area moves slowly over the particular forecast region or remains stationary over it. However, if a mean wind-based low ros-value is taken as a basis for fire-intensity estimates on sunny days, the danger level may remain underrated when convective heat transport associated with rising thermal plumes, isolated gusts, and increased turbulence (Aylor et al. 1993) is ignored (Noble et al. 1980). Fluctuating winds result in advective pre-heating of fuels at low wind speeds (Beer 1991) and rapid amplification of pyrolysis (Cheney and Gould 1995). Fire managers evaluate such fire situations as dangerous even if the burnt area per fire incidence remains relatively small. This is the practical reason why we prefer the Canadian ros formula, which gives higher fire intensities and danger ratings in the range of low wind speeds compared with the formula of Cheney et al. (1998). Some consequences can be demonstrated with the example of the Ossendorf Fire, which was sparked off during harvesting operations in a grain field near Ossendorf (eastern Germany) in the afternoon of 20 July 2006 (DOY 201). After burning an area of 4 ha, the crop fire ran into the nearby forest and destroyed a further 61 ha of coniferous woods. Weather data were recorded at a distance of approx. 10–30 km from the fire (meteorological stations: Lindenberg, Coschen), providing ha,min = 13.5–18.2%, Ta,max = 35.5–36.6°C, and u10,max = 2.5–4.0 m s−1. The last significant rain fell a week before the fire event (in the afternoon and night of 13/14 July, DOY 194/195), totalling 0.5–6.9 mm. On that fire day, based on calculated very low fuel moistures of 4% and ros values of approx. 1 m s−1 (Fig. 7a, b), the GLFI provided a higher danger rating than the FWI, whose afternoon peak was nearly at its minimum in the 10-day time series of Fig. 7c. Note that the Ossendorf Fire led to a safety recommendation for farmers declaring that, immediately before harvesting, a firebreak has to be ploughed around fields adjacent to forests (Müller 2007).
(a) Hourly fuel moisture according to GLFI and GFM models during the period of 13–23 July 2006 (DOY 194–204) at met. station Coschen. (b) Normalised ignition indicator (Qig) and rate of spread (ros). (c) GLFI’s standardised fire intensity (line) and Fosberg’s FWI (dots). The grass fire started in the afternoon of 20 July (DOY 201, indicated by a vertical arrow). (d) Aerial photo of the Ossendorf Fire spreading from the grain field into the nearby forest, with the absence of an intermittent firebreak (source: Innenministerium Brandenburg).
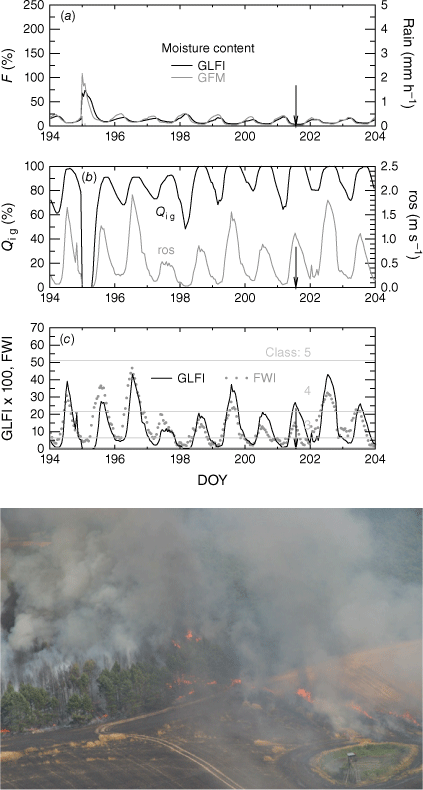
Fig. 7c shows that sinusoidal 24-h-time patterns of GLFI and FWI are similar (MAE = 5.4%), which is to be expected because fire intensity and flame length are positively correlated to each other (Byram 1959; Alexander 1982). Nevertheless, on DOY 194/195 the typical FWI artefact occurred when rain wetted the grain canopy and led to fuel moistures of 70–100%, non-ignitibility and no-spread conditions (Fig. 7a, b), but the FWI does not zero, and unlike the GLFI, rises immediately after sunrise under still moist conditions due to lacking inertia (no time-lag/memory effect).
Conclusions and outlook
The GLFI model fulfils several demands on modern rating systems:
It estimates fire danger of cured grass layers on an hourly basis throughout the diurnal cycle;
It uses meteorological energy-balance and water-budget (i.e. state-of-the art) principles;
It considers all elements of fuel moisture and different modes of water-transfer processes; and
It estimates fire behaviour based on standardised fire-reaction intensity, fire-spread rate, and ease-of-ignition measure.
The GLFI’s limitations are:
Overrating fire danger when living grasses can take up soil water via an active root system; and
Less precise fire-weather forecast at locations distant from meteorological stations (see also Cheney and Gould 1995), and under frost conditions in the cold season.
Model improvement including reliable all-season forecast is achieved by: (1) coupling of a soil-moisture based phenology model that reduces fire risk during periods of greenness; (2) testing the validity of Feq formulas and water-transfer relationships under freeze/thaw conditions and enhancing the predictive accuracy in the winter months when, for example, in the Alpine region foehn-like winds above subsidence inversions raise the fire danger (note that Alexander et al. (2013) demonstrated the benefit of grassland fire prediction in dry and snowless spells of the Canadian cold season); and (3) closure of weather-observation gaps in remote areas via grid-based modelling using countrywide re-analysed meteorological surface data (e.g. full spatial coverage is essential in complex terrain where slope and aspect may significantly affect fuel moisture and rate of fire spread, and where reversed weather situations may occur along the altitudinal gradient when an inversion layer has formed).
Model calibration and experimental validation including traditional fuel-moisture sampling in canopies with standing grasses and smaller fuel loads will be a permanent task. More test fires in the field scale, if possible, will help to verify the fire-behaviour components.
References
Alexander ME (1982) Calculating and interpreting forest fire intensities. Canadian Journal of Botany 60, 349-357.
| Crossref | Google Scholar |
Alfieri JG, Niyogi D, Blanken PD, Chen F, LeMone MA, Mitchell KE, Ek MB, Kumar A (2008) Estimation of the minimum canopy resistance for croplands and grasslands using data from the 2002 International H2O Project. Monthly Weather Review 136, 4452-4469.
| Crossref | Google Scholar |
Anderson HE (1990b) Moisture diffusivity and response time in fine forest fuels. Canadian Journal of Forest Research 20, 315-325.
| Crossref | Google Scholar |
Aylor DE, Wang Y, Miller DR (1993) Intermittent wind close to the ground within a grass canopy. Boundary-Layer Meteorology 66, 427-448.
| Crossref | Google Scholar |
Beck JA, Alexander ME, Harvey SD, Beaver AK (2002) Forecasting diurnal variations in fire intensity to enhance wildland firefighter safety. International Journal of Wildland Fire 11, 173-182.
| Crossref | Google Scholar |
Beer T (1991) The interaction of wind and fire. Boundary-Layer Meteorology 54, 287-308.
| Crossref | Google Scholar |
Beer T (1993) The speed of a fire front and its dependence on wind speed. International Journal of Wildland Fire 3, 193-202.
| Crossref | Google Scholar |
Breinl K, DiBaldassarre G, Mazzoleni M, Lun D, Vico G (2020) Extreme dry and wet spells face changes in their duration and timing. Environmental Research Letters 15, 074040.
| Crossref | Google Scholar |
Catchpole EA, Catchpole WR, Viney NR, McCaw WL, Marsden-Smedley JB (2001) Estimating fuel response time and predicting fuel moisture content from field data. International Journal of Wildland Fire 10, 215-222.
| Crossref | Google Scholar |
Cheney NP (1990) Quantifying bushfires. Mathematical and Computer Modelling 13, 9–15. 10.1016/0895-7177(90)90094-4
Cheney NP, Gould JS (1995) Fire growth in grassland fuels. International Journal of Wildland Fire 5, 237-247.
| Crossref | Google Scholar |
Cheney NP, Gould JS, Catchpole WR (1993) The influence of fuel, weather and fire shape variables on fire-spread in grasslands. International Journal of Wildland Fire 3, 31-44.
| Crossref | Google Scholar |
Cheney NP, Gould JS, Catchpole WR (1998) Prediction of fire spread in grasslands. International Journal of Wildland Fire 8, 1-13.
| Crossref | Google Scholar |
Choudhury BJ, Reginato RJ, Idso SB (1986) An analysis of infrared temperature observations over wheat and calculation of latent heat flux. Agricultural and Forest Meteorology 37, 75-88.
| Crossref | Google Scholar |
Chuvieco E, Aguado I, Dimitrakopoulos AP (2004) Conversion of fuel moisture content values to ignition potential for integrated fire danger assessment. Canadian Journal of Forest Research 34, 2284-2293.
| Crossref | Google Scholar |
Couturier DE, Ripley EA (1973) Rainfall interception in mixed grass prairie. Canadian Journal of Plant Science 53, 659-663.
| Crossref | Google Scholar |
Cruz MG, Sullivan AL, Gould JS, Hurley RJ, Plucinski MP (2018) Got to burn to learn: the effect of fuel load on grassland fire behaviour and its management implications. International Journal of Wildland Fire 27, 727-741.
| Crossref | Google Scholar |
Cruz MG, Hurley RJ, Bessell R, Sullivan AL (2020) Fire behaviour in wheat crops – effect of fuel structure on rate of fire spread. International Journal of Wildland Fire 29, 258-271.
| Crossref | Google Scholar |
Cruz MG, Alexander ME, Kilinc M (2022) Wildfire rates of spread in grasslands under critical burning conditions. Fire 5, 55.
| Crossref | Google Scholar |
Davis WS (1949) The rate of spread - fuel density relationship. Fire Control Notes 10(2), 8-9.
| Google Scholar |
Dawson TE, Goldsmith GR (2018) The value of wet leaves. New Phytologist 219, 1156-1169.
| Crossref | Google Scholar |
de Groot WJ, Wardati , Wang Y (2005) Calibrating the Fine Fuel Moisture Code for grass ignition potential in Sumatra, Indonesia. International Journal of Wildland Fire 14, 161-168.
| Crossref | Google Scholar |
Deutscher Wetterdienst (2022) German Climate Atlas 2022. Available at https://www.dwd.de/EN/climate_environment/climateatlas/climateatlas_node.html [verified 1 June 2023]
Dimitrakopoulos AP, Mitsopoulos ID, Gatoulas K (2010) Assessing ignition probability and moisture of extinction in a Mediterranean grass fuel. International Journal of Wildland Fire 19, 29-34.
| Crossref | Google Scholar |
Kidnie S, Wotton BM (2015) Characterisation of the fuel and fire environment in southern Ontario’s tallgrass prairie. International Journal of Wildland Fire 24, 1118-1128.
| Crossref | Google Scholar |
Legates DR, McCabe GJ (1999) Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resources Research 35, 233-241.
| Crossref | Google Scholar |
Liang X, Su D, Yin S, Wang Z (2009) Leaf water absorption and desorption functions for three turfgrasses. Journal of Hydrology 376, 243-248.
| Crossref | Google Scholar |
Marsden-Smedley JB, Catchpole WR (2001) Fire modelling in Tasmanian buttongrass moorlands. III. Dead fuel moisture. International Journal of Wildland Fire 10, 241-253.
| Crossref | Google Scholar |
Matthews S (2006) A process-based model of fine fuel moisture. International Journal of Wildland Fire 15, 155-168.
| Crossref | Google Scholar |
Matthews S (2010) Effect of drying temperature on fuel moisture content measurements. International Journal of Wildland Fire 19, 800-802.
| Crossref | Google Scholar |
Matthews S (2022) Australian fire danger rating system: Fire behaviour index technical guide. Available at https://www.afac.com.au/initiative/afdrs/article/fire-behaviour-index-technical-guide [verified 1 June 2023]
McGechan MB, Pitt RE (1990) The rewetting of partially dried grass swaths by rain: Part 2, Exploratory experiments into absorption and drying rates. Journal of Agricultural Engineering Research 45, 69-76.
| Crossref | Google Scholar |
Monteith JL (1965) Evaporation and environment. Symposia of the Society for Experimental Biology 19, 205-234.
| Google Scholar |
Müller C (1992) Waldbrandgefährdung und Waldbrandschutz im Land Brandenburg. Allgemeine Forstzeitschrift 18, 973-974.
| Google Scholar |
Nelson Jr RM (1983) A model for sorption of water vapor by cellulosic materials. Wood and Fiber Science 15, 8-22.
| Google Scholar |
NOAA-National Weather Service (2023) Glossary of fire weather terms. Available at https://www.weather.gov./phi/fire_glossary [verified 1 June 2023]
Noble JC (1991) Behaviour of a very fast grassland wildfire on the Riverine Plain of southeastern Australia. International Journal of Wildland Fire 1, 189-196.
| Crossref | Google Scholar |
Noble IR, Bary GAV, Gill AM (1980) McArthur’s fire-danger meters expressed as equations. Australian Journal of Ecology 5, 201-203.
| Crossref | Google Scholar |
Putuhena WM, Cordery I (1996) Estimation of interception capacity of the forest floor. Journal of Hydrology 180, 283-299.
| Crossref | Google Scholar |
Sharples JJ (2009) An overview of mountain meteorological effects relevant to fire behaviour and bushfire risk. International Journal of Wildland Fire 18, 737-754.
| Crossref | Google Scholar |
Sneeuwjagt RJ, Frandsen WH (1977) Behavior of experimental grass fires vs. predictions based on Rothermel’s fire model. Canadian Journal of Forest Research 7, 357-367.
| Crossref | Google Scholar |
Sudmeyer RA, Nulsen RA, Scott WD (1994) Measured dewfall and potential condensation on grazed pasture in the Collie River basin, southwestern Australia. Journal of Hydrology 154, 255-269.
| Crossref | Google Scholar |
Sutherland RA (1986) Broadband and spectral emissivities (2–18 µm) of some natural soils and vegetation. Journal of Atmospheric and Oceanic Technology 3, 199-202.
| Crossref | Google Scholar |
Thompson N (1981) Modelling the field drying of hay. The Journal of Agricultural Science 97, 241-260.
| Crossref | Google Scholar |
Vegas Galdos F, Álvarez C, García A, Revilla JA (2012) Estimated distributed rainfall interception using a simple conceptual model and Moderate Resolution Imaging Spectroradiometer (MODIS). Journal of Hydrology 468–469, 213-228.
| Crossref | Google Scholar |
Wilson Jr RA (1985) Observations of extinction and marginal burning states in free burning porous fuel beds. Combustion Science and Technology 44, 179-193.
| Crossref | Google Scholar |
Wittich K-P (2005) A single-layer litter-moisture model for estimating forest-fire danger. Meteorologische Zeitschrift 14, 157-164.
| Crossref | Google Scholar |
WMO (2008) ‘Guide to Meteorological Instruments and Methods of Observation. WMO-No. 8, Vol. 1, Measurement of Meteorological Variables.’ (World Meteorological Organization: Geneva) Available at https://www.weather.gov/media/epz/mesonet/CWOP-WMO8.pdf [verified 1 June 2023]
Zhou X, Mahalingam S, Weise D (2005) Modeling of marginal burning state of fire spread in live chaparral shrub fuel bed. Combustion and Flame 143, 183-198.
| Crossref | Google Scholar |
Zolina O, Simmer C, Belyaev K, Gulev SK, Koltermann P (2013) Changes in the duration of European wet and dry spells during the last 60 years. Journal of Climate 26, 2022-2047.
| Crossref | Google Scholar |


