Evaluating the Drought Code for lowland taiga of Interior Alaska using eddy covariance measurements
Eric A. Miller A * , Hiroki Iwata
A * , Hiroki Iwata  B , Masahito Ueyama
B , Masahito Ueyama  C , Yoshinobu Harazono D , Hideki Kobayashi
C , Yoshinobu Harazono D , Hideki Kobayashi  E , Hiroki Ikawa F , Robert Busey
E , Hiroki Ikawa F , Robert Busey  G , Go Iwahana
G , Go Iwahana  G and Eugénie S. Euskirchen H
G and Eugénie S. Euskirchen H
A Bureau of Land Management, Alaska Fire Service, Fort Wainwright, AK, USA.
B Department of Environmental Science, Shinshu University, Matsumoto, Nagano, Japan.
C Graduate School of Agriculture, Osaka Metropolitan University, 1-1 Gakuen-cho, Naka-ku, Sakai, Osaka 599-8531, Japan.
D Graduate School of Life and Environmental Sciences, Osaka Prefecture University, Sakai, Osaka, Japan.
E Japan Agency for Marine-Earth Science and Technology, 3173-25 Showamachi, Kanazawa-ku, Yokohama, Kanagawa, 236-0001, Japan.
F Hokkaido Agricultural Research Center, National Agriculture and Food Research Organization, Hitsujigaoka, Toyohira Ward, Sapporo, Hokkaido, 062-8555, Japan.
G International Arctic Research Center, University of Alaska Fairbanks, Fairbanks, AK, USA.
H Institute of Arctic Biology, University of Alaska Fairbanks, Fairbanks, AK, USA.
International Journal of Wildland Fire 32(8) 1226-1243 https://doi.org/10.1071/WF22165
Submitted: 20 July 2022 Accepted: 19 May 2023 Published: 30 June 2023
© 2023 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of IAWF. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Background: The Drought Code (DC) of the Canadian Fire Weather Index System (CFWIS) has been intuitively regarded by fire managers in Alaska, USA, as poorly representing the moisture content in the forest floor in lowland taiga forests on permafrost soils.
Aims: The aim of this study was to evaluate the DC using its own framework of water balance as cumulative additions of daily precipitation and substractions of actual evaporation.
Methods: We used eddy covariance measurements (EC) from three flux towers in Interior Alaska as a benchmark of natural evaporation.
Key results: The DC water balance model overpredicted drought for all 14 site-years that we analysed. Errors in water balance cumulated to 109 mm by the end of the season, which was 54% of the soil water storage capacity of the DC model. Median daily water balance was 6.3 times lower than that measured by EC.
Conclusions: About half the error in the model was due to correction of precipitation for canopy effects. The other half was due to dependence of the actual evaporation rate on the proportional ‘fullness’ of soil water storage in the DC model.
Implications: Fire danger situational awareness is improved by ignoring the DC in the CFWIS for boreal forests occurring on permafrost.
Keywords: Canadian Fire Weather Index System, duff moisture content, energy flux, evaporation, fire danger rating, permafrost, Picia mariana, wildfire.
Introduction
Fire danger rating systems are important for assessing components of the fire environment that contribute to the ignition, spread, intensity, and impact of wildland fires (Merrill and Alexander 1987; Taylor and Alexander 2006; de Groot et al. 2015). There are a number of fire danger rating systems that have been developed to represent the various hydroclimates and biophysiographies of fire characteristic biomes across the world. The Canadian Fire Weather Index System (CFWIS) was developed for the boreal forests of Canada, where the moisture content in organic soil layers is an important determinant of fire behaviour (Stocks et al. 1989). Its archetype is a closed canopy jack pine (Pinus banksiana) or lodgepole pine (Pinus contorta) forest (Van Wagner 1987). Within the CFWIS there are three moisture codes and three fire danger indices (Van Wagner 1987) (Fig. 1). The three moisture codes, the Fine Fuel Moisture Code (FFMC), Duff Moisture Code (DMC), and Drought Code (DC), feature increasing drying timelags and independently track the movement of water in soil profiles of increasing depth in a ‘bookkeeping’ system – in which today’s code is built on yesterday’s. The drying timelag of a moisture code is the time it takes to lose 1 − 1/e or ≈63% of its initial free moisture content or water storage (Van Wagner 1985). The moisture codes rely on four commonly available weather variables, air temperature, relative humidity, wind speed, and precipitation, and consist of semi-physical models of moisture movement finished with abstraction equations that cause fire danger to increase as soil moisture decreases. The three moisture codes are then combined with wind to yield three fire danger indices, the Fire Weather Index (FWI), Initial Spread Index (ISI), and Buildup Index (BUI), that correspond to the components of Byram’s (1959) equation for frontal fire intensity as the product of potential spread rate and fuel weight consumed, respectively (Van Wagner 1987; Wotton 2008).
The Canadian Fire Weather Index System. Moisture codes are outlined in black. Fire behaviour indices are outlined in grey.
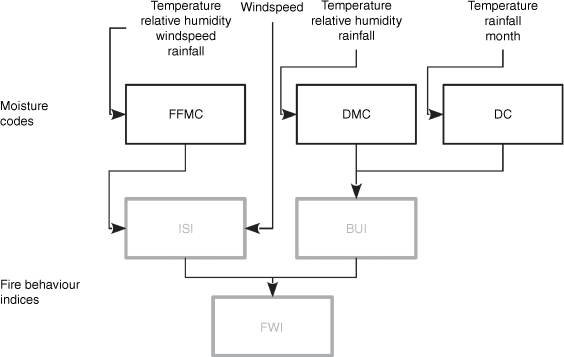
This study focuses on the Drought Code, which is meant to represent extended drought and longer drying timelags than the FFMC or the DMC. Although the DC is often considered a stand-alone code, its original purpose was to adjust the DMC by harmonic averaging in the calculation of the BUI (Van Wagner 1987). Indeed, the original name of the BUI was the ‘Adjusted DMC’ (Van Wagner 1974) and there is some value in continuing to think of the BUI in this way. Despite this purpose, the premise that the DMC actually requires adjustment for drought has never been empirically demonstrated to our knowledge.
The DC algorithm is unlike the other moisture codes that track moisture movement in physically defined fuels in units of gravimetric moisture content. The DC is based on a water balance model that tracks millimetres of water storage in a hypothetical soil by daily additions of precipitation and subtractions of actual evaporation. The precise nature of the hypothetical soil is uncertain because a broad array of soils could satisfy its drying timelag, but nearly all are likely to include mineral as well as organic layers (Johnson et al. 2013; Miller and Wilmore 2020) (Table 1). Understanding the DC requires a perspective on drying that is fundamentally different from the other moisture codes. The FFMC and DMC obtain their drying timelag from the slope of the negative exponential drying rate equation that describes moisture diffusion through the fuel bulk (Van Wagner 1979). The DC obtains its timelag from its scaling of daily actual evaporation from potential evaporation proportional to the depth of soil water remaining in storage.
| Moisture code | Smax (mm) | Timelag (days) | Depth (mm) | Weight (kg m−2) |
|---|---|---|---|---|
| FFMC | 0.6 | 0.67 | 12 | 0.25 |
| DMC | 15.0 | 12.00 | 70 | 5.00 |
| DC | 203.0 | 52.00 | Uncertain | Uncertain |
Smax is maximum storage capacity. Timelag assumes it is July, with an air temperature of 21°C and a relative humidity of 45%.
The DC has been employed or considered for use in regions outside the boreal forests of North America and for emergent applications, of which some are only peripherally related to fire danger rating, that the original Canadian Fire Danger Group could not have intended or imagined 50 years ago (Field et al. 2004; Girardin et al. 2004; de Groot et al. 2007; Dimitrakopoulos et al. 2011; Waddington et al. 2012; Varela et al. 2019; Chavardès et al. 2020; Lestienne et al. 2020; CFSFDG 2021; Coogan et al. 2021). Components of the CFWIS have been adopted or considered for application in tropical, temperate, and tundra regions in both the northern and southern hemispheres (Field et al. 2004; Taylor and Alexander 2006; de Groot et al. 2007, 2015; Xiao and Zhuang 2007; Wotton 2008; Dowdy et al. 2009; Dimitrakopoulos et al. 2011; Yang et al. 2015; Shan et al. 2017; Fernandes 2019). The DC is also used to support modelling of fire effects and carbon emission models (de Groot et al. 2009, 2015; Terrier et al. 2014). The common thread of these diverse applications is that they expect the DC to be an accurate representation of drought, but few or no studies to our knowledge have examined the performance of the DC against its own internal definition of drought as the seasonal balance of precipitation minus actual evaporation.
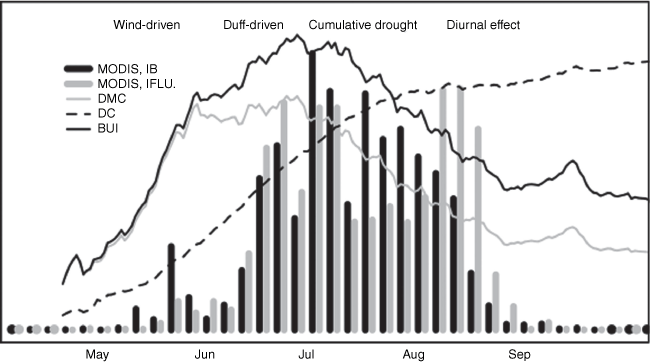
Similarity of forests and fire regimes across the North American boreal biome naturally led to adoption of the CFWIS by the Alaska fire management community in the early 1990s (Cole and Alexander 1995, 2001). Users here have been satisfied with most components of the CFWIS over the last 30 years. The CFWIS works well in Alaska in part because the Buildup Index fits the stages of the fire season better than the analogous Energy Release Component of the US National Fire Danger Rating System (Moore et al. 2021. Alaska Interagency Fire Danger Operating Plan). Fire managers in Alaska recognise four phases to the fire season: ‘Wind-Driven’, ‘Duff-Driven’, ‘Cumulative Drought’, and ‘Diurnal Effect’ (Burroughs et al. 1995. Unpublished ‘Pocket Card’ on file at the Bureau of Land Management, Alaska Fire Service, Fort Wainwright, AK, USA; Moore et al. 2020. Alaska Seasonal Strategic Analysis Tool. Unpublished report). These phases correspond well with the temporal pattern of Moderate Resolution Imaging Spectroradiometer active fire heat detections (MODIS) (Parks 2014; Ziel et al. 2020; Loboda et al. 2021), which are plotted for two prominent Interior Alaska ecoregions (Gallant et al. 1995) in Fig. 2. Whereas fire activity in much of western, temperate North America builds with drought late in the summer, most large fire days in bottomland black spruce forests occur relatively early, during the long days around the summer solstice during the Duff-Driven phase. The DC, however, persistently trends upward through September despite ameliorating day length, duff moisture content, and fire activity (Jandt et al. 2005). An analysis by Ziel et al. (2020) found that the DC was poorly related to MODIS thermal anomalies in Interior Alaska and that the performance of the BUI was very similar to the DMC, suggesting the DC adds minimal information.
MODIS heat detections (2002–2019) in the ‘Interior Bottomlands’ (IB, n = 38 056 detections) and ‘Interior Forested Lowlands and Uplands’ (IFLU, n = 124 705 detections) ecoregions of Gallant et al. (1995), Loboda et al. (2021), aggregated by 5 day periods overlaid with average (2000–2021) DMC, DC, and BUI for predictive service area AK03S (MesoWest, Alaska Fire & Fuels, akff.mesowest.org). Y-axes are normalised and not shown.
Several investigators have attempted to understand the disconnect between the DC and duff moisture content in North America using correlation analyses (Simard and Main 1982; Furguson et al. 2003; Jandt et al. 2005) that have yielded equivocal results. These studies have benchmarked the DC against field measurements of gravimetric moisture content under the a priori assumption that the DC represents one or more layers of deep, compact duff in conifer stands. Using a different approach, Miller and Wilmore (2020) compared field measurements of drying timelags and concluded that the hypothetical soil represented by the DC has an average timelag more than twice as long as whole duff columns in black spruce–feathermoss stands in Interior Alaska, and must include some proportion of mineral as well as organic soil. These analyses reflect the ‘bottom-up’ perspective of wildland fire professionals who typically link observed changes in the fire environment to moisture content in some component of the fuel bed. Another ‘top-down’ or atmospheric way to evaluate the DC is to directly compare the model’s internal water balance as cumulative additions of precipitation minus subtractions of evaporation against empirical measurements of these quantities. Three eddy covariance (EC) towers maintained in lowland taiga forests of Interior Alaska over the last decade or so make this comparison possible.
In order to better understand water balance and the rationale behind the DC algorithm, it is useful to review our current understanding of natural evaporation and transpiration, which, for the most part, is not as familiar to fire managers as is the process of drying by diffusion. In this analysis no distinction is made between ‘evaporation’ and ‘evapotranspiration’ (Brutsaert 2015). Evaporation occurs from all sources (e.g. soil, dead fuels, and plants), and EC sensors cannot distinguish the source.
The DC algorithm was developed given what was known about evaporation ~1948–1966 (Thornthwaite 1948; Thornthwaite and Mather 1955, 1957; Turner 1966, 1972; Black 2007; Shuttleworth 2007). Our understanding of natural evaporation now recognises the centrality of solar radiation. The absence of solar radiation in most fire danger rating systems is a legacy of their development many decades ago, when sensors were not prevalent and temperature was used as the best proxy (Johnson et al. 2013; CFSFDG 2021). Because the source of the energy to evaporate water comes from the sun, it is convenient to begin an explanation with energy flux. A full list of variables and subscripts is given in the Abbreviations section at the end of the article. The daily energy flux from the sun is partitioned into several components:
where Qn is net available energy, which is composed of the net solar radiation (Rn) minus the energy flux to the ground (G) and is partitioned into latent heat flux used in evaporation (λE) and sensible heat flux that raises the temperature of the landscape (H) (Dingman 2015; Hobbins and Huntington 2016). λE is converted to mm of evaporation by the latent heat of vaporisation (λ, MJ kg−1) or the energy required for the phase change from liquid to gas (Eqn 15). All terms are expressed in units of MJ m−2 day−1 (United States fire weather systems report W m−2).
Under the Advection–Aridity approach to natural evaporation, Qn drives potential evaporation (Epo) which is modelled using the Priestley–Taylor version of the Penman Combination Equation for unlimited evaporation, in which the aerodynamic term is simplified to a constant (αPT), typically 1.26 (Priestley and Taylor 1972; Brutsaert and Stricker 1979; McMahon et al. 2013):
Δ, γ, and λ in Eqn 2 are explained in Appendix 1. As the landscape dries from potential conditions, e.g. following a rainfall when water is not limiting, evaporation declines from the potential rate to the actual rate (Ea). This decline is described by the coupled feedback of the Complementary Relationship (Bouchet 1962; Kahler and Brutsaert 2006; Brutsaert 2015; Hobbins and Huntington 2016; Han and Tian 2020). In brief, any available energy unconsumed by evaporation is shunted to sensible heat flux that raises the temperature of the landscape. Under wet conditions, Ea ≈ Epo and drying proceeds at the rate of Epo in the atmosphere-controlled stage (Dingman 2015). As landscape water availability declines, Ea < Epo, and drying proceeds at the actual rate in the soil-controlled stage limited by internal bulk diffusion and plant transpiration (Baldocchi et al. 2000). As an increasing proportion of Qn is shunted to H, the complementary ratio of λE/Qn declines. This ratio, the evaporative fraction (EF), is therefore proportional to the availability of water on the landscape (Maes et al. 2019) and inversely related to fire activity. Although evaporative fraction is typically described in terms of energy, H and Qn are not known in the DC algorithm so it is convenient in our analysis to approximate it in units of evaporation rather than energy flux:
The DC Algorithm
The DC algorithm, as presented in CFWIS guidance documents (109Van Wagner and Pickett 1985, Van Wagner 1987), is not easy to understand and has led to equivocal interpretations of its physical meaning. Importantly, it conceals two components of water balance and is therefore worth explaining here. In the mid-1960s, Turner (1966, 1972) developed an index to track water storage in a soil capable of holding 8 inches (203 mm) of water to be used as an indicator of slash and duff consumption during prescribed fires. Miller (2020) reduced and reworked the algorithm to expose the values of daily depth of water storage (SDC) and actual evaporation (), allowing these values to be compared with measurements (Eqns 4–8). Turner developed the model by estimating monthly potential evaporation for 32 locations in British Columbia, Canada, using Thornthwaite and Mather’s temperature-based method for climate classification. Turner took the resulting modelled values and used linear regression to predict potential evaporation from air temperature. He found the slopes of the monthly regression lines were nearly constant at 0.0914 mm of Epo per °C of air temperature per day. This value became the slope of Eqn 5. The intercepts were not constant and varied by month. These represent additional millimetres per day of Epo above freezing and became the ‘monthly adjustments’ in Table 2. These intercepts were misleadingly renamed ‘daylength adjustments’ when Turner’s index was incorporated into the CFWIS documentation in 1974 (Van Wagner 1974).
| Month | (mm day−1) |
|---|---|
| April | 0.229 |
| May | 0.965 |
| June | 1.470 |
| July | 1.630 |
| August | 1.270 |
| September | 0.610 |
| October | 0.102 |
| November–March | −0.406 |
Turner followed Thornthwaite and Mather’s scaling of Ea from Epo, proportional to the fullness of the soil water reservoir in Eqn 6. The reservoir of 203 mm is assumed to be 96% full in the spring ( = 196 mm equivalent to the default startup value of DC = 15) (Van Wagner 1987). Rainfall (Popen) has a threshold amount, 2.8 mm day−1, below which it is ignored, and above which it is corrected for canopy interception, with the rationale that a portion does not make it to the forest floor to wet the duff (Eqn 4). Eqn 7 is the ‘water balance equation’ that adjusts yesterday’s water storage () with daily additions of precipitation (PDC) and substractions of actual evaporation (). The last step is the ‘abstraction equation’ that converts water storage to the pragmatically unitless fire danger rating moisture code of the DC, which increases exponentially with decreasing water storage. The superscript DC distinguishes water balance components of the DC algorithm from those measured by eddy covariance, which are denoted by the superscript m.
Eddy covariance
Eddy covariance is considered the most accurate way to measure land surface energy balance and evaporation. It is a technique for coupling near-instantaneous measurements of vapour flux above the vegetative canopy with turbulent wind flow in three dimensions (Aubinet et al. 2012; Dingman 2015; Hobbins and Huntington 2016). It provides estimates of the net exchange of water vapour between the land and atmosphere over a horizontal spatial scale of tens to hundreds of meters around the sensor tower (Pastorello et al. 2020). EC towers are also typically fitted with sensors to measure precipitation, solar radiation, air temperature, windspeed, and vapour pressure deficit, i.e. the variables necessary to evaluate the DC water balance model.
Material and methods
Study area
The three eddy covariance towers are located near Fairbanks in the Interior of Alaska where fire activity is greatest. The region is underlain by discontinuous permafrost. Lowland taiga on poorly drained gelisols with shallow permafrost tables is characterised by the conifer black spruce (Picea mariana). The understorey typically features high cover of nonvascular taxa (e.g. feathermosses (Hylocomium splendens and Pleurozium schreberi), sphagnum mosses, terricolous lichens) and ericaceous shrubs (e.g. Vaccinium uliginosum, V. vitis-idaea, Ledum groenlandicum) (Foote 1983). Soils thaw to a depth of 20–90 cm every summer, depending on the thickness of the duff which insulates the frozen ground (Hinzman et al. 2006b). Upland soils are typically inceptisols that are free of permafrost and feature mixed stands of white spruce (Picea glauca) and the deciduous tree species paper birch (Betula papyrifera) and aspen (Populus tremuloides). These upland forests are richer in vascular and deciduous understorey plants (e.g. Rosa acicularis, Equisetum spp., Viburnum edule, Alnus crispa, and Calamagrostis canadensis (Foote 1983)), and duff is not as deep.
The climate of Interior Alaska is continental, with cold winters and warm, relatively dry summers (Hinzman et al. 2006b). Thirty-year mean annual air temperature in Fairbanks is −2.1°C, with an average summer mean of +15.7°C. Annual precipitation is 296 mm (NCEI 2021). Snowpack typically melts in the second half of April and is equivalent to 110 mm or about 35% of annual precipitation. The organic soil (duff) in lowland taiga is 20–30 cm deep and capable of holding about 30–50 mm of water (Miller and Wilmore 2020). Maximum gravimetric moisture content is 550–725% (Skre et al. 1983; Ping et al. 2006). Day length is near 22 h on the solstice when solar elevation is 48.5°. Leaf-out occurs about mid-May. The most extensive fires occur in lowland taiga on permafrost soils. These fires occur relatively early in the season when solar radiation and air temperature are high, relative humidity and dewpoint temperature are low, and windspeed is greatest (Table 3). Ignition of fires by lightning is most common in June and July. Rainfalls are typically convective showers with low amounts in the spring and more stratiform and heavier in July and August.
| Month | Rn, avg (MJ m−2 day−1) | Ta, avg (°C) | Ta, 14 (°C) | Td, 14 (°C) | RH (%) | Popen, avg (mm) | Snowavg (mm) | CCavg (%) | Uavg (m s−1) |
|---|---|---|---|---|---|---|---|---|---|
| Apr | 14.8 | −1.4 | +10.0 | −5.7 | 37 | 6 | 70 | 62 | 2.6 |
| May | 19.3 | +8.4 | +16.6 | −0.2 | 35 | 18 | 10 | 70 | 3.0 |
| Jun | 19.7 | +14.7 | +20.1 | +7.5 | 48 | 35 | 0 | 73 | 2.9 |
| Jul | 17.6 | +15.4 | +21.1 | +10.0 | 53 | 47 | 0 | 72 | 2.6 |
| Aug | 12.3 | +12.4 | +18.2 | +9.3 | 59 | 56 | 0 | 77 | 2.5 |
| Sep | 7.9 | +6.4 | +12.7 | +3.9 | 59 | 28 | 20 | 79 | 2.5 |
The subscript avg denotes daily average from Eugster et al. (2000). The subscript 14 denotes average ‘noon’ weather measurement at 1400 hours at the SRG2 Remote Automated Weather Station near Fairbanks, Alaska, 2005–2020. Td, RH, Snow, CC, and U are dewpoint temperature, relative humidity, snowfall, cloud cover, and wind speed, respectively.
Eddy covariance towers
The analysis uses measurements of energy and water balance at three eddy covariance towers near Fairbanks (Table 4). The Bonanza Creek tower (USBZS) is located in a mature black spruce forest with cold, permafrost soils on a peat plateau in the Tanana River Lowlands 32 km southwest of Fairbanks. The Poker Flats tower (USPRR) is located in a black spruce forest 34 km north of Fairbanks (Ueyama et al. 2016). The USUAF tower is located in an open black spruce forest on permafrost on the North Campus of the University of Alaska Fairbanks (Iwata et al. 2012). All these sites occur in low-slope, lowland terrain with permafrost. Because there are 14 site-years of data across the three towers, a subset was selected to represent droughty (2013, 2017), typical (2015), and wet (2014) seasons for display in figures. The three EC datastreams were processed and standardised (Pastorello et al. 2020) and made available at the FLUXNET project data portal (https://fluxnet.org).
| Tower | Code | Lat. (°) | Long. (°) | Elev. (m) | Digital object identifier |
|---|---|---|---|---|---|
| Bonanza Creek | USBZS | 64.6964 | −148.3235 | 100 | 10.18140/FLX/1669670 |
| Poker Flats Research Range | USPRR | 65.1237 | −147.4876 | 210 | 10.18140/FLX/1440113 |
| University of Alaska Fairbanks | USUAF | 64.8663 | −147.8555 | 155 | 10.18140/FLX/1669701 |
Water balance calculations
SDC, , , and PDC were calculated by feeding weather observations from the eddy covariance towers into Eqns 4–7. The CFWIS requires noon weather observations. Mean daily air temperature in the EC data streams was corrected to ‘solar noon’ (1400 hours in Alaska) using a linear regression based on April to September obervations from the SRGA2 Remote Automated Weather Station in Fairbanks. A linear fit was excellent (P ≪ 0.0001, adj. R2 = 0.92). On average, daily air temperature was adjusted upwards by 5.9°C before feeding into the DC algorithm. Historical CFWIS spring startup dates were retrieved for the SRG2 station and applied to all three EC towers. The mean startup date was day 117 or about 26 April with a range of 100–142. Water storage was defaulted to S0 = 196 mm (DC = 15) in the spring following snowmelt (Van Wagner 1987). The end of the season was arbitrarily set as the last day of September.
The DC water balance model works in units of soil water storage but the depth of storage contributing to evaporation at the EC towers is not known and therefore cannot be directly compared. SDC was scaled to water balance (WDC) by subtracting the maximum storage capacity of the DC model:
This causes water balance to approach zero as storage approaches 203 mm. Negative water balance occurs when cumulative actual evaporation is greater than cumulative precipitation. Positive water balance is assumed to exceed the storage capacity of the soil and is considered runoff. Water balance is analogous to Eqn 7:
Measurements of water balance by eddy covariance were treated analogous to Eqn 10:
is directly measured by EC sensors. Pm was not corrected for canopy interception, i.e. Pm = Popen. was estimated by the Priestley–Taylor version of the Penman Equation (Eqn 2). We used a traditional value of αPT = 1.26, although analyses suggest that the value is temporally and biophysically variable (Barr et al. 2001; Komatsu 2005; Shuttleworth 2007; Brutsaert et al. 2017) and is generally lower for boreal conifer forests (Eugster et al. 2000; Eaton et al. 2001; Komatsu 2005; Pejam et al. 2006; Maes et al. 2019).
A comparison of the DC water balance model with EC measurements requires recognising some differences in assumptions, and these are summarised in Table 5. DCDC represents moisture content in a hypothetical soil rather than the whole landscape. The approaches cannot be compared by drying timelag because the amount of water storage that contributes to evaporation captured by EC measurements is not known. Neither precipitation or evaporation is corrected for canopy effects because EC measurements account for the entire landscape from the forest floor to the top of the canopy.
| Feature | DC water balance model | EC/Advection–Aridity |
|---|---|---|
| Fuelbed component | Organic and mineral soilA | Landscape |
| Development domain | British Columbia, Canada | Physical theory |
| Epo basis | Ta, Month | Qn, Ta |
| Ea basis | Scaled from soil water storage | Eddy covariance measurements |
| Canopy effects, Popen | Corrected | Uncorrected |
| Canopy effects, Ea | Uncorrected | Uncorrected |
| Water storage capacity | 203 mm | Unknown |
| Drying timelag | 52 days (Nominal), 60 days (AlaskaA) | Indeterminate |
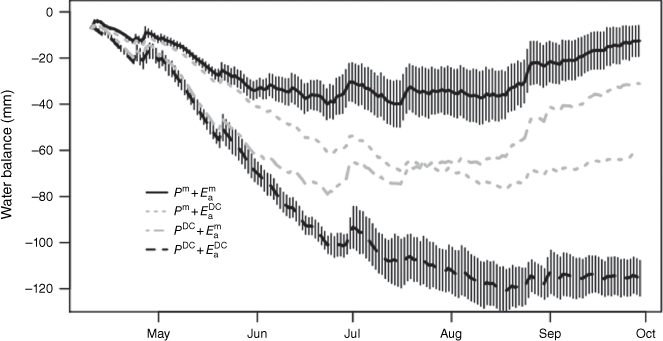
The individual error contributions of and PDC were evaluated by mixing these terms into Eqn 11 and plotting the resulting seasonal accumulations in Fig. 8.
Results
There were 2184 days in the dataset spread over three eddy covariance towers, eight seasons, and 14 site-years. The seasonal sum of averaged 179 mm or 73% of Pm, which averaged 245 mm (Table 6). On average, Pm exceeded by 66 mm per season, a ratio of 1.37. The wettest season was 2014, in which Pm exceeded by 284 mm. The driest seasons were 2013 and 2017, in which exceeded Pm by 3–66 mm.
| Season | (mm) | (mm) | ΣPm (mm) | Wm (mm) | /Pm |
|---|---|---|---|---|---|
| USPRR 2014 | 304 | 192 | 476 | +284 | 0.40 |
| USUAF 2014 | 405 | 175 | 355 | +180 | 0.49 |
| USUAF 2016 | 451 | 201 | 335 | +134 | 0.60 |
| USUAF 2018 | 371 | 127 | 247 | +120 | 0.51 |
| USBZS 2016 | 463 | 256 | 347 | +90 | 0.74 |
| USUAF 2015 | 452 | 195 | 268 | +74 | 0.72 |
| USUAF 2012 | 409 | 138 | 185 | +48 | 0.74 |
| USPRR 2011 | 341 | 169 | 202 | +32 | 0.84 |
| USUAF 2011 | 407 | 171 | 195 | +25 | 0.87 |
| USBZS 2015 | 448 | 223 | 244 | +22 | 0.91 |
| USPRR 2012 | 365 | 200 | 204 | +4 | 0.98 |
| USUAF 2013 | 387 | 149 | 146 | −3 | 1.02 |
| USPRR 2013 | 232 | 123 | 104 | −18 | 1.17 |
| USUAF 2017 | 430 | 193 | 128 | −66 | 1.51 |
| Mean | 390 | 179 | 245 | +66 | 0.73 |
averaged 2.6 mm day−1 (95th percentile 5.1 mm day−1) and averaged 3.0 mm day−1 (95th percentile 4.0 mm day−1). averaged 0.32 mm day−1 greater than but was up to 1.30 mm day−1 greater toward the end of the season (Fig. 3). peaked at 3.9 mm day−1 at week 27, 18 days later than , which peaked at 3.7 mm day−1 at week 24, roughly coincident with the peak in solar elevation.
Potential (top) and actual (bottom) evaporation by week. The asterisk denotes summer solstice.
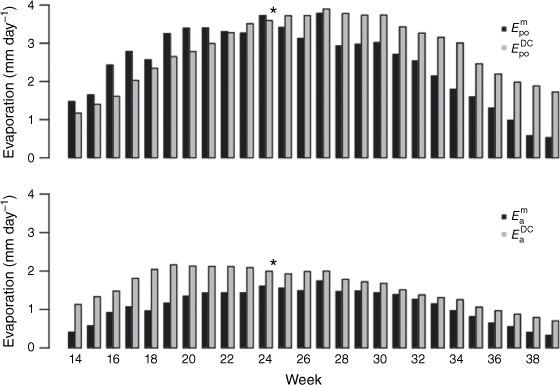
Asynchrony was also apparent in the peaks of actual evaporation, except the order was reversed. The peak in was 2.1 mm day−1 and occurred 3 weeks earlier than the peak in , which was 1.5 mm day−1. averaged 1.19 mm day−1 (95th percentile 2.2 mm day−1). averaged 1.63 mm day−1, 0.44 mm greater than , but was as much as 1.1 mm greater in the spring.
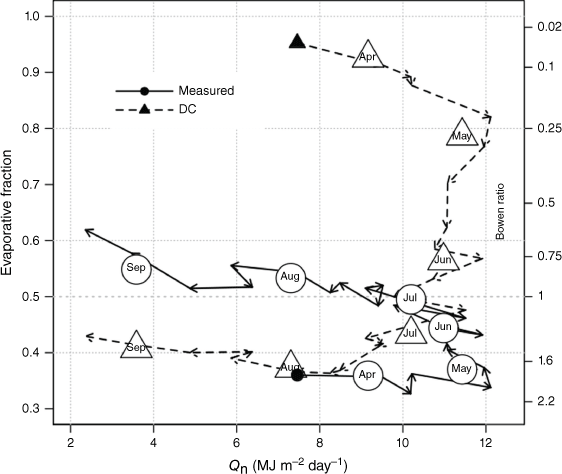
Eddy covariance measurements indicate that evaporative fraction is low following snowmelt in lowland taiga, about 0.36 in April (Fig. 4). As Qn peaks in May, EFm is still below 0.4. By mid-July EFm, climbs past 0.5 and latent heat flux (evaporation) consumes more of the available energy. EFm continues to climb toward 0.55 by September. EFDC shows a pattern that is opposite that of EFm. EFDC always starts the season at 0.96. This high value reflects the default startup value of = 196 mm, i.e. 196/203 in the scaling in Eqn 6. EFDC then decreases rapidly, reaching 0.5 and crossing EFm mid-June. EFDC continues to decline, reaching a minimum of about 0.37 in August and September.
Weekly pattern of evaporative fraction versus net available energy, Qn. The arrows mark mean weekly positions for 14 site-years. The large symbols are monthly means.
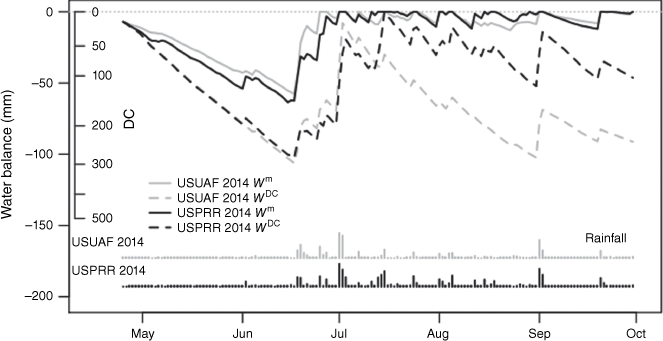
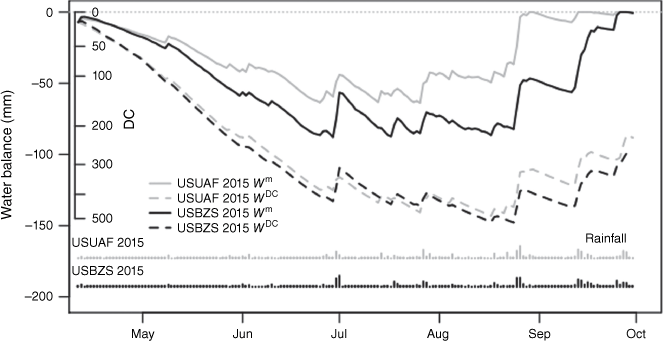
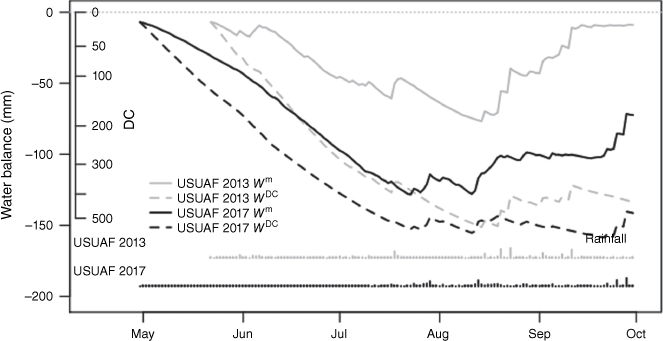
The DC water balance model consistently overestimated drought in all seasons and years (Figs 5–7). WDC reached run-off (0 mm) only 1 day out of more than 2000 in the wet 2014 season. In contrast, Wm frequently went to zero except during the drought years 2013 and 2017. Wm ended the season near zero in about three out of four seasons. In 2014, the maximum difference in water balance (Wm − WDC) occurred in June but in typical and drought years, the greatest difference occurred after August and often at the end of September (Table 7).
| Season | Site | Day of the year | Date | Max diff. (mm) Wm − WDC |
|---|---|---|---|---|
| 2011 | USPRR | 273 | 30 Sep | −134 |
| 2011 | USUAF | 273 | 30 Sep | −139 |
| 2012 | USPRR | 266 | 22 Sep | −116 |
| 2012 | USUAF | 274 | 30 Sep | −147 |
| 2013 | USPRR | 257 | 14 Sep | −73 |
| 2013 | USUAF | 273 | 30 Sep | −125 |
| 2014 | USPRR | 181 | 30 Jun | −70 |
| 2014 | USUAF | 243 | 31 Aug | −94 |
| 2015 | USBZS | 269 | 26 Sep | −107 |
| 2015 | USUAF | 255 | 12 Sep | −116 |
| 2016 | USBZS | 274 | 30 Sep | −102 |
| 2016 | USUAF | 271 | 27 Sep | −110 |
| 2017 | USUAF | 273 | 30 Sep | −69 |
| 2018 | USUAF | 224 | 12 Aug | −119 |
| Mean | 258 | 14 Sep | −109 |
Fig. 8 shows water balance averaged across the 14 site-years. WDC was always lower than Wm, and the difference increased monotonically into mid-August before levelling. The median daily water balance predicted by the DC was −99 mm, about 6.3 times greater than that measured by EC, −16 mm (n = 2184 days). Averaged over all site-years, WDC declined to −121 mm by mid-August with only weak recovery in September, and Wm declined to a minimum of about −37 mm in mid-July. The mean, maximum difference, (Wm − WDC) averaged across all years, was 109 mm (Table 7).
Fig 8 also depicts the error contributions of and PDC by mixture into Eqn 11. Half (49.7%) of the error in the DC water balance model was due to evaporation and the other half (50.3%) was due to precipitation. Errors attributable to were greatest in the early part of the season and ameliorated after the summer solstice. Errors attributable to PDC tended to occur later in the rainiest part of the season. Combined, the errors in both terms reinforced each other in the direction of overpredicting drought.
Discussion
The unique hydrological and micrometeorological features of lowland black sprucethe taiga largely derive from the presence of permafrost. Its presence influences the structure and physiology of the live fuels, e.g. leaf area, poikilohydry, and transpiration rate. It also shapes the physical attributes of the fuel bed, such as shading, sheltering, duff depth, active layer depth, root-zone temperature, and water storage capacity. Organic soils on permafrost are a paradox of sorts because they are counterintuitively waterlogged for much of the growing season despite a surprisingly arid climate (Mann et al. 2002; Jones et al. 2012; Hinzman et al. 2013). Despite high absolute amounts of water in the soil, rates of evaporation and transpiration are relatively low. Cold soils and low leaf area constrain water loss from the conifer canopy (Sullivan and Sveinbjörnsson 2011), which is relatively sparse and well spaced, allowing solar radiation to penetrate to heat the forest floor. The canopy is aerodynamically rough, which increases turbulent mixing of air (Baldocchi et al. 2000; Nakai et al. 2013) and has low albedo, resulting in higher absorption of solar radiation than hardwood stands. Because of its low albedo and low transpiration, lowland black spruce taiga loses most of its energy through sensible heat flux (Chapin et al. 2000; Eugster et al. 2000; Hinzman et al. 2006a), particularly in the spring when the ground is shallowly frozen and vegetative resistance is high (Barr et al. 2001; Arain et al. 2003; Matsumoto et al. 2008; Iwata et al. 2012; Nakai et al. 2013). High sensible heat flux leads to thermal convection, which results in a deep planetary boundary layer that entrains dry air from above, particularly in the afternoon (Baldocchi et al. 2000; Betts et al. 2001; Arain et al. 2003; Shuttleworth 2007). The resulting turbulent mixing causes plant stomata to close, further reducing latent heat flux. Although hardwood stands and wetlands may evaporate close to the equilibrium evaporation rate, as much as 5–6 mm day−1, conifer forests on permafrost typically only evaporate at about 1.5–3.5 mm day−1 (Baldocchi et al. 1997, 2000; Betts et al. 2001; Arain et al. 2003; Hinzman et al. 2006a; Iwata et al. 2012; Nakai et al. 2013). The rate in mixed conifer–deciduous forests is intermediate (Pejam et al. 2006). Although the duff in lowland taiga is capable of storing 30–50 mm of water, transpiration of deep soil moisture is weak because much of it is frozen through the summer solstice (Arain et al. 2003; Iwata et al. 2012; Miller and Wilmore 2020; Thompson et al. 2020).
The forest floor in lowland taiga is typically carpeted in poikilohydric lichens, feathermosses, and other nonvascular taxa. Ubiquitous feathermosses are weak conductors of moisture relative to vascular plants (Bond-Lamberty et al. 2011; Stoy et al. 2012; Goetz and Price 2016). The live and dead moss fuel layers (sensu Jandt et al. (2005)) are typically about 5–10 cm deep and feature very low bulk density (≈0.02 g cm−3) and high porosity (>0.96), and resist upward capillary transport of moisture (Sharratt 1997; Jandt et al. 2005; O’Donnell et al. 2009). Combined, these surface layers are capable of storing only a few millimetres of water and dry quickly (Miller and Wilmore 2020). While their high thermal resistance (O’Donnell et al. 2009; Blok et al. 2011; Loranty et al. 2018) protects the permafrost by inhibiting ground heat flux, typically 6–9% of Rn (Lafleur 1992; Sharratt 1997), the energy is displaced upward into the fuelbed. The forest floor may reach daytime temperatures much higher than the air on clear days (Stoy et al. 2012). We have radiometrically measured the surface temperature of feathermosses at greater than 55°C. Bowen ratios are high midday, indicating high sensible heat flux while λE remains flat (Crago and Brutsaert 1996; Baldocchi et al. 2000).
Much of the evaporation takes place at the forest floor. Warren et al. (2018) found that black spruce trees on a permafrost peat plateau in Canada contributed less than 1% to landscape actual evaporation. Ueyama et al. (2016) noted the importance of non-stomatal control of evaporation, which he attributed to transpiration from nonvascular mosses. Heijmans et al. (2004) measured 0.3 and 0.9 mm day−1 of actual evaporation at the surface of the moss in closed and open black spruce-feathermoss stands in Interior Alaska, about half of Epo. Bond-Lamberty et al. (2011) measured an average of 0.37 mm day−1 of bryophyte evaporation in black spruce forests of several ages and drainages in Canada. They estimated that 49–69% of total forest Ea was from the bryophyte layer on poorly drained soils. Blok et al. (2011) found that evaporation increased with removal of the moss layer, suggesting its resistance can be greater than that of bare soil.
These patterns indicate that evaporation is limited in lowland taiga, not by the evaporative demand of the air but by attributes of the forest itself (Saito et al. 2013). The seasonal pattern of this resistance to evaporation is seen as increasing evaporative fraction as the season progresses in Fig. 4. Following snowmelt in April, EFm is about 0.36. The Bowen Ratio indicates that over twice as much of the available energy goes into warming the landscape as goes into evaporating water, despite adequate soil recharge from snowmelt (Arain et al. 2003; Nakai et al. 2013). Spring Bowen Ratios in boreal conifer stands are typically 1–2.5 (Jarvis et al. 1997), but may reach 3.5 (Arain et al. 2003). EFm gradually increases in July as the soil water reservoir thaws (Betts et al. 2001; Arain et al. 2003). As lower organic soil layers thaw, they release proportionally greater amounts of water because the deeper layers are denser and their storage capacity is greater than the upper layers (Jandt et al. 2005; Hinzman et al. 2006a; Miller and Wilmore 2020). In this way the moisture content does not vary as much through the season in lowland taiga relative to upland forests on inceptisols with shallower duff (Hinzman et al. 2002, 2006a; Ping et al. 2006). As the active layer seasonally thickens, EFm continues to rise and the forest becomes increasingly energy-limited.
This pattern of evaporative fraction is starkly different from that predicted by the DC water balance model, which begins the season at 0.96, predicting that nearly all of the available energy goes toward evaporating water (Fig. 4). The model erroneously predicts that taiga enters the season in a saturated, energy-limited state. EFDC moves in a clockwise direction in Fig. 4, counter to that of EFm, suggesting that dependence of actual evaporation on water storage as modelled in Eqn 6 is inappropriate for lowland taiga. Independence is supported by the absence of a relationship between spring recharge of soil moisture by snowmelt and later fire activity in Interior Alaska. Butteri (2005) found that antecedent autumn precipitation and spring snow-water equivalent had no discernible effect on the total area burned or fire size in Interior Alaska. In a Swedish boreal conifer forest, bulk surface conductance showed little dependence on soil moisture (Grelle et al. 1999), and dependence of actual evaporation on soil water storage may be inappropriate for other forests as well (Roberts 1983).
The assumption that the actual evaporation rate depends on daily water storage can be traced to Thornthwaite and Mather’s (1955) ‘The Water Balance’, which presumed the proportionality:
Although this appears to work for many ecosystems, it performs poorly in lowland taiga and deserves scrutiny in upland and deciduous forests in Alaska and all other ecosystems where the DC is used. An analysis of a global array of eddy covariance datastreams led Maes et al. (2019) to conclude that evaporative fraction is a better indicator of ecosystem water stress than soil water storage.
A separate problem with the DC water balance model is that is based on air temperature rather than solar radiation. Turner’s potential evaporation model is a permutation of Thornthwaite and Mather’s ~1948–1957 model, which is based on mean monthly temperature. However, their work lay in classifying hydroclimates rather than predicting evaporation (Hobbins and Huntington 2016). Because air temperature peaks some time after the summer solstice, it was known even in the early 1970s that the Thornthwaite–Mather model lags solar elevation, pan evaporation measurements, and outputs of the Penman Combination Equation (Patric and Black 1968; Trigg 1971; Newman and Branton 1972). The errors round out when classifying climate on an annual basis but become problematic when adapting the model to make day-to-day predictions, as in the DC algorithm (Shuttleworth 1993). Hobbins and Huntington (2016) provide several detailed arguments against Thornthwaite-type and other temperature-based Epo models, chiefly that the synchrony and correspondence between Ta and Qn cannot be assumed, both temporally and geographically, and that other physical drivers are ignored. Using eddy covariance measurements at 107 sites in 11 biomes across the world, Maes et al. (2019) determined that radiation-based potential evaporation models, including Priestley–Taylor, performed better than temperature-based models. Xu and Singh (2001) found that many temperature-based Epo models were improved by empirically re-fitting their parameters to their locale, suggesting that temperature-based models inherently require calibration to a given hydroclimate. Continuing to rely on the temperature-based model (particularly one empirically calibrated to the climate of British Columbia) to represent subarctic taiga in Alaska seems imprudent.
Mixed modelling revealed that the error contributions of PDC and to total error over the 14 site-years were about even (Fig. 8). contributed half of the error, mostly in the early and middle parts of the season when EFDC is so much higher than EFm, the reasons for which have been previously discussed. PDC contributed the other half, mostly in the later, wetter part of the season. Errors in precipitation are much easier to isolate because they result from measurements rather than a model. They are due simply to either the minimum threshold of 2.8 mm day−1 of open precipitation or to the linear reduction in rainfall amount due to canopy effects in Eqn 4. Median daily rainfall in the dataset is 1.8 mm, so it is not surprising that 60% of daily rainfalls in Interior Alaska were below the threshold of 2.8 mm day−1 and resulted in an average of 37 mm per season ignored by the algorithm. These light showers are common in the early season. For the balance of rainfall events, the reduction in amount due to the linear correction was 68%, resulting in an additional loss of 69 mm per season. Thus the DC water balance model discarded 106 mm of rain per season or 43% of the season total (245 mm). These reductions deserve further scrutiny in future generations of the CFWIS (CFSFDG 2021), particularly for arid biomes (Jones et al. 2012). On a year-to-year basis, drought in boreal forests and tundra is influenced to a greater extent by precipitation than evaporation because of wider variance in amount (Fischer et al. 2018). The influence of a rainfall threshold and correction is particularly acute for lowland taiga given that it experiences approximately one-tenth of the annual precipitation of Pacific coastal Douglas-fir (Pseudotsuga menziesii) and western hemlock (Tsuga heterophylla) forests in Canada, for which the DC was originally designed (Turner 1972; Humphreys et al. 2003; Jones et al. 2012). Even light rainfalls contribute to water balance by reducing sensible heat flux in both the canopy (Humphreys et al. 2003) and on the landscape as a whole. Importantly, it is difficult to reconcile corrections for canopy effects on rainfall when there are no complementary corrections for actual evaporation, e.g. foliar interception of solar radiation or sheltering from wind. The rationale for rainfall corrections in fire danger rating indices and moisture codes has not been well explained, but they make more sense for models fit from empirical measurements of duff moisture content (e.g. the DMC (Van Wagner 1970), in which some proportion of rainfall did not penetrate to the forest floor to be measured) than for meteorological-based water balance models that rely on weather measurements in the open (e.g. the Keetch–Byram Drought Index (Keetch and Byram 1968) and the Finnish Forest Fire Index (Heikinhemo et al. 1998; Venalainen and Heikinheimo 2003)).
Combined, the errors in and PDC reinforce each other and cumulate to give the appearance that the DC water balance model departs from expectation in the late summer. Our measurements suggest that the departure actually begins much earlier in the season and is carried along by the bookkeeping nature of the algorithm. Steep losses of springtime actual evaporation are apparent in Figs 5–7 but are not reflected in the BUI at this time – nor are fire managers focused on drought at this point in the season. Precipitative errors, on the other hand, cumulate later with monsoonal rains, which peak in greater amounts in August. Firefighters expect drought to ameliorate with this rainfall but precipitation is reduced by the canopy correction, and water balance in the DC model continues to drop. Considering our finding that precipitation is 137% of actual evaporation in the average season, one would expect that SDC would trend toward fullness (and the DC would trend toward zero) at some point in nearly every season, but Figs 5–7 suggest this is true only for the odd rainy season. Cumulative error in water balance (Wm − WDC) averaged 109 mm by the end of the season. For context, this value is 54% of the defined storage capacity of the DC water balance model (203 mm) and 44% of average seasonal precipitation (245 mm). Median water balance predicted by the DC (−99 mm) was over six times greater in absolute amount than that measured by EC (−16 mm). The magnitude of these errors is not acceptable, particularly when our contemporary understanding of hydrology and natural evaporation offer certain improvements.
A drought index would be expected to provide useful information in places where drought is known to influence the moisture content in the fuel bed through, for example, topographic position, drainage, physiological water stress, or late-season foliar senescence and curing (Kljun et al. 2006). In temperate regions of North America a water balance approach to drought seems to fit ecosystems where transpiration by plants accounts for a high proportion of actual evaporation. For example, the Keetch–Byram Drought Index works well in the densely vegetated, humid ecosystems of the southeastern United States, and soil moisture, as Fraction of Available Water, is a significant determinant of large wildfires in the US Southern Great Plains, but only during the growing season, i.e. the period of active transpiration (Krueger et al. 2015, 2016, 2017). During the dormant season, fire activity is controlled by above-ground meteorological drivers. Applying this pattern to Alaska suggests that a water balance model in which actual evaporation is dependent on soil moisture might perform better where applied to permafrost-free upland forests that feature greater vascular plant biomass capable of transpiring deep soil moisture. Several intuitive observations support this idea. Ignition and spread of fire in upland deciduous and mixed conifer forests are resisted by transpiring vegetation in the early, greenest part of fire season, coincident with the peak in fire activity in lowland black spruce forests that is carried by the dead, dormant, or poikilohydric components of the fuelbed (Ziel 2019). Deciduous stands are often operationally regarded as barriers to fire spread in the early season but are known to burn extensively as drought persists into August and September (Bhatt et al. 2021). MODIS heat detections in upland deciduous or mixed stands of white spruce, paper birch, and aspen on relatively shallow inceptisols exhibit a peak later in the season in drought years, which suggests a response to water stress. Soils become drier later in the season because infiltration is not restricted by permafrost (Hinzman et al. 2006a, 2006b, 2013; Kljun et al. 2006). Measurements of soil moisture in the organic layer of upland inceptisols suggest greater depletion later in the season (≈0.1 m3 m−3) relative to paired lowland gelisols, which are sustained through the season at a higher volume (≈0.3–0.5 m3 m−3) (Hinzman et al. 1991; Young-Robertson et al. 2016). High springtime sensible heat flux is not a feature of boreal deciduous stands (Barr et al. 2001; Kasurinen et al. 2014), whose latent heat flux is 50–80% higher than conifer stands (Chapin et al. 2000). Nearly 90% of the precipitation in deciduous stands is returned to the atmosphere by transpiration (Baldocchi et al. 2000), indicating strong physiological coupling of the vegetation with soil moisture. A relatively strong dependence of actual evaporation on soil water storage better fits the assumption of Eqn 6 and suggests that the premise of the DC water balance model, if not its present implementation, may work better here than in lowland taiga on permafrost soils. Unfortunately there are no eddy covariance towers in upland deciduous forests currently available in Alaska to test these differences.
Conclusions and recommendations
Our measurements confirm the long-held intuition of fire managers that the DC overpredicts drought in Interior Alaska due to under-accounting of precipitation and outdated models of potential and actual evaporation. Physical-based revision of the DC water balance model based on our contemporary understanding of natural evaporation would improve its performance as a fire danger rating moisture code, not only for taiga in Alaska, but for all the global ecosystems where it is used. The concept of a fire danger rating moisture code predicated on water balance is sound, if underappreciated, and has great potential to indicate the availability of moisture in the landscape. We offer several suggestions to improve the performance and interpretation of the DC.
First, the fundamental question of whether the DMC requires adjustment for drought should be critically assessed. If the DMC adequately represents the moisture content in duff (or the component of the fuelbed with the longest drying timelag), then the DC does not add any value and the CFWIS can be simplified by setting the BUI equal to the DMC. It should be remembered that the BUI is essentially a synthetic moisture code with a drying timelag somewhere between the DMC and the DC. The question becomes is there a fuel on the landscape with a comparable drying timelag? For lowland taiga on permafrost, our measurements suggest the DC adds no value to the BUI or the CFWIS as a whole.
Second, the assumption of dependence of actual evaporation on soil water storage in the DC model, although supported for some ecosystems, does not fit taiga on permafrost soils. One untested alternative that does not make this assumption would be to use the coupled feedback of the Complementary Relationship within the Advection–Aridity approach, which relies solely on meteorological measurements to model actual evaporation (Brutsaert and Stricker 1979). Importantly, the feedback makes no assumptions about the attributes of the ecosystem to which it is applied (Dingman 2015), an advantage that is promising given that the DC is currently used globally in arctic, boreal, temperate, tropical, and other physiognomically diverse hydroclimates around the world. Other modern frameworks that reflect a physical- rather than empirical-based approach to evaporation could also result in improved or universal applicability to the diverse biomes of the world.
Third, although errors in evaporation cannot be solved without extensive revision of the DC water balance model, immediate improvement would result by omitting Eqn 4 from the algorithm. Eqn 7 would include uncorrected, open precipitation. PDC contributes half the total error and most of the bias in the late summer, the time when fire managers in Alaska have qualitatively observed departure from expectation. This simplification brings modelled water balance about halfway toward measurements, and would particularly improve performance in arid ecosystems.
Abbreviations
The following abbreviations have been used:
Variables
| e, | Vapour pressure of the air (kPa) |
| es, | Saturation vapour pressure of the air (kPa) |
| Ea, | Actual evaporation (mm day−1) |
| Epo, | Potential evaporation (mm day−1) |
| EF, | Evaporative fraction |
| G, | Ground heat flux (MJ m2 day−1) |
| H, | Sensible heat flux (MJ m2 day−1) |
| p, | Atmospheric pressure (kPa) |
| P, | Precipitation (mm day−1) |
| Popen, | Precipitation, measured in the open (mm day−1) |
| Qn, | Net available energy (MJ m2 day−1) |
| Rn, | Net solar radiation (MJ m2 day−1) |
| S, | Soil water storage (mm) |
| S0, | Soil water storage, initial (mm) |
| Smax, | Soil water storage, maximum (mm) |
| Ta, | Air temperature (°C) |
| Td, | Dewpoint temperature (°C) |
| U, | Wind speed, eye-level (m s−1) |
| W, | Water balance (mm) |
| W0, | Water balance, initial (mm) |
| αPT, | Priestley–Taylor coefficient |
| Δ, | Slope of the saturation vapour pressure versus temperature curve (kPa °C−1) |
| γ, | Psychrometric constant (kPa °C−1) |
| λ, | Latent heat of vaporisation (MJ kg−1) |
| λE, | Latent heat flux (MJ m2 day−1) |
Data availability
The data that support this study are available at https://fluxnet.org/ at DOI: 10.18140/FLX/1669670, 10.18140/FLX/1440113, 10.18140/FLX/1669701.
Declaration of funding
The US-PRR and US-UAF sites are supported by the Japan Agency for Marine-Earth Science and Technology and International Arctic Research Center, University of Alaska Fairbanks Collaboration Study, and the Arctic Challenge for Sustainability Project. Data analysis and article preparation were supported by the US Bureau of Land Management, Alaska Fire Service. The sponsors had no role in the preparation of the data or manuscript or the decision to submit for publication.
Author contributions
EAM: Project conceptualisation, data analysis, manuscript preparation, conclusions and recommendations, decision to publish. All other authors are members of the eddy covariance ‘Tower Teams’ and contributed to tower installation, maintenance, data processing, standardisation, and distribution. All authors reviewed the manuscript.
Acknowledgements
The FLUXNET network and data portal made available the eddy covariance information in analysis-ready form. The Alaska Resources Library and Information Services (ARLIS) was indispensable to the literature search. We thank Kent Slaughter, Chris Moore, Heidi Strader, Derek van der Kamp, Rikie Suzuki, Robert ‘Zeke’ Ziel, and Tricia Miller for discussions, insights, and other support that made this article possible.
References
Arain MA, Black TA, Barr AG, Griffis TJ, Morgenstern K, Nesic Z (2003) Year-round observations of the energy and water vapour fluxes above a boreal black spruce forest. Hydrological Processes 17, 3581-3600.
| Crossref | Google Scholar |
Aubinet M, Vesala T, Papale D (Eds) (2012) ‘Eddy Covariance.’ (Springer Science & Business Media) 10.1007/978-94-007-2351-1
Baldocchi DD, Vogel CA, Hall B (1997) Seasonal variation of energy and water vapor exchange rates above and below a boreal jack pine forest canopy. Journal of Geophysical Research: Atmospheres 102, 28939-28951.
| Crossref | Google Scholar |
Baldocchi D, Kelliher FM, Black TA, Jarvis P (2000) Climate and vegetation controls on boreal zone energy exchange. Global Change Biology 6, 69-83.
| Crossref | Google Scholar |
Barr AG, Betts AK, Black TA, McCaughey JH, Smith CD (2001) Intercomparison of BOREAS northern and southern study area surface fluxes in 1994. Journal of Geophysical Research: Atmospheres 106, 33543-33550.
| Crossref | Google Scholar |
Betts AK, Ball JH, McCaughey JH (2001) Near-surface climate in the boreal forest. Journal of Geophysical Research: Atmospheres 106, 33529-33541.
| Crossref | Google Scholar |
Bhatt US, Lader RT, Walsh JE, Bieniek PA, Thoman R, Berman M, Borries-Strigle C, Bulock K, Chriest J, Hahn M, Hendricks AS, Jandt R, Little J, McEvoy D, Moore C, Rupp TS, Schmidt J, Stevens E, Strader H, Waigl C, White J, York A, Ziel R (2021) Emerging Anthropogenic Influences on the Southcentral Alaska Temperature and Precipitation Extremes and Related Fires in 2019. Land 10, 82.
| Crossref | Google Scholar |
Black PE (2007) Revisiting the Thornthwaite and Mather Water Balance. Journal of the American Water Resources Association 43, 1604-1605.
| Crossref | Google Scholar |
Blok D, Heijmans MMPD, Schaepman-Strub G, van Ruijven J, Parmentier FJW, Maximov TC, Berendse F (2011) The Cooling Capacity of Mosses: Controls on Water and Energy Fluxes in a Siberian Tundra Site. Ecosystems 14, 1055-1065.
| Crossref | Google Scholar |
Bond-Lamberty B, Gower ST, Amiro B, Ewers BE (2011) Measurement and modelling of bryophyte evaporation in a boreal forest chronosequence. Ecohydrology 4, 26-35.
| Crossref | Google Scholar |
Bouchet RJ (1962) Évapotranspiration potentielle et évaporation sous abri. In ‘Biometeorology’. (Ed. SW Tromp) pp. 540–545. (Pergamon) 10.1016/B978-0-08-009683-4.50069-3
Brutsaert W (2015) A generalized complementary principle with physical constraints for land-surface evaporation. Water Resources Research 51, 8087-8093.
| Crossref | Google Scholar |
Brutsaert W, Stricker H (1979) An advection-aridity approach to estimate actual regional evapotranspiration. Water Resources Research 15, 443-450.
| Crossref | Google Scholar |
Brutsaert W, Li W, Takahashi A, Hiyama T, Zhang L, Liu W (2017) Nonlinear advection-aridity method for landscape evaporation and its application during the growing season in the southern Loess Plateau of the Yellow River basin. Water Resources Research 53, 270-282.
| Crossref | Google Scholar |
Butteri M (2005) A statistical analysis of the relationship between over-winter snowpack and large fire growth in Interior Alaska. Unpublished report. 34 pp. (Washington Institute Technical Fire Management Program: Duvall, WA, USA) Available at https://www.frames.gov/catalog/5578
CFSFDG (2021) An overview of the next generation of the Canadian Forest Fire Danger Rating System. Information Report GLC-X-26. (Natural Resources Canada, Canadian Forest Service, Great Lakes Forestry Centre: Sault Ste. Marie, ON, Canada) Available at https://cfs.nrcan.gc.ca/publications/download-pdf/40474
Chapin FS, Mcguire AD, Randerson J, Pielke R, Baldocchi D, Hobbie SE, Roulet N, Eugster W, Kasischke E, Rastetter EB, Zimov SA, Running SW (2000) Arctic and boreal ecosystems of western North America as components of the climate system. Global Change Biology 6, 211-223.
| Crossref | Google Scholar |
Chavardès RD, Daniels LD, Eskelson BNI, Gedalof Z (2020) Using Complementary Drought Proxies Improves Interpretations of Fire Histories in Montane Forests. Tree-Ring Research 76, 74-88.
| Crossref | Google Scholar |
Cole F, Alexander ME (1995) Canadian fire danger rating system proves valuable tool in Alaska. Fireline 8, 2-3.
| Google Scholar |
Cole FV, Alexander ME (2001) Rating fire danger in Alaska ecosystems: CFFDRS provides an invaluable guide to systematically evaluating burning conditions. Fireline 12, 2-3.
| Google Scholar |
Coogan SCP, Daniels LD, Boychuk D, Burton PJ, Flannigan MD, Gauthier S, Kafka V, Park JS, Wotton BM (2021) Fifty years of wildland fire science in Canada. Canadian Journal of Forest Research 51, 283-302.
| Crossref | Google Scholar |
Crago R, Brutsaert W (1996) Daytime evaporation and the self-preservation of the evaporative fraction and the Bowen ratio. Journal of Hydrology 178, 241-255.
| Crossref | Google Scholar |
de Groot WJ, Field RD, Brady MA, Roswintiarti O, Mohamad M (2007) Development of the Indonesian and Malaysian Fire Danger Rating Systems. Mitigation and Adaptation Strategies for Global Change 12, 165-180.
| Crossref | Google Scholar |
de Groot WJ, Pritchard JM, Lynham TJ (2009) Forest floor fuel consumption and carbon emissions in Canadian boreal forest fires. Canadian Journal of Forest Research 39, 367-382.
| Crossref | Google Scholar |
de Groot WJ, Wotton BM, Flannigan MD (2015) Chapter 11 - Wildland Fire Danger Rating and Early Warning Systems. In ‘Wildfire Hazards, Risks and Disasters’. (Eds JF Shroder, D Paton) pp. 207–228. (Elsevier: Oxford, UK) 10.1016/B978-0-12-410434-1.00011-7
Dimitrakopoulos AP, Bemmerzouk AM, Mitsopoulos ID (2011) Evaluation of the Canadian Fire Weather Index System in an eastern Mediterranean environment. Meteorological Applications 18, 83-93.
| Crossref | Google Scholar |
Eaton AK, Rouse WR, Lafleur PM, Marsh P, Blanken PD (2001) Surface energy balance of the Western and Central Canadian Subarctic: Variations in the energy balance among five major terrain types. Journal of Climate 14, 3692-3703.
| Crossref | Google Scholar |
Eugster W, Rouse WR, Pielke Sr RA, Mcfadden JP, Baldocchi DD, Kittel TGF, Chapin III FS, Liston GE, Vidale PL, Vaganov E, Chambers S (2000) Land–atmosphere energy exchange in Arctic tundra and boreal forest: available data and feedbacks to climate. Global Change Biology 6, 84-115.
| Crossref | Google Scholar |
Fernandes (2019) Variation in the Canadian Fire Weather Index Thresholds for Increasingly Larger Fires in Portugal. Forests 10, 838.
| Crossref | Google Scholar |
Field RD, Wang Y, Roswintiarti O, Guswanto (2004) A drought-based predictor of recent haze events in western Indonesia. Atmospheric Environment 38, 1869-1878.
| Crossref | Google Scholar |
Fischer R, Walsh JE, Euskirchen ES, Bieniek PA (2018) Regional Climate Model Simulation of Surface Moisture Flux Variations in Northern Terrestrial Regions. Atmospheric and Climate Sciences 8, 29-54.
| Crossref | Google Scholar |
Foote MJ (1983) Classification, description, and dynamics of plant communities after fire in the taiga of interior Alaska. Research Paper PNW-RP-307. (U.S. Forest Service, Pacific Northwest Forest and Range Experiment Station: Portland, OR, USA) Available at https://www.fs.usda.gov/research/treesearch/25349
Furguson SA, Ruthford J, Rorig M, Sandberg DV (2003) Measuring moss moisture dynamics to predict fire severity. In ‘The First National Congress on Fire Ecology, Prevention, and Management’, Tallahassee, FL, USA. (Eds KEM Galley, RC Klinger, NG Sugihara) pp. 211–217. (Tall Timbers Research Station: Tallahassee, FL, USA)
Girardin M-P, Tardif J, Flannigan MD, Wotton BM, Bergeron Y (2004) Trends and periodicities in the Canadian Drought Code and their relationships with atmospheric circulation for the southern Canadian boreal forest. Canadian Journal of Forest Research 34, 103-119.
| Crossref | Google Scholar |
Goetz JD, Price JS (2016) Ecohydrological controls on water distribution and productivity of moss communities in western boreal peatlands, Canada. Ecohydrology 9, 138-152.
| Crossref | Google Scholar |
Grelle A, Lindroth A, Mölder M (1999) Seasonal variation of boreal forest surface conductance and evaporation. Agricultural and Forest Meteorology 98–99, 563-578.
| Crossref | Google Scholar |
Han S, Tian F (2020) A review of the complementary principle of evaporation: from the original linear relationship to generalized nonlinear functions. Hydrology and Earth System Sciences 24, 2269-2285.
| Crossref | Google Scholar |
Heijmans MMPD, Arp WJ, Chapin FS (2004) Controls on moss evaporation in a boreal black spruce forest. Global Biogeochemical Cycles 18, GB2004.
| Crossref | Google Scholar |
Heikinhemo M, Venalainen A, Tourula T (1998) A soil moisture index for the assessment of forest fire risk in the boreal zone. In ‘Proceedings of the International Symposium on Applied Agrometeorology and Agroclimatology’, Volos, Greece. (Ed. N Dalezios) pp. 549–555. (European Commission: Volos, Greece)
Hinzman LD, Kane DL, Gieck RE, Everett KR (1991) Hydrologic and thermal properties of the active layer in the Alaskan Arctic. Cold Regions Science and Technology 19, 95-110.
| Crossref | Google Scholar |
Hinzman L, Ishikawa N, Yoshikawa K, Bolton W, Petrone K (2002) Hydrologic Studies in Caribou-Poker Creeks Research Watershed in Support of Long Term Ecological Research. Eurasian Journal of Forest Research 5, 67-71.
| Google Scholar |
Hinzman LD, Bolton WR, Petrone KC, Jones JB, Adams PC (2006a) Watershed hydrology and chemistry in the Alaskan boreal forest: the central role of permafrost. In ‘Alaska’s Changing Boreal Forest’. (Eds FS Chapin, MW Oswood, K van Cleve, LA Viereck, DL Verbyla) pp. 269–284. (Oxford University Press: New York, NY, USA)
Hinzman LD, Deal CJ, McGuire AD, Mernild SH, Polyakov IV, Walsh JE (2013) Trajectory of the Arctic as an integrated system. Ecological Applications 23, 1837-1868.
| Crossref | Google Scholar |
Humphreys ER, Black TA, Ethier GJ, Drewitt GB, Spittlehouse DL, Jork E-M, Nesic Z, Livingston NJ (2003) Annual and seasonal variability of sensible and latent heat fluxes above a coastal Douglas-fir forest, British Columbia, Canada. Agricultural and Forest Meteorology 115, 109-125.
| Crossref | Google Scholar |
Iwata H, Harazono Y, Ueyama M (2012) The role of permafrost in water exchange of a black spruce forest in Interior Alaska. Agricultural and Forest Meteorology 161, 107-115.
| Crossref | Google Scholar |
Jarvis PG, Massheder JM, Hale SE, Moncrieff JB, Rayment M, Scott SL (1997) Seasonal variation of carbon dioxide, water vapor, and energy exchanges of a boreal black spruce forest. Journal of Geophysical Research: Atmospheres 102, 28953-28966.
| Crossref | Google Scholar |
Johnson EA, Keith DM, Martin YE (2013) Comparing measured duff moisture with a water budget model and the duff and drought codes of the Canadian Fire Weather Index. Forest Science 59, 78-92.
| Crossref | Google Scholar |
Jones JA, Creed IF, Hatcher KL, Warren RJ, Adams MB, Benson MH, Boose E, Brown WA, Campbell JL, Covich A, Clow DW, Dahm CN, Elder K, Ford CR, Grimm NB, Henshaw DL, Larson KL, Miles ES, Miles KM, Sebestyen SD, Spargo AT, Stone AB, Vose JM, Williams MW (2012) Ecosystem processes and human influences regulate streamflow response to climate change at Long-Term Ecological Research Sites. BioScience 62, 390-404.
| Crossref | Google Scholar |
Kahler DM, Brutsaert W (2006) Complementary relationship between daily evaporation in the environment and pan evaporation. Water Resources Research 42, W05413.
| Crossref | Google Scholar |
Kasurinen V, Alfredsen K, Kolari P, Mammarella I, Alekseychik P, Rinne J, Vesala T, Bernier P, Boike J, Langer M, Belelli Marchesini L, van Huissteden K, Dolman H, Sachs T, Ohta T, Varlagin A, Rocha A, Arain A, Oechel W, Lund M, Grelle A, Lindroth A, Black A, Aurela M, Laurila T, Lohila A, Berninger F (2014) Latent heat exchange in the boreal and arctic biomes. Global Change Biology 20, 3439-3456.
| Crossref | Google Scholar |
Kljun N, Black TA, Griffis TJ, Barr AG, Gaumont-Guay D, Morgenstern K, McCaughey JH, Nesic Z (2006) Response of net ecosystem productivity of three boreal forest stands to drought. Ecosystems 9, 1128-1144.
| Crossref | Google Scholar |
Komatsu H (2005) Forest categorization according to dry-canopy evaporation rates in the growing season: comparison of the Priestley–Taylor coefficient values from various observation sites. Hydrological Processes 19, 3873-3896.
| Crossref | Google Scholar |
Krueger ES, Ochsner TE, Engle DM, Carlson JD, Twidwell D, Fuhlendorf SD (2015) Soil moisture affects growing-season wildfire size in the Southern Great Plains. Soil Science Society of America Journal 79, 1567-1576.
| Crossref | Google Scholar |
Krueger ES, Ochsner TE, Carlson JD, Engle DM, Twidwell D, Fuhlendorf SD (2016) Concurrent and antecedent soil moisture relate positively or negatively to probability of large wildfires depending on season. International Journal of Wildland Fire 25, 657-668.
| Crossref | Google Scholar |
Krueger ES, Ochsner TE, Quiring SM, Engle DM, Carlson JD, Twidwell D, Fuhlendorf SD (2017) Measured Soil Moisture is a Better Predictor of Large Growing-Season Wildfires than the Keetch–Byram Drought Index. Soil Science Society of America Journal 81, 490-502.
| Crossref | Google Scholar |
Lafleur PM (1992) Energy balance and evapotranspiration from a subarctic forest. Agricultural and Forest Meteorology 58, 163-175.
| Crossref | Google Scholar |
Lestienne M, Hély C, Curt T, Jouffroy-Bapicot I, Vannière B (2020) Combining the monthly Drought Code and paleoecological data to assess Holocene climate impact on Mediterranean fire regime. Fire 3, 8.
| Crossref | Google Scholar |
Loboda TV, Hall JV, Baer A (2021) ABoVE: Wildfire Date of Burning within Fire Scars across Alaska and Canada, 2001-2019. 10.3334/ORNLDAAC/1559
Loranty MM, Abbott BW, Blok D, Douglas TA, Epstein HE, Forbes BC, Jones BM, Kholodov AL, Kropp H, Malhotra A, Mamet SD, Myers-Smith IH, Natali SM, O’Donnell JA, Phoenix GK, Rocha AV, Sonnentag O, Tape KD, Walker DA (2018) Reviews and syntheses: Changing ecosystem influences on soil thermal regimes in northern high-latitude permafrost regions. Biogeosciences 15, 5287-5313.
| Crossref | Google Scholar |
Maes WH, Gentine P, Verhoest NEC, Miralles DG (2019) Potential evaporation at eddy-covariance sites across the globe. Hydrology and Earth System Sciences 23, 925-948.
| Crossref | Google Scholar |
Mann DH, Peteet DM, Reanier RE, Kunz ML (2002) Responses of an arctic landscape to Lateglacial and early Holocene climatic changes: the importance of moisture. Quaternary Science Reviews 21, 997-1021.
| Crossref | Google Scholar |
Matsumoto K, Ohta T, Nakai T, Kuwada T, Daikoku K, Iida S, Yabuki H, Kononov AV, van der Molen MK, Kodama Y, Maximov TC, Dolman AJ, Hattori S (2008) Energy consumption and evapotranspiration at several boreal and temperate forests in the Far East. Agricultural and Forest Meteorology 148, 1978-1989.
| Crossref | Google Scholar |
McMahon TA, Peel MC, Lowe L, Srikanthan R, McVicar TR (2013) Estimating actual, potential, reference crop and pan evaporation using standard meteorological data: a pragmatic synthesis. Hydrology and Earth System Sciences 17, 1331-1363.
| Crossref | Google Scholar |
Miller EA (2020) A Conceptual Interpretation of the Drought Code of the Canadian Forest Fire Weather Index System. Fire 3, 23.
| Crossref | Google Scholar |
Miller EA, Wilmore B (2020) Evaluating the Drought Code Using In Situ Drying Timelags of Feathermoss Duff in Interior Alaska. Fire 3, 25.
| Crossref | Google Scholar |
Nakai T, Kim Y, Busey RC, Suzuki R, Nagai S, Kobayashi H, Park H, Sugiura K, Ito A (2013) Characteristics of evapotranspiration from a permafrost black spruce forest in interior Alaska. Polar Science 7, 136-148.
| Crossref | Google Scholar |
NCEI (2021) ‘U.S. Climate Normals.’ (National Oceanic and Atmospheric Administration, National Centers for Environmental Information) Available at https://www.ncei.noaa.gov/products/land-based-station/us-climate-normals
Newman JE, Branton CI (1972) Annual Water Balance and Agricultural Development in Alaska. Ecology 53, 513-519.
| Crossref | Google Scholar |
O’Donnell JA, Romanovsky VE, Harden JW, McGuire AD (2009) The Effect of Moisture Content on the Thermal Conductivity of Moss and Organic Soil Horizons From Black Spruce Ecosystems in Interior Alaska. Soil Science 174, 646-651.
| Crossref | Google Scholar |
Parks SA (2014) Mapping day-of-burning with coarse-resolution satellite fire-detection data. International Journal of Wildland Fire 23, 215-223.
| Crossref | Google Scholar |
Pastorello G, Trotta C, Canfora E, Chu H, Christianson D, Cheah Y-W, Poindexter C, Chen J, Elbashandy A, Humphrey M, Isaac P, Polidori D, Reichstein M, Ribeca A, van Ingen C, Vuichard N, Zhang L, Amiro B, Ammann C, Arain MA, Ardö J, Arkebauer T, Arndt SK, Arriga N, Aubinet M, Aurela M, Baldocchi D, Barr A, Beamesderfer E, Marchesini LB, Bergeron O, Beringer J, Bernhofer C, Berveiller D, Billesbach D, Black TA, Blanken PD, Bohrer G, Boike J, Bolstad PV, Bonal D, Bonnefond JM, Bowling DR, Bracho R, Brodeur J, Brümmer C, Buchmann N, Burban B, Burns SP, Buysse P, Cale P, Cavagna M, Cellier P, Chen S, Chini I, Christensen TR, Cleverly J, Collalti A, Consalvo C, Cook BD, Cook D, Coursolle C, Cremonese E, Curtis PS, D’Andrea E, da Rocha H, Dai X, Davis KJ, Cinti BD, Grandcourt A, Ligne AD, De Oliveira RC, Delpierre N, Desai AR, Di Bella CM, Tommasi P, Dolman H, Domingo F, Dong G, Dore S, Duce P, Dufrêne E, Dunn A, Dušek J, Eamus D, Eichelmann U, ElKhidir HAM, Eugster W, Ewenz CM, Ewers B, Famulari D, Fares S, Feigenwinter I, Feitz A, Fensholt R, Filippa G, Fischer M, Frank J, Galvagno M, Gharun M, Gianelle D, Gielen B, Gioli B, Gitelson A, Goded I, Goeckede M, Goldstein AH, Gough CM, Goulden ML, Graf A, Griebel A, Gruening C, Grünwald T, Hammerle A, Han S, Han X, Hansen BU, Hanson C, Hatakka J, He Y, Hehn M, Heinesch B, Hinko-Najera N, Hörtnagl L, Hutley L, Ibrom A, Ikawa H, Jackowicz-Korczynski M, Janouš D, Jans W, Jassal R, Jiang S, Kato T, Khomik M, Klatt J, Knohl A, Knox S, Kobayashi H, Koerber G, Kolle O, Kosugi Y, Kotani A, Kowalski A, Kruijt B, Kurbatova J, Kutsch WL, Kwon H, Launiainen S, Laurila T, Leuning R, Li Y, Liddell M, Limousin JM, Lion M, Liska AJ, Lohila A, López-Ballesteros A, López-Blanco E, Loubet B, Loustau D, Lucas-Moffat A, Lüers J, Ma S, Macfarlane C, Magliulo V, Maier R, Mammarella I, Manca G, Marcolla B, Margolis HA, Marras S, Massman W, Mastepanov M, Matamala R, Matthes JH, Mazzenga F, McCaughey H, McHugh I, McMillan AMS, Merbold L, Meyer W, Meyers T, Miller SD, Minerbi S, Moderow U, Monson RK, Montagnani L, Moore CE, Moors E, Moreaux V, Moureaux C, Munger JW, Nakai T, Neirynck J, Nesic Z, Nicolini G, Noormets A, Northwood M, Nosetto M, Nouvellon Y, Novick K, Oechel W, Olesen JE, Ourcival JM, Papuga SA, Parmentier FJ, Paul-Limoges E, Pavelka M, Peichl M, Pendall E, Phillips RP, Pilegaard K, Pirk N, Posse G, Powell T, Prasse H, Prober SM, Rambal S, Rannik Ü, Raz-Yaseef N, Rebmann C, Reed D, Dios VR, Restrepo-Coupe N, Reverter BR, Roland M, Sabbatini S, Sachs T, Saleska SR, Sánchez-Cañete EP, Sanchez-Mejia ZM, Schmid HP, Schmidt M, Schneider K, Schrader F, Schroder I, Scott RL, Sedlák P, Serrano-Ortíz P, Shao C, Shi P, Shironya I, Siebicke L, Šigut L, Silberstein R, Sirca C, Spano D, Steinbrecher R, Stevens RM, Sturtevant C, Suyker A, Tagesson T, Takanashi S, Tang Y, Tapper N, Thom J, Tomassucci M, Tuovinen JP, Urbanski S, Valentini R, van der Molen M, van Gorsel E, van Huissteden K, Varlagin A, Verfaillie J, Vesala T, Vincke C, Vitale D, Vygodskaya N, Walker JP, Walter-Shea E, Wang H, Weber R, Westermann S, Wille C, Wofsy S, Wohlfahrt G, Wolf S, Woodgate W, Li Y, Zampedri R, Zhang J, Zhou G, Zona D, Agarwal D, Biraud S, Torn M, Papale D (2020) The FLUXNET2015 dataset and the ONEFlux processing pipeline for eddy covariance data. Scientific Data 7, 225.
| Crossref | Google Scholar |
Pejam MR, Arain MA, McCaughey JH (2006) Energy and water vapour exchanges over a mixedwood boreal forest in Ontario, Canada. Hydrological Processes 20, 3709-3724.
| Crossref | Google Scholar |
Priestley CHB, Taylor RJ (1972) On the assessment of surface heat flux and evaporation using large-scale parameters. Monthly Weather Review 100, 81-92.
| Crossref | Google Scholar |
Roberts J (1983) Forest transpiration: A conservative hydrological process? Journal of Hydrology 66, 133-141.
| Crossref | Google Scholar |
Saito K, Zhang T, Yang D, Marchenko S, Barry RG, Romanovsky V, Hinzman L (2013) Influence of the physical terrestrial Arctic in the eco-climate system. Ecological Applications 23, 1778-1797.
| Crossref | Google Scholar |
Shan Y, Wang Y, Flannigan M, Tang S, Sun P, Du F (2017) Spatiotemporal variation in forest fire danger from 1996 to 2010 in Jilin Province, China. Journal of Forestry Research 28, 983-996.
| Crossref | Google Scholar |
Sharratt BS (1997) Thermal Conductivity and Water Retention of A Black Spruce Forest Floor. Soil Science 162, 576-582.
| Crossref | Google Scholar |
Shuttleworth WJ (2007) Putting the “vap” into evaporation. Hydrology and Earth System Sciences 11, 210-244.
| Crossref | Google Scholar |
Simard AJ, Main WA (1982) Comparing methods of predicting Jack pine slash moisture. Canadian Journal of Forest Research 12, 793-802.
| Crossref | Google Scholar |
Skre O, Oechel WC, Miller PM (1983) Moss leaf water content and solar radiation at the moss surface in a mature black spruce forest in central Alaska. Canadian Journal of Forest Research 13, 860-868.
| Crossref | Google Scholar |
Stocks BJ, Lawson BD, Alexander ME, Van Wagner CE, McAlpine RS, Lynham TJ, Dube DE (1989) The Canadian Forest Fire Danger Rating System: an overview. The Forestry Chronicle 65, 450-457.
| Crossref | Google Scholar |
Stoy PC, Street LE, Johnson AV, Prieto-Blanco A, Ewing SA (2012) Temperature, heat flux, and reflectance of common subarctic mosses and lichens under field conditions: might changes to community composition impact climate-relevant surface fluxes? Arctic, Antarctic & Alpine Research 44, 500-508.
| Crossref | Google Scholar |
Sullivan PF, Sveinbjörnsson B (2011) Environmental controls on needle gas exchange and growth of white spruce (Picea glauca) on a riverside terrace near the Arctic treeline. Arctic, Antarctic, and Alpine Research 43, 279-288.
| Crossref | Google Scholar |
Taylor SW, Alexander ME (2006) Science, technology, and human factors in fire danger rating: the Canadian experience. International Journal of Wildland Fire 15, 121-135.
| Crossref | Google Scholar |
Terrier A, de Groot WJ, Girardin MP, Bergeron Y (2014) Dynamics of moisture content in spruce–feather moss and spruce–Sphagnum organic layers during an extreme fire season and implications for future depths of burn in Clay Belt black spruce forests. International Journal of Wildland Fire 23, 490-502.
| Crossref | Google Scholar |
Thompson DK, Schroeder D, Wilkinson SL, Barber Q, Baxter G, Cameron H, Hsieh R, Marshall G, Moore B, Refai R, Rodell C, Schiks T, Verkaik GJ, Zerb J (2020) Recent crown thinning in a boreal black spruce forest does not reduce spread rate nor total fuel consumption: results from an experimental crown fire in Alberta, Canada. Fire 3, 28.
| Crossref | Google Scholar |
Thornthwaite CW (1948) An approach toward a Rational Classification of Climate. Geographical Review 38, 55-94.
| Crossref | Google Scholar |
Trigg WM (1971) Fire season climatic zones of mainland Alaska. Research Paper PNW-RP-126. (U.S. Forest Service, Pacific Northwest Research Station: Portland, OR, USA) Available at https://www.fs.usda.gov/treesearch/pubs/25487
Turner JA (1972) The Drought Code component of the Canadian Forest Fire Behavior System. Publication No. 1316. (Environment Canada, Canadian Forestry Service, Headquarters: Ottawa, Canada) Available at http://cfs.nrcan.gc.ca/publications?id=28538
Ueyama M, Tahara N, Iwata H, Euskirchen ES, Ikawa H, Kobayashi H, Nagano H, Nakai T, Harazono Y (2016) Optimization of a biochemical model with eddy covariance measurements in black spruce forests of Alaska for estimating CO2 fertilization effects. Agricultural and Forest Meteorology 222, 98-111.
| Crossref | Google Scholar |
Van Wagner CE (1979) A laboratory study of weather effects on the drying rate of jack pine litter. Canadian Journal of Forest Research 9, 267-275.
| Crossref | Google Scholar |
Van Wagner CE, Pickett TL (1985) Equations and FORTRAN program for the Canadian Forest Fire Weather Index System. Forestry Technical Report 33. (Canadian Forest Service: Ottawa, ON, Canada) Available at https://cfs.nrcan.gc.ca/publications?id=19973
Varela V, Vlachogiannis D, Sfetsos A, Karozis S, Politi N, Giroud F (2019) Projection of forest fire danger due to climate change in the French Mediterranean Region. Sustainability 11, 4284.
| Crossref | Google Scholar |
Venalainen A, Heikinheimo M (2003) The Finnish Forest Fire Index Calculation System. In ‘Early Warning Systems for Natural Disaster Reduction’. (Eds J Zschau, A Kuppers) pp. 645–647. (Springer: Berlin, Heidelberg) 10.1007/978-3-642-55903-7_88
Waddington JM, Thompson DK, Wotton M, Quinton WL, Flannigan MD, Benscoter BW, Baisley SA, Turetsky MR (2012) Examining the utility of the Canadian Forest Fire Weather Index System in boreal peatlands. Canadian Journal of Forest Research 42, 47-58.
| Crossref | Google Scholar |
Warren RK, Pappas C, Helbig M, Chasmer LE, Berg AA, Baltzer JL, Quinton WL, Sonnentag O (2018) Minor contribution of overstorey transpiration to landscape evapotranspiration in boreal permafrost peatlands. Ecohydrology 11, e1975.
| Crossref | Google Scholar |
Wotton BM (2008) Interpreting and using outputs from the Canadian Forest Fire Danger Rating System in research applications. Environmental and Ecological Statistics 16, 107-131.
| Crossref | Google Scholar |
Xiao J, Zhuang Q (2007) Drought effects on large fire activity in Canadian and Alaskan forests. Environmental Research Letters 2, 044003.
| Crossref | Google Scholar |
Xu CY, Singh VP (2001) Evaluation and generalization of temperature-based methods for calculating evaporation. Hydrological Processes 15, 305-319.
| Crossref | Google Scholar |
Yang Y, Uddstrom M, Pearce G, Revell M (2015) Reformulation of the Drought Code in the Canadian Fire Weather Index System implemented in New Zealand. Journal of Applied Meteorology and Climatology 54, 1523-1537.
| Crossref | Google Scholar |
Young-Robertson JM, Bolton WR, Bhatt US, Cristóbal J, Thoman R (2016) Deciduous trees are a large and overlooked sink for snowmelt water in the boreal forest. Scientific Reports 6, 29504.
| Crossref | Google Scholar |
Ziel R (2019) Alaska’s fire environment: not an average place. Wildfire 28, 20-29.
| Google Scholar |
Ziel RH, Bieniek PA, Bhatt US, Strader H, Rupp TS, York A (2020) A comparison of fire weather indices with MODIS fire days for the natural regions of Alaska. Forests 11, 516.
| Crossref | Google Scholar |
Appendix 1
The variables of the Priestley–Taylor equation are explained in more detail here. Δ is the slope of the saturated vapour pressure versus temperature curve (kPa °C−1):
where Ta is air temperature (°C), ea is vapour pressure (kPa), and es is saturated vapour pressure (kPa). γ is the psychrometric constant (kPa °C−1):
where p is the air pressure (kPa). λ is the latent heat of vaporisation (MJ kg−1):
Saturation vapour pressure is obtained from the air temperature: