A phenology-driven fire danger index for northern grasslands
Johan Sjöström A * and Anders Granström
A * and Anders Granström  B
B
A Department of Fire and Safety, RISE Research Institutes of Sweden, Box 857, 501 15 Borås, Sweden.
B Department of Forest Ecology and Management, Swedish University of Agricultural Sciences, 901 83, Umeå, Sweden. Email: anders.granstrom@slu.se
Abstract
Directly after snowmelt, northern grasslands typically have highly flammable fuel-beds consisting of 100% grass litter. With green-up, the addition of high-moisture foliage leads to progressively decreasing fire hazard.
Our aim was to create a fire-danger index for northern grasslands that incorporated grass phenology.
We made use of 25 years of Swedish wildfire data and 56 experimental fires conducted during one full fire-season, merged with established models for moisture content and flame spread rates. Refined data on equilibrium moisture content of grass litter were obtained through laboratory tests.
The RING (Rate of spread In Northern Grasslands) model uses cumulative air temperature as a proxy for growing season progression. Three independent functions account for impact of wind, moisture content and the damping effect of live grass, respectively. The latter results in exponentially decaying rate of spread (ROS) with the progressing season. Following the field experiments, green grass proportion as low as 10–20% (live/dead dry-mass) resulted in model-ROS so reduced that the grassland fire season could effectively be considered over.
The model, calculated from standard meteorological data only, matches the experimental results and separately performed validation tests, as well as wildfire dispatch data.
RING has been used in Sweden since 2021 and is likely applicable to other northern regions as well.
Keywords: ecosystems, boreal, fire behaviour, northern grasslands, phenology, propagation, fire danger, fuel, wildland–urban interface.
Introduction
Globally, grass-dominated fuel beds occur in seasonally dry regions such as savannahs (Mouillot and Field 2005) and prairies (Knapp et al. 1998), but also in more mesic climates where ‘cultural’ grasslands occur around settlements and on abandoned agricultural land (Rosén and Borgegård 1999; Prishchepov et al. 2021). Grasslands cover around a third of the Earth’s land area and account for over 80% of the global burnt area (Leys et al. 2018). Grassfires differ significantly from forest fires in several aspects. They can potentially have very high rate of spread (ROS) because of the well-aerated structure and high surface-to-volume ratio of grass litter, and the fact that there are no trees to impede the wind (Cheney and Gould 1995; Cruz et al. 2022). The same factors also enable rapid adjustment of fuel moisture content to ambient weather conditions. In addition, the grass is often fully exposed to sunlight, which speeds up drying further. Grass-dominated areas can therefore transit from incombustible to highly flammable within hours (McArthur 1960; Cheney and Sullivan 2008). The high ROS puts buildings and people at risk. A recent example is the Marshall Fire in Colorado December 2021 that spread 5 km within the first hour after ignition and eventually burned 2400 ha of open grassland, destroyed 1091 buildings and caused two fatalities (Fovell et al. 2022).
Grasses undergo large phenological changes over the season, with dramatic changes in moisture content as the shoots emerge, mature and finally senesce. The transformation of live grass into dead litter fuel is commonly referred to as ‘curing’ and controls the extent of the fire-season in many grass-dominated systems. Depending on region, the drivers of the curing process can be drought, high temperatures or frost. The degree of curing is defined as oven-dried proportion of dead to total fuel mass (Kidnie et al. 2015). Based on field experiments, it is often assumed that a curing degree of ~50% is needed for fire propagation and that there is a monotonic increase in ROS towards 100% curing (see Kidnie et al. (2015) and Cruz et al. (2015)). The degree of curing is operationally assessed either from a visual inspection of grass colour and seed head development (Garvey and Millie 2000), or through destructive gravimetric moisture content determination. Attempts at modelling degree of curing through soil moisture modelling has also been tested for seasonally dry grassland, but with a low degree of precision (Krueger et al. 2023).
In northern regions, such as Canada, Fennoscandia and Russia, there is often a marked spring grass-fire season that starts after snow-melt and gradually ends when growth of new grass infiltrates the dead litter (Sjöström and Granström 2023). Here grasslands rarely cure enough from summer drought to carry fire. Instead, the curing occurs into autumn and winter because of low temperature, but during this part of the year the humidity is typically too high to enable fire propagation, even if there happens to be little or no snow. Instead, the grassfire season commences in spring after snow-melt. The fuel bed is then composed nearly exclusively of leaf litter from the previous summer, which has been largely compressed by winter’s snow. Thereafter, the fuel bed rapidly becomes less flammable with the in-growth of green grass, i.e. a reversed ‘curing’ of the fuel bed (Fig. 1).
Two contrasting aspects of the fuel situation on an abandoned former cultivated field, typical for grasslands in Northern Sweden. Photos taken from the same spot on 8 May and 6 June 2022 (photo: Anders Granström).

Although somewhat influenced by site factors such as soil conditions and nutrient availability, the growth of grass in spring is primarily controlled by weather (Gustavsson et al. 2003). The simplest phenological models therefore only take weather parameters into account. Andréasson and Gardelin (2002) defined grassfire season in Sweden using growing degree-days (GDD), in which the cumulated (daily averaged) temperature above a certain base temperature was used as a proxy for seasonal growth (Prentice et al. 1992).
For grass phenology in northern Europe, the most substantiated model was constructed by Landström (1990), using 7 years of field observations of Phleum pratense in northern Sweden. He found that growth started 3–4 days after the ground frost had thawed to a depth of 20 cm. From then on, the increase in fresh biomass during spring can be estimated by GDD (Nilsson and Hansson 2001).
In Sweden, grassland fires constitute about half of all wildfires to which suppression organisations are dispatched (Sjöström and Granström 2023). They lead to the destruction of many buildings and annually cause several injuries and deaths (Vermina Plathner et al., unpubl. data). Because of the rapidly changing fuel bed in spring to early summer, a phenologically adjusted fire danger model for grassfire spread potential is needed in order to inform the public and rescue services about the current grassfire danger. It should be noted that ‘grasslands’ often have a subcomponent of herbs (Rosén and Borgegård 1999), which broadly follow the same phenological patterns as grasses and whose litter probably do not differ with respect to flammability either. For simplicity, we hereafter refer only to ‘grass litter’ and ‘grassfires’.
All existing fire danger models for grasslands that cure under drought stress require explicit on-site information on the curing degree, because it is notoriously difficult to model (Kidnie et al. 2015; Krueger et al. 2023). For northern regions, where the fuel bed can be considered completely cured after snowmelt (Fig. 1), there is an opportunity to create a complete grassfire model from meteorological data only, by combining a phenological model of grass growth with models for fuel moisture content (MC) and ROS. Here we formulate such a model, (Rate of spread In Northern Grasslands, RING), building on data from experimental fires conducted over a full grassfire season in northern Sweden, 25 years of wildfire incident data and a set of measurements of equilibrium moisture content (EMC) in grass litter. The complete model incorporates a phenological sub-model for the ingrowth of fresh grass and its effect on ROS, an hourly weather-driven sub-model for dead fuel moisture content, and empirically based relations of ROS to wind and MC. Since 2021, the model is operationally used and updated hourly in the national warning system for grassland fires in Sweden.
Methods
A comprehensive list of nomenclature, abbreviations and their corresponding definitions is provided in Table 1 to ensure clarity and facilitate understanding of the terminology used throughout the article.
| Variable or term | Description | |
|---|---|---|
| EMC | Equilibrium moisture content. The moisture content of dead grass fuel after exposure to constant temperature and RH (%) | |
| EMCD | EMC during drying conditions (%) | |
| EMCW | EMC during wetting conditions (%) | |
| Ft(i) | Monotonically increasing time function used as a weight for adding daily temperature to GDD | |
| GDD | Growing degree-days. A phenological model for grass growth using cumulative daily average air temperature | |
| I | Global irradiance, including direct, diffuse and reflected solar radiation (kW m−2) | |
| MC | Moisture content. Mass of water to dry mass of fuel (%) | |
| N | Parameter defining the number of days over which Ft(i) increases from 8 to 92% | |
| Nav | Number of days over which air temperature is averaged, as a proxy for ground temperature (determined to 4 days in the model) | |
| Nshift | Parameter to shift the onset of growth of Ft(i) | |
| Pdispatch | Probability of a rescue service dispatch on a grassfire | |
| Pign | Probability of grass fuel igniting and burning with sustained flame | |
| Pescape | Probability of ignited grass to spread too fast for un-aided people to control it, leading to a rescue service dispatch | |
| Phenology | Changes in biological features with season, e.g. fuel characteristics | |
| RH | Relative air humidity (%) | |
| RGg | Relative humidity at the fuel surface, corrected for solar radiation heating (%) | |
| ROS | Head fire rate of spread (m min−1) | |
| RW | Head fire rate of spread in completely dry and 100% cured grass litter (m min−1) | |
| Tair | Daily average air temperature (°C) | |
| Tb | Base temperature above which cumulative temperature is calculated (°C) | |
| Tcorr | Air temperature (°C), corrected for sub-zero conditions and presence of snow | |
| Tg | Solar radiation-corrected fuel temperature (°C) | |
| Ti | Specific temperature, as a proxy for soil temperature (°C) | |
| W | 10-m open wind speed (m s−1) | |
| ΦC | Impeding, multiplicative factor for the effect of in-growth of grass on ROS | |
| ΦMC | Impeding, multiplicative factor for the effect of moisture content on ROS |
Defining the spatio-temporal extent of the grassfire season using incident data
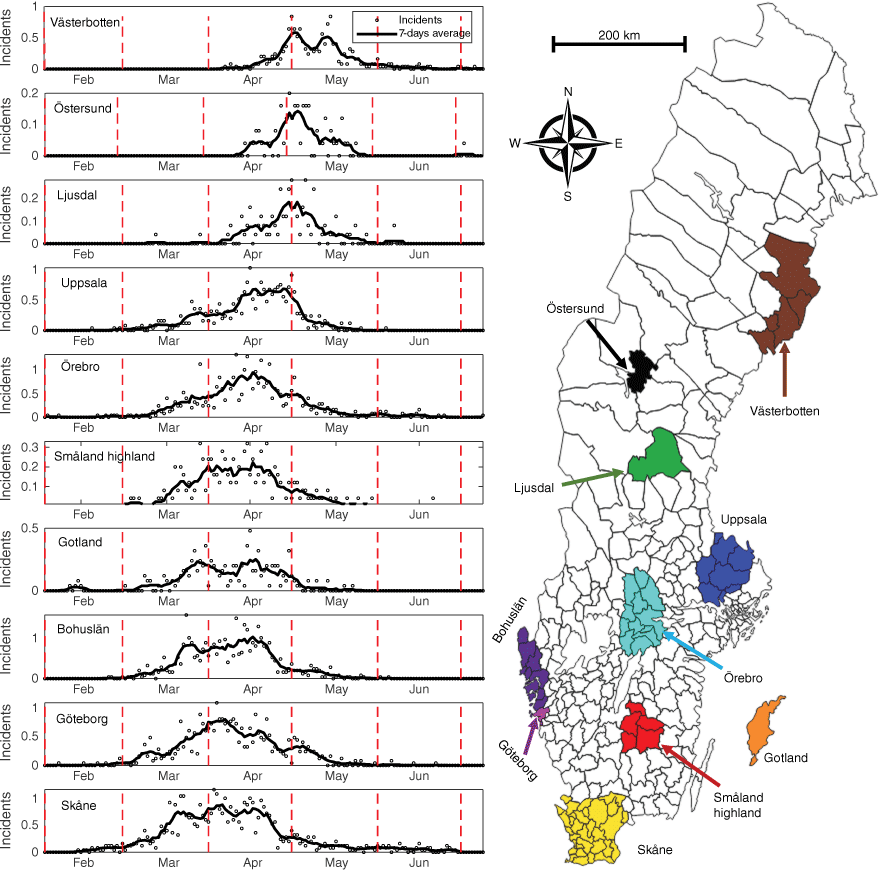
Since 1996, all wildfires that lead to a dispatch of fire fighters from the municipal rescue services are reported to a national database of incident reports managed by MSB, the Swedish Civil Contingencies Agency (Sjöström and Granström 2023). To extract temporal information on grassfires, we first delineated 10 geographically dispersed regions across Sweden that were small enough for the weather and seasonal progression to be considered homogeneous and large enough to yield a reasonable statistical basis (Fig. 2, Table 2). The boundaries for the regions coincide with the municipal borders because dispatch incident data are reported by each municipality.
Left panel: average (1996–2020) seasonal distribution of grassfires in the different regions. The circles show average number of fires per day. The lines represent 7 days running average. Right panel: regions within Sweden delineated for the incident report analysis. The North–South distance between Skåne and Västerbotten is ~1000 km and covers a considerable climatic gradient, particularly regarding the onset of spring (Jin et al. 2019).
| Region | Area (km2) | Population density (km−1) | Number of incidents 1996–2020 | |
|---|---|---|---|---|
| Västerbotten | 12 952 | 14.6 | 351 | |
| Östersund | 2208 | 29.0 | 135 | |
| Ljusdal | 5256 | 3.6 | 102 | |
| Uppsala | 8189 | 47.4 | 571 | |
| Örebro | 8546 | 35.8 | 820 | |
| Bohuslän | 3766 | 78.9 | 738 | |
| Göteborg | 448 | 1302.9 | 904 | |
| Gotland | 3134 | 19.2 | 229 | |
| Småland highland | 4974 | 23.0 | 255 | |
| Skåne | 10 965 | 117.6 | 1006 |
We selected all incidents over the 25-year period 1996–2020 that were registered in any of the regions and had only burned ‘non-tree-covered land’. Incidents with a burned area <100 m2 were removed to ignore non-spreading fires (e.g. burning refuse heaps). In this data set of over 8500 incidents, we then read through the free text description (inserted by the incident commander) of each incident to select only incidents that, by all accounts, were fires actually propagating in grassland fuel. Thus, we removed incidents that burned heather, shrubs or hay bales. We also removed late season incidents in cut hay fields or along train tracks. After this selection process, 5115 incidents remained.
For each year and region we then estimated when the grassfire season ended from the records of rescue service dispatches. Because of the somewhat haphazard occurrence of ignitions, we defined this as a time interval rather than a point in time. The day after the last reported grassfire constituted the beginning of the interval, but since termination of incidents can simply mean that the weather has turned, we counted the number of days with beneficial weather (i.e. days when weather alone should have permitted grassfires) after the last fire incident. Such days were defined as having no precipitation and a noon relative humidity below 65%. The interval duration was determined by when the number of beneficial weather days after the last reported fire reached the average number of days between the three last fires in the region (averaged over 25 years). Our reasoning here was that a number of days in sequence with good fire weather but no fire indicates that the fuel bed is no longer conducive to fire propagation. On average, the length of this interval was 10 days. For some regions and years, a qualitative assessment was inevitable, based on few or temporally isolated fire incidents. In a few cases a time interval for the end of the grassfire season could not be defined.
Phenological model for the in-growth of green grass
Similar to Nilsson and Hansson (2001), we defined a phenological grass-growth model (GDD) based on daily temperature averages, starting from 1 January, with a correction for sub-zero temperatures and for the presence of a snow cover.
The function defines a corrected daily temperature, Tcorr, as:
where Tair is the daily average air temperature. Snow observation data (SMHI 2022) from at least two weather stations in each region were used, except for the geographically small Göteborg. The weather-service criteria for registering the presence of ‘snow’ is that more than half the ground is covered by snow, as seen from the point of observation at the weather station (Brandt et al. 1999).
We then defined a specific temperature, as a proxy for soil temperature, based on several (Nav) days averages of Tcorr and limited by a base temperature Tb.
With starting date of 1 January, GDD is subsequently calculated as:
where i runs through each day of the year to the ordinal date d.
Ft(i) is a time function, monotonically growing from 0 to 1 with the ordinal day. The previous Swedish grassfire danger model (Andréasson and Gardelin 2002) also used a growing-degree model, but it severely underpredicted the length of the season in years with very mild January and February (Sjöström et al. 2021). Therefore, Ft(i)is used as a weight of the cumulative contribution from each day, decreasing the contribution from ‘warm’ days during the early period, in case of snow-free conditions. The function is a cumulative normal distribution defined as:
where N and Nshift are numerical parameters determining the function’s growth rate and onset of growth, respectively. With the weather data from each region and year, Eqn 3 was fitted by adjusting Nav, Tb, N and Nshift, such that GDD reaches 100 within the defined interval for the end of the grassfire season (see above). No parameter set fitted the estimated interval of all 250 combinations of regions and years, but the set which minimised the combined error was chosen.
An overall analysis of the influence of fuel bed phenology on grassland fire occurrence was done using the rescue service dispatch data. Because of the large number of incidents (5115), distributed over many years, the daily variation due to weather is assumed to be evened out. This leaves the phenology of the fuel bed as the single remaining factor determining fire occurrence. Thus, the GDD at the day of each fire occurrence was calculated (as described above) to obtain a statistical distribution of grassland fire dispatches with respect to GDD.
Experimental fires
A dataset of experimental fires conducted in 1998 was used to investigate the effect of the in-growth of fresh grass on head-fire rate of spread. All the results of the experimental fires were reanalysed and the experimental procedure, previously reported only in Swedish (Granström et al. 2000), is summarised here.
The campaign was run from shortly after snowmelt in the beginning of May to well into June on a large abandoned agricultural field 15 km northwest of Umeå in northern Sweden (63°57′N, 20°17′E). The fuel, which had not been cut for years, was dominated by three common grass species: creeping bentgrass (Agrostis stolonifera); tufted hairgrass (Deschampsia caespitosa); and common meadow-grass (Poa pratensis).
Beginning directly after snow melt, experimental fires were conducted on all days the fuel would carry fire. Moisture content was measured at noon for three different strata: (1) loose, well-aerated standing grass litter of ca 30 cm height (collected mainly where litter had been shielded from snow compression by small, scattered Salix shrubs); (2) upper part (~2 cm) of the snow-matted litter bed; and (3) lower part of the litter bed. Five samples per category were collected each sample day using scissors and put in airtight plastic bags. In the lab, MC was determined gravimetrically by drying for 12 h at 90°C. On 11 occasions through the season, fuel mass samples were also collected on 50 by 50 cm plots, in which all fuel was collected and sorted into live (green) and litter (dead grass from previous season). One to five samples were collected per occasion, in total 24 samples.
The approximate moisture of extinction in this type of fuel was determined by exposing grass litter from the site, with a range of pre-conditioned MC, to 5 s flame contact from a small butane burner.
During each burn day, two 9 m2 square plots were marked in matted (snow-pressed) grass fuel. Fuel depth was measured in 10 positions within each plot using a ruler inserted 50 cm from the edge of the plot. The plots were ignited along one of the sides using a large propane burner and allowed to progress with wind, while using visual observation and a stopwatch to record rate of spread. Wind speed at 2 m above ground was recorded and subsequently re-scaled to 10-m wind speed using the logarithmic wind profile and a surface roughness of 5 cm (Holmes 2007). In total, 56 test burns were conducted over the period 9 May to 25 June.
Fuel consumption was determined by visually assessing the proportion of the plot that had burn depth in four categories respectively: no consumption, as well as three burn depths of <2, 2–5 and >5 cm of the approximately 10 cm deep, snow-matted fuel bed. These categories were thereafter attributed to 0, 10, 40 and 90% consumption, respectively, of the total fuel load.
Sub-models for fuel moisture content and the influence of wind and moisture on ROS
There are several models that assess the fuel moisture content of grass-litter fuel, both of snow-matted and of standing, well-aerated grass fuel (Miller 2018). Cruz et al. (2016) evaluated different models in dead standing grass in Australia, including AM60 (the fuel moisture table of McArthur (1960) expressed as an equation by Cheney et al. (1989)), MK5 (the fuel moisture equation of the McArthur Mk 5 Grassland Fire Danger Meter (McArthur 1977), see Noble et al. (1980)), Grass Fuel Moisture Code (GFMC; Wotton 2009) and Koba (Matthews 2006). Although MK5 and AM60 performed well for Australia, they only consider instantaneous weather and will therefore underestimate moisture in a period after rain, which frequently happens during spring in northern regions. Both Koba and GFMC model the moisture content in the transition period towards a potential equilibrium moisture content (EMC), but GFMC is operationally simpler (Cruz et al. 2016) and was chosen here. Solar radiation is taken into account to estimate a radiation-corrected fuel temperature, thus affecting fuel-level relative humidity, which is important for open areas, and particularly for matted grass litter (Wotton 2009).
Equilibrium moisture content (EMC) of grass litter
The EMC values used in the GFMC (Wotton 2009) are based on scaling of experimental results obtained for pine needles. Actually, the only published experimental data on EMC for grass fuels are by Blackmarr (1971) and Van Wagner (1972), and both of these were only obtained at a single temperature of 26.7°C (80°F). To obtain data on the EMC in the temperature range typical for northern springtime, we used a climate-controlled chamber with forced convection (Weiss, model WK3-180). Two 5–10 g samples of grass leaves (4–7 mm wide, ~0.2 mm thick) and two samples of grass culms (diameter 0.5–2 mm) were allowed to acclimate in the chamber for 24 h, after which the moisture content was determined by drying at 105°C for 24 h. A series was performed during ‘drying conditions’ (i.e. from wet to consecutively drier for each equilibrium condition) at six temperatures ranging 8–26.7°C, with RH ranging 20–90%. Additionally, EMC during ‘wetting conditions’ was determined at four temperatures ranging 8–26.7°C, again with RH ranging 20–90%. The results were compared with that of the GFMC model (Wotton 2009), which upon drying is defined as:
where Tg = T + 35.07 × I × e−0.2237×w is the radiation-corrected fuel temperature (I is the global irradiance – kW m−2; W is the 10-m wind speed – m s−1) and is the fuel-level relative humidity. Eqn 5 was thereafter modified to fit the experimental results by adjusting the parameters in the dominating first term and the temperature-correcting last term (four parameters that are bold in Eqn 5), as well as the corresponding parameters in the equation for wetting conditions.
Results
Extent of the grassfire season
In all regions, grassfires were concentrated to the spring season, typically with about two-thirds of the incidents occurring within a 4–6 week period. The peak occurred ~4 weeks earlier in the southernmost regions than in the north (Fig. 2).
The parameters of Eqns 1–4 that yielded the best fit to demarcate the end of the grassfire season in the combined 250 time series (regions × years) gave Nav = 4 days, Tb = 2°C, N = 60 days, Nshift = 20 days, such that the equation for calculating the seasonal progression, where GDD(d) = 100 denote the end of the season, is:
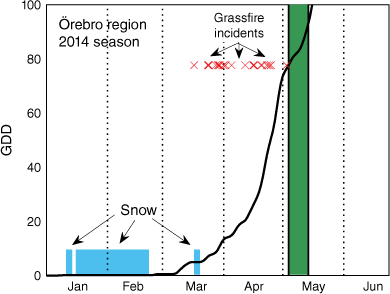
An example of the GDD development, grassfire occurrences and assumed end-of-season interval in 1 year in a south-central region of Sweden is shown in Fig. 3. Further examples are given by Sjöström et al. (2021).
Example of the progression of growing degree-days (GDD, solid line) over a season, Örebro region in 2014. X marks days with registered grassfires. The blue zones denote days with snow cover. The green shaded area represents the period during which the potential grassfire season is estimated to have ended (in this example the GDD reached 100 two days after the end-of-season interval).
Experimental burns and fuel conditions
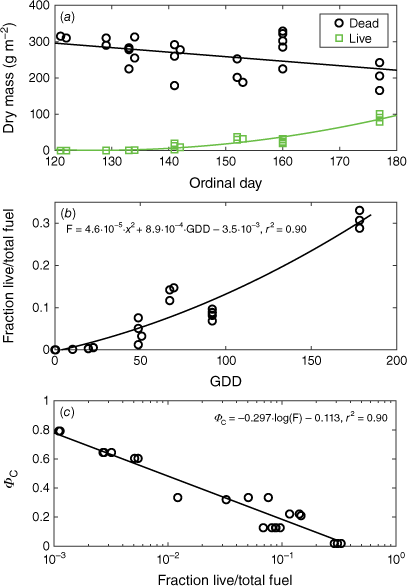
The fuel dry mass in the experiment area ranged 200–350 g m−2. The litter depth was rather constant, irrespective of total fuel mass, averaging 9.4 cm (range 8–13 cm). The dry mass of dead fuel exhibited only a weak decreasing trend over the 50-day sampling period and the in-growth of green grass increased slowly to begin with (Fig. 4a). Still, on 1 June (ordinal day 152), the green dry mass was just 10% of the dead, but by then the green grass was clearly visible over the litter. Even by the end of June, when the ‘effective’ grassfire season was well passed, the green grass dry mass was only 30% of the total dry mass, but by then the whole field appeared green, with about 30 cm tall grass.
(a) Dry mass of dead and live fuel sampled at 11 days during the campaign (n = 24). (b) Fraction of live to total dry fuel mass against growing degree-days (GDD) at the location of the test burns. (c) ΦC – the impeding effect of green grass (see Eqn 10) plotted against the fraction of live dry to dead dry fuel mass.
In all, 56 burn tests were done, during 28 days between 4 May and 25 June. No tests were done during rainy days or days with very high relative air humidity.
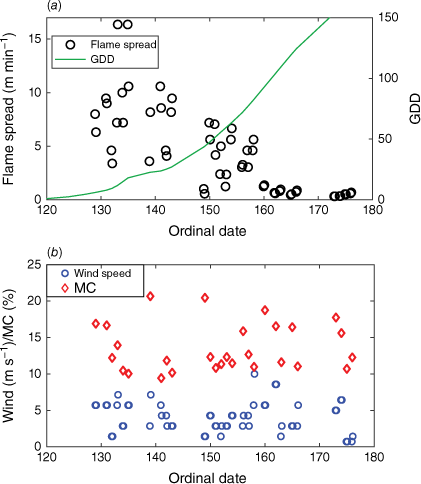
Ambient conditions varied considerably across test days, as did MC of the grass litter (Fig. 5). Due to this, ROS varied substantially from day to day, but there was also a dramatic general decrease in ROS over the period (Fig. 5). In the early part of the season, ROS was >15 m min−1 on good days. Towards the end of the test period, in late June, ROS did not exceed 1 m min−1 even when ambient conditions were beneficial, such as on day 166, when MC of the upper fuel bed was 11% and wind speed 5.7 m s−1 (Fig. 5).
(a) Results of the 56 experimental fires conducted 9 May to 25 June. Rate of spread (open symbols) was observed on 3 × 3 m plots. Progression of growing degree-days (GDD, green line, scale to the right) was calculated from Eqn 6, using reanalysed, gridded weather data. (b) 10-m wind speed (blue rings) and MC in the upper layer of the matted grass litter (red diamonds), both measured at the time of burning.
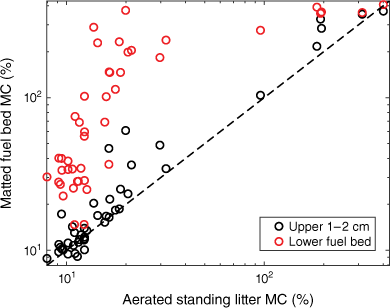
At the test site, the moisture content of the upper 1–2 cm of the snow-matted litter fuel bed was, in most cases, close to that of the loose, well aerated standing grass litter, whereas the lower section of the fuel bed often was considerably moister, sometimes by a factor 5–10 (Fig. 6). The maximum MC observed was about 400%, measured directly after rain. The critical moisture level to achieve successful ignition with sustained flaming after 5 s exposure to a small burner was <21%.
Moisture content of the two layers of the matted grass litter fuel bed relative to the moisture content of the non-compacted, standing grass litter.
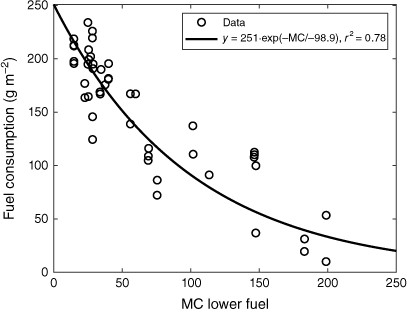
Even on days when the MC of the lower section of the fuel bed was considerably above moisture of extinction per se, parts of it was nevertheless consumed, due to the active flames above. When MC in the lower section of the fuel bed was as low as 15–30%, fuel consumption was between 200 and 250 g m−2, i.e. essentially complete (Fig. 7). With increasing MC in the lower section of the fuel bed, consumption decreased asymptotically. At MC in the lower fuel bed around 200%, only the top ~2 cm of the matted fuel bed was consumed, amounting to less than 50 g m−2 (Fig. 7).
EMC of grass litter
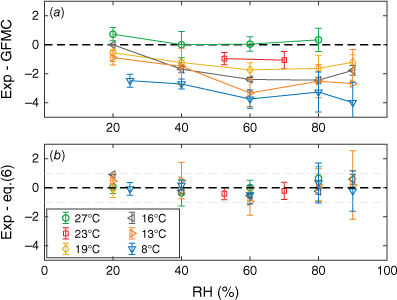
Both types of grass litter (leaves and stems) reached the same MC throughout all combinations of T and RH. At 26.7°C, our EMC observations reproduced (within 1%) the EMC assumed in the GFMC model (Wotton 2009). With decreasing temperature, however, the deviation from the GFMC prediction increased and at 8°C our EMC observations were 2.5–4% lower (Fig. 8a). A four-parameter fit of Eqn 5 to the measured values yields:
where subscripts D and W denote drying and wetting conditions, respectively, taking into account the hysteresis, depending on direction of MC change. The exponent in the last term of Eqn 5 was fitted to values so high that the last parenthesis can be omitted. After the fit, the model and experimental data agree within ±1% (Fig. 8).
(a) Difference between the experimental Equilibrium Moisture Content (EMC) results and EMC as given in the original Grass Fuel Moisture Code (GFMC) model (Wotton 2009). (b) Difference between experimental EMC and the updated, fitted model (Eqn 7). Bars indicate range. All data points shown here are from measurements in direction of drying.
Impeding effect of in-growth of green grass
To account for the effect of wind and fuel MC on ROS, we employed the model used by Cheney et al. (1998), based on a large set of experimental fires in grass fuel beds (with a mean fuel load of 350 g m−2). The rate of spread in completely cured and dry grass, RW (m min−1), depends on 10-m open wind speed (m s−1) as:
Note that the units are here changed compared with the original units in Cheney et al. (1998). The effect of dead fuel moisture content, expressed a factor acting on RW, is described by:
To isolate the effect of green grass in-growth on ROS, we divided the experimentally obtained ROS with the RW and ΦMC calculated from the wind and MC of the upper layer of the matted fuel at the time of each test. Thus, we assume that the effects of moisture and wind scale equivalently for our 3-m wide experimental fires as for infinitely wide fires and rescale the data for this size effect such that the normalised ROS equals unity for GDD = 0.
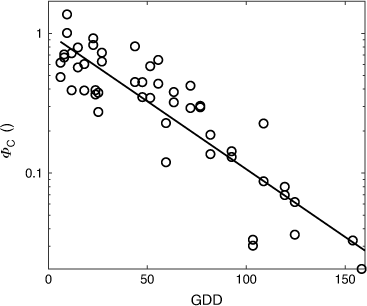
The rescaled ROS, plotted on a logarithmic axis, appear linear against GDD (Fig. 9) suggesting the impeding effect of the in-growth of fresh grass as the season progresses can be expressed as an exponentially decreasing function of GDD.
Rescaled rate of spread from the field experiments (see Fig. 5), corrected for the effect of wind and moisture content, plotted against growing degree-days (GDD). An exponential fit to the data gives ΦC = exp(−0.0224 × GDD) and r2 = 0.80.
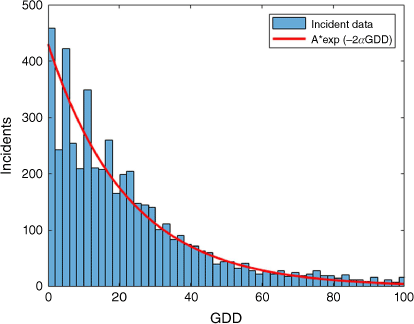
GDD distribution of grassfire incidents
The distribution of rescue service dispatches to grassfires followed an exponential decay function over GDD. The dispatch frequency was significantly reduced even as early in the season as GDD = 10. Actually, dispatch frequency over GDD decayed twice as fast as that determined for ΦC from ROS in the fire experiments (Fig. 10).
Construction of a grassland fire danger index
As a proxy for fire danger, the RING model uses ROS for a fully developed grassfire on flat ungrazed/uncut land. Because the fuel loads of typical cool-season grass in northern Europe often fall in the range 0.2–0.4 kg m−2 (own observations), we chose to define a model system of 0.3 kg m−2 ungrazed, matted grass litter, and with the proportion of new live grass determined by GDD.
Because matted litter depth does not vary substantially (own observations), any potential effect of fuel height on ROS (see discussion in Moinuddin et al. (2018), Cruz et al. (2021), Sutherland et al. (2021)) can be disregarded. Following Cheney et al. (1998), the spread rate is therefore calculated as a product of the three most contributing factors – wind, moisture content of the upper layer of matted litter and ‘curing degree’:
The three factors are given by Eqns 8–10, respectively. Most fine fuels do not allow fire spread at moisture contents above 23%, and Eqn 11 terminates spread at MC = 20% for low wind speeds and 24% for higher wind speeds.
Among the various existing models for MC in grass litter, GFMC (Wotton 2009) includes solar radiation and is operationally simple; it was therefore chosen for modelling MC in the top layer of matted grass. However, based on our tests of equilibrium MC of grass litter, we altered the EMC of the GFMC model according to Eqn 7. Additionally, our field sampling indicated a saturation MC for matted grass litter at 400%. Thus, the fuel moisture sub-model was bounded by 400% instead of 250%, as stated in the original GFMC model.
The complete model therefore delivers hourly ROS for a fully developed grassfire as influenced by weather history, current weather and degree of in-growth of new grass. The equations for the full model are given in the appendix.
Using Eqns 8–10, we also calculated the expected ROS for an infinitely wide and fully developed fire for the conditions in each experimental fire (Fig. 11). GDD was here calculated based on daily weather observations from the nearest weather station, situated ~20 km from the test site, while MC and wind was taken from measurements at the site. The estimated ROS for wide fires correlated well with the observed rates from the 3 × 3 m experimental plots (Fig. 11), but they were a factor 2.6 times higher, with a root-mean-square error of 7.1 m min−1.
The modelled Rate Of Spread (ROS) using weather data from the experimental fires, plotted against the actual measured ROS. The red symbols are from two independent sets of experimental grassfires, using plot widths of 3 and 7 m respectively (+Salsviken 10 March 2022; ▽Hunnebostrand 24 March 2022).
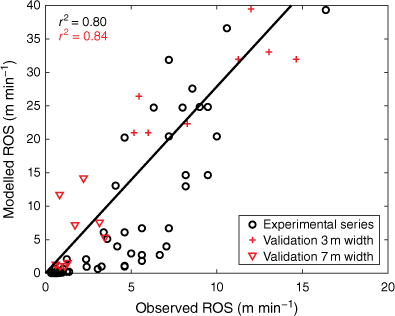
For a partial validation of the model, the same calculations were also done for ROS data from independent sets of experimental fires at two other sites, measured on plots of 3 × 3 m and 7 x 7 m, respectively. ROS was modelled based on site measurements of W and MC, whereas GDD (and thus ΦC) was calculated based on weather data from the national weather service (Fig. 11).
To achieve a relevant danger rating to issue publicly, we divided the continuous ROS scale into four levels (Table 3), on the assumption that ROS is the critical factor for grassfire danger. To test how these levels relate to grassfire occurrence, we recalculated ROS values for the whole of Sweden in a grid of 2.5 by 2.5 km, with 1 h resolution, for the 3 years 2019–2021. We then matched 633 grassfire dispatches that occurred during these years with the local ROS value at the time of the alarm. The proportion of grassfires that had occurred within each of the three highest danger level was relatively even (Table 3). Normalising grassfire occurrence by the number of times that the same danger level had occurred within the country showed that the probability of having a grassfire increased monotonically with increasing danger level (Table 2).
| Danger level | ROS (m min−1) | Portion of grassfire dispatches (%) | Portion of hourly observations (%) | Grassfire dispatches per hourly observationA | |
|---|---|---|---|---|---|
| Low | ROS ≤ 5 | 9 | 34 | 1.1 × 10−4 | |
| Moderate | 5 < ROS ≤ 15 | 31 | 28 | 4.4 × 10−4 | |
| High | 15 < ROS ≤ 25 | 32 | 22 | 5.8 × 10−4 | |
| Very high | ROS ≥ 25 | 28 | 15 | 7.3 × 10−4 |
AThe number of dispatches for each danger level divided with the number of observations during 2019–2021 that this level was observed based on recalculated, interpolated weather data. Observations that included snow or Rate of Spread (ROS) ≤0.1 m min−1 were excluded.
Discussion
Extent of the grassfire season
The wildfire dispatch data show that there is a defined grassfire season in Sweden, bounded at both ends but gradually shifting to later dates with increasing latitude. In most parts of the country, the main factor controlling the start of the season should be the duration of the snowpack. However, in the southernmost regions (e.g. Skåne), winters can be essentially snow-free, but grassfires were nevertheless rare until mid-March. The controlling factors in the winter months during snow-free periods are most likely the short days, low sun angle and high RH (Wern 2013), resulting in poor fire weather (cf. Fig. A1). The end of the season, on the other hand, is defined in all parts of the country by the gradual in-growth of fresh grass. Both southern and northern regions had the same end-of-season with respect to GDD, but the development of GDD is of course much delayed in the north, due primarily to the progressively later snow melt. Thus, the start of the season is defined by weather and the end by phenological changes in the fuel bed. This results in a grassfire season lasting roughly 6 weeks in the south and 4 weeks in the north.
Fuel bed structure and moisture relations
Moisture in grass litter adjusts quickly to the surrounding weather (Wotton 2009), but a saturating rain will naturally have an impact on fuel MC during the following hours. The litter from our fire experiments held a maximum of 400% water directly after rain. A fuel load of 0.3 kg m−2 is in line with other northern grasslands, for example the default fuel load assumed in the Canadian O-1 grass fuel model (Alexander et al. 1992). For 0.3 kg m−2, the fuel is saturated by only 1.2 mm of precipitation. Thus, precipitation ‘memory’ is not nearly as long as for most forest fuels (Van Wagner 1977), particularly because fire propagation in these fuel beds was possible even if only the upper ~2 cm was dry enough to burn.
Judging from the parallel MC sampling of different fuel strata (Fig. 6), the top 1–2 cm of the matted grass adjusted as rapidly as well-aerated standing grass to ambient weather conditions. The lower-lying part of the litter on the other hand, lagged considerably, leading to an interesting relationship between MC of the lower fuel layer and total fuel consumption. ROS might not be highly sensitive to total amount of available fuel (Cruz et al. 2018), but intensity will be, and therefore also the capacity to bridge fuel breaks (Wilson 1988). Another factor is that it is much easier to extinguish a grassfire, for example by swatting, when the lower part of the fuel bed is moist (own observation).
Matted vs standing litter
The fire experiments were conducted on snow-matted grass fuel, which would be representative for springtime conditions in most of Sweden, and boreal/hemiboreal regions generally. The dynamics of packing of grass litter fuel by snow is presently unknown, but 80% of Sweden has at least 60 days of snow cover in excess of 10 cm and an average maximum depth of ~50 cm (Wern 2015), which likely is enough to flatten the litter. However, more or less snow-free winters are common in the southernmost part of the country, resulting in less compact grass litter. Intuitively, less compaction would lead to faster drying of the entire fuel bed, with subsequent higher fuel consumption under marginal danger levels. Likewise, there might be effects on ROS (Taylor et al. 1997).
Effect of in-growth of green grass
The fire experiments show that the in-growth of green grass in spring starts to affect ROS very early in the process. The damping effect of the live component on ROS in our experiments was in fact more pronounced than for senescing Australian grasslands (Cruz et al. 2015). Already at 1% inclusion of green grass (dry mass basis), the damping effect on ROS was surprisingly large, about 50%. However, because fresh green grass usually contains at least 250% water (data not shown), a contribution of 2.5%-units of water is added to the fuel MC for each percentage of green grass. Theoretically, if the litter component is at 10% MC, green grass amounting to only 4% (dry mass) would be enough to lift the MC of the entire fuel bed to the moisture of extinction (~20%), provided it acts as one unit. This might be close to the true situation in early season, when the tender grass leaves first penetrate the matted litter and both components are intimately mixed. The water in the leaves should then be released to a large degree in the flame zone and thus directly affect combustion efficiency.
Later, the live fuel component becomes increasingly spatially separated from the dead, as the grass grows tall, and thus the damping effect per unit water should decrease. This may explain how fire propagation was at all possible towards the end of the experimental burn campaign. By then, the green grass (dry mass) accounted for around 30% of the total mass. The MC of the entire fuel bed combined would have been ~80%, i.e. well above the MC limit that allows for any fire propagation in senescing, curing grass (Cheney et al. 1998). Nonetheless, marginal fire spread occurred, but the flames were only ~10 cm long, produced a considerable amount of white smoke and would be very easy to extinguish, even on dry and windy days. The reason fire can propagate at all under such conditions is likely the physical separation of most of the moist green foliage from the litter below, where the actual combustion happens.
Rescue service dispatches vs GDD
Dispatch occurrence decreased exponentially with GDD, with an exponent twice that of the GDD effect on ROS. Note that the dispatch data does not include all occurring grassfires; ignitions that have low ROS are likely to be rapidly controlled by people nearby and thus do not lead to an alarm call and subsequent dispatch. We tentatively assume that dispatch probability is the product of (1) the likelihood of a fire igniting (and burning the fuel with sustained flaming) and (2) the likelihood that the rate of spread is too large for people on site to control it: Pdispatch = Pign × Pescape. A first order approximation is that both Pign and Pescape scale equivalently with the in-growth of green grass, as does ROS (Eqn 10). The dispatch frequency would therefore scale as Pdispatch ~ e−2α×GDD, where α = 0.0224 (derived from the fire experiments).
We believe that ROS is a highly relevant measure for grassfire danger warning, more so than it would be for forest fire danger warning, where intensity is often paramount, for example as expressed in the FWI-index of the Canadian forest fire danger system. It is the rapid spread of grassfires, often severely underestimated by the public (Sjöström and Granström 2023), and their fast response to wind gusts, that lead them to spread out of control, resulting in rescue service dispatches as well as damaged property and injured people.
Conclusions
The RING grassfire danger index is likely applicable to all northern regions where grass cures completely during winter and new growth emerges gradually through spring and early summer. Local calibration of GDD might be needed, particularly for snow-poor areas. Our fire data were from rather small experimental plots, scaled up according to established rules. Additional data from larger experimental plots would make the scaling of fire dimensions more reliable and thus increase the precision of the model, should actual ROS estimates be required, for example in prescribed burning operations. However, a relative ROS index is adequate for most situations (e.g. for danger rating to the general public). Further, our experimental data were from non-manipulated fuel beds only and it would be of interest to obtain data also from grazed or harvested grasslands in order to evaluate the effect of such measures for risk reduction. It is probable that the ROS-decrease with GDD will be even faster for treated areas, due to the decreasing proportion of dead to live grass.
Acknowledgements
The authors are grateful to Linda Berglund, Erik Hellberg Meschaks and Hasan Sokoti for assisting in field and lab work.
References
Brandt M, Eklund A, Westman Y (1999) ‘Snö I Sverige, Snödjup och vatteninnehåll i snön’ [Snow in Sweden, depth and water content in the snow], SMHI – Fakta nr 2:1999. Available at https://www.smhi.se/polopoly_fs/1.6338!/snofakta% 5B1% 5D.pdf [In Swedish]
Cheney NP, Gould JS (1995) Fire growth in grassland fuels. International Journal of Wildland Fire 5, 237-247.
| Crossref | Google Scholar |
Cheney NP, Gould JS, Catchpole WR (1998) Prediction of fire spread in grasslands. International Journal of Wildland Fire 8, 1-13.
| Crossref | Google Scholar |
Cruz MG, Gould JS, Kidnie S, Bessell R, Nichols D, Slijepcevic A (2015) Effects of curing on grassfires: II. Effect of grass senescence on the rate of fire spread. International Journal of Wildland Fire 24, 838-848.
| Crossref | Google Scholar |
Cruz MG, Kidnie S, Matthews S, Hurley RJ, Slijepcevic A, Nichols D, Gould JS (2016) Evaluation of the predictive capacity of dead fuel moisture models for Eastern Australia grasslands. International Journal of Wildland Fire 25, 995-1001.
| Crossref | Google Scholar |
Cruz MG, Sullivan AL, Gould JS, Hurley RJ, Plucinski MP (2018) Got to burn to learn: the effect of fuel load on grassland fire behaviour and its management implications. International Journal of Wildland Fire 27, 727-741.
| Crossref | Google Scholar |
Cruz MG, Sullivan AL, Gould JS (2021) The effect of fuel bed height in grass fire spread: addressing the findings and recommendations of Moinuddin et al. (2018). International Journal of Wildland Fire 30, 215-220.
| Crossref | Google Scholar |
Cruz MG, Alexander ME, Kilinc M (2022) Wildfire Rates of Spread in Grasslands under Critical Burning Conditions. Fire 5, 55.
| Crossref | Google Scholar |
Fovell RG, Brewer MJ, Garmong RJ (2022) The December 2021 Marshall Fire: Predictability and Gust Forecasts from Operational Models. Atmosphere 13, 765.
| Crossref | Google Scholar |
Jin H, Jönsson AM, Olsson C, Lindström J, Jönsson P, Eklundh L (2019) New satellite-based estimates show significant trends in spring phenology and complex sensitivities to temperature and precipitation at northern European latitudes. International Journal of Biometeorology 63, 763-775.
| Crossref | Google Scholar |
Kidnie S, Cruz MG, Gould J, Nichols D, Anderson W, Bessell R (2015) Effects of curing on grassfires: I. Fuel dynamics in a senescing grassland. International Journal of Wildland Fire 24, 828-837.
| Crossref | Google Scholar |
Krueger ES, Levi MR, Achieng KO, Bolten JD, Carlson JD, Coops NC, Holden ZA, Magi BI, Rigden AJ, Ochsner TE (2023) Using soil moisture information to better understand and predict wildfire danger: a review of recent developments and outstanding questions. International Journal of Wildland Fire 32, 111-132.
| Crossref | Google Scholar |
Landström S (1990) Influence of soil frost and air temperature in spring growth of Timothy in Northern Sweden. Swedish Journal of Agricultural Research 20, 147-152.
| Google Scholar |
Leys BA, Marlon JR, Umbanhowar C, Vannière B (2018) Global fire history of grassland biomes. Ecology and Evolution 8, 8831-8852.
| Crossref | Google Scholar |
Matthews S (2006) A process-based model of fine fuel moisture. International Journal of Wildland Fire 15, 155-168.
| Crossref | Google Scholar |
Miller EA (2018) Moisture sorption models for fuel beds of standing dead grass in Alaska. Fire 2, 2.
| Crossref | Google Scholar |
Moinuddin KAM, Sutherland D, Mell W (2018) Simulation study of grass fire using a physics-based model: striving towards numerical rigour and the effect of grass height on the rate of spread. International Journal of Wildland Fire 27, 800-814.
| Crossref | Google Scholar |
Mouillot F, Field CB (2005) Fire history and the global carbon budget: a 1° × 1° fire history reconstruction for the 20th century. Global Change Biology 11, 398-420.
| Crossref | Google Scholar |
Nilsson D, Hansson P-A (2001) Influence of various machinery combinations, fuel proportions and storage capacities on costs for co-handling of straw and reed canary grass to district heating plants. Biomass and Bioenergy 20, 247-60.
| Crossref | Google Scholar |
Noble IR, Gill AM, Bary GAV (1980) McArthur’s fire-danger meters expressed as equations. Australian Journal of Ecology 5, 201-203.
| Crossref | Google Scholar |
Prentice IC, Cramer W, Harrison SP, Leemans R, Monserud RA, Solomon AM (1992) Special Paper: A Global Biome Model Based on Plant Physiology and Dominance, Soil Properties and Climate. Journal of Biogeography 19, 117-134.
| Crossref | Google Scholar |
Prishchepov AV, Schierhorn F, Löw F (2021) Unraveling the diversity of trajectories and drivers of global agricultural land abandonment. Land 10, 97.
| Crossref | Google Scholar |
Sjöström J, Granström A (2023) Human activity and demographics drive the fire regime in a highly developed European boreal region. Fire Safety Journal 136, 103743.
| Crossref | Google Scholar |
SMHI (2022) ‘Snödjup’ [Snow depth]. Available at https://www.smhi.se/en/weather/observations/snow-depth/ [visited 29 July 2022]
Sutherland D, Sharples JJ, Mell W, Moinuddin KAM (2021) A response to comments of Cruz et al. on: ‘Simulation study of grass fire using a physics-based model: striving towards numerical rigour and the effect of grass height on the rate of spread’. International Journal of Wildland Fire 30, 221-223.
| Crossref | Google Scholar |
Wern L (2013) ‘Luftfuktighet: Variationer i Sverige’. [Humidity: Variations in Sweden]. METEOROLOGI Nr. 154. (Swedish Meteorological and Hydrological Institute: Norrköping, Sweden). urn:nbn:se:smhi:diva-2790
Wilson AAG (1988) Width of firebreak that is necessary to stop grass fires: some field experiments. Canadian Journal of Forest Research 18, 682-687.
| Crossref | Google Scholar |
Appendix 1
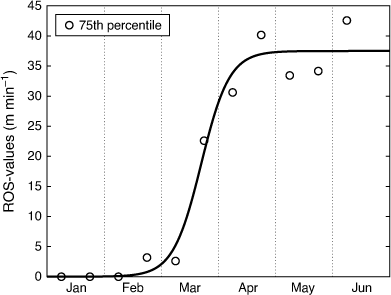
To get a rough indication of fire weather in the winter months for southern areas in Sweden that frequently lack snow cover, we calculated ROS values for the southernmost region of Skåne (cf. Fig. 2) for the period January–June, based on weather only, thus excluding the influence of green grass (i.e. according to Eqn 11 assuming Φc = 1). The data spans the three seasons of 2019–2121 (1 January–15 June), between 0800 and 2000 hours UTC on a 2.4 km square grid, using interpolated reanalysed weather observation (Mesan) data. The fire weather, exemplified by 75th percentiles of ROS for each 2-week period, was very poor until the beginning of March (Fig. A1). This would limit the occurrence of grassfires in the winter months, despite the often snow-free conditions in this southern region.
Appendix 2
Equations for calculating the fire danger index of the RING model, estimating ROS for northern uncut grasslands.
From 1 January, calculate the GDD (Tair is the 24 h average of air temperature, i is the ordinal day):
For each time step (hour), calculate the EMC
For each time step (hour), calculate the moisture content MC (P, Precipitation during last time step (mm); T, air temperature (°C); I, irradiance1 (kW m−2); W, 10 m open wind speed (m s−1); δ, length of time step (h))
For each time step, calculate the spread rate (ROS) (m min−1)
Set the grassfire danger rating based on estimated ROS values
Footnotes
1 Irradiance for the Nordic countries is calculated using a mesoscale model for solar radiation labelled STRÅNG. For more information visit https://strang.smhi.se/