Effect of flame zone depth on the correlation of flame length with fireline intensity
Mark A. Finney A * and Torben P. Grumstrup AA USDA Forest Service, Missoula Fire Sciences Laboratory, Missoula, MT 59808, USA. Email: tpg@lanl.gov
International Journal of Wildland Fire 32(7) 1135-1147 https://doi.org/10.1071/WF22096
Submitted: 26 September 2022 Accepted: 7 April 2023 Published: 27 April 2023
© 2023 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of IAWF. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Background: Previously established correlations of flame length L with fireline intensity IB are based on theory and data which showed that flame zone depth D of a line fire could be neglected if L was much greater than D.
Aims: We evaluated this correlation for wildland fires where D is typically a non-negligible proportion of L (i.e. roughly L/D < ~2).
Methods: Experiments were conducted to measure flame length L from line-source fires using a gas burner where IB and D were controlled independently (0.014 ≤ L/D ≤ 13.6).
Key results: The resulting correlation showed D significantly reduced L for a given IB over the entire range of observations and was in accord with independent data from spreading fires. Flame length is reduced because the horizontal extent of deep flame zones entrains more air for combustion than assumed by theory involving only the vertical flame profile.
Conclusions: Analysis suggested that the noted variability among published correlations of L with IB may be partly explained by varying L/D ratios typical of wildland fires.
Implications: Fire behaviour modelling that relies on correlations of L with IB for scaling of heat transfer processes would likely benefit by including the effects of D.
Keywords: backing, fireline intensity, flame length, flame zone depth, heading, line fires, Byram’s intensity.
Introduction
Correlations of flame height or length L (m) with Byram’s fireline intensity IB (kW m−1) of wildland fires (Byram 1959; Thomas 1963) are used for modelling heat transfer by radiation (for determining view factor and emissivity) and convection (for determining gas flow velocity and temperature profiles). They also have practical utility for wildland firefighters who rely on L as a visual proxy for intensity as it relates to safety and suppressibility of fires. The flame length L rather than height will be referred to here because it more generally applies to flame dimensions tilted by wind or slope, and because the effects of wind on flame length have been shown to be relatively minor (Thomas et al. 1963).
The many empirical studies of linear fire sources (see review by Alexander and Cruz 2012, 2021) have shown L to be a power function of fireline intensity IB. For example, Byram’s widely used correlation for flame length is (Byram 1959):

The coefficient and exponent among line fire correlations vary considerably for wildland fires, leading some to suspect the L–IB relationships cannot be compared among fuel types, for example grass vs shrubland (Alexander 1982; Alexander and Cruz 2012). Differences have also been attributed to the difficulty with obtaining consistent and precise measurements of fluctuating flame length (Zukoski et al. 1985; Newman and Wieczorek 2004). Importantly, some of the variation in IB derives from how it is estimated based on Byram’s (1959) formula (IB = Hm″R) for spreading fires because of uncertainty in heat yield of the fuel (H, kJ kg−1), overestimation of fuel mass consumed in flaming per unit area (m″, kg m−2), and sometimes unsteady spread rate R (m s−1). Here, we follow Byram (1959) to define the heat yield of a fuel as the total energy per unit mass of fuel released from complete combustion (i.e. heat of combustion or higher heating value) minus the combined losses of energy transferred to the environment through thermal radiation, energy for the vaporisation of water, and incomplete combustion (see also Van Wagner 1972).
Underlying the many empirical correlations, a theory of how L relates to IB for line source fires was originally developed from dimensional analysis by Thomas (1960, 1963), Thomas et al. (1961, 1963), and Steward (1964) (see eqn 4ii in Thomas 1963):

where D is the flame zone depth measured as the short direction of a rectangular flame source or parallel to the fire spread direction, Q′ is the volumetric flow rate of gaseous fuel per unit flame zone width (m3 s−1 m−1), and g (m s−2) is gravitational acceleration. Eqn 2 can be written in terms of fireline intensity using Q′=IB(ρH)−1, in which case:
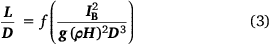
With further arguments based on entrainment, Thomas showed that if L/D was large, the functional form of Eqn 3 above can be specified as (see section entitled ‘Air Entrainment’ and eqn 11 in Thomas 1963):
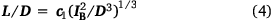
where  is an empirically determined coefficient into which the constant quantities in Eqn 3 are absorbed. Notice D cancels from Eqn 4, leading to:
is an empirically determined coefficient into which the constant quantities in Eqn 3 are absorbed. Notice D cancels from Eqn 4, leading to:

which is Thomas’ well known flame length correlation. Thomas (1963) determined the coefficient in Eqn 5 by fitting the equation to experimental flame length data.1 The absence of D in Eqn 5, along with the goodness-of-fit with experimental data, led Thomas (1963) to reason that effects of D would become negligible when flames were much longer than the flame zone was deep. This conclusion provided theoretical and experimental support for formulating flame length correlations of the form 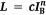 .
.
Nonetheless, the significant variation among coefficients and exponents among many studies suggests some aspect of the governing physics could be missing. This paper describes an experiment to address this shortcoming by testing the apparent theoretical and experimental support that L is independent of D for a range of fireline intensities and flame zone dimensions. We employed a laboratory sand-burner apparatus that allows precise, independent control of fireline intensity IB and flame zone depth D from a horizontal fuel source.
Methods
This paper reports on experiments conducted on a stationary, propane-fuelled sand burner in an enclosed laboratory. We examine the results in the context of earlier flame length work by Thomas and others and compare with measurements from spreading laboratory fires obtained from prior unrelated studies. The sand burner enabled repeated measurements for an arbitrary length of time, leading to measurement accuracy that would be impossible to achieve on spreading or stationary fires with solid fuels, whether in the laboratory or field. Although the physical processes of solid fuel combustion were absent in a stationary gas burner, the fluid flow, heat transfer processes, and chemical kinetics that lead to observed flame lengths were the same. Propane, along with many other hydrocarbon fuels, burns in non-premixed flaming combustion (diffusion flames) in the same temperature range as gaseous pyrolysates in wildland fires, so it has similar buoyancy. Propane and other hydrocarbon fuel types have different heat contents, stoichiometric air-fuel mixture ratios, and perhaps radiation loss fractions compared with wildland fuels, but compensating effects of each term result in minor variations in flame length compared with the shape, size, and burning rate of the fuel source (Heskestad 1983; Quintiere and Grove 1998).
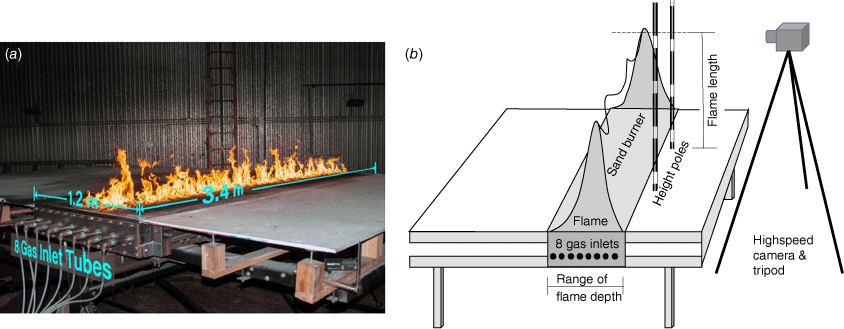
A propane-fuelled sand burner was constructed at the US Forest Service, Missoula Fire Sciences Laboratory for the purpose of studying flame structure and heat transfer from stationary flame zones (Fig. 1). This sand burner is similar to the one described by Finney et al. (2022) but double the size, having rectangular dimensions of the burner box of 1.22 m × 3.66 m. The sand box was 0.15 m deep with eight perforated tubes running the long axis (3.66 m) along the inside bottom surface under the sand. Sheet metal partitions were sealed with the bottom of the sand box between each burner tube to limit gas diffusion to the 15 cm surrounding each tube. The burner box was mounted on a tilting platform 3.66 × 7.3 m in size, with 4.8 m uphill decking made of flame-resistant Super Fire Temp®2 board 2.54 cm thick (Johns Manville Corporation, Denver, Colorado, USA, http://jm.com). The downhill decking was 1.2 m (Fig. 1) in length. Each tube was controlled separately for gas flowing from a common manifold so that any combination of tubes could be fired with a controlled flowrate of propane. Gas flow was regulated by an Alicat® mass flow controller2 (Alicat Scientific, Tucson, Arizona, USA, http://alicat.com) capable of flowing up to 1500 standard litres per minute (SLPM) with a stated precision of ±SLPM (meaning 0.42 kW m−1 for our burner). We selected propane flowrates of 300, 600, 900, 1200, and 1500 SLPM for the experiment. Heat release rate (in watts) of the propane flames was determined by multiplying the propane flowrate (in standard litres per minute) by the proportion, 1533 W (SLPM)−1. For example, 600 SLPM propane corresponds to a heat release rate of 600 × 1533 = 919.8 × 103 W. The conversion factor was calculated by multiplying the density of propane at standard temperature and pressure (1.984 kg m−3) and the lower heating value of propane (46.357 × 106 J kg−1), and then dividing by both the number of litres in a cubic meter (1000 L m−3) and the number of seconds in a minute (60 s min−1). Thus, (1.984) (46.357 × 106) (1000 × 60)−1 = 1533 W (SLPM)−1.
These experiments were conducted with the platform oriented horizontally so that length of diffusion flames could be imaged in the pure vertical dimension. Flames from the sand burner were considered buoyancy dominated because the vertical velocity of the propane issuing from the burner surface is very small. To measure flame height, two vertical graduated poles were placed at the foreground edge of the long dimension of the burner in full view of a high-speed camera (Figs 1b, 2). We chose to video the long dimension of the burner because it could more directly incorporate the spatially variable peak and trough structure of line-source flames (Finney et al. 2015), as well as the non-steady and pulsatile dynamics happening at any given location along a linear flame front (Cetegen et al. 1998). The camera was adjusted to the approximate height of the flames at each setting of propane flowrate, with field of view extending the full 3.66 m width of the burner. This ensured that the camera field of view included the expected flame height. The camera captured 10 s of video at 240 frames per second (fps) for each flow rate at each number of open burner tubes (1–8). The camera exposure time was chosen to minimise motion blur from flame movement in each frame.
Measurement of flame dimensions has never been standardised. Studies have relied upon ocular averages or photographic and video methods (discussed by Alexander and Cruz 2012), but all eventually require decisions as to how to delineate luminous flames and for averaging the time and space variation in extent of flames. Absolute comparisons among studies are difficult because of the subjectivity in estimating flame size, the axis of viewing for line fires (long or short dimension, which changes the viewed thickness of the flame profile), and estimates of fireline intensity as discussed in the introduction. In this study, we endeavour to evaluate how a precise and consistent measure of L changes as a function of experimentally controlled flame zone depth. In our case, video was processed to discriminate flaming from non-flaming in each frame using a cut-off pixel brightness value of 90% (Fig. 2b), which filtered much of the illuminated background and foreground objects, including the steel laboratory walls and the decking on the burner apparatus. Individual binary images were then processed to form a flame presence probability field for each fireline intensity–flame depth combination. Contours of flame presence probability were overlayed on a rasterised height gradient matched to the graduations on the reference poles (Fig. 2c). A visual comparison of the video with the probability image suggested that impressions of sustained flame height across the long axis of the burner coincided well with the 20% probability contour. Thus, an estimate of L for a given combination of IB and D (Fig. 2d) was calculated as the average raster height values from pixels along the 20% contour between the graduated poles to minimise effects on flame length and shape from the lateral edges.
We evaluated the applicability of the flame length–fireline intensity relationship from this gas burner experiment by comparing with data from 100 laboratory fires spreading through laser-cut cardboard fuel beds in wind and on a sloping table (Finney et al. 2013, 2015). The cardboard fuel consists of a ‘comb’ of tines of specified width, separation, and height extending from a common spine normal to the table surface. The spine is embedded in slots in the floor of the burn table, leaving only the tines exposed. The cards can then be installed at any spacing to create exact and repeatable combinations of fuel particle and fuel bed properties (e.g. fuel height, packing ratio, loading).
For these cardboard experiments, fire spread rate was obtained using longitudinal arrays of thermocouples. Flame depth was measured from overhead digital video cameras by counting the rows of cardboard fuel particles burning in the flame zone. These estimates were checked against flame zone depth calculated as the product of measured flame residence time and fire spread rate. Flame length in these studies was estimated ocularly from video cameras and reference height poles or markings on the walls of the wind tunnel. Fireline intensity was calculated from Byram’s equation (IB = Hm″R) using a heat yield of 13 000 kJ kg−1 for combustion of gaseous pyrolysates (Babrauskas 2006) and 6% fuel moisture content, fuel loading with subtraction of 25% of pre-burn fuel mass for solid residual char and mineral ash (Susott et al. 1975; Di Blasi et al. 2001), and measured spread rate.
Results
The gas burner experiment produced flame length data from a total of 40 combinations of total gas flow rates to the burner (i.e. fireline intensity IB) and number of burner tubes (i.e. flame zone depth D) (Table 1). Ratios of L/D ranged from 0.14 to 13.6. For any given fireline intensity in Fig. 3a, the flame length decreased with increasing flame zone depth. These relationships were further examined using Eqn 4. However, where Thomas (1963) specified the 1/3 exponent based on theoretical arguments, our analysis allowed for the possibility it could take other values. Nonlinear regression was applied to the experimental gas burner data (Fig. 3b) to obtain the following fit:
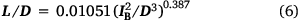
which simplifies to illustrate the non-negligible effect of D on L for the burner flames:
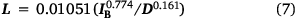
and is illustrated in in Fig. 3c. Standard error for the estimated coefficient was 0.001234 and the exponent 0.006852, and all were significant at P < 0.001. The 95% confidence interval for the exponent excluded the 1/3 value reported by Thomas (1963), indicating Eqn 6 is significantly steeper. The narrow confidence bands produced by the strong fit of the regression were nearly indistinguishable from the trend displayed on Fig. 3b; however, the confidence bands for both the fitted model and the model prediction were plotted on the linear axes in Fig. 3c. Five data points shown in open circles in Fig. 3b, c have L/D < 0.52, which Heskestad (1991) established as a criterion for distinguishing single coherent tall fires from ‘mass fires’ composed of multiple short flames, when intensity over the larger fire source is insufficient to form a single flame plume (Thomas 1967; Zukoski et al. 1985). Similar flame structures are evident on the surface of our gas burner with large flame depths, likely explaining why these points show the greatest departure from the regression line. Although not a factor in our experiments, small flames in the laminar range are also unlikely to abide correlations of the taller turbulent flames (Yuan and Cox 1996; Grove and Quintiere 2002).

|

|
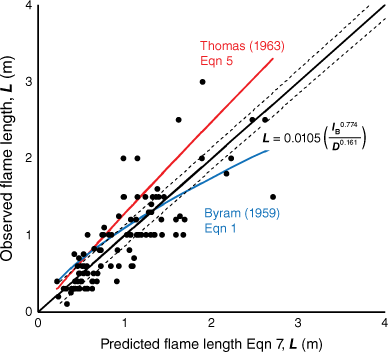
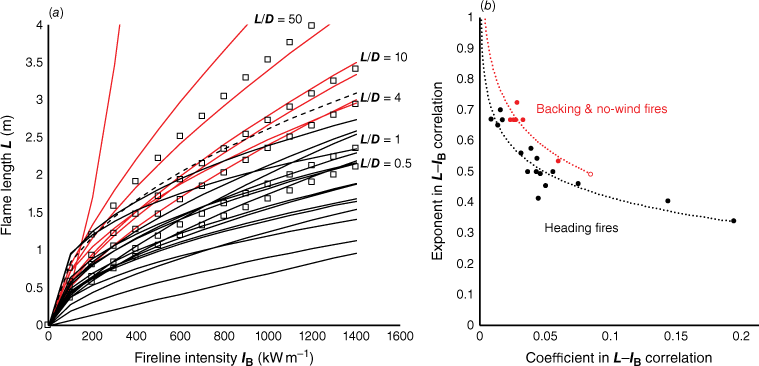
Independent data from spreading laboratory fires (Finney et al. 2013, 2015) showed that when only a function of IB, L was generally overpredicted by Thomas’ (1963) correlation and underpredicted by Byram’s (1959) at higher intensities (Fig. 4). The data trend was well approximated by the correlation from Eqn 7, where L is a function of both IB and D. Over much of the data range, predictions from Eqn 7 are significantly different from the correlations of Byram (1959) and Thomas (1963), as indicated by their exclusion from the 95% confidence intervals.
|
Discussion
The gas burner apparatus allowed precise control over fireline intensity, independent of flame source dimensions, and revealed the important role of D in determining L in these line-source fires. This result contrasts with Thomas’ (1963) data for a similar range (L/D < 7), where the exponent for the fitted correlation in Eqn 4 was found to be 1/3 (Fig. 3b) for L/D > 3 and thus cancelled the influence of D. Steward (1964) also established the theoretical exponent of 1/3 for line fires but experimentally obtained a larger exponent of 0.363 by analysis of a variety of fuel sources for which 2 < L/D < 11. The flame length data assembled by Quintiere and Grove (1998) largely conform to the 1/3 exponent, but only for L/D > 10. Such tall flames with narrow bases are unrealistic for spreading fires in the field and laboratory, suggesting the 1/3 exponent in Eqn 4 is not applicable to flames for which L/D < ~10. Indeed, the following shows that the underlying theory leads one to expect an exponent greater than 1/3 for such fires.
The length of flames is driven by the availability of oxygen for the gas phase chemical reactions of combustion. The familiar yellow–orange flames from wood or hydrocarbon fires are the result of incomplete combustion of the fuel vapour. When insufficient oxygen is present, carbon-rich molecular fuel fragments conglomerate into soot particles, which glow yellow–orange in the intense heat, forming visible flames. When adequate oxygen is available, the fragments are burned to transparent gas. Thus, for a fixed rate of fuel combustion and flame zone size, short flames mean high oxygen availability and long flames mean low oxygen availability.
The process by which oxygen becomes available for combustion in turbulent flames is entrainment. Without wind, ambient air surrounding the flames is drawn into the near field of the buoyant plume. As noted in the Introduction above, Thomas et al. (1961) and Thomas (1963) used an argument pertaining to entrainment to specify the functional form of Eqn 3 as Eqn 4. The argument is briefly summarised here. Dimensional analysis shows non-dimensional flame length for a linear fire source is some function of volumetric fuel flow rate Q′, gravity, and flame zone depth (Thomas 1960; Thomas et al. 1961) as represented by Eqn 2. This can be verified by first noting that the volumetric flow rate of air entrained into flames is the product of the average flow velocity of air entering the vertical flame profile and the surface area of the flame envelope through which entrainment occurs: 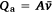 . Because we are concerned with linear fires, we can reformulate the equation to be on a per-unit-flame-zone-width basis:
. Because we are concerned with linear fires, we can reformulate the equation to be on a per-unit-flame-zone-width basis:

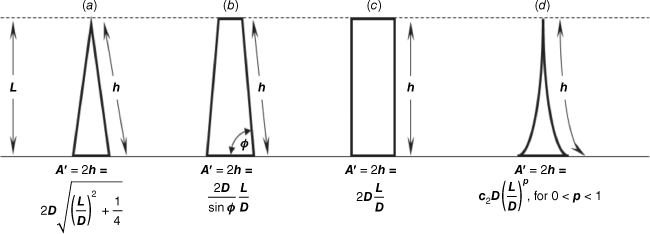
Here, A′ is the surface area of the flame envelope per unit W through which entrainment occurs. Fig. 5a–c shows A′ for three idealised flame envelope cross sections for linear fires of the type considered by Thomas et al. (1961) and Thomas (1963). The formulations for A′ appearing below these sub-figures show A′ is proportional to or on the order of D(L/D). We write D(L/D) instead of simply L to more clearly show how Eqn 8 relates to Eqn 2. Therefore, we can write A′ ∝ D(L/D)p, where p = 1 for the flame geometries in Fig. 5a–c. The exponent p appears here to facilitate the argument following below. Thomas (1963) assumed the total volumetric flow rate of entrainment air into a plume was proportional to the volumetric flow rate of fuel gas leaving the fuel bed (or burner) (i.e. 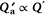 ), and that
), and that 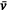 is proportional to characteristic velocity
is proportional to characteristic velocity 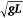 . Similar entrainment assumptions for the vertical flame profile were made by Steward (1964), Nelson (1980), Grove and Quintiere (2002), and Nelson et al. (2012). Applying these assumptions, Eqn 8 can be rewritten and rearranged to obtain the full functional form of Eqn 2:
. Similar entrainment assumptions for the vertical flame profile were made by Steward (1964), Nelson (1980), Grove and Quintiere (2002), and Nelson et al. (2012). Applying these assumptions, Eqn 8 can be rewritten and rearranged to obtain the full functional form of Eqn 2:
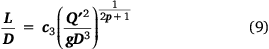
When p is set equal to 1, as in Fig. 5a–c, Eqn 9 is readily converted to Eqn 4 by using the fireline intensity substitution used to derive Eqn 3. Because the exponent is 1/3, D cancels from Eqn 4 to obtain:

which is the general form of Thomas’ (1963) flame length correlation (Eqn 5).
|
Eqn 10 demonstrates that according to the theory presented by Thomas (1963), flame length L is not a function of flame zone depth D when L/D is sufficiently large (thence, p = 1). This being the case, we should expect the flame length data compiled by Quintiere and Grove (1998) to conform to Eqn 5 only when the L/D > ~10, because the flames will exhibit p = 1 geometry. An analogous trend exists for axi-symmetric fires, where L becomes independent of D when L/D > ~3 (Thomas 1963; Heskestad 1983; Zukoski et al. 1985; Grove and Quintiere 2002).
In the absence of wind or slope, line fires with L/D > ~10 have flame profiles that are more acutely pointed and inwardly curved (as in Fig. 5d) due to the horizontal induced flow of entrainment air. Rather than being linearly proportional as before, entrainment area A′ is now some weaker function of L/D. In other words: A′ ∝ D(L/D)p for 0 < p < 1. Even without the curving profile, Thomas et al. (1961) argued that entrainment for short and wide flames should be proportional to p < 1. Consequently, the exponent of Eqn 9 becomes larger than 1/3 and D no longer cancels out as it did to arrive at Eqn 10. Instead, the equation for flame length is in the form of Eqn 7, meaning that for most spreading natural and laboratory fires, flame length for a given fireline intensity is dependent on D.
The inwardly curved shape of the flame profile in Fig. 5d means that A′ is larger than any of the other profiles for the same flame length, violating the assumption that entrainment and gas combustion occur only along the vertical portion of the flame profile (Steward 1964; Nelson 1980; Grove and Quintiere 2002; Nelson et al. 2012). This means that at least theoretically, there is a larger area over which the plume entrains air and a longer horizontal component of distance that flame gases travel during combustion for a given resulting flame height. The diagrams in Fig. 5 are idealised flame profiles, but real fires with wide bases exhibit curving flame zones in two-dimensional profile and in three-dimensions (Fig. 6). Our analysis was strictly derived from fires without wind or slope but Thomas (1963) reported only minor effects on his correlation for wind-deflected flames. The flame zones of spreading fires, whether in wind or with slope, contain three-dimensional concave flow structures (Fig. 6e–g) created by the downwash of ambient air replacing rising flames and from longitudinal vorticity (Finney et al. 2015; Katurji et al. 2021). These induced circulations increase the exposure of flame gases to ambient air within deeper flame zones.

|
Comparisons of the gas burner model (Eqn 7) with laboratory data from wind and slope-driven fires over a similar range of IB, L and D (Finney et al. 2013, 2015) show that the model was applicable to spreading fires (Fig. 4). We do not have independent confirmation of scaling beyond this range of flame lengths or intensities, but for spreading fires, Eqn 7 will generally produce lower estimates of L than Thomas’ (1963) correlation because of the significant influence of D. The deeper flame zones of surface fires may offer some explanation for preferred applicability of Byram’s correlation for heading fires (Albini 1976). Indeed, Thomas (1971) reported that his laboratory-based correlation (Eqn 5) overpredicted flame lengths observed from a variety of burns in grass, gorse, and heather, although he dismissed the influence of D on those discrepancies. Nevertheless, Eqn 5 was adopted for use in crown fires (Rothermel 1991) because Eqn 1 underpredicts tall flames (Byram 1959). Further analysis and data will be required to determine if Eqn 7 from this study applies to both surface and crown fires.
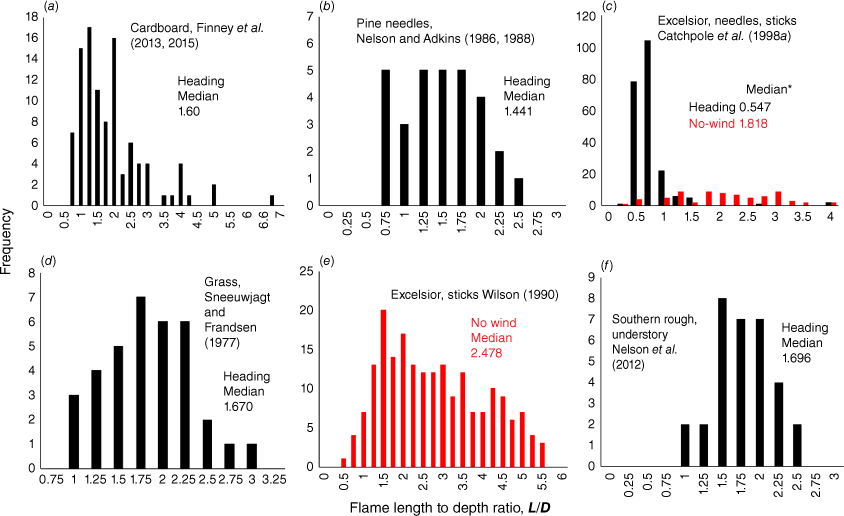
Histograms of L/D ratios from six data sets representing spreading fires in laboratory and field conditions show values of L/D < 2 for a variety of fuel and fire types (Fig. 7). In spreading fires, flame zone depth varies within the same fuel type because the flame zone geometry cannot be controlled independently from spread rate and frontal intensity. The exception occurs for fires backing into the wind (and those without wind on flat ground) that have much narrower D than fires heading with the wind (Beaufait 1965). Data from Catchpole et al. (1998a) show median L/D ratios for laboratory no-wind fires were 1.8 compared with 0.55 for heading fires (Fig. 7c). The no-wind fires of Wilson (1990) show the highest median values (2.478) among all data sets examined (Fig. 7e).
|
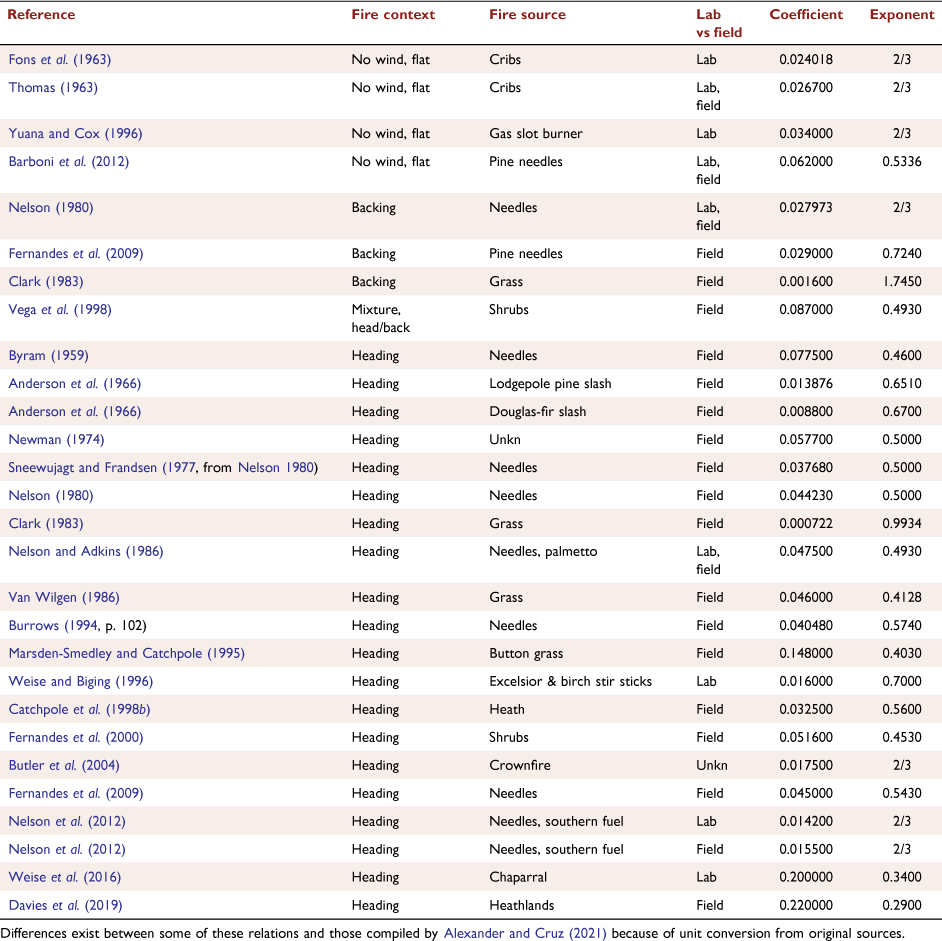
Among 28 published L–IB correlations (Table 2), those for backing and no-wind fires yielded higher flame length for a given intensity than heading fires (Fig. 8a). Three studies reported L–IB relations for backing fires with higher exponents than heading fires (2/3 vs 1/2, Nelson (1980); 0.724 vs 0.543, Fernandes et al. (2009); and 1.75 vs 0.99, Clark (1983)). However, flame length for a given intensity is a non-unique combination of the exponent and coefficient that is illustrated by a plot of these terms for all studies in Table 2 (Fig. 8b). Backing and no-wind fires have a higher exponent for a given coefficient, and a higher coefficient for a given exponent, than heading fires, and in combination lead to higher flame lengths for a given intensity. This illustrates that some variation among correlations can originate from the statistical ambiguity of curve fitting by linear or nonlinear regression, which can yield various combinations of coefficients and exponents with reasonable goodness-of-fit to experimental data. For example, instead of fitting both terms, Nelson et al. (2012) relied on the analytically derived 2/3 exponent from Thomas (1963) and only fit the coefficient.
|
|
The variability among published L–IB relations (Table 2, Fig. 8a) has invited numerous interpretations. Comparisons among studies are made difficult by the non-steadiness of flames and absence of standardised methodology for measuring flame length (Zukoski et al. 1985; Newman and Wieczorek 2004; Alexander and Cruz 2012). Biases can also arise in the fireline intensity estimates from Byram’s (1959) equation (IB = Hm″R). The spread rate R (m s−1) may not be constant (Santoni et al. 2010) and the heat yield H (kJ kg−1) may be overestimated if heat losses for radiation, moisture evaporation, and incomplete combustion are improperly accounted for (Byram 1959; Nelson and Adkins 1986) or if values of H are averaged for the gas phase and solid phase combustion (Susott et al. 1975; Babrauskas 2006). A well-known problem in wildland fire research is overestimating the fuel mass per unit area consumed in flaming m″ (kg m−2). This occurs when the measured fuel mass consumed in an experiment is attributed solely to flaming combustion, whereas in reality, both flaming combustion and solid phase combustion were responsible. The result of such an assumption is IB is calculated to be too high for observed L. To avoid this, Santoni et al. (2011) used O2 calorimetry in a spreading laboratory fire to estimate IB and the technique was subsequently employed by Barboni et al. (2012) as well. However, it is possible that residual combustion behind the spreading front may still affect measurement of heat release and lead to an exaggerated IB.
To examine the possible role of D as a source of the variability in L–IB correlations, we assumed from the congruence of burner data with Thomas’ (1963) correlation (Fig. 3a) that Eqn 5 was correct in the limit of large L/D. Hypothetical estimates of D could then be derived as a constant ratio of calculated L, and when used in Eqn 7, enabled comparison with published correlations (Fig. 8a). Although the L/D ratio is actually not constant for any given fuel type or range of intensity (Fig. 7), this exercise suggested that a substantial portion of variability among L–IB correlations was covered by the range of hypothetical L/D ratios: from 0.5 to 50 (Fig. 8a). Low L/D ratios of 0.5 and 1.0 (see examples in Fig. 6) approximated many heading fire equations, including Nelson and Adkins (1986) and Byram (1959). The middle range of L/D from 4 to 10 are similar to the no-wind fires by Thomas (1963), Fons et al. (1963), and Barboni et al. (2012). The highest L/D ratio of 50 was in the range of burner data presented by Yuan and Cox (1996), where L was 30–100 times the 0.015 m burner D. Not all of the variability among L–IB relations was within the hypothetical L/D limits, however, and the correlations showing low flame lengths for a given intensity suggest a contribution of other factors in determining L and IB as discussed above, particularly those that would inflate the value of IB.
A significant effect of D on L also leads to a previously unreported negative feedback mechanism that limits the spread rate of wildfires. Negative feedbacks are clearly implicated in limiting fire spread rate because the magnitude of spread rate and intensity reach a steady state after increasing rapidly immediately following ignition (McAlpine and Wakimoto 1991; Cheney and Gould 1997). We had earlier reported on the role of D in reducing convective heating by diminishing the gas temperature profile adjacent to the flaming edge (Finney et al. 2021, 2022). A similar effect of D on L shown here would decrease radiation view factor and reduce scaling of processes dependent upon flame length, including flame velocity. Both effects of D would work together to dynamically limit fire spread rate as the flame zone depth extends further behind the edge of an accelerating fire.
Conclusions
Experimental data from a propane sand burner demonstrated that flame zone depth D significantly reduces flame length in relation to fireline intensity in the range of 0.14 ≤ L/D ≤ 13.6. The data were analysed in context of Thomas’ (1963) dimensionless flame length formulation to obtain a new correlation that included D, which was then found to improve the fit to a data set from spreading fires. The general implications of these findings were examined using 28 published correlations and their experimental characteristics, confirming reports that backing fires (and those with no wind) had higher predicted flame length than heading fires for a given intensity. This is consistent with the effect of narrower flame zone depth D of backing and no-wind fires made apparent by the new flame length correlation. Other sources of variation likely include the well-known uncertainties involving measurement of flame length, spread rate, or fireline intensity. The low L/D ratios found in wildland fires compared with those idealised for line fires by theory of entrainment and gas combustion mean that a substantial proportion of the variability in reported flame length correlations would be reduced if flame depth was accounted for.
Nomenclature
Data availability
Data are available upon request from the authors.
Conflicts of interest
The authors have no conflicts of interest.
Declaration of funding
The study was funding by the US Forest Service, National Fire Decision Support Center.
Acknowledgements
Research was supported by the USFS, Rocky Mountain Research Station, National Fire Decision Support Center. The authors thank Jon Bergroos, Ian Grob, and Isaac Grenfell for their assistance with this work. Sara McAllister, Jason Forthofer, and three anonymous referees provided valuable reviews of the manuscript.
References
Albini FA (1976) Estimating wildfire behavior and effects. General Technical Report INT-GTR-30. (USDA Forest Service, Intermountain Research Station: Ogden, UT)Alexander ME (1982) Calculating and interpreting forest fire intensities. Canadian Journal of Botany 60, 349–357.
| Calculating and interpreting forest fire intensities.Crossref | GoogleScholarGoogle Scholar |
Alexander ME, Cruz MG (2012) Interdependencies between flame length and fireline intensity in predicting crown fire initiation and crown scorch height. International Journal of Wildland Fire 21, 95–113.
| Interdependencies between flame length and fireline intensity in predicting crown fire initiation and crown scorch height.Crossref | GoogleScholarGoogle Scholar |
Alexander ME, Cruz MG (2021) Interdependencies between flame length and fireline intensity in predicting crown fire initiation and crown scorch height. International journal of wildland fire 30, 70
| Interdependencies between flame length and fireline intensity in predicting crown fire initiation and crown scorch height.Crossref | GoogleScholarGoogle Scholar |
Anderson HE, Brackebusch AP, Mutch RW, Rothermel RC (1966) Mechanisms of fire spread research progress report 2. Research Paper INT-28. (USDA Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA)
Babrauskas V (2006) Effective heat of combustion for flaming combustion of conifers. Canadian Journal of Forest Research 36, 659–663.
| Effective heat of combustion for flaming combustion of conifers.Crossref | GoogleScholarGoogle Scholar |
Barboni T, Morandini F, Rossi L, Molinier T, Santoni PA (2012) Relationship between flame length and fireline intensity obtained by calorimetry at laboratory scale. Combustion Science and Technology 184, 186–204.
| Relationship between flame length and fireline intensity obtained by calorimetry at laboratory scale.Crossref | GoogleScholarGoogle Scholar |
Beaufait WR (1965) Characteristics of backfires and headfires in a pine needle fuel bed. Research Note INT‐39. (USDA Forest Service, Intermountain Research Station: Ogden, UT, USA)
Butler BW, Finney MA, Andrews PL, Albini FA (2004) A radiation-driven model for crown fire spread. Canadian Journal of Forest Research 34, 1588–1599.
| A radiation-driven model for crown fire spread.Crossref | GoogleScholarGoogle Scholar |
Burrows ND (1994) Experimental development of a fire management model for jarrah (Eucalyptus marginata Donn ex Sm.) forest. PhD Thesis, Australian National University, Canberra, ACT, Australia.
Byram GM (1959) Combustion of forest fuels. In ‘Forest fire: control and use’. (Ed. KP Davis) pp. 61–89, 554–555. (McGraw-Hill: New York, NY, USA)
Catchpole WR, Catchpole EA, Butler BW, Rothermel RC, Morris GA, Latham DJ (1998a) Rate of spread of free-burning fires in woody fuels in a wind tunnel. Combustion Science and Technology 131, 1–37.
| Rate of spread of free-burning fires in woody fuels in a wind tunnel.Crossref | GoogleScholarGoogle Scholar |
Catchpole WR, Bradstock RA, Choate J, Fogarty LG, Gellie N, McCarthy G, McCaw WL, Marsden-Smedley JB, Pearce G (1998b) Cooperative development of equations for heathland fire behaviour. In ‘Proceedings of the 3rd international conference on forest fire research and 14th conference on fire and forest meteorology. Vol. II’, 16–20 November 1998, Luso–Coimbra, Portugal. (Ed. DX Viegas) pp. 631–645. (University of Coimbra: Coimbra, Portugal)
Cetegen BM, Dong Y, Soteriou MC (1998) Experiments on stability and oscillatory behavior of planar buoyant plumes. Physics of Fluids 10, 1658–1665.
| Experiments on stability and oscillatory behavior of planar buoyant plumes.Crossref | GoogleScholarGoogle Scholar |
Cheney NP, Gould JS (1997) Fire growth and acceleration. International Journal of Wildland Fire 7, 1–5.
| Fire growth and acceleration.Crossref | GoogleScholarGoogle Scholar |
Clark RG (1983) Threshold requirements for fire spread in grassland fuels. PhD Dissertation, Texas Tech University, Lubbock, Texas, USA.
Davies GM, Legg CJ, Smith AA, MacDonald A (2019) Development and participatory evaluation of fireline intensity and flame property models for managed burns on Calluna-dominated heathlands. Fire Ecology 15, 30
| Development and participatory evaluation of fireline intensity and flame property models for managed burns on Calluna-dominated heathlands.Crossref | GoogleScholarGoogle Scholar |
Di Blasi C, Branca C, Santoro A, Gonzalez Hernandez EG (2001) Pyrolytic behavior and products of some wood varieties. Combustion and Flame 124, 165–177.
| Pyrolytic behavior and products of some wood varieties.Crossref | GoogleScholarGoogle Scholar |
Fernandes PM, Catchpole WR, Rego FC (2000) Shrubland fire behaviour modelling with microplot data. Canadian Journal of Forest Research 30, 889–899.
| Shrubland fire behaviour modelling with microplot data.Crossref | GoogleScholarGoogle Scholar |
Fernandes PM, Botelho HS, Rego FC, Loureiro C (2009) Empirical modelling of surface fire behaviour in maritime pine stands. International Journal of Wildland Fire 18, 698–710.
| Empirical modelling of surface fire behaviour in maritime pine stands.Crossref | GoogleScholarGoogle Scholar |
Finney MA, Forthofer J, Grenfell IC, Adam BA, Akafuah NK, Saito K (2013) A study of flame spread in engineered cardboard fuelbeds: Part I: Correlations and observations. In ‘Seventh international symposium on scale modeling (ISSM-7)’, 6–9 August, 2013, Hirosaki, Japan. 10 pp. (Intl Scale Modeling Committee)
Finney MA, Cohen JD, Forthofer JM, McAllister SS, Gollner MJ, Gorham DJ, Saito K, Akafuah NK, Adam BA, English JD (2015) Role of buoyant flame dynamics in wildfire spread. Proceedings of the National Academy of Sciences 112, 9833–9838.
| Role of buoyant flame dynamics in wildfire spread.Crossref | GoogleScholarGoogle Scholar |
Finney MA, McAllister SS, Grumstrup TP, Forthofer JM (2021) ‘Wildland fire behaviour: dynamics, principles and processes’. 360 pp. (CSIRO Publishing: Melbourne, Vic., Australia)
Finney MA, Grumstrup TP, Grenfell I (2022) Flame characteristics adjacent to a stationary line fire. Combustion Science and Technology 194, 2212–2232.
| Flame characteristics adjacent to a stationary line fire.Crossref | GoogleScholarGoogle Scholar |
Fons WL, Clements HB, George PM (1963) Scale effects on propagation rate of laboratory crib fires. Symposium (International) on Combustion 9, 860–866.
| Scale effects on propagation rate of laboratory crib fires.Crossref | GoogleScholarGoogle Scholar |
Grove BS, Quintiere JG (2002) Calculating entrainment and flame height in fire plumes of axisymmetric and infinite line geometries. Journal of Fire Protection Engineering 12, 117–137.
| Calculating entrainment and flame height in fire plumes of axisymmetric and infinite line geometries.Crossref | GoogleScholarGoogle Scholar |
Heskestad G (1983) Luminous heights of turbulent diffusion flames. Fire Safety Journal 5, 103–108.
| Luminous heights of turbulent diffusion flames.Crossref | GoogleScholarGoogle Scholar |
Heskestad G (1991) A reduced-scale mass fire experiment. Combustion and Flame 83, 293–301.
| A reduced-scale mass fire experiment.Crossref | GoogleScholarGoogle Scholar |
Katurji M, Zhang J, Satinsky A, McNair H, Schumacher B, Strand T, Valencia A, Finney M, Pearce G, Kerr J, Seto D, Wallace H, Zawar‐Reza P, Dunker C, Clifford V, Melnik K, Grumstrup T, Forthofer J, Clements C (2021) Turbulent thermal image velocimetry at the immediate fire and atmospheric interface. Journal of Geophysical Research: Atmospheres 126, e2021JD035393
| Turbulent thermal image velocimetry at the immediate fire and atmospheric interface.Crossref | GoogleScholarGoogle Scholar |
Marsden‐Smedley JB, Catchpole WR (1995) Fire behaviour modelling in Tasmanian button grass moorlands II. Fire behaviour. International Journal of Wildland Fire 5, 215–228.
| Fire behaviour modelling in Tasmanian button grass moorlands II. Fire behaviour.Crossref | GoogleScholarGoogle Scholar |
McAlpine RS, Wakimoto RH (1991) The acceleration of fire from point source to equilibrium spread. Forest Science 37, 1314–1337.
| The acceleration of fire from point source to equilibrium spread.Crossref | GoogleScholarGoogle Scholar |
Nelson Jr RM (1980) Flame characteristics for fires in southern fuels. Research Paper SE-205. (USDA Forest Service, Southeastern Forest Experiment Station: Asheville, NC, USA)
Nelson Jr RM, Adkins CW (1986) Flame characteristics of wind-driven surface fires. Canadian Journal of Forest Research 16, 1293–1300.
| Flame characteristics of wind-driven surface fires.Crossref | GoogleScholarGoogle Scholar |
Nelson Jr RM, Adkins CW (1988) A dimensionless correlation for the spread of wind-driven fires. Canadian Journal of Forest Research 18, 391–397.
| A dimensionless correlation for the spread of wind-driven fires.Crossref | GoogleScholarGoogle Scholar |
Nelson Jr RM, Butler BW, Weise DR (2012) Entrainment regimes and flame characteristics of wildland fires. International Journal of Wildland Fire 21, 127–140.
| Entrainment regimes and flame characteristics of wildland fires.Crossref | GoogleScholarGoogle Scholar |
Newman M (1974) Toward a common language for aerial delivery mechanics. Fire Management Notes 35, 18–19.
Newman JS, Wieczorek CJ (2004) Chemical flame heights. Fire Safety Journal 39, 375–382.
| Chemical flame heights.Crossref | GoogleScholarGoogle Scholar |
Quintiere JG, Grove BS (1998) A unified analysis for fire plumes. Symposium (International) on Combustion 27, 2757–2766.
| A unified analysis for fire plumes.Crossref | GoogleScholarGoogle Scholar |
Rothermel RC (1991) Predicting behavior and size of crown fires in the northern Rocky Mountains. Research Paper INT-438. (US Department of Agriculture, Forest Service, Intermountain Research Station: Ogden, UT, USA)
Santoni PA, Morandini F, Barboni T (2010) Steady and unsteady fireline intensity of spreading fires at laboratory scale. The Open Thermodynamics Journal 4, 212–219.
| Steady and unsteady fireline intensity of spreading fires at laboratory scale.Crossref | GoogleScholarGoogle Scholar |
Santoni PA, Morandini F, Barboni T (2011) Determination of fireline intensity by oxygen consumption calorimetry. Journal of Thermal Analysis and Calorimetry 104, 1005–1015.
| Determination of fireline intensity by oxygen consumption calorimetry.Crossref | GoogleScholarGoogle Scholar |
Sneeuwjagt RJ, Frandsen WH (1977) Behavior of experimental grass firesvs. predictions based on Rothermel’s fire model. Canadian Journal of Forest Research 7, 357–367.
Steward FR (1964) Linear flame heights for various fuels. Combustion and Flame 8, 171–178.
| Linear flame heights for various fuels.Crossref | GoogleScholarGoogle Scholar |
Susott RA, DeGroot WF, Shafizadeh F (1975) Heat content of natural fuels. Journal of Fire and Flammability 6, 311–325.
Thomas PH (1960) Buoyant diffusion flames. Combustion and Flame 4, 381–382.
| Buoyant diffusion flames.Crossref | GoogleScholarGoogle Scholar |
Thomas PH (1963) The size of flames from natural fires. Symposium (International) on Combustion 9, 844–859.
Thomas PH (1967) Some aspects of the growth and spread of fire in the open. Forestry: An International Journal of Forest Research 40, 139–164.
| Some aspects of the growth and spread of fire in the open.Crossref | GoogleScholarGoogle Scholar |
Thomas PH (1971) Rates of spread of some wind-driven fires. Forestry 44, 155–175.
| Rates of spread of some wind-driven fires.Crossref | GoogleScholarGoogle Scholar |
Thomas PH, Webster CT, Raftery MM (1961) Some experiments on buoyant diffusion flames. Combustion and Flame 5, 359–367.
| Some experiments on buoyant diffusion flames.Crossref | GoogleScholarGoogle Scholar |
Thomas PH, Pickard RW, Wraight HG (1963) On the size and orientation of buoyant diffusion flames and the effect of wind. Fire Research Note 516. (Fire Research Station: Borehamwood, Hertfordshire, UK)
Van Wagner CE (1972) Heat of combustion, heat yield, and fire behaviour. Information Report PS-X-35. 8 pp. (Petawawa Forest Experiment Station: Chalk River, ON, Canada)
van Wilgen BW (1986) A simple relationship for estimating the intensity offires in natural vegetation. South African Journal of Botany 52, 384–385.
Vega JA, Cuinas P, Fonturbel T, Perez-Gorostiaga P, Fernandez C (1998) Predicting fire behaviour in Galician (NW Spain) shrubland fuel complexes. In ‘Proceedings of the 3rd international conference on forest fire research and 14th conference on fire and forest meteorology. Vol. II’, 16–20 November 1998, Luso–Coimbra, Portugal. (Ed. DX Viegas) pp. 713–728. (University of Coimbra: Coimbra, Portugal)
Weise DR, Biging GS (1996) Effects of wind velocity and slope on flame properties. Canadian Journal of Forest Research 26, 1849–1858.
| Effects of wind velocity and slope on flame properties.Crossref | GoogleScholarGoogle Scholar |
Weise DR, Koo E, Zhou X, Mahalingam S, Morandini F, Balbi JH (2016) Fire spread in chaparral – a comparison of laboratory data and model predictions in burning live fuels. International Journal of Wildland Fire 25, 980–994.
| Fire spread in chaparral – a comparison of laboratory data and model predictions in burning live fuels.Crossref | GoogleScholarGoogle Scholar |
Wilson RA (1990) Reexamination of Rothermel’s fire spread equations in no‐wind and no‐slope conditions. Research Paper INT‐34. (USDA Forest Service, Intermountain Forest and Range Experiment Station: Ogden UT, USA)
Yuan L-M, Cox G (1996) An experimental study of some line fires. Fire Safety Journal 27, 123–139.
| An experimental study of some line fires.Crossref | GoogleScholarGoogle Scholar |
Zukoski EE, Cetegen BM, Kubota T (1985) Visible structure of buoyant diffusion flames. Symposium (International) on Combustion 20, 361–366.
| Visible structure of buoyant diffusion flames.Crossref | GoogleScholarGoogle Scholar |
1 The flame length correlation as it appears in Thomas (1963) is a function of fuel gas mass consumption rate per unit flame zone width:
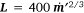 . The equation – eqn [18] in Thomas (1963) – is in centimeter-gram-second units. To obtain Eqn 4 in this document, convert Thomas’ eqn [18] to meter-kilogram-second units, substitute
. The equation – eqn [18] in Thomas (1963) – is in centimeter-gram-second units. To obtain Eqn 4 in this document, convert Thomas’ eqn [18] to meter-kilogram-second units, substitute 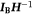 for
for 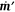 , and assume
, and assume 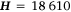 kJ kg−1 based on Albini (1976, p. 86).
kJ kg−1 based on Albini (1976, p. 86).2 The use of tradenames does not constitute an endorsement by the US Forest Service.