Slope effect on junction fire with two non-symmetric fire fronts
Carlos Ribeiro A * , Domingos Xavier Viegas A , Jorge Raposo A , Luís Reis
A * , Domingos Xavier Viegas A , Jorge Raposo A , Luís Reis  A and Jason Sharples B C
A and Jason Sharples B C
A Univ Coimbra, ADAI, Department of Mechanical Engineering, Rua Luís Reis Santos, Pólo II, 3030‐788 Coimbra, Portugal.
B School of Science, University of New South Wales (UNSW), Canberra, ACT, Australia.
C Bushfire and Natural Hazards Cooperative Research Centre, East Melbourne, Vic., Australia.
International Journal of Wildland Fire 32(3) 328-335 https://doi.org/10.1071/WF22152
Submitted: 13 July 2022 Accepted: 18 December 2022 Published: 23 January 2023
© 2023 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of IAWF. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Background: In Pedrógão Grande on 17 June 2017, two fire fronts merged and the propagation of the fire was influenced by the interaction of these non-symmetric fire fronts.
Aims: This wildfire motivated us to study a junction fire with two non-symmetrical fire fronts. The analysis of the movement of the intersection point and the angle (γ) between the bisector of the fire lines and the maximum rate of spread (ROS) direction is of particular relevance.
Methods: The study was carried out at Forest Fire Laboratory of the University of Coimbra in Lousã (Portugal) with laboratory experiments.
Key results: We found that, for small rotation angles (δ), the non-dimensional ROS of the intersection point depends on the slope angle (α) and the initial angle between fire fronts.
Conclusions: For high α, the non-dimensional ROS was highly influenced by the convection process and γ where the maximum ROS occurred, increased when δ increased. However, the radiation process was more relevant for lower α and influenced the non-dimensional ROS. For these cases, the maximum spread direction was close to that of the fire line bisector.
Implications: The present work aimed to explain fire behaviour during the Pedrógão Grande wildfire.
Keywords: convergent fire fronts, dynamic fire behaviour, extreme fire behaviour, fire acceleration, fire behaviour, fire growth, fire modelling, forest fires, junction fires, merging fires.
Introduction
Wildfire propagation is a complex and dynamic phenomenon that is not fully understood (Pastor et al. 2003; Sullivan 2009). Wildfire propagation depends not only on the classic triangle of ‘fire factors’ – topography, vegetation and meteorology – but also explicitly on time, given the dynamic interaction that it creates with the environment (Viegas 2004, 2006; Viegas et al. 2021, 2022).
The interaction of two different fire fronts during the merging of two fires (flank or spot fires) has been observed and studied by several authors in recent decades. During wildfires and prescribed fires, the interaction of the fire fronts or even some parts of the fires that merge between them cause a rapid spread of the fire and an increase in flame length (Brown and Davis 1973; Johansen 1984; Pyne 1984).
The merging of two fire-fronts that intersect at a small angle induces very high values of the rate of spread (ROS) and fire intensity of their intersection point, and follows a gradual velocity decrease in the course of time when the angle between fire fronts increases. This problem was studied by Viegas et al. (2012), who initially described this phenomenon as a ‘jump fire’, and developed a conceptual analytical model for the rate of advance of the intersection point or vertex of two oblique and symmetric fire fronts. Several research works on experimental, analytical and numerical simulation of this problem followed (Sharples et al. 2013; Viegas et al. 2013; Raposo et al. 2015, 2018; Hilton et al. 2016; Thomas et al. 2017; Sullivan et al. 2019; Filkov et al. 2021). The fire fronts were always symmetrical in relation to the vertex V and there was no fuel bed to burn outside the linear straight fire lines. The results showed that the ROS of V has a strong relationship with the initial angle between the merging fire fronts and the ROS increases suddenly from zero to values of the order of 100 times the basic ROS. A real fire situation occurred in the merging of two large fires events: one of them near Canberra, Australia, on 18 January 2003 (Doogan 2006; Raposo 2016) and more recently in Pedrógão Grande, Portugal, on 17 June 2017 (Pinto et al. 2022).
The Pedrógão Grande wildfire was considered the worst wildfire in Portugal and Europe and motivated us to study the fire behaviour when two non-symmetric fire fronts converge.
Physical problem
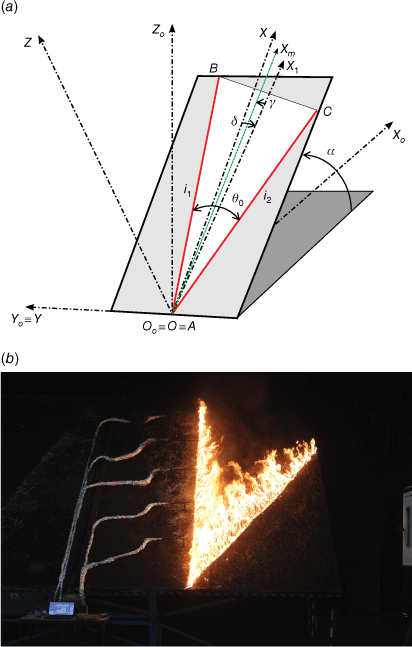
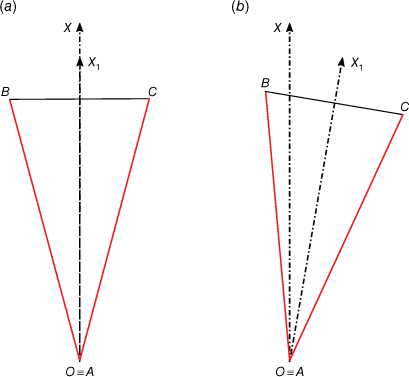
In the present study, it is assumed that the fire is produced by two straight lines i1 and i2, that intersect at point A with an initial angle θ0 between them (Fig. 1) and spread in a uniform fuel bed layer on a flat surface OXY, making a slope angle α with the horizontal datum OoXoYo. The Cartesian coordinate system OoXoYoZo is considered, in which OoZo is perpendicular to the ground. Point A coincides initially with the origin of the reference Cartesian frame with axis OX parallel to the slope gradient. The axis OX1 represents the symmetry line of the junction fire and can be defined by the rotation angle δ that represents the angle between the line with the highest slope and the bisector of the fire lines. However, for each combination of α and δ angles, the maximum ROS occurs according to axis OXm and this axis is rotated at some angle γ, which represents the angle between the bisector of the fire lines and the maximum ROS. The fuel bed area is defined by ABC and is covered by a uniform forest-type fuel layer able to support the spread of a surface fire. The merging of two linear fire fronts is illustrated schematically in Fig. 1a.
|
We consider two linear fire fronts defined by two straight lines (AB and AC), non-symmetric in the OX axis (Fig. 1a). Henceforward, the linear fire lines AB and AC are referred to as i1 and i2, respectively. In this study, it is assumed that at time ti = 0 s and during the whole experiment there is no ambient wind velocity inside the laboratory and the fire lines are straight lines, simultaneously and instantaneously ignited.
Material and methods
Laboratory experiments
The experimental study was carried out at the Canyon Table DE4 (Fig. 1b) of the Forest Fire Laboratory of the University of Coimbra in Lousã (Portugal). The Canyon Table DE4 has a working area 6 m × 8 m, but only half of the area was used in the present laboratory experiments. The slope (α) of DE4 can be varied continuously in the range of 0–40° using a hydraulic device. The fuel bed area was defined by a fixed angle between the fire fronts θ0 = 30° and a fixed length of 5.5 m, that is 8.73 m2. The selected value of θ0 = 30° was a compromise to perform our study. After an extensive test program using values of θ0 in the range of 10–90°, it was found that for smaller values of θ0 the test was very quick and it was difficult to measure the fire spread properties, while for large values of θ0 fire acceleration was not very important and the process that characterises the interaction between the two fire lines was not very relevant. This is consistent with previous work carried out on the subject of converging fronts by Viegas et al. (2012, 2013) and Raposo et al. (2018).
The fuel bed for the experiments was composed of dry particles of pine needles of Pinus pinaster with a constant load of 600 g m−2 (dry basis) (Viegas and Pita 2004; Xie et al. 2014; Raposo 2016; Raposo et al. 2018; Rodrigues et al. 2019; Viegas et al. 2021, 2022). During the preparation of each test, the air temperature (°C), relative humidity (%) and fuel moisture (mf) were monitored and the conditions of the fuel load and bulk density were controlled. The fuel bed height (hf) was aleatorily measured in five positions of the fuel bed, giving an average of 0.04 m. The approximate fuel properties follow: bulk density (ρb) of 14.50 kg m−3; fuel particle density (ρp) of 530 kg m−3; packing ratio (βf), given by the ratio of ρb to ρp, of 0.027; particle surface area to volume ratio (σf) of 4100 m−1 and High Heat of Combustion of range 19.57–21.61 MJ kg−1 (Filipe dos Santos Viana et al. 2018). The fuel moisture content was measured twice with an A&D ML50 moisture analyser for each test: before fuel bed preparation and before ignition. The time between fuel bed preparation and beginning of the burn test did not exceed 10 min, to guarantee that the moisture of the fuel bed in contact with ambient air did not change.
The basic ROS Ro (cm s−1) is a property of a given fuel bed when a linear fire front burns that fuel under no-slope and no-wind conditions and it depends principally on mf. For each series of tests performed, the value of Ro was measured using a 1 m × 1 m horizontal table with the same fuel bed properties – the corresponding values are given in Table 1.

|
The ignition of the two linear fire fronts (i1 and i2) was performed by two persons to ensure that the lines started burning simultaneously, using two wool threads soaked in a mixture of petrol (50%) and diesel fuel (50%).
All tests were monitored and recorded in continuous mode with an infrared (IR) camera (FLIR SC660) and a video camera in the visible range, placed at the top of a lifting platform. In order to avoid parallax errors, the angles between the IR camera optical axis and the ground surface of the Canyon Table DE4 were approximately 90°. The parameters considered for the IR camera were a temperature range of 300–1500°C, an emissivity value of 0.98 (Dlugogorski et al. 2014) and an acquisition rate of 15 Hz. A threshold of 350°C was used to avoid obstruction of the view by the plume of the fire (Xie et al. 2014; Liu et al. 2015). The IR videos were used to obtain the fire contour perimeter with pre-defined times adjusted for each test in accordance with α. More details about this methodology can be seen in Raposo (2016), Raposo et al. (2018) and Rodrigues et al. (2019).
In order to reduce uncertainty, three replication tests (T1, T2 and T3) were performed for each set of parameters (Table 1). For the symmetric condition (δ = 0°), we only performed one test and validated our results with previous work developed by Raposo (2016) and Raposo et al. (2018).
Evaluation of the ROS
The evaluation of the merging process of the two fire lines showed a change of the angle θ between them. The angle between the fire lines increased during the burning of the fuel bed and tended to be close to 180°, which corresponds to a straight line. According to Raposo et al. (2018), the ROS RA near the intersection point of two fire lines (point A) has a functional dependence:
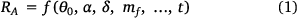
where dots represent the wide set of parameters required to define the fuel bed properties and t is the time that each test lasted after ignition. We consider t as an explicit variable because during the course of the time the fire behaviour changes as it is a dynamic process (Xavier Viegas 2004; Viegas et al. 2021, 2022).
However, the distance xA travelled by point A and the time t are not independent of each other and the distance xA at a given time t is given as follows:
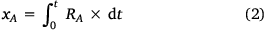
and Eqn 1 can be replaced:
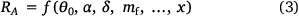
The role of θ0 has been studied extensively by several authors, showing that this is a relevant parameter in the development of junction fires (Viegas et al. 2012; Sharples et al. 2013; Thomas et al. 2015). In the present work, we consider for all experimental laboratory tests a constant value of θ0 = 30°.
The α had the following values: 10°, 20°, 30° and 40°. For each set of these parameters, the δ of linear fire fronts was 0°, 5°, 10° and 15° (Fig. 2). We assume that δ of linear fire fronts was of the same order of magnitude as the angles between the studied fire fronts θ0 = 30°. We chose this angle because we wanted to identify the smallest angle that would initiate fire behaviour changes.
|
The mf influenced the basic ROS Ro. The characteristic parameters of the fuel bed were hf, ρb and residence time to. These parameters for all experimental laboratory tests were in the same range of values. For further details about to see Viegas (2006).
The problem being analysed can be formulated as a function of either time or distance:
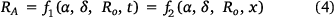
The displacement velocity of the intersection point A of the two fire lines was analysed over time from its original position O. The δ changed the symmetry of the boundary conditions of fire fronts in relation to the maximum slope angle and the intersection point. For each set of values of α and δ, the maximum ROS was along the OXm axis. In order to compare the results with other fuel bed types – although the same type of fuel bed was always used in the present experimental program – and minimise the effect of mf on RA in the tests performed under different conditions, we used non-dimensional ROS (R′A) of the intersection point defined by the following:

where Ro represents the basic ROS (cm s−1) under no-slope and no-wind conditions.
Statistical analysis
In order to reduce uncertainty, three replications (T1, T2 and T3) were performed for each set of parameters δ = 5°, 10° and 15° (Table 1). The results presented are the average of three replications for each parameter set and error bars represent ±95% confidence intervals.
We consider that the ROS of the intersection of point A can be influenced by α, which changes the flame geometry, the convection and radiation process, and by δ of the two fire lines in relation to the maximum slope. In order to check the combined influence of each variable, analysis of variance (ANOVA) was used to test for the effects of slope (α = 10°, 20°, 30° and 40°) and the δ of linear fires fronts changes (δ = 5°, 10° and 15°). An ANOVA is a statistical method for determining the existence of differences among several population means, which requires the analysis of different forms of variance associated with the random samples under study, according to Devore (2010).
Results and discussion
ROS analysis
In order to analyse the role of α and δ of the fire fronts in relation to the maximum slope, a series of laboratory experiments were carried out (Table 1). Based on general observations of fire behaviour (in loco, IR and visible videos) during the experiments, there was a large change in fire dynamics behaviour when the slope increased in comparison to the effect of the small rotations δ tested in the presented work.
In order to assess these dynamic changes, in each test, we estimated the ROS RA for the intersection point A of the two fire fronts. We used specific pre-defined times to obtain the fire perimeter plots with the IR camera according to the slope angle of each test: α = 40° and 30° for Δt = 2 s, α = 20° for Δt = 5 s and α = 10° for Δt = 10 s. The R′A was calculated according to Eqn 5 and the basic ROS (Ro) for each set of parameters is given in Table 1. The average, minimum, maximum and standard deviation (s.d.) values of R′A for three experiments (T1, T2 and T3) and for each δ (5°, 10° and 15°) were calculated (Table 2). In total, 40 experiments were performed specifically for this study and we also used 12 tests for symmetrical conditions performed earlier.

|
For each set of conditions tested, across all slope angles considered, the average R′A values ranged between 13.74 (α = 10° and δ = 5°) and 121.27 (α = 40° and δ = 15°). The average R′A was generally largest when the slope or rotation angle increased (Table 2). Two-way ANOVA with replication indicated that the R′A was significantly (P < 0.05) affected by α, but the δ considered for the two fire fronts did not significantly (P > 0.05) affect R′A. For further information about P-values please see Andrade (2019).
In order to analyse the influence of δ in the ROS of the intersection point A, we compared the values of R′A with the symmetrical boundary conditions (δ = 0°) previously developed by Raposo et al. (2018). However, for clarity, in the following figures, we represent the average results for the three repetitions run in the same conditions, with s.d. bar, representing ±95% confidence intervals. The fire spread can be described as a function of either time or space (distance), in accordance with Eqn 4, and the behaviour of fire spread was non-monotonic (cf. Viegas et al. 2021, 2022).
The average R′A values for each α and each δ were plotted as a function of time and displacement distance (Fig. 3). The R′A values for δ = 5°, 10° and 15° were compared with the R′A for the two symmetric fire fronts (δ = 0°). Despite the random nature of the fluctuations of R′A for each set of parameters used, there was a good relationship between the tests performed with δ (5°, 10° and 15°) and symmetric boundary (δ = 0°) condition, and the R′A values tended to follow the same natural fluctuations for the time and distance travelled by point A.
The behaviour of the interaction of two linear fire lines is non-monotonic (Viegas et al. 2021, 2022) and the oscillations tend to increase with the slope angle because the convection process increases and dominates the interaction of these fire fronts. Junction fires are defined by two different phases: acceleration and deceleration phases. In the cases with lower slope angles (see Fig. 3 for α = 10° and 20°) the acceleration phase was very short, whereas the deceleration phase was more evident in these cases. For the lower α, this was associated with the radiation process becoming more relevant compared to the convection process. The opposite occurred for the highest α (see Fig. 3 for α = 30° and 40°), for which the deceleration phase was not so evident and, in some experiments, the fire accelerated over the entire combustion table, possibly without reaching its maximum ROS value. The convection process was dominant for these α and the ROS of the intersection point A developed very rapidly with the highest oscillations. The measurements were difficult to acquire because point A displaced very rapidly and, in these cases, the standard deviation and the error bars tended to increase.
Angle of the maximum ROS
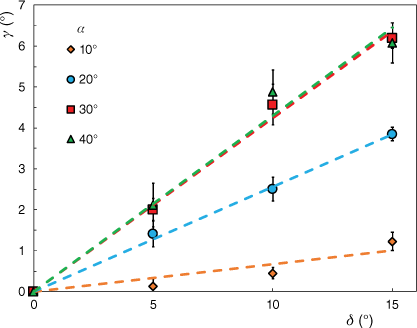
In order to assess the overall role of the parameters α and δ, the angle γ corresponding to the maximum ROS was measured for each set of parameters. The average values of γ were plotted as a function of the angle between the bisector of the linear fire lines and the line with the highest slope with the 95% confidence intervals, for all tests performed (Fig. 4). For the higher value of the slope (α = 30° and 40°), γ had a similar trend and, in those cases, the axis, where the maximum ROS occurred, was influenced more by the convection process. However, for the lower values of slope (α = 10°), γ tended to decrease and the maximum ROS was near the bisector of the fire lines (γ ~ 1°). In that case, the radiation process in the vicinity of point A was more relevant than the convection process. The fitted lines were given by the linear relationship between γ (the angle between the bisector of the fire lines and the maximum ROS) and δ (the angle between the bisector of the linear fire lines and the line with the highest slope), and can be expressed as follows:

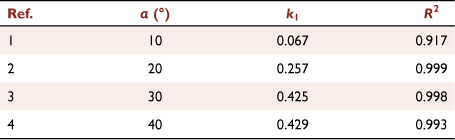
where k1 is the slope of each fitted line. For each case, we obtained the respective values of k1 and the determination coefficients (R2) of the linear regression (Table 3).
|
|
Two-way ANOVA with replication for all data values of the angle between the bisector of the fire lines and the maximum ROS (γ) indicated that γ was significantly affected (P < 0.05) by the α and δ considered for the two fire fronts.
Conclusion
Analysis of the junction fires with non-symmetric linear fire lines based on laboratory-scale experiments was performed for different inclined fuel beds (α = 10°, 20°, 30° and 40°) and different sets of rotation conditions of fire fronts (δ = 0°, 5°, 10° and 15°). The evolution of the fire front consisted mainly of the advance of the intersection point A, with an initial angle θ0 = 30° between fire lines. For the δ tested, the random fluctuations of the non-dimensional ROS R′A had a good relation between the test performed with δ (5°, 10° and 15°) and symmetric boundary condition (δ = 0°), during the time and distance travelled by point A. For α = 10° and 20°, R′A was quite similar to the symmetric condition δ = 0°. With these laboratory tests, we conclude that R′A of the intersection point A for small δ depended on α, but δ did not influence R′A. However, for higher α, the convection process was dominant and changed γ where the maximum ROS occurred; for the lower α, the variation of γ was lower and very close to 0°.
In future work, we intend to analyse in more detail the dynamic evolution of the fire and its interaction with the surrounding flow between the linear fire fronts. To better compare with wildfire situations, it is also important to increase the scale factor of the dimension of the linear fire length.
Data availability
Data are available by request to the corresponding author: Carlos Ribeiro, carlos.ribeiro@adai.pt.
Conflicts of interest
The authors declare no conflict of interest. Domingos Xavier Viegas and Jason Sharples are Guest Editors of the International Journal of Wildland Fire. To mitigate this potential conflict of interest they were blinded from the review process and were not involved at any stage in the editing of this manuscript.
Declaration of funding
The work reported in this article was carried out in the scope of project Firestorm (PCIF/GFC/0109/2017), McFire (PCIF/MPG/0108/2017), IMfire (PCIF/SSI/0151/2018), SmokeStorm (PCIF/MPG/0147/2019) and SafeFire (PCIF/SSO/0163/2019), supported by the Portuguese National Science Foundation, Region (Centro 2020, Centro-01-0246-FEDER-000015) and the European Union’s Horizon 2020 research and innovation programme under grant agreement No 101003890, FirEUrisk – DEVELOPING A HOLISTIC, RISK-WISE STRATEGY FOR EUROPEAN WILDFIRE MANAGEMENT. We thank the FCT-Foundation for Science and Technology for the PhD grant of Carlos Ribeiro with the reference SFRH/BD/140923/2018.
Author contributions
Conceptualisation: Carlos Ribeiro, Jorge Raposo and Domingos Xavier Viegas; Data curation: Carlos Ribeiro; Formal analysis: Carlos Ribeiro; Methodology: Carlos Ribeiro, Jorge Raposo and Domingos Xavier Viegas; Experimental test: Carlos Ribeiro, Jorge Raposo and Luís Reis; Supervision: Jorge Raposo and Domingos Xavier Viegas; Writing – original draft: Carlos Ribeiro; Writing – review & editing: Carlos Ribeiro, Jorge Raposo, Domingos Xavier Viegas, Luis Reis and Jason Sharples.
Acknowledgements
The support given by Nuno Luís, Gonçalo Rosa, Diogo Pires and João Carvalho in performing the laboratory experiments is gratefully acknowledged. We thank Luis Mário Ribeiro for collaboration with some images.
References
Andrade C (2019) The P Value and Statistical Significance: Misunderstandings, Explanations, Challenges, and Alternatives. Indian Journal of Psychological Medicine 41, 210–215.| The P Value and Statistical Significance: Misunderstandings, Explanations, Challenges, and Alternatives.Crossref | GoogleScholarGoogle Scholar |
Brown AA, Davis K (1973) ‘Forest Fire: Control and Use.’ (McGraw-Hill: New York)
Devore JL (2010) ‘Probability and Statistics for Engineering and the Sciences’, 8th edn. (Ed. M Julet) (Brooks/Cole, Cengage Learning: Boston, MA, USA)
Dlugogorski BZ, Hirunpraditkoon S, Kennedy EM (2014) Ignition temperature and surface emissivity of heterogeneous loosely packed materials from pyrometric measurements. Fire Safety Science 11, 262–275.
| Ignition temperature and surface emissivity of heterogeneous loosely packed materials from pyrometric measurements.Crossref | GoogleScholarGoogle Scholar |
Doogan M (2006) ‘The Canberra Firestorm. Inquests and Inquiry into Four Deaths and Four Fires between 8 and 18 January 2003.’ (ACT Coroner’s Court: Canberra, ACT)
Filipe dos Santos Viana H, Martins Rodrigues A, Godina R, Carlos de Oliveira Matias J, Jorge Ribeiro Nunes L (2018) Evaluation of the physical, chemical and thermal properties of Portuguese maritime pine biomass. Sustainability 10, 2877
| Evaluation of the physical, chemical and thermal properties of Portuguese maritime pine biomass.Crossref | GoogleScholarGoogle Scholar |
Filkov A, Cirulis B, Penman T (2021) Quantifying merging fire behaviour phenomena using unmanned aerial vehicle technology. International Journal of Wildland Fire 30, 197–214.
| Quantifying merging fire behaviour phenomena using unmanned aerial vehicle technology.Crossref | GoogleScholarGoogle Scholar |
Hilton JE, Miller C, Sharples JJ, Sullivan AL (2016) Curvature effects in the dynamic propagation of wildfires. International Journal of Wildland Fire 25, 1238–1251.
| Curvature effects in the dynamic propagation of wildfires.Crossref | GoogleScholarGoogle Scholar |
Johansen RW (1984) Prescribed Burning with Spot Fires in the Georgia Coastal Plain. Georgia Forestry Commission 49, 1–8. Available at http://www.treesearch.fs.fed.us/pubs/36481
Liu N, Wu J, Chen H, Zhang L, Deng Z, Satoh K, Viegas DX, Raposo JR (2015) Upslope spread of a linear flame front over a pine needle fuel bed: The role of convection cooling. Proceedings of the Combustion Institute 35, 2691–2698.
| Upslope spread of a linear flame front over a pine needle fuel bed: The role of convection cooling.Crossref | GoogleScholarGoogle Scholar |
Pastor E, Zárate L, Planas E, Arnaldos J (2003) Mathematical models and calculation systems for the study of wildland fire behaviour. Progress in Energy and Combustion Science 29, 139–153.
| Mathematical models and calculation systems for the study of wildland fire behaviour.Crossref | GoogleScholarGoogle Scholar |
Pinto P, Silva ÁP, Viegas DX, Almeida M, Raposo J, Ribeiro LM (2022) Influence of Convectively Driven Flows in the Course of a Large Fire in Portugal: The Case of Pedrógão Grande. Atmosphere 13, 414
| Influence of Convectively Driven Flows in the Course of a Large Fire in Portugal: The Case of Pedrógão Grande.Crossref | GoogleScholarGoogle Scholar |
Pyne SJ (1984) ‘Introduction to wildland fire: Fire Management in the United States.’ (John Wiley and Sons: New York)
Raposo JRN (2016) Extreme Fire Behaviour Associated with the Merging of Two Linear Fire Fronts. PhD Thesis, Department of Mechanical Engineering of the Faculty of Science and Technology, University of Coimbra. Available at http://hdl.handle.net/10316/31020
Raposo JR, Cabiddu S, Viegas DX, Salis M, Sharples J (2015) Experimental analysis of fire spread across a two-dimensional ridge under wind conditions. International Journal of Wildland Fire 24, 1008–1022.
| Experimental analysis of fire spread across a two-dimensional ridge under wind conditions.Crossref | GoogleScholarGoogle Scholar |
Raposo JR, Viegas DX, Xie X, Almeida M, Figueiredo AR, Porto L, Sharples J (2018) Analysis of the physical processes associated with junction fires at laboratory and field scales. International Journal of Wildland Fire 27, 52–68.
| Analysis of the physical processes associated with junction fires at laboratory and field scales.Crossref | GoogleScholarGoogle Scholar |
Rodrigues A, Ribeiro C, Raposo J, Viegas DX, André J (2019) Effect of canyons on a fire propagating laterally over slopes. Frontiers in Mechanical Engineering 5, 402–409.
| Effect of canyons on a fire propagating laterally over slopes.Crossref | GoogleScholarGoogle Scholar |
Sharples JJ, Towers IN, Wheeler G, Wheeler V-M, Mccoy JA (2013) Modelling fire line merging using plane curvature flow. In ‘MODSIM2013, 20th International Congress on Modelling and Simulation’. (Eds J Piantadosi, RS Anderssen, J Boland) pp. 256–262. Available at
| Crossref |
Sullivan AL (2009) Wildland surface fire spread modelling, 1990–2007. 3: Simulation and mathematical analogue models. International Journal of Wildland Fire 18, 387–403.
| Wildland surface fire spread modelling, 1990–2007. 3: Simulation and mathematical analogue models.Crossref | GoogleScholarGoogle Scholar |
Sullivan AL, Swedosh W, Hurley RJ, Sharples JJ, Hilton JE (2019) Investigation of the effects of interactions of intersecting oblique fire lines with and without wind in a combustion wind tunnel. International Journal of Wildland Fire 28, 704–719.
| Investigation of the effects of interactions of intersecting oblique fire lines with and without wind in a combustion wind tunnel.Crossref | GoogleScholarGoogle Scholar |
Thomas CM, Sharples JJ, Evans JP (2015) Pyroconvective interaction of two merged fire lines: curvature effects and dynamic fire spread. In ‘MODSIM2015, 21st International Congress on Modelling and Simulation’. (Eds T Weber, MJ McPhee, RS Anderssen) pp. 312–318. Available at
| Crossref |
Thomas CM, Sharples JJ, Evans JP (2017) Modelling the dynamic behaviour of junction fires with a coupled atmosphere-fire model. International Journal of Wildland Fire 26, 331–344.
| Modelling the dynamic behaviour of junction fires with a coupled atmosphere-fire model.Crossref | GoogleScholarGoogle Scholar |
Viegas DX (2006) Parametric study of an eruptive fire behaviour model. International Journal of Wildland Fire 15, 169–177.
| Parametric study of an eruptive fire behaviour model.Crossref | GoogleScholarGoogle Scholar |
Viegas DX, Pita LP (2004) Fire spread in canyons. International Journal of Wildland Fire 13, 253–274.
| Fire spread in canyons.Crossref | GoogleScholarGoogle Scholar |
Viegas DX, Raposo JR, Davim DA, Rossa CG (2012) Study of the jump fire produced by the interaction of two oblique fire fronts. Part 1. Analytical model and validation with no-slope laboratory experiments. International Journal of Wildland Fire 21, 843–856.
| Study of the jump fire produced by the interaction of two oblique fire fronts. Part 1. Analytical model and validation with no-slope laboratory experiments.Crossref | GoogleScholarGoogle Scholar |
Viegas D, Raposo J, Figueiredo A (2013) Preliminary analysis of slope and fuel bed effect on jump behavior in forest fires. Procedia Engineering 62, 1032–1039.
| Preliminary analysis of slope and fuel bed effect on jump behavior in forest fires.Crossref | GoogleScholarGoogle Scholar |
Viegas DXFC, Raposo JRN, Ribeiro CFM, Reis LCD, Abouali A, Viegas CXP (2021) On the non-monotonic behaviour of fire spread. International Journal of Wildland Fire 30, 702–719.
| On the non-monotonic behaviour of fire spread.Crossref | GoogleScholarGoogle Scholar |
Viegas DXFC, Raposo JRN, Ribeiro CFM, Reis L, Abouali A, Ribeiro LM, Viegas CXP (2022) On the intermittent nature of forest fire spread – Part 2. International Journal of Wildland Fire 31, 967–981.
| On the intermittent nature of forest fire spread – Part 2.Crossref | GoogleScholarGoogle Scholar |
Viegas DX (2004) A Mathematical Model For Forest Fires Blowup. Combustion Science and Technology 177, 27–51.
| A Mathematical Model For Forest Fires Blowup.Crossref | GoogleScholarGoogle Scholar |
Xie X, Liu N, Viegas DX, Raposo JR (2014) Experimental Research on Upslope Fire and Jump Fire. Fire Safety Science 11, 1430–1442.
| Experimental Research on Upslope Fire and Jump Fire.Crossref | GoogleScholarGoogle Scholar |



