Modelling sorption processes of 10-h dead Pinus pinaster branches
Sérgio Lopes A B C * , Sandra Santos A , Nuno Rodrigues C , Paulo Pinho
A B C * , Sandra Santos A , Nuno Rodrigues C , Paulo Pinho  B C and Domingos Xavier Viegas
B C and Domingos Xavier Viegas  A
A
A CEIF/ADAI/LAETA, Association for the Development of Industrial Aerodynamics, Rua Pedro Hispano, 12, 3031-289 Coimbra, Portugal.
B CISeD, Research Centre in Digital Services, Polytechnic Institute of Viseu, Campus Politécnico, 3504-510 Viseu, Portugal.
C Polytechnic Institute of Viseu, Campus Politécnico, 3504-510 Viseu, Portugal.
International Journal of Wildland Fire 32(6) 903-912 https://doi.org/10.1071/WF22127
Submitted: 1 July 2022 Accepted: 3 May 2023 Published: 26 May 2023
© 2023 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of IAWF. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Background: Forest fuel moisture content (FMC) is an important parameter that determines wildfire risk; therefore, its accurate prediction is of great importance. In the absence of rainfall, dead FMC changes mainly by water vapour sorption processes.
Aims: In the present work, sorption processes of 10-h dead Pinus pinaster branches (PPBs) were studied in order to develop a moisture content prediction model for this fuel type.
Methods: Laboratory tests were used to determine sorption curves, timelag and equilibrium moisture content (EMC) for different environmental conditions. Sorption curves and EMC were modelled with existing sorption models. Dead PPBs moisture content was determined in field tests carried out in central Portugal to validate the sorption models.
Key results: Sorption curves were not pure exponential functions, but had different timelag values until equilibrium was reached. EMC values allowed us to obtain a sigmoid curve and hysteresis effect.
Conclusions: Comparing predicted and observed FMCs of PPB, the Modified Henderson and Pabis models for sorption curves and the Van Wagner model for EMC show high prediction ability.
Implications: The model can be applied in early fire risk assessment, in particular in the methods that use other fuels besides fine forest fuels.
Keywords: moisture content, dead forest fuel, 10-h fuels, EMC, timelag, sorption processes, fire risk, fire management.
Introduction
Fuel moisture content (FMC) has a great influence on many aspects of forest fire behaviour, including ignition probability, rate of fire spread, flame dimensions and fuel consumption (Rothermel 1983; Viegas et al. 1992; Rossa 2017); however, its accurate prediction is difficult owing to its dependence on weather conditions, topography and vegetation (Matthews 2014). This is applicable to both dead and live fuels, but the problem is simpler for dead fuels, which are the object of the present paper, as their FMC depends mainly on meteorological parameters, as well as on physical and chemical properties of the fuels (Simard 1968). For example, fuel particle size and shape have implications on the moisture exchange rate, with atmospheric conditions affecting the ease of fire ignition (Simard 1968). In addition, surface fuel load, especially the accumulation of dead branches on the forest floor, is an important component that contributes to the spread of an active fire. It also affects fire behaviour and intensity, namely its transition from surface to crown fire (Van Wagner 1977).
In the absence of rainfall and below the fibre saturation point, dead forest fuels respond to variations in meteorological conditions through mechanisms of water transfer by sorption processes. Thus, the moisture content of a fuel particle with a given initial FMC value, when exposed to conditions of constant air temperature and relative humidity, increases or decreases until it reaches a constant value – the equilibrium moisture content (EMC) (e.g. Viney and Catchpole 1991; Catchpole et al. 2001). The moisture increase and decrease processes are designated sorption and desorption, respectively. They are characterised by either a response time, log drying rate or timelag (τ), which is the time required for the fraction of evaporable water remaining in the forest fuel to decrease from 1 to 0.368 of its initial value (Byram 1963), in the case of desorption. Timelag is divided into four categories (1-, 10-, 100- and 1000-h fuels) (Bradshaw et al. 1983) on the basis of dead forest fuels classification.
Moisture exchange process have been studied extensively for fine fuels, given their relevance to most processes of fire ignition and spread; therefore, many models to estimate FMC of dead fine fuels are available, for example Aguado et al. (2007), Matthews et al. (2010), Sharples and McRae (2011), Lopes et al. (2014), Bovill et al. (2015), Resco de Dios et al. (2015), Adab et al. (2016), Cawson et al. (2020) and Bakšić and Bakšić (2022). In the present work, the adsorption and desorption processes and EMC of medium (10-h) dead Pinus pinaster branches (PPBs) (with a diameter between 0.6 and 2.5 cm) were determined in order to develop a moisture content prediction model for this type of fuel. The medium-size dead fuels are important to estimate fire behaviour as their quantity and FMC determine the fireline intensity and the possible transition of fire from the surface to the crown (Van Wagner 1977).
Materials and methods
Laboratory tests
In the laboratory tests, samples of PPBs (0.6–2.5 cm diameter) collected in the field were used to determine sorption curves, timelag and EMC for different sets of air temperature (20, 30 and 40°C) and relative humidity (between 10 and 90%).
One sample was collected, generally once a week between 12:00 and 13:00 hours local standard time (LST) during all 2020 and 2021. Samples collected on wet days were used in desorption tests and the ones collected on dry days were used in adsorption tests. Samples were not manipulated, with the exception of adsorption tests with relative humidity below 50%, where they were previously dried.
The samples were placed inside a climatic chamber (Aralab Fitoclima 300) with a working temperature range between −20 and 100°C (accuracy ±0.5°C) and a working relative humidity range between 10 and 98% (accuracy ±2%) equipped with air temperature and relative humidity sensors and an analytical scale (precision of 0.001 g), so that continuous weight was recorded until the sample reached constant weight, determining moisture content evolution and the changing rates at which equilibrium was approached.
A total of 90 samples with an average dry weight of 11 g (±0.9 g) were used; however, in some cases, data acquisition errors did not allow partial or total curve determination.
We define the fraction of evaporable water E(t) remaining in the fuel at time t (Eqn 1):
In this equation m(t) is the fuel average moisture content at time t, m0 is the value of m at t = 0, me is the value of m as t approaches infinity (me approaches EMC).
There are several models to estimate E(t), namely:
Byram’s (1963) model, given by Eqn 2:
Page’s (1949) model, given by Eqn 3:
the Henderson and Pabis (1961) model, given by Eqn 4:
the Two-term (Henderson 1974) model, given by Eqn 5:
the Modified Henderson and Pabis (Karathanos 1999) model, given by Eqn 6:
In the previous equations, τ is the timelag (h), t is time (h), k1, k2 and k3 are the drying constants (h−1), and n, a1, a2 and a3 are empirical dimensionless constants obtained from laboratory data.
To assess the relationship between EMC of PPBs and air temperature T and relative humidity RH, the following semi-empirical and empirical models were used:
Van Wagner’s (Van Wagner 1987) model, given by Eqn 7:
the Modified Halsey (Iglesias and Chirife 1976) model, given by Eqn 8:
Nelson’s (Nelson 1984) model, given by Eqn 10:
the Modified Chung–Pfost (Pfost et al. 1976) model, given by Eqn 11:
In these equations, a, b, c, d, e and f are coefficients specific to individual models, RH is the relative humidity, T (°C) and Tk (K) are the temperatures, R is the universal gas constant (8314 J mol−1 K−1) and M is the molecular weight of water (18 g mol−1). Model constants were obtained from laboratory data.
Field tests
In the field tests, through the years 2020 and 2021 (excluding March and April 2020 owing to the COVID-19 pandemic), PPB samples were collected between 12:00 and 13:00 hours LST, generally twice a week from forest stands in central Portugal (Viseu, 40°42′30.02″N, 7°54′8.96″W) to take FMC measurements. Three samples of 0.6–2.5 cm diameter were collected and transported to the laboratory in an isothermal bag to avoid moisture changes. Here, samples were weighed and then oven-dried at 105°C to constant weight, to obtain their dry weight and therefore the dry basis moisture content calculated using Eqn 12:
where mW represents the wet mass (g) and mD represents the dry mass (g) of the samples. The final moisture content is the result from the average of the three samples collected.
Hourly meteorological conditions (air temperature, RH, wind and rainfall) measured at 5 m height in an open field from a weather station located approximately 7 km south of the sampling site were used to characterise weather conditions during field tests.
Evaluation of the sorption and EMC model performance was made using the data within the Portuguese fire risk period (May to September), excluding days with rainfall.
To assess model fitting quality, the following statistical parameters were calculated: the mean absolute error (MAE), the mean absolute percentage error (MAPE), the root-mean-squared error (RMSE) and the determination coefficient (R2). RMSE and MAPE show the accuracy of model fitting, MAE measures the bias of the model and R2 measures how well observed values are replicated by the model. Usually, higher values of R2 and lower values of MAE, MAPE and RMSE associated with randomly distributed residuals indicate a good fit.
Results
Fig. 1 shows the moisture content values of the PPBs collected from P. pinaster stands in Viseu during 2020 and 2021. A summary of weather conditions for the same period can be found in the Supplementary material. The moisture content of the PPBs varies between a minimum of 5% and a maximum of 218%. In summer months, moisture content is mainly below 15%, with the exception of periods with rainfall, although the drying of these fuels after a summer rainfall episode is very fast.
Fig. 2 shows the drying and wetting curves of PPBs represented by the evaporable water fraction (E), described in Eqn 1, as a function of time for air temperatures of 20, 30 and 40°C in a range of RH between 10 and 90% (10% steps). The drying and wetting curves show deviation from pure exponential behaviour, which means that other mathematical functions should be considered as well to represent these processes. Additionally, these curves show some fluctuations, particularly in the late stages of the experiment, caused by temperature and RH oscillations inside the climatic chamber.
Breaking up the drying and wetting curves into four periods and assuming a constant rate as fuel approaches EMC in each step, the four timelag values were calculated. Table 1 shows the average timelag constants obtained in the laboratory tests. No significant relationship of the four timelag periods with air RH was found; therefore, an average value is presented. However, a dependence of the four timelag periods on air temperature was observed.
| Process | Temperature (°C) | First timelag (h) | Second timelag (h) | Third timelag (h) | Fourth timelag (h) | ||||
| Average | s.d. | Average | s.d. | Average | s.d. | Average | s.d. | ||
| Desorption | 20 | 20.99 | 14.04 | 26.46 | 11.38 | 19.89 | 11.50 | 16.76 | 6.09 |
| 30 | 8.12 | 6.46 | 12.85 | 5.80 | 9.65 | 5.10 | 7.86 | 4.49 | |
| 40 | 8.23 | 6.43 | 9.96 | 4.24 | 9.60 | 4.02 | 7.37 | 2.62 | |
| Adsorption | 20 | 19.02 | 7.60 | 23.32 | 8.25 | 22.38 | 9.98 | 13.71 | 10.48 |
| 30 | 9.31 | 5.50 | 11.65 | 5.04 | 9.09 | 4.19 | 6.97 | 5.10 | |
| 40 | 6.29 | 3.40 | 12.09 | 11.29 | 8.89 | 4.44 | 6.65 | 3.20 | |
Table 2 shows the estimated parameters for adsorption and desorption processes based on the laboratory tests for the models described from Eqns 2–6. As can be seen, experimental drying and wetting curves are best described by the Modified Henderson and Pabis model, with an R2 of 0.694 and 0.749 and an RMSE of 0.134 and 0.116 for desorption and adsorption processes, respectively.
| Equation | Byram | Page | Henderson and Pabis | Two-term | Modified Henderson and Pabis | ||
| Model parameters | k1 | Desorption | 0.072 | 0.257 | 0.051 | 0.011 | 0.398 |
| Adsorption | 0.073 | 0.269 | 0.047 | 0.014 | 0.171 | ||
| n | Desorption | – | 0.533 | – | – | – | |
| Adsorption | – | 0.515 | – | – | – | ||
| a1 | Desorption | – | – | 0.779 | 0.267 | 0.257 | |
| Adsorption | – | – | 0.753 | 0.323 | 0.622 | ||
| k2 | Desorption | – | – | – | 0.160 | 0.106 | |
| Adsorption | – | – | – | 0.189 | 0.809 | ||
| a2 | Desorption | – | – | – | 0.718 | 0.544 | |
| Adsorption | – | – | – | 0.666 | 0.071 | ||
| a3 | Desorption | – | – | – | – | 0.007 | |
| Adsorption | – | – | – | – | 0.312 | ||
| k3 | Desorption | – | – | – | – | 0.215 | |
| Adsorption | – | – | – | – | 0.014 | ||
| Statistical parameters | R2 | Desorption | 0.542 | 0.673 | 0.595 | 0.692 | 0.694 |
| Adsorption | 0.565 | 0.730 | 0.636 | 0.748 | 0.749 | ||
| MAE | Desorption | 0.129 | 0.107 | 0.124 | 0.104 | 0.103 | |
| Adsorption | 0.131 | 0.098 | 0.123 | 0.093 | 0.093 | ||
| RMSE | Desorption | 0.163 | 0.138 | 0.154 | 0.137 | 0.134 | |
| Adsorption | 0.153 | 0.121 | 0.140 | 0.117 | 0.116 | ||
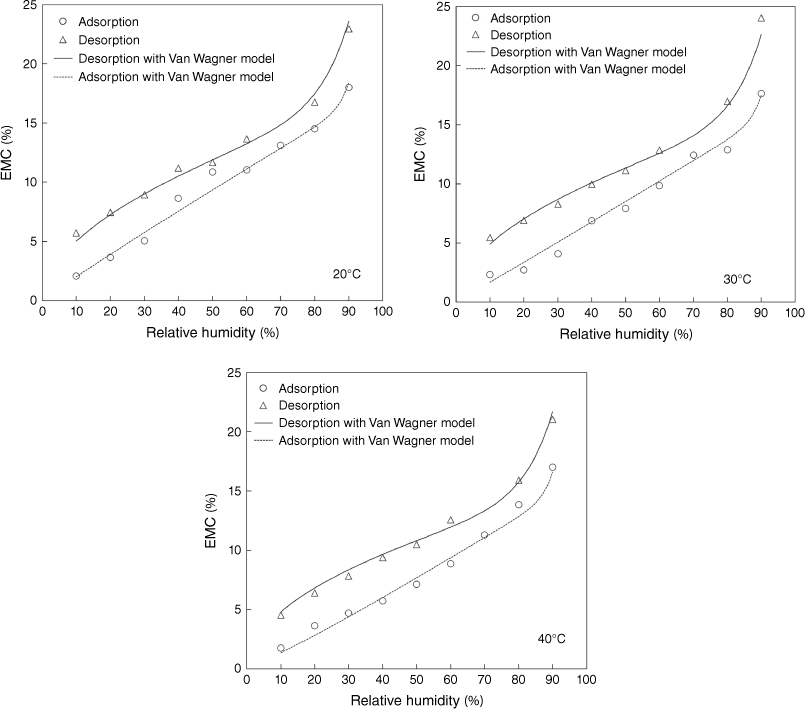
Laboratory EMC values for PPBs obtained in both adsorption and desorption tests in a range of RH between 10 and 90% for air temperatures of 20, 30 and 40°C are shown in Table 3 and plotted in Fig. 3. The desorption EMC values for 70% RH were not obtained owing to operational errors. The results were fitted to five EMC models and Table 4 shows the EMC model parameter estimate obtained for the desorption and adsorption processes described in Eqns 7–11. As an example, the estimate from the best fitted model (Van Wagner) is also shown in Fig. 3.
| Relative humidity (%) | EMCadsorption (%) | EMCdesorption (%) | ||||
| T = 20°C | T = 30°C | T = 40°C | T = 20°C | T = 30°C | T = 40°C | |
| 10 | 2.1 | 2.3 | 1.8 | 5.7 | 5.5 | 4.5 |
| 20 | 3.7 | 2.7 | 3.7 | 7.5 | 6.9 | 6.4 |
| 30 | 5.0 | 4.1 | 4.7 | 9.0 | 8.3 | 7.8 |
| 40 | 8.6 | 6.9 | 5.7 | 11.2 | 10.0 | 9.4 |
| 50 | 10.9 | 7.9 | 7.1 | 11.7 | 11.1 | 10.5 |
| 60 | 11.1 | 9.8 | 8.9 | 13.7 | 12.9 | 12.6 |
| 70 | 13.1 | 12.4 | 11.3 | – | – | – |
| 80 | 14.5 | 12.9 | 13.8 | 16.8 | 17.0 | 15.9 |
| 90 | 18.0 | 17.6 | 17.0 | 23.0 | 24.0 | 21.1 |
Equilibrium moisture content of dead Pinus pinaster branches in both the adsorption and desorption processes. Estimates obtained with Van Wagner model.
| Equation | Van Wagner | Modified Halsey | Modified Oswin | Nelson | Modified Chung–Pfost | ||
| Model parameters | a | Desorption | 1.473 | 5.767 | 12.653 | −0.183 | 0.183 |
| Adsorption | 0.218 | 4.232 | 9.409 | −0.193 | 0.193 | ||
| b | Desorption | 0.531 | 0.012 | 0.053 | 5.236 | 57.182 | |
| Adsorption | 0.958 | 0.014 | 0.052 | 4.714 | 40.913 | ||
| c | Desorption | 24.304 | 2.45 | 0.321 | – | 489.918 | |
| Adsorption | 68.193 | 2.07 | 0.390 | – | 236.158 | ||
| d | Desorption | 8.442 | – | – | – | – | |
| Adsorption | 2.863 | – | – | – | – | ||
| e1 | Desorption | −389.814 | – | – | – | – | |
| Adsorption | 0.094 | – | – | – | – | ||
| f | Desorption | 2.742 × 10−6 | – | – | – | – | |
| Adsorption | −0.042 | – | – | – | – | ||
| Statistical parameters | R2 | Desorption | 0.991 | 0.977 | 0.989 | 0.979 | 0.984 |
| Adsorption | 0.984 | 0.903 | 0.944 | 0.968 | 0.977 | ||
| MAE | Desorption | 0.428 | 0.702 | 0.384 | 0.579 | 0.421 | |
| Adsorption | 0.514 | 1.328 | 0.989 | 0.630 | 0.610 | ||
| RMSE | Desorption | 0.514 | 0.818 | 0.563 | 0.776 | 0.681 | |
| Adsorption | 0.622 | 1.530 | 1.159 | 0.873 | 0.744 | ||
| Residual distribution | Desorption | Random | Systematic | Random | Random | Random | |
| Adsorption | Random | Systematic | Random | Random | Random | ||
As can be seen, for a wide range of T and RH values, all sorption models showed good fitting with the laboratory results; however, the Van Wagner model showed the best fit for both adsorption and desorption processes. This model gives the highest R2 of 0.991 and 0.984, the lowest MAE of 0.428 and 0.514% and the lowest RMSE of 0.514 and 0.622 for desorption and adsorption processes, respectively. The residual distribution was also analysed and showed that all adsorption and desorption models showed a random residual distribution, indicating good fitting ability, with only the Halsey model presenting a systematic residual distribution.
It was seen that EMC values for the desorption process were an average of 3.4% higher than for adsorption, showing the typical hysteresis effect.
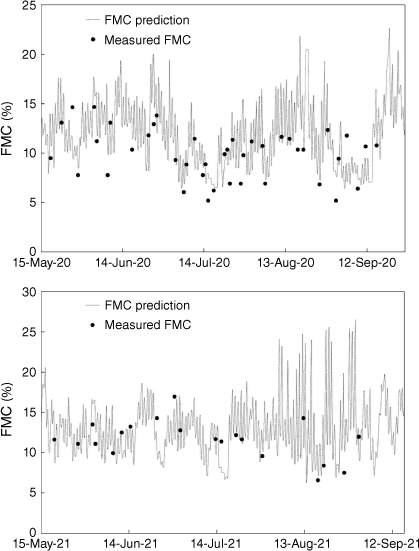
In terms of model validation, Figs 4 and 5 show the comparison between the predicted and observed values of FMC of PPBs obtained in 2020 and 2021. Predicted values are results from the Modified Henderson and Pabis model for the drying and wetting curves and the Van Wagner model for EMC, both with empirical parameters estimated in the present work, and considering the hourly meteorological conditions (air temperature and RH) from the weather station mentioned above. The observed FMC values were obtained in the field tests excluding the rainfall events.
Comparison between the predicted (line) and the observed (dots) fuel moisture content (FMC) of dead Pinus pinaster branches during 2020 and 2021 from May to September. Predicted values are results from the Modified Henderson and Pabis model for the drying and wetting curves and the Van Wagner model for equilibrium moisture content.
Comparison between the predicted and the observed fuel moisture content (FMC) of dead Pinus pinaster branches. Predicted values are results from the Modified Henderson and Pabis model for the drying and wetting curves and the Van Wagner model for equilibrium moisture content.
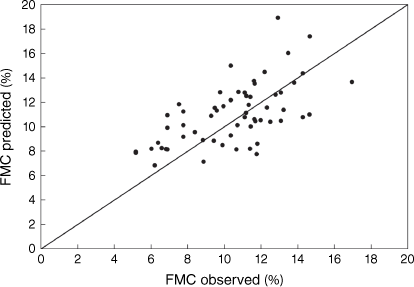
Table 5 shows the statistical parameters of the model validation procedures obtained with sorption and EMC models. Comparing the predicted and observed FMC values, in terms of MAE, MAPE and RMSE, the Modified Henderson and Pabis model for the drying and wetting curves and the Van Wagner model for EMC show high prediction ability, with an MAE of 1.96%, MAPE of 20.47% and RMSE of 2.32.
| Sorption model | Statistical parameters | Equilibrium moisture content model | ||||
| Van Wagner | Modified Halsey | Modified Oswin | Nelson | Modified Chung–Pfost | ||
| Byram | MAE | 2.81 | 2.80 | 2.86 | 2.48 | 2.79 |
| MAPE (%) | 30.25 | 29.23 | 30.05 | 26.51 | 29.84 | |
| RMSE | 3.26 | 3.27 | 3.34 | 2.87 | 3.24 | |
| Page | MAE | 2.39 | 2.38 | 2.46 | 4.58 | 2.44 |
| MAPE (%) | 25.26 | 24.33 | 25.27 | 45.07 | 25.49 | |
| RMSE | 2.79 | 2.79 | 2.88 | 5.97 | 2.84 | |
| Modified Henderson and Pabis | MAE | 1.96 | 1.98 | 4.05 | 3.94 | 2.04 |
| MAPE (%) | 20.47 | 19.98 | 39.62 | 38.65 | 20.53 | |
| RMSE | 2.32 | 2.34 | 5.35 | 5.22 | 2.44 | |
Discussion and conclusion
The drying and wetting curves of dead PPBs (0.6–2.5 cm diameter) show that they are not pure exponential functions but have different timelag values until equilibrium is reached. Additionally, the results suggest no significant relationship of the timelag period values with air RH but a dependence on air temperature. An increase in the sorption rates with temperature was observed in this study that is in agreement with the results reported by Byram (1963). However, the pure exponential equation of Byram (1963), which is frequently used in forest fire research, does not represent the drying and wetting curves of PPBs well. The Modified Henderson and Pabis model provides the best fit.
For this type of fuel, representation of the EMC values as a function of relative air humidity at a constant temperature allows us to obtain a typical sigmoid curve. The EMC values obtained were higher for the desorption process than for the adsorption process, indicating the typical hysteresis effect in these processes.
It was observed that EMCs of PPBs obtained in the present work were an average of 4.7% lower than EMCs of dead Pinus pinaster needles obtained by Lopes et al. (2014), showing that under the same environmental conditions, and given enough time to reach EMC, PPBs can reach lower values than Pinus pinaster needles. In the present work, measured timelag values were within the expected values for PPBs, with a first timelag period average of 12.0 h for adsorption and 13.7 h for desorption.
Comparing the predicted and observed FMC of PPBs, the Modified Henderson and Pabis model for the drying and wetting curves and the Van Wagner model for EMC show high prediction ability, with an MAE of 1.96%, MAPE of 20.47% and RMSE of 2.32. Lee et al. (2020) and Resco de Dios et al. (2015) obtained similar results using other models with this type of forest fuel (10 h-fuels).
Figs 4 and 5 show that, for FMC values below 8%, the prediction results are overestimated. This could result from the absence of solar radiation and wind effects in the climatic chamber tests used for model parameters determination. Observed FMC values below 8% indicate that these could be influenced by high values of direct solar radiation and/or wind effects.
The results from this study can be applied to fire behaviour models and used for the assessment of wildfire risk, improving planning and operational fire situations. Future research should be also focused on the response of the model in the presence of rainfall to understand the duration of the low-risk period of forest fire in an operational context.
Data availability
The data that support this study will be shared on reasonable request to the corresponding author.
Conflicts of interest
Domingos Xavier Viegas is an Associate Editor of International Journal of Wildland Fire. To mitigate this potential conflict of interest he was blinded from the review process and was not involved at any stage in the editing of this manuscript.
Declarations of funding
This work was financially supported by the Portuguese Foundation for Science and Technology through the project MCFire-PCIF/MPG/0108/2017 and project UIDB/05583/2020. The authors also acknowledge the financial support of the European Union’s Horizon 2020 Research and Innovation Action for the FirEUrisk project under grant agreement ID 101003890. Furthermore, we would like to thank the Research Centre in Digital Services (CISeD) and the Polytechnic of Viseu for their support.
References
Adab H, Devi Kanniah K, Beringer J (2016) Estimating and up-scaling fuel moisture and leaf dry matter content of a temperate humid forest using multiresolution remote sensing data. Remote Sensing 8, 961.
| Crossref | Google Scholar |
Aguado I, Chuvieco E, Borén R, Nieto H (2007) Estimation of dead fuel moisture content from meteorological data in Mediterranean areas. Applications in fire danger assessment. International Journal of Wildland Fire 16, 390-397.
| Crossref | Google Scholar |
Bakšić N, Bakšić D (2022) Predicting the fine fuel moisture content in Dalmatian black pine needle litter. International Journal of Wildland Fire 31(7), 708-719.
| Crossref | Google Scholar |
Bovill W, Hawthorne S, Radic J, Baillie C, Ashton A, Noske P, Lane P, Sheridan G (2015) Effectiveness of automated fuelsticks for predicting the moisture content of dead fuels in Eucalyptus forests. In ‘MODSIM2015, 21st International Congress on Modelling and Simulation’. (Eds T Weber, MJ McPhee, RS Anderssen) pp. 201–207. (Modelling and Simulation Society of Australia and New Zealand) 10.36334/MODSIM.2015.A4.Bovill
Catchpole EA, Catchpole WR, Viney NR, McCaw WL, Marsden-Smedley JB (2001) Estimating fuel response time and predicting fuel moisture content from field data. International Journal of Wildland Fire 10, 215-222.
| Crossref | Google Scholar |
Cawson JG, Nyman P, Schunk C, Sheridan GJ, Duff TJ, Gibos K, Bovill WD, Conedera M, Pezzatti GB, Menzel A (2020) Estimation of surface dead fine fuel moisture using automated fuel moisture sticks across a range of forests worldwide. International Journal of Wildland Fire 29, 548-559.
| Crossref | Google Scholar |
Chen CC (1990) Modification of Oswin EMC/ERH equation. Chinese Agricultural Research 39(4), 367-376.
| Google Scholar |
Henderson SM (1974) Progress in developing the thin layer drying equation. Transactions of the ASAE 17, 1167-1168.
| Crossref | Google Scholar |
Henderson SM, Pabis S (1961) Grain drying theory, I. Temperature effect on drying coefficient. Journal of Agricultural Engineering Research 6, 169-174.
| Google Scholar |
Iglesias HA, Chirife J (1976) Prediction of the effect of temperature on water sorption isotherms of food materials. Journal of Food Technology 11, 109-116.
| Crossref | Google Scholar |
Karathanos VT (1999) Determination of water content of dried fruits by drying kinetics. Journal of Food Engineering 39, 337-344.
| Crossref | Google Scholar |
Lee H, Won M, Yoon S, Jang K (2020) Estimation of 10-hour fuel moisture content using meteorological data: A model inter-comparison study. Forests 11, 982.
| Crossref | Google Scholar |
Lopes S, Viegas DX, Teixeira de Lemos L, Viegas MT (2014) Equilibrium moisture content and timelag of dead Pinus pinaster needles. International Journal of Wildland Fire 23, 721-732.
| Crossref | Google Scholar |
Matthews S (2014) Dead fuel moisture research: 1991–2012. International Journal of Wildland Fire 23, 78-92.
| Crossref | Google Scholar |
Matthews S, Gould J, McCaw L (2010) Simple models for predicting dead fuel moisture in eucalyptus forests. International Journal of Wildland Fire 19, 459-467.
| Crossref | Google Scholar |
Nelson Jr RM (1984) A method for describing equilibrium moisture content of forest fuels. Canadian Journal of Forest Research 14, 597-600.
| Crossref | Google Scholar |
Resco de Dios V, Fellows AW, Nolan RH, Boer MM, Bradstock RA, Domingo F, Goulden ML (2015) A semi-mechanistic model for predicting the moisture content of fine litter. Agricultural and Forest Meteorology 203, 64-73.
| Crossref | Google Scholar |
Rossa CG (2017) The effect of fuel moisture content on the spread rate of forest fires in the absence of wind or slope. International Journal of Wildland Fire 26, 24-31.
| Crossref | Google Scholar |
Sharples JJ, McRae RHD (2011) Evaluation of a very simple model for predicting the moisture content of eucalypt litter. International Journal of Wildland Fire 20(8), 1000-1005.
| Crossref | Google Scholar |
Van Wagner CE (1977) Conditions for the start and spread of crown fire. Canadian Journal of Forest Research 7, 23-34.
| Crossref | Google Scholar |
Viegas DX, Viegas MT, Ferreira AD (1992) Moisture content of fine forest fuels and fire occurrence in central Portugal. International Journal of Wildland Fire 2(4), 69-86.
| Crossref | Google Scholar |
Viney NR, Catchpole EA (1991) Estimating fuel moisture response times from field observations. International Journal of Wildland Fire 1, 211-214.
| Crossref | Google Scholar |




