Effects of fuel bed structure on heat transfer mechanisms within and above porous fuel beds in quiescent flame spread scenarios
Zakary Campbell-Lochrie A * , Carlos Walker-Ravena A , Michael Gallagher B , Nicholas Skowronski C , Eric V. Mueller A and Rory M. Hadden A
A * , Carlos Walker-Ravena A , Michael Gallagher B , Nicholas Skowronski C , Eric V. Mueller A and Rory M. Hadden A
A School of Engineering, The University of Edinburgh, Edinburgh, UK.
B Northern Research Station, USDA Forest Service, New Lisbon, NJ, USA.
C Northern Research Station, USDA Forest Service, Morgantown, WV, USA.
International Journal of Wildland Fire 32(6) 913-926 https://doi.org/10.1071/WF22129
Submitted: 1 July 2022 Accepted: 10 March 2023 Published: 31 March 2023
© 2023 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of IAWF. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Background: Further understanding of the effect of fuel structure on underlying physical phenomena controlling flame spread is required given the lack of a coherent porous flame spread theory.
Aims: To systematically investigate the effect of fuel structure on the heat transfer mechanisms within and above porous fuel beds.
Methods: Radiant and total heat fluxes were measured in two extended series of laboratory-based quiescent flame spread experiments in pine needle beds across a range of structural conditions (various fuel loadings, bulk densities, and fuel depths).
Key results: Peak radiant heat fluxes from the in-bed combustion region were greater than peak radiant heat fluxes from the above-bed flame front for all of the studied fuel conditions. However, the magnitude and duration of radiant heating from the above-bed flame increased with fuel loading (where bulk density was held constant and fuel depth allowed to vary).
Conclusions: Our study highlighted the important role of fuel structure on heat transfer mechanisms, and the relevance of development of semi-empirical and simplified physics-based models.
Implications: The interdependent effects of fuel bed properties on the underlying heat transfer mechanisms must be considered in the further development of coherent, flame spread theories.
Keywords: fire modelling, flame spread, fuel structure, heat flux, heat transfer, pitch pine, prescribed fire, thermal model.
Introduction
Recent decades have seen substantial developments in our understanding of flame spread, but there remains a need to develop a coherent theory for flame spread in wildland fuels (Finney et al. 2013). Improved theoretical understanding would support the development of modelling tools not only for use in different wildland fire scenarios but also to support prescribed burning (Hiers et al. 2020). Hiers et al. suggested that ‘adequate multiscale characterisation of vegetation structure and fuels is fundamental for predicting prescribed fire behaviour and effects’ (Hiers et al. 2020, p. 6). However, even at relatively small scale and for simple, homogeneous fuel beds, the porous nature of wildland fuels limits the applicability of experimentally demonstrated solid surface flame spread theories and requires improved physical understanding (Finney et al. 2013).
Porous fuels
Wildland fuel beds consist of numerous discrete fuel particles forming a porous (solid:gas) fuel matrix. This porous fuel structure affects both the ignition and burning behaviour of wildland fuel beds and introduces additional complexities compared with continuous solid fuels. The presence of air-filled voids between fuel elements, especially for high porosity fuel beds such as pine needle layers, results in fuel beds with low thermal conductivity. The porous nature of natural fuel beds also allows numerous heat transfer mechanisms (e.g. radiation, convection) and combustion phenomena (smouldering and flaming) to occur within the fuel bed. It is therefore desirable to understand and identify specific fuel bed descriptors to describe the effect of fuel bed structure on the burning behaviour both within and above the fuel bed.
Fuel bed descriptors
Several structural descriptors are commonly used to describe the structure of porous fuel beds such as pine needle litter layers. The fuel loading describes the overall mass of fuel per unit area. The bulk density is defined as the dry mass of fuel per unit volume. The packing ratio (β) is defined as the ratio between the fuel bed bulk density (ρb) and the particle density (ρp).
Porous fuel beds can also be described using the dimensionless value ασδ, which incorporates the fuel bed porosity (α), fuel bed depth (δ), and the surface-to-volume ratio of fuel elements (σ), and which was previously observed to be strongly correlated with spread rate in pine needle beds (Campbell-Lochrie et al. 2021). In this parameter, the fuel bed porosity is defined as the gaseous volume fraction (α = 1 − β), and is therefore a function of the packing ratio (β). The dimensionless parameter αβδ was also previously used by Wilson (1990) to describe porous fuel beds, and is therefore assessed as another relevant structural descriptor in a similar manner to the fuel loading, bulk density, and fuel depth.
Heat transfer in porous fuel beds
Many operational fire simulation models are underpinned by the semi-empirical model of Rothermel (1972), in which the energy conservation principle is applied to a unit volume of the fuel bed, with the flame spread rate described as the ratio between the propagating heat flux and the net heat required for ignition. However, during model development, the analytical solution of this energy balance was prevented because the heat transfer mechanisms were unknown, and instead empirical model closure terms were derived from laboratory experiments involving limited fuel types (½ inch sticks, ¼ inch sticks and excelsior).
Several simplified physics-based models (which do explicitly consider individual heat transfer mechanisms) have been proposed over the last century. However, given a lack of demonstrated physical proof, none of these models have seen operational use (Weber 1991; Sullivan 2009). For this class of model, significant differences in assumptions around the relative importance of different heat transfer mechanisms highlight the limitations of our existing knowledge of the flame spread process in porous wildland fuels (Finney et al. 2013). Several models have considered radiation to be dominant, particularly in no or low ambient wind conditions (Emmons 1963; Albini 1967; Van Wagner 1967), with different importance attached to the flame and within-bed radiation. However, other models allow for convective heating to dominate, for example in the modelling of flame spread through a matchstick array (Vogel and Williams 1970). Carrier et al. (1991) also described a theory for flame spread through a fuel bed of thin diameter, discrete fuel particles, in which they defined a ‘confusive’ dominant preheating mechanism that described convective and turbulent diffusion – although a thin fuel loading limit (approximately estimated as around 2 g/cm2), above which radiation contributions were similar in magnitude to convective/diffusion preheating, was also identified.
Development of a coherent flame spread theory for porous fuels requires a greater understanding of how the relative importance of different heat transfer mechanisms is altered by the flame spread scenario and fuel characteristics (e.g. porosity, fuel element spacing, fuel loading). This will also contribute to the continued development of detailed physics-based models.
Identification of heat transfer mechanism(s) represents an essential first step in the development of a flame spread theory (Williams 1977), and must consider the limits of applicability of any assumptions as the fuel, environmental, or topographical properties are altered. It has been suggested that radiation from the above-bed flame is of secondary importance in porous fuels, with heat transfer mechanisms within the fuel bed dominating (McCarter and Broido 1965; Rothermel and Anderson 1966). Rothermel and Anderson (1966) observed sustained flame spread in a pine needle bed even where heat transfer from the flame to the unburnt fuel was blocked (by shielding the fuel). Shielding the flame reduced the spread rate by 39% but it is not clear whether just radiation or also convection were blocked.
Past studies of the stationary burning of wood cribs have suggested that up to half of the radiative energy may be released from the within-bed burning region (containing glowing embers) (Fons 1963; McCarter and Broido 1965). More recently, using Fourier-transform infrared (FTIR) and infrared (IR) spectrometry to measure the emission spectra during the burning of various wildland fuels, Boulet et al. observed ‘continuous strong emissions’ from burning embers in the fuel bed similar to that of a blackbody at a 1000 K, which ‘could constitute a further contribution to fire propagation in addition to overhead flame radiation’ (Boulet et al. 2009, p. 883).
Past laboratory-based studies of heat transfer in wildland fuels have employed a wide range of approaches (Fons et al. 1960, 1962; Fons 1963; McCarter and Broido 1965; Thomas et al. 1965; Rothermel and Anderson 1966; Van Wagner 1967; Anderson 1969; Fang and Steward 1969; Konev and Sukhinin 1977; Vaz et al. 2004; Morandini et al. 2005; Frankman et al. 2010; Dupuy and Marechal 2011; Silvani et al. 2012; Morandini et al. 2013; Overholt et al. 2014; Finney et al. 2015; Tihay et al. 2014; Liu et al. 2015; Morandini et al. 2018; Silvani et al. 2018; Campbell-Lochrie et al. 2018; Bu et al. 2021; He et al. 2021; Cohen and Finney 2022a), as summarised in Fig. 1. The position and viewing angle of sensors will dictate the heating sources to which they are exposed, as well as determine the view factor between heat sources (e.g. overhead flame) and flux gauges.
Few previous studies have focused on the systematic manipulation of fuel properties in order to investigate the effect of fuel structure on the heat transfer mechanisms involved in flame spread. This restricts our ability to draw broad conclusions regarding the relative importance of different heat transfer mechanisms and to systematically explore the role of fuel bed structure.
As a result, the manner in which fuel bed properties (e.g. bulk density, porosity) physically affect the flame spread process often remains unclear. For example, previous studies have observed an effect of packing ratio on the spread rate (Fang and Steward 1969). The concept of an optimum packing ratio is embedded within the Rothermel model, where it is described as a function only of the surface-to-volume ratio of fuel elements (Rothermel 1972). However, the fundamental mechanism by which packing ratio influences the spread rate remains unclear (He et al. 2021) given the potential effects on both the fluid flow (and hence oxygen supply and convective heat transfer) and radiative attenuation.
In the present study, heat transfer within pine needle (Pinus rigida Mill.) fuel beds (from the combustion region and overhead flame) was investigated experimentally, complementing previous experimental investigations of the effect of fuel structure on the flow within and above similar fuel beds (Campbell-Lochrie et al. 2021). The relative importance of each heat energy transfer phenomenon was studied across a range of fuel bed structural conditions during two different experimental series.
Methods
Heat transfer above and within pitch pine (Pinus rigida Mill.) needle fuel beds during quiescent flame spread was investigated at a range of fuel conditions (fuel loading, bulk density, fuel depth) during two different laboratory-based experimental series. The location of heat flux gauges differed in each experimental series, allowing measurement of heat fluxes to the top and bottom surfaces of the fuel bed in the first series, and the heat flux from the in-bed combustion region in the second series.
Fuel properties
Fuel beds (1.5 m by 0.67 m) were composed of pitch pine needles only. This fuel type was chosen for consistency with an existing complementary study (Campbell-Lochrie et al. 2021). The pitch pine needles were collected from the Silas Little Experimental Forest in the New Jersey Pinelands National Reserve (Lat. 39°54′58″N, long. 74°35′55″W). The dead needles were stored indoors but otherwise unconditioned prior to use.
The Fuel Moisture Content (FMC) of each fuel bed was determined by the collection of fuel samples from each fuel bed prior to ignition with samples, then oven-dried at 60°C for 24 h. The average FMC across all experiments (dry weight basis) was 13.2% ± 4.6% (s.d. for N = 78). The geometric properties were measured by random sampling using the methods outlined by Thomas et al. (2017), with an average needle density of 706 ± 71 kg/m3 (s.d. for N = 10) and a surface-to-volume ratio of 5063 ± 640 m−1 (s.d. for N = 10).
Fuel bed construction
Several fuel bed parameters were varied to investigate the effects of different fuel bed properties and the applicability/limitations of existing fuel bed structural descriptors. The fuel loading was altered for fuel beds of constant bulk density by also allowing the fuel bed depth to vary. Similarly, the bulk density of fuel beds was varied at a constant fuel loading by altering the fuel bed depth (via compaction of the fuel bed). The interrelated effects of each of these three parameters (bulk density, fuel loading, fuel depth) on both the overall fire behaviour and the underlying heat transfer mechanisms could thus be investigated.
To allow uniform construction of fuel beds, 10% of the overall fuel load was weighed out using a precision balance (±0.01 g accuracy) and distributed into an area equal to 1/10th of the overall fuel bed area. Within each area, needles were dropped randomly, with no effort made to control the orientation of individual needles (however, the desired fuel depth was maintained for each fuel bed). Controlling fuel bed depth allowed variation of fuel loading without altering bulk density – or similarly, bulk density was varied by maintaining a constant fuel loading. Fuel bed depth was controlled by compressing the fuel bed with weighted sections similar in shape to the table surface, thereby applying uniform compression across the entire fuel bed. Random sampling of the fuel depth ensured that the desired fuel depth was achieved. Fuel loading and bulk density were defined according to the wet weight of pine needles.
Description of the fuel bed using the parameter ασδ was similar to the approach taken by previous authors (Curry and Fons 1940; Rothermel and Anderson 1966; Wilson 1990), and incorporates the effects of fuel loading and fuel bed compaction (Campbell-Lochrie et al. 2021), which can otherwise cancel in similar previously suggested dimensionless parameters (e.g. αβδ as described in Wilson 1990). The range of bulk densities (10–40 kg/m3) investigated reflected the limiting extremes of porosity that could be easily constructed with the chosen fuel type, but also represented typical field conditions based upon available fuel loading and fuel depth data for Pinus rigida Mill. litter layers (Gallagher et al. 2017; Mueller et al. 2017). For example, the fuel characteristics (including fuel loading and fuel bed depth) measured pre- and post-treatment for 22 prescribed burns and four wildfires conducted in the New Jersey Pinelands, as reported by Gallagher et al. (2017).
Flame spread table
Both experimental series involved laboratory-based flame spread experiments conducted on a flame spread table (1.5 m by 0.67 m) in quiescent conditions (no wind or slope). The flame spread table had a vermiculite base and insulated sidewalls. Sidewalls were adjusted to a height of 0.03 m above the fuel bed surface to prevent lateral entrainment of air. 10 mL of acetone, distributed equally over a 0.67 m × 0.02 m (l × w) strip of alumina-silica fibre, provided a line ignition source across the entire fuel bed width.
Each experiment was recorded, allowing video analysis of flame height and spread rate. Flame spread rate was calculated through linear regression analysis based on the flame front position over time, and flame height was estimated from the video.
The table was located underneath a 1 MW calorimetry hood, allowing calculation of the Heat Release Rate (HRR) by oxygen consumption calorimetry, with combustion gases extracted via an exhaust hood with an extraction flow rate of 1000 L/s. Over-spilling was prevented by steel curtain walls on each of the four sides of the extraction hood. Three species gas analysis (O2, CO2 and CO) was conducted with all calorimetry data logged at a frequency of 1 Hz. The HRR was calculated using oxygen consumption calorimetry (Janssens 1991), assuming an energy constant of 14.15 kJ/kgO2 based on an average for wildland fuels (Bartoli 2011). The history and principles of oxygen consumption calorimetry are described in detail elsewhere (Babrauskas and Grayson 1992).
Heat fluxes
The first experimental series (Experimental Series 1) focused on comparison of (radiant and total) heat fluxes measured at the top and bottom surfaces of the fuel bed. Heat flux gauges were therefore positioned either with the sensor surface flush with the top surface of the fuel bed (±0.5 mm) or flush with the bottom surface (±0.5 mm) of the fuel bed (represented by gauge numbers 2 and 10 respectively in Fig. 1). The focus of the second series (Experimental Series 2) was the measurement of (radiant and total) heat fluxes transferred laterally through the fuel bed. Heat flux gauges were therefore positioned horizontally within the fuel bed (midpoint of the gauge at a height of 12.7 mm above the table surface) with the sensor surfaces perpendicular to the direction of flame spread and viewing the within-bed combustion region (represented by gauge number 4 in Fig. 1).
Heat fluxes (radiant and total) were measured using water-cooled heat flux gauges (Hukseflux SBG01®, Hukseflux, Delft, Netherlands) calibrated up to 100 kW/m2 (<±6.5% calibration error, k = 2 coverage factor). The gauges (25.4 mm total diameter, 1 mm sensor diameter) have a response time of 200 µs and an emissivity of 0.95. For radiative heat flux measurements, a window was attached to the gauge as described in ISO 14934 (2014), with an uncoated sapphire lens (2.3 mm thick) preventing convective heat transfer to the sensor element. These windows have a spectral transmission range of 0.2–5.5 µm compared with 0.2–50 µm for the un-windowed gauges, which may result in a slight underestimate of the incident radiant flux. Sapphire windows were used in several previous wildland flame spread studies (Anderson 1969; Silvani and Morandini 2009; Silvani et al. 2012, 2018; Frankman et al. 2013; Tihay et al. 2014; Morandini et al. 2019; Fayad et al. 2022). Heat flux measurements were recorded at a minimum of 5 Hz (25 out of 29 experiments at 10 Hz). A zero error of ±0.12 kW/m2 was observed during the background period prior to ignition.
Experimental Series 1
In Experimental Series 1, four heat flux gauges were placed vertically and positioned in two pairs (radiant and total gauge in each pair). One pair was positioned such that the sensors were flush with the table surface (represented by Gauge Position 10 in Fig. 1), and the second pair was positioned with the sensors flush with the top surface of the fuel bed (represented by Gauge Position 2 in Fig. 1). All four gauges were located near the fuel bed centreline, at a distance of 1.3 m from the ignition line and 0.2 m from the end of the fuel bed, as shown in Fig. 2. Thermocouples (0.25 mm Type K) were located at a height of 10 mm above the table surface, at a distance of 0.3, 0.6 and 0.9 m from the ignition line, and along with the observed spread rate, allowed for estimation of the flame front arrival time.
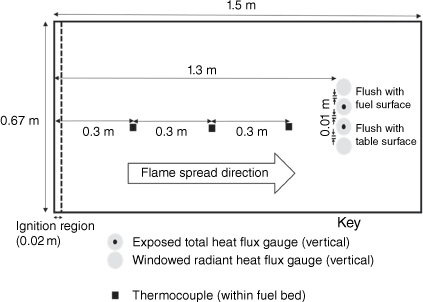
|
The fuel bed conditions studied in this first experimental series are summarised in Table 1.
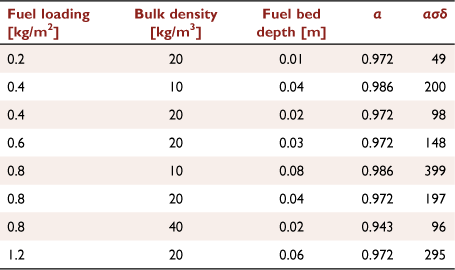
|
Experimental Series 2
In the second set of experiments, only two heat flux gauges (radiant and total) were used. These gauges were placed horizontally and located within the fuel bed (represented by Gauge Position 4 in Fig. 1), with the midpoint of the gauge at a height of 12.7 mm above the table surface. These gauges were located at a horizontal distance of 0.9 m from the ignition line and 0.6 m from the end of the fuel bed (as shown in Fig. 3). Thermocouples (0.25 mm Type K) were positioned at a height of 10 mm above the fuel bed, at a distance of 0.6, 0.8, 0.85 and 0.9 m from the ignition line, and along with the spread rate, allowed for estimation of the flame front arrival time.
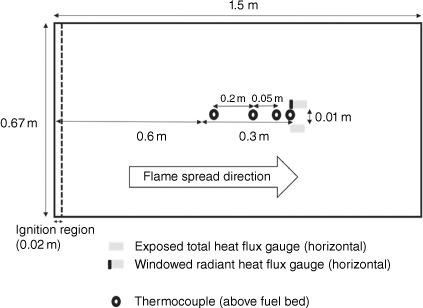
|
For this series, the flame spread table was positioned on a load cell (sampling frequency of 1 Hz, accuracy of ±1 g), allowing calculation of the burning rate. The range of fuel bed conditions studied in this experimental series are summarised in Table 2.
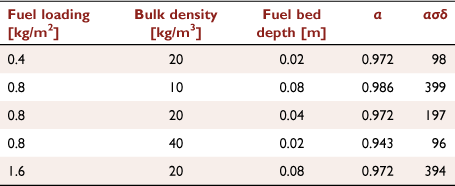
|
Results & discussion
Effect of fuel bed structure on fire behaviour
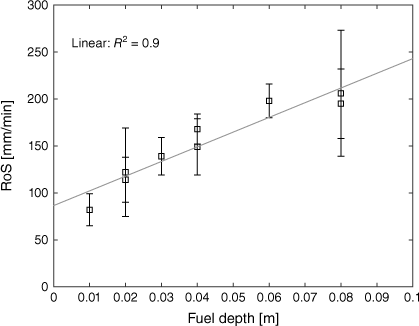
The observed fire behaviour (spread rate, flame height, HRR) at each fuel condition is summarised in Table 3. As shown in Fig. 4, a relatively linear relationship (R2 = 0.9) was observed between fuel depth and spread rate, but the bulk density and fuel loading of the fuel beds varied across the range of fuel depths studied. The interdependence of fuel bed parameters must be considered along with the manner in which the fuel depth was altered in each case. For a constant packing ratio, increased fuel loading (where fuel depth also varied) was associated with increased spread rate in this quiescent flame spread scenario, but the effects of packing ratio cannot be isolated from fuel loading and depth.

|
|
This interdependence and correlation between fuel parameters was previously discussed by Rossa and Fernandes (2018). For example, they highlighted that the correlation between fuel depth and fuel loading (for a fixed bulk density) must be considered. A similar observation was made by Catchpole et al. (1998), p. 27, who stated that ‘the relationship of spread rate with load is dependent on how the increase in loading is obtained’ for example whether the packing ratio or fuel depth is fixed.
The experiments in this study exhibited periods of constant Mass Loss Rate (MLR), and the average MLR across this period was therefore reported. This is in line with the approach discussed by Viegas et al. (2018). MLR was calculated as the derivative of the mass over a given timestep with a 5 s moving average applied.
At most fuel conditions the onset of quasi-steady state flame spread involving a single, linear flame front was quickly observed, but this was not the case at the lowest fuel loading (0.2 kg/m2). In this case, visual observations (shown in Fig. 5) also highlighted the absence of a smouldering region behind the flame front (present at all other fuel conditions). In all other cases studied, the continuous flame front width was equal to the fuel bed width (0.67 m), with the flame front remaining largely perpendicular to the direction of flame spread.

|
These variations in the flame spread behaviour may reflect the importance of individual particle effects at this lowest fuel loading, where the fuel bed visually displays greater discontinuity. However, further systematic study at these low fuel loadings is required before conclusive findings can be drawn regarding the importance of particle effects (and the responsible mechanisms) in this scenario and fuel type.
Flame spread behaviour at the individual particle scale has been studied by previous authors (Weber and De Mestre 1990), with Lai et al. investigating the mechanisms responsible for the effect of inclination angles on fire propagation along wooden rods (Lai et al. 2020). Fang and Steward (1969) also observed a significant increase in spread rate through excelsior fuel beds (of fixed voidage and fuel loading) as the particle length was increased (and thus the connectivity of fuel elements altered).
Further understanding of the interaction of the individual fuel particle properties and the resulting fuel bed structure, including the connectivity of particles, is required. For example, Dupuy previously suggested a term to estimate the characteristic distance between pine needles as a function of packing ratio and surface-to-volume ratio (Dupuy 1995). The effect of other fuel bed parameters (e.g. fuel loading) may require consideration when estimating this average separation distance and the influence of this term.
Effect of fuel structure on heat fluxes
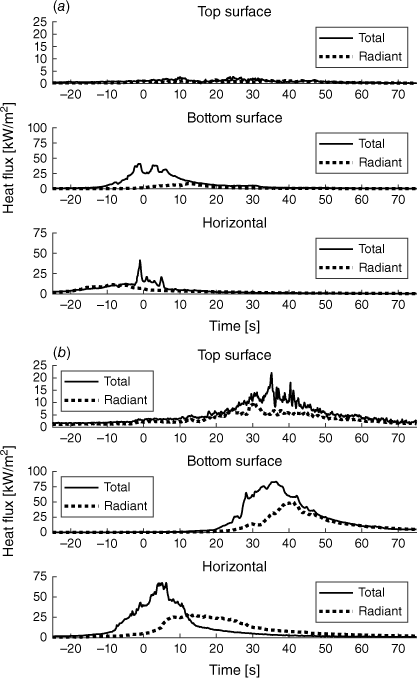
The typical heating profile consisted of an initial steady growth period as the flame front approached the gauge, with a subsequent sharp rate of increase followed by characteristic peak-decay behaviour, as illustrated in Fig. 6. Peak (radiant and total) heat fluxes are summarised in Table 4, where average values (and max/min range) at each fuel condition are reported for each measurement location. Where the peak total heat flux was greater than the maximum of the calibration range (100 kW/m2), its absolute value should be interpreted with caution.
|

|
For all fuel bed conditions, radiant heating from the above-bed flame to the fuel bed surface remained low (max. of 11 kW/m2 and less than 5 kW/m2 for the majority of the studied fuel conditions). A maximum peak radiant heat flux at the top surface of the fuel bed of 11 kW/m2 was measured for the fuel bed of 1.6 kg/m2 fuel loading. It should be considered, however, that past studies have shown that even relatively low imposed radiant fluxes can significantly influence the flame spread rate (a summary of studies in various fuel types was previously provided by Drysdale (2011)), although further investigation and understanding of the heating response of vegetation particles is required (see for example (Cohen and Finney 2022a)).
Peak radiant heat fluxes were similar to those previously measured in both pine needle beds (Morandini et al. 2005) and laser-cut cardboard fuel arrays (He et al. 2021). At the lowest fuel loading (0.2 kg/m2), a negligible radiant flux (0.2 kW/m2) was measured at the top fuel bed surface. However, this may partly reflect the dependence of the flame proximity to the gauge on the structure of individual needles given the greater average separation distance between pine needles at this condition.
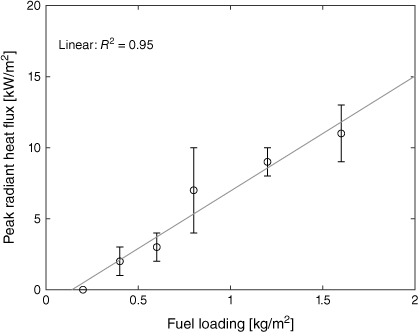
Peak radiant fluxes measured at the top surface of the fuel bed increased with increasing fuel loading (for a constant packing ratio with fuel bed depth allowed to vary), with a relatively linear trend observed (R2 = 0.95 for 20 kg/m3 fuel beds of various fuel loadings with fuel depth allowed to vary), as shown in Fig. 7. As fuel loading increased from 0.4 to 1.6 kg/m2 (for 20 kg/m3 fuel beds, fuel depth varying from 0.02 to 0.08 m), peak radiant heat fluxes measured at the top surface increased by 450%. Little effect of bulk density (or packing ratio) on the radiant heat flux at the top surface of fuel bed was observed (for fuel beds of fixed fuel loading and varying fuel depth). Over the widest range of bulk densities (10–40 kg/m3 for 0.8 kg/m2 fuel beds with fuel depth varying from 0.08 to 0.02 m) an initial increase in surface radiative flux occurred as the bulk density increased (10–20 kg/m3), followed by a decline as the fuel bed was further compressed (20–40 kg/m3).
|
Peak total heat flux measured at the top surface of the fuel bed also increased with increasing fuel loading (for a constant bulk density with fuel depth allowed to vary). A negligible peak total heat flux (0.1 kg/m2) was measured for the lowest fuel loading (0.2 kg/m2), with the peak total flux at the top surface gauge increasing as the fuel loading was increased from 0.4 to 1.6 kg/m2 (for 20 kg/m3 fuel beds with fuel depth allowed to vary). As with radiant fluxes, variations in total peak heat fluxes – measured at the top surface of the fuel bed of different bulk density (but constant fuel loading with fuel depth allowed to vary) – are typically within the range of experimental uncertainty; however, a sharp decline was observed for the highest bulk density case (0.8 kg/m2, 40 kg/m3).
As previously mentioned, caution is required when interpreting these peak total heat flux magnitudes because the convective heat transfer is dependent upon the gauge properties and does not represent the actual convective heat flux experienced by a pine needle. The response to heating of particles will depend upon the particle properties (Cohen and Finney 2022b). Peak total heat fluxes measured by the gauges at the top surface of the fuel bed were greater than the peak radiant heat flux for all fuel bed conditions other than the lowest fuel loading (0.2 kg/m2), where both were negligible. For the other fuel conditions, ratios of peak total to peak radiant heat flux at the top surface ranged from 1.5 to 4.5.
Compression of fuel beds (increasing the bulk density by reducing the fuel depth) also reduces the average distance between fuel elements. For 0.8 kg/m2 fuel beds, the peak radiant flux transferred horizontally through the fuel bed to the gauge was reduced by 48% as the bulk density was increased from 10 to 40 kg/m3. A slight increase in radiant heat fluxes (within the experimental error) was observed for the intermediate bulk density case (20 kg/m3). Therefore, further investigation of this non-linear behaviour is required.
Relative contribution of above-bed flame and within-bed combustion region
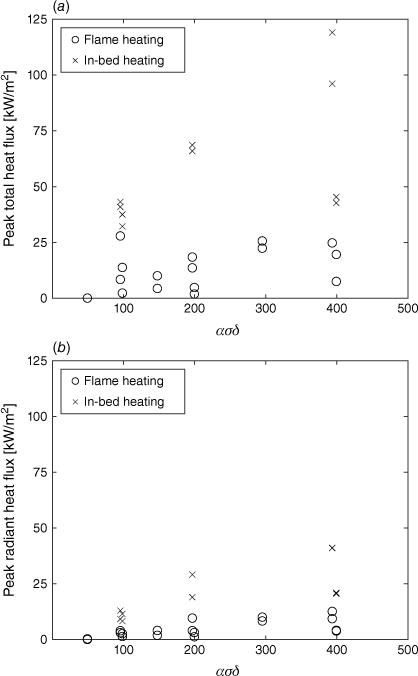
Significant variations between peak heat fluxes measured at each gauge location for a given fuel bed condition can also be observed in Table 4 and Fig. 8. This allows the relative importance of the within-bed heating and above-bed heating to be explored as a function of fuel structure. The greatest peak (radiant and total) fluxes were measured by gauges at the bottom surface of the fuel bed or the horizontal gauges located within the fuel bed, which primarily measure heat flux transferred from the within-bed combustion region.
|
As shown in Table 4, peak heat fluxes measured at the top surface of the fuel bed are significantly lower than at either of the other two measurement locations. Greater heat transfer is observed from the within-bed combustion region than from the overhead flame. Across all fuel bed conditions, the ratio of peak total heat flux at the bottom surface to that at the top fuel bed surface ranged from 2.2 to 14. This agrees with previous qualitative observations in pine needle beds and wood cribs (McCarter and Broido 1965; Rothermel and Anderson 1966), and with previous measurements of within-bed and above-bed radiant fluxes in wood shaving fuel beds (Fang and Steward 1969).
For the studied fuel conditions, the ratio of peak radiant heat flux transferred horizontally through the fuel bed from the within-bed combustion region to the peak radiant heat flux at the top surface of the fuel bed ranged from 2.8 to 6.0 (excluding the lowest fuel loading case). This is similar to previous observations in wood shaving fuel beds (Fang and Steward 1969), where radiant heating through the fuel bed (from the ‘burning embers’) was greater than the overhead flame heating with the ‘burning zone transfer(ing) about three times the radiant energy to the unburnt to the unburnt fuel at short distance of one inch or less’ (Fang and Steward 1969, p. 396).
In a similar manner to earlier work (Fang and Steward 1969), the radiant heat flux from the overhead flame and burning zone are each shown relative to the distance ahead of the flame front in Fig. 9. For each fuel condition, a 1 s moving average was applied to the radiant heat flux profiles from each experiment. The average profiles (established relative to the time at which the peak heat flux occurs) are reported for each fuel bed condition with the position of the flame front established based upon the average spread rate at each fuel condition.
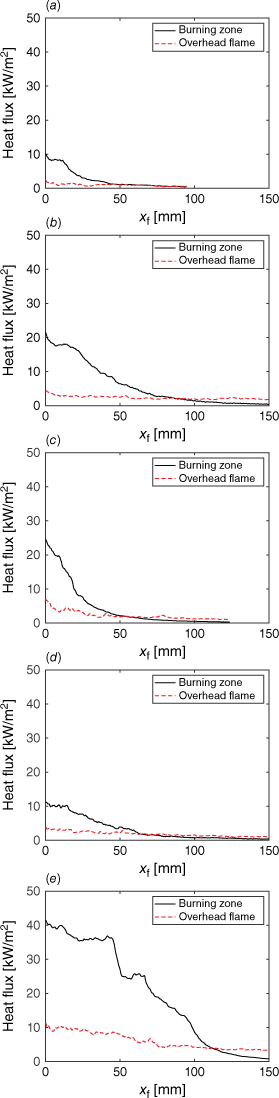
|
As the flame front approaches the heat flux gauge, the difference between the magnitude of radiant heating from the burning zone and from the flame region increases. The ratio between flame and burning zone radiant heat flux varied with fuel loading and bulk density (where in each case fuel depth was allowed to vary). This is important because fuel bed structure (including fuel loading) was not considered in this context by Fang and Steward (1969), who presented a radiant heating plot for a single, unidentified fuel bed of wood shavings; however, in the present study, the influence of fuel loading, bulk density and fuel depth are observed and the interdependence of fuel parameters must be considered.
Effective heating distance
The flux density distribution ahead of the flame front was calculated using the observed flame spread rate and the flame arrival time at the thermocouple locations. This allowed calculation of the effective heating distance (the distance ahead of the flame front at which the radiant heat flux received by the gauge first exceeds background levels). The maximum effective heating distance was less than 250 mm. However, the peak heat flux occurred after the initial flame front arrival. This is partly due to an extended heating duration after the initial flame front arrival, when the trailing flaming and smouldering regions continue to propagate over the gauges.
Given the dual influence of view factor and fuel bed attenuation, the radiant heat flux transferred through the fuel bed to the gauge varies as a function of the distance from the flame front. The view factor will vary by gauge location, depending upon the geometric arrangement of the gauge and the radiator (flame or combustion region). A view factor can be estimated for each gauge location by assuming the radiator to be well-approximated by a rectangle (as described by McGuire (1952)). The heat flux gauge orientations used in this study can be represented by either a parallel or perpendicular discrete element receiver. The resulting view factors, as a function of distance between gauge and radiator and also fuel bed depth, are shown in Fig. 10. It should be noted that while the peak view factor is significantly lower for the perpendicularly aligned gauge, the presence of the radiator directly in front of the gauge surface at the arrival time means that it may be more appropriate to describe both gauge orientations as parallel to the radiator at the time of flame/combustion region arrival.
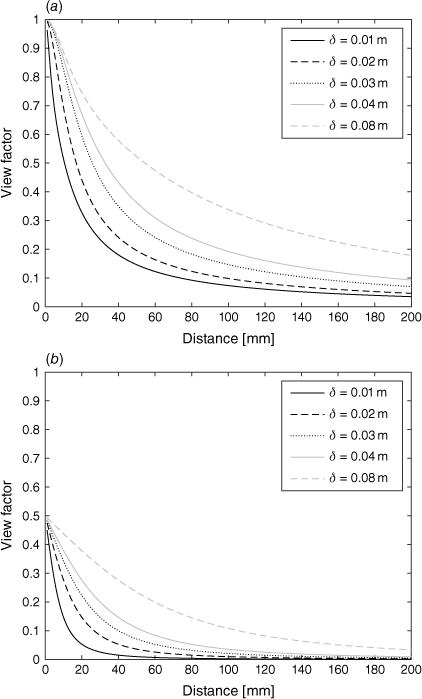
|
Heat flux duration
Comparison of the effective heating distance is complicated by the variation in spread rates between the different fuel conditions. Considering the radiant flux as a function of time (rather than as a function of distance ahead of the flame front) provided greater insight into the heat flux duration, which is important for understanding the heating and ignition of fuel particles.
The overall heat flux duration was calculated by applying a threshold of 1 kW/m2 to the measured heat flux values. This period in which radiant heating is observed can then be plotted as a function of time from the initial radiant heating onset time. As shown in Fig. 11, for fuel beds of fixed bulk density, altering the fuel loading by varying the fuel bed depth also affected the overall radiant heat flux duration at the top surface of the fuel bed. The overall radiant heat flux duration at the top surface of the fuel bed increased with increased fuel loading (for fuel beds of constant bulk density with fuel depth allowed to vary). For 20 kg/m3 fuel beds, the overall radiant heat flux duration (above the 1 kw/m2 threshold) to the top surface of the fuel bed increased from an average of 57 ± 10 s for a 0.4 kg/m2 (0.02 m depth) fuel bed to 164 ± 11 s for a 1.6 kg/m2 (0.08 m depth) fuel bed (±max/min). This increased overall radiant heat flux duration occurs despite the increased spread rate with greater fuel loading (for fuel beds of constant bulk density with fuel bed depth allowed to vary).
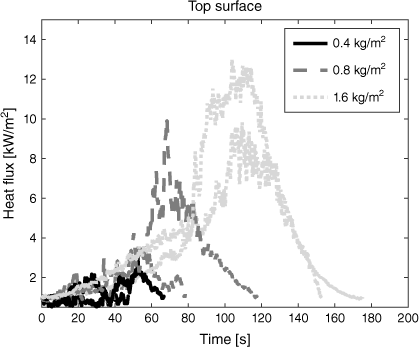
|
A similar trend was observed for the duration of radiant heat flux (above the 1 kw/m2 threshold) for the gauge positioned flush with the lower surface of the fuel bed. For 20 kg/m3 fuel beds, the overall radiant heat flux duration (above the 1 kw/m2 threshold) to the bottom surface of the fuel bed increased from an average of 41 ± 6 s for a 0.4 kg/m2 (0.02 m depth) fuel bed to 135 ± 25 s for a 1.6 kg/m2 (0.08 m depth) fuel bed (±max/min).
Conclusions
Two experimental series, involving different heat flux measurement locations, address an existing need for experimental observation of the effect of fuel structure on the heat transfer in natural, porous fuel beds, and the resulting flame spread rate and fire behaviour (flame height, HRR, burning rate). Heat flux gauges measured the heat flux from the above-bed flame and the within-bed combustion region at each fuel condition. Heat transfer through the fuel bed (from the in-bed combustion region) was dominant for all fuel bed conditions.
The contribution from the above-bed flame typically increased for higher ασδ values or higher fuel loadings (for a fixed packing ratio with fuel depth allowed to vary). However, it remained low across all fuel conditions (max radiant heat flux of 11 kW/m2 at max fuel loading and highest flame height case, and less than 5 kW/m2 for the majority of fuel conditions). The overall duration of radiant heat flux (above a 1 kW/m2 threshold) at the top surface of the fuel bed also increased for higher fuel loadings (for a fixed packing ratio with fuel depth allowed to vary).
As stressed throughout this study, the interaction of different fuel parameters (e.g. fuel bed depth also varies when the fuel loading is altered at a constant packing ratio) must be remembered when considering these conclusions. The approach taken in this study therefore offers additional insight to supplement observations from related previous studies that have often simultaneously varied fuel loading and packing ratio. Flame height was also observed to vary with fuel loading (for a fixed bulk density where fuel depth was therefore also varied) and with bulk density (for a fixed fuel loading where fuel depth was therefore also varied), affecting the above-bed heat transfer and effective heating distance. However, radiant heat fluxes from the combustion region also varied non-linearly with bulk density (for a fixed fuel loading with fuel depth allowed to vary), with a 48% lower peak radiant flux for a compressed 40 kg/m3 fuel bed compared with a higher porosity 10 kg/m3 fuel bed of equal fuel loading (0.8 kg/m2).
At all but the lowest fuel loading (0.2 kg/m2), the peak total heat flux to the gauges exceeded the peak total radiant flux. However, in this study, the dependence of the convective heat transfer profile on the gauge properties must be considered because the response of fuel particles would differ. The interdependence of the different fuel bed parameters (fuel loading, bulk density, fuel bed depth) should also be considered when interpreting these results, given that previous authors have highlighted the potential for regime changes as the fuel loading (and/or fuel bed depth) vary. Additionally, the role of fine-scalefuel bed structure (e.g. inter-needle connections, needle orientation) requires further investigation given the observed effects of needle sparsity at the lowest fuel loadings investigated in this study.
Data availability
The data that support this study will be shared upon reasonable request to the corresponding author.
Conflicts of interest
The authors declare no conflicts of interests.
Declaration of funding
The authors wish to thank the US Department of Defense – Strategic Environmental Research and Development Program (SERDP) for their financial support under the project grant RC-2641.
References
Albini FA (1967) A physical model for firespread in brush. Symposium (International) on Combustion 11, 553–560.| A physical model for firespread in brush.Crossref | GoogleScholarGoogle Scholar |
Anderson HE (1969) Heat transfer and fire spread. Research Paper INT-69, USDA Forest Service, Ogden, UT, USA.
| Crossref |
Babrauskas V, Grayson S (1992) ‘Heat Release in Fires.’ (Elsevier Applied Science: New York, NY, USA)
Bartoli P (2011) Feux de forêt : amélioration de la connaissance du couplage combustible-flamme. PhD Thesis, Universite di Corsica-Pasquale Paoli, Corte, France and The University of Edinburgh, Scotland. [In French]
Boulet P, Parent G, Collin A, Acem Z, Porterie B, Clerc JP, Consalvi JL, Kaiss A (2009) Spectral emission of flames from laboratory-scale vegetation fires. International Journal of Wildland Fire 18, 875–884.
| Spectral emission of flames from laboratory-scale vegetation fires.Crossref | GoogleScholarGoogle Scholar |
Bu R, Zhou Y, Shi L, Fan C (2021) Experimental study on combustion and flame spread characteristics in horizontal arrays of discrete fuels. Combustion and Flame 225, 136–146.
| Experimental study on combustion and flame spread characteristics in horizontal arrays of discrete fuels.Crossref | GoogleScholarGoogle Scholar |
Campbell-Lochrie Z, Walker-Ravena C, Mueller E V, Hadden RM (2018) The effect of interstitial flow on the burning dynamics of porous fuel beds. In ‘Advances in Forest Fire Research 2018’. (Ed. Viegas DX) (Imprensa da Universidade de Coimbra: Coimbra, Portugal)
| Crossref |
Campbell-Lochrie Z, Walker-Ravena C, Gallagher M, Skowronski N, Mueller EV, Hadden RM (2021) Investigation of the role of bulk properties and in-bed structure in the flow regime of buoyancy-dominated flame spread in porous fuel beds. Fire Safety Journal 120, 103035
| Investigation of the role of bulk properties and in-bed structure in the flow regime of buoyancy-dominated flame spread in porous fuel beds.Crossref | GoogleScholarGoogle Scholar |
Carrier GF, Fendell FE, Wolff MF (1991) Wind-aided firespread across arrays of discrete fuel elements. I. Theory. Combustion Science and Technology 75, 31–51.
| Wind-aided firespread across arrays of discrete fuel elements. I. Theory.Crossref | GoogleScholarGoogle Scholar |
Catchpole WR, Catchpole EA, Butler BW, Rothermel RC, Morris GA, Latham DJ (1998) Rate of spread of free-burning fires in woody fuels in a wind tunnel. Combustion Science and Technology 131, 1–37.
| Rate of spread of free-burning fires in woody fuels in a wind tunnel.Crossref | GoogleScholarGoogle Scholar |
Cohen JD, Finney MA (2022a) Fuel particle heat transfer part 2: radiation and vonvection during dpreading laboratory fires. Combustion Science and Technology
| Fuel particle heat transfer part 2: radiation and vonvection during dpreading laboratory fires.Crossref | GoogleScholarGoogle Scholar |
Cohen JD, Finney MA (2022b) Fuel particle heat transfer part 1: convective cooling of irradiated fuel particles. Combustion Science and Technology
| Fuel particle heat transfer part 1: convective cooling of irradiated fuel particles.Crossref | GoogleScholarGoogle Scholar |
Curry JR, Fons WL (1940) Forest-fire behavior studies. Mechanical Engineering 62, 219–225.
Drysdale D (2011) ‘An Introduction to Fire Dynamics.’ (John Wiley & Sons: Chichester, UK)
Dupuy JL (1995) Slope and fuel load effects on fire behavior: laboratory experiments in pine needles fuel beds. International Journal of Wildland Fire 5, 153–164.
| Slope and fuel load effects on fire behavior: laboratory experiments in pine needles fuel beds.Crossref | GoogleScholarGoogle Scholar |
Dupuy JL, Maréchal J (2011) Slope effect on laboratory fire spread: contribution of radiation and convection to fuel bed preheating. International Journal of Wildland Fire 20, 289–307.
| Slope effect on laboratory fire spread: contribution of radiation and convection to fuel bed preheating.Crossref | GoogleScholarGoogle Scholar |
Emmons H (1963) Fire in the Forest. In ‘Fire Research Abstracts and Reviews. Vol. 5’. (National Academies Press: Washington, DC, USA) (Ed. W. G. Berl). pp. 163–178.
| Crossref |
Fang JB, Steward FR (1969) Flame spread through randomly packed fuel particles. Combustion and Flame 13, 392–398.
| Flame spread through randomly packed fuel particles.Crossref | GoogleScholarGoogle Scholar |
Fayad J, Rossi L, Frangieh N, Awad C, Accary G, Chatelon F-J, Morandini F, Marcelli T, Cancellieri V, Cancellieri D, Morvan D, Pieri A, Planelles G, Costantini R, Meradji S, Rossi J-L (2022) Numerical study of an experimental high-intensity prescribed fire across Corsican Genista salzmannii vegetation. Fire Safety Journal 131, 103600
| Numerical study of an experimental high-intensity prescribed fire across Corsican Genista salzmannii vegetation.Crossref | GoogleScholarGoogle Scholar |
Finney MA, Cohen JD, Mcallister SS, Jolly WM (2013) On the need for a theory of wildland fire spread. International Journal of Wildland Fire 22, 25–36.
| On the need for a theory of wildland fire spread.Crossref | GoogleScholarGoogle Scholar |
Finney MA, Cohen JD, Forthofer JM, McAllister SS, Gollner MJ, Gorham DJ, Saito K, Akafuah NK, Adam BA, English JD (2015) Role of buoyant flame dynamics in wildfire spread. Proceedings of the National Academy of Sciences 112, 9833–9838.
| Role of buoyant flame dynamics in wildfire spread.Crossref | GoogleScholarGoogle Scholar |
Fons WL (1963) Forest fire modelling. In ‘ASME-ASCE Meeting, August 1963, Boston, MA’. pp. 164–175. (US Forest Service: Washington, DC, USA)
Fons WL, Bruce HD, Pong WY, Richards S (1960) Project Fire Model Summary Progress Report. Period 1 November 1958 to 30 April 1960. Pacific Southwest Forest and Range Experiment Station, Berkeley, CA, USA. Available at https://archive.org/details/CAT31365383/page/n1/mode/2up
Fons WL, Clements HB, Elliot ER, George P (1962) Project Fire Model – Summary Progress Report II. Period 1 May 1960 to 30 April 1962. Southern Forest Fire Laboratory, Macon, GA, USA. Available at https://www.srs.fs.usda.gov/pubs/ja/1960/ja_1960_fons_001.pdf
Frankman D, Webb BW, Butler BW (2010) Time-resolved radiation and convection heat transfer in combusting discontinuous fuel beds. Combustion Science and Technology 182, 1391–1412.
| Time-resolved radiation and convection heat transfer in combusting discontinuous fuel beds.Crossref | GoogleScholarGoogle Scholar |
Frankman D, Webb BW, Butler BW, Jimenez D, Forthofer JM, Sopko P, Shannon KS, Hiers JK, Ottmar RD (2013) Measurements of convective and radiative heating in wildland fires. International Journal of Wildland Fire 22, 157–167.
| Measurements of convective and radiative heating in wildland fires.Crossref | GoogleScholarGoogle Scholar |
Gallagher MR, Clark KL, Thomas JC, Mell WE, Hadden RM, Mueller EV, Kremens RL, El Houssami M, Filkov AI, Simeoni AA, Skowronski NS (2017) New Jersey fuel treatment effects: pre-and post-burn biometric data. Forest Service Research Data Archive, Washington, DC, USA
| Crossref |
He Q, Liu N, Xie X, Zhang L, Zhang Y, Yan W (2021) Experimental study on fire spread over discrete fuel bed. Part I: effects of packing ratio. Fire Safety Journal 126, 103470
| Experimental study on fire spread over discrete fuel bed. Part I: effects of packing ratio.Crossref | GoogleScholarGoogle Scholar |
Hiers JK, O’Brien JJ, Varner JM, Butler BW, Dickinson M, Furman J, Gallagher M, Godwin D, Goodrick SL, Hood SM, Hudak A, Kobziar LN, Linn R, Loudermilk EL, McCaffrey S, Robertson K, Rowell EM, Skowronski N, Watts AC, Yedinak KM (2020) Prescribed fire science: the case for a refined research agenda. Fire Ecology 16, 11
| Prescribed fire science: the case for a refined research agenda.Crossref | GoogleScholarGoogle Scholar |
ISO 14934-4:2014 (2014) Fire tests – Calibration and use of heat flux meters – Part 4 : guidance on the use of heat flux meters in fire tests. International Organization for Standardization (ISO), Geneva, Switzerland. Available at https://www.iso.org/obp/ui/-iso:std:iso:14934:-4:ed-1:v1:en
Janssens ML (1991) Measuring rate of heat release by oxygen consumption. Fire Technology 27, 234–249.
| Measuring rate of heat release by oxygen consumption.Crossref | GoogleScholarGoogle Scholar |
Konev EV, Sukhinin AI (1977) The analysis of flame spread through forest fuel. Combustion and Flame 28, 217–223.
| The analysis of flame spread through forest fuel.Crossref | GoogleScholarGoogle Scholar |
Lai Y, Wang X, Rockett TBO, Willmott JR, Zhou H, Zhang Y (2020) The effect of preheating on fire propagation on inclined wood by multi-spectrum and schlieren visualisation. Fire Safety Journal 118, 103223
| The effect of preheating on fire propagation on inclined wood by multi-spectrum and schlieren visualisation.Crossref | GoogleScholarGoogle Scholar |
Liu N, Wu J, Chen H, Zhang L, Deng Z, Satoh K, Viegas DX, Raposo JR (2015) Upslope spread of a linear flame front over a pine needle fuel bed: the role of convection cooling. Proceedings of the Combustion Institute 35, 2691–2698.
| Upslope spread of a linear flame front over a pine needle fuel bed: the role of convection cooling.Crossref | GoogleScholarGoogle Scholar |
McCarter RJ, Broido A (1965) Radiative and convective energy from wood crib fires. Pyrodynamics 2, 65–85.
McGuire JH (1952) The calculation of heat transfer by radiation. Fire Research Note No. 20. International Association for Fire Safety Science. Available at https://publications.iafss.org/publications/frn/20/-1/view/frn_20.pdf
Morandini F, Simeoni A, Santoni PA, Balbi JH (2005) A model for the spread of fire across a fuel bed incorporating the effects of wind and slope. Combustion Science and Technology 177, 1381–1418.
| A model for the spread of fire across a fuel bed incorporating the effects of wind and slope.Crossref | GoogleScholarGoogle Scholar |
Morandini F, Perez-Ramirez Y, Tihay V, Santoni PA, Barboni T (2013) Radiant, convective and heat release characterization of vegetation fire. International Journal of Thermal Sciences 70, 83–91.
| Radiant, convective and heat release characterization of vegetation fire.Crossref | GoogleScholarGoogle Scholar |
Morandini F, Silvani X, Dupuy JL, Susset A (2018) Fire spread across a sloping fuel bed: flame dynamics and heat transfers. Combustion and Flame 190, 158–170.
| Fire spread across a sloping fuel bed: flame dynamics and heat transfers.Crossref | GoogleScholarGoogle Scholar |
Morandini F, Toulouse T, Silvani X, Pieri A, Rossi L (2019) Image-based diagnostic system for the measurement of flame properties and radiation. Fire Technology 55, 2443–2463.
| Image-based diagnostic system for the measurement of flame properties and radiation.Crossref | GoogleScholarGoogle Scholar |
Mueller E V, Skowronski N, Clark K, Gallagher M, Kremens R, Thomas JC, El Houssami M, Filkov A, Hadden RM, Mell W, Simeoni A (2017) Utilization of remote sensing techniques for the quantification of fire behavior in two pine stands. Fire Safety Journal 91, 845–854.
| Utilization of remote sensing techniques for the quantification of fire behavior in two pine stands.Crossref | GoogleScholarGoogle Scholar |
Overholt KJ, Kurzawski AJ, Cabrera J, Koopersmith M, Ezekoye OA (2014) Fire behavior and heat fluxes for lab-scale burning of little bluestem grass. Fire Safety Journal 67, 70–81.
| Fire behavior and heat fluxes for lab-scale burning of little bluestem grass.Crossref | GoogleScholarGoogle Scholar |
Rossa CG, Fernandes PM (2018) Empirical modeling of fire spread rate in no-wind and no-slope conditions. Forest Science 64, 358–370.
| Empirical modeling of fire spread rate in no-wind and no-slope conditions.Crossref | GoogleScholarGoogle Scholar |
Rothermel RC (1972) A mathematical model for predicting fire spread in wildland fuels. Research Paper INT-115. USDA Forest Service, Intermountain Forest and Range Experiment Station, Ogden, UT, USA
Rothermel RC, Anderson HE (1966) Fire spread characteristics determined in the laboratory. Research Paper INT-30. US Forest Service, Intermountain Forest & Range Experiment Station, Ogden, UT, USA
Silvani X, Morandini F (2009) Fire spread experiments in the field: temperature and heat fluxes measurements. Fire Safety Journal 44, 279–285.
| Fire spread experiments in the field: temperature and heat fluxes measurements.Crossref | GoogleScholarGoogle Scholar |
Silvani X, Morandini F, Dupuy JL (2012) Effects of slope on fire spread observed through video images and multiple-point thermal measurements. Experimental Thermal and Fluid Science 41, 99–111.
| Effects of slope on fire spread observed through video images and multiple-point thermal measurements.Crossref | GoogleScholarGoogle Scholar |
Silvani X, Morandini F, Dupuy JL, Susset A, Vernet R, Lambert O (2018) Measuring velocity field and heat transfer during natural fire spread over large inclinable bench. Experimental Thermal and Fluid Science 92, 184–201.
| Measuring velocity field and heat transfer during natural fire spread over large inclinable bench.Crossref | GoogleScholarGoogle Scholar |
Sullivan AL (2009) Wildland surface fire spread modelling, 1990–2007. 1: Physical and quasi-physical models. International Journal of Wildland Fire 18, 349–368.
| Wildland surface fire spread modelling, 1990–2007. 1: Physical and quasi-physical models.Crossref | GoogleScholarGoogle Scholar |
Thomas PH, Simms DL, Wraight HG (1965) Fire spread in wooden cribs. Part II. Heat transfer experiments in still air. Fire Safety Science 599, 1
Thomas JC, Hadden RM, Simeoni A (2017) Experimental investigation of the impact of oxygen flux on the burning dynamics of forest fuel beds. Fire Safety Journal 91, 855–863.
| Experimental investigation of the impact of oxygen flux on the burning dynamics of forest fuel beds.Crossref | GoogleScholarGoogle Scholar |
Tihay V, Morandini F, Santoni PA, Perez-Ramirez Y, Barboni T (2014) Combustion of forest litters under slope conditions: burning rate, heat release rate, convective and radiant fractions for different loads. Combustion and Flame 161, 3237–3248.
| Combustion of forest litters under slope conditions: burning rate, heat release rate, convective and radiant fractions for different loads.Crossref | GoogleScholarGoogle Scholar |
Van Wagner CE (1967) Calculations on forest fire spread by flame radiation. Forestry Branch Departmental Publication No. 1185. Available at https://cfs.nrcan.gc.ca/pubwarehouse/pdfs/24717.pdf
Vaz GC, André JCS, Viegas DX (2004) Fire spread model for a linear front in a horizontal solid porous fuel bed in still air. Combustion Science and Technology 176, 135–182.
| Fire spread model for a linear front in a horizontal solid porous fuel bed in still air.Crossref | GoogleScholarGoogle Scholar |
Viegas DX, Pinto C, Raposo J (2018) Burning rate. In ‘Encyclopedia of wildfires and wildland-urban interface (WUI) fires’. (Ed. S Manzello) pp. 1–8. (Springer: Cham)
| Crossref |
Vogel M, Williams FA (1970) Flame propagation along matchstick arrays. Combustion Science and Technology 1, 429–436.
| Flame propagation along matchstick arrays.Crossref | GoogleScholarGoogle Scholar |
Weber RO (1991) Modelling fire spread through fuel beds. Progress in Energy and Combustion Science 17, 67–82.
| Modelling fire spread through fuel beds.Crossref | GoogleScholarGoogle Scholar |
Weber RO, De Mestre NJ (1990) Flame spread measurements on single Ponderosa pine needles: effect of sample orientation and concurrent external flow. Combustion Science and Technology 70, 17–32.
| Flame spread measurements on single Ponderosa pine needles: effect of sample orientation and concurrent external flow.Crossref | GoogleScholarGoogle Scholar |
Williams FA (1977) Mechanisms of fire spread. Symposium (International) on Combustion 16, 1281–1294.
| Mechanisms of fire spread.Crossref | GoogleScholarGoogle Scholar |
Wilson RA (1990) Reexamination of Rothermel fire spread equations in no-wind and no-slope conditions. Research Paper INT-434. USDA Forest Service, Intermountain Research Station, Ogden, UT, USA.



