Severe convection-related winds in Australia and their associated environments
Andrew Brown A B and Andrew Dowdy AA Bureau of Meteorology, Melbourne, Vic., Australia.
B Corresponding author. Email: andrew.brown@bom.gov.au
Journal of Southern Hemisphere Earth Systems Science 71(1) 30-52 https://doi.org/10.1071/ES19052
Submitted: 11 May 2020 Accepted: 20 November 2020 Published: 29 January 2021
Journal Compilation © BoM 2021 Open Access CC BY-NC-ND
Abstract
Severe surface wind gusts produced by thunderstorms have the potential to damage infrastructure and are a major hazard for society. Wind gust data are examined from 35 observing stations around Australia, with lightning observations used to indicate the occurrence of deep convective processes in the vicinity of the observed wind gusts. A collation of severe thunderstorm reports is also used to complement the station wind gust data. Atmospheric reanalysis data are used to systematically examine large-scale environmental measures associated with severe convective winds. We find that methods based on environmental measures provide a better indication of the observed severe convective winds than the simulated model wind gusts from the reanalysis data, noting that the spatial scales on which these events occur are typically smaller than the reanalysis grid cells. Consistent with previous studies in other regions and idealised modelling, the majority of severe convective wind events are found to occur in environments with steep mid-level tropospheric lapse rates, moderate convective instability and strong background wind speeds. A large proportion of events from measured station data occur with relatively dry environmental air at low levels, although it is unknown to what extent this type of environment is representative of other severe wind-producing convective modes in Australia. The occurrence of severe convective winds is found to be well represented by a number of indices used previously for forecasting applications, such as the weighted product of convective available potential energy (CAPE) and vertical wind shear, the derecho composite parameter and the total totals index, as well as by logistic regression methods applied to environmental variables. Based on the systematic approach used in this study, our findings provide new insight on spatio-temporal variations in the risk of damaging winds occurring, including the environmental factors associated with their occurrence.
Keywords: climate, climatology, convection, downburst, extremes, hazards, reanalysis, thunderstorms, wind.
1 Introduction
Severe convective winds (SCWs) can be caused by thunderstorm downdrafts and outflow, including phenomena such as downbursts and gust fronts. The Australian Bureau of Meteorology (BoM) defines severe-wind producing thunderstorms based on 3-second average wind gust speeds exceeding 25 m s−1. SCWs present a major risk to some industries, including for the energy sector, which is susceptible to transmission line failures from SCWs (Bureau of Meteorology 2016; Australian Energy Market Operator 2017). Therefore, understanding risk factors associated with the occurrence of SCWs is valuable for planning and enhanced resilience in relation to damaging wind events.
The sparseness of high-quality wind observations is one of the limiting factors for understanding SCWs in Australia. Reports of severe thunderstorms can be used (Allen et al. 2011), although these are biased towards areas of greater population density, are not consistent over time and may overestimate wind speeds in some instances (Edwards et al. 2018). Geerts (2001) and Holmes et al. (2018) used station wind data to estimate some observed climatological characteristics in Australia, although these investigations were regional, for the individual Australian states of New South Wales and South Australia, respectively. Based on the observational data limitations and research done to date, considerable knowledge gaps remain for the climatology of SCWs in general throughout Australia.
Given these limitations for SCW observations, some studies have examined atmospheric environments in which convective hazards occur. Environmental conditions based on model data have been found to provide a useful indication of the occurrence of severe thunderstorms globally (Brooks et al. 2003), in Europe (Taszarek et al. 2019) and in Australia (Allen and Karoly 2014). Such methods have also been used in Australia to estimate the mean occurrence of hail events (Niall and Walsh 2005; Bednarczyk and Sousounis 2012; Bedka et al. 2018), cool-season tornadoes (Kounkou et al. 2009) as well as thunderstorms and convective rainfall (Dowdy 2020). Recently, this method has been applied to SCWs throughout Australia using model environments on a seasonal-mean basis (Spassiani 2020). However, environmental analysis on an event basis is yet to be achieved, noting that Brown and Dowdy (2019) examined SCW events and their associated environments in the state of South Australia.
Previous severe weather research has provided knowledge of SCW environments, although the extent to which these environments are applicable across the Australian continent has not been systematically tested. Early findings from field campaigns indicated that days with thunderstorms that produce downbursts can be differentiated from days with thunderstorms that do not produce downbursts, based on the profile of temperature and humidity near an event (Wakimoto 1985; Atkins and Wakimoto 1991). Similarly, idealised numerical model studies have investigated downburst occurrences in relation to atmospheric environments (Srivastava 1985; Proctor 1989), with the results of such studies suggesting that favorable environments include a relatively dry subcloud layer and melting level, with steep temperature lapse rates. Conceptually, dry low-levels assist downdraft intensification by allowing for increased melting and evaporation of precipitation within a thunderstorm, with the associated latent heat change leading to cooler and therefore heavier air parcels. In addition, high amounts of liquid water and ice may also aid downdraft initiation through precipitation loading, although this depends on other factors such as the steepness of the lapse rate (Srivastava 1985). Meanwhile, a steep temperature lapse rate creates a more unstable atmosphere, indicating a favorable environment for convection to form. Those previous studies suggest a broadly similar set of large-scale environments to those identified by various recent observational studies (Doswell and Evans 2003; Kuchera and Parker 2006; Hurlbut and Cohen 2014), including based on a combination of strong lapse rates and moisture sources, while noting a wide range of other factors that can potentially influence the occurrence of hazardous weather phenomena associated with severe thunderstorms, which may vary with convective mode.
Environmental diagnostics are often used in operational weather forecasting applications to indicate the chance of severe thunderstorms occurring. Statistical regression methods based on a wide range of environmental conditions are also sometimes used, including for systematic studies of thunderstorm occurrences over long time periods (i.e. complementary to case studies or weather forecasting of individual events). For example, binary logistic regression has been applied in relation to hail occurrence in the United States (Allen et al. 2015), Germany (Mohr et al. 2015) and Spain (Gascón et al. 2015), lightning activity in Australia (Bates et al. 2018) as well as convective hazards in China (Pang et al. 2019).
Two historical model datasets (or reanalyses) are used here to investigate environments associated with SCWs in Australia. The reanalysis datasets are the BoM Atmospheric Regional Reanalysis for Australia (BARRA: Su et al. 2019) and ERA5, from the European Centre for Medium-Range Weather Forecasts (Hersbach et al. 2020). We examine various established diagnostics commonly used in forecasting severe thunderstorms, in addition to wind gusts as provided in the reanalysis datasets, in relation to their ability to indicate the observed SCWs. This is done using two observed SCW datasets: one dataset based on station wind observations, with lightning data used to indicate the occurrence of deep convective processes in the vicinity of the observed wind gusts; as well as another dataset based on severe thunderstorm reports as collated by BoM. A set of logistic regression models is then developed for indicating the chance of SCWs occurring, which is shown to improve skill over traditional indices.
In this work, the ‘Data and methods’ section contains the observed event datasets, the reanalysis datasets, the environmental diagnostics tested, and the logistic regression approach. The ‘Results’ includes evaluation of the environmental diagnostics and reanalysis wind gust data in relation to the observed SCW datasets, as well as the development of a logistic regression model for indicating the chance of SCWs occurring; followed by the ‘Discussion and conclusion’.
2 Data and methods
2.1 Observed wind gusts
Two observed SCW datasets are used, spanning 2005–2018. The first of these, referred to throughout this study as “measured” SCW events, is from station wind gust data with lightning observations used to indicate the occurrence of deep convective processes in the vicinity of the station (as detailed below). The second of these, referred to as “reported” SCW events, is from severe wind events listed in the reports collated by BoM for severe thunderstorm hazards.
For the measured SCW dataset, daily wind gust data are provided from automatic weather stations (AWS) managed by the BoM. The speed, direction and local time of the daily maximum 3-second average gust at a height of 10 m above ground level is archived. We use data from 35 AWS stations which have a long and reliable wind gust record covering most of the continent (Azorin‐Molina et al. 2019). Data is available at most stations for the full 14-year observational period, with the exceptions being Amberley (12.1 years), East Sale (12.1 years), Coffs Harbour (10.4 years) and Halls Creek (4.6 years). The data have been quality controlled by the BoM and gusts flagged for potentially large measurement error are removed. The AWS stations are listed in Table 1 along with the length of each record, with their locations shown in Fig. 1.

|

|
Daily maximum values of the measured station gusts are used throughout this study and are classed as ‘convective’ based on lightning data. The lightning data are combined stroke counts from two ground-based networks of lightning detectors: the World-Wide Lightning Location Network (WWLLN; Virts et al. 2013) and the Global Position and Tracking System (GPATS). The lightning data are collated on a 0.25° latitude-longitude grid with 6-hourly periods used for the temporal spacing, covering 2005–2018 (defining the observational period used in this study). A wind gust is classed as convective for the purposes of this study only if there are two or more lightning strokes detected within 50 km of the AWS station that recorded the wind gust during the 6-hourly time period of the lightning data that corresponds to when the gust occurred. A gust of 25 m s−1 or above is classed as severe, otherwise it is classed as non-severe. Although these thresholds used for the lightning data are somewhat arbitrary in their specific magnitudes, this method can provide observation-based evidence that deep convection occurred around the region and time that a severe wind gust was recorded. This is based on the idea that lightning is caused by strong potential differences from electrically charged regions of a cloud and that these charged regions are generated by strong updrafts resulting from deep convective processes (Lang and Rutledge 2002).
The reported event dataset is the BoM Severe Thunderstorm Archive (STA), which has been used previously for severe thunderstorm analysis (Allen et al. 2011). Each report contains a latitude-longitude location, the time of the report and an estimated wind gust speed. It is noted that there are significant biases within this dataset, for example, the tendency of reports to be located in regions of high population density and for gust speeds to be overestimated (Edwards et al. 2018). In addition, the STA has not been maintained in some regions of Australia from 2015 onwards, and so periods of null reports may be present during the latter portion of the archive. Reports are only used if they are within 50 km of the 35 AWS locations in Table 1 during the 2005–2018 period, so that each observational dataset is sampling the same locations and types of atmospheric environment. If there is more than one report at a location on a single day, only the report with the highest estimated wind gust speed is retained.
In addition, events with nearby tropical cyclones (TCs) from the BoM best-track database are removed. This is due to the high potential for synoptic-scale processes and winds associated with TCs to be mis-classified as SCWs (as considered for the purposes of this study with a focus on thunderstorm-related wind gusts), while noting that TCs also have convective processes embedded in their structure as a key aspect of their development. Consequently, severe wind gusts are not considered in this study if the center of a TC is within 500 km of the AWS station on the same day as the gust. This process eliminates eight measured severe wind gusts and 14 reported events, leaving a remainder of 202 measured and 510 reported events from 2005–2018.
The spatial distribution of reported and measured SCWs in Australia is presented in Fig. 1 for the 35 locations examined in this study. The population density bias in the reported dataset is clear, with local maxima in each of the mainland state capital cities (including Perth Airport, Darwin Airport, Adelaide Airport, Melbourne Airport, Sydney Airport and Amberly near the city of Brisbane). Therefore, there is low confidence in this reported SCW dataset for indicating spatial characteristics of SCWs, although this is not a focus of this study.
The annual time series of each dataset is also shown in Fig. 1, showing relatively large interannual variability, ranging from 24 to 66 events in a year in the reported dataset, and 5 to 20 in the measured dataset. There appears to be little association in variability between the two datasets in terms of the interannual time series, although it is noted that the STA is not consistently maintained across all Australian states and territories.
2.2 Environmental diagnostics from reanalyses
The environmental conditions associated with SCWs are investigated using various convective diagnostics based on data obtained from two atmospheric reanalyses: BARRA and ERA5. The choice of environmental diagnostics to consider in this study was informed by previous studies of thunderstorms and convective hazards including severe wind gusts, and includes both diagnostic variables and diagnostic indices, the distinction of which is discussed by Doswell and Schultz (2006).
Diagnostic variables are broadly defined here as either basic observable quantities, physical quantities derived from observable variables, or the result of a mathematical/statistical operation on those observed/derived variables. The diagnostic variables investigated here are listed in the Appendix (Table A1), including things such as the temperature lapse rate between two layers, water vapour mixing ratio averaged over various vertical layers, the magnitude of vertical wind shear between two layers, storm relative helicity, wind speed at various heights and averaged over certain vertical layers, the parametrised hourly maximum model wind gust at a height of 10 m and convective available potential energy (CAPE). Note that the computation of CAPE uses four different starting parcel definitions (see Table A1) and provides equilibrium level (EL), lifting condensation level (LCL) and convective inhibition (CIN) as additional diagnostics.
In contrast to the above definition of diagnostic variables, diagnostic indices are broadly defined as the combination of variables into formulae, which may be based on physical processes, or arbitrarily designed to match observations such as based on statistical regression. The full list of indices used is provided in Table A1. Generally, all diagnostics are identical to their definition within the National Oceanic and Atmospheric Administration (NOAA) Storm Prediction Center (SPC), unless noted otherwise in Table A1.
Diagnostics are calculated on hourly BARRA and ERA5 reanalysis data, using all pressure levels below 100 hPa and including surface level data. These environmental diagnostics calculated from the reanalysis data are spatiotemporally matched to the observed SCW events using the following method. For each of the observed SCW events, the diagnostics are calculated from the grid cell of the reanalysis data that is closest (using land points only) to the location of the station where the observed SCW was recorded. This is done for the most recent hourly time-step prior to the time that the observed SCW event was listed as occurring in the station record or report database. There is an exception to this method for the parameterised model wind gust from the reanalyses, where the time-step after each observed wind gust is used, given that this diagnostic is defined as the maximum in the previous hour. A range of different time steps and spatial proximity definitions were tested for associating diagnostics with SCW events, with the resulting skill generally insensitive to the method used (see Section 3.1 and Appendix Figs. A2, A3). Given that the pre-convective environment is being sampled, and both models use convective parameterization, convective contamination in the reanalysis environmental conditions is not considered to be a limiting factor for the purposes of this study (noting that Appendix Fig. A1 shows that the environmental diagnostics calculated from reanalyses are broadly consistent with those calculated from observations using radiosonde soundings).
Both reanalysis datasets have hourly data, as used in this study for calculating the environmental diagnostics. ERA5 has horizontal grid spacing of 0.25° on 37 pressure levels (27 of which are at or below 100 hPa), whereas BARRA data has horizontal grid spacing of 0.11° (37 pressure levels, 22 levels below 100 hPa).
To calculate the diagnostics listed in Table A1, multiple software packages using Python were applied to three-dimensional fields of air temperature, relative humidity, geopotential height, zonal wind, meridional wind and vertical wind. In addition, some diagnostics were taken directly from the reanalysis data (e.g. the modelled wind gust at 10 m as provided in the reanalysis datasets). For the calculation of all CAPE diagnostics and some vertical interpolation routines, wrf-python (Ladwig 2017) was used. MetPy (May et al. 2019) was utilised for the computation of various physical quantities. SHARPpy (Blumberg et al. 2017) provided some routines for SPC-defined convective indices, and SkewT (https://pypi.org/project/SkewT/) provided parcel lifting routines which were adapted to calculate downdraft convective available potential energy (DCAPE). Further details on the diagnostics are provided in the Appendix section, including examining values based on radiosonde data in addition to reanalysis data.
2.3 Diagnostic testing: Heidke skill score and the relative operating characteristic curve
Model diagnostics are tested on their ability to identify the occurrence of observed SCW events by using the optimal Heidke skill score (HSS) with a fixed threshold for event identification, as well as the area under the relative operating characteristic (ROC) curve (area under curve; AUC). The HSS is a measure of skill relative to random chance and uses all elements of the contingency table (Joint Working Group on Forecast Verification Research 2015). For a given diagnostic, an optimal HSS/threshold is considered in this study only if the diagnostic correctly identifies at least two-thirds of the SCW events. Note that in addition to testing diagnostics, the HSS is also used to optimise the set of predictors used in the logistic regression model (Section 2.4).
It has been suggested that the HSS is appropriate for rare event forecasting (Doswell et al. 1990), given that it includes correct negatives (when the diagnostic correctly identifies a null-event) in a controlled way. The HSS ranges from –1 to 1 (with 1 being a perfect forecast and 0 representing no skill), but is sensitive to the number of events, so tends towards zero for extremely rare events (such as SCWs as examined here). This is examined further in the Appendix (Fig. A4) and is not expected to impact on results regarding the relative skill of each diagnostic or statistical model.
The ROC curve shows the false positive rate and false negative rate for a diagnostic over a range of thresholds and is therefore indicative of the overall usefulness of a diagnostic. The AUC quantifies the area under the ROC curve and is a measure of how a diagnostic can separate events from non-events, which can be shown to be equivalent to the Mann–Whitney U-statistic (Mason and Graham 2002). The AUC ranges from 0 to 1, with 1 representing a perfect separation of events and non-events, and 0.5 representing the baseline for skill.
2.4 Application of logistic regression with environmental diagnostics
For SCW environment identification, we develop a statistical model using binary logistic regression, utilizing both the Python Scikit-learn package (Pedregosa et al. 2011) and the statsmodels package (Seabold and Perktold 2010). The logistic regression model will be fit to observed events and use environmental diagnostic variables from reanalyses as predictors (diagnostic indices are ignored). The general form of the equation resulting from the logistic regression is

where P is the probability of an environment supportive of SCW, and z is a linear combination of diagnostic variables plus an intercept term. The optimal set of diagnostic variables for use in Eqn 1 is achieved by a stepwise forward selection algorithm, similar to previous studies using logistic regression for convective hazards (Gascón et al. 2015; Mohr et al. 2015; Prein and Holland 2018). This type of selection ensures that variables which have the greatest multivariate skill are included in the model. The process is as follows.
Begin by fitting a logistic regression model to observed events without using any variables, resulting in a null model (intercept only with HSS = 0).
For each variable which has been attained from the reanalyses (n = 72, ignoring indices), add the variable to the model from the previous step, and fit the model again.
For each new model from step 2 (n = 72), calculate the probability that each regression term is statistically significant (coefficient is different from zero), and that a statistically significant increase in the HSS is achieved by the model (estimated by 1000-time bootstrap procedure using random resampling).
If, for any of the new models from step 2, the null hypothesis is rejected for each test in step 3 (α = 0.05), then the variable which provided the greatest increase in HSS is retained for use in the model. If not, the procedure is halted.
Repeat steps 2–4 until no further improvement is made.
This process is repeated for both reanalyses and for both observed datasets, resulting in four logistic regression models. When reporting the HSS for the fitted models, cross-validation is used to ensure there has been no over-fitting. Cross-validation is achieved by randomly resampling 80% of each observed dataset to use as a training dataset, 16 times, and using the remaining 20% of the dataset for testing, with the mean, maximum and minimum HSS reported in Section 3.2.
3 Results
3.1 Relative skill of environmental diagnostics
Diagnostics are tested here on their ability to identify SCW events at 35 locations around Australia. As discussed in Section 2.3, our method is to apply a range of thresholds for each diagnostic to optimise the HSS, in addition to requiring a successful detection of at least two-thirds of events. As noted in Section 2.2, the closest model spatial point to each event has been used for all diagnostics at the most recent instantaneous hourly time step (with the exception of the modeled wind gust), although skill scores are generally similar for other methods of spatial and temporal proximity, shown in the Appendix (Figs. A2, A3). Note that the overall magnitude of the HSS shown here is not a reflection of the absolute skill of the diagnostics considered, but rather the rarity of SCW events in the observed datasets (see Section 2.3 and discussion in the Appendix, Fig. A4). Diagnostic skill is also demonstrated in the Appendix by using ROC curves and the AUC score, which is not sensitive to event frequency and incorporates a range of possible thresholds for event identification (Fig. A5). However, here we focus on the HSS, given that relative skill for an optimal threshold is of greater interest.
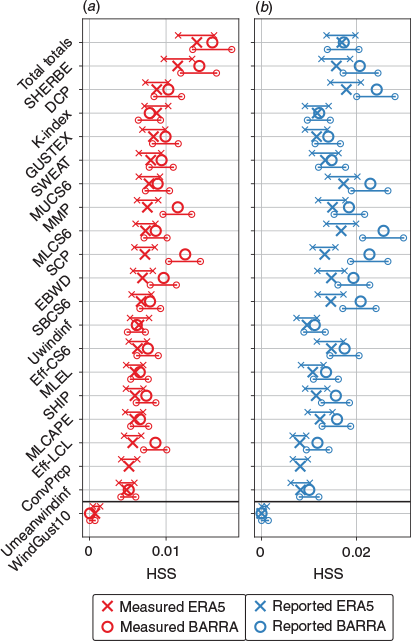
For the ERA5 and BARRA reanalyses, results indicate that total totals is the most skillful diagnostic (i.e. based on the highest HSS value) for identifying the occurrence of measured SCW events (Fig. 2a). Total totals is based on the temperature lapse rate in the 850–500 hPa layer and the 850 hPa dewpoint, and has traditionally been used as an indicator for thunderstorm development in forecasting. Its ability to identify hazardous convective environments using model data has been noted previously (Dowdy 2015; Miller and Mote 2018), as well as its usefulness in predicting downbursts from satellite data (Ellrod 1989).
|
In addition to indicating environments favorable for convection, the relative skill of the total totals diagnostic may result from it being a simple index of convective instability that could be more reliably represented at the relatively coarse scale resolved in reanalysis datasets, in contrast to some of the other stability diagnostics which integrate throughout the vertical (such as CAPE and other related quantities). Another possibility may be that the vertical layer used to compute total totals is more frequently unstable within the reanalyses in comparison to other levels which are considered by vertically integrated diagnostics. The emphasis on mid-level instability may relate to SCW mechanisms but could also suppress non-meteorological factors and biases. For example, model bias in surface variables is often greater than for above the boundary layer (as for some wind diagnostics demonstrated in Appendix Section A2, for example).
For reported SCW events, MLCS6 is the most skillful diagnostic from BARRA, whereas the derecho composite parameter (DCP) is the most skillful from ERA5 (Fig. 2b). MLCS6 represents the weighted product of mixed-layer CAPE and vertical wind shear following Brooks et al. (2003), which has been adapted for Australia by climatological studies using reanalyses (Allen and Karoly 2014; Dowdy 2020). The DCP has been developed for environments supporting mesoscale squall lines, which are a leading mode of SCW production in the United States (Smith et al. 2012). In contrast to the environmental diagnostics, the results in Fig. 2 also reveal that model wind gusts (WindGust10) do not provide a good indication of the observed SCW events.
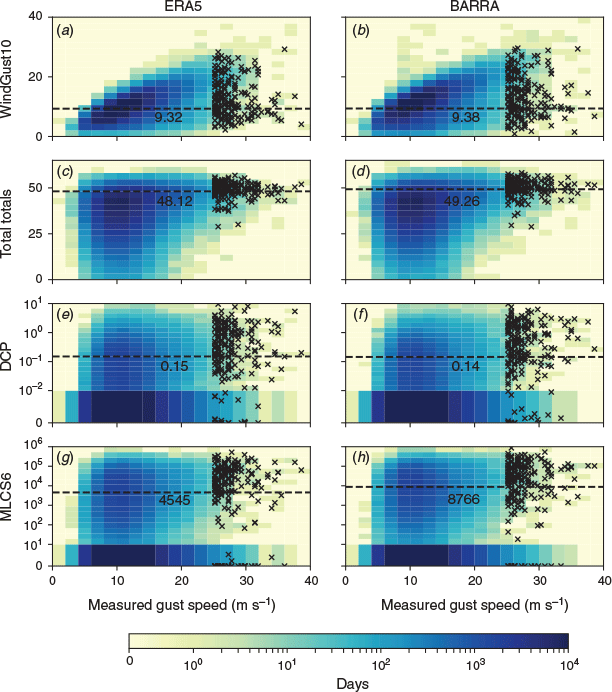
The above-mentioned environmental diagnostics (total totals, MLCS6, DCP as well as WindGust10) are examined further in Fig. 3, showing their occurrence frequency distributions as a function of measured wind gust speeds. SCW events are highlighted in Fig. 3 using black crosses. This shows that the wind gust speeds from the reanalysis datasets (WindGust10) underestimate the magnitude of the observed severe wind gusts. The WindGust10 values follow the observed values reasonably well for the lower magnitudes, but this is not the case for the more extreme values, particularly for those associated with convective processes (i.e. the SCW events shown in black). It is noted that reanalysis gusts are intended to be representative of an area larger than the spatial scale of SCWs, and it follows that BARRA and ERA5 are not expected to be used for convective extremes. However, gridded datasets are often used for studying extreme events (including for wind), so it is useful to document this limitation of reanalyses for simulating SCW events. However, reanalyses may potentially be suitable for examining extreme winds when the spatial scale approaches the reanalysis grid spacing, such as for synoptic events including cyclones and fronts.
|
The other three environmental diagnostics (total totals, DCP and MLCS6) have threshold values higher than many of their commonly occurring values (i.e. the dark blue shaded regions in Fig. 3), which results in better skill for indicating the occurrence of SCW events, as compared to the skill for the wind gust data from reanalyses. The threshold for the DCP (~0.15) shown in Fig. 3 is lower than the conventional forecasting guidance of 1 as is sometimes used for operational severe weather prediction, and the threshold of MLCS6 (~9000 for BARRA, ~5000 for ERA5) is lower than the value of 25 000 used for severe thunderstorms in Allen and Karoly (2014). Although, the thresholds reported here are broadly similar to the values around 10 000 used for classifying thunderstorms and convective rainfall climatology throughout Australia (Dowdy 2020). The threshold for total totals (~48) compares well with traditional guidance (e.g. Miller (1972) suggests values above 44 are useful for indicating thunderstorm occurrences). Variations in diagnostic thresholds such as these could be expected to some degree due to the different datasets used for different applications and studies. For example, station observations, radiosonde data and fine-resolution numerical weather prediction (NWP) data are often used for operational weather forecasting applications, whereas coarser-scale data such as gridded reanalyses are often used for longer-term climatological studies. In addition, SCW gusts are known to be produced by a wide range of convective modes, some of which may not require large amounts of instability (see Section 3.2 for further discussion). This could somewhat explain the relatively low thresholds for the DCP and MLCS6.
3.2 Logistic regression model development
Logistic regression models for indicating the occurrence of SCWs are considered in this section, with models constructed based on combining a selected set of environmental diagnostics. Selection is achieved through a stepwise forward selection process (Section 2.4), based on the inclusion of diagnostics which provide the largest multivariate increase in HSS. The results of the selection process, presented for each reanalysis model and observed dataset, is shown in Table 2 and discussed here. The final logistic regression models, including variable coefficients and cross-validated skill, are presented in Table 3. As for the diagnostics presented in the previous section, SCW environments are identified by the logistic regression models using a fixed diagnostic threshold based on optimizing the HSS (Section 2.3), and these thresholds are also shown in Table 3.

|
For the BARRA and ERA5 logistic models fitted to reported SCW events, the first two variables selected are similar. These are, in order of selection, the effective bulk wind difference (EBWD) and the pressure-weighted mean wind speed. For BARRA, the mean wind speed from 800 to 600 hPa is selected (Umean800–600), whereas for ERA5, the 0–6 km layer above ground level is used. For ERA5, CAPE using a mixed-layer starting parcel (MLCAPE) and the temperature lapse rate from 1–3 km above ground level (LR13) are then selected, resulting in a model with four predictors. For BARRA, LR13 is also then selected, followed by the equilibrium level of the mixed-layer convective parcel (MLEL) and the minimum relative humidity over the 1–3 km layer above ground level (RHMin13), resulting in five predictors. MLEL quantifies the height at which the mixed-layer convective parcel becomes neutrally buoyant with respect to the environment and can be interpreted as the potential height of convection (e.g. convective cloud-top height), based on the available energy in the environment for lifting the parcel. RHMin13 is hypothesised by Kuchera and Parker (2006) to promote dry air entrainment, which is relevant for downdrafts. MLCAPE and LR13 both relate to atmospheric and convective instability, whereas Umean06 and Umean800–600 are relevant for convective organization and mixing of strong upper-level winds to the surface. EBWD is defined as the magnitude of vertical wind shear between the base of the effective layer and half of the equilibrium level, and therefore relates to convective organization and separation of updrafts and downdrafts in the cloud layer. In addition, the EBWD contains information about CAPE and convective inhibition (CIN), given that the effective layer is defined as a contiguous layer of pressure levels that have CAPE greater than 100 J.kg−1 and CIN less than 250 J.kg−1 (Thompson et al. 2007). If no effective layer is present, then the value of this diagnostic (or any other diagnostic which uses the effective layer) is zero.
For models that are fitted to measured SCW events, the first three variables selected are similar between reanalyses, and to those chosen for the reports-based models. These are the EBWD, LR13 and the pressure weighted mean wind speed (Umean03 for BARRA and Umean800–600 for ERA5). As discussed above, these diagnostics are most likely related to instability, convective organization and vertical mixing. The discrepancy between the mean wind speed layer selected between ERA5 and BARRA could potentially relate to the vertical resolution of each dataset, which is greater for ERA5 than for BARRA (Section 2.2). For BARRA, the next two variables selected are the MLEL and RHMin03 (similar to RHMin13 as discussed above), resulting in five predictors. For ERA5, the next variables selected are RHMin13, the effective-layer storm relative helicity (SRHE), the water vapor mixing ratio at the height of the melting level (Q-Melting), and the effective-layer parcel lifting condensation level (Eff-LCL), resulting in seven predictors. SRHE is related to the potential for a convective system with a persistent, rotating updraft or mesocyclone, such as a supercell. In addition to supercells, Grams et al. (2012) show that effective layer diagnostics such as SRHE can be useful for discrete and clustered convective modes. Eff-LCL approximates the height of the cloud base using an effective-layer convective parcel, whereas Q-Melting relates to the moisture available for evaporative cooling within a downdraft (Srivastava 1985).
To demonstrate that each selected variable provides a statistically meaningful separation of the observed datasets, relative operating characteristic (ROC) curves, along with the area under the curve (AUC) is computed for each variable. The AUC quantifies the extent to which each diagnostic can separate SCW events from non-events and is equivalent to the Mann–Whitney U-statistic (Section 2.3), which is a commonly used test for the significance of statistical predictors, but potentially not as useful as the AUC for very large datasets given that it is based on hypothesis testing. The AUC results shown in Table 2 suggest that all predictors are skillful in a univariate sense for separating measured and reported SCW events from non-events (i.e. the AUC is significantly greater than 0.5), with the AUC ranging from 0.835 for the EBWD to 0.667 for RHMin03 (Table 2).
To further investigate the relationship between candidate variables and SCW at these 35 locations, a probability density function (PDF) for each diagnostic is calculated, as presented in Fig. 4. The PDFs are calculated by using a Gaussian kernel estimate, and can be interpreted as the likelihood of the diagnostic being inside a continuous range of values, for a given subset of the event space. This method is used to compare the occurrence frequencies of environmental variable magnitudes for SCW events, non-severe convective gusts and non-convective gusts based on measured wind gusts and lightning.
All distributions are shifted towards higher diagnostic values for SCW events as compared to gusts not classed as convective. Convective instability diagnostics or diagnostics which use the effective layer (MLEL, MLCAPE, Eff-LCL, EBWD and SRHE) are higher for convective gusts compared to non-convective gusts, as are Q-Melting, RHMin13 and RHMin03. The lapse rate distribution (LR13) for gusts classed as convective become attenuated at around the typical value of the moist adiabatic lapse rate (5°C km−1), whereas days classed as non-convective tend to have lower environmental lapse rates. The distribution of the environmental wind speed (Umean800–600, Umean03, Umean06) is broadly similar for days classed as convective and non-severe, and non-convective.
Comparing non-severe and severe convective gust distributions, it appears that LR13 is generally higher for the severe events. This is also the case for wind diagnostics (Umean800–600, Umean03, Umean06), SRHE and EBWD. CAPE is more frequently moderate (from 250 to 1000 J kg−1) and less frequently high (>1000 J kg−1) for SCW events relative to non-severe convective events. Less frequent high values of CAPE occur with relatively low equilibrium levels during SCW events, indicating the potential for SCWs to occur in reduced-buoyancy environments, as has been suggested by previous research (Geerts 2001; Sherburn et al. 2016). In addition, it appears the environment is relatively dry at low levels during measured SCW events relative to non-severe events, which is evident in the distributions of RHMin13 and RHMin03, potentially reflecting the prominence of dry-microburst events in the measured dataset.
It is noted that all distributions during observed events have been constructed without knowledge of the convective mode. This is important given that different convective modes may have distinct environmental characteristics (Grams et al. 2012). It follows that uncertainty is introduced in, for example, the role of low-level moisture (RHMin13 and RHMin03) in identifying SCW environments in general. Low-level moisture diagnostics may vary considerably between, for example, a supercell compared with a dry microburst producing-mode. Therefore, the distributions in Fig. 4 may reflect the dominant convective mode within the measured events, and this potential limitation will be explored further in the discussion.
These results for variable selection are now used for producing the logistic regression models. This is done individually for both reanalysis datasets and both observed datasets, resulting in four different statistical models. The details for each of these models are presented in Table 3, including the scaling coefficients used for each model, noting that all coefficients are positive. Each logistic regression model out-performs the most skillful diagnostics from Fig. 2 in terms of cross-validated HSS (Table 3), and also in terms of AUC (shown in the Appendix). It is noted that co-linearity can be a problem for logistic regression, and so this is quantified for each model with results shown in the Appendix (Section A6). It is concluded that co-linearity is not significant in any of the models, based on the variance influence factor (VIF).
3.3 Evaluation of SCW environment characteristics relative to observations
To provide some further insight on the environmental diagnostic approaches examined in previous sections, we compare their climatological characteristics to those of the SCW observations including their mean monthly and hourly occurrence frequencies, as well as for their measured gust direction. This is presented for the statistical models based on logistic regression (Table 3) and for the best-performing diagnostics from Section 3.1 (total totals, MLCS6 and DCP).
Fig. 5 presents the normalised occurrence frequency distributions for each month and hour as well as for measured wind direction. This is presented for the two observed SCW datasets and for times when a favorable environment is identified by the diagnostic variables and logistic regression models. A favorable environment is defined using hourly reanalysis data, applying the same thresholds producing the optimal cross-validated HSS as shown previously in Table 3. Reanalysis wind gust direction distributions are constructed using hourly station observations when a favorable environment is detected. Hourly gust direction observations have been provided by the BoM at the same set of locations as in Table 1.

|
The monthly frequency distributions of measured and reported observed SCWs have maxima during the warmer months of the year (from around September to March). The considerable agreement between the two independent observed SCW datasets suggests that they have a suitable level of reliability for the purposes of this study. Each environmental diagnostic can broadly replicate the warm-season SCW peak, although total totals has a bi-modal distribution indicating too many cool-season events. MLCS6 and the DCP also broadly represent the warm-season peak but with potentially too few cool-season events, noting that the MLCS6 diagnostic has been developed for warm-season convection (Allen et al. 2011). The logistic regression models generally lag behind the observed event datasets in terms of the annual cycle, with the peak shifted to later in the warm season, as has been found for logistic regression techniques by other studies (Allen et al. 2015).
The observed SCWs have a diurnal distribution that is broadly as expected for convective activity with a strong peak in the mid/late afternoon (Fig. 5b, e), accompanied by some evening events and a small number of nocturnal events. SCW reports entered in the STA without a time are assigned 00:00 UTC, hence there may be an artificially increased number of reports at around 10:00 LST in that dataset. All of the diagnostics can reproduce the observed peak during the afternoon, although each has a flatter distribution than the results for the observed SCW datasets. This could be related to biases in the reanalyses in terms of the diurnal cycle, but also potentially due to relevant environmental factors not being represented by these diagnostics, such as convective inhibition and initiation which could have some diurnal variation. In addition, the relatively small diurnal variability could be related to the use of hourly reanalysis, compared with daily maximum observations.
The ERA5 diagnostic distributions all reach their maxima somewhat too early in the day relative to observations. For BARRA diagnostics, MLCS6, the logistic regression model fitted to measured events, and the total totals diagnostic peak slightly too late in the day, whereas the logistic regression model fitted to the reported events has a peak timing which is slightly before the observed peak. A somewhat earlier timing of these diagnostic measures as compared to the observed SCWs might be expected for environmental approaches such as these, which identify some of the pre-cursor environments that can be associated with the occurrence of convective hazards.
Observed SCW events are most frequently westerly in direction (Fig. 5c, f). Westerly measured wind gust direction occurs 11% of the time in the report database and 18% of the time for measured events. It is noted that there is an observational bias towards cardinal compass points, which is evident in the distribution for all hourly observations (shown in Fig. 5c, f). The wind direction distribution is broadly replicated by the logistic regression models, including a peak in the westerly direction. Total totals, MLCS6 and the DCP have a slightly flatter wind direction distribution than is the case for the observed SCWs, with more frequently easterly and southerly gusts. There is an artificial northerly peak in all distributions using hourly gust observations, due to directions associated with zero wind speed reported as 0°.
These findings indicate that broad-scale characteristics of observed SCWs can be replicated by environmental measures in some cases, with variations depending on the method applied. The discrepancies for the environmental diagnostics as compared to the observed SCWs are largest for total totals in relation to the monthly distributions, also noting cool-season environments are less frequently identified by MLCS6 and DCP, consistent with definitions based on warm-season severe thunderstorms. Examples such as these suggest that although these types of indices may be useful in representing some types of environments associated with severe thunderstorms, logistic regression methods that consider a broad range of variables could be beneficial for some specific applications (such as the focus of this study on SCW identification).
4 Discussion and conclusion
In this study, we examined SCW environments in Australia using a combination of observations and environmental measures based on reanalysis data. This includes two, independent observed SCW event datasets and environmental measures based on two atmospheric reanalyses (BARRA and ERA5). The observed characteristics of SCWs indicate a similar seasonal and diurnal distribution to previous events for the state of NSW in eastern Australia (Geerts 2001), as well as to national severe thunderstorm reports (Allen et al. 2011) and other proxies for thunderstorms in Australia (Kuleshov et al. 2002). The similar features include more frequent events in the convective warm season and late-afternoon/evening, as well as relatively few cool-season and nocturnal events. We found that the SCW events were most often observed with a westerly measured gust direction.
The parametrised model wind gusts from the reanalyses were found to not provide a good representation of observed SCW events, also noting that the spatial scale on which these events occur are generally smaller than the model grid-cells. The skill metrics associated with the model wind gusts suggests that they are not suitable for analysis of convective wind events. Skill is greatly improved upon using model diagnostics which represent aspects of the larger-scale environments in which these events occur, and it is preferable to use these diagnostics to identify SCWs rather than model wind gusts. We find that the most skillful environmental diagnostics for indicating the observed SCW occurrences are total totals, MLCS6 and the DCP. Total totals has previously been used to indicate hail (Niall and Walsh 2005) and lightning activity in Australia (Dowdy 2015) and has been identified as a useful parameter for SCW identification in the United States including for applications using model data during events with minimal synoptic forcing (Miller and Mote 2018). Although the performance of total totals may somewhat reflect its relatively simple definition (which could have potential benefits for application to coarse-scale data including some gridded reanalyses), the individual terms used in this diagnostic are conceptually relevant for convective hazards (including mid-tropospheric lapse rates and moisture measures). MLCS6 has been developed as a discriminate for warm season STA reports in Australia (Allen et al. 2011), and this definition is consistent with the high skill for convective wind reports presented here. The DCP was developed for the identification of environments supportive of quasi-linear MCS (Evans and Doswell 2001), which are a leading mode of SCW generation (Smith et al. 2012), such that the results presented here are consistent with expectations that this could likely be a useful environmental diagnostic for indicating the occurrence of SCW events as examined in this study. Based on the results of variable selection for use in logistic regression, it is likely that the relationship between the DCP and SCW events is driven by CAPE and Umean06, which are both used by the DCP, and are selected as predictors based on the reported dataset using ERA5.
We found a range of thermodynamic variables to be useful for indicating SCW events, including measures based on vertical temperature gradients (LR13), convective instability (MLEL, MLCAPE and Eff-LCL), low-level moisture (RHMin13 and RHMIN03), as well as environmental wind speeds and shear (Umean800–600, Umean03, Umean06, EBWD and SRHE). Increased mid-level lapse rates appear to enhance the probability of SCW occurrence, likely due to greater instability providing the potential for more intense convection. SCWs are also associated with high values of environmental wind speed, which is likely related to storm organization, downwards mixing of horizontal momentum and/or strong synoptic forcing (Evans and Doswell 2001). Meanwhile, increased low and mid-level moisture (as measured by RHMin13 and RHMin03) is found to enhance the probability of convective gusts relative to non-convective gusts. CAPE is more often moderate for observed events relative to other convective environments, with lower equilibrium levels, which has been found by other studies (Geerts 2001; Sherburn et al. 2016).
The variables mentioned above were combined using logistic regression techniques, with the resultant statistical models shown to provide some improvements (higher HSS values) as compared to the use of individual diagnostics for indicating the observed SCW events. The statistical models were able to replicate the observed climatological characteristics of the SCW datasets, including the general features of the seasonal and diurnal cycles as well as the measured wind direction distribution. In addition, the logistic regression models are able to provide some utility in identifying hazardous low-CAPE environments, as evident in the relative frequency of cool-season identification (Fig. 5) and selected case studies (not shown). However, some differences with observed characteristics were noted, including a lagged annual cycle with a flatter and somewhat earlier peak indicated during the day from the regression methods as compared to the observed events, which may relate to the representation of the diurnal cycle within reanalysis models in general. The timing of the diurnal cycle could also potentially reflect the use of environmental measures associated with the pre-cursor environments that deep and moist convection can potentially occur in (e.g. CAPE).
Results suggest that dry air at lower levels appears somewhat more conducive for SCW occurrence, relative to non-severe convective gust environments (Fig. 4), although it is not clear to what extent this result is a general feature of SCW environments in Australia, or if it may simply reflect the dominant convective modes of the measured event dataset. The relationship between low-level dryness and measured SCWs is broadly consistent with the understanding of dry microburst-producing storm environments, in which sub-cloud dryness increases evaporative cooling, resulting in the acceleration of downdrafts (Wakimoto 1985). However, it is also noted that supercell thunderstorms, which can occur in environments with moist low-levels, are capable of producing SCW events in Australia (Richter et al. 2014). This has been investigated by comparing the distribution of environmental variables for measured SCW events with the distributions for reported events. Results (shown in the Appendix) suggest that the method of this study is fairly robust with respect to the observed dataset, although differences between the distributions of RHMin13 and RHMin03 confirm that there is considerable variation surrounding the role of low-level moisture, which might be related to the occurrence of specific convective modes (e.g. dry microburst or supercell modes). It follows that the logistic regression models fitted to measured SCW events, which have relatively low relative humidity values (as shown from their distribution Fig. 4 and in the Appendix), could potentially be more suited for dry microburst environments, whereas models fitted to reported events may possibly be more related to supercell-type modes with more moisture in the low levels. Future work to improve the methods of this paper could include examining this in more detail, or consideration of individual convective modes with respect to SCW in Australia, including with seasonal variation.
Our findings are intended to have potential uses in relation to improved preparedness for severe winds and the damages that they can cause in Australia, including for helping inform infrastructure design and risk assessments. The results could help provide general guidance for severe weather forecasting applications, such as those used operationally within the Bureau of Meteorology based on the types of convective diagnostics examined here. Insight is provided on factors relating to the mean climatology of severe convective wind events in Australia, noting that improved understanding of the average risk of occurrence of these events is important for planning and design standards given the damages that they can cause to buildings and other property (e.g. infrastructure used for essential services such as electricity distribution towers). These results could also help enable future studies, such as the application of environmental measures to gridded data throughout Australia (i.e. complementary to the method employed here based on 35 individual locations) which could include the analysis of the spatial distribution of SCW environments as well as climate variations.
Data and code availability
AWS wind gust data, the STA and BARRA are available from the BoM; ERA5 is available from the Copernicus Climate Data Store. Lightning data can be made available upon request. All analysis code is available in the following Git repository: https://github.com/andrewbrown31/SCW-analysis, which contains a log file detailing how the code was used for the results shown here.
Conflicts of interest
The authors declare that they have no conflicts of interest.
Acknowledgements
This project is funded by the Australian Government Department of Industry, Science, Energy and Resources through the Electricity Sector Climate Information Project, as well as by the National Environmental Science Program (NESP). Comments provided on earlier versions of the manuscript by Joshua Soderholm and Robert Taggart from the Bureau of Meteorology are gratefully acknowledged, as are comments by two anonymous reviewers.
References
Allen, J. T., and Karoly, D. J. (2014). A climatology of Australian severe thunderstorm environments 1979–2011: inter-annual variability and ENSO influence. Int. J. Climatol. 34, 81–97.| A climatology of Australian severe thunderstorm environments 1979–2011: inter-annual variability and ENSO influence.Crossref | GoogleScholarGoogle Scholar |
Allen, J., Karoly, D., and Mills, G. (2011). A severe thunderstorm climatology for Australia and associated thunderstorm environments. Aust. Meteorol. Oceanogr. J. 61, 143–158.
| A severe thunderstorm climatology for Australia and associated thunderstorm environments.Crossref | GoogleScholarGoogle Scholar |
Allen, J. T., Tippett, M. K., and Sobel, A. H. (2015). An empirical model relating US monthly hail occurrence to large-scale meteorological environment. J. Adv. Model. Earth Syst. 7, 226–243.
| An empirical model relating US monthly hail occurrence to large-scale meteorological environment.Crossref | GoogleScholarGoogle Scholar |
Atkins, N. T., and Wakimoto, R. M. (1991). Wet microburst activity over the southeastern United States: implications for forecasting. Wea. Forecast 6, 470–482.
| Wet microburst activity over the southeastern United States: implications for forecasting.Crossref | GoogleScholarGoogle Scholar |
Australian Energy Market Operator. (2017). Black system, South Australia, 28 September 2016. Available at https://www.aemo.com.au/-/media/Files/Electricity/NEM/Market_Notices_and_Events/Power_System_Incident_Reports/2017/Integrated-Final-Report-SA-Black-System-28-September-2016.pdf [verified 25 November 2020]
Azorin‐Molina, C., Guijarro, J. A., McVicar, T. R., Trewin, B. C., Frost, A. J., and Chen, D. (2019). An approach to homogenize daily peak wind gusts: an application to the Australian series. Int. J. Climatol. 39, 2260–2277.
| An approach to homogenize daily peak wind gusts: an application to the Australian series.Crossref | GoogleScholarGoogle Scholar |
Bates, B. C., Dowdy, A. J., and Chandler, R. E. (2018). Lightning prediction for Australia using multivariate analyses of large-scale atmospheric variables. J. Appl. Meteorol. and Climatol. 57, 525–534.
| Lightning prediction for Australia using multivariate analyses of large-scale atmospheric variables.Crossref | GoogleScholarGoogle Scholar |
Bedka, K. M., Allen, J. T., Punge, H. J., Kunz, M., and Simanovic, D. (2018). A long-term overshooting convective cloud-top detection database over Australia derived from MTSAT Japanese advanced meteorological imager observations. J. Appl. Meteorol. and Climatol. 57, 937–961.
| A long-term overshooting convective cloud-top detection database over Australia derived from MTSAT Japanese advanced meteorological imager observations.Crossref | GoogleScholarGoogle Scholar |
Bednarczyk, C., and Sousounis, P. (2012). Hail climatology of Australia based on lightning and reanalysis. Available at https://ams.confex.com/ams/27SLS/webprogram/Manuscript/Paper255889/extendedAbstract_pdf.pdf [verified 25 November 2020]
Blumberg, W. G., Halbert, K. T., Supinie, T. A., Marsh, P. T., Thompson, R. L., and Hart, J. A. (2017). Sharppy: an open-source sounding analysis toolkit for the atmospheric sciences. Bull. Am. Meteorol. Soc. 98, 1625–1636.
| Sharppy: an open-source sounding analysis toolkit for the atmospheric sciences.Crossref | GoogleScholarGoogle Scholar |
Brooks, H. E., Lee, J. W., and Craven, J. P. (2003). The spatial distribution of severe thunderstorm and tornado environments from global reanalysis data. Atmos. Res. 67–68, 73–94.
| The spatial distribution of severe thunderstorm and tornado environments from global reanalysis data.Crossref | GoogleScholarGoogle Scholar |
Brown, A., and Dowdy, A. (2019). Extreme wind gusts and thunderstorms in South Australia analysed from 1979–2017. Bureau Research Report No. 034. Available at http://www.bom.gov.au/research/publications/researchreports/BRR-034.pdf [verified 25 November 2020]
Bunkers, M. J., Klimowski, B. A., Zeitler, J. W., Thompson, R. L., and Weisman, M. L. (2000). Predicting supercell motion using a new hodograph technique. Wea. Forecast 15, 61–79.
| Predicting supercell motion using a new hodograph technique.Crossref | GoogleScholarGoogle Scholar |
Bureau of Meteorology. (2016). Severe thunderstorm and tornado outbreak South Australia 28 September 2016. Available at http://www.bom.gov.au/announcements/sevwx/sa/Severe_Thunderstorm_and_Tornado_Outbreak_28_September_2016.pdf [verified 25 November 2020]
Coniglio, M. C., Stensrud, D. J., and Wicker, L. J. (2006). Effects of upper-level shear on the structure and maintenance of strong quasi-linear mesoscale convective systems. J. Atmos. Sci. 63, 1231–1252.
| Effects of upper-level shear on the structure and maintenance of strong quasi-linear mesoscale convective systems.Crossref | GoogleScholarGoogle Scholar |
Doswell, C. A., and Evans, J. S. (2003). Proximity sounding analysis for derechos and supercells: an assessment of similarities and differences. Atmos. Res. 67–68, 117–133.
| Proximity sounding analysis for derechos and supercells: an assessment of similarities and differences.Crossref | GoogleScholarGoogle Scholar |
Doswell, C. A., and Schultz, D. M. (2006). On the use of indices and parameters in forecasting severe storms. E-Journal of Severe Storms Meteorology 1, .
Doswell, C. A., Davies-Jones, R., and Keller, D. A. (1990). On summary measures of skill in rare event forecasting based on contingency tables. Wea. Forecast 5, 576–585.
| On summary measures of skill in rare event forecasting based on contingency tables.Crossref | GoogleScholarGoogle Scholar |
Dowdy, A. J. (2015) Large-scale modelling of environments favourable for dry lightning occurrence. In ‘Proceedings of 21st International Congress on Modelling and Simulation, Gold Coast, Australia, 29 November to 4 December 2015’. 1524–1530. (Modelling and Simulation Society of Australia and New Zealand.)
Dowdy, A. J. (2020). Climatology of thunderstorms, convective rainfall and dry lightning environments in Australia. Clim. Dyn. 54, 3041–3052.
| Climatology of thunderstorms, convective rainfall and dry lightning environments in Australia.Crossref | GoogleScholarGoogle Scholar |
Edwards, R., Allen, J. T., and Carbin, G. W. (2018). Reliability and climatological impacts of convective wind estimations. J. Appl. Meteorol. and Climatol. 57, 1825–1845.
| Reliability and climatological impacts of convective wind estimations.Crossref | GoogleScholarGoogle Scholar |
Ellrod, G. (1989). Environmental conditions associated with the Dallas microburst storm determined from satellite soundings. Wea. Forecast 4, 469–484.
| Environmental conditions associated with the Dallas microburst storm determined from satellite soundings.Crossref | GoogleScholarGoogle Scholar |
Evans, J. S., and Doswell, C. A. (2001). Examination of derecho environments using proximity soundings. Wea. Forecast 16, 329–342.
| Examination of derecho environments using proximity soundings.Crossref | GoogleScholarGoogle Scholar |
Gascón, E., Merino, A., Sánchez, J. L., Fernández-González, S., García-Ortega, E., López, L., and Hermida, L. (2015). Spatial distribution of thermodynamic conditions of severe storms in southwestern Europe. Atmos. Res. 164–165, 194–209.
| Spatial distribution of thermodynamic conditions of severe storms in southwestern Europe.Crossref | GoogleScholarGoogle Scholar |
Geerts, B. (2001). Estimating downburst-related maximum surface wind speeds by means of proximity soundings in New South Wales, Australia. Wea. Forecast 16, 261–269.
| Estimating downburst-related maximum surface wind speeds by means of proximity soundings in New South Wales, Australia.Crossref | GoogleScholarGoogle Scholar |
Grams, J. S., Thompson, R. L., Snively, D. V., Prentice, J. A., Hodges, G. M., and Reames, L. J. (2012). A climatology and comparison of parameters for significant tornado events in the United States. Wea. Forecast 27, 106–123.
| A climatology and comparison of parameters for significant tornado events in the United States.Crossref | GoogleScholarGoogle Scholar |
Hersbach, H., Bell, B., Berrisford, P., et al. (2020). The ERA5 global reanalysis. Quart. J. Roy. Meteorol. Soc. 146, 1999–2049.
| The ERA5 global reanalysis.Crossref | GoogleScholarGoogle Scholar |
Holmes, J., Wang, C.-H., and Oliver, S. (2018). Extreme winds for six South Australian locations. In ‘Proceedings of the 19th Australasian Wind Engineering Society Workshop. Torquay, Victoria’. (Australasian Wind Engineering Society.)
Hurlbut, M. M., and Cohen, A. E. (2014). Environments of Northeast US severe thunderstorm events from 1999 to 2009. Wea. Forecast 29, 3–22.
| Environments of Northeast US severe thunderstorm events from 1999 to 2009.Crossref | GoogleScholarGoogle Scholar |
Joint Working Group on Forecast Verification Research (2015). Forecast verification methods across time and space scales. Available at https://www.cawcr.gov.au/projects/verification/ [verified 25 November 2020]
King, A. T., and Kennedy, A. D. (2019). North American supercell environments in atmospheric reanalyses and RUC-2. J. Appl. Meteorol. Climatol. 58, 71–92.
| North American supercell environments in atmospheric reanalyses and RUC-2.Crossref | GoogleScholarGoogle Scholar |
Kounkou, R., Mills, G., and Timbal, B. (2009). A reanalysis climatology of cool-season tornado environments over southern Australia. Int. J. Climatol. 29, 2079–2090.
| A reanalysis climatology of cool-season tornado environments over southern Australia.Crossref | GoogleScholarGoogle Scholar |
Kuchera, E. L., and Parker, M. D. (2006). Severe convective wind environments. Wea. Forecast 21, 595–612.
| Severe convective wind environments.Crossref | GoogleScholarGoogle Scholar |
Kuleshov, Y., De Hoedt, G., Wright, W., and Brewster, A. (2002). Thunderstorm distribution and frequency in Australia. Aust. Met. Mag. 51, 145–154.
Ladwig, W. (2017). wrf-python (version 1.1.0) [Software]. (UCAR/NCAR: Boulder, CO.) Available at
Lang, T. J., and Rutledge, S. A. (2002). Relationships between convective storm kinematics, precipitation, and lightning. Mon. Wea. Rev. 130, 2492–2506.
| Relationships between convective storm kinematics, precipitation, and lightning.Crossref | GoogleScholarGoogle Scholar |
Mason, S. J., and Graham, N. E. (2002). Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: statistical significance and interpretation. Quart. J. Roy. Meteorol. Soc. 128, 2145–2166.
| Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: statistical significance and interpretation.Crossref | GoogleScholarGoogle Scholar |
May, R. M., Arms, S. C., Marsh, P., Bruning, E., Leeman, J. R., Goebbert, K., et al. (2019). MetPy: a Python package for meteorological data. (Unidata: Boulder, C).) Available at
McCann, D. W. (1994). WINDEX-A new index for forecasting mircoburst potenitial. Wea. Forecast 9, 532–541.
| WINDEX-A new index for forecasting mircoburst potenitial.Crossref | GoogleScholarGoogle Scholar |
Miller, R. C. (1972). Notes on analysis and severe-storm forecasting procedures of the air force global weather central. Tech. Rep. 200, Air Weather Service.
Miller, P. W., and Mote, T. L. (2018). Characterizing severe weather potential in synoptically weakly forced thunderstorm environments. Nat. Hazards and Earth Syst. Sci. 18, 1261–1277.
| Characterizing severe weather potential in synoptically weakly forced thunderstorm environments.Crossref | GoogleScholarGoogle Scholar |
Mohr, S., Kunz, M., and Keuler, K. (2015). Development and application of a logistic model to estimate the past and future hail potential in Germany. J. Geophys. Res. 120, 3939–3956.
| Development and application of a logistic model to estimate the past and future hail potential in Germany.Crossref | GoogleScholarGoogle Scholar |
Niall, S., and Walsh, K. (2005). The impact of climate change on hailstorms in southeastern Australia. Int. J. Climatol. 25, 1933–1952.
| The impact of climate change on hailstorms in southeastern Australia.Crossref | GoogleScholarGoogle Scholar |
Pang, G., He, J., Huang, Y., and Zhang, L. (2019). A binary logistic regression model for severe convective weather with numerical model data. Adv. Meteorol. 2019, 6127281.
| A binary logistic regression model for severe convective weather with numerical model data.Crossref | GoogleScholarGoogle Scholar |
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830.
Prein, A. F., and Holland, G. J. (2018). Global estimates of damaging hail hazard. Wea. Clim. Extrem. 22, 10–23.
| Global estimates of damaging hail hazard.Crossref | GoogleScholarGoogle Scholar |
Proctor, F. H. (1989). Numerical simulations of an isolated microburst. Part II: sensitivity experiments. J. Atmos. Sci. 46, 2143–2165.
| Numerical simulations of an isolated microburst. Part II: sensitivity experiments.Crossref | GoogleScholarGoogle Scholar |
Pryor, K. L. (2007). The GOES microburst windspeed potential index, (2004), 15. Available at https://cds.cern.ch/record/1024106/files/0703162.pdf [verified 25 November 2020]
Richter, H., Peter, J., and Collis, S. (2014). Analysis of a destructive wind storm on 16 November 2008 in Brisbane, Australia. Mon. Wea. Rev. 142, 3038–3060.
| Analysis of a destructive wind storm on 16 November 2008 in Brisbane, Australia.Crossref | GoogleScholarGoogle Scholar |
Seabold, S., and Perktold, J. (2010). Statsmodels: econometric and statistical modeling with python. In ‘Proceedings of the 9th Python in Science Conference (SciPy 2010)’, Austin Texas. (Eds S. van der Walt and J. Millman) pp. 92–96. (SciPy.org)
Sherburn, K. D., Parker, M. D., King, J. R., and Lackmann, G. M. (2016). Composite environments of severe and nonsevere high-shear, low-CAPE convective events. Wea. Forecast 31, 1899–1927.
| Composite environments of severe and nonsevere high-shear, low-CAPE convective events.Crossref | GoogleScholarGoogle Scholar |
Smith, B. T., Castellanos, T. E., Winters, A. C., Mead, C. M., Dean, A. R., and Thompson, R. L. (2012). Measured severe convective wind climatology and associated convective modes of thunderstorms in the contiguous United States, 2003–09. Wea. Forecast 28, 229–236.
| Measured severe convective wind climatology and associated convective modes of thunderstorms in the contiguous United States, 2003–09.Crossref | GoogleScholarGoogle Scholar |
Spassiani, A. C. (2020) Climatology of severe convective wind gusts in Australia. PhD thesis. The University of Queensland School of Civil Engineering
Srivastava, R. C. (1985). A simple model of evaporatively driven downdraft: application to microburst downdraft. J. Atmos. Sci. 42, 1004–1023.
| A simple model of evaporatively driven downdraft: application to microburst downdraft.Crossref | GoogleScholarGoogle Scholar |
Su, C.-H., Eizenberg, N., Steinle, P., Jakob, D., Fox-Hughes, P., White, C. J., et al. (2019). BARRA v1.0: the Bureau of Meteorology atmospheric high-resolution regional reanalysis for Australia. Geosci. Model Dev. Discuss 12, 2049–2068.
| BARRA v1.0: the Bureau of Meteorology atmospheric high-resolution regional reanalysis for Australia.Crossref | GoogleScholarGoogle Scholar |
Taszarek, M., Allen, J., Púčik, T., Groenemeijer, P., Czernecki, B., Kolendowicz, L., et al. (2019). A climatology of thunderstorms across Europe from a synthesis of multiple data sources. J. Climate 32, 1813–1837.
| A climatology of thunderstorms across Europe from a synthesis of multiple data sources.Crossref | GoogleScholarGoogle Scholar |
Thompson, R. L., Edwards, R., and Mead, C. M. (2004). ‘An update to the supercell composite and significant tornado parameters.’ (Storm Prediction Center: Norman, OK.)
Thompson, R. L., Mead, C. M., and Edwards, R. (2007). Effective storm-relative helicity and bulk shear in supercell thunderstorm environments. Wea. Forecast 22, 102–115.
| Effective storm-relative helicity and bulk shear in supercell thunderstorm environments.Crossref | GoogleScholarGoogle Scholar |
Virts, K. S., Wallace, J. M., Hutchins, M. L., and Holzworth, R. H. (2013). Highlights of a new ground-based, hourly global lightning climatology. Bull. Amer. Meteorol. Soc. 94, 1381–1391.
| Highlights of a new ground-based, hourly global lightning climatology.Crossref | GoogleScholarGoogle Scholar |
Wakimoto, R. M. (1985). Forecasting dry microburst activity over the High Plains. Mon. Wea. Rev. 113, 1131–1143.
| Forecasting dry microburst activity over the High Plains.Crossref | GoogleScholarGoogle Scholar |
Appendix 1. Convective diagnostics
Table A1 presents a complete list of all diagnostics tested for SCW identification (Section 3.1), as well as for logistic model development (Section 3.2). This includes environmental variables (e.g. MLCAPE, Umean06), model variables (e.g. ConvPrcp and WindGust10) and diagnostic indices (e.g. DCP and SCP). Some of the diagnostics in Table A1 are not mentioned directly in the main manuscript text, as only the top-performing diagnostics are reported on. However, these are still listed here for completeness. Diagnostics are used here as they are commonly defined in the literature including by the Storm Prediction Center (SPC), unless otherwise noted.

|
Appendix 2. Environmental diagnostics applied to radiosonde data and reanalysis data
For comparison with the reanalysis datasets, environmental diagnostics were also computed using radiosonde data from the BoM at four locations around Australia: Darwin, Sydney, Adelaide and Woomera (Table 1). Radiosonde data are available at a frequency of once, twice or three times a day depending on the location and are compared to the hourly reanalysis time steps which are closest to the launches and spatially nearest to the stations (considering land points only). Observed diagnostics are calculated in the same way as for the models, and we impose the restriction that profiles must have at least 12 data points (noting that the average number of points is between 45 and 65 for these locations), start below 850 hPa, and finish above 200 hPa. Comparisons are performed on the mixed-layer parcel CAPE, CIN and equilibrium level (MLCAPE, MLCIN, MLEL), downdraft convective available potential energy (DCAPE), total totals, wind shear from 0–6 km above ground level (S06), as well as the pressure-weighted mean wind speed from 800–600 hPa and 0–1 km above ground level (Umean800–600 and Umean01).
Fig. A1 shows there is good agreement between both models and the observed diagnostics (r ≥ 0.80), except for CIN (r = 0.68 for BARRA and r = 0.71 for ERA5) and DCAPE (r = 0.71 for BARRA and r = 0.79 for ERA5). Poor model representation of CIN has been found by previous studies and is likely related to unresolved thin inversion layers (King and Kennedy 2019). Relatively large errors in DCAPE are likely due to similar issues, given that downdraft energy is calculated for the parcel with minimum equivalent potential temperature, from the surface to 400 hPa above ground level. Another notable aspect of Fig. A1 is the better representation in the reanalysis data of simple instability diagnostics (total totals) relative to more complex ones (MLCAPE, DCAPE) based on comparisons to the observed values (from radiosonde data). This could relate back to the skill of these relatively simple variables when applied to the reanalysis data for indicating the occurrence of SCW events (Fig. 2). Also, it appears that incomplete model representation of the boundary layer may lead to poorer skill for diagnostics which use near-surface values, relative to diagnostics that don’t (e.g. Umean01 versus Umean800–600).
The general performance of model-derived diagnostics compared with observations gives confidence that each reanalysis dataset could potentially be used to investigate climatological SCW identification. It is noted that observed profiles from these radiosondes could have already been assimilated into the reanalyses, and correlations may degrade with distance from these sites. In addition, it appears that the diagnostic values based on ERA5 are somewhat better correlated with the observations data (e.g. larger values of r in Fig. A1) than is the case based on BARRA, noting that the differences are relatively small in general.
Appendix 3. Other proximity definitions for model diagnostics
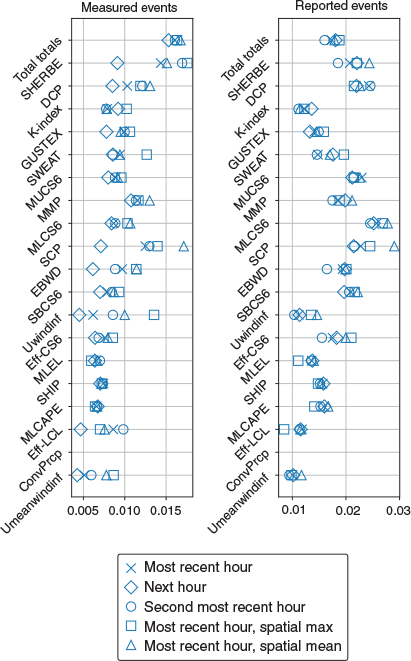
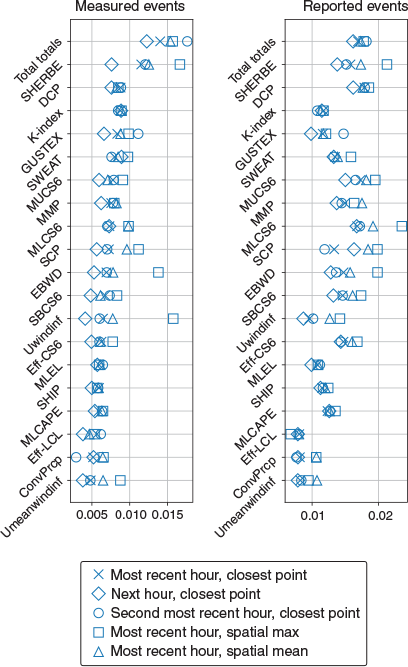
As described in Section 2.2, the method used for associating reanalysis diagnostics with SCW events is to use the closest spatial point from each model, and the most recent hourly time step before the observed events, representing instantaneous pre-event conditions. Here, it is tested to what extent the HSS shown in Fig. 2 is sensitive to this definition. This is done by comparing the HSS using the most recent hourly time step and closest spatial point with four other definitions. These are; the most recent hour using a spatial average (with a 50 km radius), the same but with a spatial maximum, the second most recent hour using the closest spatial point (representing instantaneous pre-event conditions) and the following hourly time step using the closest spatial point (representing post-event instantaneous conditions). Results, shown in Fig. A2 for ERA5 and Fig. A3 for BARRA, suggest that the relative skill between diagnostics is generally insensitive to the choice of proximity definition, except for some outlying scores associated with using the spatial maximum for effective-layer wind diagnostics associated with measured SCW events.
|
Appendix 4. Sensitivity of the HSS to event frequency
The magnitude of HSS in the results (for example, the identification of reported and measured SCW in Fig. 2) is largely a result of the frequency of observed events in each dataset. However, the change in HSS between diagnostics is indicative of the relative skill. This can be demonstrated by examining the optimal HSS for two diagnostics from ERA5 (DCP and total totals) in their ability to identify measured SCW events, and subsetting the observed dataset for a varying number of randomly selected non-events. The relationship between the proportion of non-events chosen (relative to the full set of non-events) and the HSS is shown in Fig. A4. Fig. A4 reveals that there is an exponential decrease in HSS for increasing non-event proportion in the dataset, although for all proportions, total totals performs better than the DCP (i.e. the relative skill between diagnostics is constant and consistent with results in Fig. 2). In addition, the skill is always significantly greater than zero.
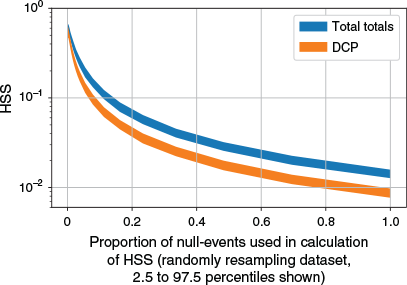
|
Appendix 5. The relative operating characteristic curve and area under curve for SCW events
Other skill scores, which are not sensitive to event frequency and do not require a fixed threshold, can be used to gain a sense of the overall usefulness of diagnostics in predicting SCW events. The relative operating characteristic (ROC) curve, along with the area under the curve (AUC) can be used to assess diagnostic performance by considering a range of thresholds. Fig. A5 shows ROC curves and AUC scores for each event dataset and reanalyses, which compare the performance of the top diagnostic indices (i.e. total totals, the DCP and MLCS6) with the logistic regression models developed in Section 3.2.
ROC curves and the AUC suggest that the top-performing diagnostics for each observed dataset and reanalysis model, as well as each logistic regression model, are skillful in distinguishing SCW events from non-events (i.e. the ROC curve is far from the ‘no-skill’ line along the diagonal, and accordingly, the AUC is ≫0.5). In addition, the logistic regression models perform better than each environmental diagnostic in terms of AUC.
Appendix 6. Notes on co-linearity in the logistic regression models
Co-linearity in logistic regression (i.e. correlation between variables) leads to large standard errors in fitted coefficients, due to confounding the effects of predictands on the predicted variable. Here, it is investigated whether or not the four logistic regression models presented in Table 3 contain significant co-linearity, using the variance inflation factor (VIF) following the method of Mohr et al. (2015). The VIF is a measure of the variance explained for each predictor using all other predictors in the model, where a value greater than 5 is often considered to represent significant co-linearity. It is found that for each of the four models, the VIF for each predictor indicates insignificant co-linearity (Table A2).

|
Appendix 7. Environmental diagnostic distributions for reported SCW events
Fig. A6 shows probability density functions (PDFs) for the same set of variables as in Fig. 4, constructed separately for measured and reported SCW events. Results suggest that the measured event environments have a relatively dry low-level compared with reported event environments, as shown by RHMin13 and RHMin03. Distributions for other variables are broadly similar between the two event datasets. These findings may have relevance for inferring the dominant convective modes within each dataset, as discussed in the ‘Discussion and conclusion’ (Section 4).

|