Interdecadal modulation of the effect of ENSO on rainfall in the southwestern Pacific
Tony Weir A D , Ravind Kumar B and Arona Ngari CA Fenner School of Environment and Society, Australian National University.
B Deceased. Formerly of Fiji Meteorological Service.
C Cook Islands Meteorological Service.
D Corresponding author. Email: tony.weir@anu.edu.au
Journal of Southern Hemisphere Earth Systems Science 71(1) 53-65 https://doi.org/10.1071/ES19053
Submitted: 5 March 2020 Accepted: 22 December 2020 Published: 1 March 2021
Journal Compilation © BoM 2021 Open Access CC BY-NC-ND
Abstract
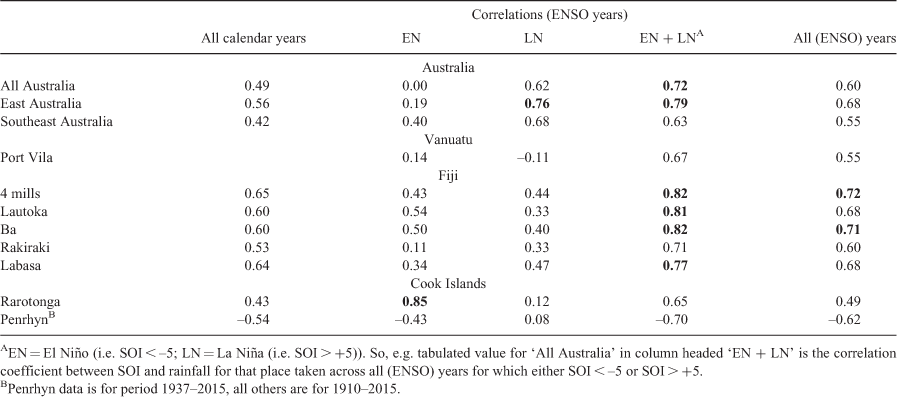
The El Niño-Southern Oscillation (ENSO) is the dominant driver of interannual variability on rainfall in many Pacific Islands and in countries bordering the tropical Pacific Ocean. From 1916 through to 1975, the correlation coefficient between the Southern Oscillation Index (SOI) and interannual variability in rainfall in eastern Australia was strong in negative phases of the Interdecadal Pacific Oscillation (IPO) but weak in positive phases. By examining records of rainfall over the past hundred years in central Vanuatu and on the ‘dry side’ of Fiji, which both lie near the southern edge of the South Pacific Convergence Zone (SPCZ), we find that such modulation by IPO has been much weaker there than in eastern Australia. This paper examines possible reasons for this difference. We also find that the correlation between rainfall and the SOI remained strong throughout each of the past three phases of the IPO, in all these places, including eastern Australia. However, at Rarotonga in the southern Cook Islands, whose position is also near the southern edge of the SPCZ, but at the southeastern end, the displacement of the SPCZ by ENSO events is greater there than further west. Consequently, the correlation between rainfall and SOI is so strong at Rarotonga in El Niño years with SOI < −5 that SOI alone becomes a good predictor of wet-season rainfall there. The difference in modulation of rainfall in eastern Australia between the two positive phases of IPO (1926–1941 and 1978–1998) may be due to the influence on Australia of other climatic oscillations, such as the Indian Ocean Dipole, though other factors may also have played a role.
Keywords: Australia, Cook Islands, El Niño-Southern Oscillation (ENSO), Fiji, Interdecadal Pacific Oscillation (IPO), rainfall, Southern Oscillation Index (SOI), Southwest Pacific.
1 Introduction
The El Niño-Southern Oscillation (ENSO) drives much of the interannual variation in rainfall in the Pacific Islands (PCCSP 2011b; Murphy et al. 2014). The relationship between ENSO and rainfall has been much explored in both the Pacific Islands and Australia, particularly since the extreme El Niño event of 1982–1983, because of the possibility of using the state of ENSO to predict rainfall a season or two ahead (McBride and Nicholls 1983; Sarachik and Cane 2010; Cottrill and Kuleshov 2014) and the economic importance of doing so (Nicholls 1985; Smith and Ubilava 2017). In some locations and farming types, application of a skilled seasonal forecast can yield additional profit of more than AU$50/ha, such as in combined sheep and wheat farms in the ‘Mediterranean’ climate of Western Australia (Asseng et al. 2012).
In many Pacific Islands, there are long-established vernacular words for El Niño, which literally mean ‘hunger’ or ‘nothing left in the sun’ (Robson Tigona, pers. comm.). An attempt by Solofa and Aung (2004) to establish a statistical relation between agricultural productivity and ENSO for Samoa was thwarted by lack of data on subsistence production. Availability of freshwater is a priority issue for the numerous low-lying islands with no surface water, including small islands and atolls, which are subject to ENSO-related droughts (Sinclair et al. 2012). Tropical cyclones are the most common disaster-related events in the Pacific Islands, accounting for 157 (76%) of reported disasters from 1950 to 2004 (Bettencourt et al. 2006). Since cyclones arise in regions of unusually warm sea surface temperatures (SSTs) and a major manifestation of El Niño events is increased SSTs in the central or eastern Pacific, it is not surprising that El Niño is associated with an increased frequency of cyclones in the more eastern parts of the southwest Pacific (Terry 2007).
The state of ENSO varies from year to year, with an oscillation period varying typically from 4 to 7 years. An extreme El Niño features lower than average rainfall in the southwest Pacific and higher than average rainfall in South America; the reverse is true of an extreme La Niña. The strength of the relationship between rainfall and ENSO is shown by the strong correlations between annual rainfall and various indicators of the state of ENSO, of which the Southern Oscillation Index (SOI) is the longest established and still widely used, including in this paper. The SOI is essentially a normalised measure of the difference (air pressure at Tahiti) minus that at Darwin (see Appendix 1 for more detail.) El Niño events are characterised by a negative SOI (<–5) and La Niña events by a positive SOI (>+5). Another widely used measure is the Niño 3.4 index, which is essentially the anomaly in SSTs in the Niño 3.4 region of the central Pacific, which covers 5°N–5°S and 170°W–120°W (see Appendix 1). An El Niño condition is characterised by a positive SST departure from normal greater or equal to +0.5°C (NOAA 2016). There is a very strong negative correlation between SOI and the Niño 3.4 index (r = −0.92, ENSO year data). The evolution of an ENSO event (except perhaps for its inception) is now reasonably well understood in terms of the interaction between ocean and atmosphere in the tropical Pacific Ocean (Clarke 2008; Sarachik and Cane 2010). However, there remains considerable scope for improvement in the predictability of ENSO events (Santoso et al. 2019); the new CMIP6 suite of global climate models may offer some improvement over the older CMIP5 suite for this purpose (Wang et al. 2020).
The Interdecadal Pacific Oscillation (IPO) is a less well understood measure of the state of the ocean and atmosphere in the Pacific. As its name implies, it varies over time frames of decades. It directly affects a much wider range of latitude than ENSO, and indeed was first noticed by its effect on Canadian fisheries (Mantua et al. 1997). The state of the IPO can be measured by the Tripole Index (TPI) of Henley et al. (2015), which is essentially the difference between the SST anomaly (SSTA) in the tropical central Pacific Ocean and the average of the extratropical SSTA in the southwest and northwest Pacific (see Appendix 1). Although it can be calculated monthly, the TPI is most revealing when averaged over periods of several years. Periods of positive TPI resemble El Niño events in that both are characterised by anomalously high SSTs in the central Pacific. But, for the IPO, this effect is smoothed over time, and a state of positive TPI is spread over a wider range of latitude than in an El Niño. This smoothing is usually attributed to the influence of related oceanic processes, which operate over longer time scales than those of ENSO (Henley 2017). Thus, the IPO partially reflects interdecadal variability in ENSO-driven SST variability (e.g. Power et al. 2006; Henley 2017).
Power et al. (1999) showed that in eastern Australia the strength of the relation between ENSO and rainfall varies with the phase of the IPO, whereas Kumar et al. (2014) found no such modulation in Fiji.
The aim of this paper is to investigate possible reasons for this difference. To do so, we draw on rainfall data from 1910–2014 not only from Australia and Fiji, but also from Vanuatu (to the west of Fiji) and Cook Islands (to the east of Fiji), and examine in turn the three hypotheses below.
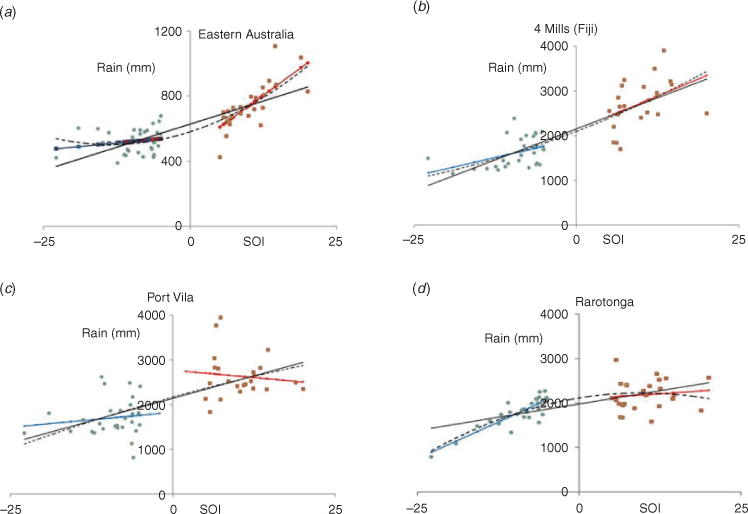
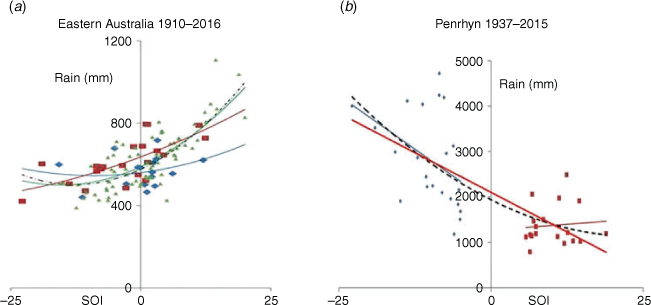
Hypothesis 1: the difference between Fiji and Australia might be related to the fact that the relationship between rainfall against SOI observed in eastern Australia (Fig. 1a) is strikingly non-linear, unlike that in Fiji (Fig. 1b). This hypothesis is explored in sections 3 and 4 of this paper.
Hypothesis 2: in the islands of the southwest Pacific, one of the main manifestations of the phase of ENSO is movement in the position of the South Pacific Convergence Zone (SPCZ), which is a band of high rainfall stretching in a southeasterly direction from the Solomon Islands to the Cook Islands. Therefore, we hypothesise that much of the difference in the effect of ENSO on rainfall is because movements in the SPCZ have less effect in eastern Australia than in the islands. This hypothesis is investigated in section 5.
Hypothesis 3: the differences in the relationship between rainfall and SOI between eastern Australia and the islands of the southwest Pacific may be because influences other than ENSO and IPO have greater effect on rainfall in eastern Australia than in the islands. This hypothesis is investigated in section 6.
2 Data and methods
Australian monthly rainfall data from 1910 onwards were obtained as regional averages from the website of the Australian Bureau of Meteorology (BOM), (http://www.bom.gov.au/climate/change/index.shtml#tabs = Tracker&tracker = timeseries). In this paper, Australia is represented by ‘eastern Australia’ (i.e. Queensland, New South Wales, Australian Capital Territory, Victoria and Tasmania) as the region most directly affected by ENSO. Fiji is represented by ‘4 mills’ (i.e. the average of the monthly rainfalls of the four individual sugar mills). The Fiji sugar mills are all on the ‘dry’ side of the larger islands for agricultural reasons; they are sheltered by hills from the southeast trade winds, which prevail on the windward (‘wet’) sides of those islands from May to October and therefore show much stronger correlations between rainfall and SOI than other Fiji sites (Kumar et al. 2014).
The underlying raw data from the Pacific Islands is monthly rainfall for each of Port Vila (Vanuatu; 17.74°S, 168.32°E), Rarotonga (Cook Islands; 21.20°S, 159.80°W) and the four sugar mills in Fiji (Lautoka at 17.60°S, 177.45°E; Ba at 17.55°S, 177.70°E; Rakiraki at 17.37°S, 178.17°E; and Labasa at 16.43°S, 179.38°E) (see maps in section 5 for approximate location of these stations.) These are the only stations in those countries with reliable records extending as far back as 1910. Each of them has a distinct wet season (November–April) and dry season (May–October). All of this data is held by the respective national meteorological services.
Records for major stations in the Pacific Islands were all carefully curated as part of the Pacific Climate Change Science Program (PCCSP) and the Pacific–Australia Climate Change Science Adaptation Planning Program sponsored by Australia (Power et al. 2011), with much of it now available through the Pacific Climate Change Data Portal at http://www.bom.gov.au/climate/pccsp/. However, we obtained data directly from the respective national meteorological services. For Fiji, in years for which data for an individual mill is missing (about two or three years for each mill), we used the average taken over the other mills. The few years for which data for Port Vila are missing were discarded from the analysis (see Appendix 3 for more details about missing data). Some data from Penrhyn in the northern Cook Islands (9.03°S, 158.05°W) was also analysed, but this data goes back only to 1937.
All analyses in this paper are in terms of ‘ENSO years’ running from May through to April in the following calendar year. ENSO year 1910 here refers to May 1910–April 1911, and so on. This convention was chosen to match the division between ‘wet’ and ‘dry’ seasons commonly used in the southwest Pacific; it differs slightly from the June–May ‘ENSO years’ used by Chung and Power (2017). Since ENSO events usually begin in the ‘dry’ season but have their main impact on rainfall in the South Pacific Islands in the immediately following ‘wet’ season, using ‘ENSO years’ better represents ENSO events than using calendar years (which tends to split prelude and consequence). Unless otherwise noted, the data for all stations examined runs from 1910 to 2014.
SOI was obtained (as monthly averages) from the BOM website (http://www.bom.gov.au/climate/current/soihtm1.shtml). We defined an El Niño year as one for which SOI < −5 and a La Niña year as one for which SOI > +5, with SOI averaged over that ‘ENSO year’. Values for TPI (an index of the state of the IPO) were taken from the National Oceanic and Atmospheric Administration (NOAA) website referred to by Henley et al. (2015) (see Appendix 1 for further details).
The rainfall maps shown in section 5 were selected from a set provided to us by BOM, who produced them based on data extracted from NOAA’s CMAP database of monthly analyses of global precipitation. This NOAA database is on a 2.5° × 2.5° latitude/longitude grid and extends back to 1979; it is based on observations from land-based rain gauges, merged with precipitation estimates from several satellite-based algorithms (infrared and microwave) (see http://www.cpc.ncep.noaa.gov/products/global_precip/html/wpage.cmap.html).
3 SOI/rainfall correlations by IPO phase: Australia is different
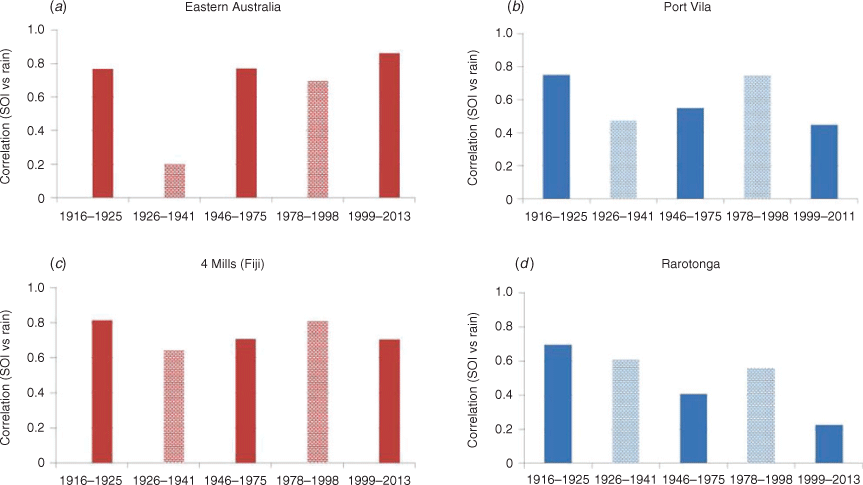
Fig. 2 compares the correlation between SOI and rainfall (both averaged over ENSO years) for five phases of IPO, for eastern Australia, Fiji (‘4 mills’), Port Vila and Rarotonga. Periods of the IPO phases used here are based on 13-year filtered data for the TPI of Henley et al. (2015), as detailed in Appendix 1. Note that, as indicated in Fig. 2, there are several small gaps between successive periods of positive and negative TPI used in our analyses to allow for ‘transition’ periods. All correlations shown are significant at the 0.05 level except for eastern Australia (1926–1941), Port Vila (1929–1941 and 1999–2011) and Rarotonga 1999–2013, where correlations have r < 0.5.
The chart for eastern Australia (Fig. 2a) features strong correlations (>0.7) for periods of negative TPI, but dips very markedly for the earlier period of positive TPI (1926–1941) to low correlation (<0.2). But this pattern does not persist for the next period of positive TPI (1978–1998), when the correlation remains almost as high (>0.6).
The Fiji chart (‘4 mills’) (Fig. 2c) shows high correlations (0.6–0.8) in periods of negative TPI (1916–1925, 1976–1975 and 1999–2013), slightly lower correlations for the period 1926–1941 (when TPI was positive) but an even higher correlation for the period 1978–1998 (when TPI was again positive). Port Vila (Fig. 2b) shows a similar pattern to Fiji, except that all the correlations are slightly lower – most notably for the most recent negative phase (1999–2013). Rarotonga (Fig. 2d), near the southeastern end of the SPCZ, shows a strikingly different pattern to the others, with the correlation in the most recent negative phase being quite low (<0.25).
The correlation between SOI and rainfall in the positive IPO phase of 1978–1998 was strengthened by including two of the strongest El Niño events (ENSO years 1982 and 1997), which were both exceptionally dry across the whole region, except for 1997 in eastern Australia. Wang and Hendon (2007) suggest that the difference between 1982 and 1997 ‘El Niño’ rainfalls in eastern Australia was due to rainfall there being more sensitive to SST on the eastern edge of the warm pool, rather than SST in the central Pacific (measured by the Niño 3.4 index) – a conclusion consistent with those two years having the two lowest rainfalls on record at Rarotonga, the easternmost station analysed in our paper. The only two El Niño events in the previous positive phase (ENSO years 1940 and 1941) were not quite so strong.
4 Rainfall/SOI correlations in El Niño and La Niña years
Power et al. (2006) observed that the quadratic best-fit to a plot of Australian rainfall against SOI is non-linear. A large positive SOI anomaly during June–December is closely linked to a large Australian response (i.e. Australia, not just eastern Australia, usually becomes much wetter in a La Niña event), whereas the magnitude of a negative (El Niño) SOI anomaly is a poorer guide to how dry Australia will actually become. They also found that in both the observations and in their coupled general circulation model, the relationship between ENSO and Australian climate (both temperature and rainfall) is strong in the positive phase of IPO but much weaker in the negative phase of IPO. Noting the physical resemblance (e.g. in SST) between a period of positive IPO and an El Niño event, they suggested that the non-linearity described above provides a mechanism via which ENSO teleconnections could be modulated on decadal time scales in a partially predictable fashion. King et al. (2013) found that similar non-linearity and effect of IPO applies also to extreme rainfall events in eastern Australia. However, Cai et al. (2010) found that since 1980, this asymmetry no longer operates in southeast Queensland; that La Niña events no longer induce a rainfall increase, leading to the observed rainfall reduction there; and that a similar asymmetric rainfall teleconnection with ENSO Modoki exists and shares the same temporal evolutions.
One could hypothesise that the non-linearity of this relationship was weakened in the 1978–1998 period by the two very strong El Niño events, making for significantly reduced rainfall, and thus making the quadratic best-fit curve of rainfall against SOI more linear even in a positive IPO phase. Alternatively, the change in effect of IPO may be due to broader climate change between the 1930s and the 1980s. The latter hypothesis can only be tested by data from a subsequent positive phase of IPO; one such phase began around 2015 but has not yet continued for long enough to test. Section 6 examines the hypotheses that one of the periods 1926–1943 or 1978–1998 is exceptional, especially in Australia.
A comparison of scatter plots of rainfall against SOI is shown in Fig. 1. For clarity, data from neutral or near-neutral years (–5 < SOI < +5) is omitted from the charts in Fig. 1 and from the calculation of the best-fit curves shown in that figure. For all stations examined, curves (lines) of best-fit are almost unaffected by omitting the neutral years, but the correlation coefficients are significantly increased (e.g. from 0.68 to 0.79 for eastern Australia – see Appendix 4).
These charts in Fig. 1 show an interesting trend in the quadratic ‘best-fit’ curves as we move eastward from eastern Australia (~150E, Fig. 1a) through Vanuatu (~168E, Fig. 1c) and Fiji (~178E, Fig. 1b) to Cook Islands (~160 W, Fig. 1d). For eastern Australia, the curve is concave upwards, i.e. flattening out for negative SOI, consistent with the plots presented by Power et al. (2006) and Chung and Power (2017). Part of the explanation for this is that southern Australian summers are usually fairly dry, so there is a limit to how much drier they can become.
In contrast, the quadratic best-fit curve for Fiji (4 mills) is almost indistinguishable from the best-fit line, which slopes uniformly upwards, indicating that the increase of rainfall with increase in SOI is similar for negative and positive SOI. That is, in Fiji (and also in central Vanuatu), but much less so in Australia, a stronger El Niño event implies a much drier summer than a weak El Niño or neutral year. Summer is the wet season in the sugar cane districts of Fiji (for which these charts apply), so there is scope for greater decreases in its rainfall, particularly in strong El Niño events.
For Rarotonga, the quadratic curve is concave downwards, i.e. the reverse of that for eastern Australia. Indeed, the rainfall for El Niño years shows a positive correlation with SOI (r = 0.85), which is significant at 0.01 level and so strong that it suggests a single physical effect is dominating. In contrast, there is almost no correlation (r = 0.12) in La Niña years.
Thus, if mid-year SOI (or equivalently SST in Niño 3.4 region) indicates an El Niño, this makes for a very good numerical prediction of wet-season rainfall at Rarotonga in those years. This enables much better rainfall predictions than simply using correlations across all years, as is done (in effect) in the predictions currently made on the Island Climate Update (https://niwa.co.nz/climate/island-climate-update) widely used by island national meteorological services. In the next section, we explain this difference by looking at the dynamics of the SPCZ.
According to the theory outlined by Power et al. (2006), the modulation by IPO of the rainfall/SOI correlation in Australia, with that correlation being weak when TPI is negative, is linked to the quadratic best-fit curve of rainfall against SOI being concave upwards. We would therefore expect to see no such modulation for Fiji, where the corresponding curve is nearly linear; which is indeed what Fig. 2c shows. Similarly, that theory would predict a weakened correlation between the SOI and Rarotonga rainfall during IPO positive phases and a strengthened correlation during IPO negative phases, since the quadratic curve of rainfall against SOI is concave downwards (i.e. the reverse of Australia). On the contrary, according to Fig. 2d, the observed correlation is weakest when TPI is negative. In the next section, we suggest that the dynamics of the SPCZ are more important at Rarotonga than the effect suggested by Power et al. (2006).
The separate best-fit lines for El Niño and La Niña years shown in Fig. 1 (and the corresponding correlation coefficients) confirm the story told by the quadratic curves. Indeed, the separate correlations for El Niño and La Niña periods were moderate in Fiji and effectively zero for Port Vila.
Freund et al. (2019) reported that since about 1980, El Niño events have more often had their strongest warm anomaly of SST in the central Pacific (EN-CP, also called El Niño Modoki) as opposed to ‘classical’ El Niño events, in which the warm anomaly is in the eastern Pacific (EN-EP). We found that distinguishing these two ‘flavours’ of El Niño does not noticeably affect the results of this section. However, we noted that of the El Niño events since 1950, EN-CP events predominate for moderately strong events (–10 < SOI < −5) while very strong events are mainly of the EN-EP type.
5 Effect on station rainfall of movement of the SPCZ in response to ENSO
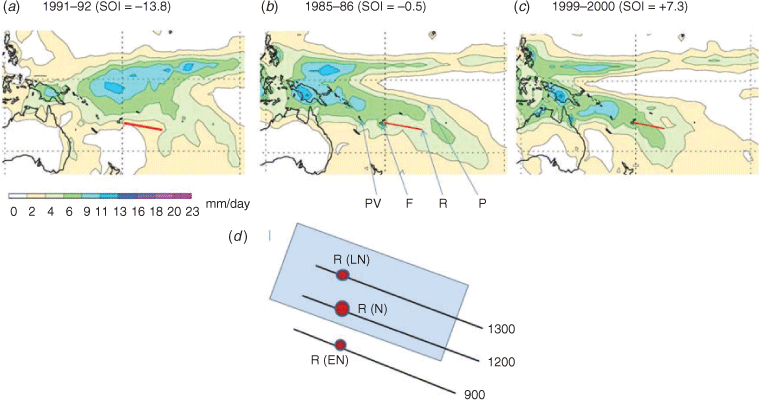
The rainfall maps for November–April in Fig. 3 clearly show the SPCZ as a prominent band of rainfall and indicate how its position varies between neutral, La Niña and El Niño years. The SPCZ is the band stretching in a southeasterly direction approximately from the Solomon Islands to east of the Cook Islands in Fig. 3b and c, but running more easterly in Fig. 3a. Note that PCCSP (2011b) cautions that ‘the image of a continuous SPCZ with a line of high rainfall and strong convection represents the seasonal or long-term average, rather than the conditions on any single day’. The SPCZ is normally strongest in December–February and weaker and less defined in June–August. Therefore, the maps in Fig. 3 depict the average rainfall over each November–April season.
The movement of the SPCZ casts some light on why Rarotonga behaves so differently from the more westerly stations in its response to IPO and SOI, particularly in more recent years (as indicated in Figs 3 and 4). The interannual variability of the SPCZ is dominated by ENSO events, with the SPCZ moving north and east during El Niño events and south and west during La Niña events (Salinger et al. 2014). These movements away from the ‘neutral’ position of Fig. 3b are evident in Fig. 3a and Fig. 3c respectively. Each of the maps shown in Fig. 3 share their main features with other years of similar SOI (±1), at least in the period for which similar maps are available (i.e. 1979–2009), although of course details differ in individual years.
Although the SPCZ is more difficult to discern in the Fiji ‘dry’ season (May–October), in effect the associated rainfall also moves seasonally towards the northeast in the ‘dry’ season and towards southwest in the ‘wet’ season. In addition to this movement, there is also a similar but more-or-less independent longer-term movement associated with the IPO, with the SPCZ moving to the northeast in the positive phase and to the southwest in the negative phase of IPO (Folland et al. 2002; PCCSP 2011b; Salinger et al. 2014). The movements can be of several hundred kilometres (as an indication of scale, the distance from Fiji to Rarotonga – indicated by the red line in Fig. 3 – is about 2500 km). Indeed, in both of the extreme El Niño events for which maps are available (1982 and 1997), the SPCZ moved so far to the northeast that it merged into the Intertropical Convergence Zone (visible in Fig. 3b as the northern band of rain running from west to east).
It is clear that the range of displacements at Rarotonga was roughly double that at Port Vila. The mean position of the southern edge of the SPCZ rain belt was very close to that of the typical ‘neutral’ year shown in Fig. 3b, which shows Rarotonga lying just inside that edge, as indicated in the schematic diagram, Fig. 3d. Therefore, as the SPCZ moved to the southwest in a La Niña, Rarotonga, which was just inside the rain belt (position N in Fig. 3d), was well inside the rain belt (position La Niña in Fig. 3d), which did not result in much change in the November–April rainfall, which went from wet (1200 mm) to only slightly wetter (1300 mm). Conversely, as the SPCZ moved to the northeast in an El Niño, Rarotonga was outside the rain belt (position El Niño in Fig. 3d), thus causing a more dramatic shift in November–April rainfall from wet (1200 mm) to relatively dry (900 mm) (the numbers are approximately those for the years of Fig. 3a–c). Hence, the correlation of rainfall with SOI at Rarotonga would be stronger in El Niño s than in La Niña events.
The resolution of the rainfall maps of Fig. 3 is too coarse (~2°) to distinguish the ‘dry’ (leeward) side’ of Fiji, where the 4 mills are situated, from the ‘wet’ side, which generally has considerable higher rainfall than the ‘dry’ side in November, December and April because it is exposed to the southeast trade winds (compare the charts for Nadi and Suva in PCCSP 2011a). Thus, the southward dip around Fiji of the high rainfall zone in Fig. 3b does not well represent the 4 mills, where the wet-season rainfall is more subject to ENSO through the movement of the SPCZ than Fig. 3 would suggest (Kumar et al. 2014). Allowing for this ‘resolution effect’ in interpreting the maps allows one to more clearly discern the movement of the SPCZ around Fiji and to see that it would result in roughly equal increases and decreases in rainfall in La Niña and El Niño years respectively, as is observed in Fig. 1. Likewise, it can also be seen that the displacement (distance moved) was less than at Rarotonga. Similar ‘resolution’ and displacement effects apply to Port Vila, which lies on the leeward side of a hilly island in central Vanuatu, but to a lesser extent because that island (Efate) is both smaller and lower than the main islands of Fiji.
The maps in Fig. 3 also show some of the effect of ENSO on rainfall in eastern Australia, particularly the increase in rainfall in La Niña years. In northeast Australia (coastal Queensland), November–April is normally the wet season, but in La Niña years the rainfall was much higher than normal, usually accompanied by a rise in the number of tropical cyclones making landfall there. In southeast Australia, on the other hand, summer (December, January, February) was usually the driest season.
6 Time series of rainfall and ENSO-related parameters
6.1 Time series of rainfall
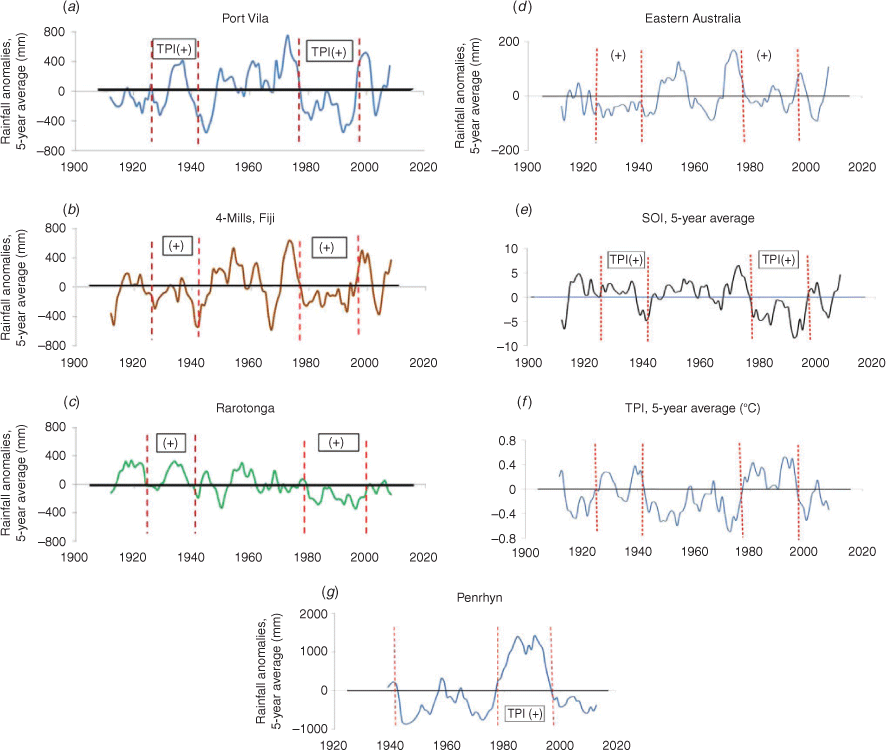
Fig. 4 shows time series of the 5-year average P5 of rainfall at each station (as anomalies). In the positive IPO phase of 1978–1998, P5 at all the island sites is clearly lower than its long-term average, except for Penrhyn, which is consistent with the tendency of the rain-bearing SPCZ to move northeastward (i.e. away from each of the sites except Penrhyn) in positive phases of IPO (Salinger et al. 2014).
6.2 Low-frequency variation of SOI
Data presented in Fig. 4e and f provide a check that SOI and TPI are strongly correlated and that the periods used in Figs 2 and 5a correctly reflect the phases of the IPO.
|
Table 1 indicates that La Niña events are more frequent in negative phases of IPO and El Niño events are more frequent in positive phases of IPO. However, a notable difference between the two positive phases is that ENSO events were significantly more frequent in 1978–1998 than in 1926–1941. Indeed, the frequency of ENSO events was much lower in 1926–1941 than in any other of the periods examined here; this was also noted by Sarachik and Cane (2010, p.9).
This suggests that the low SOI/rainfall correlation in eastern Australia in 1926–1941 may be related to the unusual behaviour of ENSO in this period, although we consider this is unlikely to be a full ‘explanation’.
6.3 Eastern Australia
For eastern Australia, the most striking feature in Fig. 4d is that rainfall was markedly low throughout the IPO positive phase of 1926–1941 (the ‘Depression Drought’ which bankrupted many small farmers), which is also the period in which the correlation of rainfall with SOI was markedly low (see Fig. 2). In contrast, smoothed rainfall (P5) in eastern Australia in the later positive phase (1978–1999), when the rainfall–SOI correlation was high, was around the long-term average.
Fig. 5a shows little support for the hypothesis that the two very strong El Niño events in 1978–1998 made for extra low rainfall and thereby rendered the plot of rainfall against SOI more linear (i.e. more like that in Fiji), as would be consistent with the ‘curvature hypothesis’ of Power et al. (1999).
A more likely factor could be the influence of other large-scale climatic oscillations that affect Australia, notably the Indian Ocean Dipole (IOD) and the Southern Annular Mode (SAM), all of which favoured drought for at least part of this period (Verdon-Kidd and Kiem 2009). The ‘bushfire summer’ of 2019–2020, with its record high temperatures provides a recent dramatic demonstration that these latter influences (IOD and SAM) can override the ‘effect’ of a more-or-less neutral ENSO (BOM 2020). Such influences may also explain the lower than average rainfall in southeastern Australia in the La Niña event of 2007 (Gallant and Karoly 2009). Modelling by Cai and van Rensch (2013) showed that in austral spring (September, October, November) the IOD and ENSO were often coherent, thereby reinforcing the effect of ENSO on rainfall in Australia, and similarly for the Indian Ocean Basin Mode in austral summer (December, January, February).
6.4 Long-term movements of SPCZ
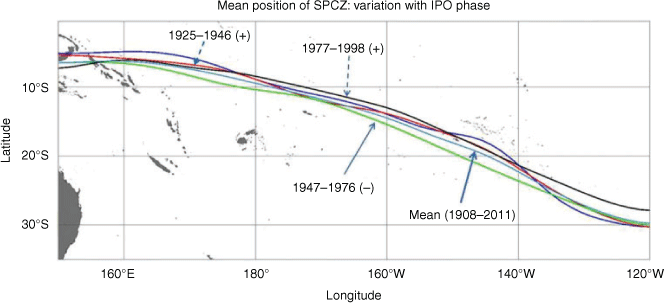
Global satellite-based rainfall maps, on which Fig. 3 is based, were available only from around 1979. However, analyses by Harvey et al. (2018, 2019) used data from NOAA’s ‘20th century REANALYSIS (v2c)’ project going back to 1908 to identify the locus of maximum precipitation in the southwest Pacific region in each austral summer (December, January, February). One of their maps (reproduced here as Fig. 6) shows a clear northeastward movement of the mean SPCZ between the IPO negative period of 1947–1975 and the following IPO positive period of 1978–1998, with a northerly displacement of about 250 km at the longitude of the Cook Islands (i.e. ~160°W). This is consistent with the marked increase in rainfall at Penrhyn during 1978–1998 and in El Niño (during which the SPCZ also moves northeastward).
|
The SPCZ Index (SPCZI, Appendix 2) introduced by Salinger et al. (2014) as an index of SPCZ position can also provide some long-term information, as it can be traced back to around 1900. Unfortunately, the SPCZI varies monotonically but non-linearly with displacement of the SPCZ (especially in the region south east of Samoa), so little can be inferred from the magnitude of the SPCZI. Nevertheless, a time series of SPCZI (Fig. A1b) shows little visible or statistical difference between the displacements in the two positive phases of IPO, and thus no indication of any difference due to climate change between 1926–1941 and 1978–1998.
6.5 Penrhyn
On the basis of a similar argument about movement of the SPCZ to that for Rarotonga (Fig. 3d), but in reverse, one would expect that at Penrhyn, which lies near the northern edge of the mean position of the SPCZ El Niño would correspond to wetter years and La Niña to drier years, i.e. the reverse of the situation at Rarotonga. Such is indeed the case, as shown in Fig. 5b. The correlation coefficient between rainfall and SOI taken over 1937–2015 (i.e. all available data) is strongly negative (r = −0.70), excluding years with –5 < SOI < +5. Penrhyn had very large variation of rainfall in El Niño years (ranging from 1176 mm to 4721 mm) and relatively small variation of rainfall in La Niña years.
The difference in rainfall between IPO phases was much greater at Penrhyn than at any of the other island sites, with average rainfall there in the IPO positive phase 1978–1998 nearly double that than in the preceding or following negative phases (see Fig. 4g). Indeed the 9 years of highest rainfall (>3500 mm) all fell in periods of positive IPO, and all of the 19 driest years (<1500 mm) fell in phases of negative IPO.
7 Conclusions
Our results confirm that rainfall in eastern Australia and several Pacific Islands is strongly affected by ENSO. The correlations between ‘annual’ rainfall and SOI are stronger if calculated using ‘ENSO years’ from May to the next April, as we have done, than using calendar years.
Sites on the ‘dry’ side of the larger islands of Fiji are sheltered from the moist trade winds of the austral winter and therefore showed much stronger correlations between rainfall and SOI than other Fiji sites. For such sites, the correlation remained high (r > 0.6) throughout the study period (1916–2013), and the quadratic best-fit curve of rainfall against SOI was almost linear. The results for Port Vila in central Vanuatu were broadly similar to those from the ‘dry’ side of Fiji, though the correlations in each IPO phase are all somewhat weaker than for Fiji.
The results for Rarotonga in the southern Cook Islands differed markedly from those for the other island sites and for eastern Australia, particularly since 1946, with the correlation stronger in the positive IPO period 1978–1998 than in the preceding and following periods of negative IPO, in both of which r < 0. 4. Indeed the quadratic best-fit curve of rainfall against SOI for Rarotonga is concave downwards, with rainfall varying only weakly with SOI in La Niña years, but so strongly correlated with SOI in El Niño years (r = 0.85) that SOI alone became a good predictor of wet-season rainfall when SOI < −5.
All of the 4 mills in Fiji, Port Vila and Rarotonga lie close to the southern edge of the mean position of the SPCZ. This explains the difference between El Niño and La Niña years at Rarotonga. In La Niña years, the SPCZ moved to the southwest but still lay over Rarotonga; but in El Niño years, the SPCZ moved to the northeast, resulting in a band with a strong gradient of rainfall over Rarotonga. This effect was more marked at Rarotonga than at the other island stations because the displacement (in km) of the SPCZ was greater at Rarotonga, which was furthest from the ‘pivot’ at the warm pool. The reverse effect applied for Penrhyn in the northern Cook Islands, which was near the northern edge of the SPCZ.
The correlation between rainfall in Australia and SOI was strongly modulated by the IPO for much of the 20th century, being high (>0.7) in IPO negative phases (1916–1925 and 1946–1975) and low (<0.2) in the positive phase 1926–1941. Power et al. (1999) attributed this effect to: (a) the curve of rainfall against SOI, which is concave upwards, since rainfall there does not vary much between dry years (strong El Niño) and very dry years (extreme El Niño); and (b) the broad similarity of SST across the Pacific in an El Niño to that when IPO was positive. However, contrary to that finding, the correlation remained consistently high (i.e. effectively unmodulated) through the subsequent positive phase (1978–1998) and negative phase (1999–2013).
Our results across the southwest Pacific region suggest that the drop in SOI/rainfall correlation in the earlier positive IPO phase in eastern Australia in 1925–1941 may have been more of an anomaly than the high values in the second positive IPO phase (1978–1998). This may have related to the rainfall in eastern Australia being significantly lower in 1926–1941 than in any of the other IPO phases in this study, which was not the case for the island sites. It may also have related to the relatively low frequency of ENSO events in that period and to the influence on Australia of other climatic oscillations, such as the IOD and the SAM. An alternative interpretation could be the anomalous period is that of positive TPI in Australia during 1978–1998, perhaps resulting from central Pacific El Niño events becoming the more frequent type. It is also possible that climate change has changed the modulating effect of IPO on SOI/rainfall correlation since 1977. However, the only period of positive TPI since 1998 was that beginning around 2015, which is not yet far enough advanced to test this hypothesis.
Nevertheless, this study has confirmed that the phase of IPO can have a significant influence on the correlation between rainfall and SOI and thus on the usefulness of SOI and other ENSO-related parameters in predicting seasonal rainfall in both eastern Australia and the islands of the southwest Pacific. Since projections indicate that ENSO and the SPCZ are likely to continue as major features of the climate in the southwest Pacific (Cai et al. 2012; Cai et al. 2014), knowing how they influence rainfall in the region will continue to be of scientific and economic importance.
Conflicts of interest
The authors declare that they have no conflicts of interest.
Acknowledgements
This paper builds on work at the University of the South Pacific (USP) with our former colleague Mark Stephens, and preliminary versions of this analysis were presented at the 2017 and 2018 conferences of the Australian Meteorological and Oceanographic Society. We thank the Australian Bureau of Meteorology (BOM), the Fiji Meteorological Service, and the Cook Islands Meteorological Service for supplying their data and for their permission to use it in this study. Publicly available rainfall data for Port Vila, compiled by and owned by the Vanuatu Meteorological Service, was obtained from the Pacific Climate Change Data Portal on the BOM website. We also acknowledge helpful comments on various iterations of this paper from Scott Power (BOM), who inspired much of the analysis presented here; Ben Henley (University of Melbourne); Robson Tigona (USP and Vanuatu Meteorology and Geo-hazards Department); and two anonymous but very diligent referees. This research did not receive any specific funding.
References
Asseng, S., Thomas, D., McIntosh, P., Alves, O., and Khimashia, N. (2012). Managing mixed wheat-sheep farms with a seasonal forecast. Agric. Syst. 113, 50–56.| Managing mixed wheat-sheep farms with a seasonal forecast.Crossref | GoogleScholarGoogle Scholar |
Bettencourt, S., Croad, R., Freeman, P., Hay, J., Jones, R., King, P., Lal, P., Mearns, A., Miller, G., Pswarayi-Riddihough, I., Simpson, A., Teuatabo, N., Trotz, U. and Van Aalst, M. (2006). Not if but when: Adapting to natural hazards in the Pacific Island region: a policy note. (World Bank: Washington.)
BOM (2020). Annual Climate Statement 2019. Bureau of Meteorology: Melbourne. Available at http://www.bom.gov.au/climate/current/annual/aus/
Cai, W., and van Rensch, P. (2013). Austral Summer Teleconnections of Indo-Pacific Variability: Their Nonlinearity and Impacts on Australian Climate. J. Climate 26, 2796–2810.
| Austral Summer Teleconnections of Indo-Pacific Variability: Their Nonlinearity and Impacts on Australian Climate.Crossref | GoogleScholarGoogle Scholar |
Cai, W., van Rensch, P., Cowan, T., and Sullivan, A. (2010). Asymmetry in ENSO teleconnection with regional rainfall, its multidecadal variability and impact. J. Climate 23, 4944–4955.
| Asymmetry in ENSO teleconnection with regional rainfall, its multidecadal variability and impact.Crossref | GoogleScholarGoogle Scholar |
Cai, W., Lengaigne, M., Borlace, S., Collins, M., Cowan, T., McPhaden, M. J., Timmermann, A., Power, S., Brown, J., Menkes, C., Ngari, A., Vincent, E. M., and Widlansky, M. J. (2012). More extreme swings of the South Pacific convergence zone due to greenhouse warming. Nature 488, 365–370.
| More extreme swings of the South Pacific convergence zone due to greenhouse warming.Crossref | GoogleScholarGoogle Scholar | 22895343PubMed |
Cai, W., Borlace, S., Lengaigne, M., Rensch, P. V., Collins, M., Vecchi, G., Timmermann, A., Santoso, A., McPhaden, M. J., Lixin, W., England, M. H., Guojian, W., Guilyardi, E., and Jin, F.-F. (2014). Increasing frequency of extreme El Niño events due to greenhouse warming. Nature Climate Change 4, 111–116.
| Increasing frequency of extreme El Niño events due to greenhouse warming.Crossref | GoogleScholarGoogle Scholar |
Chung, C. T. Y., and Power, S. B. (2017). The non-linear impact of El Niño, La Niña and the Southern Oscillation on seasonal and regional Australian precipitation. J. South. Hemisph. Earth Syst. Sci. 67, 25–45.
| The non-linear impact of El Niño, La Niña and the Southern Oscillation on seasonal and regional Australian precipitation.Crossref | GoogleScholarGoogle Scholar |
Clarke, A. J. (2008). An Introduction to the Dynamics of El Niño and the Southern Oscillation. (Academic Press: San Diego.)
Cottrill, A., and Kuleshov, Y. (2014). An assessment of rainfall seasonal forecasting skill from the statistical model SCOPIC using four predictors. Aust. Meteorol. Oceanogr. J. 64, 273–281.
| An assessment of rainfall seasonal forecasting skill from the statistical model SCOPIC using four predictors.Crossref | GoogleScholarGoogle Scholar |
Folland, C. K., Renwick, J. A., Salinger, M. J., and Mullan, A. B. (2002). Relative Influences of the Interdecadal Pacific Oscillation and ENSO on the South Pacific Convergence Zone. Geophys. Res. Lett. 29, 211–214.
| Relative Influences of the Interdecadal Pacific Oscillation and ENSO on the South Pacific Convergence Zone.Crossref | GoogleScholarGoogle Scholar |
Freund, M. B., Henley, B. J., Karoly, D. J., McGregor, H. V., Abram, N. J., and Dommenget, D. (2019). Higher frequency of Central Pacific El Niño events in recent decades relative to past centuries. Nature Geosci. 12, 450–455.
| Higher frequency of Central Pacific El Niño events in recent decades relative to past centuries.Crossref | GoogleScholarGoogle Scholar |
Gallant, A. J. E., and Karoly, D. J. (2009). Atypical influence of the 2007 La Niña on rainfall and temperature in southeastern Australia. Geophys. Res. Lett. 36, L14707.
| Atypical influence of the 2007 La Niña on rainfall and temperature in southeastern Australia.Crossref | GoogleScholarGoogle Scholar |
Harvey, T., Renwick, J. and Lorrey, A. (2018). The South Pacific Convergence Zone in Reanalysis and satellite products. In ‘Pacific Climate Change Conference’, 21–23 February 2018, Wellington, New Zealand.
Harvey, T., Renwick, J. A., Lorrey, A. M., and Ngari, A. (2019). The representation of the South Pacific convergence zone in the twentieth century reanalysis. Mon. Wea. Rev. 147, 841–851.
| The representation of the South Pacific convergence zone in the twentieth century reanalysis.Crossref | GoogleScholarGoogle Scholar |
Henley, B. J. (2017). Pacific decadal climate variability: indices, patterns and tropical-extratropical interactions. Glob. Planet. Change 155, 42–55.
| Pacific decadal climate variability: indices, patterns and tropical-extratropical interactions.Crossref | GoogleScholarGoogle Scholar |
Henley, B. J., Gergis, J., Karoly, D. J., Power, S., Kennedy, J., and Folland, C. K. (2015). A Tripole Index for the Interdecadal Pacific Oscillation. Climate Dyn. 45, 3077–3090.
| A Tripole Index for the Interdecadal Pacific Oscillation.Crossref | GoogleScholarGoogle Scholar |
King, A. D., Alexander, L. V., and Dona, M. G. (2013). Asymmetry in the response of eastern Australia extreme rainfall to low-frequency Pacific variability. Geophys Res Lett 40, 2271.
| Asymmetry in the response of eastern Australia extreme rainfall to low-frequency Pacific variability.Crossref | GoogleScholarGoogle Scholar |
Kumar, R., Stephens, M., and Weir, T. (2014). Rainfall trends in Fiji. Int. J. Climatol. 34, 1501–1510.
| Rainfall trends in Fiji.Crossref | GoogleScholarGoogle Scholar |
Mantua, N. J., Hare, S. R., Zhang, Y., Wallace, J. M., and Francis, R. C. (1997). A Pacific interdecadal climate oscillation with impacts on salmon production. Bull. Amer. Meteorol. Soc. 78, 1069–1079.
| A Pacific interdecadal climate oscillation with impacts on salmon production.Crossref | GoogleScholarGoogle Scholar |
McBride, J., and Nicholls, N. (1983). Seasonal relationships between Australian rainfall and the Southern Oscillation. Mon. Wea. Rev. 111, 1998–2004.
| Seasonal relationships between Australian rainfall and the Southern Oscillation.Crossref | GoogleScholarGoogle Scholar |
Murphy, B., Power, S., and McGree, S. (2014). The varied impacts of El Niño -Southern Oscillation on Pacific island climates. J. Climate 27, 4015–4036.
| The varied impacts of El Niño -Southern Oscillation on Pacific island climates.Crossref | GoogleScholarGoogle Scholar |
Nicholls, N. (1985). Impact of the Southern Oscillation on Australian crops. J Climate 5, 553–560.
| Impact of the Southern Oscillation on Australian crops.Crossref | GoogleScholarGoogle Scholar |
NOAA (2016). Equatorial Pacific Sea Surface Temperatures. National Oceanic and Atmospheric Administration. Available at https://www.ncdc.noaa.gov/teleconnections/ENSO/indicators/sst/
PCCSP (2011a). Climate Change in the Pacific: Scientific Assessment and New Research. Volume 2: Country Reports. Pacific Climate Change Science Program (Australian Bureau of Meteorology and CSIRO: Melbourne.) www.pacificclimatechangescience.org
PCCSP (2011b). Climate Change in the Pacific: Scientific Assessment and New Research. Volume 1: Regional Overview. Pacific Climate Change Science Program (Australian Bureau of Meteorology and CSIRO: Melbourne.) www.pacificclimatechangescience.org
Power, S., Casey, T., Folland, C., Colman, A., and Mehta, V. (1999). Inter-decadal modulation of the impact of ENSO on Australia. Climate Dyn. 15, 319–324.
| Inter-decadal modulation of the impact of ENSO on Australia.Crossref | GoogleScholarGoogle Scholar |
Power, S., Haylock, M., Colman, R., and Wang, S. (2006). The predictability of interdecadal changes in ENSO activity and ENSO teleconnections. J. Climate 19, 4755–4771.
| The predictability of interdecadal changes in ENSO activity and ENSO teleconnections.Crossref | GoogleScholarGoogle Scholar |
Power, S. B., Schiller, A., Cambers, G., Jones, D., and Hennessy, K. (2011). The Pacific Climate Change Science Program. Bull. Amer. Meteorol. Soc. 92, 1409–1411.
| The Pacific Climate Change Science Program.Crossref | GoogleScholarGoogle Scholar |
Salinger, M., Mcgree, S., Beucher, F., Power, S., and Delage, F. (2014). A new index for variations in the position of the South Pacific convergence zone 1910/11-2011-2012. Climate Dyn. 43, 881–892.
| A new index for variations in the position of the South Pacific convergence zone 1910/11-2011-2012.Crossref | GoogleScholarGoogle Scholar |
Santoso, A., Hendon, H., Watkins, A., Power, S., Dommenget, D., England, M. H., Frankcombe, L., Holbrook, N. J., Holmes, R., Hope, P., Lim, E.-P., Luo, J.-J., McGregor, S., Neske, S., Nguyen, H., Pepler, A., Rashid, H., Gupta, A. S., Taschetto, A. S., Wang, G., Abellán, E., Sullivan, A., Huguenin, M. F., Gamble, F., and Delage, F. (2019). Dynamics and predictability of El Niño-Southern oscillation: An Australian perspective on progress and challenges. Bull. Amer. Meteorol. Soc. 100, 403–420.
| Dynamics and predictability of El Niño-Southern oscillation: An Australian perspective on progress and challenges.Crossref | GoogleScholarGoogle Scholar |
Sarachik, E. S. and Cane, M. A. (2010). The El Niño-Southern Oscillation Phenomenon. (Cambridge University Press: Cambridge, UK.)
Sinclair, P., Atumurirava, F. and Samuela, J. (2012). Rapid Drought Assessment Tuvalu. SOPAC Technical Report PR38, Secretariat of the Pacific Community: Suva, Fiji.
Smith, S. C., and Ubilava, D. (2017). The El Niño Southern Oscillation and economic growth in the developing world. Glob. Environ. Change 45, 151–164.
| The El Niño Southern Oscillation and economic growth in the developing world.Crossref | GoogleScholarGoogle Scholar |
Solofa, D., and Aung, T. (2004). Samoa’s 102 year meteorological record and a preliminary study on agricultural product and ENSO variability. The South Pacific Journal of Natural Science 22, 46–50.
| Samoa’s 102 year meteorological record and a preliminary study on agricultural product and ENSO variability.Crossref | GoogleScholarGoogle Scholar |
Terry, J. (2007). Tropical Cyclones: climatology and impacts in the South Pacific. (Springer: Cham, Switzerland.)
Verdon-Kidd, D. C., and Kiem, A. S. (2009). Nature and causes of protracted droughts in southeast Australia: Comparison between the Federation, WWII, and Big Dry droughts. Geophys. Res. Lett. 36, L22707.
| Nature and causes of protracted droughts in southeast Australia: Comparison between the Federation, WWII, and Big Dry droughts.Crossref | GoogleScholarGoogle Scholar |
Wang, G., and Hendon, H. H. (2007). Sensitivity of Australian Rainfall to Inter–El Niño Variations. J. Climate 20, 4211–4226.
| Sensitivity of Australian Rainfall to Inter–El Niño Variations.Crossref | GoogleScholarGoogle Scholar |
Wang, G., Cai, W., and Santoso, A. (2020). Stronger increase in the frequency of extreme convective than extreme warm El Niño events under greenhouse warming. J. Climate 33, 675–690.
| Stronger increase in the frequency of extreme convective than extreme warm El Niño events under greenhouse warming.Crossref | GoogleScholarGoogle Scholar |
Definitions
A1.1. Southern Oscillation Index (SOI)
The SOI gives an indication of the development and intensity of El Niño or La Niña events in the Pacific Ocean. The SOI is calculated using the pressure differences between Tahiti and Darwin. There are a few different methods for calculating the SOI. The method used by the Australian Bureau of Meteorology is the Troup SOI, which is the standardised anomaly of the mean sea level pressure (MSLP) difference between Tahiti and Darwin.
Calculation:
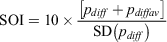
where:
pdiff = (average Tahiti MSLP for the month) − (average Darwin MSLP for the month),
pdiffav = long term average of pdiff for the month in question, and
SD(pdiff) = long term standard deviation of pdiff for the month in question.
The above text and monthly data used in this paper were taken from http://www.bom.gov.au/climate/current/soihtm1.shtml.
A1.2. Niño 3.4 index
The Niño 3.4 index (sometimes referred to by National Oceanic and Atmospheric Administration as the Oceanic Niño Index, ONI) is essentially the anomaly in sea surface temperatures (SSTs) in the Niño 3.4 region of the central Pacific, which covers 5°N–5°S and 170°W–120°W. The anomaly is measured monthly relative to a centred 30-year base period, which is updated every 5 years. An El Niño (La Niña) condition is characterised by a positive (negative) departure from normal SSTs, greater than or equal to +0.5°C (less than or equal to –0.5°C) of the running 3-month average (NOAA 2016).
A1.3. Interdecadal Pacific Oscillation Tripole Index (TPI)
The TPI was calculated using the methods below.
Step 1. Subtract the monthly climatology from each SST grid cell (1° × 1°) to remove the seasonal cycle and compute the monthly mean SST anomalies in each of the three TPI regions using a chosen base period (1971–2000 used here). The regions are:
region 1, 25°N–45°N, 140°E–145°W;
region 2, 10°S–10°N, 170°E–90°W;
region 3, 50°S–15°S, 150°E–160°W.
Step 2. Compute the unfiltered TPI as:
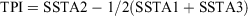
Step 3. Apply a 13-year Chebyshev low-pass filter to obtain the filtered version of the index (filtered TPI).
Monthly (unfiltered) and 13-year ‘filtered’ data for TPI are available at: https://psl.noaa.gov/data/timeseries/IPOTPI/.
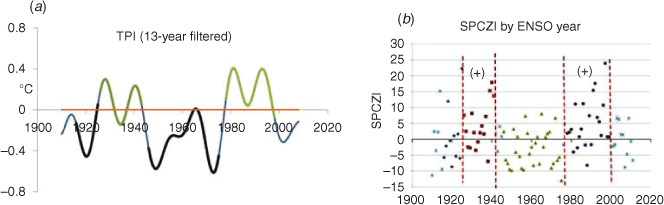
The initial selection of TPI phases for our analysis was based on the 13-year filtered index, which was recommended by Henley et al. (2015) for such purposes, shown in Fig. A1a. For consistency with our other data, the TPI plotted in Fig. 4f is a 5-year running average of the monthly data. As can be seen in Fig. 4, the phases are consistent with that version also.
|
Appendix 2. Time series of the South Pacific Convergence Zone Index (SPCZI)
The SPCZI of Salinger et al. (2014) is based on the sea level pressure difference between a pair of stations roughly equidistant to the northeast and southwest of the SPCZ, namely Apia (Samoa) and Suva (Fiji). As the SPCZ moves to the northeast, the pressure increases in Apia relative to ‘normal’, so the SPCZI is positive. Unfortunately, because the SPCZI varies monotonically but non-linearly with displacement of the SPCZ (especially in the region south east of Samoa), little can be inferred from the magnitude of the SPCZI. Nevertheless, one can say that there is little visible or statistical difference in Fig. A1b between the displacements in the two positive phases of IPO, and in particular no indication of any difference due to climate change between 1926–1941 and 1978–1998.
Appendix 3. Treatment of missing data
Fiji. For each of the 4 mills, any El Niño-Southern Oscillation (ENSO) year with rainfall data missing for at least one month was regarded as ‘missing data’ and omitted from the analysis. For any such year, the rainfall for ‘4 mills’ was taken as the average over the remaining mills (i.e. those with adequate data for that year). 1930 is the only year for which more than one mill had missing data. For each station, the ENSO years affected were: Lautoka 1930, 1931, 1937 and 1945; Labasa none; Rarawai (Ba) 1930, Penang (Rakiraki) 1925, 1927, 1978 and 1987. Thus, there is usable data for ‘4 mills’ for the whole period 1910–2014.
Vanuatu. Port Vila is the only station in Vanuatu with a long enough run of data to be used in this paper. In the period 1910–2014, data was ‘missing’ (as defined above) for 1927, 1928, 1942, 1943, 1951. That is why slightly different periods are plotted for Port Vila in Fig. 2.
Cook Islands. There was no missing data for Rarotonga in the southern Cook Islands; but for Penrhyn in the northern Cook Islands, data for the following ENSO years was unavailable: 1910–1936 (no records), 1947, 1949, 1996, 2001 and 2004.
Eastern Australia. No missing data.
Appendix 4. SOI/rainfall correlations: ENSO years versus calendar years
Analyses in this paper is in terms of ‘ENSO years’ running from May through to April in the following calendar year. ENSO year 1910 here refers to May 1910–April 2011. Table A1 shows that the correlation coefficient between annual rainfall and annual SOI was typically about 10% greater when calculated using ENSO years rather than calendar years.
|