Observations of wildfire spread dynamics in southern Australian grasslands
Miguel G. Cruz A * , Musa Kilinc B , James S. Gould A and Wendy R. Anderson C
A * , Musa Kilinc B , James S. Gould A and Wendy R. Anderson C
A
B
C
Abstract
Wildfire propagation is inherently non-steady, although forecasts of their spread focus on a pseudo-steady state assumption.
To investigate the variability in rate of fire spread of wildfires in southern Australian grassland landscapes, and the effect of landscape features in inhibiting fire propagation. To evaluate the adequacy of grassfire rate of spread models currently used in Australia.
We reconstructed the propagation of six wildfires in grassland fuels and characterised the unsteady nature of rate of spread. We also analysed the effect of barriers to fire spread in slowing or halting wildfire propagation.
Headfire rate of spread in wildfires was observed to be non-steady, with peaks in forward rate of spread being on average 2.6-times higher than mean values. The rate of spread had an average coefficient of variation of 88%. Areas of fuel discontinuity, such as roads, did not stop fires under moderate burning conditions, but resulted in slowing the average rate of fire spread.
Analysis of wildfire observations is key to understand fire behaviour features that are not replicable in experimental or modelling environments. Findings from the analysis can support fire-fighting safety awareness and inform landscape fire propagation modelling.
Keywords: fire barriers, fire behaviour, fire environment, grass curing, non-steady fire propagation, rate of fire spread, wildfire documentation.
Introduction
As a wildfire moves across the landscape, the speed at which its headfire travels in the direction of its primary spread is non-steady, fluctuating over short to long time scales (Viegas et al. 2021, 2022). Small scale non-steady periodic behaviour within the flame zone is suggested to be the result of turbulent interactions between the buoyant forces of the fire and the inertial forces driving it (Finney et al. 2015). As the time and space length scales increase, the non-steady behaviour is determined by a number of factors. For example, the variability in wind speed associated with gust and lull cycles result in direct changes in the rate of fire spread, as described by Albini (1982) and observed in large scale experimental fires (Cheney et al. 1993; Clark et al. 1999; Taylor et al. 2004; Viegas et al. 2022). Linked to these cycles are also fire–atmosphere interactions. Cheney and Sullivan (2008) provide a description of the interaction between fire generated convective cells and the transient wind flow, with the generation of up- and down-drafts and their effect on grassfire propagation. As the size of the fire increases, it will integrate a larger range of burning conditions and larger, more drastic, variations in the environmental conditions (e.g. stronger wind gusts) are necessary to affect fire behaviour. At such scales, the fire–atmosphere interactions are characterised by larger cycles (e.g. Nelson et al. 2012; Viegas et al. 2022) as observed in the pulsating dynamics of strong convection columns. Topography, by affecting local fire behaviour, such as the increase in rate of spread and intensity in upslope runs (Luke and McArthur 1978: Butler et al. 1998; Viegas et al. 2021), will also influence the non-steady behaviour of larger fires. Spot fire dynamics, such as the occurrence of concentrated spot ignitions associated with upslope runs and the pulsating nature of the plume, is a further factor influencing the variability in observed fire spread (Luke and McArthur 1978). Through their spatial variability, fuels are another variable determining the local energy output that will affect how a wildfire will interact with the environment and atmosphere around it and its non-steady propagation. Non-steady propagation is also observed under constant boundary conditions in laboratory experiments (e.g. Catchpole et al. 1998; Viegas et al. 2022).
The transient nature of fire spread has been shown to be cyclic. For example, Albini (1982) showed theoretically how transient, or non-steady, wind speed and associated flame front characteristics, such as energy release and flame front residence time, affect the periodicity in rate of fire spread. The periodicity of the unsteady behaviour is suggested to be related to the length scales determining the cycles (Albini 1982; Finney et al. 2015; Viegas et al. 2022). From the analysis of experimental and wildfire case study data, Viegas et al. (2022) made the argument that the variation in a headfire rate of spread is the result of several superimposed cycles occurring at distinct frequencies and amplitudes. The longer the fire run and more variable the fire environment (e.g. different fuel types, propagation across multiple drainages with upslope and downslope runs), the more cycles should be observed.
For practical purposes, fire spread models used operationally (e.g. Rothermel 1972; Forestry Canada Fire Danger Group 1992; Cheney et al. 1998, 2012) assume a pseudo-steady state propagation in equilibrium with environmental conditions. This propagation is generally calculated over a time period of 30 min or longer (Rothermel 1983; Andrews et al. 2007; Cheney and Sullivan 2008). In operational situations, this is often aligned with the time resolution of the weather forecasts and does not attempt to describe short-term fluctuations or cyclic patterns in fire propagation. Considering wind speed is the most dynamic and variable input in fire spread models, Albini (1982) provided a justification for modelling fire spread as a steady state process given that variations in this input occur at frequencies below 0.001 Hz (i.e. cycles with a periodicity above ≈15 min).
The variability in rate of fire spread is a poorly studied aspect of fire behaviour, and to our knowledge, only a relatively small number of studies have quantified fluctuations in rate of spread on relatively large experimental fires over small time-scales (e.g. Burrows et al. 1991; Taylor et al. 2004; McRae et al. 2005; Cruz et al. 2013; Butler et al. 2016). Rothermel (1991) used data from a selected number of well documented wildfires in the conifer forests of the western United States to characterise the relationship between the average and maximum rate of fire spread over periods of several hours. In the most comprehensive treatment of the problem, Viegas et al. (2022) combined data from laboratory and field experiments with wildfire data, to explore the frequency and amplitude of observed oscillations in fire propagation.
The wide variability in fire spread and behaviour at short time scales in wildfires make it unlikely that adequate prediction tools can be developed to describe the minute-by-minute propagation of a wildfire in the foreseeable future with any degree of confidence (Rothermel 1991). Nonetheless, documenting such fire behaviour is of interest in understanding and quantifying, even if only in coarse terms, the non-steady propagation where one observes short-lived periods of rates of spread several times faster than the average value. This knowledge has obvious practical implications for modelling fire spread across the landscape and understanding how processes dependent on fireline intensity, such as firebrand generation, spot fire transport distances, onset of crowning and fire breaching of roads and fuel breaks, influence overall fire propagation. Similarly, unsteady behaviour and the occurrence of unexpectedly faster and more intense fire runs have relevance in fireline safety considerations (e.g. Rothermel and Mutch 1986; Rothermel 1993; Cheney et al. 2001; Butler 2014; Viegas et al. 2022).
The existence of roads, farm lanes and purpose-built firebreaks within grassland landscapes can have significant impacts on fire propagation and determine the variability in rate of fire spread. These features, called ‘barriers to fire spread’ (after Cheney et al. 1998), affect the overall rate of fire propagation across the landscape by: (1) stopping a fire under low fire spread potential; or (2) slowing a fire under moderate to high burning conditions (Cheney et al. 1998). They also aid more effective direct suppression action, namely around flanks (Cheney and Sullivan 2008). Understanding how different roads and other barriers to fire spread affect fire propagation is important for the accurate forecasting of the potential for fire propagation in grasslands.
We used observations from wildfires in grasslands to characterise the: (1) variability in rate of fire spread; and (2) effect of barriers to spread, such as roads, in slowing or halting fire propagation. We also used these data to test the adequacy of models currently used to predict wildfire propagation in southern Australian grassland landscapes.
Materials and methods
Wildfire spread data were collected by operational personnel from Victorian land management and fire-fighting agencies (see acknowledgements) involved in suppression operations within the first few hours (i.e. response phase) of wildfire events in grasslands. The dataset included fires occurring between 2021 and 2023 in western Victoria. The analysis focused on wildfires spreading predominately in pastures and winter crops (primarily wheat, barley and canola). All fires analysed in this study used Air Observer intelligence gathering tools that included photography utilising FireMapper Tablet software and video capture utilising forward and sideways facing cameras from aircraft. Additional wildfire incident data from radio dispatch logs, personnel logbooks and interviews with identified key individuals involved in suppression were used in the generation of wildfire propagation data. The amount of imagery per fire depended on its duration and competing operational requirements (e.g. aircraft could be deployed elsewhere for other emergencies). After each wildfire event, photographic (Figs 1 and 2) and video imagery was accessed, and only imagery with identifiable landscape markers and fire progression was used. Fire perimeters extracted from the imagery were digitised and geolocated using ArcGIS software (ESRI). Headfire rate of spread was calculated for each pair of adjacent perimeters from the distance travelled by the leading edge of the flame front between each perimeter divided by the time difference between perimeters. This defined a fire spread segment. Average headfire, or forward, rate of spread for overall fire runs, henceforth called ‘fire run’, encompassing several fire spread segments was calculated as the ratio of the overall distance travelled by the total time taken (i.e. not as an average of the segments; Gould and Sullivan 2020).
View of the Glenloth fire spread at 11:38 hours on 18 December 2021 as recorded from the air attack supervisor aircraft.

Final fire perimeter of the Glenloth fire at 13:09 hours on 18 December 2021. Oblique photograph shows the landscape mosaic of grass and crop types, and condition (e.g. harvested vs unharvested).

Onsite post-fire assessments were made between 1 and 5 days after events to determine grass or crop type, and condition (e.g. grazed, eaten out, harvested, etc.). Biomass quantity was destructively sampled using typically three 1 × 1-m quadrats in adjacent, unburned paddocks, deemed representative of the fuel supporting propagation of the main fire runs. Firebreaks and other barriers to fire propagation in the path of the fire were identified and their width measured to the nearest metre. Suppression activities were identified using vehicle tracking data and through interviews with landowners and firefighters. Aerial suppression conducted by rotary- and fixed-wing aircraft was assessed by mapping the aircraft tracking and drop timings.
Weather data from the nearest Commonwealth Bureau of Meteorology Automatic Weather Station (AWS) network, including 10-min averages of ambient air temperature, relative humidity, 10-m open wind speed and direction, and wind gust associated with the measurement period, were compiled for each fire.
Fire behaviour modelling and error statistics
Fire danger was calculated through the Grassland Fire Danger Index (McArthur 1966) using the Mk 3 equation of Noble et al. (1980). The Cheney et al. (1998) grass fire rate of spread models for natural and grazed grasslands were evaluated against the average observed rates of fire spread. These models predictions relied on estimated moisture content of dead grass fuels using Cheney et al. (1989) parameterisation of McArthur (1960) fuel moisture tables. Fire spread model fit was evaluated through the calculation of the mean absolute error (MAE), mean bias error (MBE) and mean absolute percentage error (MAPE) (Willmott 1982). Residuals were calculated as observed minus predicted, with positive and negative bias indicating under- and over-prediction, respectively. All statistical analyses were conducted with R software (R Core Team 2024). Fireline intensity, as per Byram (1959), was estimated using the measured fine fuel load and a low heat content of 18,600 kJ kg−1.
Results
Dataset characteristics
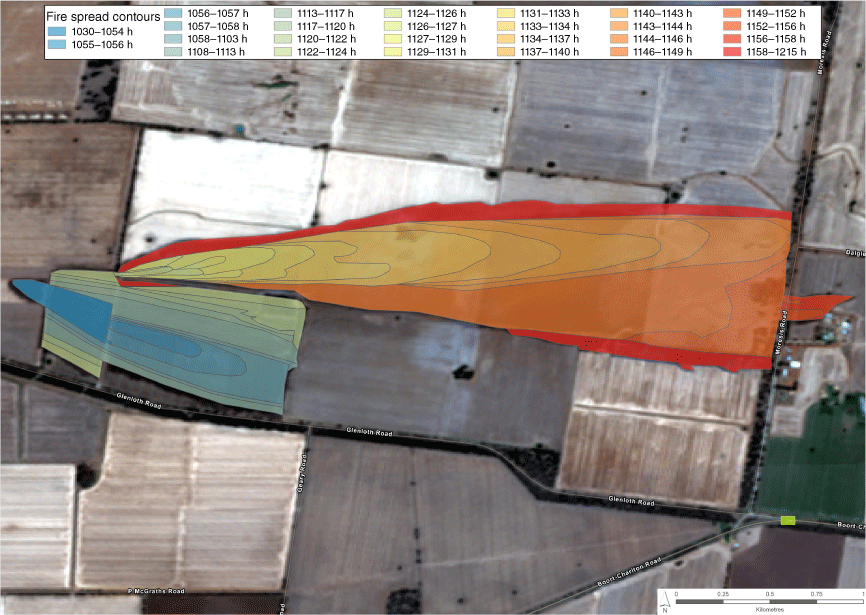
A dataset of six wildfires burning through grassland fuel types was assembled (Table 1). Two other available wildfires were not included as they did not meet data quality requirements. The wildfires in the dataset ranged in size between 31 and 502 ha (average 187 ha). A total of 75 fire spread segments were identified. After removing fire spread segments with uncertain start or end times, or involving wind direction changes greater than 45°, a total of 68 segments were used in the analysis. Fire spread segment period and distance averaged 200 s (3.3 min) and 261 m, respectively. The longest segment run was 1067 m. Two of the wildfires, the Glenloth East (Figs 1–3) and the Tahara, each had two independent or separate fire runs (e.g. Fig. 3, Table 1). Average wind speeds and estimated dead fuel moisture content varied between 11 and 32 km h−1 and 4.7 and 9.1% oven-dry weight, respectively (Table 2). Grasslands were observed to be 100% cured, although the curing level could have been lower in some localised gullies and creek lines.
| Fire | Date | Ignition location | Time period (fire run duration) | Number of fire runs | Nearest Bureau of Meteorology AWS, distance to fire | Main fuel type | Fire area (ha) | |
|---|---|---|---|---|---|---|---|---|
| Glenloth East run 1 | 18 December 2021 | 36.11S, 143.57E | 10:42–10:58 (16 min) | 4 | Charlton, 25 km | Barley, unharvested | 59 | |
| Glenloth East run 2 | 18 December 2021 | 36.11S, 143.57E | 11:24–11:58 (34 min) | 16 | Charlton, 25 km | Barley, unharvested | 166 | |
| Woodhouse | 13 January 2022 | 37.77S, 142.40E | 13:54–14:08 (14 min) | 6 | Westmere, 45 km | Pasture, ungrazed | 31 | |
| Tahara run 1 | 13 December 2022 | 37.73S, 141.70E | 12:47–13:18 (31 min) | 8 | Casterton, 30 km | Pasture, grazed | 169 | |
| Tahara run 2 | 13 February 2022 | 37.74S, 141.72E | 13:33–14:05 (32 min) | 9 | Casterton, 30 km | Pasture, grazed | 122 | |
| MurraWarra | 17 January 2023 | 36.43S, 142.28E | 16:50–17:02 (12 min) | 6 | Warracknabeal, 15 km | Wheat and lentils, harvested | 59 | |
| Hillside | 23 February 2023 | 37.37S, 143.11E | 12:17–12:54 (37 min) | 12 | Westmere, 40 km | Pasture, grazed | 496 | |
| Steele Rd | 19 November 2023 | 35.15S, 142.23E | 14:47–15:15 (28 min) | 7 | Walpeup, 23 km | Barley, harvested | 502 |
Map of the Glenloth Rd fire progression. Figure highlights the mosaic of different grass and crop conditions in the path of a wildfire typical of the southern Australia grassland environment. This fire had two independent runs, with the first run (cool colours) being stopped at a road after spreading for 1.3 km; the second run (warm colours) originated at the rear northern flank of the first run approximately 26 min after the first run stopped, and spread approximately 3.7 km before being largely suppressed at a major road. These two runs were considered independent for fire behaviour analysis. Background image is from 21 December 2021.
| Fire | 10-m open wind speed (km h−1) | Wind gust/mean ratio | Air temp (°C) | Relative humidity (%) | Observed mean rate of fire spread (km h−1) | Coefficient of variation (%) | Max/Mean rate of fire spread | Predicted dead fuel moisture content (%) | Predicted rate of fire spread (km h−1) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Glenloth East run 1 | 21 | 1.53 | 34 | 19 | 4.7 | 173 | 4.6 | 5.2 | 6.1 (nat) | |
| Glenloth East run 2 | 21 | 1.34 | 34 | 19 | 8.7 | 39 | 1.6 | 5.2 | 5.6 (nat) | |
| Woodhouse | 27 | 1.31 | 32 | 32 | 4.4 | 82 | 2.6 | 7.6 | 4.8 (cut) | |
| Tahara run 1 | 20 | 1.29 | 30 | 18 | 9.7 | 62 | 2.1 | 5.9 | 4.2 (cut) | |
| Tahara run 2 | 20 | 1.24 | 30 | 18 | 4.5 | 79 | 2.6 | 5.9 | 4.2 (cut) | |
| MurraWarra | 17 | 1.26 | 38 | 21 | 7.2 | 110 | 3.0 | 4.7 | 4.1 (cut) | |
| Hillside | 32 | 1.19 | 28 | 38 | 3.7 | 133 | 2.5 | 9.1 | 4.7 (cut) | |
| Steele Rd | 13 | 1.78 | 33 | 16 | 5.0 | 52 | 1.9 | 5.1 | 3.0 (cut) |
Cheney et al. (1998) fire spread rate model: nat, natural grass; cut, cut or grazed grass.
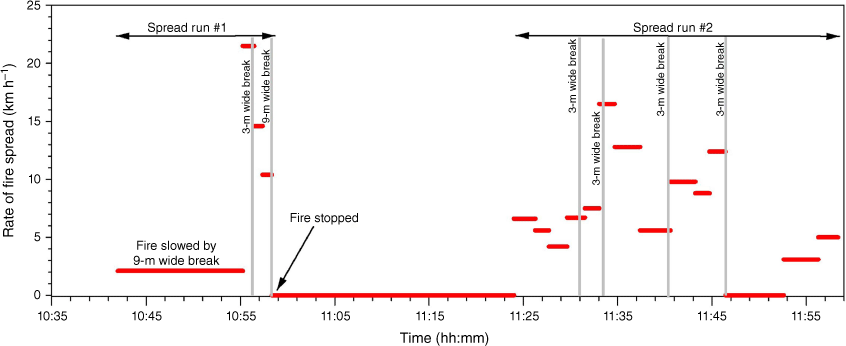
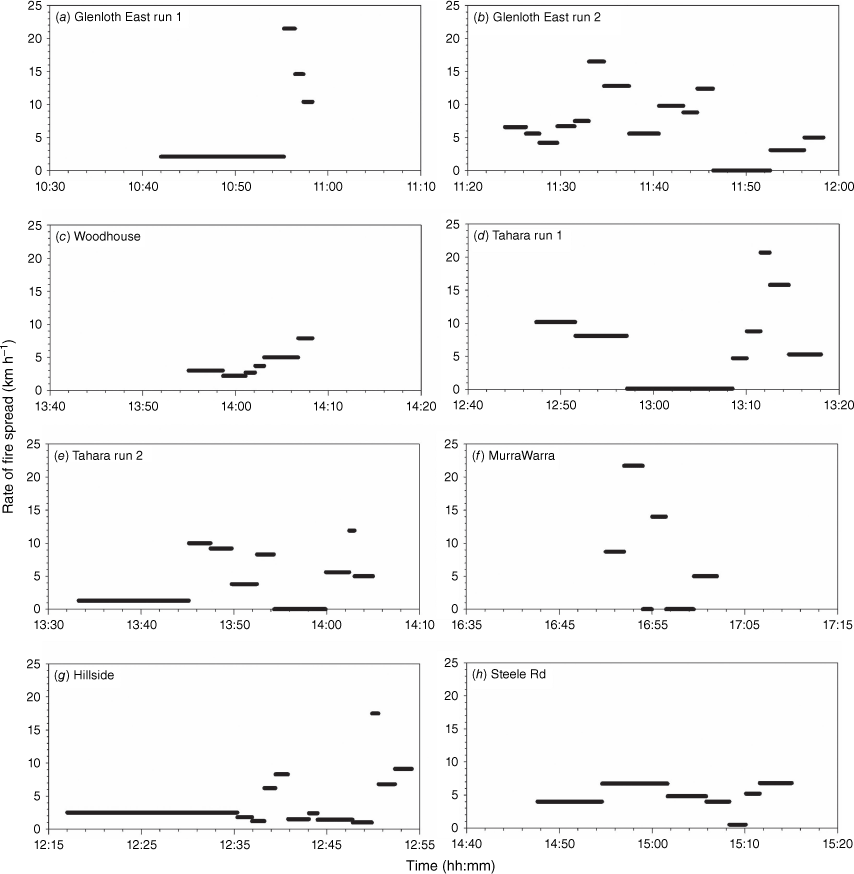
The Grassland Fire Danger Index (McArthur 1966) varied between 12 (Steele Rd fire) and 23 (Hillside fire), values within the High (8 < GFDI < 20) and Very High (20.5 < GFDI < 50) rating classes (Table 3). Segment rate of fire spread varied between 0.0 and 21.7 km h−1. Spread rates of zero refer to periods of time when the fire was held up for several minutes, at times up to 10 min (Fig. 4), by some sort of a barrier. Such barriers were eventually breached, allowing the fire to continue to propagate (Fig. 3). The average wildfire rate of spread for overall fire runs, varied between 3.7 and 9.7 km h−1 (Table 2). All observations were conducted within the first hour of propagation, although we could not identify any fire spread trend that would suggest a fire was still accelerating from its initial point source ignition (Fig. A1). All overall fire runs considered were assumed to be spreading in equilibrium with the environment having previously completed the fire acceleration phase after ignition.
| Fire | GFDI | Number and size of breaks crossed | Effect of Fire behaviour | Fuel relevance | Break effect on propagation | |
|---|---|---|---|---|---|---|
| Glenloth East | 21 | n = 9, 3–9 m wide. | Breaks had negligible effect when rate of spread was above 5 km h−1 | Fire stopped in breaks within harvested or fallow fields. | Fire spread unimpeded in most breaks, stopping at two breaks, a 9 and a 5.5-m wide break, with limited fuel continuity on the downwind side of break. | |
| Woodhouse | 22 | n = 5, 3–5 m wide. | Fire spreading between 2 and 12 km h−1. poorly maintained breaks were breached by slow spreading fire. | Paddocks were ungrazed; shelterbelt changed wind speed and fuel moisture around fire break. | Fire was slowed down while crossing the small farm breaks, but did not stop. Fire stopped at breaks with shelterbelt, believed to be due to its effect on grass curing, moisture content and wind field. | |
| Tahara | 18 | n = 6, 4–5.5-m wide roads | Fire spreading between 2.6 and 11.9 km h−1 when passing through roads | Harvested canola, and a mixture of pastures ranging from grazed to eaten out. | Roads (5.5-m wide) were able to hold fire for periods up to 5 min, after which fire would break out. Fire was able to spread over several well-maintained farm breaks, at times through spotting (200–300 m) from roadside vegetation. Fire eventually contained after headfire breached a 5.5-m wide road and break up. | |
| MurraWarra | 17 | n = 5; 5–6-m wide road. | Fire encountering breaks while spreading at 8.7–21 km h−1. | Mixture of harvested and unharvested cereals and legumes. Road side vegetation well managed. | Fire crossed most roads without noticeable slowing. Fire was stopped momentarily as it reached a 6-m wide road. Fire eventually broke through, but its narrow front was suppressed. | |
| Hillside | 23 | n = 5, 5-m wide roads; 20-m wide gullies. | Fire encountering breaks while spreading with a speed of 1.2–6.2 km h−1 | Combination of grazed and natural pastures; not fully cured grasses in gullies. | Fire slowed down while crossing most of breaks. Often momentarily stopping and then crossing in a number of different points. | |
| Steele Rd | 12 | n = 3, 10–15-m wide roads. | Fire encountering breaks while spreading at 4–9.4 km h−1 | Harvested barley | Two 15-m wide, poorly maintained breaks, halted propagation momentarily, resulting in a considerably slowing down of the fire. The 10-m wide, well-maintained road held the headfire region while the fire was spreading at about 9 km h−1. Spot fires formed downwind, but were successfully suppressed while small. |
Variability in observed rate of fire spread in the Glenloth Road Fire. Red horizontal lines represent the average segment rate of fire spread; grey vertical lines represent barriers such as fire breaks. Fire was reported at 10:30, and the first fire behaviour observation was conducted at 10:37 hours.
Fire spread variability
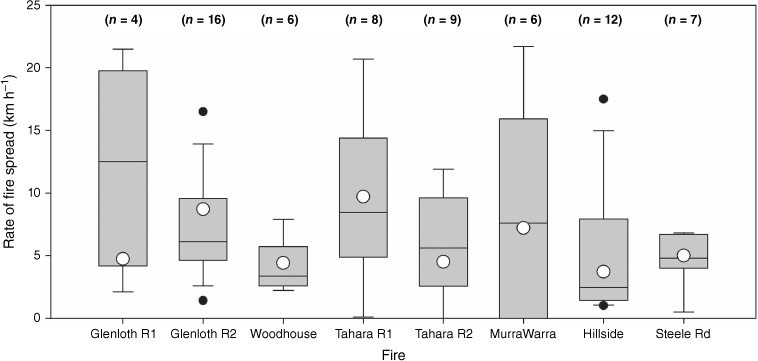
The variability of the headfire rate of spread for the six wildfires analysed is illustrated in Fig. 5 (also Fig. A1). The fastest segment fire spread rate, 21.7 km h−1 on the Glenloth East fire, was 4.6-times greater than the average for the overall fire run. The ratio between the maximum and the mean rate of fire spread averaged 2.6 for the eight fire runs; i.e. on average the maximum rate of spread was approximately 2.6-times the overall fire run average. This ratio varied between 1.9 and the above mentioned 4.6. The coefficient of variation of rate of fire spread averaged 88%, varying between 39 and 173% (Table 2).
Variability in observed rate of fire spread in the eight wildfires runs used in the analyses. Boxes define the upper and lower quartiles, with the thin line within representing the median. The open circle is the fire run average rate of spread. The outer horizontal lines outside the box reflect maximum and minimum values excluding outliers (black circles), defined as more than 3/2-times the upper quartile.
Rate of fire spread was dynamic or non-steady in all fires (Fig. A1). Very slow rates of spread were associated with periods where the headfire was held up by, but eventually crossing, a barrier. We could not identify a clear acceleration trend in the segments downwind of a barrier once the fire breached it. The rate of spread of the fire segment after being held and overcoming a barrier was often quite high (e.g. Fig. A1a, e, f). We were only able to observe a cyclic trend in the longer duration runs (Fig. A1b, d, e, f). Smaller runs (Fig. A1a, c, e) did not have the duration to establish time series where a cycle was observable.
Effect of barriers on grassland fire propagation
Of the 68 fire spread segments used in this analysis, a total 41 segments had fire crossing, or breaching, barriers such as roads or other types of breaks. Barrier characteristics varied from firebreaks and farm lanes, typically 3-m wide, to gullies (often with non-fully cured grasses) about 20-m in width (Table 3). Firebreaks and roads ranged from poorly maintained (e.g. some fuel might be present) to well-maintained, with surrounding vegetation managed (e.g. cut or well grazed grass).
Under the burning conditions associated with the dataset, no road, firebreak or gully stopped a wildfire per se. We observed that most poorly maintained barriers with widths of up to 3.0 m did not affect the propagation of a wildfire if it was spreading vigorously. Wider barriers, such as roads, tended to slow the overall wildfire propagation, and at times facilitated its containment.
The effect of a barrier on fire propagation was dependent on the speed and intensity of the fire at the time it reached the barrier, the width and condition of the barrier, the grass fuel condition surrounding the barrier (e.g. eaten-out vs natural or unharvested crop), and the existence of trees or shelterbelt on the windward side. Collected data did not allow for a quantitative analysis of the effect of barriers on fire propagation, although the data were in agreement with Wilson (1988) firebreak breach model.
Evaluation of Cheney et al. (1998) grass fire spread models
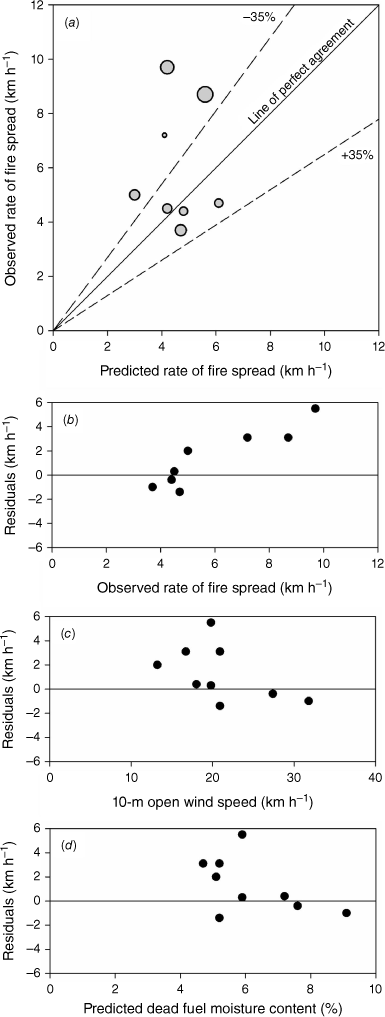
The grass fire spread models of Cheney et al. (1998) were evaluated using the overall fire runs (Tables 1 and 2). With the exception of one shorter fire run (i.e. MurraWarra fire, 1.8 km in 12 min), all other fire runs lasted approximately 30 min or more. Fire runs incorporated all the fire segments within its spread footprint, also encompassing periods of slow propagation due to the effect of barriers as envisioned by Cheney et al. (1998). Fire spread predictions used the most appropriate fire spread model for the prevailing grass fuel condition: cut and grazed model for mid-summer pastures (Cheney and Sullivan 2008) and harvested crops (Cruz et al. 2020); and natural grass model for unharvested crops (Cruz et al. 2020). The models predicted the dataset with an MAE of 1.72 km h−1, and a MAPE of 26%. Mean bias was 1.16 km h−1. Four of the eight fire runs evaluated were within the ±35% error band (Cruz and Alexander 2013). The fastest fires were under-predicted (Fig. 6a, b). Interestingly, these fires had moderate wind speeds (i.e. between 13 and 21 km h−1) and very low estimated fine dead fuel moisture contents, between 4.5 and 5.2% (Fig. 6c, d). No other available variables, such as run duration (Table 1) or wind gustiness (Table 2), explained the under-prediction of the four fastest fires.
Plots of (a) observed rate of fire spread vs predictions of the Cheney et al. (1998) fire spread models, with bubble size proportional to the fire run duration (range, 12–37 min), (b) residuals vs observed rate of fire spread, (c) residuals vs 10-m open wind speed, and (d) residuals vs predicted dead fuel moisture content. The dashed lines around the line of perfect agreement in (a) indicate the ±35% error interval.
Discussion
The detailed dynamics of the observed wildfire rates of spread followed the conceptual process as described by Cheney et al. (1998) and Cheney and Sullivan (2008) for grassfire propagation in southern Australia pastoral and cropland areas. Fire spread rates increased during periods of wind gusts, slowed down during lulls in wind or when the flame front reached areas with low fire spread potential (e.g. creek lines), and were momentarily halted when roads and other barriers were of such a size that they limited propagation by reduced convective or radiative energy heat transfer. It should also be noted that the fires occurred within fire danger rating levels (High and low range of Very High) amenable for effective suppression (Cheney and Gould 1995).
Fire spread variability
The fire variability data analysed had length scales between the observations in experimental fire behaviour studies, e.g. tens of meters and less than 2 min (e.g. Burrows et al. 1991; Taylor et al. 2004; Butler et al. 2016), and wildfire data, e.g. longer than a kilometre and an hour (Rothermel 1991; Viegas et al. 2022). All wildfire runs showed an unsteady dynamic in rate of fire spread, with the longer runs showing a cyclic variation in spread rate (Fig. A1). It is unclear if the main determinant of the amplitude and frequency of the observed cycles was due to changes in wind speed, fuel condition, suppression, or fire-atmosphere interactions; however, it was observed that in a number of occasions fires would temporarily halt while reaching barriers. The dataset does not contain the detail necessary to investigate the drivers of the cyclic fire dynamics, mainly because the wind measurements were conducted tens of kilometres from the active headfire region.
The data collected give insights into the variability in rate of fire spread expected to occur in wildfires burning in similar conditions in southern Australia, with spread rate having an average coefficient of variation of 88%. Probably of more relevance for suppression operations is the finding that on average, the peak rate of fire spread can be almost three times higher than the observed or predicted fire run average value. This value is higher than the average of 1.7 presented by Rothermel (1991) for a series of wildfires burning in conifer forests of the northern Rocky Mountains, USA; and 1.8-times observed in experimental crown fires carried out in the boreal conifer forest in the north-west Territories of Canada (Taylor et al. 2004). Sudden changes in fire behaviour have the potential to disrupt effective suppression operations (Plucinski 2019) and place firefighters in danger.
The high maximum:mean rate of fire spread ratio observed in our dataset suggests a higher amplitude in rate of fire spread cycles in grassland fuels. This is likely because the prevailing open environment, very fine dead fuels, and relatively smaller energy release rates make the flame front more reactive to changes in wind, which has implications for fireline safety and risk analysis. It is important to emphasise the relatively small size of the dataset used in this analysis limits any more definitive conclusions. The effect of barriers to spread in grassfires, causing fires to momentarily stop at a location, will also reduce the average rate of spread of a fire run, which in turn will result in a higher max/mean rate of fire spread ratio. Analysis of a larger dataset, such as that of Cadril et al. (2023), will be necessary in order to more comprehensively explore the variable behaviour of wildfires.
Effect of barriers to fire spread
Data characteristics, namely the limited size of the database, did not allow for a robust quantitative analysis of the effect of the barriers on fire propagation. Despite this fact, the observations in the dataset did allow for a number of qualitative inferences. Landscape fuel discontinuities, in the case of southern Australian grasslands being mostly barriers such as roads, have a visible effect on overall fire propagation and suppression effectiveness (McArthur et al. 1982). Wider barriers, such as established roads 5–10 m wide, tended to significantly slow the overall wildfire propagation, and at times facilitated containment. When a wildfire reached such a barrier, the headfire would stop momentarily, with discrete ignition points observed to occur downwind of the barrier. It was observed that such ignitions could occur immediately or take minutes to materialise; up to approximately 10 min in some cases. This process was often repeated several times in the longer runs (e.g. Glenloth East fire, Fig. 4). This momentary halting of overall fire propagation and associated reduction in fireline intensity often allowed for successful containment of the fire at that location. However, we could not identify situations where the barriers, at times consisting of 15-m wide tracks, stopped a fire solely by itself. From the observations, it was evident that small wind shifts on the flanks or back of the fire allowed a new headfire to develop and breach the barrier; in some cases, this occurred on multiple occasions before the barrier was finally breached. It is uncertain as to whether these breaches across barriers were due to wind gusts increasing the flame length and thereby enabling direct flame contact across the barrier, short distance ember transport, or a combination of both.
Small barriers, such as 3-m wide roads, showed negligible effect on slowing down the headfire region, with flame fronts often progressing unimpeded across these barriers without any observable variations in rate of fire spread.
Successful containment with ground resources supported by aerial firefighting often occurred after the flame front reached a barrier and was momentarily held up. This highlights the fact that these areas had the highest chance of successful fire suppression, with this occurring even under conditions conductive to high intensity fire propagation.
The observations discussed here have implications for simulating landscape fire propagation in the context of how the existence of barriers to fire spread and their impacts are considered. If a simulator uses an empirical fire spread model such as Cheney et al. (1998), a model that implicitly includes the effects of barriers in momentarily slowing down wildfire propagation (see next section), then the simulator should not explicitly include the effect of the barriers in fire propagation. Doing so can result in doubling the barrier effect in slowing down fire propagation, leading to an under-prediction in rate of fire spread. Considering practical applications, this is likely only relevant for low to moderate burning conditions. Under heightened fire danger conditions, the resultant higher fireline intensities will be above most thresholds for barrier breaching (Wilson 1988) and the simulations should overcome barriers without slowing the fire down. Testing of spatially explicit wildfire propagation simulators with the present wildfire dataset will improve our understanding of how wildfire growth simulators should incorporate the effect of barriers on fire propagation.
Evaluation of current models
The evaluation of the Cheney et al. (1998) fire spread models yielded a mean absolute percent error of 26%, a relatively low value when compared with other results obtained from the evaluation of grass fire spread models against wildfire data, such as a value close to 80% for the same models in Kilinc et al. (2012; also Cruz et al. 2018a) or just below 40% in Cardil et al. (2023). Previous evaluation of the models against experimental data in pastures and croplands (Cruz et al. 2018b, 2020), with wind, fuel structure and fuel moisture content measured, produced percent errors varying between 22 and 35%, an error range similar to what was found in our analysis. See Sneeuwjagt and Frandsen (1977), Rothermel and Rinehart (1983), van Wilgen and Wills (1988) and Gould (1991) for further studies evaluating fire spread models against experimental and prescribed fire data in grassland fuels.
The evaluation results showed an under-prediction bias, with the four fastest wildfires being under-predicted. This is likely the result of a skewed dataset rather than a model limitation. The collection of fire spread data in wildfires spreading under moderate to high fire danger rating conditions as done in the current study is subject to a bias. Generally data from experimental fire observations or unsuppressed wildfires will be symmetrically distributed around the mean (expected prediction from model; e.g. fig. 4 in Cheney et al. (1998)). But in the case of the present study, the wildfires that spread faster than the expectation (above the mean expectation for the conditions) are more likely to escape initial control, propagate across the landscape and in turn be documented. Conversely, the fires spreading slower than the mean expectation are more likely to be contained while small, and thus not be subjected to documentation as a free spreading wildfire. As such, a dataset such as that assembled for this study will be biased to the fires spreading faster than the mean expectation. The skewed nature of the dataset due to the absence in the analysis of some fires spreading slower than expected yielded an under-prediction bias.
Concluding remarks
This study highlights the importance of wildfire observational data in understanding aspects of fire propagation that are only witnessed at large temporal and spatial scales. Wildfire data have the advantage of enabling the observation of fire characteristics that are not apparent at experimental scales. However, these types of data can suffer from high uncertainty (e.g. weather, fuel, perimeter location) and might not be complete (e.g. missing fuel data). Although we were able to accurately map fire perimeters at short time-intervals (see also Liu et al. 2018 and Cadril et al. 2023), there is a need to further develop rapid deployment or ‘drop-and-forget’ sensors and methods for measurement of critical environment variables, such as those associated with the prevailing meteorology, close to the headfire region. Such data are necessary to reduce the uncertainty in wildfire datasets and enable more conclusive analysis of their dynamics.
Our analysis focused on relatively small overall fire runs, averaging 26 min in duration and 2.8 km in spread distance, showing only parts of cycles in fire activity. None of the wildfires analysed had a time series with more than two cycles. Given the duration of the wildfire runs, it might be the case that some higher order cycles were not captured in the observations. Data encompassing longer fire runs (i.e. several hours) are needed to better understand and quantify the amplitude and frequency of the highest order cycles. The characterisation of these cycles is required to then investigate their dependence on environmental variables and time.
Despite early interest in the unsteady nature of wildfire propagation (e.g. Albini 1982), most applied fire behaviour research has focused on quantifying pseudo steady state propagation. As a result, understanding of the unsteady dynamics of wildland fire has not progressed significantly. Viegas et al. (2022) put forward a framework to better understand and quantify the process. There will be an interest in incorporating aspects of non-steady fire propagation, such as its time dependence, and amplitude and frequency of cycles, into wildfire propagation forecasts in order to improve firefighter safety and suppression effectiveness, and better understand fire effects on ecosystem components.
Declaration of funding
This research was funded by the Commonwealth Scientific and Industrial Research Organisation and Country Fire Authority of Victoria.
Acknowledgements
We thank volunteers and staff within Country Fire Authority of Victoria (CFA) involved in the incident management during and after the wildfire events for providing their invaluable time and insights. We also thank staff within CFA, Department of Energy, Environment and Climate Action (DEECA), Emergency Management Victoria (EMV), Fire Rescue Victoria (FRV) and State Emergency Services (SES) with data collection and to Harry Smiles for providing mapping support. The authors acknowledge the valuable comments provided by Andrew Sullivan, Marty Alexander, William Swedosh, Matt Plucinski and two anonymous reviewers on an earlier draft of this paper.
References
Albini FA (1982) Response of free-burning fires to nonsteady wind. Combustion Science and Technology 29, 225-241.
| Crossref | Google Scholar |
Andrews P, Finney M, Fischetti M (2007) Predicting wildfires. Scientific American 297, 46-55.
| Crossref | Google Scholar | PubMed |
Burrows N, Ward B, Robinson A (1991) Fire behaviour in spinifex fuels on the Gibson Desert Nature Reserve, Western Australia. Journal of Arid Environments 20, 189-204.
| Crossref | Google Scholar |
Butler BW (2014) Wildland firefighter safety zones: a review of past science and summary of future needs. International Journal of Wildland Fire 23, 295-308.
| Crossref | Google Scholar |
Butler B, Teske C, Jimenez D, O’Brien J, Sopko P, Wold C, Vosburgh M, Hornsby B, Loudermilk E (2016) Observations of energy transport and rate of spreads from low-intensity fires in longleaf pine habitat – RxCADRE 2012. International Journal of Wildland Fire 25, 76-89.
| Crossref | Google Scholar |
Cardil A, Monedero S, SeLegue P, Navarrete MÁ, de-Miguel S, Purdy S, Marshall G, Chavez T, Allison K, Quilez R, Ortega M, Silva CA, Ramirez J (2023) Performance of operational fire spread models in California. International Journal of Wildland Fire 32, 1492-1502.
| Crossref | Google Scholar |
Catchpole WR, Catchpole EA, Rothermel RC, Morris GA, Butler BW, Latham DJ (1998) Rate of spread of free-burning fires in woody fuels in a wind tunnel. Combustion Science and Technology 131, 1-37.
| Crossref | Google Scholar |
Cheney NP, Gould JS (1995) Separating fire spread prediction and fire danger rating. CALMScience Supplement 4, 3-8.
| Google Scholar |
Cheney NP, Gould JS, Catchpole WR (1993) The influence of fuel, weather and fire shape variables on fire-spread in grasslands. International Journal of Wildland Fire 3, 31-44.
| Crossref | Google Scholar |
Cheney NP, Gould JS, Catchpole WR (1998) Prediction of fire spread in grasslands. International Journal of Wildland Fire 8, 1-13.
| Crossref | Google Scholar |
Cheney P, Gould J, McCaw L (2001) The dead-man zone - a neglected area of firefighter safety. Australian Forestry 64, 45-50.
| Crossref | Google Scholar |
Cheney NP, Gould JS, McCaw WL, Anderson WR (2012) Predicting fire behaviour in dry eucalypt forest in southern Australia. Forest Ecology and Management 280, 120-131.
| Crossref | Google Scholar |
Clark TL, Radke L, Coen J, Middleton D (1999) Analysis of small-scale convective dynamics in a crown fire using infrared video camera imagery. Journal of Applied Meteorology 38, 1401-1420.
| Crossref | Google Scholar |
Cruz MG, Alexander ME (2013) Uncertainty associated with model predictions of surface and crown fire rates of spread. Environmental Modelling & Software 47, 16-28.
| Crossref | Google Scholar |
Cruz MG, McCaw WL, Anderson WR, Gould JS (2013) Fire behaviour modelling in semi-arid mallee-heath shrublands of southern Australia. Environmental Modelling & Software 40, 21-34.
| Crossref | Google Scholar |
Cruz MG, Alexander ME, Sullivan AL, Gould JS, Kilinc M (2018a) Assessing improvements in models used to operationally predict wildland fire rate of spread. Environmental Modelling & Software 105, 54-63.
| Crossref | Google Scholar |
Cruz MG, Sullivan AL, Gould JS, Hurley RJ, Plucinski MP (2018b) Got to burn to learn: the effect of fuel load on grassland fire behaviour and its management implications. International Journal of Wildland Fire 27, 727-741.
| Crossref | Google Scholar |
Cruz MG, Hurley RJ, Bessell R, Sullivan AL (2020) Fire behaviour in wheat crops – effect of fuel structure on rate of fire spread. International Journal of Wildland Fire 29, 258-271.
| Crossref | Google Scholar |
Finney MA, Cohen JD, Forthofer JM, McAllister SS, Gollner MJ, Gorham DJ, Saito K, Akafuah NK, Adam BA, English JD (2015) Role of buoyant flame dynamics in wildfire spread. Proceedings of the National Academy of Sciences of the United States of America 112, 9833-9838.
| Crossref | Google Scholar | PubMed |
Gould JS, Sullivan AL (2020) Two methods for calculating wildland fire rate of forward spread. International Journal of Wildland Fire 29, 272-281.
| Crossref | Google Scholar |
Liu X, He B, Quan X, Yebra M, Qiu S, Yin C, Liao Z, Zhang H (2018) Near real-time extracting wildfire spread rate from Himawari-8 satellite data. Remote Sensing 10, 1654.
| Crossref | Google Scholar |
McRae DJ, Jin JZ, Conard SG, Sukhinin AI, Ivanova GA, Blake TW (2005) Infrared characterization of fine-scale variability in behavior of boreal forest fires. Canadian Journal of Forest Research 35, 2194-2206.
| Crossref | Google Scholar |
Nelson RM, Butler BW, Weise DR (2012) Entrainment regimes and flame characteristics of wildland fires. International Journal of Wildland Fire 21, 127-140.
| Crossref | Google Scholar |
Noble IR, Bary GAV, Gill AM (1980) McArthur’s fire danger meters expressed as equations. Australian Journal of Ecology 5, 201-203.
| Crossref | Google Scholar |
Plucinski MP (2019) Contain and control: wildfire suppression effectiveness at incidents and across landscapes. Current Forestry Reports 5, 20-40.
| Crossref | Google Scholar |
Rothermel RC, Mutch RW (1986) Behavior of the live-threatening Butte fire: August 27–29, 1985. Fire Management Notes 47(2), 14-24.
| Google Scholar |
Sneeuwjagt RJ, Frandsen WH (1977) Behavior of experimental grass fires vs. predictions based on Rothermel’s fire model. Canadian Journal of Forest Research 7, 357-367.
| Crossref | Google Scholar |
Taylor SW, Wotton BM, Alexander ME, Dalrymple GN (2004) Variation in wind and crown fire behaviour in a northern jack pine black spruce forest. Canadian Journal of Forest Research 34, 1561-1576.
| Crossref | Google Scholar |
van Wilgen BW, Wills AJ (1988) Fire behaviour prediction in savanna vegetation. South African Journal of Wildlife Research 18, 41-46.
| Google Scholar |
Viegas DXFC, Raposo JRN, Ribeiro CFM, Reis LCD, Abouali A, Viegas CXP (2021) On the non-monotonic behaviour of fire spread. International Journal of Wildland Fire 30, 702-719.
| Crossref | Google Scholar |
Viegas DXFC, Raposo JRN, Ribeiro CFM, Reis L, Abouali A, Ribeiro LM, Viegas CXP (2022) On the intermittent nature of forest fire spread – Part 2. International Journal of Wildland Fire 31, 967-981.
| Crossref | Google Scholar |
Willmott CJ (1982) Some comments on the evaluation of model performance. Bulletin of the American Meteorological Society 63, 1309-1313.
| Crossref | Google Scholar |
Wilson AAG (1988) Width of firebreak that is necessary to stop grass fires - some field experiments. Canadian Journal of Forest Research 18, 682-687.
| Crossref | Google Scholar |
Appendix
Variability in segment observed rate of fire spread and duration for the eight fire runs used in the analysis.
| Time start | Time end | Run Duration (s) | Barrier present (Y, N) | Barrier width (m) | Barrier effect held (Y, N) | Fuel condition | Fuel Type | Fuel load (kg m–2) | Run length (m) | ROS (km h−1) | Fireline Intensity (MW m−1) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Woodhouse | ||||||||||||
| 13:54:55 | 13:58:39 | 224 | N | Natural | Pasture | 0.16 | 188 | 3 | 2.5 | |||
| 13:58:39 | 14:01:05 | 146 | Y | 3 | N | Natural | Pasture | 0.16 | 91 | 2.2 | 1.8 | |
| 14:01:05 | 14:02:07 | 62 | Y | 3 | N | Natural | Pasture | 0.16 | 47 | 2.7 | 2.2 | |
| 14:02:07 | 14:03:05 | 58 | N | Natural | Pasture | 0.24 | 60 | 3.7 | 4.6 | |||
| 14:03:05 | 14:06:45 | 220 | Y | 3 | Y | Natural | Pasture | 0.22 | 304 | 5 | 5.7 | |
| 14:06:45 | 14:08:18 | 93 | N | Natural | Pasture | 0.22 | 205 | 7.9 | 9.0 | |||
| Glenloth East | ||||||||||||
| 10:42:00 | 10:55:15 | 795 | Y | 9 | N | Natural | Lentil | 0.43 | 468 | 2.1 | 4.7 | |
| 10:55:15 | 10:56:27 | 72 | N | Unharvested | Barley | 0.65 | 430 | 21.5 | 72.2 | |||
| 10:56:27 | 10:57:21 | 54 | Y | 3 | Unharvested | Barley | 0.65 | 219 | 14.6 | 49.0 | ||
| 10:57:21 | 10:58:20 | 59 | Y | 9 | N | Unharvested | Barley | 0.65 | 171 | 10.4 | 34.9 | |
| 11:24:00 | 11:26:16 | 136 | N | Harvested | Barley | 0.62 | 250 | 6.6 | 21.1 | |||
| 11:26:16 | 11:27:43 | 87 | N | Harvested | Barley | 0.62 | 135 | 5.6 | 17.9 | |||
| 11:27:43 | 11:29:39 | 116 | N | Harvested | Barley | 0.62 | 134 | 4.2 | 13.5 | |||
| 11:29:39 | 11:31:31 | 112 | Y | 3.1 | N | Harvested | Barley | 0.62 | 207 | 6.7 | 21.5 | |
| 11:31:31 | 11:33:03 | 92 | N | Unharvested | Barley | 0.66 | 191 | 7.5 | 25.6 | |||
| 11:33:03 | 11:34:41 | 98 | Y | 3 | N | Unharvested | Barley | 0.66 | 448 | 16.5 | 56.3 | |
| 11:34:41 | 11:37:23 | 162 | N | Unharvested | Barley | 0.66 | 577 | 12.8 | 43.6 | |||
| 11:37:23 | 11:40:35 | 192 | Y | 3 | N | Unharvested | Barley | 0.66 | 298 | 5.6 | 19.1 | |
| 11:40:35 | 11:43:14 | 159 | N | Unharvested | Barley | 0.66 | 435 | 9.8 | 33.4 | |||
| 11:43:14 | 11:44:44 | 90 | Y | 3 | N | Fallow | Barley | 0.1 | 219 | 8.8 | 4.5 | |
| 11:44:44 | 11:46:26 | 102 | N | Fallow | Barley | 0.1 | 351 | 12.4 | 6.4 | |||
| 11:46:26 | 11:49:46 | 200 | N | Fallow | Barley | 0.1 | 278 | 5 | 2.6 | |||
| 11:49:46 | 11:52:36 | 170 | Y | 5.5 | Y | Fallow | Barley | 0.1 | 211 | 4.5 | 2.3 | |
| 11:52:36 | 11:56:16 | 220 | N | Harvested | Wheat | 0.31 | 189 | 3.1 | 5.0 | |||
| 11:52:36 | 11:56:16 | 220 | N | Harvested | Wheat | 0.31 | 85 | 1.4 | 2.2 | |||
| 11:56:16 | 11:58:21 | 125 | N | Harvested | Wheat | 0.31 | 172 | 5 | 8.0 | |||
| Tahara Murndal | ||||||||||||
| 12:47:21 | 12:51:35 | 254 | Y | 5.5 | Natural | Pasture | 0.41 | 720 | 10.2 | 21.6 | ||
| 12:51:35 | 12:57:08 | 333 | Y | Natural | Pasture | 0.41 | 752 | 8.1 | 17.2 | |||
| 12:57:08 | 13:08:32 | 18 | N | Natural | Pasture | 0.41 | 18 | 0.1 | 0.2 | |||
| 13:08:32 | 13:10:03 | 91 | Y | 20 | Eaten out and natural | Pasture | 0.24 | 120 | 4.7 | 5.8 | ||
| 13:10:03 | 13:11:32 | 89 | N | Eaten out and natural | Pasture | 0.24 | 218 | 8.8 | 10.9 | |||
| 13:11:32 | 13:12:32 | 60 | N | Eaten out and natural | Pasture | 0.24 | 345 | 20.7 | 25.7 | |||
| 13:12:32 | 13:14:35 | 123 | N | Eaten out and natural | Pasture | 0.24 | 541 | 15.8 | 19.6 | |||
| 13:14:35 | 13:18:03 | 208 | N | Eaten out and natural | Pasture | 0.24 | 305 | 5.3 | 6.6 | |||
| 13:33:16 | 13:45:09 | 713 | N | Eaten out and natural | Pasture | 0.24 | 264 | 1.3 | 1.6 | |||
| 13:45:09 | 13:47:29 | 140 | N | Eaten out and natural | Pasture | 0.24 | 389 | 10 | 12.4 | |||
| 13:47:29 | 13:49:46 | 137 | N | Eaten out and natural | Pasture | 0.24 | 350 | 9.2 | 11.4 | |||
| 13:49:46 | 13:52:29 | 163 | Y | Eaten out and natural | Pasture | 0.24 | 172 | 3.8 | 4.7 | |||
| 13:52:29 | 13:54:19 | 110 | Y | 5.5 | N | Eaten out and natural | Pasture | 0.24 | 253 | 8.3 | 10.3 | |
| 13:54:19 | 13:59:54 | 335 | Y | 5.5 | - | - | 0 | 0 | 0 | |||
| 13:59:54 | 14:02:26 | 152 | Y | Natural | Pasture | 0.36 | 237 | 5.6 | 10.4 | |||
| 14:02:26 | 14:03:00 | 34 | Y | Natural | Pasture | 0.36 | 112 | 11.9 | 22.1 | |||
| 14:03:00 | 14:05:00 | 120 | Y | 4 | Natural | Pasture | 0.36 | 166 | 5 | 9.3 | ||
| Murra Warra | ||||||||||||
| 16:50:00 | 16:52:00 | 120 | Y | 5 | N | Unharvested | Chickpea | 0.3 | 290 | 8.7 | 13.5 | |
| 16:52:00 | 16:54:00 | 120 | Y | 5 | N | Harvested | Cereal | 0.35 | 723 | 21.7 | 39.2 | |
| 16:54:00 | 16:55:00 | 60 | Y | 6 | Y | Harvested | Cereal | 0.35 | 0.1 | 0 | 0.0 | |
| 16:55:00 | 16:56:30 | 90 | Y | 6 | N | Harvested | Lentil | 0.2 | 350 | 14 | 14.5 | |
| 16:56:30 | 16:59:30 | 180 | Y | 6 | Y | Harvested | Lentil | 0.15 | 0.1 | 0 | 0.0 | |
| 16:59:30 | 17:02:00 | 150 | N | Harvested | Lentil | 0.15 | 270 | 6.5 | 5.0 | |||
| Hillside Rd | ||||||||||||
| 12:17:00 | 12:35:20 | 1100 | Y | 5 | N | Natural | Pasture | 0.35 | 760 | 2.5 | 4.5 | |
| 12:35:20 | 12:36:56 | 96 | Y | 20 | Natural | Pasture | 0.35 | 48 | 1.8 | 3.3 | ||
| 12:36:56 | 12:38:15 | 79 | Y | 20 | Natural | Pasture | 0.35 | 27 | 1.2 | 2.2 | ||
| 12:38:15 | 12:39:27 | 72 | Y | 20 | Natural | Pasture | 0.35 | 124 | 6.2 | 11.2 | ||
| 12:39:27 | 12:40:48 | 81 | N | Grazed | Pasture | 0.35 | 187 | 8.3 | 15.0 | |||
| 12:40:48 | 12:43:03 | 135 | Y | 5 | Eaten Out | Pasture | 0.35 | 56 | 1.5 | 2.7 | ||
| 12:43:03 | 12:43:59 | 56 | N | Natural | Pasture | 0.1 | 37 | 2.4 | 1.2 | |||
| 12:43:59 | 12:47:46 | 227 | N | Natural | Pasture | 0.35 | 90 | 1.4 | 2.5 | |||
| 12:47:46 | 12:49:51 | 125 | N | Natural | Pasture | 0.35 | 34 | 1 | 1.8 | |||
| 12:49:51 | 12:50:33 | 42 | N | Natural | Pasture | 0.35 | 204 | 17.5 | 31.6 | |||
| 12:50:33 | 12:52:20 | 107 | N | Natural | Pasture | 0.35 | 203 | 6.8 | 12.3 | |||
| 12:52:20 | 12:54:09 | 109 | N | Natural | Pasture | 0.35 | 275 | 9.1 | 16.5 | |||
| Steele Rd | ||||||||||||
| 14:47:39 | 14:54:36 | 417 | N | Harvested | Barley | 0.33 | 465 | 4 | 6.8 | |||
| 14:54:36 | 15:01:40 | 424 | N | Harvested | Barley | 0.33 | 789 | 6.7 | 11.4 | |||
| 15:01:40 | 15:05:50 | 250 | N | Harvested | Barley | 0.33 | 331 | 4.8 | 8.2 | |||
| 15:05:50 | 15:08:19 | 149 | Y | 15 | N | Harvested | Barley | 0.33 | 166 | 4 | 6.8 | |
| 15:08:19 | 15:10:06 | 107 | Y | 15 | N | Harvested | Barley | 0.33 | 15 | 0.5 | 0.9 | |
| 15:10:06 | 15:11:36 | 90 | N | Harvested | Barley | 0.33 | 131 | 5.2 | 8.9 | |||
| 15:11:36 | 15:15:03 | 207 | N | Harvested | Barley | 0.33 | 389 | 6.8 | 11.6 | |||


