The distributed strategy for asynchronous observations in data-driven wildland fire spread prediction
Mengxia Zha A B , Zheng Wang
A B , Zheng Wang  A B , Jie Ji A B * and Jiping Zhu A B
A B , Jie Ji A B * and Jiping Zhu A B
A
B
Abstract
Asynchronous observations refer to observations that are obtained at multiple moments. The observation moments of fire fronts may differ throughout an entire wildfire area. Asynchronous observations include historical data, which hinders the effectiveness of data assimilation due to the lack of timely updates on changing fire fronts.
This paper proposed a distributed strategy combined with the Ensemble Transform Kalman filter (ETKF-distributed) for asynchronous observations. It can assimilate fire fronts immediately at any location by using new matching schemes between prediction and observation.
The ETKF-distributed undergoes testing using a wildland fire generated based on real terrain, vegetation, and historical weather data from the local area. In addition, the ETKF and ETKF-centralised proposed in our previous work were employed as comparisons. Observing System Simulation Experiments were conducted to generate asynchronous observation fire fronts.
The benefit of immediate assimilation enables the new method to maintain high accuracy predictions.
The allocation of observation resources can be focused in regions with high rates of speed when employing ETKF-distributed.
The ETKF-distributed has high efficiency and adaptability, making it highly promising for implementation in wildfire prediction.
Keywords: asynchronous observations, data assimilation, distributed strategy, Ensemble Transform Kalman filter, high-accuracy prediction, immediate assimilation, Observing System Simulation Experiments, wildland fire.
Introduction
Climate change has led to a global increase in devastating wildfires in recent years (Schultz et al. 2008; Cardil et al. 2021; Collins et al. 2021). Wildfires tend to grow at compounding rates, meaning that as fire becomes larger, its potential for rapid growth also increases (Juang et al. 2022). It is frequently disregarded that although large-scale wildfires are not very common, they significantly impact the total area burned (Liu et al. 2021). Canada experiences over 8000 wildfires annually, with just 3% of these fires having a burning area exceeding 200ha (Stocks et al. 2002; Flannigan et al. 2009; Lagerquist et al. 2017). However, these larger fires account for 97% of the total burned area. Massive wildfires have a significant impact on the economy, ecology, and the environment. Therefore, it is imperative to precisely forecast the propagation of wildfires, as it can aid in firefighting strategies and facilitate timely evacuations.
Throughout the years, many scholars have developed a sequence of wildfire propagation models. Referring to Sullivan’s classification scheme (Sullivan 2009a, 2009b, 2009c), these models can be divided into three categories. The first type is physical and quasi-physical models (Sullivan 2009a), which are based on the fundamental chemistry and physics of combustion and fire spread (Balbi et al. 1999, 2010). The second type is empirical and quasi-empirical models (Sullivan 2009b), which rely solely on statistical analysis of experimental data, with or without a physical framework (Rothermel 1972; Anderson et al. 1982). The third type is mathematical analogues and simulation models (Sullivan 2009c), which are based on empirical or quasi-empirical models and are used to simulate the spread of fire across a modelled landscape. Notable models in this category include FARSITE (Finney 1998), PROMETHEUS (Tymstra et al. 2010), and FOREFIRE (Filippi et al. 2013b), which are widely used by fire management agencies to predict the spread of large-scale wildfires.
However, the propagation of wildfires is a highly intricate process that is impacted by multiple factors (Sutherland et al. 2023). For instance, the spread of fire is impacted by meteorological conditions (Clark et al. 1996) and in turn, the fire affects the temperature and wind conditions in the local area (Filippi et al. 2013b). The moisture content of the vegetation depends on meteorological conditions during a short, even long period (Viegas et al. 2001) and significantly influences fire behaviour (Ruffault et al. 2018). The topographical conditions can also affect meteorological conditions (Abdalhaq et al. 2006), particularly regional wind fields. To put it succinctly, forecasting the propagation of wildfires is an exceedingly intricate matter. Despite the development of various coupled atmosphere-wildfire models, such as WRF-SFIRE (Mandel et al. 2011), MesoNH/Blaze (Costes et al. 2021), and WRF-FIRE (Coen et al. 2013), their prediction results are often unsatisfactory (Albini 1976). Fire propagation models in these simulators contain complex differential equations that need approximated numerical solutions to be solved (Gillespie 1977), resulting in inherent uncertainty (Cruz and Alexander 2013). Furthermore, the aforementioned parameters that influence the development of wildfires are dynamic and interrelated, making it difficult to provide accurate initial input data and boundary conditions for these simulators (Bianchini et al. 2010).
Previous researchers have introduced data assimilation (DA) as a means to enhance the reliability of model prediction outcomes (Abdalhaq et al. 2006; Mandel et al. 2008). DA incorporates the observed data into the prediction process to make the optimal estimation of the input parameters; e.g. fuel and wind (Mandel et al. 2012; Rochoux et al. 2014; Srivas et al. 2017; Zhang et al. 2017; Zhou et al. 2020) and the state parameters, e.g. fire front position and temperature (Rochoux et al. 2015; Fang et al. 2017; Zhang et al. 2019; Zhou et al. 2019, 2021). The Kalman filter is a widely used algorithm for sequential data assimilation. It was presented in 1960 by Kalman for signal estimation (Kalman 1960). Its effectiveness is restricted due to its assumption of linear dynamics between the control variables and model outputs. Nevertheless, the spread of a wildfire is a typical complex nonlinear problem. For addressing nonlinear issues, extensions of the KF were proposed, such as the Ensemble Kalman filtering (EnKF) (Evensen 1994), which relies on a stochastic description of the model behaviour. The EnKF has been employed to forecast wildfires in recent years (Rochoux et al. 2014, 2015; Srivas et al. 2016, 2017). According to our previous study (Zhou et al. 2019), the Ensemble Transform Kalman filter (ETKF) (Bishop et al. 2001) can avoid ‘perturbed observations’ to eliminate the additional source of sampling error. In the application of ETKF, the observation data assimilated each time is the entire fire perimeter, which is assumed to be observed at the same moment. However, acquiring such ideal observation data in a real wildfire is extremely challenging.
Currently, the main ways of monitoring wildfires are satellite remote sensing, watch towers, and aerial detection (Allison et al. 2016). One limitation of satellites is their limited temporal resolution, which means they require a long time to re-survey the same area (Xie et al. 2018). Consequently, satellites are mostly employed for fire detection rather than continuously tracking fire fronts (Benali et al. 2016). Regarding watchtowers, their coverage is limited, and their immobile nature makes it costly to monitor extensive forested areas (Zhang et al. 2020). Aerial detection, such as unmanned aerial vehicles (UAVs), has gradually become mainstream wildfire monitoring equipment due to its mobility and relatively affordable cost (Jian et al. 2019). However, the task of accurately tracking the fire perimeter by the UAV is extremely challenging for several reasons. First, the terrain surrounding wildfires is intricate, and the climate conditions are severe, both of which are unfavourable for UAV operations. Second, the fire front exhibits dynamic spread, necessitating precise flight path planning for the UAV. Predecessors have developed many UAV path planning algorithms with the aim of improving the efficiency of fire perimeter tracking. For example, it was proposed that a partially observable Markov decision process that enables UAVs to autonomously track fire perimeters developing in random directions (Shobeiry et al. 2021). Other researchers have developed a vector field-based algorithm to navigate UAVs to preferentially track parts of fire perimeters with higher spreading rates (Feng and Katupitiya 2022). Regardless of the fire front tracking algorithm chosen, there is an unavoidable issue: it is difficult to rapidly collect a complete fire perimeter using only one UAV, especially in large-scale burned areas (Choi et al. 2019). Therefore, some scholars have proposed employing multiple UAVs to coordinate operations (Casbeer et al. 2005, 2006; Ren and Beard 2008; Merino et al. 2012; Choi et al. 2019). Nevertheless, the restricted range of communication poses challenges in achieving information synchronisation across several UAVs (Yu et al. 2020; Oubbati et al. 2022). Therefore, the fire perimeter collected by UAVs consists of fire fronts from different moments, which we refer to as asynchronous observations.
In previous studies, the entire fire perimeter was artificially synthesised (Srivas et al. 2016; Fang et al. 2017; Gu 2017; Long and Hu 2017; Srivas et al. 2017) or extracted from an infra-red image when the burned area was small (Rochoux et al. 2015; Rios et al. 2016; Valero et al. 2017). The entire fire perimeter data obtained in the above methods came from the same observation moment. It is not considered that the entire fire perimeter will likely be asynchronous. In the framework of EnKF or ETKF, the entire fire perimeter data is incorporated into the prediction model at a single analysis step, and this moment is called the analysis moment. The input observations for a single analysis step were collected between the present and the last analysis moment. This means that if the observation is asynchronous, the assimilated fire fronts may be collected long before the present analysis moment. The assimilation effect will be worse because the fire front collected in the past has been spreading forward.
Our previous research proposed a centralised extrapolation strategy based on the standard ETKF (ETKF-centralised) for assimilating asynchronous observations. This method can extrapolate the fire fronts collected in the past time by the prediction system. Its core idea is to convert asynchronous fire perimeters into ideal synchronous observations. It has significantly reduced the time lag error of observations to a certain extent. Still, there is no guarantee that the fire fronts can be extrapolated to their exact location when the observation time lag is too large, owing to the imperfect prediction system.
This paper proposed a distributed strategy based on ETKF (ETKF-distributed), which eliminates the need for extrapolation. This distributed strategy allows for the instantaneous integration of fire fronts acquired from any moment and location. Since the incorporated observation is a part of the fire perimeter, only a part of the forecast fire perimeter will be corrected during the analysis step. A matching scheme between the forecast fire perimeter and the observed fire front segment was designed to identify the update range. We conducted a large-scale wildfire simulation experiment to evaluate the prediction effects of the new strategy. Observing System Simulation Experiments (OSSEs) were performed by PROMETHEUS to generate asynchronous observation fire perimeters. FARSITE is then used as a fire spread model, which combines ETKF, ETKF-centralised, and ETKF-distributed to predict the location of fire perimeters, respectively. Finally, we summarise their characteristics and applicable conditions by comparing the prediction results.
Materials and methods
Numerical procedure
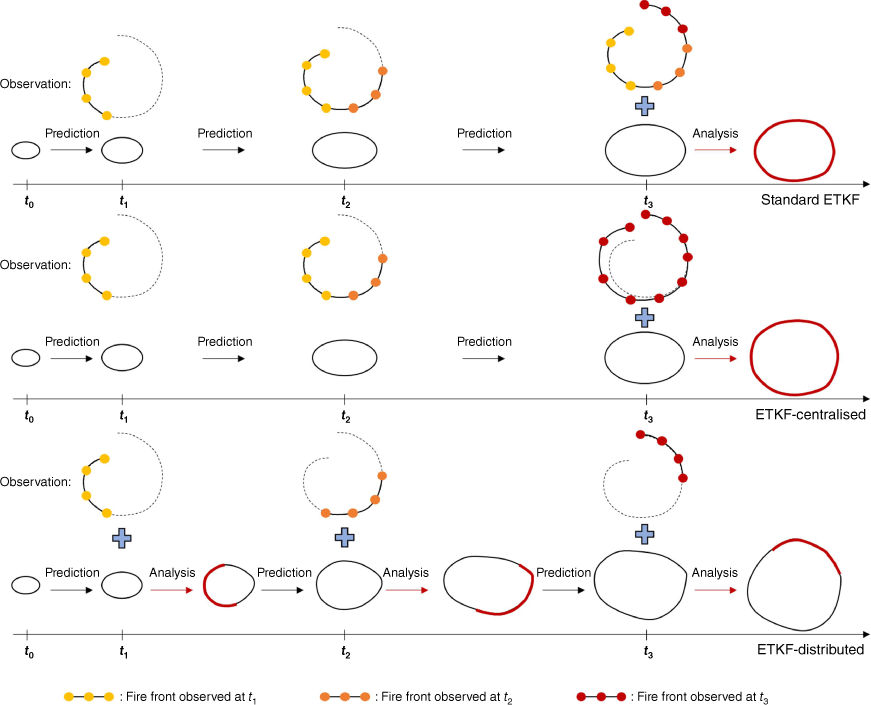
Fig. 1 shows the schematic diagram of the standard Ensemble Transform Kalman filter (ETKF), ETKF-centralised and ETKF-distributed. The observed fire perimeter in the figure comprises three fire front segments collected at t1, t2, and t3. The standard ETKF and ETKF-centralised performed the analysis step at time t3 to incorporate observations. The standard ETKF did not process the asynchronous observation data when performing the analysis step, but ETKF-centralised extrapolated the observed fire front segments to make them close to the ideal synchronous observations. ETKF-distributed performed analysis steps at t1, t2, and t3, enhancing the effectiveness of DA.
Algorithmic theory
Fig. 2 shows the derivation steps of the standard ETKF, ETKF-centralised, and ETKF-distributed for comparison.
Standard ETKF
Assuming the number of forecast ensemble members is m, we use X to represent the state of the forecast ensemble. M is a nonlinear prediction operator, which refers to FARSITE in this study. The propagation of the member j from time t0 to time tn can be written as Eqn 1. The error covariance of the forecast ensemble Pf at the time tn could be expressed as Eqn 2. At the analysis step, the mean of the forecast ensemble xf and the error covariance of the forecast ensemble Pf will be updated, as shown in Eqns 3–6. s is the scaled innovation vector (Sakov et al. 2010). The matrix G and the transform matrix T can be written as expressions only about S. If we use Z to represent observation data, R represents the observation error, and H represents the mapping matrix between prediction and observation, then s, and S can be written as Eqns 7 and 8.
ETKF combined with centralised extrapolation strategy
In addition to the prediction and analysis steps, the extrapolation step is added when adopting the centralised extrapolation strategy in the standard ETKF (Fig. 2). Its core idea is to process asynchronous fire perimeters into ideal synchronous observations by a prediction system. Assuming there are n segments of the observation fire front, the original observations can be expressed as , where the observation vectors correspond to different observed moments t1, t2, t3, …, tn. The extrapolation process for each fire front segment is shown in Eqn 11, Eqn 12 and Eqn 13. The prediction system used in this research is FARSITE. The extrapolated fire perimeter can be expressed as: . Finally, the Zposterior will replace the original observation Zpriori to participate in the next analysis step. That is, replace the observation in Eqn 18 with Zposterior.
ETKF combined with distributed extrapolation strategy
Unlike the centralised extrapolation strategy, the distributed strategy performs analysis immediately. This means that the forecast fire perimeter will be updated as soon as the fire front segment is observed (Fig. 2). The observation time of the first fire front segment is t1, so the prediction step only proceeds to t1. Since the observation obtained at t1 is a fire front segment, only a part of the forecast fire points can be corrected. We use λX to represent the part of the forecast ensemble that will be updated, and the error covariance of this part is in Eqn 21. The . is the mean of this part of the forecast ensemble. The mean value and error covariance of the forecast ensemble that will not be updated are expressed by and , respectively. and are updated in the same way as the standard ETKF, as shown in Eqns 22–25. Finally, the updated analysis fire front and the non-updated prediction fire front are connected in series to form a complete analysis fire perimeter. Complete assimilation results can be written as Eqns 28 and 29. They will enter the next prediction and analysis step when the next fire front segment is observed, and so on.
Matching scheme of prediction and observation
Achieving a one-to-one correspondence between the observed fire point and the forecast fire point is crucial during the analysis step of DA. Ideally, the observation is a complete fire perimeter (Fig. 3a). The predicted and observed fire perimeters comprise a series of fire points. The entire forecast fire perimeter will be updated at this time. However, the dimensions of the forecast and observed fire points may differ due to different scales and resolutions. Interpolation can be used to achieve a one-to-one correspondence between the fire perimeters in different dimensions (Srivas et al. 2016; Yoo and Song 2023).
Traditional matching scheme of forecast fire front and observed fire front. (a) The observed fire front is complete. (b) The observed fire front is incomplete.
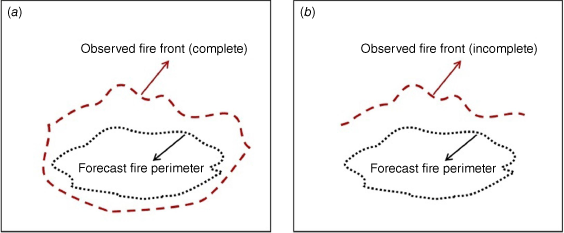
Fig. 3b shows the observation fire front segment. Only part of the forecast fire will be updated at this time. Therefore, it is not feasible to use interpolation directly. The most direct method to filter out the forecast fire points corresponding to the observed fire front is to use the criterion of the closest distance. Each observed fire point with its closest forecast fire point was paired (Rochoux et al. 2014, 2015). This scheme works well when the scale of the burned area is small (the number of fire points is small) and the local terrain is flat. When dealing with a large-scale real terrain, the fire front consists of numerous fire points and exhibits a very intricate shape. There may be many forecast fire points closest to one observed fire point, which makes it challenging to employ the criterion of the closest distance.
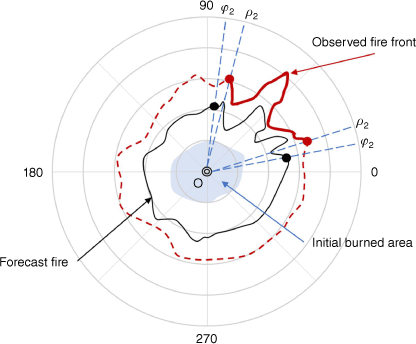
The application of Huygens’ concept in modelling surface fire growth is prevalent. This principle assumes that fire growth occurs in an elliptical form, and each vertex can act as an independent source for elliptical expansion (Lopes et al. 2002). These ellipses will be infinitely close to perfect circles under ideal circumstances (flat terrain, no wind, and uniform vegetation), and the fire spread trajectory will naturally form a series of concentric circles. All the fire points at different times are located on the ray originating from the centre of the circle. Inspired by this, this paper proposes a matching scheme between prediction and observation based on the polar coordinate system, which is used to determine the range of the forecast fire perimeter that requires dynamic correction.
Fig. 4 shows the initial burning area as the blue region, while the black curve shows the current forecast fire perimeter determined by the model. The red curve PQ is the observed fire front at the current moment, and the red dotted line indicates the unobserved part. First, locate the centroid O of the initial combustion area and build a polar coordinate system using O as the origin. Then, calculate the angles ρ1 and ρ2 of the two endpoints of the observed fire front segment. In order to maintain the physical coherence of the analysed fire and avoid unrealistic shapes, it is necessary for observational information to be diffused to neighbouring areas of the update range. Therefore, we introduce a scaling factor ε to scale the update range. If the predicted spread rate is smaller than the true spread rate, the observed fire front will appear outside the predicted fire perimeter (as shown in the Fig. 4). The updated range is enlarged, and the obtained φ1 and φ2 are in Eqn 30. If the predicted spread rate exceeds the true spread rate, the observed fire front will appear inside the predicted fire perimeter. The update range will be reduced, and the update ranges φ1 and φ2 are in Eqn 31. The optimal outcome is achieved when the value of ε is roughly 0.1, as confirmed by verification. Once the update range for the forecast fire is determined, the interpolation method can be employed to make the dimensions of the observed fire points consistent with the forecast fire points. Finally, the observation fire points and forecast fire points can be matched one to one.
Application of data assimilation algorithm to large-scale wildland fire
Based on data from CAL FIRE (https://www.fire.ca.gov/incidents/), Mariposa, CA, USA, experienced over 40 wildfires in the preceding 10years, with eight classified as large (Table 1). It can be seen that large-scale wildfires last for a long time; some even last more than 100 days. Furthermore, these wildfires are primarily focused on July and August annually. The incidence and growth of wildfires are favoured during this period due to the warm and dry climate (Cruz et al. 2020).
| Name | Date started | Active time (day) | Coordinates | Burned area (km2) | |
|---|---|---|---|---|---|
| El Portal Fire | 26 July 2024 | 15 | / | 18.98 | |
| Meadow Fire | 16 August 2014 | 119 | / | 19.31 | |
| Detwiler Fire | 16 July 2017 | 177 | 37.62N, 120.21W | 331.14 | |
| Empire Fire | 1 August 2017 | 161 | 37.64N, 119.62W | 32.76 | |
| South Fork Fire | 14 August 2017 | 148 | 37.54N, 119.60W | 28.33 | |
| Ferguson Fire | 13 July 2018 | 175 | 37.65N, 119.89W | 392.14 | |
| River Fire | 11 July 2021 | 8 | 37.35N, 119.87W | 39.08 | |
| Washburn Fire | 7 July 2022 | 28 | 37.50N, 119.61W | 19.77 |
Observing system simulation experiments performed in PROMETHEUS
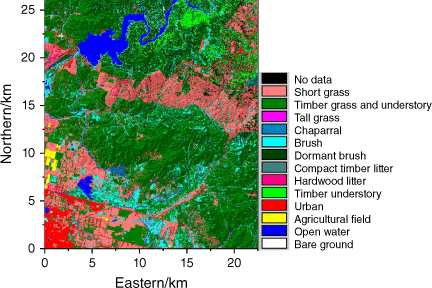
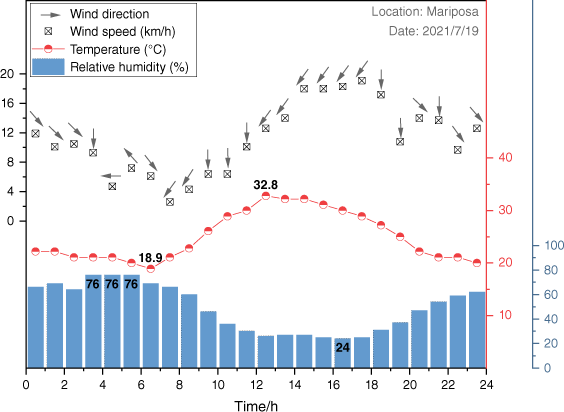
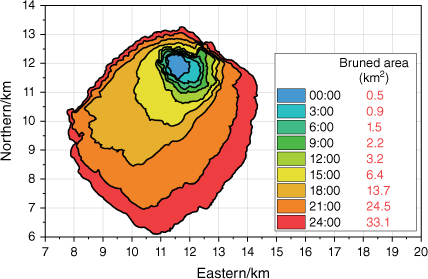
In order to verify the proposed algorithm, we conducted OSSEs that are typically designed to generate synthetically observation (Masutani et al. 2010). The OSSEs consist of two main steps: (1) simulation of a wildfire using real terrain, vegetation, and weather, referred to as ‘true fire’; and (2) extraction of the fire front as observations. We used PROMETHEUS to simulate true fire. It needs spatial input data on topography (slope, aspect, and elevation), vegetation types, and weather. We selected an area (36.85N to 37.05N, 119.5W to 119.7W) around Mariposa, where the terrain and vegetation data are downloaded from an online American geospatial database called LANDFIRE (https://www.landfire.gov/) (Fig. 5). We also found local historical weather data for 29 July 2021 (during the River fire) from a website named World Weather (https://world-weather.info/forecast/) (Fig. 6). On that particular day, the highest temperature exceeded 30°C, but the lowest relative humidity was only 24%. The maximum wind speed exceeded 16 km/h, and the wind direction was mainly south-east and south-west.
Fig. 7 shows the spread of the true fire and the corresponding burned area. It is not difficult to find that the rate of fire propagation significantly accelerated after 15:00. The extent of the burnt region expanded by 7.3 km2 within 3 h after 15:00 hours, surpassing the total area scorched in the preceding 15 h. The burned area even increased by 18 km2 from 18:00 hours to 21:00 hours. This mutation often occurs in wildfires (Liu et al. 2021), caused by the collective effect of terrain, vegetation, and weather. Regardless of the fire propagation model, predicting mutations is extremely difficult. DA will give feedback on this mutation information to the prediction model in time by integrating observation data, thereby reducing the model’s prediction error.
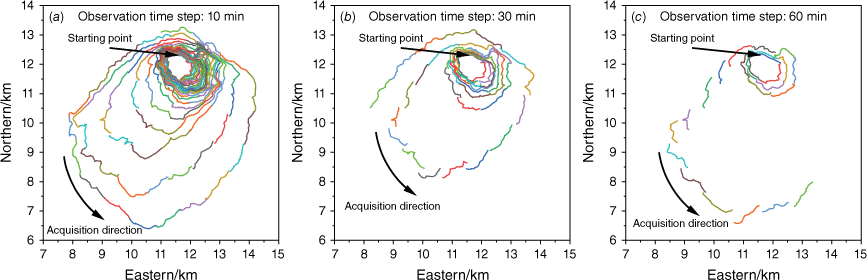
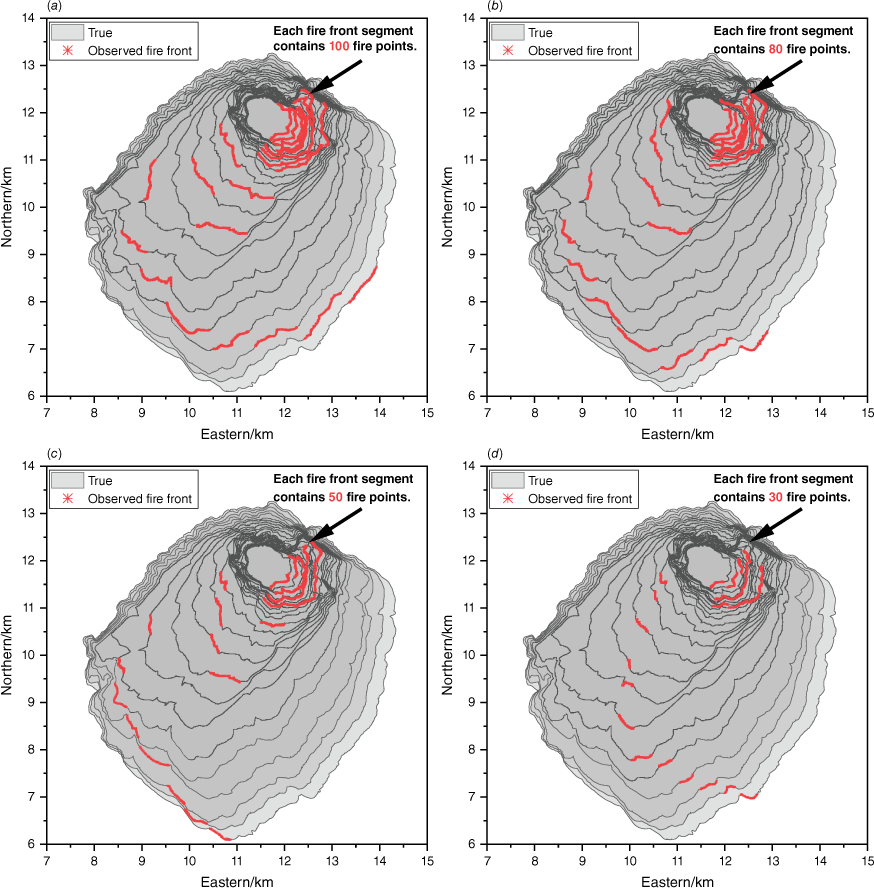
Three assumptions were established for the collection of observation fire fronts: (1) the observation time step is fixed; (2) the length of the fire front collected each time by UAV is about 1 km (each fire front segment contains 100 fire points, and the resolution of adjacent fire points is 30 m); and (3) the starting point of the UAV is set north of the burning area, and the acquisition is conducted counter-clockwise around the burning area. The observation fire front is in Fig. 8. There are three observation collection time steps (60, 30, and 10 min). The different colours distinguish the observation moments of these fire fronts.
DA cases design
The PROMETHEUS was employed to simulate the true fire, and we will now choose another prediction model to perform DA. The purpose is to reflect that the spread mechanisms of real wildfire are not yet fully understood (Gollner et al. 2015). We chose FARSITE as the basic fire propagation model, which is widely used for wildfire prediction. Real terrain, fuel type, and the daily minimum and maximum temperature and humidity were input during the prediction. Fuel adjustment factors and wind parameters were randomly generated.
Table 2 lists nine cases of DA experiments. According to different observation time steps, they are divided into three groups: 60; 30; and 10 min. Three algorithms were applied to perform DA for each group. ETKF and ETKF-centralised methods require a complete observation fire perimeter to perform analysis operations, so their analysis moment is identical. The ETKF-distributed can conduct analysis operations immediately, resulting in the analysis moment being equivalent to the observation moment. The free run fire, directly used FARSITE without the DA algorithm, was set up to compare the effectiveness of the DA.
| Case | Observation time step (min) | DA algorithm | Analysis moment | |
|---|---|---|---|---|
| A1 | 60 | ETKF |  | |
| A2 | ETKF-centralised | |||
| A3 | ETKF-distributed |  | ||
| B1 | 30 | ETKF |  | |
| B2 | ETKF-centralised | |||
| B3 | ETKF-distributed |  | ||
| C1 | 10 | ETKF |  | |
| C2 | ETKF-centralised | |||
| C3 | ETKF-distributed |  |
The observation errors of fire fronts are similar to offsets and mainly come from the acquisition, positioning, and identification processes. Due to the obscuration of thick smoke and the lack of unique visual features of terrain and vegetation, the root mean square error of fire fronts collected by UAV may exceed 40 m (Santana et al. 2022). The observation fire fronts used in this research are synthetic without errors (resolution between fire points is 30 m). However, the analysis scheme in the Kalman filter requires that the error covariance matrices of the observations be known every time measurements are available (Evensen 1994). Therefore, noise needs to be added manually. It is assumed that the observation error of each fire front segment is 50 m; that is, each fire front segment will translate in a random direction, with an average translation distance of 50 m.
Results of application
We hope to comprehensively compare the impact of different algorithms on wildfire spread prediction accuracy. We qualitatively and quantitatively analyzed the prediction results of different algorithms, respectively.
Qualitative results discussion
Fig. 9 shows the DA results from 03:00 hours to 07:00 hours; the observation time step is 60 min. The grey area represents the spread of the true fire. The red dot represents the observed fire front to which noise has been artificially added. It is not difficult to find that the analysis fire perimeters only appear at 03:00 hours and at 07:00 hours in the results based on ETKF and ETKF-centralised. The reason is that ETKF and ETKF-centralised will update the forecast fire to obtain the analysis fire when the observed fire front segments form a complete fire perimeter. As shown in Fig. 8c, the first complete fire perimeter is formed by three fire front segments collected from 01:00 hours to 03:00 hours. Similarly, the second complete fire perimeter is formed by four fire front segments collected from 04:00 hours to 07:00 hours. There is always an analysis fire in ETKF-distributed results, indicating that the forecast fire has been updated at every hour.
The comparison of fire perimeter obtained using three methods at 03:00 hours (a, b and c), 04:00 hours (d, e and f), 05:00 hours (g, h and i), 06:00 hours (j, k and l), and 07:00 hours (m, n and o).
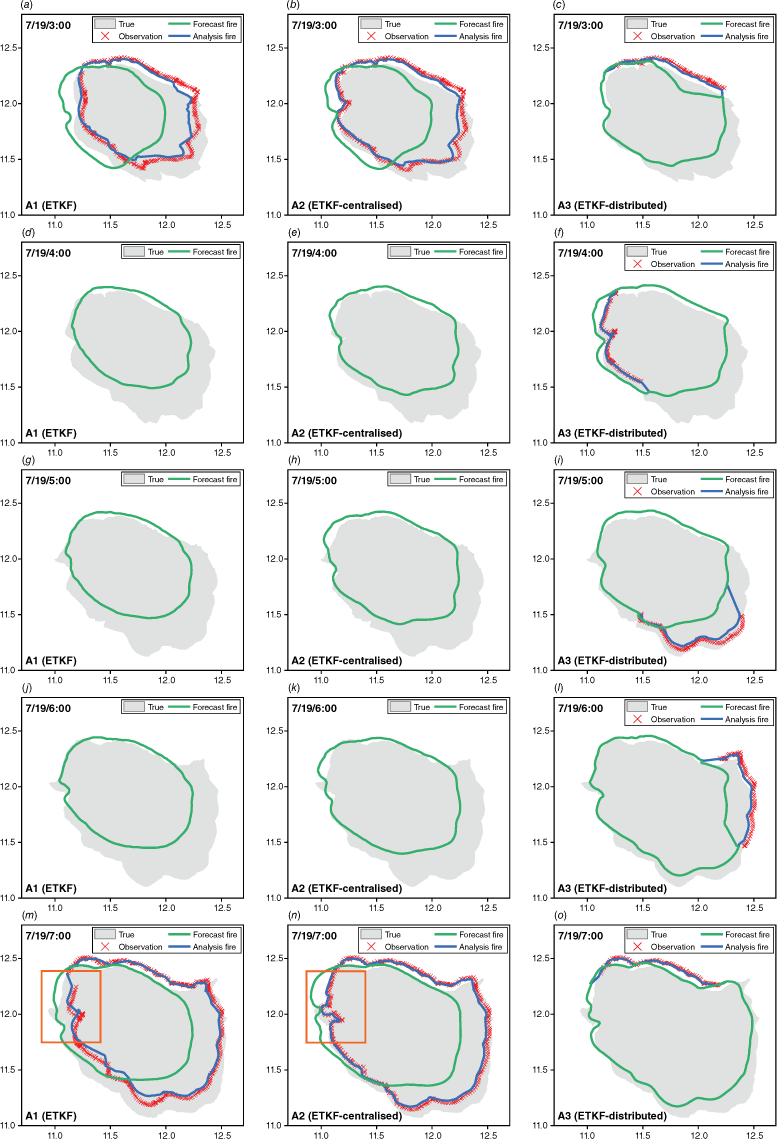
The analysis fire is closer to the true fire compared with the forecast fire, indicating that all three methods can improve the accuracy of forecast results. Still, the degree of improvement is different. For example, the analysis fire of ETKF-centralised is significantly closer to the true fire within the orange box. The reason is that ETKF-centralised extrapolates the observation fire front before updating, which reduces the error caused by the time lag. Nevertheless, there are uncertainties in the prediction system and the input environmental parameters used in the extrapolating process, resulting in a gap between the analysis fire of ETKF-centralised and the true fire. The performance of ETKF-distributed throughout the entire stage is relatively good and stable compared with them. The distance between its forecast fire and the true fire is significantly smaller, particularly at 03:00 hours and at 07:00 hours, attributed to the continuous real-time analysis operation.
Fig. 10 shows the forecast fire from 18:00 hours to 24:00 hours obtained by different algorithms. The burned area of true fire is rapidly expanding, as indicated by the black curve. It is not difficult to see that the forecast fire based on ETKF and ETKF-centralised deviate far from the true fire. The direct reason for the deviation is that there has been a lack of observations for a long tiime. The fundamental reason is that FARSITE did not predict the rapid increase of true fire. It is worth noting that the forecast fires of ETKF and ETKF-centralised have always been close. This is because the observation time step is only 10 min. Hence, the collection time lag for observation fire fronts that comprise the entire fire perimeter is relatively small, resulting in a small extrapolation distance of observation fire fronts. Thus, their assimilation results are very close. The difference between the ETKF-distributed forecast fire and the true fire is much smaller compared to them.
When the observation time step is 10 min, the comparison of the forecast fire obtained by using three methods at 18:00 hours (a), 20:00 hours (b), 22:00 hours (c), and 24:00 hours (d).
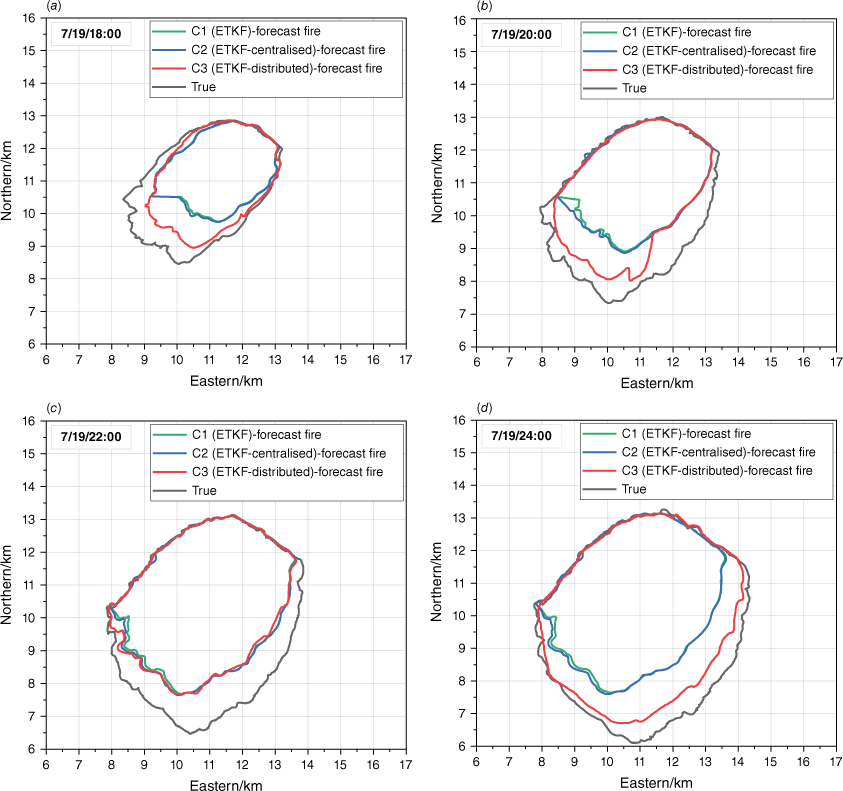
Interestingly, the forecast fires of ETKF and ETKF-centralised almost overlapped with the forecast fire of ETKF-distributed at 22:00 hours, but a significant gap reappeared at 24:00 hours. The reason is that ETKF and ETKF-centralised performed the last analysis step at 21:40 hours (Table 2). The fire front segments collected after 21:40 hours cannot form a complete fire perimeter, so they cannot participate in DA. ETKF-distributed effectively used all observed fire fronts in comparison. Consequently, the prediction results of ETKF-distributed are relatively more reliable.
Quantitative results discussion
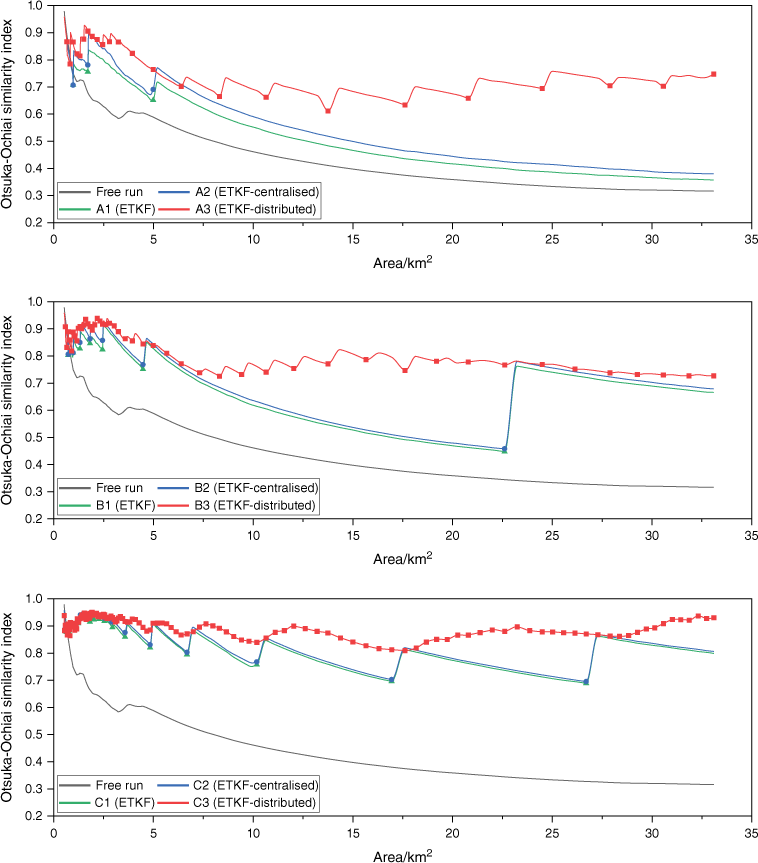
In order to quantitatively assess the prediction accuracy, we used the Otsuka-Ochiai similarity index (Filippi et al. 2013a) (Eqn 32). S1 and S2 are the burning areas enclosed by forecast and true fire perimeter, respectively. The value of SI ranges from 0 to 1. SI equal to 1 means a complete coincidence.
We calculated the burned area of the true fire and the SI between the forecast fire and the true fire at 10-min intervals. A graph was then plotted using the burned area as the x-axis and the SI as the y-axis, resulting in a set of curves (Fig. 11). The symbols represent the analysis steps. It can be seen that the SI of free run has been declining. The cases performed DA are much better, indicating that integrating observations improved prediction accuracy. Overall, the prediction accuracy improves significantly as the observation time step decreases. Therefore, increasing the frequency of observation can improve the efficiency of DA in practical applications.
Whether the observation time step is 60, 30, or 10 min, ETKF-distributed always has higher prediction accuracy and more minor fluctuations compared to ETKF and ETKF-centralised. It is worth noting that as the observation time step increases, the difference between the three algorithms becomes more significant. Additionally, the gap between ETKF-distributed and the other two algorithms becomes significantly more extensive when the burned area exceeds 5 km2. This is because the time required to collect the entire fire perimeter increases as the observation time step and burned area increase. The performance of ETKF and ETKF-centralised will be adversely affected by a prolonged absence of observations. The ETKF-distributed has a notable advantage in its ability to integrate observed fire fronts at any given time.
Table 3 shows the mean SI and computation time for each case. All the cases were completed on a computer equipped with an Intel Core i5-10400 CPU running at 2.90 GHz. The cases that performed ETKF-distributed take lots of computing time because they require frequent analysis steps and have high computational complexity. It is always hoped that the most accurate predictions will be obtained with minimal computing resources. Therefore, it is recommended to use ETKF or ETKF-centralised when the observation time step is small (such as less than 10 min), particularly when the wildfire spread is also small (such as less than 5 km2). In contrast, they can ensure good prediction accuracy and consume fewer computing resources.
Further research on ETKF-distributed
Optimised acquisition scheme
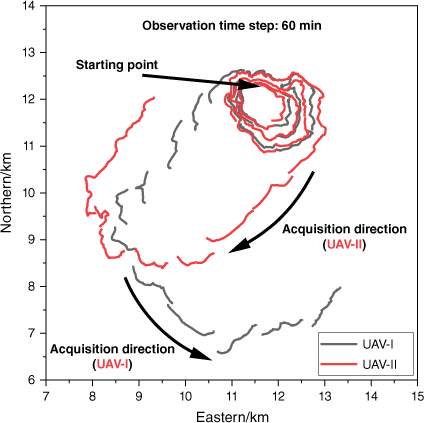
We have demonstrated that higher observation frequency improves the accuracy of DA algorithm predictions. In addition to the observation frequency, the prediction accuracy may be influenced by other parameters related to the observation collection process, including the number of UAVs, the trajectory of UAVs, the length of the fire fronts, and so on. We took case A3 as an example, kept the observation collection step size unchanged at 60 min, and changed other parameters to obtain five different fire front collection strategies (Table 4). In case A3-DU, two UAVs use clockwise and counter-clockwise circulation around the burned area to collect fire fronts. The obtained observation fire fronts are in Fig. 12. In case A3-P, a single UAV adopted a priority tracking strategy to collect the fire fronts. This means that it will preferentially collect fire fronts with a high rate of speed (ROS) in the entire burned area. Then we changed the length of the fire front based on case A3-P so that the number of fire points contained in each fire front segment will be 80, 50, and 30, respectively, as shown in case A3-P_80, A3-P_50, and A3-P_30%. The observation fire fronts obtained by the priority tracking strategy are in Fig. 13. The graph shows the hourly true fire spread so that areas with high ROS can be seen. ETKF-distributed was employed to perform DA after adding 50m noise to these observation fire fronts.
| Case | Number of UAVs | Observation collection strategy | The number of fire points collected by a single drone each time | |
|---|---|---|---|---|
| A3 | 1 | Circle tracking | 100 | |
| A3-DU | 2 | Circle tracking | 100 | |
| A3-P | 1 | Prioritise tracking | 100 | |
| A3-P_80% | 1 | Prioritise tracking | 80 | |
| A3-P_50% | 1 | Prioritise tracking | 50 | |
| A3-P_30% | 1 | Prioritise tracking | 30 |
Results of data assimilation
Fig. 14 shows the DA results with different observation strategies. The x-axis represents the burned area of the true fire. It can be seen that both the red curve and the blue curve are significantly higher than the black curve, particularly when the burned area exceeds 5 km2 (Fig. 14a). Consequently, increasing the number of UAVs or adopting the priority tracking strategy can improve the accuracy of the prediction. The former method enhances the average SI by 3.5% through a direct increase in the number of observations, while the latter method improves the quality of observations by concentrating observation resources on areas with high ROS, resulting in an average SI increase of 8.3%. It is important to mention that the result of case A3-P is better than the result of case A3-DU, suggesting that optimising the fire front tracking strategy to obtain high-quality data is more efficient than simply increasing the number of observations.
The DA results with different observation strategies. (a) CaseA3, CaseA3-DU and Case A3-P. (b) CaseA3, CaseA3-P_80%, CaseA3-P_50% and CaseA3-P_30%.
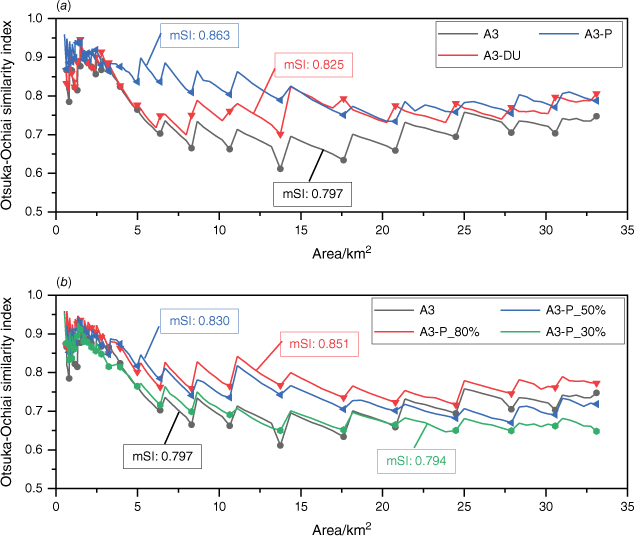
Fig. 14b shows the SI of the forecast fire under different lengths of observation fire fronts. The red curve is significantly higher than the black curve, and the blue and green curves are also higher than the black curve in the early stage. It means that the priority tracking strategy can maintain good prediction accuracy even if the observed fire fronts are short. Therefore, observation resources can be concentrated in the direction of high ROS to improve overall prediction accuracy. It should be pointed out that the underlying principle of this collection strategy is that no objects need to be focused on in the surrounding environment of wildfires, such as residential areas and important infrastructure. Otherwise, deploying observation resources specifically in these directions is advisable to guarantee that the fire fronts are updated promptly.
Results show that the curve of cases A3-P_50 and A3-P_30% are significantly lower than that of cases A3 when the burned area exceeds 20 km2. This suggests that the priority tracking strategy is no longer advantageous. The number of fire points contained in the entire fire perimeter has exceeded 1500 when the wildfire spreads more than 20 km2, while the initial fire perimeter only contains about 200 fire points. It means that the fire front collected each time by case A3-P_50% and case A3-P_30% only account for about 2–3% of the entire fire perimeter. It can be concluded that the assimilation effect of ETKF-distributed will become worse when the length of the observed fire front is less than 3% of the entire fire perimeter.
Discussion
Our results show that these algorithms have their characteristics and are suitable for different situations. When predicting wildfires, selecting the right strategy depends on the extent of the burned area and the available monitoring capabilities. For instance, the standard ETKF can be applied when the measurement equipment fully covers the burned area. The observation data is probably asynchronous when a wildfire reaches more than 5 km2. Assessing the ability to collect observation data in the field is critical in this situation. If it takes a long time, such as several hours, to collect the entire fire perimeter, it is best to choose ETKF-distributed. If the observation frequency is high and the entire fire perimeter can be collected within 1 h, it is recommended to use the ETKF-centralised. The reason is that it has better prediction performance and consumes fewer computational resources. It should be emphasised that these methods are not conflicting but can be combined. For example, when applying ETKF-centralised, ETKF-distributed can also be employed simultaneously to incorporate the fire front in a certain direction, particularly when it is necessary to prioritise important regions.
ETKF-distributed has the capability to carry out real time adjustments to the fire perimeter. The updated fire perimeter improves the initial conditions of the prediction model, allowing it to improve the accuracy of wildfire spread predictions. Nevertheless, the part of the fire perimeter without observation data has not been processed. Accurate estimation of environmental factors, such as wind, is crucial for effectively adjusting the entire fire perimeter in the future.
Conclusions
The entire fire perimeter must be collected multiple times in large-scale wildfires, leading to asynchronous observations. This paper adopted a distributed strategy based on the standard ETKF for asynchronous observations. We simulated a wildland fire that lasted 24 h and burned more than 30 km2. Observing System Simulation Experiments were carried out to generate asynchronous fire front segments, and their acquisition time intervals were 60, 30, and 10 min. Standard ETKF, ETKF combined with a distributed strategy (ETKF-distributed), and ETKF combined with a centralised extrapolation strategy (ETKF-centralised) were employed to predict the location of fire perimeters, respectively. Further investigation was conducted on the performance of ETKF-distributed by increasing the number of UAVs, adopting a priority tracking fire front strategy, and changing the fire front length. From the results, we conclude that: (1) both ETKF-centralised and ETKF-distributed can reduce errors caused by asynchronous observations; however, the ETKF-distributed method exhibits superior prediction accuracy and less significant fluctuations; (2) the larger the observation time step, the more obvious the advantages of the ETKF-distributed; (3) the ETKF-distributed method consumes more computing resources due to the frequent execution of analysis operations; (4) the ETKF-distributed is more flexible and can be better applied to complex practical application scenarios; and (5) concentrating observation resources in areas with a high rate of speed can maximise the advantages of ETKF-distributed.
Data availability
The data that support this study are available in FigShare at https://doi.org/10.6084/m9.figshare.23507919.
Declaration of funding
This work was supported by the National Key R&D Program of China (No. 2022YFC3003101), the Fundamental Research Funds for the Central Universities (Grant No. WK2320000050), and the Fundamental Research Funds for the Central Universities under (Grant No. KY2320000039).
Acknowledgements
This work was supported by the National Key R&D Program of China (No. 2022YFC3003101), the Fundamental Research Funds for the Central Universities (Grant No. WK2320000050), and the Fundamental Research Funds for the Central Universities under Grant No. KY2320000039 which are gratefully acknowledged. Numerical computations were performed at Hefei's advanced computing center.
References
Abdalhaq B, Cortés A, Margalef T, Bianchini G, Luque E (2006) Between classical and ideal: enhancing wildland fire prediction using cluster computing. Cluster Computing 9, 329-343.
| Crossref | Google Scholar |
Allison RS, Johnston JM, Craig G, Jennings S (2016) Airborne optical and thermal remote sensing for wildfire detection and monitoring. Sensors 16(8), 1310.
| Crossref | Google Scholar | PubMed |
Anderson DH, Catchpole EA, De Mestre NJ, Parkes T (1982) Modelling the spread of grass fires. The ANZIAM Journal 23(4), 451-466.
| Crossref | Google Scholar |
Balbi JH, Santoni PA, Dupuy J-L (1999) Dynamic modelling of fire spread across a fuel bed. International Journal of Wildland Fire 9(4), 275-284.
| Crossref | Google Scholar |
Balbi J-H, Rossi J-L, Marcelli T, Chatelon F-J (2010) Physical modeling of surface fire under nonparallel wind and slope conditions. Combustion Science and Technology 182(7), 922-939.
| Crossref | Google Scholar |
Benali A, Russo A, Sá ACL, Pinto RMS, Price O, Koutsias N, Pereira JMC (2016) Determining fire dates and locating ignition points with satellite data. Remote Sensing 8(4), 326.
| Crossref | Google Scholar |
Bianchini G, Denham M, Cortés A, Margalef T, Luque E (2010) Wildland fire growth prediction method based on multiple overlapping solution. Journal of Computational Science 1(4), 229-237.
| Crossref | Google Scholar |
Bishop CH, Etherton BJ, Majumdar SJ (2001) Adaptive sampling with the ensemble transform Kalman filter. Part I: Theoretical aspects. Monthly Weather Review 129(3), 420-436.
| Crossref | Google Scholar |
Cardil A, Rodrigues M, Ramirez J, de-Miguel S, Silva CA, Mariani M, Ascoli D (2021) Coupled effects of climate teleconnections on drought, Santa Ana winds and wildfires in southern California. Science of The Total Environment 765, 142788.
| Crossref | Google Scholar | PubMed |
Casbeer DW, Beard RW, McLain TW, Li S-M, Mehra RK (2005) Forest fire monitoring with multiple small UAVs. In ‘Proceedings of the 2005, American Control Conference’, 2005. (IEEE) 10.1109/ACC.2005.1470520
Casbeer DW, Kingston DB, Beard RW, McLain TW (2006) Cooperative forest fire surveillance using a team of small unmanned air vehicles. International Journal of Systems Science 37(6), 351-360.
| Crossref | Google Scholar |
Choi Y, Choi Y, Briceno S, Mavris DN (2019) Multi-UAS path-planning for a large-scale disjoint disaster management. In ‘2019 International Conference on Unmanned Aircraft Systems (ICUAS)’. (IEEE) 10.1109/ICUAS.2019.8797950
Clark TL, Jenkins MA, Coen J, Packham D (1996) A coupled atmosphere fire model: convective feedback on fire-line dynamics. Journal of Applied Meteorology and Climatology 35(6), 875-901.
| Crossref | Google Scholar |
Coen JL, Cameron M, Michalakes J, Patton EG, Riggan PJ, Yedinak KM (2013) WRF-Fire: coupled weather–wildland fire modeling with the weather research and forecasting model. Journal of Applied Meteorology and Climatology 52(1), 16-38.
| Crossref | Google Scholar |
Collins L, Bradstock RA, Clarke H, Clarke MF, Nolan RH, Penman TD (2021) The 2019/2020 mega-fires exposed Australian ecosystems to an unprecedented extent of high-severity fire. Environmental Research Letters 16(4), 044029.
| Crossref | Google Scholar |
Costes A, Rochoux MC, Lac C, Masson V (2021) Subgrid-scale fire front reconstruction for ensemble coupled atmosphere-fire simulations of the FireFlux I experiment. Fire Safety Journal 126, 103475.
| Crossref | Google Scholar |
Cruz MG, Alexander ME (2013) Uncertainty associated with model predictions of surface and crown fire rates of spread. Environmental Modelling & Software 47, 16-28.
| Crossref | Google Scholar |
Cruz MG, Alexander ME, Fernandes PM, Kilinc M, Sil  (2020) Evaluating the 10% wind speed rule of thumb for estimating a wildfire’s forward rate of spread against an extensive independent set of observations. Environmental Modelling & Software 133, 104818.
| Crossref | Google Scholar |
Evensen G (1994) Sequential data assimilation with a nonlinear quasi‐geostrophic model using Monte Carlo methods to forecast error statistics. Journal of Geophysical Research: Oceans 99(C5), 10143-10162.
| Crossref | Google Scholar |
Fang H, Srivas T, de Callafon RA, Haile MA (2017) Ensemble-based simultaneous input and state estimation for nonlinear dynamic systems with application to wildfire data assimilation. Control Engineering Practice 63, 104-115.
| Crossref | Google Scholar |
Feng L, Katupitiya J (2022) Navigation for prioritized wildfire boundary tracking. In ‘International Conference on Autonomous Unmanned Systems’. (Springer) 10.1007/978-981-99-0479-2_59
Filippi J-B, Mallet V, Nader B (2013a) Representation and evaluation of wildfire propagation simulations. International Journal of Wildland Fire 23(1), 46-57.
| Crossref | Google Scholar |
Filippi J-B, Pialat X, Clements CB (2013b) Assessment of ForeFire/Meso-NH for wildland fire/atmosphere coupled simulation of the FireFlux experiment. Proceedings of the Combustion Institute 34(2), 2633-2640.
| Crossref | Google Scholar |
Flannigan MD, Krawchuk MA, de Groot WJ, Wotton BM, Gowman LM (2009) Implications of changing climate for global wildland fire. International Journal of Wildland Fire 18(5), 483-507.
| Crossref | Google Scholar |
Gillespie DT (1977) Exact stochastic simulation of coupled chemical reactions. The Journal of Physical Chemistry 81(25), 2340-2361.
| Crossref | Google Scholar |
Gollner M, Trouve A, Altintas I, Block J, de Callafon R, Clements C, Cortes A, Ellicott E, Filippi JB, Finney M (2015) Towards data-driven operational wildfire spread modeling: a report of the NSF-funded WIFIRE workshop. 10.13016/M2Z70R
Gu F (2017) Localized recursive spatial-temporal state quantification method for data assimilation of wildfire spread simulation. Simulation 93(4), 343-360.
| Crossref | Google Scholar |
Jian L, Li Z, Yang X, Wu W, Ahmad A, Jeon G (2019) Combining unmanned aerial vehicles with artificial-intelligence technology for traffic-congestion recognition: electronic eyes in the skies to spot clogged roads. IEEE Consumer Electronics Magazine 8(3), 81-86.
| Crossref | Google Scholar |
Juang CS, Williams AP, Abatzoglou JT, Balch JK, Hurteau MD, Moritz MA (2022) Rapid growth of large forest fires drives the exponential response of annual forest‐fire area to aridity in the western United States. Geophysical Research Letters 49(5), e2021GL097131.
| Crossref | Google Scholar | PubMed |
Kalman RE (1960) A new approach to linear filtering and prediction problems. Journal of Basic Engineering 82, 35-45.
| Crossref | Google Scholar |
Lagerquist R, Flannigan MD, Wang X, Marshall GA (2017) Automated prediction of extreme fire weather from synoptic patterns in northern Alberta, Canada. Canadian Journal of Forest Research 47(9), 1175-1183.
| Crossref | Google Scholar |
Liu N, Lei J, Gao W, Chen H, Xie X (2021) Combustion dynamics of large-scale wildfires. Proceedings of the Combustion Institute 38(1), 157-198.
| Crossref | Google Scholar |
Long Y, Hu X (2017) Spatial partition-based particle filtering for data assimilation in wildfire spread simulation. ACM Transactions on Spatial Algorithms and Systems (TSAS) 3(2), 1-33.
| Crossref | Google Scholar |
Lopes AMG, Cruz MG, Viegas DX (2002) FireStation—an integrated software system for the numerical simulation of fire spread on complex topography. Environmental Modelling & Software 17(3), 269-285.
| Crossref | Google Scholar |
Mandel J, Bennethum LS, Beezley JD, Coen JL, Douglas CC, Kim M, Vodacek A (2008) A wildland fire model with data assimilation. Mathematics and Computers in Simulation 79(3), 584-606.
| Crossref | Google Scholar |
Mandel J, Beezley JD, Kochanski AK (2011) Coupled atmosphere-wildland fire modeling with WRF-Fire version 3.3. Geoscientific Model Development Discussions 4(1), 497-545.
| Crossref | Google Scholar |
Mandel J, Beezley JD, Kochanski AK, Kondratenko VY, Kim M (2012) Assimilation of perimeter data and coupling with fuel moisture in a wildland fire–atmosphere DDDAS. Procedia Computer Science 9, 1100-1109.
| Crossref | Google Scholar |
Masutani M, Schlatter TW, Errico RM, Stoffelen A, Andersson E, Lahoz W, Woollen JS, Emmitt GD, Riishøjgaard L-P, Lord SJ (2010) Observing system simulation experiments. In ‘Data Assimilation: Making Sense of Observations’. (Eds W Lahoz, B Khattatov, R Menard) pp. 647–679. (Springer) 10.1007/978-3-540-74703-1_24.
Merino L, Caballero F, Martínez-de-Dios JR, Maza I, Ollero A (2012) An unmanned aircraft system for automatic forest fire monitoring and measurement. Journal of Intelligent & Robotic Systems 65, 533-548.
| Crossref | Google Scholar |
Oubbati OS, Atiquzzaman M, Lim H, Rachedi A, Lakas A (2022) Synchronizing UAV teams for timely data collection and energy transfer by deep reinforcement learning. IEEE Transactions on Vehicular Technology 71(6), 6682-6697.
| Crossref | Google Scholar |
Ren W, Beard RW (2008) ‘Distributed consensus in multi-vehicle cooperative control.’ (Springer) 10.1007/978-1-84800-015-5
Rios O, Pastor E, Valero MM, Planas E (2016) Short-term fire front spread prediction using inverse modelling and airborne infrared images. International Journal of Wildland Fire 25(10), 1033-1047.
| Crossref | Google Scholar |
Rochoux MC, Ricci S, Lucor D, Cuenot B, Trouvé A (2014) Towards predictive data-driven simulations of wildfire spread–Part I: Reduced-cost Ensemble Kalman Filter based on a Polynomial Chaos surrogate model for parameter estimation. Natural Hazards and Earth System Sciences 14(11), 2951-2973.
| Crossref | Google Scholar |
Rochoux MC, Emery C, Ricci S, Cuenot B, Trouvé A (2015) Towards predictive data-driven simulations of wildfire spread–Part II: Ensemble Kalman Filter for the state estimation of a front-tracking simulator of wildfire spread. Natural Hazards and Earth System Sciences 15(8), 1721-1739.
| Crossref | Google Scholar |
Ruffault J, Martin-StPaul N, Pimont F, Dupuy J-L (2018) How well do meteorological drought indices predict live fuel moisture content (LFMC)? An assessment for wildfire research and operations in Mediterranean ecosystems. Agricultural and Forest Meteorology 262, 391-401.
| Crossref | Google Scholar |
Sakov P, Evensen G, Bertino L (2010) Asynchronous data assimilation with the EnKF. Tellus A: Dynamic Meteorology and Oceanography 62(1), 24-29.
| Crossref | Google Scholar |
Santana B, Cherif EK, Bernardino A, Ribeiro R (2022) Real-time georeferencing of fire front aerial images using iterative ray-tracing and the bearings-range extended Kalman filter. Sensors 22(3), 1150.
| Crossref | Google Scholar | PubMed |
Schultz MG, Heil A, Hoelzemann JJ, Spessa A, Thonicke K, Goldammer JG, Held AC, Pereira JMC, van Het Bolscher M (2008) Global wildland fire emissions from 1960 to 2000. Global Biogeochemical Cycles 22(2), GB2002.
| Crossref | Google Scholar |
Shobeiry P, Xin M, Hu X, Chao H (2021) Uav path planning for wildfire tracking using partially observable markov decision process. In ‘AIAA Scitech 2021 Forum’. 10.2514/6.2021-1677
Srivas T, Artés T, de Callafon RA, Altintas I (2016) Wildfire spread prediction and assimilation for FARSITE using ensemble Kalman filtering. Procedia Computer Science 80, 897-908.
| Crossref | Google Scholar |
Srivas T, de Callafon RA, Crawl D, Altintas I (2017) Data assimilation of wildfires with fuel adjustment factors in farsite using ensemble kalman filtering. Procedia Computer Science 108, 1572-1581.
| Crossref | Google Scholar |
Stocks BJ, Mason JA, Todd JB, Bosch EM, Wotton BM, Amiro BD, Flannigan MD, Hirsch KG, Logan KA, Martell DL (2002) Large forest fires in Canada, 1959–1997. Journal of Geophysical Research: Atmospheres 107(D1), FFR 5-1-FFR 5-12.
| Crossref | Google Scholar |
Sullivan AL (2009a) Wildland surface fire spread modelling, 1990–2007. 1: Physical and quasi-physical models. International Journal of Wildland Fire 18(4), 349-368.
| Crossref | Google Scholar |
Sullivan AL (2009b) Wildland surface fire spread modelling, 1990–2007. 2: Empirical and quasi-empirical models. International Journal of Wildland Fire 18(4), 369-386.
| Crossref | Google Scholar |
Sullivan AL (2009c) Wildland surface fire spread modelling, 1990–2007. 3: Simulation and mathematical analogue models. International Journal of Wildland Fire 18(4), 387-403.
| Crossref | Google Scholar |
Sutherland D, Rashid MA, Hilton JE, Moinuddin KAM (2023) Implementation of spatially-varying wind adjustment factor for wildfire simulations. Environmental Modelling & Software 163, 105660.
| Crossref | Google Scholar |
Tymstra C, Bryce RW, Wotton BM, Taylor SW, Armitage OB (2010) Development and structure of Prometheus: the Canadian wildland fire growth simulation model. Information Report NOR-X-417. (Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre: Edmonton, AB) Available at https://central.bac-lac.gc.ca/.item?id=31775&op=pdf&app=Library
Valero MM, Rios O, Mata C, Pastor E, Planas E (2017) An integrated approach for tactical monitoring and data-driven spread forecasting of wildfires. Fire Safety Journal 91, 835-844.
| Crossref | Google Scholar |
Viegas DX, Piñol J, Viegas MT, Ogaya R (2001) Estimating live fine fuels moisture content using meteorologically-based indices. International Journal of Wildland Fire 10(2), 223-240.
| Crossref | Google Scholar |
Xie Z, Song W, Ba R, Li X, Xia L (2018) A spatiotemporal contextual model for forest fire detection using Himawari-8 satellite data. Remote Sensing 10(12), 1992.
| Crossref | Google Scholar |
Yoo S, Song J (2023) Rapid prediction of wildfire spread using ensemble Kalman filter and polyline simplification. Environmental Modelling & Software 160, 105610.
| Crossref | Google Scholar |
Yu Z, Zhang Y, Liu Z, Qu Y, Su C-Y, Jiang B (2020) Decentralized finite-time adaptive fault-tolerant synchronization tracking control for multiple UAVs with prescribed performance. Journal of the Franklin Institute 357(16), 11830-11862.
| Crossref | Google Scholar |
Zhang C, Rochoux M, Tang W, Gollner M, Filippi J-B, Trouvé A (2017) Evaluation of a data-driven wildland fire spread forecast model with spatially-distributed parameter estimation in simulations of the FireFlux I field-scale experiment. Fire Safety Journal 91, 758-767.
| Crossref | Google Scholar |
Zhang C, Collin A, Moireau P, Trouvé A, Rochoux MC (2019) State-parameter estimation approach for data-driven wildland fire spread modeling: application to the 2012 RxCADRE S5 field-scale experiment. Fire Safety Journal 105, 286-299.
| Crossref | Google Scholar |
Zhang F, Zhao P, Xu S, Wu Y, Yang X, Zhang Y (2020) Integrating multiple factors to optimize watchtower deployment for wildfire detection. Science of The Total Environment 737, 139561.
| Crossref | Google Scholar | PubMed |
Zhou T, Ding L, Ji J, Li L, Huang W (2019) Ensemble transform Kalman filter (ETKF) for large-scale wildland fire spread simulation using FARSITE tool and state estimation method. Fire Safety Journal 105, 95-106.
| Crossref | Google Scholar |
Zhou T, Ding L, Ji J, Yu L, Wang Z (2020) Combined estimation of fire perimeters and fuel adjustment factors in FARSITE for forecasting wildland fire propagation. Fire Safety Journal 116, 103167.
| Crossref | Google Scholar |
Zhou T, Ding L, Ji J, Luo S (2021) VWETKF for wildfire propagation prediction employing observations with missing values and/or spatial variations of error variance. Proceedings of the Combustion Institute 38(3), 5091-5099.
| Crossref | Google Scholar |