Sydney downslope windstorm event on 31 October 2023
Jiwon Park A *
A *
A
Handling Editor: Christopher Reason
Abstract
A moderate-strength downslope windstorm occurred in the Sydney Metropolitan Area during the early morning of 31 October 2023. It was a rare event in view of the climatology of Sydney, as some stations reported the highest wind gusts in the last 20 years. The event was initiated by a rapidly propagating disturbance in a vertically sheared wind environment ahead of the passage of a trough. With the assumption of a quasi-steady condition, the phase speed of the disturbance translated to a reduction of the effective cross-barrier winds, which resulted in the wave breaking in the low to mid-troposphere. The flow transition from sub- (F < 1) to supercritical (F > 1) across a low mountain barrier ~900 m high was possible owing to the alignment of several factors. These include the right tuning of the phase speed relative to the ambient westerly winds, the split flows and wave breaking at the right altitude, and the linear wind shear upstream, which caused a hydraulic jump response, and the downslope acceleration on the lee side of the Great Dividing Range. The close match of the barrier height of the Oberon Plateau to the critical ridgetop height was remarkable, suggesting that the wind speed observed during the event was likely the maximum attainable wind speed. Further analysis shows that a classical Boulder-style downslope windstorm involving a deep tropospheric layer and forcing by a slow-moving synoptic system is unlikely in Sydney.
Keywords: Badgerys Creek, downslope windstorm, Foehn effect, hydraulic jump, New South Wales, Oberon Plateau, severe wind event, wave breaking, Western Sydney.
1Introduction
Strong wave-induced downslope windstorms occur when an airstream with static stability flows over high mountains. Local names of downslope windstorms include the chinook of the Rocky Mountains, USA, bora of the Yugoslavian mountains, Alpine foehn of the European Alps and Argentine zonda (Durran 1990). These windstorm events are characterised by high-pressure drag, wave breaking and hydraulic jump signatures (Durran 1986, 1990). Although not well documented, similar wave-induced downslope windstorms are thought to occur to a lesser extent in the Australian Alps and their immediate lee in New South Wales and Victoria due to the prevalence of strong westerly winds over elevated terrain.
In the early morning of 31 October 2023, the Sydney Metropolitan Area was affected by vigorous westerly winds lasting 3–4 h between 01:00 and 05:00 hours Australian Eastern Daylight Time (AEDT, +11 UTC). The windstorm resulted in 425 State Emergency Service (SES) jobs across the SES Metro Zone (covering the Sydney metropolitan area), mainly related to fallen trees and roof damage to residential and commercial properties. The south-western suburbs of Sydney were hardest hit with some record wind gusts, with wind damage focused on Liverpool, Campbelltown, Penrith, Camden and Fairfield (SES Operational Update – Severe Weather NSW 33/2324 numbers 1–2, NSW State Emergency Services, unpubl. data). The highest wind gust recorded during the event was 104 km h–1 (02:52 hours) at Badgerys Creek, followed by 98 km h–1 (02:53 hours) at Camden and 94 km h–1 (04:12 hours) at Horsley Park. The wind gust at Badgerys Creek was the equal highest record at the site. Camden and Horsley Park also had the highest October records at each site. Based on the history of observations at Badgerys Creek (opened 1995) and Horsley Park (opened 1997), the recurring interval of such a wind event in Western Sydney appears to be at least once every 20 years. This event was unique because the damaging winds (gusts >90 km h–1) in Western Sydney are typically observed in association with thunderstorm cells or a convection line following a cold front. Yet this event was dry, purely driven by synoptic westerlies. Because of pressure-driven channelling through the valleys or east–west-oriented corridors (Webb and Park 2023), westerly winds are typically stronger in Illawarra and the Lower Hunter than in Sydney. Also, the Western Sydney suburbs are generally protected from the westerlies by the topographic shielding of the Blue Mountains and the Oberon Plateau. However, it is noteworthy that Western Sydney suburbs saw stronger winds than Illawarra and the Lower Hunter during the event. A notable foehn effect was also observed in association with the windstorm, with a significant temperature rise to overnight (e.g. 27–29°C), contrary to the diurnal trend. The analysis of the observations and computer model outputs also revealed that the strong westerly winds in Sydney arose from the breaking of mountain waves in the low to mid-troposphere (Clark and Peltier 1977, 1984) and the transition of the cross-barrier flow from tranquil (subcritical, F < 1) to shooting (supercritical, F > 1) at the ridgetop (Long 1954). These caused a significant downslope acceleration as the shooting flow plunged underneath a turbulent layer created by the wave breaking above the lee of the ranges, and a jump-like disturbance formed further downstream (Smith 1985). In the present paper, both the flow transition and its characteristic jump-like disturbance are referred to as a hydraulic jump. Kepert (2017) noted that downslope winds induced by mountain waves on moderate topography were responsible for several large fires in Australia in recent decades, including the Margaret River Fire in Western Australia in 2011, the State Mine Fire in New South Wales in 2013 and the Aberfeldy Fire in Victoria in 2013. Wilke et al. (2022) also observed that trapped lee waves were a major contributor to the downslope winds that brought extreme fire behaviour during the Tathra Fire in New South Wales in 2018. Similarly, Park et al. (2022) found that hydraulic jumps and wave breaking were the main causes of a downslope windstorm event on 14 February 2018 during the PyungChang Winter Olympics that occurred on the lee of the Taebaek Mountains in eastern South Korea, which have similar mountain heights (~1000 m) to the Great Dividing Range in eastern New South Wales. In light of these studies, a similar wave-induced or hydraulic jump-style downslope windstorm affecting the Sydney Metropolitan Area is not out of the question. However, to the best of the author’s knowledge, such a possibility has not been adequately investigated in the past. Yet this event deserves special attention because it teaches us that such a downslope windstorm can occur in Sydney. This paper endeavours to explain the event by referencing well-known mechanisms of downslope windstorms, including hydraulic jumps and wave breaking, and examines why the south-western suburbs of Sydney were hit hardest during the event. Answers to such questions may be necessary for public safety in view of the rapid population growth in Western Sydney and aviation safety at Sydney’s second international airport in Badgerys Creek, which is currently under construction.
The term windstorm in other parts of the world is generally reserved for high-end downslope wind events with gusts up to 50–60 m s–1 (~100–120 knots) (Klemp and Lilly 1975; Lilly 1978; Durran 1990), whereas this event was moderately strong at best according to the international standard. Nevertheless, this event is referred to as the Sydney Downslope Windstorm Event (SDWE) to emphasise its uniqueness with regard to the climatology of the Sydney Metropolitan Area.
2The topography around Sydney and the data used
Fig. 1 shows the topography of the central eastern areas of New South Wales (NSW), with the Sydney Metropolitan Area (SMA) at the centre of the coastline. SMA is an ~50- × 50-km square of low-lying area (elevation near sea level to 200 m) along the central part of the NSW Coast, with Sydney Harbour and the Sydney central business district (CBD) ~7 km from the coastline. Sydney Airport (YSSY, 5-m elevation) is located on the northern shore of Botany Bay, ~10 km to the south of the Sydney CBD. The aviation code and the elevation of each key location are shown in parentheses. The narrow areas between the coast and the CBD form the eastern suburbs, whereas the western suburbs extend from the Sydney CBD westwards to the Hawkesbury–Nepean Rivers just before the foothills of the Great Dividing Range (GDR), with Campbelltown and Camden (YSCN, 70 m) at the south-western corner, Penrith (PENR, 25 m) at the western end and Richmond (YSRI, 20 m) at the north-west. The topography rises westwards from the western ends of SMA until the Blue Mountains, ~70–100 km west of the Sydney CBD, which form a part of the GDR, with elevations between 700 and 1100 m. Mount Victoria (MVI, 1050 m) is a critical location in the Blue Mountains for aircraft flying under visual flight rules. To the south-west of the Blue Mountains is the township of Oberon (elevation, 1100 m), marked X in Fig. 1. The areas surrounding Oberon, often called the Oberon Plateau, have higher elevations than the Blue Mountains, generally between 1100 and 1300 m, with a couple of peaks reaching ~1350 m. The Central Tablelands district encompasses both the Blue Mountains and Oberon Plateau, and it continues further west to Orange (YORG, 900 m), the regional centre of the district, with nearby Mountain Canobolas (~1400 m), which is the highest peak in the Central Tablelands, before its topography gently slopes downward towards the western plains. The Central West Slopes and Plains district encompasses the western slopes of the GDR and adjacent plains. Forbes (YFBS, 230 m), Parkes (YPKS, 320 m) and Cowra (YCWR, 300 m) are the towns in the region, with elevation ranges between 200 and 300 m. To the south-west of Sydney is the Southern Highlands – the higher parts of the Illawarra district, with elevations between 500 and 900 m with Bowral (YXOW, 690 m) as the centre. Sharp escarpments divide the coastal parts of the Illawarra from the Southern Highlands. The Illawarra Coast is ~130 km long, oriented SSW to NNE, with the City of Wollongong and its suburbs (Albion Park YSHL being one) on the northern side, and Nowra (YSNW, 100 m), Kangaroo Valley and Jervis Bay on the southern side. As the wind event did not extend to the areas north of SMA, a description of the topography to the north of Sydney will not be elaborated here.
Topographic map of central eastern New South Wales. Red squares are the locations of the major international airports of the capital cities – Sydney and Canberra. Blue squares are the sites of the regional aerodromes or transport infrastructure where the Bureau of Meteorology’s Automatic Weather Stations (AWSs) are located. The AWS sites relevant for this study with their aviation codes are: Sydney AP (YSSY), Badgerys Creek (YSBC), Camden (YSCN), Richmond (YSRI) and Forbes (YFBS). Marked by X is the township of Oberon in the Central Tablelands. Inserted in the bottom right corner is the map of the Sydney Metropolitan Area, with Bureau of Meteorology’s AWS sites marked as black squares.

The Bureau of Meteorology maintains a network of Automatic Weather Stations (AWSs) across the state. Key observation sites with AWSs are marked in Fig. 1 as blue squares with aviation codes, and the major city centres and regional towns are marked as red squares. A separate map of AWS sites in SMA is inserted in the lower right corner. The AWS observations of 1-min peak gusts will be used for wind gusts, and the Meteorological Aerodrome Report (METAR) 10-min mean wind speeds every 30 min will be used for mean wind speeds and directions. The temperatures will be from the 1-min mean temperature observations. In addition to the surface-level observations from the AWS network, upper-air observations are carried out at Sydney Airport (AP) employing a 1280-MHz wind profiler and a routine upper-air sounding between 18 and 19Z (05:00–06:00 hours). These observations at Sydney AP provide detailed aerological information downstream, but no upstream upper air observations are available. Therefore, the aerological conditions over the mountain ranges or the windward side of the GDR can only be deduced from either computer models or reanalysis data. For this purpose, the ERA5 reanalysis data (Hersbach et al. 2020) and the outputs from the 12Z 30 October 2023 run of the operational ACCESS-Global model (ACCESS-G, 12.5-km horizontal resolution) will be used as appropriate (Bureau of Meteorology 2016, 2019). Additionally, the model cross-sections from the 06Z and 12Z 30 October 2023 runs of the operational ACCESS-City (ACCESS-C) model will be analysed in detail to investigate the evidence of amplification of mountain waves, wave breaking and a hydraulic jump. ACCESS-C has a horizontal resolution of 1.5 km and 70 vertical levels from the surface to 0.009 hPa (~80-km altitude). The vertical grid spacing varies from 25 to 150 m below 1000-m altitude, and from 150 to 300 m between 1000- and 4500-m altitude (Bureau of Meteorology 2016, 2019). High-resolution models in research mode are typically used to capture non-linear features like wave breaking or hydraulic jumps adequately. For example, Park et al. (2022) used 333 by 200 m for horizontal and vertical resolutions, and Wilke et al. (2022) employed a 100-m horizontal resolution model. Although the 1.5-km horizontal resolution of the operational ACCESS-C model may be considered somewhat coarse compared with the research models, it is sufficient to capture the main features, including the amplification of mountain waves, wave breaking, hydraulic jumps and the subsequent downslope winds in the low level.
3Observations
3.1 Synoptic features and surface observations
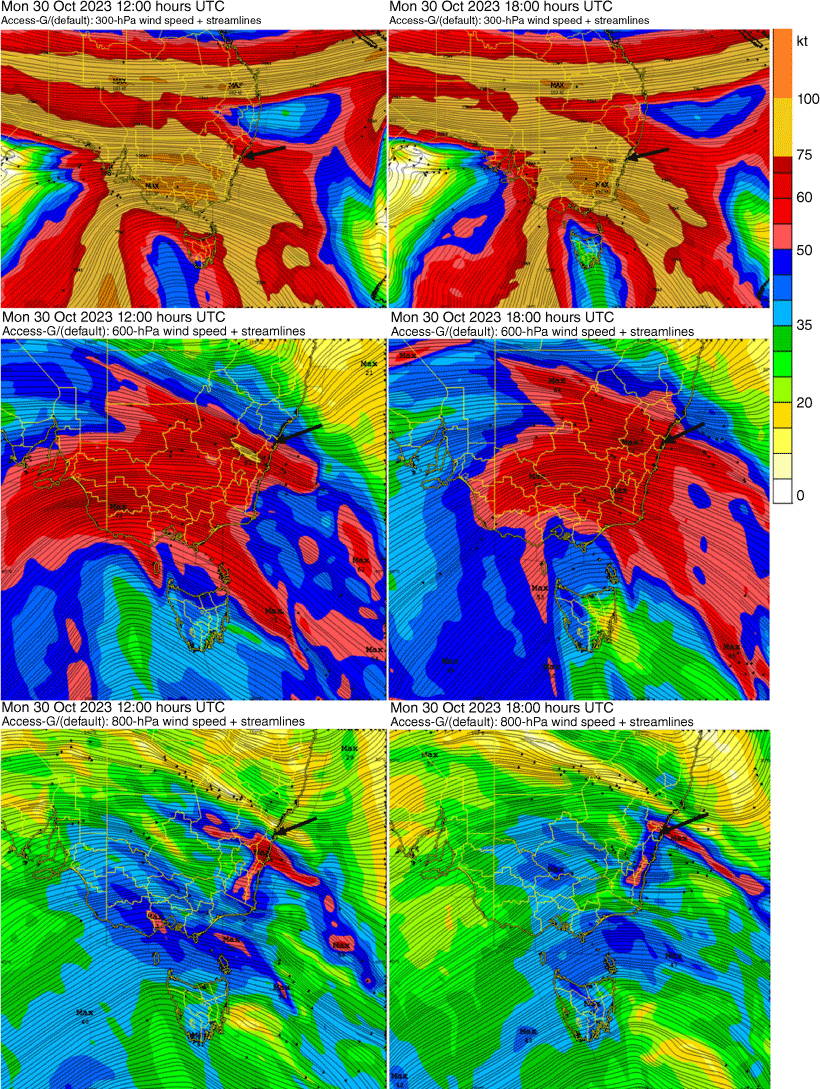
Fig. 2 is an infrared (IR) image of eastern NSW at 1300Z on 30 October 2023 UTC date (00:00 hours AEDT on 31 October 2023) with manual analysis of synoptic features overlaid. Fig. 3 shows ACCESS-G model winds and isotachs at 300-, 600- and 800-hPa levels at 12Z and 18Z. The wind barbs of AWS observations and the ASCAT winds (satellite-derived winds) in Fig. 2 indicate two trough features in addition to a cold front (a) crossing southern NSW. The first trough (b) extends from the western plains to the northern areas of the Southern Tablelands, then to the Illawarra Coast. The second trough (c) extends from northern inland NSW to the Upper Hunter, then to the Central Coast. A cloud band is seen between (b) and (c), and the ACCESS-G model winds at 12Z (23:00 hours) and 18Z (05:00 hours) in Fig. 3 (middle and bottom) show that there was a WNW jet in the low to mid-level of the troposphere ahead of (b) and underneath the cloud band. Fig. 3 (top) also shows that central eastern NSW, including SMA, Central Tablelands and Illawarra districts, was in the right exit region of a broad upper-level jet where ageostrophic winds would be expected to promote upper-level confluence and downward motion. The troughs (b) and (c) were mobile and heading NE as front (a) moved across southern NSW and Victoria during the overnight period between 30 and 31 October 2023. While trough (b) was crossing the Illawarra, gusty WNW winds were observed along the Illawarra Coast, most notably at Nowra station, which recorded an 89 km h–1 wind gust at 22:12 hours on 30 October. Sydney suburbs started experiencing strong and gusty downslope winds from c. 01:00–02:00 hours on 31 October as trough (b) headed north towards SMA, and the WNW jet ahead of the trough interacted with the mountain ranges of the Central Tablelands west of Sydney. Winds in the south-western suburbs of Sydney were particularly strong. Fig. 4 shows the meteograms of the wind gusts, half-hourly 10-min average wind speeds and directions, and screen temperatures from selected AWS in Sydney. Observations from the south-western suburbs where the impact of the damaging winds (gust > 90 km h−1) were most significant are grouped in Fig. 4a–c. According to the temperature graphs for Bankstown AP (d2), Sydney AP (e2) and Richmond AP (g2) in Fig. 4, the nocturnal inversion broke between 00:00 and 02:00 hours, causing temperatures to rise by 5–10°C at these sites, contrary to the diurnal cycle, until they plateaued at 27–28°C. These temperatures were 5–6°C higher than the average maximum temperature in October at Sydney Observatory Hill (CBD) and 2–4°C higher in western Sydney. However, the temperatures in the south-western suburbs (a2, b2, c2) and Penrith (f2) were already at 27–28°C from midnight, or soon after for c2, indicating earlier inversion breaking there.
IR image, wind barbs from AWS and ASCAT winds (satellite-derived winds), and the surface analysis of the synoptic systems crossing eastern New South Wales at 13Z on 30 October 2023 UTC date. (a) Cold front. (b, c) Pre-frontal troughs. The number on each wind barb is the gust speed in knots (1 knot = ~1.9 km h–1). The downslope windstorm in Sydney occurred in association with the trough (b).

ACCESS-G model streamlines and isotachs at 12Z (left) and 18Z (right). The levels are at 300 hPa (top), 600 hPa (middle) and 800 hPa (bottom). The arrow indicates the position of Sydney AP. Colour contours denote isotachs, with blue, >35 knots (~65 km h–1); red, >50 knots (~93 km h–1); amber, >75 knots (~139 km h–1); and orange, >100 knots (~185 km h–1).
Time series of AWS 10-m winds (left) and screen temperatures from 1-min data (right) from selected AWS sites in the Sydney Metropolitan Area between 00:00 and 09:00 hours on 31 October 2023. Shown in the time series of winds (left) are 1-min peak wind gusts (blue), METAR 10-min mean wind speeds every 30 min (red), and METAR wind directions (DIR, black crosses). Letters in the label designate AWS sites: (a1–2) Badgerys Creek, (b1–2) Camden, (c1–2) Horsley Park, (d1–2) Bankstown, (e1–2) Sydney AP, (f1–2) Penrith, (g1–2) Richmond.

The same period also saw an increase in wind speeds across all stations, most notably in Badgerys Creek (a1), Camden AP (b1) and Sydney AP (e1), marking the onset of the downslope windstorm. Temporal variation of gust speeds shows that there were two periods of surge of downslope winds. The first period of surge spanned 01:45 to 03:00 hours after inversion breaking, and the earliest peaks were observed at places like Camden (b1, 79.6 km h–1 at 01:43 hours) and Sydney AP (e1, 70.2 km h–1 at 02:16 hours). More substantial peaks were observed towards the end of the period at places like Badgerys Creek (a1, 104 km h–1 at 02:52 hours – the strongest gust of the event) and Camden (b1, 98 km h–1 at 02:53 hours – the strongest gust for the site) before an interlude of relatively weaker winds between 03:00 and 04:00 hours, which was most noticeable in Badgerys Creek (a1), Camden (b1) and Sydney AP (e1). The second surge period spanned 04:00 to 05:00 hours, and then the event gradually wound up between 05:00 and 06:00 hours. Some sites in south-western Sydney that did not show noticeable gusts during the first surge recorded wind gust peaks this time, including Horsley Park (c1, 94.3 km h–1 04:12 hours) and Bankstown AP (d1, 79.6 km h–1 at 04:36 hours). Badgerys Creek also recorded the second-strongest peak gust close to the earlier peak (a1, 103.7 km h–1 at 04:21 hours). Similarly, Sydney AP recorded the strongest gust for the site (e1, 79.6 km h–1 at 04:21 hours). The spatial extent of the second surge suggests that it was broader than the first one. As the event was coming to a finish, Bankstown (64.8 km h–1 at 05:41 hours), Penrith Lake (63.0 km h–1 at 05:26 hours) and Sydney AP (59.4 km h–1 at 06:00 hours) displayed relatively minor peaks between 05:30 and 06:00 hours. However, this last peak was absent in Camden (b1) as trough (b) already had gone through. The timing of surge and gust peaks appears to be delayed by ~30 min at Richmond (g1), but this was likely due to the northernmost position of Richmond AP compared with other stations.
Up until c. 06:00 hours, wind direction remained between 280 and 310° at most stations; then, wind speeds dropped significantly with a SW wind change after the passage of trough (b), marking the end of the event. The SW change arrived earliest at Camden AP at c. 04:50 hours, then slowly moved across much of SMA between 05:00 and 07:00 hours, crossing Richmond AP at c. 07:15 hours. The most notable change was observed at Sydney AP, where a sharp wind direction change from WNW to SE was accompanied by a rapid temperature drop of 5°C at c. 06:30 hours.
The wind speed eased after the arrival of the SW change, which caused the decoupling of the boundary layer and the formation of a nocturnal inversion, bringing further drops in wind speeds and temperatures. Winds became completely calm at Horsley Park between 07:00 and 07:30 hours, and the winds were generally light and variable in many places between 06:30 and 08:00 hours. Then, winds picked up as the insolation broke the nocturnal inversion again, and the winds turned westerly as the cold front (a) continued to move across south-east NSW through the rest of the morning.
3.2 Vertical profile and hydraulic jump signature
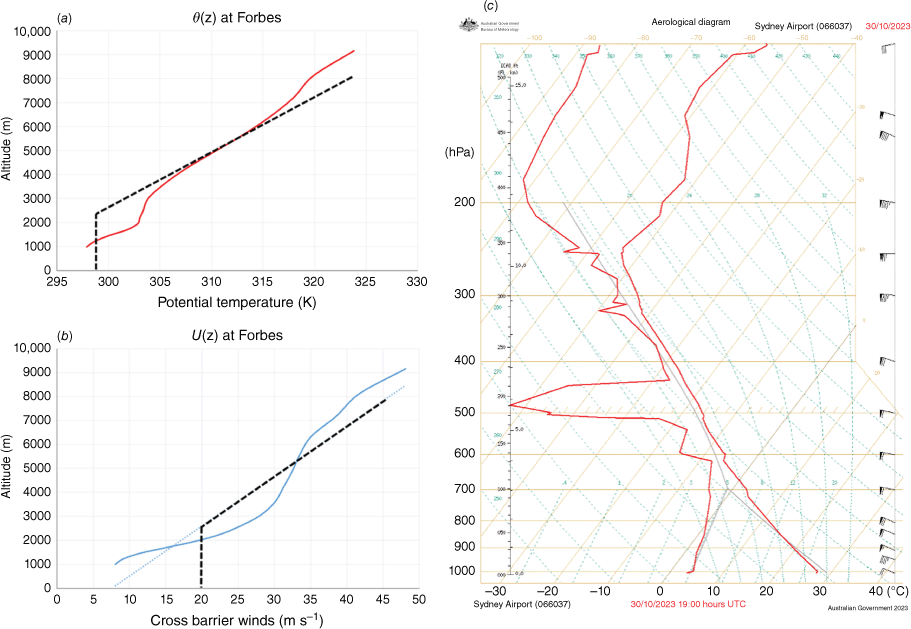
Shown on the left side of Fig. 5 are the vertical profiles of the potential temperatures (Fig. 5a) and the cross-barrier wind speeds (Fig. 5b) in the upstream region near Forbes (33.40°S, 148.00°E). The wind speeds are measured along the 110–290° direction (perpendicular to the general orientation of the GDR in NSW), and the data are from ERA5 reanalysis (Hersbach et al. 2020). The 6-h temporal averages of wind speeds and potential temperatures between 12Z and 18Z were used to filter out temporal fluctuations. The vertical gradient of the potential temperatures between 4000 and 6500 m is almost constant, indicating uniform static stability in the mid level, apart from a relatively warm layer between 2000- and 3000-m altitudes. The upstream cross-barrier winds show positive shear with a steady increase in wind speeds with height. Although the increase is not strictly linear, an approximation by linear shear following the line of best fit (dotted line) appears reasonable. The boundary layer is stable owing to night-time radiative cooling and the presence of a warm layer above, which complicates the interaction with the topography. Inserted (in broken lines) are the hypothetical profiles where a well-mixed boundary layer is assumed between the ground and 2500 m (750 hPa). The next section will use a simplified theoretical approach based on this hypothetical profile. Fig. 5c shows the upper air sounding taken at Sydney AP (33.95°S, 151.17°E) between 18Z and 19Z (05:00–06:00 hours), close to the end of the event. It represents the profiles in the downstream region. The lapse rate in the low level is almost uniform and slightly less than dry adiabat, with the surface level temperature ~28°C in line with the AWS screen temperatures in Fig. 4. Wind barbs on the far right of the aerological diagram show a concentration of westerly momentum in the low level between 1000 and 2000 m (or 900 and 800 hPa) with a maximum wind speed of 70 knots (~130 km h–1). Then, there is a relative lull in the mid level up to 500 hPa (~5600 m) before winds increase again in the upper level to tropopause. The profiler winds at Sydney AP, shown in Fig. 6, reinforce this observation and highlight some additional points. There were two surges of a jet (>50 knots, ~93 km h–1) in the near-surface level below 1200 m. The first one happened between 1445Z and 1600Z (01:45–03:00 hours), and the second one between 1700Z and 1830Z (04:00–05:30 hours), with an interlude between 1600Z and 1700Z (03:00–04:00 hours), all in agreement with the time series of AWS surface winds in Fig. 4. The surge of strong low to mid-level winds between 1200 and 3500 m lasted longer and was more continuous than those below 1200 m, spanning 1430Z to 1815Z (01:30–05:15 hours). At 17Z, the strongest westerly winds in this layer reached 70–80 knots (~130–149 km h–1) between 1700- and 2000-m altitude. It is also interesting to note a lull or wind reversal in the low level from the profiler winds, marking the beginning and end of the event. In Fig. 6, a lull of low-level winds of only 10–15 knots (~19–28 km h–1) from WNW was seen between 1300- and 1700-m altitude for ~30 min between 1315Z and 1345Z (00:15–00:45 hours) before a significant increase of winds in the low to mid-level. Towards the end of the event, a similar wind reversal was seen in the same altitudes between 1815 and 1845Z (05:15–05:45 hours), consistent with rotor flow or wave overturning.
Vertical profiles at Forbes (left), and at Sydney AP (right), representing the conditions on the windward side and the lee side of the Oberon Plateau respectively. The potential temperatures (a) were averaged over the 6 h from 12Z to 18Z, and the wind component (b) was perpendicular to the mountain barrier in the plain from the 290 to 110° direction, averaged over the same 6-h period. Both sets of data were from ERA 5 reanalysis. The dotted blue line in (b) is the line of best fit for the winds. The dashed black lines in (a) and (b) represent the idealised vertical wind and temperature profiles for theoretical investigation. (c) is the aerological diagram from the upper air sounding at Sydney AP between 18 and 19Z.
Profiler wind observations at Sydney AP during the 6 h between 13Z and 19Z, or 00:00 and 06:00 hours on 31 October 2023. Wind barbs represent the airflow in the horizontal plane. Note that the discontinuity at 2000-m altitude is due to the difference in the thresholds of the colour contours used.

Shown in Fig. 7a, b are the vertical cross-sections of operational ACCESS-C (Sydney) model winds and isentropes at 09Z, 10Z, 12Z (Fig. 7a), and between 14 and 18Z (Fig. 7b). These are along the route, oriented 280–110°, following the mean wind directions in the low to mid-level from the Sydney AP profiler winds, sonde observations and the upstream winds from ERA5 reanalysis. The route, marked as a broken line in Fig. 1, is 375 km long, and it starts from Forbes and joins Oberon, Badgerys Creek and Sydney AP, then finishes at S34 E152 offshore. At 09Z (Fig. 7a), the isentropes, the proxy for streamlines, displayed only trapped lee waves with ripples vertically stacked up in the mid to upper-level troposphere. Between 10Z and 12Z, the wave crest over the foothills began to amplify, and a low-level jet emerged between 900 and 750 hPa on the lee side due to the flow separation in the mid-troposphere. At 14Z (Fig. 7b), the development of large-amplitude waves could be seen over the foothills west of Badgerys Creek between 800 and 600 hPa. On the lee side, the tongue of a low-level jet of 50–60 knots (~93–111 km h–1) became pronounced, and a bundle of tightly packed isentropes was observed between 900 and 800 hPa (1000–2000 m). Above the jet, a region of sparser isentropes with NW wind directions and weaker cross-barrier wind components was found between 750 and 600 hPa (2500–4200 m), hinting at the development of wave breaking. The low-level jet may have formed owing to the transition of the airflow in the low to mid level from tranquil to shooting at the ridgetop, which in theory occurs for Froude number (F) < 1 and >1 respectively (Durran 1990). At 15Z, large-amplitude mountain waves over the foothill became even more pronounced as the dipping of isentropes created a deep wave trough. Near the trough, the 305-K isentrope dropped ~1500-m altitude. With the amplification of mountain waves, the low-level jet strengthened to ~65–70 knots (~120–130 km h–1), and this is consistent with the low-level jet reaching the near-surface level by downward momentum transport. It coincided with the first wind surge at the near-surface level. At 16Z, a similar 1500-m dip of the 303-K isentrope from ~2000- to ~500-m altitude is seen east of Badgerys Creek, together with a tightly packed bundle of isentropes underneath the 303-K line over Sydney suburbs and nearby coastal water. The concentration of isentropes close to the ground is consistent with the maximum downward momentum transport at approximately this time, which agrees with the timing of the strongest wind gusts at Badgerys Creek and Camden. The position of the dip in the model indicates that the features in the ACCESS-C model were moving ahead of the actual unfolding of the event by ~15–30 min at this time step, which was a reasonable timing error in the Numerical Weather Prediction (NWP) system, enough to be useful for forecasting. Another notable feature at 16Z was a jump-like disturbance (hydraulic jump) of the isentropes ~30 km offshore from Sydney AP with a steep rise of ~1000 m from near-surface level. It contrasts with the cross section at 15Z, where the rise of the isentrope near-surface level was more gradual than sharp, indicating that the hydraulic jump fully developed by 16Z. The coastal winds further offshore on the eastern side of the jump decreased to 15–25 knots (~28–46 km h–1) as the shooting flow (F > 1) on the lee side transitioned back to tranquil flow (F < 1). The wave breaking also became apparent above the low-level jet and the hydraulic jump, with 305- and 306-K isentropes displaying wave overturning between 700 and 600 hPa east of Sydney AP. In contrast to all these developments below 600 hPa between 14Z and 16Z, the isentropes above 550 hPa remained non-turbulent, exhibiting flow separation from below. The only noticeable features above 550 hPa were long-wave components and general lee side deceleration in mid-level winds.
(a) ACCESS-C model vertical cross sections of winds and isentropes along the route oriented in the 100–280° direction following the wind direction in low to mid-troposphere, connecting Forbes, Badgerys Creek, Sydney A, and an offshore point S34 E152, at 09Z, 10Z and 12Z (20:00–23:00 hours the day before the event). The route is marked in a dashed black line in Fig. 1. Wind barbs represent the horizontal flow (1 knot = ~1.9 km h–1). The hatched blue area at the bottom of each cross-section indicates topography. Cross sections are from 06Z 30 October 2023 model run. (b) ACCESS-C model vertical cross sections of winds and isentropes along the same route as Fig. 7a, between 14Z and 17Z (01:00–04:00 hours on the day of SDWE). Cross sections are from 12Z 30 October 2023 model run.

At 17Z, the low-level jet is still visible at the near-surface level, with less tight bundling of isentropes, weaker wind speeds (50–55 knots, ~93–102 km h–1) within the jet and the hydraulic jump shifting further offshore. The column of the strongest 900–750-hPa winds, which corresponds to the surge of low to mid-level winds between 1200 and 3500 m in the profiler winds (Fig. 6), has also shifted offshore between the jump region and Sydney AP, which does not agree with the profiler wind observation at Sydney AP. Given that the actual surge moved through Sydney AP only after 18Z (Fig. 6), the ACCESS-C model was running at least 1 h ahead of the actual observations by this time. As a result, the ACCESS-C model failed to capture the whole duration of the event adequately and missed the second wind surge altogether. Nevertheless, the model captured the mesoscale features and their temporal evolutions well, offering useful additional insight.
4Theoretical investigation
4.1 Long equation and the assumption of quasi-steady condition
Although a high-resolution model like ACCESS-City can accurately depict mesoscale features and provide reliable forecast guidance, a theoretical investigation can provide further insight into the physics of downslope windstorms. Some generally accepted physical mechanisms include the optimal superposition of partially reflected gravity waves in a multi-layer structure atmosphere (or simply partial reflection) (Klemp and Lilly 1975), wave breaking or overturning of large-amplitude mountain waves and subsequent amplification of the surface drag due to the reflection at the critical level (Clark and Peltier 1977, 1984), and hydraulic jumps (Long 1954, Smith 1985, Durran and Klemp 1987; Smith and Sun 1987). Among these three theories, the hydraulic jump theory is the oldest and most intuitive owing to its direct analogy to hydraulics. Long (1954) was the first to point out the connection between the hydraulic jump exhibited by stratified fluid crossing a barrier and a downslope windstorm in the atmosphere. Provided the elevation of the mountain barrier does not vary rapidly and disregarding the contributions from short-wave components, the governing equation of the streamlines of stratified fluid is (Long 1953, 1955):
where u0, θ0 and are respectively the horizontal winds, ambient potential temperature and the static stability (Brunt–Väisälä frequency) in the upstream region, and δ = z – z0 is the vertical displacement of the streamline at z from its original position z0. The letter subscripts denote partial derivatives. The equation admits sinusoidal solutions when u0 is constant but is generally non-linear otherwise. Smith (1985) and Smith and Sun (1987) obtained an analytic solution of Eqn 1 for constant u0 by assuming a dividing streamline that divides a stable tropospheric layer from a fully turbulent layer, or so-called dead zone, where wave breaking and overturning occurs. The hydraulic model developed by Long (1954), Smith (1985) and Smith and Sun (1987) (or simply the hydraulic jump model from now on) is appealing owing to its analytic solutions and simplicity, yet its extension is desirable for two reasons. Firstly, the temporal variation terms would play a part when the synoptic system concerned is mobile or when there is a wind surge, which was the case with the SDWE. Secondly, they assume no upstream wind shear, but the inclusion of wind shear is important as it reduces the critical ridgetop height for the flow transition, as will be shown later.
To incorporate temporal variation terms, we assume a quasi-steady condition in the sense that the time-dependent terms are approximately related to the spatial terms by a travelling wave with phase velocity c in the x-direction, i.e.
In Eqn 2, u, w and ρ are respectively the horizontal and vertical velocities of the flow, and the density of air. The origin of the travelling wave may be due to the motion of the synoptic system, wind surge, or development of the synoptic systems concerned, but this will not be elaborated here. With limited information, the estimation of c has room for subjective interpretation. For SDWE, the vertical cross sections in Fig. 7b show the head of a hydraulic jump and its associated wind surge in the near-surface level travelling eastwards at 40–50 km h–1 between 15Z and 17Z. From this, c = 12.5 m s–1 appears to be a reasonable estimate for the event. Another justification for this choice comes from the position of the wave breaking during the event. As it turns out, the assumption of a quasi-steady state with phase speed c is crucial in obtaining the right altitude for a wave-induced critical level that agrees with the wind profiler observation (Fig. 6) and the model cross-sections (Fig. 7b). Additionally, wave breaking is a prerequisite for a free boundary condition δz = 0 along the dividing streamline in the hydraulic jump model. Therefore, these points need to be addressed before proceeding to the hydraulic jump model.
4.2 Linear wave model in a single-layer atmosphere
The position of the wave-induced critical level, which indicates where the wave breaking takes place, can be estimated from the solution of the linearised wave equations (Clark and Peltier 1977, Aihara and Hirasawa 1988). For this purpose, the linearised Eqn 1 in a single-layer atmosphere with a uniform shear σ ≅ 0.0022 s−1 and a uniform static stability N ≅ 0.012 s−1 are considered. The values of σ and N are based on the upstream cross barrier speeds U0 ≅ 20 m s–1 at the surface level and U1 ≅ 30 m s–1 at 550 hPa, and the mean static stability following the slope of the black broken line in Fig. 5a. With that,
Following the method employed by Aihara and Hirasawa (1988), the wave-induced first-order horizontal wind component u1 satisfying the Eliassen–Palm radiation condition (Eliassen and Palm 1960) is:
Note that Eqn 4 is a typical solution for stationary mountain waves, except that u1 and U0 are replaced by u1 − c and U0 − c respectively, owing to Eqn 2, which translates to the reduction of the resultant cross-barrier winds (effective cross-barrier winds) by c. Here, m(k) is the normalised spectral function of the topography, and Q(z, k) is a function that depends on ρ(z) and l(z), which is close to unity in the low to mid-troposphere. Further, l(z) is the Scorer parameter, l0 = 0.0016 m−1, and r = 0.18 is the ratio of shear to static stability, which is related to the upstream gradient Richardson number (Ri0) by . hM and B respectively are the ridgetop height and the half-width of the mountain range. The last step in Eqn 4 is based on the assumption that the predominant horizontal wavelength forced by the topography is Lx ~ 2B. As the elevation of Oberon and the surrounding area in the plateau is generally between 1100 and 1250 m, and the elevation of the western slopes of the GDR and the adjacent western plain is ~200–300 m, hM ~ 900 m is an appropriate estimation for the ridgetop height.
According to the Eliassen–Palm theorem in the context of stationary linear wave theory, the energy flux of stationary mountain waves in the vertical direction is proportional to u0, and the downward momentum flux is constant in the z-direction provided u0 is not zero (Eliassen and Palm 1960). If a travelling wave with phase speed c modulates the background flow, u0 needs to be replaced by u0 − c. Further, if u1 is comparable with the background flow itself, the level where u – c = u0 + u1 – c ≅ 0 constitutes a wave-induced critical level where the wave breaking occurs, resulting in zero wave-energy flux across the critical level and divergent momentum flux in the z-direction. The existence of a wave-induced critical level can be tested from the solutions of Eqn 4 and 5 at z = zc, where . Here, the subscript c stands for the locations where u1 attains a minimum u1 = NhM ≅ −11 m s–1. Hence, zc is the height where the wave-induced horizontal flow opposes the mean flow the most. Alternatively, the wave-induced critical level can be estimated by looking at the convective instability. The temperature profile may become locally convective owing to the modification of the lapse rate by wave motion. This may cause a reduction of local Richardson number (Ri) and wave overturning and promote a wave-induced critical level. The condition of convective instability is approximately:
Table 1 lists the calculated values of zc, u – c and dθ/dz from Eqn 4–6, at the ridgetop (πx/B = 0), foothill (πx/B = π/2) and on the lee (πx/B = π), when c = 12.5 m s–1 and when c = 0. Fig. 8 is a schematic diagram visualising the result of Table 1 when c = 12.5 m s–1. The left-hand columns in Table 1 (c = 12.5 m s–1) represent the current quasi-state model for SDWE, whereas the right-hand columns (c = 0 m s–1) are the classical steady-state model for comparison. In the first case with c = 12.5 m s–1, because both u – c and dθ/dz change signs between the foothill and the lee, it predicts the first appearance of the wave-induced critical level and wave breaking and overturning between the foothill and lee between 2700- and 1100-m altitudes (i.e. between the two zc values at the foothill and lee). Then, the wave-induced critical level splits into the upper and lower branches and cascades to the lee side, with the wave breaking and overturning region between the two (Fig. 8). This picture is consistent with the model cross-sections in Fig. 7b, which depict wave breaking above 1000 m and the tightening of the streamlines below 1000 m on the lee between 15Z and 18Z. It is also in line with the wind reversal seen in the profiler winds between 1300- and 1700-m altitudes between 18Z and 19Z (Fig. 6), consistent with rotor flow or wave overturning in the level. When c = 0, neither a critical level nor wave breaking is predicted owing to the strong prevailing westerly winds and the positive wind shear. Therefore, the positions where wave breaking occurred during SDWE support c = 12.5 m s–1.
| c | c = 12.5 m s–1 | c = 0 m s–1 | |||||
|---|---|---|---|---|---|---|---|
| Location (πx/B) | Ridgetop (0) | Foothill (π/2) | Lee (π) | Ridgetop (0) | Foothill (π/2) | Lee (π) | |
| ϕc | 3π/2 | π | π/2 | 3π/2 | π | π/2 | |
| zc (m) | 4670 | 2650 | 1140 | 12500 | 7080 | 3030 | |
| u0 (m s–1) | 30.4 | 25.9 | 22.4 | 47.8 | 35.6 | 26.7 | |
| u = u0 + u1 (m s–1) | 19.4 | 14.9 | 11.4 | 36.8 | 24.6 | 15.7 | |
| u – c (m s–1) | 6.9 | 2.4 | −1.0 | 36.8 | 24.6 | 15.7 | |
| dθ/dz (K km–1) | 1.70 | 0.79 | −0.44 | 3.39 | 3.04 | 2.59 | |
The condition u – c = 0 stands for the wave-induced critical level, and dθ/dz ≤ 0 means convective instability. The phase speeds c = 12.5 m s–1 (left) and c = 0 m s–1 (right) were chosen to represent SDWE and the classical model with steady forcing respectively.
A schematic diagram of the wave-induced critical level in the single-layer linear wave model. The far left side shows the mean upstream flow relative to the phase speed (u0 – c) and the wave-induced first-order horizontal flows (u1) on the ridge, foothill and lee. The combined horizontal flow (u – c = u0 + u1 – c) at various locations above an idealised topography is shown on the right. Estimated locations of the wave-induced critical levels (u – c = 0) are traced in broken red curves.

4.3 Hydraulic jump model
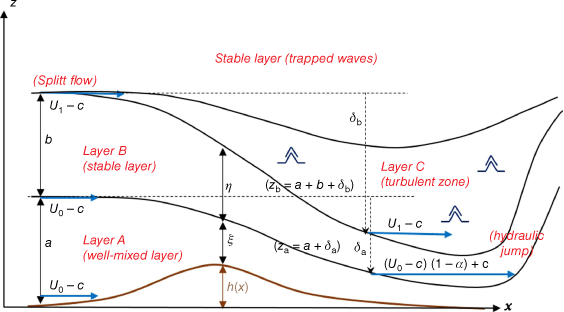
Having established the occurrence of wave breaking and the value of c, the hydraulic jump model will now be employed for further theoretical investigation. Fig. 9 is a schematic diagram of the two-layer atmosphere model adapted from Smith and Sun (1987). The model consists of three layers: A (boundary layer), B (stable tropospheric layer) and C (dead zone), all underneath a stable layer in the mid to upper troposphere, which is unaffected by flow transition in layers A and B. It is referred to as a two-layer model because only layers A and B are important for calculating the critical ridgetop height and the downslope wind speed, and their initial depths are denoted by a and b respectively. The streamlines z = za and z = zb originating from (za)0 = a and (zb)0 = a + b upstream mark the divisions between A and B, and between B and C respectively. In particular, a special term dividing streamline is used to designate z = zb as the model assumes the flow separation at (zb)0 = a + b (z = zb being the lower branch of the streamline), and wave breaking is assumed to occur in the region between these two splitting streamlines, forming a fully turbulent layer – the dead zone (layer C). The streamlines z = za and z = zb are displaced from their initial positions by δa = za − a and δb = zb – (a + b) respectively, as the flow accelerates downslope and plunges underneath layer C. The boundary conditions at the dividing streamline and the topography produce a relationship between δa, δb and h(x). For wave breaking and a hydraulic jump to occur, the actual ridgetop height (hM) should match the critical ridgetop height (hm) required for a hydraulic jump, that is, hm = max(h) imposed by the solution. If hM ≫ hm, the fluid is shooting (supercritical) both upstream and downstream, and neither wave breaking nor a hydraulic jump occurs, although some travelling waves (columnar disturbances) may propagate upstream (Long 1954; Lin and Wang 1996). If hM < hm, the fluid is tranquil (subcritical) and upstream blocking may occur. Wave breaking and a hydraulic jump may still occur with reduced intensity if the upstream Froude number is not too low compared with unity (Lin and Wang 1996).
A schematic diagram of a two-layer atmosphere system, adapted from Smith and Sun (1987). Layer A is a well-mixed boundary layer, and layer B is a stable layer. Layer C is a fully turbulent layer due to wave breaking and overturning. The dividing streamline z = zb is the lower branch of the streamline where flow separation occurs upstream at (zb)0 = a + b.
Let the upstream wind profile u0(z0) be constant in layer A and increase linearly in height in layer B (note that this is a slight modification of Eqn 3):
Also, the boundary layer (layer A) is assumed to be well mixed. Taking into account the reduction of the effective cross-barrier wind speed by c (Eqn 2) and substituting Eqn 7, 8 into Eqn 1, the Long equation becomes:
Once the solution is known, the horizontal wind speed is obtained from:
Turbulence in layer C implies uniformity of the mean density and the mean flow speed within it. With hydrostatic approximation, it translates to a free boundary condition along the dividing streamline z = zb (Eqn 11) (Smith 1985).
Other boundary conditions are the continuity of δ and δz at za = a + δa, and the matching boundary condition z = h(x) = δ(x, h(x)) at the topography.
By changing the variables and rescaling by Scorer’s parameter :
In Eqn 13, s and y are respectively the transformed vertical coordinates of the streamline at x and upstream (x → −∞).
With this, Eqn 9 in layer B becomes:
Eqn 14 is integrated numerically from the initial condition (s, y, ys) = (b̂ + δ̂b, b̂,1) to obtain zero for s and ys at y = 0, which we denote s0 and (ys)0 respectively. The value of δ̂a and its z derivative α = (δ̂a)ẑ are obtained from the continuity of the solution at z = za:
The solution of Eqn 9 in layer A is a linear function in z:
The topography h and the downslope wind speed ud in layer A are related to α by:
Although some differences exist between the assumptions of this model and the actual upstream vertical wind and temperature profiles of SDWE (Fig. 5a, b), the analysis focuses on a hypothetical daytime equivalence where a well-mixed boundary layer is assumed with a constant potential temperature of 299 K to 2500-m altitude (or to ~750 hPa) for the sake of simplicity. Based on Fig. 5a, b, and from the fact that the elevation of Forbes is ~250 m, we estimate a ≅ 2250 m, U0 ≅ 40 knots (~21 m s–1). Also, following the slope of the black dashed line in Fig. 5a for the mean static stability and the slope of the regression line in Fig. 5b (blue dotted line) for the wind shear, we estimate σ ≅ 0.0044 s−1, N ≅ 0.012 s−1, r ≅ 0.37 and l0 ≅ 0.0016 m−1. Note that N and l0 are unchanged from the earlier analysis of the single-layer linear model, whereas r and σ double this time owing to splitting the single layer into two layers with equal depth. The dashed lines in Fig. 5a, b reflect the simplified upstream conditions for layers A and B with these parameter values. Although a determination of the initial altitude of the dividing streamline (zb)0 = a + b is not straightforward, we take b ≅ 2250 m and U1 ≅ 60 knots = ~31 m s–1 based on a relative lull area of the wind speeds found between 4500 and 5000 m in the Sydney AP sonde observation (Fig. 5c). Interestingly, according to Eqn 5 in the single-layer linear model, this choice of the upstream altitude of the dividing streamline and splitting flow corresponds to a 1.47π radian phase shift, and it is also not far from zc = 4670 m over the ridgetop for c = 12.5 m s–1 in Table 1, where . This condition in SDWE agrees well with the optimal position of the critical level at upstream (λz, vertical wavelength of the gravity wave) for the resonant growth of waves by reflection at the critical level stipulated by Clark and Peltier (1984). From this observation, the condition of Klemp and Lilly (1975), that is, phase shift at the top of the layer for the optimal superposition of partially reflected gravity waves, appears inapplicable to SDWE.
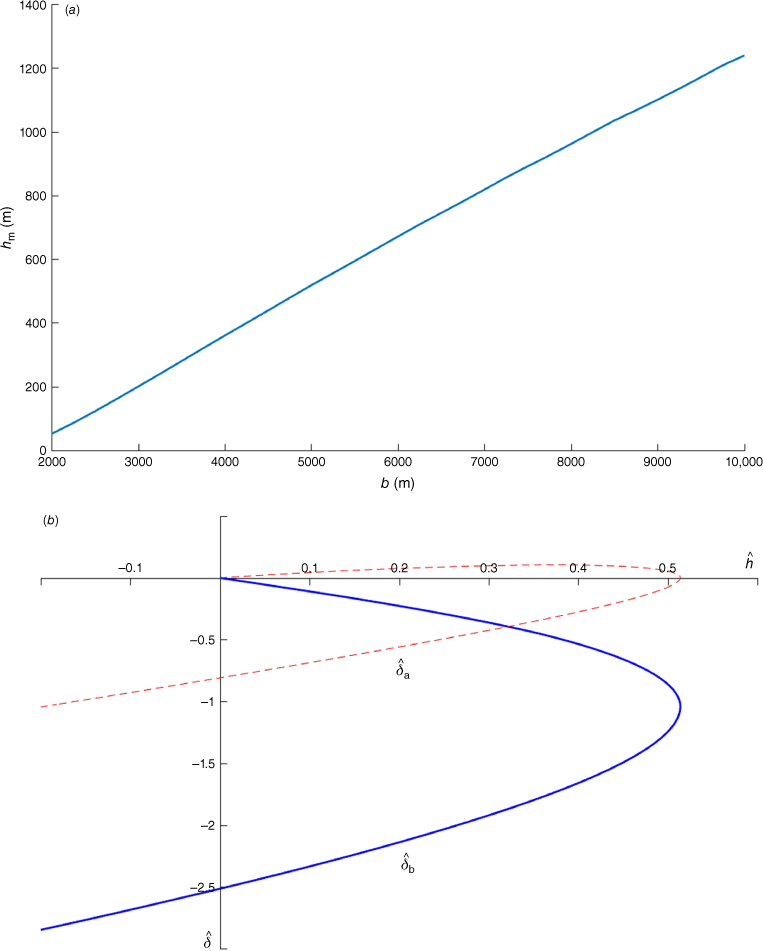
The values of the environmental parameters for SDWE now established, Eqn 14 and 16 can be integrated to obtain the critical ridgetop height. Fig. 10 is a plot of δ̂a and δ̂b as a function of ĥ, similar to fig. 3 of Smith and Sun (1987) in the context of SDWE. The plot covers the fourth quadrant and a portion of the third quadrant because they are the only physically meaningful ranges. The plot shows that the critical ridgetop height (i.e. the maximum ĥ where δ̂a,b branch out) was ĥm = 1.37, or hm = 854 m in metric measure, which agrees well with the actual ridgetop height hM = ~900 m. Alternatively, hm is a function of the upstream Froude number F0, so hm can be obtained independently. For this, we define the Froude number F (which was implicitly assumed in the preceding discussions) as follows:
Here, v̄ is the layer-mean wind speed relative to the phase speed c, H is the effective flow depth of the combined layers A and B in Fig. 9, g′ = N2b is the reduced gravity based on the density difference across layer B and α is as defined in Eqn 15. Their upstream values v̄0, H0 and F0 are given by:
Requiring F = 1 at the ridgetop, the relationship between hm and F0 is given by:
The plots of δ̂a (broken red) and δ̂b (solid blue) v. ĥ of SDWE from the hydraulic jump model, with c = 12.5 m s–1 and the idealised upstream wind/temperature profiles in Fig. 5a, b. The dash–dot black line indicates the elevation of the Sydney Metropolitan Area relative to the western slopes of the Great Dividing Range, as the elevation difference between the two regions corresponds to ĥ = −0.3 on the lee side. The critical ridgetop height for both δ̂a and δ̂b is ĥm = −1.37, which translates to hm = 854 m.

Both Long (1954) and Smith and Sun (1987) derived Eqn 22 assuming that the upstream wind profile is constant in height. Eqn 22 is still valid with reasonable accuracy when the shear is linear and not large, provided the modified parameters in Eqn 20 and 21 are used. A complete derivation of this method is provided in the Appendix.
For SDWE, with the environmental parameters U0 ≅ 20 m s–1, U1 ≅ 30 m s–1, c ≅ 12.5 m s–1, H0 ≅ 3375 m and N ≅ 0.012 s−1, Eqn 20 and 21 give ≅ 13.5 m s–1 and F0 ≅ 0.408. From these upstream parameter values, Eqn 22 yields the critical ridgetop height hm = 871 m, which agrees with the previous result of Fig. 10 within 2% accuracy.
Note that alternative definitions of F0 are also possible, and Eqn 23 is an example.
where hw is the critical height for the wave breaking rather than the flow transition. An advantage of Eqn 23 is that it affords a direct comparison with the flow regimes of non-structured fluid (i.e. single U and N) studied by Lin and Wang (1996). The upstream Froude number employed by Lin and Wang was , and this definition is equivalent to Eqn 23 when there is no ambient wind shear. Although the actual thresholds of wind regimes in SDWE may differ slightly from the thresholds given by Lin and Wang owing to the shear, it may be reasonable to assume that the findings of Lin and Wang would be largely valid when the shear is not large.
With hw ∼ hm ≅ 850 m and hM ≅ 900 m, Eqn 23 yields F̂0 ≅ 0.95, which falls into regime II (0.9 < F̂ < 1.12) of Lin and Wang. This regime is characterised by wave breaking above the lee, a jump-like disturbance (hydraulic jump) at the downstream edge of the wave breaking region and the absence of upstream blocking, which is consistent with the observations in SDWE. It is also the interval with the strongest surface drag, which is a proxy measure of the severity of downslope winds, and this reinforces that the wind speed observed in SDWE was the maximum attainable from the given environmental condition.
Having ascertained that the critical ridgetop height for a full hydraulic jump-like response was between 850 and 900 m during SDWE, an explanation of why the wind damage was concentrated in south-western Sydney (Camden, Badgerys Creek) during the event, and why wind speeds were relatively weaker in the far western end (Penrith) or the north-west corner (Richmond) of SMA, is offered as follows: as was seen in Fig. 1 and 3, the trajectory of downslope winds that reached south-western Sydney crossed the Oberon Plateau earlier, where the barrier height matched the critical ridgetop height for a hydraulic jump. However, the airstream that reached Penrith or Richmond crossed the Blue Mountains, which are generally 100 to 200 m lower than the Oberon Plateau. Hence, a hydraulic jump response was not fully realised along the latter path. Similarly, the elevation of the mountain barriers along the path reaching the Illawarra Coast was lower than the Oberon Plateau by 200–500 m, and the highest ridges were located well away from the Illawarra coastline. This explains why the Illawarra Coast, which typically experiences stronger westerly winds than Sydney from pressure-driven channelling, did not experience damaging westerly winds this time except for a couple of hours at a near-damaging threshold at Nowra. Hence, the topography of the Oberon Plateau made a significant difference to wind speeds between south-western Sydney and the surrounding region during the event.
Also, the agreement between the final downslope wind speed ud predicted by the hydraulic jump model and the observed wind speed during SDWE was remarkable. The elevation difference between the Western Slopes of the GDR (windward side) and SMA (lee side) translates to ĥ ≅ −0.3 on the lee side. The downslope wind speed in SMA is calculated from Eqn 18 at ĥ ≅ −0.3, yielding ud ≅ 37.8 m s–1 or 136 km h–1 (~73.5 knots) in layer A, which is 30% larger than the highest wind gust observed from 10-m winds during SDWE, but it is close to the maximum speed of the low-level jet seen in the upper air sounding (Fig. 5c) and the Sydney AP profiler winds (Fig. 6). Alternatively, ud on the lee can be expressed in terms of F0 if the elevation difference between the windward and lee sides is small compared with :
With U0 ≅ 20 m s–1, c ≅ 12.5 m s–1 and F0 ≅ 0.408 for SDWE, Eqn 24 gives ud ≅ 35.0 m s–1, which is within 8% of the numerical solution.
Smith (1985) suggested that the development of Kelvin–Helmholtz instability (KHI) at the top of the stable layer may reduce the actual downslope wind speed from the prediction of the hydraulic jump model. However, it is interesting to note that the supposed effect of KHI was inconsequential in SDWE. A clue is the Richardson number Ri in layer B, given by Eqn 25:
Any internal gravity wave becomes unstable when Ri < ¼ owing to the energy feed from shear (Miles 1961). Recalling that b̂ = ĥ ≅ −3.6 = 3.6, r = 0.37 in SDWE, and that r is related to the upstream Richardson number by (Eqn 13), Ri = ¼ is solved for δ̂b to identify the location where KHI first occur along the dividing streamline, as it is the supposed boundary of the turbulent region. Eqn 25 gives δ̂b ≅ −5.5, which is lower than the lowest value of δ̂b for ĥ > −0.3 in Fig. 10, implying that KHI was not initiated. Therefore, the flow maintained the condition Ri > ¼ along the dividing streamline. The reason is that the positive wind shear of the ambient flow acted in opposition to the negative wind shear arising from the downstream acceleration, reducing the resultant local wind shear and suppressing the energy feed to turbulent eddies.
4.4 Investigation of alternative cases
Similar numerical calculations were carried out for two alternative cases to investigate the contributions of the wind shear and the phase speed c. The first case is when the wind shear is set to zero whereas all other environmental parameters, including c, are kept unchanged. If the cross-barrier winds are constant U1 = U2 = Ū = 22.5 m s–1 (~44 knots) (this is the mean average wind speed across layers A and B in the original set-up), numerical calculation yields ĥm = −1.43, not far from the original value ĥm = −1.37 in Fig. 10. However, owing to the decrease in l, the metric value of the critical height increases to hm = 1193 m, ~340 m higher than the original and perhaps too high for the mountain ranges in the Central Tablelands. The critical ridgetop height hm would be the same as the original (~850 m) if Ū were to increase to 25.5 m s–1 (~50 knots). Therefore, given the relatively low mountain barriers of the Oberon Plateau, the wind shear was necessary to reduce the critical ridgetop height.
The second alternative case to investigate is when c = 0 and b increases freely so that layer B becomes a deep tropospheric layer. This scenario resembles the classical high-end wave-induced downslope windstorms in Boulder on the lee of the Rocky Mountains in the USA. Durran (1990) lists three circumstances that may lead to Boulder-style downslope windstorms: (1) large enough mountain height to induce breaking of mountain waves aloft; (2) Scorer parameter layering with the presence of a stable layer near ridgetop level; (3) capping by a mean-state critical layer. For case (1), as demonstrated by case c = 0 in Table 1, the topography of the Oberon Plateau is too low in the sense that the wave-induced wind component resulting from topography (u1 ≅ NhM ≅ 10 m s–1 ≅ 20 knots = ~11 m s–1) is insufficient to counter the strong ambient westerly winds with positive shear to produce a wave-induced critical level. The second possibility to consider is case 3. The same hydraulic jump model as in the previous section is used to locate the altitude of the mean-flow critical level, with the same environmental parameters as in SDWE, except that c = 0 and b varies freely. Recalling that N ≅ 0.012 s−1 and U0 ≅ 20 m s–1, the Scorer’s parameter is now l0 = U0 ≅ 0.0006 m–1. Shown in Fig. 11a is a plot of a plot of hm v. b under these conditions. The plot shows that hm does not exceed 1300 m even when b reaches near tropopause level at 10 km, confirming the earlier finding that ambient wind shear reduces the critical ridgetop height compared with a typical critical height of ~2000 m under no or little shear. From Fig. 11a, hm is approximately the same as in the original (~850 m) when b ≅ 7250 m and the depth of the combined tropospheric layers is a + b ≅ 9500 m. The only possibility of realising this case in SMA is when a north–south oriented upper-level jet creates a mean-flow critical level at ~9500-m altitude above the deep tropospheric layers with westerly winds, which seems unlikely in NSW from the author’s experience. However, the mean-flow critical level appears to be a major factor with easterly downslope winds in other parts of Australia, such as Adelaide gully winds in South Australia or Perth escarpment winds in Western Australia. Despite its remote chance in Sydney, further investigation of case 3 is worthwhile to see what to expect when Boulder-style downslope windstorms eventuate in SMA and how they compares with SDWE. Fig. 11b is the plot of δ̂a and δ̂b v. ĥ when b = 7250 m and c = 0. The graph shows ĥm ≅ 0.51, which still translates to the same critical height hm ≅ 850 m as in Fig. 10. The low value of ĥm is consistent with the findings of Durran and Klemp (1987), which reported strong downslope winds and strong pressure drag at ĥm as low as 0.4. The theoretical downslope wind speed calculated from Fig. 11b is ud ≅ 50 m s–1, ~33% higher than the previous cases with c = 12.5 m s–1. It is also interesting to note that the phase shift across the depth ~(a + b) ≅ 9500 m corresponds to 0.98π (rad) ≅ according to Eqn 5 when the linear model in a single-layer atmosphere (Section 4.2) is applied with l0 = 0.0006 m−1 and r = 0.37. Provided that either the mean-flow critical level or tropopause is located at this level, it will be the optimal condition for the superposition of partially reflected gravity waves as stipulated by Klemp and Lilly (1975). Therefore, under this condition, all three mechanisms, including partial reflection, wave breaking and a hydraulic jump, may work together to bring the downslope windstorm. Additionally, the outcome of this case is distinguished from the c = 12.5 m s–1 cases as the wave breaking takes place in the mid to upper-level of the troposphere rather than in the low to mid-level, as wave breaking first occurs in the upper troposphere or lower stratosphere before extending downwards to the mid-troposphere with Boulder-style windstorms (Clark and Peltier 1984).
(a) hm v. b when c = 0, otherwise the same environmental parameters are used as in Fig. 10. (b) A plot of δ̂a (broken red) and δ̂b (solid blue) v. ĥ, with c = 0 and b = 7250 m. The critical ridgetop height is ĥm = −0.51, which translates to hm = 857 m.
Case 2 appears to be a probable set-up for the majority of gale force winds on the peaks in the Australian Alps, as sustained gale force north-westerly winds are often observed, most notably at Thredbo Top station (elevation 1957 m), when a thermally stable layer or a strong inversion forms at the ridgetop level by pre-frontal warm air advection. The gale to storm force winds reaching the immediate lee of the Australian Alps as downslope windstorms are quite possible under such a setting, although it is difficult to verify owing to the sparsity of AWS in the area. In this kind of a multi-layer structure, optimal superposition of the partially reflected waves at the interface of the layers may lead to non-linear amplification of mountain waves and significantly stronger downslope windstorms than a single-layer structure if the depths of layers are rightly tuned (Klemp and Lilly 1975; Durran 1986). Shin et al. (2022) listed partial reflection, along with the hydraulic jump and the wave breaking, as the main causes of downslope windstorms on the lee of the Taebaek Mountains, which have similar mountain heights to the Great Dividing Range in south-east Australia. In view of these observations, the possibility of downslope windstorms in SMA by Case 2 leaves room for further investigation.
Besides consideration of the three circumstances listed in Durran (1990), Boulder-style downslope windstorms in SMA appear unfavourable from a synoptic consideration. The condition c = 0 implies completely stationary mountain waves arising from the slow change or movement of synoptic systems. With famous Boulder windstorms in the lee of the Rocky Mountains, strong cross-barrier winds are often seen maintained for 12–24 h with the slow movement of synoptic systems (Lilly 1978). Numerical simulations of high-end downslope windstorms also demonstrate that it takes at least 2–6 h, or more, to reach a high surface drag state under steady forcing (Clark and Peltier 1984, Durran 1986, Aihara and Hirasawa 1988). Strong westerly winds in central eastern NSW with aerological profiles similar to SDWE are usually caused by fast-moving frontal systems crossing south-east Australia in spring, and such conditions lasting more than 12 h in the region seem improbable owing to the mobility of the systems. Hence, a hypothetical Boulder-style downslope windstorm in Sydney appears unlikely.
5Conclusion
The Sydney downslope windstorm event (SDWE) during the early morning of 31 October 2023 was a moderately strong downslope windstorm event accompanied by significant temperature rises at night. The event was notable because it demonstrated that, despite the Oberon Plateau’s relatively low topography, the Sydney Metropolitan Area can still experience a foehn-type downslope windstorm when the atmospheric conditions are just right. One necessary condition is strong cross-barrier winds with linear wind shear within a stable layer upstream in the low to mid-level of the troposphere, which were provided by warm pre-frontal WNW airstreams during SDWE. Secondly, the cross-barrier wind speeds and the movement speed of the synoptic system (manifested by the phase speed of the disturbance) must be tuned so that the effective cross-barrier winds are just right to initiate wave breaking and a hydraulic jump.
The Sydney AP profiler wind observations and ACCESS-C model cross-sections all indicated the presence of a hydraulic jump and wave breaking in the low to mid-troposphere. Further mathematical analysis showed that these two mesoscale features worked together as the main driving mechanism for the downslope windstorm. The transition of the flow from tranquil to shooting over the ridgetop, coupled with the trapping of wave energy under the wave-induced critical level, caused the plunging of flow underneath the turbulent layer and subsequent downward momentum transport. This resulted in the formation of a strong low-level jet that reached the ground as a downslope windstorm. The agreement between the critical ridgetop height predicted by the hydraulic jump model and the barrier height of the Oberon Plateau was remarkable, highlighting the importance of the Oberon Plateau in the event. This was consistent with the concentrated wind damage in south-western Sydney during the event, including Campbelltown, Liverpool and Badgerys Creek. The hydraulic jump model’s prediction of the final downslope wind speed agreed well with the observed wind speed of the low-level jet during the event. This suggests that the positive wind shear of the ambient flow suppressed the development of KHI along the dividing streamline. Lastly, it was shown that classical Boulder-style downslope windstorms by slow-moving synoptic systems are unlikely in central eastern New South Wales from a synoptic and climatological viewpoint. It highlights the importance of the mobility of the synoptic systems in relation to the downslope windstorm potential in the Sydney Metropolitan Area.
Although the hydraulic jump model provides a useful insight into the mechanism of the Sydney Downslope Windstorm Event, its application to forecasting remains challenging and perhaps even impractical in its current form. The theory relies on at least two unknowns – the initial position of the dividing streamline (b) relative to the boundary layer and the phase speed (c) arising from the movement or development of the synoptic system – which can only be worked out in the post-event analysis. Therefore, a practical method of estimating these two unknowns will be the key to its future application for forecasting downslope windstorms. However, the reliable depiction of the event by ACCESS-City model cross-sections was remarkable, and this reiterates the importance of high-resolution models as the main forecasting tool for predicting windstorm events with 6–24 h lead time.
This paper focused only on a single event in the Sydney Metropolitan Area. Similar downslope windstorms may have been responsible for several severe wind events, extreme fire behaviours, or severe clear air turbulence in the past in other parts of south-east Australia, including the Australian Alps, the South Coast of NSW and Gippsland in Victoria, where the topography may be considered more favourable than Sydney. Wilke et al. (2022) showed that studies for downslope windstorms in the area have significant value for fire weather forecasting and public safety. Future research may look into documenting more case studies from past or future events and investigate the mesoscale mechanisms and synoptic patterns that led to those events. Shin et al. (2022) used 41 years of data to classify the synoptic patterns relevant to each generating mechanism of downslope windstorms in the Taebaek Mountains in South Korea. A similar study could be conducted to classify the synoptic patterns conducive to various types of topographically enhanced flows in south-east Australia, including foehn-type downslope winds (SDWE being an example) and channelling flow through the known corridors like Hunter Valley or Goulburn corridor in NSW (Webb and Park 2023).
Data availability
The surface observation data from AWS and the upper air sounding data at Sydney AP that support this study were obtained from the Bureau of Meteorology, Australia. They are available either free of charge from the Bureau of Meteorology website (see http://www.bom.gov.au) or can be requested with charge at cost recovery basis (see http://www.bom.gov.au/climate/data-services/station-data.shtml). The ERA5 reanalysis data that support this study were obtained from the climate datastore of COPERNICUS/ECMWF (see https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-pressure-levels?tab=overview).
Acknowledgements
I express my deep gratitude to Dr Kevin Tory of The Bureau of Meteorology and Assoc. Prof. Jung-Hoon Kim of Seoul National University for their valuable suggestions and comments. A significant improvement in this work was possible because of their feedback.
References
Aihara M, Hirasawa M (1988) On severe downslope wind due to the mountain wave-induced critical level. Papers in Meteorology and Geophysics 39, 59-77.
| Crossref | Google Scholar |
Bureau of Meteorology (2016) BNOC Operations Bulletin Number 105: APS2 Upgrade to the ACCESS-G Numerical Weather Prediction System. 16 March 2016. (Bureau National Operations Centre, The Bureau) Available at http://www.bom.gov.au/australia/charts/bulletins/APOB105.pdf.
Bureau of Meteorology (2019) NOC Operations Bulletin Number 125: APS3 upgrade of the ACCESS-G/GE Numerical Weather Prediction system. 20 October 2019. (National Operational Centre, The Bureau) Available at http://www.bom.gov.au/australia/charts/bulletins/opsbull_G3GE3_external_v3.pdf
Clark TL, Peltier WR (1977) On the evolution and stability of finite-amplitude mountain waves. Journal of the Atmospheric Sciences 34, 1715-1730.
| Crossref | Google Scholar |
Clark TL, Peltier WR (1984) Critical level reflection and the resonant growth of non-linear mountain waves. Journal of the Atmospheric Sciences 41, 3122-3134.
| Crossref | Google Scholar |
Durran DR (1986) Another look at downslope windstorms. Part I: the development of analogs to supercritical flow in an infinitely deep, continuously stratified fluid. Journal of the Atmospheric Sciences 43, 2527-2543.
| Crossref | Google Scholar |
Durran DR (1990) Mountain waves and downslope winds. AMS Monograph 23, 59-83.
| Google Scholar |
Durran DR, Klemp JB (1987) Another look at downslope windstorms. Part II: non-linear amplification beneath wave-overturning layers. Journal of the Atmospheric Sciences 44, 3402-3412.
| Crossref | Google Scholar |
Eliassen A, Palm E (1960) On the transfer of energy in stationary mountain waves. Geofysiske Publikasjoner 22(3), 1-23.
| Google Scholar |
Hersbach H, et al. (2020) The ERA5 global reanalysis. Quarterly Journal of the Royal Meteorological Society 146, 1999-2049.
| Crossref | Google Scholar |
Kepert JD (2017) Mountain waves and extreme fire behaviours. Fire Australia 2017(2), 22-24.
| Google Scholar |
Klemp JB, Lilly DK (1975) The dynamics of wave-induced downslope winds. Journal of the Atmospheric Sciences 32, 320-339.
| Crossref | Google Scholar |
Lilly DK (1978) A severe downslope windstorm and aircraft turbulence event induced by a mountain wave. Journal of the Atmospheric Sciences 35, 59-77.
| Crossref | Google Scholar |
Lin YL, Wang TA (1996) Flow regimes and transient dynamics of two-dimensional stratified flow over an isolated mountain ridge. Journal of the Atmospheric Sciences 53(1), 139-158.
| Crossref | Google Scholar |
Long RR (1953) Some aspects of the flow of stratified fluids, I. A theoretical investigation. Tellus 5, 42-58.
| Crossref | Google Scholar |
Long RR (1954) Some aspects of the flow of stratified fluids, II. Experiments with a two-fluid system. Tellus 6, 97-115.
| Crossref | Google Scholar |
Long RR (1955) Some aspects of the flow of stratified fluids, III. Continuous density gradients. Tellus 7, 341-357.
| Crossref | Google Scholar |
Miles JW (1961) On the stability of heterogeneous shear flows. Journal of fluid Mechanics 10, 496-508.
| Crossref | Google Scholar |
Park J-R, Kim J-H, Shin Y, Kim S-H, Chun H-Y, Jang W, Tsai C-L, Lee G (2022) A numerical simulation of a strong windstorm event in the Taebaek Mountain Region in Korea during the ICE-POP 2018. Atmospheric Research 272, 106158.
| Crossref | Google Scholar |
Shin Y, Kim J-H, Chun H-Y, Jang W, Son S-W (2022) Classification of synoptic patterns with mesoscale mechanisms for downslope windstorms in Korea using a self-organizing map. Journal of Geophysical Research: Atmospheres 127, e2021JD35867.
| Crossref | Google Scholar |
Smith RB (1985) On severe downslope winds. Journal of the Atmospheric Sciences 42, 2597-2603.
| Crossref | Google Scholar |
Smith RB, Sun J (1987) Generalised hydraulic solutions pertaining to severe downslope winds. Journal of the Atmospheric Sciences 44, 2934-2939.
| Crossref | Google Scholar |
Webb C, Park J (2023) Channelling flows in the Hunter Valley. Journal of Southern Hemisphere Earth Systems Science 73, 194-211.
| Crossref | Google Scholar |
Wilke D, Kepert JD, Tory KJ (2022) The meteorology of the Tathra Bushfire. Weather and Forecasting 37, 581-600.
| Crossref | Google Scholar |
Appendix
Defining the Froude number as the ratio of the flow speed (u) to the phase speed of the shallow-water gravity waves (H, flow depth), Long (1954) derived a relationship between the critical barrier height hm and the upstream Froude number F0 of a single fluid layer system (the subscript 0 denotes the upstream values).
The condition of the critical height is equivalent to F = 1, implying the flow transition from tranquil (F < 1) to shooting (F > 1) at the ridgetop. Smith and Sun (1987) proved that Eqn A1 is also valid in a two-layer system consisting of a well-mixed lower layer (layer A) and a thin, stable upper layer (layer B) subject to the free boundary condition at the top of B if the upstream flow speed u0 is constant in both layers, and g is replaced by the reduced gravity . Fig. 9 is the schematic diagram adapted from Smith and Sun (1987). They further claimed without proof that Eqn A1 can be extended to the general two-layer system in a surprisingly accurate fashion even if the upper layer is not thin, provided H0 is replaced by the effective altitude Heff = a + γb, where a and b are the layer depths in Fig. 9 and γ = 0.5 ± 0.05 over most of the parameter ranges. In summary, the claim is that layer B can be compressed to a thin layer at the mean altitude with equal density difference while layer A is expanded to Heff to produce a physically equivalent system. Although the claim seems plausible, it may be worthwhile revisiting Smith and Sun’s proof to give more rigorous proof while expanding the problem to include wind shear in layer B. Here, layer B does not need to be thin, provided an approximation by bulk-mean values of the layer is acceptable. Also, c is set to be zero for now, and its inclusion will be discussed at the end. Integrating Eqn 14:
Here, α = (δa)z is the derivative of δ at z = za, η = zb − zb = b + δb − δa is the depth of layer B, and y̅ is the centroid of the layer B upstream. Hats denote the quantities scaled by Scorer’s parameter .
Noting that ys = 1 − δz, the integration of dy across layer B and the requirement of mass conservation for layer A with its depth ξ = za – h = a + δa − h yield:
Defining the mean displacement , and letting u̅ = U0(1+ry̅) be the upstream wind at the centroid level, we recover a version of the Bernoulli Eqn given by Smith and Sun (1987),
where g′ = N2b is the reduced gravity. As δa = h + ξ − a and δb = h + ξ + η − a − b,
Here, is the mean altitude of layer B upstream, and we define to be the effective flow depth of the combined layers A and B. Although the ratio of to its preceding term is non-negligible, taking up the value of one-sixth in the upstream region (α → 0) if a and b are equal, this ratio decreases downstream as |α| increases. Also, the absolute value of ε vanishes upstream as |α| → 0. Hence, ε will be omitted as it greatly simplifies mathematics. Defining the upstream Froude number and substituting the above expression of δ̅ to Eqn A5 yields:
Provided that the elevation difference between the windward side and the lee side is small compared with H0, Eqn A6 is solved for to obtain αl and ud on the lee:
Also, differentiating Eqn A6 by α, the condition for the critical ridgetop height is:
If we introduce the effective flow speed of the system ū = ū0(1 − α), and use a subscript m to denote the critical values, the above condition at the critical ridgetop height reduces to:
Note that Eqn 22, A1 and A11 are all identical. This proves the validity of the original equation of Long (1954) in the two-layer model (Fig. 9), as well as the claim of Smith and Sun (1987) that a thick stable layer may be approximated by a thin density interface of equal strength located at the mean position.
Here, u̅ is not to be confused with the bulk mean flow speed of layer B, which is . Rather, it is the flow speed of the boundary layer if layer B is compressed into a thin layer with upstream wind speed u̅0 at the interface between layers A and B.
Returning to the calculation of the centroid, we note that, as s → y upstream:
As ,
It reduces to u̅0 = U0 when r = ΔU0 / Nb → 0. Despite several approximations made through the steps, the values of hm thus obtained appear to be in reasonable agreement with those obtained by numerical integration when r is not large. For example, when a = b = 2250 m, U0 = 7.5 m s–1, the difference is within 5% if 0 ≤ r ≤ 0.5. However, the method becomes unreliable if r > 0.5, as it predicts significantly smaller values for hm. Lastly, for a quasi-steady case where c is non-zero, U0 and U1 in Eqn A12 need to be replaced by wave-relative flow speeds U0 − c and U1 − c respectively. This will alter u̅0 and F0, yet r is unchanged, and the main Eqn A11 remains valid. For example, because c = 12.5 m s–1 in SDWE, U0 = 20 m s–1 and U1 = 30 m s–1 need be replaced by U0 – c = 7.5 m s–1 and U1 – c = 17.5 m s–1 in Eqn A12. With these values, Eqn A10 and A11 yield F0 = 0.408 and hm = 871 m. Eqn A8 is also modified to:
Eqn A13 gives ud = 35.0 m s–1 for the parameter values above, close to the maximum speed of the low-level jet observed during the SDWE.

