Additive main effects and multiplicative interaction for grain yield of rice (Oryza sativa) genotypes for general and specific adaptation to salt stress locations
S. L. Krishnamurthy A * , B. M. Lokeshkumar A , Suman Rathor A , A. S. Warraich A , N. M. Vinaykumar B and P. C. Sharma A *
A * , B. M. Lokeshkumar A , Suman Rathor A , A. S. Warraich A , N. M. Vinaykumar B and P. C. Sharma A *
A
B
Handling Editor: Mohd. Kamran Khan
Abstract
Salt stress is one of the major, ever-increasing abiotic stresses that hinders rice production across arable land around the world. In order to sustain the production of rice (Oryza sativa) in these salt-affected areas, high-yielding stable salt tolerant genotypes must be identified.
The additive main effects and multiplicative interaction (AMMI) model was carried out to identify high-yielding stable rice genotypes under both saline and alkali stress.
Nineteen promising rice genotypes including five standard checks were evaluated using randomized block design under nine salt stress environments using three replications in 2017 and 2018.
The AMMI model II is thought to be the best model for genotype identification based on prediction accuracy with high GEIS and low GEIN (genotype and environment interaction noise). According to AMMI model II, six genotypes were identified as the top performers under salt stress: one genotype (CSR RIL-01-IR 165) yielded the best in three environments; another genotype (CSR 2711-17) yielded highly in in two environments; and the remaining three genotypes (RP5989-2-4-8-15-139-62-6-9, RP 6188-GSR IR1-8-S6-S3-S1, RP6189-HHZ17-Y16-Y3-SAL1) as well as one control genotype (CHK2) yielded well in single environments.
Based on AMMI stability study, genotypes RP5989-2-4-8-15-139-62-6-9, CSR2711-17, CSR RIL-01-IR 165, CSR-2748-4441-195, CSR-2748-4441-193), and CSRRIL-01-IR 75 were determined to be higher yielding and more stable than the national control genotype (CSR23).
The high-yielding stable genotypes identified in this study could be planted for salt-affected areas to sustain the production of rice.
Keywords: adaptation, alkalinity, AMMI, G × E interaction, mega environments, rice, salinity, stability.
Introduction
Soil health degradation has a direct negative impact on agricultural production across the globe. The GSASmap (Global Salt Affected Soil map) reported that more than 424 million ha of topsoil (0–30 cm) and 833 million ha of subsoil (30–100 cm) are salt-affected (FAO and ITPS 2015). The rising problem of salt stress is a serious threat to the production in salt-sensitive crops like rice (Oryza sativa). Approximately one-third of the irrigated rice-growing areas encounter salinity issues. A recent study shows that each day around 2000 ha of cultivable land are losing their productivity due to salinization (Shahid et al. 2018). The ICAR-Central Soil Salinity Research Institute (CSSRI) has categorized 6.7 million ha (Mha) in India as salt-affected, with 3.8 Mha classified as alkali and 2.9 Mha as saline, posing a severe threat to the livelihood security of the farming community. According to Sharma et al. (2015), salt-affected soils cause India to lose 16.84 million tonnes of crop output (including cereals, oilseeds, pulses, and cash crops) annually, resulting in estimated economic losses of Indian Rupee (INR)230 billion. Salinity causes osmotic stress in rice plants by disrupting their morphological and physiological balance, especially at the seedling and reproductive stage, which results in poor growth and reduced grain yield. Grain yield reductions range from 27% to 50% at an electrical conductivity (ECe) of 8 dS m−1 across various rice cultivars (Mohammadi et al. 2013). It is estimated that for every increase of one unit in electrical conductivity (ECe) beyond the threshold of 4 dS m−1, there is a 12% reduction in grain yield, and under extreme saline conditions, yields can plummet to zero, leading to plant death. Farm income declines with rising salt levels, with annual potential and actual losses per hectare reaching INR10,714 and INR7737, respectively, due to the adverse effects of salt. Therefore, continuous efforts are underway to tackle this issue using various approaches like soil reclamation and the adoption of more tolerant crop species. However, these methods face constraints due to economic factors associated with reclamation, nutritional requirements, and the marketability of alternative crops. The problem of salinity and alkalinity has been addressed through better management practices and by introducing salt-tolerant varieties that harvestable performance in soils with variable salt concentrations (Krishnamurthy et al. 2021). Globally, numerous salt-tolerant rice varieties have been developed and released for cultivation to address the challenges posed by saline soils. The pioneering variety, Pokkalli, was introduced in 1939 from Ceylon (now Sri Lanka), marking the beginning of efforts to breed rice capable of thriving in saline conditions. India and the Philippines have made significant contributions by developing several salt-tolerant rice varieties, including Kala Rata 1–24, Nona Bokra, Bhura Rata, SR 26B, Chin.13, and 349 Jhona. Additionally, Bangladesh, Thailand, Japan, the United States, South Korea, and Russia have each developed various salt-tolerant rice varieties (Qin et al. 2020). In India, the ICAR-Central Soil Salinity Research Institute (CSSRI) in Karnal has been exclusively focused on the development of salt-tolerant rice varieties. Their efforts have resulted in the release of approximately 13 such varieties including CSR 10, CSR 13, CSR 23, CSR 27, Basmati CSR 30, CSR 36, CSR 43, CSR 46, CSR 49, CSR 52, CSR 56, CSR 60, and CSR 76, which have significantly contributed to agricultural productivity in the country’s saline regions (Krishnamurthy et al. 2024).
Rice yield is a complex trait influenced by genotypes, environment, and the interaction of both. Hence, the evaluation of lines for grain yield across the different ranges of salt stress environments is crucial for the development of farmers’ accepted salt-tolerant varieties (Krishnamurthy et al. 2017). These kinds of trials are called multi-environmental trials (METs) and they help in quantifying Genotype × Environment interaction (GEI) with the help of various statistical methods (Sa’diyah and Hadi 2016). These trials are very informative as all the components of variability viz genotype, environment, and their interaction effect can be studied. In addition, GEI leads ranking of different genotypes across the environments (de Leon et al. 2016). Earlier biometricians explained GEI in a single dimension with the help of ANOVA and linear regression (Finlay and Wilkinson 1963; Eberhart and Russell 1966; Perkins and Jinks 1968). However, complex GEI occurs in nature, which can now be explained by biplot-based methods; namely, genotype main effect, genotype × environment (GGE) (Yan et al. 2000; Yan and Rajcan 2002), and Additive Main effects and Multiplicative Interactions (AMMI) (Gauch 1992).
AMMI analysis serves as a more accurate model to understand genotype-environment interactions. It combines the univariate technique of ANOVA with PCA-based multivariate analysis to find out GEI thereby significantly improving the probability of successful identification of stable genotypes. In the case of METs related to salt tolerance in rice, several researchers have successfully used AMMI analysis in pursuit of identifying stable salt-tolerant genotypes (Krishnamurthy et al. 2015, 2016a; Islam et al. 2016). In this study, the AMMI model was used to analyze the data generated from screening of 19 rice genotypes across nine salt-affected environments to identify stable rice genotypes for salt stress and to process the delineation of environments into mega-environments.
Materials and methods
Plant materials and testing locations
The study evaluated 14 advanced rice (Oryza sativa L.) lines developed for salt-affected soils, alongside five check varieties (Table 1). Among these FL 478, CSR 23, Jaya, CSR 36 and CSR 10 were salt-tolerant checks, while Jaya served as a salt-sensitive check. The genotypes were evaluated in salt-stressed microplotsat Karnalwith a plot area of 0.6 m2 and spacing of 20 cm × 15 cm (N = 20), as well as in salt-affected farmer fields with an area of 5 m2 and spacing of 20 cm × 20 cm (N = 125). The experiments were laid out in a Randomized Complete Block Design (RCBD) with three replications across all environments. The experiment spanned two consecutive years: (1) kharif 2017–2018 across four salt stress environments (saline micro plot in Karnal, Haryana; sodic microplot in Karnal, Haryana; sodic farmer’s field in Gautam Buddha Nagar, UP; and sodic field in Lucknow, UP); and (2) kharif 2018–2019 across five salt stress environments (saline microplot in Karnal, Haryana; sodic microplot in Karnal, Haryana; sodic field in Kurukshetra, Haryana; sodic farmer’s field in Gautam Buddha Nagar, UP; and sodic field in Lucknow, UP) (Table 2). Stress conditions were induced in the microplots through the application of various salts in appropriate proportion. The electrical conductivity of the saline microplots (ECe ~8.0 dS m−1) was maintained by irrigating with a saline solution (7 NaCl : 1 Na2SO4 : 2 CaCl2) twice a week. The desired soil pH of the microplots (pH ~9.7–9.8) was achieved using sodium bicarbonate (NaHCO3) and sodium carbonate (Na2CO3) solutions. In field conditions, irrigation was administered at appropriate intervals as recommended by agronomic best practices. Soil salinity, indicated by ECe (8.0 dS m−1) and alkalinity by pH 9.5–9.8, was measured before transplanting, at maturity, and post-harvest (Table 2). Grain yield data were recorded on a plot basis and converted to kg ha−1. Data from nine environments were analyzed using AMMI to identify the most stable and salt-tolerant genotypes.
| Genotype number | Genotype code | Name of the genotypes | |
|---|---|---|---|
| 1 | GN01 | CSR 2711-17 | |
| 2 | GN02 | RP 6185-GSR IR 1-5-S14-S2-Y1 | |
| 3 | GN03 | CSR RIL-01-IR 75 | |
| 4 | GN04 | RP 6276-GSR IR1-12-S8-Y1-Y2 | |
| 5 | GN05 | CSR-2748-4441-195 | |
| 6 | GN06 | RP 6112-MS-T193-5-22-55-33-1-3 | |
| 7 | GN07 | TR 13083 | |
| 8 | GN08 | RP 6189-HHZ 17-Y16-Y3-SAL1 | |
| 9 | GN09 | RNR 11718 | |
| 10 | GN10 | CSR RIL-01-IR 165 | |
| 11 | GN11 | CSR-2748-4441-193 | |
| 12 | GN12 | RP 6188-GSR IR1-8-S6-S3-S1 | |
| 13 | GN13 | RP 6265-GSR IR 1-5-S12-D3-Y2 | |
| 14 | GN14 | RP 5989-2-4-8-15-139-62-6-9 | |
| 15 | CHK1 | FL 478 | |
| 16 | CHK2 | CSR 23 | |
| 17 | CHK3 | Jaya | |
| 18 | CHK4 | CSR 36 | |
| 19 | CHK5 | CSR 10 |
| Location number | Location code | Location | Latitude and longitude | Year | Stress type | Av. ECe (dS m−1) | Av. pH | Month | No. of days with rain | Total rainfall (mm) | Avg. max. temp. (°C) | Avg. min. temp. (°C) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | E1 | Saline microplot CSSRI, Karnal, Haryana | 29°42′N, 76°57′E | 2017 | Saline | 8 | 7.5 | June | 9 | 237.1 | 36.8 | 24.7 | |
| July | 9 | 112 | 33.6 | 26.4 | |||||||||
| August | 7 | 239.9 | 32.7 | 25.5 | |||||||||
| September | 5 | 247.6 | 32.7 | 22.6 | |||||||||
| October | 0 | 0 | 32.9 | 16.7 | |||||||||
| November | 0 | 0 | 25.1 | 10.3 | |||||||||
| Total/Range | 30 | 836 | 25.1–36.8 | 10.3–26.4 | |||||||||
| 2 | E2 | Sodic microplot CSSRI, Karnal, Haryana | 29°42′N, 76°57′E | 2017 | Alkaline | 1.2 | 9.6 | June | 9 | 237.1 | 36.8 | 24.7 | |
| July | 9 | 112 | 33.6 | 26.4 | |||||||||
| August | 7 | 239.9 | 32.7 | 25.5 | |||||||||
| September | 5 | 247.6 | 32.7 | 22.6 | |||||||||
| October | 0 | 0 | 32.9 | 16.7 | |||||||||
| November | 0 | 0 | 25.1 | 10.3 | |||||||||
| Total/Range | 30 | 836 | 25.1–36.8 | 10.3–26.4 | |||||||||
| 3 | E3 | Sodic field Gautam Buddh Nagar, Uttar Pradesh | 28.3383°N, 77.6078°E | 2017 | Alkaline | 1.2 | 9.6 | June | 2 | 35 | 36.4 | 24 | |
| July | 6 | 112 | 32.7 | 24.8 | |||||||||
| August | 11 | 243 | 32.1 | 24.9 | |||||||||
| September | 5 | 246 | 32.85 | 21.62 | |||||||||
| October | – | – | 31.9 | 16.3 | |||||||||
| November | – | – | 26.5 | 10.8 | |||||||||
| Total/Range | 23 | 636 | 26.536.4 | 10.8–24.9 | |||||||||
| 4 | E4 | Sodic field Lucknow, Uttar Pradesh | 26°47′N, 80°46′E | 2017 | Alkaline | 1.2 | 9.8 | June | 4 | 48.3 | 39.2 | 23.1 | |
| July | 19 | 213.5 | 31.9 | 21.6 | |||||||||
| August | 15 | 356.1 | 33 | 21.9 | |||||||||
| September | 5 | 60.6 | 34.5 | 21.3 | |||||||||
| October | 0 | 0 | 34.1 | 16.2 | |||||||||
| November | 0 | 0 | 27.8 | 8.5 | |||||||||
| Total/Range | 43 | 678 | 27.8–39.2 | 8.5–23.1 | |||||||||
| 5 | E5 | Saline microplot CSSRI, Karnal, Haryana | 29°42′N, 76°57′E | 2018 | Saline | 8 | 7.5 | June | 6 | 168.9 | 36.9 | 25.3 | |
| July | 8 | 281.5 | 33.7 | 25.9 | |||||||||
| August | 5 | 207.9 | 32.7 | 25.4 | |||||||||
| September | 7 | 185.2 | 31.2 | 22.7 | |||||||||
| October | 0 | 0 | 30.9 | 15.9 | |||||||||
| November | 0 | 0 | 27 | 10.9 | |||||||||
| Total/Range | 26 | 843.5 | 27.0–36.9 | 10.9–25.9 | |||||||||
| 6 | E6 | Sodic microplot CSSRI, Karnal, Haryana | 29°42′N, 76°57′E | 2018 | Alkaline | 1.2 | 9.8 | June | 6 | 168.9 | 36.9 | 25.3 | |
| July | 8 | 281.5 | 33.7 | 25.9 | |||||||||
| August | 5 | 207.9 | 32.7 | 25.4 | |||||||||
| September | 7 | 185.2 | 31.2 | 22.7 | |||||||||
| October | 0 | 0 | 30.9 | 15.9 | |||||||||
| November | 0 | 0 | 27 | 10.9 | |||||||||
| Total/Range | 26 | 843.5 | 27.0–36.9 | 10.9–25.9 | |||||||||
| 7 | E7 | Sodic field Gautam Buddh Nagar, Uttar Pradesh | 28.3383°N, 77.6078°E | 2018 | Alkaline | 1.2 | 9.6 | June | 4 | 48.1 | 38.5 | 25 | |
| July | 15 | 494.5 | 33.7 | 25 | |||||||||
| August | 8 | 209.9 | 33 | 25.5 | |||||||||
| September | 9 | 180.4 | 41.7 | 23.5 | |||||||||
| October | 1 | 4 | 31.5 | 17.2 | |||||||||
| November | – | 1.3 | 26.9 | 12.1 | |||||||||
| Total/Range | 37 | 938.2 | 26.9–41.7 | 12.1–25.5 | |||||||||
| 8 | E8 | Sodic field Lucknow, Uttar Pradesh | 26°47′N, 80°46′E | 2018 | Alkaline | 1.2 | 9.8 | June | 4 | 48.1 | 38.5 | 25 | |
| July | 15 | 494.5 | 33.7 | 25 | |||||||||
| August | 8 | 209.9 | 33 | 25.5 | |||||||||
| September | 9 | 180.4 | 41.7 | 23.5 | |||||||||
| October | 1 | 4 | 31.5 | 17.2 | |||||||||
| November | – | 1.3 | 26.9 | 12.1 | |||||||||
| Total/Range | 37 | 938.2 | 26.9–41.7 | 12.1–25.5 | |||||||||
| 9 | E9 | Farmer field Kurukshetra, Haryan | 29.9695°N, 76.8783°E | 2018 | Alkaline | 1.2 | 9.5 | June | 7 | 167.9 | 36.9 | 22.3 | |
| July | 7 | 280.5 | 33.6 | 24.9 | |||||||||
| August | 6 | 205.9 | 32.7 | 24.4 | |||||||||
| September | 6 | 186.2 | 32.7 | 21.6 | |||||||||
| October | 0 | 0 | 32.9 | 15.8 | |||||||||
| November | 0 | 0 | 24.1 | 10.9 | |||||||||
| Total/Range | 26 | 840.5 | 24.1–36.9 | 10.9–24.9 |
Data analysis
The statistical analysis was done using the AMMISOFT and MATMODEL ver. 3 statistical package (Gauch 2008; Gauch 2013). AMMI analysis forms a series of model families and then identifies the best family with the help of the FR test (Cornelius 1993). Using analysis of variance (ANOVA), it splits the variations into three components: (1) genotype (G); (2) environment (E); and (3) genotype × environment interaction (GEI) It also applies singular value decomposition (SVD) or principal component analysis (PCA) to GE after removing the genotypic effect. AMMI1 biplot and IPC1 were used to interpret the results of the AMMI model and to analyze the stability of genotypes and the interaction between genotypes and environments. An IPC1 score of zero determines the stability of a genotype in multiple environments, and a negative or positive IPC1 score is proportional to the specific adaptation of genotypes to the environments. AMMI model equation explains the analysis of variance (ANOVA) and principal component analysis as:
where Yge is the yield of genotype g in environment e, μ is the grand mean, αg is the genotype deviation from the grand mean, βe is the environment deviation, λn is the singular value for IPC n and correspondingly λn2 is its eigenvalue, γgn is the eigenvector value for genotype g and component n, δen is the eigenvector value for environment e and component n, with both eigenvectors scaled as unit vectors, and ρge is the residual. The interaction scores are commonly scaled as λn0.5γgn and λn0.5δen so that their products estimate interactions directly, without the need of yet another multiplication by λ.
Model diagnosis
To select the most suitable AMMI family, the analysis employed model diagnosis and accuracy gain (accurate for forecasting the actual means) as explained by Ebdon and Gauch (2002a, 2002b) and Gauch (2013). Using 171,000 validations with the 171 treatment real data, the actual root mean square predictive differences (RMS PD) were calculated. Model diagnosis and accuracy improvement were conducted using AMMISOFT (Gauch 2013) and MATMODEL ver. 3 (Gauch 2008). Robustness tests, such as the Gollob F-test (1968) and the FR test (Cornelius 1993), were used alongside cross-validation to evaluate the model’s performance and identify significant IPCs. The yield ratio for AMMI winners within each environment (indicated in the first column of AMMI rankings) was computed by dividing the overall yield of the best performing variety (Gauch 2013). Gauch (2013) defines a winning genotype across environments as one with a ratio of one. A ratio of 1.10 or higher is considered to be suggestive of narrow adaptation, which measures the relevance of narrow adaptations owing to GEI effects.
Results
Yield performance under saline and sodic conditions
Among the 14 genotypes in nine environments in saline and sodic conditions, genotype RP 5989-2-4-8-15-139-62-6-9 (GN14) gave the highest mean grain yield of 3353 kg ha−1. It was followed by genotypes CSR-2748-4441-195 (GN05) and CSR-2748-4441-193 (GN11) with a mean grain yield of 3237 kg ha−1 and 3231 kg ha−1, respectively. Genotypes CSR-2748-4441-195 (GN05), CSR-5989-2-4-8-15-139-62-6-9 (GN14), and CSR-2748-4441-193 (GN11) all performed well under sodic stress conditions, providing grain at rates of 3437 kg ha−1, 3275 kg ha−1, and 3225 kg ha−1, respectively. In contrast, genotypes CSR RIL-01-IR (GN10), CSR-2748-4441-193 (GN11), and CSR 2711-17 (GN01) fared well under saline stress conditions, with mean grain yields of 3311 kg ha−1, 3256 kg ha−1, and 3128 kg ha−1, respectively (Table 3). For details on ANOVA, mean, coefficient of variation (CV%), l.s.d. at 5%, and mean significant difference (MSD) at 5%, along with tests for homogeneity of variances and normality for grain yield in rice genotypes under saline and alkaline conditions, see Supplementary Tables S1, S2, and S3.
| Genotype number | Genotypes | Saline environments | Sodic environments | Sodic and saline environment | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E1 | E5 | Mean | E2 | E3 | E4 | E6 | E7 | E8 | E9 | Mean | Mean | Rank | |||
| 1 | GN01 | 3322 | 2933 | 3128 | 3863 | 3627 | – | 3319 | 4004 | 2976 | 4193 | 3140 | 3137 | 5th | |
| 2 | GN02 | 1804 | 811 | 1308 | 1916 | 2386 | 283 | 926 | 1352 | 2857 | 1185 | 1558 | 1502 | 17th | |
| 3 | GN03 | 3150 | 2889 | 3020 | 3982 | 3512 | 500 | 3326 | 4010 | 3244 | 3985 | 3223 | 3178 | 4th | |
| 4 | GN04 | 2589 | 778 | 1684 | 3433 | 2834 | 778 | 2785 | 3518 | 3304 | 3444 | 2871 | 2607 | 12th | |
| 5 | GN05 | 3233 | 2978 | 3106 | 3763 | 3488 | 444 | 3311 | 3907 | 3988 | 4022 | 3275 | 3237 | 2nd | |
| 6 | GN06 | 1891 | 667 | 1279 | 1378 | 2531 | – | 533 | 1895 | 1310 | 815 | 1209 | 1224 | 19th | |
| 7 | GN07 | 2263 | 2678 | 2471 | 3033 | 2306 | 1356 | 2859 | 3647 | 2173 | 3444 | 2688 | 2640 | 11th | |
| 8 | GN08 | 2041 | 778 | 1410 | 3448 | 2206 | 2433 | 904 | 1029 | 3363 | 1252 | 2091 | 1939 | 15th | |
| 9 | GN09 | 2044 | 104 | 1074 | 3009 | 2507 | – | 496 | 1270 | 2768 | 889 | 1563 | 1454 | 18th | |
| 10 | GN10 | 3244 | 3378 | 3311 | 3763 | 3680 | 456 | 378 | 3899 | 4256 | 4170 | 2943 | 3025 | 6th | |
| 11 | GN11 | 3256 | 3256 | 3256 | 3740 | 3736 | 778 | 3319 | 4057 | 2976 | 3970 | 3225 | 3232 | 3rd | |
| 12 | GN12 | 2661 | 2600 | 2631 | 3189 | 3048 | 1244 | 2770 | 3263 | 4286 | 3385 | 3026 | 2939 | 9th | |
| 13 | GN13 | 2582 | 2689 | 2636 | 3322 | 3080 | 1122 | 2844 | 3692 | 3899 | 3600 | 3080 | 2981 | 8th | |
| 14 | GN14 | 3144 | 2978 | 3061 | 3727 | 3969 | 1322 | 3304 | 4019 | 3512 | 4207 | 3437 | 3354 | 1st | |
| 15 | CHK1 | 978 | 2611 | 1795 | 1544 | 1655 | – | 2719 | 3501 | 3065 | 3370 | 2265 | 2160 | 14th | |
| 16 | CHK2 | 2411 | 2944 | 2678 | 3179 | 2950 | 478 | 3296 | 3827 | 3839 | 4148 | 3102 | 3008 | 7th | |
| 17 | CHK3 | 456 | 2611 | 1534 | 1278 | 980 | 1567 | 2696 | 3307 | 3542 | 3304 | 2382 | 2193 | 13th | |
| 18 | CHK4 | 2481 | 1778 | 2130 | 3056 | 3070 | 739 | 726 | 962 | 1458 | 1511 | 1646 | 1753 | 16th | |
| 19 | CHK5 | 2611 | 2633 | 2622 | 3236 | 3064 | 967 | 2622 | 3213 | 4226 | 3430 | 2965 | 2889 | 10th | |
Predictive accuracy, model diagnosis, and AMMI analysis of variance
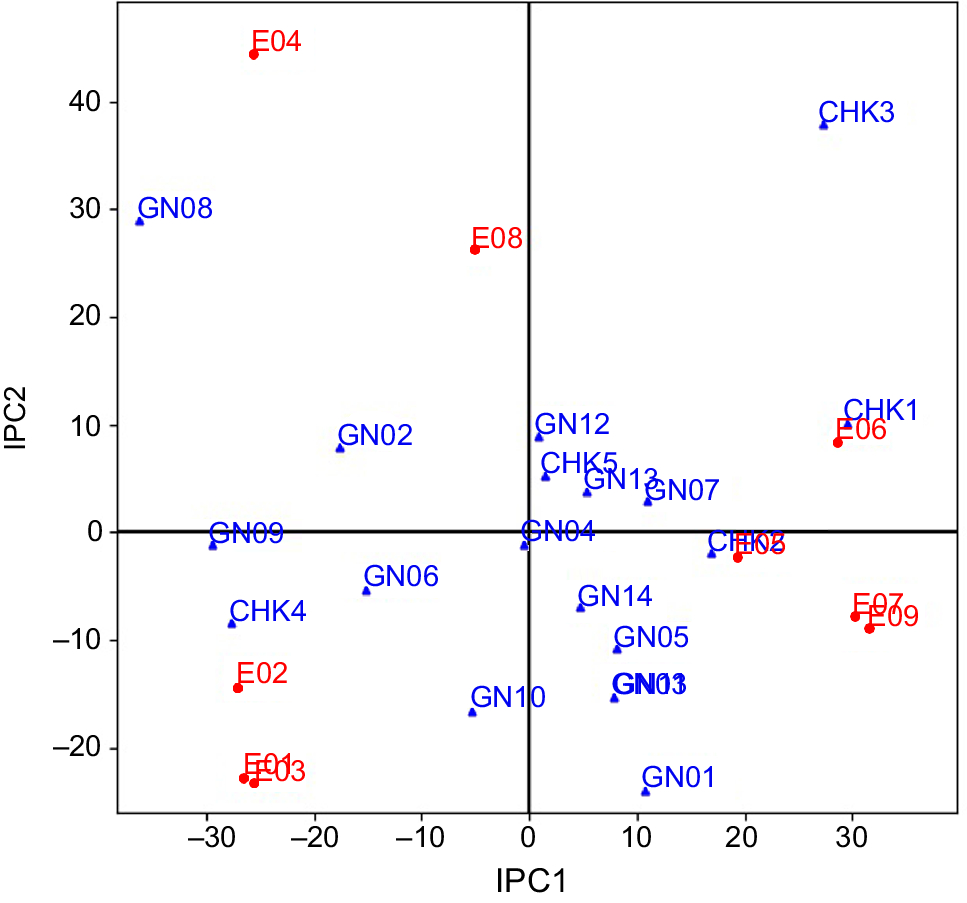
Yield data from two seasons across nine environmental conditions subjected to AMMI analyses through yield-stability statistics (Yge). In this study, available variability in grain yield was partitioned into various components using ANOVA of the AMMI model (Table 4). About 85.16% of the total variability among genotypes for grain yield explained the variations in the treatment, and the rest was an experimental error due to residual error. Total treatment variations were classified into three key causative components: (1) genotype (G); (2) environment (E); and (3) their interaction (GEI). All three components differed significantly at a probability level of P ≤ 0.001 and the maximum proportion variation was explained by environment (32%). Contribution from G and GEI accounted for 27% and 26% of the total treatment variation, respectively. The GEI component was further subdivided into seven Interaction Principal Components (IPC1–IPC7), the first four of which (IPC1–IPC4) were determined to be significant. A total of 93% of the GEI for grain yield was supplied by the first four IPCs, with the IPC1 (48%) making the largest contribution. The results of this model demonstrated that 80% of total treatment variations were due to GEIS (GEI signal), whereas the remaining 20% was attributable to GEIN (GEI noise). Components E and GEIN account for approximately 44% of the variation in this data, which is inconsequential to a breeder. Only the remaining 57% variation, represented by G and GEIS, is meaningful from a practical point of view. Sum of squares of component G was 1.3 and 5.4 times larger than that of GEIS and GEIN, respectively. Results from model diagnosis through cross-validation identified the AMMI-4 model as having the smallest RMS PD, indicating the highest predictive accuracy for grain yield (Table 5). This model is closer to the true means compared to the raw data (AMMI-F model). The AMMI gain factor for grain yield was 1.3. To determine the best model for this data, both the FR-test (at P < 0.01) and Gollob’s F-test were employed, as AMMI analysis relies on family diagnosis rather than a single model. The only discrepancy between the two F-tests was that six IPCAs were identified as significant by Gollob’s F-test, while only four IPCAs were selected by the FR test. The results indicated that IPC1 and IPC2, representing AMMI families AMMI1 and AMMI2, respectively, accounted for 72% and 90% of the GEIS variations. AMMI biplot1 was used to demonstrate the principal additive influence of genotypes and environment on the x-axis, as well as the multiplicative effect of GEI on the y-axis in terms of mean and IPC1 (Fig. 1). AMMI biplot2 was created by combining IPC1 and IPC2, and it may be used to identify genotypes or environments with low, medium, or large interaction effects (Fig. 2).
| Source of variance | d.f. | MSS | Gollob’s F-test | Proportion of variation | ||||
|---|---|---|---|---|---|---|---|---|
| Total variation (%) | Main and interaction variation (%) | GEI variation (%) | GEIS variation (%) | |||||
| Treatment | 170 | 4223251.1*** | 85.1 | |||||
| Genotype | 18 | 12845039.6*** | 27.4 | |||||
| Environment | 8 | 33751438.5*** | 32.0 | |||||
| Interaction (G × E) | 144 | 1505072.7*** | 25.7 | |||||
| IPC1 | 25 | 4161852.7*** | 120.6*** | 48.0 | 59.9 | |||
| IPC2 | 23 | 2257536.2*** | 65.4*** | 24.00 | 29.9 | |||
| IPC3 | 21 | 1246629.2*** | 36.1*** | 12.1 | 15.1 | |||
| IPC4 | 19 | 986072.5** | 28.6*** | 8.6 | 10.8 | |||
| IPC5 | 17 | 449794.1 | 13.0*** | 3.5 | 4.4 | |||
| IPC6 | 15 | 442937.7 | 12.8*** | 3.1 | 0.00 | |||
| IPC7 | 13 | 90468.9 | 2.6 | 0.5 | 0.00 | |||
| Residual | 11 | 34506.1 | 0.2 | 0.00 | ||||
| Error | 342 | 365793.2 | 14.8 | |||||
| Blocks/Env | 18 | 1573170.6*** | 3.4 | |||||
| Pure Error | 324 | 298716.8 | 11.5 | |||||
| Total | 512 | 1646589.8 | 100 | 100 | 100 | |||
MSS, Mean sum of squares; GEI, genotype × environment Interaction; GEIs, genotype × environment Interaction of signal; IPC, interaction principal component tested based on FR.
**P < 0.01; ***P < 0.001.
| Model | d.f. | RMS PD | |
|---|---|---|---|
| AMMI1 | 25 | 751.5 | |
| AMMI2 | 23 | 735.6 | |
| AMMI3 | 21 | 734.9 | |
| AMMI4 | 19 | 722.2* | |
| AMMI5 | 17 | 730.0 | |
| AMMIF | 170 | 751.4 |
AMMI additive main effects and multiplicative interaction.
Identification of ‘winner’ genotype from AMMI model family
A central element of AMMI analysis is the identification and ranking of winning genotypes across various mega-environments. Genotypes were ranked according to their IPC1 scores, with the highest-scoring genotype listed first and subsequent genotypes ranked in descending order of IPC1 values (Table 6). Eight model families (AMMI0 to AMMIF) were developed based on the number of components included in the analysis. The AMMI0 model family incorporates no components, while the AMMIF model family includes all available components. The AMMI0 model family identified only one winning genotype, as it was based on a single mega-environment. In contrast, the AMMIF model family included seven genotypes that achieved victories across seven environments. The genotype RP 5989-2-4-8-15-139-62-6-9 (GN14) was successful across all AMMI model families and in the majority of scenarios. This genotype performed the best in 9, 6, 1, 1, 2, 2, 3, 2 and 2 environments according to the AMMI0, AMMI1, AMMI2, AMMI3, AMMI4, AMMI5, AMMI6, and AMMIF model families, respectively (Table 6). The AMMI0 model family, which does not account for any components, results in only one mega-environment and provides limited predictive power. Conversely, the AMMIF model family, which includes all components, generates multiple mega-environments but with greater environmental noise. Based on the low RMS PD model diagnosis analysis, the AMMI-4 model emerged as the most effective predictive model. This model identified four ‘winning’ genotypes across four mega-environments. Specifically, genotypes CSR 2711-17 (GN01) and CSR RIL-01-IR 165 (GN10) achieved mean grain yields of 3137 kg ha−1 and 3025 kg ha−1, respectively, and were successful in three environments each. The genotype RP 5989-2-4-8-15-139-62-6-9 (GN14) achieved a mean grain yield of 3353.5 kg ha−1 and won in two environments, while the genotype RP 6189-HHZ 17-Y16-Y3-SAL1 (GN08), with a mean grain yield of 1939.3 kg ha−1, yield the highest in one environment. In the AMMI1 model, both the genotype RP 5989-2-4-8-15-139-62-6-9 (GN14) and the check genotype CSR 23 (CHK2) were successful in two distinct mega-environments. The AMMI2 model delineated six genotypes; CSR 2711-17 (GN01) yielded best in two environments, and CSR RIL-01-IR 165 (GN10) yielded best in three environments.
| Genotype number | Genotype code | Grain yield kg ha−1 | AMMI model family | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AMMI0 | AMMI1 | AMMI2 | AMMI3 | AMMI4 | AMMI5 | AMMI6 | AMMI7 | AMMIF | ||||
| 16 | CHK2 | 3008.1 | 3 | 1 | ||||||||
| 1 | GN01 | 3137.4 | 2 | 3 | 3 | 2 | 1 | 1 | ||||
| 11 | GN11 | 3231.9 | 1 | 1 | 2 | 1 | ||||||
| 3 | GN03 | 3177.6 | 2 | 2 | 2 | |||||||
| 14 | GN14 | 3353.5 | 9 | 6 | 1 | 1 | 2 | 2 | 3 | 2 | 2 | |
| 12 | GN12 | 2938.4 | 1 | 1 | 1 | 1 | ||||||
| 10 | GN10 | 3024.9 | 3 | 3 | 3 | 3 | 1 | 1 | 1 | |||
| 8 | GN08 | 1939.3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||
| Mega-environments | 1 | 2 | 6 | 5 | 4 | 5 | 6 | 6 | 7 | |||
Delineation of mega-environments based on AMMI1
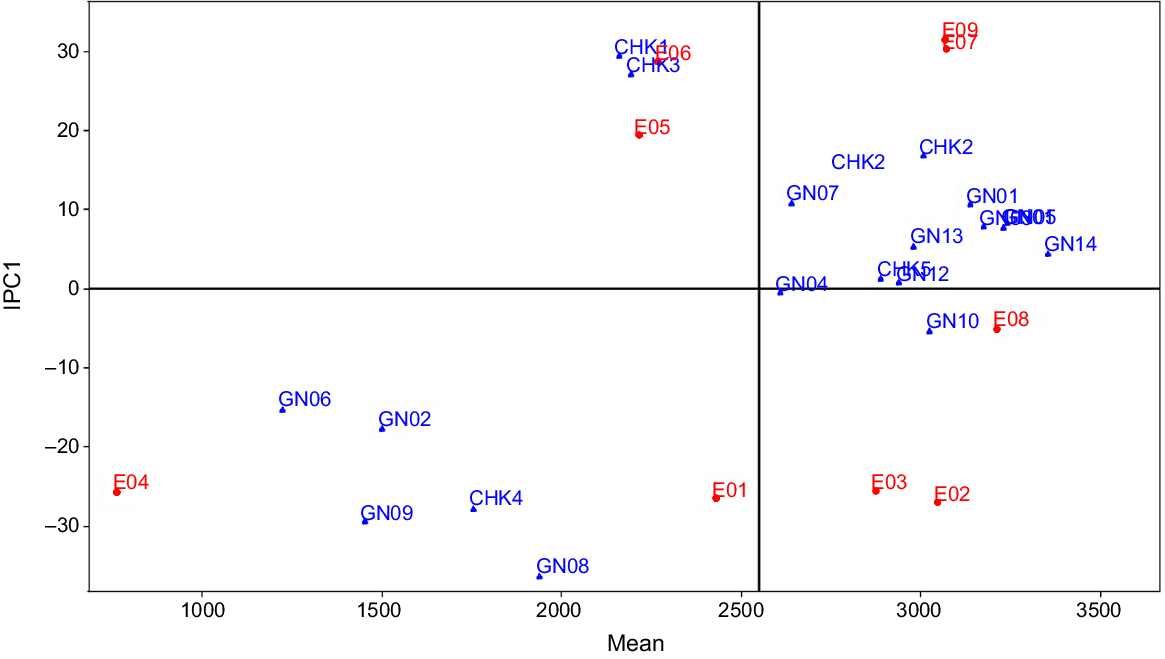
The AMMI1 model family with the highest GEIS and the least amount of GEIN gives a better understanding of the suitability of different genotypes in different environments. The nine settings in the current investigation were listed in decreasing order of their IPC1 value (Table 7). According to the AMMI1 model, the current study divided nine environments into two mega-environments: (1) Mega-envrionment I that contains six environments; and (2) Mega-environment II that contains just three habitats (Fig. 3). The environments with the highest IPC1 values (E9, E7, and E6) are defined in Mega-environment II, while the remaining six environments (E1, E2, E3, E4, E5, and E8) are grouped in Mega-environment I. According to the AMMI1 model, genotype RP 5989-2-4-8-15-139-62-6-9 (GN14) yielded the best in all six environments of Mega-environment I, whereas CSR 23 (CHK2) yielded the best in the three environments of Mega-environment II, followed by RP 5989-2-4-8-15-139-62-6-9 (GN14), which ranked second place in Mega-environment II. Three genotypes, CSR-2748-4441-195 (GN05), CSR-2748-4441-193 (GN11), and CSR 2711-17(GN01), placed third, fourth, and fifth in Mega-environment II. The raw data-based AMMIF algorithm identified seven mega-environments with seven ‘winning’ genotypes.
| Mega-environment | Environment code | IPC1 score | Ratio | AMMI1 Ranks | AMMIF Ranks | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | |||||
| II | E09 | 31.61 | 1.010 | CHK2 | GN14 | GN05 | GN11 | GN01 | GN14 | GN01 | GN10 | CHK2 | GN05 | |
| E07 | 30.25 | 1.006 | CHK2 | GN14 | GN05 | GN11 | GN01 | GN11 | GN14 | GN03 | GN01 | GN05 | ||
| E06 | 28.68 | 1.002 | CHK2 | GN14 | GN05 | GN11 | GN01 | GN03 | GN01 | GN11 | GN05 | GN14 | ||
| I | E05 | 19.38 | 1.000 | GN14 | GN05 | GN11 | GN1 | CHK2 | GN10 | GN11 | GN05 | GN14 | CHK2 | |
| E08 | −5.06 | 1.000 | GN14 | GN05 | GN11 | GN03 | GN01 | GN12 | GN10 | CHK5 | GN05 | GN13 | ||
| E03 | −25.62 | 1.000 | GN14 | GN10 | GN11 | GN05 | GN03 | GN14 | GN11 | GN10 | GN01 | GN03 | ||
| E04 | −25.69 | 1.000 | GN14 | GN10 | GN11 | GN05 | GN03 | GN08 | CHK3 | GN07 | GN14 | GN12 | ||
| E01 | −26.50 | 1.000 | GN14 | GN10 | GN11 | GN05 | GN03 | GN01 | GN11 | GN10 | GN05 | GN03 | ||
| E02 | −27.06 | 1.000 | GN14 | GN10 | GN11 | GN05 | GN03 | GN03 | GN01 | GN05 | GN10 | GN11 | ||
AMMI1 mega-environment display for 19 rice genotypes evaluated under nine environments of saline and sodic condition. Environment means are shown on the abscissa and interaction principal component (IPC1) scores on the ordinate.
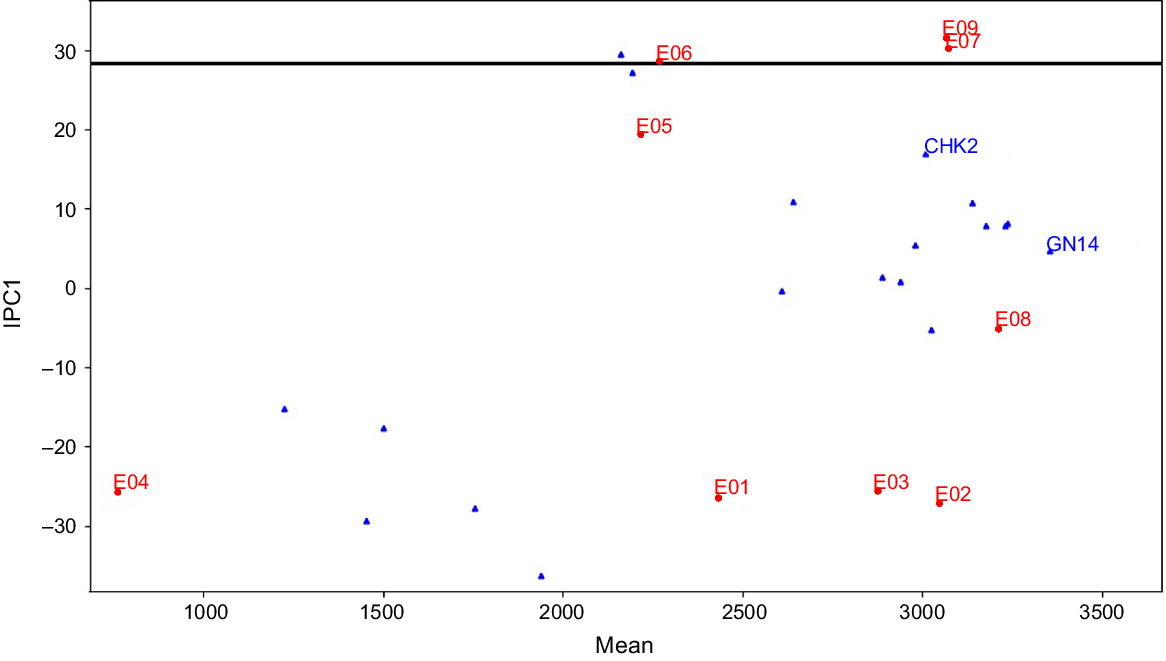
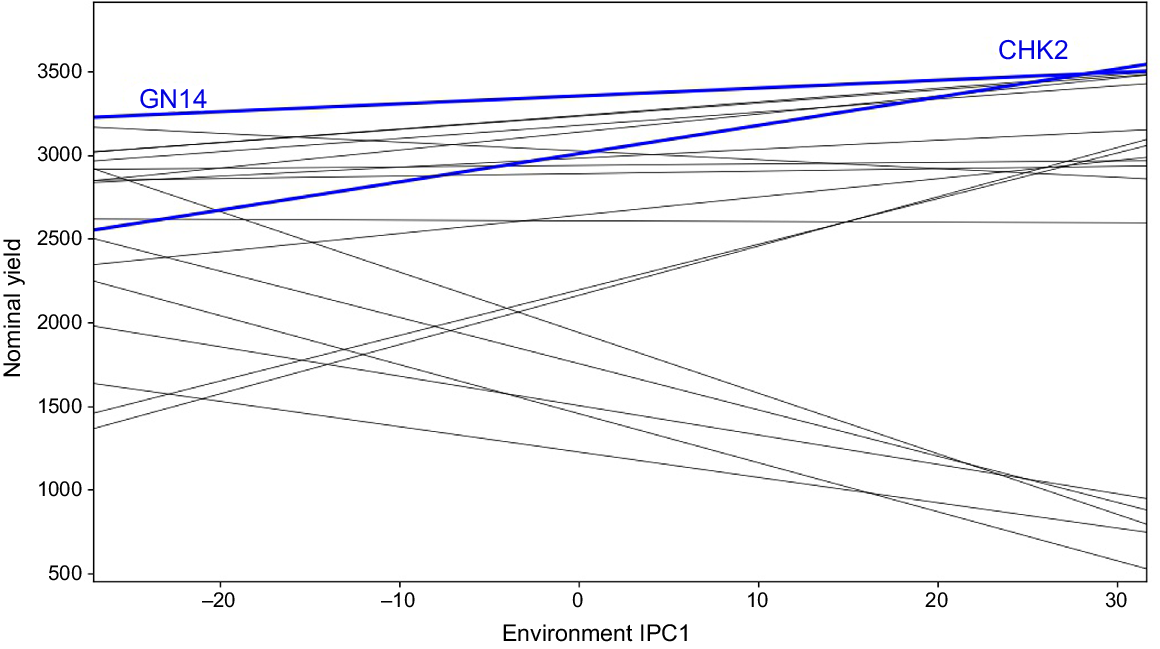
The primary purpose of all multi-environment experiments is to identify stable genotypes. In this experiment, the nominal yield of several genotypes was plotted against the environmental IPC1 score, indicating that RP 5989-2-4-8-15-139-62-6-9 (GN14), with an average grain production of 3353 kg ha−1, demonstrated broad adaptability for all of the environments of mega-environment I (Fig. 4). The ratio of the grain yield of a ‘winner’ genotype in a particular environment to the yield of the overall ‘winner’ is used to identify genotypes with specific or general adaptability. In our experiment, CSR 23 (CHK2) with an average yield of 3008 kg ha−1 yielded the best in all the environments of mega-environment II with yield ratios larger than one, indicating limited adaptation. The genotype CHK2 had a yield advantage of 3353 × 1.01 = 3386 kg ha−1; i.e. 3386–3008 = 378 kg ha−1 (13%) yield advantage over broad adaption under environment E09.
Discussion
Utilizing waste and degraded land represents a viable strategy for increasing agricultural yield. Most waste and degraded soils result from the accumulation of salt in the upper soil layers, rendering them unsuitable for agricultural use. Consequently, it is crucial to develop cultivars capable of thriving under various conditions, including those involving degraded soils. GEI is a significant challenge for plant breeders (Lin and Binns 1988). Agricultural traits are frequently affected by external conditions throughout a plant’s life cycle (Kumar et al. 2015). To effectively evaluate genotype performance, it is crucial to test them in various environments. If genotypes are only assessed in one environment during early breeding stages, there is a risk of overlooking beneficial genetic variations that might perform better under different conditions. This limited testing approach can lead to the loss of valuable genes. Integrating GEI analysis into the breeding process can therefore improve genotype selection and enhance cultivation outcomes in specific target environments (Hassani et al. 2018).
Yield is a highly complex variable that is influenced by genetic and environmental factors as well as their interactions. Special statistical methods such as G main effect plus GGE and AMMI are necessary for the analysis of complicated environmental data that may draw valid inferences under variable environments. However, researchers prefer the latter strategy because of its ability to extract the signal component from noise (Gauch 2006; Yan et al. 2007; Gauch et al. 2008; Yang et al. 2009; Yan and Holland 2010). The main factor that makes the AMMI model more accurate than the GGE biplot analysis is the division of the treatment variation into G, E, and G × E components, followed by the application of singular value decomposition (SVD) to G × E. AMMI-based analysis is also better than linear regression model due to its accuracy in partitioning of interaction sum of squares into component variables (Nachit et al. 1992).
This study aimed to assess the environmental stability of grain yield under salt stress conditions. The experiment was conducted across nine salt stress environments, which were combinations of different locations and years. Descriptive statistics for grain yields indicated the presence of significant variation in this trait among the genotypes. The ANOVA of AMMI divides the treatment variation from residual error or variations caused by unknown factors. The sum of squares of G, E, and G × E significance is used to evaluate the appropriateness of the AMMI model. At a P-value of ≤0.001, all three components are highly significant. The environment is the most important component in this variability, but both G and GEI contribute approximately equally. Likewise, several studies have reported that environmental components contribute the most to the total variation (Ghaed-Rahimi et al. 2014; Islam et al. 2016; Hassani et al. 2018; Shahriari et al. 2018; Krishnamurthy et al. 2021). Both signal (GEIS) and noise (GEIN) are present in the GEI component. The degree of freedom of GEI is multiplied by the mean sum of squares of the experimental error to generate the SS for GEIN. To get GEIS, GEIN is then subtracted from SS of GEI (Gauch 2013). As compared to the genotypic main effect, the SS for GEIS and GEIN is 0.8 and 0.2 times higher, respectively. The current findings are consistent with earlier studies in which evaluations of rice genotypes were carried out under various salt-affected soil conditions and significant contributions of G, E, and GEI for grain yield were discovered (Anandan et al. 2009; Krishnamurthy et al. 2015, 2021; Islam et al. 2016).
Model families ranging from AMMI0 to AMMIF are produced during AMMI analysis. Because the AMMI0 family lacks both GEIS and GEI, the genotypes were compared in the original set of mega-environments. In contrast, the AMMIF family keeps all of the GEIS and GEIN as this model uses the original set of data or raw data. The model family in between these two extremes can be used for a particular set of data. The selection of the best model family depends on three parameters: (1) statistical significance; (2) interpretability; and (3) accuracy (Gauch 2013). In this study, the seven IPCs (IPC1–IPC7) accounted for 76% of the total GEI distribution, with the remaining 24% attributable to residual effects on grain yield. Of these seven IPCs, only the first four were statistically significant according to FR statistics, while the Gollob F-test identified six out of the seven IPCs as significant. A similar contrast result was observed by Hassani et al. (2018) in root and sugar yield. The F-test methods depend on distributional assumptions and data normality, with some tests like FR being either liberal (Akbarpour et al. 2014) or conservative in detecting significant IPCs (Annicchiarico 1997). In our study, data normality was confirmed by Shapiro–Wilk (1965) tests (Table S2). Model diagnosis is essential to determine the most suitable model family for a given dataset and research objective. Two primary approaches for model diagnosis are cross-validation and hypothesis testing about the number of components, which help in identifying the optimal number of multiplicative terms for dissecting GEI mean squares (Cornelius 1993; Gauch 2013). Both approaches were employed in this study to enhance the predictive accuracy of AMMI model families. In our study, the AMMI model accounted for 80% of the GEI sum of squares (GEIS) and 20% of the GEIN. Cross-validation results identified AMMI4 as the most predictive and accurate model, as indicated by its low root mean square predictive differences (RMS PD) value. Therefore, AMMI4 is recommended for the current model to maximize prediction accuracy (Agahi et al. 2020). Similarly, other researchers have used RMS PD to assess the predictive accuracy of AMMI models (Ghaed-Rahimi et al. 2014; Hassani et al. 2018; Shahriari et al. 2018). Krishnamurthy et al. (2021) found that IPC1, IPC2, and IPC3 together explained 60.5% of the GEI variation and 67% of the GEIS variation for rice under salt stress conditions. Studies on GEI often show significant discrepancies between the results of different diagnostic methods and predictive accuracy (Hassani et al. 2018). Practical constraints typically limit the number of feasible mega-environments to two or three, or possibly a few more, which often requires a simpler AMMI model (AMMI-1 or AMMI-2) rather than a more complex one determined solely by statistical criteria (Gauch 2013). This highlights a trade-off between statistical and practical considerations that can guide the selection of appropriate and parsimonious models in GEI studies.
Within a mega-environment, the habitats exhibit similar characteristics, resulting in consistent responses from genotypes (Yan and Rajcan 2002). However, fluctuations in genotype rankings due to environmental factors can complicate the identification of the most stable genotype. AMMI analysis addresses this issue by separating noise from the true GEI component, thereby facilitating a more accurate comparison of genotypes. Modern model families like AMMI5, AMMI6, and AMMI7 capture more GEIN, resulting in the formation of several mega-environments. In the current instance, AMMI6 and AMMI7 both recognized six mega-environments, but AMMIF detected seven mega-environments. The fraction of GEIS drops from AMMI1 to AMMI7, whereas the GEIN component grows in the same way. Therefore, the AMMI1 family provides the finest foundation for the division of environments into mega-environments (Gauch 2006). Using the AMMI1 model family as a foundation, the original nine environments are divided into two mega-environments with two ‘winners’. RP 5989-2-4-8-15-139-62-6-9 (GN14) yielded the best in all six environments of Mega-environment I, while CSR 23 (CHK2) took first place in each of the three mega-environments of Mega-environment II. The primary additive effect of genotypes and environments is represented on 2D surfaces using the AMMI biplot1, which makes it simple to identify related genotypes and environments. The AMMI biplot1 groups together the environments that fall under the same mega-environments or the genotypes that exhibit a similar pattern of behavior. The AMMI2 model family also defined six mega-environments, like AMMI6 and AMMI7, but it caught a greater proportion of GEIS than AMMI6 and AMMI7, which gives it a higher level of prediction accuracy for the current dataset. In the six mega-environments based on the AMMI2 model family, CSR RIL-01-IR 165 (GN10) and CSR 2711-17 (GN01), respectively, took first place in three and two environments. The first two IPC can be used to determine genotypes or locations with low, medium, or high GEI. The genotypes close to the biplot’s origin have a low IPC1 score and are more stable as a result of less environmental interaction. The IPC1 score grows in either a positive or negative direction as we approach away from the origin, and as a result, the interaction effect increases significantly (Anandan et al. 2009). Points nearer to a score of 1 suggest two environments or genotypes with comparable interaction patterns. According to Gauch (2013) the most reliable genotype in terms of stability across many conditions is one with a ratio of 1. In this instance, genotype RP 5989-2-4-8-15-139-62-6-9 (GN14) is the clear victor and is advised for widespread adaption. A genotype is suited for a limited range of environments when the ratio for that genotype approaches or exceeds 1. Because it produces better results in that environment. For narrow adaptation in this environment, the check genotype CSR 23 (CHK2), which has a yield advantage of 12% under E09, is advised (Kumar et al. 2010, 2011; Anandan et al. 2009; Ali et al. 2013; Krishnamurthy et al. 2014, 2016b, 2016c, 2017).
Conclusion
In response to increasing salt stress, this study aimed to assess potential salt-tolerant rice lines across nine environments, encompassing both saline and sodic stress conditions, using the AMMI stability model. Significant genetic variability in grain yield was observed, which could be leveraged in rice breeding programs. Genotypes RP 5989-2-4-8-15-139-62-6-9 (GN14) and CSR-2748-4441-195 (GN05) exhibited exceptional performance under sodic stress conditions. Conversely, CSR RIL-01-IR (GN10), CSR-2748-4441-193 (GN11), and CSR 2711-17 (GN01) demonstrated strong performance under saline stress conditions. According to the low RMS PD model diagnosis analysis, the AMMI-4 model emerged as the most predictive. In the AMMI-4 model, four ‘winning’ genotypes were identified across four mega-environments: (1) CSR 2711-17 (GN01); (2) CSR RIL-01-IR 165 (GN10); (3) RP 5989-2-4-8-15-139-62-6-9 (GN14)’ and (4) RP 5989-2-4-8-15-139-62-6-9 (GN14). Using the AMMI1 model family as a basis, the nine environments were categorized into two mega-environments, each featuring two top-performing genotypes: (1) RP 5989-2-4-8-15-139-62-6-9 (GN14); and (2) CSR 23 (CHK2). The superior performing and ‘winning’ genotypes can be recommended for cultivation in saline and alkaline soils and can also be utilized in breeding programs aimed at enhancing rice productivity in salt-affected areas, thereby contributing to increased rice production to meet the needs of the growing population.
Data availability
The data that support this study will be shared upon reasonable request to the corresponding author.
Author contributions
SLK and PCS: designed the experiments, BML, SR, ASW: recorded the field data, BML, SR, ASW, and NMV: analyzed the data, All the authors contributed to manuscript writing.
Acknowledgements
The authors acknowledge the Director, ICAR-CSSRI and Network Project on functional genomics and genetic modification in crops (NPFGGM) and Incentivizing in Agricultural Research for providing all essential resources for research work.
References
Agahi K, Ahmadi J, Oghan HA, Fotokian MH, Orang SF (2020) Analysis of genotype × environment interaction for seed yield in spring oilseed rape using the AMMI model. Crop Breeding and Applied Biotechnology 20(1), e26502012.
| Crossref | Google Scholar |
Akbarpour O, Dehghani H, Sorkhi B, Gauch HG (2014) Evaluation of genotype × environment interaction in barley (Hordeum vulgare L.) based on AMMI model using developed SAS program. Journal of Agricultural Science & Technology 16, 909-920.
| Google Scholar |
Ali S, Gautam RK, Mahajan R, Krishnamurthy SL, Sharma SK, Singh RK, Ismail AM (2013) Stress indices and selectable traits in SALTOL QTL introgressed rice genotypes for reproductive stage tolerance to sodicity and salinity stresses. Field Crops Research 154, 65-73.
| Crossref | Google Scholar |
Anandan A, Eswaran R, Sabesan T, Prakash M (2009) Additive main effects and multiplicative interactions analysis of yield performances in rice genotypes under coastal saline environments. Advances in Biological Research 3(1-2), 43-47.
| Google Scholar |
Annicchiarico P (1997) Joint regression vs AMMI analysis of genotype-environment interactions for cereals in Italy. Euphytica 94, 53-62.
| Crossref | Google Scholar |
Cornelius PL (1993) Statistical tests and retention of terms in the additive main effects and multiplicative interaction model for cultivar trials. Crop Science 33(6), 1186-1193.
| Crossref | Google Scholar |
de Leon ND, Jannink J-L, Edwards JW, Kaeppler SM (2016) Introduction to a special issue on genotype by environment interaction. Crop Science 56(5), 2081-2089.
| Crossref | Google Scholar |
Ebdon JS, Gauch HG, Jr. (2002a) Additive main effect and multiplicative interaction analysis of national turfgrass performance trials: I. Interpretation of genotype × environment interaction. Crop Science 42, 489-496.
| Crossref | Google Scholar |
Ebdon JS, Gauch HG, Jr. (2002b) Additive main effect and multiplicative interaction analysis of national turfgrass performance trials: II. Cultivar recommendations. Crop Science 42, 497-506.
| Crossref | Google Scholar |
Eberhart SA, Russell WA (1966) Stability parameters for comparing varieties 1. Crop Science 6(1), 36-40.
| Crossref | Google Scholar |
Finlay KW, Wilkinson GN (1963) The analysis of adaptation in a plant-breeding programme. Australian Journal of Agricultural Research 14(6), 742.
| Crossref | Google Scholar |
Gauch HG, Jr. (2006) Statistical analysis of yield trials by AMMI and GGE. Crop Science 46(4), 1488-1500.
| Crossref | Google Scholar |
Gauch HG, Jr. (2013) A simple protocol for AMMI analysis of yield trials. Crop Science 53(5), 1860-1869.
| Crossref | Google Scholar |
Gauch HG, Jr., Piepho H-P, Annicchiarico P (2008) Statistical analysis of yield trials by AMMI and GGE: further considerations. Crop Science 48(3), 866-889.
| Crossref | Google Scholar |
Ghaed-Rahimi L, Heidari B, Dadkhodaie A (2014) Genotype × environment interactions for wheat grain yield and antioxidant changes in association with drought stress. Archives of Agronomy and Soil Science 61(2), 153-171.
| Crossref | Google Scholar |
Hassani M, Heidari B, Dadkhodaie A, et al. (2018) Genotype by environment interaction components underlying variations in root, sugar and white sugar yield in sugar beet (Beta vulgaris L.). Euphytica 214, 79.
| Crossref | Google Scholar |
Islam MR, Sarker MRA, Sharma N, Rahman MA, Collard BCY, Gregorio GB, Ismail AM (2016) Assessment of adaptability of recently released salt tolerant rice varieties in coastal regions of South Bangladesh. Field Crops Research 190, 34-43.
| Crossref | Google Scholar |
Krishnamurthy SL, Sharma SK, Gautam RK, Kumar V (2014) Path and association analysis and stress indices for salinity tolerance traits in promising rice (Oryza sativa L.) genotypes. Cereal Research Communications 42(3), 474-483.
| Crossref | Google Scholar |
Krishnamurthy SL, Pundir P, Singh YP, Sharma SK, Sharma PC, Sharma DK (2015) Yield stability of rice lines for salt tolerance using additive main effects and multiplicative interaction analysis - AMMI. Journal of Soil Salinity and Water Quality 7(2), 98-106.
| Google Scholar |
Krishnamurthy SL, Sharma PC, Sharma SK, Batra V, Kumar V, Rao LVS (2016a) Effect of salinity and use of stress indices of morphological and physiological traits at the seedling stage in rice. Indian Journal of Experimental Biology 54(12), 843-850.
| Google Scholar | PubMed |
Krishnamurthy SL, Sharma SK, Sharma DK, Sharma PC, Singh YP, Mishra VK, Burman D, Maji B, Bandyopadhyay BK, Mandal S, Sarangi SK, Gautam RK, Singh PK, Manohara KK, Marandi BC, Singh DP, Padmavathi G, Vanve PB, Patil KD, Thirumeni S, Verma OP, Khan AH, Tiwari S, Shakila M, Ismail AM, Gregorio GB, Singh RK (2016b) Analysis of stability and G × E interaction of rice genotypes across saline and alkaline environments in India. Cereal Research Communications 44(2), 349-360.
| Crossref | Google Scholar |
Krishnamurthy SL, Gautam RK, Sharma PC, Sharma DK (2016c) Effect of different salt stresses on agro-morphological traits and utilisation of salt stress indices for reproductive stage salt tolerance in rice. Field Crops Research 190, 26-33.
| Crossref | Google Scholar |
Krishnamurthy SL, Sharma PC, Sharma DK, Ravikiran KT, Singh YP, Mishra VK, Burman D, Maji B, Mandal S, Sarangi SK, Gautam RK, Singh PK, Manohara KK, Marandi BC, Padmavathi G, Vanve PB, Patil KD, Thirumeni S, Verma OP, Khan AH, Tiwari S, Geetha S, Shakila M, Gill R, Yadav VK, Roy SKB, Prakash M, Bonifacio J, Ismail A, Gregorio GB, Singh RK (2017) Identification of mega-environments and rice genotypes for general and specific adaptation to saline and alkaline stresses in India. Scientific Reports 7(1), 7968.
| Crossref | Google Scholar |
Krishnamurthy SL, Sharma PC, Sharma DK, Singh YP, Mishra VK, Burman D, Maji B, Mandal S, Sarangi SK, Gautam RK, Singh PK, Manohara KK, Marandi BC, Chattopadhyay K, Padmavathi G, Vanve PB, Patil KD, Thirumeni S, Verma OP, Khan AH, Tiwari S, Geetha S, Gill R, Yadav VK, Roy B, Prakash M, Anandan A, Bonifacio J, Ismail AM, Singh RK (2021) Additive main effects and multiplicative interaction analyses of yield performance in rice genotypes for general and specific adaptation to salt stress in locations in India. Euphytica 217, 20.
| Crossref | Google Scholar |
Krishnamurthy SL, Rathor S, Lokeshkumar BM, Warriach AS, Vinaykumar NM, Sharma PC, Gautam RK, Singh RK (2024) Genetic improvement of rice for inland saline and alkaline areas of North-Western India. In ‘Genetic improvement of rice for salt tolerance’. (Eds RK Singh, M Prakash, RK Gautam, SL Krishnamurthy, S Thirumeni) pp. 77–100. (Springer Nature Singapore Pte Ltd) 10.1007/978-981-99-3830-8
Kumar BMD, Shadakshari YG, Krishnamurthy SL (2010) Genotype x Environment interaction and stability analysis for grain yield and its components in Halugidda local rice mutants. Electronic Journal of Plant Breeding 1(5), 1286-1289.
| Google Scholar |
Kumar BMD, Gangaprsad S, Krishnamurthy SL, Mallikarjunaiah H (2011) Stability analysis of puttabatta rice mutants. Karnataka Journal of Agricultural Sciences 24(4), 527-528.
| Google Scholar |
Lin CS, Binns MR (1988) A superiority measure of cultivar performance for cultivar × location data. Canadian Journal of Plant Science 68, 193-198.
| Crossref | Google Scholar |
Mohammadi R, Mendioro MS, Diaz GQ, Gregorio GB, Singh RK (2013) Mapping quantitative trait loci associated with yield and yield components under reproductive stage salinity stress in rice (Oryza sativa L.). Journal of Genetics 92(3), 433-443.
| Crossref | Google Scholar | PubMed |
Nachit MM, Nachit G, Ketata H, Gauch HG, Jr, Zobel RW (1992) Use of AMMI and linear regression models to analyze genotype-environment interaction in durum wheat. Theoretical and Applied Genetics 83(5), 597-601.
| Crossref | Google Scholar | PubMed |
Perkins JM, Jinks JL (1968) Environmental and genotype-environmental components of variability IV. Non-linear interactions for multiple inbred lines. Heredity 23(4), 525-535.
| Crossref | Google Scholar |
Qin H, Li Y, Huang R (2020) Advances and challenges in the breeding of salt-tolerant rice. International Journal of Molecular Sciences 21(21), 8385.
| Crossref | Google Scholar | PubMed |
Sa’diyah H, Hadi AF (2016) AMMI model for yield estimation in multi-environment trials: a comparison to BLUP. Agriculture and Agricultural Science Procedia 9, 163-169.
| Crossref | Google Scholar |
Shahriari Z, Heidari B, Dadkhodaie A (2018) Dissection of genotype × environment interactions for mucilage and seed yield in Plantago species: application of AMMI and GGE biplot analyses. PLoS ONE 13(5), e0196095.
| Crossref | Google Scholar | PubMed |
Yan W, Holland JB (2010) A heritability-adjusted GGE biplot for test environment evaluation. Euphytica 171(3), 355-369.
| Crossref | Google Scholar |
Yan W, Rajcan I (2002) Biplot analysis of test sites and trait relations of soybean in Ontario. Crop Science 42(1), 11-20.
| Crossref | Google Scholar | PubMed |
Yan W, Hunt LA, Sheng Q, Szlavnics Z (2000) Cultivar evaluation and mega-environment investigation based on the GGE biplot. Crop Science 40(3), 597-605.
| Crossref | Google Scholar |
Yan W, Kang MS, Ma B, Woods S, Cornelius PL (2007) GGE biplot vs. AMMI analysis of genotype-by-environment data. Crop Science 47(2), 643-653.
| Crossref | Google Scholar |
Yang R-C, Crossa J, Cornelius PL, Burgueño J (2009) Biplot analysis of genotype × environment interaction: proceed with caution. Crop Science 49, 1564-1576.
| Crossref | Google Scholar |