Predicting daily initial attack aircraft targets in British Columbia
S. W. Taylor A * and K. Nadeem BA Pacific Forestry Centre, Natural Resources Canada, Victoria, BC, Canada.
B Department of Mathematics and Statistics, University of Guelph, Guelph, ON, Canada.
International Journal of Wildland Fire - https://doi.org/10.1071/WF21090
Submitted: 24 June 2021 Accepted: 19 January 2022 Published online: 4 April 2022
© 2022 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of IAWF. This is an open access article distributed under the Creative Commons Attribution- NonCommercial 4.0 International License (CC BY-NC)
Abstract
We developed spatially explicit models of the daily probability of aircraft use in initial attack (IA) on a fire (hereafter the conditional models), and estimates of the unconditional probability of daily aircraft IA targets to support preparedness planning in the province of British Columbia, Canada, using a grid cell × day lasso-logistic framework. Novel aspects of our work include: (1) inclusion of an historical aircraft baseline covariate to account for missing or poorly estimated factors in our models; and of 2 day lead weather and Forest Fire Weather Index (FWI) covariates as proxies for fire potential trend, and (2) linking the conditional models of aircraft use in IA to models of daily fire occurrence to estimate the daily number of aircraft IA targets. The baseline risk of using an aircraft, population and road density were highly influential spatial covariates in both aircraft conditional models. The probability of sustained flaming, temperature, and FWI lead, and Sheltered Duff Moisture Code, temperature, and the Showalter Index were the three most influential meteorological variables in the conditional airtanker and helicopter IA models, respectively. We demonstrate the application of the models to portray the distribution of the expected number of daily aircraft IA targets.
Keywords: aerial suppression, fire danger, fire management, forecasting, initial attack, preparedness planning, resource demand prediction, statistical learning.
Introduction
The objective of initial attack (IA) is to contain fires during their incipient growth phase when there is a greater likelihood that IA resources can construct holding fireline faster than the fire perimeter is expanding, in order to limit fire size and potential damage. Aircraft (fixed wing and helicopters) are important to facilitating rapid IA in many jurisdictions. Airtankers can deliver long-term fire retardant to create retardant lines, or water/foam to extinguish flames and wet fuels in and ahead of the combustion zone. Helicopters are used to transport ground crews and water buckets, reconnoiter or conduct fire assessments (Trethewey 2007). Wildfire aviation costs (capital or contract costs, fuel, flight time and retardant) are a large portion of the budget of many fire agencies and thus aircraft need to be used efficiently (Aircraft costs make up ~20% of British Columbia’s fire suppression budget, ranging from approximately $CA 0 to 120 million annually; T. Nessman, Manager of Wildfire Operations, BC Wildfire Service, pers. comm.).
The management of many aircraft located at multiple bases to service a variable daily fire demand of varying severity is a complex multi-stage decision process with four primary components (D. L. Martell, University of Toronto, unpubl. data, 9 November 2011): (1) capacity planning of the number of aircraft and bases required; (2) location or siting of bases; (3) allocation of aircraft to bases that are located closer to expected fire targets on a seasonal or daily basis (termed home basing and day basing, respectively); (4) utilisation of aircraft, including potential deployment to multiple fires with differing and changing priority within a daily operational period, and the selection of attack tactics for different fire conditions.
The broad objective of wildfire aviation management is to minimise the total cost of fire response plus fire losses. Tactical and operational aircraft location and allocation decisions usually seek to minimise or meet a response time target at the least cost – it is assumed that the probability of a fire escaping IA is directly related to response time (Calkin et al. 2014). Managers who are day-basing aircraft must consider the potential threat of new fires occurring during the upcoming or following day that will require aircraft (hereafter called targets) in the operating range of each base, the number, capacity and air speed of the available aircraft and ferrying costs between bases, and allocate resources to minimise potential cost plus losses across the whole system. The wildfire threat includes the likely number of new fires, their intensity and growth rate, the values at risk and the availability of other air and ground resources within the operating area of each base – if other fire suppression resources are already heavily committed to active fires, then IA success maybe more critical. Furthermore, in a large jurisdiction with multiple bases, aircraft may preferentially be located at central bases where they can provide overload or surge capacity to other regions more quickly and at a lower cost than more distant bases (M. Benson, FP Innovations Wildfire Operations Research, previously Superintendent of Airtanker Operations, BC Wildfire Service, pers. comm.) when locally based aircraft are committed. Berry (2012) summarised the challenge in British Columbia as managing a supply chain delivering ‘10 731 tons of retardant per year by aircraft anywhere within 1 000 000 square kilometers, with an average response time of 17 minutes.’
Mathematical modelling over several decades has provided many insights into airtanker and helicopter management for fire response. Simulation, coverage and optimisation models have been used to examine how many or what types of airtankers and bases are needed at particular locations to service the demand for aerial IA in different jurisdictions. For additional background, see Islam et al. (2009), Martell (2007, 2015) and Wei et al. (2015). Of particular interest here, several allocation/deployment models have been developed to optimally assign aircraft resources to multiple bases in a jurisdiction (Hodgson and Newstead 1978; McLellan and Martell 1996; Islam et al. 2009; Chow and Regan 2011; Lee et al. 2013; Zeferino 2020). The daily aircraft IA demand input to these models is obtained by replaying or sampling fire weather or fire ignitions from historic fire seasons, or by stochastic simulation to obtain representative fire locations (Lee et al. 2013). Islam et al. (2009) suggest that their airtanker day-basing simulation model for Ontario could be used with real-time estimates of fire occurrence. Chow and Regan (2011) found that using their coverage model with forecasts of the Buildup Index of the US National Fire Danger Rating System to dynamically relocate aircraft outperformed standard response rules in severe fire weather in California. However, few allocation models have been used in fire operations (Martell 2015). Several authors note that more information on when and where fires will occur is needed to better plan the distribution of resources (Greulich 2003) and improve response times (Calkin et al. 2014).
The demand for aircraft for IA is connected to the spatio-temporal fire occurrence point process (Xi et al. 2019). Several spatially explicit statistical models of daily fire occurrence have been developed to estimate the potential location and number of new fires (e.g. Preisler et al. 2004; Wotton and Martell 2005; Magnussen and Taylor 2012; Nadeem et al. 2020; Woolford et al. 2021). Aircraft will be requested and dispatched on a proportion of new fire starts, or targets, depending on the observed and expected fire behaviour and values at risk from the fire, access and travel distance for ground resources, and availability of other resources in the event the fire escapes IA. We develop a set of statistical models incorporating indicators of fire danger, values at risk and road access to provide spatially explicit forecasts of the number of daily aircraft IA targets in the province of British Columbia, Canada. The BC Wildfire Service (BCWFS) makes extensive use of airtankers and helicopters in wildfire response. Electronic records of the movements of these aircraft and of weather and fire characteristics that have accrued over several decades provide a rich historical database for modelling. These models will provide new information for aircraft day-basing decisions that is only qualitatively represented by fire danger measures presently used to guide decisions.
Objectives
The objectives of our research are to: (1) evaluate the importance of some of the environmental and geographic factors that influence airtanker and helicopter use in IA, and (2) develop predictive models of the probability of an airtanker or helicopter being used in IA that can implemented in a fire management information system to forecast the likely number and location of new initial air attack targets.
We use an approach that combines models of the conditional probability of aircraft use in IA (hereafter the conditional models) with models of fire occurrence in BC developed by Nadeem et al. (2020). Specifically, we model the unconditional probability that a fire will occur at a population level P(B) irrespective of any other event, the conditional probability of an aircraft A being required given that a fire has occurred P(A|B) and the joint probability of an aircraft IA target P(A, B) = P(A|B) × P(B). This approach was inspired by models of large fire occurrence and of fire costs in the United States developed by Preisler et al. (2009, 2011) that employ a joint probability framework.
In addition to the joint modelling approach, several novel variables and model applications are introduced. In the ‘Variable Selection, data sources and compilation’ subsection, we introduce the use of airtanker and helicopter IA-caused base rates (a ranking of the average number of historical aircraft IA targets per grid cell since 1986) as covariates. The baseline rates were used to account for spatial variation in aircraft use that is not well explained by specific geographic variables (e.g. road density, distance to communities). We also introduce the use of lead (as opposed to lag) Fire Weather Index (FWI) System variables as indicators of expected fire weather in upcoming days. As in Nadeem et al. (2020), we used a measure of vegetation greenness (Normalized Differential Vegetation Index, NDVI) derived from remote sensing to represent seasonal variation in fire potential that is not otherwise accounted for by daily weather and fire danger measures, as well as a number of atmospheric stability indices derived from a reanalysis dataset that may represent atmospheric influences on fire behaviour that are not included in fire danger measures calculated for the land surface. In the ‘Unconditional models’ subsubsection, we link the two conditional aircraft IA models with two unconditional models of fire occurrence that we developed in Nadeem et al. (2020). The resulting grid-based unconditional probabilities are additive over the grid to estimate the expected number of aircraft IA targets in a geographic area on any day.
Materials and methods
Study area
An average of 1758 fires occurred annually in the province of BC, Canada, during 1986–2014 in a land area of approximately 93 million ha; 63 and 46% of these fires were lightning- and human-caused, respectively (Nadeem et al. 2020). The BCWFS has the primary responsibility for fire prevention, preparedness and response to protect life, property, timber and other natural resource values, in accordance with higher-level plans (BCWFS 2010). A variety of resources and tactics are used in fire response. Three-person IA crews are quickly deployed by ground or air to contain most newly reported fires. If initial assessment indicates that the new fire will likely not be contained by an IA crew, air tankers or helicopters may be used. Twenty-person extended attack (unit) crews, heavy equipment, helicopters and air tankers are utilised to contain and extinguish those fires escaping IA. Fires that are not a threat to human or resource values receive a modified response, which in some cases may only be observation. The demand for response resources varies across the province with the distribution of population, infrastructure, and the type and intensity of forest resource use, and through the fire season with weather and ignitions; human-caused fire starts have a bimodal distribution peaking in April and August, while lightning-caused fires have a unimodal distribution with a peak in July (Magnussen and Taylor 2012). Lightning storms can result in surges of dozens to hundreds of new fire ignitions in as little as 1–3 days.
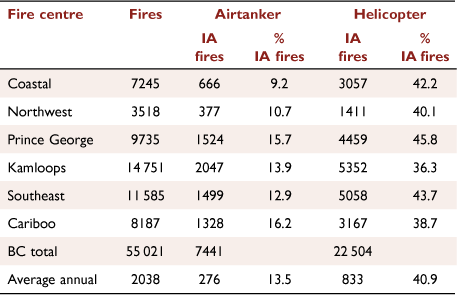
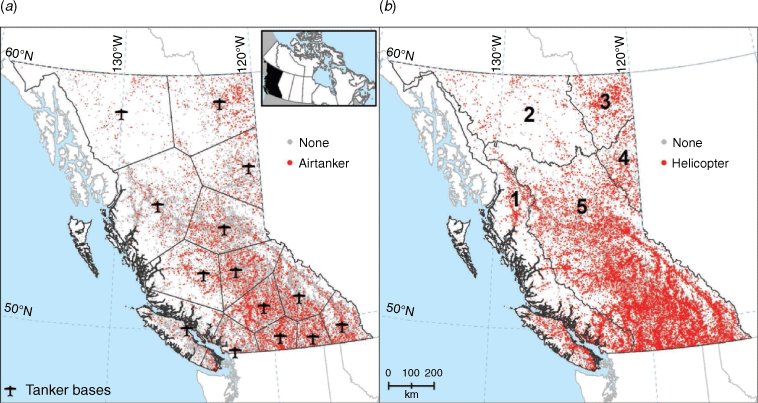
The BCWFS has long-term contracts for 30 airtankers that are based at one or more of 13 tanker bases during the fire season (Fig. 1a). Decisions about where to home-base airtankers in the fire season are made in late winter for a fixed contract period, depending on the historical amount of retardant use at a base. There is typically a seasonal pattern to fire occurrence, beginning at low elevations in the south at the beginning of the fire season, moving to the northern boreal region before leaf-out of deciduous trees, followed by a peak in fire starts in the central interior in summer. During the fire season, airtankers are repositioned, or day-based, to different tanker bases by the Airtanker Control Officer depending on a number of factors. These include fire danger (e.g. Buildup Index (BUI) of the Canadian FWI System exceeding 60 or 100 indicating significant fire potential in the Prince George and southern fire centres, respectively), expected ignitions and values at risk in the operating areas of each base, the ongoing fire load, including aircraft use on high-priority active fires in different regions, and the availability of ground resources. When a forest officer carrying out an assessment of a new fire requests airtanker assistance, the Provincial Air Tanker Centre may dispatch an air tanker, usually from the closest base to the fire, or reroute an airborne tanker to the fire, depending on fire potential and priority and aircraft availability. Helicopters are contracted from private firms on a day to medium term basis (e.g. 10–60 days), and are dispatched through one of six regional fire centres. Helicopters can be located at almost any site where they can refuel. During periods of elevated fire danger, helicopters and IA crews can be prepositioned to high-risk areas. Airtankers and helicopters are used in IA on an average of 13.5 and 40.9% of fires, respectively (Fig. 1, Table 1).
|
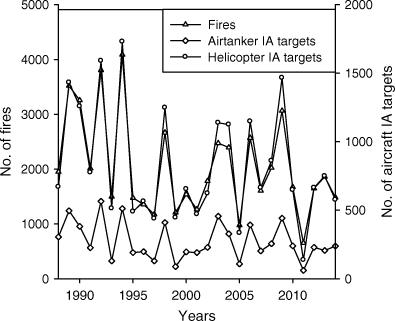
Annual aircraft use in IA tracks the annual number of fires (Fig. 2), although there is somewhat greater variability in the number of aircraft IA fires than fires (coefficients of variation are 43 and 57% for the annual number of fires and number fires with aircraft use in IA, respectively); proportionally more aircraft are used in IA in years with more fires. Average airtanker use in IA ranges from 9 to 16% in six regional fire centres (shown in Fig. 3) – it is highest in central BC and lowest in coastal BC. Average helicopter use in IA varies from 36 to 46%, and is highest in north central and southeast BC and the lowest in central BC.
|
Modelling approach
Spatio-temporal variation in the requirement for aircraft for IA is a considerable challenge in daily preparedness planning. Thus, our objective is to estimate the likelihood of a new airtanker or helicopter IA target fire at any grid location across BC on a daily basis for application in a predictive model to inform decision making. The sample space is all days in each fire season, defined as a 7-month period from 16 March to 14 October for the years 1988–2014 over the province of BC. The sampling unit is a space-time voxel vij, which represents a 24-h period j (starting at midnight) for a 20 × 20 km cell i; the 400-km2 resolution grid over BC comprises 2541 cells. This discretised approach allows the use of spatially explicit logistic regression models to estimate the probability of an event. We used a two-stage procedure in our modelling framework. First, we estimated the conditional probability of an aircraft being used in IA in vi,j, given at least one fire occurrence in the voxel (there are few grid cells with more than one ignition per voxel at the 20 km scale). Secondly, the unconditional probability of an aircraft IA target was estimated as the joint probability of aircraft use and the probability of one or more ignitions in a voxel. The latter probability was estimated from the daily human- and lightning-caused fire occurrence models that we developed in Nadeem et al. (2020). Our conditional models represent the average concurrent relationship between a set of explanatory variables (represented by a data matrix X) and the Bernoulli model of aircraft use (0, 1) in IA (represented by the response vectors Y) conditional on a fire occurrence Z = 1 (represented by the response vector Z).
Variable selection, data sources and compilation
The first step in model development was to populate the data frame consisting of a data matrix X and the response vectors Y and Z associated with the voxels V. The 80 variables listed in Table 2 were included as candidate explanatory variables X for both of the models of airtanker and helicopter use in initial attack. They include spatially varying but temporally static baseline, geographic, vegetation and ecumene variables, and dynamic spatio-temporally varying meteorological variables; the meteorological, vegetation and geographic variables are collectively indicators of potential fire severity and difficulty of control, while the ecumene variables are measures of access and distance to values in the built environment. The explanatory variables, along with aircraft and fire occurrence records, are a mixture of point and gridded and categorical and continuous data in their raw form. The response and explanatory variables were imputed to each day × cell voxel, or interpolated to the centroid of each cell, for approximately 15 million voxels (2541 cells × 34 years × 214 days) as described in the following section. Random subsets of voxels from this large spatio-temporal dataset were used for model fitting, as described in the response-based sampling section that follows.
Incidents and aircraft response. We obtained records of ~70 000 fires that occurred during the years 1986–2014 from the BCWFS Incident database, including the fire number (a unique fire identifier within a year), fire location (latitude, longitude), fire centre, and discovery and IA dates. We also obtained records of ~250 000 flights that took place during 1986–2014 that were recorded in the BCWFS Aircraft Management System (AMS) database, including the flight date, aircraft model, tail (registration) number, hours of use, number of legs flown, and associated fire number and fire centre – that is, the number of legs and hours flown by a particular aircraft on a particular fire on a particular day. We then categorised the aircraft models (approximately 145 rotary and fixed wing aircraft models) in the database into five broad types: airtanker, other fixed wing, and light, medium and heavy helicopter (e.g. Tretheway 2007) and discarded the records for the ‘other fixed wing’ group. When necessary, the Canadian Civil Aircraft Register (https://wwwapps.tc.gc.ca/saf-sec-sur/2/ccarcs-riacc/RchSimp.aspx, accessed 1 November 2021) was used to match tail numbers to aircraft models. We determined whether an aircraft was used in IA by first sorting the aircraft records by fire number and date, then merging them with the incident database by fire number and fire discovery date/first aircraft flight date. The resulting 60 000 records of fire number, fire discovery date, latitude, longitude, airtanker and helicopter IA counts were mapped to our space–time voxels by latitude, longitude and fire discovery date. At the spatial resolution of our analysis (20 × 20 km), most of the daily aircraft IA counts are reduced to either 0s or 1s.
Baseline, environment and ecumene covariates. The base rate of airtanker and helicopter use in IA across BC was estimated from the total count of these events in a cell over 29 years (Fig. 3). We assume that these counts reflect the long-term expectation of the response variable over the spatial grid, and are used in the models as rank transformed covariates (baseline airtanker and helicopter ranks in Table 2) assuming a stationary spatial pattern and not accounting for uncertainty in the estimates.

|
Most of the meteorological, vegetation and geographic variables (representing fire potential) and measures of the ecumene (representing access and values at risk) that may influence the likelihood of airtanker or helicopter use in IA (Table 2) were drawn from the dataset used to model daily human- and lightning-caused fire occurrence in Nadeem et al. (2020). Briefly these include:
Geography – ecozone, elevation, topographic roughness and elevation;
Vegetation – the proportion of vegetated and non-vegetated area, treed and non-treed area; area covered by coniferous and deciduous tree species, the proportion of the treed area in conifer, deciduous or mixed-wood classes (>75, 26–75, and <25% needle-leaf proportion, respectively) and the average daily NDVI (as a measure of the average seasonal trend in vegetation greenness in a grid cell).
Surface weather and fire danger: temperature, relative humidity, wind speed and 24 h precipitation at 1200 hours, the daily Fine Fuel Moisture Code, Duff Moisture Code, Drought Code, Initial Spread Index, Buildup Index and Fire Weather Index (FFMC, DMC, DC, ISI, BUI, FWI, respectively) of the Fire Weather Index System (Van Wagner 1987) and the sheltered duff moisture code or SDMC (Wotton and Martell 2005).
Atmospheric stability: daily values of the K, Showalter, Totals and Continuous Haines Indexes (Mills and McCaw 2010; Stull 2015), the 500 mb geopotential height anomaly, and the 500 mb height pressure tendency.
Ecumene: the total length of roads (km) and population in each cell, and the proportion of a cell composed of or the distance from the cell midpoint to a WUI or WII feature.
The data sources and methods that were used to estimate these variables are described more fully in Nadeem et al. (2020). Squared and square root terms were also included for a number of the covariates to account for the possibility of non-linear response, while a number of lag terms and interactions wre included with the meteorological variables. Four new variables were introduced in the present study: the average of the wind speed, precipitation, ISI and FWI values on the discovery date and the following 2 days, which we term WINDSPEED, PRECIPITATION, ISI and FWI LEAD3. The lead variables were included to represent information on the expected near-term fire weather and danger tendency that is available to all fire personnel through daily or twice daily weather briefings during the fire season; we expect that this information may influence fire managers' perception of risk in the upcoming days.
Response-based sampling, model development and variable ranking
We split the 29 years of study dataset into training (1986–2008) and test datasets (2009–2014) for both the AT-IA and HELI-IA models. The training dataset comprises ~81% of the IA fires. Our model development and variable ranking procedures use an ensemble approach based in response-based sampling of the XYZ data frame. Approximately 60 000 of the 18 million voxels spanning 29 fire seasons (1986–2014) have one or more fire occurrences; we estimate that an airtanker or helicopter was used in IA in 13 and 41% of these voxels, respectively (Table 1).
We used a response-based downsampling scheme (see Nadeem et al. 2020) to improve the class-balance, where all of the case observations Y = 1|Z = 1 (Y = aircraft use, Z = fire occurrence) are retained as well as a simple balanced random sample of the controls (Y = 0|Z = 1); this procedure was repeated to create 500 balanced samples. We opted for a large number of datasets in our ensemble because it better explores the control sample space and so improves the predictive skill of the ensemble mean, and results in more stable variable rankings.
We fitted individual Lasso-logistic regression models to the 500 samples to predict day–cell probabilities of aircraft use in IA over grid voxels, using the R package glmnet (Friedman et al. 2010) for the two aircraft types: (i) an AT-IA model of the likelihood of airtanker use in IA, and (ii) a HELI-IA model of the likelihood of helicopter use in IA. The relationship between the covariate values and the conditional probability of an aircraft being used in IA on a given cell-day was estimated using a logistic regression model (following the approach of Preisler et al. (2011) for large fire prediction) as:
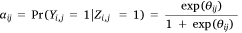
where αi,j is the conditional probability of an aircraft being used in cell j on day i, Yi,j is the binary aircraft utilisation variable (0,1) in cell i on day j, and Zi,j is the binary indicator variable for the presence of at least one fire at ij. The linear predictor θ in cell i on day j is calculated as:
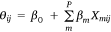
where Χm,i,j is the value of a covariate Χm in cell i on the jth day, β0 is the intercept and β = (β1, β1,…, βm)t is the vector of regression coefficients.
The Lasso-logistic regression model (Tibshirani 1996) is a regularised version of ordinary logistic regression with automatic variable selection that shrinks covariate coefficients to zero if they do not contribute to the model fit – thus, the regression coefficients of the retained covariates reflect their contribution to model fit. The regularisation imposes a penalty 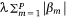 on the coefficients vector β. The tuning parameter λ, which controls the amount of shrinkage, was estimated using k-fold cross-validation (Tibshirani 1996). The case-control sampling procedure also introduces a deterministic offset intercept term log(p1/p0), in the linear predictor θ, where p1 = 1 for our balanced sample and p0 is the ratio of the number of controls to the number of cases in the full dataset (Hosmer and Lemeshow 2000). After carrying out 500 model fits using the same model form and covariates, we determined the average value of each coefficient
on the coefficients vector β. The tuning parameter λ, which controls the amount of shrinkage, was estimated using k-fold cross-validation (Tibshirani 1996). The case-control sampling procedure also introduces a deterministic offset intercept term log(p1/p0), in the linear predictor θ, where p1 = 1 for our balanced sample and p0 is the ratio of the number of controls to the number of cases in the full dataset (Hosmer and Lemeshow 2000). After carrying out 500 model fits using the same model form and covariates, we determined the average value of each coefficient 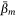 that was selected in the ensemble; these average coefficients are used in predictive applications. It is noteworthy that each of the individual model fits may select a slightly different suite of variables, and that the rank order of the covariates will be different in each model fit.
that was selected in the ensemble; these average coefficients are used in predictive applications. It is noteworthy that each of the individual model fits may select a slightly different suite of variables, and that the rank order of the covariates will be different in each model fit.
Two methods were used to rank variable importance that exploit properties of the Lasso-logistic model and the ensemble approach, which are detailed in the supplement to Nadeem et al. (2020). In the first method, we compute the standardised regression coefficients 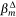 in each of 500 model fits and determine the rank order of the non-zero standardised coefficients
in each of 500 model fits and determine the rank order of the non-zero standardised coefficients 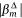 > 0. We then determine the average rank for each of the P covariates over the 500 model fits. In the second method, we utilise the automatic variable selection function in lasso-logistic regression to compute an index
> 0. We then determine the average rank for each of the P covariates over the 500 model fits. In the second method, we utilise the automatic variable selection function in lasso-logistic regression to compute an index 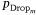 notated as:
notated as:
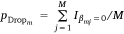
that represents the proportion of times that the mth covariate is dropped in the 500 model fits (where 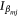 is an indicator of whether a covariate βm was included in the jth model fit or not). That is, those variables that are most influential have lower
is an indicator of whether a covariate βm was included in the jth model fit or not). That is, those variables that are most influential have lower 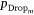 values. The covariates selected in the conditional AT-IA and HELI-IA model, their rank, ordered average standardised coefficients
values. The covariates selected in the conditional AT-IA and HELI-IA model, their rank, ordered average standardised coefficients 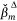 , and
, and 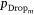 values are listed in Appendix Table A2, Table A3. Note that
values are listed in Appendix Table A2, Table A3. Note that 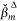 is the average of standardised coefficients where
is the average of standardised coefficients where 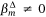 over the set of 500 coefficients for Χm.
over the set of 500 coefficients for Χm.
(1) Unconditional models. Our AT-IA and HELI-IA models estimate the probability of airtanker or helicopter use in initial air attack in a voxel vij, conditional on one or more fires occurring in the voxel (day × grid cell). In previous work, we used a similar spatio-temporal framework to develop three models of daily fire occurrence in BC (Nadeem et al. 2020), which are termed HCF, OLCF and PLCF (Human Caused Fire, Observed Lightning Caused Fire and Potential Lightning Caused Fire models, respectively). In this second stage, we develop unconditional models of aircraft IA targets as a joint probability of fire occurrence and aircraft use (the two lightning-caused fire models employ different covariates to represent lighting potential – the OLCF model includes observed and lagged lightning strikes, whereas the PLCF model includes measures of atmospheric stability as proxies for thunderstorm potential; the OLCF and PLCF models are intended to be used in nowcasting (after a lightning storm) and forecasting applications, respectively). As an intermediate step, we combine the human- and lightning-caused fire occurrence models to estimate the marginal probability of a fire of any cause as:
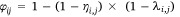
where φi,j, ηi,j, and λi,j are the probability a fire, a human-caused fire, and a lightning caused fire in cell i on day j, respectively. We assume that human and lightning fire occurrences are conditionally independent given the values of the covariates because they arise from independent ignition processes. Also, because fires are rare events at the scale of our model (400 km2 cell × 1 day), it is unlikely that a lightning and person-caused fire would occur in the same voxel.
The unconditional probability of a fire requiring an airtanker or helicopter for IA τ in cell i on the jth day is then estimated as the product of the conditional and marginal models:
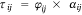
We developed four estimates of τij, which we term AT-IAO, AT-IAP, HELI-IAO and HELI-IAP, that result from combining the two conditional airtanker and helicopter models (AT-IA, HELI-IA) and the two marginal fire occurrence models φij that incorporate either the HCF and OLCF models (O), or the HCF and PLCF models (P), respectively; hereafter, we will refer to these four estimates as models.
2. Number of aircraft IA targets. A property of our modelling framework is that, although some of the covariates may be spatially correlated, we assume that the response variable Yi,j, is independently distributed over day-cell combinations conditional on the values of the spatially and temporally specific explanatory variables. Thus, we obtain a count of the total number of events NG,j on the jth day as the sum of the probabilities 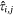 over all G grid cells (Preisler et al. 2009) as:
over all G grid cells (Preisler et al. 2009) as:
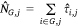
where 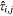 is the estimated probability of at least one aircraft IA target occurring in voxel (i, j). For the conditional models,
is the estimated probability of at least one aircraft IA target occurring in voxel (i, j). For the conditional models, 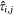 is summed over only those cells in G with a fire occurrence Z = 1 on the jth day. By including temporally and spatially explicit covariate values, it is possible to have a different expected probability in a cell on different days and in nearby cells on the same day (Preisler et al. 2004).
is summed over only those cells in G with a fire occurrence Z = 1 on the jth day. By including temporally and spatially explicit covariate values, it is possible to have a different expected probability in a cell on different days and in nearby cells on the same day (Preisler et al. 2004).
Model evaluation
After fitting the conditional models with the training dataset, we evaluate the performance of all of the models with the test dataset in terms of the AUC (Area under Receiver Operating Characteristic (ROC) curve) (Hosmer and Lemeshow 2000) and the sensitivity (true positive rate) and specificity (true negative rate). In calculating the sensitivity and specificity, the threshold for classifying aircraft target probabilities as 0 (false or no target) or 1 (positive or at least one target) was based on the Youden index criterion associated with the computed ROC curves (Youden 1950; Hand 2012). The conditional models are evaluated with respect to those voxels in the test dataset where one or more fires occurred (Z = 1), and the unconditional models are evaluated with respect to all voxels in the test dataset (2009–2014). We also compare the predicted 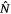 and observed values N of aircraft use in IA with the same evaluation data.
and observed values N of aircraft use in IA with the same evaluation data.
Results
We developed two models of the conditional probability of using an airtanker (AT-IA and HELI-IA) that, when combined with two estimates of the marginal probability of a fire, yielded four estimates of the unconditional probability of an airtanker or helicopter IA target (AT-IAO, AT-IAP, HELI-IAO and HELI-IAP, which we also refer to as models). In this section, we contrast the variable importance of the two conditional models and the predictive performance of all six models, and demonstrate an application of the models to estimate the number and locations of aircraft IA targets on 4 days in the test dataset.
Variable importance in the conditional models
The variable rank score, average standardised regression coefficient 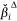 and pDrop index for all of the variables that were included in the AT-IA and HELI-IA models are in Appendix Table A2, Table A3 in rank order. We reiterate that the average non-standardised coefficients,
and pDrop index for all of the variables that were included in the AT-IA and HELI-IA models are in Appendix Table A2, Table A3 in rank order. We reiterate that the average non-standardised coefficients,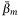 , (not reported here) are implemented in model prediction applications. The rank score and pDrop have a negative relationship (Fig. 4); we consider that covariates with pDrop below 0.2 are the most important predictors in their respective models. We emphasise that pDrop and importance rank values reveal different aspects of how a covariate influences the predictive skill of the ensemble model. Rank describes a covariate’s influence relative to all other covariates, whereas pDrop measures how often that covariate was selected (or rejected) in the 500 model fits.
, (not reported here) are implemented in model prediction applications. The rank score and pDrop have a negative relationship (Fig. 4); we consider that covariates with pDrop below 0.2 are the most important predictors in their respective models. We emphasise that pDrop and importance rank values reveal different aspects of how a covariate influences the predictive skill of the ensemble model. Rank describes a covariate’s influence relative to all other covariates, whereas pDrop measures how often that covariate was selected (or rejected) in the 500 model fits.
|
|
We screened 38 static spatial variables and 42 dynamic temporal variables in the conditional AT-IA and HELI-IA models. Of these, 76 and 70 variables were selected in at least 1% of an ensemble of 500 model fits of the AT-IA and HELI-IA models respectively (Appendix Table A2, Table A3). However, we consider the 27 and 32 variables that were selected in at least 80% of the 500 model fits in the AT-IA and HELI-IA models, respectively (pdrop index ≤ 0.20) influential (Table 3). Among these variables, 6 dynamic and 13 static variables were common to both models. The meteorologically related dynamic variables PSUF, TEMPERATURE, FWI LEAD3, K INDEX, SDMC and WINDSPEED all had a positive effect in both models.

|
The static spatial variables BASE RATE, POPULATION, ELEVATION2, WII DISTANCE, WUI AREA, %MIXEDWOOD, LATITUDE and TREED had a positive effect in both models. ROAD LENGTH0.5, POPULATION0.5 and ROUGHNESS had a negative effect, which suggests greater probability of aircraft use in IA in forested areas with lower road density and in less rugged terrain, and that the population effect has a levelling-off function. MONTANE CORDILERRA and TAIGA PLAIN ecoregions were also influential covariates; however, it is more difficult to interpret the effect of ecoregions due to confounding with the base rate covariate.
Among the covariates unique to the AT-IA model, ISI LEAD3 and WII AREA have a positive influence. PRECIPITATION LAG1, PRECIPITATION LAG2, LONGITUDE, 500 MB ANOMALY, DC and WINDSPEED LEAD3 had a negative influence. That is, there is increasing probability of airtanker use in IA west to east and with falling atmospheric pressure. The seemingly contrary effect of DC may be due to DC increasing steadily over the fire season, whereas fire occurrence peaks in the middle of the season in BC. The negative influence of WINDSPEED LEAD3 may be because increasing wind speed can be associated with a drying trend, neutral drying conditions or a wetting trend, whereas increasing ISI and FWI are almost always associated with a drying trend or neutral drying conditions.
In the HELI-IA model, RELATIVE HUMIDITY, WII DISTANCE2, ISI2, BUI, AVERAGE NDVI2, DC2 and %CONIFER2 had a positive influence. SHOWALTER INDEX, FWI*TEMPERATURE, TOTALS INDEX, 500 MB TENDENCY, CHI and PRECIPITATION LAG3 had a negative influence. However, an increasingly negative SHOWALTER indicates instability, consistent with positive influence of the K INDEX, although the TOTALS INDEX and CHI stability indexes have an opposite influence.
Model skill
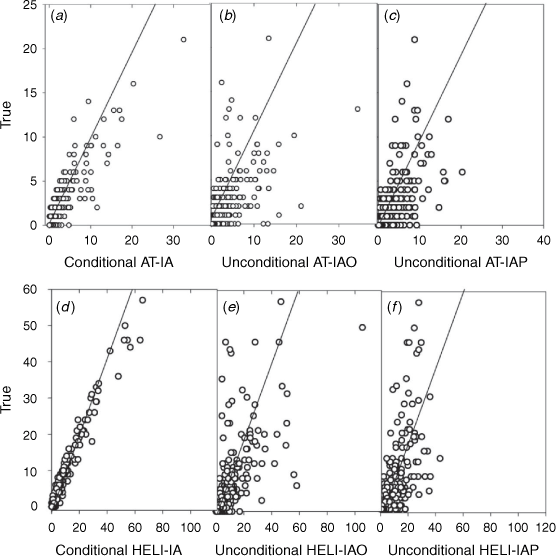
We assessed the predictive skill of the two conditional models and four unconditional estimators with regard to ROC characteristics, provincial scale time series, and plots of predicted vs observed values using 5 years of out-of-sample data for all cell × day voxels, and for only those voxels where fires were observed. The accuracy of all the models in predicting aircraft use for all cell–day combinations in the test data was very good (AUC > 0.9) but only fair (0.60–0.76 for the cell–days (Z = 1) where fires occurred. The AUC for Z = 1 cases and sensitivity for all cases were higher for the airtanker than the comparable helicopter models, while the specificity was similar (Table 4). Sensitivity (true positive rate) was greater than specificity (true negative rate) for all models; specificity was greater for the unconditional models with observed lightning strikes (AT-IAO, HELI-IAO) than with lightning indicators (AT-IAP, HELI-IAP) but sensitivity was opposite.
|
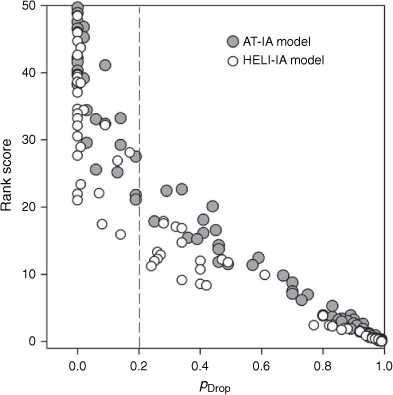
We examined the performance of the six models in predicting daily aircraft IA targets at a provincial scale by comparing the predicted (sum of the cell-based probability values over all cells on a particular day) vs the observed daily fire counts in the test years (Fig. 5). All of the models track the daily variation in aircraft IA targets quite well. As expected, the conditional models were better than the unconditional models at capturing the larger peaks in the number of daily targets, which is also evident in the predicted/observed plots in Fig. 6. However, the conditional models have less practical value in a predictive application because the fires have already occurred. The AT-IAO and HELI-IAO models seem to have better sensitivity on days with a higher number of targets, approximately more than 10 and 30 targets respectively, while the AT-IAP and HELI-IAP models may have better specificity on days with a lower number of targets. The spatial residuals for the unconditional AT-IAP and AT-IAP models are shown in Fig. 7. Not surprisingly, absolute error is higher in areas with high aircraft use as shown in Fig. 3, but it appears to be as underprediction.
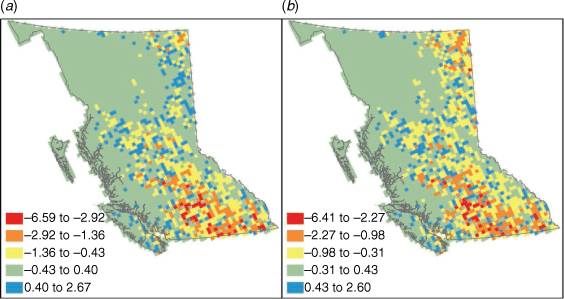
|
Discussion
The aircraft IA use base rates were very influential covariates in the airtanker and helicopter models, as were the base fire occurrence rates in the fire occurrence models in Nadeem et al. (2020). The base rates reported here were rank transformations of the count of aircraft IA targets, regardless of the number of fires that occurred in a cell (e.g. absolute vs proportional or conditional values). We also calculated a base rate as the proportion of fires with aircraft use in IA in a cell, which resulted in 2–3% higher AUC values for the Z = 1 (fire only) cases, and fewer highly influential variables, indicating better model fits. However, the proportional base rate probability values are spurious for cells with only a few fire occurrences. Further consideration will be given to modelling an appropriate conditional base rate. It is noteworthy that our base rates are from 29 years of data; base rate estimates may be poorer in jurisdictions with shorter data records.
The influence of access (ROAD LENGTH) and POPULATION was contrary in both the AT-IA and HELI-IA models, suggesting both a greater use of aircraft for IA near populated places, but also with decreasing accessibility; this is consistent with findings for federally contracted large airtanker use in the US (Stonesifer et al. 2016). The six indexes of the FWI System were less influential than temperature, windspeed, PSUF (probability of sustained flaming) and SDMC in the conditional airtanker and helicopter models. We only included one (a model for lodgepole pine forests) of many PSUF models for different forest fuel types; other PSUF models derived for different fuel types could be evaluated in future. The importance of the lead variable FWI LEAD3 (average FWI for today, tomorrow and overmorrow) was surprising and may be because we are modelling the human decision to allocate an aircraft, conditional on a request, not a physical process. All fire personnel receive or have access to daily to twice daily weather briefings during the fire season ‒ the positive influence of FWI LEAD3 may reflect a greater tendency to request and dispatch aircraft when there is an expectation of increasing fire danger.
We examined a number of atmospheric stability indices representing the potential for convective storms (K, Totals, and Showalter Indexes) or convection (CHI) that are composed of stability and moisture terms calculated from temperature and dewpoint temperature in different combinations of 850, 700 and 500 hPa layers. Among these, the K-Index1 was influential in both the airtanker and helicopter models, whereas the Totals Index, Showalter Index or CHI were also influential in the helicopter model.
Although it is a good indicator of lighting occurrence, Potter et al. (2003) suggest that the K Index may not be the most suitable fire danger indication as high KI values can result from both high atmospheric moisture as well high instability. However, the variation in atmospheric moisture (as reflected in the dewpoint) may be less for days and locations where fires occurred (Z = 1), and the instability term may predominate. Although it is difficult to interpret why the K Index is more influential that the Totals Index, Showalter Index or CHI in our models, atmospheric instability is clearly important, likely owing to its influence on the rapid early growth of the aircraft IA target fires. Atmospheric stability indexes are not included among the fire danger indexes of the FWI System, and this finding provides support for further investigation.
Our interest is in developing unconditional models of daily aircraft IA targets to inform aircraft day-basing decisions by linking conditional models of aircraft use with daily fire occurrence models developed in earlier work, and in predictive performance over explanation. Thus, we took the approach of fitting an ensemble of 500 conditional models to a balanced dataset with lasso logistic regression in a manner that was compatible with the fire occurrence models of Nadeem et al. (2020), although the aircraft dataset has far fewer observations and is less imbalanced. A potential issue with our approach is that errors may be spatially correlated; however, the large number of explanatory variables used in the models may mitigate this problem. Other techniques such as deep learning could be examined for their potential to improve predictive performance in future work.
The sensitivity and specificity of the conditional AT-IA model was greater than for the HELI-IA model, perhaps because the airtankers are used for only one IA function (delivering fire retardant) that is strongly related to the threat of the target fire (e.g. potential fire behaviour and values at risk), whereas helicopters are used for a number of tasks in IA and on more fires with a potentially wider range of fire behaviour. Our work is a further demonstration of the application of fire occurrence models in a joint probability framework to estimate a number of other events, where the event is conditional on a fire occurring.
The predictive performance of the unconditional models is based in part and ultimately limited by the skill of the three fire occurrence models in Nadeem et al. (2020), which followed the series OLCF > PLCF > HCF (observed lightning, predicted lightning and human-caused fire occurrence, respectively). The AUC, sensitivity and specificity of the AT-IAO is comparable with the OLCF and greater than HCF, whereas that of the AT-IAP is similar to the PLCF and greater that HCF. The AUC, sensitivity and specificity of the HELI-IAO and HELI-IAP models are similar to the HCF. Future improvements in the skill of the daily fire occurrence models, and particularly the HCF model (see discussion in Nadeem et al. 2020) will improve the unconditional airtanker IA models, and any other conditional model linked to fire occurrence.
A caveat of our statistical learning approach is that it reflects past decisions both to request and dispatch or not an aircraft for IA that we assume are mainly correct in our large sample. It would be useful to better understand and examine ways to assess the conditions associated with Type I decision errors (where aircraft are requested/dispatched but the true fire threat is overestimated), and particularly for Type II errors (where the true fire threat is underestimated and aircraft are either not requested or dispatched) as well as the influence of Type II errors in IA success. One possible means that has been used to examine air ambulance tasking is a retrospective review of a sample of dispatch decisions (Wilmer et al. 2015), but we leave this for future work.
Potential application
The counts of the probable number of aircraft IA targets and maps of probable aircraft IA target locations will provide fire managers with more information on the potential demand for aircraft to consider when making day-basing decisions than maps of FWI System values that are used at present. Figs 8, 9 provide examples of predicted aircraft IA target probabilities vs observed fire locations for 4 days in the test dataset with low (1 July 2009) and high–very high (9, 27, 28 July) numbers of aircraft IA targets. The unconditional models provide a sharper spatial picture of the location of probable aircraft IA targets (specificity) than do the conditional models as well as estimates of the likely number of targets, and a much sharper lens than maps of the BUI of the FWI System (Appendix Fig. A1) that are often used as an indicator of potential airtanker demand. The AT-IAO and HELI-IAO models could be used with observed and forecast lightning strike counts (cf. Burrows et al. 2005) on the present and following 2 days, while the AT-IAP and HELI-IAP models could be used with medium-term weather forecast models (e.g. 3–14 days) to provide an estimate of demand over a 2-weekplanning period. Estimates of the number and location of IA targets may facilitate future work to optimise coverage and minimise response time. However, this study is an early exploration of the predictability of the number and location of aircraft IA targets. More time will be required to evaluate the skill of the models with forecast data. We also reiterate that the number of targets is only one component of daily demand, particularly for air tankers, and one factor in aircraft day-basing decisions. The amount of fire retardant required to be delivered from a tanker base on any day, which is influenced by potential fire behaviour and growth, is a more complete measure of demand and another area for future investigation.
The importance of managing aircraft resources in BC is likely to increase with changing climate. It is noteworthy that 8 of the 33 anomalously high-area-burned years in the 100-yearperiod 1921–2020 occurred between 2001 and 2020, including two very severe seasons (Taylor 2021), despite increasing suppression effort over the century. Indeed, the record-breaking 2018 fire season in BC with approximately 1.5 million ha burned was estimated to be 2–5 times more likely due to anthropogenic climate change (Kirchmeier-Young et al. 2019). Predictive models of the location of potential aircraft IA target fires that can better inform day-basing decisions may help maintain IA success, and could be used with climate projections to simulate future aircraft demand with climate change.
Data availability
The data that support this study were obtained in part from the BC Wildfire Service by permission. Data will be shared upon reasonable request to the corresponding author with permission from the BC Wildfire Service.
Conflicts of interest
The authors declare no conflict of interest.
Declaration of funding
This research did not receive any specific funding.
Acknowledgements
The cooperation of the BC Wildfire Service in providing Aircraft Management System data is gratefully acknowledged. M. Benson and D. Marek (formerly of the BC Wildfire Service) contributed insights about airtanker and helicopter management. K. Omendje assisted with data compilation and G. Thandi prepared the maps. Many thanks to K. Lertzman, C. Dean, D. Martell, F. Zwiers, M. Krawchuk, C. Kolden, the associate editor and two anonymous reviewers for helpful comments on earlier drafts of the paper.
References
B.C. Wildfire Service (BCWFS) (2010) Wildland fire management strategy. Available at https://www2.gov.bc.ca/assets/gov/public-safety-and-emergency-services/wildfire-status/governance/bcws_wildland_fire_mngmt_strategy.pdf [Accessed 7 September 2020]Berry J (2012) Managing airtankers for measurable performance. Wildland Fire Canada 2012 Conference, 1–4 October 2012, Kananaskis, AB.
Burrows WR, Price C, Wilson LJ (2005) Warm season lightning probability prediction for Canada and the northern United States. Weather and Forecasting 20, 971–988.
| Warm season lightning probability prediction for Canada and the northern United States.Crossref | GoogleScholarGoogle Scholar |
Calkin DE, Stonesifer CS, Thompson MP, McHugh CW (2014) Large airtanker use and outcomes in suppressing wildland fires in the United States. International Journal of Wildland Fire 23, 259–271.
| Large airtanker use and outcomes in suppressing wildland fires in the United States.Crossref | GoogleScholarGoogle Scholar |
Chow JYJ, Regan AC (2011) Resource location and relocation models with rolling horizon forecasting for wildland fire planning. Informs 49, 31–43.
| Resource location and relocation models with rolling horizon forecasting for wildland fire planning.Crossref | GoogleScholarGoogle Scholar |
Friedman J, Hastie T, Tibshirani R (2010) Regularization paths for generalized linear models via coordinate Descent. Journal of Statistical Software 33, 1–22.
| Regularization paths for generalized linear models via coordinate Descent.Crossref | GoogleScholarGoogle Scholar | 20808728PubMed |
Greulich FE (2003) Airtanker initial attack: a spreadsheet-based modeling procedure. Canadian Journal of Forest Research 33, 232–242.
| Airtanker initial attack: a spreadsheet-based modeling procedure.Crossref | GoogleScholarGoogle Scholar |
Hand DJ (2012) Assessing the performance of classification methods. International Statistical Review 80, 400–414.
| Assessing the performance of classification methods.Crossref | GoogleScholarGoogle Scholar |
Hodgson MJ, Newstead RG (1978) Location-allocation models for one-strike initial attack of forest fires by airtankers. Canadian Journal of Forest Research 8, 145–154.
| Location-allocation models for one-strike initial attack of forest fires by airtankers.Crossref | GoogleScholarGoogle Scholar |
Hosmer DW, Lemeshow S (2000) ‘Applied Logistic Regression’, 2nd edn. (Wiley: New York, NY)
Islam KS, Martell DL, Posner MJ (2009) A time-dependent spatial queueing model for the daily deployment of airtankers for forest fire control. INFOR: Information Systems and Operational Research 47, 319–333.
| A time-dependent spatial queueing model for the daily deployment of airtankers for forest fire control.Crossref | GoogleScholarGoogle Scholar |
Kirchmeier‐Young MC, Gillett NP, Zwiers FW, Cannon AJ, Anslow FS (2019) Attribution of the influence of human‐induced climate change on an extreme fire season. Earth’s Future 7, 2–10.
| Attribution of the influence of human‐induced climate change on an extreme fire season.Crossref | GoogleScholarGoogle Scholar |
Lee Y, Fried JS, Albers HJ, Haight RG (2013) Deploying initial attack resources for wildfire suppression: spatial coordination, budget constraints, and capacity constraints. Canadian Journal of Forest Research 43, 56–65.
| Deploying initial attack resources for wildfire suppression: spatial coordination, budget constraints, and capacity constraints.Crossref | GoogleScholarGoogle Scholar |
MacLellan JI, Martell DL (1996) Basing airtankers for forest fire control in Ontario. Operations Research 44, 677–686.
| Basing airtankers for forest fire control in Ontario.Crossref | GoogleScholarGoogle Scholar |
Magnussen S, Taylor SW (2012) Prediction of daily lightning-and human-caused fires in British Columbia. International Journal of Wildland Fire 21, 342–356.
| Prediction of daily lightning-and human-caused fires in British Columbia.Crossref | GoogleScholarGoogle Scholar |
Martell DL (2007) Forest Fire Management: current practices and new challenges for operational researchers. In ‘Handbook of Operations Research in Natural Resources’. (Eds A Weintraub, C Romero, R Trond Bjorndal, R Epstein, J Miranda) pp. 489–509. (Springer Science+Business Media: New York, NY)
Martell DL (2015) A review of recent forest and wildland fire management decision support systems research. Current Forestry Reports 1, 128–137.
| A review of recent forest and wildland fire management decision support systems research.Crossref | GoogleScholarGoogle Scholar |
Mills GA, McCaw L (2010) Atmospheric stability environments and fire weather in Australia – extending the Haines Index. CAWCR Technical Report No. 20. (CSIRO and the Bureau of Meteorology: Melbourne, Vic.)
Nadeem K, Taylor SW, Woolford DG, Dean CB (2020) Mesoscale spatiotemporal predictive models of daily human-and lightning-caused wildland fire occurrence in British Columbia. International Journal of Wildland Fire 29, 11–2.
| Mesoscale spatiotemporal predictive models of daily human-and lightning-caused wildland fire occurrence in British Columbia.Crossref | GoogleScholarGoogle Scholar |
Potter BE, Goodrick S, Brown T (2003) Development of a statistical validation methodology for fire weather indices. In ‘Proceedings of 2nd International Wildland Fire Ecology and Fire Management Congress, 5th Symposium on Fire and Forest Meteorology’ 16–20 November 2003, Orlando, FL. (American Meteorological Society: Boston, MA)
Preisler HK, Brillinger DR, Burgan RE, Benoit JW (2004) Probability based models for estimation of wildfire risk. International Journal of Wildland Fire 13, 133–142.
| Probability based models for estimation of wildfire risk.Crossref | GoogleScholarGoogle Scholar |
Preisler HK, Burgan RE, Eidenshink JC, Klaver JM, Klaver RW (2009) Forecasting distributions of large federal-lands fires utilizing satellite and gridded weather information. International Journal of Wildland Fire 18, 508–516.
| Forecasting distributions of large federal-lands fires utilizing satellite and gridded weather information.Crossref | GoogleScholarGoogle Scholar |
Preisler HK, Westerling AL, Gebert KM, Munoz-Arriola F, Holmes TP (2011) Spatially explicit forecasts of large wildland. fire probability and suppression costs for California. International Journal of Wildland Fire 20, 508–517.
| Spatially explicit forecasts of large wildland. fire probability and suppression costs for California.Crossref | GoogleScholarGoogle Scholar |
Stonesifer CS, Calkin DE, Thompson MP, Stockmann KD (2016) Fighting fire in the heat of the day: an analysis of operational and environmental conditions of use for large airtankers in United States fire suppression. International Journal of Wildland Fire 25, 520–533.
| Fighting fire in the heat of the day: an analysis of operational and environmental conditions of use for large airtankers in United States fire suppression.Crossref | GoogleScholarGoogle Scholar |
Stull R (2015) Thunderstorm Fundamentals. Chapter 14. In ‘Practical meteorology: an algebra-based survey of atmospheric science’. (University of BC: Vancouver, BC)
Taylor SW (2021) Frameworks for and Predictive Models to Support Wildland Fire Management Preparedness Decisions. PhD thesis. Simon Fraser University, Vancouver, BC. Available at https://theses.lib.sfu.ca/file/thesis/6579 [Accessed 1 December 2020].
Tibshirani R (1996) Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society Series B 58, 267–288.
| Regression shrinkage and selection via the lasso.Crossref | GoogleScholarGoogle Scholar |
Trethewey D (2007) Development of an index for quick comparison of helicopter costs and benefits. International Journal of Wildland Fire 16, 444
| Development of an index for quick comparison of helicopter costs and benefits.Crossref | GoogleScholarGoogle Scholar |
Van Wagner CE (1987) Development and structure of the Canadian Forest Fire Weather Index System. Forestry Technical Report 35, Canadian Forestry Service, Ottawa, ON.
Wei Y, Bevers M, Belval EJ (2015) Designing seasonal initial attack resource deployment and dispatch rules using a two-stage stochastic programming procedure. Forest Science 61, 1021–1032.
| Designing seasonal initial attack resource deployment and dispatch rules using a two-stage stochastic programming procedure.Crossref | GoogleScholarGoogle Scholar |
Wilmer I, Chalk G, Davies GE, Weaver AE, Lockey DJ (2015) Air ambulance tasking: mechanism of injury, telephone interrogation or ambulance crew assessment? Emergency Medicine Journal 32, 813–816.
| Air ambulance tasking: mechanism of injury, telephone interrogation or ambulance crew assessment?Crossref | GoogleScholarGoogle Scholar | 25527473PubMed |
Woolford DG, Martell DL, McFayden CB, Evens J, Stacey A, Wotton BM, Boychuk D (2021) The development and implementation of a human-caused wildland fire occurrence prediction system for the province of Ontario, Canada. Canadian Journal of Forest Research 51, 303–325.
| The development and implementation of a human-caused wildland fire occurrence prediction system for the province of Ontario, Canada.Crossref | GoogleScholarGoogle Scholar |
Wotton BM, Martell DL (2005) A lightning fire occurrence model for Ontario. Canadian Journal of Forest Research 35, 1389–1401.
| A lightning fire occurrence model for Ontario.Crossref | GoogleScholarGoogle Scholar |
Xi DDZ, Taylor SW, Woolford DG, Dean CB (2019) Statistical models of key components of wildfire risk. Annual Review of Statistics and its Application 6, 197–222.
| Statistical models of key components of wildfire risk.Crossref | GoogleScholarGoogle Scholar |
Youden WJ (1950) Index for rating diagnostic tests. Cancer 3, 32–35.
| Index for rating diagnostic tests.Crossref | GoogleScholarGoogle Scholar | 15405679PubMed |
Zeferino JA (2020) Optimizing the location of aerial resources to combat wildfires: a case study of Portugal. Natural Hazards 100, 1195–1213.
| Optimizing the location of aerial resources to combat wildfires: a case study of Portugal.Crossref | GoogleScholarGoogle Scholar |
1 KI = (T850 − T500) − DP850 − (T700 – D700) where T and DP are temperature and dewpoint temperature respectively, and the subscripts are pressure levels in hPa.

|

|

|




 ) and pDrop criterion of the most influential variables in the conditional AT-IA (27 of 76 variables) and HELI-IA model (34 of 73 variables).
) and pDrop criterion of the most influential variables in the conditional AT-IA (27 of 76 variables) and HELI-IA model (34 of 73 variables).

