An empirically based approach to defining wildland firefighter safety and survival zone separation distances
Wesley G. Page A B and Bret W. Butler A BA USDA Forest Service, Rocky Mountain Research Station, Fire, Fuel and Smoke Science Program, 5775 Highway 10 W, Missoula, MT 59808, USA.
B Corresponding authors. Email: wesleygpage@fs.fed.us; bwbutler@fs.fed.us
International Journal of Wildland Fire 26(8) 655-667 https://doi.org/10.1071/WF16213
Submitted: 5 December 2016 Accepted: 19 May 2017 Published: 8 August 2017
Journal Compilation © IAWF 2017 Open Access CC BY-NC-ND
Abstract
Wildland firefighters in the US are mandated to identify areas that provide adequate separation between themselves and the flames (i.e. safety zones) to reduce the risk of burn injury. This study presents empirical models that estimate the distance from flames that would result in a low probability (1 or 5%) of either fatal or non-fatal injuries. The significant variables for the fatal injury model were fire shelter use, slope steepness and flame height. The separation distances needed to ensure no more than a 1 or 5% probability of fatal injury, without the use of a fire shelter, for slopes less than 25% were 20 to 50 m for flame heights less than 10 m, and 1 to 4 times the flame height for flames taller than 10 m. The non-fatal injury model significant variables were fire shelter use, vehicle use and fuel type. At the 1 and 5% probability thresholds for a non-fatal injury, without the use of a fire shelter, the separation distances were 1 to 2, 6 to 7, and 12 to 16 times greater than the current safety zone guideline (i.e. 4 times the flame height) for timber, brush and grass fuel types respectively.
Additional keywords: fire behaviour, firefighter entrapment, flame height, safe separation distance.
Introduction
Wildland fire occurs in complex environments where multiple physical processes interact to influence fire behaviour on a variety of spatial and temporal scales (Barrows 1951; Van Wagner 1985; Finney et al. 2013). Wildland firefighters work in these complex environments to protect human lives and property but also to preserve natural values at risk such as watersheds or wildlife habitat (Scott et al. 2014). Sometimes while working towards accomplishing these goals, firefighters can become exposed to rapidly changing weather and fire conditions that result in unanticipated consequences such as injury or death (National Wildfire Coordinating Group 1997; Cheney et al. 2001; Werth et al. 2011). In order to minimise the risk posed by these threats, a variety of safety protocols or orders have been developed within the USA (e.g. McArdle 1957; National Wildfire Coordinating Group 2014); among these is the requirement that firefighters identify safety zones, i.e. preplanned areas of refuge that can be utilised without the use of fire shelters in case of entrapment (National Wildfire Coordinating Group 1996). When those areas are not available, smaller areas that are large enough to prevent fatal injury but likely to result in some kind of injury may be used as a last resort, sometimes referred to as survival (without fire shelter) or deployment (with fire shelter) zones (National Wildfire Coordinating Group 1996). Generally, the development, evolution and intent of firefighting safety protocols have been to avoid entrapments altogether by using the protocols as rules for engagement (Brauneis 2002), systems for operational safety (Gleason 1991) and ways to reinforce important tactical decisions (Thorburn and Alexander 2001).
Despite the recognition of the dangers posed by wildland fires, numerous accounts of wildland firefighter fatalities are reported year after year in fire-prone regions across the globe. Recent historical summaries in Australia (1901–2011) and Greece (1977–2013) indicated that firefighter fatalities accounted for ~11 and 23% of the total deaths caused by wildfire respectively, an average of ~1 death per year (Blanchi et al. 2014; Diakakis et al. 2016). In Spain, 48% of the total wildland fire-related fatalities between 1980 and 2010 were either firefighters or volunteer firefighters, an average of ~4 per year (Cardil and Molina 2015). Likewise, in Canada, Alexander and Buxton-Carr (2011) reported 165 wildland fire suppression-related fatalities from 1941 to 2010, an average of at least 2 fatalities per year. In the USA, between 1990 and 2006, there were 310 deaths during wildland fire operations of which 64 were related to burnovers or entrapments, an average of ~4 per year (Mangan 2007). In an effort to facilitate improvements in firefighter safety, these deaths or near-misses are often followed by attempts to gather, compile and report the factual circumstances that led to the entrapment through official investigations or more informal processes, like the Facilitated Learning Analysis (Mangan 1995; USDA Forest Service 2015). These investigations are sometimes the catalyst for major organisational or policy changes (e.g. McArdle 1957; USDA and USDI 1995) but their effectiveness in increasing wildland firefighter safety is rarely quantitatively assessed.
In order to provide wildland firefighters with estimates of the separation distance between themselves and the flames necessary for protection, several models and guidelines have been developed. The models are generally based on identification of the fire energy source strength, the time–temperature thresholds for burn injury to bare skin and the distance necessary to prevent injury (Butler 2014a). The earliest known guideline was developed by Green and Schimke (1971) in relation to fuel breaks for high-intensity brush fires based on radiant heating. A more recent model advanced by Butler and Cohen (1998a) was also developed based on radiant heating, which was distilled to a general guideline suggesting that the separation distance between the firefighters and the flames should be at least 4 times the flame height (Butler and Cohen 1998b; National Wildfire Coordinating Group 2014). Additionally, Zárate et al. (2008) and Rossi et al. (2011) produced other physically based radiant heat transfer models of safe separation distance using similar approaches with different assumptions regarding flame front temperature and width. Despite the wide use of these models in operational settings, they have known limitations in regards to their assumptions of using only radiant heating, no wind or slope influence, failing to incorporate mechanisms of injury other than burns to bare skin, and the lack of direct validation in the field (Butler 2014a). Recent measurements have shown that convective energy transport can exceed radiative transport in wildland fires (Yedinak et al. 2010; Frankman et al. 2013). Recognising this, Butler et al. (2015) discussed the need for using field-measured radiative and convective values to improve existing safety zone guidelines.
Although the requirement to identify and use safety or survival zones by wildland firefighters can vary by country, they are credited as being essential components of operational safety systems (Gleason 1991; Thorburn and Alexander 2001). Owing to their potential importance and the limitations with current physically based models, we endeavoured to determine if observations of the fire environment, size of the refuge area and type of injury (i.e. fatal or non-fatal) during actual firefighter entrapments could be used to develop empirical models. In the present study, we define survival zone separation distance to be a distance of sufficient length from the flames that could result in non-fatal injury but a low probability (1 or 5%) of fatal injury to entrapped firefighters. Likewise, we define safety zone separation distance to be a distance of sufficient length that would result in a low probability (1 or 5%) of any injury to entrapped firefighters. The specific objectives of the present study were to (1) determine if adequate data are available from existing reports and investigations of firefighter entrapments to build empirical models; (2) if so, then build models capable of predicting the likelihood of either a fatal or non-fatal injury; (3) use those models to determine the separation distances required to ensure a low probability of fatal or non-fatal injury; and (4) compare results with existing physically based models and observations from a set of experimental fires.
Methods
Data collection
Documents that were available as of March 2016 in the Wildland Fire Lessons Learned Center Incident Review database (available at http://www.wildfirelessons.net, accessed 28 April 2017) that were classified as wildland firefighter entrapments in the USA for the years 1910 to 2015 were downloaded and studied. The documents were mostly agency-produced investigative reports but additional supplementary material was sometimes provided, which included staff ride information (Keller 2002), newspaper articles and summary presentations. All of the data compiled in the present study were obtained from these information sources except for the Mann Gulch fire, where a more recent review and critique of the entrapment has been undertaken (Alexander et al. 2009a).
The documents were reviewed for specific information about the entrapment in terms of how the individual(s) were affected physically (fatal injury, non-fatal injury, or neither), the wildland fire environment (fuels, weather and topography) in and around the entrapment area, fire behaviour at the time of entrapment, and the spatial dimensions of the entrapment area. Particular emphasis was placed on gathering information related to the key variables identified in previous research (Butler and Cohen 1998a; Zárate et al. 2008; Rossi et al. 2011; Butler 2014a), such as flame height (or flame length) and separation distance from the flames. An attempt was made to estimate the variables of interest when they were not explicitly described using photographs or other descriptive information. Those incidents that did not have or did not allow a reasonable estimate of separation distance from the flames during the entrapment were excluded from the analysis. Additionally, those incidents in which the entrapped were not stationary while taking refuge during the initial passage of the fire front (i.e. they ran or drove through the flames) were also excluded from the analysis. When a particular incident had multiple entrapments that were separated in time and space, each entrapment was treated as a unique case. Therefore, each entrapment in the study represents a particular set of conditions related to a specific time and location that may have contained multiple firefighters.
Variables of interest for each entrapment were as follows: number entrapped, number of fire shelters deployed, number of fatalities, number of injuries, the presence and use of vehicles or buildings during the entrapment, fuel model (Anderson 1982; Scott and Burgan 2005), fuel type, fuel height, fuel load, entrapment site slope steepness, weather source, air temperature, relative humidity, wind speed at eye-level, 1-, 10- and 100-h fuel moisture, live fuel moisture, rate of spread, flame length, fireline intensity, flame height and separation distance from the flames. We defined injuries to include any injury described in the report that required medical attention, which encompassed burns as well as smoke-related injuries. Fatalities were also included in the injury tallies in order to aid in the analysis (see below), as some entrapments had no survivors, and would have otherwise been counted as having no injuries. The presence of a vehicle or building was included in the analysis if it was used as a refuge or a shield and 6 m above ground level (20-foot) wind speed was adjusted to eye-level using a wind adjustment factor of 0.4 for timber and 0.5 for brush and grass fuel types (Rothermel 1983). If flame height was not reported but flame length was, it was assumed that flame height and flame length were equivalent (Butler and Cohen 1998a). Furthermore, when the separation distance of the entrapped firefighters from the flames was not directly reported, it was estimated based on the dimensions described, which when entrapment area size was given in acres was taken to be the radius of a circle with an equivalent area. If the values for the variables were reported as a range, the midpoint was used as input for the analysis. It should be noted that the underlying data quality is largely unknown and likely varies from report to report. As there was no basis to confirm or refute the reported measurements, we assume they were made with minimal bias.
Data analysis
Two separate analyses of the same dataset were completed based on whether a fatal injury was reported during an entrapment, referred to as the fatal injury model, or whether a non-fatal injury was reported during an entrapment, referred to as the non-fatal injury model. Both analyses used all available data with the occurrence of a fatal or non-fatal injury coded as 0 (no) or 1 (yes).
As the primary dependent variables were binomial, logistic regression was used to estimate the likelihood of occurrence given the set of observed independent variables by means of the R statistical package, ver. 3.3.1 (R Core Team 2015). All relevant interactions between independent variables were initially evaluated in the models with inclusion based on a stepwise selection procedure using Akaike’s Information Criterion (AIC) (stepAIC). Multicollinearity was assessed in the final models by calculating the variance inflation factors for each independent variable. Owing to the low sample size of the dataset, those independent variables that were marginally non-significant (0.1 > P > 0.05) were retained in the final models whereas others not meeting that criteria were removed. Goodness-of-fit statistics for the selected models included reduction in deviance compared with the null model and the le Cassie–van Houwelingen–Copas–Hosmer (le Cassie) unweighted sum of squares test (Hosmer et al. 1997) as implemented in the rms package (Harrell 2016). The predictive power of the final models was evaluated using the area under the receiver operating characteristics curve (AUC) and McFadden’s pseudo R2 (McFadden 1974) as implemented in the pscl package (Jackman 2015). Variable importance was assessed by determining the drop in model deviance obtained by adding the additional variable. To aid in interpretation of the final models, the coefficients were also reported as odds ratios.
The models obtained from each analysis were used to estimate the separation distances required to ensure that there was either a 1 or 5% probability of a fatal or non-fatal injury. Specifically, the final fatal and non-fatal injury models were rearranged to solve for separation distance given the fixed probabilities using the standard multiple logistic regression model form (Hosmer and Lemeshow 2000):
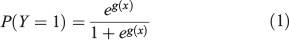
with the logit given by
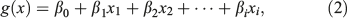
where P(Yi = 1) is the probability that a fatal or non-fatal injury will occur, xi are the independent variables, β0 is the intercept, and βi are the coefficients. The selection of the acceptable probability levels for fatal and non-fatal injuries as 1 or 5% was somewhat arbitrary, being based on the importance of life and the low probability threshold that wildland firefighters would likely find acceptable. In reality, wildland firefighters would judge their level of acceptable risk based on the potential benefits v. the potential costs or losses for a specific situation (Clancy 2011). The results of the logistic regression analysis are presented with their coefficients so readers can use Eqns 1 and 2 to either directly estimate the probability of a fatal or non-fatal injury for a specific situation or calculate their own separation distance using a different risk tolerance threshold.
A one-way analysis of variance was used to determine if the mean responses for each independent variable varied among fuel and consequence type (fatality, injury, or neither). In this part of the analysis, fatality cases were those entrapments where at least one firefighter perished, whereas injury cases were entrapments where at least one firefighter was injured, exclusive of fatalities. If a significant difference was found (α < 0.05), Tukey’s Honest Significant Difference (HSD) multiple comparison test (Tukey 1949) was used to control the family-wise error rate and evaluate individual differences among fuel and consequence type.
Model evaluation
The models developed to predict the likelihood of a fatal or non-fatal injury were compared against a set of independently gathered field data. Specifically, the Wildfire Operations Research branch of FPInnovations has undertaken a series of experimental outdoor fires in which heat flux and smoke (carbon monoxide) data were collected in either natural or man-made openings similar to oil well sites (Alexander et al. 2009b), to determine if firefighters could survive an entrapment (available at http://wildfire.fpinnovations.ca/Research/ProjectPage.aspx?ProjectNo=1, accessed 17 April 2017). Firefighter survivability appears to have been approximately estimated using a heat flux threshold of 7 to 10 kW m−2; however, final conclusions from their work have not yet been published, thus the comparisons are considered preliminary.
Results
Data summary
A total of 242 entrapment incidents that occurred in the USA between 1910 and 2015 were reviewed, of which 65 had sufficient data to conduct the analysis (see online supplementary material for a complete listing of the data used to conduct the analysis). Seven of the included incidents had multiple entrapments, which produced a total of 72 unique entrapment cases. The dataset covered a significant range of environmental and fire behaviour conditions (Fig. 1, Table 1). The entrapments occurred between 1937 and 2015, mostly in the western USA, with the years 2000–09 having the highest number of entrapment cases with a fatality (Fig. 2). Entrapments were most common (ordered by number of cases) in August, July and June, with the primary fuel types being timber (38 cases), brush (26 cases) and grass (8 cases). The cases occurring in timber fuel types had the highest mean number of people entrapped, shelters deployed, fuel height and flame height. Other differences in fuel and flame height between the grass and brush fuel types were not statistically significant as there was considerable variation in their heights.

|

|
Analysis of several independent variables grouped by consequence type (fatality, injury, or neither) indicated that most of the mean values were similar (Table 2). The main difference among consequence type was seen with the mean separation distance and the ratio of separation distance to flame height (SDFH). Specifically, as consequence of the entrapment increased (neither < injury < fatality), the mean separation distance and SDFH decreased (Fig. 3). Separation distances for entrapments when a fatality occurred were on average less than 10 m whereas those entrapments lacking either a fatality or an injury had on average separation distances greater than ~15 m.

|
Fatal injury model (survival zone separation distance)
The best-fitting model predicting the likelihood of a fatal injury during an entrapment contained four significant independent variables: slope steepness, separation distance, the use of a fire shelter and flame height (Table 3). Overall model fit was good based on change in deviance (deviance = 52.3, P > χ2 = 0.91) and the le Cassie goodness-of-fit test (P = 0.189); null hypothesis was that the selected model was adequate. The predictive power of the final model was moderate based on McFaddens R2 (0.35) and AUC (0.89) with the variance inflation factors indicating little evidence of multicollinearity, i.e. value < 2.5. Variable importance analysis, as measured by the contribution to a drop in model deviance, indicated that separation distance was the most important variable, followed by the use of a fire shelter, slope steepness and flame height. The modelled odds ratios suggested that for each unit increase in slope (%) and flame height (m), the odds of a fatal injury increased by 3 and 4% respectively. Conversely, for each metre increase in separation distance, the odds of a fatal injury decreased by 11%.

|
The predicted probabilities plotted by separation distance, slope steepness, flame height and fire shelter use demonstrated the relative importance of these variables on the likelihood of a fatal injury (Fig. 4). Clearly, the importance of a fire shelter in decreasing the probability of a fatal injury is confirmed (column 1 v. column 2); however, it appears the effect decreases as slope steepness increases (Fig. 4e, f).
The separation distances (expressed as the ratio of separation distance to flame height) needed to ensure that the probability of a fatal injury is no more than 1 or 5% were plotted by slope steepness, flame height and fire shelter use along with predictions from existing physically based safety zone models (Fig. 5). Inspection of the plots at the 1% probability level indicates that for flame heights below 10 m and slopes less than 25%, the separation distances required for surviving an entrapment without and with a fire shelter range from 40 to 50 m and 20 to 30 m respectively. At the 5% probability level, the required separation distances for flame heights less than 10 m and slopes less than 25% range from 20 to 30 m and 5 to 15 m without and with a fire shelter respectively. These values are generally higher than the values predicted for safety zones using the physically based models. However, at flame heights exceeding 10 m, for all combinations of fire shelter use and probability level, the required SDFH ratios decrease and eventually become lower than Butler and Cohen’s (1998a) model but similar to the models proposed by Zárate et al. (2008) and Rossi et al. (2011), generally ranging from 1 to 4 times the flame height.

|
Non-fatal injury model (safety zone separation distance)
The best-fitting model predicting the likelihood of a non-fatal injury during an entrapment contained four significant independent variables: the use of a fire shelter, separation distance, fuel type and the use of a vehicle (Table 4). Overall model fit was good based on change in deviance (deviance = 72.2, P > χ2 = 0.252) and the le Cassie goodness-of-fit test (P = 0.878). The predictive power of the final model was poor to moderate based on McFaddens R2 (0.26) and AUC (0.84), with the variance inflation factors indicating little evidence of multicollinearity. Variable importance analysis indicated that the use of a fire shelter was the most important variable followed by separation distance, the use of a vehicle, fuel type and the fire shelter–vehicle interaction. The modelled odds ratios showed that for each metre increase in separation distance, the odds of a non-fatal injury decreased by 3%. Additionally, a change in fuel type from brush to grass and from brush to timber decreased the odds of a non-fatal injury as well as the use of a fire shelter or a vehicle. However, the use of a vehicle and a fire shelter during an entrapment increased the odds of a non-fatal injury.

|
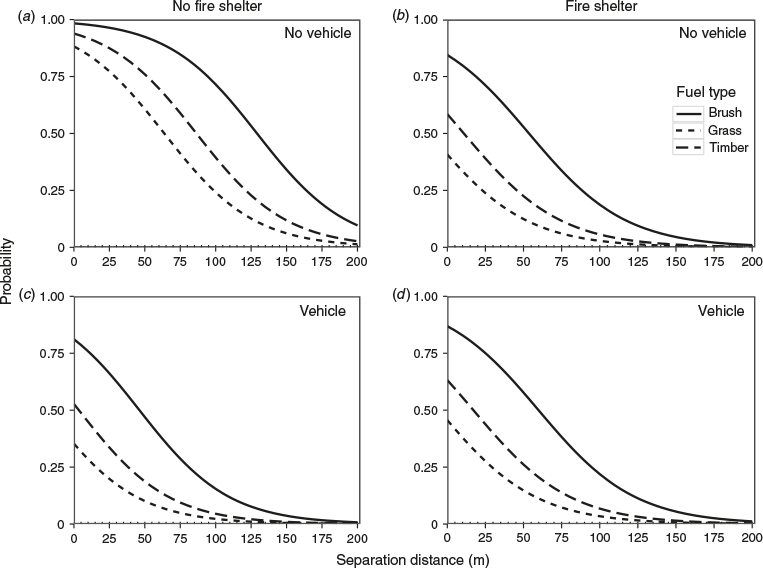
The predicted non-fatal injury probabilities plotted by fire shelter use, vehicle use and fuel type confirmed that the use of a fire shelter or a vehicle during an entrapment was important to decreasing the probability of a non-fatal injury, although the effect was not present when both a fire shelter and a vehicle were used together (Fig. 6). Across all scenarios, entrapments occurring in a brush fuel type had the greatest probability of a non-fatal injury, followed by the timber and grass fuel types.
The separation distances required to ensure that the probability of a non-fatal injury during an entrapment was either 1 or 5% were plotted by fuel type, vehicle use and fire shelter use (Fig. 7). Without a fire shelter or vehicle, the required separation distances at the 1% probability level were 275, 209 and 232 m for the brush, grass and timber fuel types respectively. Compared with this maximum level, the required separation distances dropped by 52 and 83 m across all fuel types when either the probability threshold changed to 5% or a vehicle was used respectively. When a vehicle was used and the probability threshold was set to 5%, the separation distances decreased by ~136 m across all fuel types, compared with the maximum separation distances. Additionally, the use of a fire shelter decreased the required separation distances by ~76 m for both the 1 and 5% probability thresholds, without a vehicle, across all fuel types.

|
Comparison of the results with the rule-of-thumb for safety zone separation distance in the USA (i.e. 4 times the flame height) when the observed median flame heights by fuel type were used indicates that the predicted separation distances from the empirical model were higher in the majority of cases. Specifically, the current rule-of-thumb guidelines suggested that separation distances should be at least 38 m for brush, 13 m for grass and 122 m for timber fuel types. These values are ~7, 15 and 2 times lower than the maximum predicted values using the empirical model for the brush, grass and timber fuel types respectively, at the 1% probability level without a fire shelter or a vehicle.
Model evaluation
Comparison of the predictions from the empirical models developed in the current study with the results from seven experimental fires conducted in northern Canada by FPInnovations indicated that there was a significant likelihood that entrapped firefighters would be injured in all cases, with a mean probability of a non-fatal injury of 88% (Table 5). This is in agreement with the purpose of the experimental fires, that is ‘to characterise the size of the ideal survival zone’ (Baxter 2009), with the understanding that firefighters could be in a very uncomfortable situation if they had to use such an area. Those experimental fires that were deemed potentially survivable had a mean probability of fatal injury of 16%, which was lower than the mean value of 25% for those fires that were considered not-survivable. Only one experimental fire appeared to meet our definition of a survival zone with a probability of a fatal injury less than 5%, which was for the fire that had a separation distance of 25 m.

|
Discussion
The development and testing of tools to predict the separation distances needed to protect wildland firefighters during entrapments is an important yet largely understudied area of wildland fire research. Most attempts to quantify safety zone separation distance have been based on modelling the physical processes dictating radiant energy transfer and burn injury to bare skin. The results of the current study represent the first attempt to use data collected following wildland firefighter entrapments to build empirical models. Several important findings have been revealed as a result of using this alternative approach.
The value of fire shelters or vehicles as an option of last resort has been described by entrapment survivors for years (Mangan 1997; Butler and Putnam 2001; Anderson 2003; Putnam and Butler 2004); however, their effect on changing the likelihood of a fatality or an injury has never been quantified. The results from the present study confirm that the use of fire shelters significantly lowers the likelihood of any kind of injury under conditions experienced during entrapment events. However, steep slopes seem to limit fire shelter effectiveness, possibly owing to the impacts of increased convective heating on the fire shelter material (Butler and Putnam 2001; Butler et al. 2015). Additionally, the empirical models support the belief that vehicles (including dozers) can be used as places of refuge or as shields during entrapments (Mangan 1997). Despite the effectiveness of fire shelters and vehicles, the use of both during an entrapment seems to slightly increase the likelihood of a non-fatal injury. The underlying reason for this relationship is unclear but it may be an artefact of our methodology. We treated each entrapment (potentially containing many firefighters) rather than each firefighter as our sampling unit. Thus, during a given entrapment, different firefighters may have used different secondary protection strategies. This potentially masks the true effect of using both a fire shelter and a vehicle during an entrapment for a single or small group of firefighters, as is sometimes done with fire curtains (available at http://www.stormkingmtn.com/index.cfm?Section=23andpagenum=190, accessed 21 April 2017).
The effect of wind and slope on separation distance was only partially incorporated into the empirical models. Slope steepness has been reasoned as a potential contributor to safety zone size (Rossi et al. 2011; Butler 2014b) as it is well recognised in aiding convective and radiative heat transfer and thus forward rate of spread (Rothermel 1972; Van Wagner 1977; Dupuy and Maréchal 2011). Here, we found that the probability of a fatal injury was directly related to slope steepness, where for each percentage point increase in slope, the odds of a fatal injury increased by 3%. However, the effect of slope steepness was not significant in the model developed to predict the likelihood of a non-fatal injury. Likewise, we failed to find a significant wind speed effect for both models, which is also a substantial contributor to convective and radiative heat transfer (Cheney et al. 1993; Catchpole et al. 1998; Frankman et al. 2013). Slope and wind can alter flame geometry through changes in flame angle, which increases flame length (Weise and Biging 1996) and heat transfer by radiation (Albini 1985). However, flame length is difficult to measure in the field (Rothermel and Rinehart 1983). In the present study, we used flame height to represent flame geometry, although flame length was used when flame height was not reported. The lack of statistical significance of wind speed could be related to our use of both flame height and flame length and also to the lack of quality on-site measurements immediately before the entrapments.
The significant independent variables included in the final models were generally similar to those determined to be important in the physically based models but they were not consistent between models. For example, the model for non-fatal injuries did not contain a significant flame height effect, but rather fuel type was determined to be a better predictor of non-fatal injury, where the brush fuel type was found to be the most dangerous followed by the timber and grass fuel types. Given that flame heights are generally different among fuel types, the average effect of flame height was indirectly incorporated into the final non-fatal injury model through the fuel type dependence. The consequence of this model form is that the predicted separation distances for safety zones are static and do not change based on predicted or observed changes in fire behaviour. This simplifies the selection and determination of adequate safety zones but also leads to an overestimation of separation distance, especially for environmental conditions that produce less than extreme fire behaviour. The overprediction is quite apparent in the estimated separation distances for the grass fuel type using the probability of a non-fatal injury model (separation distance >200 m). This distance seems quite extreme, especially when the median value for flame height based on the eight entrapment cases was 3.2 m, which is 60–70 times lower than the estimated separation distance. The excessively high separation distance may be related to the high proportion of these incidents with injuries (50%), the frequent utilisation of fire shelters found in these eight cases, and the limited size of the dataset.
The proposed non-fatal injury model suggests that safety zone separation distances should be substantially larger than currently recommended by physically based models, especially when the risk tolerance threshold is set to a value representative of the importance of life. Several factors could be causing this difference, which include addressing a known underprediction bias in the physical models, determination of the actual probability level that is acceptable for non-fatal injuries and model quality. Underprediction of separation distance in the current set of physically based models is likely related to the failure to include the effects of convective heat transfer on safety zone size (Zárate et al. 2008; Butler 2014a, 2014b) and the use of burns to bare skin as the only mechanism of injury. A safety zone should be an area of sufficient size to ensure that firefighters remain uninjured from all possible injury mechanisms including excessive inhalation of smoke or hot combustion gases (National Wildfire Coordinating Group 1996). Wildland firefighter sensitivity to smoke, both short- and long-term, has been previously recognised as a significant health risk (Reinhardt and Ottmar 1997; Broyles 2013) and as such, it is likely a source of respiratory-based injuries. Thus, safety zone separation distance should increase beyond the burn injury limit to accommodate the effects of excessive smoke exposure. Differences between the physical and empirical models may also be related to an overestimate of separation distance caused by difficulties in determining and justifying an acceptable likelihood of an injury. Owing to underlying model form, predicted non-fatal injury probabilities never reach zero and tend to have long right-skewed tails, which produces large increases in required separation distance for relatively small changes in probability. For example, we provide details for two risk tolerance thresholds (1 and 5%) and found that in the case of the non-fatal injury model, the required separation distances dropped by over 50 m for all fuel types when the level of risk increased from 1 to 5%.
The model evaluation results indicated that both the fatal and non-fatal injury empirical models were sensitive to changes in separation distance, fuel type and flame height across the range of values reported in the set of experimental fires. The high probability of non-fatal injury for all seven experimental fires confirmed that none of the areas tested were suitable to be used as safety zones, which was in agreement with the purpose of the experimental fires. However, of the four fires that were considered potentially survivable, only one met our criteria of a survival zone, having a probability of a fatal injury less than 5%. This discrepancy could potentially be attributed to the status of the experimental fire project, i.e. the results are preliminary, and the criteria used to determine survivability for both the experimental fires (7–10 kW m−2 heat flux threshold) and in the current study (<5% probability). A more complete evaluation could be undertaken with a more detailed and finalised field dataset and more rigorous criteria for determining survivability.
Study limitations
As with all empirically based models, their interpretation and applicability is limited to the range of values used to develop them. In the present study, the data capture a fairly broad array of fire behaviour conditions but lack a large number of cases where separation distances are greater than ~80 m. Additionally, there were only five cases where no injury (fatal or non-fatal) was reported and a fire shelter was not used. The low sample size under these less-than-extreme conditions can be attributed to the nature of the circumstances in which the data were compiled (i.e. data mostly come from reports of entrapments that resulted in an injury or fatality). Although the results may be useful for comparisons with other parts of the world, they should only be considered pertinent to fuel conditions that are similar to those encountered in the USA. However, other countries and regions may find the methodology useful for conducting an analysis specific to their unique environments.
Based on the nature of the dataset and the low risk tolerance thresholds used, the separation distances presented are conservative in nature and potentially overpredicting what may actually be required when conditions are less than severe. As such, it is recommended that the results primarily be used to guide application of current safety zone guidelines, to identify research needs and for comparisons with future models that attempt to incorporate the effects of convective heat transfer on safety zone size (Butler 2014b). However, wildland firefighters may find the results of both the fatal and non-fatal injury models useful for discussion, such as to why the large distances may be needed, the relative benefits of seemingly slight increases in separation distances and to aid in identification of potential survival and deployment zones if escape routes to safety zones become cut off.
Owing to the issues described above, the dataset could be improved through the inclusion of cases where no fatalities or injuries occurred and no secondary means of protection was necessary (i.e. a fire shelter or vehicle), in other words, a success. Although these types of cases may happen frequently, they are generally not reported. Additionally, a better adherence to the guidelines proposed by Mangan (1995) by investigation teams in future wildland firefighter entrapment reports, particularly when describing the entrapment area and fire environment, would likely benefit future attempts to build and improve empirically based models.
Conclusions
The analysis of documents produced in response to wildland firefighter entrapments in the USA have demonstrated the potential use of these data to better understand the factors that influence the likelihood of fatal and non-fatal injuries. The results have confirmed the important role that fire shelters play in protecting wildland firefighters and how the use of a vehicle for refuge or as a shield can also help safeguard firefighters. The analysis similarly showed the potential for the data to be used to estimate the separation distances needed to protect firefighters from death or injury. Comparisons of the results with existing physically based safety zone models indicate that the empirical models are generally more conservative in terms of the required separation distances (i.e. they require greater separation distances when the risk tolerance threshold is representative of the importance of protecting life). The reasons for the differences could be related to several factors, including the nature of the dataset used to construct the models, the underestimation of separation distance in the physically based models and model quality.
Continued improvement in the ability of empirically based methods to accurately estimate wildland firefighter safety and survival zone separation distances is likely when the importance of specific details in entrapment investigation reports is more fully recognised, especially in terms of descriptions of the entrapment area and the fire environment, and where additional data are collected when safety zones perform as designed. Additionally, a common poor practice is to evaluate safety zones separately from the paths to those safety zones (i.e. escape routes), when in reality neither can be successful without the other. Many entrapments occur while firefighters are en route to some perceived safety zone. Thus, additional work should include an evaluation of methods to assess escape route viability. This coupled with ongoing improvements using physically based methods will no doubt give firefighters a better understanding of the factors that affect safety zone size, escape route locations, and how they can be better incorporated into operational planning.
Conflicts of interest
The authors declare that they have no conflicts of interest.
Acknowledgements
This work was supported by the Joint Fire Science Program, the National Fire Plan through the Washington Office of Forest Service Research, the National Wildfire Coordinating Group (NWCG) Fire Behaviour Subcommittee and the Wildland Fire Management Research Development and Application Program. We gratefully acknowledge review of the manuscript by M. E. Alexander and T. J. Adams as well as by other anonymous reviewers. Support and encouragement for this effort from many fire practitioners is also appreciated.
References
Albini FA (1985) A model for fire spread in wildland fuels by radiation. Combustion Science and Technology 42, 229–258.| A model for fire spread in wildland fuels by radiation.Crossref | GoogleScholarGoogle Scholar |
Alexander ME, Buxton-Carr P (2011) Wildland fire suppression related fatalities in Canada, 1941–2010: a preliminary report. In ‘Proceedings of the 11th International Wildland Fire Safety Summit’, 4–8 April 2011, Missoula, MT. (Ed. RL Fox) (CD-ROM) (International Association of Wildland Fire: Missoula, MT, USA)
Alexander ME, Ackerman MY, Baxter GJ (2009a) An analysis of Dodge’s escape fire on the 1949 Mann Gulch Fire in terms of a survival zone for wildland firefighters. In ‘Proceedings of the 10th International Wildland Fire Safety Summit’, 27–30 April 2009, Phoenix, AZ, USA. (International Association of Wildland Fire: Missoula, MT, USA) Available at http://www.wildlandfire.com/docs/2009/lessons-learn/dodge-escape-fire-analysis.pdf [Verified 14 November 2016].
Alexander ME, Baxter GJ, Ackerman MY (2009b) Is a wellsite opening a safety zone for a wildland firefighter or a survival zone, or neither? In ‘The ’88 Fires: Yellowstone and Beyond’, 22–27 September 2008, Jackson Hole, WY, USA. (Eds RE Masters, KEM Galley, DG Despain) Tall Timbers Miscellaneous Publication 16, p. 110. (Tall Timbers Research Station: Tallahassee, FL, USA)
Anderson HE (1982) Aids to determining fuel models for estimating fire behavior. USDA Forest Service, Intermountain Forest and Range Experiment Station, General Technical Report INT-122. (Ogden, UT, USA)
Anderson L (2003) The new-generation fire shelter. National Wildfire Coordinating Group, Fire Equipment Working Team, NWCG PMS 411. (Boise, ID, USA)
Barrows JS (1951) Fire behavior in northern Rocky Mountain forests. USDA Forest Service, Northern Rocky Mountain Forest and Range Experiment Station, Station Paper 29. (Missoula, MT, USA)
Baxter G (2009) Survival zones for wildland firefighters: data collection in five experimental openings in grass. FPInnovations Wildfire Oper. Res. Proj. Updat., p. 5. (Hinton, AB, Canada)
Baxter G (2010) Survival zones for wildland firefighters: data collection in five more experimental openings in grass. FPInnovations Wildfire Oper. Res. Proj. Updat., p. 7. (Hinton, AB, Canada) Available at http://wildfire.fpinnovations.ca/1/Update_FiveGrassOpenings_2010.pdf [Verified June 2017]
Baxter G (2012a) Survival zones for wildland firefighters: data collection in one experimental opening in timber. FPInnovations Wildfire Oper. Res. Proj. Updat., p. 5. (Hinton, AB, Canada) Available at http://wildfire.fpinnovations.ca/1/Update_OneTimberOpening_2012.pdf [Verified June 2017].
Baxter G (2012b) Survival zones for wildland firefighters: data collection in two experimental openings in grass. FPInnovations Wildfire Oper. Res. Proj. Updat., p. 4. (Hinton, AB, Canada) Available at http://wildfire.fpinnovations.ca/1/Update_TwoGrassOpenings_2012.pdf [Verified June 2017]
Baxter G (2014) Survival zones for wildland firefighters: data collection in a natural opening in timber (No. 2). FPInnovations Wildfire Oper. Res. Proj. Updat., p. 4. (Hinton, AB, Canada) Available at http://wildfire.fpinnovations.ca/1/Update_NaturalOpeningTimber_No2_v2.pdf [Verified June 2017]
Blanchi R, Leonard J, Haynes K, Opie K, James M, Dimer de Oliveira F (2014) Environmental circumstances surrounding bushfire fatalities in Australia 1901–2011. Environmental Science & Policy 37, 192–203.
| Environmental circumstances surrounding bushfire fatalities in Australia 1901–2011.Crossref | GoogleScholarGoogle Scholar |
Brauneis K (2002) Fire orders: do you know their original intent? Fire Management Today 62, 27–29.
Broyles G (2013) Wildland firefighter smoke exposure. USDA Forest Service, National Technology and Development Program, 1351 1803. 5100-Fire Management. (Boise, ID, USA) Available at https://www.fs.fed.us/t-d/pubs/pdfpubs/pdf13511803/pdf13511803dpi100.pdf [Verified June 2017].
Butler BW (2014a) Wildland firefighter safety zones: a review of past science and summary of future needs. International Journal of Wildland Fire 23, 295–308.
| Wildland firefighter safety zones: a review of past science and summary of future needs.Crossref | GoogleScholarGoogle Scholar |
Butler BW (2014b) A study of the impact of slope and wind on firefighter safety zone effectiveness. Joint Fire Science Program, Final Report, Project 07–2-1–20. (Boise, ID, USA)
Butler BW, Cohen JD (1998a) Firefighter safety zones: a theoretical model based on radiative heating. International Journal of Wildland Fire 8, 73–77.
| Firefighter safety zones: a theoretical model based on radiative heating.Crossref | GoogleScholarGoogle Scholar |
Butler BW, Cohen JD (1998b) Firefighter safety zones: how big is big enough? Fire Management Notes 58, 13–16.
Butler BW, Putnam T (2001) Fire shelter performance in simulated wildfires: an exploratory study. International Journal of Wildland Fire 10, 29–44.
| Fire shelter performance in simulated wildfires: an exploratory study.Crossref | GoogleScholarGoogle Scholar |
Butler B, Parsons R, Mell W (2015) Recent findings relating to firefighter safety zones. In ‘Proceedings of the Large Wildland Fires Conference’, 19–23 May 2014, Missoula, MT, USA. (Eds RE Keane, M Jolly, R Parsons, K Riley) USDA Forest Service, Rocky Mountain Research Station, Proceedings RMRS-P-73, pp. 30–34. (Fort Collins, CO, USA) Available at https://www.treesearch.fs.fed.us/pubs/49166 [Verified June 2017]
Cardil A, Molina DM (2015) Factors causing victims of wildland fires in Spain (1980–2010). Human and Ecological Risk Assessment 21, 67–80.
| Factors causing victims of wildland fires in Spain (1980–2010).Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3sXhvFCqt7fE&md5=9d59c797b406394900705eb081805d3cCAS |
Catchpole WR, Catchpole EA, Butler BW, Rothermel RC, Morris GA, Latham DJ (1998) Rate of spread of free-burning fires in woody fuels in a wind tunnel. Combustion Science and Technology 131, 1–37.
| Rate of spread of free-burning fires in woody fuels in a wind tunnel.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1cXjs1Ggsbo%3D&md5=66ac3b45fdc5617b834ea4ab199d47bfCAS |
Cheney NP, Gould JS, Catchpole WR (1993) The influence of fuel, weather and fire shape variables on fire-spread in grasslands. International Journal of Wildland Fire 3, 31–44.
| The influence of fuel, weather and fire shape variables on fire-spread in grasslands.Crossref | GoogleScholarGoogle Scholar |
Cheney NP, Gould JS, McCaw L (2001) The Dead-Man Zone – a neglected area of firefighter safety. Australian Forestry 64, 45–50.
| The Dead-Man Zone – a neglected area of firefighter safety.Crossref | GoogleScholarGoogle Scholar |
Clancy D (2011) Can acceptable risk be defined in wildland firefighting? In ‘Proceedings of the Second Conference on the Human Dimensions of Wildland Fire’, 27–29 April 2010, San Antonio, TX, USA. (Eds SM McCaffrey, CL Fisher) USDA Forest Service, Northern Research Station, NRS-P-84, pp. 1–8. (Newtown Square, PA, USA) Available at https://www.treesearch.fs.fed.us/pubs/38507 [Verified June 2017].
Diakakis M, Xanthopoulos G, Gregos L (2016) Analysis of forest fire fatalities in Greece: 1977–2013. International Journal of Wildland Fire 25, 797–809.
| Analysis of forest fire fatalities in Greece: 1977–2013.Crossref | GoogleScholarGoogle Scholar |
Dupuy JL, Maréchal J (2011) Slope effect on laboratory fire spread: contribution of radiation and convection to fuel bed preheating. International Journal of Wildland Fire 20, 289–307.
| Slope effect on laboratory fire spread: contribution of radiation and convection to fuel bed preheating.Crossref | GoogleScholarGoogle Scholar |
Finney MA, Cohen JD, Mcallister SS, Jolly WM (2013) On the need for a theory of wildland fire spread. International Journal of Wildland Fire 22, 25–36.
| On the need for a theory of wildland fire spread.Crossref | GoogleScholarGoogle Scholar |
Frankman D, Webb BW, Butler BW, Jimenez D, Forthofer JM, Sopko P, Shannon KS, Hiers JK, Ottmar RD (2013) Measurements of convective and radiative heating in wildland fires. International Journal of Wildland Fire 22, 157–167.
| Measurements of convective and radiative heating in wildland fires.Crossref | GoogleScholarGoogle Scholar |
Gleason P (1991) LCES – a key to safety in the wildland fire environment. Fire Management Notes 52, 9
Green LR, Schimke HE (1971) Guides for fuel-breaks in the Sierra Nevada mixed-conifer type. USDA Forest Service, Pacific Southwest Forest and Range Experiment Station, report. (Berkeley, CA, USA)
Harrell FE (2016) rms: Regression modeling strategies. Available at https://cran.r-project.org/package=rms [Verified 3 October 2016].
Hosmer DW, Lemeshow S (2000) ‘Applied Logistic Regression’, 2nd edn. (Wiley: New York, NY, USA)
Hosmer DW, Hosmer T, Le Cessie S, Lemeshow S (1997) A comparison of goodness-of-fit tests for the logistic regression model. Statistics in Medicine 16, 965–980.
| A comparison of goodness-of-fit tests for the logistic regression model.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DyaK2szgsVaiuw%3D%3D&md5=bc5f454bb424b72b900293af514acb47CAS |
Jackman S (2015) pscl: Classes and methods for R developed in the Political Science Computational Laboratory, Stanford University. Available at http://pscl.stanford.edu/ [Verified 3 October 2016].
Keller P (2002) What’s a staff ride? Fire Management Today 64, 6–7.
Mangan R (1995) Investigating wildland fire entrapments. USDA Forest Service, Technology and Development Program, 9551–2845-MTDC. (Boise, ID, USA)
Mangan R (1997) Surviving fire entrapments: Comparing conditions inside vehicles and fire shelters. USDA Forest Service, Technology and Development Program, 9751–2817-MTDC. (Boise, ID, USA)
Mangan R (2007) Wildland firefighter fatalities in the United States: 1990–2006. National Wildfire Coordinating Group, Safety and Health Working Team, National Interagency Fire Center, Technical Report PMS 841. (Boise, ID, USA)
McArdle RE (1957) Standard firefighting orders. Fire Control Notes 18, 151–152.
McFadden D (1974) Conditional logit analysis of qualitative choice behavior. In ‘Frontiers in econometrics’. (Ed. P Zarembka) pp. 105–142. (Academic Press Inc.: New York, NY, USA)
National Wildfire Coordinating Group (1996) Glossary of wildland fire terminology. National Interagency Fire Center, PMS 822, NFES 1849. (Boise, ID, USA)
National Wildfire Coordinating Group (1997) Historical wildland firefighter fatalities 1910–1996. National Interagency Fire Center, PMS 205, NFES 1832. (Boise, ID, USA)
National Wildfire Coordinating Group (2014) Incident response pocket guide. National Interagency Fire Center, PMS 461, NFES 001077. (Boise, ID, USA)
Putnam T, Butler BW (2004) Evaluating fire shelter performance in experimental crown fires. Canadian Journal of Forest Research 34, 1600–1615.
| Evaluating fire shelter performance in experimental crown fires.Crossref | GoogleScholarGoogle Scholar |
R Core Team (2015) R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. Available at http://www.R-project.org/.
Reinhardt T, Ottmar R (1997) Smoke exposure among wildland firefighters: a review and discussion of current literature. USDA Forest Service, Pacific Northwest Research Station, General Technical Report GTR-373. (Portland, OR, USA)
Rossi JL, Simeoni A, Moretti B, Leroy-Cancellieri V (2011) An analytical model based on radiative heating for the determination of safety distances for wildland fires. Fire Safety Journal 46, 520–527.
| An analytical model based on radiative heating for the determination of safety distances for wildland fires.Crossref | GoogleScholarGoogle Scholar |
Rothermel RC (1972) A mathematical model for predicting fire spread in wildland fuels. USDA Forest Service, Intermountain Forest and Range Experiment Station, Research Paper INT-115. (Ogden, UT, USA)
Rothermel RC (1983) How to predict the spread and intensity of forest and range fires. USDA Forest Service, Intermountain Forest and Range Experiment Station, General Technical Report INT-143. (Ogden, UT, USA)
Rothermel RC, Rinehart GC (1983) Field procedures for verification and adjustment of fire behavior predictions. USDA Forest Service, Intermountain Forest and Range Experiment Station, General Technical Report INT-142. (Ogden, UT, USA)
Scott AC, Bowman DMJS, Bond WJ, Pyne SJ, Alexander ME (Eds) (2014) Fire management. In ‘Fire on Earth: an Introduction’. pp. 259–290. (Wiley: Hoboken, NJ, USA)
Scott JH, Burgan RE (2005) Standard fire behavior fuel models: a comprehensive set for use with Rothermel’s surface fire spread model. USDA Forest Service, Rocky Mountain Research Station, General Technical Report GTR-153. (Fort Collins, CO, USA)
Thorburn RW, Alexander ME (2001) LACES versus LCES: adopting an ‘A’ for ‘anchor points’ to improve wildland firefighter safety. In ‘Proceedings of the 2001 International Wildland Fire Safety Summit’, 6–8 November 2001, Missoula, MT, USA. (Eds BW Butler, D Mangan) (International Association of Wildland Fire: Missoula, MT, USA) Available at http://www.iawfonline.org/proceedings.php [Verified June 2017].
Tukey JW (1949) Comparing individual means in the analysis of variance. Biometrics 5, 99–114.
| Comparing individual means in the analysis of variance.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DyaH1M%2FltlGgsA%3D%3D&md5=138ded18c97da89817bab706bb0aef00CAS |
USDA and USDI (1995) Federal wildland fire management policy and program review. Final Report, December 18, 1995.
USDA Forest Service (2015) Facilitated learning analysis implementation guide. Available at http://www.wildfirelessons.net/viewdocument/facilitated-learning-analysis-imple-1 [Verified 20 April 2017]
Van Wagner CE (1977) Effect of slope on fire spread rate. Canadian Forestry Service Bi-monthly Research Notes 33, 7–8.
Van Wagner CE (1985) Fire behavior modelling – how to blend art and science. In ‘Eighth Conference on Fire and Forest Meteorology’, 29 April–2 May 1985, Detroit, MI, USA. (Eds LR Donoghue, RE Martin) pp. 3–5. (Society of American Foresters: Washington, DC, USA)
Weise DR, Biging GS (1996) Effects of wind velocity and slope on flame properties. Canadian Journal of Forest Research 26, 1849–1858.
| Effects of wind velocity and slope on flame properties.Crossref | GoogleScholarGoogle Scholar |
Werth PA, Potter BE, Clements CB, Finney MA, Goodrick SL, Alexander ME, Cruz MG, Forthofer JA, McAllister SS (2011) Synthesis of knowledge of extreme fire behavior: Volume I for fire managers. USDA Forest Service, Pacific Northwest Research Station, General Technical Report GTR-854. (Portland, OR, USA)
Yedinak KM, Cohen JD, Forthofer J, Finney MA (2010) An examination of flame shape related to convection heat transfer in deep-fuel beds. International Journal of Wildland Fire 19, 171–178.
| An examination of flame shape related to convection heat transfer in deep-fuel beds.Crossref | GoogleScholarGoogle Scholar |
Zárate L, Arnaldos J, Casal J (2008) Establishing safety distances for wildland fires. Fire Safety Journal 43, 565–575.
| Establishing safety distances for wildland fires.Crossref | GoogleScholarGoogle Scholar |