A comparative analysis of wildfire initial attack containment objectives and modelling strategies in Ontario, Canada
Kennedy Korkola A # * , Melanie Wheatley A B # , Jennifer Beverly C , Patrick M. A. James A and Mike Wotton A D
C , Patrick M. A. James A and Mike Wotton A D
A
B
C
D
Abstract
Fire management agencies use the proportion of fires classified as initial attack (IA) success as a suppression performance metric, making IA success a common indicator of suppression effectiveness in research. The criteria and definition for IA success vary based on operational objectives, making comparisons across studies difficult.
To examine the sensitivity of different time and size-based IA success definitions on model predictive accuracy and compare different modelling approaches.
Using 30 years of historical fire report data from Ontario, Canada (n = 26,171), we developed logistic regression models, bagged classification trees and random forest models to predict IA success for eight different definitions. Model predictive accuracy, sensitivity and specificity were assessed on an independent validation dataset.
The eight definitions classified between 79 and 98% of fires as IA successes. There was no clear pattern between model strength across prediction metrics and IA success definition. Logistic regression generally outperformed machine learning methods in classifying IA escapes.
The definition of IA success does not greatly impact model performance across the modelling techniques used. Models of IA success and suppression-system performance metrics should be set with specific research or operational objectives in mind.
Keywords: containment probability, fire containment, fire management, forest fire, initial attack success, logistic regression, machine learning, suppression effectiveness, wildland fire.
Introduction
In fire-prone landscapes, wildfires are typically managed by government agencies to protect public safety and values while also supporting a range of land management objectives. Wildfires are an essential natural disturbance in the Canadian boreal forest (Bonan and Shugart 1989; Burton et al. 2008), burning an average of nearly 3 million ha of forest a year (Hanes et al. 2019). When these fires spread to where people, infrastructure and forest resources are threatened, wildfire suppression is used to avert potential disastrous consequences on the landscape.
The initial action taken to halt or slow the spread of a fire by the first firefighting resources that arrive at the fire is referred to as the initial attack (IA) phase of wildfire suppression (Merrill and Alexander 1987). In Canada’s boreal forests, IA typically involves ground crews of four to seven wildland firefighters using various tactics, such as power pump and hose, to extinguish flames and break up fuels, working directly on the fire’s edge to contain the fire (Canadian Interagency Forest Fire Centre (CIFFC) 2023). Fires that escape these IA efforts contribute significantly to the area burned on the landscape and dramatically increase suppression costs (Martell 2001; Arienti et al. 2006).
To provide a consistent means of characterising their IA system, fire management agencies and researchers studying suppression systems develop objective and quantifiable indicators of suppression effectiveness that they apply to individual fires. Given the fire suppression goal of keeping a fire small and eliminating its growth potential quickly, performance metrics are often based on achieving a state of fire containment before the fire reaches some set size or by a specific time after the start of IA (Gordon 2014). The proportion of successful IAs over a fire season is often used as a performance measure of fire suppression effectiveness by fire management agencies (e.g. Ontario Ministry of Natural Resources and Forestry 2014).
Although the use of common terminology is promoted across fire management agencies for consistent communication, IA success is defined in several different ways. Fire management agencies throughout Canada define IA success using different thresholds, which reflect the specific fire management objectives associated with a given jurisdiction (Gordon 2014). For instance, in British Columbia and the Northwest Territories, a fire must be controlled within the first 24 h, or before the next burning period, the time at which fires are typically most active, to be deemed an IA success (Gordon 2014). In Alberta, IA must occur before the fire exceeds 2 ha in size and the fire must be contained by 10:00 hours the following day to be considered an IA and containment success (Gordon 2014; Beverly 2017). A size-based definition of IA success, such that a fire is kept to 10 ha or less, is used in Saskatchewan. In Manitoba, there is a set final size limit of 5 ha or the fire must be controlled by 10:00 hours the day following IA to be labelled a success (Gordon 2014). In Ontario, time and size constraints are combined, requiring containment by 13:00 hours the day following IA or the final size of 4 ha or less (Ontario Ministry of Natural Resources and Forestry 2014). Specific IA success metrics are not used in Quebec, and instead, response system performance is measured with four operational objectives (Gordon 2014; Cardil et al. 2019): fires are discovered at a size <0.5 ha, IA occurs within 1h of fire detection anywhere in the full response zone, fires are contained before 10:00 hours and fires are extinguished before they burn 3 ha.
Metrics of IA success are also used extensively in research investigations as an indicator of landscape-scale fire suppression effectiveness (Plucinski 2019). Research studies commonly rely on historical fire agency reporting archives, paired with supplemental weather observations and geographic feature data, to model suppression effectiveness across broad temporal and spatial scales. These studies use an indicator of IA success that is generally representative of the fire management agency performance metrics reviewed above. For example, these studies have defined IA success using fire size criteria, such as a containment size of 2 ha used by Beverly (2017), or final fire size thresholds of 3 ha (Arienti et al. 2006), 4 ha (Podur and Wotton 2010), 5 ha (Plucinski 2012a; Plucinski et al. 2023), or 20 ha (Plucinski 2012a). Time-based definitions of fire containment within 4, 12 and 24-h periods have also been used (Plucinski 2012b; Collins et al. 2018; Marshall et al. 2022). Some studies further differentiate between response and containment failures (Arienti et al. 2006; Plucinski 2012a; Cardil et al. 2019). A response failure occurs when IA is not initiated before a specific size or time threshold, whereas a containment failure occurs when the IA crew cannot contain the fire within the specified constraints (Arienti et al. 2006).
Past studies have modelled the success or failure of IA using statistical modelling or machine learning methods. Multiple logistic regression is often used to model the binary outcome of IA success or failure (e.g. Arienti et al. 2006; Beverly 2017; Wheatley et al. 2022; Plucinski et al. 2023), with machine learning methods such as random forest (e.g. Collins et al. 2018; Marshall et al. 2022) and classification trees (e.g. Plucinski et al. 2011; Plucinski 2012b) common approaches for considering large, comprehensive sets of predictor variables. These methods have been used to identify the most influential predictors of IA success and to model how the probability of successful containment on IA changes in response to variations in environmental and wildfire context.
The probability of IA success is influenced by a broad range of factors including environmental and operational factors. Environmental factors such as weather, fuel type and connectivity (within and between stands), and landscape characteristics such as topography affect IA success probability by influencing fire behaviour. Consequently, fire behaviour and related indices that represent potential fire behaviour in a given location tend to be highly influential predictors of IA success. The Canadian Forest Fire Weather Index (FWI) System (Van Wagner 1987) uses daily weather temperature, relative humidity, wind speed and precipitation observations to calculate fuel moisture and fire behaviour outputs. These outputs are commonly used in IA success modelling to replace observations of fire behaviour, which are often unavailable. For example, as demonstrated in the provinces of Alberta and Ontario, the probability of IA success is known to decrease with increasing values of the Initial Spread Index (ISI), a unitless indicator of potential fire spread calculated using fuel moisture and wind speed (Arienti et al. 2006; Podur and Martell 2007; Beverly 2017; Wheatley et al. 2022). The influence of fuels on IA success is often represented through forest fuel type (Cardil et al. 2019) or time since last disturbance (Beverly 2017; Reimer et al. 2019); both factors influence fire behaviour and support high-intensity and fast spreading fires, which are associated with a decrease in IA success. For topography, increases in slope have been associated with decreases in IA success (Collins et al. 2018; Marshall et al. 2022; Plucinski et al. 2023).
Operational factors such as agency response times, resource allocation and the size of the fire at IA have also been found to influence IA success (Arienti et al. 2006; Flannigan et al. 2006; Podur and Wotton 2010; Beverly 2017; Cardil et al. 2019; Collins et al. 2018). Longer response times for suppression resources allows more time for fires to grow, leading to both response failures (Arienti et al. 2006) and IA failures (Plucinski 2012a). Response time, combined with environmental attributes, can influence the size of a fire and perimeter length requiring containment at the time suppression resources arrive. Large fires with lengthy perimeters increase the time allocated per suppression resource unit to fully contain the fire, making it more difficult to contain the fire at a small size or by the short time-to-containment definitions of IA success. Indeed, in numerous research studies, a larger fire size at IA has been associated with a decrease in IA success (Arienti et al. 2006; Beverly 2017; Marshall et al. 2022; Wheatley et al. 2022).
Despite several studies identifying predictors of IA success, comparing results and inferences across these studies is challenging owing to inconsistent definitions of IA success. In particular, there is uncertainty about how sensitive classifications of IA success are to the specific definition used. Additionally, different modelling methodologies themselves (e.g. statistical modelling versus machine learning) may influence results and interpretability. Using historical fire data from the province of Ontario, we compare different definitions of IA success and modelling methods to explore differences in predictive accuracy. We developed restrictive models including only the influential covariates of fire spread potential (ISI) and fire size at the onset of firefighting as identified in previous literature (e.g. Arienti et al. 2006; Beverly 2017; Wheatley et al. 2022). We compared the predictive accuracy of models developed using different IA success definitions used by fire management agencies and researchers. For each definition, we then compared different modelling methods, including statistical modelling and machine learning techniques (i.e. bagged classification trees and random forest), to evaluate the variability in IA success prediction accuracy. These comparisons of IA success model definitions and methods will enhance the understanding and cross comparison of fire containment models across the literature.
Methods
Historical fire and weather data
Historical fire data, including information on IA success, were provided by the Ontario Ministry of Natural Resources (OMNR) and include operational records for all forest fires in the province of Ontario from 1990 to 2019. Since 2014, Ontario’s official fire suppression strategy is known as ‘Appropriate Response’ – a risk-based approach to fire management where fires receive an appropriate response based on the behaviour and potential impacts of the fire. To encourage the beneficial ecological role of fire, fire management agencies may opt to monitor fires that do not threaten values (Ontario Ministry of Natural Resources and Forestry 2014). Only fires that received suppression by IA were included in the analysis. Fires were also omitted if they occurred outside the core fire season, which we defined as 1 May to 30 September.
Initial spread index observations for the day of IA were obtained from the OMNR daily weather archive. The archive consists of fire weather indices calculated from weather station observations of temperature, relative humidity, wind speed and 24-h precipitation at 13:00 Local Daylight Time (LDT) and are representative of peak daily fire behaviour conditions (≈17:00 LDT) at each weather station in the OMNR weather station network. Daily ISI values were interpolated to each fire’s location on the day of IA using a thin-plate spline method in the ‘fields’ package in R (Nychka et al. 2017). The ISI was the only fire weather index used in our modelling owing to its strong association with IA success identified in previous studies (e.g. Arienti et al. 2006; Podur and Martell 2007; Beverly 2017; Wheatley et al. 2022).
Defining initial attack success
Eight definitions of IA success were derived from previously used definitions in the literature and standard fire management agency-specific definitions (Table 1). A binary outcome variable was created to represent IA success (0 = IA failure, 1 = IA success) for each of the eight different IA success definitions based on time, final fire size, or fire growth thresholds. Time-based thresholds specify the time of fire containment or when the fire is assigned an operations status of ‘being held’ (BHE) by Ontario’s fire management agency. Fires are assigned a BHE status when fire growth is not anticipated past its expected boundaries given the observed and forecast weather conditions and current resources committed (Canadian Interagency Forest Fire Centre (CIFFC) 2023).
| Threshold type | Threshold name | Description of containment success | Previous reference | Proportion of fires classified as IA success (%) | |
|---|---|---|---|---|---|
| Time or size | Time or size | Fire is assigned a BHE status by 13:00 hours the day following IA or the fire has a final size ≤4 ha | Ontario Ministry of Natural Resources (2004), LaCarte (2019) | 98 | |
| Size | Final size 4 ha | Final fire size ≤4 ha | Podur and Wotton (2010) | 97 | |
| Growth | 2 ha growth | Final fire size is no more than 2 ha greater than size at IA | LaCarte (2019) | 96 | |
| Time | BHE 1900 | Fire is assigned a BHE status by 19:00 hours the day following IA (i.e. at the end of the next day’s ‘burning period’) | Modified from NWCG (National Wildfire Coordinating Group) (2022) | 95 | |
| Size | Final size 2 ha | Final fire size ≤2 ha | Alberta Sustainable Resource Development (2001); modified from Beverly (2017) | 94 | |
| Time | BHE 1300 | Fire assigned a BHE status by 13:00 hours the day following IA (i.e. before the beginning of a the next day’s ‘burning period’) | Modified from NWCG (National Wildfire Coordinating Group) (2022), Wheatley et al. (2022) | 92 | |
| Growth | 20% growth | Final fire size is no more than 20% greater than the fire size at IA | Modified growth definition | 81 | |
| Growth | Zero growth | Fire size at IA is equal to the final fire size (i.e. no observed growth) | Tremblay et al. (2018) | 79 |
Abbreviations used are: BHE, being held; IA, initial attack.
Data analysis
Multiple logistic regression methods (e.g. Hosmer et al. 2013) were used to predict the probability of IA success for each of the eight IA success definitions shown in Table 1. We developed simple models predicting IA success using ISI and fire size at IA as covariates:
where P(success) is the probability of IA success, β0 is the regression coefficient of the model intercept, β1 and β2 are the regression coefficients associated with fire size at IA (SIZE, in hectares) and ISI, respectively.
Logistic regression assumes a linear relationship between the log-odds of interest (i.e. the empirical proportion of IA success) and the given covariate. We examined this assumption before fitting the logistic regression models by visually examining empirical log-odds plots, which partitioned each covariate into equal decile bins and plotted the bin’s empirical log-odds against each decile’s median value. These plots were examined for each of the eight IA success definitions for both ISI and fire size at IA. Multicollinearity between ISI and fire size at IA was examined to ensure no strong association between these two covariates. All statistical modelling and data tests were executed using R statistical software (R Core Team 2022).
Machine learning methods, including bagged classification trees and random forest modelling, were used to model the binary outcome of IA success. These machine learning methods are useful when dealing with complex relationships as they are not restricted by assumptions of Gaussian relationships or by their distributions (De’Ath and Fabricius 2000). Classification tree methods use combinations of explanatory variables to explain variation in a categorical response variable by continually splitting the data into more uniform groupings based on the Gini index (De’Ath and Fabricius 2000). These splits aim to make the groups as homogeneous as possible based on the proportion of IA success or IA failure in the data using size at IA and ISI as predictors. However, classification trees alone tend to have high variance, and therefore bagging is necessary. Bagging is the process in which many bootstrapped training sets are made from a subsample of the observations and then averaged together to improve accuracy (James et al. 2013). We developed eight models using the bagged classification tree method, one for each of our IA success definitions.
Random forest modelling is like bagged classification trees in that the model creates many decision trees to calculate the proportion of IA success and IA failure based on a set of predictors. The main difference between the two machine learning methods is the decorrelation between trees (James et al. 2013). In building a random forest model, the algorithm is only allowed to consider a random subsample of m predictors, which removes the model’s ability to use only the strongest predictor at each split, which would create a similar collection of decision trees. Instead, each tree uses different subsets of predictors to determine splitting, which decreases the variance in the averaged trees (James et al. 2013). We developed eight models predicting IA success using the random forest method, one for each definition of IA success, including the ISI and fire size at IA predictors in the models. The ‘randomForest’ package (Liaw and Wiener 2002) in R was used for the bagged classification trees and random forest modelling. For the bagged classification trees, the number of predictors for each decision tree was set to m = 2 to include both ISI and fire size at IA at each split; otherwise, default parameters were used for both methods to make general comparisons between models.
We compared predictive accuracy and sensitivity across the three modelling methods and eight definitions of IA success. Historical fire data were separated into testing and training data for cross-validation using a randomised split, with 80% of observations used for model training and the remaining 20% reserved for testing and validation. Bootstrapping was used to ensure internal validation of each model. Overall, 24 different models were developed.
For each model, we calculated the area under the Receiver Operating Characteristic (ROC) curve for the training data and testing data observed and predicted values. The area under the ROC curve (AUC) measures the model’s ability to discriminate between the observations that endorse the outcome of interest versus those that do not. This value ranges from 0.5 to 1.0, where values above 0.7, 0.8 and 0.9 indicate acceptable, excellent and outstanding discrimination, respectively (Hosmer et al. 2013). For the machine learning methods, we also compared the out-of-bag mean square error (OOB MSE), which provides an estimate of the model’s prediction error using bootstrapped samples in the training data while building the classification trees (James et al. 2013). Metrics of overall predictive accuracy (i.e. the total proportion of correctly classified fires), sensitivity (i.e. the proportion of IA success fires classified correctly) and specificity (i.e. the proportion of IA failure fires classified correctly) were examined, along with the MSE of prediction residuals, as represented by the Brier score (Brier 1950). We used the Youden index criterion, a value derived from the training ROC curve, to determine the optimal threshold for distinguishing between IA successes and IA failures for model prediction (Youden 1950). This threshold is used to determine metrics of accuracy, sensitivity and specificity.
Results
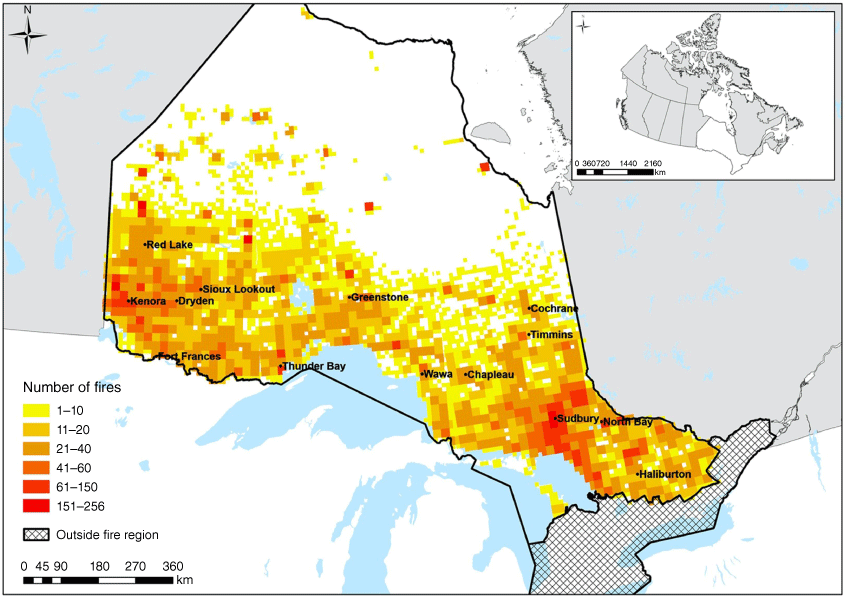
In Ontario, 34,836 fires were reported from 1990 to 2019. Fires that did not receive suppression on detection (n = 3254) were omitted, as were those that occurred before 1 May or after September 30 (n = 5315). Fires were also omitted from analysis if the size at IA was missing and or the final size was less than the IA size (n = 96). Our final dataset included 26,171 fires across Ontario (Fig. 1).
Ontario forest fire management area. Fire Management Headquarters across the province are denoted by black dots and represent locations where initial attack wildland firefighter crews are prepositioned for deployment. Historical fire frequency (i.e. number per 20 km2) is indicated by shading and includes all fires that received IA between May 1 and September 30 from 1990 to 2019 inclusive (n = 26,171).
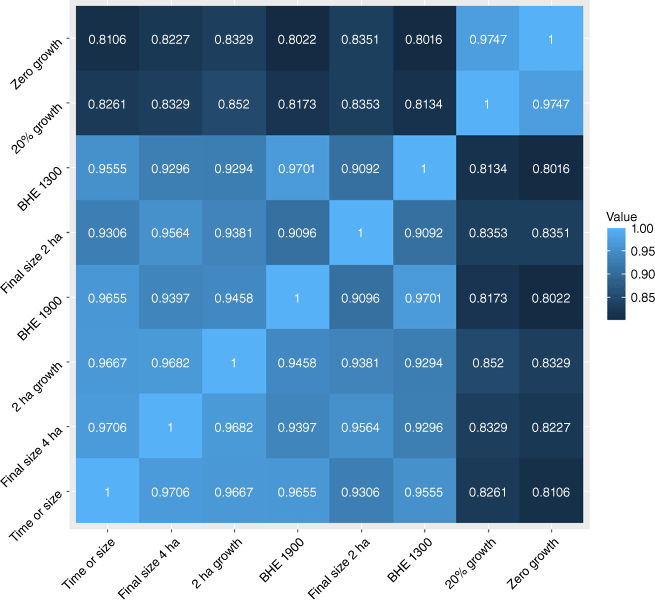
Three of our IA success definitions include a final size criterion that required further sub-sets of the data to ensure that our modelling of IA success was capturing successful IA operations as opposed to agency ‘response failures’ (i.e. fires where action was taken when they were greater than the IA success final size threshold; Arienti et al. 2006). For both the ‘time or size’ and ‘final size ≤4 ha’ definitions, the data were put in a subset to include only fires that had a size at IA of ≤4 ha, as any fire that was attacked at a size greater than 4 ha would automatically be considered an IA failure, even though this fire had no chance to be successfully contained. Similarly, for the ‘final size ≤2 ha’, the data were placed in a subset to include only fires with an IA size of ≤2 ha. The resulting dataset had 25,121 and 24,286 fires for modelling the 4 and 2-ha size constraints, respectively. Overall, it is important to note that although the eight definitions may yield proportions of IA success ranging from 79 to 98%, these definitions predominantly categorise a similar subset of fires. Specifically, 74% of the fires are considered an IA success across all eight definitions. In general, there is a high degree of consistency in how the different definitions classify fires, with size and time-constraint definitions demonstrating high levels of agreement with each other, as depicted in Fig. 2.
The proportion of fires that are considered an initial attack (IA) success for all combinations of IA success modelling definitions. A value close to 1 indicates a higher consistency in IA success classification, highlighting the similarity between those two definitions. Abbreviation used is: BHE, being held.
The assumption of linearity for the logistic regression models was not met for the fire size at IA predictor; therefore, we used logarithmic transformations on this variable for all IA success models. ISI was not linearly associated with the log-odds of IA success for both the BHE 1300 and BHE 1900 success definitions; therefore, a second-order polynomial transformation was used for modelling with ISI for both models. The logistic regression model summaries, including regression coefficients, are shown in Supplementary material S1.
Comparison of IA containment definitions
The model summaries for the AUC, OOB MSE, overall prediction accuracy and Brier score are shown in Table 2. Performance of the eight different IA success models was similar; there is no clear pattern between the collective strength of the model across all metrics examined and the proportion of fires that are classified as an IA success (e.g. a model with 98% of fires considered an IA success does not necessarily have greater accuracy than a model with 93% of fires considered an IA success). Overall model accuracy was generally lower for both time-based definitions (i.e. BHE 1300 and BHE 1900) and the zero growth definition. However, the bagged classification tree method showed no discernable differences in accuracy across the models developed. The Brier score was relatively similar across each of the eight definitions. However, for the zero growth model, the mean residual error was generally greater, a finding likely due to the higher proportion of IA failures (19%) in this IA success definition.
| Modelling method | Metric | Time or size | Final size 4 ha | 2 ha growth | BHE 1900 | Final size 2 ha | BHE 1300 | 20% growth | Zero growth | |
|---|---|---|---|---|---|---|---|---|---|---|
| Logistic regression | AUC (train) | 0.88 (0.004) | 0.91 (0.003) | 0.91 (0.002) | 0.83 (0.004) | 0.90 (0.003) | 0.82 (0.003) | 0.76 (0.002) | 0.79 (0.002) | |
| AUC (test) | 0.89 (0.02) | 0.91 (0.01) | 0.91 (0.01) | 0.83 (0.01) | 0.90 (0.01) | 0.82 (0.01) | 0.76 (0.01) | 0.79 (0.01) | ||
| Accuracy | 0.86 (0.03) | 0.88 (0.01) | 0.86 (0.01) | 0.82 (0.03) | 0.84 (0.02) | 0.79 (0.01) | 0.66 (0.01) | 0.71 (0.01) | ||
| Brier Score | 0.01 (0.001) | 0.02 (0.001) | 0.03 (0.002) | 0.04 (0.002) | 0.03 (0.002) | 0.06 (0.002) | 0.13 (0.002) | 0.13 (0.003) | ||
| Bagged classification trees | OOB MSE (%) | 2.41 (0.07) | 3.81 (0.10) | 5.86 (0.13) | 7.31 (0.14) | 5.16 (0.11) | 10.42 (0.15) | 25.50 (0.25) | 26.31 (0.25) | |
| AUC (train) | 0.999 (0.0007) | 0.999 (0.0004) | 1.000 (0.0003) | 0.997 (0.0005) | 0.999 (0.0003) | 0.998 (0.0004) | 0.999 (0.0002) | 0.999 (0.0001) | ||
| AUC (test) | 0.75 (0.03) | 0.81 (0.02) | 0.84 (0.01) | 0.77 (0.01) | 0.81 (0.01) | 0.76 (0.01) | 0.69 (0.01) | 0.72 (0.01) | ||
| Accuracy | 0.98 (0.002) | 0.96 (0.003) | 0.94 (0.003) | 0.92 (0.003) | 0.95 (0.002) | 0.89 (0.004) | 0.74 (0.006) | 0.73 (0.006) | ||
| Brier score | 0.02 (0.001) | 0.03 (0.002) | 0.04 (0.002) | 0.05 (0.002) | 0.04 (0.002) | 0.08 (0.002) | 0.18 (0.004) | 0.18 (0.004) | ||
| Random forest | OOB MSE (%) | 3.12 (0.07) | 2.52 (0.06) | 4.27 (0.09) | 5.12 (0.09) | 3.28 (0.07) | 7.34 (0.1) | 18.48 (0.2) | 19.55 (0.2) | |
| AUC (train) | 0.996 (0.0003) | 0.998 (0.0002) | 0.992 (0.0005) | 0.980 (0.001) | 0.997 (0.0002) | 0.967 (0.001) | 0.875 (0.003) | 0.889 (0.002) | ||
| AUC (test) | 0.91 (0.01) | 0.93 (0.01) | 0.86 (0.01) | 0.78 (0.01) | 0.94 (0.006) | 0.78 (0.01) | 0.74 (0.008) | 0.77 (0.008) | ||
| Accuracy | 0.95 (0.003) | 0.95 (0.003) | 0.92 (0.005) | 0.85 (0.008) | 0.94 (0.003) | 0.81 (0.01) | 0.64 (0.01) | 0.68 (0.01) | ||
| Brier score | 0.02 (0.002) | 0.02 (0.002) | 0.04 (0.002) | 0.04 (0.002) | 0.03 (0.002) | 0.06 (0.003) | 0.2 (0.004) | 0.2 (0.004) |
Mean and standard deviation in parentheses from the bootstrapped iterations are presented. Models were fit using a training dataset of n = 20,936 fires for most definitions. ‘Time or size’ and ‘final size ≤4 ha’ used n = 20,099 observations to fit the model. ‘Final size ≤2 ha’ used 19,428 observations to fit the model.
Abbreviations used are: AUC, area under the receiver operating characteristic curve; OOB MSE, out of bag mean squared error; BHE, being held.
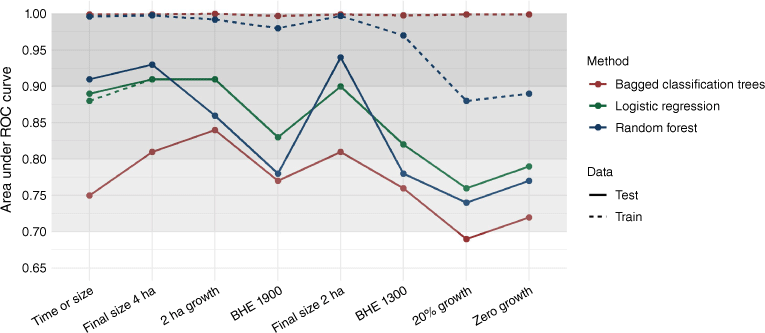
When comparing the AUC, specifically for the training dataset, across each definition for each modelling method (Fig. 3), we see no consistent pattern or differences across the definitions used, meaning that the proportion of IA successes is not influencing the discriminatory ability of the model. All three modelling methods generally show a decline in AUC, moving across the x-axis in Fig. 4, from the ‘2 ha growth’ definition to the ‘20% growth definition’; however, the peak at the ‘Final size 2 ha’ definition signifies that this trend is likely due to the underlying constraints in the definitions themselves rather than the proportion of IA successes. Generally, the IA success thresholds defined by absolute size constraints (e.g. final size ≤4 ha) have a greater AUC compared with IA success thresholds defined by time constraints (e.g. BHE by 19:00 hours) or fire growth (e.g. 20% growth).
Area under the ROC curve for the training and testing validation data for each of the eight initial attack (IA) success definitions and three modelling methods. The IA success definitions used for modelling are ordered along the x axis according to descending percentage of IA success. The shaded areas represent the interpretation of discriminatory ability from the area under the ROC curve as described by Hosmer et al. (2013), with values above 0.7 indicating acceptable discriminatory ability, values above 0.8 indicating excellent discriminatory ability, and values above 0.9 indicating outstanding discriminatory ability. Abbreviations used are: BHE, being held; ROC, receiver operating characteristic.
Comparison of model (a) sensitivity (i.e. the proportion of initial attack (IA) successes classified correctly), and (b) specificity (i.e. the proportion of IA escapes classified correctly) for each model. The IA success definitions used for modelling are ordered along the x axis according to descending percentage of IA success. Abbreviation used is: BHE, being held.
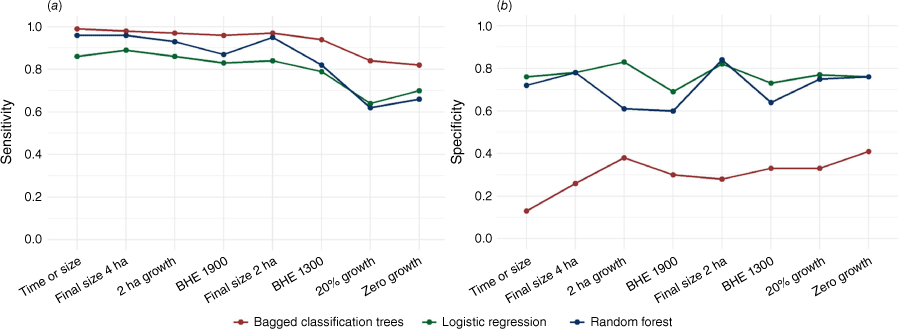
To emphasise each model’s ability to classify IA success versus IA failures correctly, Table 3 presents the sensitivity, or the model’s ability to classify the IA successes, and specificity, or the model’s ability to correctly classify the IA failures, for each definition of IA success for the three modelling methods. Overall, there are no noticeable increasing or decreasing relationships between the proportion of IA success fires and the model’s ability to correctly classify IA successes versus IA failures (Fig. 4). For the zero growth IA success model, with the highest proportion of IA failures, the specificity is generally the highest for each modelling method, and sensitivity is generally the lowest. This result is likely due to the model’s ability to better capture attributes related to IA failure owing to a more balanced dataset. Sensitivity is also lower for the time-based IA success definitions for both logistic regression and random forest.
| Time or size | Final size 4 ha | 2 ha growth | BHE 1900 | Final size 2 ha | BHE 1300 | 20% growth | Zero growth | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Sensitivity | Logistic regression | 0.86 (0.04) | 0.89 (0.01) | 0.86 (0.01) | 0.83 (0.03) | 0.84 (0.02) | 0.79 (0.01) | 0.64 (0.01) | 0.70 (0.01) | |
| Bagged classification trees | 0.99 (0.002) | 0.98 (0.002) | 0.97 (0.003) | 0.96 (0.003) | 0.97 (0.002) | 0.94 (0.004) | 0.84 (0.006) | 0.82 (0.007) | ||
| Random forest | 0.96 (0.003) | 0.96 (0.004) | 0.93 (0.006) | 0.87 (0.01) | 0.95 (0.004) | 0.82 (0.01) | 0.62 (0.02) | 0.66 (0.01) | ||
| Specificity | Logistic regression | 0.76 (0.05) | 0.78 (0.03) | 0.83 (0.02) | 0.69 (0.04) | 0.82 (0.03) | 0.73 (0.02) | 0.77 (0.02) | 0.76 (0.01) | |
| Bagged classification trees | 0.13 (0.03) | 0.26 (0.04) | 0.38 (0.03) | 0.30 (0.02) | 0.28 (0.03) | 0.33 (0.02) | 0.33 (0.02) | 0.41 (0.02) | ||
| Random forest | 0.72 (0.03) | 0.78 (0.03) | 0.61 (0.03) | 0.60 (0.03) | 0.84 (0.02) | 0.64 (0.03) | 0.75 (0.02) | 0.76 (0.01) |
Sensitivity and specificity are reported for the testing validation dataset. Mean sensitivity and specificity across the bootstrapped models is presented with standard deviation in parenthesis.
Abbreviation used is: BHE, being held.
Comparison of modelling methods
We examined the AUC developed on both the training and testing datasets for each IA success model. Examining the difference between the AUC for a single model can provide an indication of model overfit. When a model is overfitting, the AUC for the training data will be exceptionally high, approaching 1, while the AUC for the testing data will be substantially lower. The random forest and bagged classification tree models have AUC values that are considered outstanding, approaching a near-perfect 1.0 for the training data. When we use the testing data (Fig. 3), the AUC is substantially less, suggesting that these machine learning methods are overfitting the data, in part likely owing to the default parameters used in model development. Out of the three modelling methods, bagged classification trees consistently perform the worst across all IA success definitions when comparing AUC, with values typically less than 0.8, which is the threshold for acceptable discrimination. For the logistic regression methods, all models have acceptable or even excellent ability to discriminate between IA successes versus IA failures as demonstrated by the AUC for both the training and testing data.
Overall model prediction accuracy varies across methods (Table 2), with models developed using random forest and bagged classification trees outperforming logistic regression methods when predicting IA success. The Brier score showed comparable residual errors for logistic regression and bagged classification trees, with random forest reporting the lowest mean residual error. In predicting IA failures or model specificity, all three methods perform less accurately compared with predicting IA successes or model sensitivity (Table 3). Logistic regression outperforms bagged classification trees and random forest modelling for classifying IA failures on nearly every IA success definition, except for the 2 ha growth definition. Therefore, the ability to accurately capture the rarer, but operationally impactful, IA failure is best modelled by logistic regression.
Discussion
There is no consistent definition for classifying fires as successfully contained on IA to study landscape-scale suppression effectiveness. Similarly, fire management agencies use different performance metrics when evaluating system-level suppression success using the simplified binary indicator of ‘IA success’ or ‘IA failure’ (Gordon 2014). Using historical fire data from the province of Ontario, we tested the sensitivity of eight different IA success definitions, all defined using final fire size or time to containment criteria. We used three different modelling strategies to compare predictive accuracy for modelling across various IA success definitions. The proportion of fires classified as an IA success varied according to the definition. In Ontario, 79–98% of fires were classified as an IA success depending on the definition. However, regardless of the specific threshold used to define IA success, most fires are classified similarly across various definitions (Fig. 2), meaning that these metrics set by fire management agencies are providing consistent measures of the effectiveness of the IA system. This consistency across thresholds can allow the comparison of IA success between operational and research-based objectives or when definitions of IA containment change.
We found no consistent evidence to suggest that the overall proportion of IA successes associated with an IA success criterion impacted the model’s ability to classify or differentiate between IA successes and IA failures accurately. This finding is supported by consistent measures of predictive accuracy, sensitivity and specificity across all eight definitions (Fig. 4). For example, there is no clear indication that a model predicting a 98% IA success outcome (i.e. time or size definition) performed better than a model predicting a 79% IA success outcome (i.e. zero growth definition). However, there is some evidence to support that the underlying criteria for each IA success threshold can influence the model’s discriminatory ability and predictive accuracy. Time-based definitions, which set thresholds for containment by the day’s next burning period, generally exhibit lower discriminatory power compared with definitions based on absolute fire size (e.g. final fire size less than or equal to 4 ha) (Fig. 3). We attribute this finding largely to the human influence involved in deciding to declare a fire ‘being held’ within these time-based definitions, as opposed to fire size definitions grounded in the physical aspects of the fire environment. The variability in declaring a fire ‘being held’ depends on the physical requirements for fire containment and the individual Incident Commander’s confidence in reporting that the fire is contained and is not expected to grow past anticipated boundaries. We also recognise that including size at IA as a predictor may have a stronger influence on models with outcomes based on size-based thresholds of IA success (i.e. final size less than 2 or 4 ha), leading to improved predictive accuracy compared with time-based and growth definitions.
Generally, the ‘zero growth’ and ‘20% growth’ definitions of IA success exhibited reduced model discriminatory ability as demonstrated by the AUC (Fig. 3) and the predictive accuracy (Fig. 4) compared with the final fire size definitions. The ‘zero growth’ definition is not a realistic performance measure or suppression IA success standard. This definition assumes such minimal fire behaviour that the fire exhibits no active spread from when the wildland firefighters began IA. Even if a wildland firefighter crew promptly engages in IA and works on wrapping the fire immediately, some growth is still anticipated, as the crews need time to lay hose on the entirety of the fire perimeter. The ‘20% growth’ definition shares similarities with the ‘zero growth’ definition in restricting growth owing to the fire size classifications reported by the OMNR. In its fire report archives, the OMNR reports the smallest fire size as 0.1 ha; this includes all fires up to and including this size. This baseline fire size of 0.1 ha represents approximately 50% of fires in our data. Sizes are reported in hectares only to the first decimal place; therefore, the next allowable fire size in the archive system is 0.2 ha, which is a 100% growth increase. Consequently, by default, these fires classified as a size of 0.1 ha are considered an IA failure if they experience any growth. This is evident in Fig. 2, where the agreement percentage between the ‘zero growth’ and ‘20% growth’ definitions is 97%. These thresholds essentially define the same set of fires, and their stringent constraints on fire growth result in lower model predictive accuracy estimates compared with other definitions.
Our results provide insight about different modelling methods available for predicting IA success. The use of statistical and machine learning approaches, such as random forest and bagged classification trees, allows a relative comparison of these commonly used methods in previous IA success modelling studies (e.g. Arienti et al. 2006; Plucinski et al. 2011; Plucinski 2012a, 2012b; Beverly 2017; Cardil et al. 2019; Collins et al. 2018; Marshall et al. 2022; Wheatley et al. 2022). Although model performance was similar among methods, machine learning techniques tended to overfit the training data, resulting in reduced model discriminatory ability for the testing data, represented by the AUC (Fig. 3). Logistic regression methods consistently exhibited the highest discriminative ability across most models, except for the ‘time or size,’ ‘final size 4 ha’ and ‘final size 2 ha’ definitions, a finding that likely reflects the tendency of the traditional machine learning approaches to overfit training data when not optimised for their specific use. Notably, the bagged classification trees method displayed the largest disparity between the training and testing AUCs, possibly owing to its overall weaker predictive power arising from the tendency of decision trees in this method to correlate with all sets of predictor variables considered at each tree split (James et al. 2013).
A model designed to represent the IA response system, whether for modelling suppression effectiveness or for determining performance metrics in fire management, should prioritise accurate classification of IA failures (model specificity) over IA success (model sensitivity) if achieving equality between both metrics is not feasible. Models that overpredict the number of IA failures are preferred as they err on the side of being risk-averse. Predicting escaped fires is crucial because escapes pose greater potential for disastrous effects than fires that are quickly contained, and contribute to the majority of area burned (Stocks et al. 2002; Hanes et al. 2019), entail greater suppression costs (Calkin et al. 2005) and consume significant suppression resource time. Fire management agencies must plan and prepare both short-term and long-term suppression resource forecasting, and it is critical to have or send an excess of resources to a fire rather than too few.
When examining these IA failures (Fig. 4a), logistic regression outperforms both random forest and bagged classification trees in correctly predicting IA failures, with a range of 69–83% of IA failures classified correctly depending on the definition used. All three modelling methods exhibit a higher capability to correctly classify IA successes compared with IA failures (Fig. 4b), likely owing to the higher proportion of IA successes in the data. Generally, when modelling rare occurrences such as IA failures, the classification rate for the rare event is lower than non-rare events, as observed in previous IA success modelling studies (Wheatley et al. 2022) and fire occurrence prediction modelling (Phelps and Woolford 2021). However, our analysis reveals that logistic regression models tend to correctly classify a similar proportion of IA successes and IA failures, with 64–89% accuracy for IA successes. This relatively equal classification between IA successes and IA failures is desirable for developing decision-support models to inform fire operation planning and resource forecasting.
Although logistic regression methods outperformed machine learning methods in classifying these IA failures, this result should not be taken as evidence that machine learning methods are not suited for IA success modelling. Instead, it underscores the importance of considering model optimisation strategies to accurately classify as many IA failures as possible. In the Ontario historical fire data, the proportion of IA successes to IA failures is not equal, and depending on the definition, IA failures can be a rare occurrence, with some definitions having only a 2% occurrence of IA failure. When modelling binary outcome data with imbalanced occurrence rates, it is common to consider balancing the outcome to represent a 50–50 split of positive and negative cases (e.g. Phelps and Woolford 2021). Although not presented in the current paper, we repeated each model using balanced input data for the proportion of IA successes and IA failures for each definition. We observed no differences in the trade-off between sensitivity and specificity for models using balanced and unbalanced data (Supplementary material S2).
Statistical modelling and machine learning methods are common when modelling fire suppression system performance measures, and modelling objectives should be considered when using one approach over another. For example, when modelling with a comprehensive set of predictor variables to evaluate the most influential fire behaviour and fire environment factors on successful IA containment, machine learning methods such as classification trees (e.g. Plucinski et al. 2011; Plucinski 2012b) and random forest (e.g. Collins et al. 2018; Rodrigues et al. 2019; Marshall et al. 2022; Xu et al. 2023) may be of interest as these methods can easily incorporate a large number of input variables and identify variable importance metrics (James et al. 2013). Other modelling objectives may be to examine specific predictors known a priori as potential influencers based on logical arguments or previous literature. In these cases, a specific relationship between this known construct is being isolated and explained, such as the relationship between time since prior wildfire and IA success (e.g. Beverly 2017) or how suppression effort on IA influenced successful containment or failure (e.g. Wheatley et al. 2022; Rezaei et al. 2023). In these cases, statistical modelling may be better suited as it allows isolation and close examination of the association between two variables and manipulation of these associations using powerful smoothers.
In this study, our goal was not to create predictive models to be used in an operational capacity. Instead, we sought to compare models using different thresholds for IA containment and the methods used to model the IA system, not necessarily to build the best predictive model of IA success. Therefore, although they are important and influential, we did not incorporate other environmental and human-related predictors commonly used in other studies, such as the fuels the fire is burning in, fire behaviour attributes (e.g. spread rate and fireline intensity) and fire response time. We used default parameters when building our models for each modelling method to allow relative comparisons between models; however, despite our simplistic model design, the majority of models had predictive accuracy values over 0.8 (Table 2), and our model discriminative ability represented by the test data AUC is similar to those reported in other studies (e.g. Collins et al. 2018; Wheatley et al. 2022; Plucinski et al. 2023) that consider a comprehensive set of predictor variables. Each modelling method used in the present study can be optimised to provide more accurate predictions of IA success, which should be explored when developing models for predictive purposes.
Conclusion
The binary indicator of IA success or IA failure is used throughout fire suppression research studies as a metric of suppression effectiveness and used by fire management agencies for summarising performance metrics across fire seasons. In exploring eight definitions of IA success, we observed that collective model strength did not vary strongly across definitions. Consequently, the specific definition chosen for a particular modelling exercise will not significantly impact the sensitivity of results. This means that suppression performance metrics set by fire management agencies are not strongly biased by the specific definition of IA success used. This consistency across definitions allows the comparison of IA success through time and across research and operational studies of IA success. Through a comparative analysis of statistical modelling and machine learning methods, we found that, in general, logistic regression and random forest modelling perform the best regarding model discriminatory ability, predictive accuracy, sensitivity and specificity. However, the choice of modelling method should be tailored to specific study objectives. Future work should investigate whether these results are consistent across Canada, as we only tested these IA threshold and modelling methods using historical fire data in Ontario.
Conflicts of interest
Mike Wotton and Jen Beverly are Associate Editors of International Journal of Wildland Fire. To mitigate this potential conflict of interest they had no editor-level access to this paper during the peer review process. The authors declare no other conflicts of interest.
Declaration of funding
We acknowledge the support of the Natural Sciences and Engineering Research Council of Canada – Doctoral Canadian Graduate Scholarship to Kennedy Korkola and the OMNR through a Collaborative Research Agreement with The University of Toronto (Patrick James).
Acknowledgements
The OMNR provided data used in this study and their staff engaged in helpful conversations around initial attack and suppression operations.
References
Alberta Sustainable Resource Development (2001) Wildfire management in Alberta. Available at https://open.alberta.ca/publications/0778513785 [verified 29 August 2023]
Arienti MC, Cumming SG, Boutin S (2006) Empirical models of forest fire initial attack success probabilities: the effects of fuels, anthropogenic linear features, fire weather, and management. Canadian Journal of Forest Research 36, 3155-3166.
| Crossref | Google Scholar |
Beverly JL (2017) Time since prior wildfire affects subsequent fire containment in black spruce. International Journal of Wildland Fire 26, 919-929.
| Crossref | Google Scholar |
Bonan GB, Shugart HH (1989) Environmental factors and ecological processes in boreal forests. Annual Review of Ecology and Systematics 20(1), 1-28.
| Crossref | Google Scholar |
Brier GW (1950) Verification of forecasts expressed in terms of probability. Monthly Weather Review 78(1), 1-3.
| Crossref | Google Scholar |
Burton PJ, Parisien MA, Hicke JA, Hall RJ, Freeburn JT (2008) Large fires as agents of ecological diversity in the North American boreal forest. International Journal of Wildland Fire 17(6), 754-767.
| Crossref | Google Scholar |
Calkin DE, Gebert KM, Jones JG, Neilson RP (2005) Forest service large fire area burned and suppression expenditure trends, 1970-2002. Journal of Forestry 103, 179-183.
| Crossref | Google Scholar |
Canadian Interagency Forest Fire Centre (CIFFC) (2023) Canadian wildland fire glossary. Available at https://www.ciffc.ca/sites/default/files/2023-05/CWFM_glossary_v2023-04-24-EN.pdf [verified 3 January 2024]
Cardil A, Lorente M, Boucher D, Boucher J, Gauthier S (2019) Factors influencing fire suppression success in the province of Quebec (Canada). Canadian Journal of Forest Research 49, 531-542.
| Crossref | Google Scholar |
Collins KM, Price OF, Penman TD (2018) Suppression resource decisions are the dominant influence on containment of Australian forest and grass fires. Journal of Environmental Management 228, 373-382.
| Crossref | Google Scholar | PubMed |
De’ath G, Fabricius KE (2000) Classification and regression trees: a powerful yet simple technique for ecological data analysis. Ecology 81(11), 3178-3192.
| Crossref | Google Scholar |
Flannigan MD, Amiro BD, Logan KA, Stocks BJ, Wotton BM (2006) Forest fires and climate change in the 21st century. Mitigation and Adaptation Strategies for Global Change 11(4), 847-859.
| Crossref | Google Scholar |
Gordon (2014) Developing more common language, terminology and data standards for wildland fire management in Canada. Available at https://www.ciffc.ca/sites/default/files/2019-03/Developing_More_Common_Terminolgy_-_Final_Report.pdf [verified 23 March 2022]
Hanes CC, Wang X, Jain P, Parisien MA, Little JM, Flannigan MD (2019) Fire-regime changes in Canada over the last half century. Canadian Journal of Forest Research 49, 256-269.
| Crossref | Google Scholar |
Liaw A, Wiener M (2002) Classification and regression by randomForest. R News 2, 18-22.
| Google Scholar |
Marshall E, Dorph A, Holyland B, Filkov A, Penman TD (2022) Suppression resources and their influence on containment of forest fires in Victoria. International Journal of Wildland Fire 31(12), 1144-1154.
| Crossref | Google Scholar |
Martell DL (2001) Forest Fire Management. In ‘Forest Fires’. pp. 527-583. (Academic Press) 10.1016/b978-012386660-8/50017-9
National Wildfire Coordinating Group (NWCG) (2022) ‘Glossary of wildland fire terminology.’ (National Wildfire Coordinating Group) Available at https://www.nwcg.gov/glossary/a-z [verified 28 March 2022]
Nychka D, Furrer R, Paige J, Sain S (2017) fields: tools for spatial data. (R Package version 10.3). 10.5065/D6W957CT
Ontario Ministry of Natural Resources and Forestry (2014) ‘Wildland fire management strategy.’ (Queen’s Printer for Ontario: Toronto, ON, Canada) Available at https://www.ontario.ca/page/wildland-fire-management-strategy [verified 21 November 2023]
Phelps N, Woolford DG (2021) Guidelines for effective evaluation and comparison of wildland fire occurrence prediction models. International Journal of Wildland Fire 30(4), 225-240.
| Crossref | Google Scholar |
Plucinski MP (2012a) Factors affecting containment area and time of Australian forest fires featuring aerial suppression. Forest Science 58, 390-398.
| Crossref | Google Scholar |
Plucinski MP (2012b) Modelling the probability of Australian grassfires escaping initial attack to aid deployment decisions. International Journal of Wildland Fire 22(4), 459-468.
| Crossref | Google Scholar |
Plucinski MP (2019) Contain and control: wildfire suppression effectiveness at incidents and across landscapes. Current Forestry Reports 5, 20-40.
| Crossref | Google Scholar |
Plucinski MP, McCarthy GJ, Hollis JJ, Gould JS (2011) The effect of aerial suppression on the containment time of Australian wildfires estimated by fire management personnel. International Journal of Wildland Fire 21(3), 219-229.
| Crossref | Google Scholar |
Plucinski MP, Dunstall S, McCarthy NF, Deutsch S, Tartaglia E, Huston C, Stephenson AG (2023) Fighting wildfires: predicting initial attack success across Victoria, Australia. International Journal of Wildland Fire 32(12), 1689-1703.
| Crossref | Google Scholar |
Podur JJ, Martell DL (2007) A simulation model of the growth and suppression of large forest fires in Ontario. International Journal of Wildland Fire 16(3), 285-294.
| Crossref | Google Scholar |
Podur J, Wotton M (2010) Will climate change overwhelm fire management capacity? Ecological Modelling 221(9), 1301-1309.
| Crossref | Google Scholar |
R Core Team (2022) ‘R: A language and environment for statistical computing.’ (R Foundation for Statistical Computing: Vienna, Austria) Available at https://www.r-project.org/ [verified 17 March 2022]
Reimer J, Thompson DK, Povak N (2019) Measuring initial attack suppression effectiveness through burn probability. Fire 2, 60.
| Crossref | Google Scholar |
Rezaei M, Lee I, Beverly J (2023) The effect of wildfire suppression resources: targeting fire groups with enhanced treatment effect. SSRN Electronic Journal. 10.2139/ssrn.4554313
Rodrigues M, Alcasena F, Vega-García C (2019) Modeling initial attack success of wildfire suppression in Catalonia, Spain. Science of The Total Environment 666, 915-927.
| Crossref | Google Scholar | PubMed |
Stocks BJ, Mason JA, Todd JB, Bosch EM, Wotton BM, Amiro BD, Flannigan MD, Hirsch KG, Logan KA, Martell DL, Skinner WR (2002) Large forest fires in Canada, 1959–1997. Journal of Geophysical Research: Atmospheres 107, FFR 5-1-FFR 5-12.
| Crossref | Google Scholar |
Tremblay PO, Duchesne T, Cumming SG (2018) Survival analysis and classification methods for forest fire size. PLoS One 13, e0189860.
| Crossref | Google Scholar | PubMed |
Wheatley M, Wotton BM, Woolford DG, Martell DL, Johnston JM (2022) Modelling initial attack success on forest fires suppressed by air attack in the province of Ontario, Canada. International Journal of Wildland Fire 31(8), 774-785.
| Crossref | Google Scholar |
Xu Y, Zhou K, Zhang F (2023) Modeling wildfire initial attack success rate based on machine learning in Liangshan, China. Forests 14(4), 740.
| Crossref | Google Scholar |
Youden WJ (1950) Index for rating diagnostic tests. Cancer 3, 32-35.
| Crossref | Google Scholar | PubMed |


