Factors influencing travel time and getaway time of helitack crews on wildfires in the province of Quebec
Frédéric Brunet A * , Jonathan Boucher B and Mathieu Bouchard AA
B
Abstract
Reducing the delay between the detection of a fire and the arrival of the initial attack (IA) crew can have a significant impact on the likelihood of the IA’s success.
The objective of this study was to identify factors influencing same-day getaway time, next-day getaway time and travel time of helitack IA crews in the province of Quebec, Canada.
Using generalised linear modelling and model selection, we analysed the impact of multiple factors on these three distinct times.
Our results show that factors such as the distance between the departure base and the fire, the number of flight legs to reach a fire, dispatch hour, departure base location, the fire’s rate of spread, Julian date, the number of active fires, fuel type and the fire’s size at detection all influenced getaway time and travel time with varying degrees of influence.
The factors with the highest influence were distance for travel time and dispatch hour for both same-day and next-day getaway times.
Addressing these high-impact factors through the modification of deployment policies and the positioning of helitack crews could help reduce response times.
Keywords: Deployment policies, fire management, fire suppression, helitack, initial attack, presuppression, resource deployment, response time, travel time, wildfire.
Introduction
Wildfires play an important role in many forest ecosystems and are considered one of the main natural disturbances in eastern Canada (Payette 1992). With the effects of climate change, wildfires will become more difficult to control: the number of fires, total area burned, fire intensity and the associated workload are all expected to increase over the next century (Wotton et al. 2010, 2017; Tymstra et al. 2019). Some solutions have been proposed to address these issues. These include strengthening community risk reduction programs, increasing the use of modified response to fire and enhancing fire suppression capacity (Hope et al. 2016; Tymstra et al. 2019).
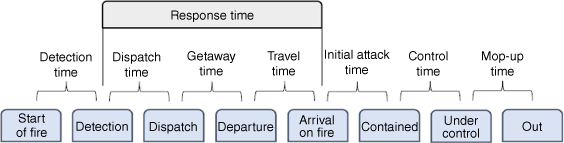
Fire suppression involves several phases (Fortin 1989; Fig. 1). Of all the fire suppression phases, the initial attack (IA) is the most critical for limiting the final size of a fire (Ntaimo et al. 2013; Reimer et al. 2019). IA is defined as the actions taken to halt the progression of a new wildfire by the first firefighting forces to arrive at the fire (CIFFC Training Working Group 2023) and its primary objective is to contain the fire as quickly as possible (Lee et al. 2013). IA occurs on the first day of suppression operations on a fire and typically ends when the fire is considered contained. A fire is considered contained when its progression is temporarily halted along its perimeter under prevailing conditions. If a fire is not contained on the first day, the IA phase transitions to the sustained attack phase.
Wildfire suppression chronology based on Fortin (1989), CIFFC (2021) and NWCG (2024). Initial attack time transitions to sustained attack time when the IA is exceeded. Sustained action continues until the fire is contained.
Once a crew arrives at a fire, multiple factors can influence the time it takes to contain its perimeter. One of the most important parameters that influences IA success is the size of the fire on arrival (Hirsch et al. 2004; Plucinski 2012; Beverly 2017). The larger the fire, the lower the chances are to successfully contain it. This highlights the importance of minimising the response time to a fire, to limit the period during which the fire can grow without suppression efforts (Parks 1964).
One of the most influential factors affecting the success of the IA is the time to get crews on a fire, as no suppressive action is taken during this period (Arienti et al. 2006; Plucinski 2012; Beverly 2017). Response time encompasses dispatch, getaway and travel time (Fig. 1). Depending on the studies, these components are sometimes studied individually, but they are often grouped together and referred to as response time. Plucinski et al. (2023) looked at the effect of response time and its individual components on IA success, and concluded that travel time was a significant predictor. In the present study, Dispatch time is defined as the interval between the initial reporting of a new fire and the dispatch of an IA crew to the fire by a local fire manager. Getaway time is defined as the delay between the moment a crew is dispatched to a fire, and the IA crew’s departure. Travel time is defined as the delay between the crew’s departure and the moment the crew arrives at the fire site.
Getaway time and travel time vary depending on multiple factors. The distance between the dispatch base and the fire has been shown to influence response time for helitack crews in Catalonia, Spain (Rodrigues et al. 2019), as well as travel time in Australia (Plucinski 2012). Longer distances are associated with higher response and travel times. The time of day at which a fire is assigned has also been shown to impact getaway time. Late-day fire detection led to longer getaway times, sometimes because they were delayed to the next day (Plucinski 2012; Paudel et al. 2019). Weather conditions and fire weather indices, such as those of the Canadian Forest Fire Weather Index System (FWI System, Van Wagner 1987) are also taken into account by fire management agencies in their decision-making process leading to dispatch and impact the response time (Rapp et al. 2021). The Initial Spread Index (ISI) of the FWI System, which is a metric representing the expected fire rate of spread (Van Wagner 1987), has been shown to be one of the major drivers (Paudel 2014). A fire with a high ISI will spread more rapidly, compelling the fire manager to dispatch a crew faster to a fire in order to be able to contain it. A higher number of active fires in an area has been shown to increase response time (Paudel et al. 2019) because of a limited amount of IA resources available at a given point in time, with its impact evaluated both in Alberta, Canada (Cumming 2005) and in northwestern Ontario, Canada (Paudel et al. 2019). Deployment strategies can also impact response time; positioning crews in areas where fire starts are expected was shown to reduce response time in Alberta, Canada (Cumming 2005).
The objective of this study is to analyse the factors that influence travel and getaway time on fires attacked by helitack crews in the province of Quebec, Canada. Analyses treat travel time and getaway time as separate entities, because they are deemed to be influenced by different processes. In this study, we considered that getaway time is mainly influenced by decisions made by the fire manager, whereas travel time is only influenced by physical factors (D. Chalifour, fire manager, pers. comm., 2022). Dispatch time is not analysed considering it takes a maximum of 20 min following internal policies and has little variation. Although many factors have been proved to influence response time on wildfires, no study to our knowledge has separately analysed factors influencing travel time and getaway time for helitack crews. This paper bridges this gap and also provides a more regional perspective to factors influencing helitack IA in Quebec. Separating the analyses allows specification of the impact of each factor on specific time periods, instead of overall response time. We hypothesise: (1) that the distance from the base to the fire and the number of flight legs as well as the IA crew’s departure base will influence travel time; and (2) that the date of initial attack, the time of dispatch, the agency’s workload (number of active fires), the predicted fire behaviour and the fire size at detection as well as the IA crew’s departure base will influence the getaway time.
Methods
Study area and operational context
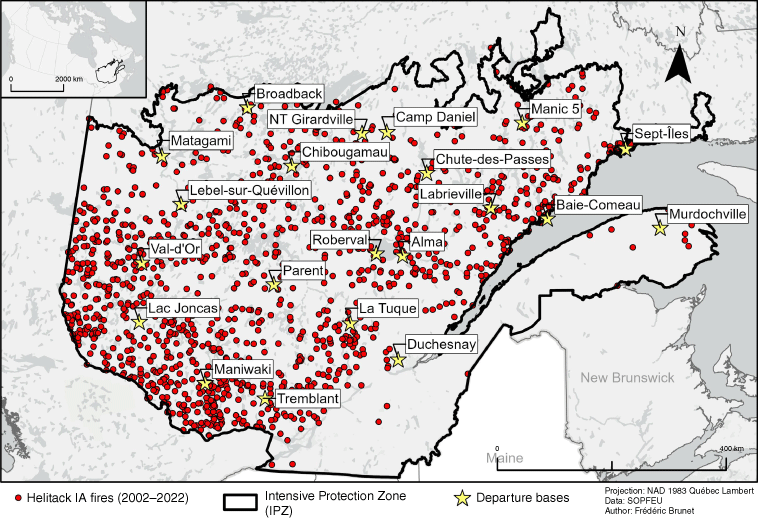
The study area is in the Intensive Protection Zone (IPZ) located in the southern part of the province of Quebec, Canada (Fig. 2). All forest fires that take place in this zone receive full response from the fire protection agency. The IPZ boundaries correspond to the limits of commercial forestry in the province of Quebec. This was done to limit the effects of wildfires on the forestry industry. Fires that take place in the sparsely populated and sparsely forested regions north of the IPZ are not systematically controlled unless they threaten infrastructure or communities (Tymstra et al. 2019). The IPZ covers approximately 52 million ha (45°–52°N, 64°–80°W, Fig. 2) (Chabot et al. 2009).
Fires (n = 1333, red dots) that received an initial attack by a helitack crew that ignited between 2002 and 2022 in the Intensive Protection Zone (IPZ; black outline) of the province of Quebec, Canada, and that were used in the statistical analyses. Departure bases used in this study (apart from the Active fire category) are also shown (yellow stars with label).
In Quebec, Canada, the agency responsible for the suppression of wildland fires is the Société de protection des forêts contre le feu (SOPFEU). Initial attacks are usually done by ground crews, either transported by truck or by helicopter. They can also be supported by airtankers when fire behaviour is too extreme. Ground crews are composed of three to four firefighters, with suppression equipment that typically includes hand tools (e.g. shovel and Pulaski) and a power pump kit with hoses. Helitack crews are used for fires that have been identified as a priority considering their faster travel time.
Helitack crews can be deployed to any of 18 primary deployment sites covering the province, each with a 113 km coverage radius, representing approximately 30 min of flight from its centre to its outer limits. When a new fire is detected, SOPFEU has as an operational objective to have personnel on the fire within the next hour (Cardil et al. 2019). It is first reported to the provincial fire centre (Centre provincial de lutte, CPL). The CPL then has 15 min to complete the fire report and assign the fire to one of the three regional fire centres (Centre regional de lutte, CRL). The CRL then has 5 min to dispatch the fire to a local fire manager who will be responsible for a particular deployment site, and will send out an IA crew to the fire. The crew has to take off within 10 min of being dispatched when there is ordered deployment. Ordered deployment can start as early as 08:00 hours when there is extreme fire weather and will start at the latest time of 13:00 hours when fire weather is milder. It ends typically between 17:00 and 20:00 hours, also depending on the predicted fire weather and remaining daylight. If there is no ordered deployment, crews have up to 60 min to leave.
Data
Data used in this study were sourced from two different databases obtained from SOPFEU, spanning 2002 to 2022. The first database is SOPFEU’s Operational Objectives Database, which contains general information for every day of activity on all fires that have occurred in Quebec. The second database is SOPFEU’s helicopter flight leg database, which holds aircraft flights information such as time of departure and motor shutdown times. The number of flight legs required to get to a fire varies between one and two. Fires requiring two flights legs to get to the destination are due to either the helicopter having to refuel to get to the destination or picking up additional crew members/or suppression equipment. The aviation flight leg database is primarily used for billing purposes but was essential to find the departure base linked to each fire. However, one of the main drawbacks of using this database was the lack of uniformity in the data, caused by the manual entry of most of the data. This led to the rejection of multiple fires because the exact departure point of a flight, or the exact take-off time was not indicated in the database or could not be linked to the corresponding fire. Fires originating from departure bases with fewer than a total of five departures for separate fires were rejected, because they were used too sparsely to extrapolate any significant information. Overall, between 2002 and 2022, 2427 fires were serviced by a helitack crew to perform an IA in the IPZ. Of this number, 1094 fires were rejected during data screening based on insufficient data to establish the different response times.
Factors used for the analyses were included based on previous studies as well as those hypothesised by the authors to influence both travel and getaway times. Fire behaviour and the number of active fires can be represented by multiple variables. The variables considered to represent fire behaviour are the ISI, FWI, Rate of Spread (ROS) and Head Fire Intensity (HFI) (Van Wagner 1987; Forestry Canada Fire Danger Group 1992). The FWI is a general index of fire danger that takes into account the ISI and the Buildup Index (BUI), which represents the total amount of fuel available for combustion. ROS represents the predicted fire speed at the head of the fire, taking into account spotting and the fuel type. HFI is the predicted intensity at the head of the fire (Forestry Canada Fire Danger Group 1992). Fuel type was also analysed, because it directly influences fire behaviour. Twelve of the 17 fuel categories found in the Canadian Fire Behaviour Prediction System (FBP) (Forestry Canada Fire Danger Group 1992) were considered. For the number of active fires, both the number of fires across the province of Quebec as well as the number in a 150 km radius of the fire were considered to represent the local and provincial fire load on a deployment base. The number of daily fire starts across the province as well as the number of daily fire starts in a 150 km radius of the fire were also considered. A high number of fires could have an impact on response times locally, while the fire load is relatively low across the province.
The operational objectives database was used to extract the following variables: date of the IA, hour of dispatch, ISI, FWI, ROS, HFI, number of active fires, number of active fires in a 150 km radius, number of daily fire starts, number of daily fire starts in a 150 km radius and fuel type as well as time of departure. The ISI and FWI were calculated based on the Canadian Forest FWI System (Van Wagner 1987), while the ROS and HFI were calculated based on the Canadian Forest FBP System (Forestry Canada Fire Danger Group 1992). These calculations used fuels at the coordinates of the fire’s ignition point and the observed daily fire weather, obtained from the nearest weather station. Fuel information was extracted from a spatial layer and crosschecked using data collected on the fire.
The flight leg database was used to obtain the departure base, number of flight legs and travel time. Only the first and second flight legs recorded for a fire were kept, which represent the flight legs associated with the IA. Departure bases include 24 separate bases or deployment sites, as well as an ‘Active fire’ category. This category applies when crews are redeployed directly from an ongoing fire to a new fire. Thus, ‘Active fire’ acted as a departure base for our analyses in these specific cases.
The distance separating the fire from the departure base was calculated with the haversine formula using their respective coordinates. The haversine formula is used to find the shortest distance between two points on a sphere using given longitudes and latitudes (Dauni et al. 2019). For fires that required more than one flight leg (n = 95), distance was calculated between the departure and intermediate base, and then from the intermediate base to the fire.
Data exploration
Data exploration was conducted following the protocol of Zuur et al. (2010). This protocol is used to detect outliers, heterogeneity of variance, collinearity, dependence of observations and problems with interaction as well as the distribution of data. The data were analysed separately for getaway time and travel time. All of the 1333 fires were used in the analyses for travel time.
However, some explanatory variables related to fire weather data were missing for the analyses of getaway time, and we rejected 384 fires for this reason in the getaway time analyses. Missing data were often linked to incorrect or absent fuel type data, which is necessary when calculating the ROS and HFI fire behaviour metrics. Furthermore, getaway time followed a bimodal distribution, and could not be analysed with general linear regression. This distribution was caused by fires with a very late dispatch hour. In the province of Quebec, IA helicopters are not equipped to fly at night, and can thus only fly from 30 min before sunrise to 30 min after sundown following Canadian Aviation Regulations (Transport Canada 1996). When crews receive a dispatch notice late in the evening, helitack crews can only reach the fire the next morning because they cannot fly at night. This creates a significant increase in getaway time, thus leading to a bimodal distribution. To remedy this situation, the getaway time dataset was subdivided into two categories: fires attacked on the same day as dispatch (n = 844) and fires attacked on the next day (n = 105).
Data exploration also confirmed that the observations were not independent when segmented on a yearly basis. The year of the fire was thus included as a random effect in the analyses. The year of a fire can encompass the effects of policy changes throughout the years, fire weather patterns that change between seasons (Arienti et al. 2006) and the number of resources that were available that year.
Statistical analyses
Owing to its ability to handle non-normal response distributions and random effects, general linear mixed modelling (GLMM) was used to test which variables have a significant impact on travel time and getaway time. Three different models were used, one for the same-day getaway time (SD getaway time), one for next-day getaway time (ND getaway time) and one for travel time. All analyses were performed using R statistical software (v 4.2.1; R Core Team 2022). Models were fitted using the R package glmmTMB (Brooks et al. 2017); assumptions were verified using the DHARMa and Performance packages (Lüdecke et al. 2021; Hartig 2022). The following assumptions were verified: low collinearity between explanatory variables, homogeneity of variance, normality of random effect, normality of residuals, linearity between predicted value and response variable, mean equal to the variance, values of zero (i.e. null values) followed expected distribution. In some cases, residuals were not independent, indicating a non-linear relation between the predicted value and the response variable. This was corrected by applying polynomial functions and cubic root transformations to certain variables to eliminate patterns in residuals. The year of the fire was used in all three models as a random effect coded on the intercept of the function. It is assumed that the year would not have an effect on the slope of the function, but rather it might change the covariates baseline levels, without changing their effect’s size. A quasi-Poisson distribution was used for the travel time model, and a negative binomial distribution was used for the SD getaway time and ND getaway time models. These distributions were chosen to best address the overdispersion observed in all the models. All three models used a log link function.
Model building was conducted using a forward stepwise approach, supported by the Akaike Information Criterion (AIC) (Symonds and Moussalli 2011) as well as a pseudo-R2 (Burnham and Anderson 2004). Variables were added to the model until the lowest AIC and the highest pseudo-R2 were attained. Variables previously identified as having a potential effect on either getaway time or travel time were included. This process also helped identify variables to be used for the number of active fires and potential fire behaviour, which can be represented by multiple variables. However, to avoid collinearity, only one variable per category was included because they encompass similar effects (Table 1).
| Response variable | Explanatory variables | Random effect | R2 | AIC | |
|---|---|---|---|---|---|
| SD getaway time | JD | Year | 0.047 | 7768.82 | |
| SD getaway time | JD + DH | Year | 0.201 | 7535.80 | |
| SD getaway time | JD + DH + FWI | Year | 0.209 | 7530.752 | |
| SD getaway time | JD + DH + HFI | Year | 0.211 | 7527.920 | |
| SD getaway time | JD + DH + ISI | Year | 0.214 | 7528.671 | |
| SD getaway time | JD + DH + ROS | Year | 0.214 | 7527.090 | |
| SD getaway time | JD + DH + ROS + DB | Year | 0.257 | 7523.647 | |
| SD getaway time | JD + DH + ROS + DB + FS | Year | 0.263 | 7518.190 | |
| SD getaway time | JD + DH + ROS + DB + FS + FT | Year | 0.285 | 7510.590 | |
| SD getaway time | JD + DH + ROS + DB + FS + FT + DF150 | Year | 0.284 | 7511.680 | |
| SD getaway time | JD + DH + ROS + DB + FS + FT + DFP | Year | 0.287 | 7509.400 | |
| SD getaway time | JD + DH + ROS + DB + FS + FT + AF150 | Year | 0.287 | 7506.684 | |
| SD getaway time | JD + DH + ROS + DB + FS + FT + AFP | Year | 0.295 | 7503.250 | |
| ND getaway time | DH | Year | 0.647 | ||
| Travel time | D | Year | 0.409 | 11,495.53 | |
| Travel time | D + NOF | Year | 0.478 | 11,206.05 | |
| Travel time | D + NOF + DB | Year | 0.501 | 11,191.03 |
Getaway time models that were considered are ranked by AIC. AIC was not calculated for ND getaway time and travel time, because only one model was tested in each case. The following explanatory variables were used: Julian date (JD), Dispatch hour (DH), Fire Weather Index (FWI), Head Fire Intensity (HFI), Rate of Spread (ROS), Active fires in a 150 km radius (AF150), Active fires in the province of Quebec (AFP), Daily fire starts in a 150 km radius (DF150), Daily fire starts in the province of Quebec (DFP), Departure base (DB), Distance (D), Fuel type (FT), Fire size at detection (FS), Number of flight legs (NOF).
Final models best explaining the data and used for subsequent analyses are presented in bold.
Finally, a Type II ANOVA was performed on all three models (i.e. SD getaway time, ND getaway time and travel time models) to verify the effects of categorical variables (Table 2). A Type II ANOVA can be used as no interaction is being tested, for which case a Type III would have been preferable. The number of fires per departure base was unbalanced, which could cause problems with a sequential Type I ANOVA. A Tukey’s range test was done as a post hoc analysis to evaluate the differences between departures bases, using the multcomp package (Hothorn et al. 2008).
| SD getaway time | ||||||
|---|---|---|---|---|---|---|
| GLMM | Term | Estimate | s.e. | Z value | P-value | |
| Intercept | 2.146 | 0.493 | 4.355 | <0.001 | ||
| Julian date | 0.003 | 0.001 | 3.877 | <0.001 | ||
| Dispatch hour (1) | −11.081 | 0.861 | −12.868 | <0.001 | ||
| Dispatch hour (2) | −10.910 | 0.874 | −12.485 | <0.001 | ||
| Rate of spread | −0.020 | 0.006 | −3.119 | 0.001 | ||
| Fire size at detection | 0.027 | 0.010 | 2.590 | 0.010 | ||
| Active fires | 0.004 | 0.001 | 2.710 | 0.007 | ||
| Year (random effect) | 0.015 | 0.124 | ||||
| ANOVA | Term | Chi-square | d.f. | P-value | ||
| Julian date | 11.658 | 1 | <0.001 | |||
| Dispatch hour | 170.341 | 2 | <0.001 | |||
| Rate of spread | 10.125 | 1 | 0.001 | |||
| Active fires | 7.358 | 1 | 0.006 | |||
| Fire size at detection | 6.707 | 1 | 0.010 | |||
| Fuel type | 32.127 | 11 | <0.001 | |||
| Departure base | 47.711 | 21 | <0.001 | |||
| ND getaway time | ||||||
|---|---|---|---|---|---|---|
| GLMM | Term | Estimate | s.e. | Z value | P-value | |
| Intercept | 6.735 | 0.014 | 473.114 | <0.001 | ||
| Dispatch hour (1) | −1.969 | 0.146 | −13.503 | <0.001 | ||
| Dispatch hour (2) | −0.405 | 0.146 | −2.766 | 0.006 | ||
| Year (random effect) | 0.000 | 0.000 | ||||
| ANOVA | Term | Chi-square | d.f. | P-value | ||
| Dispatch hour | 299.189 | 2 | <0.001 | |||
| Travel time | ||||||
|---|---|---|---|---|---|---|
| GLMM | Term | Estimate | s.e. | Z value | P-value | |
| Intercept | 2.978 | 0.092 | 32.190 | <0.001 | ||
| Distance | 0.223 | 0.009 | 24.460 | <0.001 | ||
| Number of flights | 0.584 | 0.029 | 20.230 | <0.001 | ||
| Year (random effect) | 0.004 | 0.02 | ||||
| ANOVA | Term | Chi-square | d.f. | P-value | ||
| Distance | 598.298 | 1 | <0.001 | |||
| Number of flights | 409.322 | 1 | <0.001 | |||
| Departure base | 64.344 | 24 | <0.001 | |||
GLMM results and the subsequent type II ANOVA performed on the GLMM results are shown for each model.
Results
From the fires that received an IA by a helitack crew, we estimate that the median same-day getaway time was 20 min (ranging from 0 to 628 min; n = 843) and that the next-day getaway time was 829 min (ranging from 402 to 1437 min; n = 105). The median travel time was 47 min (ranging from 2 to 195 min; n = 1333). The random effect of the year varied across models, where its influence was most significant on the SD getaway model, increasing the pseudo-R2 by 1.7%. The average getaway time varied by over 18 min between years. For the travel time model, the variation between years was minimal, with the pseudo-R2 increasing by only 0.2%. In the ND getaway time model, the random effect explained less than 0.1% of the variation.
Same-day getaway time
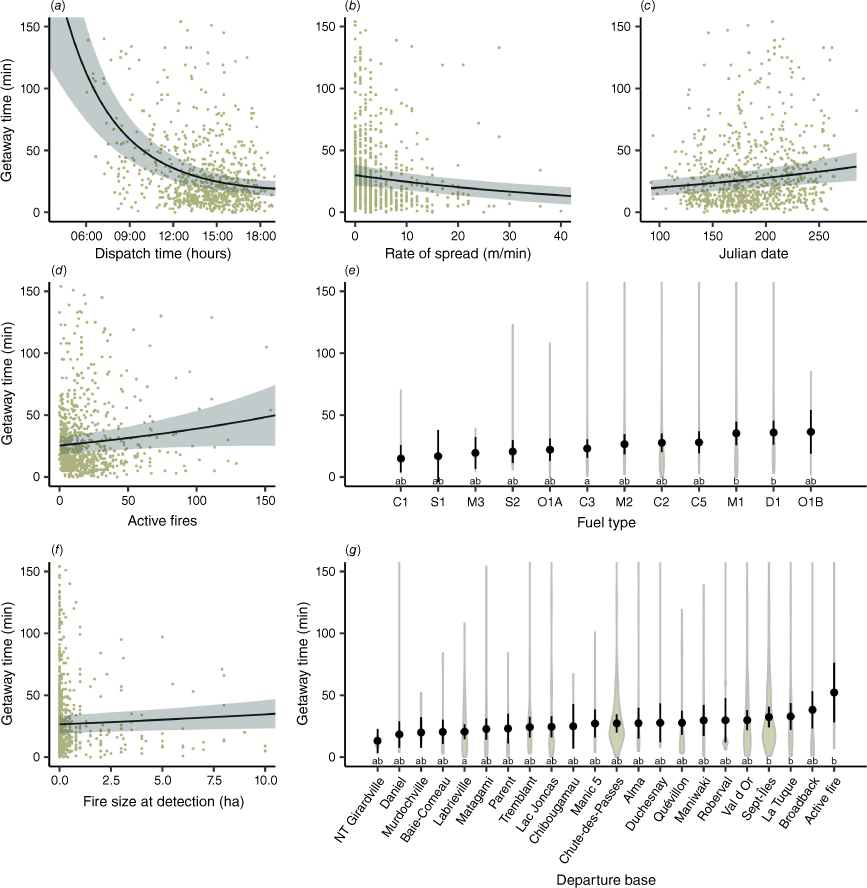
For SD getaway time, the model that yielded the lowest AIC score was the one using ROS (to express a component of fire behaviour) and number of active fires in the province (as a metric of provincial or agency workload). It was influenced by the dispatch hour, ROS, Julian date, departure base, fuel type and number of active fires as well as the fire’s size at detection (Fig. 3, Table 2). Dispatch hour had the highest impact on SD getaway time, following a second-degree polynomial function relation with SD getaway time. Between a fire dispatched at 08:00 hours and a fire dispatched to at 13:00 hours, there was a 47.4 ± 15.7 min decrease in predicted SD getaway time. An increase from 1 to 25 m/min in ROS decreased predicted SD getaway time by 12.3 ± 7.8 min. For the Julian date, predicted getaway time increased by 11.7 ± 8.3 min between 1 May and 1 September. As an example for the effect of the departure base, there was an increase of 15.3 ± 7.2 min in predicted SD getaway time between the Baie-Comeau and Val D’Or bases. The difference between departure bases was only significant between certain categories, between the Baie-Comeau and the Val-d’Or bases, La Tuque base and Active Fire category. For fuel types, predicted SD getaway time increased by 12.1 ± 7.8 min between Mature Jack or Lodgepole pine (C3) and Boreal Mixedwood – Leafless (M1) fuel FBP types. The difference between fuel types was only significant between the C3 fuel type and the M1, Leafless Aspen (D1) fuel types. Results also show an increase of 1–40 active fires in the province only increased predicted getaway time by 5.1 ± 7.8 min and that for fire size at detection, predicted SD getaway time increased 8.3 ± 9.4 min between a fire detected at 0.1 ha and a fire detected at 10 ha.
Graphs presenting (a) the impact of dispatch hour on SD getaway time; (b) the impact of the Rate of spread on SD getaway time; (c) the impact of the Julian date on SD getaway time; (d) the impact of the number of active fires in the province of Quebec on SD getaway time; (e) the impact of the fuel type on SD getaway time; (f) the impact of the fire size at detection on SD getaway time; (g) the impact of the departure base on SD getaway time. The predicted effect from the SD getaway time model is shown in black. The confidence interval (CI) is shaded in grey for the continuous data and is shown in black for the violin plots (CI 95%). Raw data are shown behind in green. Violin plots are proportional to the count data per category. Tukey’s range test results are presented with compact letter display under the violin plots, with groups sharing the same letter indicating no significant difference. Each graph represents the partial effect of the independent variable, with other variables kept at constant.
Next-day getaway time
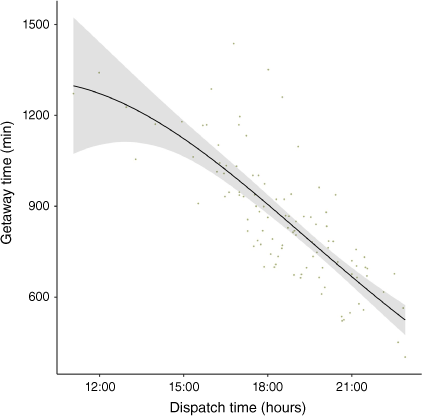
For the ND getaway time model, dispatch hour was the only variable to have an effect (Fig. 4, Table 2). Julian date, number of active fires, departure base, fuel type, fire size at detection and ROS did not have a significant effect and were removed from the final model. The effect of dispatch hour followed a second-degree polynomial function. An increase in dispatch hour decreased predicted ND getaway time. A fire dispatched at 21:00 hours compared with a fire dispatched at 15:00 hours lowered the predicted ND getaway time by 480.6 ± 62.5 min.
Graph presenting the impact of dispatch hour on next-day getaway time. The predicted effect from the ND getaway time model is shown in black, with the confidence interval in grey (CI 95%). Raw data are shown behind in green. The effect of the dispatch hour is shown, with the year variable kept at constant.
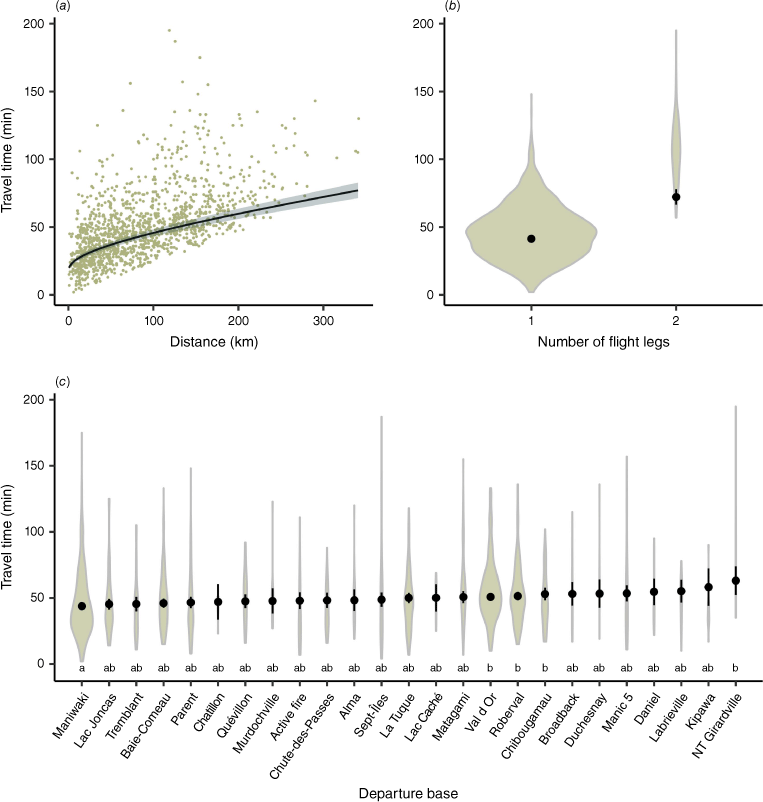
Travel time
The distance between the departure base and the fire and the number of flight legs as well as the departure base all had an impact on travel time (Fig. 5, Table 2). In our model, distance had the highest impact on travel time, following a cubic root transformation (distance1/3). With an increase of 150 km, the model predicted an increase in travel time of 36.9 ± 2.4 min. The second-most important factor was the number of flight legs. The increase between one and two flight legs increased the predicted travel time by 34.5 ± 4.1 min. The last significant factor was the departure base. For example, the difference in travel time between the Maniwaki and Roberval bases was predicted to be an increase of 7.6 ± 2.9 min. Only the difference between the higher travel time departure bases of NT Girardville, Chibougamau, Roberval and Val d’Or compared with the lower travel time departure base of Maniwaki could be considered significant. Overlap between the confidence intervals of the other bases did not permit drawing significant conclusions on their effect on travel time, which was shown with the Tukey’s range test results (Fig. 5c). The confidence interval range was also highly influenced by the number of fires associated with each departure base.
Graphs presenting (a): the impact of the distance separating departure base and fire on travel time; (b) the impact of the number of flight legs it takes a helitack crew to get to a fire on travel time; (c) the impact of the identity of the departure base on travel time. The predicted effect from the travel time model is shown in black. The confidence interval is shaded in grey for the distance and is shown in black for the violin plots (CI 95%). Raw data are shown behind in green. Violin plots are proportional to the count data per category. Tukey’s range test results are presented with compact letter display under the violin plots, with groups sharing the same letter indicating no significant difference. Each graph represents the partial effect of the independent variable, with other variables kept at constant.
Discussion
The data and statistical analysis used helped identify factors influencing both getaway time (i.e. SD and ND getaway time) and travel time for fires attacked by IA helitack crews. Results showed that for same-day getaway time, the dispatch hour, ROS, number of active fires, Julian date, departure base and fire size at detection as well as fuel type had an influence. For next-day getaway time, only dispatch hour had an influence. The distance between the departure base and the fire, the number of flight legs needed to reach the fire and the departure base all influenced travel time. Although all the previous factors have been identified as having a significant impact on travel and getaway time, the effect of these factors had a varying degree of importance.
Same-day getaway time
The primary factor influencing same-day getaway time was dispatch hour. Fires dispatched early in the morning (before 10:00 hours) had a longer getaway time than fires dispatched during the afternoon. This is contrary to what is stated by Paudel et al. (2019) and Plucinski (2012). Longer getaway times were expected for fires with later dispatch hours, but in the present study, fires attacked on the next day were separated into a different model, explaining the lack of a late-day dispatch effect. The opposite is observed with longer getaway times for early morning dispatch hours, which may be explained by the ordered deployment time, which starts in most situations at 13:00 hours, and can start as early as 08:00 hours when predicted fire weather is extreme. Fires detected outside of standard ordered deployment hours had longer getaway times (Fig. 3).
ROS (or rather expected ROS as a function of the FBP fuel at the point of ignition and of observed local fire weather) was the second factor influencing getaway time. A higher value in ROS was linked to shorter getaway times. This shows that fire managers will tend to send out crews faster when the fire weather is more favourable to fire growth.
Julian date was the third variable to have an impact on getaway time. Fires happening later in the season tend to have longer getaway times. Fire season and standard deployment procedures usually operate between 15 May and 15 August. During these dates, there is constant deployment of helitack crews, with minimal deployment when fire weather conditions are very mild. Minimal deployment consists of three crews throughout the province, and there can be up to 30 crews deployed when fire weather is extreme. These dates can be extended if spring arrives earlier or if conditions favourable to fire extend further in the summer. Outside of these dates, deployment of helitack crews will only be done based on fire weather conditions. When fire weather is less extreme during the fall (autumn), there can be longer getaway times because there is no ordered deployment of helitack crews; pilots and crews have to travel from where they are staying to the base before flying to a fire.
The fourth factor influencing getaway time was the departure base. For the category ‘Active fire’, longer getaway times can be attributed to crews already working on an active fire before flying off to a new fire start. In these situations, crews must regroup their equipment and load the helicopter before going on a newer fire, increasing getaway time. Further investigation could identify bases with a longer getaway time to see what could be done to reduce it. Some bases have helipads located next to the crew’s standby site, whereas at other bases, crews must travel a certain distance by vehicle to arrive at the helipad. Identifying bases with less efficient helipad location could further explain longer getaway times. Regional differences in departure policies between bases in situations when there is no ordered deployment can also explain longer getaway times, because outside of the ordered deployment, the responsibility for deployment and subsequent getaway time falls under the regional bases.
The fifth factor influencing getaway time was fuel type. Longer getaway times were observed for both M1 and D1 compared with C3. This shows that fire managers seem to send out crews faster in coniferous forest types compared with deciduous and mixed forest types. No significant effect was observed between the Boreal Spruce (C2) fuel type and the deciduous forest types, which is contrary to what was expected considering that it C2 has the highest potential for extreme fire behaviour.
The sixth factor influencing getaway time was the number of active fires in the province. A high number of active fires often limits resources, and helicopters are shared between multiple fires, increasing getaway times for example when the helicopter assigned to IA is not readily available to service a new fire. For both the number of active fires and fire size at detection, predicted values only surpassed the confidence interval overlap when comparing low and very high values. It is only in these situations where their effect can be considered significant.
The last factor to influence getaway time was the fire’s size at detection. Fires detected at very large sizes (>20 ha) showed longer getaway times, indicating that fire managers take more time before sending out crews on large fires owing to low chances of IA success (J. Boucher, unpubl. data). Oftentimes, fires of these sizes will require airtanker drops and the helitack crew will either wait for them to finish, or work on the flanks and at the back of the fire where intensity is lower. Fire size at detection ranged from 0.0 to 97.0 ha, with only 87 fires detected at a size greater than 1 ha. Fires detected at large sizes are thus rare occurrences.
One factor that was not analysed in the current model but could be of interest is the presence of population or critical infrastructure near the fire. In Quebec, every fire located in the IPZ is attacked as soon as possible. In cases where resources are not sufficient to respond to every new fire start, response priorities are established as follows: (1) human life, (2) public and private infrastructure critical to public safety, (3) likelihood of attaining operational objectives, and (4) forest resource values (Cardil et al. 2019; Tymstra et al. 2019). Thus, in situations where the province cannot intervene on every new fire start, the proximity of the fire to one of these priorities could influence getaway time.
Next-day getaway time
Fires with earlier dispatch hours on the day before the initial attack had longer getaway times than fires with a later dispatch hour. Multiple factors can explain a fire being serviced on the next day. The most important one is the duration of sunlight left for the helicopter to safely fly to a fire and come back. Other factors can include the danger posed by a fire, and the availability of IA crews. Fires with dispatch hours as early as 12:00 hours are sometimes serviced on the next day (Fig. 4), explained by the fire manager deeming these fires as low priority rather than a lack of remaining sunlight hours.
Travel time
The most influential factor on travel time was the distance between the departure base and the fire. This confirms what is already present in the literature for other regions and countries (Plucinski 2012; Paudel et al. 2019). Actions taken to reduce distance, such as modifying deployment policies to place crews closer to new potential fire starts, will have the highest impact on reducing travel time compared with actions taken on other factors.
The number of flight legs was the second factor in importance on predicted travel time. Though only 7% (n = 95) of fires in our dataset necessitated two legs to reach the fire, an increase from one to two legs increased travel time. The main reason for a helicopter flight to have two legs to get to a destination is to refuel. If the helicopter pilot deems that fuels levels are too low to get to a fire and have a sufficient reserve to fly back to the closest fuel cache, the helicopter will have to land to refuel on the way to the IA. Pilots must then complete a full motor shutdown to start fuelling procedures, which explains the steep increase in predicted travel time of 34.5 ± 4.1 min. Efforts should be taken to reduce situations in which two flight legs are required to get to a new fire. These can include increasing the spatial density of deployed helicopters where new fire starts are expected as well as higher amounts of fuel at take off to increase flight autonomy. Increasing the amount of fuel comes with the drawback of having to diminish the helicopters payload, either by bringing less suppression equipment or reducing IA crew size.
The third factor influencing travel time was the departure base. The ANOVA results showed a significant effect of the departure base on travel time, but further analysis revealed that an actual trend can only be observed between certain bases, with the confidence interval overlap being too high in most cases to determine a significant difference between bases. The mechanism explaining the difference in travel time between bases is not clearly defined in the exploratory context of this study. It is hypothesised that these differences could be explained by the effective coverage of each departure base. Whereas some departure bases cover a very limited amount of territory, other bases often intervene at greater distances, mostly for the bases that are at the northern limit of the IPZ, thus affecting travel time.
An additional factor that was not included in the travel time model is the helicopters’ overall speed variability, which includes both cruising speed and the wind’s influence (which can either push the aircraft or create resistance). These factors were not included because they are hard to evaluate on a large-scale model: wind speeds can vary greatly during a single flight, and helicopter travel speed varies based on its payload and motor type. They could, however, be considered when analysing travel time for specific flights.
Limitations and future research
One of the main difficulties in the analysis was determining the departure base for every fire using historical data, owing to some missing data in the flight leg database. This challenge is not unique to our study, with data screening being a common issue in statistical modelling with wildfire agencies databases (Taylor et al. 2013). Among the three models, the SD getaway time model yielded the lowest pseudo-R2 (29.5%). The lower pseudo-R2 for the SD getaway time model was anticipated, as the variables included in the model are proxies of the fire manager’s decision-making process. Each fire is unique, and the decision process guiding the departure of the crew can be influenced by numerous factors that are not recorded. Nevertheless, the inclusion of factors such as population density around the fire or the presence of nearby critical infrastructure could also influence same-day getaway time, potentially improving the overall model. Additionally, including the presence or absence of ordered deployment at the time of fire dispatch could influence SD and ND getaway time models. However, this variable was not included because it is not recorded in historical databases.
Further research could be carried out to find solutions to minimise the impact of the factors influencing same and next day getaway time, as well as travel time. Focusing efforts on reducing the factors with the greatest influence could lead to a reduction in the overall response time of IA helitack crews. For getaway time, reviewing internal policies for available resources could diminish the impact of the dispatch hour on getaway time, notably for early fires that are dispatched before ordered deployment. For travel time, these solutions could include changing the agency’s deployment policies, either by optimising the disposition of deployment bases or increasing the number of available helicopters to further reduce the distance between departure bases and new fire starts. The use of optimisation models to help deploy helitack crews could reduce travel time through the use of stochastic modelling (Arrubla et al. 2014) or more standard optimisation problems such as the maximal coverage location problem (Lee et al. 2014). Using helicopters with higher payload capacity could allow increased fuel autonomy without reducing IA crew size and equipment quantity. This would reduce the number of situations where two flight legs are needed, especially for bases further north in the IPZ that often respond to distant fires. Overall, improving the understanding of how various factors influence total response time could enable fire managers to deploy appropriate resources by weighting predicted response time to predicted fire growth before suppression efforts arrive. Additional research could also be conducted to identify factors that influence ground crew getaway and travel times, for both IA purposes and for supporting helitack operations.
Conclusion
This study identified factors that influenced getaway time and travel time of helitack crews responding to fires in Quebec’s IPZ. Through statistical analyses, we found that dispatch hour, rate of spread, Julian date, the number of active fires, departure base and fuel type as well as the fire’s size at detection influenced same-day getaway time. For fires attacked on the next day following dispatch, dispatch hour influenced getaway time. Travel time was influenced by distance, the number of flight legs and departure base. For both same-day and next-day getaway time, the factor with the most influence was the dispatch hour. For travel time, the distance between the departure base and the fire had the greatest influence, closely followed by the number of flight legs. Overall, identifying factors that influence getaway and travel time gives fire managers a better insight into which factors should be prioritised to reduce response times to fires. In some cases, reducing response time might not be necessary, for example, when fire weather is unfavourable to fire spread or if the fire is of low priority (e.g. burning on an island). For high-priority fires, notably near communities or critical infrastructure, working on the identified factors could have a positive impact on reducing response time, thus increasing the chances of containing new fire starts.
Declaration of funding
Funding for this research was provided by grant from the Fonds de recherche du Québec-Nature et technologies (FRQNT) and the Ministère des Ressources naturelles et des Forêts du Québec, in the program: Contribution of the forest sector to the attenuation of the effects of climate change (project no. 308324).
Acknowledgements
We acknowledge the participation of the Société de protection des forêts contre le feu (SOPFEU) in this project. Specifically, we want to thank Caroline Plante and Christine Bussières for their assistance with SOPFEU’s data and insights, and we also thank Joëlle Brault for providing the necessary geospatial data. Appreciation is also extended to Olivier Lundqvist of the Direction des services prédictifs, as well as Sylvain Guitard and Luc Dugas of the Direction principale des operations stratégiques et aériennes, for their additional contributions and expertise.
References
Arienti MC, Cumming S, Boutin S (2006) Empirical models of forest fire initial attack success probabilities: the effects of fuels, anthropogenic linear features, fire weather, and management. Canadian Journal of Forest Research 36, 3155-3166.
| Crossref | Google Scholar |
Arrubla JAG, Ntaimo L, Stripling C (2014) Wildfire initial response planning using probabilistically constrained stochastic integer programming. International Journal of Wildland Fire 23, 825-838.
| Crossref | Google Scholar |
Beverly JL (2017) Time since prior wildfire affects subsequent fire containment in black spruce. International Journal of Wildland Fire 26, 919.
| Crossref | Google Scholar |
Brooks M, Kristensen K, van , Benthem K, Magnusson A, Berg CW, Nielsen A, Skaug H, Mächler M, Bolker B (2017) glmmTMB balances speed and flexibility among packages for zero-inflated generalized linear mixed modeling. R Journal 9, 378-400.
| Crossref | Google Scholar |
Burnham KP, Anderson DR (Eds) (2004) ‘Model selection and multimodel inference.’ (Springer New York: New York, NY, USA) 10.1007/b97636.
Cardil A, Lorente M, Boucher D, Boucher J, Gauthier S (2019) Factors influencing fire suppression success in the province of Quebec (Canada). Canadian Journal of Forest Research 49, 531-542.
| Crossref | Google Scholar |
Chabot M, Blanchet P, Drapeau P, Fortin J, Gauthier S, Imbeau L, Lacasse G, Lemaire G, Nappi A, Quenneville R, Thiffault E (2009) ‘Manuel de foresterie.’ (Editions MultiMondes: Québec City, CANADA) Available at http://ebookcentral.proquest.com/lib/ulaval/detail.action?docID=3374931
Canadian Interagency Forest Fire Centre (CIFFC) (2021) Glossaire Canadien des termes employés en gestion des incendies forestiers. (CIFFC). Available at https://ciffc.ca/sites/default/files/2020-12/Glossaire%20Canadien%20des%20termes%20employ%C3%A9s%20en%20gestion%20des%20incendies%20forestiers%202021.pdf.
CIFFC Training Working Group (2023) Canadian wildland fire glossary. Available at https://ciffc.ca/sites/default/files/2023-05/CWFM_glossary_v2023-04-24-EN.pdf.
Cumming SG (2005) Effective fire suppression in boreal forests. Canadian Journal of Forest Research 35, 772-786.
| Crossref | Google Scholar |
Dauni P, Firdaus MD, Asfariani R, Saputra MIN, Hidayat AA, Zulfikar WB (2019) Implementation of Haversine formula for school location tracking. Journal of Physics: Conference Series 1402, 077028.
| Crossref | Google Scholar |
Forestry Canada Fire Danger Group (1992) Development and Structure of the Canadian Forest Fire Behavior Prediction System. ST-X-3. (Hull). (Minister of Supply and Services Canada). Available at https://cfs.nrcan.gc.ca/publications?id=10068
Hartig F (2022) DHARMa: residual diagnostics for hierarchical (multi-level/mixed) regression models. Available at https://CRAN.R-project.org/package=DHARMa
Hirsch K, Podur J, Janser R, McAlpine R, Martell D (2004) Productivity of Ontario initial-attack fire crews: results of an expert-judgement elicitation study. Canadian Journal of Forest Research 34, 705-715.
| Crossref | Google Scholar |
Hope ES, McKenney DW, Pedlar JH, Stocks BJ, Gauthier S (2016) Wildfire suppression costs for Canada under a changing climate. PLoS One 11, e0157425.
| Crossref | Google Scholar | PubMed |
Hothorn T, Bretz F, Westfall P (2008) Simultaneous inference in general parametric models. Biometrical Journal 50, 346-363.
| Crossref | Google Scholar | PubMed |
Lee Y, Fried JS, Albers HJ, Haight RG (2013) Deploying initial attack resources for wildfire suppression: spatial coordination, budget constraints, and capacity constraints. Canadian Journal of Forest Research 43, 56-65.
| Crossref | Google Scholar |
Lee Y, Lee B, Kim KH (2014) Optimal spatial allocation of initial attack resources for firefighting in the republic of Korea using a scenario optimization model. Journal of Mountain Science 11, 323-335.
| Crossref | Google Scholar |
Lüdecke D, Ben-Shachar M, Patil I, Waggoner P, Makowski D (2021) performance: An R Package for assessment, comparison and testing of statistical models. Journal of Open Source Software 6, 3139.
| Crossref | Google Scholar |
Ntaimo L, Gallego-Arrubla JA, Gan J, Stripling C, Young J, Spencer T (2013) A simulation and stochastic integer programming approach to wildfire initial attack planning. Forest Science 59, 105-117.
| Crossref | Google Scholar |
National Wildfire Coordinating Group (NWCG) (2024) NWCG glossary of wildland fire. Available at https://www.nwcg.gov/publications/pms205/nwcg-glossary-of-wildland-fire-pms-205
Parks GM (1964) Development and application of a model for suppression of forest fires. Management Science 10, 760.
| Crossref | Google Scholar |
Paudel A (2014) Characterizing the forest fire initial attack system in northeastern Ontario, Canada. (University of Toronto). Available at https://central.bac-lac.gc.ca/.item?id=TC-OTU-68051&op=pdf&app=Library&oclc_number=1033009755
Paudel A, Martell DL, Woolford DG (2019) Factors that affect the timing of the dispatch of initial attack resources to forest fires in northeastern Ontario, Canada. International Journal of Wildland Fire 28, 15-24.
| Crossref | Google Scholar |
Payette S (1992) Fire as a controlling process in the North American boreal forest. In ‘A systems analysis of the global boreal forest’. (Eds GB Bonan, HH Shugart, R Leemans) pp. 144–169. (Cambridge University Press: Cambridge) 10.1017/CBO9780511565489.006.
Plucinski MP (2012) Factors affecting containment area and time of Australian forest fires featuring aerial suppression. Forest Science 58, 390-398.
| Crossref | Google Scholar |
Plucinski MP, Dunstall S, McCarthy NF, Deutsch S, Tartaglia E, Huston C, Stephenson AG (2023) Fighting wildfires: predicting initial attack success across Victoria, Australia. International Journal of Wildland Fire 32, 1689-1703.
| Crossref | Google Scholar |
Rapp CE, Wilson RS, Toman EL, Jolly WM (2021) Assessing the role of short-term weather forecasts in fire manager tactical decision-making: a choice experiment. Fire Ecology 17, 35.
| Crossref | Google Scholar |
R Core Team (2022) R: A Language and Environment for Statistical Computing. Available at https://www.R-project.org/
Reimer J, Thompson DK, Povak N (2019) Measuring initial attack suppression effectiveness through burn probability. Fire 2, 60.
| Crossref | Google Scholar |
Rodrigues M, Alcasena F, Vega-García C (2019) Modeling initial attack success of wildfire suppression in Catalonia, Spain. Science of the Total Environment 666, 915-927.
| Crossref | Google Scholar | PubMed |
Symonds MRE, Moussalli A (2011) A brief guide to model selection, multimodel inference and model averaging in behavioural ecology using Akaike’s information criterion. Behavioral Ecology and Sociobiology 65, 13-21.
| Crossref | Google Scholar |
Taylor SW, Woolford DG, Dean CB, Martell DL (2013) Wildfire prediction to inform fire management: statistical science challenges. Statistical Science 28, 586-615.
| Crossref | Google Scholar |
Transport Canada (1996) Canadian Aviation Regulations. Available at https://laws-lois.justice.gc.ca/PDF/SOR-96-433.pdf
Tymstra C, Stocks B, Cai X, Flannigan M (2019) Wildfire management in Canada: review, challenges and opportunities. Progress in Disaster Science 5, 100045.
| Crossref | Google Scholar |
Van Wagner CE (1987) Development and structure of the Canadian Forest Fire Weather Index System. (Canadian Foresty Service: Ottawa). Available at https://cfs.nrcan.gc.ca/pubwarehouse/pdfs/19927.pdf
Wotton M, Nock C, Flannigan M (2010) Forest fire occurrence and climate change in Canada. International Journal of Wildland Fire 19, 253-271.
| Crossref | Google Scholar |
Wotton BM, Flannigan MD, Marshall GA (2017) Potential climate change impacts on fire intensity and key wildfire suppression thresholds in Canada. Environmental Research Letters 12, 095003.
| Crossref | Google Scholar |
Zuur AF, Ieno EN, Elphick CS (2010) A protocol for data exploration to avoid common statistical problems. Methods in Ecology and Evolution 1, 3-14.
| Crossref | Google Scholar |


