Field and laboratory analysis of the junction fire process in the catastrophic fire of Pedrógão Grande in June 2017

Domingos X. Viegas; Carlos Ribeiro; Miguel Almeida; Paulo Pinto; Luís M. Ribeiro; Álvaro Silva

doi:10.1071/WF22161

RESEARCH ARTICLE (Open Access)

Previous Next Contents Vol 32(6)

Field and laboratory analysis of the junction fire process in the catastrophic fire of Pedrógão Grande in June 2017

Domingos X. Viegas

^A ^* , Carlos Ribeiro

^A , Miguel Almeida

^A , Paulo Pinto ^B , Luís M. Ribeiro

^A and Álvaro Silva ^B

+ Author Affiliations

- Author Affiliations

^A Univ Coimbra, ADAI, Department of Mechanical Engineering, Rua Luís ReisSantos, Pólo II, 3030‐788 Coimbra, Portugal.

^B Portuguese Institute for Sea and Atmosphere (IPMA), Rua C do Aeroporto, 1749-077 Lisbon, Portugal.

^* Correspondence to: xavier.viegas@dem.uc.pt

International Journal of Wildland Fire 32(6) 951-967 https://doi.org/10.1071/WF22161
Submitted: 14 July 2022 Accepted: 8 April 2023 Published: 15 May 2023

© 2023 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of IAWF. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)

Abstract

Background: Two fire ignitions in Pedrógão Grande on 7 June 2017 had very fast due to unusual physical processes associated with the interaction between an overhead thunderstorm and the fire and the subsequent merging of the fires as a junction fire, killing 66 persons in 2 h.

Aims: Using a laboratory simulation of the merging process, we explain the fire spread conditions and verify that the junction of the two fires was responsible for the very intense fire development.

Methods: The real fire spread was reconstructed from an extensive field survey and physical modelling tests were performed in the Fire Research Laboratory combustion tunnel using various fuels and scale modelling laws.

Key results: The spread and merging of the two fires in the tests agree very well with field observations, namely the periods of rate of spread (ROS) increase and decrease, peak values of ROS and area growth process using scaling laws.

Conclusions: Analysis of the Pedrógão Grande fire evolution and its physical simulation at laboratory scale showed the importance of the mechanisms of two fires merging in producing very important convective processes.

Implications: Our study showed the validity of performing the experimental analysis of complex fire spread situations provided that the similarity conditions are fulfilled.

Keywords: convergent fire fronts, dynamic fire behaviour, extreme fire behaviour, fire acceleration, fire and atmosphere interaction, fire behaviour, fire growth, forest fires, junction fires, merging fires, physical modelling, scaling laws.

Introduction

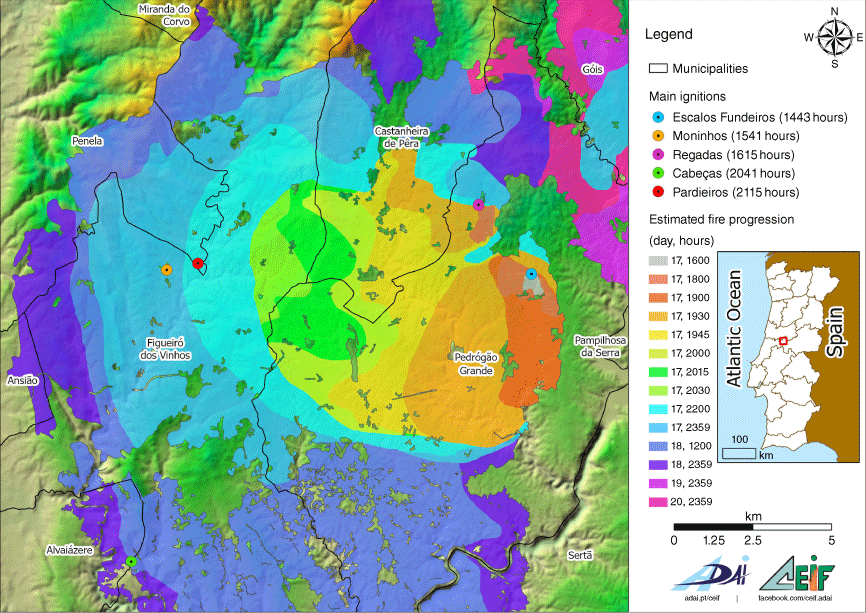
The fires that started in the early afternoon of 17 June 2017 near Pedrógão Grande (PG) will be remembered as the worst on record in Portugal as they destroyed ~45 000 ha of vegetation and forestry land but above all because they caused the death of 66 persons. Several authors have analysed this fire and produced reports studying various aspects of this very complex event, namely Guerreiro et al. (2017), Viegas et al. (2017) and San-Miguel-Ayanz et al. (2021).

The fire was initiated by a 15 kV electrical power line at two locations separated by 3 km (Fig. 1). The interaction between a thunderstorm, organised as a mesoscale convective system (MCS), and the two fires was extensively analysed in Pinto et al. (2022) using weather station, satellite and radar observation data. As a result of this interaction, the two insufficiently manned fires began to spread out of control. The present work complements the previous research, as the very unusual conditions that resulted from that interaction produced the merging of the two fires during the late evening of that day, which are described here in detail. This process is designated a junction fire (Viegas et al. 2012; Raposo et al. 2018) and is accompanied by very strong convective processes resulting in very fast fire spread, which in this case caused the death of 66 persons in a period of 2 h.

Fig. 1.

Map of Portugal and of the area of the fire of Pedrógão Grande with fire ignition points and the fire spread shown.

The spread of the fire was reconstructed by the authors from extensive field data and in the present work, a physical laboratory simulation of the fire spread was performed using modelling and scaling laws that provided good agreement with the fire phenomena observations, including the development of the very tall smoke column and the violent convective processes that were reported in Viegas et al. (2017). Artés et al. (2021) based on analysis of the vertical profiles of the atmosphere above wildfires proposed an alternative to the use of traditional fire danger indices and they take as an example the Pedrógão Grande Fire. The objective of the present study was to show the relevance of the merging processes of the two separate ignitions on the PG fire development, namely, to show that the fire development would have been quite different if only one of the fire ignitions had occurred, and to assess the capacity of simulating complex fire phenomena using laboratory-scale experiments and appropriate scaling laws.

Analysis of the fire

Fire ignition and spread

The PG fire occurred in the district of Leiria, in central Portugal (Fig. 1), in a period of drought with air temperatures above 40°C and very low relative humidity. The wind flow in the region was from the NW and not very strong. A large MCS developed over the central-western Iberian Peninsula and moved W-NW, causing several fires due to lightning, but at 1430 hours (all indicated times are local time, which is UTC (Coordinated Universal Time) plus 1 h), when the PG fire started, the most active part of this system was still nearly 100 km away and electrical strikes were not registered in the area of the fire until 1800 hours (Pinto et al. 2022).

The PG fire was actually caused by two ignitions that occurred near Escalos Fundeiros (EF) at 1430 hours and near Regadas (RE) at 1540 hours (Fig. 2). Both ignitions were caused by an electrical power line touched by the foliage of trees below and very close to the lines. The two places are 3.2 km apart but the road from EF to RE was not very accessible for heavy vehicles.

Fig. 2.

Aerial view of the location of the ignition points of (a) Escalos Fundeiros (EF), and (b) Regadas (RE).

As there were other fire ignitions in the area, firefighting resources were dispersed and there were not sufficient ground and aerial means capable of coping with the very difficult spread of the EF fire, which at 1530 hours started to spot and threaten houses in the village of EF. When the RE fire was detected, there also were no resources to deploy there, and the fire was left spreading practically on its own. Between 1800 and 1815 hours, a downflow from the MSC, which was not yet over the region of the fire, forced the fire column to tilt towards the SW, spreading flames over a wide area and making control of the fire virtually impossible from that time. This process was recorded continuously by video cameras installed in the Fire Brigade of PG Station. Two frames recorded at 1800 and 1815 hours by the north-facing camera are shown in Fig. 3. The process of this downflow was carefully studied by the authors using various methods, namely radar and ground sensors, to analyse the very complex flow produced by the thunderstorm and by the fire in Pinto et al. (2022).

Fig. 3.

Views of the column of the fire of Escalos Fundeiros at 1800 hours and at 1815 hours, showing the interaction with the downflow produced by the mesoscale convective flow.

The EF fire started to spread towards the town of Pedrógão Grande, sweeping through a large number of villages. At the same time, the RE fire, which was smaller, also spread completely out of control, towards the NW, forming the right side of a large pincer that was now advancing like a curved fire front more than 20 km long, threatening an approximately circular area of 10-km diameter where hundreds of people lived, who felt their life threatened by this very violent and roaring fire (cf. Fig. 1).

Merging of the two fires

There is evidence that after 1930 hours, both fires had their inner flanks very close to each other, making a small angle between them, therefore with the ideal conditions to merge as a junction fire, studied by Viegas et al. (2012), Raposo et al. (2018) and Ribeiro et al. (2023). Between 1930 and 2030 hours, the process of merging induced very strong winds in the area ahead of the fire. The rate of spread (ROS) of the head fire was of the order of 14 km h⁻¹. The quick combustion of a very large amount of vegetation produced a convection column that reached 12 000 m at 2010 hours and remained at that height for several hours. Flames of the order of 50–100 m long separated from the vegetation were recorded, creating an environment near the ground like the inside of a furnace. There are reports of tree stands starting to burn from their tops to the ground (Fig. 4). Persons in the area of the fire were in pitch dark and reported that the air was full of fireballs. Besides this, there were pieces of wood, branches and bark flying all around, sometimes igniting new fires. In at least two very localised areas, wind tornadoes twisted and broke a large number of trees more than 20 cm in diameter, breaking them like toothpicks. The wind velocity required to cause this is estimated to be of the order of 200 km h⁻¹.

Fig. 4.

Some images of fire phenomena during its spread in the late afternoon of 17 June 2017.

Similar phenomena were observed in the merging process of the McIntyre and Bendora fires near Canberra on 18 January 2003, with a very fast spreading fire (27 km h⁻¹) and a tornado that broke trees trunks larger than 30 cm in diameter (Doogen 2006).

The perception of the violence of the fire caused by the noise produced by its very tall and roaring flames that threatened to destroy everything in their path caused many citizens to decide to flee from their houses. Some of them took this decision in spite of knowing that their houses would normally sustain the passage of a fire, which most of them did. While escaping in their cars, many persons, sometimes entire families, were caught by the smoke, loss of visibility and flames and lost their lives. Particularly dramatic was the situation of a stretch of 200 m of Road N326-1, between Figueiró dos Vinhos and Castanheira de Pêra (Fig. 4), in which 30 persons were killed inside or near their cars.

The lack of maintenance of vegetation – including trees – in the vicinity of the main roads contributed to the lack of survival conditions for the citizens. We identified one particular pine tree that was very close to the road edge and fell over the road with the very strong fire-induced wind, crossing it from one side to the other. This tree and a group of cars that crashed into each other created a trap from which the cars could not drive out. Based on the testimony of survivors and of persons who passed by that road before or during the accident, we were able to identify at least 16 persons whose death can be directly attributed to this tree.

The main fire was controlled on 22 June by 2350 hours with the effort of more than 1400 firefighters and other agents after burning a total area of 45 328 ha.

Materials and methods

Scaling laws

Similarity conditions

In this paper, we present a methodology to model the spread of the fire in the case of PG based on physical laboratory experiments. Given the need to perform these experiments at a relatively small scale and to make approximations regarding several physical processes and parameters that govern the phenomena at both scales, we describe the modelling laws that were developed, and the assumptions made.

Scaling distance and fire spread

Here, we address the problem of transposing the results of fire spread onto two domains S₁ and S₂, covered with a surface fuel bed, potentially with different properties and with different dimensions, but assuming that there is a geometrical similarity between the two domains and a physical similarity between the fire propagation processes. This means that the laws of fire spread at a given location and time in system S₁ are the same as those at the corresponding location and time in system S₂.

In the general case, the fuel cover can be arbitrary in both systems, respecting geometrical similarity, provided that the local fire spread properties are known to be similar at each pair of corresponding points. In the present work, for simplification, we assume that the fuel cover is homogeneous in both systems.

Under the above conditions of geometrical similarity, we develop scaling laws to transpose the conditions of fire spread properties from a given point P₁ in domain S₁ to the corresponding point P₂ in the domain S₂.

At the two corresponding points in both domains, the local ROS R is given respectively by:

(1)

R_{1} = f_{1} \times R_{o1}

and

(2)

R_{2} = f_{2} \times R_{o2} .

In these equations, we use as reference ROS values the so-called basic ROS R_o, (Viegas and Pita 2004; Raposo et al. 2014, 2018; Xie et al. 2014; Rodrigues et al. 2019; Viegas et al. 2021, 2022; Ribeiro et al. 2022, 2023) that corresponds to a linear fire spreading in the same fuel under no-wind and no-slope conditions.

The value of R_o characterises the combustibility properties of the fuel bed, namely its composition, fuel load, compactness and moisture content. The non-dimensional function f_i characterises the physical properties of the spreading fire, namely the role of wind, topography and induced convection, on the heat transfer processes and on the combustion of the fuel bed particles.

If we have a reference ROS R_ref1 at a given point in domain S₁, then the value of the reference value in domain S₂ is R_ref2. We define the physical similarity parameter:

(3)

k_{f_{ref}} = \frac{f_{1_{ref}}}{f_{2_{ref}}}

Full physical similarity between the fire spread conditions would be achieved if we had:

(4)

k_{f_{ref}} = 1

meaning that both physical processes were similar. We assume that quasi-complete similarity is achieved if the ratio k_f between both functions is of the order of 1.

If a given line has a length $ℓ_{1}$ in one system and $ℓ_{2}$ in the other, we can define the length scale factor ε by:

(5)

ε = \frac{ℓ_{1}}{ℓ_{2}}

If a section of the fire front is displaced in a given time step in System 1 by:

(6)

d x_{1} = f_{1} \times R_{o1} \times d t_{1}

the corresponding displacement in the other system will be:

(7)

d x_{2} = f_{2} \times R_{o2} \times d t_{2}

Using the length scale factor, we can see that:

(8)

ε = \frac{d x_{1}}{d x_{2}} = \frac{f_{1} \times R_{o 1} \times d t_{1}}{f_{2} \times R_{o 2} \times d t_{2}} = k_{f} \times \frac{R_{o1} \times d t_{1}}{R_{o2} \times d t_{2}}

From this equation, we can derive the time scale factor τ:

(9)

τ = \frac{d t_{1}}{d t_{2}} = \frac{ε}{k_{f}} \times (\frac{R_{o2}}{R_{o1}}) = ε \times \frac{R_{2}}{R_{1}}

The time scale factor shows that when analysing linear displacements of the fire front, a given time interval Δt₁ in S₁ corresponds to a time lapse of Δt₂ in S₂ multiplied by the length scale factor and the ratio of the reference ROS values.

Scaling areas

If we consider an elementary area growth in the two systems, this is given respectively by:

(10)

d A_{1} = d x_{1} \times d y_{1} = f_{x_{1}} R_{o1} d t_{1} \times f_{y_{1}} R_{o1} d t_{1}

(11)

d A_{2} = d x_{2} \times d y_{2} = f_{x_{2}} R_{o2} d t_{2} \times f_{y_{2}} R_{o2} d t_{2}

In these equations, f_xi and f_yi are the factors of the ROS function for the component along OX and OY axes respectively and i = 1 or 2 (Fig. 5). We assume that the ratio of the non-dimensional functions at both scales is the same:

(12)

\frac{f_{x_{1}}}{f_{x_{2}}} = \frac{f_{y_{1}}}{f_{y_{2}}} = k_{f}

As dA₁ = ε²dA₂, we can determine the time scale factor τ_A for areas burned in both systems in the corresponding periods of time:

(13)

τ_{A} = {(\frac{d t_{1}}{d t_{2}})}_{A} = (\frac{ε}{k_{f}}) \times (\frac{R_{o2}}{R_{o1}}) = ε \times \frac{R_{2}}{R_{1}} = τ

As can be seen, the time scale factor for areas is the same as that for distances.

Experimental setting

The authors performed laboratory experiments in the combustion tunnel of the Forest Fire Research Laboratory of the University of Coimbra to simulate the development of the two ignition fires. As shown in Fig. 5a, the combustion tunnel has a horizontal test section of 6 m by 8 m limited by 2 m high vertical lateral walls and is open at the top. The flow in the test section is produced by two axial fans and can reach a maximum value of 8 m s⁻¹. The flow is of the boundary layer type near the horizontal surface of the test section and fairly uniform.

Fig. 5.

(a) General view of the combustion tunnel of the Fire Research Laboratory during test PG 42. (b) Layout of the fuel bed and the ignition lines.

The physical problem is described schematically in Fig. 5b. Let us consider an absolute reference frame O_oX_oY_oZ_o in which the horizontal datum plane is defined by the axis O_oX_oY_o. The system OXYZ is coincident with the absolute reference. The fuel bed surface test was a rectangle defined by ABDE with dimension AB equal to 5 m and BD equal to 4 m. The straight line OC represents the middle of the fuel bed on the OY axis and the wind flow U_o is the flow velocity vector (m s^–1) produced by two fans is parallel to the OX axis (represented as bold short black arrows in Fig. 5b).

In order to simulate the spread of the two fires of EF and RE after 1830 hours and their merging, we marked two straight lines FG and HI to represent the EF and RE fires at that time, respectively. Henceforth, these lines are designated L_EF (Escalos Fundeiros) and L_RE (Regadas). The angles between these fire lines and the OY axis are θ₁ (EF) and θ₂ (RE), as indicated in Fig. 5b. In the present work, for each set of parameters, the angles θ₁ and θ₂ were 25° and 48°, respectively.

Given the geometrical similarity between the position, orientation and length of each fire line at the laboratory and at the field scales, we were able to determine the length scale parameter. Using the ratio of the linear dimensions of the EF fire length in both systems at the nominal time of t_i, we find that (dimensions are in metres):

(14)

ε = \frac{ℓ_{1}}{ℓ_{2}} = \frac{ℓ_{r}}{ℓ_{m}} \approx \frac{4400}{1.5} = 2933

In the tests, we covered a test area of 4 × 5 m² with a uniform fuel bed of particles of either dead needles of Pinus pinaster (PP), straw (ST) or shrub fine branches and foliage (SH), with a fuel load of 600 g m⁻² (dry basis).

During the preparation of each test, the fuel load and bulk density were controlled. The laboratory air temperature, relative humidity and fuel moisture (m_f) were monitored. The time between preparation of the fuel bed and the start of the test did not exceed 10 min to avoid changes in moisture content of the fuel bed. The fuel moisture content was measured twice: at the beginning of the preparation of the fuel bed and immediately before each test was started using a moisture analyser (A&D ML50). In Table 1, the values of fuel moisture content immediately before each test started are presented. The equipment used in each test was the moisture analyser (A&D ML50).

Table 1. Parameters of the tests performed in the present research.

Ref.	Fuel	U_o [m s⁻¹]	Designation^A	m_f (%)	R_o (cm s⁻¹)	R′_max
1	PP	0	PG 10	11.73	0.36	1.27
2	PP	2	PG 12*	11.34	0.34	47.05
3	PP	3	PG 13*	11.34	0.35	95.70
4	PP	4	PG 14*	12.87	0.35	112.82
5	ST	2	PG 22*	10.50	0.71	45.00
6	SH	2	PG 32*	10.38	1.35	23.10
7	PP	2	PG E 12	11.24	0.43	50.05
8	ST	2	PG E 22	12.11	0.80	45.00
9	SH	2	PG E 32	9.89	1.34	23.10
10	PP	2	PG EF 12*	12.11	0.37	34.48
11	PP	2	PG RE 12*	11.36	0.33	18.29
12	ST	2	PG 22A	11.34	0.34	93.97
13	PP	2	PG 42*	11.40	0.24	41.28

^AThe tests marked with (*) are the ones used in the present work.

An infrared camera (FLIR SC660) was used to record the position of the fire perimeter evolution in all tests. A temperature range between 300 and 1500°C was used with a rate of acquisition of 15 Hz. IR recording was continuous, and it was possible to estimate the local value of ROS at every point of the fuel bed. The IR images were automatically analysed with an open-source program Fire_ROS_Calculator (Abouali and Viegas 2019).

The tests were monitored using a photographic camera (Canon EOS 550D) and one video camera in top view (Sony AVCHD MPEG2 SD). The Canon photographic camera was used to take instantaneous images during the test.

Before each test, the corresponding value of the basic ROS (R_o) was determined. This test was performed on a horizontal table of 1 × 1 m² with the same type of fuel cover without slope or wind.

Most of the experiments were carried out in 2019 and although data collection and analysis were performed and completed then, very few quantitative results were disseminated by the authors. With the recorded images of Test PG 12, we created a video superimposing the IR and video images onto a map of the area with some of the main roads and the location of the accidents in which 66 persons were killed, to illustrate the mechanism of fire merging and explain the difficulty that people had in escaping from the fire. We have used this video in several lectures and training sessions to present our perspective of the events of this fire.

Test PG 42, with the same conditions as PG 12, was performed in 2022 to check the repeatability of the experiments, using the same methodology and sensors, although with an improved IR camera and more updated data analysis methods and systems. The results obtained were very similar to those found previously.

As can be seen in Table 1, we performed preliminary experiments with different fuels and wind velocities to test the role of these parameters, finding that the processes were similar in all cases although they were intensified for larger values of U_o. In the present work, we only use the results from the tests indicated with an asterisk in Table 1.

In the experiments, ignition of the two fire lines was performed simultaneously by two persons. For safety reasons, the flow velocity in the wind tunnel was turned on only after the two persons had left the test chamber. This time lapse created an uncertainty in determining the start of the test. In our experiments, we intended to simulate the fire spread after time t_o (1830 hours in real conditions) but owing to this delay, this time did not coincide with the time of ignition t_i that corresponded to the start of data recording.

Differences in this time lapse may explain some discrepancies in the time-dependent laws of the results obtained in the experiments. As we shall see, the time lapse Δt_i = t_i − t_o of a few seconds in the laboratory experiment corresponded to several minutes in the real-case fire. This time lapse was considered in the subsequent analysis.

Assessment of similarity conditions

One of the requisites to have physical similarity between the processes at both scales is the geometrical similarity of the terrain and fire ignition location at the start of the fire. The area of the PG fire considered in this study has an average slope of 6° (10.5%), which can be considered negligible to allow the simulation of the fire on a horizontal surface at the laboratory scale. The terrain at full scale consists of undulating ground with variations of height of the order of 100 m and with maximum slopes of 36%. The terrain roughness created by these elements of topography over a length of 8 km can be considered negligible in comparison with the vertical development of the fire and the overwhelming role of fire-induced convection, to allow us to use a flat surface to represent the terrain at the laboratory scale.

The fuel cover at the full scale is composed mainly of a mixture of eucalyptus and pine trees, with shrub in the understorey. Some areas had acacia and broadleaved trees, and agricultural cultures, but the dominant fuel was composed of unmanaged mature eucalyptus plantations (Xavier Viegas et al. 2017; Pinto et al. 2022).

We know that, generically, the fuel bed structure can be considered constant for the duration of a specific single fire behaviour simulation (Scott 2012). Most commonly, when spatially describing a landscape for fire behaviour simulation, vegetation is physically characterised using fuel models (Anderson 1982; Scott and Burgan 2005; Heinsch 2020). These models are used to address surface fire behaviour (Rothermel 1972), namely, to estimate the spread in the direction of the wind and slope (Sullivan 2009). This estimate also includes an indication of Byram’s fire intensity (Byram 1959), which usually determines what fuels are consumed during a fire (Cruz et al. 2014) like large woody fuels during glowing combustion (Hollis et al. 2011a, 2011b) or fine fuels in low-intensity fires (e.g. McCarthy 2003).

In the case of Pedrógão Grande, given the very high intensity of the fire spread, the differences between fuel types and species was very much attenuated, allowing us to consider that the behaviour of the fire was equivalent to a homogeneous fuel bed with the average properties of the real vegetation. Therefore, we also use a homogeneous fuel bed at the laboratory scale.

In the PG fire, there is a characteristic value of the ROS that is the maximum value R_MAX of the head fire after the merging of both fires. Choosing this value as a reference velocity, in order to have physical similarity we must have the same or very similar values of R′_MAX at both scales.

In the laboratory experiments, we have a variable parameter that is the incident wind flow velocity U_o. Considering the set of experiments PG 12, PG 13 and PG 14, performed with pine needles with a velocity of 2, 3 and 4 m s⁻¹, respectively, we can see that the corresponding values of R′_MAX given in Table 1 are of the same order as the value of 72.3 for the real fire. Calculating the values of k_f for each case, we find that for PG 12, PG 13 and PG 14, the values of k_f are respectively 1.54, 0.757 and 0.642, which are close to 1. Therefore, we consider that the physical similarity of fire spread conditions is closely fulfilled in the present set of experiments.

Results and discussion

Isochrones of fire spread

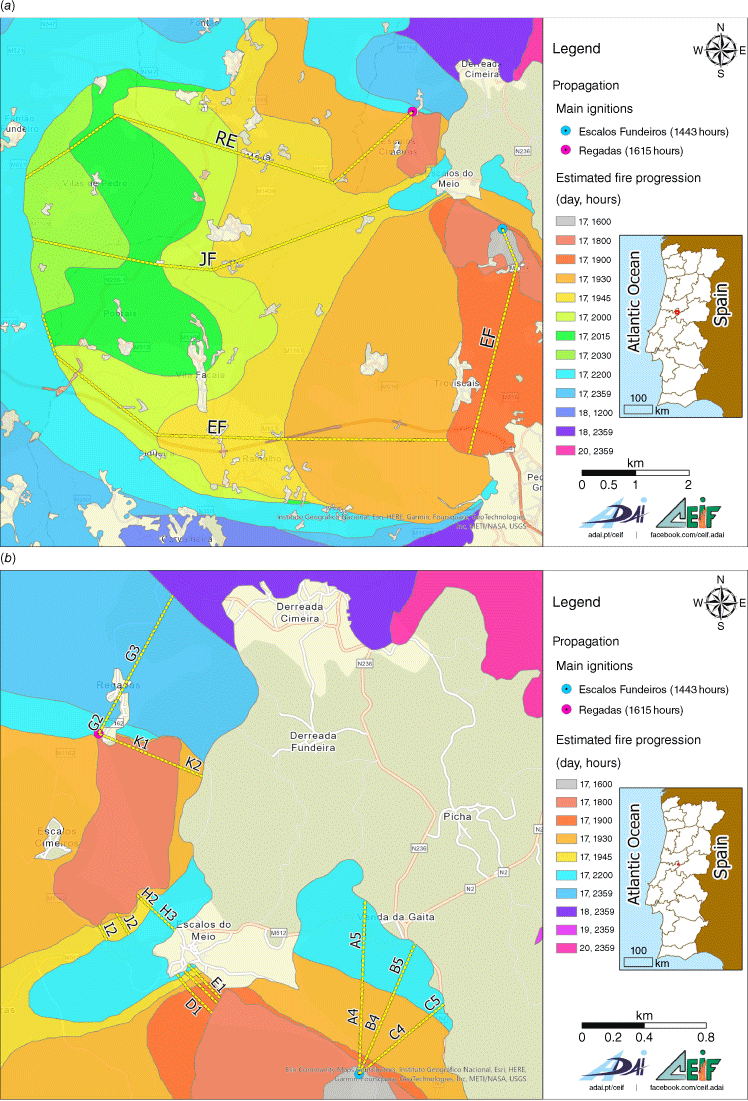
The isochrones of the fire spread in the full-scale situation, which we designated ‘real’ conditions, are shown as shaded areas in Fig. 1 and are illustrated more in detail in Fig. 6. In Fig. 6a, the trajectories of the three main head fires Escalos Fundeiro (EF), Regadas (RE) and Junction Fire (JF) are indicated while in Fig. 6b, some trajectories of back fires and flank fires are shown. These lines were used to estimate respectively the head fire ROS and the flank fire ROS, which was compared with the basic ROS for the real fire (R_or).

Fig. 6.

(a) Isochrones of the PG fire based on reconstruction of the fire evolution with the trajectories of the three head fires. (b) Some trajectories of back and flank fires of the PG fire.

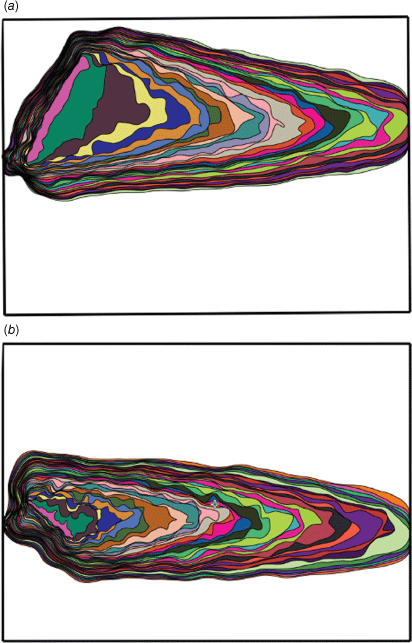
The isochrones of fire spread obtained in the test Ref 2: PG 12 with both ignitions, performed with pine needles, at a time step of 20 s are shown in Fig. 7.

Fig. 7.

Map with the isochrones of fire spread of the physical simulation of the two fires in the combustion tunnel of the University of Coimbra. The initial position of the fires (pink areas) corresponds at the situation at ~1830–1930 hours. The time lapse between the lines is 20 s.

The corresponding lines for tests Ref. 10: PG EF 12 and Ref. 11: PG RE 12, with only one ignition each, respectively for EF and RE are shown in Fig. 8. We have the isochrones of all the tests referred to in Table 1, which were the basis of the analysis of fire spread in each test.

Fig. 8.

(a) Map with the fire spread isochrones of the physical simulation of the EF fire (Ref. 10: PG EF 12) in the combustion tunnel of the University of Coimbra. (b) Isochrones for fire spread of the RE fire line (Ref. 11: PG RE 12). The time lapse between the lines is 20 s in both cases.

Rate of spread analysis

Non-dimensional ROS

As usual in the analysis of ROS values at different scales, we use the non-dimensional ROS R′ defined by:

(15)

R' = \frac{R}{R_{o}}

In this equation, R is the actual value of the modulus of the ROS at a given point and R_o is a reference ROS value, which is a characteristic property of the fuel bed.

As mentioned above, this property was measured systematically in the laboratory for each set of test conditions and the corresponding value of R_o is given in Table 1.

Nevertheless, for the field conditions, given the heterogeneity and diversity of the fuel bed properties, we had to estimate the reference velocity from fire spread in backing and flanking sections of the fire perimeter. It is known that the ROS in these cases is very close to R_o (cf. Viegas 2004; Sharples et al. 2010; Raposo et al. 2015; Rossa et al. 2015; Rossa and Fernandes 2018).

Using the trajectories of the back and flank fires shown in Fig. 6b, we estimated the local values of the ROS along those lines and calculated their arithmetical mean R_or = 5.37 cm s⁻¹. This value was taken as a reference to determine non-dimensional values for the field scale.

Scale factors for field and laboratory systems

In the present study, we consider the development of the scale factors for two situations: (i) transposing the results from the full scale of the fire to the model laboratory experiments; and (ii) transposing the results from laboratory experiments performed at the same scale with different fuels.

Field and laboratory results

In this case, system S₁ ≡ S_r is the field or real fire domain and S₂ ≡ S_m is the model laboratory domain. Using Eqns 9 and 13 and the given values of R₁ or R₂for each case, we can estimate the time scale factors for linear dimensions and for the area evaluation in each case. The corresponding values are given in Table 2.

Table 2. Time scale factors for the transposition of linear and area measurements from laboratory experiments and the real fire.

Test ref.	Fuel bed	R _o (cm s⁻¹)	τ _A	Ignition time (hours)
PG 12	PP	0.34	120.68	1830
PG 13	PP	0.35	252.68	1830
PG 14	PP	0.35	297.89	1823
PG 22	ST	0.71	241.03	1803
PG 32	SH	1.35	235.26	1721
PG 42	PP	0.23	71.63	1754
Field	Forest	5.37	1	1930

Laboratory experiments with different fuels

When comparing the time-dependent results from laboratory experiments performed with different fuels, in order to convert the time scale to a common reference, we used the following definition of reduced time t*:

(16)

t^{⁎} = t_{o}^{⁎} + \frac{R_{MAXk}}{R_{MAX}^{⁎}} \times t_{k}

In this equation, $R_{MAX}^{⁎}$ is the maximum ROS of the test used as reference, and R_MAXk and t_k are respectively the maximum ROS and the time of the test that is being analysed. The parameter $t_{o}^{⁎}$ was introduced to correct for errors due to differences of the initial time lapse Δt_i, as described above.

It must be noted that Eqn 16 is equivalent to Eqn 9 with ε = 1, as we are comparing laboratory experiments performed at the same linear scale. In the present study, we use as reference the data from test PG 12; therefore, the reduced time t* refers to this particular test.

Comparison between tests performed with different fuels

Using Eqn 16, we estimated the reduced time t* for tests PG 12, PG 22 and PG 32 performed respectively with pine needles, straw and shrub fuel beds. The evolution of the head fire of EF, RE and JF as a function of t* is shown respectively in Fig. 9a–c. In all cases, we considered that $t_{o}^{⁎} = 0$ .

Fig. 9.

Comparison between non-dimensional ROS from tests with different fuels as a function of reduced time (t*). The fuels used are pine needles (PP): PG 12, straw (ST): PG 22 and shrubs (SH): PG 32. (a) EF; (b) RE; and (c) JF.

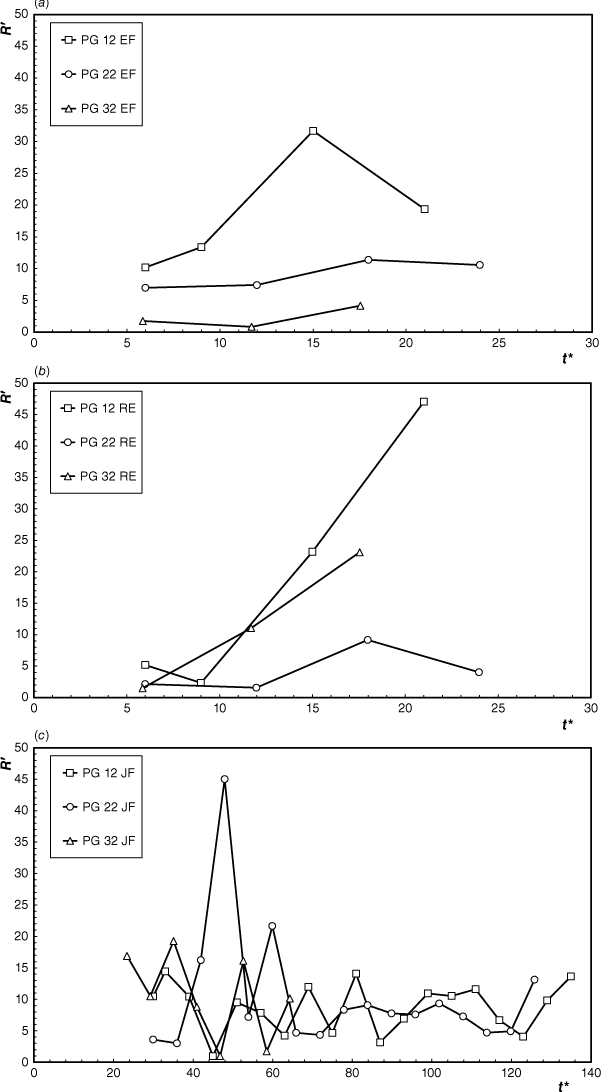
As can be seen in these figures, the evolution of the head fires follows the same trend in all cases but with some differences that can be attributed to the different ignition conditions and to the response time of the combustion process in each fuel, associated with the residence time of the flames (Viegas 2006). The maximum value of R′ of 45 is reached in test PG 12 on the RE head fire, whereas for PG 22, with straw, it is reached by the JF. In test PG 32 with shrub, the ROS increase is much slower, given the higher residence time, and the maximum value of R′ achieved in this test is of 22, much lower than observed in the other fuels and in the field (cf. Fig. 9).

Comparison between single and joint ignitions

One of the objectives of the experimental study was to show the difference in fire spread conditions between the actual situation of having two simultaneous merging fires in comparison with having only one of them. For this, we performed two tests similar to PG 12: PG EF 12, with only the ignition of EF, as shown in Fig. 8a, and PG RE 12, with only the ignition of RE, Fig. 8b.

The analysis of those figures shows clearly that the areas burned by the single fires are much lower than those burnt by the joint fires (Fig. 7), as would be expected. This was actually one reason motivating the residents in the path of the JF fire to attempt to run away from this very fast spreading fire coming towards their area of residence, without realising that they were in the middle of a very large bowl of fire, created by these two large pincers of fire. Many survivors told us that wherever they attempted to drive, they were always surrounded by fire.

In order to highlight the great acceleration induced at the head of the merging fires, we compare in Fig. 10 the values of R′ for the head fires of the two isolated fires with those of the joint fires in test PG 12. As can be seen in this figure, although in test PG EF 12 a fairly high value of 34 is reached at the beginning of the spread by the EF fire, in test PG 12, a much higher value of 48 is reached by this fire; the corresponding values for the RE fire are respectively 32 for PG 12 and 13 for PG RE 12 tests.

Fig. 10.

Comparison between the non-dimensional ROS of the EF and RE head fires of the PG 12 tests where both ignitions were performed with the results of the same head fires with isolated ignitions.

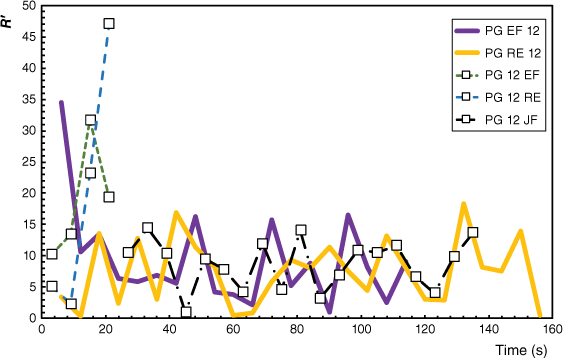
These results confirm the intensification of fire spread produced in the merging fires, which results in much higher values of burned area and ROS and also in the existence of the very strong convective processes that were observed and described above.

Comparison between model and real scales

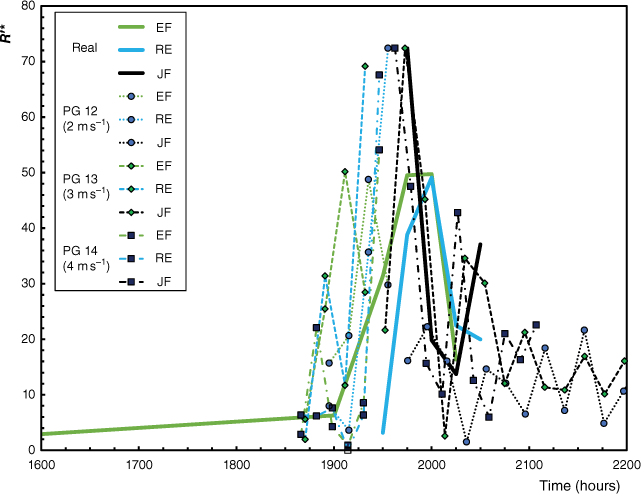
In Fig. 11, we plotted the values of R′ for the three head fires in the real fire based on the fire reconstruction shown in Figs 1 and 2a as a function of local time during 17 June of 2017. As can be seen in this figure, the peak values of R′ reach 72.4 for the JF fire and values close to 50 for both the EF and the RE fires.

Fig. 11.

Comparison between non-dimensional normalised ROS of the EF, RE and JF head fires from the real fire and from tests performed with pine needles (PP) and different wind velocities: PG 12 (2 m s⁻¹), PG 13 (3 m s⁻¹) and PG 14 (4 m s⁻¹).

Using the time scaling equations described above, we used the following equation to transpose the model experiments time to the time for the full-scale conditions:

(17)

t_{r j} = t_{i j} + τ_{j} \times t_{j}

In this equation, t_rj is the real time, at full scale, corresponding to the results of test j, τ_j is the corresponding time scale factor, given in Table 2, for each test, and t_j is the time since fire ignition in test j. The parameter t_rj is the fictious ignition time, to account for the ignition delay in the test. The values of t_rj were adjusted for each test to obtain better overall agreement; the corresponding values are given in Table 2.

The results of tests PG 12, PG 13 and PG 14, performed with pine needles but with three different flow velocities, are plotted in Fig. 11 using the real time scale of the fire, according to the proposed model.

As can be seen in this figure, the results of the physical modelling of the large PG fire during its very intense propagation in the late afternoon 17 June 2017, using the scaling laws proposed in the present paper agree quite well with the observed characteristics of the real fire. The overall tendency of fire growth for the various head fires as well as the order of magnitude of the non-dimensional ROS and its temporal variation, obtained in 1:2933 scale experiments with different flow velocities has very good agreement with the full-scale observations, showing that the use of laboratory experiments is a valid tool to model extreme fire behaviour in wildfire events.

Area growth analysis

Tests with different fuels

The growth of burned area over the course of time is a very important parameter to assess fire suppression capacity or effectiveness and also to estimate the release of energy and smoke to the atmosphere.

In Fig. 12a, we compare the evolution of the burned area during experiments PG 12, PG 22 and PG 32 performed with three different fuels. In each case, measurement of the area was stopped when the head fire reached the border of the fuel bed.

Fig. 12.

Evolution of the burned area in three tests performed with different fuels: pine needles PG 12, straw PG 22 and shrubs PG 32: (a) as a function of physical time; (b) as a function of reduced time.

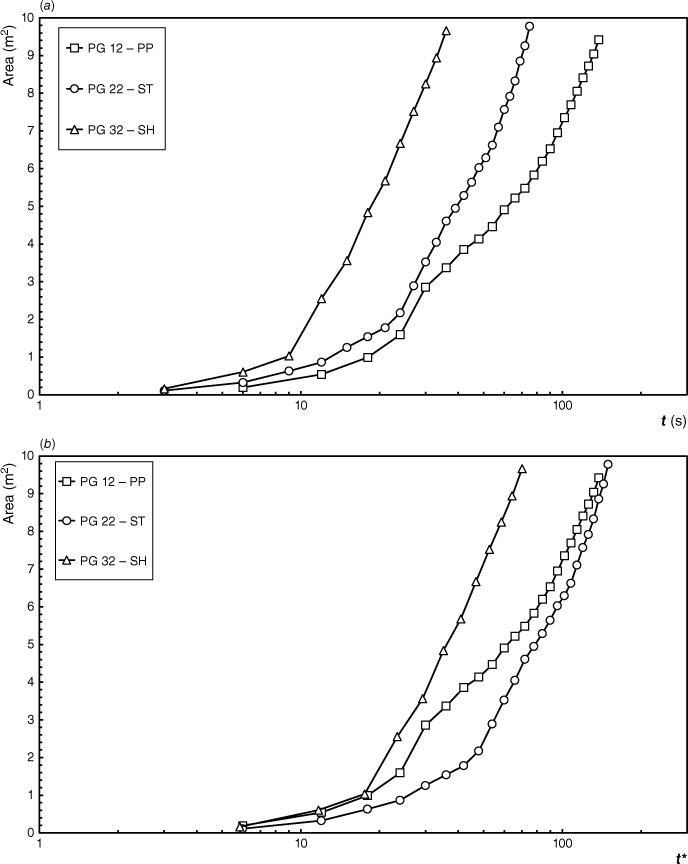
The temporal trend of the three curves is similar but the time taken to burn a given area is inversely proportional to the respective value of R_MAX, as expected. This is clearly shown in Fig. 12b in which we used the reduced time t* corresponding to test PG 12, as the three curves almost merge into a single one. In these figures, no corrections were made to account for the ignition time delay.

Comparison of burned area variation between model and full-size scales

We now analyse and compare the area growth in the real conditions after 1930 hours, which corresponds nominally to the start of the laboratory experiments, when the two fire lines started to spread freely without any extinction effort, using the results of tests PG 12, PG 13 and PG 14, which are considered to have closest similarity to the real fire spread conditions. For this, we use the area A₂ burned by the three head fires (EF, RE and JF) since 1930 hours; for this reason, in the graph we considered that the area of the fire at this time was equal to zero, when in reality it was already 3154 ha for the real fire. For the time scale factor τ_A, we used the respective values given in Table 2.

As can be seen in Fig. 13 in which the four curves are plotted, the experimental results show that initially the area growth rate was very high, but after 2030 hours, this rate decayed, as happened with the real fire. Although the overall tendency of area growth is reproduced by the experiments as well as its order of magnitude, it is clear that using the scale modelling assumptions of the present work, we obtained much lower values of the burned area, prompting us to analyse the possible reasons for this.

Fig. 13.

Comparison between the burned area growth in tests PG 12, PG 13 and PG 14 with the real fire between 1930 and 2200 hours.

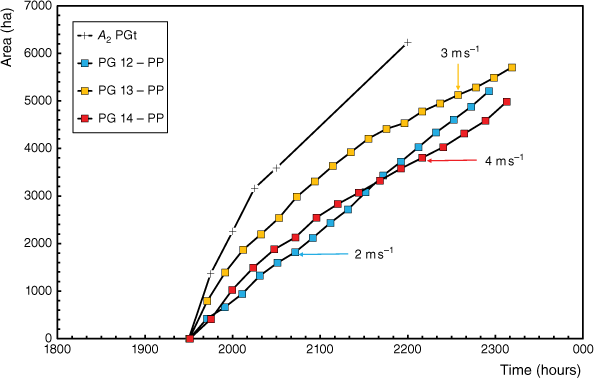
More obvious is the fact that the fire spread processes in the laboratory experiments became very different from those at the full scale as the fire became a very intense fire storm. After 2000 hours in the real fire, there were extensive spotting and crown fires, which are not replicated in the laboratory-scale experiments. As a consequence, the actual values of the fire spread parameters from the model experiments, like the burned area and its rate of growth, do not fully agree with the full scale, but they follow the same temporal trend and are of the same order of magnitude, therefore showing the usefulness and interest of the present method of physical and scale modelling to analyse complex and intense fires that cannot be otherwise simulated with current state simulators.

In spite of these discrepancies, it is worth noting the great similarity between the overall fire behaviour that was observed at both scales. This is due to the overwhelming effect of the convective flows produced by the junction fires, causing the very significant acceleration of the head fires even on flat ground.

Conclusion

The fire that occurred on 17 June 2017 near Pedrógão Grande covered an area of 45 000 ha, resulted in the destruction of more than 1000 houses and structures, and caused the death of 66 persons. This fire had very intense spread over a couple of hours due to the convergence of unusual circumstances that were analysed in this paper. In the first place, the fire had two separate ignitions that started 3 km apart, caused by a power line, at 1430 hours and at 1350 hours. Owing to insufficient resources, these fires were not controlled when by 1800 hours a downflow from a thunderstorm that was passing overhead interacted with the two fires and caused them to spread out of control. The merging of these fires produced so-called junction fire spread with very high ROS and very intense convective processes over a very wide area, surprising hundreds of persons who were in the area and eventually causing the death of 66 persons.

To the knowledge of the authors, this type of fire behaviour has not previously been reported and is not well predicted by current fire simulators.

Based on extensive field data, the authors were able to reconstruct the evolution of the fire, and evaluate the spread of the main head and flank fires. These results were compared with those obtained in a series of laboratory experiments (at a scale close to 1:3000) performed in similar geometrical conditions. A scale modelling method was proposed to transpose the results of linear displacements or of area growth measurements from laboratory experiments to the real fire scale. Our results show that in spite of the differences in the geometry of the terrain and in some of the mechanisms of fire spread that surely existed between the real fire and the laboratory-scale tests, the results obtained in the laboratory experiments follow the same trends of fire spread configuration, fire acceleration and burned area growth that were observed in the full-scale conditions.

The present work shows that the physical modelling of fire spread in laboratory scale experiments is a useful tool to replicate and interpret the properties of some complex fires, provided that the appropriate modelling rules and parameter transformation equations are used.

In future work, we intend to explore the results of the spread of the fire to better explain some processes associated with the fire of Pedrógão Grande, like the emission and dispersion of smoke and the various accidents that occurred in the area. We intend also to extend the application of the present method of physical modelling to the analysis of other cases.

Symbols

α	Slope angle (°)
m_f	Moisture content of the fuel bed particles (dry basis)
R_o	Basic rate of spread (cm s⁻¹)
R₁	Rate of spread in domain S₁ (cm s⁻¹)
R₂	Rate of spread in domain S₂ (cm s⁻¹)
R_o1	Basic rate of spread in domain S₁ (cm s⁻¹)
R_o2	Basic rate of spread in domain S₂ (cm s⁻¹)
R	Rate of spread (ROS) (cm s⁻¹)
R′	Non-dimensional ROS
k_f	Ratio between fire spread functions of each domain
ε	Length scale factor
dx₁	Fire front displacement in domain S₁ (m)
dx₂	Fire front displacement in domain S₂ (m)
τ	Time scale factor for distances
dA₁	Burned area in domain S₁ (m²)
dA₂	Burned area in domain S₂ (m²)
τ_A	Time scale factor for areas
O_oX_oY_oZ_o	Absolute reference frame
O_oX_oY_o	Horizontal datum plane
ABDE	Fuel bed surface
U_o	Flow velocity vector (m s⁻¹)
t_o	Time in real Pedrógão Grande Fire – 1830 hours
t_i	Time of ignition
t*	Reduced time
θ₁	Angle between the Escalos Fundeiros fire line and OY axis
θ₂	Angle between the Regadas fire line and OY axis
S₁	Domain 1, which represents the real domain during the fire
S₂	Domain 2, which represents the laboratory domain
$ℓ_{1}$	Length in Domain S₁ (m)
$ℓ_{2}$	Length in Domain S₂ (m)
$ℓ_{r}$	Length in real fire (m)
$ℓ_{m}$	Length in laboratorial model (m)
A₁	An elementary area of domain S₁
A₂	An elementary area of domain S₂
R_MAX	Maximum rate of spread
t_rj	Real time at full scale of the test j

Nomenclature

PG	Pedrógão Grande
EF	Escalos Fundeiros
RE	Regadas
MCS	Mesoscale Convective System
L_EF	Line designated by Escalos Fundeiros
L_RE	Line designated by Regadas

ST	Straw
SH	Shrub fine branches and foliage
PP	Pinus pinaster

Supplementary material

Supplementary material is available online.

Data availability

Data are available only under request to the corresponding author: Domingos X. Viegas, xavier.viegas@dem.uc.pt.

Conflicts of interest

The authors declare no conflict of interest. Domingos Xavier Viegas an Associate Editor of International Journal of Wildland Fire. Miguel Almeida is also a Guest Editor for the issue. To mitigate this potential conflict of interest, they were blinded from the review process and were not involved at any stage in the editing of this manuscript.

Declaration of funding

The work reported in this article was carried out in the scope of projects IMfire (PCIF/SSI/0151/2018) and SmokeStorm (PCIF/MPG/0147/2019) supported by the Portuguese National Science Foundation and European Union’s Horizon 2020 research and innovation programme under grant agreement No. 101003890, FirEUrisk – Developing a Holistic, Risk-wise Strategy for European Wildfire Management. We would like to thank the FCT-Foundation for Science and Technology for the PhD grant of Carlos Ribeiro with the reference SFRH/BD/140923/2018.

Author contributions

Conceptualisation: Domingos Xavier Viegas and Carlos Ribeiro; data curation: Domingos Xavier Viegas, Luis M. Ribeiro and Carlos Ribeiro; formal analysis: Domingos Xavier Viegas and Carlos Ribeiro; methodology: Domingos Xavier Viegas and Carlos Ribeiro; experimental tests: Domingos Xavier Viegas and Carlos Ribeiro; supervision: Domingos Xavier Viegas; writing – original draft: Domingos Xavier Viegas; writing – review and editing – Domingos Xavier Viegas; Carlos Ribeiro; Miguel Almeida; Paulo Pinto; Luís M. Ribeiro and Álvaro Pimpão.

Acknowledgements

The support given by Jorge Raposo, Luis Reis, André Rodrigues, Abdelrahman Abouali, Nuno Luis, Gonçalo Rosa, Diogo Pires and João Carvalho in performing the laboratory experiments is gratefully acknowledged.

References

Abouali A, Viegas DX (2019) Fire ROS Calculator: a tool to measure the rate of spread of a propagating wildfire in a laboratory setting. Journal of Open Research Software 7, 24.
| Crossref | Google Scholar |

Anderson HE (1982) Aids to determining fuel models for estimating firebehavior. USDA Forest Service, Intermountain Forest and Range Experiment Station General Technical Report INT‐122. (Ogden,UT). Available at https://www.fs.usda.gov/treesearch/pubs/6447

Artés T, Castellnou M, Houston Durrant T, San-Miguel J (2022) Wildfire-atmosphere interaction index for extreme fire behaviour. Natural Hazards and Earth System Sciences 509-522.
| Crossref | Google Scholar |

Byram GM (1959) Combustion of forest fuels. In ‘Forest fire: control anduse’. (Ed. KP Davis) pp. 90–123. (McGraw‐Hill: New York, NY)

Doogen M (2006) ‘The Canberra Firestorm Inquests and Inquiry into Four Deaths and Four Fires Between 8 and 18 January 2003.’ (ACT Coroner’s Court: Canberra, ACT)

Cruz MG, Sullivan AL, Leonard R, Malkin S, Matthews S, Gould JS, Mccaw WL, Alexander ME (2014) ‘Fire behaviour knowledge in Australia: a synthesis of disciplinary and stakeholder knowledge on fire spread prediction capability and application.’

Guerreiro J, Fonseca C, Salgueiro A, Fernandes P, Lopez E, de Neufville R, Mateus F, Castellnou M, Silva JS, Moura J, Rego F, Mateus P (2017) Análise e apuramento dos factos relativos aos incêndios que ocorreram em Pedrogão Grande, Castanheira de Pera, Ansião, Alvaiázere, Figueiró dos Vinhos, Arganil, Góis, Penela, Pampilhosa da Serra, Oleiros e Sertã, entre 17 e 24 de junho de 2017. [In Portuguese]

Heinsch FA (2020) Fuel model. In ‘Encyclopedia of Wildfires and Wildland–Urban Interface (WUI) Fires’. (Ed. SL Manzello) pp. 520–538. (Springer International Publishing: Cham) doi:10.1007/978-3-319-52090-2_178

Hollis JJ, Anderson WR, McCaw WL, Cruz MG, Burrows ND, Ward B, Tolhurst KG, Gould JS (2011a) The effect of fireline intensity on woody fuel consumption in southern Australian eucalypt forest fires. Australian Forestry 74, 81-96.
| Crossref | Google Scholar |

Hollis JJ, Matthews S, Anderson WR, Cruz MG, Burrows ND (2011b) Behind the flaming zone: Predicting woody fuel consumption in eucalypt forest fires in southern Australia. Forest Ecology and Management 261, 2049-2067.
| Crossref | Google Scholar |

McCarthy G (2003) Fire management Drought Factor (fine fuel consumption) prediction from field measurement of Fine Fuel Moisture Content.

Pinto P, Silva ÁP, Viegas DX, Almeida M, Raposo J, Ribeiro LM (2022) Influence of convectively driven flows in the course of a large fire in Portugal: the case of Pedrógão Grande. Atmosphere 13, 414.
| Crossref | Google Scholar |

Raposo J, Viegas DX, Xie X, Almeida M, Naian L (2014) Analysis of the jump fire produced by the interaction of two oblique fire fronts: comparison between laboratory and field cases. In ‘Advances in forest fire research’. (Ed. DX Viegas) pp. 88–94. (Imprensa da Universidade de Coimbra) 10.14195/978-989-26-0884-6_8

Raposo JR, Cabiddu S, Viegas DX, Salis M, Sharples J (2015) Experimental analysis of fire spread across a two-dimensional ridge under wind conditions. International Journal of Wildland Fire 24, 1008-1022.
| Crossref | Google Scholar |

Raposo JR, Viegas DX, Xie X, Almeida M, Figueiredo AR, Porto L, Sharples J (2018) Analysis of the physical processes associated with junction fires at laboratory and field scales. International Journal of Wildland Fire 27, 52-68.
| Crossref | Google Scholar |

Ribeiro C, Reis L, Raposo J, Rodrigues A, Viegas DX, Sharples J (2022) Interaction between two parallel fire fronts under different wind conditions. International Journal of Wildland Fire 31, 492-506.
| Crossref | Google Scholar |

Ribeiro C, Xavier Viegas D, Raposo J, Reis L, Sharples J (2023) Slope effect on junction fire with two non-symmetric fire fronts. International Journal of Wildland Fire 32, 328-335.
| Crossref | Google Scholar |

Rodrigues A, Ribeiro C, Raposo J, Viegas DX, André J (2019) Effect of canyons on a fire propagating laterally over slopes. Frontiers in Mechanical Engineering 5, 41.
| Crossref | Google Scholar |

Rossa CG, Fernandes PM (2018) An empirical model for the effect of wind on fire spread rate. Fire 1, 31.
| Crossref | Google Scholar |

Rossa CG, Davim DA, Viegas DX (2015) Behaviour of slope and wind backing fires. International Journal of Wildland Fire 24, 1085-1097.
| Crossref | Google Scholar |

Rothermel RC (1972) A mathematical model for predicting fire spread in wildland fuels. USDA Forest Service, Intermountain Forest and Range Experiment Station, Research Paper INT-RP-115. (Ogden, UT)

San-Miguel-Ayanz J, Oom D, Artès T, Viegas DX, Fernandes P, Faivre N, Freire S, Moore P, Rego F, Castellnou M (2021) Forest fires in Portugal in 2017. Science for Disaster Risk Management 2020: Acting Today, Protecting Tomorrow. (EUR 30183 EN, Publications Office of the European Union, Luxembourg)

Scott JH (2012) Introduction to Wildfire Behavior Modeling. National Interagency Fuels, Fire, & Vegetation Technology Transfer. Available at www.niftt.gov

Scott JH, Burgan RE (2005) Standard fire behavior fuel models: a comprehensive set for use with Rothermel’s surface fire spread model. Gen. Tech. Rep. RMRS‐GTR‐153. Fort Collins, CO: U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station.

Sharples JJ, McRae RHD, Weber RO (2010) Wind characteristics over complex terrain with implications for bushfire risk management. Environmental Modelling & Software 25, 1099-1120.
| Crossref | Google Scholar |

Sullivan AL (2009) Wildland surface fire spread modelling, 1990–2007. 3: Simulation and mathematical analogue models. International Journal of Wildland Fire 18, 387-403.
| Crossref | Google Scholar |

Viegas DX (2004) On the existence of a steady-state regime for slope and wind driven fires. International Journal of Wildland Fire 13, 101-117.
| Crossref | Google Scholar |

Viegas DX (2006) Parametric study of an eruptive fire behaviour model. International Journal of Wildland Fire 15, 169-177.
| Crossref | Google Scholar |

Viegas DX, Pita LP (2004) Fire spread in canyons. International Journal of Wildland Fire 13, 253-274.
| Crossref | Google Scholar |

Viegas DX, Raposo JR, Davim DA, Rossa CG (2012) Study of the jump fire produced by the interaction of two oblique fire fronts. Part 1. Analytical mViegasodel and validation with no-slope laboratory experiments. International Journal of Wildland Fire 21, 843-856.
| Crossref | Google Scholar |

Viegas DX, Almeida M, Ribeiro L, Raposo J, Viegas MT, Oliveira R, Alves D, Pinto C, Humberto J, Rodrigues A, Lucas D, Lopes S, Silva L (2017) O complexo de incêndios de Pedrógão Grande e concelhos limítrofes, iniciado a 17 de junho de 2017. (Coimbra, Portugal) [In Portuguese]

Viegas DXFC, Raposo JRN, Ribeiro CFM, Reis LCD, Abouali A, Viegas CXP (2021) On the non-monotonic behaviour of fire spread. International Journal of Wildland Fire 30, 702-719.
| Crossref | Google Scholar |

Viegas DXFC, Raposo JRN, Ribeiro CFM, Reis L, Abouali A, Ribeiro LM, Viegas CXP (2022) On the intermittent nature of forest fire spread – Part 2. International Journal of Wildland Fire 31, 967-981.
| Crossref | Google Scholar |

Xie X, Liu N, Viegas DX, Raposo JR (2014) Experimental research on upslope fire and jump fire. Fire Safety Science 11, 1430-1442.
| Crossref | Google Scholar |