Parametric evaluation of heat transfer mechanisms in a WUI fire scenario
Cesare Fiorini A , Hélder D. Craveiro A * , Aldina Santiago A , Luís Laím A and Luís Simões da Silva AA University of Coimbra,Institute for Sustainability and Innovationin Structural Engineering (ISISE), Advanced Production and Intelligent Systems ‐ Associated laboratory (ARISE), Department of Civil Engineering, Coimbra, Portugal.
Abstract
Wildland–urban interface (WUI) fires are becoming more frequent and catastrophic as they are associated with the effects of climate change, demographic pressure, human activities, abandonment of rural areas and activities promoting dangerous fuel continuity. For example, in the central regions of Portugal, Chile and California, severe direct and indirect impacts have been observed, with a catastrophic number of fatalities.
Mitigating and reducing the impacts of wildfires in the WUI requires understanding heat transfer mechanisms from forest fires and understanding how structures ignite is crucial to define and implement new mitigation strategies.
Adopting Computational Fluid Dynamics is essential to assess the WUI fire problem by simulating fire behaviour and quantifying its characteristics. In this paper, a building is exposed to several wildfire scenarios, assessing the influence of parameters such as materials, fuels, topography and meteorological conditions.
The investigated scenarios were developed considering validated Fire Dynamics Simulator (FDS) models of single trees on fire and the influence of governing parameters was quantified.
For the selected scenarios, the impacts on the building were assessed and compared, quantifying heat release rates, radiative heat flux and adiabatic surface temperature.
This research contributes to a Performance-Based Design (PBD) approach for buildings in the WUI.
Keywords: adiabatic surface temperature, built environment, convection, Fire Dynamics Simulator (FDS), heat transfer, incident heat flux, performance-based approach, physics-based model, radiation, wildland–urban interface (WUI).
Introduction
Fires have been a persistent problem over recent decades, burning millions of hectares around the world, according to Quarles and Standohar-Alfano (2018), and becoming increasingly frequent, as confirmed by Bento-Gonçalves and Vieira (2020). Climate change (Barbero et al. 2015), the abandonment of forests and rural areas (Mantero et al. 2020), increasing fuel continuity (Knorr et al. 2016) and human activities (Krawchuk et al. 2009) are among the main causes for the increase in the occurrence and intensity of fires. As a result, catastrophic consequences for human society and the environment are being observed, as stated by Syphard et al. (2017) and Bento-Gonçalves and Vieira (2020). Different kinds of fires can be classified in relation to location and conditions, such as forest fire, rural fire, urban fire, bushfire, shrub fire, wildfire, large outside fire and wildland–urban interface (WUI) fire (Manzello et al. 2018). The present paper is focused on the WUI, which refers to the area where structures meet or intermingle with wildland and vegetative fuels and where a wildland fire can potentially ignite buildings (Bento-Gonçalves and Vieira 2020). The high risk associated with this kind of problem is the uncontrolled spread of fires due to fuel continuity, as described by Moinuddin and Sutherland (2017). As an example of fires in the WUI, Manzello et al. (2018) mention several burned areas in the Mediterranean countries of Portugal, Spain, Italy, France and Greece. Specifically, in Portugal, at least three megafires can be cited (Oliveira et al. 2018; Bento-Gonçalves and Vieira 2020). In 2016, the island of Madeira was affected by a big fire. As a consequence, 177 houses were destroyed and three people died (Couto et al. 2021; Ribeiro et al. 2021). Further, the estimated damage was approximately €61 million (Couto et al. 2021). One year later, another two catastrophic fires occurred in Portugal: the Pedrogão Grande fire in June 2017 and the megafire in October 2017. Regarding the Pedrogão Grande fire, in total 66 people were killed and 253 were injured, more than 458 homes were destroyed and 49 businesses were directly affected by the fire, as stated by Ribeiro et al. (2020). Concerning the October 2017 megafire that occurred in the central region of Portugal, 521 industrial buildings were partially damaged or destroyed (Guerreiro et al. 2018), 47 people were killed and 2100 km2 burned (Viegas et al. 2017; Oliveira et al. 2018). Another tragic incident is the Valparaiso fires in Chile. According to Manzello et al. (2018), Valparaiso has been affected by wildfires at least five times between 2013 and 2017, with 15 people killed, 533 injured and 3000 homes destroyed (Reszka and Fuentes 2015). It is notable that the Valparaiso fires had an economic impact of more than €100 million (Manzello et al. 2018). Unfortunately, more examples exist and can be found in the literature such as in Ryan and Opperman (2013), Molina-Terrén et al. (2019) and Finney (2021).
Fernandez et al. (2018) highlighted that the essence of the problem is not wildland fire control, but rather house ignitability (vulnerability of a structure to ignition mechanisms). Fires can start owing to exposure to heat flow from flames or firebrands generated by a forest fire (Sandström 2013); however, as stated by Potter and Leonard (2011), 90% of building ignitions are due to firebrand exposure events. Fire in the WUI still requires extensive research, especially concerning the different heat transfer mechanisms and the ignition potential of buildings located in the vicinity of forest areas.
According to Vacca et al. (2020), the complexity of the WUI fire problem is due to the interaction of multiple phenomena of different causes occurring at different scales, namely the macroscale, mesoscale and microscale. Focusing on the microscale, three main fire sources can be identified: the wildfire front, burning natural fuels (e.g. grassland, shrubland, forest stand, logging slash) and burning non-natural fuels (for example, as defined in Instructor Guide NWCG S-190 (2019), artificial materials like houses, sheds, fences, pipelines and trash piles). Based on the species of fuels and their level of maintenance (i.e. trimming, pruning and watering), wildfires vary greatly and manifest a specific intensity (vegetation burning) throughout the flaming phase (Vacca et al. 2020). At the microscale level, the ‘home ignition zone’ (HIZ), first conceived by Cohen (2000), can be defined as a place where preventive actions are necessary, like regular cleaning of the outside area (defensible space), avoiding accumulation of fuels, and maintaining a distance between the vegetation and the building, as described by Vacca et al. (2020).
Another important relationship to be considered in the analysis of the WUI fire problem is between the meteorology (such as temperature, humidity and wind) and the fire growth mechanisms involved. Wind can impact firebrands, radiant heat flux and flame contact. Also, topography (elevation and slope) and vegetation (type of cover, fire load, moisture content, height and species) influence fire behaviour (Cohen and Saveland 1997). Viegas (2004) investigated the effects of upslope and favourable wind with different velocities on fire spread and found that the rate of spread increases with higher wind velocity. Linn et al. (2010) confirmed the acceleration of fire when it spreads upslope through several simulations of slope and fuel structure effects on coupled wildfire behaviour. Regarding measurements of convective and radiative heating in wildfires, Frankman et al. (2013) stated that crown fires reached higher radiative values compared with surface fires. Drissi (2014) investigated the influence of different parameters (wind and moisture content, among others) on the rate of spread of fire, showing that the key parameters are wind velocity and fuel load. Countryman (1976) explained that moisture content affects the pyrolysis process and consequently ignition, confirming that the burning rate of wildland fuel slows when moisture content increases. Tihay et al. (2014) calculated the following parameters for the combustion of forest litter under slope conditions: burning rate, heat release rate, convective and radiant fractions for various loads. As a result, they demonstrated that with increasing slope, the heat release rate (HRR) increases and that the contribution of convective heat release decreases with increasing slope, whereas radiation increases with increasing fuel load. Kim et al. (2016) focus on tree crown spacing and slope interaction effects, demonstrating how increasing tree spacing and reducing the slope decreases HRR and increases the time to reach peak HRR. Safdari (2018), with particular attention to different heat transfer mechanisms, states that it is still not clear whether convective or radiant heat transfer is predominant during wildfires and that a combined radiation and convection mode is more relevant. Castillo Soto et al. (2022) focus their study on safety distances in the case of real fires in Chile and Spain (calculating the corresponding radiative heat flux). As a result, the need for a gradual reduction in fuel load to mitigate radiant heat transfer is stated. Abu-Zidan et al. (2022) contributed with observations on the effect of wind velocity and direction on façade fire spread in an isolated rectangular building. One of the main findings of the wind–fire interaction was that the façade fire spread was heavily influenced by the near-wall flow fields generated by the building geometry. Also, the presence of external wind influenced the temperature and HRR of façade fires.
Performance-based design (PBD) must be used in the field of fire safety engineering to improve the development of design specifications for buildings in the vicinity of forest areas, understanding the conditions promoting ignitions in the built environment and the behaviour of buildings exposed to this extreme external action.
The use of computational fluid dynamics (CFD) tools, such as those described by Papalou and Baros (2019), allows modelling different fire scenarios at the microscale level, assessing and quantifying HRRs and temperatures, for instance. According to Mell et al. (2009), Fire Dynamics Simulator (FDS) (McGrattan et al. 2021) is a well-validated tool for modelling compartment fires and burning vegetation and has been used to model WUI fire scenarios by several authors, including Ghaderi et al. (2021), Suzuki and Manzello (2021) and Vanella et al. (2021). However, further validation and developments of the numerical models are needed, especially concerning the generation of firebrands and their interaction with structures (different levels of vulnerability of structures may lead to new secondary fires).
In this work, the main objective is to identify and quantify the basic heat transfer mechanisms occurring from fire to buildings (impact on the structure), assessing the influence and importance of parameters such as topography, meteorology, materials and fuels. Thermal quantities such as HRR, radiative heat fluxes, gas temperatures and adiabatic surface temperature (AST) are measured. Beshir et al. (2021) outlined the importance of the assessment of AST, which is commonly used to investigate the behaviour of structures subjected to thermal stresses. The AST can be defined as the temperature of a surface that cannot absorb or lose heat to the environment. The use of this concept is very convenient because it describes with a single quantity the thermal exposure of a solid surface. This parameter is provided automatically by FDS. AST is used as an input parameter for a structural model assessed with finite element method (FEM) software (Wickstrom et al. 2007). As a result, by coupling the thermal and structural analyses (using CFD and FEM), extreme wildfire action in the WUI is more thoroughly investigated. This type of research improves the PBD approach for buildings near forests, contributing to a better understanding of the heat transfer phenomena involved and their impact on the built environment. Note that severe limitations still exist in the current modelling tools, namely when discussing ignitions due to firebrands, and new and additional developments are still needed in this field.
Methodology
The FDS is widely used to simulate and reproduce fire scenarios, especially compartment fires, and in recent years, its field of applicability has been extended to wildfires in the WUI. FDS is suitable for modelling microscale wildfire scenarios in the vicinity of buildings. This CFD software numerically solves a form of the Navier–Stokes equations appropriate for low-speed, thermally driven fluid, focusing on smoke and heat transport from fires (McGrattan et al. 2022). Fluid dynamics is solved using three governing equations referring to the conservation of mass, momentum and energy (McGrattan et al. 2022). The FDS algorithm was created with a focus on low Mach number approximation. This means that gas moves at a low speed due to chemical heat release and buoyancy forces. Consequently, pressure behaviour, internal energy and enthalpy are influenced by this approach. Regarding the simulation mode, FDS uses a very large eddy simulation (VLES) model with a Cartesian three-dimensional grid. Specifically, a staggered grid is used to represent scalar quantities and vector components (McGrattan et al. 2022).
Among different models for representing wildland fire spread, FDS provides the Lagrangian particle model (LPM). In LPM, the vegetation (surface and raised) is assumed to be a collection of Lagrangian particles that are heated via radiation and convection, as explained by Vanella et al. (2021). One advantage of Lagrangian particles is that they overcome the geometry constraints imposed by the numerical grid. Grass, trees, firebrands, etc. are normally modelled using Lagrangian particles, as found in Wadhwani et al. (2017). Cheney et al. (1998) showed the validation process, where the mathematical model prediction was compared with an experimental assessment (short and tall burning grass). The experimental work performed by Mell et al. (2009) presented in detail the behaviour of a single Douglas fir tree on fire with different heights of 2 and 5 m and moisture content of 14 and 49%, respectively. Using such experimental results, numerical models were first developed and calibrated. The numerical model for representing grass and trees was based on the LPM using cylindrical particles and a linear thermal degradation sub-model to simulate a tree burning, as implemented in Wildland Fire Dynamics Simulator (WFDS). In FDS, the pyrolysis model, and consequently the chemical kinetics involved, can be considered infinitely fast or obey an Arrhenius rate law (McGrattan et al. 2022). The Arrhenius rate law defines a finite-rate reaction where the temperature-dependent reactions are characterised and based on the activation energy and Boltzmann distribution (Batiot et al. 2021). In the present study, the FDS was run applying the Arrhenius rate law to the trees and the grass (McGrattan et al. 2022).
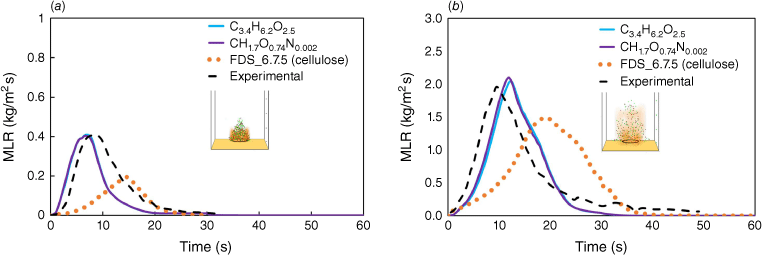
Before proceeding with the study of the numerical case, the pyrolysis model was calibrated based on the mass loss rate (MLR) results, which reproduced the thermo-physical fuel properties of the experimental tests described by Mell et al. (2009) using FDS 6.7.7 (McGrattan et al. 2021). Following a similar approach to the one used by Moinuddin and Sutherland (2019), physics-based simulations were performed, unlike what was implemented by Hostikka et al. (2008), where HRR values per ground area were used for crown and surface fires. The experiments aimed to assess the behaviour of Douglas fir trees in fire considering different heights, ranging from 2 to 5 m, and moisture content, ranging from 14 to 49%. In Table 1, the physical and thermal properties used in the calibration model are summarised, and in Fig. 1, a comparison between experimental and numerical results in terms of MLR is plotted. Fig. 1 shows four different curves, namely an experimental curve (solid black line) and three FDS numerical curves. The fuel chemical compositions of the three curves are: C3.4H6.2O2.5 (Hostikka and McGrattan 2001), CH1.7O0.74N0.002 (McGrattan et al. 2021) and C6H10O5 (i.e. cellulose) as found in Browne (1958). The heat of combustion was 14 516 kJ/kg (Vacca and Àgueda 2020). In Fig. 1a, for the case of a tree of 2-m height and moisture content (MC) of 14%, the peak MLR values are 2.03 and 1.97 kg/m2 s, respectively, for C3.4H6.2O2.5 (cyan line) and the experimental curve (black dashed line). This means a peak-to-peak MLR difference of 3%. In addition, for a tree of 5-m height and MC of 26% (see Fig. 1b), the peak-to-peak MLR difference is 2%, with the peak MLR values of 0.409 and 0.418 expressed in kilograms per square metre per second (kg/m2 s) for C3.4H6.2O2.5 and the experimental curve. Hence, the chemical composition C3.4H6.2O2.5 was adopted in the parametric studies. The ignition was done through a burner with a heat release rate per unit area (HRRPUA) of 1500 kW/m2.
| Quantity | Value | Quantity | Value | |
|---|---|---|---|---|
| HRRPUA ignitor (kW/m2) | 1500 | Heat of combustion (kJ/kg) | 14 516F | |
| Duration of ramp fire (s) | 13 | Soot yield (kg/kg) | 0.02 | |
| Wood/wood/cellulose | CH1.7O0.74N0.002/C3.4H6.2O2.5/C6H10O5 | Initial temperature (°C) | 28 | |
| Time (s) | 120 | Heat of reaction (kJ/kg) | 416 | |
| Grid size cell (cm) | 10–25 | Specific heat capacityB (kJ/kg K) | 2.0|1.5|4.184 | |
| Fuel geometry tree | Cone | Thermal conductivityA (W/m K) | 0.1A | |
| Crown width (radius) (m) | 1.45 | DensityB (kg/m3) | 1000|100|1300 | |
| Crown base height (m) | 0 | Reference temperature (°C) | 300C, 100D | |
| Tree height (m) | 5 | Vegetation density (kg/m3) | 514 | |
| Shape | Cylindrical | Moisture vegetation (%) | 14 | |
| N_PARTICLES_PER_CELL | 1 | Drag coefficient | 2.8 | |
| PACKING_RATIO (s, m, l)E | 68, 48, 44 |
AMoisture, vegetation and char.
BMoisture, charred vegetation and dirt.
CGrass vegetation.
DMoisture.
Es, m, l, small, medium, large.
Mass loss rate (MLR): (a) height 2 m, MC 14%; (b) height 5 m, MC 26% (McGrattan et al. 2022).
Referring to grid size, two mesh sizes were tested: 25 and 10 cm; 10 cm was the same computational grid used by Mell et al. (2009).
Case study
Scenario description
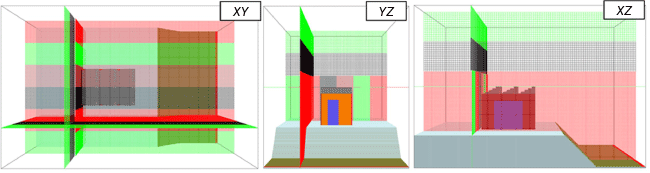
In Fig. 2, an industrial warehouse set in a WUI scenario is depicted. The warehouse is representative of a real building. Owing to the high computational resources needed, the building is slightly smaller than a real industrial building but still representative. The warehouse has a rectangular base of 15 × 10 m2 (x and y directions) and a height of 12 m (z direction). The structure has a sawtooth roof and three descending planes in the western direction. Two doors (3.5 × 8 m2) are located on the eastern and western sides. Two square gates (8 × 8 m2) are placed on the northern and southern wall perimeters. The panel walls thickness is 25 cm. The doors and gates have 15 mm thick glass surfaces (see black surfaces in Fig. 2). The warehouse is located on higher ground (west side), where there is no vegetation. The flat ground has an extent of 37 × 36 m2. The ground is covered in grass and measures 20 × 36 m2 (top view). Considering the base scenario depicted, several parameters influencing fire behaviour were varied to quantify the impact of different fire scenarios in WUI fire exposure of the building.
Schematic representation of the base scenario investigated (1) Position coordinates for measurement of devices (DVC) type, (2) Fire load, (3) Wind, (4) Slope with inclination of angle α, (5) Distance (δ) from the façade and (6) Building materials.
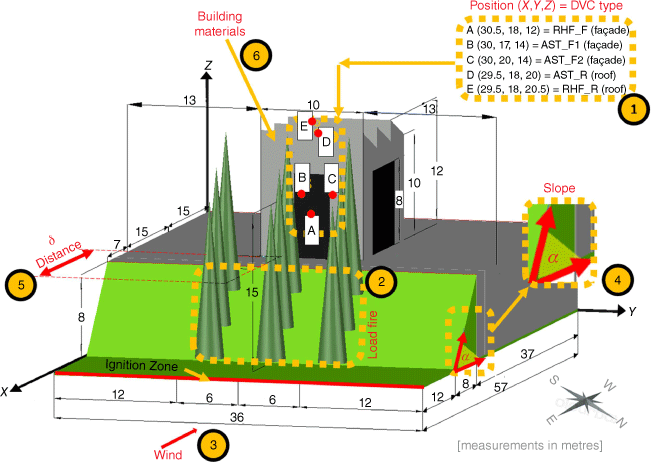
The trees have a conical shape, with a base radius of 1.45 m and a height of 15 m. These sizes represent the average height for a eucalyptus tree at 10 years of age, as found in Tomé et al. (2001). The distances between trees are 3 and 6 m in the x and y directions, respectively.
Relative to wind and assuming a neutral stratification of the atmosphere (upstream wind field), Porterie et al. (2007) and Vanella et al. (2021) describe, based on Monin–Obukhov, the attributes of airflow properties (i.e. height, surface roughness, turbulent friction, etc.).
The thermal devices are positioned on the eastern façade, as depicted in Fig. 2. Three AST devices are located on the concrete wall (point C), on the glass (point B) and the roof top (point D). Radiative heat flux gas sensors are placed in front of the eastern façade (Point A), as well as on the roof top (Point E). Slices of thermal parameters (temperature, radiation loss, velocity) are placed in planes X (30.5 and 36 m), Y (18 m) and Z (18.5 and 20 m).
Regarding the material description, in this investigation, the house materials considered were non-combustible, namely concrete and glass, but other structural materials (for instance, steel and timber) will be considered in the future. All thermophysical properties used in the numerical models are listed in Table 2.
Numerical simulation
The FDS 6.7.7 release was used to conduct the numerical simulations. The computational domain is X = 57 m, Y = 36 m, Z = 40 m. The domain is divided into eight meshes (see Fig. 3), six meshes with a cubic cell of 25 cm for a range of Z = 0–24 m, and two meshes with (50 cm)3 for a range Z = 24–40 m. A total of 3 414 528 cells are generated. The domain boundary is open in the E–W direction and at the top, namely in (Xmin = 0, Xmax = 57) and (Zmax = 40), while it is periodic (i.e. it repeats itself indefinitely) in the N–S direction (Ymin = 0, Ymax = 36). The dimension of the grid size cell chosen (equal to 25 cm) is in agreement with Moinuddin et al. (2018) and Khan et al. (2019) for simulating similar computational domains and purposes. Specifically, Moinuddin et al. (2018), in their investigation, developed a grid sensitivity analysis.
The wood chemical composition formula used is C3.4H6.2O2.5 (Hostikka and McGrattan 2001). Heat combustion, moisture fraction and drag coefficient have been defined in Table 1. Ignition starts on the eastern bound, occupying 75 cm (see Fig. 2). The ignition is started by the burner, with an HRR per unit area (HRRPUA) of 1500 kW/m2. To simulate the ignition process, a time ramp lasting 13 s at the beginning of the simulation is applied to the ignition process. The time of the simulation is 120 s (2 min). The goal is to use a physics-based model capable of accurately assessing and quantifying heat transfer phenomena as a function of the number of trees (fire load, FL), wind direction (WD), wind velocity (WV), slope (topography, S), distance between the façade and the trees (DIST) and finally the moisture content of the vegetation (MC).
Design of experiments with several factors
In the present study, the independent effects of a group of factors as well as their combined effects are studied through CFD fire simulations, assessing in detail the magnitude of all heat transfer mechanisms and impacts on the built environment. To do this, two-factorial design approaches are applied: an analysis based on the change of factors one at a time (OFAT) and a full factorial design (FFD). In total, 35 numerical simulations were performed: 19 for the OFAT and 16 for the FFD (see Supplementary material S1a, b, respectively).
A parameter sweep is applied by changing one factor at a time (OFAT). As shown in Table 3, the OFAT is implemented with four levels for six factors. The factors used for assessing wildfire behaviour are: fire load (FL), slope (SL), wind velocity (WV), wind direction (WD), distance (DIST) and moisture content (MC). These parameters are used for measuring time variations of quantities and their peak values, such as HRR, AST and radiative heat flux (RHF). In terms of fire load, the space between trees was kept constant at 3 m, as in the numerical experiment of Kim et al. (2016). Only the number of trees was changed. The variation in the angle of the wind direction was selected to study the wind effect specifically on the closest façade to the trees. The chosen wind velocity interval was based on data extracted from a real field test involving a crown fire type, as reported by Morvan and Frangieh (2018) and as found for Portuguese conditions in Trigo et al. (2006). Upslope topography was chosen for analysis because the combined wind effects are significant. In this way, flat terrain was excluded. Pimont et al. (2012) studied the influence of slope by varying it from 0 to 100%. In the present investigation, a smaller range of slopes (from 16° to 46°, i.e. from 30% to ~100%) was considered. Recently, Castillo Soto et al. (2022) investigated values for safety distance (defined as the distance from the edge of the vegetation to a building). The distances used in our analysis belong in Priority Zone one (0–10 m) and Priority Zone two (10–20 m) as defined in Partners in Protection (2003). Finally, MC variation was based on the experiment described by Mell et al. (2009) and by Ribeiro et al. (2021).
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
|---|---|---|---|---|---|---|---|
| Level | Fire load (FL) | Wind direction (WD) | Wind velocity (WV) | Slope (α) (SL) | Distance (δ) (DIST)B | Moisture content (MC) | |
| (–) | (no. trees) | (°) | (m/s) | (°) | (m) | (%) | |
| LV1 | 6 | 67.5 | 4.15 | 16 | (9) | 13 | |
| LV2 | (9) | (90) | (5) | 30 | 12 | (26) | |
| LV3 | 12 | 112.5 | 5.85 | 38 | 15 | 39 | |
| LV4 | 15 | 135 | 6.70 | (46) | 18 | 52 |
AValues in parentheses are considered as benchmark values.
BThe distance between the eastern façade and the closest tree row is measured in the x direction.
To further understand the interactions between the different governing factors, a second set of numerical simulations was performed, and the results were investigated considering an FFD. Other authors, like Drissi (2014) and Bearinger et al. (2021), used an FFD as well. The ability to evaluate the main effects and their interactions is one of the benefits of a full-factorial analysis. In this paper, the FFD is based on four factors expected to influence the heat transfer mechanisms. The factors involved are defined at two levels (high and low). A complete list of the factors involved in the 16 cases is provided in Supplementary material S1b. In Table 4, the four factors (FL, SL, WV and MC) are designated in the first column with the letters A, B, C and D, respectively. Wind direction and distance were not changed, considering that the perpendicular direction (90°) and the closest distance (9 m) represent two of the main factors in the baseline scenario.
Results
Varying single factors
In this section, the FDS results are discussed when a single factor is modified at a time with particular attention to peak HRR values and peak AST values.
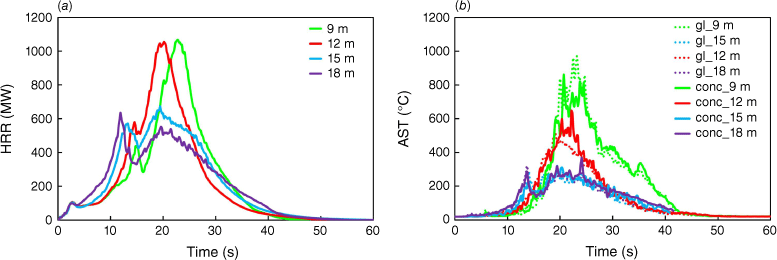
To investigate the influence of fire load, given by the increasing number of trees, the base scenario was fixed; i.e. considering a slope of 46°, wind direction of 90°, velocity of 5 m/s, distance from the building to the trees of 9 m and MC of 26%. The graphical representation of the scenarios investigated is depicted in Supplementary material S2. In Fig. 4a, b the main results in terms of HRR (in MW) and AST (in °C) are depicted. For HRR, as expected, the higher the number of trees, the higher the HRR (owing to the increase in fuel quantity). The first period (between 0 and 13 s) corresponds to the ignition phase. The second phase (13–20 s) is characterised by the increase of HRR. Maximum values are 1985, 1564, 1016 and 563 MW for 15, 12, 9 and 6 trees, respectively. Similar results were reported by Wickramasinghe et al. (2022) for different wildfire scenarios but using similar modelling strategies. The four peak HRR values happened within 5 s (between 20 and 25 s). Additional figures are provided for different simulation times in Supplementary material S3, such as the instant when the maximum value of HRR was attained and the corresponding slice temperature visualisation. MLR graphics and roof AST plots are depicted in Supplementary material S4a, b, respectively.
Evolution of HRR and AST as a function of time for different fire loads: (a) HRR; (b) AST for glass (gl; dashed lines) and concrete (conc; solid lines) surfaces.
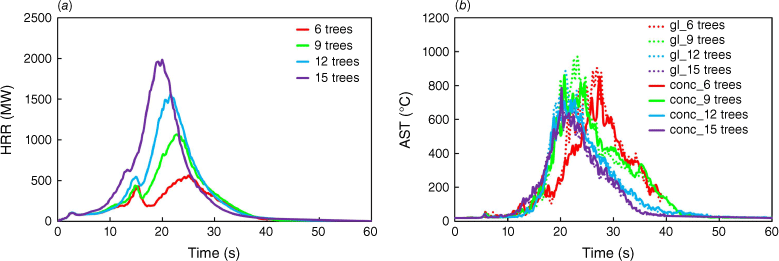
Considering the monitoring devices located in the building, it was possible to assess the evolution of the AST (points C and B in Fig. 2) as a function of time for the different scenarios. The results obtained for the devices located on the glass (dashed lines) and concrete walls (solid lines) are presented in Fig. 4b, whereas for the devices located on the roof, the results are presented in Supplementary material S4b. From the graphs shown in Fig. 4b, the difference in terms of AST evolution is clear in the interval ranging from 21 to 28 s, where the difference between the scenario with 15 and 6 trees reached the maximum value of approximately 330°C. This difference is due to the fact that with the smaller number of trees, there is a delay in the increase of the heat release rate per unit volume (HRRPUV) because there is a larger distance between the fire origin and the first row of trees. It is worth noting that (see Supplementary material S3), in the scenario with six trees, flame deflection is less pronounced and the flame height smaller, hence impacting the façade of the building directly. This explains why the ASTs measured are some of the highest for the scenario with only six trees.
For the roof (see point E in Fig. 2), it was observed that increasing the number of trees led to higher ASTs during a longer period (see Supplementary material S4b). The maximum AST values recorded in the simulations were 622, 580, 516 and 616°C, respectively, for the scenarios with 6, 9, 12 and 15 trees.
Additionally, two thermocouple (TP) devices were placed to monitor the gas temperature of the two burning trees closest to the building and aligned with the x-direction (in the plane Y = 18 m). TP1 (see Supplementary material S5) refers to the burning tree 9 mand TP2 to the tree 12 m away from the building at a height of 9 m. The temperatures recorded by the thermocouple devices are presented in Supplementary material S5. Looking at the graph (see Supplementary material S5), the curves for TP2 increase faster than the curves for TP1. This is justified by position as TP2 is closer to the ignition zone. Also, the temperature reached by the solid lines (TP2) is always higher than that of solid lines (TP1). This means that combustion of the second tree is more complete. The solid red line (for six trees) shows that the flame did not reach the height of 9 m above ground level. Excluding the case of six trees, the average peak-to-peak difference in the cases of 9 and 15 trees is ~200°C for TP1 and TP2.
To investigate the influence of wind velocity, the same base scenario is considered, assuming the existence of nine trees, a slope of 46°, wind direction of 90°, distance from the building to the trees of 9 m and a moisture content of 26%. Fig. 5 is an example of the outputs obtained with FDS for a wind velocity of 4.15 m/s. In detail, three HRRPUV frames are presented, respectively, from the top, frontal and lateral views.
Example of multiple views detailing the fire spread in the simulated scenario considering a wind velocity of 4.15 m/s.

The evolution of HRR (MW) and AST (°C) as a function of time and for different wind velocities is presented in Fig. 6a, b. In detail, the simulated wind velocities are: 4.15, 5.00, 5.85 and 6.70 m/s (i.e. 15, 18, 21, and 24 km/h). The highest values are obtained when the wind velocity is the lowest, at 4.15 m/s (purple line). As found in Wang and Chateil (2007), the pyrolysis and flame height (and consequently combustion) are related to the wind velocity, showing how with increasing wind velocity, pyrolysis decreases. Also, Abu-Zidan et al. (2022) confirmed that the presence of wind causes a reduction in the intensity of a façade fire and that with higher wind velocities, greater reductions are caused in HRR and AST owing to the presence of a high-pressure stagnation region in front of the building. The peak HRR value in the present study is 1170 MW (at 23.4 s). Increasing the wind velocity from 4.15 to 6.7 m/s leads to a reduction in the HRR of approximately 307 MW.
Evolution of HRR and AST as a function of time for different wind velocities: (a) HRR; (b) AST for glass (gl) and concrete (conc) surfaces.
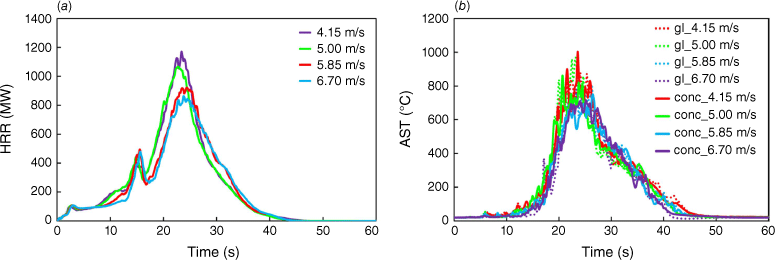
As previously mentioned, the varying parameters are considered to assess in detail the AST on the façade (see Fig. 6a). Supplementary material S6a, b depicts the plots of MLR and the roof AST. For the façades, the highest ASTs were obtained for the lower wind velocity, whereas in the roof, the highest AST was obtained for the higher wind velocity. This behaviour is governed by the wind velocity causing flame deflection. On the façade in front of trees, there is a major presence of flames (involving the building from the ground to the roof) when the wind velocity is lower (4.15 m/s). For the highest velocity (6.70 m/s), the flames are more inclined toward the façade (as highlighted by the red circle and the blue arrow drawn in the Supplementary material S7, when the wind is blowing at 6.70 m/s, the first section of the roof is almost completely covered by flames). These observations are further supported by the slice temperature visualisation depicted in Supplementary material S8. The pictures presented in Supplementary material S8a–d correspond to the instant when the highest AST was attained, whereas the ones presented in Supplementary material S8e–l correspond to the instant when the highest HRR was recorded.
The gas temperature was also monitored; results are plotted in Supplementary material S9. The highest peak TP value reached is 1375°C (blue solid curve). This curve shows a rapid decrease phase, meaning that with the highest wind velocity (6.70 m/s), the entire combustion process is completed more quickly compared with lower wind velocity. The other curves present a longer period of stable temperature (almost 10 s).
Fig. 7a, b depicts HRR and AST evolution with wind directions ranging from 67.5° to 135°. In the HRR plot, the green curve for a wind direction of 90° has the highest value of 1016 MW at 24.3 s. The second highest value (blue line) was ~20% less than the first, i.e. 802 MW (at 25 s). Similar behaviour was observed for wind directions 67.5°, 112.5° and 135°. In Supplementary material S10a, b, the plots of MLR and the roof AST are depicted. The combination of trees aligned with wind direction and the presence of a block representing the structure after the group of trees may explain why the peak HRR is higher with the wind blowing at 90°. It is possible to infer that alignment causes the unburned trees to be completely covered by flames. Furthermore, the structure’s presence as an obstacle allows the heat to remain in the region longer, increasing the HRR. Abu-Zidan et al. (2022) reported a similar conclusion, describing this condition as a high-pressure stagnation region in front of the building. The fire plume, however, experiences very strong tilting in the direction of the wind; the specific combined effect of building geometry and wind direction causes it to reach the highest temperature for a 135° wind direction.
Evolution of HRR and AST as a function of time for different wind directions: (a) HRR; (b) AST for glass (gl) and concrete (conc) surfaces.
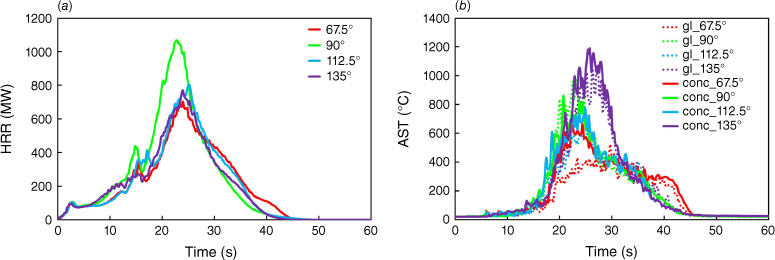
Fig. 7b shows AST graphics for the walls (glass, concrete). For a wind direction of 135°, both curves for glass and concrete (see purple line, solid and dotted) have the highest values: 1064 and 1188°C, respectively, at 27 and 25.7 s, despite the fact it is one of the scenarios with the smallest HRR measured (Fig. 7a). For the façade materials adopted (concrete and glass), the ASTs obtained are relatively similar for the following wind directions, 67.5° and 90°. For these wind directions, the observed maximum ASTs in concrete were 665 and 659°C, respectively. In the roof, (see Supplementary material S7b) the highest AST was observed for the wind direction of 67.5°, where a maximum AST of 649°C was recorded, whereas the lowest maximum AST of 329°C was recorded for the scenario with a wind direction of 112.5°. Considering that a fixed wind velocity of 5 m/s was assumed for all simulations, it is clear that the wind direction plays a role in the way heat transfer mechanisms impact the building. These observations are further supported by the slice temperature visualisation depicted in Supplementary materials S11 and S12. When the wind is blowing in a 135° direction, the temperature recorded on the façade for glass and concrete is higher. This is because the flames impinge on those areas for a longer period, causing an increase in temperature (see red circles in the Supplementary material S13). However, for a 67.5° direction, the flames do not overlap and the façade is not engulfed by flames, while the top roof is covered by flames (see the blue circles in the Supplementary material S13).
Different slopes were considered in this investigation, ranging from 16° to 46°. Fig. 8a, b depicts the evolution of HRR and AST considering different slopes. The peak HRR values (Fig. 8a) consistently increase as the slope increases: 583, 764, 842 and 1016 MW respectively for the 16°, 30°, 38° and 46° slopes. A significant difference (decrease of approximately 43%) was observed between the scenario with the highest (46°) and the lowest (16°) slope. The steeper the slope, the higher the HRR and the AST owing to the pre-heating effect of the burning vegetation. The radiant heat pre-heats the fuel ahead, increasing the intensity and rate of spread, as can be seen in Fig. 8a. The higher the slope, the faster the maximum HRR and AST were attained. In Fig. 8b, maximum glass AST values for all curves (481, 602, 635 and 775°C) are higher than the maximum AST for concrete (472, 597, 630 and 660°C). The monitored AST increased as the slope increased.
Evolution of HRR and AST as a function of time for different slopes: (a) HRR; (b) AST for glass (gl) and concrete (conc) surfaces.

In Supplementary material S14a, b the plots of MLR and the roof AST are shown. Regarding the evolution of AST on the roof, the highest values were obtained for the steepest slopes. The highest value was 656°C for a slope of 38°, whereas the lowest was 437°C for a slope of 16°.
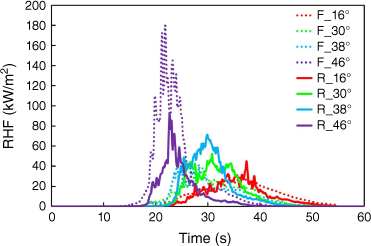
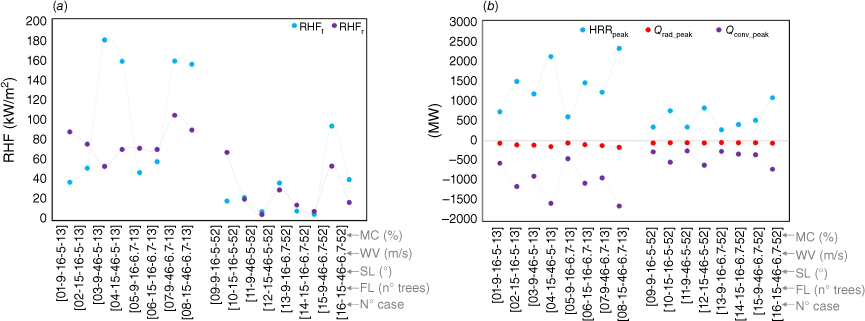
In this assessment, RHF was also monitored in the simulations at points A and E depicted in Fig. 2, located on the façade (F) and the roof (R). The results are depicted in Fig. 9. It is worth mentioning that for all scenarios, the recorded values of RHF show a severe impact on the fire scenarios tested on the building. Concerning the RHF values for the façade, considering different slopes, an average peak RHF value of 74 kW/m2 was obtained. For the roof, the average peak RHF value was 65 kW/m2. For all the selected cases, the measured RHF is high or very high, clearly indicating that for all scenarios, the flames directly impact the building. This also explains the sustained high ASTs recorded and presented for all tested scenarios. The magnitude of the measured RHF is consistent with the scenarios described by Khan et al. (2019).
The effect of the distance between the first row of trees and the façade of the warehouse was also assessed, ranging from 9 to 18 m (see Supplementary material S15). The other parameters were fixed as detailed in Table 3. HRR and AST curves are depicted in Fig. 10a, b. For the smallest distances, 9 and 12 m, the maximum HRR value of 1035 MW was observed respectively at 20.2 and 24.3 s. The average maximum HRR value of 654 MW was observed for the biggest distances, 15 and 18 m, representing a decrease of 37% (i.e. 381 MW) compared with the shortest distances. In Supplementary material S16a, b the plots of MLR and the roof AST are shown. In terms of MLR, some differences can be seen and can be explained by the position of the trees. Note that for some scenarios, all trees are on the slope (distance = 9 m), whereas for other scenarios, some trees are on the slope and others are in the flat part of the terrain (distance of 12 and 15 m) and finally, for the final scenario, all the trees are located in the flat part of the terrain (18 m). Consequently, the HRR is smaller for the scenarios with the biggest distance to the building and with some or all trees on the flat part of the terrain. Both the influence of distance and slope can be observed simultaneously with these simulations. The lack of pre-heating of the vegetation ahead in the simulations with the largest distances to the building (fewer trees on the slope) lead to a smaller HRR.
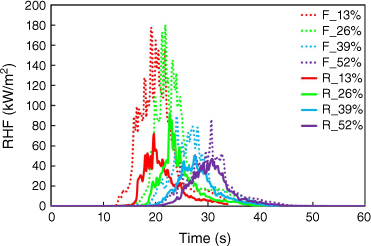
The MC of the vegetation was also varied, considering values ranging from 13 to 52%, as detailed in Table 3, and HRR and AST curves are depicted in Fig. 11a, b. Generally, the lower the MC, the higher the recorded values of HRR. The difference in terms of peak HRR values (1212 and 829 MW) between the scenario with the lowest and highest MC is approximately 32%. The MC influences the quantity of heat released.
Evolution of HRR and AST as a function of time for different moisture contents: (a) HRR; (b) AST for glass (gl) and concrete (conc) surfaces.
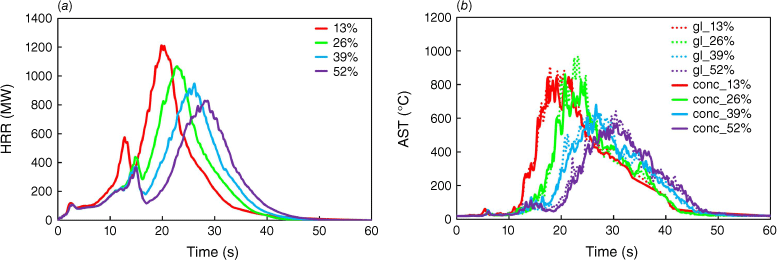
In terms of the recorded AST, a decreasing trend is observed with increasing MC, and the time to reach maximum AST increases with increasing MC. As an example, the peak AST values for the glass are 906, 775, 655 and 644°C at 17.8, 25.7, 25.2, 30.4 s for 13, 26, 39 and 52% MC. The plots of MLR and the roof AST are given in Supplementary material S17a, b.
Concerning the measured RHF (recorded at points A and E of Fig. 2) depicted in Fig. 12 as a function of time and for different values of vegetation MC, it was observed that the lower the MC, the higher the RHF. For an MC of 13%, the maximum RHFs obtained for the façade and roof were 177 and 72 kW/m2, respectively. It is worth noting that for all scenarios, the recorded values of RHF show a severe impact of the fire scenarios tested on the building. Similar observations for different scenarios were reported by Khan et al. (2019).
OFAT study
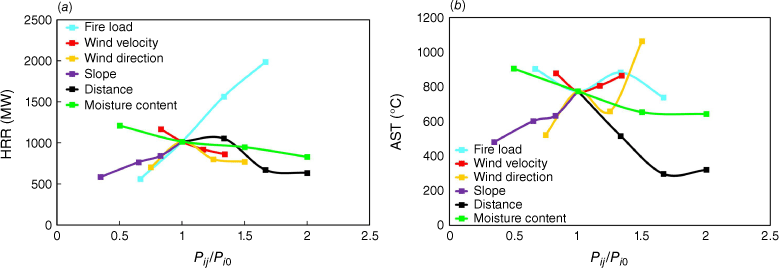
Fig. 13 shows two graphics about HRR and glass AST, represented as mono-factor trends. The x-axis on the graph in Fig. 13 represents a dimensionless parameter, Pij/Pi0. This dimensionless parameter is defined as the ratio between the jth value (from LV1 to LV4 in Table 3) of the selected ith parameter (from column 2 to 7 of Table 3) and its reference parameter value (in parentheses in Table 3). As an example, for the fire load curve (blue line), the four dimensionless values are (6/9; 9/9; 12/9; and 15/9). The denominator (9) represents the reference parameter value for the fire load, and the numerators are the values changed for that parameter (found in the second column of Table 3).
In the peak HRR shown in Fig. 13, fire load (blue line) and slope (cyan line) show growing trends, with FL higher than SL (in detail, the inclination of the straight line is almost double compared with the slope line; this implies that fire load has more influence than slope on the peak HRR values). The trend of increasing peak HRR is influenced by the quantity of fuel available for combustion, as found by Baker (2011). Furthermore, the increasing trend of peak HRR coincides with the increasing trend of the slope parameter. This is explained by preheating caused by flame radiation and hot gas convection, as also stated by Drissi (2014). With regard to wind velocity (red line), distance (black line) and MC (green line), all show a decreasing trend; in particular, the decrease in wind velocity and MC is nearly linear. The increase in wind velocity causes a fluctuating and changing fire plume orientation, with a consequent reduction in peak HRR values, as stated by Abu-Zidan et al. (2022). Regarding the MC effect on peak HRR, the higher the MC, the lower the HRR peaks, as confirmed in previous studies by Babrauskas (2002). For the distance parameter, the number of trees on the slope is changing. For the 9-m distance, there are nine trees on the slope, and for the 18-m distance, all the trees are on the flat terrain.
In Fig. 13, the peak AST values for the glass are rising owing to factors such as increasing slope (cyan line) and wind direction (yellow line). Observing the trends of the following factors – fire load, wind velocity, moisture content and distance – all are diminishing, with a stronger intensity for distance. As shown by the peak AST glass values reached in the experiments carried out by Ni et al. (2012), glass breaks between 600 and 800°C. The failure of the glass parts was not explicitly considered in the present simulations, but it can be stated that such a scenario would most likely lead to a compartment fire in the building. Regarding the peak glass AST trend, the curves for slope, distance and MC present very similar behaviour compared with the same curves plotted for peak HRR values in Fig. 13. For the wind velocity curve, the behaviour initially decreases and then increases. This is driven by the movement and persistence of flames toward the warehouse’s main façade. Regarding the heat transfer mechanism, the evaluation represented in Fig. 14 was made.
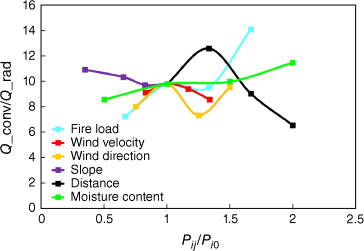
The ratio Qconv/Qrad is the ratio between the convection energy peak and the radiation energy peak. These values are directly obtained by the FDS software, in kilowatts, for convective and radiative heat flow. These heat transfers to the building in the computational domain represent parcels of the energy-conservation principle. This ratio ranges from 7 to 14, showing a predominant convective heat transfer mechanism. As found by Finney et al. (2015), the heat flux from radiation alone is insufficient to support fire spread, and convective heating appears to be the critical heat transfer mechanism causing the ignition and spread of wildfires.
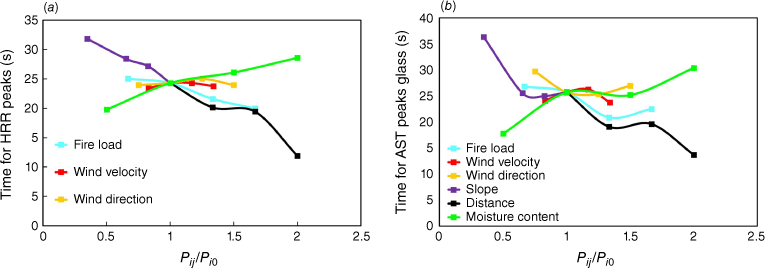
Two plots in Fig. 15a, b show the time required to reach the peak HRR and peak AST, respectively. The increase in value from LV 1 to LV 4 (as shown in Table 3) for the slope distance and fire load parameters causes a reduction in time to attain peak HRR values, as shown in Fig. 15a. The time reductions are 8, 12 and 5 s, i.e. 20, 24 and 51% reductions of the initial time, respectively. This is explained by the increase in MLR. Regarding the wind factors (velocity and direction), the change in terms of time to peak HRR values is minor (less than 0.5 s). This means that these two factors do not govern the observed maximum values. Regarding the MC parameter, going from LV1 to LV4, the time increase is 8 s, corresponding to a 44% increase based on the time needed to reach the peak HRR value at LV1. Both graphs shown in Fig. 15 have substantially the same trends. In the second graph (Fig. 15b), it is possible to see that the peak AST values for glass are reached later compared with the peak HRR values.
Full factorial design
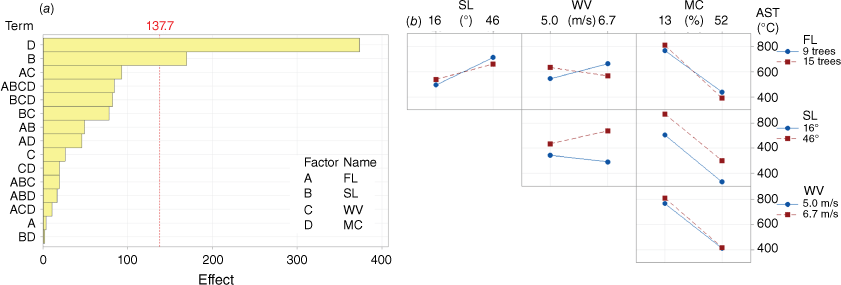
Results obtained by running a full factorial design are represented in Fig. 16 using Pareto charts. In previous studies, Drissi (2014) and Bearinger et al. (2021) also used Pareto charts to assess how factors affect WUI fires and heat transfer. One of the advantages of this data visualisation is that it illustrates the impact of every single factor included in the FFD, as well as existing interaction effects. The results present a 95% confidence level with a 5% significance level. This means that the horizontal bars crossing the red vertical dashed line indicate which factors are significant, as depicted in Fig. 16. In detail, looking at Fig. 16a, the peak HRR values show that (in order of importance) the main single factors are MC, fire load and slope (D, A and B, respectively). Furthermore, AD has a strong interaction factor. Regarding the peak MLR values represented in Fig. 16b, the most important factors are the same as those shown in Fig. 16a. Note that for both cases in Fig. 16, wind velocity (C) is the only single factor that is not relevant. Moreover, the other combined interacting factors are not relevant either. However, parameter C is more relevant when combined with parameter B (i.e. BC). So, for peak HRR and peak MLR, a single factor (in this case, the wind velocity) is more important than the interacting factors, as was found by Drissi (2014).
Fig. 17a shows the main effect of the factors on the mean of the peak HRR. The least important factor is WV as, in the range between 5 and 6.7 m/s, the mean of the peak HRR stays unchanged (less than 1% a difference). Observing FL and SL within their respective increases, both factors contribute to increasing the peak result. However, MC is the main factor with the highest impact, inducing a difference of 40% on the peak HRR mean values, because the lower the MC, the more efficient the combustion. The influence of combined factors on peak HRR is depicted in Fig. 17b. The majority are nearly parallel lines or at least do not intersect, showing that there is no interaction.
Fig. 18a, b show glass AST as a Pareto chart and its interaction plot. In Fig. 18a, the main effects of factors on the mean of the peak AST values are MC and slope (D and B), with a higher contribution by MC. Wind velocity and fire load (C and A) and the remaining combined factors are not significant. In Fig. 18b, FL interacts with SL, WV and MC. This may be caused by the amount of fuel to be burned, where a greater quantity likely eliminates the need to increase wind velocity to reach higher temperatures.
Fig. 19a, b shows the RHF value measured at the façade as a Pareto chart and its interaction plot. In Fig. 19a, three main factors are relevant: D, B and their mutual interaction (DB). Contrary to the previous cases, D and B as single factors have nominally the same importance; the difference in bar length is very small (5%). The interaction plot shown in Fig. 19 indicates that SL and FL, as well as WV and FL, interact. The remaining combination shows the same behaviour.
In summary, the wind velocity (C) selected in the FFD, ranging from 5 to 6.70 m/s, was found to be not significant for the HRR, RHF and AST. However, Cruz and Alexander (2014) explained that the rate of fire spread has already passed the transition point from surface to crown fire when considering these low wind velocities (5–6.70 m/s), showing in this way the importance of this range of velocities beyond the reason previously explained in the OFAT section. Future research will look at whether higher wind velocities significantly affect HRR, RHF and AST.
Data overview
It can be seen from the graphs in Fig. 20 that the peak RHF is higher when the slope is higher (46%) and the MC is lower (13%). In this case, the peak RHF values of the façade are ~160–180 kW/m2, versus ~50 kW/m2 in the case with the smaller slope. Also, for MC (52%), the highest peak RHF values are reached at the façade. Also, in this case, 52% MC (right panel of Fig. 20), the RHF value difference between the façade and roof is very low in the majority of cases (five out of eight): a maximum difference of 7 kW/m2. Another aspect to show (regarding the two cases: 01 and 09) is that for both, RHFf (at façade) is less than RHFr (at the roof), and for both cases, the difference is almost the same (~49 kW/m2). A possible explanation for this is that, in these conditions, the difference in MC percentage does not influence this relative difference. In agreement with Castillo Soto et al. (2022), the maximum heat supported by the structural and decorative house materials ranges from 12.5 kW/m2 (wooden structures) to 400 kW/m2 (solid brick wall), so for the RHF obtained in this simulation, the warehouse is still safe.
In terms of energy balance, when the MC is lower, the peak HRR values are higher, as depicted in right panel of Fig. 20. In the extreme case, HRR can double in value, as shown by comparing the HRR extreme values for Case 8 (2300 MW) and Case 16 (1100 MW). Furthermore, when MC is at 52%, the oscillation of peak HRR values is reduced, varying between 350 and 1100 MW. Peak radiative heat is lower than fromconvection mechanism. Considering the 16 cases, the mean peak Qrad value reached is 72 MW. This value is less significant than the mean peak Qconv (equal to 712 MW). This shows a correspondence of ~ 10% between the two contributions of the heat transfer mechanism (as deduced from Fig. 14).
In Fig. 21, the time, expressed in seconds, to reach the extreme values of HRR and AST for the three different positions shows that for Cases 1–8 with MC equal to 13%, Case 5 takes the longest (~33 s) and Case 8 takes the shortest time (~16 s). This can be explained by the combined effect of fire load and slope on accelerating the process to reach peak values. On the other side, for the second group (Cases 9–16), all with MCs of 52%, there is a larger variance in timing (almost 35 s). The times to reach peak HRR (blue line) are always shorter than those to reach peak AST values. This can be explained by the slow process of heat transfer that happens when the MC is higher.
Discussion
To assess and quantify the impact of different wildfire scenarios in a microscale scenario, several comparisons were established considering the studied parameters. The main observations are:
Increasing the number of trees sequentially (adding a group of three trees), the increase in HRR is approximately 500 MW.
Increasing the wind velocity from 4.15 to 6.7 m/s, the measured HRR decreases by approximately 26%, mainly owing to the incomplete combustion of the trees due to the large deflection of the flames.
Concerning wind direction, the HRR decreases when the wind is not blowing perpendicular to the façade (90°). The HRR reduction is approximately 31, 21 and 24%, respectively, for wind blowing at 67.5°, 112.5° and 135°.
Increasing the slope leads to an almost linear increase in the HRR due to the influence of preheating of the vegetation ahead and also reduces the time to reach the highest values of HRR.
Increasing the distance and considering the singularity of the geometric configuration of the terrain, a reduction in the HRR is observed, mainly because for the smallest distance to the building, the trees are all on the slope, and for the intermediate distances of 12 and 15 m, some trees are on the slope and others in the flat part of the terrain, and finally, for the largest distance of 18 m, all trees are on the flat part of the terrain. This influences fire behaviour significantly, replicating the effect observed when the slope was varied.
The higher the MC, the lower the HRR. For the selected case study, a reduction of 32% was observed.
For the AST monitored on the façade of the building, significant variations were observed. The difference (between extreme values) was 450°, 550° and 260° respectively for the following factors: distance, wind direction and MC. AST increased by a factor of 1.5 to 2 times for each of the three parameters.
The highest values reached for HRR, glass AST and RHF were respectively ~2300 MW, 1000°C and 180 kW/m2. Quantifying the impacts of wildfires in the built environment enables the adoption of a PBD approach for the design of structures in the WUI.
The time necessary to reach the highest values of AST increases when the slope decreases and also when the MC increases.
The key factors that are most relevant to the results obtained are slope and MC.
Conclusions and future research
Based on a calibrated numerical model of a single burning Douglas fir tree, a parcel-scale WUI fire scenario was investigated reproducing a typical industrial scenario. In this study, FDS was employed, and the LPM was considered to represent the fuel. The heat transfer mechanisms from the wildfire to the building were assessed considering the influence of the number of trees, wind direction and velocity, slope, distance between the façade and the trees, and finally MC of the vegetation. An OFAT (for six factors at one level) and an FFD (for four factors at two levels) were used to assess the impact of some parameters on the WUI and heat transfer mechanisms. Based on these analyses, the main factors and interaction factors were identified. Results obtained show the relationship and importance of single factors as well as combined factors. Also, depending on the parameters assessed (RHF, AST, HRR and time), the influence of a single factor changes. It was possible to understand and quantify in detail ASTs in the building and radiative heat flux. Generally, it can be considered that the impact of a wildfire on the building is severe with sustained direct flame contact for all the scenarios modelled. The AST recorded may indicate that severe damage to the structure with a high ignition potential could occur.
The information obtained allows CFD results to be coupled with finite-element software, enabling the mechanical analysis of buildings in the WUI and consequently the analysis and design of fire-resistant and resilient buildings.
Finally, it is worth noting that severe limitations still exist when using advanced computational tools to model microscale WUI fire scenarios, especially when simulating firebrands and secondary spot fires that can originated from these. Hence, extensive research is still needed in this field, focusing on new mathematical models capable of better describing their behaviour and interaction with the surroundings (vegetation or buildings). Such developments will enable the effective use of physics-based tools to model complex WUI fire scenarios, and consequently to develop and improve new and existing codes for the design of buildings in the WUI, incorporating performance-based principles.
Data availability
The data used to generate the results in the paper are available and can be provided on request, including the input files and results of the simulations.
Declaration of funding
This work was financed by national funds through FCT – Foundation for Science and Technology, under grant agreement 2021.08194.BD attributed to the fist author and under grant agreement 2020.03588.CEECIND attributed to the second author. The authors gratefully acknowledge the Portuguese Foundation for Science and Technology (FCT) for its support under the framework of the research project PCIF/AGT/0062/2018 – INTERFACESEGURA – Segurança e Resiliência ao Fogo das Zonas e Interface Urbana–Florestal, financed by FCT through National funds and to the research project ‘Modelling fire spread from forest to the built environment at the wildland–urban interface (WUI) using Fire Dynamics Simulator’, with reference 2022.15641.CPCA.A1 (National Network for Advanced Computing – NNAC). This work was partly financed by FCT/MCTES through national funds (PIDDAC) under the R&D Unit Institute for Sustainability and Innovation in Structural Engineering (ISISE), under reference UIDB/04029/2020, and under the Associate Laboratory Advanced Production and Intelligent Systems ARISE under reference LA/P/0112/2020.
Author contributions
Cesare Fiorini: research and numerical modelling; writing the original draft and formal analysis and interpretation of the results. Hélder D. Craveiro: funding acquisition; supervision; preliminary design and planning of research; numerical modelling; formal analysis and interpretation of results. writing original draft; writing – review and editing; Luís Simões da Silva: analysis and interpretation of the results; writing – review and editing. Aldina Santiago: supervision; writing – review and editing. Luís Laím: writing – review and editing.
Acknowledgements
The authors acknowledge the Laboratory for Advanced Computing at the University of Coimbra for providing {High Performance Computing, consulting} resources that contributed to the research results reported within this paper. URL: https://www.uc.pt/lca.
References
Abu-Zidan Y, Rathnayaka S, Mendis P, Nguyen K (2022) Effect of wind speed and direction on façade fire spread in an isolated rectangular building. Fire Safety Journal 129, 103570.
| Crossref | Google Scholar |
Baker E (2011) Burning Characteristics of Individual Douglas-Fir Trees in the Wildland–Urban Interface. MSc thesis, Fire Protection Engineering Faculty of the Worchester Polytechnic Institute, MA, USA. Available at https://web.wpi.edu/Pubs/ETD/Available/etd-082411-183323/unrestricted/thesis.pdf
Barbero R, Abatzoglou JT, Larkin NK, Kolden CA, Stocks B (2015) Climate change presents increased potential for very large fires in the contiguous United States. International Journal of Wildland Fire 24, 892-899.
| Crossref | Google Scholar |
Batiot B, Rogaume T, Richard F, Luche J, Collin A, Guillaume E, Torero JL (2021) Origin and Justification of the Use of the Arrhenius Relation to Represent the Reaction Rate of the Thermal Decomposition of a Solid. Applied Sciences 11(9), 4075.
| Crossref | Google Scholar |
Bearinger E, Lattimer BY, Hodges JL, Rippe C, Kapahi A (2021) Statistical Assessment of Parameters Affecting Firebrand Pile Heat Transfer to Surfaces. Frontiers in Mechanical Engineering 7, 702181.
| Crossref | Google Scholar |
Bento-Gonçalves A, Vieira A (2020) Wildfires in the wildland-urban interface: Key concepts and evaluation methodologies. Science of The Total Environment 707, 135592.
| Crossref | Google Scholar |
Beshir M, Wang Y, Centeno F, Hadden R, Welch S, Rush D (2021) Semi-empirical model for estimating the heat release rate required for flashover in compartments with thermally thin boundaries and ultra-fast fires. Fire Safety Journal 120, 103124.
| Crossref | Google Scholar |
Browne FL (1958) Theories of the combustion of wood and its control. Report No 2136. (USDA Forest Service, Forest Products Laboratory) Available at https://docslib.org/doc/9175988/theories-of-the-combustion-of-wood-and-its-control
Castillo Soto ME, Molina Martínez JR, Bonilla B S, Moreno García RA (2022) Calculating minimum safety distance against wildfires at the wildland–urban interface in Chile and Spain. Heliyon 8, e11238.
| Crossref | Google Scholar |
Cheney NP, Gould JS, Catchpole WR (1998) Prediction of fire spread in grasslands. International Journal of Wildland Fire 8(1), 1-13.
| Crossref | Google Scholar |
Cohen J, Saveland J (1997) Structure ignition assessment can help reduce fire damages in the WUI. Fire Management Notes 57(4), 19-23 Available at https://www.fs.usda.gov/research/treesearch/4690.
| Google Scholar |
Cohen JD (2000) Preventing disaster: Home ignitability in the wildland–urban interface. Journal of Forestry 98(3), 15-21.
| Crossref | Google Scholar |
Countryman CM (1976) ‘Heat conduction and wildland fire. Heat – its role in wildland fire – Part 3.’ (Forest Service Pacific Southwest Forest and Range Exeperiment Station USDA: Berkely, CA) Available at https://www.frames.gov/documents/behaveplus/publications/Countryman_1976_Part3_HeatConductionWildlandFire_blue_ocr.pdf
Couto FT, Salgado R, Guiomar N (2021) Forest Fires in Madeira Island and the Fire Weather Created by Orographic Effects. Atmosphere 12(7), 827.
| Crossref | Google Scholar |
Cruz MG, Alexander ME (2014) The start, propagation, and spread rate of crown fires. Fire Management Today 73(4), 17-23 Available at https://www.frames.gov/documents/catalog/cruz_and_alexander_2014b.pdf.
| Google Scholar |
Drissi M (2014) Modeling the spreading of large-scale wildland fires. In ‘Proceedings of the large wildland fires conference’, 19–23 May 2014, Missoula, MT. Proceedings RMRS-P-73. (Eds RE Keane, M Jolly, R Parsons, K Riley) pp. 278-285. (USDA Forest Service, Rocky Mountain Research Station: Fort Collins, CO) 10.13140/RG.2.1.1638.4483
Fernandez F, Guillaume B, Porterie B, Ganteaume A, Guerra F (2018) Modelling fire spread and damage in wildland–urban interfaces. In ‘Advances in Forest Fire Research’. (Ed. DX Viegas) pp. 818–825. (Universidade de Coimbra) 10.14195/978-989-26-16-506_90
Finney MA (2021) The wildland fire system and challenges for engineering. Fire Safety Journal 120(48) 103085. 10.1016/j.firesaf.2020.103085
Finney MA, Cohen JD, Forthofer JM, McAllister SS, Gollner MJ, Gorham DJ, Saito K, Akafuah NK, Adam BA, English JD (2015) Role of buoyant flame dynamics in wildfire. Proceedings of the National Academy of Sciences 112(32), 9833-9838.
| Crossref | Google Scholar |
Frankman D, Webb BW, Butler BW, Jimenez D, Forthofer JM, Sopko P, Shannon KS, Hiers JK, Ottmar RD (2013) Measurements of convective and radiative heating in wildland fires. International Journal of Wildland Fire 22(2), 157-167.
| Crossref | Google Scholar |
Ghaderi M, Ghodrat M, Sharples JJ (2021) LES Simulation of Wind-Driven Wildfire Interaction with Idealized Structures in the Wildland-Urban Interface. Atmosphere 12, 21.
| Crossref | Google Scholar |
Guerreiro J, Fonseca C, Salgueiro A, Fernandes P, Lopez Iglésias E, de Neufville R, Mateus F, Castellnou Ribau M, Sande Silva J, Moura JM, Castro Rego F, Caldeira DN (2018) ‘Comissão Técnica Independente. Avaliação dos incêndios ocorridos entre 14 e 16 de outubro de 2017 em Portugal Continental’. Relatório Final. 274 pp. (Assembleia da República: Lisboa) Available at https://www.parlamento.pt/Documents/2018/Marco/RelatorioCTI190318N.pdf [In Portuguese]
Hostikka S, McGrattan KB (2001) ‘Large Eddy Simulation of Wood Combustion’. pp. 755–762. (Interflam) Available at https://tsapps.nist.gov/publication/get_pdf.cfm?pub_id=861077
Hostikka S, Mangs J, Mikkola E (2008) Comparison of Two and Three Dimensional Simulations of Fires at Wildland Urban Interface. Fire Safety Science 9, 1353-1364.
| Crossref | Google Scholar |
Khan N, Sutherland D, Wadhwani R, Moinuddin K (2019) Physics-Based Simulation of Heat Load on Structures for improving Construction Standards for Bushfire Prone Areas. Frontiers in Mechanical Engineering 5, 35.
| Crossref | Google Scholar |
Kim DW, Chung W, Lee B (2016) Exploring tree crown spacing and slope interaction effects on fire behavior with a physics-based fire model. Forest Science and Technology 12(4), 167-175.
| Crossref | Google Scholar |
Knorr W, Jiang L, Arneth A (2016) Climate, CO2 and human population impacts on global wildfire emissions. Biogeosciences 13, 267-282.
| Crossref | Google Scholar |
Krawchuk MA, Moritz MA, Parisien MA, Van Dorn J, Hayhoe K (2009) Global Pyrogeography: the Current and Future Distribution of Wildfire. PLoS One 4(4), e5102.
| Crossref | Google Scholar |
Linn RR, Winterkamp JL, Weise DR, Edminster C (2010) A numerical study of slope and fuel structure effects on coupled wildfire behaviour. International Journal of Wildland Fire 19, 179-201.
| Crossref | Google Scholar |
Mantero G, Morresi D, Marzano R, Motta R, Mladenoff DJ, Garbarino M (2020) The influence of land abandonment on forest disturbance regimes: a global review. Landscape Ecology 35, 2723-2744.
| Crossref | Google Scholar |
Manzello SL, Blanchi R, Gollner MJ, Gorham D, McAllister S, Pastor E, Planas E, Reszka P, Suzuki S (2018) Summary of workshop large outdoor fires and the built environment. Fire Safety Journal 100, 76-92 PMCID: PMC6459202.
| Crossref | Google Scholar |
McGrattan K, McDermott R, Hostikka S, Weinschenk C, Overholt K (2021) ‘Fire Dynamics Simulator, User’s guide’. FDS Version 6.7.7. 402 pp. (National Institute of Standards and Technology Special Publication 1019) 10.6028/NIST.SP.1019
McGrattan K, McDermott R, Hostikka S, Weinschenk S, Overholt K (2022) ‘Fire Dynamics Simulator, Technical Reference Guide, Vol. 1: Mathematical Model’. FDS Version 6.7.8. (National Institute of Standards and Technology) 10.6028/NIST.SP.1018
Mell W, Maranghides A, McDermott R, Manzello SL (2009) Numerical simulation and experiments of burning douglas fir trees. Combustion and Flame 156(10), 2023-2041.
| Crossref | Google Scholar |
Moinuddin KAM, Sutherland D (2017) Numerical Modelling of fires on forest floor and canopy fires. Report No. 352.2017. (Bushfire and Natural Hazards CRC: Melbourne) Available at https://www.bnhcrc.com.au/sites/default/files/managed/downloads/numerical_modelling_of_fires_-_floor_and_canopy.pdf
Moinuddin KAM, Sutherland D (2019) Simulations of radiation heat flux on a structure from a fire in an idealised shrubland. Australian Journal of Emergency Management 4, 26-31 Available at https://www.researchgate.net/publication/339150332.
| Google Scholar |
Moinuddin KAM, Sutherland D, Mell W (2018) Simulation study of grass fire using a physics-based model: striving towards numerical rigour and the effect of grass height on the rate of spread. International Journal of Wildland Fire 27(12), 800-814.
| Crossref | Google Scholar |
Molina-Terrén DM, Xanthopoulos G, Diakakis M, Ribeiro L, Caballero D, Delogu GM, Viegas DX, Silva CA, Cardil A (2019) Analysis of forest fire fatalities in Southern Europe: Spain, Portugal, Greece and Sardinia (Italy). International Journal of Wildland Fire 28, 85-98.
| Crossref | Google Scholar |
Morvan D, Frangieh N (2018) Wildland fires behaviour: wind effect versus Byram’s convective number and consequences upon the regime of propagation. International Journal of Wildland Fire 27(9), 636-641.
| Crossref | Google Scholar |
Ni Z, Lu S, Peng L (2012) Experimental study on fire performance of double-skin glass façades. Journal of Fire Sciences 30(5), 457-472.
| Crossref | Google Scholar |
NWCG S-190 (2019) National Wildfire Coordinating Group (Instructor Guide) S-190 Unit 2: Fuels. Available at https://www.nwcg.gov/sites/default/files/training/docs/s-190-ig02.pdf
Oliveira R, Oliveira S, Zêzere J, Viegas D (2018) Human perception of fire hazard in wildland urban interface areas: a Portuguese survey analysis of spot fires. In ‘Advances in Forest Fire Research’. (Ed. DX Viegas) pp. 1130–1136. (Universidade de Coimbra) 10.14195/978-989-26-16-506_126
Papalou A, Baros D (2019) Assessing Structural Damage after a Severe Wildfire: A case study, Buildings 9 171. 10.3390/buildings9070171
Pimont F, Dupuy J-L, Linn RR (2012) Coupled slope and wind effects on fire spread with influences of fire size: a numerical study using FIRETEC. International Journal of Wildland Fire 21(7), 828-842.
| Crossref | Google Scholar |
Porterie B, Consalvi JL, Loraud JC, Giroud F, Picard C (2007) Dynamics of wildland fires and their impact on structures. Combustion and Flame 149, 314-328.
| Crossref | Google Scholar |
Potter M, Leonard J (2011) Spray System Design for Ember Attack - research findings and discussion paper. (Report to Bushfire CRC) Available at https://hdl.handle.net/102.100.100/103658?index=1
Quarles SL, Standohar-Alfano C (2018) Wildfire Research, Ignition potential of decks subjected to an ember exposure. Technical Report. (Insurance Institute for Business & Home Safety) Available at https://docslib.org/doc/8868049/ignition-potential-of-decks-subjected-to-an-ember-exposure
Reszka P, Fuentes A (2015) The Great Valparaiso Fire and Fire Safety Management in Chile. Fire Technology 51, 753-758.
| Crossref | Google Scholar |
Ribeiro LM, Rodrigues A, Lucas D, Viegas DX (2020) The Impact on Structures of the Pedrógão Grande Fire Complex in June 2017 (Portugal). Fire 3(4), 57.
| Crossref | Google Scholar |
Ribeiro LM, Almeida M, Viegas DX, Alves D, Barbosa T, Modarres M (2021) ‘Planeamento da gestão de combustíveis. Efeito da distância e da frequência das intervenções na proteção das estruturas e rede viária’. 160 pp. (ForestWISE (Coord) Projetos AGIF 2021 (P32100231): Vila Real) Available at https://www.agif.pt/app/uploads/2022/07/Relato’rio-Projeto-Distancia-e-frequencia-de-intervenções_FW_final_06072022.pdf [In Portuguese]
Ryan KC, Opperman TS (2013) LANDFIRE – A national vegetation/fuels data base for use in fuels treatment, restoration, and suppression planning. Forest Ecology and Management 294, 208-216.
| Crossref | Google Scholar |
Safdari SM (2018) Characterization of Pyrolysis Products from Fast Pyrolysis of Live and Dead Vegetation. PhD thesis, Department of Chemical Engineering, Faculty of Brigham Young University, Provo, UT, USA. Available at https://www.et.byu.edu/~tom/Papers/Saeed_Safdari_Dissertation.pdf
Sandström J (2013) Thermal Boundary Conditions Based on Field Modelling of Fires. Licentiate thesis, Division of Structural and Construction Engineering, Department of Civil Engineering, Environmental and Natural resources Engineering, Lualea University of Technology, Sweden. Available at https://www.diva-portal.org/smash/get/diva2:990371/FULLTEXT01.pdf
Suzuki S, Manzello SL (2021) Investigating the Effect of Structure to Structure Separation Distance on Firebrand Accumulation. Frontiers in Mechanical Engineering 6, 628510.
| Crossref | Google Scholar |
Syphard AD, Brennan TJ, Keeley JE (2017) The importance of building construction materials relative to other factors affecting structure survival during wildfire. International Journal of Disaster Risk Reduction 21, 140-147.
| Crossref | Google Scholar |
Tihay V, Morandini F, Santoni PA, Perez-Ramirez Y, Barboni T (2014) Combustion of forest litters under slope conditions: Burning rate, heat release rate, convective and radiant fractions for different loads. Combustion and Flame 161, 3237-3248.
| Crossref | Google Scholar |
Trigo RM, Pereira JMC, Pereira MG, Mota B, Calado TJ, Dacamara CC, Santo FE (2006) Atmospheric conditions associated with the exceptional fire season of 2003 in Portugal. International Journal of Climatology 26, 1741-1757.
| Crossref | Google Scholar |
Vacca P, Àgueda A (2020) Deliverable D6.2 Set of FDS codes of baseline vulnerability and sheltering experiments. D6.2_F_Set of FDS codes of baseline vuln. and shelt. Exp. Available at https://wuiview.webs.upc.edu/download/D6.2_F_Set% 20of% 20FDS% 20codes.pdf
Vacca P, Caballero D, Pastor E, Planas E (2020) WUI fire risk mitigation in Europe: A performance-based design approach at home-owner level. Journal of Safety Science and Resilience 1, 97-105.
| Crossref | Google Scholar |
Vanella M, McGrattan K, McDermott R, Forney G, Mell W, Gissi E, Fiorucci P (2021) A Multi-Fidelity Framework for Wildland Fire Behavior Simulations over Complex Terrain. Atmosphere 12(273), 273.
| Crossref | Google Scholar |
Viegas DX (2004) Slope and wind effects on fire propagation. International Journal of Wildland Fire 13(2), 143-156.
| Crossref | Google Scholar |
Viegas DX, Almeida M, Ribeiro LM, Raposo J, Alves D (2017) An overview of the Fires in Portugal in 2017. Global Observations of Forest Cover (GOFC Copernicus Meeting) London. Available at https://gofcgold.org/sites/default/files/fireit_meetings/GOFC_Fire_IT_2017/day2/Viegas.pdf
Wadhwani R, Sutherland D, Ooi A, Moinuddin K, Thorpe G (2017) Verification of a Lagrangian particle model for short-range firebrand transport. Fire Safety Journal 91, 776-783.
| Crossref | Google Scholar |
Wang HY, Chateil B (2007) Numerical Simulation of Wind-Aided Flame Spread over Horizontal Surface of Condensed Fuel in a Confined Channel. International Journal on Engineering Performance-Based Fire Codes 9(2), 65-77 Available at https://www.bse.polyu.edu.hk/researchCentre/Fire_Engineering/summary_of_output/journal/IJEPBFC/V9/p65-77.pdf.
| Google Scholar |
Wickramasinghe A, Khan N, Moinuddin K (2022) Determining firebrand generation rate using physics-based modelling from experimental studies through inverse analysis. Fire 5, 6.
| Crossref | Google Scholar |
Wickstrom U, Duthinh D, McGrattan K (2007) Adiabatic Surface Temperature for Calculating Heat Transfer to Fire Exposed Structures. In ‘Proceedings of the Eleventh International Interflam Conference’. (Royal Holloway College, University of London. Interscience Communications) Available at https://tsapps.nist.gov/publication/get_pdf.cfm?pub_id=900083