On the non-monotonic behaviour of fire spread
Domingos Xavier Filomeno Carlos Viegas A B C , Jorge Rafael Nogueira Raposo B , Carlos Fernando Morgado Ribeiro
B , Carlos Fernando Morgado Ribeiro  B , Luís Carlos Duarte Reis B , Abdelrahman Abouali B and Carlos Xavier Pais Viegas B
B , Luís Carlos Duarte Reis B , Abdelrahman Abouali B and Carlos Xavier Pais Viegas B
A Department of Mechanical Engineering, University of Coimbra, Coimbra 3030-788, Portugal.
B Association for the Development of Industrial Aerodynamics (ADAI)/Associated Laboratory on Energy, Transportation and Aeronautics (LAETA), University of Coimbra, Coimbra 3030-289, Portugal.
C Corresponding author. Email: xavier.viegas@dem.uc.pt
International Journal of Wildland Fire 30(9) 702-719 https://doi.org/10.1071/WF21016
Submitted: 4 February 2021 Accepted: 6 July 2021 Published: 16 August 2021
Journal Compilation © IAWF 2021 Open Access CC BY-NC-ND
Abstract
A conceptual model based on the dynamic interaction between fire, the fuel bed and the surrounding flow to explain the non-monotonic or intermittent behaviour of fires is proposed. According to the model, even in nominally permanent and uniform boundary conditions, the fire-induced flow modifies the geometry of the flame and its rate of spread. After an initial acceleration, there is a reduction in the rate of spread followed by one or more cycles of growth. Carefully controlled experiments of fires in slopes and canyons show that the evolution of fire properties, namely flame angle and rate of spread, have high-frequency oscillations superimposed on the low-frequency fire growth cycle described above.
Keywords: dynamic fire behaviour, fire acceleration, fire environment coupling, fire growth, fire modelling, forest fire behaviour, oscillatory fire behaviour.
Introduction
Forest fire spread is a complex process that is not fully understood in spite of the variety of approaches used over several decades of research, from purely empirical to fully theoretical, aiming to achieve a full capacity to model and predict fire behaviour. Pastor et al. (2003) and Sullivan (2009) give a state of the art on the field of fire behaviour research and provide a large number of references that illustrate the complexity of the problem and the difficulty of reaching a general and complete solution. At present, we are able to predict fire behaviour only in a very limited set of conditions (Thomas et al. 2017), missing some of the cases that may be of greater practical importance, like the very intense or rapidly changing fires that create major concerns for fire managers and endanger people’s lives (Bowman et al. 2017).
A fundamental step in the process of fire modelling is to understand how fires modify their properties over the course of time, owing to dynamic interaction between the fire and its surroundings. In previous work (cf. Viegas 2004a, 2004b), we observed that, in the general case, fire behaviour is a dynamic process in the sense that even under permanent boundary conditions, fire behaviour properties depend explicitly on time. In Viegas (2002), it was shown that the transverse convection along the fire line modifies the rate of spread (ROS) of the fire, producing its rotation movement. In Viegas (2004c), it was shown that the fire-induced convection produces acceleration of the fire, causing what was designated an eruption, which is often observed in canyons or steep slopes. This problem is also addressed by Dold et al. (2006). In Raposo et al. (2018), the merging of two linear fires with a small angle between them, causing strong radiation and convection effects, and producing the highest values of ROS observed both in the laboratory and in the field, was analysed. This problem was also studied by Thomas et al. (2017).
In the present paper, we address the problem of natural oscillatory or intermittent behaviour of the fire and show that these oscillations are due to dynamic interaction between the fire, the fuel bed and the surrounding flow. This natural process is non-permanent as it involves fluctuations of various frequencies and amplitudes superimposed on an overall quasi-static process, which is in itself controlled by these fluctuations. We propose a conceptual model to describe the fluctuations of flame and ROS properties and present the results of a set of laboratory-scale experiments to support it.
Several authors have studied the spread of a point or line ignition fire on a slope, namely Mendes-Lopes et al. (2003), Dupuy et al. (2011), Silvani et al. (2018), but in spite of recognising the variability of the fire spread, they assume that it propagates in a steady state and provide essentially average values of fire spread properties.
Albini (1982) studied the variability of wind-aided fires, stating that the ROS of fires in natural fuels is very sensitive to wind speed, but in many cases the spread rate can also vary substantially with time even though the fuel and meteorological conditions remain essentially constant. Based on the spectral density of wind fluctuations at frequencies below 0.1 Hz, Albini predicted that the response of the fire would be oscillatory, with a spectral response that depended on the type of fuel and also on the average value of the wind velocity. According to this model, there is a dominant amplitude of oscillation of the ROS for a frequency between 0.01 and 0.02 Hz but apparently the average value of the ROS is not changed. Although Albini’s study grasped some of the features of dynamic fire behaviour, it did not consider the natural fluctuations that occur even in the absence of wind and the large amplitude variations of the ROS that are considered in the present paper. Finney et al. (2015, 2019) and Silvani et al. (2018) also addressed the problem of fluctuations in fire properties due to turbulence in fire-induced convection.
Conceptual model of fire evolution
The present conceptual model considers a head fire created by a flaming fire front on a flat surface covered by a homogeneous fuel bed. We assume that there is a uniform and permanent ambient flow over the fuel bed surface characterised by a reference velocity Uo (cf. Viegas and Neto 1991; for a full list of symbols and abbreviations see Table A1 in Appendix 1). Alternatively, we may consider that the fire is spreading along a slope or a canyon with constant inclination α in relation to a horizontal datum.
We are aware that the fires are always 3D processes and the fluctuations of the fire and flow properties described in this paper along the Ox-axis occur along the Oy-axis as well, creating cells of convection as observed by Finney et al. (2015). In the present paper, we are concerned with the phenomena along the main direction of fire spread, which are relevant for practical applications in the case of fires that are driven by slope or wind.
In Fig. 1, we present the conceptual evolution of the fire spread properties, namely the flame length and angle with the horizontal surface (β) as a function of time. When the fire starts (Stage 1 in Fig. 1), the flame is almost vertical (β = 90°) and the natural convection flow is symmetrical on both sides of the fire. The presence of a constant wind (or constant slope or topography effect) will incline the flame, decreasing its angle, and increase the ROS (Stage 2). The fire growth due to the presence of the flame and the prevailing wind can be explained by the feedback effect described in Viegas (2004c) for the process of fire growth in a canyon.

|
The larger value of ROS will increase the flame depth and therefore the amount of fuel that is burning simultaneously. Because of this, the flame will be thicker and start to become vertical, increasing the value of β given the larger amount of fuel burning and the increased buoyancy (Stage 5). In the process of fire acceleration, the local flow on both sides of the flame will increase as well. The increase of the ROS and flame length with local flow velocity and decrease of its inclination angle with either wind or slope is amply supported in the literature (cf. Dupuy 1995) and is documented below.
The increased modulus of the flow velocity on the leeward of the flame will contribute to its deceleration and after reaching a value of β ≈ 90° (Stage 7), the ROS will decrease, reaching a local minimum, and then a new cycle of acceleration starts (Stage 8) but with a larger and deeper flame front than at Stage 1. This cycle can be repeated if the boundary conditions persist.
ROS evolution
In order to analyse the fire front evolution, following many authors, namely Byram (1959), Byram and Nelson (1951), Rothermel (1972, 1983), Albini (1981, 1982), Alexander and Cruz (2012), Tolhurst (2009), Sharples (2009), Butler et al. (2007), we use the concept of ROS of the head fire as it gives a very important indication of the development and intensity of the fire. Several fire-related properties such as the fireline intensity, flame length, energy release rate, residence time, heat impact on the soil, gas emissions and others can be derived from knowledge of the local ROS (cf. Freeborn et al. 2008; Canfield et al. 2014; Moinuddin et al. 2018). Accurate knowledge of the head fire evolution linked to other information on terrain, fuel cover and topography can also provide an overall assessment of the fire spread and of the perimeter or the burned area evolution over the course of time.
As a consequence of the process described above, according to the present model, the ROS of the fire front will have the temporal evolution shown in Fig. 2, with a sort of yoyo effect. There will be an initial increase of the ROS until Stage 7, then a decrease until Stage 8, followed by another cycle. At the start of this second cycle, normally the fire will have a higher ROS than at Stage 1, given the growth of the flame up to Stage 6. Over time, the cycle can be repeated one or more times as illustrated in Fig. 2 and as was observed in fire experiments that are presented below and in some real fires as well (cf. Anderson 1968; Wade and Ward 1973). Superimposed on the general cycle of ROS evolution is a process of higher frequency – short period of time – and low-amplitude fluctuations derived from the dynamic interactions between the fire and the surrounding turbulent flow. These fluctuations are not illustrated in Fig. 2 for the sake of clarity, but are clearly shown below in the laboratory-scale experiments.

|
The conceptual evolution of the inclination angle β of the flame over the course of time is also plotted in Fig. 2 with the same time scale but with an arbitrary vertical scale. At the start of the fire, the value of β is close to 90° and then decreases to a value of the order of 30°, and increases while the ROS continues to increase, reaching a local maximum close to 90°, after which another cycle starts.
As plotted in Fig. 2 the growth of the ROS R is gradual and then followed by a sudden decrease, as confirmed by the experiments, giving the characteristic oscillatory or intermittent pattern to fire behaviour. This sudden decrease produced by the overall fire dynamics induced by the fire explains why an eruptive fire in a canyon does not reach infinite values of R as predicted in the mathematical model of Viegas (2004c, 2006) after a finite time, as the changes in the flame and flow properties at this stage decrease the value of R to a significant degree.
The present model deals mainly with kinematic properties of the fire and of the surrounding flow but it must be taken into account that the modifications induced by the flow in the geometry of the flame are associated with a change in the combustion processes as well as in the balance of forces and heat transfer processes of the flame system, resulting in a change of the ROS over the course of time. This time dependency of the fire properties induced by the fire itself prompts us to define this process as dynamic as opposed to other approaches that consider mainly average values of fire properties.
Reference flow velocities
In order to analyse the flow in the vicinity of the fire front, we refer to the temporal evolution of the flow velocity component U′ = Ux – Uo parallel to the fuel bed at a point P positioned at a certain distance above it, as a function of the time t′ = tP – t, elapsed since the passage of the flame at time tP (cf. figure below). Assuming that the flow induced by the fire has opposite directions on both sides of the flame, we consider the time tP when the relative velocity U′ changes sign as the time of arrival of the fire at P. As shown in our experiments, on the windward side of the flame, the flow velocity increases, owing to the indraft produced by the fire, reaching a maximum value U′max. Then, the flow velocity decreases, being equal to zero at the trailing edge – the rear of the flame, becoming negative on the leeward side of the flame and reaching a minimum value U′min, ahead of the leading edge or front of the flame. We use these values of U′max and U′min as reference flow velocities respectively for the windward and leeward flows, near the flame.
In the present study, validation of the conceptual curve shown in Fig. 3 was made with the experimental results performed in no-wind conditions (Uo = 0), in which case the value of U′ = Ux.
|
If the process of fire spread is transient, knowing the evolution of the rate of spread R(t), it is possible to estimate the distance xf(t) of the flame to point P from:
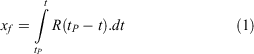
Negative and positive values of xf correspond respectively to the windward or leeward side of the fire.
Validation
In order to validate the conceptual model, we present a series of laboratory experiments of point ignition fires under controlled permanent conditions. Given the difficulty of physically producing a flow with uniform velocity over a large area, we chose to perform tests under the effect of constant slope in no-wind conditions. Using the analogy between slope and wind effect on fire spread, we extend the considerations above for the development of a fire under a constant wind to the case of a fire on a constant slope.
We consider two cases, first the spread of a point ignition on a slope, and then in a symmetrical canyon. As we shall see in the canyon fire, when we increase the slope of the water line of the canyon to 30° or 40°, the ROS increases and then decreases as described in the conceptual model. In order to validate the present conceptual model, we shall mainly use the slope tests, as this configuration is easier to analyse and provides a better description of the flame properties during the initial phase of fire acceleration.
Material and methods
Experimental simulation
Standard fuel bed
All experiments described in this paper were performed with our ‘standard fuel bed’ composed of dead Pinus Pinaster needles with a fuel load of 600 g m−2 (dry basis) that has consistently been used by our research group through the years in a wide series of experiments (cf. Viegas and Pita 2004; Xie et al. 2014; Raposo 2016; Raposo et al. 2018; Rodrigues et al. 2019). The pine needles were kept inside the laboratory at indoor ambient conditions; therefore, their moisture content mf could change from one test to another. We measured mf before each test in order to prepare the total mass of particles required for the test to compensate for the mass of water in the fuel. The height of the fuel bed was between 5 and 7 cm.
Basic ROS
The ROS of a linear fire front under no-slope and no-wind conditions, which we designate the basic ROS Ro, is an intrinsic property of the fuel bed. For a given fuel bed, its value will depend mainly on the moisture content mf of the fuel particles.
In order to minimise the effect of mf on R in tests performed under different conditions, we use the non-dimensional ROS R′, defined as:

Fire spread on a slope
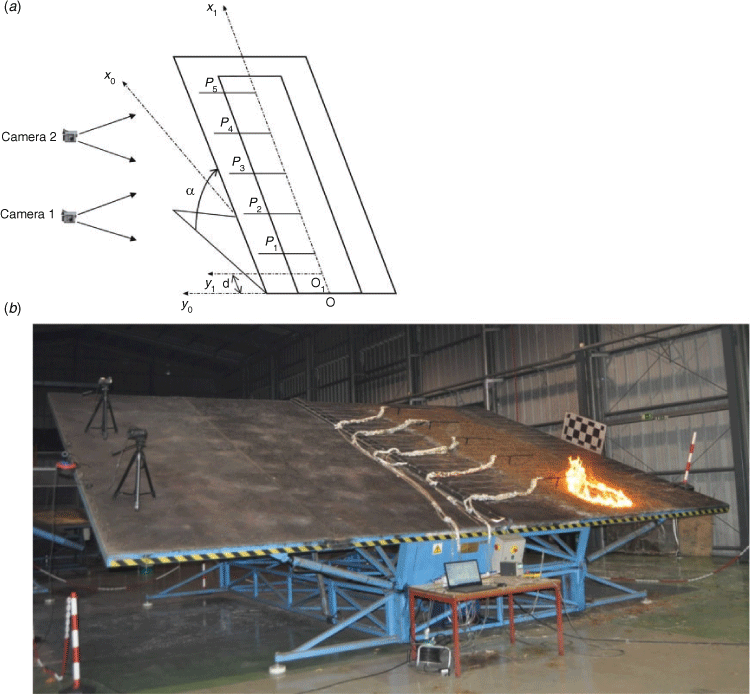
We performed tests with a point ignition fire on a slope on the CT3 combustion table of the Forest Fire Research Laboratory of the University of Coimbra. A schematic view of the experimental layout is shown in Fig. 4a and a photo of the test rig taken during test SP303 is shown in Fig. 4b. The dimensions of the table are 6 × 8 m2 but only half was used in the present experiments. The fuel bed was a rectangle of 5.5 × 2 m2 (in some tests, the dimensions were 5 × 2 m2) and ignition was at the centre line 50 cm above the lower border of the fuel. Five S-Pitot tubes placed 15 cm above the surface of the table measured the Ux component of the flow.

|
One infrared camera recorded an oblique top view of the spread of the fire and two video cameras recorded the flame properties during the tests.
The slope angle α of the table was set to 20°, 30° and 40° and four repetitions were made for each configuration. The test parameters are given in Table 1.

|
Fire spread in canyons
Fires in canyons can ‘blow up’ or exhibit eruptive behaviour, with the ROS increasing continuously over the course of time (cf. Viegas and Pita 2004; Viegas 2004c, 2006; Dold and Zinoviev 2009; Viegas and Simeoni 2011; Xie et al. 2020). A canyon is composed of two lateral faces that make an angle δ with a reference horizontal plane, and their intersection – the water line – makes an angle α with the horizontal datum (Fig. 5a).

|
Experiments reported in Viegas and Pita (2004) performed on a 3 × 3 m2 canyon-shaped table with pine needles as fuel bed showed the tendency of a non-monotonic variation of the ROS. The mathematical model proposed in Viegas (2004c) estimates that the ROS of the head fire along the water line of the canyon will reach very high values after a finite time.
In the present study, a set of experiments was performed in this test rig using δ = 40° (measured when α = 0°) for different values of the inclination angle α of the water line. We performed three repetitions for each configuration and these test parameters are given in Table 2.

|
More details on the experimental methodology can be found in Viegas and Pita (2004).
Data analysis
Rate of spread
The tests were recorded using an infrared camera (FLIR SC660) in the range of 300–1500°C, with a rate of acquisition of 15 Hz. The threshold of 350°C was used to avoid obstruction of the view by the fire plume. The frames from the IR camera recordings were extracted and analysed to obtain the fire contour at pre-defined times. The time between frames was adapted for each test. The Cartesian coordinates of the frame were converted into true physical Cartesian coordinates in the plane of the combustion table in order to determine the evolution of the fire front to compute the instantaneous values of ROS at each point of the fire line and the isochrones of the fire following the methodology described in Raposo et al. (2018) and Rodrigues et al. (2019).
In the analysis of the positions of the fire advance along the Ox-axis of the table, the positions Pi (xi, ti), and Pi+1(xi+1, ti+1) at predefined times were determined. For the slope tests, these points coincided with the head of the fire. In some configurations of the canyon fires, there was a bifurcation of the fire with two heads, one on each slope, but analysis was always carried out on the intersection line of the two faces of the canyon, corresponding to the axis Ox (see Fig. 5). From these data, we can determine the ‘instantaneous’ ROS Rj (xj, tj):

We calculate this value for time tj given by:

As we intend to correlate the fire properties (flame angle and length) with Rj, they are determined for the corresponding time tj for each data point.
Flame geometry
Two video cameras were placed laterally on the surface of the combustion table to record the propagation of the head fire during each test, as shown in Fig. 3. The two cameras were a Sony AVCHD MPEG2 SD and Sony HD DCR-SR87 that recorded 20 frames per second. Although each camera could view the entire length of the fire spread, in order to minimise parallax errors, we used Camera 1 to analyse the spread of the fire in the first half of the table and Camera 2 for the remaining part. Reference direction and scale marks were used to estimate the flame angle and length. It is estimated that the errors of the angle and length measurement are less than 1° and 2 cm respectively in the entire field of vision of each camera.
The flame length L is defined by the length of a line joining the tip of the continuous flame to the middle of the base of the flame, as indicated in Fig. 4. The flame angle β is the angle between the base of the fuel bed and the above-mentioned line, as shown in Fig. 4.
To estimate L and β at a given time tj, we used three frames, captured at an interval of 1 s, at tj – 1 s, tj and tj + 1 s. The properties of the flame are the average of these three values.
As the experiments used in this work are controlled by the terrain slope α, in the analysis of the flame angle, following Cruz and Alexander (2020), we considered the possibility of using another flame angle βo, defined by (see Fig. 5):

The angle βo between the flame and the horizontal surface would be more meaningful for describing the role of gravity or buoyancy in the development of the flame and of fire spread. We nevertheless found that this is applicable mainly at the initial stages of the fire development, as fire-induced convection soon becomes the dominant mechanism controlling the flame geometry and fire spread.
Flow velocity
Five S-Pitot tubes were installed along the Ox axis 15 cm above the surface of the table at the following distances from the lower edge of the fuel bed: 1, 2, 3, 4 and 5 m. Each Pitot measured the flow temperature Ti and velocity Ui (i = 1 to 5) parallel to the fuel bed at every second. From the temperature record at each Pitot position, with a rate of acquisition of 1 Hz using K-type thermocouples (nickel chromium/nickel aluminium, metallic shielded, with a diameter of 0.5 mm, connected to an NI cDAQ-9174 with an NI 9213TC module that allows synchronous data-logging), it was possible to determine the time of arrival tp of the flame at each Pitot position assessed by the temperature reaching 350°C. The Pitot tubes were connected by pipes to differential pressure transducers (Gems 5266–50L Very Low Range Differential Pressure Transmitter (0 to 50 Pa)). These transducers were connected to the NI cDAQ-9174 with an NI 9205 voltage module that performs the data-logging of the signal also with a frequency of 1 Hz. The transducers are bi-directional so that when the flow is upslope along the Ox axis, the signal is positive and when it is opposite, it is negative. With the data collected by this method, using the values of synchronous temperature measurements by the application of a calibration, it was possible to estimate the flow velocity induced by the fire phenomena.
More details on the use and calibration of S-Pitot tubes can be found in Kang et al. (2015). Pinto et al. (2020) found that the error due to misalignment between the flow velocity and the probe axis is negligible for an angle below 6°; if the misalignment is in the range between 6 and 30°, the error can be up to 9%.
Results and discussion
Fire spread on slopes
Time evolution of ROS and flame angle
In order to illustrate the processes described in the conceptual model, we picked sample slope tests of each configuration to analyse the evolution of R′ and β as a function of time. The results are shown in Figs 6–8, which include video images of each test at selected times. In spite of the accuracy and detail of the experiments, we recognise that there are some high-frequency oscillations of both parameters that are not easy to interpret or explain owing to the discrete nature of our data, meaning that we may not observe the extreme values of R′ or β as they may not occur exactly at the times of observation.

|
In test SP202 (Fig. 6) for α = 20°, the ROS increases and the flame angle decreases corresponding to points 1, 2 and 3 in Fig. 2. There is a period of acceleration between 25 and 275 s with an oscillation of both R′ and β. In this period, R′ varies between 1.28 and 2.64 and β oscillates around 65°. Between 275 and 325 s, β decreases to 51°, while R′ drops from 2.68 to 2.32. From this time till the end of the test, β increases again while R′ undergoes a full cycle of growth and decrease. The three photos on the right side of Fig. 6 are of video images taken at 325, 425 and 525 s corresponding to a period of increasing values of β, while R′ increases up to 2.65 and then decreases to 1.93.
In test SP 302 (Fig. 7) for α = 30°, the ROS and the flame angle variation correspond essentially to the same phase as in the previous case. There is a period of overall increase of R′ till it reaches a value of 6.49 at 230 s. During this period, two oscillations of R′ and β are observed. Between 230 and 330 s, there is a period of R′ decrease from 6.49 to 2.04, also with two oscillations. Then, two peak values of R′ occur at 350 and at 410 s with oscillations in between. From this time till 450 s, R′ decreases to 4.12 with an overall increase of β with at least two oscillations. The three photos shown in Fig. 7 correspond to video images taken at 170, 210 and 270 s illustrating the decrease of β and the increase of R′ between 170 and 210 s and the opposite trend in the second period of time.
Test SP 403 (Fig. 8) for α = 40° is possibly more straightforward to interpret as the value of R′ increases from 1.2 at the beginning to 8.74 at 230 s. The ROS and the flame angle increase, corresponding to points 4, 5 and 6 in Fig. 2. In this period, there are several oscillations of both R′ and β. During the whole test, β increases with oscillations, some of them in phase with the oscillations of R′. Between 230 and 390 s, R′ and β have two oscillations. The photos from this test, taken at 130, 250 and 330 s, illustrate a period of general increase of β and R′ with two marked oscillations.
Rate of spread
The results of the non-dimensional ROS R′ as a function time elapsed since the origin of the four tests performed for each configuration for slope angles α = 20°, 30° and 40° are shown in Fig. 9a–c respectively. In spite of the random nature of the fluctuations of R′, good repeatability is observed for tests performed in each configuration. For α = 20° (Fig. 9a), we see that on average R′ increases from an initial value close to 1.5 to ~2.5 and then decreases slightly. For α = 30° (Fig. 9b), we see that on average R′ increases to values close to 5 and then decreases with two or more cycles. For α = 40° (Fig. 9c), we see that on average R′ increases to values close to 8, and although there is indication of a decreasing phase of R′, the length of the fuel bed was not sufficient to observe it in full.

|
We do not have yet an interpretation for the relationship between the relatively high-frequency and low-amplitude fluctuations and the low-frequency and-high amplitude oscillations. It seems that high-amplitude oscillations occur mainly for values of R′ > 4, meaning that possibly, for this fuel, the amount of energy involved in the combustion process is sufficient to feed greater variations of the R′(t) curve.
Flame properties
The results of the flame angle β and flame length L as a function of time since the origin for all tests performed for each configuration for slope angles α = 20°, 30° and 40° are plotted in Fig. 10a–c respectively. Good repeatability of the experiments is shown in the four tests performed for each configuration for both parameters. Following the pattern of variation of R′, for α = 20° (Fig. 9a), the flame angle decreases from the initial value of 70° (which corresponds to βo ≈ 90°), to ~50° at the end of the test. For α = 30° (Fig. 10b), the initial values of β are ~60° then decrease to ~40°, remain constant and then tend to increase, at least for some tests. For α = 40° (Fig. 10c), the flame angle β starts with values of the order of 50° (corresponding to βo ≈ 90°) and increases to 60° and even to 70°.
Silvani et al. (2018) experimentally studied the spread of a linear fire front in an excelsior fuel on a 3 × 6 m2 inclinable bench for two slope angles of 0° and 30° and for three values of fuel load. For the 30° slope, they refer to oscillations in the flame geometry describing the latter as spherical (‘fireball’) or elongated, which is consistent with the fluctuations that we observed for both L and β, but they do not provide detailed data on the evolution of fire properties with time.
Mendes-Lopes et al. (2003) experimentally studied the propagation of a linear fire on a 2 × 0.7 m2 fuel bed of Pinus pinaster needles with a fuel load of 0.5 kg m−2 for various slope and wind velocity conditions. Fuel moisture content was controlled during the experiments and two values of the moisture content, 10% and 18%, were used. Slope was varied between ±15° and wind velocity between ±3 m s−1. Although for practical reasons not all combinations of slope and wind were tested, 192 tests were performed for different combinations of the three control parameters. The authors provide results of the time variation of the flame angle for two cases without slope. In the no-wind case, the values of β oscillate around 90° with small fluctuations, but for 1 m s−1 wind, the flame angle varies between 40° and 90° with an average value of 70°. For 3 m s−1 flow, in the first 120 s the height of the flame increases from 15 to 45 cm, with some oscillations; it then decreases to values close to 20 cm after 20 s, but the authors only provide average values of all parameters.
Reference flow velocities
The flow velocity was measured by S-type Pitot tubes, as described in the Methods section, at five points 15 cm above the ground, in all tests. Using average values of the flow velocity every 5 s, the time tP of passage of the flame past each Pitot tube position was estimated from the trace of U′(t) when the flow velocity changed from essentially positive to essentially negative values of U′. The results obtained for each configuration were very consistent and the results of one sample test for each configuration are shown in Fig. 11.

|
To simplify our analysis, we consider the flame to be static at the position of the Pitot (x = xP). When the flow approaches the leeward side of the flame (negative values of xP – x and of tP – t), the value of U′ increases to a maximum as anticipated in the conceptual model, then decreases owing to the presence of the flame, which acts as a solid body, producing a stagnation point in the present test conditions. On the leeward side of the flame, the flow velocity U′ becomes negative with a well-defined minimum value. Very similar results can be found in Yang et al. (2018) and in Liu et al. (2015).
The values of Umax and Umin obtained in each test as a function of the local value of R′ are plotted respectively in Figs 12 and 13. As can be seen in Fig. 12, Umax tends to increase with R′, as would be expected, although the present data indicate that this growth is not monotonic. For the present fuel bed, a local maximum value of Umax for R′ ≈ 4 seems to exist.

|

|
The distribution of Umin also shows a tendency to decrease with R′, as shown in Fig. 14, but possibly not in a monotonic form as well.

|
Silvani et al. (2018) employed an innovative particle image velocimetry (PIV) technique to analyse the flow field in a vertical plane. Their flow visualisation and measurement techniques confirm the existence of a positive fire-induced wind on the windward side of the flame and a negative flow towards the flame on its leeward side.
Overall flame angle and flame length
The distribution of values of flame angle β for all tests as a function of R′ is shown in Fig. 14. In the initial stages of fire spread, when R′ < 2, βo could possibly describe the evolution of the flame angle better, as suggested before, but the fire-induced flow velocity increases rapidly with R′ and the fire becomes dominated by convective flow and less dependent on terrain slope, as shown in Fig. 14.
In spite of the data scatter, it is possible to see the trend of reduction of β from 90° for R′ = 0 to a minimum value between 30° and 40° for R′ ≈ 4. For R′ > 5, β increases to values close to 70°.
This trend is also visible in the line of βave(R′) shown in Fig. 14. The lines corresponding to βave ± Δβ, in which Δβ is the standard deviation computed at each interval of R′, are shown as well.
It must be noted that in this figure, we have values of β corresponding to periods of fire acceleration (increase of R′) or deceleration, which may contribute to the scatter of data.
The distribution of values of flame length L for all tests as a function of R′ is shown in Fig. 15. The data scatter is larger than for β but from the experimental points and the Lave line, it is possible to see a trend of increasing L for 1.5 < R′ < 3. There is possibly a local maximum value of L for R′ ≈ 4, corresponding to the minimum of β. For R′ > 5, there seems to be a second stage of increase of L, but the present data are too scarce in this range of tests to confirm this assertion.

|
Our results show that for a given fuel bed, there is univocal relationship between the ROS and the flame angle and flame length, but this relationship is not bi-univocal as many fire spread models assume. For a given fire spread condition – terrain slope in the present case – some values of β or L may correspond to different values of R′. As shown in the present analysis, this is due to the oscillatory behaviour of fire spread, caused by the interaction between fire-induced convection and the combustion process.
Fire spread in canyons
We now present the results of the head fire ROS in the canyon along its Ox axis, which cover a higher range of values of R′ and therefore better illustrate the non-monotonic behaviour of fire spread that is predicted in our conceptual model. Owing to practical difficulties, flow and flame properties were not analysed in this test configuration.
In Fig. 16a–c, the non-dimensional ROS R′ values of the head fire along the centre line of the canyon every 5 s are plotted as a function of time, for the three tests performed with α = 20°, 30° and 40°, together with the curves of R′ave and of R′ave ± ΔR′. Given the relatively high temporal resolution of the fire spread analysis, the existence of fluctuations in the ROS values with time is clearly shown.

|
The fluctuations of the ROS can be considered as an instability or a perturbation of the equilibrium conditions in the fire (cf. Finney et al. 2015). In some cases, the amplitude of this oscillation is sufficient to cause a relatively large increase of the ROS, leading to an ‘eruption’, but in other cases these oscillations are damped by the fire–environment system and the ROS value returns almost to its initial value, as predicted in the conceptual model. This is clearly shown in Fig. 16a for the test with α = 20° in which the average value of R′ increases steadily from ~1.5 at the start to 4 at the end of the test. Given the random nature of the turbulent flow fluctuations, each test is different from the other and the scatter of the ROS values is not necessarily associated with lack of accuracy or other systematic measurement errors but rather with the random nature of the fire fluctuations. Therefore, the averaging process provides only an indication of the overall tendency of the evolution of R′(t).
In the case of α = 30° (Fig. 16b), the fluctuations continue to exist, but when the value of R′ > 7, the amplitude of the fluctuations becomes very large and sudden fire acceleration occurs. As predicted by the Viegas (2004a) model, the value of R′ increases very rapidly, reaching ~35. After this maximum value, there are one or more oscillations with an overall tendency of ROS reduction. The same happens for α = 40° (Fig. 16c) with R′ increasing to ~40, although in this case the reduction phase is not completed owing to the limited size of the fuel bed.
Conclusion
In this work, a conceptual model of fire spread based on the interaction between fire-induced convection, the fuel and the surrounding flow that modifies flame geometry and therefore the fire spread characteristics is proposed to interpret and justify the non-monotonic growth of a fire. According to this model, there is a process of relatively high-frequency fluctuations, associated with the turbulent flame and flow properties, superimposed onto a lower-frequency evolution, related to the fuel bed and its combustion properties, namely the flame geometry, owing to its interaction with the surrounding ambient environment, that induces an oscillatory or intermittent behaviour in fire spread. This concept was validated in carefully controlled laboratory experiments of point ignition fires on a simple slope or in a canyon in the absence of external flow. It was observed that over the course of time, the ROS of the head fire undergoes a cycle of growth followed by a sudden decrease, particularly in the case of canyon fires, with higher-frequency and smaller-amplitude oscillations. Careful analysis of the flow through the flame highlights the modifications induced by the presence of the flame on the flow in the windward or leeward regions of the flame, with two characteristic velocities. For a given fuel bed, these velocities increase in modulus with the ROS but possibly not in a monotonic way. The flame angle in relation to the fuel bed has a characteristic non-monotonic variation with R′, decreasing from a relatively high value – corresponding to an initially vertical flame – to a minimum value of the order of 30°, for R′ ≈ 4 for this fuel, and then increases to values close to 70°. The flame length increases with R′ but also shows a local maximum near the minimum flame angle.
In future work, we intend to analyse the fluctuations of R′ and of other flow and fire-related parameters for a wider range of values of R′ for the standard fuel used in these experiments and for other fuels as well. A mathematical model to interpret the present conceptual model and its application to the analysis of real fires reported in the literature will be addressed as well.
Conflicts of interest
The authors declare that they have no conflicts of interest.
Declaration of funding
The work reported in this article was carried out in the scope of project Firestorm (PCIF/GFC/0109/2017) supported by the Portuguese National Science Foundation and the European Union’s Horizon 2020 research and innovation programme under grant agreement Nº 101003890. We would like to thank the FCT-Foundation for Science and Technology for the PhD grant of Carlos Ribeiro with the reference SFRH/BD/140923/2018.
Acknowledgements
The support of Nuno Luís, António Cardoso and Filipe Ferreira in the laboratory experiments is gratefully acknowledged.
References
Albini FA (1981) A model for the wind-blown flame from a line fire. Combustion and Flame 43, 155–174.| A model for the wind-blown flame from a line fire.Crossref | GoogleScholarGoogle Scholar |
Albini FA (1982) Response of free-burning fires to non-steady wind. Combustion Science and Technology 29, 225–241.
| Response of free-burning fires to non-steady wind.Crossref | GoogleScholarGoogle Scholar |
Alexander ME, Cruz MG (2012) Interdependencies between flame length and fireline intensity in predicting crown fire initiation and crown scorch height. International Journal of Wildland Fire 21, 95–113.
| Interdependencies between flame length and fireline intensity in predicting crown fire initiation and crown scorch height.Crossref | GoogleScholarGoogle Scholar |
Anderson HE (1968) Fire spread and flame shape. Fire Technology 4, 51–58.
| Fire spread and flame shape.Crossref | GoogleScholarGoogle Scholar |
Bowman DMJS, Williamson GJ, Abatzoglou JT, Kolden CA, Cochrane MA, Smith AMS (2017) Human exposure and sensitivity to globally extreme wildfire events. Nature Ecology & Evolution 1, 0058
| Human exposure and sensitivity to globally extreme wildfire events.Crossref | GoogleScholarGoogle Scholar |
Butler BW, Anderson WR, Catchpole EA (2007) Influence of slope on fire spread rate. In ‘The fire environment – innovations, management, and policy; conference proceedings’, 26–30 March 2007, Destin, FL. (Eds Butler, Bret W., Cook, Wayne) USDA Forest Service, Rocky Mountain Research Station, Proceedings RMRS-P-46CD, pp. 75–82. (Fort Collins, CO)
Byram GM (1959) Combustion of forest fuels. In ‘Forest Fire: Control and Use’. (Ed. KP Davis) pp. 61–89, 554–555. (McGraw-Hill: New York, NY)
Byram GM, Nelson RM (1951) The possible relation of air turbulence to erratic fire behavior in the Southeast. Fire Control Notes 63, 46–51.
Canfield JM, Linn RR, Sauer JA, Finney M, Forthofer J (2014) A numerical investigation of the interplay between fireline length, geometry, and rate of spread. Agricultural and Forest Meteorology 189–190, 48–59.
| A numerical investigation of the interplay between fireline length, geometry, and rate of spread.Crossref | GoogleScholarGoogle Scholar |
Cruz MG, Alexander ME (2020) Flame Dimensions. In ‘Encyclopedia of Wildfires and Wildland-Urban Interface (WUI) Fires’. (Ed. SL Manzello) pp. 468–472. (Springer: Cham)
Dold JW, Zinoviev A (2009) Fire eruption through intensity and spread rate interaction mediated by flow attachment. Combustion Theory and Modelling 13, 763–793.
| Fire eruption through intensity and spread rate interaction mediated by flow attachment.Crossref | GoogleScholarGoogle Scholar |
Dold JW, Zinoviev A, Weber RO (2006) Non-local flow effects in bushfire spread rates. In ‘Proceedings of the V International Conference on Forest Fire Research’, 27–30 November 2006, Figueira da Foz, Portugal. (Ed. DX Viegas) pp. 1–8.
Dupuy JL (1995) Slope and fuel load effects on fire behavior: laboratory experiments in pine needles fuel beds. International Journal of Wildland Fire 5, 153–164.
| Slope and fuel load effects on fire behavior: laboratory experiments in pine needles fuel beds.Crossref | GoogleScholarGoogle Scholar |
Dupuy JL, Maréchal J, Portier D, Valette JC (2011) The effects of slope and fuel bed width on laboratory fire behaviour. International Journal of Wildland Fire 20, 272–288.
| The effects of slope and fuel bed width on laboratory fire behaviour.Crossref | GoogleScholarGoogle Scholar |
Finney MA, Cohen JD, Forthofer JM, McAllister SS, Gollner MJ, Gorham DJ, Saito K, Akafuah NK, Adam BA, English JD, Dickinson RE (2015) Role of buoyant flame dynamics in wildfire spread. Proceedings of the National Academy of Sciences of the United States of America 112, 9833–9838.
| Role of buoyant flame dynamics in wildfire spread.Crossref | GoogleScholarGoogle Scholar | 26183227PubMed |
Finney MA, Smith CT, Maynard TB (2019) Experiments on wildfire ignition by exploding targets. USDA Forest Service, Rocky Mountain Research Station, Research Paper RMRS-RP-108. (Fort Collins, CO)
Freeborn PH, Wooster MJ, Hao WM, Ryan CA, Nordgren BL, Baker SP, Ichoku C (2008) Relationships between energy release, fuel mass loss, and trace gas and aerosol emissions during laboratory biomass fires. Journal of Geophysical Research, D, Atmospheres 113, D01301
| Relationships between energy release, fuel mass loss, and trace gas and aerosol emissions during laboratory biomass fires.Crossref | GoogleScholarGoogle Scholar |
Kang W, Trang ND, Lee SH, Choi HM, Shim JS, Jang HS, Choi YM (2015) Experimental and numerical investigations of the factors affecting the S-type Pitot tube coefficients. Flow Measurement and Instrumentation 44, 11–18.
| Experimental and numerical investigations of the factors affecting the S-type Pitot tube coefficients.Crossref | GoogleScholarGoogle Scholar |
Liu N, Wu J, Chen H, Zhang L, Deng Z, Satoh K, Viegas DX, Raposo JR (2015) Upslope spread of a linear flame front over a pine needle fuel bed: The role of convection cooling. Proceedings of the Combustion Institute 35, 2691–2698.
| Upslope spread of a linear flame front over a pine needle fuel bed: The role of convection cooling.Crossref | GoogleScholarGoogle Scholar |
Mendes-Lopes JMC, Ventura JMP, Amaral JMP (2003) Flame characteristics, temperature–time curves, and rate of spread in fires propagating in a bed of Pinus pinaster needles. International Journal of Wildland Fire 12, 67–84.
| Flame characteristics, temperature–time curves, and rate of spread in fires propagating in a bed of Pinus pinaster needles.Crossref | GoogleScholarGoogle Scholar |
Moinuddin KAM, Sutherland D, Mell W (2018) Simulation study of grass fire using a physics-based model: striving towards numerical rigour and the effect of grass height on the rate of spread. International Journal of Wildland Fire 27, 800–814.
| Simulation study of grass fire using a physics-based model: striving towards numerical rigour and the effect of grass height on the rate of spread.Crossref | GoogleScholarGoogle Scholar |
Pastor E, Zárate L, Planas E, Arnaldos J (2003) Mathematical models and calculation systems for the study of wildland fire behaviour. Progress in Energy and Combustion Science 29, 139–153.
| Mathematical models and calculation systems for the study of wildland fire behaviour.Crossref | GoogleScholarGoogle Scholar |
Pinto C, André J, Viegas DX (2020) Double S-type Pitot tube for velocity field study of fire whirls. Flow Measurement and Instrumentation 76, 101806
| Double S-type Pitot tube for velocity field study of fire whirls.Crossref | GoogleScholarGoogle Scholar |
Raposo J (2016) Extreme fire behaviour associated with merging of two linear fire fronts. PhD thesis, University of Coimbra, Coimbra, Portugal. Available at http://hdl.handle.net/10316/31020
Raposo JR, Viegas DX, Xie X, Almeida M, Figueiredo A, Porto L, Sharples J (2018) Analysis of the physical processes associated with junction fires at laboratory and field scales. International Journal of Wildland Fire 27, 52–68.
| Analysis of the physical processes associated with junction fires at laboratory and field scales.Crossref | GoogleScholarGoogle Scholar |
Rodrigues A, Ribeiro C, Raposo J, Viegas DX, André J (2019) Effect of canyons on a fire propagating laterally over slopes. Frontiers of Mechanical Engineering 5, 402–409.
| Effect of canyons on a fire propagating laterally over slopes.Crossref | GoogleScholarGoogle Scholar |
Rothermel RC (1972) A mathematical model for predicting fire spread in wildland fuels. USDA Forest Service, Intermountain Forest and Range Experiment Station, Research Paper INT-RP-115. (Ogden, UT)
Rothermel RC (1983) How to predict the spread and intensity of forest and range fires. USDA Forest Service, Intermountain Forest and Range Experiment Station, General Technical Report INT-143. (Ogden, UT)
Sharples JJ (2009) An overview of mountain meteorological effects relevant to fire behaviour and bushfire risk. International Journal of Wildland Fire 18, 737–754.
| An overview of mountain meteorological effects relevant to fire behaviour and bushfire risk.Crossref | GoogleScholarGoogle Scholar |
Silvani X, Morandini F, Dupuy JL, Susset A, Vernet R, Lambert O (2018) Measuring velocity field and heat transfer during natural fire spread over large inclinable bench. Experimental Thermal and Fluid Science 92, 184–201.
| Measuring velocity field and heat transfer during natural fire spread over large inclinable bench.Crossref | GoogleScholarGoogle Scholar |
Sullivan AL (2009) Wildland surface fire spread modelling, 1990–2007. 3: Simulation and mathematical analogue models. International Journal of Wildland Fire 18, 387–403.
| Wildland surface fire spread modelling, 1990–2007. 3: Simulation and mathematical analogue models.Crossref | GoogleScholarGoogle Scholar |
Thomas CM, Sharples JJ, Evans JP (2017) Modelling the dynamic behaviour of junction fires with a coupled atmosphere-fire model. International Journal of Wildland Fire 26, 331–344.
| Modelling the dynamic behaviour of junction fires with a coupled atmosphere-fire model.Crossref | GoogleScholarGoogle Scholar |
Tolhurst K (2009) Report on the Physical Nature of the Victorian Fires occurring on 7th February 2009.
Viegas DX (2002) Fire line rotation as a mechanism for fire spread on a uniform slope. International Journal of Wildland Fire 11, 11–23.
| Fire line rotation as a mechanism for fire spread on a uniform slope.Crossref | GoogleScholarGoogle Scholar |
Viegas DX (2004a) On the existence of a steady state regime for slope and wind driven fires. International Journal of Wildland Fire 13, 101–117.
| On the existence of a steady state regime for slope and wind driven fires.Crossref | GoogleScholarGoogle Scholar |
Viegas DX (2004b) Slope and wind effects on fire propagation. International Journal of Wildland Fire 13, 143–156.
| Slope and wind effects on fire propagation.Crossref | GoogleScholarGoogle Scholar |
Viegas DX (2004c) A mathematical model for forest fires blowup. Combustion Science and Technology 177, 27–51.
| A mathematical model for forest fires blowup.Crossref | GoogleScholarGoogle Scholar |
Viegas DX (2006) Parametric study of an eruptive fire behaviour model. International Journal of Wildland Fire 15, 169–177.
| Parametric study of an eruptive fire behaviour model.Crossref | GoogleScholarGoogle Scholar |
Viegas DX, Neto LPC (1991) Wall shear-stress as a parameter to correlate the rate of spread of a wind-induced forest fire. International Journal of Wildland Fire 1, 177–188.
| Wall shear-stress as a parameter to correlate the rate of spread of a wind-induced forest fire.Crossref | GoogleScholarGoogle Scholar |
Viegas DX, Pita LP (2004) Fire spread in canyons. International Journal of Wildland Fire 13, 253–274.
| Fire spread in canyons.Crossref | GoogleScholarGoogle Scholar |
Viegas DX, Simeoni A (2011) Eruptive behaviour of forest fires. Fire Technology 47, 303–320.
| Eruptive behaviour of forest fires.Crossref | GoogleScholarGoogle Scholar |
Wade DD, Ward DE (1973) An analysis of the Air Force Bomb Range Fire. USDA Forest Service, Southeastern Forest Experiment Station, Research Paper SE-105. (Asheville, NC)
Xie X, Liu N, Viegas DX, Raposo JR (2014) Experimental research on upslope fire and jump fire. Fire Safety Science 11, 1430–1442.
| Experimental research on upslope fire and jump fire.Crossref | GoogleScholarGoogle Scholar |
Xie X, Liu N, Raposo JR, Viegas DX, Yuan X, Tu R (2020) An experimental and analytical investigation of canyon fire spread. Combustion and Flame 212, 367–376.
| An experimental and analytical investigation of canyon fire spread.Crossref | GoogleScholarGoogle Scholar |
Yang Z, Zhang H, Zhang L, Chen H (2018) Experimental study on downslope fire spread over a pine needle fuel bed. Fire Technology 54, 1487–1503.
| Experimental study on downslope fire spread over a pine needle fuel bed.Crossref | GoogleScholarGoogle Scholar |
Appendix 1

|





