Guidelines for effective evaluation and comparison of wildland fire occurrence prediction models
Nathan Phelps A B and Douglas G. Woolford A CA Department of Statistical and Actuarial Sciences, University of Western Ontario, London N6A 3K7, Canada.
B Department of Computer Science, University of Western Ontario, London N6A 3K7, Canada.
C Corresponding author. Email: dwoolfor@uwo.ca
International Journal of Wildland Fire 30(4) 225-240 https://doi.org/10.1071/WF20134
Submitted: 28 August 2020 Accepted: 16 December 2020 Published: 29 January 2021
Journal Compilation © IAWF 2021 Open Access CC BY-NC-ND
Abstract
Daily, fine-scale spatially explicit wildland fire occurrence prediction (FOP) models can inform fire management decisions. Many different data-driven modelling methods have been used for FOP. Several studies use multiple modelling methods to develop a set of candidate models for the same region, which are then compared against one another to choose a final model. We demonstrate that the methodologies often used for evaluating and comparing FOP models may lead to selecting a model that is ineffective for operational use. With an emphasis on spatially and temporally explicit FOP modelling for daily fire management operations, we outline and discuss several guidelines for evaluating and comparing data-driven FOP models, including choosing a testing dataset, choosing metrics for model evaluation, using temporal and spatial visualisations to assess model performance, recognising the variability in performance metrics, and collaborating with end users to ensure models meet their operational needs. A case study for human-caused FOP in a provincial fire control zone in the Lac La Biche region of Alberta, Canada, using data from 1996 to 2016 demonstrates the importance of following the suggested guidelines. Our findings indicate that many machine learning FOP models in the historical literature are not well suited for fire management operations.
Keywords: area under curve (AUC), Brier score, logarithmic score, mean absolute error (MAE), model selection, precision-recall curve, receiver operating characteristic curve, visual diagnostics, wildfire occurrence.
Introduction
Although wildland fires are a natural part of many ecosystems that have several positive impacts (Johnston et al. 2020), they also pose a risk to public safety, infrastructure, property and forest resources (Martell 2007). Fire management agencies are faced with the difficult task of balancing the benefits and losses of wildland fires in order to get ‘the right amount of fire to the right place at the right time at the right cost’ (Martell 2007). Consequently, fire management decisions are made on a variety of spatial and temporal scales from daily, incident-level tactical decisions all the way to long-term, large-scale strategic planning. These can include developing strategies to detect fires and optimising resource allocation for responding to fires.
Wildland fire management can be viewed as a form of risk management (e.g. Xi et al. 2019; Johnston et al. 2020). One of the key components of wildland fire risk management is accurately quantifying the likelihood or probability of wildland fire occurrence (i.e. the hazard). A recent review of wildland fire management in Canada by Tymstra et al. (2020) noted that improvement of wildland fire occurrence prediction (FOP) was a ‘specific gap’ in preparedness research.
This need to predict when, where and how many fires can occur is a critical piece of information for fire management operations. In Canada, the Canadian Forest Fire Danger Rating System (CFFDRS) is used daily by fire management personnel. Although the CFFDRS includes an FOP system as one of its four linked subsystems, at the time of its release, that FOP System was conceptual (Stocks et al. 1989) and a national FOP subsystem is still yet to be published (Wang et al. 2017). Natural Resources Canada (2020) notes that some regions do have systems. For example, the lightning-caused FOP system of Wotton and Martell (2005) combined with the human-caused FOP system of Woolford et al. (2020) represent the fine-scale, spatially explicit FOP system used by the Ministry of Natural Resources and Forestry in the Province of Ontario, Canada.
FOP aids preparedness planning tasks such as the repositioning or deployment of detection and/or initial attack suppression resources. Consequently, spatially and temporally explicit FOP models have been developed and integrated into fire management information systems (e.g. Woolford et al. 2016). FOP models also feed into other decision support tools, such as those that aid aerial detection planning (e.g. McFayden et al. 2020).
Ideally, an FOP model used in an information system or for decision support should produce predictions on a space–time scale that provides enough detail for use in daily fire management planning. As noted in reviews of global research on wildland fire occurrence (Plucinski 2012; Costafreda-Aumedes et al. 2017), there are two distinct approaches to FOP. Fire occurrences can be modelled as a binary process (i.e. fire or no fire) or as a count of the number of occurrences (e.g. Cunningham and Martell 1973; Todd and Kourtz 1991; Plucinski et al. 2014). In this study, we focus on the binary approach, as have most past FOP studies. To develop a fine-scale, spatially and temporally explicit FOP model, space–time is typically partitioned into a set of voxels (e.g. 10 × 10-km daily cells), which map counts of fires essentially to a presence or absence (i.e. fire or no fire) process and facilitate the use of the binary modelling approach. This procedure results in a highly imbalanced classification problem for researchers to model in the sense that the number of fire observations is many orders of magnitude smaller than the number of non-fire observations (Taylor et al. 2013).
Many different methods for FOP have been used historically in this context of fine-scale, spatially and temporally explicit FOP modelling, including logistic regression (e.g. Martell et al. 1987, 1989; Vega-Garcia et al. 1995), regularised (e.g. LASSO) logistic regression (e.g. Nadeem et al. 2020), logistic generalised additive models (e.g. Brillinger et al. 2003; Preisler et al. 2004, 2011; Vilar et al. 2010; Woolford et al. 2011, 2016; Magnussen and Taylor 2012) and a variety of machine learning methods, including neural networks, support vector machines and random forests (e.g. Vega-Garcia et al. 1996; Vasconcelos et al. 2001; Alonso-Betanzos et al. 2003; Stojanova et al. 2006, 2012; Sakr et al. 2010, 2011; Bar Massada et al. 2013; Rodrigues and de la Riva 2014; Van Beusekom et al. 2018).
Owing to the wide range of modelling approaches, it is not uncommon to use multiple methods to develop a set of candidate FOP models for a given region and then choose a final model. Given that such a model could be used by fire management, such as in an information system displaying spatially explicit FOP predictions based on current conditions, it is crucial to be able to objectively evaluate and compare models for final model selection. We have noticed that the procedures often used for comparing FOP models could lead to choosing a model that may not be the optimal choice for use in practice.
Our objective is to outline guidelines for comparing FOP models with the intent of systematically choosing the best fine-scale spatially explicit model for daily use as a decision support tool for wildland fire management operations. We discuss appropriate choices for a testing dataset and evaluation metrics, as well as the importance of addressing the variability in these metrics. Furthermore, because FOP models could be used in fire management practice, we argue that it is crucial to collaborate with end users to ensure models meet their needs and to use temporal and spatial visualisations that assess models in the context in which they will be used. Through a case study analysis for a provincial fire control zone in the Lac La Biche region in the Province of Alberta, Canada, over the period 1996–2016, we show how to reduce the risk of issues, such as failing to identify poor calibration, in a variety of FOP models. Although we demonstrate our objective using models from several different FOP modelling approaches in our case study, we note that these guidelines should be followed even if only a single approach is taken.
Model evaluation and comparison for wildland fire occurrence prediction
A review
Here, we briefly review several FOP studies, focusing on studies that have fitted more than one type of model (i.e. using both statistical and machine learning methods) and the ways in which they have evaluated and compared their models. For comprehensive recent reviews of wildland fire occurrence research, see Plucinski (2012) and Costafreda-Aumedes et al. (2017). Plucinski summarised a wide variety of models, stratified by their objectives, such as spatial v. temporal models and count v. occurrence modelling methods, summarising common factors that have been found to affect fire occurrence. Costafreda-Aumedes et al. presented a global perspective of the various methods that have been used for modelling counts and individual incidences of human-caused wildland fires on a variety of spatial and temporal scales and they also noted a need for FOP models to be linked to management.
Several studies focus on modelling only spatial patterns of wildland fire occurrence, commonly referred to as wildland fire ignition susceptibility. Examples include Vasconcelos et al. (2001) and Bar Massada et al. (2013), who modelled ignitions directly, as well as Rodrigues and de la Riva (2014), who modelled areas of high and low wildland fire occurrence. These are relevant because their modelling approaches could be used for fine-scale spatially and temporally explicit FOP modelling, which is the focus of our work herein. For brevity, we also refer to these articles as FOP studies throughout this paper.
To our knowledge, the comparison of Vega-Garcia et al. (1996) of a neural network and logistic regression for FOP in the Whitecourt Forest of Alberta, Canada, is the first comparison of statistical and machine learning methods for FOP. Their study region was split into eight subregions and, for every day in each of five fire seasons, the presence or absence of a human-caused wildland fire in the subregion was recorded, resulting in over 8000 observations in the training dataset. Only 157 of these observations were fire occurrences, so they sampled 157 non-fire observations from the training dataset in order to balance the data before model fitting. A separate 2 years of data (3294 observations, 58 of which were fire occurrences) were reserved to evaluate and compare models. Other FOP studies (e.g. Vasconcelos et al. 2001; Stojanova et al. 2006, 2012; Bar Massada et al. 2013; Rodrigues and de la Riva 2014) have also used machine learning approaches and compared their results with logistic regression. For these cases, fire occurrences have composed 22 to 50% of the observations in the dataset.
In such studies, a confusion matrix and the metrics associated with it were often used for model evaluation and comparison. For a binary response process, a confusion matrix is a 2 × 2 table of the actual (fire/no fire observed) and modelled values (fire/no fire predicted). This requires a model’s outputs to be in the form of a classification, not a probability. Yet many models that are viewed as classifiers were actually developed to model the probability of an event (Harrell 2015). In this context, fitted and predicted values are mapped to a classification according to whether the probabilistic output is above a given threshold. Metrics such as accuracy, precision, recall (sensitivity), specificity, omission error, commission error and kappa have all been used in FOP studies (e.g. Vega-Garcia et al. 1996; Vasconcelos et al. 2001; Stojanova et al. 2006, 2012; Sakr et al. 2010, 2011) and are derived from the values in a confusion matrix.
Another metric that has also been used for FOP model evaluation (e.g. Vasconcelos et al. 2001; Bar Massada et al. 2013; Rodrigues and de la Riva 2014; Nadeem et al. 2020) is area under the receiver operating characteristic curve (AUC-ROC) (Hanley and McNeil 1982). This is a threshold-independent metric that depends only on a model’s ability to rank observations (i.e. relative probability of fire occurrence matters, but the values themselves are irrelevant). An AUC-ROC value of 0.5 corresponds to no discrimination between the classes; values from 0.7 to 0.8 correspond to acceptable discrimination; values from 0.8 to 0.9 correspond to excellent discrimination; and values greater than 0.9 correspond to outstanding discrimination (Hosmer et al. 2013). Some reported AUC-ROC scores in FOP literature have fallen short of the 0.7 threshold for acceptable discrimination, but others have eclipsed 0.90.
Although uncommon, a few FOP studies have also assessed another form of model performance, calibration. A well-calibrated FOP model produces predictions that represent the true probability of a fire occurrence. Sakr et al. (2010, 2011) used customised metrics to assess the error in predicting the number of fires on a given day, whereas Nadeem et al. (2020) used root-mean-squared error (RMSE) after aggregating the predictions either spatially or temporally.
In addition to metrics, some FOP studies have used visualisations in order to qualitatively assess their models. Several studies illustrated their models’ predictions using spatial maps of fire occurrence probability (e.g. Vasconcelos et al. 2001; Stojanova et al. 2012; Bar Massada et al. 2013; Rodrigues and de la Riva 2014). Vasconcelos et al. (2001) also used a calibration plot to compare the observed probability of fire occurrence with their models’ predictions, whereas Nadeem et al. (2020) plotted observed and predicted counts.
Pitfalls with current approaches
The purpose of evaluating models on a testing dataset is to gain insight about how we can expect a model to perform in practice. In order to do this in a meaningful way, the distribution of the testing dataset must be the same as the distribution of the observations the model will encounter in practice. As noted, fine-scale FOP modelling can produce a dataset that is highly imbalanced in terms of fire and non-fire observations. Although it is reasonable to use subsampling techniques to create training datasets, such as response-based sampling for logistic-based FOP modelling (e.g. Vega-Garcia et al. 1995; Brillinger et al. 2003; Vilar et al. 2010; Woolford et al. 2011, 2016; Nadeem et al. 2020), these techniques should not be applied to the testing dataset, because subsampling is not used when models are implemented as decision support tools. This requirement is important because the distribution of the observations in the testing dataset can affect the metrics used in model comparison. For example, subsampling of the non-fire observations in a testing set can lead to an overestimation of the precision. Also, some metrics are computed by calculating an error for each prediction–observation pair and summing (or averaging) these errors. These metrics can be computed independently for fire and non-fire observations (i.e. stratified scores); thus, the aggregate score of such metrics can be thought of as a weighted function of the stratified scores. If we artificially change the fire/no-fire distribution in the testing dataset, we are reweighting these stratified scores. This reweighting impacts the aggregate score and can change the ranking of the candidate models, possibly leading to selecting a model that performs worse in practice than one (or more) of the other candidate models.
The metrics associated with a confusion matrix are common evaluation tools in the machine learning community (e.g. Géron 2017), but they are not particularly well suited for evaluating FOP models; they are more suitable for evaluating models that make final decisions (i.e. models that make a decision rather than support a decision) such as an email spam filter, which makes final decisions without human input. Consequently, two problems with the use of threshold-dependent metrics for the evaluation of FOP models become clear:
For a threshold t and sufficiently small tolerance ϵ, the difference between a probability of a fire occurrence of t – ϵ and t + ϵ is negligible in practice, but not in the value of the metric.
Probabilistic output from two competing FOP models can be very different but could also be mapped to the same classification output and a threshold-dependent metric would not distinguish between these two predictions.
In addition, if a testing dataset is used that represents the true distribution of fire occurrences in practice, some of the metrics associated with a confusion matrix are a poor choice. Recalling that wildland fires are very rare events when modelling on a fine space–time scale, wildland fire data are very imbalanced in terms of the distribution of their dichotomous (fire/no fire) response variable. Some metrics are inappropriate for use in problems with imbalanced data. For example, it is well documented that overall prediction accuracy is a poor measure for assessing model performance in such cases (e.g. Chawla et al. 2004; Orriols-Puig and Bernadó-Mansilla 2009; Jeni et al. 2013). This is because accuracy fails to consider the trade-off between false positives and false negatives. A model can obtain a very good classification accuracy simply by predicting the majority class every time, but then the false negative rate is maximised. Threshold-independent metrics can also be unsuitable for such situations. Jeni et al. (2013) noted that it seems AUC-ROC may not highlight poor model performance in situations with highly imbalanced data. Potential issues with the use of AUC-ROC for FOP model comparisons have been identified previously (Bar Massada et al. 2013).
A model’s ability to rank observations in terms of their relative likelihood of fire occurrence is not the only component of model evaluation that should be considered; a model’s calibration is also important. However, very few FOP studies have used metrics to assess calibration and none have directly assessed the calibration on the scale of the predictions, namely on the prediction–observation pairs. Although the primary goal of FOP may be simply to identify regions with higher relative likelihood of fire occurrence, a secondary but still important goal of FOP should be to produce well-calibrated (i.e. true) probabilities. Well-calibrated fire occurrence predictions are much easier for a fire management agency to interpret, whereas miscalibrated probabilities and a scale from low to high danger (without a probabilistic interpretation or a connection to the expected number of fires) are more difficult to interpret and thus are less useful as a decision support tool. In addition, the output of FOP models may be used as input in other decision support tools such as the aerial detection planning tool described in McFayden et al. (2020) or in wildland fire risk modelling (see Xi et al. 2019; Johnston et al. 2020 for summaries). The risk to a resource or asset (e.g. a house, a power line) from a specific fire is the product of that fire reaching the entity (through ignition at some location and spread to the entity) and the impact of that fire on the entity. Thus, the total risk attributed to an entity needs to account for all possible fires. Like with the metrics discussed earlier in this section, this total risk can be thought of as a weighted summation of the impacts across all individual fires. Consequently, miscalibrated probabilities of fire occurrence can lead to the belief that one entity is at higher risk than another when the opposite may be the case. Even if the observations are correctly ranked from low to high probability of fire occurrence, this error can still occur because the magnitudes of the probabilities are important for risk computations. Consequently, proper calibration of output is a critical aspect of FOP models that must be evaluated.
When FOP models are used in fire management operations as decision support tools, fire management agencies may only have a few minutes to interpret a model’s outputs and decide how to act (Alexander et al. 2015). Visualisations have been suggested to facilitate efficient interpretation of model outputs for FOP (e.g. Xi et al. 2019). For example, daily predictions are commonly presented spatially, and predicted values over the grid for a region of interest on a given day are aggregated to produce an estimate for the expected number of new fires to arrive that day. Consequently, the comparison of FOP models using only metrics is not satisfactory as they do not assess their performance in the context for which they will be used in practice. Bar Massada et al. (2013) noted that metrics may reveal only small differences in performance, while visualisations can reveal more substantial differences. Although some FOP studies have used visualisations to assess and compare models (e.g. Vasconcelos et al. 2001; Stojanova et al. 2012; Bar Massada et al. 2013; Rodrigues and de la Riva 2014; Nadeem et al. 2020), we note that several studies have relied entirely on quantitative metrics. Consequently, we advocate for the use of visualisations to qualitatively evaluate a model’s performance and to compare competing models.
Guidelines
We provide six guidelines to follow to effectively evaluate and compare FOP models in order to select a model well suited for fire management operations.
Guideline 1: Ensure that the testing dataset is representative of what will be observed in practice
In order to evaluate a model’s performance for use in practice, it is imperative to use a testing dataset that is independent of the training dataset. This requirement is generally met in FOP literature. This guideline follows from the well-known fact that using data that the model used in training leads to optimistic estimates of model performance (e.g. Géron 2017). When splitting the data into training and testing sets, we recommend reserving the most recent years for model testing because this represents how the model would perform if used operationally in the recent past, which may be useful for engaging with fire management end users. An alternative would be to randomly sample years from the dataset. Regardless, we suggest a block sampling approach of full years so that performance can be assessed over full fire seasons.
The distribution of the testing dataset must also be representative of the distribution expected in practice (i.e. highly imbalanced in terms of the response variable of interest). This applies even if a response-dependent sampling method or some other subsampling method was used to reduce the size of the training dataset.
Guideline 2: Use area under the precision-recall curve (AUC-PR) to assess a model’s ability to rank observations
In cases with imbalanced data, it has been suggested that AUC-PR be used to assess model performance instead of AUC-ROC (e.g. Jeni et al. 2013; Saito and Rehmsmeier 2015). Like AUC-ROC, AUC-PR is a threshold-independent metric that evaluates a model’s ability to rank observations in terms of their relative likelihood of fire occurrence. Unlike AUC-ROC, this metric does not have a level of model performance associated with different ranges of values as described previously. The baseline AUC-PR is the overall proportion of positive observations in the data and a model whose AUC-PR exceeds the AUC-PR of another model is interpreted as having better predictive performance. This metric has been shown to be more effective than AUC-ROC in differentiating between models’ early retrieval performance (Saito and Rehmsmeier 2015), which for FOP corresponds to the performance of a model for the observations deemed most probable to be a fire occurrence.
Guideline 3: Quantitatively assess the calibration of a model using appropriate metrics
Nadeem et al. (2020) assessed the calibration of their models by aggregating their predictions across space or over time. As will be discussed in Guideline 5, these metrics may be used in conjunction with spatial or temporal visualisations. Although this evaluation is helpful, we suggest also computing error terms directly from prediction–observation pairs. The former approach does not provide a way of choosing between two models if the spatial and temporal metrics are not in agreement, but our proposed approach facilitates using only a single metric to compare the calibration of models. We consider three well-known scoring rules for evaluating calibration in this manner; mean absolute error (MAE) (e.g. Willmott and Matsuura 2005), Brier score (BS) (Brier 1950) and logarithmic score (LS) (e.g. Bickel 2007) are defined as follows:


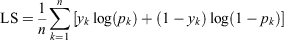
where k indexes the observations, n is the number of observations, pk is the modelled probability of occurrence, and yk is an indicator variable indicating whether or not the event was observed. A smaller value is better for MAE and BS, but for LS a larger (less negative) value indicates improved performance.
An advantage of MAE is that it provides an intuitive interpretation of how far off a model’s predictions are from actual observations. However, unlike BS and LS, it is not a proper scoring rule. Proper scoring rules have the property that their values are optimised by the true probabilities (e.g. Benedetti 2010). The fact that MAE does not have this property can lead to surprising, unwanted results when comparing models. Consider a situation with 1000 independent observations, each with a probability of fire occurrence of 1 in 1000. Suppose that there are the following two candidate models: a ‘correct’ (i.e. perfect) model that predicts fire occurrence with probability 1 in 1000 for each observation, and a ‘no fire’ model that always predicts zero probability of a fire. Consider the situation that corresponds to what is expected on average from the underlying process, namely exactly 1 of the 1000 observations is a fire. The MAE for the ‘correct’ model is 0.001998, but the MAE for the ‘no fire’ model is only 0.001, approximately half the MAE of the ‘correct’ model. In fact, the use of MAE would lead to choosing the ‘no fire’ model in any scenario where less than 500 fires occurred. Note that the probability of seeing more than even 10 fires in this hypothetical scenario is less than 1 in 100 million, meaning that the ‘no fire’ model would essentially always be chosen over the correct model if MAE was the scoring criteria. However, such a model would be of no use to fire management operations because it would never predict a fire. Although this is an overly simplified example because each observation has the same probability of fire occurrence, it illustrates that MAE can suggest the use of a model that is clearly inferior to another candidate model for use in practice. BS would not yield results as misleading as MAE, but it has also been shown that BS is a poor choice of scoring rule for use with imbalanced data (Benedetti 2010). For the situation as described above with exactly one fire occurring, the improvement in BS from using the ‘correct’ model instead of the ‘no fire’ model is only 0.1%. Benedetti advocates for the use of LS, particularly in cases with imbalanced data.
Of the three metrics considered, we suggest the use of LS for evaluating FOP models. However, a potential downside of this metric is that it places equal importance on identifying fire observations and non-fire observations, even though a fire management agency may wish to place more emphasis on identifying the former. This can be done by using a customised metric from the Beta family of scoring rules (Merkle and Steyvers 2013), which is defined as follows:
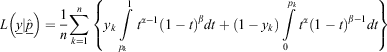
where 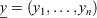 is a vector of observed responses,
is a vector of observed responses, 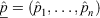 is a vector of corresponding predictions, and the parameters, α > −1, β > −1, control the shape of the scoring rule. Specifically, the term α/(α + β) can be set to reflect the relative cost of false positives to false negatives. If positive values are chosen such that β > α, the metric places larger emphasis on identifying the minority class (fire observations) than the majority class (non-fire observations). Note also that BS and LS are special cases from this Beta family of scoring rules with parameter values α = β = 1 and α = β = 0 respectively; see Merkle and Steyvers (2013) for more details.
is a vector of corresponding predictions, and the parameters, α > −1, β > −1, control the shape of the scoring rule. Specifically, the term α/(α + β) can be set to reflect the relative cost of false positives to false negatives. If positive values are chosen such that β > α, the metric places larger emphasis on identifying the minority class (fire observations) than the majority class (non-fire observations). Note also that BS and LS are special cases from this Beta family of scoring rules with parameter values α = β = 1 and α = β = 0 respectively; see Merkle and Steyvers (2013) for more details.
Guideline 4: Recognise that there is variability in performance metrics
It is important to recognise that a model’s performance on a testing dataset has an element of uncertainty associated with it. Specifically, if different datasets were used for testing models, we would (likely) obtain different values for each metric for each model. Hence, each metric can also be viewed as a realisation of a random variable drawn from a given sampling distribution. If interested in a statistical comparison of models, a paired t-test can be performed, using as inputs the individual error terms for each prediction–observation pair. It should be noted that these error terms do not exist for the ranking metrics (AUC-ROC and AUC-PR) and that the non-parametric alternative to the t-test, the Wilcoxon signed rank test (Wilcoxon 1992), is not an appropriate statistical test for comparing FOP models. The latter is more robust to outliers, but for FOP, the outliers are the fire occurrences (the observations in which we have the most interest), so the robustness to outliers is not a desirable property. For the ranking metrics, visualisations of the receiver operating characteristic and precision-recall curves can be used to assess if a subset of observations dramatically impacts the metric.
Guideline 5: Use visualisations to qualitatively evaluate models
As mentioned, FOP models should be evaluated not only quantitatively but also qualitatively. We advocate for the use of time series plots of observed and predicted counts of fires aggregated daily over the study region (e.g. Woolford et al. 2011; Magnussen and Taylor 2012) and colour-coded maps of predicted fire outcomes (e.g. Magnussen and Taylor 2012; Stojanova et al. 2012; Nadeem et al. 2020), both of which can be paired with calibration metrics for predictions aggregated over space or time. These maps of predictions can be presented for a variety of time periods (e.g. daily, weekly, monthly). For sufficiently short time periods, observed fires can be overlaid as points, but this is impractical for longer time periods because there will be too many fires in some regions. In these cases, a colour-coded map can be created for the observed fire occurrences as well, and the visualisations can be compared side by side.
Guideline 6: Collaborate with end users to ensure models meet their needs
As mentioned in the third guideline, end users may value different aspects when it comes to evaluating model performance. It is necessary to collaborate with end users in order to understand their priorities and develop and select models that meet their needs, which may extend beyond model performance. Fire management agencies tend to be reluctant to trust FOP models (Xi et al. 2019); thus, interpretability should be considered in the model development and selection process. Although complex models (e.g. random forests, neural networks) have been developed for FOP, they have infrequently been used for decision support in fire management operations, possibly owing to their lack of interpretability (Costafreda-Aumedes et al. 2017). Even if a model is shown to have statistically significantly better performance than another – keeping in mind that statistical significance does not imply practical significance – if the latter model is more easily interpreted, it may be more effective for operational use because its outputs are more trusted by fire management agencies. When developing, evaluating and comparing FOP models, it is important to consider the needs of the end users in determining the overall efficacy of each model.
Case study: fire occurrence prediction in Lac La Biche, Alberta, Canada
Here, we illustrate the importance of our guidelines through a case study analysis. We note that our objective here is not to determine the ‘gold standard’ for FOP modelling in the study region. Rather, our objective is to demonstrate the importance of these guidelines when evaluating and comparing a variety of data-driven modelling methods that are commonly used for spatially and temporally explicit fine-scale FOP. All analyses were performed in R (R Core Team 2017).
Study region
Our case study is for a 23 000 km2 region that approximates Fire Control Zone 42 in Alberta, a western province of Canada (Fig. 1). We refer to our study area as the Lac La Biche region because wildland fires in this area are managed by an office of Alberta Ministry of Agriculture and Forest located in the town of Lac La Biche (Sherry et al. 2019). This region is in the Boreal Plains ecozone of Canada, which experiences moderately warm summers and contains a mix of coniferous (black spruce, jack pine and tamarack) and deciduous (white birch, trembling aspen and balsam poplar) trees (Ecological Stratification Working Group 1995).
We analysed data for the Lac La Biche study region for the 1996–2016 fire seasons (March through October). In order to develop spatially and temporally explicit FOP models, our study region and period were partitioned into a set of space–time voxels. These voxels have a spatial resolution of 10 × 10 km and a temporal resolution of 1 day. The Wildfire Management Branch of Alberta Agriculture and Forestry (AF) was consulted in this choice and they provided the spatial grid. Fire Control Zone 42 is an irregularly shaped region; some cells in our study region extend beyond the fire control zone, while other cells along the zone’s border are classified as part of another fire control zone and thus do not belong to our study region. The study region falls along the eastern border of Alberta, so some cells on the boundary have a lower spatial resolution, as is common in FOP modelling over a grid.
Data from various sources provided by AF were compiled into a single dataset for modelling, recorded at the voxel level. Data sources included the following: historical AF fire records; historical daily fire-weather records observed at a set of weather stations across the province that were then interpolated to the centroid of each voxel; the Infrastructure Interface (INF), Wildland Industry Interface (WII) and Wildland–Urban Interface (WUI) of Johnston and Flannigan (2018) and geographic information system (GIS) layers that represent human-land use patterns such as roads and railways, as well as ecological characteristics such as CFFDRS fuel types (e.g. Stocks et al. 1989) and ecological classifications (Ecological Stratification Working Group 1995).
Specific covariates available for use as predictors for FOP modelling included both static and dynamic variables. Static variables included ecological information, such as fuel type inventories (e.g. percentage of cell covered in a CFFDRS fuel type, water and non-fuel) as well as variables that record specific information about land use such as the percentage of the cell that is WII, WUI and INF, and lengths of roads, railways, etc. Dynamic variables included weather (e.g. precipitation, relative humidity, temperature) as well as Canadian Fire Weather Index (FWI) System variables, which were computed using the cffdrs package (Wang et al. 2017). For information about the CFFDRS and its FWI System, including a description of FWI variables, see Wotton (2009) and references therein.
Both lightning and human-caused fires occur in our study region. Stratifying occurrences by cause (lightning v. human) for FOP modelling across Canada is common (e.g. Martell et al. 1987; Vega-Garcia et al. 1995, 1996; Magnussen and Taylor 2012; Woolford et al. 2016; Nadeem et al. 2020) because of different drivers of fire occurrence between lightning and human-caused fires, including the fact that lightning-caused fires have the potential to smoulder in the duff layer for an extended period of time before detection (e.g. Kourtz and Todd 1991; Wotton and Martell 2005). This is not the case for human-caused fires, which commonly ignite in dry surface fine fuels in areas where quick detection is likely (Woolford et al. 2020). For the purpose of our illustrative case study, we focused on human-caused fire occurrences. At the space–time scale of the voxels, counts of human-caused fires were effectively reduced to a dichotomous (i.e., 0/1) variable with 1 denoting that cell experiencing a fire day (i.e. one or more human-caused fires occurred, with occurrences of more than one fire in a voxel being extremely rare) and 0 indicating that no human-caused fires occurred in that local region on that given day.
Modelling
Data from 1996–2011 were chosen as a training dataset and data from 2012–16 were reserved as a testing dataset to facilitate evaluating and comparing the performance of the models on unseen data. As previously noted, this block sampling retains full fire seasons for model testing. Our training dataset had over 900 000 observations, but there were only 550 voxels in which a fire occurred. As several past FOP studies have used balanced or approximately balanced training datasets (e.g. Vega-Garcia et al. 1995, 1996; Alonso-Betanzos et al. 2003; Stojanova et al. 2006, 2012), we sampled 550 non-fire occurrences from the training dataset in order to create a balanced training dataset that was needed for some of the modelling methods. A separate balanced dataset was also created from the testing data. Models were evaluated and compared using this as well as the unsampled (imbalanced) testing dataset in order to illustrate how the choice of testing data can impact model assessments and comparisons.
In order to facilitate showing the importance of the guidelines we suggest, we used four different types of models that have all previously been used for FOP: logistic regression (e.g. Martell et al. 1987, 1989; Vega-Garcia et al. 1995), bagged classification trees (e.g. Stojanova et al. 2006, 2012), random forests (e.g. Stojanova et al. 2006, 2012; Bar Massada et al. 2013; Rodrigues and de la Riva 2014; Van Beusekom et al. 2018) and neural networks (e.g. Vega-Garcia et al. 1996; Vasconcelos et al. 2001; Alonso-Betanzos et al. 2003; Sakr et al. 2011). For more information on the framework of any of the models, see the cited studies. However, it should be noted that the modelling approach can differ even within the same type of model. For example, Vega-Garcia et al. (1996) trained their neural network using backpropagation, whereas Vasconcelos et al. (2001) employed a genetic algorithm. We implemented logistic regression using the mgcv package (Wood 2011), the bagged classification trees and random forest using the randomForest package (Liaw and Wiener 2002), and the neural network using the keras package (Chollet and Allaire 2017).
As appropriate, we used the default settings for both the bagged classification trees and random forest. The neural network was a multilayer perceptron trained using binary cross entropy loss with the Adam optimiser (Kingma and Ba 2014). Early stopping (e.g. Prechelt 1998) was used to prevent the model from overfitting. In order to facilitate early stopping, a validation dataset was needed. One hundred observations were taken from the training dataset to form a validation dataset, leaving 1000 observations remaining in the neural network’s training dataset. This random splitting was performed in a way that ensured both datasets were balanced. A maximum of 300 epochs were used for training, but if the loss on the validation dataset had not improved after the most recent 30 epochs, the model-fitting process was stopped. The neural network had three layers: an input layer that performed batch normalisation (Ioffe and Szegedy 2015), a single hidden layer with 10 neurons that used the rectified linear unit (ReLU) activation function (Nair and Hinton 2010), and an output layer that used the sigmoid activation function.
All four types of models were trained using the same set of covariates. We included the components of the FWI System, namely the Fine Fuel Moisture Code (FFMC), Duff Moisture Code (DMC), Drought Code (DC), Initial Spread Index (ISI), Build-up Index (BUI), FWI and Daily Severity Rating (DSR). Temperature, relative humidity, wind speed and precipitation were also used as measures of the weather. The proportion of each cell classified as WII, WUI and INF was used to represent where people are and their interactions with the forest. In addition, the proportion of the cell covered in water was incorporated. To capture intra-annual trends as well as spatial trends that are unaccounted for by other predictors, we included covariates for day of year, latitude and longitude. Many of these predictors were correlated with one another, but this was not a concern because our focus was on prediction, not inference, and good predictions can still be obtained even with strong multicollinearity (e.g. Paul 2006).
We also fitted a second logistic regression model to the entire (unsampled) training dataset using only FFMC as a predictor, because FFMC has been well established as a key driver of human-caused fire occurrence, starting with the work of Cunningham and Martell (1973). This very simple model can be treated as a baseline for the other models when evaluating the performance of each model on an unsampled testing dataset. We refer to this model as the baseline logistic regression model and the other logistic regression model, which used several covariates, as the multiple logistic regression model.
Model evaluation and comparison
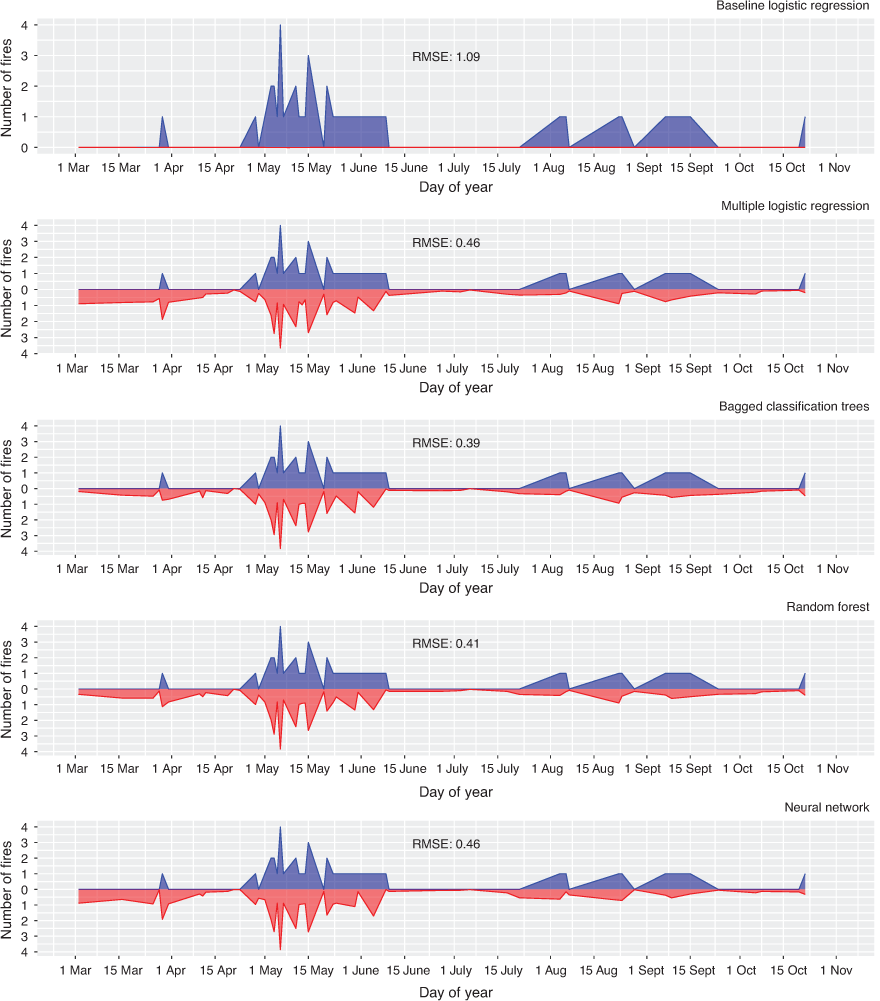
As previously noted, we evaluated and compared the models using both a balanced testing dataset and an unsampled (imbalanced) testing dataset. Fig. 2 shows a temporal ‘mirror’ plot and RMSE for each of the models for the 2013 fire season, using a balanced testing dataset. Except for the baseline logistic regression model, the models appear to do an excellent job identifying fire occurrences. However, our interpretation of their performance changes dramatically if the unsampled testing dataset is used, which is what would occur if such models were implemented in practice. Fig. 3 displays the temporal plots and RMSEs for 2013 using the unsampled testing data. It is immediately clear that the models fitted using balanced training data provide grossly overestimated predictions of the number of fires throughout the fire season. In Fig. 4, we show spatial prediction maps for the models for 5 May 2013. The most notable observation from these visualisations is that the baseline logistic regression model outputs nearly uniform predictions. (A different scale was used for that plot to illustrate that there are some minor spatial differences in predictions.) Although not nearly as noticeable, the multiple logistic regression model also appears to offer less spatial discrimination than the machine learning models.

|
In addition to the visualisations, we compared the performance of the models using several metrics commonly used in past FOP studies as well as other metrics as suggested herein. Metrics associated with a confusion matrix, namely accuracy, precision, recall, specificity and kappa, were computed using the caret package (Kuhn 2008) using a threshold probability of 0.5. The package PRROC (Grau et al. 2015) was used to compute both AUC-ROC and AUC-PR. It uses two different ways to calculate AUC-PR, a linear interpolation approach (Davis and Goadrich 2006) and an integration approach (Boyd et al. 2013; Keilwagen et al. 2014). We have found that these values are typically quite similar, so only the values from the most recent approach are presented. In order to assess calibration, we computed BS, negative logarithmic score (NLS), and a customised metric from the Beta family that placed more importance on identifying fire occurrences by setting parameters to α = 1 and β = 99. We used NLS instead of LS so that a smaller value indicates better performance regardless of the calibration metric under consideration.
The top part of Table 1 shows the values obtained for each metric using the balanced testing dataset. The three machine learning models performed very similarly, in general outperforming the logistic regression models. For the machine learning models, the calibration metrics are not in agreement in ranking the models. The values for BS suggest that the random forest and bagged classification trees outperformed the neural network. However, the values obtained for NLS and the customised metric suggest the opposite. Paired t-tests were performed to compare the tree-based approaches with the neural network for BS and the customised metric, but none of these tests provided strong evidence of a difference (0.12 ≤ P ≤ 0.78 for all four tests). These tests were not performed for NLS because both tree-based methods incorrectly predicted events with certainty (i.e. a probability of 0 or 1), causing infinite scores for NLS.
The values for each metric using the unsampled testing dataset are shown in the bottom of Table 1. There are several cases where a model appeared to have outperformed another when using a balanced testing dataset, but the latter model performed better on the unsampled testing dataset. For example, in terms of BS, bagged classification trees were better calibrated than random forests when using the balanced testing dataset (although a paired t-test did not find statistically significant evidence of this statement with P ≈ 0.51), but the opposite was true when using the unsampled testing dataset (P ≪ 0.001). This demonstrates that the ranking of models can change as a result of distorting the distribution of the testing dataset. The baseline logistic regression model easily achieved the highest accuracy simply by classifying every observation as a non-fire occurrence. However, it is clear from both the AUC-ROC and AUC-PR that this model was inferior to the others in terms of ranking the observations, which is unsurprising given the uniformity of its predictions. In terms of percentage change, AUC-PR shows much more substantial changes in model performance than AUC-ROC. For example, with imbalanced testing data, the percentage changes from the worst model to the best model (in terms of AUC-ROC and AUC-PR) are 24 and 795% for AUC-ROC and AUC-PR respectively. When comparing the random forest with the neural network, the percentage changes are 1.5 and 69% respectively. These relatively large changes corroborate past studies that have suggested that AUC-PR may be able to highlight differences in model performance that are not shown by AUC-ROC in cases with imbalanced data (e.g. Jeni et al. 2013; Saito and Rehmsmeier 2015).
Discussion
We have outlined several pitfalls of model evaluation and comparison in FOP literature and provided a set of guidelines to aid in selecting a model that is well suited for operational use. These include the following six recommendations: (1) ensure the testing dataset always represents the distribution of the data encountered in practice; (2) use AUC-PR to compare the models’ ability to rank observations; (3) quantitatively assess the calibration of a model using appropriate metrics (such as the LS and/or a customised metric from the Beta family); (4) address variability in performance metrics; (5) use temporal and spatial visualisations to qualitatively evaluate the models; (6) and collaborate with end users to ensure that models meet their needs. Such guidelines for evaluating models should be followed even if one is developing a single type of model and not comparing across a set of different types of FOP modelling methods. We emphasise that the focus of these guidelines is model evaluation and comparison, not model fitting, and that details on an appropriate model development process (e.g. if the aim is to identify significant relationships, handling possible multicollinearity) are outside the scope of this paper.
Through a case study, we have demonstrated that the use of model selection processes that do not follow such guidelines may select a model that is a poor choice for operational use. By following these guidelines, we were able to clearly determine that all five models in our case study were poor choices for use in practice. The baseline logistic regression model offered very little spatial discrimination and therefore would not be helpful in determining how to allocate resources across the study region. As expected owing to the assessment of fit using the mirror plots and RMSE values contained in Fig. 3, all three calibration metrics (BS, NLS and the customised metric from the Beta family of scoring rules) indicate that the four models fitted using a balanced training dataset were all very poorly calibrated. These four other models all predicted far too many fires, indicating that they would provide misleading guidance for long-term planning and distort computations of risk. Had we used some of the evaluation and comparison approaches used in FOP literature, we may not have identified the deficiencies in our models. For example, both the accuracy and AUC-ROC obtained by these models are competitive with values obtained in past FOP studies (e.g. Vega-Garcia et al. 1995, 1996; Vasconcelos et al. 2001; Alonso-Betanzos et al. 2003; Stojanova et al. 2006, 2012; Bar Massada et al. 2013; Rodrigues and de la Riva 2014; Van Beusekom et al. 2018; Nadeem et al. 2020). However, the use of an unsampled testing dataset, along with visualisations and metrics that assess calibration, revealed that the models were very poorly calibrated.
As noted in the meta-analysis of Costafreda-Aumedes et al. (2017), it can be difficult to synthesise results across different studies and model types. When comparing metrics across different models (as was done in our study and has been done in other past studies), it is important to recognise that they could vary with the fitted model and the given testing dataset. Ideally, the testing dataset should be large enough to ensure that the calculated metrics are relatively stable. However, the limited number of positive observations in an imbalanced dataset can lead to a large amount of variability when calculating a metric. For example, our testing dataset had 291 312 observations, but only 193 fire occurrences. As shown in Appendix 1, by swapping the ranking of only two predictions, the AUC-PR can change by as much as 0.0039, which is a relatively large change considering the small scores for all five models (Table 1). In future work, we plan to develop a set of better-suited candidate models from which to select a final human-caused FOP model for this region. As mentioned in Guideline 4, when doing so, it will be important to plot precision-recall curves in order to determine if differences in AUC-PRs were caused by very minor differences in predictions. Claiming that one model is better than another based on a small difference in AUC-PR may be very misleading to end users.
In our evaluation of the models, we presented spatial prediction maps for only a single day (Fig. 4). It should be noted that this sample day was shown for illustrative purposes and that examining only a single day is not a sufficient procedure for evaluating and comparing FOP models. In general, a variety of scenarios should be examined for a thorough comparison and evaluation of models when developing an FOP system for use by fire management. These scenarios should be chosen in consultation with fire management staff. For example, daily fire activity over the course of several fire seasons in the testing dataset could be classified as low, moderate and high and then a random sample of days within each of these strata could be examined. Alternatively, one could create a dynamic visualisation that showed the progression of maps over the course of several fire seasons reserved for testing, which could be viewed by fire management personnel and the researchers to qualitatively assess a model’s performance.
Conclusion
We have proposed a set of guidelines for evaluating and comparing FOP models. These guidelines cover the choice of testing data, the use of appropriate metrics and visualisations for model evaluation, variability in performance metrics, and collaboration with end users. Using these guidelines, we have shown that all five models developed in our case study are not well suited for decision support in fire management operations. All models that were fitted using a balanced training dataset systematically overpredicted the number of fire occurrences. Given that many machine learning models in FOP literature have been trained using a response-based sample of the data like the one used in this study, our results suggest that several past machine learning models designed for FOP could also be very poorly calibrated and thus not suitable for operational use to predict the number of fire occurrences. This may also be true for some logistic FOP models, but several recent studies have accounted for this biased sample by incorporating an offset term into the logistic model (e.g. Brillinger et al. 2003; Vilar et al. 2010; Woolford et al. 2011, 2016; Nadeem et al. 2020), as was first done for FOP modelling by Vega-Garcia et al. (1995). To our knowledge, machine learning FOP models have never been trained in a manner that reflects the biased training data, but techniques such as Platt’s Scaling (Platt 1999) and an equation proposed by Dal Pozzolo et al. (2015) can be used to account for this bias. Future studies that use machine learning for FOP should consider these or other approaches to improve model calibration.
Conflicts of interest
The authors declare no conflicts of interest.
Acknowledgements
We acknowledge the support of the Natural Sciences and Engineering Research Council of Canada (NSERC), (RGPIN-2015-04221, and its USRA program), the Institute for Catastrophic Loss Reduction, as well as of the Government of Alberta who is also thanked for providing the data. B. Moore, A. Stacey and M. Wotton are thanked for their assistance in preparing the data for modelling. C. Tymstra, B. Moore, D. Finn, M. Wotton and M. Flannigan are thanked for helpful conversations related to wildland fire occurrence in Alberta. C. Tymstra is also acknowledged for his strong advocation for the use of FOP in Alberta. Helpful comments made by an anonymous associate editor and a set of reviewers that led to significant improvements in the manuscript are gratefully acknowledged.
References
Alexander ME, Taylor SW, Page WG (2015) Wildland firefighter safety and fire behavior prediction on the fireline. In ‘Proceedings of the 13th international wildland fire safety summit & 4th human dimensions wildland fire conference’. Boise, Idaho, USA. pp. 20–24. (International Association of Wildland Fire, Missoula, Montana, USA)Alonso-Betanzos A, Fontenla-Romero O, Guijarro-Berdiñas B, Hernández-Pereira E, Andrade MIP, Jiménez E, Soto JLL, Carballas T (2003) An intelligent system for forest fire risk prediction and firefighting management in Galicia. Expert Systems with Applications 25, 545–554.
| An intelligent system for forest fire risk prediction and firefighting management in Galicia.Crossref | GoogleScholarGoogle Scholar |
Bar Massada A, Syphard AD, Stewart SI, Radeloff VC (2013) Wildfire ignition-distribution modelling: a comparative study in the Huron–Manistee National Forest, Michigan, USA. International Journal of Wildland Fire 22, 174–183.
| Wildfire ignition-distribution modelling: a comparative study in the Huron–Manistee National Forest, Michigan, USA.Crossref | GoogleScholarGoogle Scholar |
Benedetti R (2010) Scoring rules for forecast verification. Monthly Weather Review 138, 203–211.
| Scoring rules for forecast verification.Crossref | GoogleScholarGoogle Scholar |
Bickel JE (2007) Some comparisons among quadratic, spherical, and logarithmic scoring rules. Decision Analysis 4, 49–65.
| Some comparisons among quadratic, spherical, and logarithmic scoring rules.Crossref | GoogleScholarGoogle Scholar |
Boyd K, Eng KH, Page CD (2013) Area under the precision-recall curve: point estimates and confidence intervals. In ‘Joint European conference on machine learning and knowledge discovery in databases’, 23–27 September 2013, Prague, Czech Republic. (Eds H Blockeel, K Kersting, S Nijssen, F Železný), pp. 451–466. (Springer: Berlin, Germany)
Brier GW (1950) Verification of forecasts expressed in terms of probability. Monthly Weather Review 78, 1–3.
| Verification of forecasts expressed in terms of probability.Crossref | GoogleScholarGoogle Scholar |
Brillinger DR, Preisler HK, Benoit JW (2003) Risk assessment: a forest fire example. Lecture Notes -Monograph Series 40, 177–196.
| Risk assessment: a forest fire example.Crossref | GoogleScholarGoogle Scholar |
Chawla NV, Japkowicz N, Kotcz A (2004) Special issue on learning from imbalanced data sets. SIGKDD Explorations 6, 1–6.
| Special issue on learning from imbalanced data sets.Crossref | GoogleScholarGoogle Scholar |
Chollet F, Allaire JJ (2017) R interface to keras. Available at https://keras.rstudio.com/index.html [Verified 17 December 2020]
Costafreda-Aumedes S, Comas C, Vega-Garcia C (2017) Human-caused fire occurrence modelling in perspective: a review. International Journal of Wildland Fire 26, 983–998.
| Human-caused fire occurrence modelling in perspective: a review.Crossref | GoogleScholarGoogle Scholar |
Cunningham AA, Martell DL (1973) A stochastic model for the occurrence of man-caused forest fires. Canadian Journal of Forest Research 3, 282–287.
| A stochastic model for the occurrence of man-caused forest fires.Crossref | GoogleScholarGoogle Scholar |
Dal Pozzolo A, Caelen O, Johnson RA, Bontempi G (2015) Calibrating probability with undersampling for unbalanced classification. In ‘2015 IEEE symposium series on computational intelligence’, 7–10 December 2015, Cape Town, South Africa. pp. 159–166. (IEEE)
Davis J, Goadrich M (2006) The relationship between Precision-Recall and ROC curves. In ‘Proceedings of the 23rd international conference on machine learning’, 25–29 June 2006, Pittsburgh, USA. pp. 233–240. (ACM)
Ecological Stratification Working Group (1995) A national ecological framework for Canada. Report and national map at 1 : 7 500 000 scale. Agriculture and Agri-Food Canada, Research Branch, Centre for Land and Biological Resources Research and Environment Canada, State of the Environment Directorate, Ecozone Analysis Branch. (Ottawa/Hull, Canada).
Géron A (2017) ‘Hands-on machine learning with Scikit-Learn and TensorFlow: concepts, tools, and techniques to build intelligent systems’. (O’Reilly Media, Inc.: Sebastopol, CA, USA)
Grau J, Grosse I, Keilwagen J (2015) PRROC: computing and visualizing precision-recall and receiver operating characteristic curves in R. Bioinformatics 31, 2595–2597.
| PRROC: computing and visualizing precision-recall and receiver operating characteristic curves in R.Crossref | GoogleScholarGoogle Scholar | 25810428PubMed |
Hanley JA, McNeil BJ (1982) The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 143, 29–36.
| The meaning and use of the area under a receiver operating characteristic (ROC) curve.Crossref | GoogleScholarGoogle Scholar | 7063747PubMed |
Harrell FE, Jr (2015) ‘Regression modeling strategies: with applications to linear models, logistic and ordinal regression, and survival analysis.’ (Springer: Berlin, Germany)
Hosmer DW, Jr, Lemeshow S, Sturdivant RX (2013) ‘Applied logistic regression.’ (John Wiley & Sons)
Ioffe S, Szegedy C (2015) Batch normalization: accelerating deep network training by reducing internal covariate shift. Journal of Machine Learning Research 37, 448–456.
Jeni LA, Cohn JF, De La Torre F (2013) Facing imbalanced data – recommendations for the use of performance metrics. In ‘2013 Humaine Association conference on affective computing and intelligent interaction’, 2–5 September 2013, Geneva, Switzerland. pp. 245–251. (IEEE)
Johnston LM, Flannigan MD (2018) Mapping Canadian wildland fire interface areas. International Journal of Wildland Fire 27, 1–14.
| Mapping Canadian wildland fire interface areas.Crossref | GoogleScholarGoogle Scholar |
Johnston LM, Wang X, Erni S, Taylor SW, McFayden CB, Oliver JA, Stockdale C, Christianson A, Boulanger Y, Gauthier S, Arseneault D, Wotton BM, Parisien MA, Flannigan MD (2020) Wildland fire risk research in Canada. Environmental Reviews 28, 164–186.
| Wildland fire risk research in Canada.Crossref | GoogleScholarGoogle Scholar |
Keilwagen J, Grosse I, Grau J (2014) Area under precision-recall curves for weighted and unweighted data. PLoS One 9, e92209
| Area under precision-recall curves for weighted and unweighted data.Crossref | GoogleScholarGoogle Scholar | 24651729PubMed |
Kingma D, Ba J (2014) Adam: a method for stochastic optimization. In ‘Proceedings of the 3rd international conference on learning representations’, 7–9 May 2015, San Diego, USA.
Kourtz P, Todd B (1991) Predicting the daily occurrence of lightning-caused forest fires. Forestry Canada, Petawawa National Forest Institute, Information Report PI-X-112. (Chalk River, ON).
Kuhn M (2008) Building predictive models in R using the caret package. Journal of Statistical Software 28, 1–26.
| Building predictive models in R using the caret package.Crossref | GoogleScholarGoogle Scholar |
Liaw A, Wiener M (2002) Classification and regression by randomForest. R News 2, 18–22.
Magnussen S, Taylor SW (2012) Prediction of daily lightning-and human-caused fires in British Columbia. International Journal of Wildland Fire 21, 342–356.
| Prediction of daily lightning-and human-caused fires in British Columbia.Crossref | GoogleScholarGoogle Scholar |
Martell DL (2007) Forest fire management: current practices and new challenges for operational researchers. In ‘Handbook of operations research in natural resources’. (Eds A Weintraub, C Romero, T Bjørndal, R Epstein) pp. 489–509. (Springer: Berlin, Germany)
Martell DL, Otukol S, Stocks BJ (1987) A logistic model for predicting daily people-caused forest fire occurrence in Ontario. Canadian Journal of Forest Research 17, 394–401.
| A logistic model for predicting daily people-caused forest fire occurrence in Ontario.Crossref | GoogleScholarGoogle Scholar |
Martell DL, Bevilacqua E, Stocks BJ (1989) Modelling seasonal variation in daily people-caused forest fire occurrence. Canadian Journal of Forest Research 19, 1555–1563.
| Modelling seasonal variation in daily people-caused forest fire occurrence.Crossref | GoogleScholarGoogle Scholar |
McFayden CB, Woolford DG, Stacey A, Boychuk D, Johnston JM, Wheatley MJ, Martell DL (2020) Risk assessment for wildland fire aerial detection patrol route planning in Ontario, Canada. International Journal of Wildland Fire 29, 28–41.
| Risk assessment for wildland fire aerial detection patrol route planning in Ontario, Canada.Crossref | GoogleScholarGoogle Scholar |
Merkle EC, Steyvers M (2013) Choosing a strictly proper scoring rule. Decision Analysis 10, 292–304.
| Choosing a strictly proper scoring rule.Crossref | GoogleScholarGoogle Scholar |
Nadeem K, Taylor SW, Woolford DG, Dean CB (2020) Mesoscale spatio-temporal predictive models of daily human and lightning-caused wildland fire occurrence in British Columbia. International Journal of Wildland Fire 29, 11–27.
| Mesoscale spatio-temporal predictive models of daily human and lightning-caused wildland fire occurrence in British Columbia.Crossref | GoogleScholarGoogle Scholar |
Nair V, Hinton GE (2010) Rectified linear units improve restricted Boltzmann machines. In ‘Proceedings of the 27th international conference on machine learning’, 21–24 June 2010, Haifa, Israel. (Eds J Fürnkranz, T Joachims) pp. 807–814. (Omnipress: Madison, WI, United States)
Natural Resources Canada (2020) Canadian Forest Fire Danger Rating System (CFFDRS) summary. Available at https://cwfis.cfs.nrcan.gc.ca/background/summary/fdr [Verified 7 December 2020]
Orriols-Puig A, Bernadó-Mansilla E (2009) Evolutionary rule-based systems for imbalanced data sets. Soft Computing 13, 213–225.
| Evolutionary rule-based systems for imbalanced data sets.Crossref | GoogleScholarGoogle Scholar |
Paul RK (2006) Multicollinearity: causes, effects and remedies. IASRI 1, 58–65.
Platt J (1999) Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Advances in Large Margin Classifiers 10, 61–74.
Plucinski MP (2012) A review of wildfire occurrence research. Bushfire Cooperative Research Centre. (Melbourne, Vic., Australia)
Plucinski MP, McCaw WL, Gould JS, Wotton BM (2014) Predicting the number of daily human-caused bushfires to assist suppression planning in south-west Western Australia. International Journal of Wildland Fire 23, 520–531.
| Predicting the number of daily human-caused bushfires to assist suppression planning in south-west Western Australia.Crossref | GoogleScholarGoogle Scholar |
Prechelt L (1998) Early stopping – but when? In ‘Neural networks: tricks of the trade’. (Eds GB Orr, K-R Müller) pp. 55–69. (Springer: Berlin, Germany)
Preisler HK, Brillinger DR, Burgan RE, Benoit JW (2004) Probability-based models for estimation of wildfire risk. International Journal of Wildland Fire 13, 133–142.
| Probability-based models for estimation of wildfire risk.Crossref | GoogleScholarGoogle Scholar |
Preisler HK, Westerling AL, Gebert KM, Munoz-Arriola F, Holmes TP (2011) Spatially explicit forecasts of large wildland fire probability and suppression costs for California. International Journal of Wildland Fire 20, 508–517.
| Spatially explicit forecasts of large wildland fire probability and suppression costs for California.Crossref | GoogleScholarGoogle Scholar |
R Core Team (2017) R: A language and environment for statistical computing. (R Foundation for Statistical Computing: Vienna, Austria). Available at https://www.R-project.org/ [Verified 17 December 2020]
Rodrigues M, de la Riva J (2014) An insight into machine-learning algorithms to model human-caused wildfire occurrence. Environmental Modelling & Software 57, 192–201.
| An insight into machine-learning algorithms to model human-caused wildfire occurrence.Crossref | GoogleScholarGoogle Scholar |
Saito T, Rehmsmeier M (2015) The precision-recall plot is more informative than the ROC plot when evaluating binary classifiers on imbalanced datasets. PLoS One 10, e0118432
| The precision-recall plot is more informative than the ROC plot when evaluating binary classifiers on imbalanced datasets.Crossref | GoogleScholarGoogle Scholar | 26469698PubMed |
Sakr GE, Elhajj IH, Mitri G, Wejinya UC (2010) Artificial intelligence for forest fire prediction. In ‘2010 IEEE/ASME international conference on advanced intelligent mechatronics’. pp. 1311–1316. (IEEE)
Sakr GE, Elhajj IH, Mitri G (2011) Efficient forest fire occurrence prediction for developing countries using two weather parameters. Engineering Applications of Artificial Intelligence 24, 888–894.
| Efficient forest fire occurrence prediction for developing countries using two weather parameters.Crossref | GoogleScholarGoogle Scholar |
Sherry J, Neale T, McGee TK, Sharpe M (2019) Rethinking the maps: a case study of knowledge incorporation in Canadian wildfire risk management and planning. Journal of Environmental Management 234, 494–502.
| Rethinking the maps: a case study of knowledge incorporation in Canadian wildfire risk management and planning.Crossref | GoogleScholarGoogle Scholar | 30641360PubMed |
Stocks BJ, Lynham TJ, Lawson BD, Alexander ME, Wagner CV, McAlpine RS, Dube DE (1989) Canadian Forest Fire Danger Rating System: an overview. Forestry Chronicle 65, 258–265.
| Canadian Forest Fire Danger Rating System: an overview.Crossref | GoogleScholarGoogle Scholar |
Stojanova D, Panov P, Kobler A, Džeroski S, Taskova K (2006) Learning to predict forest fires with different data mining techniques. In ‘Conference on data mining and data warehouses’. pp. 255–258. (SIKDD: Ljubljana, Slovenia)
Stojanova D, Kobler A, Ogrinc P, Ženko B, Džeroski S (2012) Estimating the risk of fire outbreaks in the natural environment. Data Mining and Knowledge Discovery 24, 411–442.
| Estimating the risk of fire outbreaks in the natural environment.Crossref | GoogleScholarGoogle Scholar |
Taylor SW, Woolford DG, Dean CB, Martell DL (2013) Wildfire prediction to inform management: statistical science challenges. Statistical Science 28, 586–615.
| Wildfire prediction to inform management: statistical science challenges.Crossref | GoogleScholarGoogle Scholar |
Todd JB, Kourtz PH (1991) Predicting the daily occurrence of people-caused forest fires. Forestry Canada, Petawawa National Forestry Institute, Information Report PI-X-103. (Chalk River, ON, Canada)
Tymstra C, Stocks BJ, Cai X, Flannigan MD (2020) Wildfire management in Canada: review, challenges and opportunities. Progress in Disaster Science 5, 100045
| Wildfire management in Canada: review, challenges and opportunities.Crossref | GoogleScholarGoogle Scholar |
Van Beusekom AE, Gould WA, Monmany AC, Khalyani AH, Quiñones M, Fain SJ, Andrade-Núñez MJ, González G (2018) Fire weather and likelihood: characterizing climate space for fire occurrence and extent in Puerto Rico. Climatic Change 146, 117–131.
| Fire weather and likelihood: characterizing climate space for fire occurrence and extent in Puerto Rico.Crossref | GoogleScholarGoogle Scholar |
Vasconcelos MJP, Silva S, Tome M, Alvim M, Pereira JC (2001) Spatial prediction of fire ignition probabilities: comparing logistic regression and neural networks. Photogrammetric Engineering and Remote Sensing 67, 73–81.
Vega-Garcia C, Woodard PM, Titus SJ, Adamowicz WL, Lee BS (1995) A logit model for predicting the daily occurrence of human caused forest-fires. International Journal of Wildland Fire 5, 101–111.
| A logit model for predicting the daily occurrence of human caused forest-fires.Crossref | GoogleScholarGoogle Scholar |
Vega-Garcia C, Lee BS, Woodard PM, Titus SJ (1996) Applying neural network technology to human-caused wildfire occurrence prediction. AI Applications 10, 9–18.
Vilar L, Woolford DG, Martell DL, Martín MP (2010) A model for predicting human-caused wildfire occurrence in the region of Madrid, Spain. International Journal of Wildland Fire 19, 325–337.
| A model for predicting human-caused wildfire occurrence in the region of Madrid, Spain.Crossref | GoogleScholarGoogle Scholar |
Wang X, Wotton BM, Cantin AS, Parisien MA, Anderson K, Moore B, Flannigan MD (2017) cffdrs: an R package for the Canadian Forest Fire Danger Rating System. Ecological Processes 6, 5
| cffdrs: an R package for the Canadian Forest Fire Danger Rating System.Crossref | GoogleScholarGoogle Scholar |
Wilcoxon F (1992) Individual comparisons by ranking methods. In ‘Breakthroughs in statistics’. (Eds S Kotz, NL Johnson) pp. 196–202. (Springer: New York, NY, USA)
Willmott CJ, Matsuura K (2005) Advantages of the mean absolute error (MAE) over the root-mean-square error (RMSE) in assessing average model performance. Climate Research 30, 79–82.
| Advantages of the mean absolute error (MAE) over the root-mean-square error (RMSE) in assessing average model performance.Crossref | GoogleScholarGoogle Scholar |
Wood SN (2011) Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. Journal of the Royal Statistical Society. Series B, Statistical Methodology 73, 3–36.
| Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models.Crossref | GoogleScholarGoogle Scholar |
Woolford DG, Bellhouse DR, Braun WJ, Dean CB, Martell DL, Sun J (2011) A spatiotemporal model for people-caused forest fire occurrence in the Romeo Malette forest. Journal of Environmental Statistics 2, 2–16.
Woolford DG, Wotton BM, Martell DL, McFayden C, Stacey A, Evens J, Caputo J, Boychuk D, Kuyvenhoven R, Leonard D, Leroux G, McLarty D, Welch F (2016) Daily lightning- and person-caused fire prediction models used in Ontario. Poster presented at Wildland Fire Canada 2016 Conference, Kelowna, BC, Canada. Available at http://www.wildlandfire2016.ca/wp-content/uploads/2019/11/McFayden-Fire-Occurence-Prediction-Poster-Ontario-2016-10-17V2Final.pdf [Verified 22 May 2020]
Woolford DG, Martell DL, McFayden C, Evens J, Stacey A, Wotton BM, Boychuk D (2020) The development and implementation of a human-caused wildland fire occurrence prediction system for the province of Ontario, Canada. Canadian Journal of Forest Research
| The development and implementation of a human-caused wildland fire occurrence prediction system for the province of Ontario, Canada.Crossref | GoogleScholarGoogle Scholar |
Wotton BM (2009) Interpreting and using outputs from the Canadian Forest Fire Danger Rating System in research applications. Environmental and Ecological Statistics 16, 107–131.
| Interpreting and using outputs from the Canadian Forest Fire Danger Rating System in research applications.Crossref | GoogleScholarGoogle Scholar |
Wotton BM, Martell DL (2005) A lightning fire occurrence model for Ontario. Canadian Journal of Forest Research 35, 1389–1401.
| A lightning fire occurrence model for Ontario.Crossref | GoogleScholarGoogle Scholar |
Xi DD, Taylor SW, Woolford DG, Dean CB (2019) Statistical models of key components of wildfire risk. Annual Review of Statistics and Its Application 6, 197–222.
| Statistical models of key components of wildfire risk.Crossref | GoogleScholarGoogle Scholar |
Appendix 1.
Consider two models yielding identical predictions for all but two observations. These observations have the two highest probabilities of a fire for both models. One of the observations is a fire and the other is not. For Model 1, the highest probability is for the observation with the fire and for Model 2 the highest probability is for the other observation. Below is a computation of the approximate change in AUC-PR for the testing dataset, which has 193 fires.


When the PR curves of the models diverge:

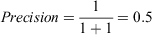
For Model 1:
When the decision threshold moves past the second largest prediction, the recall for Model 1 stays the same, but precision does not.

For Model 2:
When the threshold moves past the second largest prediction, both recall and precision change.
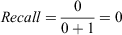
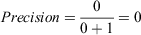
Computing the change in AUC-PR:
For Model 2, assume that the line segment drawn from (0.005181347, 0.5) to (0, 0) is straight (i.e. the area can be computed as a triangle).