An efficient, multi-scale neighbourhood index to quantify wildfire likelihood

Douglas A. G. Radford; Holger R. Maier; Hedwig van Delden; Aaron C. Zecchin; Amelie Jeanneau

doi:10.1071/WF23055

RESEARCH ARTICLE (Open Access)

Next Contents Vol 33(5)

An efficient, multi-scale neighbourhood index to quantify wildfire likelihood

Douglas A. G. Radford

^A ^* , Holger R. Maier ^A , Hedwig van Delden ^A ^B , Aaron C. Zecchin ^A and Amelie Jeanneau ^A

+ Author Affiliations

- Author Affiliations

^A The University of Adelaide, Adelaide, SA, Australia.

^B Research Institute for Knowledge Systems, Maastricht, The Netherlands.

^* Correspondence to: douglas.radford@adelaide.edu.au

International Journal of Wildland Fire 33, WF23055 https://doi.org/10.1071/WF23055

Submitted: 25 April 2023 Accepted: 4 April 2024 Published: 26 April 2024

© 2024 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of IAWF. This is an open access article distributed under the Creative Commons Attribution 4.0 International License (CC BY).

Abstract

Background

To effectively reduce future wildfire risk, several management strategies must be evaluated under plausible future scenarios, requiring models that provide estimates of how likely wildfires are to spread to community assets (wildfire likelihood) in a computationally efficient manner. Approaches to quantifying wildfire likelihood using fire simulation models cannot practically achieve this because they are too computationally expensive.

Aim

This study aimed to develop an approach for quantifying wildfire likelihood that is both computationally efficient and able to consider contagious and directionally specific fire behaviour properties across multiple spatial ‘neighbourhood’ scales.

Methods

A novel, computationally efficient index for quantifying wildfire likelihood is proposed. This index is evaluated against historical and simulated data on a case study in South Australia.

Key results

The neighbourhood index explains historical burnt areas and closely replicates patterns in burn probability calculated using landscape fire simulation (ρ = 0.83), while requiring 99.7% less computational time than the simulation-based model.

Conclusions

The neighbourhood index represents patterns in wildfire likelihood similar to those represented in burn probability, with a much-reduced computational time.

Implications

By using the index alongside existing approaches, managers can better explore problems involving many evaluations of wildfire likelihood, thereby improving planning processes and reducing future wildfire risks.

Keywords: burn probability, fire behaviour, fire management, fire simulation modelling, neighbourhood index, planning, risk, wildfire likelihood.

Introduction

Wildfires can have significant negative impacts on community ‘assets’ (Gill et al. 2013), including loss of life and damage to infrastructure, cultural values and the environment. These impacts can be seen across the globe (Gill et al. 2013), including in south-eastern Australia (Filkov et al. 2020), and are likely to get worse due to climate change. The changing climate has already resulted in an increase in the intensity and frequency of global wildfire weather (Jones et al. 2022), has already caused a notable increase in the area burnt in Australian forests (Canadell et al. 2021) and will increasingly reduce the efficacy of landscape interventions, such as fuel treatments (Clarke et al. 2022). A key component in planning to reduce the likelihood of these impacts is quantifying the relative likelihood of any wildfire spreading to specific assets or locations of interest (henceforth referred to as ‘wildfire likelihood’).

To understand wildfire likelihood, it is important to understand the way fire spreads across a landscape. The spread of fire is commonly considered a multi-scaled (McKenzie et al. 2011) and spatially contagious process (Peterson 2002; McKenzie and Kennedy 2011; Newman et al. 2019). Contagion is a function of both connectivity and momentum (McKenzie and Kennedy 2011; Newman et al. 2019). Connectivity describes the spatial arrangement of fuels that may transmit fire spread across a landscape, and momentum describes the potential energy driving fire spread. To quantify the momentum of fire spread, much effort has been spent to understand the relationships among weather, fuels and topography factors and their joint influence on the potential behaviour of wildfires (Rothermel 1983; Cruz et al. 2015). These factors are commonly considered as either top-down (i.e. climate and weather) or bottom-up (i.e. fuel and topography) in the way they influence fire behaviour (Heyerdahl et al. 2001; Parisien et al. 2010; Falk et al. 2011). Relevant quantitative measures of fire behaviour include potential rate of spread (ROS), head fire intensity (HFI) and ember-generation properties. In general, higher magnitude fire behaviour properties are related to the increased spread of fires and higher wildfire likelihood, either through faster fire spread or a reduced ability to suppress intense wildfires.

Landscape managers can reduce wildfire likelihood by taking actions that might reduce the potential momentum of fire spread (i.e. fire behaviour) or interrupt connectivity and stop the spread of fire toward an asset. These actions can reduce (or remove completely) fuel loads, change fuel structure and/or improve the ability to suppress fire. When considering these options at the landscape level, managers must make decisions across several dimensions (Ott et al. 2023). These include (i) where to locate treatments (e.g. whether close to assets or in the open landscape) and how large the treatment area will be, (ii) what style of intervention will be carried out (e.g. prescribed burn, mechanical fuel load reduction, or other activity), and (iii) when the intervention will be carried out, which is often based on both timing with fire seasons and scheduling alongside other actions. Given these different dimensions of decision making, acting to reduce wildfire likelihood is a complex planning problem.

To support these complex planning decisions, managers can simulate and evaluate available treatment options using different models that represent wildfire likelihood (Miller and Ager 2013). These models fall into two broad classes: landscape fire simulation or asset-centric models.

Landscape fire simulation models are the most widely used to assist decision making. A review by Parisien et al. (2019) considered almost 50 studies that explore fuel treatments using the burn probability outputs of landscape fire simulation models. Such models make use of fire growth simulators (for example, FARSITE (Finney 1998), Prometheus (Tymstra et al. 2010), Phoenix (Tolhurst et al. 2008) or Spark (Miller et al. 2015)) to model many individual fire events across a landscape, simulated under different combinations of input ignition and weather parameters (Finney 2005; Miller and Ager 2013). The relative number of times a location is burnt by one of these fire events can be aggregated to create a map of simulated burn probability, which is a direct measure of wildfire likelihood (Parisien et al. 2019). Because fire simulation models aim to represent the physics of wildfires as realistically as possible, they are able to represent the contagious nature of fire spread (Peterson 2002) and exhibit a range of observed, directionally specific and physically realistic patterns, such as fire shadows (Finney 2005). These patterns are a result of top-down and bottom-up interactions of fire behaviour that occur across multiple spatial scales (Parisien et al. 2010; Parks et al. 2011).

The major disadvantage of using landscape fire simulation models is that they are computationally expensive, sometimes taking in the order of days or weeks to run (Parisien et al. 2019). This high computational time stems from the need to simulate many thousands of fire events, depending on factors such as the size of the study area and the combination(s) of ignition points and weather conditions considered. Although computationally possible, especially when cloud or supercomputing facilities are used (Parisien et al. 2019), the computational feasibility of this approach decreases significantly where the generation of a large number of burn probability maps is required. These types of problems are common in socio-environmental contexts, including problems with future uncertainties such as scenario analysis, those exploring model or system sensitivities and those involving the consideration of many alternative combinations of management options, such as optimisation. Landscape fire simulation models have been used successfully to explore some of these problems, including those exploring fuel treatment prioritisation (Ager et al. 2010), temporal dynamics in vegetation succession (Barros et al. 2019) and/or other future scenarios (Gazzard et al. 2020; Ager et al. 2021), but this has only been done for systems with limited complexity. In addition, more computationally expensive analyses, such as the optimisation of treatment options at a landscape scale, are not feasible in realistic problem settings (Miller and Ager 2013; Chung 2015).

To overcome the computational cost associated with generating the burn probability outputs of landscape fire simulation models, especially when exploring more complex, multi-faceted decision-making problems, asset-centric models can be used. In contrast to simulation-based models, asset-centric models do not directly simulate fire events moving across a landscape. Instead, they survey local features in the vicinity of assets to provide a measure of wildfire likelihood at the location of the asset. These features are often linked to the momentum or connectivity of the surrounding region and their effect on wildfire likelihood. For example, the presence of certain features at or near assets can increase wildfire likelihood (e.g. high momentum due to high potential ROS or HFI fuels) or decrease it (e.g. low connectivity due to barriers to spread such as water bodies). Similarly, the absence of certain features can increase wildfire likelihood (e.g. fuel breaks) or decrease it (e.g. burnable fuels). To consider these local features, the structure of asset centric models is typically based on user-defined (heuristic asset-centric models) or statistically informed relationships (statistical asset-centric models).

Heuristic asset-centric models, such as those presented by Beverly et al. (2021), Verde and Zêzere (2010) and Liberatore et al. (2021), use process-based or expert-informed rules to define the model structure. For example, Beverly et al. (2021) make use of the empirical evidence that highly ‘local’ features influence wildfire likelihood and subsequent building losses (Caggiano et al. 2020). They present a model that spatially aggregates the presence or absence of hazardous fuels within a predefined radius of an asset (for example, within 500 m) and provide a novel methodology for examining the directionally specific landscape arrangement of these hazardous fuels relative to a point of interest (Beverly and Forbes 2023). Alternatively, Verde and Zêzere (2010) combine several chosen weather, fuel and topography factors in a multiplicative fashion to provide a measure of wildfire likelihood, and Liberatore et al. (2021) use the connectivity of treatable fuel polygons as a surrogate for wildfire likelihood. These heuristic models have the flexibility to allow for the inclusion of expert-informed knowledge of wildfire processes and tend to have the desirable property of being easy to interpret.

Statistical asset-centric models have substantially increased in use across several wildfire management contexts, including wildfire likelihood (sometimes referred to as wildfire susceptibility) estimation (Jain et al. 2020; Arif et al. 2021). Statistical asset-centric models, such as those provided by Sharma et al. (2022) and Price et al. (2015a), quantify wildfire likelihood by calibrating statistical or machine-learning models on observed wildfire activity and underlying input features such as weather, fuel and topography. For example, Sharma et al. (2022) calibrate six different machine-learning algorithms on satellite-detected wildfire hotspots to create a model for wildfire likelihood. These statistical models can explore the complex top-down and bottom-up interactions of weather, fuel and topography factors that influence wildfires without necessarily requiring a priori knowledge of how these factors interact (Leuenberger et al. 2018). Alternatively, the model proposed by Price et al. (2015a) incorporates both an a priori heuristic model structure (that fire must spread from an ignition point to a receiver point) and a statistical model structure (statistically derived relationships between input variables, including those on a linear path between ignition and receiver points). This model is calibrated on historical ignition points and burnt areas and was found to be highly accurate for the historical validation data within the study region presented. Statistical models have also been combined with burn probability outputs to either provide regional guidance on intervention effectiveness (Penman et al. 2014; Cirulis et al. 2020) or to analyse the drivers of burn probability (Parks et al. 2011; Furlaud et al. 2018).

Because asset-centric models do not rely on the simulation of thousands of fire events, they are typically significantly more computationally efficient than landscape fire simulation models, in some cases reducing run times from the order of days or weeks to hours or seconds. This computational saving is critical when exploring problems such as scenario and sensitivity analysis or optimisation that rely on many evaluations of wildfire likelihood at a given time, as mentioned above. In fact, the use of asset-centric models has made it possible to tackle optimisation-based decision-making problems (Lauer et al. 2017; Williams et al. 2017; Liberatore et al. 2021) that would most likely be computationally infeasible when using landscape fire simulation models (Chung 2015). For example, the treatment placement optimisation problem formulated by Liberatore et al. (2021), which describes the connectivity of treatable polygons as a surrogate for wildfire likelihood, takes only seconds to run when asset-centric models are used.

However, this increase in the computational efficiency of asset-centric models comes at the expense of the ability to represent contagious and directionally specific patterns in wildfire likelihood with the same level of detail as landscape fire simulation models. The first reason for this is that asset-centric models generally consider a fixed spatial scale, such as the use of a fixed neighbourhood radius (Beverly et al. 2021), fixed polygons (Liberatore et al. 2021) or a fixed resolution of input variables (Sharma et al. 2022). Fixed scale models like these are unable to represent the multi-scale nature of contagious fire spread processes that influence wildfire likelihood (Parisien et al. 2010; Parks et al. 2011; Thompson and Calkin 2011). The second reason is that asset-centric models generally do not consider the directionally specific interactions of weather, fuel and topography factors that govern wildfire processes (Beverly et al. 2021). Asset-centric models that do not consider directionality are unable to represent patterns in wildfire likelihood such as fire shadows (Parisien et al. 2020), which are inherently directionally specific. As a result, many asset-centric models do not accurately reflect wildfire likelihood or the influence of barriers to fire spread, including those created by the interventions implemented by managers (Parisien et al. 2020). The model of Price et al. (2015a) is an exception, because it is able to incorporate multiple scales and directionally specific interactions between weather, fuel and topography factors into an estimate of wildfire likelihood, making it suitable for problems like evaluating landscape interventions (Price and Bedward 2020). However, this model only considers linear paths between ignition and receiver points, making it incapable of accounting for fire to spread in a variety of directions, including around obstacles.

Given the low computational efficiency of landscape fire simulation models and the reduced level of detail with which asset-centric models represent certain wildfire processes, there is an opportunity to develop a new modelling approach that can overcome these limitations. Such an approach would make it possible to perform computationally demanding analyses such as sensitivity and scenario analysis or optimisation, as mentioned earlier, while representing wildfire processes with an increased level of detail. Consequently, the first objective of this paper is to introduce a novel approach to quantifying wildfire likelihood that is both computationally efficient and able to represent wildfire processes in a more detailed manner. This is achieved by proposing a neighbourhood index that is conceptually similar to heuristic asset-centric models, and hence computationally efficient, but unlike existing asset-centric models, is able to represent the contagious, multi-scale and directionally specific interactions of fire behaviour factors that govern wildfire processes explicitly. The second objective of this paper is to assess the utility of the proposed neighbourhood index for a case study region in the Adelaide Hills in South Australia by: (i) comparing estimates of wildfire likelihood obtained using the proposed neighbourhood index with (a) corresponding burn probability estimates obtained using simulation-based models and (b) historical burnt areas; and (ii) comparing the computational effort required to obtain estimates of wildfire likelihood using the proposed neighbourhood index with that required by a simulation-based model.

To achieve the above objectives, the remainder of this paper is structured as follows: First, the conceptual basis for the proposed neighbourhood index is outlined. The study area is then introduced, including the input data used for the study and the process of applying the proposed index to the study area, followed by the approach used to test the utility of the proposed neighbourhood index. The case study results are then presented and discussed, followed by a summary, conclusions and recommended future research directions.

Methods

Proposed neighbourhood index

The proposed neighbourhood index describes whether and how easily fire may spread toward a point of interest (point i within map X) from its ‘local’ neighbourhood surroundings (points $j \in J_{i}^{w}$ ) defined under a given set of specific weather conditions (denoted by the super script w). The formulation of the index reflects several key principles of fire spread and likelihood, including multi-scalar momentum and connectivity associated with contagion, directionally specific fire spread and top-down controls of fire weather.

In order to capture the multi-scale nature of wildfires and their ability to spread over these scales, the proposed index aggregates fire behaviour properties (denoted by fbp_j for point j) across several neighbourhoods of different spatial scales surrounding the point of interest i (Fig. 1). The potential momentum driving fire spread at different scales is directly captured through this aggregation of fire behaviour properties within each neighbourhood. This aggregation also implicitly considers connectivity, because cells within a neighbourhood that cannot burn do not contribute to the momentum within the neighbourhood.

Fig. 1.

Calculation of the neighbourhood index for a point of interest, i.

Neighbourhoods are designed to capture local momentum and connectivity in the areas that have the biggest influence on wildfire likelihood at the point of interest. The sizes of the neighbourhoods can be calibrated to local conditions to reflect known relationships between fire size and frequency (Hantson et al. 2015), for example, by considering the distribution of observed fire sizes within the local region. In addition, the index is calculated under different weather conditions and then probabilistically aggregated, thereby accounting for the top-down control of weather on potential fire behaviour and spread.

Specifically, the above factors are incorporated into the neighbourhood index through a four-step process, an overview of which is given in Fig. 1. This process can be followed to calculate the neighbourhood index for any point of interest, such as at specific assets for which the arrival of a fire may be adverse, or for all points in a landscape. The first three steps are completed separately for each distinct set of weather conditions (indexed by w = 1, …, W, where W is the total number of unique weather conditions considered), and the fourth step aggregates across the entire set of weather conditions. To undertake the first three steps, a raster map X of input properties is required, where the input properties ${fbp}_{j, i}^{w}$ reflect the potential fire behaviour or momentum driving fire spread from point j toward point i under specific weather conditions w.

In the first step, the number, size, shape and spatial resolution of neighbourhoods (indexed by n = 1, …, N) are defined with respect to local conditions (Step 1; Fig. 1). In the second step, individual neighbourhood indices ${NI}_{i}^{n, w}$ are calculated for the point of interest i (for weather condition w and neighbourhood n) by summing potential weather- and topography-adjusted fire behaviour properties ( ${fbp}_{j, i}^{w}$ properties of raster map X) within each neighbourhood of cells $j \in J_{i}^{n, w}$ (Step 2; Fig. 1). In the third step, the weather-specific neighbourhood index ${NI}_{i}^{w}$ is calculated as a weighted sum of the normalised index value of each individual neighbourhood (Step 3; Fig. 1). Normalisation in this step ensures that the contribution of each neighbourhood to the weather-specific index value is adjusted for each neighbourhood’s size. Finally, the weather-specific neighbourhood index is probabilistically aggregated over the weather conditions considered (NI_i, Step 4; Fig. 1). In addition to the overview of each of these steps provided in Fig. 1, greater detail is provided by the mathematical formulation of each step below.

Step 1. Define Neighbourhoods: Select the number of neighbourhoods N, and for each neighbourhood n = 1, …, N, specify the set of cells belonging to that neighbourhood $J_{i}^{n, w} \subset X$ for each given weather condition w = 1, …, W.

As shown in Fig. 1, the first step involves the determination of each neighbourhood set $J_{i}^{n, w}$ $(J_{i}^{n, w} \subset X)$ for all points i, weather conditions w and neighbourhoods n = 1, …, N. The spatial resolution at which neighbourhood level n is defined, with corresponding map denoted as X_n, is controlled by the resolution factor RFⁿ, which is assigned during the parameterisation of the index (note that X_n is a uniformly down-sampled version of X, where cell properties of the coarser resolution X_n correspond to averaged values of the cells in X). A higher resolution ensures local, bottom-up fire behaviour features are captured, but is also more computationally expensive (i.e. the highest resolution is where X_n = X). A lower resolution will capture broader-scale landscape features more efficiently, at the expense of local features. The set of cells within each neighbourhood is controlled by neighbourhood shape, which is defined by the user. In this study, the neighbourhoods are circular sectors defined by shape and distance parameters, denoted as α and D, respectively. The α parameter dictates the ‘field of view’ or angular range deviation from the direction of prevailing wind to be considered. The D parameter dictates the distance from the point of interest to be considered. That is, for point i (x_i = (x_i,y_i) in Euclidian space) and wind direction θ^w for weather condition w, the representation of the shape parameterised by α and D in Euclidian space is given by

(x, y) \in {x : | x - x_{i} | \leq D, - \frac{α}{2} \leq \arg (x_{i} - x) - θ^{w} \leq \frac{α}{2}}

where x = (x,y), and the sets $J_{i}^{n, w}$ are clearly indices of discrete points in this space (note that here, arg is defined in the 2-D real vector space). Jointly, the α and D parameters reflect the directionally specific spread of fire and represent a similar concept to the length-to-breadth ratio that is used to describe the spread of fire in elliptical models (Van Wagner 1969). A larger α:D ratio represents the possibility that over the defined distance, fires may be expected to reach the point of interest from a larger range of directions (Fig. 1). A smaller α:D ratio represents a narrower range of directions from which fires are expected to reach the point of interest over the given distance (Fig. 1). At relatively small distances, fires may typically arrive as heading fires, flanking fires and/or backing fires, so α is typically larger (see n = 1; Fig. 1). At relatively large distances, the fires that reach the point of interest are assumed to have largely travelled as heading fires in the direction of prevailing winds, so α is typically smaller (see n = N; Fig. 1).

Step 2. Calculate Individual Neighbourhood Indices: Calculate ${NI}_{i}^{n, w}$ , the neighbourhood index of point i for the nth neighbourhood under weather conditions w, as the sum of fire behaviour properties ${fbp}_{j, i}^{w}$ at points $J_{i}^{n, w}$ . That is,
${NI}_{i}^{n, w} = \sum_{j \in J_{i}^{n, w}} {fbp}_{j, i}^{w}$

In the second step, potential fire behaviour properties calculated at the cells within each neighbourhood are aggregated to calculate a neighbourhood index for each individual neighbourhood ${NI}_{i}^{n, w}$ . Potential fire behaviour properties (fbp_j) may be represented by measures such as HFI or ROS, because these measures incorporate weather, fuel and topographic interactions that directly drive fire spread. Relatively high fire behaviour properties reflect high momentum and a higher likelihood that fire will continue to spread through each cell within the neighbourhood, for example, due to fast-spreading (high ROS) or intense burning (high HFI) fuels. Relatively low or zero values (i.e. barriers such as dense urban areas or water bodies) reflect lower momentum and/or connectivity and a lower likelihood that a fire will continue to spread through each cell within the neighbourhood. Prior to aggregation, fire behaviour properties may be adjusted for a specific wind direction and local topography acting between points i and j (i.e. to compute ${fbp}_{j, i}^{w}$ from fbp_j) using the apparent slope metric (Duff and Penman 2021). Within Step 2, the aggregation process disregards the spatial distribution of fire behaviour properties inside each neighbourhood. However, features in the spatial distribution of fire behaviour properties that are considered to have a potentially significant effect on wildfire likelihood may be captured through appropriate parameterisation of the neighbourhoods in Step 1.

Step 3. “Calculate Weather specific Neighbourhood Index: Calculate ${NI}_{i}^{w}$ , the weather-specific neighbourhood index of point i under weather conditions w. Each ${NI}_{i}^{n, w}$ is normalised by the maximum index value at any point i ∈ X (denoted as ${NI}_{\max}^{n, w}$ ) and weighted by $p^{n, w}$ , the neighbourhood's relative importance, given weather condition w, and is given by”:
${NI}_{i}^{w} = \sum_{n = 1}^{N} p^{n, w} (\frac{{NI}_{i}^{n, w}}{{NI}_{\max}^{n, w}})$
where ${NI}_{\max}^{n, w} = \max_{i \in X} {{NI}_{i}^{n, w}}$ , $0 \leq p^{n, w} \leq 1$ , and $\sum_{n = 1}^{N} p^{n, w} = 1$ .

In the third step, the multi-scale nature of wildfire likelihood is captured by considering the combination of the set of N neighbourhood index values ${NI}_{i}^{n, w}$ . The aggregation of these neighbourhoods is controlled by the relative importance of each neighbourhood in influencing the spread of fire to the point of interest (the weight term $p^{n, w}$ used in Step 3).

Once calculated for a given set of weather conditions, a relatively higher weather-specific neighbourhood index ( ${NI}_{i}^{w}$ in Step 3) suggests higher wildfire likelihood due to higher connectivity and momentum acting in the direction of the point of interest from within the neighbourhoods. That is, higher connectivity and momentum within the neighbourhoods increase the likelihood of a fire spreading to the point of interest from within the considered neighbourhoods. A lower index suggests lower wildfire likelihood due to either lower momentum acting in the direction of the point of interest and/or barriers to spread that interrupt connectivity within the neighbourhoods, thus decreasing the likelihood of a fire spreading to the point of interest from within the neighbourhood(s). Interventions in the landscape may be evaluated by their ability to reduce momentum (i.e. fire behaviour) and/or interrupt the connectivity of fuels within the neighbourhoods, consequently reducing wildfire likelihood as represented by the neighbourhood index.

Step 4. Aggregate over Weather Conditions: Repeat steps 1–3 across all weather conditions w = 1, …, W, aggregate and weight by the relative probability of each set of weather conditions occurring (p^w):
${NI}_{i} = \sum_{w = 1}^{W} p^{w} {NI}_{i}^{w}$
where $0 \leq p^{w} \leq 1, \sum_{w = 1}^{W} p^{w} = 1$ .

In the final step, the weather-specific neighbourhood indices calculated for each set of weather conditions are probabilistically aggregated to provide the overall neighbourhood index (NI_i). Each weather-specific neighbourhood index is multiplied by the relative probability of its weather conditions occurring p^w. As a result, NI_i is the expected value of ${NI}_{i}^{w}$ across the different weather conditions considered w = 1, …, W. This enables the overall neighbourhood index to reflect the top-down and probabilistic control of climate and weather conditions driving fire spread in specific directions with different degrees of momentum. For example, even if a point of interest is exposed to highly hazardous fire behaviour properties to the east, if dangerous fire weather does not frequently occur from this direction then it may be less likely for fire to spread to assets from that direction. Weather conditions that are considered within this step can be informed by statistical analysis of historical weather patterns, expected future weather patterns or the priorities of the user.

Study area

The case study area within which the utility of the proposed neighbourhood index is assessed is the Adelaide Hills region of South Australia (Fig. 2). The Adelaide Hills region is located to the east of the city of Adelaide, the capital of South Australia. Given the coincidence of high wildfire activity and human populations within the region, there exists a need for tools that support proactive planning of treatments to reduce wildfire likelihood. The region itself covers approximately 140,000 ha (Fig. 2) and has a growing population of approximately 80,000 people (Australian Bureau of Statistics 2021). Development within the region is typical of the peri-urban interface, with residential housing often scattered throughout densely vegetated sclerophyllous landscapes (Bardsley et al. 2015). In addition to people and infrastructure, the landscape also contains significant value for cultural connection and biodiversity conservation (Bardsley et al. 2015). Grasslands and eucalypt forests are the predominant fuel types across the landscape (Fig. 3). Prior to colonial invasion, wildfire risk in this area was likely reduced by landscape management undertaken by local Indigenous Peoples (Fletcher et al. 2021), here including the Peramangk, Ngarrindjeri, Ngadjuri and Kaurna (Bardsley et al. 2019). Since colonial invasion and urban development in the Adelaide hills, wildfires have caused significant recorded burnt area and losses.

Fig. 2.

Adelaide Hills case study region in the geographical context of south eastern Australia.

Fig. 3.

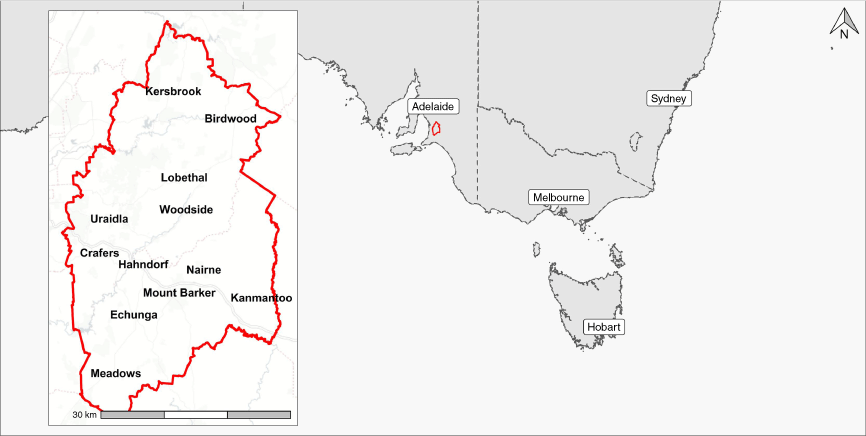
Top: historical wildfires intersecting the Adelaide Hills region (left). The Cudlee Creek fire is depicted in a darker shade as a notable recent historical occurrence. Fire behaviour models (middle) and topographic elevation (right) are also shown. Bottom: Cumulative annual burnt area of recorded fires intersecting the study area. Separate fire polygons representing events are delineated by alternating colours within the stacked bar chart.

The governmental records of wildfire activity used in this study contain 242 wildfire events of size greater than 1 ha, which have intersected with the region since 1955 (Department for Environment and Water 2021). Over this time, the cumulative area burnt is almost 100,000 ha (Fig. 3). Importantly, and as summarised by others (Gill and Allan 2008), the majority of historical burnt area in the region is due to only a small number of extreme wildfire events (Fig. 3). One such event was the Cudlee Creek fire in December 2019 (Fig. 3), in which over 20,000 ha were burnt and 85 homes were lost (South Australian Country Fire Service 2022).

Input data

Vegetation mapping of 30 m resolution was provided by the South Australian Department for Environment and Water (DEW, pers. comm.). The mapping of vegetation communities provided was last updated in 2019. Vegetation classes were reclassified into relevant fire behaviour models (Fig. 3). Fire behaviour models were selected from Cruz et al. (2015), except for the Pine model, which was adapted from Wang et al. (2017). Locally calibrated Olson curves (DEW, pers. comm.) were used to estimate fuel loads. A constant fuel age of 30 years was assumed to reflect a ‘worst-case’ scenario of fuel load accumulation. This scenario is consistent with maximum fuel load scenarios used within south-eastern Australia (State of Victoria 2015; Gazzard et al. 2020). The maximum fuel scenario was also chosen to reflect a limited effect of historical fires on moderating fire spread within the region, as exemplified by the absence of, or low and negative, ‘leverage’ (Price et al. 2015b) and the limited influence of fuel age on preventing fire spread in similar Australian sclerophyll landscapes (Price and Bradstock 2010). Vegetation classes that reflect urban and other developed land uses (e.g. mine sites) were considered ‘unburnable’ and assigned a potential ROS of zero.

To source information on weather for the study region, the Bureau of Meteorology Atmospheric high-resolution Regional Reanalysis for Australia (BARRA) dataset was used (Su et al. 2019). This dataset contains hourly and sub-hourly information for temperature, relative humidity, wind speed and direction at a 1.5 km resolution across the study region. For use in this study, the spatially and temporally explicit weather data were aggregated to form representative weather streams. Representative weather streams and their relative probability of occurrence are provided in Table 1 (AH1–AH8). To generate these streams using the BARRA dataset, the days on record that constitute days of potential fire danger are determined using a threshold for the Forest Fire Danger Index (McArthur 1967; Noble et al. 1980) at which more than 95% of the historical burnt area had occurred. The values of each weather parameter across the landscape on potential fire danger days from the hours of 12–5 pm were extracted. Wind direction was split into eight classes (W = 8) based on cardinal and ordinal wind directions, and the remaining parameters were split into quantiles for a total of 512 data bins (eight sets of three variables, each with four quantile classes). Each bin is represented by the median value of the parameters within that bin. The frequency of weather parameters falling into each bin at each timestep was recorded. The most common bin of weather parameters from each wind direction was selected to be used as the eight representative weather conditions, with the relative probability of occurrence normalised to one (Table 1).

Table 1.Aggregated weather parameters and relative probabilities for the study region.

Weather code, w	Wind direction (°)	Temperature (°C)	Relative humidity (%)	Wind magnitude (km/h)	Relative probability (p^w,%)
AH1	0	37.5	10.1	15.3	19
AH2	45	23.8	42.1	27.4	19
AH3	90	23.8	42.1	27.4	22
AH4	135	23.8	42.1	15.3	6
AH5	180	33.0	15.3	10.4	5
AH6	225	33.0	15.3	10.4	7
AH7	270	23.8	21.5	27.4	6
AH8	315	37.5	10.1	27.4	16

The topographic information required for model implementation was sourced from a Digital Elevation Model (DEM) provided by Geoscience Australia (2010) and resampled to the same resolution as the vegetation map (30 m; Fig. 3). Slope and apparent slope were calculated using this DEM and the terra package (Hijmans 2022) in R (R Core Team 2022).

Neighbourhood index application

To calculate the neighbourhood index for the study region, a publicly available GitHub repository (Firehoods, https://github.com/DougRadford/Firehoods) has been created. The repository provides a function written in R (R Core Team 2022) using the terra package (Hijmans 2022), which takes as inputs a wind direction, a raster layer of properties to be aggregated (for example, the ROS adjusted for topography and wind direction using apparent slope) and a parameter table of the same format as Table 2. The parameters within this table (N, Dⁿ, αⁿ and RFⁿ) match those described in Step 1 of the neighbourhood index formulation (Fig. 1) and are determined for the Adelaide Hills study region as outlined below.

Table 2.Parameterisation of neighbourhood index.

Neighbourhood scale (n)	Distance, Dⁿ (m)	αⁿ (°)	Resolution factor, RFⁿ
1	300	360.00	1
2	500	360.00	1
3	830	360.00	2
4	1650	360.00	4
5	2690	180.00	8
6	5040	90.00	16
7	9620	45.00	32
8	12,600	22.50	40
9	25,810	11.25	80

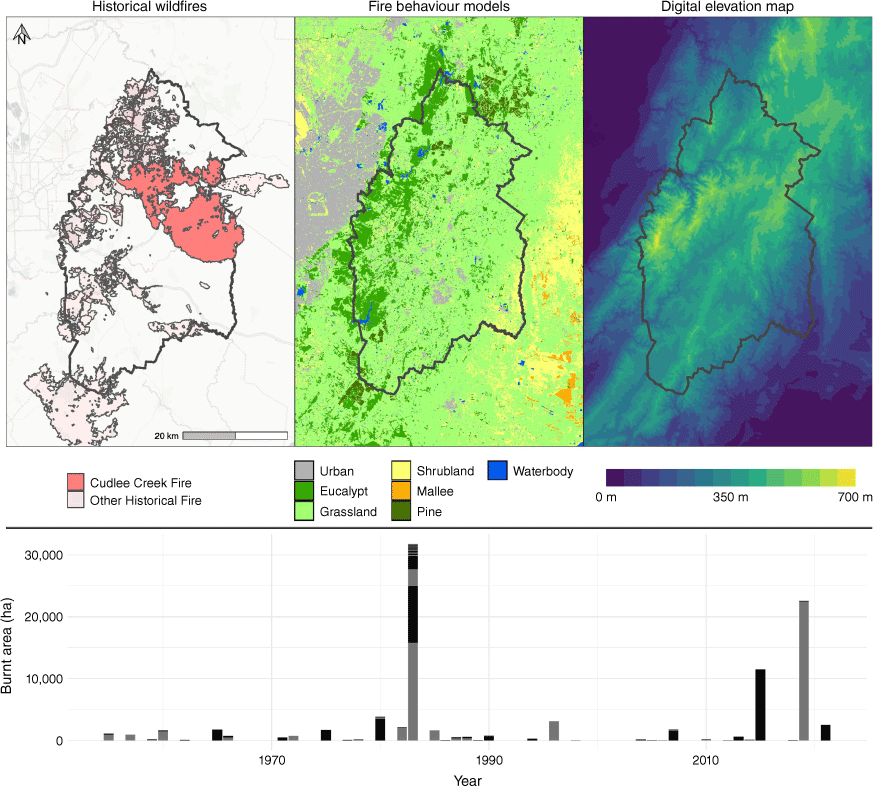
The relevant number of neighbourhoods (N; Table 2) was determined to be nine (N = 9) using a power–law analysis of the frequency-size distribution (Grassberger and Manna 1990; Hantson et al. 2015) of historical wildfires that have intersected the study region (Fig. 4). This approach to defining classes was chosen because it provides a link between the multiple scales of wildfire events and their relative frequency or importance (Hantson et al. 2015). It is noted that within the analysis, historical wildfires smaller than 1 ha in size were omitted, because these do not represent spreading wildfires and would overly influence the power–law fit (Hantson et al. 2015).

Fig. 4.

Power–law function relating wildfire size and frequency in Adelaide Hills region, as calculated using historical wildfires of size greater than 1 ha that intersect the region (total number = 242).

To generate the distance parameters (Dⁿ; Table 2), bounding boxes around each historical fire scar were created, recording the length of the diagonal. The median diagonal length of each nth class defined in the power–law analysis was used as the distance parameter for the corresponding neighbourhood (Dⁿ; Table 2).

The appropriate shape parameters (αⁿ; Table 2) were estimated based on the distance parameter of each neighbourhood (Table 2) and the approximately inverse relationship between the α and distance parameters discussed in the formulation of the neighbourhood index. That is, relatively small distance parameters are assigned larger α parameters (e.g. D¹ = 300 m, α¹ = 360°), and larger distance parameters are given smaller α parameters (e.g. D⁹ = 25,810 m, α¹ = 11.25°). As discussed, this reflects the assumption that across small distances, wildfires may arrive as heading, flanking or backing fires, whereas across larger distances, it is more likely they arrive only as heading fires travelling with the prevailing wind direction.

The resolution factors (RFⁿ; Table 2) were set to keep the ratio between the distance parameters and the resolution of the input properties for each neighbourhood approximately constant. Where the resolution factor is greater than one, the resolution of input properties (originally 30 m) was reduced by averaging these properties to the lower resolution (e.g. for a resolution factor of two this involves averaging four 30 m cells up to a new input layer at 60 m resolution). The utility of this approach was demonstrated by calculating and comparing the neighbourhood index with and without any adjustment to the resolution (Fig. A1).

Within the second step (Fig. 1), it was necessary to define the fire behaviour properties to be aggregated. Two configurations of the neighbourhood index were tested, using either the ROS or HFI as the input properties. These properties were adjusted for the apparent slope $({fbp}_{j, i}^{w})$ with respect to each wind direction prior to neighbourhood aggregation. A computational simplification was made such that the direction from j to i is always considered as the direction of the prevailing wind. This generalisation holds true for most cells j within large neighbourhoods of low α values but is less valid for neighbourhoods with high α values.

In the third step (Fig. 1), the relative importance of each neighbourhood was considered equal in weight $(p^{n, w} = \frac{1}{N}, n = 1, \dots, N)$ , given the linear relationship between bins in the power–law analysis (Fig. 4) used to define neighbourhoods.

In the fourth step (Fig. 1), the weather-specific neighbourhood indices calculated under each set of weather conditions (AH1–AH8; Table 1) were multiplied by the relative probability (p^w) of the weather conditions occurring and then summed. The result is NI_i, the overall neighbourhood index of the point of interest. To distinguish between the overall neighbourhood indices calculated using different fire behaviour properties, we label the overall neighbourhood index calculated using ROS as NI-ROS and that calculated using HFI as NI-HFI.

We note that the process described above is only one possible approach for parameterising the neighbourhood index. Within the above approach, chosen parameters and neighbourhood weights are not varied by weather conditions $(D^{n, w} = D^{n}, α^{n, w} = α^{n}, {RF}^{n, w} = {RF}^{n}, p^{n, w} = \frac{1}{9}, w = 1, \dots, W)$ , given the historically based power–law analysis undertaken was independent of weather conditions, making it suitable for long-term strategic analyses.

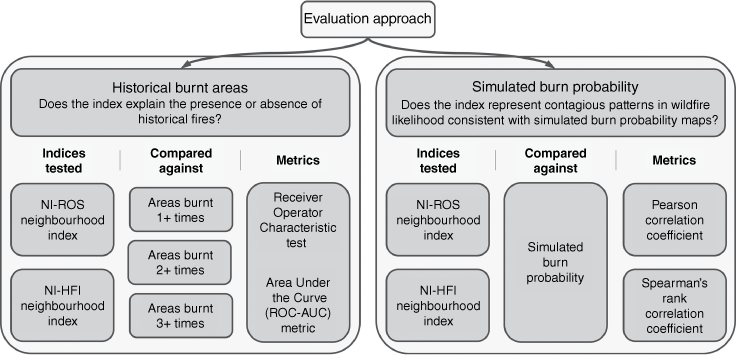
Assessment of the utility of the neighbourhood index

To evaluate whether the proposed neighbourhood index provides reasonable and computationally efficient estimates of contagious wildfire likelihood, its values were compared with historical burnt areas and simulated burn probability using both quantitative metrics and visual inspection (see Fig. 5). The former provides an indication of the ability of the neighbourhood index to distinguish between areas that historically have been burnt and those that have not, whereas the latter provides an indication of the ability of the index to estimate simulated burn probability values.

Fig. 5.

Overview of the two-part validation approach used to test two variants of the neighbourhood index, calculated with either ROS (NI-ROS) or HFI (NI-HFI) as the aggregated fire behaviour properties. Each index version is tested independently against historical burnt areas and simulated burn probability.

The advantage of comparing against historical burnt areas is that these areas are reflective of real fire spread. However, the limitation of the comparison with historical burnt areas is that burnt areas are influenced by the stochastic chance of ignition occurrences (Parisien et al. 2020) and are representations of only one possible realisation of the past. Furthermore, limited data were available within our study area to reflect this past and any changes in landscape composition over time (i.e. changes in vegetation classes were not available). In comparison, the advantages of testing each index against simulated burn probability are several. Firstly, landscape fire simulation models represent directionally specific and contagious wildfire spread, with their simulated burn probability outputs representing desirable observed patterns like fire shadows. Secondly, when comparing against simulated outputs, the input data is controlled and identical to that used to calculate the neighbourhood index. Finally, there is no influence of stochasticity related to ignition points, because these are sufficiently enumerated within the structured Monte Carlo process used to calculate burn probability. The limitation of comparing against simulated burn probability is that the patterns in wildfire likelihood represented are limited in realism to that of the underlying fire growth simulator and conditions modelled.

The pre-processing of historical data, calculation of simulated burn probability and quantitative metrics used to evaluate the performance of the two variants of the proposed neighbourhood index considered (Fig. 5) are discussed in detail in the subsequent sections. When evaluating the performance of each index variant, the quantitative tests do not consider cells that are assigned unburnable fuel types (e.g. reservoirs).

Comparison with historical burnt areas

To quantitatively evaluate the performance of each variant of the neighbourhood index considered against historical burnt areas, the Receiver-Operator Characteristic (ROC) test and Area Under the Curve (AUC-ROC) metric were chosen. The ROC test was chosen due to its applicability to natural hazard models (Beguería 2006) and prior application to wildfire studies (Parisien and Moritz 2009; Sharma et al. 2022). To undertake the ROC test, the number of times each cell within the study area has burnt within the entire record (1955–2021) was summed. Within the study area, approximately 41% of burnable cells had burnt at least once, 9% at least twice and 1% the maximum of three times. The ROC test is a binary classification test, so was undertaken independently against areas burnt: (i) at least once; (ii) at least twice; or (iii) three times. These three independent ROC tests help to account for the influence of stochasticity of historical ignition occurrences and to assess the ability of each index variant to discriminate areas that have burnt more frequently (assumed to be more indicative of higher wildfire likelihood). When evaluating each index variant using the AUC-ROC metric, values less than 0.7 are considered a poor discrimination between areas burnt or unburnt, and values above 0.7, 0.8 and 0.9 are considered acceptable, excellent and outstanding, respectively (Hosmer et al. 2013). Only the results of the best-performing neighbourhood index variant are presented in the body of the paper, with the results for the other variant provided in Table A1.

Comparison with simulated burn probability

To evaluate the neighbourhood index performance against simulated burn probability, quantitative correlation metrics were used alongside a qualitative visual assessment of model agreement. Correlation metrics were used because they provide a quantitative measure of the strength of the relationship between the two variants of the proposed neighbourhood index and burn probability, though this is spatially aggregated across the study region. In contrast, the visual assessment provides a spatially explicit depiction of model performance and allows for the assessment of how well the index captures contagious and directional patterns in burn probability (i.e. fire shadows), albeit in a qualitative manner. Additionally, to quantify the relative computational efficiency of the proposed neighbourhood index and landscape fire simulation models, the run time of each model was compared. Runtimes were recorded as the wall clock runtime without parallelisation on an Intel^® Core™ i9-12900KF CPU @3200 Mhz machine with 16 Cores and 128 Gb RAM.

To calculate burn probability, a basic implementation of Spark version 1.1.3 (Miller et al. 2015) was used to simulate a total of 54,000 fires, each assumed to be 5 h in duration. Potential ignition points were arranged in a uniform grid, which was constructed iteratively to ensure that edge effects were removed within the study region and that the ignition density was sufficient to reduce uncertainty in output burn probability. For each set of weather conditions (AH1–AH8; Table 1), the number of times each cell was burnt by a simulated wildfire was calculated. This was then aggregated across weather conditions by multiplying by the relative probability (p^w; Table 1) of each set of weather conditions occurring and summing across these weather conditions. Next, the burn probability was calculated by rescaling the probability adjusted number of times burnt to the range [0, 1], aligning with the scales of the neighbourhood index. Note that although Spark has the flexibility to model more complex processes related to wildfire spread (i.e. suppression and ember-based spread), these are not included in this study.

The Pearson and Spearman’s rank correlations were used to measure the strength of the relationship between each variant of the neighbourhood index and simulated burn probability. The Pearson correlation was used to test the strength of the linear relationship between the index and burn probability, and Spearman’s rank correlation was used to test the strength of this relationship without assuming linearity. Higher correlations indicate a stronger relationship between the index and burn probability. Only the results of the best-performing index variant are presented in the body of the paper, with the results for the other variant provided in Table A2.

To visually assess the spatially explicit ability of the neighbourhood index to capture the contagious patterns in wildfire likelihood represented by burn probability outputs (i.e. fire shadows), the relative magnitude of each measure of wildfire likelihood across the study area was compared. To achieve this, each measure of wildfire likelihood was divided into five equal classes using quintiles, because this has been shown to be the most reliable symbology for presenting burn probability maps (Beverly and McLoughlin 2019). To explore differences among maps, the difference between the quintile classes of each measure of wildfire likelihood at each cell was calculated, termed quintile class difference. To further assess areas of agreement or disagreement, as represented by the quintile class differences between the neighbourhood index and burn probability, the quintile classes of each individual neighbourhood’s index value ( ${NI}_{i}^{n, w}$ , Step 2; Fig. 1) were also explored.

Results and discussion

Historical burnt areas

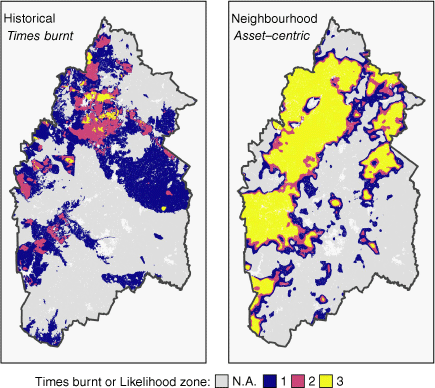
The performance of the neighbourhood index (NI-HFI) is strongly dependent on the frequency with which the areas compared against have burned (shown in Fig. 6). The neighbourhood index performs poorly (AUC-ROS = 0.64) when discriminating against any area that has only been burnt once; however, this performance increases monotonically to the category of acceptable (AUC-ROC = 0.77) or excellent (AUC-ROC = 0.82) when comparing against only areas that have burnt at least twice or the maximum of three times, respectively. As the threshold for the number of times a cell has been burnt increases, the neighbourhood index becomes increasingly better at discriminating that cell as having a relatively higher wildfire likelihood. This suggests that the neighbourhood index captures the landscape contagion properties that have led to certain cells being burnt repeatedly. The poorer performance of the neighbourhood index on areas burnt only once may reflect the high dependency of these areas on where ignitions have occurred and under what conditions, aligning with the limitations of historical comparisons discussed by Parisien et al. (2020). This is also reflected by the relatively large area assigned to the highest likelihood of burning by the neighbourhood index (Likelihood zone 3, Fig. 6), which suggests that even though not all areas have burnt frequently, their neighbourhood properties suggest they might have done so under a different realisation of the past.

Fig. 6.

Historical Burnt Areas (left) and the wildfire likelihood zones generated using the best-performing neighbourhood index (NI-HFI, right). Likelihood zones 1, 2 and 3 are generated for visualising the results of each asset-centric model using thresholds defined following a similar method to that of Parisien and Moritz (2009) and based on the AUC-ROC tests against areas burnt at least once, twice or three times.

The neighbourhood index calculated using HFI properties (NI-HFI Average AUC-ROC = 0.744) performed significantly better than the neighbourhood index calculated using ROS properties (NI-ROS Average AUC-ROC = 0.420; Table A1). This suggests that aggregating high HFI properties across multiple scales using the neighbourhood index is more informative for identifying areas that have burnt repeatedly within the region considered. This is likely because the region contains significant suppression resources and the NI-HFI implicitly captures processes associated with intense fires that cannot be easily suppressed (Hirsch and Martell 1996) and spread faster through higher ember production (Rothermel 1983). These considerations are not represented by the NI-ROS version of the neighbourhood index. The ability of the NI-HFI to implicitly represent these processes is an advantage of the proposed neighbourhood index over landscape fire simulation models, which must explicitly model suppression and ember spread during fire growth, if at all. Explicitly incorporating more information about suppression (e.g. Telfer 2019) or ember production potential (e.g. Roberts et al. 2021) into the neighbourhood index may improve its performance further. Because the proposed neighbourhood index shows explanatory power with respect to historical burnt areas, there exists potential to incorporate the neighbourhood index into statistical asset-centric models, such as that of Price et al. (2015a).

Simulated burn probability

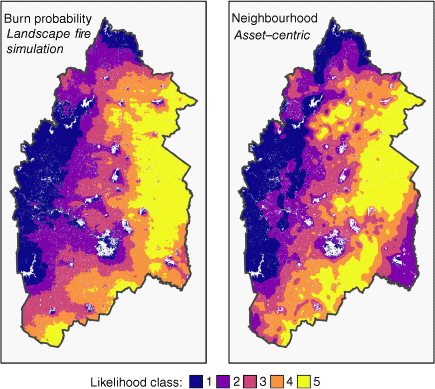
Results indicate that the proposed neighbourhood index (NI-ROS) is highly correlated with the burn probability results (Pearson correlation, ρ = 0.83 and Spearman rank correlation, ρ = 0.85). This suggests that the neighbourhood index is able to capture the contagious patterns in wildfire likelihood that are represented in landscape fire simulation models with a high degree of similarity (Fig. 7). This is a significant finding because it is the first example of an asset-centric model providing estimates of contagious wildfire likelihood that are comparable to those of simulation-based models.

Fig. 7.

Comparison of the best-performing neighbourhood index (NI-ROS) against simulated burn probability. Likelihood classes are defined by the quintiles of the simulated burn probability and neighbourhood index separately.

In contrast to the comparison with historical burnt areas, the neighbourhood index calculated using ROS properties (NI-ROS) out-performs the neighbourhood index calculated using HFI properties when comparing against simulated burn probability (NI-HFI Pearson correlation ρ = −0.24; Table A2). This is likely because the fire growth model used to calculate burn probability in this study simulates fire spread as a function of ROS only and does not incorporate ember-based spread modes or the effect of suppression on reducing the spread of low-intensity fires. This reinforces that the neighbourhood index has the potential to capture contagious and directionally specific processes of fire spread, as represented in either historical occurrences or burn probability outputs, provided it is parameterised appropriately.

Although the neighbourhood index estimates the relative wildfire likelihood portrayed by the burn probability results well across the Adelaide Hills region (as shown by high correlations), there remain areas of disagreement due to differences in the model representation of fire spread processes in ‘unburnable’ areas, as seen in Fig. 8. In this figure, areas of over-prediction are commonly down-wind of large areas that have zero rate of spread (i.e. urban areas or reservoirs; Fig. 3). This is due to the different handling of these unburnable areas in the fire growth model and the calculation of the neighbourhood index. In the basic setup of the fire growth model used in this study (Spark), the ‘unburnable’ barriers to spread are explicitly represented and interrupt the connectivity of the landscape. The difference between a low ROS patch of fuel and a zero ROS urban area is significant (a simulated fire may still propogate across a low ROS patch, but a zero ROS patch acts as a hard barrier). By contrast, in the proposed neighbourhood index, barriers to spread and landscape connectivity are only implicitly represented. For the neighbourhood index, the difference between a low ROS patch of fuel and a zero ROS urban area is not as significant in the summation of the fire behaviour properties within larger neighbourhoods (Step 2; Fig. 1).

Fig. 8.

Comparison of the weather-specific neighbourhood index (NI-ROS^w=AH1) with the simulated burn probability results under a single set of weather conditions (AH1 for all panels). White cells indicate unburnable fuel types. Quintile class difference is calculated by subtracting the quintile class (1–5) of the simulated burn probability from the quintile class of the neighbourhood index on a cell-by-cell basis. A zero quintile class difference represents areas of broad agreement. Positive or negative difference indicates that the neighbourhood index over-predicts or under-predicts burn probability, respectively.

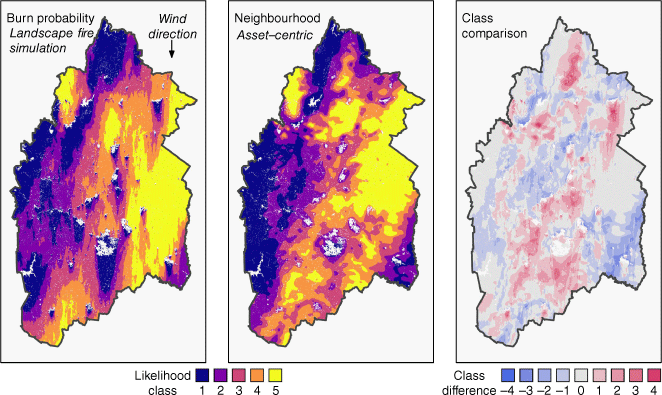
Although it is unlikely that the urban areas are truly ‘unburnable’ as currently configured in Spark, and consequently that fire shadows may be over-represented in the simulated burn probability map, they may also be under-represented by the neighbourhood index. Two areas of notable over-prediction of wildfire likelihood that exemplify this include the fire shadows on the down-wind side of both the Mt Barker and Woodside regions (shown by the quintile class difference; Fig. 9). These fire shadows are both clearly present in the simulated burn probability results and are created by urban settlements. The first, Mt Barker, is a densely populated urban area. Its fire shadow is only slightly discernable in the weather-specific neighbourhood index (NI-ROS^w=AH1, Fig. 8) and some of the individual neighbourhood index values (NI-ROS^{n, w=AH1}, 5 ≤ n ≤ 9, Fig. 9), though at different distances downwind of Mt Barker. By contrast, the Woodside region is an area with several less dense, urban centres (Woodside, Lobethal and Charleston), and its fire shadow is not consistently discernible in the weather-specific neighbourhood index, nor the individual neighbourhood index values. More explicitly incorporating barriers to spread into the formulation of the neighbourhood index may further improve its ability to estimate simulated burn probability. The methodology of O’Donnell et al. (2011) presents an example where barriers to spread have been explicitly represented in wildfire studies previously.

Fig. 9.

Left: quintile class difference between simulated burn probability and weather-specific neighbourhood index (NI-ROS^w=AH1) under AH1 weather conditions (chosen nominally). Notable areas of disagreement are highlighted using callouts. The histogram shows the relative frequency of cells within each category of quintile class difference. Right: individual neighbourhood indices (NI-ROS^n, w=AH1) for each set of parameters in Table 2 under AH1 weather conditions.

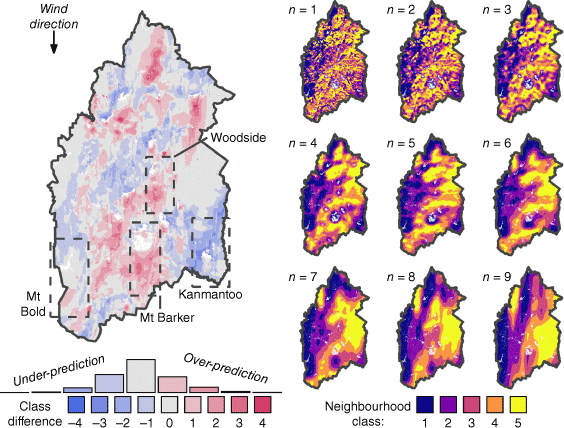
A further explanation for areas of disagreement between the neighbourhood index and burn probability may be related to the complex interactions across different scales of fire spread, which influence wildfire likelihood. Across these scales, any given location can present significantly different individual neighbourhood properties (Fig. 9). This is consistent with the emergent nature of wildfire likelihood, which is influenced by contagious processes occurring across different scales (Newman et al. 2019). The region south of Mt Bold reservoir (highlighted in Fig. 9), for example, shows high individual neighbourhood index values (NI-ROS^n, w=AH1) across small-to-medium scales (1 ≤n ≤ 6) and very low individual neighbourhood index values at large scales (7 ≤n ≤ 9). Both the landscape fire simulation and asset-centric models identify this area as having relatively low wildfire likelihood, with only a slight over-prediction in some areas by the weather-specific neighbourhood index (NI-ROS^w=AH1). Conversely, the Kanmantoo region shows low individual neighbourhood index values across the same small-to-medium scales and high individual neighbourhood index values at large scales, with the weather-specific neighbourhood index (NI-ROS^w=AH1) under-predicting wildfire likelihood as represented by burn probability. An improved estimation against simulated burn probability that may better account for these interactions between scales may be achieved by calibrating the neighbourhood index parameters (i.e. Dⁿ, αⁿ, p^n,w) against the simulated burn probability results directly – and by allowing for interactions between the neighbourhood indices of different scales in the mathematical formulation of the proposed neighbourhood index. These improvements may be achieved by increasing the complexity with which neighbourhoods are aggregated, for example, by using statistical models such as machine learning algorithms that take the individual neighbourhood indices as inputs. Such an approach may address the slight non-linearity in the relationship between the neighbourhood index and burn probability currently observed, indicated by the Spearman’s rank correlation exceeding Pearson’s correlation. Furthermore, alternative approaches to calibrating the neighbourhood index may remove the reliance of the presented methodology on historical observations and allow for studies that explore future wildfire likelihood.

Although it provides an estimate of wildfire likelihood that is highly correlated with simulated burn probability, the neighbourhood index is significantly more computationally efficient than the landscape fire simulation modelling approach. The neighbourhood index (NI-ROS) provides its estimate of wildfire likelihood in 0.26% of the computational time (7.9 min) required by the simulation-based model (3071.3 min). This is because the asset-centric neighbourhood index does not require the simulation of many individual fire events to estimate wildfire likelihood and only considers the fire behaviour properties within the neighbourhoods surrounding each point.

The neighbourhood index appears to be able to represent contagious patterns in wildfire likelihood and has a low computational cost, so it is useful for answering problems that require many evaluations of wildfire likelihood, such as scenario and sensitivity analysis or the optimisation of fuel treatment placement. The reduced computational cost of the proposed neighbourhood index may also make it useful for other cases that require fast runtimes, including use in workshop planning settings, calculation of large-scale daily or sub-daily fire risk indices that do not currently incorporate measures of wildfire likelihood (i.e. the Australian Fire Danger Rating System), or improvements within global fire models that do not capture the influence of fuel continuity on wildfire likelihood (Jones et al. 2022).

Based on the results obtained, it appears the neighbourhood index offers the ability to efficiently disentangle the complex interactions between the multiple scales of contagious fire spread processes that govern wildfire likelihood (e.g. through visualising individual neighbourhood indices; Fig. 9). By being able to identify the most relevant neighbourhood scales for each asset or location, use of the proposed neighbourhood index could enable landscape managers to directly select asset-specific risk-reduction strategies that match relevant scales. For example, in the aforementioned Mt Bold example, treatments to reduce wildfire likelihood might be focused on the small-to-medium scales that have high index values (NI-ROS^n,w=AH1, 1 ≤ n ≤ 6), whereas in the Kanmantoo example, treatments might be better focused on the larger scales (7 ≤n ≤ 9). Furthermore, given the low computational cost of the index, these treatment strategies and their effect on reducing contagious wildfire likelihood can be easily compared by recalculating the neighbourhood index with inputs that reflect each alternative treatment strategy.

The neighbourhood index has performed well for the case study, but it should be noted that only spatially homogenous ignition probabilities and static weather conditions were considered (i.e. a fixed wind direction). These factors are simple to incorporate into landscape fire simulation models that explicitly consider individual wildfire events but have not been previously incorporated into heuristic asset-centric models. Although the current formulation of the neighbourhood index does not handle these considerations, we suggest that future work may make this possible. For example, spatially heterogeneous controls on ignition likelihood may be considered alongside the proposed neighbourhood index, as suggested conceptually in fig. 6b of Beverly et al. (2021), or incorporated directly into the formulation of the neighbourhood index by considering ignition probabilities within the neighbourhoods from which fires may spread. Additionally, temporally dynamic weather conditions, including dangerous conditions associated with a change in wind direction, might be incorporated more explicitly by jointly considering weather-specific neighbourhood indices calculated under two or more sets of weather conditions.

Conclusion

We introduce the conceptual basis for, and mathematical formulation of, a computationally efficient asset-centric neighbourhood index that considers contagious and directionally specific fire behaviour properties across multiple spatial ‘neighbourhood’ scales. This enables the proposed neighbourhood index to mimic contagious and directionally specific wildfire spread patterns, including ‘fire shadows’ and the ability of a wildfire to spread around landscape barriers across different spatial scales. Representation of these patterns has not been achieved by other models of wildfire likelihood without the computationally expensive simulation of many thousands of individual fire events.

This paper demonstrates the application of the proposed neighbourhood index to a case study in the Adelaide Hills, Australia. The proposed neighbourhood index demonstrates an excellent ability to (i) discriminate the historical areas that have been burnt most frequently and (ii) capture physical processes represented by fire growth models. This represents the first example of a heuristic asset-centric model providing results comparable to those of landscape fire simulation models. However, these estimates are provided at a very small fraction of the computational time required by landscape fire simulation models to calculate burn probability. This makes it possible to carry out studies that require many evaluations of wildfire likelihood, such as sensitivity or scenario analysis and the optimisation of fuel treatment placements, without sacrificing detail in the representation of wildfire likelihood. Such studies have previously not been possible for problems with realistic levels of scale and complexity, given the computational expense of generating burn probability outputs and lack of alternative models that represent the contagious and directionally specific processes of wildfire likelihood.

Despite its excellent performance, the proposed neighbourhood index also has several limitations. As discussed, it does not currently incorporate spatially heterogenous ignition probability or temporally dynamic weather conditions. Ongoing development in these directions, alongside others, will improve its utility. One option for addressing these limitations is to incorporate the index into statistical models, such as artificial neural networks (Maier et al. 2023).

In developing this index, the authors wish to support statements of other researchers suggesting that models should be chosen based on the problems they answer and used in combination to support decisions (Parisien et al. 2020; Price and Bedward 2020). By more closely integrating the neighbourhood index with both landscape fire simulation and statistical asset-centric models, there exists opportunity to create a suite of highly complementary tools for modelling wildfire likelihood and exploring problems that, to date, have been computationally infeasible to explore while also considering contagious and directionally specific fire behaviour properties across multiple spatial scales.

Although there exist several avenues for further improvement, the results of this study clearly demonstrate the potential for an asset-centric model to provide computationally efficient estimates of wildfire likelihood that also consider a more detailed representation of underlying physical processes affecting fire spread. As mentioned above, this opens the door to exploring problems that require many evaluations of wildfire likelihood, including sensitivity analysis, optimisation of treatment planning and exploration of future uncertainties associated with land use and climate change scenarios. This is significant, given previous challenges in addressing these types of problems and the increasing need to proactively intervene to reduce future wildfire risk.

Data availability

The data supporting this study will be shared upon reasonable request to the corresponding author. Some data that support this study were obtained from third parties by permission. Where relevant, data will be shared with permission from the third parties.

Conflicts of interest

The authors declare no conflicts of interest.

Declaration of funding

This research was undertaken while the lead author was supported by funding from the Australian Department of Education Skills and Employment, Research Training Program, and from Westpac Scholars Trust, Future Leaders Scholarship.

Acknowledgements

We thank Mr Mike Wouters and Mr Simeon Telfer from the South Australian Department for Environment and Water for their support in model development and data provision. Thank you to the Spark development team from CSIRO for providing the Spark software and support. This work was supported with supercomputing resources provided by Mr Fabien Voisin and the Phoenix HPC service at the University of Adelaide, to whom we are grateful. We also thank the two anonymous reviewers and Associate Editor, whose comments have assisted with improving the quality of this paper and its contributions significantly. This work was completed on Kaurna Country.

References

Ager AA, Vaillant NM, Finney MA (2010) A comparison of landscape fuel treatment strategies to mitigate wildland fire risk in the urban interface and preserve old forest structure. Forest Ecology and Management 259, 1556-1570.
| Crossref | Google Scholar |

Ager AA, Evers CR, Day MA, Alcasena FJ, Houtman R (2021) Planning for future fire: scenario analysis of an accelerated fuel reduction plan for the western United States. Landscape and Urban Planning 215, 104212.
| Crossref | Google Scholar |

Arif M, Alghamdi KK, Sahel SA, Alosaimi SO, Alsahaft ME, Alharthi MA, Arif M (2021) Role of machine learning algorithms in forest fire management: a literature review. Journal of Robotics and Automation 5, 212-226.
| Crossref | Google Scholar |

Australian Bureau of Statistics (2021) 2021 Census All persons QuickStats. Available at https://www.abs.gov.au/census/find-census-data/quickstats/2021/40102 [Verified 15 April 2024]

Bardsley DK, Weber D, Robinson GM, Moskwa E, Bardsley AM (2015) Wildfire risk, biodiversity and peri-urban planning in the Mt Lofty Ranges, South Australia. Applied Geography 63, 155-165.
| Crossref | Google Scholar |

Bardsley DK, Prowse TAA, Siegfriedt C (2019) Seeking knowledge of traditional Indigenous burning practices to inform regional bushfire management. Local Environment 24, 727-745.
| Crossref | Google Scholar |

Barros AMG, Ager AA, Day MA, Palaiologou P (2019) Improving long-term fuel treatment effectiveness in the National Forest System through quantitative prioritization. Forest Ecology and Management 433, 514-527.
| Crossref | Google Scholar |

Beguería S (2006) Validation and evaluation of predictive models in hazard assessment and risk management. Natural Hazards 37, 315-329.
| Crossref | Google Scholar |

Beverly JL, Forbes AM (2023) Assessing directional vulnerability to wildfire. Natural Hazards 117, 831-849.
| Crossref | Google Scholar |

Beverly JL, McLoughlin N (2019) Burn probability simulation and subsequent wildland fire activity in Alberta, Canada – Implications for risk assessment and strategic planning. Forest Ecology and Management 451, 117490.
| Crossref | Google Scholar |

Beverly JL, McLoughlin N, Chapman E (2021) A simple metric of landscape fire exposure. Landscape Ecology 36, 785-801.
| Crossref | Google Scholar |

Caggiano MD, Hawbaker TJ, Gannon BM, Hoffman CM (2020) Building loss in WUI disasters: evaluating the core components of the Wildland–Urban Interface definition. Fire 3, 73.
| Crossref | Google Scholar |

Canadell JG, Meyer CP, Cook GD, Dowdy A, Briggs PR, Knauer J, Pepler A, Haverd V (2021) Multi-decadal increase of forest burned area in Australia is linked to climate change. Nature Communications 12, 6921.
| Crossref | Google Scholar | PubMed |

Chung W (2015) Optimizing fuel treatments to reduce wildland fire risk. Current Forestry Reports 1, 44-51.
| Crossref | Google Scholar |

Cirulis B, Clarke H, Boer M, Penman T, Price O, Bradstock R (2020) Quantification of inter-regional differences in risk mitigation from prescribed burning across multiple management values. International Journal of Wildland Fire 29, 414-426.
| Crossref | Google Scholar |

Clarke H, Cirulis B, Penman T, Price O, Boer MM, Bradstock R (2022) The 2019–2020 Australian forest fires are a harbinger of decreased prescribed burning effectiveness under rising extreme conditions. Scientific Reports 12, 11871.
| Crossref | Google Scholar | PubMed |

Cruz MG, Gould JS, Alexander ME, Sullivan AL, McCaw WL, Matthews S (2015) ‘A Guide to Rate of Fire Spread Models for Australian Vegetation.’ (CSIRO Land and Water: Canberra, ACT, and AFAC: Melbourne, Vic.)

Department for Environment and Water (2021) Bushfires and Prescribed Burns History. Available at https://data.sa.gov.au/data/dataset/e5434c77-9815-48e6-8ea7-fb35c78f6786 [accessed 02 August 2021]

Duff TJ, Penman TD (2021) Determining the likelihood of asset destruction during wildfires: modelling house destruction with fire simulator outputs and local-scale landscape properties. Safety Science 139, 105196.
| Crossref | Google Scholar |

Falk DA, Heyerdahl EK, Brown PM, Farris C, Fulé PZ, McKenzie D, Swetnam TW, Taylor AH, Van Horne ML (2011) Multi-scale controls of historical forest-fire regimes: new insights from fire-scar networks. Frontiers in Ecology and the Environment 9, 446-454.
| Crossref | Google Scholar |

Filkov AI, Ngo T, Matthews S, Telfer S, Penman TD (2020) Impact of Australia’s catastrophic 2019/20 bushfire season on communities and environment. Retrospective analysis and current trends. Journal of Safety Science and Resilience 1, 44-56.
| Crossref | Google Scholar |

Finney MA (1998) FARSITE: Fire Area Simulator-model development and evaluation. (U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station) 10.2737/RMRS-RP-4

Finney MA (2005) The challenge of quantitative risk analysis for wildland fire. Forest Ecology and Management 211, 97-108.
| Crossref | Google Scholar |

Fletcher MS, Hall T, Alexandra AN (2021) The loss of an indigenous constructed landscape following British invasion of Australia: an insight into the deep human imprint on the Australian landscape. Ambio 50, 138-149.
| Crossref | Google Scholar | PubMed |

Furlaud JM, Williamson GJ, Bowman DMJS (2018) Simulating the effectiveness of prescribed burning at altering wildfire behaviour in Tasmania, Australia. International Journal of Wildland Fire 27, 15-28.
| Crossref | Google Scholar |

Gazzard T, Walshe T, Galvin P, Salkin O, Baker M, Cross B, Ashton P (2020) What is the ‘appropriate’ fuel management regime for the Otway Ranges, Victoria, Australia? Developing a long-term fuel management strategy using the structured decision-making framework. International Journal of Wildland Fire 29, 354-370.
| Crossref | Google Scholar |

Geoscience Australia (2010) 3 second SRTM Digital Elevation Model (DEM) v01. Bioregional Assessment Source Dataset. Available at https://data.gov.au/data/dataset/12e0731d-96dd-49cc-aa21-ebfd65a3f67a [accessed 31 July 2021]

Gill AM, Allan G (2008) Large fires, fire effects and the fire-regime concept. International Journal of Wildland Fire 17, 688-695.
| Crossref | Google Scholar |

Gill AM, Stephens SL, Cary GJ (2013) The worldwide “wildfire” problem. Ecological Applications 23, 438-454.
| Crossref | Google Scholar | PubMed |

Grassberger P, Manna SS (1990) Some more sandpiles. Journal de Physique 51, 1077-1098.
| Crossref | Google Scholar |

Hantson S, Pueyo S, Chuvieco E (2015) Global fire size distribution is driven by human impact and climate. Global Ecology and Biogeography 24, 77-86.
| Crossref | Google Scholar |

Heyerdahl EK, Brubaker LB, Agee JK (2001) Spatial controls of historical fire regimes: a multiscale example from the interior west, USA. Ecology 82, 660-678.
| Crossref | Google Scholar |

Hijmans R (2022) terra: Spatial Data Analysis. R package version 1.6-41. Available at https://CRAN.R-project.org/package=terra [accessed 18 November 2022]

Hirsch K, Martell D (1996) A review of initial attack fire crew productivity and effectiveness. International Journal of Wildland Fire 6, 199-215.
| Crossref | Google Scholar |

Hosmer DW, Lemeshow S, Sturdivant RX (2013) ‘Applied logistic regression.’ 3rd edn. (John Wiley and Sons: Hoboken, NJ, USA)

Jain P, Coogan SCP, Subramanian SG, Crowley M, Taylor S, Flannigan MD (2020) A review of machine learning applications in wildfire science and management. Environmental Reviews 28, 478-505.
| Crossref | Google Scholar |

Jones MW, Abatzoglou JT, Veraverbeke S, Andela N, Lasslop G, Forkel M, Smith AJP, Burton C, Betts RA, Van Der Werf GR, Sitch S, Canadell JG, Santín C, Kolden C, Doerr SH, Le Quéré C (2022) Global and regional trends and drivers of fire under climate change. Reviews of Geophysics 60, 1-76.
| Crossref | Google Scholar |

Lauer CJ, Montgomery CA, Dietterich TG (2017) Spatial interactions and optimal forest management on a fire-threatened landscape. Forest Policy and Economics 83, 107-120.
| Crossref | Google Scholar |

Leuenberger M, Parente J, Tonini M, Pereira MG, Kanevski M (2018) Wildfire susceptibility mapping: deterministic vs. stochastic approaches. Environmental Modelling & Software 101, 194-203.
| Crossref | Google Scholar |

Liberatore F, León J, Hearne J, Vitoriano B (2021) Fuel management operations planning in fire management: a bilevel optimisation approach. Safety Science 137, 105181.
| Crossref | Google Scholar |

Maier HR, Galelli S, Razavi S, Castelletti A, Rizzoli A, Athanasiadis IN, Sànchez-Marrè M, Acutis M, Wu W, Humphrey GB (2023) Exploding the myths: an introduction to artificial neural networks for prediction and forecasting. Environmental Modelling & Software 167, 105776.
| Crossref | Google Scholar |

McArthur AG (1967) ‘Fire behaviour in eucalypt forest.’ Leaflet 107. (Commonwealth of Australia, Forestry and Timber Bureau: Canberra, ACT, Australia)

McKenzie D, Kennedy MC (2011) Scaling laws and complexity in fire regimes. In ‘The Landscape Ecology of Fire’. (Eds D McKenzie, C Miller, DA Falk) pp. 27–49. (Springer: Berlin/Heidelberg, Germany)

McKenzie D, Miller C, Falk DA (2011) Toward a theory of landscape fire. In ‘The Landscape Ecology of Fire’. (Eds D McKenzie, C Miller, DA Falk) pp. 3–25. (Springer: Berlin/Heidelberg, Germany)

Miller C, Ager AA (2013) A review of recent advances in risk analysis for wildfire management. International Journal of Wildland Fire 22, 1-14.
| Crossref | Google Scholar |

Miller C, Hilton J, Sullivan A, Prakash M (2015) SPARK – A Bushfire Spread Prediction Tool. In ‘International Symposium on Environmental Software Systems’, Melbourne, Vic. (Eds R Denzer, RM Argent, G Schimack, J Hřebíček) pp. 262–271. (Springer International Publishing: Melbourne, Vic., Australia) 10.1007/978-3-319-15994-2_26 [accessed 4 May 2022]

Newman EA, Kennedy MC, Falk DA, McKenzie D (2019) Scaling and complexity in landscape ecology. Frontiers in Ecology and Evolution 7, 1-16.
| Crossref | Google Scholar |

Noble IR, Gill AM, Bary GAV (1980) McArthur’s fire-danger meters expressed as equations. Australian Journal of Ecology 5, 201-203.
| Crossref | Google Scholar |

O’Donnell AJ, Boer MM, McCaw WL, Grierson PF (2011) Vegetation and landscape connectivity control wildfire intervals in unmanaged semi-arid shrublands and woodlands in Australia. Journal of Biogeography 38, 112-124.
| Crossref | Google Scholar |

Ott JE, Kilkenny FF, Jain TB (2023) Fuel treatment effectiveness at the landscape scale: a systematic review of simulation studies comparing treatment scenarios in North America. Fire Ecology 19, 10.
| Crossref | Google Scholar |

Parisien M-A, Moritz MA (2009) Environmental controls on the distribution of wildfire at multiple spatial scales. Ecological Monographs 79, 127-154.
| Crossref | Google Scholar |

Parisien M-A, Miller C, Ager AA, Finney MA (2010) Use of artificial landscapes to isolate controls on burn probability. Landscape Ecology 25, 79-93.
| Crossref | Google Scholar |

Parisien M-A, Dawe DA, Miller C, Stockdale CA, Armitage OB (2019) Applications of simulation-based burn probability modelling: a review. International Journal of Wildland Fire 28, 913-926.
| Crossref | Google Scholar |

Parisien M-A, Ager AA, Barros AM, Dawe D, Erni S, Finney MA, McHugh CW, Miller C, Parks SA, Riley KL, Short KC, Stockdale CA, Wang X, Whitman E (2020) Commentary on the article “Burn probability simulation and subsequent wildland fire activity in Alberta, Canada – Implications for risk assessment and strategic planning” by J.L. Beverly and N. McLoughlin. Forest Ecology and Management 460, 117698.
| Crossref | Google Scholar |

Parks SA, Parisien M-A, Miller C (2011) Multi-scale evaluation of the environmental controls on burn probability in a southern Sierra Nevada landscape. International Journal of Wildland Fire 20, 815-828.
| Crossref | Google Scholar |

Penman TD, Bradstock RA, Price OF (2014) Reducing wildfire risk to urban developments: simulation of cost-effective fuel treatment solutions in south eastern Australia. Environmental Modelling & Software 52, 166-175.
| Crossref | Google Scholar |

Peterson GD (2002) Contagious disturbance, ecological memory, and the emergence of landscape pattern. Ecosystems 5, 329-338.
| Crossref | Google Scholar |

Price OF, Bedward M (2020) Using a statistical model of past wildfire spread to quantify and map the likelihood of fire reaching assets and prioritise fuel treatments. International Journal of Wildland Fire 29, 401-413.
| Crossref | Google Scholar |

Price OF, Bradstock RA (2010) The effect of fuel age on the spread of fire in sclerophyll forest in the Sydney region of Australia. International Journal of Wildland Fire 19, 35-45.
| Crossref | Google Scholar |

Price O, Borah R, Bradstock R, Penman T (2015a) An empirical wildfire risk analysis: the probability of a fire spreading to the urban interface in Sydney, Australia. International Journal of Wildland Fire 24, 597-606.
| Crossref | Google Scholar |

Price OF, Penman TD, Bradstock RA, Boer MM, Clarke H (2015b) Biogeographical variation in the potential effectiveness of prescribed fire in south-eastern Australia. Journal of Biogeography 42, 2234-2245.
| Crossref | Google Scholar |

R Core Team (2022) ‘R: A language and environment for statistical computing.’ (R Foundation for Statistical Computing: Vienna, Austria) Available at https://www.R-project.org/ [accessed 16 March 2022]

Roberts ME, Rawlinson AA, Wang Z (2021) Ember risk modelling for improved wildfire risk management in the peri-urban fringes. Environmental Modelling & Software 138, 104956.
| Crossref | Google Scholar |

Rothermel RC (1983) ‘How to Predict the Spread and Intensity of Forest and Range Fires.’ (United Stated Department of Agriculture Forest Service: Ogden, UT)

Sharma LK, Gupta R, Fatima N (2022) Assessing the predictive efficacy of six machine learning algorithms for the susceptibility of Indian forests to fire. International Journal of Wildland Fire 31, 735-758.
| Crossref | Google Scholar |

South Australian Country Fire Service (2022) Bushfire History. Available at https://www.cfs.sa.gov.au/about/about/bushfire-history/ [accessed 19 September]

State of Victoria (2015) Measuring bushfire risk in Victoria. Available at https://www.safertogether.vic.gov.au/__data/assets/pdf_file/0031/126949/DELWP0017_BushfireRiskProfiles_rebrand_v5.pdf [accessed 27 October 2023]

Su C-H, Eizenberg N, Steinle P, Jakob D, Fox-Hughes P, White CJ, Rennie S, Franklin C, Dharssi I, Zhu H (2019) BARRA v1.0: the Bureau of Meteorology atmospheric high-resolution regional reanalysis for Australia. Geoscientific Model Development 12, 2049-2068.
| Crossref | Google Scholar |

Telfer S (2019) Bushfire Simulation and Suppression Probability Weighting for Strategic Bushfire Planning. In ‘6th International Fire Behaviour and Fuels Conference’, Sydney, Australia. (International Association of Wildland Fire: Missoula, MT, USA)

Thompson MP, Calkin DE (2011) Uncertainty and risk in wildland fire management: a review. Journal of Environmental Management 92, 1895-1909.
| Crossref | Google Scholar | PubMed |

Tolhurst KG, Shields BJ, Chong DM (2008) Phoenix: development and application of a bushfire risk management tool. Australian Journal of Emergency Management 23, 47-54.
| Google Scholar |

Tymstra C, Bryce R, Wotton B, Taylor S, Armitage O (2010) Development and structure of Prometheus: the Canadian wildland fire growth simulation model. Information Report NOR-X-417. (Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre: Edmonton, AB)

Van Wagner CE (1969) A simple fire-growth model. The Forestry Chronicle 45, 103-104.
| Crossref | Google Scholar |

Verde JC, Zêzere JL (2010) Assessment and validation of wildfire susceptibility and hazard in Portugal. Natural Hazards and Earth System Sciences 10, 485-497.
| Crossref | Google Scholar |

Wang X, Wotton BM, Cantin AS, Parisien M-A, Anderson K, Moore B, Flannigan MD (2017) cffdrs: an R package for the Canadian Forest Fire Danger Rating System. Ecological Processes 6, 5.
| Crossref | Google Scholar |

Williams BA, Shoo LP, Wilson KA, Beyer HL (2017) Optimising the spatial planning of prescribed burns to achieve multiple objectives in a fire‐dependent ecosystem. Journal of Applied Ecology 54, 1699-1709.
| Crossref | Google Scholar |

Appendix 1.Preliminary analysis of neighbourhood index sensitivity to resolution factor

Fig. A1.

Comparison of neighbourhood index (NI-ROS) calculated with fixed resolution factor and variable resolution factor. The Pearson correlation coefficient between the two indices is 0.9997. The computation time of the variable resolution factor index is 473 s. The computation time of the fixed resolution factor index is significantly higher (209,725 s).

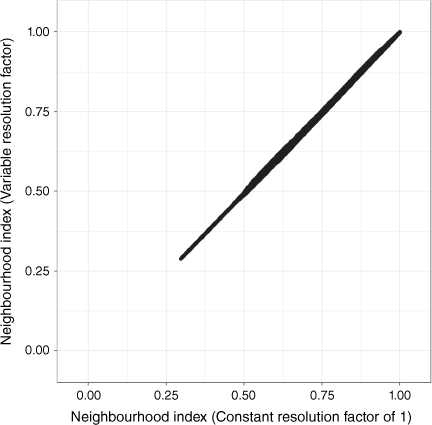
Appendix 2.Extended results for all computational experiments

Table A1.Receiver-Operator Characteristic Area Under Curve results for the different neighbourhood indices when testing against areas burnt at least once, at least twice or three times in the historical record.

Index and version	AUC-ROC metric
	Minimum number of times areas compared against have burnt			Average
	1	2	3	Average
NI-ROS	0.456	0.370	0.434	0.420
NI-HFI	0.641	0.771	0.819	0.744

The average AUC-ROC score is used to select the best-performing index for comparison within the Results & discussion section.

Table A2.Pearson and Spearman rank correlations between the different neighbourhood indices and simulated burn probability.

Index and version	Correlation metric		Average correlation
Index and version	Pearson	Spearman	Average correlation
NI-ROS	0.83	0.85	0.84
NI-HFI	−0.24	−0.28	−0.26

Average correlation is used to select the best-performing index for comparison within the Results & discussion section.