High-resolution fire danger forecast for Poland based on the Weather Research and Forecasting Model
Alan Mandal A , Grzegorz Nykiel A B , Tomasz Strzyzewski A D , Adam Kochanski C , Weronika Wrońska A , Marta Gruszczynska A and Mariusz Figurski
A B , Tomasz Strzyzewski A D , Adam Kochanski C , Weronika Wrońska A , Marta Gruszczynska A and Mariusz Figurski  A
A
A Institute of Meteorology and Water Management, National Research Institute, 01-673 Warsaw, Poland.
B Faculty of Civil and Environmental Engineering, Gdansk University of Technology, 80-233 Gdansk, Poland.
C Department of Meteorology and Climate Science, San Jose State University, San Jose, CA 95192-0104, USA.
D Corresponding author. Email: tomasz.strzyzewski@imgw.pl
International Journal of Wildland Fire 31(2) 149-162 https://doi.org/10.1071/WF21106
Submitted: 5 August 2021 Accepted: 10 November 2021 Published: 23 December 2021
Journal Compilation © IAWF 2022 Open Access CC BY-NC-ND
Abstract
Due to climate change and associated longer and more frequent droughts, the risk of forest fires increases. To address this, the Institute of Meteorology and Water Management implemented a system for forecasting fire weather in Poland. The Fire Weather Index (FWI) system, developed in Canada, has been adapted to work with meteorological fields derived from the high-resolution (2.5 km) Weather Research and Forecasting (WRF) model. Forecasts are made with 24- and 48-h lead times. The purpose of this work is to present the validation of the implemented system. First, the results of the WRF model were validated using in situ observations from ~70 synoptic stations. Second, we used the correlation method and Eastaugh’s percentile analysis to assess the quality of the FWI index. The data covered the 2019 fire season and were analysed for the whole forest area in Poland. Based on the presented results, it can be concluded that the FWI index (calculated based on the WRF model) has a very high predictive ability of fire risk. However, the results vary by region, distance from human habitats, and size of fire.
Keywords: fire weather index, FWI, fire danger, forecasting, forest fires, Weather Research and Forecasting Model, WRF, Poland.
Introduction
Fires are one of the greatest threats to forest ecosystems. They can negatively affect the composition and structure of fauna (Smith 2000) and flora (Brown and Smith 2000), as well as air (Sandberg et al. 2002), soil, and water quality (Neary et al. 2005). Additionally, they cause economic losses (González-Cabán 2013) and pose dangers to human health and life (Xu et al. 2020). As indicated by many studies (Lavorel et al. 2006; Hantson et al. 2015; Jolly et al. 2015; Barbero et al. 2020), progressive global climate change may in future cause an increase in the frequency and intensity of forest fires in most regions of the Earth. Although no increase in fire activity has been observed in Poland (Grajewski 2017) from 1990 to 2016, work on its monitoring and forecasting should begin now – in preparation for future increases in fire activity that may be further exacerbated by increasing human activities, urbanisation, and settlement growth (Chas-Amil et al. 2013; Bowman et al. 2011; Syphard et al. 2007; Narayanaraj and Wimberly 2012). Effective forest fire management activities, consisting of prevention, detection, control, suppression, and restriction of fire, are necessary to minimise the effects of wildfire (Martell 2001). Prescribed burning is also increasingly being used as an effective fire management tool (Francos and Úbeda 2021). In the decision-making activities associated with these activities, assessing and forecasting forest fire danger is particularly important (Wotton 2009).
Forest fire danger is understood as an assessment of the constant and dynamic factors that determine the ease of ignition, the spread rate, the difficulty of control, and the impact of fires (Stacey 2012). The most important of these include weather conditions, human behaviour, vegetation characteristics, fuel availability, and topography (Flannigan and Wotton 2001). Depending on the spatial and temporal variability of each factor, its impact on the assessment of forest fire risk can be different (de Rigo et al. 2017). According to this variability, the fire hazard can be predicted using static (long-term) and dynamic (short-term) indicators (San-Miguel-Ayanz 2002). Static indicators use factors that do not change in a short time, for example topography and type of vegetation. They are mainly used for long-term planning, for example decisions on the construction of fire protection infrastructure. Dynamic indicators support the operational activities of forest fire management. They assess fuel availability and weather conditions by which they determine the possible ease of ignition and the ability to spread fire (San-Miguel-Ayanz 2002). Most of the dynamic indicators are based mainly on meteorological data, because they are relatively easy to obtain and provide a good forecast of moisture in the fuel (Chuvieco et al. 2009).
The Canadian Forest Fire Weather Index (FWI) (Wagner 1987; Lawson and Armitage 2008) is one of the most widely used dynamic indices worldwide for predicting forest fire danger. Besides Canada, it has some usage in Alaska and the Great Lakes region of the USA (Mölders 2008; Horel et al. 2014), China (Tian et al. 2014), Great Britain (de Jong et al. 2016), Spain (Romero et al. 2014), Portugal (Carvalho et al. 2008), Italy (Cane et al. 2008) and Greece (Varela et al. 2015), among others. It has also been adopted by the European Forest Fire Information System (EFFIS) (de Rigo et al. 2017; Di Giuseppe et al. 2020). Although it was developed for Canadian pine forests, it works well for other forest types (Taylor and Alexander 2006). FWI provides a uniform way to predict forest fire danger based on weather conditions (air temperature, relative humidity, wind speed, and precipitation), by which the moisture content of three layers of forest floor (litter, duff, deep layer) and potential fire behaviour (rate of spread and intensity) are determined. Only meteorological data are needed for FWI calculations, so that the index can be estimated directly using data from numerical weather prediction (NWP) models (Di Giuseppe et al. 2016).
One of the NWP models used for fire weather forecasting is the Weather Research and Forecasting (WRF) model (Skamarock et al. 2019). Mölders (2008) used this model to predict fire weather for the interior of Alaska in June 2005. He found that WRF is well suited for this task. Although some of the meteorological parameters were slightly overestimated or underestimated, the trends of the fire index were appropriately predicted and the fire indices derived from the daily mean forecast meteorological parameters were quite reliable. Simpson et al. (2014) used WRF to model the 2009–2010 fire season in New Zealand. They used predicted meteorological parameters to calculate the FWI and the continuous Haines index (CHI). They showed that due to model errors in wind speed forecasting and rainfall, the model underestimated the FWI values associated with periods of high fire hazard. Furthermore, due to problems with modelling meteorological fields at 850 hPa, the CHI values were only moderately in agreement with observations. On the other hand, Rodríguez et al. (2018) and Papagiannaki et al. (2020) showed, based on the example of Argentina and the Mediterranean region, that WRF can be used successfully and efficiently used for FWI forecasting. One of the important factors in using any NWP model is the correct choice of parameterisation to predict as accurately as possible the meteorological parameters, which are critical in the context of fire danger.
In this paper, we validate the high-resolution FWI forecasting system implemented in Poland that is driven by meteorological data derived from the WRF. The rationale for conducting the research is mainly associated with the high number of forest fires occurrence in Poland, which have not decreased for many years, and the risk of worsening of this trend in connection with projected global climate changes. Presently, the low-resolution fire forecast is in place in Poland, created by the Forest Research Institute, which divides the country into 60 forecast zones (more details in the Forest fire data subsection). However, there is no forest fire risk prediction system that would provide sufficient spatial resolution to identify the most fire-prone areas. The paper is organised as follows. First, data and methodology are described, including the fire database and the WRF model. Next, we present validation results utilising methods applied to the whole country and its separated regions, which are followed by a discussion of the obtained results and statistics. Last, we provide some concise conclusions and future plans.
Data and methodology
Study area
Poland is located in central Europe on the Baltic Sea. The area of Poland is 312 705 km2, of which 93 289 km2, or~30.5%, is forest (Rozkrut 2019). Poland is located between the oceanic and continental climate. The average annual temperature in the period 1971–2000 in north-eastern Poland (Suwalki) is 6.4°C, and in western Poland (Slubice) it is 8.6°C. Annual precipitation in mountain areas is more than 1000 mm, in the highland belt, and in the north of the country is 600–700 mm, while in central Poland it is ~550 mm (all data from the Institute of Meteorology and Water Management).
The lowlands (areas with altitudes of less than 300m above mean sea level (MSL)) cover 91.3% of the country, and the average height of the terrain is 173 m MSL. The lowest point is 1.8 m below sea level and the highest point is 2499 m above sea level. There are mountain areas in the south of the country and the relief gradually slopes towards the north.
The highest population density is in the south of the country in the agglomerations of Katowice and Kraków. Population clusters also occur around the largest cities and are distributed relatively regularly throughout the country. The areas of north-eastern Poland are the least populated.
Most of the forested lands are owned by the State Treasury. The national forest comprises 81% of the total forested land, with private forests making up the remainder. The economic function of forests is associated with construction, timber, and cellulose for paper production. Coniferous vegetation accounts for 87% of forests (mainly Pinus sylvestris and Larix decidua – 75.5%) (Rozkrut 2019). The distribution of forests in Poland is not geographically uniform. The most forested areas are in the western and northern parts of the country. Some forests are present in mountain areas in the southern part of the country and in the north-eastern regions, and central Poland is the least forested area.
Due to the diversity of natural conditions in the State Forests, a division into eight regions was introduced (Zielony and Kliczkowska 2012). The division is based on:
-
Total annual precipitation;
-
Average annual air temperature;
-
Length of the growing season;
-
Annual temperature amplitude;
-
Range of glacial periods;
-
Natural landscape classes;
-
Range of natural occurrence of Abies alba, Picea abies, and Fagus sylvatica; and
-
The occurrence and distribution of the major classes of potential natural vegetation and plant landscapes.
The result of the division of the country into eight regions is presented in Fig. 1 and some basic characteristics of these regions are presented in Table 1.

|
In each region (except Sudeten), the main species is Pinus sylvestris (the average for the whole of Poland is 60%). The largest share of Pinus Sylvestris (81%) is in the Poland–Pomeranian area in central Poland, and the smallest is in the coastal areas (Baltic), where it is 50%. The main species in the Sudetes is Picea abies (56%). Except for the Sudetes, all regions have a similar structure of stand age (58–66 years) and forestation (21.7–28.6%). The population density in the regions varies, with the lowest in Masurian-Podlasie in north-eastern Poland and the highest in Lesser Poland in southern Poland. The average height above sea level increases from the north (sea coast) to the south (mountains).
Forest fire data
According to the report of the European Commission (San-Miguel-Ayanz et al. 2019), in 2009–2018, Poland ranks fourth in Europe in terms of the average annual number of forest fires (7141) and 12th in terms of the average annual burnt area (3572 ha). Regarding the average burned area of a single forest fire (0.44 ha), Poland ranks 24th, suggesting that fires are usually extinguished at an early stage of their development (Grajewski 2017). The specificity of forest fires in Poland, compared with other European countries, is a large number of them with a much smaller burned area. Almost all forest fires throughout the year (97%) occur in Poland from March to September (Szczygieł and Kwiatkowski 2020). The key element controlling the danger of forest fires in Poland is the atmospheric conditions. Poland is located at the interface between continental and oceanic climates, resulting in frequent weather anomalies, such as prolonged droughts that favour fire occurrence or strong winds that cause rapid fire spread.
During the fire season, the activities of Polish forest fire management are supported by forest fire danger forecasts, which are prepared for 60 forecast zones up to 24 h in advance. Fire danger forecasts are based on weather conditions (temperature, relative humidity, and daily amount of precipitation) and moisture content of forest litter, using indicators and an algorithm developed by the Polish Forest Research Institute (Szczygieł and Kwiatkowski 2020). The forecasts are made on a 4-grade scale: no threat; low threat; medium threat; and high threat, at 0900 and 1300 hours local time.
To have complete and detailed information on the fires that occurred in 2019, additional data were requested from the Polish State Fire Service. The data obtained contained information on the exact location of the fire (latitude and longitude), the reported ignition time and time of containment, the burnt area, the cause of the fire, and the type of vegetation affected by the fire. This research focuses only on forest fires that occurred during the fire season from March 1 to September 30. The 2019 fire season was active, and provided extensive data records required for statistical analysis. General fire statistics show that it can be taken as representative of the decade. During the fire season, 8338 forest fires were reported with a total burned area of 3431 ha. The season from March 1 to September 30 accounted for 93.7% of all fire events and 97.9% of the total burned area. Most of the forest fires were small: 90.7% of them did not exceed 1 ha, and 58.4% were less than 0.1 ha. Larger fires, which exceeded 5 ha, accounted for 1.2%. The average area of the fire was 0.41 ha. Most of the forest fires (88.8%) were human caused. Lightning discharges caused only 0.8% of fires, and 10.4% of the fire causes were not identified. The largest forest fire (40.2%) occurred in April, and the burned area in this month represented 57.3% of the entire season. On 23 April, there were 383 active forest fires throughout the country, with a total burned area of 493 ha (14.4% of the entire season).
For the purposes of this research, the number of forest fires and burned areas were classified by region, season, size, and distance from the nearest city. The period from March to May was considered the spring season and the period from June to September was assumed to be the summer season. The distance from the city was determined on the basis of the administrative city borders. The numbers of the fires and the size of burned area for specific regions are presented in Fig. 2. The spatial distributions of the fires and burned areas, clustered in a 2.5 × 2.5-km grid (same as NWP data), are shown in Fig. 3.

|

|
Canadian Forest Fire Weather Index (FWI) system
The FWI system consists of six elements. There are three fuel moisture codes that assess fuel moisture content:
-
Fine Fuel Moisture Code (FFMC) represents the moisture level of the upper layer of the litter (approximately 1–2 cm deep). FFMC considers temperature, humidity, precipitation, and wind. The code is susceptible to rapidly changing meteorological conditions. FFMC is used to describe the ease of ignition and the probability of its occurrence (De Groot 1987);
-
The Duff Moisture Code (DMC) describes the upper layers of the forest floor where litter starts to decay (approximately 5–10 cm deep). They have a longer drying time than FFMC fuels, which causes a delay of 12 days. DMC is influenced by temperature, wind, and precipitation, and has been proven to be helpful in predicting ignition caused by lightning discharges; and
-
Drought Code (DC) expresses the moisture status of the deepest (compact) organic layers (approximately 10–20 cm deep) corresponding to the ground fuel. This class is affected by temperature and rain, and slowly dries with a delay of 52 days.
There are three indicators describing the behaviour of fire:
-
Initial Spread Index (ISI) combines FFMC and wind speed, and indicates the rate at which fires spread;
-
Buildup Index (BUI) combines two moisture codes, DMC and DC. It expresses the amount of fuel available to the fire during a fire spread, taking into account the humidity of organic layers. BUI is used for fire suppression planning; and
-
The FWI indicator integrates all these elements, and indicates the intensity of the fire in the event of ignition on the basis of the combined rate of spread and the amount of fuel available. It is used to represent fire risk conditions.
To describe fire risk, usually six classes are distinguished: very low; low; moderate; high; very high; and extreme (Wagner 1987; Wotton 2009), where low code values indicate a lower fire susceptibility, and high values indicate a higher fire risk.
The FWI system was developed for the standard forest (mature Jack Pine (Pinus banksiana Lamb) and Lodgepole Pine (Pinus contorta)) (Wotton 2009). However, the behavioural characteristics of these species during fire are similar and can also be found in other forest types (Stocks et al. 1989). Taylor and Alexander (2006) proved that the FWI system can also work well in such cases.
Weather Research and Forecasting model data
The FWI parameters were estimated on the basis of the meteorological fields derived from the non-hydrostatic WRF model ver. 4.2.1 (Skamarock et al. 2019). As initial and boundary conditions, data from the Global Forecast System (GFS) were applied with a spatial resolution of 0.25°. We designed two nested domains with one way of nesting with a coefficient of 5. This allowed us to get two domains in the Lambert Conformal projection, with 12.5-km and 2.5-km resolution. In this study, we used only fields from the nested high-resolution grid, which covered the whole area of Poland. In the vertical, the forecasts were performed for 50 levels up to 50 hPa. Simulations were started at 1200 hours UTC with a forecast duration of 48 h, which allowed us to obtain FWI parameters with a 24- and 48-h lead time for each WRF run. Initialisation of the FWI moisture code elements were done using 1-month simulation. All calculations were carried out on the high performance Tryton computer, located at the Academic Computer Center in Gdansk, with 552 cores allocated to computations and 16 cores supporting I/O operations.
We used a single-moment microphysics scheme with six hydrometeor classes (WSM6) (Zaidi and Gisen 2018), Grell–Freitas convective parameterisation (Grell and Freitas 2014) for the 12.5-km domain, and explicit wet process physics for the 2.5-km domain. The model used RRTMG radiative scheme (Iacono et al. 2008), the Mellor Yamada Nakanishi Niino (MYNN) turbulence scheme (Nakanishi and Niino 2009) with 2.5-order closure for boundary layer processes, and the MYNN level 3 scheme for parametrisation of the near-surface layer (Nakanishi and Niino 2006). The topography, land use, and soil type used in the model were derived from the IGBP MODIS and USGS GMTED2010 datasets. These models, with 30 arc-second resolution, also contain seasonal variability of selected parameters. To remove numerical noise at the start of the simulations, digital filter initialisation (DFI) was used (Peckham et al. 2016).
The FWI was calculated on the basis of modelled meteorological parameters, such as air temperature, wind speed, relative humidity, and precipitation, at noon every day. Therefore, to evaluate the accuracy of the WRF model, we compared the predicted values of these parameters with in situ measurements at 62 synoptic stations. Comparison was made for the hours when FWI was counted (noon). In terms of temperature, wind speed, and relative humidity, we compared biases and root mean square error (RMSE). All analyses conducted for the 24- and 48-h lead time are presented in Fig. 4. The air temperature average bias for all stations was –0.1 ± 0.5°C and –0.2 ± 0.5°C for the 24- and 48-h forecasts respectively. The largest biases were observed for stations located on the coast and in the mountains (southern Poland), mostly due to the relatively low resolution of terrain data used in the WRF simulations. Outside these areas, the temperature biases did not exceed ±1.0°C. The 48-h forecast was generally characterised by 1.5 times higher RMSE values compared with the 24-h simulation. The average RMSE values were 2.3 ± 0.3°C (with a maximum of 3.2°C) and 3.9 ± 0.3°C (with a maximum of 4.8°C) for the 24- and 48-h forecasts respectively. In the case of wind speed, the biases were similar for both time leads, with an average of 0.6 ± 0.6 m s−1. However, the RMSE values were significantly higher for longer simulations and equal to 2.5 ± 0.2 m s−1. For air humidity (at 2 m above the surface), the biases were small for both forecasts, but we obtained high RMSEs that averaged 13 ± 2% and 17 ± 2% for 24- and 48-h time leads respectively. For stations where precipitation was recorded, we analysed the probability of detection (POD) and the critical success index (CSI), which were calculated using a 2 × 2 contingency table. A threshold equal to 0.1 mm of accumulated precipitation was adopted. For both lead times, we obtained similar results (Fig. 4d). POD and CSI had values of ~50 ± 10%. For some stations, those values were significantly higher, reaching almost 70%.
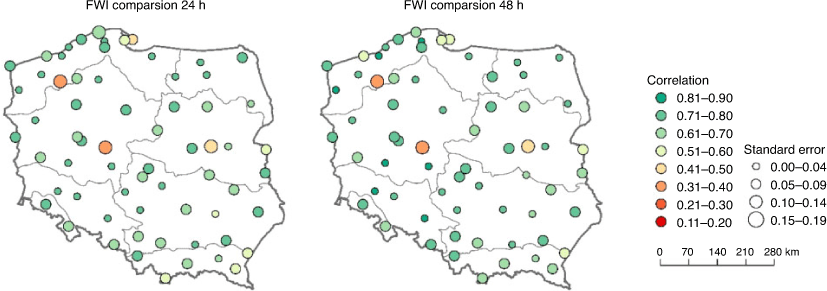
Based on these simulated meteorological parameters, we estimated the FWI values for all synoptic stations. Example of FWI time series calculated from meteorological observations and both 24- and 48-h time leads, WRF forecasts are presented in Fig. 5. The high correlation of 0.8 between solutions is clearly visible. The similarity of the calculated FWI was assessed for all stations analysed using the Pearson’s correlation coefficient and the standard error of linear regression. The results are presented together in Fig. 6. For both forecast lead times, the results obtained were very similar. Most of the stations were characterised with correlations greater than 0.7 (average 0.65 ± 0.15). Furthermore, standard errors were relatively small and did not exceed 0.18.
Based on the comparison presented with in situ measurements at meteorological stations, we concluded that the forecasted meteorological parameters provided an accurate prediction of FWI with 24- and 48-h lead times.
Results and discussion
It is worth emphasising that before operational use of the forest fire danger index occurs, it must be tested, evaluated, and validated to prepare a detailed description of the relationships between its value and fire activity, as well as other related limitations (Potter et al. 2003). Due to the short operating time of the WRF model in Poland, we analysed one fire season (March–September 2019). In our study, we focus on the following aspects:
-
How the predicted daily FWI values correlate with daily fire activity measures, such as number of fires and areas burned;
-
Whether the variability of the predicted daily FWI values can be used as a proxy for fire occurrence; and
-
How efficiently the FWI thresholds (proposed by EFFIS to assess the level of fire danger in Europe) reflected the fire danger expressed by the observed number of fires and the burned area.
It should be noted that although we focused on the analysis of data provided from 24-h FWI forecasts, the very high correlation between the 24-h and 48-h FWI forecast suggests that similar performance should be expected for FWI forecasts with a 48-h lead time.
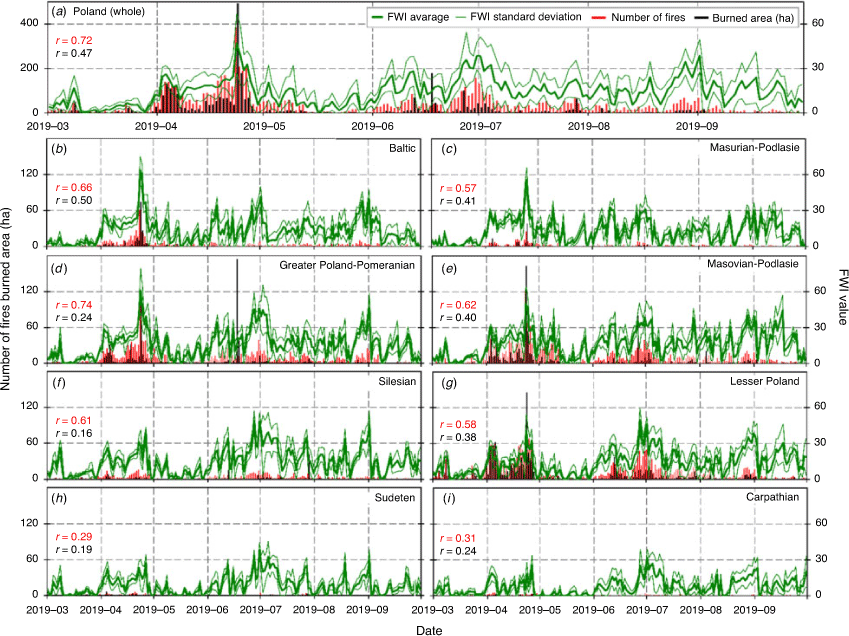
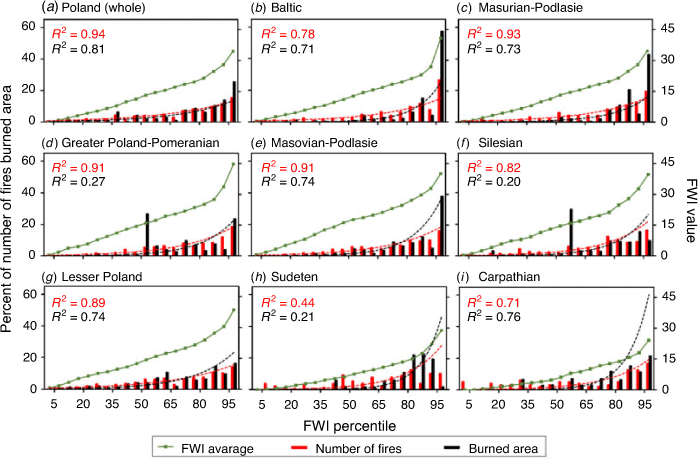
In the following section, we present an analysis of the relationship between the predicted FWI and the observed fire activity. To assess the correlation between these parameters, we determined the Pearson’s correlation coefficient for the data collected on the national and regional scale. This analysis was performed by comparing the time series of the average daily FWI values with the time series of the daily number of fires and the daily burned area. For this purpose, the datasets were individually prepared for each day and spatial unit (country or region). Average daily FWI values were calculated separately for a particular spatial unit based on the 2.5-km WRF data. Additionally, to take into account the uneven distribution of daily FWI values during the fire season, we calculated the values of the 5th–95th percentile of FWI (with increments of 5) for the same spatial units and the same dataset. Then, based on the percentile values, 20 classes were defined (percentile range: 0–5, 5–10, 10–15, … 95–100). These classes covered 10 or 11 days of the analysed season. For each class, according to the methodology of Alves et al. (2018), we calculated the total number of fires, the burned area, and the average FWI value. The number of fires and burned areas were converted into a percentage for the entire season. The relationships between the average FWI, the percentage of the number of fires, and the percentage of the burned area were determined using the coefficient of determination R2.
Our analyses showed a relatively high degree of correlation between the predicted daily FWI values and the observed daily measures of fire activity, with respect to both the raw values (Fig. 7) and the values based on the percentile method (Fig. 8). Both analyses showed stronger correlations with respect to the daily number of fires than to the daily burned areas. Higher correlations were obtained by analysing the calculated values for the entire country: 0.72 and 0.47 for comparisons with the numbers of fires and with burnt areas respectively. The correlations calculated for the regions were also generally relatively high. The lowest correlations in both analyses were observed in Sudeten (0.29 and 0.19). These low values were probably influenced by the low number of fires (128) and the burned areas (29 ha), which occurred during the studied fire season. Compared with the whole country, in the last decade, this region has always been characterised by such a low level of fire activity, which is related to the smallest forest area in the country (Table 1), and to the cooler and more humid climate of the highlands and mountainous areas (and thus also to lower values of FWI in the season, which was reflected in the fire season studied). It should be noted that this region is the only one distinguished by a dominant Picea abies forest type, whereas the other regions are dominated by Pinus sylvestris; FWI was developed in Canada on this forest type. Low correlations were also recorded in the Carpathian region (0.31 and 0.24), which had the lowest number of fires (95) and burned area (17 ha) in the country, and which is also related to small forest areas and a cooler and wetter climate. However, this region recorded a high coefficient of determination in the percentile method (0.71 and 0.76), indicating a significant relationship between FWI and fire activity in this region. The predicted FWI values for the Silesian and Greater Poland–Pomeranian regions were also characterised, in both analyses, by a low relationship with the burned area. Several large fires were recorded in these regions on days when we forecast non-high FWI values. These fires were most likely caused by human intentions and certainly affected the lower correlations.
Our analysis of the relationship between daily FWI values and fire activities showed that on 23 April 2019, when the highest FWI values were forecast, the season’s highest numbers of fires and burned areas were also observed in most of the regions. It should be noted that April is the period of the most frequent intentional burning of grasses on agricultural land. Days in the summer season with high FWI values were generally characterised by lower fire activity than were days with similar values in the spring season. The percentage classes analysis shows that days with the highest FWI values in the fire season were generally characterised by the highest number of fires and burned area. For example, 10–11 days with the highest FWI in the season (percentile 95–100) accounted for 10 to 27% of fires in the season and up to 57% of burned area (depending on the region analysed).
The presented results indicate that the presented FWI forecasting system has the potential to provide information on future fire activity with a lead time of 24 h. However, the similarity between the 24- and 48-h forecasts suggests that the performance of the 48-h FWI forecast should also be similar. We expect the FWI forecast to be useful in planning preventive measures for forest fire management on national and regional scales.
The predictive abilities of FWI indicators can be conditioned by the size of the fires, regions, season, and distance from the cities. To verify this, we used the rank–percentile method proposed by Eastaugh et al. (2012). This approach is based on an assessment of the slope of the ranked fire-day percentiles and the intercept of this slope. Daily FWI values for each 2.5 × 2.5-km grid cell (where a fire occurred) were converted to particular percentiles over the full range of days for the analysed period. Then, the percentiles corresponding to days when the fire occurred were determined and ranked from lowest to highest, making it possible to plot the ranked percentile curves. The intercepts were calculated by following the Theil–Sen method (Theil 1950; Sen 1968), which provided the median of all possible particular intercepts of that slope.
From the percentile curves we can see that the intercepts with the ‘index percentile on fire day’ at high values (e.g. close to 100) indicate very high predictive skills, whereas those at low values (close to 0) indicate no predictive skills. The results presented in Fig. 9a show that in terms of fire size, the highest predictive skills were achieved for fires larger than 5 ha, whereas the lowest predictive skills were observed for the smallest fires (<1 ha). According to the mechanism of FWI, the higher the index value, the greater the intensity of the fire after ignition. Fire should spread faster and be more difficult to extinguish. In the analysed season, the ignition of most fires was caused by a human, with many factors potentially responsible for further spread: weather conditions and humidity of combustible materials (expressed in FWI); human and firefighting response; fuel type; topography; and others. Large fires were easier to predict than small fires because many were discarded from the analyses. Small fires have a negative impact on the predictive score because most of them were caused by intentional arson, but occurred at low values of FWI, which do not allow fire to expand over a large area.

|
Analysis of the predictive ability of FWI for specific regions (Fig. 9b) showed that regions with lower fire activity (Carpathian, Baltic, Sudeten, Masurian–Podlasie, Silesia) obtained better ability to forecast fire occurrence than regions with much higher activity (Lesser Poland, Greater Poland–Pomeranian, Masovian–Podlasie). This relationship was most probably affected by the fact that in the regions with higher fire activity, a higher number of human-caused fires were observed at low FWI. Slightly better abilities were found for fires observed further away from cities (Fig. 9c), as well as those that occurred during the summer season (compared with spring) (Fig. 9d). These two relationships are also explained by the higher number of intentionally human-caused fires. During the spring, many farmers conduct numerous grass burnings. On the other hand, areas close to the city, are more likely to be chosen for recreation and activity.
Research using the rank–percentile method allowed us to distinguish between areas that correspond to very strong and weak predictive skills. Five types of prediction areas have been identified:
-
Very low, where fires occurred on days with FWI values from 0 to 25th percentile (Fig. 10a);
-
Low abilities (25 ≤ percentile < 50) (Fig. 10b);
-
Mean (50 ≤ percentile < 75) (Fig. 10c);
-
Good (75 ≤ percentile < 90) (Fig. 10d); and
-
Very good (90 ≤ percentile ≤ 100) (Fig. 10e).

|
In the case of areas with more than one fire, the percentile values were averaged. The results obtained show that in 48% of the areas analysed, the predictive abilities were good or very good. These areas accounted for 47% of the fire events and 53% of the total burned area. Very low or low skills were found in 27% of the analysed areas, where 28% of the fires and 25% of the burned area occurred. Areas with very low, low or medium predictive abilities were largely concentrated in regions within the range of socioeconomic influence of the largest agglomerations in the country, especially the capital Warsaw.
The fire index can have an informative and warning function for forest fire management and the public, but only if its values are assigned to the levels (classes) of fire risk. In this study, we decided to use EFFIS-developed thresholds that are universal for Europe (Table 2), and assess their predictive ability during the investigated fire season in Poland. The number of correctly predicted fires (in a season) was compared with the number of incorrectly predicted ones. A fire occurrence in the moderate, high, very high and extreme class was considered a correct forecast, whereas a fire in the low and very low class was considered incorrect. The number of hazard classes in which no fires were recorded was also analysed. Grid cells in the moderate, high, very high and extreme classes were classified as false positives. All grid cells (with and without fire) were also analysed. However, the structure of the results was almost identical to that of grid cells without fires – therefore we omit these results here. Additionally, the percentage of burnt area in the predicted FWI classes was examined. The results presented in Fig. 11 show that on national and regional scales, 68–83% of the fires were correctly predicted, and 17–32% were predicted erroneously. The highest number of matches was recorded in the Baltic and Greater Poland–Pomeranian region, and the lowest was recorded in the Sudeten and Carpathian regions. From 38% to 68% of the analysed grid cells can be considered false positives. The lowest number of false alarms was found in the Baltic and Carpathian regions and the highest in the Masovian–Podlasie, Silesian and Greater Poland–Pomeranian regions. In all regions, the number of accurate forecasts was greater than the number of false positives, indicating the predictive ability of the hazard classes. When analysing the burned area, we found that from 68–92% of the total burned area (in a given region) occurred during fires in the moderate, high, very high and extreme classes. In the two northern regions of the Masurian–Podlasie and the Baltic, the FWI classes were particularly successful in capturing the events that contributed to the overall burnt area. In these regions, fires associated with extreme FWI contributed to 35% and 20% of the burned area respectively.

|

|
The FWI fire hazard classes proposed by EFFIS have shown potential to be used in fire risk assessment in Poland. The very low number of forecasts in the extreme and very high classes (2–7% depending on the region) may suggest that some improvement can be made by lowering the FWI thresholds for these classes, or by combining them into one (especially in the coldest regions, such as high-elevation mountainous areas). It should be noted, though, that the limited number of days falling into the extreme and very high categories may be absolutely acceptable, considering relatively modest fire activity during the analysed period. Longer (multiyear) data records would need to be analysed to conclusively assess to what degree the general EFFIS thresholds fit the fire regime in Poland. It is also possible that as the climate warms and the fire activity increases, events falling into the current extreme and very high classes of EFFIS will become more common.
Conclusions
In this work, we presented validations of a high-resolution fire danger forecast system for Poland, which is based on the Canadian FWI index, fed with meteorological data from the WRF model. Analyses were presented for the March–September 2019 fire season using 24- and 48-h forecasts and consisted of two major steps. The first was to assess the accuracy of meteorological parameters forecasted by the WRF model and to assess the accuracy of the FWI forecasted values. We obtained a high correlation between the FWI values calculated from meteorological observations and those from the forecasted values, ~0.8 for both lead times: 24- and 48-h. The second step involved describing the relationship between the predicted FWI and the fire activity. By examining the correlations between the forecast daily FWI and the daily number of fires and burned area, we observed that the higher the forecast value of FWI in a given area (nationwide or on the scale of regions), the higher the fire activity in that area tended to be. Nationwide, we obtained correlations of 0.72 and 0.47 when comparing the number of fires and the burned area respectively. In testing the ability of FWI to predict the occurrence of fires, we found that FWI was better at predicting larger fires during the summer season, and in areas farther from cities. In our opinion, this is directly related to human activities. For the assessment of fire danger, we adopted classes according to EFFIS, which showed relatively high predictive skills in Poland. Further work focused on extending the period of analysis will aim, among other things, to define these classes specifically for the area of Poland.
The presented results refer only to one fire season, so they should not be overgeneralised. Nevertheless, in this work, we have shown that FWI in combination with the high-resolution WRF model can be a valuable tool for determining the fire danger forecast.
Data availability
The WRF FWI data are available under the CC BY-NC-ND licence (Nykiel and Figurski 2020).
Conflict of interest
The authors declare no conflicts of interest.
Declaration of funding
The study was performed as part of the research task “Development of forecasting methods to improve existing products and develop new application solutions (S-6/2021)” financed by the Ministry of Science and Higher Education (Poland), statutory activity of the Institute of Meteorology and Water Management-National Research Institute in 2021.
Acknowledgements
The Authors thank Polish National State Fire Service for providing detailed data about the fires. Calculations were carried out at the Academic Computer Centre in Gdansk.
References
Alves D, Ribeiro LM, Viegas DX (2018) Calibration of the Canadian FWI system for the territory of Europe. In ‘Advances in Forest Fire Research’. pp. 33–43. (Imprensa da Universidade de Coimbra)| Crossref |
Barbero R, Abatzoglou JT, Pimont F, Ruffault J, Curt T (2020) Attributing increases in fire weather to anthropogenic climate change over France. Frontiers in Earth Science 8, 104.
| Attributing increases in fire weather to anthropogenic climate change over France.Crossref | GoogleScholarGoogle Scholar |
Bowman DMJS, Balch J, Artaxo P, Bond WJ, Cochrane MA, D’Antonio CM, DeFries R, Johnston FH, Keeley JE, Krawchuk MA, Kull CA, Mack M, Moritz MA, Pyne S, Roos CI, Scott AC, Sodhi NS, Swetnam TW (2011) The human dimension of fire regimes on Earth: the human dimension of fire regimes on Earth. Journal of Biogeography 38, 2223–2236.
| The human dimension of fire regimes on Earth: the human dimension of fire regimes on Earth.Crossref | GoogleScholarGoogle Scholar |
Brown JK, Smith JK (2000) Wildland fire in ecosystems: effects of fire on flora. US Department of Agriculture, Forest Service, Rocky Mountain Research Station, Ogden, UT.
| Crossref |
Cane D, Ciccarelli N, Gottero F, Francesetti A, Pelfini F, Pelosini R (2008) Fire Weather Index application in north-western Italy. Advances in Science and Research 2, 77–80.
| Fire Weather Index application in north-western Italy.Crossref | GoogleScholarGoogle Scholar |
Carvalho A, Flannigan MD, Logan K, Miranda AI, Borrego C (2008) Fire activity in Portugal and its relationship to weather and the Canadian Fire Weather Index System. International Journal of Wildland Fire 17, 328–338.
| Fire activity in Portugal and its relationship to weather and the Canadian Fire Weather Index System.Crossref | GoogleScholarGoogle Scholar |
Chas-Amil ML, Touza J, García-Martínez E (2013) Forest fires in the wildland–urban interface: a spatial analysis of forest fragmentation and human impacts. Applied Geography (Sevenoaks, England) 43, 127–137.
| Forest fires in the wildland–urban interface: a spatial analysis of forest fragmentation and human impacts.Crossref | GoogleScholarGoogle Scholar |
Chuvieco E, González I, Verdú F, Aguado I, Yebra M (2009) Prediction of fire occurrence from live fuel moisture content measurements in a Mediterranean ecosystem. International Journal of Wildland Fire 18, 430–441.
| Prediction of fire occurrence from live fuel moisture content measurements in a Mediterranean ecosystem.Crossref | GoogleScholarGoogle Scholar |
De Groot WJD (1987) Interpreting the Canadian Forest Fire Weather Index (FWI) System. In ‘Proceedings: Fourth Central Regional Fire Weather Committee Scientific and Technical Seminar,’ 2 April 1987, Winnipeg, Manitoba. Canadian Forestry Service, Northern Forestry Centre, Edmonton, Alberta, pp. 3–13.
de Jong MC, Wooster MJ, Kitchen K, Manley C, Gazzard R, McCall FF (2016) Calibration and evaluation of the Canadian Forest Fire Weather Index (FWI) System for improved wildland fire danger rating in the United Kingdom. Natural Hazards and Earth System Sciences 16, 1217–1237.
| Calibration and evaluation of the Canadian Forest Fire Weather Index (FWI) System for improved wildland fire danger rating in the United Kingdom.Crossref | GoogleScholarGoogle Scholar |
de Rigo D, Libertà G, Houston Durrant T, Artés Vivancos T, San-Miguel-Ayanz J (2017) Forest fire danger extremes in Europe under climate change: variability and uncertainty. Publications Office of the European Union: Luxembourg.
| Crossref |
Di Giuseppe F, Pappenberger F, Wetterhall F, Krzeminski B, Camia A, Libertá G, San Miguel J (2016) The potential predictability of fire danger provided by numerical weather prediction. Journal of Applied Meteorology and Climatology 55, 2469–2491.
| The potential predictability of fire danger provided by numerical weather prediction.Crossref | GoogleScholarGoogle Scholar |
Di Giuseppe F, Vitolo C, Krzeminski B, San-Miguel J (2020) Fire weather index: the skill provided by ECMWF ensemble prediction system. Other hazards (e.g., glacial and snow hazards, karst, wildfires hazards, and medical geo-hazards), preprint.
| Crossref |
Eastaugh CS, Arpaci A, Vacik H (2012) A cautionary note regarding comparisons of fire danger indices. Natural Hazards and Earth System Sciences 12, 927–934.
| A cautionary note regarding comparisons of fire danger indices.Crossref | GoogleScholarGoogle Scholar |
Flannigan MD, Wotton BM (2001) Climate, weather, and area burned. In ‘Forest Fires’ pp. 351–373 (Academic Press, New York, USA)
Francos M, Úbeda X (2021) Prescribed fire management. Current Opinion in Environmental Science & Health 21, 100250.
| Prescribed fire management.Crossref | GoogleScholarGoogle Scholar |
González-Cabán A (2013) The economic dimension of wildland fires. In ‘Vegetation Fires and Global Change – Challenges for Concerted International Action. A white paper directed to the United Nations and international organizations’ pp. 229–237. (Kassel Publishing House, Germany)
Grajewski S (2017) Effectiveness of forest fire security systems in Poland. Infrastructure and Ecology of Rural Areas IV, 1563–1576.
| Effectiveness of forest fire security systems in Poland.Crossref | GoogleScholarGoogle Scholar |
Grell GA, Freitas SR (2014) A scale and aerosol aware stochastic convective parameterization for weather and air quality modeling. Atmospheric Chemistry and Physics 14, 5233–5250.
| A scale and aerosol aware stochastic convective parameterization for weather and air quality modeling.Crossref | GoogleScholarGoogle Scholar |
Hantson S, Pueyo S, Chuvieco E (2015) Global fire size distribution is driven by human impact and climate: spatial trends in global fire size distribution. Global Ecology and Biogeography 24, 77–86.
| Global fire size distribution is driven by human impact and climate: spatial trends in global fire size distribution.Crossref | GoogleScholarGoogle Scholar |
Horel JD, Ziel R, Galli C, Pechmann J, Dong X (2014) An evaluation of fire danger and behaviour indices in the Great Lakes Region calculated from station and gridded weather information. International Journal of Wildland Fire 23, 202–214.
| An evaluation of fire danger and behaviour indices in the Great Lakes Region calculated from station and gridded weather information.Crossref | GoogleScholarGoogle Scholar |
Iacono MJ, Delamere JS, Mlawer EJ, Shephard MW, Clough SA, Collins WD (2008) Radiative forcing by long–lived greenhouse gases: calculations with the AER radiative transfer models. Journal of Geophysical Research 113, D13103.
| Radiative forcing by long–lived greenhouse gases: calculations with the AER radiative transfer models.Crossref | GoogleScholarGoogle Scholar |
Jolly WM, Cochrane MA, Freeborn PH, Holden ZA, Brown TJ, Williamson GJ, Bowman DMJS (2015) Climate-induced variations in global wildfire danger from 1979 to 2013. Nature Communications 6, 7537.
| Climate-induced variations in global wildfire danger from 1979 to 2013.Crossref | GoogleScholarGoogle Scholar | 26172867PubMed |
Lavorel S, Flannigan MD, Lambin EF, Scholes MC (2006) Vulnerability of land systems to fire: interactions among humans, climate, the atmosphere, and ecosystems. Mitigation and Adaptation Strategies for Global Change 12, 33–53.
| Vulnerability of land systems to fire: interactions among humans, climate, the atmosphere, and ecosystems.Crossref | GoogleScholarGoogle Scholar |
Lawson BD, Armitage OB (2008) Weather Guide for the Canadian Forest Fire Danger Rating System. Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre, Edmonton, AB, Canada.
Martell DL (2001) Chapter 15 – Forest Fire Management. In ‘Forest Fires’ (Eds EA Johnson, K Miyanishi) pp. 527–583. (Academic Press: San Diego, CA, USA)
| Crossref |
Mölders N (2008) Suitability of the Weather Research and Forecasting (WRF) Model to predict the June 2005 fire weather for Interior Alaska. Weather and Forecasting 23, 953–973.
| Suitability of the Weather Research and Forecasting (WRF) Model to predict the June 2005 fire weather for Interior Alaska.Crossref | GoogleScholarGoogle Scholar |
Nakanishi M, Niino H (2006) An improved Mellor–Yamada level 3 model: its numerical stability and application to a regional prediction of advecting fog. Boundary-Layer Meteorology 119, 397–407.
| An improved Mellor–Yamada level 3 model: its numerical stability and application to a regional prediction of advecting fog.Crossref | GoogleScholarGoogle Scholar |
Nakanishi M, Niino H (2009) Development of an improved turbulence closure model for the atmospheric boundary layer. Journal of the Meteorological Society of Japan 87, 912.
| Development of an improved turbulence closure model for the atmospheric boundary layer.Crossref | GoogleScholarGoogle Scholar |
Narayanaraj G, Wimberly MC (2012) Influences of forest roads on the spatial patterns of human- and lightning-caused wildfire ignitions. Applied Geography (Sevenoaks, England) 32, 878–888.
| Influences of forest roads on the spatial patterns of human- and lightning-caused wildfire ignitions.Crossref | GoogleScholarGoogle Scholar |
Neary DG, Ryan KC, DeBano LF (2005) Wildland fire in ecosystems: effects of fire on soils and water. USDA Forest Service, Rocky Mountain Research Station, Ogden, UT.
| Crossref |
Nykiel G, Figurski M (2020) Fire Weather Index data for Poland (March–September 2019) based on high-resolution Weather Research and Forecasting Model [Dataset]. Gdańsk University of Technology.
| Crossref |
Papagiannaki K, Giannaros TM, Lykoudis S, Kotroni V, Lagouvardos K (2020) Weather-related thresholds for wildfire danger in a Mediterranean Region: the case of Greece. Agricultural and Forest Meteorology 291, 108076.
| Weather-related thresholds for wildfire danger in a Mediterranean Region: the case of Greece.Crossref | GoogleScholarGoogle Scholar |
Peckham SE, Smirnova TG, Benjamin SG, Brown JM, Kenyon JS (2016) Implementation of a Digital Filter Initialization in the WRF Model and its application in the rapid refresh Monthly Weather Review 144, 99–106.
| Implementation of a Digital Filter Initialization in the WRF Model and its application in the rapid refreshCrossref | GoogleScholarGoogle Scholar |
Potter BE, Goodrick S, Brown T (2003) Development of a statistical validation methodology of fire weather indices. In ‘Proceedings of 2nd International Wildland Fire Ecology and Fire Management Congress, 5th Symposium on Fire and Forest Meteorology’, 16–20 November 2003, Orlando, FL. (American Meteorological Society: Boston, MA)
Rodríguez H, Lighezzolo A, Martina A, Zigarán G, Viscardi DA, Rodriguez A, Baudo F, Scavuzzo C, Bellis L, Arganaraz J (2018) Towards the operational implementation of the Fire Weather Index FWI based on the High-Resolution WRF Model. In ‘IEEE Biennial Congress of Argentina (ARGENCON)’, pp. 1–6. (IEEE)
| Crossref |
Romero R, Mestre A, Botey R (2014) A new calibration for Fire Weather Index in Spain (AEMET). In ‘Advances in Forest Fire Research’. pp. 1044–1053. (Imprensa da Universidade de Coimbra)
| Crossref |
Rozkrut D (2019) Statistical Yearbook of Forestry. (Statistics Poland: Warsaw). Available at https://stat.gov.pl/en/topics/statistical-yearbooks/statistical-yearbooks/statistical-yearbook-of-forestry-2019,12,2.html
San-Miguel-Ayanz J (2002) Methodologies for the evaluation of forest fire risk: from long-term (static) to dynamic indices. In ‘Forest Fires: Ecology and Control’. (Eds T Anfodillo, V Carraro) pp. 117–132. (University degli Studi di Padova)
San-Miguel-Ayanz J, Durrant T, Boca R, Maianti P, Liberta G, Artes Vivancos T, Jacome Felix Oom D, Branco A, De Rigo D, Ferrari D, et al. (2019) Forest Fires in Europe, Middle East and North Africa 2018, Joint Research Centre Technical Report, JRC117883. Publications Office of the European Union, Luxembourg
| Crossref |
Sandberg DV, Ottmar RD, Peterson JL (2002) Wildland fire in ecosystems: effects of fire on air. Ogden, UT: USDA Forest Service, Rocky Mountain Research Station.
| Crossref |
Sen PK (1968) Estimates of the regression coefficient based on Kendall’s tau. Journal of the American Statistical Association 63, 1379–1389.
| Estimates of the regression coefficient based on Kendall’s tau.Crossref | GoogleScholarGoogle Scholar |
Simpson CC, Pearce HG, Sturman AP, Zawar-Reza P (2014) Verification of WRF modelled fire weather in the 2009–10 New Zealand fire season International Journal of Wildland Fire 23, 34–45.
| Verification of WRF modelled fire weather in the 2009–10 New Zealand fire seasonCrossref | GoogleScholarGoogle Scholar |
Skamarock WC, Klemp JB, Dudhia J, Gill DO, Liu Z, Berner J, Wang W, Powers JG, Duda MG, Barker D, Huang XY (2019) A Description of the Advanced Research WRF Model Version 4. NCAR Technical Notes No. NCAR/TN-556+STR. National Center for Atmospheric Research, Boulder, CO.
| Crossref |
Smith JK (2000) Wildland fire in ecosystems: effects of fire on fauna. USDA Forest Service, Rocky Mountain Research Station, Ogden, UT.
| Crossref |
Stacey R (2012) European Glossary for Wildfires and Forest Fires, European Union-INTERREG IVC.
Stocks BJ, Lawson BD, Alexander ME, Van Wagner CE, McAlpine RS, Lynham TJ, Dubé DE (1989) The Canadian Forest Fire Danger Rating System: an overview Forestry Chronicle 65, 450–457.
| The Canadian Forest Fire Danger Rating System: an overviewCrossref | GoogleScholarGoogle Scholar |
Syphard AD, Radeloff VC, Keeley JE, Hawbaker TJ, Clayton MK, Stewart SI, Hammer RB (2007) Human influence on California fire regimes. Ecological Applications 17, 1388–1402.
| Human influence on California fire regimes.Crossref | GoogleScholarGoogle Scholar | 17708216PubMed |
Szczygieł R, Kwiatkowski M (2020) Dynamic forest fire risk evaluation in Poland. Folia Forestalia Polonica 62, 139–144.
| Dynamic forest fire risk evaluation in Poland.Crossref | GoogleScholarGoogle Scholar |
Taylor SW, Alexander ME (2006) Science, technology, and human factors in fire danger rating: the Canadian experience. International Journal of Wildland Fire 15, 121–135.
| Science, technology, and human factors in fire danger rating: the Canadian experience.Crossref | GoogleScholarGoogle Scholar |
Theil H (1950) A rank-invariant method of linear and polynomial regression analysis. Indagationes Mathematicae 12, 85–91.
Tian X, Zhao F, Shu L, Wang M (2014) Changes in forest fire danger for south-western China in the 21st Century. International Journal of Wildland Fire 23, 185–195.
| Changes in forest fire danger for south-western China in the 21st Century.Crossref | GoogleScholarGoogle Scholar |
Varela V, Sfetsos A, Vlachogiannis D, Gounaris N (2015) Fire Weather Index (FWI) classification for fire danger assessment applied in Greece. Tethys, Journal of Weather and Climate of the Western Mediterrania 15, 31–40.
| Fire Weather Index (FWI) classification for fire danger assessment applied in Greece.Crossref | GoogleScholarGoogle Scholar |
Wagner CE (1987) Development and Structure of the Canadian Forest Fire Weather Index System. Forestry technical report, Canada Communication Group Publ: Ottawa, ON, Canada.
Wotton BM (2009) Interpreting and using outputs from the Canadian Forest Fire Danger Rating System in research applications. Environmental and Ecological Statistics 16, 107–131.
| Interpreting and using outputs from the Canadian Forest Fire Danger Rating System in research applications.Crossref | GoogleScholarGoogle Scholar |
Xu R, Yu P, Abramson MJ, Johnston FH, Samet JM, Bell ML, Haines A, Ebi KL, Li S, Guo Y (2020) Wildfires, global climate change, and human health. The New England Journal of Medicine 383, 2173–2181.
| Wildfires, global climate change, and human health.Crossref | GoogleScholarGoogle Scholar | 33034960PubMed |
Zaidi SM, Gisen JIA (2018) Evaluation of Weather Research and Forecasting (WRF) microphysics single moment class-3 and class-6 in precipitation forecast. MATEC Web of Conferences 150, 03007.
| Evaluation of Weather Research and Forecasting (WRF) microphysics single moment class-3 and class-6 in precipitation forecast.Crossref | GoogleScholarGoogle Scholar |
Zielony R, Kliczkowska A (2012) Natural-forest regionalization of Poland 2010. Centrum Informacyjne Lasów Państwowych. Warsaw, Poland [in Polish].