Modelling chamise fuel moisture content across California: a machine learning approach

Keywords: Adenostoma, chamise, live fuel moisture content, new growth, old growth, wildfire, machine learning, California, live fuel moisture, numerical weather modelling, WRF, random forest, LFMC.

Live fuel moisture content (LFMC) plays an integral role in the propagation and intensity of wildfires because it affects combustion and heat transfer rates within vegetation (Dimitrakopoulos and Papaioannou 2001; Chuvieco et al. 2004; Jurdao et al. 2012). Although the moisture content is higher within the herbaceous portion of the plant (new growth) compared with the woody material (old growth), both exhibit the same annual cycle in California, typically peaking in the spring (March–May) and declining to minima in early autumn (August–September). This annual cycle is shaped by the amount and frequency of winter/spring precipitation and the return of summer drought (Keeley et al. 2009; Pivovaroff et al. 2019). Tracking LFMC’s rate of decline from its spring maximum is very important because it affects the onset and severity of larger fire activity (Nolan et al. 2016). Importantly, summer/autumn LFMC minima coincide with the return of the Southern California Santa Ana wind season, creating a favourable environment for large and destructive wildfires (Dennison et al. 2008; Rolinski et al. 2016).

LFMC has long been used by fire agencies, particularly fire managers, to evaluate wildfire danger across their supported territories. Wildfire danger is assessed and predicted using a variety of fire behaviour metrics, including rates of spread, flame length, and fireline intensity, all of which are a function of LFMC. More recently, most of California’s electric utilities are also beginning to use LFMC to assess wildfire potential. Specifically, LFMC is used extensively by Southern California Edison (SCE), where they have started sampling LFMC bi-weekly within their service area to help understand the vegetation’s susceptibility to wildfire and to bolster their situational awareness, especially during periods of critical fire weather.

LFMC is generally measured bi-weekly by physically extracting small portions of the plant and performing a gravimetric process on the sample to determine its water content. The calculation for LFMC is expressed as a percentage using the following equation:

Because the vegetation water weight can exceed that of the dry matter, LFMC can exceed 100%. In California, LFMC is sampled by various federal, state, and local fire agencies, with the most commonly sampled species consisting of: chamise (Adenostoma fasciculatum); buckwheat (Fagopyrum esculentum); sagebrush (Artemisia tridentata); hoaryleaf and bigpod ceanothus (Ceanothus crassifolius and ceanothus megacarpus); and manzanita (Arctostaphylos). Although there are other native species across the landscape, these are most frequently sampled due to their abundance and ease of access within wildfire-prone regions. This paper focuses on chamise, which has relatively abundant observation data, a prerequisite for building a skilful LFMC model.

LFMC is modulated by plant phenology, and both are affected by short-term (days) and long-term (months) changes in weather and root zone soil moisture. Important weather variables include incoming solar radiation, near-surface air temperature and relative humidity, and precipitation. Root zone soil moisture is influenced by both soil type and time integrations of these weather variables, all of which can be a function of location, elevation and proximity to large bodies of water. Additionally, soil moisture is impacted by rainfall runoff (to and from the location of interest), evaporation (from the surface and evapotranspiration), and soil water recharge. All of the above factors can influence plant photosynthesis, the timing of reproduction cycles, and LFMC (Dennison and Moritz 2009; Holden and Jolly 2011; Qi et al. 2014).

Although LFMC observations are critical to understanding the environmental conditions that may lead to significant fire activity, they are severely undersampled (temporally and spatially). This problem is exacerbated when regular sampling is disrupted due to changes in staffing (such as when key personnel are committed to fire incidents), and/or when a fire consumes the vegetation within the sampling collection site. For these reasons, there is a need for a daily gridded LFMC product. Higher spatial and temporal resolution LFMC data can be used to assess fire danger in between sparse observation locations as well as provide inputs for high-resolution fire spread modelling simulations.

Many efforts to model LFMC have been made in recent years, most of which include the use of remote sensing technologies to measure leaf water content (Chuvieco 2003; Danson and Bowyer 2004; Peterson et al. 2008; Qi et al. 2012; Yebra et al. 2013; García et al. 2020; McCandless et al. 2020; Rao et al. 2020; Michael et al. 2021). Specifically, the use of Moderate Resolution Imaging Spectroradiometer (MODIS) and Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) has been reported by Serrano et al. (2000), Yebra et al. (2008) and Myoung et al. (2018). Additionally, a combination of the Normalized Difference Vegetation Index (NDVI) and surface temperature was used to estimate LFMC by Chuvieco et al. (2004). These remote-sensed based products help fill in the spatial and temporal gaps left by in situ LFMC observations.

In comparison, several studies have used in situ meteorological predictors in their LFMC models, without using remotely sensed data. Viegas et al. (2001) estimated LFMC in various plant species in Catalunya and Central Portugal as a function of several fire weather indices calculated based on the Canadian Forest Fire Weather Index System. In addition to these fire weather indices, Castro et al. (2003) also explored numerous other predictors in their LFMC model for Cistus monspeliensis in the Catalonia region of Spain, including temperature, relative humidity and soil water reserve. Dimitrakopoulos and Bemmerzouk (2003) modelled LFMC in three plant species in the Mediterranean region of Crete, Greece as a linear function of the Keetch–Byram Drought Index (KBDI). Their study was extended by Pellizzaro et al. (2007) by including other well known drought indices. More recently, Ruffault et al. (2018) have evaluated the usefulness of various drought indexes in modelling LFMC.

In this paper, we adopt an approach similar to the latter, with a goal of providing historical and near real-time chamise LFMC estimates across California. This is accomplished by building a random forest machine learning model relating in situ LFMC observations to high-resolution, validated numerical weather model data. In contrast with previous studies that use automatic weather station data, this effort uses LFMC meteorological predictors (Table 1) taken from a gridded product. This is necessary to generate a high-resolution gridded LFMC product. Our method is also advantageous over the remote sensing approach in that it can provide not only historical LFMC values well before the satellite era, but also near real-time LFMC forecasts afforded by operational weather forecasting.

Table 1.  List of LFMC model predictors
All predictors are standardised before being used to build random forest models. All temperature and relative humidity (RH) variables are at 2 m above the ground, wind speed is at 10 m above the ground and incoming shortwave radiation is at the surface

This paper will present the methodology used to develop our machine learning model to approximate new- and old-growth chamise LFMC within California. First, we will illustrate the types of data collected and generated for this modelling effort, which includes in situ LFMC observations and high-resolution weather data. Second, we will describe the predictor screening process and the random forest model construction and validation process. Third, we will assess our model performance using correlation, bias and root mean squared error (RMSE), and compare our model skill with other studies. Finally, we will summarise our results and discuss future work.

For the purpose of developing our models, we acquired historical chamise new- and old-growth LFMC observations from the National Fuel Moisture Database (NFMD) web-based interface. This database serves as a central repository for national LFMC observations, thus eliminating the time-consuming task of contacting and gathering measurements from each fire agency separately. LFMC measurements were initially retrieved for more than 100 sites across California. However, this initial site count decreased as measurements were carefully screened before building the machine learning model.

Because multiple fire agencies contribute data to the national archive, the data need to be vetted to make sure LFMC new- and old growth are consistently categorised among sites. Some fire agencies sample both new- and old-growth chamise and store and label the data as such, while others do not. To categorise the LFMC data as either new or old growth for unclearly labelled sites, we applied a historical pattern analysis by taking the following steps. First, we calculated the typical magnitude of yearly LFMC ranges for both new- and old growth based on the clearly labelled sites. LFMC typically ranges from 50% to 200% for new growth and 40% to 150% for old growth. Then, we tentatively categorised a site with the magnitude of yearly LFMC ranges greater than or equal to 150% as a new-growth site or less than or equal to 110% as an old-growth site. Sites that did not fall into these two categories were discarded. Finally, we conducted one-tailed two-sample t-tests at 5% significance level to evaluate if the mean of the LFMC time series resembles either the new-growth population mean of 89% or the old-growth population mean of 67%. Those time series that passed our tests were either designated as new or old growth. Data that did not meet our LFMC new- or old-growth criteria described above were discarded. After vetting our data, 52 chamise new-growth sites and 41 chamise old-growth sites were retained for our study (Fig. 1). Tables 2 and 3 provide the site name and associated start date, end date and record count for each new- and old-growth site location. The earliest vetted LFMC data start in 1983, with most sites having data through 2020.

Fig. 1.  Map showing the region of interest containing portions of California, Nevada and Arizona. Colour scheme represents vegetation density ranging from urban areas (white), deserts (tan) to forests (green). Figure inset top right shows all three of the WRF domain extents (red boxes). In the main portion of the figure, the innermost WRF domain (red box) encompasses the National Fuel Moisture Database observation locations for new-growth chamise (open black circles) and old-growth chamise (filled red circles).

Table 2.  Site level chamise new-growth random forest model summary table ranked by testing RMSE in increasing order
All 11 021 new-growth LFMC records are used to calculate overall statistics. RMSE and bias have units of  %. Dates formatted as year–month–day

Table 3.  Site level chamise old-growth random forest model summary table ranked by testing RMSE in increasing order
All 4917 old-growth LFMC records are used to calculate overall statistics. RMSE and bias have units of  %. Dates formatted as year–month–day

To produce a gridded LFMC product, a high spatial and temporal resolution historical weather dataset was built providing data at all of the screened site observation locations and time spans reported in Tables 2 and 3. These historical weather data were generated using a validated configuration of the Advanced Research Weather Research and Forecast model (WRF) version 4.0.3 (Skamarock et al. 2019). WRF dynamically downscaled the National Centers for Environmental Prediction Climate Forecast System Reanalysis (CFSR) (Saha et al. 2010) using 52 vertical levels and three domains consisting of an outer 18-km resolution domain with two inner 6- and 2-km resolution nested domains (Fig. 1). Multiple potential WRF configurations were validated using three observation data sources: Remote Automated Weather Stations (RAWS) (Zachariassen et al. 2003), Automated Surface Observation System (ASOS; ASOS 1998), and SCE’s weather stations. The WRF configuration that minimised the near-surface wind speed, temperature and dew point verification metrics (e.g. RMSE, correlation) was selected. This configuration includes the Morrison double-moment microphysics scheme (Morrison et al. 2009), the new Goddard longwave and shortwave radiation schemes (Chou and Suarez 1999), the Mellor–Yamada Nakanishi and Niino Level 3 (MYNN3) PBL (Nakanishi and Niino 2006), the Noah-MP (multi-physics) Land Surface Model (Niu et al. 2011) and the Kain–Fritsch cumulus scheme (Kain 2004), which was activated in the outermost domain only. Historical weather data from the WRF grid cell closest to each LFMC site were matched to LFMC measurements, with hourly WRF data temporally aggregated to obtain daily values. Potential predictor variables (e.g. air temperature, relative humidity, soil moisture and precipitation) across various time spans were then created for LFMC model development.

To model daily LFMC as a function of weather predictors, we adopted a random forest (RF) regression method. RF was found to minimise the LFMC error compared with several other machine learning methods, according to a recent study by McCandless et al. (2020). Separate chamise new- and old-growth RF models were trained using predictors from the gridded high-resolution weather data. Feature selection and parameter tuning was performed to achieve optimised RF models. Following peer-reviewed literature, we derived many predictors from the gridded weather data output, with temporal scales ranging from short-term (1–7 days) to long-term (30–240 days) periods. We then screened each predictor based on the incremental change in LFMC RMSE resulting from the inclusion or exclusion of that predictor. The end result is a set of optimised RF models relating a set of key predictors to LFMC, which are listed in Table 1.

Different RF parameter configurations were tested to minimise LFMC RMSE. Tuneable RF parameters include node size, number of trees, and percentage of randomly selected variables (Probst et al. 2019). Our algorithm converged when the number of random forest trees reached 200. The LFMC RMSE were minimised with a parameter node size of five and the percentage of randomly selected variables of 80%. The importance rank plot for the final new- and old-growth model is presented in Figs 2 and 3, respectively. Long-term precipitation predictors (90–240 days) emerge as the most important predictors in both new- and old-growth models. This makes physical sense given that plant material development is a moisture limited process and root zone soil moisture is a function of cumulative precipitation, potential evapotranspiration as well as soil physical properties (e.g. texture, depth, stone cover, etc.). In fact, Dennison and Moritz (2009) indicated that long-term precipitation accumulations (previous one-month to three-month period) impact the timing of LFMC decline and are strongly correlated with historical California wildfires. Day length is also a key predictor for the new-growth model, and long-term (150 days) near-surface air temperature is crucial for the old-growth model. Both of these predictors change with the seasons and modulate plant activity and development. Finally, our RF new- and old-growth models, now trained using the full dataset with optimal parameter settings, are stored for historical and operational implementation.

Fig. 2.  Importance rank panel plots for top chamise new-growth predictors. The left panel shows the percentage increase in the mean squared error if the predictor is permuted. The right panel shows the increase in node purity if the predictor is permuted. In both panels, the importance of each predictor increases along the abscissa.

Fig. 3.  Importance rank panel plots for top chamise old-growth predictors. The left panel shows the percentage increase in the mean squared error if the predictor is permuted. The right panel shows the increase in node purity if the predictor is permuted. In both panels, the importance of each predictor increases along the abscissa.

Our goal is to produce a gridded high-resolution daily chamise LFMC hindcast and forecast model for California, assuming chamise grows across the state. Given the sparse NFMD site locations (52 chamise new-growth sites and 41 chamise old-growth sites), we must test whether our models perform reasonably well at locations without observations. To do this, we perform many cross-validation iterations. For each validation iteration, we leave one site out for testing and use LFMC observations from all other sites to train an RF model using optimal model settings. Overall, we conducted a 52-fold (41-fold) cross-validation assessment for the new (old) growth model that corresponds to the number of sites available in each chamise fuel category. This allows us to determine if the model trained at sites with observations can be applied at locations without chamise observations across California, where modelled LFMC is influenced by the spatial and temporal variability of the weather predictors.

To assess the performance of the RF models, we collected testing results from all cross-validation iterations for all sites. In Fig. 4, observed LFMC is plotted against model-predicted LFMC for both new- and old-growth sites. Our models perform well, with an overall correlation, RMSE and bias of 0.89, 15.34% and 0.26%, respectively, for new-growth LFMC and 0.79, 8.81% and 0.11% for old-growth LFMC (see Tables 2 and 3). Furthermore, the predicted and observed LFMC are distributed along the perfect fit line (y = x) for both new- and old-growth models. Nevertheless, the old-growth LFMC model underestimates observations for the few outliers that are greater than 100%. For the new-growth model, the scatter increases as observed LFMC values increase, indicative of a model performance degradation as LFMC approaches extremely high values.

Fig. 4.  Scatter plots of predicted and observed LFMC for old- (left) and new-growth models (right). The red dotted line indicates a perfect fit.

Clearly, the fluctuations within the lower range of the LFMC spectrum play a significant role in the propagation and intensity of wildfires (Peterson et al. 2008). To assess the model performance for this critical range, we also conducted more targeted model validations during periods when observed LFMC dropped to 100% or below for new-growth sites and 90% or below for old-growth sites. Within these LFMC ranges, our model has an overall correlation, RMSE and bias of 0.73, 11.02% and 3.46% for new growth, respectively, and 0.80, 7.20% and 1.07% for old growth. Although there is minimal change in correlation and bias, the LFMC RMSE is reduced by ~4% and ~2% for the new- and old-growth sites, respectively. This suggests that the LFMC model will capture the late spring to early summer vegetation drying period, which precedes the start of peak wildfire season in California.

To further evaluate the model, we calculated training and testing error statistics for each of the 52 new-growth and 41 old-growth sites. In Table 2, the 52 new-growth sites (consisting of a total of 11 021 LFMC vetted records) are ranked from the best to worst performance according to the testing RMSE.

For most new-growth sites, the training RMSE are below 9.0%, indicating that the RF model fits the data reasonably well. Not surprisingly, the testing RMSE are somewhat larger, ranging from 7.3% to 26.5%. The degradation in model performance for testing may be attributable in part to the sparseness and inconsistency in LFMC sampling, as discussed in the introduction. Another possible culprit may be the modelling errors in weather predictors, which arise in part from the intrinsic limitation on weather predictability over regions with complex terrain (Doyle et al. 2011). Nevertheless, the overall testing RMSE (15.34%) calculated from all new-growth LFMC site testing data remains relatively small compared with the magnitude of the new-growth LFMC, which typically ranges from 50% to 200%, but can occasionally exceed 240%. As for model biases, the training bias is near zero, typically ranging from –2% to 2% among new-growth sites. In comparison, the testing bias is somewhat larger, typically ranging from –6% to 6%. However, the overall training (0.09%) and testing (0.26%) biases are near zero, which indicates that the new-growth model provides an approximately unbiased LFMC estimation.

In Table 3, the 41 old-growth sites (consisting of a total of 4917 vetted records) are ranked according to testing RMSE. Both training and testing biases are centred near zero, mostly between –1.5% and 1.5%. Similar to the new-growth LFMC model, approximately unbiased predictions can be expected when we implement the old-growth model within California. The testing RMSE of LFMC are typically much smaller for the old-growth sites compared with the new-growth sites. For example, 78% of the old-growth sites have a testing RMSE below 10%, whereas 81% of the new-growth sites have a testing RMSE less than 20%. This is consistent with the fact that woody material contains less water and tends to have less annual variability than the herbaceous portion of the plant (Countryman and Dean 1979; see Figs 5 and 6 as well).

Fig. 5.  Observed (black line and dots) and modelled (red line and dots) daily new-growth LFMC time series for the Bitter Canyon Castaic site during 2 years. Each LFMC observation (black dots) is paired with modelled LFMC from the same location and day (red dots). The light blue line is the observed historical monthly mean LFMC for the Bitter Canyon Castaic site. The year 2015 (left plot) is a relatively dry year and the year 2017 (right plot) is a relatively wet year.

Fig. 6.  Observed (black line and dots) and modelled (red line and dots) daily old-growth LFMC time series for the Irish Hills site during 2 years. Each LFMC observation (black dots) is paired with modelled LFMC (red dots) from the same location and day. The light blue line is the observed historical monthly mean LFMC for the Irish Hills site. The year 2015 (left plot) is a relatively dry year and the year 2017 (right plot) is a relatively wet year.

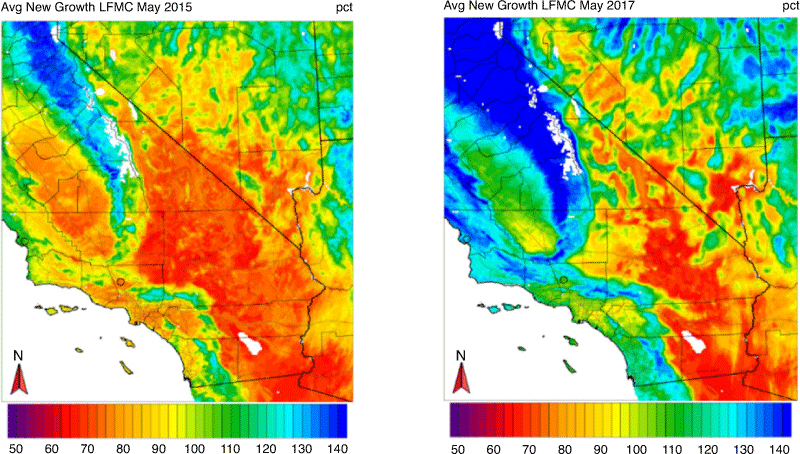
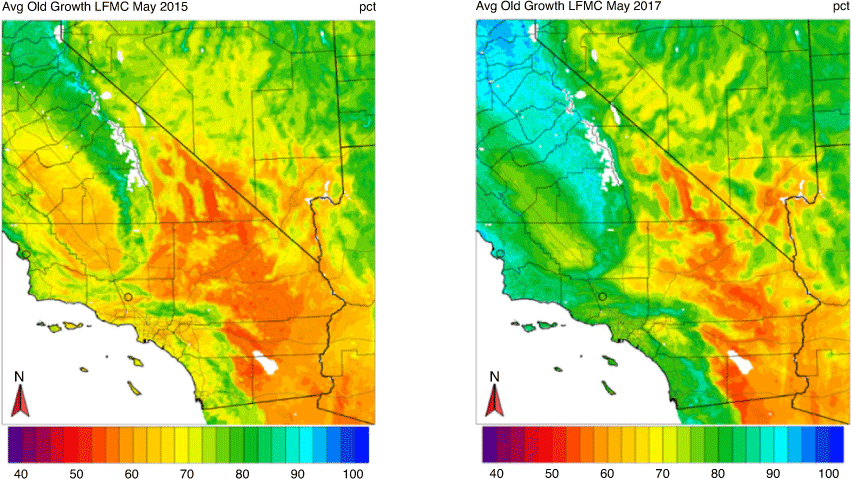
To assess whether the RF model can capture the inter-annual variability in LFMC, we compared the LFMC time series for a recent dry year (2015) and wet year (2017) at two different sites: Bitter Canyon Castaic and Irish Hills. Bitter Canyon Castaic is a new-growth LFMC site and Irish Hills is an old-growth LFMC site. Both sites have the most LFMC observations during these 2 years compared with other sites. Figures 5 and 6 compare the observed and modelled LFMC time series for both years at the Bitter Canyon Castaic and Irish Hills sites respectively. Each site’s observed historical monthly mean LFMC time series is plotted to help detect the differences between wet and dry years. For both old and new-growth LFMC sites, our RF model captures the observed LFMC wet and dry year contrast with relatively higher LFMC values throughout most of the year in 2017 compared with 2015. These LFMC differences are more pronounced earlier in the year and trend towards smaller differences at the end of each year. As expected for old-growth LFMC, the annual observed and modelled LFMC time series comparison between 2017 and 2015 yields a less dramatic difference at the Irish Hills site.

The various testing verification metrics presented above were obtained via cross-validation, which leaves one site out as the testing data at each iteration. The high correlations, relatively low RMSE and near-zero biases give us confidence that our models can provide reliable LFMC estimates at locations without observations. To demonstrate that, we computed LFMC at all locations within our domain using the RF LFMC model and gridded weather predictors for both 2015 and 2017. Figures 7 and 8 show the geographic distributions of the new- and old-growth LFMC in May of 2015 and 2017 respectively. In all maps, the LFMC spatial variability appears to be realistic, with the coast and higher elevations being moister than interior low- to mid-elevation locations. This confirms that our model can capture spatial variability in LFMC, when combined with a good sample of significant predictors that may vary considerably from one location to another. Furthermore, there is a noticeable distinction in LFMC between dry and wet years for both the new (Fig. 7) and old growth (Fig. 8), which confirms that our model can adequately capture inter-annual LFMC variability.

Fig. 7.  Monthly average chamise new-growth LFMC model output valid May 2015 (left) and May 2017 (right) across a portion of California. Model output is provided for all land locations below 3300 m (approximate elevation of the tree line in California), regardless of whether or not chamise exists. Black circles indicate Irish Hills and Bitter Canyon Castaic sampling site locations.

Fig. 8.  Monthly average chamise old-growth LFMC model output valid May 2015 (left) and May 2017 (right) across a portion of California. Model output is provided for all land locations below 3300 m (approximate elevation of the tree line in California), regardless of whether or not chamise exists. Black circles indicate Irish Hills and Bitter Canyon Castaic sampling site locations.

As discussed in the introduction, many LFMC models have been developed in the past. It is therefore beneficial to compare model performance between our LFMC model and others. The LFMC model in Rao et al. (2020) has an overall R², RMSE and bias of 0.63, 25.0% and 1.9%; the Yebra et al. (2018) model has an overall R² and RMSE of 0.58 and 40.0%; the Qi et al. (2012) model has an overall R² and MAE of 0.27 and 28.1%; the Ruffault et al. (2018) model has an R² and RMSE of 0.3 and 20%; and the McCandless et al. (2020) model has an overall RMSE of ~22% (all figures respective). The R² in various LFMC models proposed in Viegas et al. (2001) range from 0.12 to 0.79. Our random forest model has an overall R², RMSE and bias of 0.79, 15.34% and 0.26% for chamise new growth and an overall R², RMSE and bias of 0.63, 8.81% and 0.11% for chamise old growth (all figures respective). Based on these verification metrics, our model appears to compare favourably with the LFMC models developed in those studies. However, we acknowledge that a more vigorous comparison is required to make a meaningful assessment about the performance of various LFMC models, because different studies have focused on different vegetation species at different locations while using different validation methods.

Model accuracy suffers when attempting to capture peak chamise LFMC values. We believe this can be mostly attributed to having fewer observed peak values because the majority of LFMC values are below 100%, especially for old-growth chamise (Fig. 4). However, we are less concerned about model performance associated with peak values because higher fire danger occurs with lower LFMC values (Peterson et al. 2008). Capturing the rate of change and values at the lower spectrum are more important for determining the yearly timing of the onset of large fire occurrence as well as wildfire spread and behaviour (Dennison et al. 2008). Our reported reduced RMSE for lower LFMC ranges indicates that our model performs reasonably well in this regard.

Several studies document the use of in situ observations that include meteorological predictors. For example, Castro et al. (2003) demonstrated skill in estimating LFMC in Cistus monspeliensis across the Catalonia region of Spain using some of the same meteorological variables used herein. Of particular interest was the use of the summation of temperatures and precipitation over multiple-day periods in their regression models. This provides an indirect form of validation for our model construction since we found these types of predictors to be important as well.

Given the success of our LFMC model, we have begun to produce multiple day forecasts for California utilities operationally. These forecasts are provided on a 2-dimensional grid in different domains within California. We have also applied our models to dynamically downscaled historical weather data and obtained a multi-decadal historical LFMC dataset for California utilities to facilitate their wildfire research initiatives. It is important to note that although our LFMC model can provide hindcasts and forecasts for any location with necessary weather data, this model output should be used only over regions where chamise is the dominant vegetation type. Such information is typically provided by a gridded fuel category dataset (e.g. LANDFIRE 2008).

Future work may include several research topics. First, the 2-km resolution WRF simulations, which are employed in this study, do not perfectly resolve terrain features including slope and aspect, and soil type features. Therefore, there is a need to use higher resolutions to improve the accuracy of weather predictors used in our LFMC model. This will be made possible by the ever-increasing power of computational resources. Second, our models can be retrained to improve performance as more observations become available. With more LFMC observations, we will also be able to explore other machine learning approaches such as various deep learning methods (Jain et al. 2020) to further improve LFMC modelling. Finally, a similar methodology may be developed to model LFMC in other vegetation types that are common within the wildland environment and have abundant observations as suggested by many other studies.

The data that support this study cannot be publicly shared due to ethical or privacy reasons and may be shared upon reasonable request to the corresponding author if appropriate.

The authors declare no conflicts of interest.

Funding for this work was provided by Atmospheric Data Solutions, LLC.