Modelling chamise fuel moisture content across California: a machine learning approach
Scott B. Capps A C , Wei Zhuang A , Rui Liu A , Tom Rolinski B and Xin Qu AA Atmospheric Data Solutions, LLC, 15275 South Wagon Road, #59, Jackson, WY 83001, USA.
B Southern California Edison, 6000 Irwindale Avenue, Irwindale, CA 91702, USA.
C Corresponding author. Email: scapps@atmosdatasolutions.com
International Journal of Wildland Fire 31(2) 136-148 https://doi.org/10.1071/WF21061
Submitted: 11 May 2021 Accepted: 23 November 2021 Published: 9 December 2021
Journal Compilation © IAWF 2022 Open Access CC BY-NC-ND
Abstract
Live fuel moisture content plays a significant and complex role in wildfire propagation. However, in situ historical and near real-time live fuel moisture measurements are temporally and spatially sparse within wildfire-prone regions. Routine bi-weekly sampling intervals are sometimes exceeded if the weather is unfavourable and/or field personnel are unavailable. To fill these spatial and temporal gaps, we have developed a daily gridded chamise (Adenostoma fasciculatum) live fuel moisture product that can be used, in conjunction with other predictors, to assess current and historical wildfire danger/behaviour. Chamise observations for 52 new- and 41 old-growth California sites from the National Fuel Moisture Database were statistically related to dynamically downscaled high-resolution weather predictors using a random forest machine learning model. This model captures reasonably well the temporal and spatial variability of chamise live fuel moisture content within California. Compared with observations, model-predicted live fuel moisture values have an overall R2, root mean squared error (RMSE) and bias of 0.79, 15.34% and 0.26%, respectively, for new growth and 0.63, 8.81% and 0.11% for old growth. Given the success of the model, we have begun to use it to produce daily forecasts of chamise live fuel moisture content for California utilities.
Keywords: Adenostoma, chamise, live fuel moisture content, new growth, old growth, wildfire, machine learning, California, live fuel moisture, numerical weather modelling, WRF, random forest, LFMC.
Introduction
Live fuel moisture content (LFMC) plays an integral role in the propagation and intensity of wildfires because it affects combustion and heat transfer rates within vegetation (Dimitrakopoulos and Papaioannou 2001; Chuvieco et al. 2004; Jurdao et al. 2012). Although the moisture content is higher within the herbaceous portion of the plant (new growth) compared with the woody material (old growth), both exhibit the same annual cycle in California, typically peaking in the spring (March–May) and declining to minima in early autumn (August–September). This annual cycle is shaped by the amount and frequency of winter/spring precipitation and the return of summer drought (Keeley et al. 2009; Pivovaroff et al. 2019). Tracking LFMC’s rate of decline from its spring maximum is very important because it affects the onset and severity of larger fire activity (Nolan et al. 2016). Importantly, summer/autumn LFMC minima coincide with the return of the Southern California Santa Ana wind season, creating a favourable environment for large and destructive wildfires (Dennison et al. 2008; Rolinski et al. 2016).
LFMC has long been used by fire agencies, particularly fire managers, to evaluate wildfire danger across their supported territories. Wildfire danger is assessed and predicted using a variety of fire behaviour metrics, including rates of spread, flame length, and fireline intensity, all of which are a function of LFMC. More recently, most of California’s electric utilities are also beginning to use LFMC to assess wildfire potential. Specifically, LFMC is used extensively by Southern California Edison (SCE), where they have started sampling LFMC bi-weekly within their service area to help understand the vegetation’s susceptibility to wildfire and to bolster their situational awareness, especially during periods of critical fire weather.
LFMC is generally measured bi-weekly by physically extracting small portions of the plant and performing a gravimetric process on the sample to determine its water content. The calculation for LFMC is expressed as a percentage using the following equation:

Because the vegetation water weight can exceed that of the dry matter, LFMC can exceed 100%. In California, LFMC is sampled by various federal, state, and local fire agencies, with the most commonly sampled species consisting of: chamise (Adenostoma fasciculatum); buckwheat (Fagopyrum esculentum); sagebrush (Artemisia tridentata); hoaryleaf and bigpod ceanothus (Ceanothus crassifolius and ceanothus megacarpus); and manzanita (Arctostaphylos). Although there are other native species across the landscape, these are most frequently sampled due to their abundance and ease of access within wildfire-prone regions. This paper focuses on chamise, which has relatively abundant observation data, a prerequisite for building a skilful LFMC model.
LFMC is modulated by plant phenology, and both are affected by short-term (days) and long-term (months) changes in weather and root zone soil moisture. Important weather variables include incoming solar radiation, near-surface air temperature and relative humidity, and precipitation. Root zone soil moisture is influenced by both soil type and time integrations of these weather variables, all of which can be a function of location, elevation and proximity to large bodies of water. Additionally, soil moisture is impacted by rainfall runoff (to and from the location of interest), evaporation (from the surface and evapotranspiration), and soil water recharge. All of the above factors can influence plant photosynthesis, the timing of reproduction cycles, and LFMC (Dennison and Moritz 2009; Holden and Jolly 2011; Qi et al. 2014).
Although LFMC observations are critical to understanding the environmental conditions that may lead to significant fire activity, they are severely undersampled (temporally and spatially). This problem is exacerbated when regular sampling is disrupted due to changes in staffing (such as when key personnel are committed to fire incidents), and/or when a fire consumes the vegetation within the sampling collection site. For these reasons, there is a need for a daily gridded LFMC product. Higher spatial and temporal resolution LFMC data can be used to assess fire danger in between sparse observation locations as well as provide inputs for high-resolution fire spread modelling simulations.
Many efforts to model LFMC have been made in recent years, most of which include the use of remote sensing technologies to measure leaf water content (Chuvieco 2003; Danson and Bowyer 2004; Peterson et al. 2008; Qi et al. 2012; Yebra et al. 2013; García et al. 2020; McCandless et al. 2020; Rao et al. 2020; Michael et al. 2021). Specifically, the use of Moderate Resolution Imaging Spectroradiometer (MODIS) and Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) has been reported by Serrano et al. (2000), Yebra et al. (2008) and Myoung et al. (2018). Additionally, a combination of the Normalized Difference Vegetation Index (NDVI) and surface temperature was used to estimate LFMC by Chuvieco et al. (2004). These remote-sensed based products help fill in the spatial and temporal gaps left by in situ LFMC observations.
In comparison, several studies have used in situ meteorological predictors in their LFMC models, without using remotely sensed data. Viegas et al. (2001) estimated LFMC in various plant species in Catalunya and Central Portugal as a function of several fire weather indices calculated based on the Canadian Forest Fire Weather Index System. In addition to these fire weather indices, Castro et al. (2003) also explored numerous other predictors in their LFMC model for Cistus monspeliensis in the Catalonia region of Spain, including temperature, relative humidity and soil water reserve. Dimitrakopoulos and Bemmerzouk (2003) modelled LFMC in three plant species in the Mediterranean region of Crete, Greece as a linear function of the Keetch–Byram Drought Index (KBDI). Their study was extended by Pellizzaro et al. (2007) by including other well known drought indices. More recently, Ruffault et al. (2018) have evaluated the usefulness of various drought indexes in modelling LFMC.
In this paper, we adopt an approach similar to the latter, with a goal of providing historical and near real-time chamise LFMC estimates across California. This is accomplished by building a random forest machine learning model relating in situ LFMC observations to high-resolution, validated numerical weather model data. In contrast with previous studies that use automatic weather station data, this effort uses LFMC meteorological predictors (Table 1) taken from a gridded product. This is necessary to generate a high-resolution gridded LFMC product. Our method is also advantageous over the remote sensing approach in that it can provide not only historical LFMC values well before the satellite era, but also near real-time LFMC forecasts afforded by operational weather forecasting.

|
This paper will present the methodology used to develop our machine learning model to approximate new- and old-growth chamise LFMC within California. First, we will illustrate the types of data collected and generated for this modelling effort, which includes in situ LFMC observations and high-resolution weather data. Second, we will describe the predictor screening process and the random forest model construction and validation process. Third, we will assess our model performance using correlation, bias and root mean squared error (RMSE), and compare our model skill with other studies. Finally, we will summarise our results and discuss future work.
Data collection
For the purpose of developing our models, we acquired historical chamise new- and old-growth LFMC observations from the National Fuel Moisture Database (NFMD) web-based interface. This database serves as a central repository for national LFMC observations, thus eliminating the time-consuming task of contacting and gathering measurements from each fire agency separately. LFMC measurements were initially retrieved for more than 100 sites across California. However, this initial site count decreased as measurements were carefully screened before building the machine learning model.
Because multiple fire agencies contribute data to the national archive, the data need to be vetted to make sure LFMC new- and old growth are consistently categorised among sites. Some fire agencies sample both new- and old-growth chamise and store and label the data as such, while others do not. To categorise the LFMC data as either new or old growth for unclearly labelled sites, we applied a historical pattern analysis by taking the following steps. First, we calculated the typical magnitude of yearly LFMC ranges for both new- and old growth based on the clearly labelled sites. LFMC typically ranges from 50% to 200% for new growth and 40% to 150% for old growth. Then, we tentatively categorised a site with the magnitude of yearly LFMC ranges greater than or equal to 150% as a new-growth site or less than or equal to 110% as an old-growth site. Sites that did not fall into these two categories were discarded. Finally, we conducted one-tailed two-sample t-tests at 5% significance level to evaluate if the mean of the LFMC time series resembles either the new-growth population mean of 89% or the old-growth population mean of 67%. Those time series that passed our tests were either designated as new or old growth. Data that did not meet our LFMC new- or old-growth criteria described above were discarded. After vetting our data, 52 chamise new-growth sites and 41 chamise old-growth sites were retained for our study (Fig. 1). Tables 2 and 3 provide the site name and associated start date, end date and record count for each new- and old-growth site location. The earliest vetted LFMC data start in 1983, with most sites having data through 2020.
To produce a gridded LFMC product, a high spatial and temporal resolution historical weather dataset was built providing data at all of the screened site observation locations and time spans reported in Tables 2 and 3. These historical weather data were generated using a validated configuration of the Advanced Research Weather Research and Forecast model (WRF) version 4.0.3 (Skamarock et al. 2019). WRF dynamically downscaled the National Centers for Environmental Prediction Climate Forecast System Reanalysis (CFSR) (Saha et al. 2010) using 52 vertical levels and three domains consisting of an outer 18-km resolution domain with two inner 6- and 2-km resolution nested domains (Fig. 1). Multiple potential WRF configurations were validated using three observation data sources: Remote Automated Weather Stations (RAWS) (Zachariassen et al. 2003), Automated Surface Observation System (ASOS; ASOS 1998), and SCE’s weather stations. The WRF configuration that minimised the near-surface wind speed, temperature and dew point verification metrics (e.g. RMSE, correlation) was selected. This configuration includes the Morrison double-moment microphysics scheme (Morrison et al. 2009), the new Goddard longwave and shortwave radiation schemes (Chou and Suarez 1999), the Mellor–Yamada Nakanishi and Niino Level 3 (MYNN3) PBL (Nakanishi and Niino 2006), the Noah-MP (multi-physics) Land Surface Model (Niu et al. 2011) and the Kain–Fritsch cumulus scheme (Kain 2004), which was activated in the outermost domain only. Historical weather data from the WRF grid cell closest to each LFMC site were matched to LFMC measurements, with hourly WRF data temporally aggregated to obtain daily values. Potential predictor variables (e.g. air temperature, relative humidity, soil moisture and precipitation) across various time spans were then created for LFMC model development.
LFMC machine learning models
Model construction
To model daily LFMC as a function of weather predictors, we adopted a random forest (RF) regression method. RF was found to minimise the LFMC error compared with several other machine learning methods, according to a recent study by McCandless et al. (2020). Separate chamise new- and old-growth RF models were trained using predictors from the gridded high-resolution weather data. Feature selection and parameter tuning was performed to achieve optimised RF models. Following peer-reviewed literature, we derived many predictors from the gridded weather data output, with temporal scales ranging from short-term (1–7 days) to long-term (30–240 days) periods. We then screened each predictor based on the incremental change in LFMC RMSE resulting from the inclusion or exclusion of that predictor. The end result is a set of optimised RF models relating a set of key predictors to LFMC, which are listed in Table 1.
Different RF parameter configurations were tested to minimise LFMC RMSE. Tuneable RF parameters include node size, number of trees, and percentage of randomly selected variables (Probst et al. 2019). Our algorithm converged when the number of random forest trees reached 200. The LFMC RMSE were minimised with a parameter node size of five and the percentage of randomly selected variables of 80%. The importance rank plot for the final new- and old-growth model is presented in Figs 2 and 3, respectively. Long-term precipitation predictors (90–240 days) emerge as the most important predictors in both new- and old-growth models. This makes physical sense given that plant material development is a moisture limited process and root zone soil moisture is a function of cumulative precipitation, potential evapotranspiration as well as soil physical properties (e.g. texture, depth, stone cover, etc.). In fact, Dennison and Moritz (2009) indicated that long-term precipitation accumulations (previous one-month to three-month period) impact the timing of LFMC decline and are strongly correlated with historical California wildfires. Day length is also a key predictor for the new-growth model, and long-term (150 days) near-surface air temperature is crucial for the old-growth model. Both of these predictors change with the seasons and modulate plant activity and development. Finally, our RF new- and old-growth models, now trained using the full dataset with optimal parameter settings, are stored for historical and operational implementation.
Model validation
Our goal is to produce a gridded high-resolution daily chamise LFMC hindcast and forecast model for California, assuming chamise grows across the state. Given the sparse NFMD site locations (52 chamise new-growth sites and 41 chamise old-growth sites), we must test whether our models perform reasonably well at locations without observations. To do this, we perform many cross-validation iterations. For each validation iteration, we leave one site out for testing and use LFMC observations from all other sites to train an RF model using optimal model settings. Overall, we conducted a 52-fold (41-fold) cross-validation assessment for the new (old) growth model that corresponds to the number of sites available in each chamise fuel category. This allows us to determine if the model trained at sites with observations can be applied at locations without chamise observations across California, where modelled LFMC is influenced by the spatial and temporal variability of the weather predictors.
Results
To assess the performance of the RF models, we collected testing results from all cross-validation iterations for all sites. In Fig. 4, observed LFMC is plotted against model-predicted LFMC for both new- and old-growth sites. Our models perform well, with an overall correlation, RMSE and bias of 0.89, 15.34% and 0.26%, respectively, for new-growth LFMC and 0.79, 8.81% and 0.11% for old-growth LFMC (see Tables 2 and 3). Furthermore, the predicted and observed LFMC are distributed along the perfect fit line (y = x) for both new- and old-growth models. Nevertheless, the old-growth LFMC model underestimates observations for the few outliers that are greater than 100%. For the new-growth model, the scatter increases as observed LFMC values increase, indicative of a model performance degradation as LFMC approaches extremely high values.

|
Clearly, the fluctuations within the lower range of the LFMC spectrum play a significant role in the propagation and intensity of wildfires (Peterson et al. 2008). To assess the model performance for this critical range, we also conducted more targeted model validations during periods when observed LFMC dropped to 100% or below for new-growth sites and 90% or below for old-growth sites. Within these LFMC ranges, our model has an overall correlation, RMSE and bias of 0.73, 11.02% and 3.46% for new growth, respectively, and 0.80, 7.20% and 1.07% for old growth. Although there is minimal change in correlation and bias, the LFMC RMSE is reduced by ~4% and ~2% for the new- and old-growth sites, respectively. This suggests that the LFMC model will capture the late spring to early summer vegetation drying period, which precedes the start of peak wildfire season in California.
To further evaluate the model, we calculated training and testing error statistics for each of the 52 new-growth and 41 old-growth sites. In Table 2, the 52 new-growth sites (consisting of a total of 11 021 LFMC vetted records) are ranked from the best to worst performance according to the testing RMSE.
For most new-growth sites, the training RMSE are below 9.0%, indicating that the RF model fits the data reasonably well. Not surprisingly, the testing RMSE are somewhat larger, ranging from 7.3% to 26.5%. The degradation in model performance for testing may be attributable in part to the sparseness and inconsistency in LFMC sampling, as discussed in the introduction. Another possible culprit may be the modelling errors in weather predictors, which arise in part from the intrinsic limitation on weather predictability over regions with complex terrain (Doyle et al. 2011). Nevertheless, the overall testing RMSE (15.34%) calculated from all new-growth LFMC site testing data remains relatively small compared with the magnitude of the new-growth LFMC, which typically ranges from 50% to 200%, but can occasionally exceed 240%. As for model biases, the training bias is near zero, typically ranging from –2% to 2% among new-growth sites. In comparison, the testing bias is somewhat larger, typically ranging from –6% to 6%. However, the overall training (0.09%) and testing (0.26%) biases are near zero, which indicates that the new-growth model provides an approximately unbiased LFMC estimation.
In Table 3, the 41 old-growth sites (consisting of a total of 4917 vetted records) are ranked according to testing RMSE. Both training and testing biases are centred near zero, mostly between –1.5% and 1.5%. Similar to the new-growth LFMC model, approximately unbiased predictions can be expected when we implement the old-growth model within California. The testing RMSE of LFMC are typically much smaller for the old-growth sites compared with the new-growth sites. For example, 78% of the old-growth sites have a testing RMSE below 10%, whereas 81% of the new-growth sites have a testing RMSE less than 20%. This is consistent with the fact that woody material contains less water and tends to have less annual variability than the herbaceous portion of the plant (Countryman and Dean 1979; see Figs 5 and 6 as well).
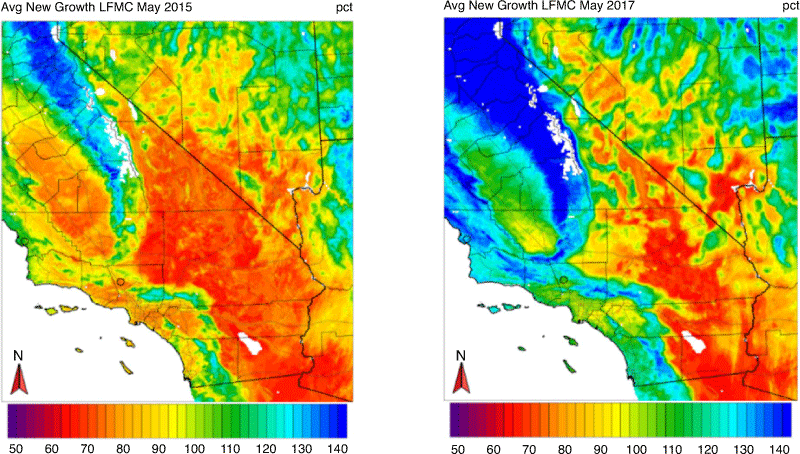
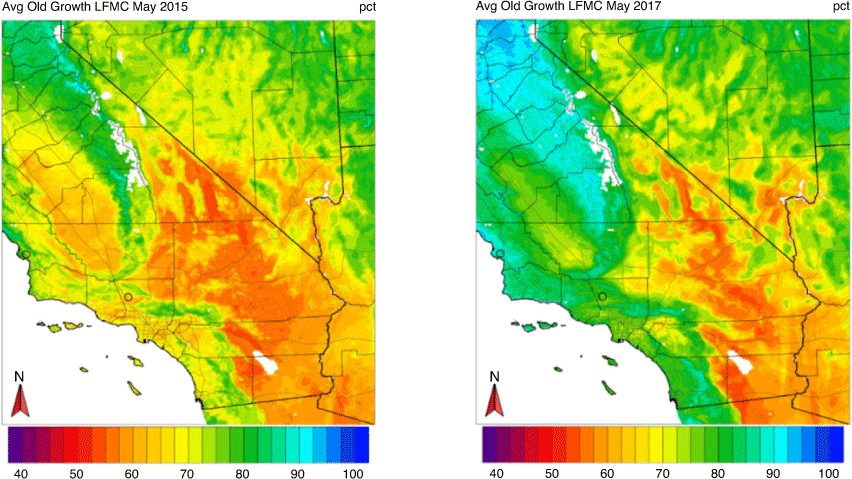
To assess whether the RF model can capture the inter-annual variability in LFMC, we compared the LFMC time series for a recent dry year (2015) and wet year (2017) at two different sites: Bitter Canyon Castaic and Irish Hills. Bitter Canyon Castaic is a new-growth LFMC site and Irish Hills is an old-growth LFMC site. Both sites have the most LFMC observations during these 2 years compared with other sites. Figures 5 and 6 compare the observed and modelled LFMC time series for both years at the Bitter Canyon Castaic and Irish Hills sites respectively. Each site’s observed historical monthly mean LFMC time series is plotted to help detect the differences between wet and dry years. For both old and new-growth LFMC sites, our RF model captures the observed LFMC wet and dry year contrast with relatively higher LFMC values throughout most of the year in 2017 compared with 2015. These LFMC differences are more pronounced earlier in the year and trend towards smaller differences at the end of each year. As expected for old-growth LFMC, the annual observed and modelled LFMC time series comparison between 2017 and 2015 yields a less dramatic difference at the Irish Hills site.
The various testing verification metrics presented above were obtained via cross-validation, which leaves one site out as the testing data at each iteration. The high correlations, relatively low RMSE and near-zero biases give us confidence that our models can provide reliable LFMC estimates at locations without observations. To demonstrate that, we computed LFMC at all locations within our domain using the RF LFMC model and gridded weather predictors for both 2015 and 2017. Figures 7 and 8 show the geographic distributions of the new- and old-growth LFMC in May of 2015 and 2017 respectively. In all maps, the LFMC spatial variability appears to be realistic, with the coast and higher elevations being moister than interior low- to mid-elevation locations. This confirms that our model can capture spatial variability in LFMC, when combined with a good sample of significant predictors that may vary considerably from one location to another. Furthermore, there is a noticeable distinction in LFMC between dry and wet years for both the new (Fig. 7) and old growth (Fig. 8), which confirms that our model can adequately capture inter-annual LFMC variability.
Discussion and conclusion
As discussed in the introduction, many LFMC models have been developed in the past. It is therefore beneficial to compare model performance between our LFMC model and others. The LFMC model in Rao et al. (2020) has an overall R2, RMSE and bias of 0.63, 25.0% and 1.9%; the Yebra et al. (2018) model has an overall R2 and RMSE of 0.58 and 40.0%; the Qi et al. (2012) model has an overall R2 and MAE of 0.27 and 28.1%; the Ruffault et al. (2018) model has an R2 and RMSE of 0.3 and 20%; and the McCandless et al. (2020) model has an overall RMSE of ~22% (all figures respective). The R2 in various LFMC models proposed in Viegas et al. (2001) range from 0.12 to 0.79. Our random forest model has an overall R2, RMSE and bias of 0.79, 15.34% and 0.26% for chamise new growth and an overall R2, RMSE and bias of 0.63, 8.81% and 0.11% for chamise old growth (all figures respective). Based on these verification metrics, our model appears to compare favourably with the LFMC models developed in those studies. However, we acknowledge that a more vigorous comparison is required to make a meaningful assessment about the performance of various LFMC models, because different studies have focused on different vegetation species at different locations while using different validation methods.
Model accuracy suffers when attempting to capture peak chamise LFMC values. We believe this can be mostly attributed to having fewer observed peak values because the majority of LFMC values are below 100%, especially for old-growth chamise (Fig. 4). However, we are less concerned about model performance associated with peak values because higher fire danger occurs with lower LFMC values (Peterson et al. 2008). Capturing the rate of change and values at the lower spectrum are more important for determining the yearly timing of the onset of large fire occurrence as well as wildfire spread and behaviour (Dennison et al. 2008). Our reported reduced RMSE for lower LFMC ranges indicates that our model performs reasonably well in this regard.
Several studies document the use of in situ observations that include meteorological predictors. For example, Castro et al. (2003) demonstrated skill in estimating LFMC in Cistus monspeliensis across the Catalonia region of Spain using some of the same meteorological variables used herein. Of particular interest was the use of the summation of temperatures and precipitation over multiple-day periods in their regression models. This provides an indirect form of validation for our model construction since we found these types of predictors to be important as well.
Given the success of our LFMC model, we have begun to produce multiple day forecasts for California utilities operationally. These forecasts are provided on a 2-dimensional grid in different domains within California. We have also applied our models to dynamically downscaled historical weather data and obtained a multi-decadal historical LFMC dataset for California utilities to facilitate their wildfire research initiatives. It is important to note that although our LFMC model can provide hindcasts and forecasts for any location with necessary weather data, this model output should be used only over regions where chamise is the dominant vegetation type. Such information is typically provided by a gridded fuel category dataset (e.g. LANDFIRE 2008).
Future work may include several research topics. First, the 2-km resolution WRF simulations, which are employed in this study, do not perfectly resolve terrain features including slope and aspect, and soil type features. Therefore, there is a need to use higher resolutions to improve the accuracy of weather predictors used in our LFMC model. This will be made possible by the ever-increasing power of computational resources. Second, our models can be retrained to improve performance as more observations become available. With more LFMC observations, we will also be able to explore other machine learning approaches such as various deep learning methods (Jain et al. 2020) to further improve LFMC modelling. Finally, a similar methodology may be developed to model LFMC in other vegetation types that are common within the wildland environment and have abundant observations as suggested by many other studies.
Data availability statement
The data that support this study cannot be publicly shared due to ethical or privacy reasons and may be shared upon reasonable request to the corresponding author if appropriate.
Conflicts of interest
The authors declare no conflicts of interest.
Declaration of funding
Funding for this work was provided by Atmospheric Data Solutions, LLC.
Acknowledgements
We are especially grateful to Southern California Edison for providing the multi-decadal historical WRF weather data. Live fuel moisture observations were retrieved from the National Fuel Moisture Database (http://www.wfas.net/index.php/national-fuel-moisture-database-moisture-drought-103). Figures and analyses were produced using the R programming language (R Development Core Team, www.r-project.org/foundation/) ncdf4, randomForest and ggplot2 packages, the NCAR Command Language (NCL) and Python (www.python.org). We are grateful for the constructive comments and suggestions provided by two anonymous reviewers. Finally, we thank Jerry Kalkhof for his help with the NFMD dataset.
References
ASOS (Automated Surface Observation System) (1998) Automated surface observation system users guide. Available at http://www.nws.noaa.gov/asos/pdfs/aum-toc.pdf [Verified 23 November 2021]Castro FX, Tudela A, Sebastià MT (2003) Modeling moisture content in shrubs to predict fire risk in Catalonia (Spain). Agricultural and Forest Meteorology 116, 49–59.
| Modeling moisture content in shrubs to predict fire risk in Catalonia (Spain).Crossref | GoogleScholarGoogle Scholar |
Chou MD, Suarez MJ (1999) A solar radiation parameterization (CLIRAD-SW) developed at Goddard Climate and Radiation Branch for atmospheric studies. NASA Technical Memorandum, NASA/TM-1999–104606.
Chuvieco E (2003) ‘Wildland fire danger estimation and mapping: the role of remote sensing data.’ (World Scientific Publishing: Singapore)
Chuvieco E, Cocero D, Riaño D, Martín MP, Martínez-Vega J, De La Riva J, Pérez F (2004) Combining NDVI and surface temperature for the estimation of live fuel moisture content in forest fire danger rating. Remote Sensing of Environment 92, 322–331.
| Combining NDVI and surface temperature for the estimation of live fuel moisture content in forest fire danger rating.Crossref | GoogleScholarGoogle Scholar |
Countryman CM, Dean WH (1979) Measuring moisture content in living chaparral: a field user’s manual. USDA, Forest Service Pacific Southwest Forest and Range Experiment Station, General Technical Report PSW-36. (Berkeley, CA, USA)
Danson FM, Bowyer P (2004) Estimating live fuel moisture content from remotely sensed reflectance. Remote Sensing of Environment 92, 309–321.
| Estimating live fuel moisture content from remotely sensed reflectance.Crossref | GoogleScholarGoogle Scholar |
Dennison PE, Moritz MA (2009) Critical live fuel moisture in chaparral ecosystems: a threshold for fire activity and its relationship to antecedent precipitation. International Journal of Wildland Fire 18, 1021–1027.
| Critical live fuel moisture in chaparral ecosystems: a threshold for fire activity and its relationship to antecedent precipitation.Crossref | GoogleScholarGoogle Scholar |
Dennison PE, Moritz MA, Taylor RS (2008) Evaluating predictive models of critical live fuel moisture in the Santa Monica Mountains, California. International Journal of Wildland Fire 17, 18–27.
| Evaluating predictive models of critical live fuel moisture in the Santa Monica Mountains, California.Crossref | GoogleScholarGoogle Scholar |
Dimitrakopoulos AP, Bemmerzouk AM (2003) Predicting live herbaceous moisture content from a seasonal drought index. International Journal of Biometeorology 47, 73–79.
| Predicting live herbaceous moisture content from a seasonal drought index.Crossref | GoogleScholarGoogle Scholar | 12647093PubMed |
Dimitrakopoulos AP, Papaioannou KK (2001) Flammability assessment of Mediterranean forest fuels. Fire Technology 37, 143–152.
| Flammability assessment of Mediterranean forest fuels.Crossref | GoogleScholarGoogle Scholar |
Doyle JD, Gaberšek S, Jiang Q, Bernardet L, Brown JM, Dörnbrack A, Filaus E, Grubišić V, Kirshbaum DJ, Knoth O, Koch S, Schmidli J, Stiperski I, Vosper SB, Zhong S (2011) An intercomparison of T-REX mountain-wave simulations and implications for mesoscale predictability. Monthly Weather Review 139, 2811–2831.
| An intercomparison of T-REX mountain-wave simulations and implications for mesoscale predictability.Crossref | GoogleScholarGoogle Scholar |
García M, Riaño D, Yebra M, Salas J, Cardil A, Monedero S, Ramirez J, Martín MP, Vilar L, Gajardo J, Ustin S (2020) Live fuel moisture content product from Landsat TM satellite time series for implementation in fire behavior models. Remote Sensing 12, 1714
| Live fuel moisture content product from Landsat TM satellite time series for implementation in fire behavior models.Crossref | GoogleScholarGoogle Scholar |
Holden ZA, Jolly WM (2011) Modeling topographic influences on fuel moisture and fire danger in complex terrain to improve wildland fire management decision support. Forest Ecology and Management 262, 2133–2141.
| Modeling topographic influences on fuel moisture and fire danger in complex terrain to improve wildland fire management decision support.Crossref | GoogleScholarGoogle Scholar |
Jain P, Coogan SCP, Subramanian SG, Crowley M, Taylor S, Flannigan MD (2020) A review of machine learning applications in wildfire science and management. Environmental Reviews 28, 478–505.
| A review of machine learning applications in wildfire science and management.Crossref | GoogleScholarGoogle Scholar |
Jurdao S, Chuvieco E, Arevalillo JM (2012) Modelling fire ignition probability from satellite estimates of live fuel moisture content. Fire Ecology 8, 77–97.
| Modelling fire ignition probability from satellite estimates of live fuel moisture content.Crossref | GoogleScholarGoogle Scholar |
Kain JS (2004) The Kain–Fritsch convective parameterization: an update. Journal of Applied Meteorology 43, 170–181.
| The Kain–Fritsch convective parameterization: an update.Crossref | GoogleScholarGoogle Scholar |
Keeley JE, Safford H, Fotheringham CJ, Franklin J, Moritz M (2009) The 2007 southern California wildfires: lessons in complexity. Journal of Forestry 107, 287–296.
LANDFIRE (2008) Existing Vegetation Type Layer, LANDFIRE 1.1.0, US Department of the Interior, Geological Survey, and US Department of Agriculture. Available at http://landfire.cr.usgs.gov/viewer/ [Verified 29 November 2021]
McCandless TC, Kosovic B, Petzke W (2020) Enhancing wildfire spread modelling by building a gridded fuel moisture content product with machine learning. Machine Learning: Science and Technology 1, 035010
Michael Y, Helman D, Glickman O, Gabay D, Brenner S, Lensky IM (2021) Forecasting fire risk with machine learning and dynamic information derived from satellite vegetation index time-series. The Science of the Total Environment 764, 142844
| Forecasting fire risk with machine learning and dynamic information derived from satellite vegetation index time-series.Crossref | GoogleScholarGoogle Scholar | 33158519PubMed |
Morrison H, Thompson G, Tatarskii V (2009) Impact of cloud microphysics on the development of trailing stratiform precipitation in a simulated squall line: comparison of one and two-moment schemes. Monthly Weather Review 137, 991–1007.
| Impact of cloud microphysics on the development of trailing stratiform precipitation in a simulated squall line: comparison of one and two-moment schemes.Crossref | GoogleScholarGoogle Scholar |
Myoung B, Kim SH, Nghiem SV, Jia S, Whitney K, Kafatos MC (2018) Estimating live fuel moisture from MODIS satellite data for wildfire danger assessment in Southern California USA. Remote Sensing 10, 87
| Estimating live fuel moisture from MODIS satellite data for wildfire danger assessment in Southern California USA.Crossref | GoogleScholarGoogle Scholar |
Nakanishi M, Niino H (2006) An improved Mellor–Yamada Level 3 Model: its numerical stability and application to a regional prediction of advection fog. Boundary-Layer Meteorology 119, 397–407.
| An improved Mellor–Yamada Level 3 Model: its numerical stability and application to a regional prediction of advection fog.Crossref | GoogleScholarGoogle Scholar |
Niu G-Y, Yang Z-L, Mitchell KE, Chen F, Ek MB, Barlage M, Kumar A, Manning K, Niyogi D, Rosero E, Tewari M, Xia Y (2011) The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. Journal of Geophysical Research 116, D12109
| The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements.Crossref | GoogleScholarGoogle Scholar |
Nolan RH, Boer MM, Resco de Dios V, Caccamo G, Bradstock RA (2016) Large-scale, dynamic transformations in fuel moisture drive wildfire activity across southeastern Australia. Geophysical Research Letters 43, 4229–4238.
| Large-scale, dynamic transformations in fuel moisture drive wildfire activity across southeastern Australia.Crossref | GoogleScholarGoogle Scholar |
Pellizzaro G, Cesaraccio C, Duce P, Ventura A, Zara P (2007) Relationships between seasonal patterns of live fuel moisture and meteorological drought indices for Mediterranean shrubland species. International Journal of Wildland Fire 16, 232–241.
| Relationships between seasonal patterns of live fuel moisture and meteorological drought indices for Mediterranean shrubland species.Crossref | GoogleScholarGoogle Scholar |
Peterson SH, Roberts DA, Dennison PE (2008) Mapping live fuel moisture with MODIS data: a multiple regression approach. Remote Sensing of Environment 112, 4272–4284.
| Mapping live fuel moisture with MODIS data: a multiple regression approach.Crossref | GoogleScholarGoogle Scholar |
Pivovaroff AL, Emery N, Sharifi MR, Witter M, Keeley JE, Rundel PW (2019) The effect of ecophysiological traits on live fuel moisture content. Fire 2, 28
| The effect of ecophysiological traits on live fuel moisture content.Crossref | GoogleScholarGoogle Scholar |
Probst P, Wright MN, Boulesteix AL (2019) Hyperparameters and tuning strategies for random forest. Wiley Interdisciplinary Reviews. Data Mining and Knowledge Discovery 9, e1301
| Hyperparameters and tuning strategies for random forest.Crossref | GoogleScholarGoogle Scholar |
Qi Y, Dennison PE, Spencer J, Riano D (2012) Monitoring live fuel moisture using soil moisture and remote sensing proxies. Fire Ecology 8, 71–87.
| Monitoring live fuel moisture using soil moisture and remote sensing proxies.Crossref | GoogleScholarGoogle Scholar |
Qi Y, Dennison PE, Jolly WM, Kropp RC, Brewer SC (2014) Spectroscopic analysis of seasonal changes in live fuel moisture content and leaf dry mass. Remote Sensing of Environment 150, 198–206.
| Spectroscopic analysis of seasonal changes in live fuel moisture content and leaf dry mass.Crossref | GoogleScholarGoogle Scholar |
Rao K, Williams AP, Flefil JF, Konings AG (2020) SAR-enhanced mapping of live fuel moisture content Remote Sensing of Environment 245, 111797
| SAR-enhanced mapping of live fuel moisture contentCrossref | GoogleScholarGoogle Scholar |
Rolinski T, Capps SB, Fovell RG, Cao Y, D’Agostino BJ, Vanderburg S (2016) The Santa Ana wildfire threat index: methodology and operational implementation. Weather and Forecasting 31, 1881–1897.
| The Santa Ana wildfire threat index: methodology and operational implementation.Crossref | GoogleScholarGoogle Scholar |
Ruffault J, Martin-StPaul N, Piment F, Dupuy J (2018) How well do meteorological drought indices predict live fuel moisture content (LFMC)? An assessment for wildfire research and operations in Mediterranean ecosystems. Agricultural and Forest Meteorology 262, 391–401.
| How well do meteorological drought indices predict live fuel moisture content (LFMC)? An assessment for wildfire research and operations in Mediterranean ecosystems.Crossref | GoogleScholarGoogle Scholar |
Saha S, Moorthi S, Pan HL, Wu X, Wang J, Nadiga S, Tripp P, Kistler R, Woollen J, Behringer D, Liu H (2010) The NCEP climate forecast system reanalysis. Bulletin of the American Meteorological Society 91, 1015–1058.
| The NCEP climate forecast system reanalysis.Crossref | GoogleScholarGoogle Scholar |
Serrano L, Ustin SL, Roberts DA, Gamon JA, Penuelas J (2000) Deriving water content of chaparral vegetation from AVIRIS data. Remote Sensing of Environment 74, 570–581.
| Deriving water content of chaparral vegetation from AVIRIS data.Crossref | GoogleScholarGoogle Scholar |
Skamarock WC, Klemp JB, Dudhia J, Gill DO, Liu Z, Berner J, Huang XY (2019) A description of the Advanced Research WRF Model Version 4 (No. NCAR/TN-556+STR) (National Center for Atmospheric Research: Boulder, CO, USA).
Viegas DX, Piñol J, Viegas MT, Ogaya R (2001) Estimating live fine fuels moisture content using meteorologically-based indices. International Journal of Wildland Fire 10, 223–240.
| Estimating live fine fuels moisture content using meteorologically-based indices.Crossref | GoogleScholarGoogle Scholar |
Yebra M, Chuvieco E, Riaño D (2008) Estimation of live fuel moisture content from MODIS images for fire risk assessment. Agricultural and Forest Meteorology 148, 523–536.
| Estimation of live fuel moisture content from MODIS images for fire risk assessment.Crossref | GoogleScholarGoogle Scholar |
Yebra M, Dennison PE, Chuvieco E, Riano D, Zylstra P, Hunt ER, Danson FM, Qi Y, Jurdao S (2013) A global review of remote sensing of live fuel moisture content for fire danger assessment: moving towards operational products. Remote Sensing of Environment 136, 455–468.
| A global review of remote sensing of live fuel moisture content for fire danger assessment: moving towards operational products.Crossref | GoogleScholarGoogle Scholar |
Yebra M, Quan X, Riaño D, Larraondo PR, van Dijk AIJM, Cary GJ (2018) A fuel moisture content and flammability monitoring methodology for continental Australia based on optical remote sensing. Remote Sensing of Environment 212, 260–272.
| A fuel moisture content and flammability monitoring methodology for continental Australia based on optical remote sensing.Crossref | GoogleScholarGoogle Scholar |
Zachariassen J, Zeller KF, Nikolov N, McClelland T (2003) A review of the Forest Service Remote Automated Weather Station (RAWS) network. USDA Forest Service, Rocky Mountain Research Station, General Technical Report RMRS-GTR-119. (Fort Collins, CO, USA)