Some observations on the biogeochemical cycling of zinc in the Australian sector of the Southern Ocean: a dedication to Keith Hunter
Michael J. Ellwood A , Robert Strzepek B , Xiaoyu Chen A , Thomas W. Trull C and Philip W. Boyd BA Research School of Earth Sciences, Australian National University, Canberra, ACT 2601, Australia.
B Institute for Marine and Antarctic Studies, University of Tasmania, Hobart, Tas. 7004, Australia.
C CSIRO Oceans and Atmosphere, Hobart, Tas. 7004, Australia.
D Corresponding author. Email: michael.ellwood@anu.edu.au
Marine and Freshwater Research 71(3) 355-373 https://doi.org/10.1071/MF19200
Submitted: 30 May 2019 Accepted: 7 September 2019 Published: 3 December 2019
Journal Compilation © CSIRO 2020 Open Access CC BY-NC-ND
Abstract
In this study we investigated the distribution of dissolved and particulate zinc (dZn and pZn respectively) and its isotopes in the Subantarctic Zone as part of a Geotraces Process voyage. dZn and pZn depth profiles contrasted each other, with dZn showing depletion within the euphotic zone while pZn profiles showed enrichment. Fitting a power law equation to the pZn profiles produced an attenuation factor of 0.82, which contrasted values for particulate phosphorus, cadmium and copper. The results indicate that zinc has a longer regeneration length scale than phosphorus and cadmium, but shorter than copper. The differential regeneration of pZn relative to that of particulate phosphorus likely explains why dZn appears to have a deeper regeneration profile than that of phosphate. The dZn isotope (δ66Zndissolved) profiles collected across the Subantarctic Zone showed differing profile structures. For one station collected within an isolated cold-core eddy (CCE), δ66Zndissolved showed surface enrichment relative to deep waters. The corresponding pZn isotope profiles within the CCE did not show enrichment; rather, they were subtly depleted in surface waters and then converged to similar values at depth. Zinc isotope fractionation can be explained through a combination of fractionation processes associated with uptake by phytoplankton, zinc complexation by natural organic ligands and zinc regeneration from particulate matter.
Introduction
Zinc is an essential micronutrient for phytoplankton because it is involved in several key enzyme reactions within cells. The oceanic distribution of zinc is similar to that of silicic acid, which has puzzled researchers for many years (Bruland et al. 1978; Hunter and Boyd 1999). Recent modelling efforts suggest that the coupling of these two nutrients may result from: (1) physical circulation within the Southern Ocean and biogeochemical modification of these waters by diatoms (Vance et al. 2017; de Souza et al. 2018); and (2) biological uptake in the Southern Ocean coupled with the reversible scavenging of zinc onto sinking particles (Roshan et al. 2018; Weber et al. 2018). These modelling studies rely heavily on the concentration and isotope composition of zinc in the dissolved phase. Further, in all these modelling scenarios, the Southern Ocean is critical in determining the initial biogeochemical status of zinc, silicic acid and phosphate in surface and subsurface waters, which is then propagated globally by mode and intermediate water masses (Sarmiento et al. 2004).
The Subantarctic Zone (SAZ) of the Southern Ocean represents ~50% of the total area of the Southern Ocean and is an important contributor to the export of nutrients from the Southern Ocean into the global ocean thermocline. The SAZ is bound by the Subtropical Front (STF) to the north and the Subantarctic Front (SAF) and the Polar Front (PF) to the south (Fig. 1). The SAZ is a major contributor to oceanic uptake of CO2, with an annual flux >1 Gt C year–1 (Metzl et al. 1999; Frölicher et al. 2015). Although primary production within the SAZ makes a major contribution to global CO2 uptake, primary production in SAZ waters is limited by silica, iron and light availability (Boyd et al. 1999; Hutchins et al. 2001; Petrou et al. 2011; Westwood et al. 2011). In SAZ surface waters, silicic acid concentrations typically range between ~0.5 and 3 µM (Lourey and Trull 2001), which are on the cusp of being growth limiting (Paasche 1973; Franck et al. 2005).

|
To date, there have only been a handful of studies looking at zinc cycling in the SAZ. Work by Ellwood (2008), Samanta et al. (2017) and Butler et al. (2013) for the south-west Pacific sector of the Southern Ocean all showed depletion of zinc and silicic in surface waters, with concentrations ranging between 0.06 and 0.36 nmol kg–1. Although these zinc concentrations are low, there is little evidence to suggest that they are low enough to limit phytoplankton growth (Ellwood 2004; Butler et al. 2013). Understanding the processes that affect the cycling of zinc in the SAZ is important because this region is where Subantarctic Mode Water (SAMW) forms and ventilates lower latitudes (Sarmiento et al. 2004; Sallée et al. 2006).
To date, little work has looked at zinc isotope cycling between the dissolved and particulate phases (dZn and pZn respectively). The aim of the work presented here was to understand the cycling of dZn and pZn in the subantarctic waters south of Australia. This work forms part of the international GEOTRACES program.
Materials and methods
Sampling sites
The Southern Ocean Time Series (SOTS) site is located at 47°S, 142°E, south-west of Tasmania, Australia (Fig. 1). This has been a long-term mooring site where biophysicochemical water column measurements have been made since 1998 and it presently forms part of the Australian Integrated Marine Observing System (IMOS). The SOTS site is located on the northern edge of the SAZ, with typical sea surface temperatures ranging between ~9 and 13°C (Fig. 1; Herraiz-Borreguero and Rintoul 2011). The site is in deep water (>4500 m) and is located on the western side of the Tasman Rise. Although the site is located on the northern edge of the SAZ, upper ocean oceanography at the site can be complex. The oceanographic properties of the site are generally representative of the Australian sector of the SAZ, but the site is also affected by Tasman Sea Outflow water, which forms part of the return flow to the South Pacific super gyre (Ridgway 2007; Oliver and Holbrook 2014). This westward-flowing water exhibits some properties of subtropical water sourced from the Tasman Sea, but is also affected by eddy circulation near Tasmania that is associated with the westward leakage of the East Australia Current (Weeding and Trull 2014; Shadwick et al. 2015). For the present study, the SOTS site was occupied between 18 and 21 March 2016 and again between 19 and 27 March 2017.
The cyclonic cold-core eddy (CCE) site was studied between 28 March and 3 April 2016 (Fig. 1), with its centre located at ~50.4°S, 147.1°E. The eddy was ~190 km in diameter and was a stable feature that had formed in mid-February 2016, ~1.2° further south of the sampling site near the SAF (Moreau et al. 2017). After formation, the eddy moved slowly northward across the northern extension of the SAF with a rotation speed of 0.527 rad day–1 (Moreau et al. 2017; Patel et al. 2019). The biogeochemical properties of this eddy differ from external waters (Moreau et al. 2017; Patel et al. 2019). Because this eddy became ‘structurally closed’ after development, its ability to entrain and detrain nutrients, dissolved iron, phytoplankton and zooplankton was restricted. That is, it behaved much like a static mesocosm.
The other site of interest was located at 51.90°S, 148.51°E within the SAZ and was designated as the ‘SAZ’ site (Fig. 1). It was located north of the northern extension of the SAF and is regarded as having biogeochemical properties typical of the SAZ. The site was sampled between 7 and 11 April 2016.
Equipment cleaning
All equipment used in this study had been extensively acid cleaned. Typically, sample bottles were soaked for 1 week in 15% aqua regia (HCl : HNO3 3 : 1) reagent grade, rinsed and then soaked for 1 further week in 2% HNO3. Water used to rinse bottles was purified using a water purification system (Millipore, Melbourne, Vic., Australia). The final step in the process was to fill bottles with 0.5% (w/w) Teflon-distilled (designated here as ‘t-acid’; Savillex, Minneapolis, MN, USA) HNO3 (Mattinson 1972) and then double-bag them. Laboratory plasticware was acid cleaned by heating in aqua regia followed by heating with 0.5% t-HNO3.
Conductivity, temperature and depth and nutrient sampling
Conductivity, temperature and depth (CTD) profile data and water samples for nutrient and biological parameters were collected with a winch-lowered package consisting of an SBE 911plus CTD (Seabird, Seattle, WA, USA), a Turner Designs (San Jose, CA, USA) fluorometer and a 24-bottle SBE 32 Carousel water sampler (Seabird). Salinities were standardised to standard seawater (Ocean Scientific International Ltd, Portsmouth, UK). Samples for macronutrients, phosphate, nitrate, nitrite, ammonia and silicic acid were collected and analysed at sea on unfiltered samples using a Seal AA3 segmented flow system (Seal Analytical, Mequon, WI, USA) following the procedures outlined by Armstrong et al. (1967) and Wood et al. (1967). Horizontal CTD profile measurements of the water column were made using a towed undulating (0–200 m) SBE 911plus CTD system (TRIAXUS; MacArtney, Esbjerg, Denmark).
Primary production measurements
Net primary production (i.e. 14C uptake rates) were determined for water column samples collected at six depths from 0 to 100 m (Boyd et al. 2005). These measurements involved spiking samples with radioactive carbon (NaH14CO3) and incubating them for 24 h. The light conditions for the six collection depths were simulated using neutral density screening for each incubator chamber. After 24 h, samples were filtered, rinsed reducing titanium solution to remove extracellular 14C and archived for scintillation counting ashore.
Trace metal sampling
Seawater samples for trace metal and isotope determination were collected using acid-cleaned, Teflon-coated, externally sprung 12-L Niskin bottles attached to an autonomous rosette (Seabird) equipped with an SBE 911plus CTD unit (Seabird). Upon retrieval, the Niskin bottles were transferred to a clean container laboratory. Seawater samples for dissolved trace metal analysis were filtered through acid-cleaned, 0.2-µm capsule filters (Supor AcroPak 200; Pall, New York, NY, USA) and acidified with t-HNO3 to a final pH of ≤1.8. The sampling protocols followed recommendations in the GEOTRACES Cruise and Methods Manual (Cookbook) (http://www.geotraces.org/science/intercalibration/222-sampling-and-sample-handling-protocols-for-geotraces-cruises, accessed 10 November 2015).
Particulate trace metal samples were collected in situ onto acid-leached 0.2-µm Supor (142-mm diameter) filters (Pall) using six large-volume dual-head pumps (McLane Research Laboratories, East Falmouth, MA, USA), deployed at various water depths. For most profiles, one pump depth was used as a blank check whereby only 4–8 L of water was pumped through the filter.
Trace metal analysis
Purification and separation of zinc from the seawater matrix was performed by solid-phase extraction using chelating ion chromatography followed by anion exchange chromatography (Samanta et al. 2016, 2017). For dZn isotope (δ66Zndissolved) determination, seawater samples (2 L) were spiked with a 67Zn–68Zn double spike (3–6 : 1 spike : sample ratio; Samanta et al. 2016, 2017). Samples were left overnight to equilibrate and then preconcentrated at a pH of 4.5 by passing them over 0.5-mL columns packed with Nobias PA Chelate PA1L resin (Hitachi-Hitech, Tokyo, Japan) at a flow rate of 2 mL min–1. Samples were rinsed with 4 mL of ammonium acetate buffer solution (1% w/w) followed by elution with 4 mL of 1 M t-HNO3. Samples were evaporated to dryness and redissolved with 0.5 mL of 6 M t-HCl. Samples were further purified using the anion exchange procedure described by Poitrasson and Freydier (2005). This procedure involved loading samples onto ~200-µL columns filled with cleaned AG-MP1 resin (Bio-Rad, Sydney, NSW, Australia). Salts and other elements not of interest were eluted from columns by passing 3 × 1 mL of 6 M t-HCl followed by 3 × 1 mL of 0.5 M t-HCl. This fraction was saved for iron isotope analysis. Zinc was eluted from each column by passing 3 × 1 mL of 0.5 M t-HNO3 over the AG-MP1 resin. The collected zinc samples were evaporated to dryness and redissolved in 2% (w/w) HNO3.
Particulate samples for trace element and δ66Zn determination were thawed and processed using the acid digestion protocol of Eggimann and Betzer (1976), as described by Ellwood et al. (2015).
Zinc isotopes were determined using a NeptunePlus multi-collector ICPMS (ThermoScientific, Sydney, NSW, Australia) with an APEX-IR introduction system (ESI, Omaha, NB, USA) and with X-type skimmer cones. At the start of each measurement session, the instrument was tuned for intensities on mass 62Ni, 63Cu, 65Cu, 64Zn, 66Zn, 67Zn and 68Zn. Samples were analysed in medium resolution mode in groups of three, bracketed with the IRMM-3702 standard (Institute for Reference Materials and Measurements, Geel, Belgium). A 2% (v/v) HNO3 blank measurement was made before each sample or standard measurement. All measurements were made as one block of 45 cycles with a 4-s integration time. On-peak blank correction of sample isotope intensities was undertaken by subtracting the average intensity of the 45 cycle measurements for each of the measured isotopes from the isotope intensities measured for each blank.
All zinc isotope measurements were collected relative to the standard reference material IRMM-3702, which is isotopically indistinguishable from the new zinc standard ‘AA-ETH Zn’ (Archer et al. 2017). The IRMM-3702 standard is offset by 0.30 ± 0.05‰ (s.d) with respect to the Johnson Matthey (JMC) Lyon standard (Cloquet et al. 2008; Moeller et al. 2012; Archer et al. 2017). Zinc isotope values were subsequently related to the JMC Lyon standard by adding 0.30‰ to all our results. Thus, the δ66Zn values are reported using the following equation:
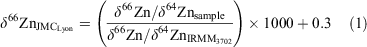
Zinc isotope reproducibility was tested by processing an in-house seawater standard multiple times. This standard was collected at a depth of 3500 m during the PINTS (‘Primary productivity induced by Iron and Nitrogen in the Tasman Sea’) campaign in 2010 from Station P3 (Hassler et al. 2014). Full processing of the sample produced a mean (±2 s.d.) δ66ZnJMCLyon value of 0.63 ± 0.02 (n = 3), which is isotopically indistinguishable from the mean (±2 s.d.) value of 0.60 ± 0.05 (n = 6) obtained by Samanta et al. (2017; Table 1).

|
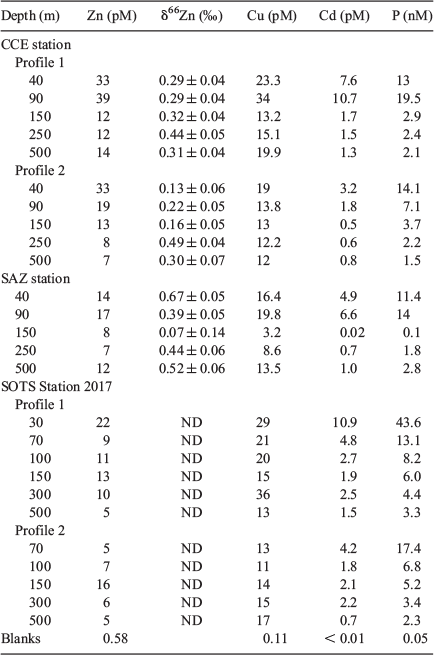
Elemental analysis for dissolved and particulate copper, cadmium, nickel, manganese, aluminium and phosphorus was made by removing aliquots from preconcentrated digests destined for zinc isotope analysis. These were measured by high-resolution inductively coupled plasma–mass spectrometry (ICP-MS; Element XR; ThermoScientific) in medium resolution mode. Iron concentrations were obtained from iron isotope analysis (M. J. Ellwood, unpubl. data). Blanks associated with the collection and processing of particulate samples are given in Tables 1 and 2, along with results for the analysis of an in-house standard for dissolved trace metals. Overall, the dissolved results produced in this study are comparable to the results obtained by Samanta et al. (2017) for zinc, Thompson and Ellwood (2014) for copper and previous measurements made at the Australian National University for iron and nickel in 2011.
|
One-dimensional biogeochemical modelling
The potential processes that affect the distribution of dZn relative to that of nitrate or phosphate and phytoplankton biomass were explored using a one-dimensional (1-D) model (Fig. 2). During the development of the model, we were mindful that some processes, (e.g. lateral advection) are not parameterised by the model. Some of the biological processes parameterised within the model are also simplified. The rationale for using this 1-D model is to explore the relative effect (and interplay) that processes such as phytoplankton utilisation of zinc, zinc complexation to natural organic ligands and regeneration have on dZn and pZn isotope profiles. One should be mindful that this model is not three-dimensional in nature and only extends to 500 m (i.e. it lacks the ability to simulate the global processes). That said, this 1-D model is a useful tool for exploring processes that influence the cycling of zinc within the CCE.
The 1-D model is based on the model developed by Schlosser et al. (2014) and includes one phytoplankton group and references key nutrients, including nitrate, phosphate, zinc and iron (Fig. 2). Note that the model has an iron component, which will not be presented in this paper. The model includes mixing, which supplies nutrients into the euphotic zone and the main loss process for nutrients and zinc from the euphotic zone (organic matter export; Fig. 2). The zinc component within the model also includes complexation to natural organic ligands. In the model presented, scavenging of zinc from solution and isotope fractionation associated with this potential process are considered in a limited number of runs (John and Conway 2014; Weber et al. 2018). We justify this because our model focuses on the upper water column where zinc predominantly complexes to natural organic ligands, which will tend to reduce the free Zn2+ concentration such that scavenging would be a minor component of its overall cycling in the upper water column.
As mentioned, the model does not include advection, which is justifiable for several reasons: (1) vertical advection (i.e. upwelling) occurs in the Southern Ocean primarily south of the PF and not in the SAZ and SAF regions examined here (Speer et al. 2000); (2) zonal advection brings in waters with similar properties from upstream in the Antarctic Circumpolar Current (Trull et al. 2001b), and can thus be ignored; and (3) meridional transport is dominated by northward Ekman transport, and although this does supply nutrients over the annual mean, in late summer surface concentrations between the SAF and PF zone are very uniform (Trull et al. 2001a), so this term can also be ignored.
In the model, phytoplankton production (γphyto) is expressed as a function of nitrogen biomass. The limiting term (i.e. the minimum, min) for γphyto is expressed as follows (the definitions for all symbols and their values are given in Table 3):
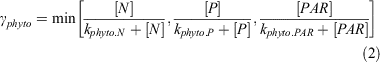
In the upper water column, at and above the depth of peak biomass (i.e. the deep chlorophyll maximum), the regeneration of nutrients back into solution is expressed as a linear function relative to biomass. Below this depth the rate of nutrient regeneration decreases following the Martin particulate organic carbon (POC) attenuation expression power law (Martin et al. 1987):
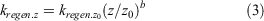
where z is depth with respect to z0, which was set to depth below the peak in biomass. This function effectively trends the sinking particles as transitioning from fresh to refractory with depth. For simplicity, the model used single values of kregen (0.35 day–1) and the power law exponent b (0.858; Martin et al. 1987) for all components. As shown in the results, it is likely that b varies among elements, and the ramifications of choosing a single value are explored in the Discussion.
For dissolved inorganic nitrogen (NO3), Eqn 4 and 5 express its uptake by phytoplankton, its exchange between boxes above (j) and below (j–2) and its regeneration from phytoplankton (expressed here as particulate organic nitrogen, PON):
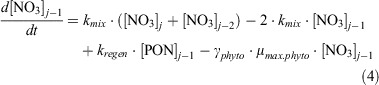
Note that the maximum uptake rate μmax.phyto is in units of nitrogen here, and thus scaling to the observed 14C uptake rates requires adjustment by the Redfield C : N ratio.
Overall, the change in PON can be expressed as follows:
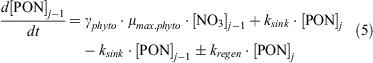
In this expression (Eqn 5), and for the other particle expressions (Eqn 7, 11; see below), the mixing terms do not appear because the sinking rate of particles (at 10 m day–1) overwhelms the mixing (range 1.2–6 m day–1) contribution to their distributions, especially during spring and summer as the mixing term reduces.
For dissolved inorganic phosphate (PO4), the following equations express its uptake by phytoplankton to form particulate organic phosphorus (POP), its exchange between boxes and its regeneration from phytoplankton:
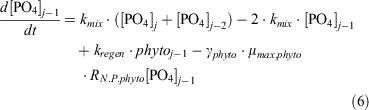
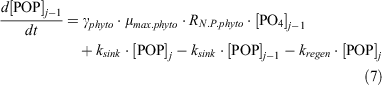
For dZn, the following equation expresses its uptake by phytoplankton, its exchange between boxes and its regeneration from particulate matter (Znphyto):
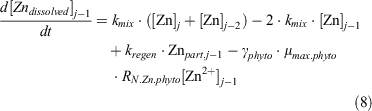
The partitioning of zinc was between complexed and uncomplexed zinc (i.e. free inorganic zinc, Zn2+) and was simulated using the following equation (Ellwood and van den Berg 2000):
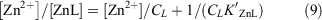
which was rearranged to give:
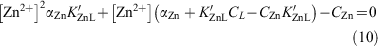
where the concentration of free zinc [Zn2+] in seawater was calculated as [Zn′] = αZn[Zn2+] and CZn is the total dZn concentration, K′ZnL presents the conditional stability constant for the zinc–ligand complex, CL is the total concentration of zinc-binding ligands in solution and αZn is the coefficient for inorganic complexation of Zn2+ in seawater. Here K′ZnL, CL and αZn were set to 1010, 1 nM and 2.1 respectively (Ellwood and van den Berg 2000; Ellwood 2004). Eqn 10 was solved within each iterative model cycle.
The overall change in particulate zinc concentration can be expressed as follows:
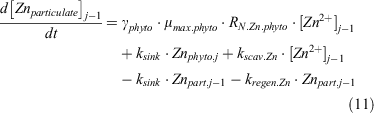
For the deepest model box, box j–n, nitrate, phosphate and dZn were supplied into this box from below. These inputs were required to balance the loss of PON, POP and pZn associated with sinking matter that sinks out of this box.
For model runs, we simulated dissolved nitrate, phosphate and zinc profiles to a depth of 500 m with depth intervals of 20 m. Seasonality was introduced into the model by varying the light (photosynthetically activate radiation, PAR) and mixing component using a cosine function such that the light field was highest at the summer solstice (22 December) and mixing was highest during at the winter solstice (21 June), consistent with deep winter mixing during winter (Fig. 2; Tagliabue et al. 2014).
The model was run to an annual steady state with respect to the deeper ocean (>250 m). The model was ‘calibrated’ to reference profiles of nitrate and dZn from within the CCE by adjusting the supply of nutrients into the deepest box, box j–n (Table 3; Fig. 3).
|
Isotope fractionation was simulated by applying fractionation factors (α) to the following processes: Zn2+ uptake by phytoplankton, Zn2+ regeneration from organic matter, Zn2+ complexation by natural organic ligands and Zn2+ scavenging from solution. For each of these processes, the fractionation is in the expected direction for kinetic fractionation (i.e. 64Zn reacts faster than 66Zn), except for zinc scavenging from solution (John and Conway 2014). Thus, during uptake, phytoplankton form with isotopically lighter compositions than the dissolved Zn substrate, which, in turn, becomes progressively heavier. Regeneration preferentially releases 64Zn, lightening the dZn isotope pool and rendering the remnant particle pool isotopically heavier. Understanding the effect of the ligand complexation process on dZn and pZn isotope compositions is dependent on the operational definition of ‘dissolved’. As measured here, the operational separation of pZn and dZn is by filtration through a 0.2-µm pore size such that the dZn measurement is the sum of free Zn2+ and ligand-bound zinc. As discussed below, the ligand-bound component dominates the total dissolved pool, especially in surface waters. Thus, the Zn2+ released from ligands and taken up by phytoplankton is lighter than that of the operationally measured dZn, which, in turn, leads to a lighter pZn isotope composition that would arise without the influence of ligand complexation.
Finally, special treatment is applied to the top and bottom boxes in the model. At the top, no flux enters from above. At the bottom, particles are allowed to exit the j–n box, and this is balanced by an upward supply flux of dZn and nutrients into this box. The isotope composition of the upward supply zinc is set to match the value of 0.45‰ measured for the deep Southern Ocean.
Results and discussion
Hydrography
The SOTS, CCE and SAZ stations were physically and chemically distinct (Fig. 1). The SOTS station is located along the northern edge of the SAZ close to the STF. The surface water temperature at SOTS was 12.6°C, salinity was 34.7 and nitrate and silicate concentrations were 4.5 and 1.6 µM respectively (Fig. 4), all typical of northern SAZ water properties (Rintoul and Trull 2001). The upper water column also experiences frequent incursions for subtropical water. Below the surface, SAMW and Antarctic Intermediate Water (AAIW) are present at depths of approximately 200–400 and 600–1200 m respectively (Fig. 4).

|
The CCE station was located at 50.4°S, 147°E within the SAZ (Fig. 1). However, the surface water temperature was 7.2°C, salinity was 33.8 (Fig. 5) and nitrate and silicate concentrations were 22 and silicate was 3.3 µM respectively, all typical of polar waters located further south of the northern extension of the SAF (Moreau et al. 2017; Patel et al. 2019). Satellite analysis revealed that the eddy had formed in early February 2016 and moved northward ~1.2° of latitude at the time of sampling (Patel et al. 2019). Satellite analysis of the eddy also revealed that it had a lower chlorophyll concentration than surrounding waters, consistent with its development further south in less-productive polar waters (Fig. 1, 5). Below the surface, AAIW appear to be present at depths between ~300 and 800 m within the eddy (Fig. 4).

|
The SAZ station was located south-east of the CCE station within the SAZ (Fig. 1). The surface water temperature for the SAZ station was 9.2°C, salinity was 34.3 and nitrate and silicate concentrations were 14.5 and 1.3 µM respectively (Fig. 4), again consistent with SAZ water properties (Rintoul and Trull 2001). Subsurface SAMW and AAIW were present at depths between ~200 and 1200 m (Fig. 4).
Biological and nutrient data
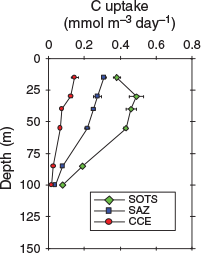
Aqua moderate-resolution imaging spectroradiometer (MODIS) satellite chlorophyll images reveal higher concentrations of chlorophyll at the SOTS and SAZ stations that at the CCE station (Fig. 1). Primary production rates between the three sites also varied, with the CCE station having the lowest rates, whereas the SOTS station had the highest (Fig. 6). The rates of primary production across all stations are consistent with previous measurements made for the region south of Australia (Boyd et al. 1999; Westwood et al. 2011).
|
The decline in the rate of primary production between stations (SOTS > SAZ > CCE) matched the decline in the dissolved iron concentration between stations within the upper water column (15–70 m) with mean (±s.d.) values of 61 ± 4, 48 ± 12 and 21 ± 3 pmol kg–1 for the SOTS, SAZ and CCE stations respectively (Table 1). The low rates of primary production within the CCE were matched by higher transmissivity (lower particulate mass within the water column) and lower TRIAXUS chlorophyll fluorescence than surrounding waters (Fig. 5). Our results are consistent with the prevalence of iron limitation in subantarctic and polar waters south of Australia (Boyd et al. 1999; Sedwick et al. 1999).
Upper water column concentrations for phosphate and nitrate showed varying degrees of depletion, with the SOTS station having the lowest surface water concentrations and the CCE station the highest (Fig. 7). Conversely, silicate was depleted at all three stations.
Concentrations of dZn and pZn
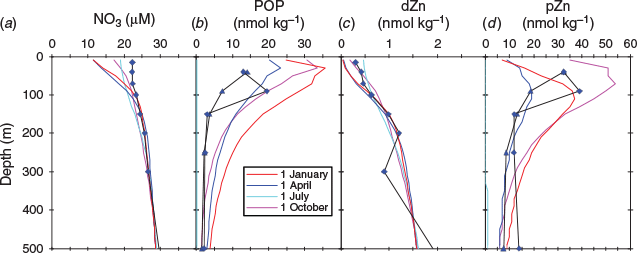
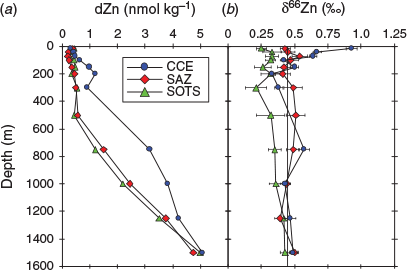
dZn concentrations for the three stations ranged between 0.21 and 5.06 nmol kg–1 across a depth range of 15–1500 m (Table 1; Fig. 7), with zinc depletion in surface waters and increasing zinc concentrations with depth. The zinc profiles, along with other dissolved profiles for iron, copper, nickel, cadmium and aluminium, were all oceanographically consistent, suggesting that contamination during sampling and analysis was minimal. For the CCE profile, there was a ‘step’ in the dZn concentration profile between 200 and 300 m wherein the zinc concentration decreased from 1.21 to 0.9 nmol kg–1. This ‘step’ in zinc concentration paralleled a step-wise increase in the concentration of dissolved iron and aluminium and a slight decline in the concentration of dissolved copper, and is coincident with a change in water mass between 200 and 300 m within the CCE (Fig. 7). Analysis of temperature and salinity depth profiles for the CCE indicates that there is a change in the physical properties at ~270 m with the intrusion of water with slightly elevated temperature and salinity (Fig. 4). This ‘intruding’ water has a lower zinc concentration.
pZn profiles were obtained for the CCE and SAZ stations, and for at the 2017 SOTS occupation. The concentrations of pZn varied between 0.1 and 19.5 pmol kg–1 across a depth range of 40–500 m, decreasing with depth and thus exhibiting trends opposite to the dZn profiles. The change in pZn concentration with depth is similar to that for particulate phosphorous (Fig. 8). Cadmium and copper, two metals that are also biologically used by phytoplankton, both showed enriched concentrations in the euphotic zone (Fig. 8). The particulate profiles for cadmium and copper present a nice contrast to that of zinc because dissolved cadmium is generally not expected to be scavenged from seawater, whereas dissolved copper is believed to be scavenged from seawater even though it is organically complexed. This leads to its ‘hybrid’ profile structure, with partial depletion in surface waters and an increase in concentration with depth (Bruland and Lohan 2003).

|
The attenuation of zinc with depth was modelled using the Martin equation:
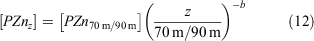
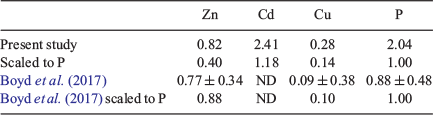
where [PZnz] represents the particulate zinc concentration at depth z, [PZn70 m/90 m] represents the particulate zinc concentration close to the base of the mixed layer at either 70 or 90 m and b represents the vertical attenuation factor. It should be noted that this equation was developed to model the sinking flux for particulate organic carbon and other various elements (Martin et al. 1987; Boyd et al. 2017), whereas we have used it to fit the attenuation profiles of suspended and sinking zinc, phosphorous, cadmium and copper concentration v. depth. That is, the suspended particle pool is dominantly produced by the attenuation of the sinking flux (Bishop 1989), with little effect of mixing. The vertical attenuation factor obtained for zinc (0.82) is less than the attenuation factors for phosphorous (2.41) and cadmium (2.41), but more than that of copper (0.28; Table 4). When normalised against phosphorous, attenuation factors for zinc, cadmium and copper are comparable to those compiled by Boyd et al. (2017). This sequence indicates that zinc has a longer regeneration length scale than phosphorous and cadmium, but less than that of copper (Fig. 8). That is, the regeneration of zinc is slower than that of phosphorous and cadmium but faster than that of copper. These differences in the regeneration length scale reflect the release of these metals and phosphorous from suspended and sinking cells and detrital matter. For example, zinc is used in zinc-finger proteins associated with RNA and DNA expression, carbonic anhydrase and alkaline phosphatase, all of which have different affinities for zinc (Twining et al. 2014). By contrast, phosphorous is a significant component of RNA and DNA, membrane phospholipids, low molecular weight water-soluble phosphate esters and metabolically active inorganic orthophosphate (Raven 2013). These differences in the regeneration of these two elements will also be reflected in the zinc : phosphorus ratio v. depth.
|
A plot of the zinc : phosphorus ratio v. depth revealed an increase in the ratio with increasing depth (Fig. 8). This contrasts with the results of Twining et al. (2014), who observed no significant change in the zinc : phosphorus ratio v. depth for material sinking from a diatom-dominated phytoplankton bloom from subtropical waters. Because the sampling at the SOTS, CCE and SAZ sites occurred late in the growing season, the phytoplankton community was primarily dominated by small prokaryote and eukaryote phytoplankton, which may explain the difference between these two studies.
The differential regeneration of zinc relative to phosphorus should also be reflected in the dissolved phase for these two elements, whereby it is expected that the increase in dZn concentration with depth should be lower than that of phosphate. A plot of zinc v. phosphate shows curvature where the slope for the relative change in the dZn and phosphate concentration (ΔZn/ΔP) increases with depth (Fig. 9), which can be interpreted as faster phosphorus regeneration relative to zinc.
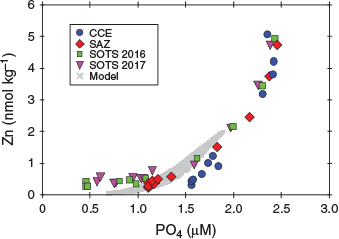
|
Recent ocean modelling work of the biogeochemical zinc cycle used a range of approaches to simulate its cycling. In general, the uptake and regeneration of zinc in these models is tied to that of phosphorus (Vance et al. 2017; de Souza et al. 2018; Roshan et al. 2018; Weber et al. 2018). Our modelling results also show that there is a decoupling between zinc and phosphate (and nitrate) cycling resulting from differences in the stoichiometric Zn : P uptake ratio relative to the deep-water Zn : P supply ratio (Fig. 9; Sunda and Huntsman 1992). This decoupling is likely to be amplified by differences in the regeneration length scale between these two elements: in most models, the regeneration rate of these two elements is assumed to be similar (e.g. Vance et al. 2017). Our field results suggest that this is not quite the case; rather, we find that zinc is less labile than phosphorous, leading to a longer regeneration length scale. These differences in regeneration length scales may seem small, but they strongly affect the biogeochemical coupling, or the lack thereof, for these two elements.
Zinc isotope analysis
The isotope composition of dZn (δ66Zndissolved) varied between 0.21 and 0.93‰, with most of the variability occurring in the upper water column at the CCE station, where values ranged from 0.93 to 0.33‰ between depths of 40 and 200 m (Fig. 10, 11). For the other two stations, δ66Zndissolved showed less variability, with values ranging between 0.32 and 0.54‰ at depths between 40 and 200 m. Mean (±2 s.d.) deep-water (≥1000 m) values for δ66Zndissolved were 0.46 ± 0.06, 0.44 ± 0.11 and 0.40 ± 0.08‰ for the CCE, SAZ and SOTS stations respectively. These deep-water values are consistent with other Southern Ocean deep-water (≥700 m) measurements (e.g. Wang et al. 2018), where mean (±2 s.d.) δ66Zndissolved was 0.40 ± 0.05‰ (n = 13).
|
The δ66Zndissolved values measured at the SOTS station between 300 and 1000 m were isotopically lighter than measurements made across the same depth range at the other two stations (Fig. 10). That said, these lower δ66Zndissolved values at the SOTS station were consistent with measurements made by Samanta et al. (2017) across a similar depth range for a station located east (Station P3; located at 46.2°S, 159.5°E) of the SOTS site, but at a similar latitude. This light δ66Zndissolved signal at the SOTS station may represent the influence the Tasman Sea Outflow (Oliver and Holbrook 2014), which forms part of the South Pacific super gyre (Ridgway 2007).
The isotope composition of particulate zinc (δ66Znparticulate) varied between 0.07 and 0.67‰ (Fig. 11). For the CCE station, δ66Znparticulate values were lighter in the upper water column and increased to values ~0.44‰ at a depth of 250 m. These lighter δ66Znparticulate values occur within the euphotic zone (40 m) when δ66Zndissolved is isotopically heavy, suggesting that uptake of isotopically light zinc by cells (John et al. 2007; Samanta et al. 2017) resulted in the dZn pool becoming isotopically heavy (Fig. 11).
By contrast, δ66Znparticulate values for the SAZ site profile varied between 0.07 and 0.67‰, with the minimum occurring at 150 m below the euphotic zone (Fig. 11). This minimum occurs at the transition from higher to lower nitrate and ammonia concentrations, which is indicative of particulate organic matter regeneration (Fig. 7). Below 150 m, mean (±2 s.d.) δ66Znparticulate increases to values near the deep-water average of 0.44 ± 0.11‰ for the SAZ site. Note that we did not collect particulate samples during the 2016 SOTS site occupation, so we do not have δ66Znparticulate values to compare with the δ66Zndissolved profile obtained at this site.
Upper ocean δ66Zndissolved fractionation
Observations
The upper water column values (0–100 m) within the CCE and at the SAZ station revealed an increase in δ66Zndissolved values with increasing dZn concentration. The δ66Zndissolved distribution is consistent with preferential loss of 64Zn through uptake by phytoplankton accompanying the observed surface deficit of dZn concentrations. To explore this further, we plotted δ66Zndissolved against ln[Zn] for the CCE because it is essentially a closed system with regard to the surrounding waters, thus allowing us to use a closed-system Rayleigh fractionation model to model the data (Fig. 12). Fitting the model to the δ66Zndissolved data produced a mean (±s.d.) fractionation factor (α) of 0.999 33 ± 0.000 04 (ϵ = –0.67‰) for samples collected within the euphotic zone (0–100 m). Interestingly, the δ66Znparticulate data did not conform to either the instantaneous or expected integrated fractionation process associated with the closed-system model (Fig. 12). The expectation is that as dZn is depleted and δ66Zndissolved increases towards the surface, δ66Znparticulate will also increase for both the instantaneous product (for which δ66Znparticulate should track δ66Zndissolved with a constant offset of –0.67) and for the accumulated product (Fig. 12). Instead, δ66Znparticulate varies little with changes in dZn concentration. The primary production profiles offer a possible explanation for this discrepancy: because pZn is generated primarily in the euphotic zone at depths less than 50 m where primary production is highest (Fig. 6), the difference in the δ66Znparticulate and δ66Zndissolved distributions is driven by the different mechanisms of their vertical redistribution. Hence, the δ66Znparticulate signature is distributed downward without modification by sinking, whereas changes in the δ66Zndissolved with depth (or dZn concentration) across the euphotic likely represents a mixing curve.
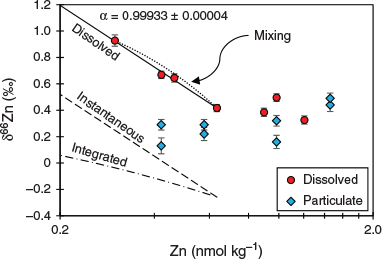
|
Below the depth of maximum biomass (i.e. below ~100 m), the δ66Znparticulate signature increases subtly (Fig. 11). One interpretation is that this occurs as a result of remineralisation, which preferentially releases 64Zn so the remaining pZn pool becomes heavier and, correspondingly, the δ66Zndissolved pool becomes lighter where they converge near 250m (Fig. 12). We tested this idea with our 1-D model.
1-D modelling
The changes in δ66Zndissolved between 0 and 100 m, resulting in the apparent ϵ of –0.67‰, could be a consequence of several processes including: (1) complexation to natural organic ligands; (2) biological fractionation within the euphotic zone; and (3) isotope fractionation upon zinc regeneration from organic matter. Here we explore these processes further in the 1-D model by running it over a yearly cycle to mimic the seasonal conversion of dZn to pZn within the euphotic zone followed by the remineralisation of pZn at depth. Data were then extracted data close to the time of sampling of the CCE.
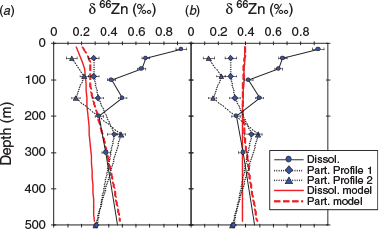
It has been argued that the fractionation of zinc isotopes in phytoplankton culture studies results from its partitioning between inorganic and organic complexes (e.g. by EDTA, which is used to buffer the inorganic zinc concentration of the medium; John et al. 2007). Zinc-EDTA isotope fractionation is ~0.3‰ between complexed and Zn2+ with the zinc-EDTA being isotopically heavy (Ban et al. 2002; Ding et al. 2010; Marković et al. 2017). In seawater, zinc speciation is dominated by its complexation with natural organic ligands (Bruland 1989; Ellwood and van den Berg 2000; Ellwood 2004) with ligand concentrations ranging between 1 and 2 nM. Using a natural ligand concentration for the subantarctic waters of 1 nM with a conditional stability constant of 1010 (Ellwood 2004), we found that complexation results in δ66Zndissolved (which reflects the sum of the ligand-bound and free Zn2+ components) becoming isotopically heavy in surface waters when using a value of ϵcomplexation = 0.3‰ (δ66ZnZn2+ – δ66Zndissolved; αcomplexation = 1.0003). However, the extent of the change in both δ66Zndissolved and δ66Znparticulate did not match our observations particularly well for the time of sampling of the CCE (Fig. 13).
Zinc isotope fractionation can also occur during Zn2+ uptake by phytoplankton (John et al. 2007; Köbberich and Vance 2017; Samanta et al. 2018). Using fractionation factors of ϵuptake = –0.3‰ (δ66Zndissolved – δ66Znparticulate; αuptake = 0.9997) or –0.67‰ (Fig. 12) for zinc uptake by phytoplankton, δ66Zndissolved becomes isotopically heavy in surface waters of the model. However, the extent of change in both δ66Zndissolved and δ66Znparticulate did not match our observations well; rather, the model simulation was isotopically heavy compared with the field data (Fig. 13).
We simulated the effect of fractionation associated with both zinc complexation with natural organic ligands and Zn2+ uptake by phytoplankton using ϵcomplexation set to 0.3‰ and ϵuptake = –0.3‰. The combined influence of these process produced a δ66Zndissolved that was similar in structure to the measured values for the CCE station (Fig. 13). However, the modelled δ66Znparticulate did not fit the measured data particularly well for the time of sampling of the CCE. Indeed, the measured data are subtly lighter within and below the euphotic zone, whereas the modelled data remain close to the deep-water input value.
Experimentation with the 1-D model revealed that including fractionation of zinc upon its regeneration from particulate organic matter improved the best fit to the CCE dataset. Setting a value for ϵregeneration to –0.15‰ (δ66Znparticulate – δ66Zndissolved; αcomplexation = 0.99985) in combination with ϵcomplexation and ϵuptake values of 0.3 and –0.3‰ respectively produced the best fit to the measured values for both δ66Zndissolved and δ66Znparticulate datasets (Fig. 13). That is, it appears that the combined effect of zinc isotope fractionation occurs as a result of complexation with natural organic ligands, zinc uptake and zinc regeneration from sinking particulate organic matter. These 1-D model results also confirm that sinking can redistribute the δ66Znparticulate signature so that it is homogeneous above 150 m. It also confirms that remineralisation can cause the δ66Zndissolved and δ66Znparticulate signatures to converge at depths between 150 and 250 m (Fig. 14d).
Using a 1-D model, John and Conway (2014) were able to demonstrate that the scavenging (αscavenging ranging between 1.00058 and 1.001) of zinc from solution onto particles can lead to a light δ66Zndissolved composition and heavy δ66Znparticulate composition. This is akin to what we model for zinc being regenerated for sinking particulate matter (Fig. 15). We found the role of scavenging is weak in the upper portion of the profile as a result of zinc complexation with natural organic ligands, which reduces the concentration dissolved free zinc available to be scavenged. Note that the model of John and Conway (2014) did not include organic complexation of zinc, so its effect in their model was not tested. As our results show (Fig. 15), a combination of processes can reproduce the structure seen for the in-eddy δ66Zndissolved and δ66Znparticulate profiles, without the specific requirement for scavenging. Indeed, zinc isotope fractionation during organic matter regeneration needs to be considered in global-scale models along with differential zinc regeneration relative to the release of nutrients from sinking particles.
|
The nutrient and zinc concentrations and isotope distributions should be considered as reflecting autumn conditions for phytoplankton production, export and remineralisation. Our 1-D model runs show that phytoplankton production, export and remineralisation vary seasonally and that the isotope signatures of dZn and pZn zinc are dynamic (Fig. 14). Interestingly, the period when δ66Zndissolved and δ66Znparticulate signatures do diverge and show Rayleigh-like fractionation characteristics is during the initial phytoplankton development between August and September (Fig. 14). This occurs as a result of strong winter mixing, which resets water column biogeochemistry to near deep-water values and low particulate production during winter months as a result of light limitation. These two factors, combined with the remineralisation and vertical redistribution of the low number of particles present during winter, allow the system to be reset to conditions comparable to a ‘classic’ closed system.
Overall, our work shows that the δ66Zn signature for both the dZn and pZn phases is affected by chemical (complexation), biological (uptake and regeneration) and physical (mixing and particle sinking) processes that, combined, influence the dissolved and particulate isotopic fields. Zinc scavenging onto particles appears to play a minor role in setting the δ66Zn signature for both dZn and pZn when zinc-complexing ligands are undersaturated. It is only through the use of a model, which included seasonality, that we could evaluate the relative importance of these processes.
Conclusions
Profiles of dZn concentration v. depth collected at three stations located in the SAZ showed depletion in surface waters and enrichment at depth. By contrast, profiles of pZn concentration v. depth profiles showed enrichment within the euphotic zone, followed by a decline in concentration with depth. The structure of the pZn concentration profile was similar to that of particulate phosphorus and cadmium, but contrasted that of copper. Modelling of these particulate profiles produced variable vertical attenuation factors of 0.82, 2.04, 2.41 and 0.28 for zinc, phosphorus, cadmium and copper respectively. Our results indicate that zinc has a longer regeneration length scale than phosphorus and cadmium, but a shorter one than copper. These differences likely help explain differences in the structures of the dissolved concentration v. depth profiles for these elements.
Profiles of δ66Zndissolved v. depth showed enrichment (mean ± 2 s.e., 0.93 ± 0.04‰) in surface waters relative to deep (>1000 m) waters (0.46 ± 0.06‰) for the CCE station. Because of its isolated nature, the δ66Zndissolved from the CCE station likely retains the signals of isotope fractionation, whereas at the SOTS and SAZ stations these may have been lost or diluted through physical processes such as mixing. Using a 1-D model, we showed that the isotopic structure of the δ66Zndissolved and δ66Znparticulate profiles from the CCE station can be explained by the combined effects of isotope fractionation associated with uptake by phytoplankton, complexation of zinc with natural organic ligands and the regeneration of zinc from particulate matter. It appears that the role of scavenging is minor in the upper ocean where zinc complexation dominates.
Conflicts of interest
M. J. Ellwood is a Guest Editor of the research front dedicated to Prof. Keith Hunter. Despite this relationship, he did not at any stage have editorial-level access to the manuscript while it was in peer review. Marine and Freshwater Research encourages its editors to publish in the journal and they are kept totally separate from the decision-making processes for their manuscripts. The authors have no further conflicts of interest to declare.
Declaration of funding
This research was supported financially under the Australian Research Council’s Discovery Program (DP170102108; DP130100679) and ship time from Australia’s Marine National Facility (IN2016_V02 and IN2017_V02).
Acknowledgements
This paper is dedicated to Prof. Keith Hunter, who passed away on 24 October 2018. To the senior authors of this paper, Keith was an inspiration. Keith was a true academic with an in-depth knowledge of all things marine and anything else he turned his attention too. As a testament, many of the figures generated in this paper were undertaken using a spreadsheet program (ViewFinder) written by Keith. Keith was also a great leader and mentor, and his wise counsel will be missed by the senior authors of this paper. The authors are grateful to the officers, crew and research staff of the Marine National Facility RV Investigator for their help with sample collection and generation of hydrochemistry data.
References
Ammerman, J. W., Hood, R. R., Case, D. A., and Cotner, J. B. (2003). Phosphorus deficiency in the Atlantic: an emerging paradigm in oceanography. Eos 84, 165–170.| Phosphorus deficiency in the Atlantic: an emerging paradigm in oceanography.Crossref | GoogleScholarGoogle Scholar |
Archer, C., Andersen, M. B., Cloquet, C., Conway, T. M., Dong, S., Ellwood, M., Moore, R., Nelson, J., Rehkamper, M., Rouxel, O., Samanta, M., Shin, K.-C., Sohrin, Y., Takano, S., and Wasylenki, L. (2017). Inter-calibration of a proposed new primary reference standard AA-ETH Zn for zinc isotopic analysis. Journal of Analytical Atomic Spectrometry 32, 415–419.
| Inter-calibration of a proposed new primary reference standard AA-ETH Zn for zinc isotopic analysis.Crossref | GoogleScholarGoogle Scholar |
Armstrong, F. A. J., Stearns, C. R., and Strickland, J. D. H. (1967). The measurement of upwelling and subsequent biological process by means of the Technicon Autoanalyzer and associated equipment. Deep-Sea Research and Oceanographic Abstracts 14, 381–389.
| The measurement of upwelling and subsequent biological process by means of the Technicon Autoanalyzer and associated equipment.Crossref | GoogleScholarGoogle Scholar |
Ban, Y., Aida, M., Nomura, M., and Fujii, Y. (2002). Zinc isotope separation by ligand exchange chromatography using cation exchange resin. Journal of Ion Exchange 13, 46–52.
| Zinc isotope separation by ligand exchange chromatography using cation exchange resin.Crossref | GoogleScholarGoogle Scholar |
Bishop, J. K. B. (1989). Regional extremes in particulate matter composition and flux: effects on the chemistry of the ocean interior. In ‘Productivity of the Ocean: Present and Past’. (Eds W. H. Berger, V. S. Smetacek, and G. Wefer.) pp. 117–137. (Wiley: New York, NY, USA.)
Boyd, P., LaRoche, J., Gall, M., Frew, R., and McKay, R. M. L. (1999). Role of iron, light, and silicate in controlling algal biomass in subantarctic waters SE of New Zealand. Journal of Geophysical Research – Oceans 104, 13395–13408.
| Role of iron, light, and silicate in controlling algal biomass in subantarctic waters SE of New Zealand.Crossref | GoogleScholarGoogle Scholar |
Boyd, P. W., Law, C. S., Hutchins, D. A., Abraham, E. R., Croot, P. L., Ellwood, M., Frew, R. D., Hadfield, M., Hall, J., Handy, S., Hare, C., Higgins, J., Hill, P., Hunter, K. A., LeBlanc, K., Maldonado, M. T., McKay, R. M., Mioni, C., Oliver, M., Pickmere, S., Pinkerton, M., Safi, K., Sander, S., Sanudo-Wilhelmy, S. A., Smith, M., Strzepek, R., Tovar-Sanchez, A., and Wilhelm, S. W. (2005). FeCycle: attempting an iron biogeochemical budget from a mesoscale SF6 tracer experiment in unperturbed low iron waters. Global Biogeochemical Cycles 19, GB4S2.
| FeCycle: attempting an iron biogeochemical budget from a mesoscale SF6 tracer experiment in unperturbed low iron waters.Crossref | GoogleScholarGoogle Scholar |
Boyd, P. W., Ellwood, M. J., Tagliabue, A., and Twining, B. S. (2017). Biotic and abiotic retention, recycling and remineralization of metals in the ocean. Nature Geoscience 10, 167–173.
| Biotic and abiotic retention, recycling and remineralization of metals in the ocean.Crossref | GoogleScholarGoogle Scholar |
Bruland, K. W. (1989). Complexation of zinc by natural organic ligands in the Central North Pacific. Limnology and Oceanography 34, 269–285.
| Complexation of zinc by natural organic ligands in the Central North Pacific.Crossref | GoogleScholarGoogle Scholar |
Bruland, K. W., and Lohan, M. C. (2003). 6.02 – Controls of trace metals in seawater A2 – Holland, Heinrich D. In ‘Treatise on Geochemistry’. (Ed. K. K. Turekian.) pp. 23–47. (Pergamon: Oxford, UK.)
Bruland, K. W., Knauer, G. A., and Martin, J. H. (1978). Zinc in north-east Pacific water. Nature 271, 741–743.
| Zinc in north-east Pacific water.Crossref | GoogleScholarGoogle Scholar |
Butler, E. C. V., O’Sullivan, J. E., Watson, R. J., Bowie, A. R., Remenyi, T. A., and Lannuzel, D. (2013). Trace metals Cd, Co, Cu, Ni, and Zn in waters of the subantarctic and Polar Frontal Zones south of Tasmania during the ‘SAZ-Sense’ project. Marine Chemistry 148, 63–76.
| Trace metals Cd, Co, Cu, Ni, and Zn in waters of the subantarctic and Polar Frontal Zones south of Tasmania during the ‘SAZ-Sense’ project.Crossref | GoogleScholarGoogle Scholar |
Cloquet, C., Carignan, J., Lehmann, M., and Vanhaecke, F. (2008). Variation in the isotopic composition of zinc in the natural environment and the use of zinc isotopes in biogeosciences: a review. Analytical and Bioanalytical Chemistry 390, 451–463.
| Variation in the isotopic composition of zinc in the natural environment and the use of zinc isotopes in biogeosciences: a review.Crossref | GoogleScholarGoogle Scholar | 17952419PubMed |
de Souza, G. F., Khatiwala, S. P., Hain, M. P., Little, S. H., and Vance, D. (2018). On the origin of the marine zinc–silicon correlation. Earth and Planetary Science Letters 492, 22–34.
| On the origin of the marine zinc–silicon correlation.Crossref | GoogleScholarGoogle Scholar |
Ding, X., Nomura, M., and Fujii, Y. (2010). Zinc isotope effects by chromatographic chelating exchange resin. Progress in Nuclear Energy 52, 164–167.
| Zinc isotope effects by chromatographic chelating exchange resin.Crossref | GoogleScholarGoogle Scholar |
Eggimann, D. W., and Betzer, P. R. (1976). Decomposition and analysis of refractory oceanic suspended materials. Analytical Chemistry 48, 886–890.
| Decomposition and analysis of refractory oceanic suspended materials.Crossref | GoogleScholarGoogle Scholar |
Ellwood, M. J. (2004). Zinc and cadmium speciation in subantarctic waters east of New Zealand. Marine Chemistry 87, 37–58.
| Zinc and cadmium speciation in subantarctic waters east of New Zealand.Crossref | GoogleScholarGoogle Scholar |
Ellwood, M. J. (2008). Wintertime trace metal (Zn, Cu, Ni, Cd, Pb and Co) and nutrient distributions in the Subantarctic Zone between 40–52°S; 155–160°E. Marine Chemistry 112, 107–117.
| Wintertime trace metal (Zn, Cu, Ni, Cd, Pb and Co) and nutrient distributions in the Subantarctic Zone between 40–52°S; 155–160°E.Crossref | GoogleScholarGoogle Scholar |
Ellwood, M. J., and van den Berg, C. M. G. (2000). Zinc speciation in the northeastern Atlantic Ocean. Marine Chemistry 68, 295–306.
| Zinc speciation in the northeastern Atlantic Ocean.Crossref | GoogleScholarGoogle Scholar |
Ellwood, M. J., Hutchins, D. A., Lohan, M. C., Milne, A., Nasemann, P., Nodder, S. D., Sander, S. G., Strzepek, R., Wilhelm, S. W., and Boyd, P. W. (2015). Iron stable isotopes track pelagic iron cycling during a subtropical phytoplankton bloom. Proceedings of the National Academy of Sciences of the United States of America 112, E15–E20.
| Iron stable isotopes track pelagic iron cycling during a subtropical phytoplankton bloom.Crossref | GoogleScholarGoogle Scholar | 25535372PubMed |
Franck, V. M., Smith, G. J., Bruland, K. W., and Brzezinski, M. A. (2005). Comparison of size-dependent carbon, nitrate, and silicic acid uptake rates in high- and low-iron waters. Limnology and Oceanography 50, 825–838.
| Comparison of size-dependent carbon, nitrate, and silicic acid uptake rates in high- and low-iron waters.Crossref | GoogleScholarGoogle Scholar |
Frölicher, T. L., Sarmiento, J. L., Paynter, D. J., Dunne, J. P., Krasting, J. P., and Winton, M. (2015). Dominance of the Southern Ocean in anthropogenic carbon and heat uptake in CMIP5 models. Journal of Climate 28, 862–886.
| Dominance of the Southern Ocean in anthropogenic carbon and heat uptake in CMIP5 models.Crossref | GoogleScholarGoogle Scholar |
Harrison, W. G., Harris, L. R., and Irwin, B. D. (1996). The kinetics of nitrogen utilization in the oceanic mixed layer: nitrate and ammonium interactions at nanomolar concentrations. Limnology and Oceanography 41, 16–32.
| The kinetics of nitrogen utilization in the oceanic mixed layer: nitrate and ammonium interactions at nanomolar concentrations.Crossref | GoogleScholarGoogle Scholar |
Hassler, C. S., Ridgway, K. R., Bowie, A. R., Butler, E. C. V., Clementson, L. A., Doblin, M. A., Davies, D. M., Law, C., Ralph, P. J., van der Merwe, P., Watson, R., and Ellwood, M. J. (2014). Primary productivity induced by iron and nitrogen in the Tasman Sea: an overview of the PINTS expedition. Marine and Freshwater Research 65, 517–537.
| Primary productivity induced by iron and nitrogen in the Tasman Sea: an overview of the PINTS expedition.Crossref | GoogleScholarGoogle Scholar |
Herraiz-Borreguero, L., and Rintoul, S. R. (2011). Subantarctic mode water: distribution and circulation. Ocean Dynamics 61, 103–126.
| Subantarctic mode water: distribution and circulation.Crossref | GoogleScholarGoogle Scholar |
Hunter, K. A., and Boyd, P. (1999). Biogeochemistry of trace metals in the ocean. Marine and Freshwater Research 50, 739–753.
| Biogeochemistry of trace metals in the ocean.Crossref | GoogleScholarGoogle Scholar |
Hutchins, D. A., Sedwick, P. N., DiTullio, G. R., Boyd, P. W., Quéguiner, B., Griffiths, F. B., and Crossley, C. (2001). Control of phytoplankton growth by iron and silicic acid availability in the subantarctic Southern Ocean: experimental results from the SAZ Project. Journal of Geophysical Research – Oceans 106, 31559–31572.
| Control of phytoplankton growth by iron and silicic acid availability in the subantarctic Southern Ocean: experimental results from the SAZ Project.Crossref | GoogleScholarGoogle Scholar |
John, S. G., and Conway, T. M. (2014). A role for scavenging in the marine biogeochemical cycling of zinc and zinc isotopes. Earth and Planetary Science Letters 394, 159–167.
| A role for scavenging in the marine biogeochemical cycling of zinc and zinc isotopes.Crossref | GoogleScholarGoogle Scholar |
John, G. S., Geis, R. W., Saito, M. A., and Boyle, E. A. (2007). Zinc isotope fractionation during high-affinity and low-affinity zinc transport by the marine diatom Thalassiosira oceanica. Limnology and Oceanography 52, 2710–2714.
| Zinc isotope fractionation during high-affinity and low-affinity zinc transport by the marine diatom Thalassiosira oceanica.Crossref | GoogleScholarGoogle Scholar |
Köbberich, M., and Vance, D. (2017). Kinetic control on Zn isotope signatures recorded in marine diatoms. Geochimica et Cosmochimica Acta 210, 97–113.
| Kinetic control on Zn isotope signatures recorded in marine diatoms.Crossref | GoogleScholarGoogle Scholar |
Lourey, M. J., and Trull, T. W. (2001). Seasonal nutrient depletion and carbon export in the Subantarctic and Polar Frontal Zones of the Southern Ocean south of Australia. Journal of Geophysical Research – Oceans 106, 31463–31487.
| Seasonal nutrient depletion and carbon export in the Subantarctic and Polar Frontal Zones of the Southern Ocean south of Australia.Crossref | GoogleScholarGoogle Scholar |
Marković, T., Manzoor, S., Humphreys-Williams, E., Kirk, G. J. D., Vilar, R., and Weiss, D. J. (2017). Experimental determination of zinc isotope fractionation in complexes with the phytosiderophore 2′-deoxymugeneic acid (DMA) and its structural analogues, and implications for plant uptake mechanisms. Environmental Science & Technology 51, 98–107.
| Experimental determination of zinc isotope fractionation in complexes with the phytosiderophore 2′-deoxymugeneic acid (DMA) and its structural analogues, and implications for plant uptake mechanisms.Crossref | GoogleScholarGoogle Scholar |
Martin, J. H., Knauer, G. A., Karl, D. M., and Broenkow, W. W. (1987). VERTEX – carbon cycling in the northeast Pacific. Deep-Sea Research – A. Oceanographic Research Papers 34, 267–285.
| VERTEX – carbon cycling in the northeast Pacific.Crossref | GoogleScholarGoogle Scholar |
Mattinson, J. M. (1972). Preparations of hydrofluoric, hydrochloric and nitric acids at ultralow lead levels. Analytical Chemistry 44, 1715–1716.
| Preparations of hydrofluoric, hydrochloric and nitric acids at ultralow lead levels.Crossref | GoogleScholarGoogle Scholar |
Metzl, N., Tilbrook, B., and Poisson, A. (1999). The annual fCO2 cycle and the air–sea CO2 flux in the sub-Antarctic Ocean. Tellus – B. Chemical and Physical Meteorology 51, 849–861.
| The annual fCO2 cycle and the air–sea CO2 flux in the sub-Antarctic Ocean.Crossref | GoogleScholarGoogle Scholar |
Moeller, K., Schoenberg, R., Pedersen, R.-B., Weiss, D., and Dong, S. (2012). Calibration of the new certified reference materials ERM-AE633 and ERM-AE647 for copper and IRMM-3702 for zinc isotope amount ratio determinations. Geostandards and Geoanalytical Research 36, 177–199.
| Calibration of the new certified reference materials ERM-AE633 and ERM-AE647 for copper and IRMM-3702 for zinc isotope amount ratio determinations.Crossref | GoogleScholarGoogle Scholar |
Moreau, S., Penna, A. D., Llort, J., Patel, R., Langlais, C., Boyd, P. W., Matear, R. J., Phillips, H. E., Trull, T. W., Tilbrook, B., Lenton, A., and Strutton, P. G. (2017). Eddy-induced carbon transport across the Antarctic Circumpolar Current. Global Biogeochemical Cycles 31, 1368–1386.
| Eddy-induced carbon transport across the Antarctic Circumpolar Current.Crossref | GoogleScholarGoogle Scholar |
Oliver, E. C. J., and Holbrook, N. J. (2014). Extending our understanding of South Pacific gyre ‘spin-up’: modeling the East Australian Current in a future climate. Journal of Geophysical Research – Oceans 119, 2788–2805.
| Extending our understanding of South Pacific gyre ‘spin-up’: modeling the East Australian Current in a future climate.Crossref | GoogleScholarGoogle Scholar |
Orsi, A. H., Whitworth, I. I. I. T., and Nowlin, J. W. D. (1995). On the meridional extent and fronts of the Antarctic Circumpolar Current. Deep-sea Research – I. Oceanographic Research Papers 42, 641–673.
| On the meridional extent and fronts of the Antarctic Circumpolar Current.Crossref | GoogleScholarGoogle Scholar |
Paasche, E. (1973). Silicon and the ecology of marine plankton diatoms. I. Thalassiosira pseudonana (Cyclotella nana) grown in a chemostat with silicate as limiting nutrient. Marine Biology 19, 117–126.
| Silicon and the ecology of marine plankton diatoms. I. Thalassiosira pseudonana (Cyclotella nana) grown in a chemostat with silicate as limiting nutrient.Crossref | GoogleScholarGoogle Scholar |
Patel, R. S., Phillips, H. E., Strutton, P. G., Lenton, A., and Llort, J. (2019). Meridional heat and salt transport across the subantarctic front by cold-core eddies. Journal of Geophysical Research – Oceans 124, 981–1004.
| Meridional heat and salt transport across the subantarctic front by cold-core eddies.Crossref | GoogleScholarGoogle Scholar |
Petrou, K., Hassler, C. S., Doblin, M. A., Shelly, K., Schoemann, V., van den Enden, R., Wright, S., and Ralph, P. J. (2011). Iron-limitation and high light stress on phytoplankton populations from the Australian Sub-Antarctic Zone (SAZ). Deep-sea Research – II. Topical Studies in Oceanography 58, 2200–2211.
| Iron-limitation and high light stress on phytoplankton populations from the Australian Sub-Antarctic Zone (SAZ).Crossref | GoogleScholarGoogle Scholar |
Poitrasson, F., and Freydier, R. (2005). Heavy iron isotope composition of granites determined by high resolution MC-ICP-MS. Chemical Geology 222, 132–147.
| Heavy iron isotope composition of granites determined by high resolution MC-ICP-MS.Crossref | GoogleScholarGoogle Scholar |
Raimbault, P., and Garcia, N. (2008). Evidence for efficient regenerated production and dinitrogen fixation in nitrogen-deficient waters of the South Pacific Ocean: impact on new and export production estimates. Biogeosciences 5, 323–338.
| Evidence for efficient regenerated production and dinitrogen fixation in nitrogen-deficient waters of the South Pacific Ocean: impact on new and export production estimates.Crossref | GoogleScholarGoogle Scholar |
Raven, J. A. (2013). The evolution of autotrophy in relation to phosphorus requirement. Journal of Experimental Botany 64, 4023–4046.
| The evolution of autotrophy in relation to phosphorus requirement.Crossref | GoogleScholarGoogle Scholar | 24123454PubMed |
Ridgway, K. R. (2007). Seasonal circulation around Tasmania: an interface between eastern and western boundary dynamics. Journal of Geophysical Research 112, C10016.
| Seasonal circulation around Tasmania: an interface between eastern and western boundary dynamics.Crossref | GoogleScholarGoogle Scholar |
Rintoul, S. R., and Trull, T. W. (2001). Seasonal evolution of the mixed layer in the Subantarctic Zone south of Australia. Journal of Geophysical Research – Oceans 106, 31447–31462.
| Seasonal evolution of the mixed layer in the Subantarctic Zone south of Australia.Crossref | GoogleScholarGoogle Scholar |
Roshan, S., DeVries, T., Wu, J., and Chen, G. (2018). The internal cycling of zinc in the ocean. Global Biogeochemical Cycles 32, 1833–1849.
| The internal cycling of zinc in the ocean.Crossref | GoogleScholarGoogle Scholar |
Sallée, J. B., Wienders, N., Speer, K., and Morrow, R. (2006). Formation of subantarctic mode water in the southeastern Indian Ocean. Ocean Dynamics 56, 525–542.
| Formation of subantarctic mode water in the southeastern Indian Ocean.Crossref | GoogleScholarGoogle Scholar |
Samanta, M., Ellwood, M. J., and Mortimer, G. E. (2016). A method for determining the isotopic composition of dissolved zinc in seawater by MC-ICP-MS with a 67Zn–68Zn double spike. Microchemical Journal 126, 530–537.
| A method for determining the isotopic composition of dissolved zinc in seawater by MC-ICP-MS with a 67Zn–68Zn double spike.Crossref | GoogleScholarGoogle Scholar |
Samanta, M., Ellwood, M. J., Sinoir, M., and Hassler, C. S. (2017). Dissolved zinc isotope cycling in the Tasman Sea, SW Pacific Ocean. Marine Chemistry 192, 1–12.
| Dissolved zinc isotope cycling in the Tasman Sea, SW Pacific Ocean.Crossref | GoogleScholarGoogle Scholar |
Samanta, M., Ellwood, M. J., and Strzepek, R. F. (2018). Zinc isotope fractionation by Emiliania huxleyi cultured across a range of free zinc ion concentrations. Limnology and Oceanography 63, 660–671.
| Zinc isotope fractionation by Emiliania huxleyi cultured across a range of free zinc ion concentrations.Crossref | GoogleScholarGoogle Scholar |
Sarmiento, J. L., Gruber, N., Brzezinski, M. A., and Dunne, J. P. (2004). High-latitude controls of thermocline nutrients and low latitude biological productivity. Nature 427, 56–60.
| High-latitude controls of thermocline nutrients and low latitude biological productivity.Crossref | GoogleScholarGoogle Scholar | 14702082PubMed |
Schlosser, C., Klar, J. K., Wake, B. D., Snow, J. T., Honey, D. J., Woodward, E. M. S., Lohan, M. C., Achterberg, E. P., and Moore, C. M. (2014). Seasonal ITCZ migration dynamically controls the location of the (sub)tropical Atlantic biogeochemical divide. Proceedings of the National Academy of Sciences of the United States of America 111, 1438–1442.
| Seasonal ITCZ migration dynamically controls the location of the (sub)tropical Atlantic biogeochemical divide.Crossref | GoogleScholarGoogle Scholar | 24367112PubMed |
Sedwick, P. N., DiTullio, G. R., Hutchins, D. A., Boyd, P. W., Griffiths, F. B., Crossley, A. C., Trull, T. W., and Queguiner, B. (1999). Limitation of algal growth by iron deficiency in the Australian Subantarctic region. Geophysical Research Letters 26, 2865–2868.
| Limitation of algal growth by iron deficiency in the Australian Subantarctic region.Crossref | GoogleScholarGoogle Scholar |
Shadwick, E. H., Trull, T. W., Tilbrook, B., Sutton, A. J., Schulz, E., and Sabine, C. L. (2015). Seasonality of biological and physical controls on surface ocean CO2 from hourly observations at the Southern Ocean Time Series site south of Australia. Global Biogeochemical Cycles 29, 223–238.
| Seasonality of biological and physical controls on surface ocean CO2 from hourly observations at the Southern Ocean Time Series site south of Australia.Crossref | GoogleScholarGoogle Scholar |
Speer, K., Rintoul, S. R., and Sloyan, B. (2000). The diabatic deacon cell. Journal of Physical Oceanography 30, 3212–3222.
| The diabatic deacon cell.Crossref | GoogleScholarGoogle Scholar |
Strzepek, R. F., Hunter, K. A., Frew, R. D., Harrison, P. J., and Boyd, P. W. (2012). Iron–light interactions differ in Southern Ocean phytoplankton. Limnology and Oceanography 57, 1182–1200.
| Iron–light interactions differ in Southern Ocean phytoplankton.Crossref | GoogleScholarGoogle Scholar |
Sunda, W. G., and Huntsman, S. A. (1992). Feedback interactions between zinc and phytoplankton in seawater. Limnology and Oceanography 37, 25–40.
| Feedback interactions between zinc and phytoplankton in seawater.Crossref | GoogleScholarGoogle Scholar |
Tagliabue, A., Sallée, J.-B., Bowie, A. R., Levy, M., Swart, S., and Boyd, P. W. (2014). Surface-water iron supplies in the Southern Ocean sustained by deep winter mixing. Nature Geoscience 7, 314–320.
| Surface-water iron supplies in the Southern Ocean sustained by deep winter mixing.Crossref | GoogleScholarGoogle Scholar |
Thompson, C. M., and Ellwood, M. J. (2014). Dissolved copper isotope biogeochemistry in the Tasman Sea, SW Pacific Ocean. Marine Chemistry 165, 1–9.
| Dissolved copper isotope biogeochemistry in the Tasman Sea, SW Pacific Ocean.Crossref | GoogleScholarGoogle Scholar |
Trull, T., Rintoul, S. R., Hadfield, M., and Abraham, E. R. (2001a). Circulation and seasonal evolution of polar waters south of Australia: implications for iron fertilization of the Southern Ocean. Deep-sea Research – II. Topical Studies in Oceanography 48, 2439–2466.
| Circulation and seasonal evolution of polar waters south of Australia: implications for iron fertilization of the Southern Ocean.Crossref | GoogleScholarGoogle Scholar |
Trull, T. W., Bray, S. G., Manganini, S. J., Honjo, S., and Francois, R. (2001b). Moored sediment trap measurements of carbon export in the Subantarctic and Polar Frontal Zones of the Southern Ocean, south of Australia. Journal of Geophysical Research – Oceans 106, 31489–31509.
| Moored sediment trap measurements of carbon export in the Subantarctic and Polar Frontal Zones of the Southern Ocean, south of Australia.Crossref | GoogleScholarGoogle Scholar |
Twining, B. S., Nodder, S. D., King, A. L., Hutchins, D. A., LeCleir, G. R., DeBruyn, J. M., Maas, E. W., Vogt, S., Wilhelm, S. W., and Boyd, P. W. (2014). Differential remineralization of major and trace elements in sinking diatoms Limnology and Oceanography 59, 689–704.
| Differential remineralization of major and trace elements in sinking diatomsCrossref | GoogleScholarGoogle Scholar |
Vance, D., Little, S. H., de Souza, G. F., Khatiwala, S., Lohan, M. C., and Middag, R. (2017). Silicon and zinc biogeochemical cycles coupled through the Southern Ocean. Nature Geoscience 10, 202–206.
| Silicon and zinc biogeochemical cycles coupled through the Southern Ocean.Crossref | GoogleScholarGoogle Scholar |
Wang, R. M., Archer, C., Bowie, A. R., and Vance, D. (2018). Zinc and nickel isotopes in seawater from the Indian Sector of the Southern Ocean: the impact of natural iron fertilization versus Southern Ocean hydrography and biogeochemistry. Chemical Geology 12, 12–34.
Weber, T., John, S., Tagliabue, A., and DeVries, T. (2018). Biological uptake and reversible scavenging of zinc in the global ocean. Science 361, 72–76.
| Biological uptake and reversible scavenging of zinc in the global ocean.Crossref | GoogleScholarGoogle Scholar | 29976823PubMed |
Weeding, B., and Trull, T. W. (2014). Hourly oxygen and total gas tension measurements at the Southern Ocean Time Series site reveal winter ventilation and spring net community production. Journal of Geophysical Research – Oceans 119, 348–358.
| Hourly oxygen and total gas tension measurements at the Southern Ocean Time Series site reveal winter ventilation and spring net community production.Crossref | GoogleScholarGoogle Scholar |
Westwood, K. J., Brian Griffiths, F., Webb, J. P., and Wright, S. W. (2011). Primary production in the Sub-Antarctic and Polar Frontal Zones south of Tasmania, Australia; SAZ-Sense survey, 2007. Deep-sea Research – II. Topical Studies in Oceanography 58, 2162–2178.
| Primary production in the Sub-Antarctic and Polar Frontal Zones south of Tasmania, Australia; SAZ-Sense survey, 2007.Crossref | GoogleScholarGoogle Scholar |
Wood, E. D., Armstrong, F. A. J., and Richards, F. A. (1967). Determination of nitrate in sea water by cadmium-copper reduction to nitrite. Journal of the Marine Biological Association of the United Kingdom 47, 23–31.
| Determination of nitrate in sea water by cadmium-copper reduction to nitrite.Crossref | GoogleScholarGoogle Scholar |








