Feedback loops between mathematics and microbiology
Douglas R. Brumley A *A School of Mathematics and Statistics, The University of Melbourne, Parkville, Vic. 3010, Australia.

Dr Douglas Brumley, BSc (Hons), PhD (Cantab) is a Senior Lecturer at The University of Melbourne. He leads an interdisciplinary research group that utilises mathematics, microfluidics and microscopy to study a range of dynamic processes in biology including bacterial motility, symbioses, nutrient cycling and flows around coral reefs. |
Microbiology Australia 43(1) 32-35 https://doi.org/10.1071/MA22010
Submitted: 3 March 2022 Accepted: 21 March 2022 Published: 19 April 2022
© 2022 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of the ASM. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
The combination of mathematical modelling and quantitative video-microscopy provides exciting opportunities for elucidating the mechanisms behind key processes in microbial ecology, ranging from cell navigation and nutrient cycling to biofilm establishment and symbioses. Central to this approach is the iterative process, whereby experiments and modelling inform one another in a virtuous cycle: vast quantities of experimental data help to test and refine mathematical models, the predictions from which feed back to the experimental design itself. This paper discusses recent technologies, emerging applications, and examples where calibrated mathematical models enable calculation of quantities that are otherwise extremely difficult to measure.
Keywords: applied mathematics, chemotaxis, fluid dynamics, microbial ecology, microfluidics, motility, navigation, video-microscopy.
Microorganism behaviour and interactions unfold at the microscale and are inherently dynamic. Ecological processes depend on spatial structure of the environment, as well as the arrangement and behaviour of microbes. For example, the capacity for microbes to actively navigate heterogeneous environments using chemotaxis can dramatically influence their nutrient acquisition and establishment of symbioses;1 ubiquitous fluid flows in the environment (e.g. ocean, groundwater, gut, mucus) influence the motility of microbes and reshape the environment;2 and Brownian motion can affect encounter rates between microorganisms.3 While functional complexity of microbes is well documented, it can be very difficult to examine spatiotemporal processes using traditional tools in microbiology. The combination of visualisation in controlled environments and mathematical modelling is uniquely positioned to resolve dynamic features of microbial lifestyles, and the ways in which these scale up to ecosystem-level processes.
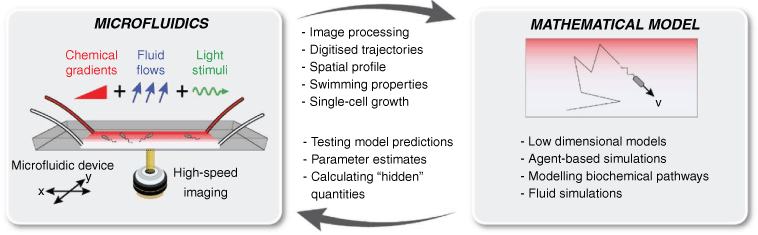
The growing use of microfluidics and video-microscopy has facilitated the direct imaging of microbial behaviour in a range of realistic controlled microenvironments. Typically fabricated from flexible, optically transparent elastomers such as polydimethylsiloxane (PDMS), microfluidic devices can be used to create precisely controlled physicochemical conditions.4 Steady gradients or transient pulses of oxygen, amino acids, and sugars can be used to interrogate the chemotactic ability of microorganisms.5,6 Microscale fluid flows can be generated with exquisite precision using ultraslow syringe pumps, with flow fields exactly solvable using known dimensions. Various other additional stimuli – including light illumination patterns, electric and magnetic fields7 – can readily be overlayed. Taken together, this enables the user to accurately recreate physical and chemical features of realistic microenvironments – for example from the ocean or soil – in a device small enough to fit on a microscope slide (Fig. 1).
Mathematical modelling has been applied extensively over many decades to model phenomena in microbial ecology. These approaches can involve directly simulating the motion of individual cells (agent-based models); abstracting organisms or chemicals as continuous fields which vary in space and time (continuum models); modelling sensory pathways or physical processes using reduced-order dynamical systems; and using statistical models to process and interpret sequencing data. For example, understanding of pattern formation in growing domains,8 limits to chemoreception,9 and motility patterns of swimming microorganisms10 stemmed from mathematical models. More broadly across microbiology, mathematical modelling has been used to investigate metabolism in microbial communities and the transmission of infection in disease epidemiology. The success of mathematical models hinges on accurately identifying the essential features of the biological system that shape the ecological processes, and detailed parameterisation of the model.
The feedback loop between experiments and mathematical modelling is essential for understanding various processes in microbial ecology. Previous works have highlighted the utility of microfluidic devices for visualising dynamic processes.4 However, these technologies realise their full potential when combined with mathematical modelling, particularly through iteration between experiments and theory. Because experimental environments (e.g. chemical gradients, flow, light, fields) can be independently and continuously varied, the predictions of mathematical models can be thoroughly scrutinised. Where differences occur, models can be updated, and further experiments conducted (Fig. 1).
What are the key elements that facilitate this iterative loop? Video-microscopy of microbes in carefully controlled arenas enables collection of vast quantities of data, for example in the form of high-speed movies, time-lapse photographs, or fluorescence intensity. Image processing algorithms – often conducted in MATLAB, Python, ImageJ – result in digitised trajectories, for example, the position of all motile bacteria at all time-steps11 or the growth dynamics and lineages of cells throughout a biofilm.12 From these data, cell concentration profiles, swimming speeds, turning angles, and attachment events13 can be quantified with great precision. Although visualisation is a key step, this methodology is not merely ‘observational’. The extracted information can be either used to parameterise mathematical models or directly compare with the predictions of simulations or modelling efforts.
Many aspects of microorganisms’ environment and lifestyle can be modelled explicitly using known governing equations and physical principles. The Navier–Stokes equations can be used to precisely calculate how fluid flows and local shear transport and rotate microbes;14 the transport and spread of dissolved organic matter can be solved using the advection-diffusion equation; and buoyancy forces, gravitational torques and magnetic fields can be readily included.15 Explicit calculation of the hydrodynamic flow fields around swimming microorganisms16 allows one to determine how organisms physically interact with one another17 as well as in dense suspensions.18 Mathematical modelling can also shed light on complex biochemical pathways and whole cell dynamics. These range from low-dimensional models, where a full sensory pathway can be abstracted as a dynamical system with few parameters,19 through to systems biology approaches that involve high-dimensionality modelling of many processes in a cell.20 Despite their apparent simplicity, minimal models have elucidated how different bacteria navigate chemical profiles using for example logarithmic sensing21 or fold change detection,22 and how the discrete molecular nature of chemical attractants places limits on gradient detection.23 These models, which enable prediction of microbial dynamics in arbitrary settings with great accuracy (~1% fitting error)24 despite few parameters, were developed and validated with the large quantities of data obtained through microfluidics and microbial tracking.
To close the feedback loop, model predictions must be able to inform refinements of experimental design. In the simplest case, this can be using mathematical models to identify the key regions of parameter space to be studied experimentally, for example, determining the domain size, imaging timescales or nutrient concentrations at which specific phenomena are likely to occur. Pioneering work of Berg and Purcell,9 later extended by others, calculated the strength of a chemical gradient necessary to elicit a chemotactic response. Experiments can also be designed to test the robustness of the model – for example, would a model for chemotaxis still work if the gradients were increased by a factor of 10 or 100? Challenging models through a suite of different experiments removes the likelihood of coincidental agreement between experiments and modelling.
Mathematical models can reveal specific phenomena that might not otherwise be seen in experimental systems. Knowledge of how fluid gradients reorient cells suggested that swimming microbes exhibit different behaviours as fluid shear is varied; advection–diffusion modelling suggests that external flow can dramatically influence quorum sensing of microbial communities;25 and theoretical work on confined active suspensions26 hinted that confining boundaries could stabilise bacterial suspensions into vortical flow patterns.
Mathematical modelling enables one to calculate important parameters and quantities that cannot currently be measured directly. Marine nutrient cycling and biogeochemistry is underpinned by the concerted action of microbial populations, and determining precisely how microbial behaviour (e.g. motility, navigation) influences nutrient uptake, represents a key challenge. Resource acquisition is readily measured using bulk techniques, for example by examining cell growth rates and dry mass measurements. At the single-cell level, Nanoscale secondary ion mass spectrometry (NanoSIMS) and other quantitative imaging tools27 provide highly quantitative measurements for nutrient uptake, but can be prohibitively expensive and time-consuming. However, in microfluidic arenas where the nutrient landscape can be spatially controlled and the bacterial positions readily measured,24 it is straightforward to calculate single-cell nutrient exposure across the entire bacterial population. Quantities such as the energetic cost of swimming, which can be extremely challenging to measure biochemically, can be readily calculated using fluid dynamical models which consider the shape, swimming speed, and hydrodynamic drag on a cell body.28 This enables quantitative predictions about optimal strategies for microorganisms in various realistic environments. For example, the competition between non-motile and chemotactic bacteria is shown to depend sensitively on the local ocean productivity.29
Perhaps the most powerful aspect of mathematical modelling is the capacity to investigate the implications of varying key physical parameters and examining how sensitive results are to changes in microbial behaviour. For example, how does the nutrient uptake change as chemotactic sensitivity is modified, and is there an optimal value? How does IgA-mediated agglutination of pathogens vary as antibody stickiness and cell growth rates change? Mechanistic models can either examine key metrics for given parameters, or allow these parameters to vary over time, known as in silico evolutionary experiments.
Future directions. We have discussed the iteration between experiments and modelling, communicated through data and model outputs. The greatest advances thus far have been in relation to single microbial species or simple communities. Community analysis is typically performed at a very high level, e.g. through metagenomics, but is not well suited to exploring spatial and temporal effects, and physical processes involved in the microbial lifestyles. An important area for future exploration will be examining interaction between multiple species and assessing the role of spatial heterogeneity and resource diversity in natural communities.
Another clear future area of research is the application of machine learning (ML) and artificial intelligence (AI). In the shorter time, this is likely to assist with the extraction of data from experimental results (e.g. image segmentation, cell identification), which can be fed to mathematical models as outlined earlier. However, in the longer term, AI will likely assist in the modelling phase itself, proposing and testing reduced order models, or guiding human intuition.30 Through exposure to large datasets, AI may be able to ‘learn’ how microorganisms behave, either as individuals (e.g. chemotaxis, motility patterns, growth rates), or communities (e.g. symbiosis partnerships, community dynamics). This offers the tantalising possibility of extrapolating behaviour from small numbers of different species – for example, chemotaxis towards specific compounds, symbiosis between pairs of organisms – to complex communities with multiple metabolic interactions. Despite these possibilities, ML and AI find it difficult to provide reasoning for their predictions. So, there will be a trade-off between accurate prediction of dynamics and revealing underlying mechanisms or physical principles (at least in the short term). Taken together, the combination of quantitative video-microscopy, mathematical modelling, and machine learning, is promising for providing quantitative understanding of how complex microbial communities behave.
Data availability
Data sharing is not applicable as no new data were generated or analysed during this study.
Conflicts of interest
The author declares no conflicts of interest.
Declaration of funding
This work was supported by an Australian Research Council Discovery Early Career Researcher Award DE180100911 and a Gordon & Betty Moore Foundation Symbiosis in Aquatic Systems grant.
References
[1] Raina, J-B et al.. (2019) The role of microbial motility and chemotaxis in symbiosis. Nat Rev Microbiol 17, 284–294.| The role of microbial motility and chemotaxis in symbiosis.Crossref | GoogleScholarGoogle Scholar | 30923350PubMed |
[2] Bhattacharjee, T et al.. (2021) Chemotactic migration of bacteria in porous media. Biophys J 120, 3483–3497.
| Chemotactic migration of bacteria in porous media.Crossref | GoogleScholarGoogle Scholar | 34022238PubMed |
[3] Barr, JJ et al.. (2015) Subdiffusive motion of bacteriophage in mucosal surfaces increases the frequency of bacterial encounters. Proc Natl Acad Sci 112, 13675–13680.
| Subdiffusive motion of bacteriophage in mucosal surfaces increases the frequency of bacterial encounters.Crossref | GoogleScholarGoogle Scholar | 26483471PubMed |
[4] Son, K et al.. (2015) Live from under the lens: exploring microbial motility with dynamic imaging and microfluidics. Nat Rev Micro 13, 761–775.
| Live from under the lens: exploring microbial motility with dynamic imaging and microfluidics.Crossref | GoogleScholarGoogle Scholar |
[5] Menolascina, F et al.. (2017) Logarithmic sensing in Bacillus subtilis aerotaxis. Npj Syst Biol Appl 3, 16036.
| Logarithmic sensing in Bacillus subtilis aerotaxis.Crossref | GoogleScholarGoogle Scholar | 28725484PubMed |
[6] Kalinin, Y et al.. (2010) Responses of Escherichia coli bacteria to two opposing chemoattractant gradients depend on the chemoreceptor ratio. J Bacteriol 192, 1796–1800.
| Responses of Escherichia coli bacteria to two opposing chemoattractant gradients depend on the chemoreceptor ratio.Crossref | GoogleScholarGoogle Scholar | 20118262PubMed |
[7] Rismani Yazdi, S et al.. (2018) Magnetotaxis enables magnetotactic bacteria to navigate in flow. Small 14, 1702982.
| Magnetotaxis enables magnetotactic bacteria to navigate in flow.Crossref | GoogleScholarGoogle Scholar |
[8] Crampin, EJ et al.. (1999) Reaction and diffusion on growing domains: scenarios for robust pattern formation. Bull Math Biol 61, 1093–1120.
| Reaction and diffusion on growing domains: scenarios for robust pattern formation.Crossref | GoogleScholarGoogle Scholar | 17879872PubMed |
[9] Berg, HC and Purcell, EM (1977) Physics of chemoreception. Biophys J 20, 193–219.
| Physics of chemoreception.Crossref | GoogleScholarGoogle Scholar | 911982PubMed |
[10] Taylor, GI (1951) Analysis of the swimming of microscopic organisms. Proc R Soc Lond A Math Phys Sci 209, 447–461.
[11] Carrara, F et al.. (2020) Generating controlled, dynamic chemical landscapes to study microbial behavior. J Vis Exp 155, e60589.
| Generating controlled, dynamic chemical landscapes to study microbial behavior.Crossref | GoogleScholarGoogle Scholar |
[12] Drescher, K et al.. (2016) Architectural transitions in Vibrio cholerae biofilms at single-cell resolution. Proc Natl Acad Sci 113, E2066–E2072.
| Architectural transitions in Vibrio cholerae biofilms at single-cell resolution.Crossref | GoogleScholarGoogle Scholar | 26933214PubMed |
[13] Yawata, Y et al.. (2014) Competition–dispersal tradeoff ecologically differentiates recently speciated marine bacterioplankton populations. Proc Natl Acad Sci 111, 5622–5627.
| Competition–dispersal tradeoff ecologically differentiates recently speciated marine bacterioplankton populations.Crossref | GoogleScholarGoogle Scholar | 24706766PubMed |
[14] Guasto, JS et al.. (2012) Fluid mechanics of planktonic microorganisms. Annu Rev Fluid Mech 44, 373–400.
| Fluid mechanics of planktonic microorganisms.Crossref | GoogleScholarGoogle Scholar |
[15] Pedley, TJ and Kessler, JO (1992) Hydrodynamic phenomena in suspensions of swimming microorganisms. Annu Rev Fluid Mech 24, 313–358.
| Hydrodynamic phenomena in suspensions of swimming microorganisms.Crossref | GoogleScholarGoogle Scholar |
[16] Drescher, K et al.. (2010) Direct measurement of the flow field around swimming microorganisms. Phys Rev Lett 105, 168101.
| Direct measurement of the flow field around swimming microorganisms.Crossref | GoogleScholarGoogle Scholar | 21231017PubMed |
[17] Darveniza, C et al.. (2022) Pairwise scattering and bound states of spherical microorganisms. Phys Rev Fluids 7, 013104.
| Pairwise scattering and bound states of spherical microorganisms.Crossref | GoogleScholarGoogle Scholar |
[18] Wensink, HH et al.. (2012) Meso-scale turbulence in living fluids. Proc Natl Acad Sci 109, 14308–14313.
| Meso-scale turbulence in living fluids.Crossref | GoogleScholarGoogle Scholar | 22908244PubMed |
[19] Long, J et al.. (2017) Feedback between motion and sensation provides nonlinear boost in run-and-tumble navigation. PLOS Comput Biol 13, e1005429.
| Feedback between motion and sensation provides nonlinear boost in run-and-tumble navigation.Crossref | GoogleScholarGoogle Scholar | 28264023PubMed |
[20] Le Novère, N et al.. (2005) Minimum information requested in the annotation of biochemical models (MIRIAM). Nat Biotechnol 23, 1509–1515.
| Minimum information requested in the annotation of biochemical models (MIRIAM).Crossref | GoogleScholarGoogle Scholar | 16333295PubMed |
[21] Kalinin, YV et al.. (2009) Logarithmic sensing in Escherichia coli bacterial chemotaxis. Biophys J 96, 2439–2448.
| Logarithmic sensing in Escherichia coli bacterial chemotaxis.Crossref | GoogleScholarGoogle Scholar | 19289068PubMed |
[22] Lazova, MD et al.. (2011) Response rescaling in bacterial chemotaxis. Proc Natl Acad Sci 108, 13870–13875.
| Response rescaling in bacterial chemotaxis.Crossref | GoogleScholarGoogle Scholar | 21808031PubMed |
[23] Hein, AM et al.. (2016) Physical limits on bacterial navigation in dynamic environments. J R Soc Interface 13, 20150844.
| Physical limits on bacterial navigation in dynamic environments.Crossref | GoogleScholarGoogle Scholar | 26763331PubMed |
[24] Brumley, DR et al.. (2019) Bacteria push the limits of chemotactic precision to navigate dynamic chemical gradients. Proc Natl Acad Sci 116, 10792–10797.
| Bacteria push the limits of chemotactic precision to navigate dynamic chemical gradients.Crossref | GoogleScholarGoogle Scholar | 31097577PubMed |
[25] Kim, MK et al.. (2016) Local and global consequences of flow on bacterial quorum sensing. Nat Microbiol 1, 15005.
| Local and global consequences of flow on bacterial quorum sensing.Crossref | GoogleScholarGoogle Scholar | 27571752PubMed |
[26] Woodhouse, FG et al.. (2012) Spontaneous circulation of confined active suspensions. Phys Rev Lett 109, 168105.
| Spontaneous circulation of confined active suspensions.Crossref | GoogleScholarGoogle Scholar | 23215137PubMed |
[27] Raina, J-B et al.. (2017) Subcellular tracking reveals the location of dimethylsulfoniopropionate in microalgae and visualises its uptake by marine bacteria. Elife 6, e23008.
| Subcellular tracking reveals the location of dimethylsulfoniopropionate in microalgae and visualises its uptake by marine bacteria.Crossref | GoogleScholarGoogle Scholar | 28371617PubMed |
[28] Lauga, E and Powers, TR (2009) The hydrodynamics of swimming microorganisms. Reports Prog Phys 72, 096601.
| The hydrodynamics of swimming microorganisms.Crossref | GoogleScholarGoogle Scholar |
[29] Smriga, S et al.. (2016) Chemotaxis toward phytoplankton drives organic matter partitioning among marine bacteria. Proc Natl Acad Sci 113, 1576–1581.
| Chemotaxis toward phytoplankton drives organic matter partitioning among marine bacteria.Crossref | GoogleScholarGoogle Scholar | 26802122PubMed |
[30] Davies, A et al.. (2021) Advancing mathematics by guiding human intuition with AI. Nature 600, 70–74.
| Advancing mathematics by guiding human intuition with AI.Crossref | GoogleScholarGoogle Scholar | 34853458PubMed |