Boundary layer height above the Great Barrier Reef studied using drone and Mini-Micropulse LiDAR measurements
Robert G. Ryan A * , Christian Eckert B , Brendan P. Kelaher B , Daniel P. Harrison B and Robyn Schofield
A * , Christian Eckert B , Brendan P. Kelaher B , Daniel P. Harrison B and Robyn Schofield  A
A
A
B
Abstract
The planetary boundary layer height (PBLH) is an important meteorological feature defining the boundary between surface processes and the free troposphere. The PBLH plays a key role in cloud formation and the vertical extent of aerosols and air pollutants. Measurements of PBLH were made by meteorological sensors mounted to a multi-copter drone over the southern Great Barrier Reef, Australia. We then compared these drone-based measurements to remote-sensed PBLH observations, using a Mini-Micropulse (MP) LiDAR system. Across the measurement campaign (1 March–2 April 2023), the mean PBLH value using the drones was 801 ± 203 m. Using the gradient method for MP LiDAR normalised relative backscatter profiles, the mean PBLH was 811 ± 260 m. Using an ideal MP LiDAR profile fitting method the mean was 912 ± 202 m and using a wavelet covariance transform method the mean was 862 ± 298 m. The boundary layer was consistently well mixed, without convective instability or a strong diurnal PBLH cycle. The three MP LiDAR methods compared well to the drone measurements overall with Pearson’s R correlation coefficients >0.60; however, estimates from the MP LiDAR were typically ~10% higher than from the drone. These results indicate congruence between the backscatter- and thermodynamically derived PBLH at One Tree Island, which is robust to variations in sampling conditions and the choice of MP LiDAR PBLH retrieval method.
Keywords: atmospheric mixing, atmospheric structure, drones, Great Barrier Reef, LiDAR, One Tree Island, PBLH, planetary boundary layer height, remote sensing.
1.Introduction
The planetary boundary layer is the layer of the troposphere closest to, and most affected by, the Earth’s surface. The planetary boundary layer height (PBLH) determines the extent of turbulent mixing of momentum, energy, gases and aerosols in the lower atmosphere and is the exchange point between the surface and the free troposphere (Stull 1988). The PBLH is often characterised by a temperature inversion and is a meteorological parameter crucial to understanding atmospheric thermodynamics, cloud formation and pollutant dispersion (Hennemuth and Lammert 2006).
Diurnal variation in the PBLH in marine environments is often muted compared to over land due to the absence of a strong diurnal cycle in surface sensible heat flux over the ocean (Hennemuth and Lammert 2006). Despite this simplification, observational and physical challenges inherent to the offshore environment make modelling of the boundary layer in marine environments difficult (Sullivan and McWilliams 2010; Shaw et al. 2022). Physical factors driving the marine PBLH include convection when cold air flows over warmer water, as well as boundary layer stratification when warm air flows over cold water (Archer et al. 2016). Uncertainty in marine boundary layer dynamics due to ocean current and sea surface temperature variations (Skyllingstad et al. 2007), including coral reefs (MacKellar et al. 2013), and the frequent occurrence of marine stratocumulus cloud at the top of the boundary layer (Wood 2012) also limit our ability to simulate the marine PBLH.
A paucity of observations in marine environments limits validation of PBLH modelling estimates (Shaw et al. 2022). This is especially the case in the Australian region, including over the Great Barrier Reef (GBR), a vast and fragile marine ecosystem off the north-east coast of Australia that is under threat due to climate change (Ainsworth et al. 2016; Mentzel et al. 2024). There are a limited number of studies detailing boundary layer measurements over the GBR (MacKellar et al. 2013; Chen et al. 2019; McGowan et al. 2022). MacKellar et al. (2013) and McGowan et al. (2022) examined boundary layer thermodynamics over Heron Island in the southern GBR. They found that the boundary layer structure is modulated by the complex variations in sea surface temperature and roughness associated with coral reefs. Chen et al. (2019) used LiDAR measurements to retrieve the PBLH at Mission Beach, a coastal site adjacent to the northern GBR. In that study, large discrepancies were found between Mini-Micropulse (MP) LiDAR-observed PBLH and the values simulated by the Weather Research and Forecasting model, with the model not capturing the PBLH diurnal variation and differing from the observations by over 1 km.
Growing interest in atmospheric chemistry and composition over the GBR necessitates an understanding of the local atmospheric structure. Work by Swan et al. (2017), Jones et al. (2018) and Fiddes et al. (2022) attempted to address the role of reef-derived dimethyl sulfide in reef-aerosol-cloud climate feedbacks. As part of the Reef Restoration and Adaptation Program: Cooling and Shading Subprogram, ongoing studies are examining the potential of artificially enhanced atmospheric sea-salt concentrations to promote marine cloud brightening and mitigate coral bleaching (Harrison et al. 2019; Hernandez-Jaramillo et al. 2023, 2024; Harrison 2024). Knowing the PBLH, and hence the extent of aerosol dispersion from their surface emission points, is critical for understanding the effect of these natural and anthropogenic aerosol emissions on the radiation balance over the GBR.
LiDAR and ceilometer measurements are routinely used to determine the PBLH on the basis of aerosol scattering (Lewis et al. 2013; Li et al. 2017; Su et al. 2017; Dang et al. 2019; Wang et al. 2021; Osibanjo et al. 2022). LiDAR measurements provide vertical backscatter profiles and, in a cloud-free atmosphere, the strongest backscatter is provided by aerosols, which are predominantly contained within the boundary layer. Therefore, the PBLH is often characterised by a decrease in aerosol backscatter. There are three mathematical methods commonly used for determining the PBLH altitude from LiDAR data: gradient, idealised profile (IP), and wavelet transform methods (Li et al. 2017). The gradient method defines the PBLH as the altitude of the most negative peak of the derivative of the range-corrected LiDAR signal (Hayden et al. 1997). The IP method is similar to the gradient method; however, the minimum gradient is calculated from an idealised backscatter profile fit to the data (Steyn et al. 1999). In the wavelet transform method, the LiDAR signal is decomposed using a wavelet mother function (e.g. the Haar function) (Baars et al. 2008; de Arruda Moreira et al. 2014; Li et al. 2017).
For many years balloon launches with attached radiosondes were the dominant methodology to measure vertical profiles of meteorological variables such as temperature, relative humidity and air pressure (Durre et al. 2006). Drones are increasingly used in atmospheric science, particularly for providing vertical profiles of atmospheric composition and key meteorological parameters (Greatwood et al. 2017; Eckert et al. 2023). This information can be used to estimate the PBLH on thermodynamic grounds, by analysing the gradient of the potential temperature (Θ) (Hennemuth and Lammert 2006) or applying the 1.5-theta method, which specifies that the PBLH corresponds to the altitude at which Θ first exceeds the minimum +1.5 K during ascent (Nielsen-Gammon et al. 2008; Hu et al. 2010). To our knowledge, no previous comparison of thermodynamic and backscatter-derived PBLH retrieval methods has been carried out using drones or radiosondes in the GBR, or the broader Australian region.
Throughout March and April 2023, drone and MP LiDAR vertical profiling were carried out simultaneously at One Tree Island as part of the Restoration and Adaptation Program: Cooling and Shading Subprogram fieldwork. The One Tree Island drone vertical profiles were first described, and validated against surface meteorological observations, in Eckert et al. (2023). One Tree Island is situated ~85 km from Gladstone off the east coast of Australia (23.508°S, 152.092°E), a designated scientific marine reserve in the Capricorn Bunker Group of the southern GBR (Fig. 1). Concurrent drone and MP LiDAR measurements over the course of a month provide a unique opportunity to use these two methods to examine the thermodynamic and backscatter-derived PBLH at the GBR.
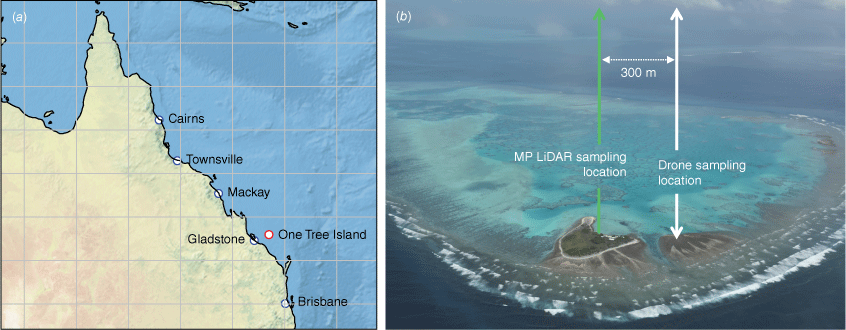
Location of drone and Mini-Micropulse (MP) LiDAR boundary layer height sampling. (a) Map showing the location of One Tree Island off the coast of Queensland in north-eastern Australia, in relation to major Queensland cities. (b) Photograph of One Tree Island taken from a drone, showing the location of the island inside the coral reef lagoon (photo credit: M. Goolmeer). The viewing direction of this image is north-west. The MP LiDAR was located at the research station and the vertical drone sampling was conducted ~300 m to the east.
2.Materials and methods
2.1. Drone sampling
Drone-based meteorological profiles were obtained between late February and early April 2023. The flights, conducted using a DJI Matrice 300 (M300) quadcopter drone, reached altitudes of up to 1.5 km. Therefore, all flights were beyond visual line of sight and approved by the Australian Civil Aviation Safety Authority. Flights were conducted daily at 09:00, 12:00 and 15:00 hours Australian eastern standard time. Temperature, pressure and relative humidity were measured on the drones using InterMet Systems iMet-XQ2 UAV (iMet) sensors. For a more in-depth explanation of the drone sampling methodology, refer to Eckert et al. (2023). The 3-D position of the mounted iMet sensors and flight patterns (ascent, mission peak and descent) are determined using the drone’s flight logs rather than relying on barometric measurements or the built-in global navigation satellite system recordings from the atmospheric sensors.
Potential temperature Θ (K) is the temperature that an unsaturated parcel of dry air would have if it were brought adiabatically and reversibly from its initial state to a standard pressure level (typically 1000 hPa), as shown in Eqn 1. Because the difference between the potential temperature of unsaturated moist air and that of dry air remains small, no distinction needs to be made for most practical purposes (World Meteorological Organization 1966):
where R ÷ cP = 2 ÷ 7, R represents the ideal gas constant for dry air (8.314 J K−1 mol−1) and cp represents the specific heat capacity at constant pressure (29.14 kJ kmol−1 K−1). To determine the PBLH from the drone Θ profile, using the 1.5-theta method, we first calculate the mean Θ in the lowest 300 m of the profile (Θ300 m), as Θ varied little in range 0–300 m and it was expected that the PBLH would be significantly above 300-m altitude during the daytime in this location. The PBLH is then identified as the first altitude at which Θ = Θ300 m + 1.5 K (Nielsen-Gammon et al. 2008; Hu et al. 2010).
2.2. MP LiDAR sampling
The MP LiDAR used at One Tree Island (Droplet Measurement Technologies; https://www.dropletmeasurement.com/product/mini-mpl/) was located on the upper part of the beach in front of the main research station. The laser is green (532-nm wavelength), eye-safe and operating at a frequency of 2500 Hz. The integration time was 30 s and vertical resolution was 30 m as recommended by the manufacturer. We utilise data from both co-polarised and cross-polarised channels. The MP LiDAR scans were taken at 90, 45 and 0° relative to the horizon. Horizontal scans were used employed for calibration, and we use only the vertical scans for PBLH analysis in this work.
Several corrections must be applied to the MP LiDAR signal before proceeding, as outlined in Campbell et al. (2002). Firstly, the background signal and after-pulse effect must be subtracted. The background signal accounts for any ambient light at 532 nm, whereas the after-pulse signal arises from detector saturation due to the laser flash, at the very beginning of a sampling period. Raw MP LiDAR signals are also divided by an overlap function that accounts for the drop off in near-field signal due to the combination of a narrow receiver field of view and a wide transmitting aperture. The overlap range of MP LiDAR signals is typically ~5 km. Overlap and after-pulse calibrations were carried out routinely throughout the campaign period following the procedures outlined in Welton et al. (2000, 2002). The dead time correction, resulting from saturation caused by photon avalanche events, was unaltered from that supplied by the manufacturer.
The raw MP LiDAR signal P as a function of range r comprises contributions from aerosol scattering, Rayleigh scattering, background (mostly solar) photons at 532 nm, and instrumental noise:
where β denotes backscatter coefficients, σ denotes extinction coefficients, subscripts R and A indicate Rayleigh and aerosol scattering, NB denotes the 532-nm background atmospheric contribution and E relates to the laser energy. The raw MP LiDAR signal is a combination of co-polarised and cross-polarised return, calculated according to Córdoba-Jabonero et al. (2021) and Flynn et al. (2007):
The normalised relative backscatter (NRB) is calculated from the raw signal by subtracting NB and the after-pulse signal (A(r)) then dividing by the overlap function O(r) and finally multiplying by the square of the range (r2). Key sources of uncertainty associated with NRB calculation include the choice of after-pulse and overlap calibration functions and laser energy fluctuations (Welton and Campbell 2002). Overall uncertainty in the NRB retrieval is typically less than 5% (Welton et al. 2000).
2.3. MP LiDAR cloud filtering
To ensure we sampled the PBLH in clear-sky conditions, we implemented a cloud-filtering algorithm based on the raw LiDAR signals and a co-located all-sky cloud camera (Solmirus All Sky Imaging System M1v, https://solmirus.com/asis-m1v). To validate cloud detection from the MP LiDAR signals, we looked for cloud-masked pixels in a circular region with 5° radius from the centre of each all-sky camera image (Fig. 2). Given that the receiving field of view of the MP LiDAR is 220 mrad (0.01°), this results in a very conservatively strict cloud-flagging. The cloud-masking in the all-sky images were determined by the all-sky camera manufacturer’s (Solmirus) internal algorithm, with cloud-flagged pixels shown in white in the top row of Fig. 2.
Cloud detection using the all-sky camera and Mini-Micropulse (MP) LiDAR. Top row shows all-sky camera images from 27 February 2023 at OTI for scenes that are (a) predominantly cloud obscured, (b) slightly cloud obscured and (c) cloud-free. Colours indicate the ratio of green to blue pixels with cloud-flagged pixels in white. Red circles indicate the 5° radius region in the centre of each image, relevant for validating the MP LiDAR cloud-detection algorithm. Bottom row shows MP LiDAR raw count vertical profiles, and the gradient of this signal, at the same time as each camera image. Red dashed lines indicate flagging of a cloud-base in the MP LiDAR signal. Note that cloud-flagging was carried out through the depth of the troposphere (MP LiDAR signal 0–10-km altitude) but only the lowest 3 km of the profile is shown for clarity here.
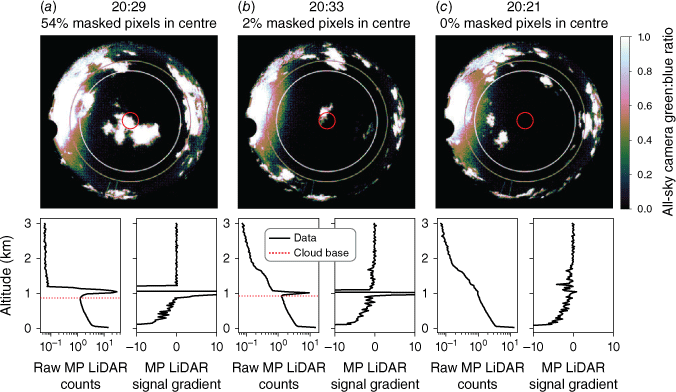
Here, we develop and test a threshold-based MP LiDAR detection algorithm that, as in Wang and Sassen (2001), is based on the raw LiDAR signal rather than the range-corrected signal or calibrated NRB. The algorithm begins by calculating the derivative of the entire raw LiDAR signal. The raw MP LiDAR signal typically decreases with altitude, and a cloud or aerosol layer base may be present when the signal slope increases with altitude (gradient becomes positive). Example vertical profiles of the raw MP LiDAR signal and gradient on 27 February 2023 are shown in the bottom panels of Fig. 2. To exclude single-layer noise spikes, we only flag a potential layer base if the gradient exceeds zero in three successive layers (over 90-m altitude). We then examine the characteristics of the signal and the gradient in the 20 altitude bins above each flagged layer base. Guided by threshold characteristics in Wang and Sassen (2001), we tuned the following threshold values by comparing to the cloud camera images. A cloud layer is flagged if (a) the layer’s maximum raw signal exceeds 0.4 counts μs−1 and the minimum gradient is less than −0.5 counts μs−1 m−1, (b) the layer peak’s raw signal is more than twice the raw signal at the base, and the altitude is below 4 km or (c) the layer’s peak’s raw signal is more than 1.2 times the raw signal at the base, and the altitude is above 4 km. Once a cloud is identified in a profile, the algorithm goes on to search the remainder of the profile and can retrieve multiple cloud layers in one profile. The cloud-flagging is sensitive to predominantly cloudy scenes such as Fig. 2a where >50% of the all-sky camera’s centre pixels are marked as cloud, and to scenes were as little as 2% of the centre pixels are cloud marked (Fig. 2b). Sky scenes with no cloud-marked pixels, such as Fig. 2c, do not result in a cloud detection in the MP LiDAR profile.
2.4. MP LiDAR PBLH calculation
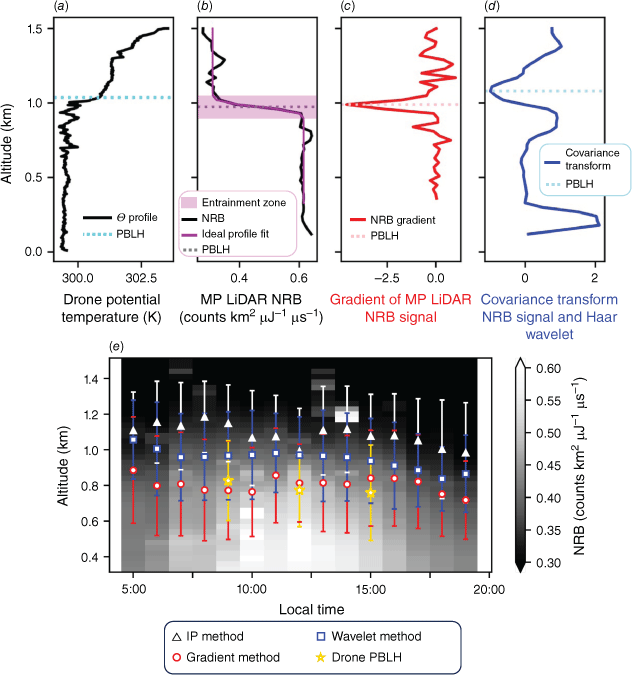
We used 30-min averaged MP LiDAR NRB profiles to calculate the PBLH, encompassing the time taken to complete a drone ascent and descent. The simplest method employed for calculating the PBLH from cloud-free MP LiDAR NRB profiles is the gradient method. The PBLHGrad was determined to be the altitude of the most negative NRB signal gradient. An example drone potential temperature profile, including the 1.5-theta PBLH, is shown in Fig. 3a. Alongside this, an example vertical NRB profile, taken on 6 March 2023 (Fig. 3b), shows the gradient of that signal, indicating the PBLH detection at the minimum value of the gradient. Signal-to-noise in MP LiDAR NRB profiles decreases with altitude, so to isolate the minimum gradient applicable to the PBLH rather than noise, we took the minimum gradient between 0- and 3-km altitude. As there are no sources of uncertainty other than those inherent to the NRB calculation, we take the gradient method PBLH uncertainty to be 5%, following the upper estimate of typical NRB uncertainty in Welton et al. (2000).
(a) An example potential temperature profile from the drone at midday on 6 March 2023, showing the planetary boundary layer height (PBLH) determined by the 1.5-theta method. (b) An example normalised relative backscatter (NRB) profile taken at the same time by the Mini-Micropulse (MP) LiDAR, showing the fitted ideal profile shape and associated ideal profile method-derived PBLH. (c) Gradient of the MP LiDAR NRB signal and associated gradient method PBLH. (d) Covariance transform of the Haar wavelet function and the NRB signal, showing the wavelet method PBLH. (e) Greyscale image showing the mean cloud-free MP LiDAR NRB in each daylight hour (local time) throughout the campaign. Overlayed are the campaign mean PBLH estimates from each MP LiDAR method. The means of all estimated drone PBLH values at 09:00, 12:00 and 15:00 hours are represented by yellow stars. Error bars are the standard deviations of the means.
The IP method aims to fit an idealised four-parameter equation for the shape of the NRB signal, following Steyn et al. (1999) and as outlined in Li et al. (2017) and Dang et al. (2019). The IP is given as follows:
The error function denoted by ε is defined in Dang et al. (2019). The fit parameter Zm is the PBLH and s is the thickness of the transition region between the boundary layer and the free troposphere (the entrainment zone). The fit parameters Bm and Bu refer to the backscatter below and above the entrainment zone, respectively. The standard error on the fit for parameter Zm is calculated and added in quadrature to the NRB uncertainty to produce the overall IP method PBLH uncertainty. The shape of B(z) is shown in magenta in Fig. 3b, where the IP function has been fitted to the measured NRB signal. The entrainment zone defined by s in Eqn 4 is indicated in Fig. 3b by the magenta-shaded region.
The wavelet method determines the PBLH by covariance transform between a wavelet profile and the LiDAR NRB profile. Here we use the Haar wavelet shape h (Gamage and Hagelberg 1993) and covariance transform w(s, b) (Brooks 2003):
where z is the profile altitude, s is the dilation of the wavelet shape and b is the translation of the wavelet. The lower and upper bounds of the LiDAR profile NRB(z) are given by z0 and z0 respectively. Although other wavelet shapes can be used, the Haar wavelet has been shown to be robust for PBLH detection in Baars et al. (2008), Dang et al. (2019) and Wang et al. (2021). The value of b when the minimum of w(a, b) is found, is taken as the PBLH. This relies on a suitable value of s, which physically represents the thickness of the entrainment zone, as for the IP method, and as indicated for an example NRB profile in Fig. 3b. On inspecting the NRB profiles, the entrainment zone was determined to typically be ~200 m thick, hence a value of s = 0.2 km is used throughout for wavelet method PBLH detection. We make a conservative estimate of the uncertainty of this approach by calculating the standard deviation of Haar wavelet PBLH values retrieved with s = 0.1, 0.2, 0.3 and 0.4 km. The standard error calculated from this is added in quadrature to the 5% NRB uncertainty to produce an overall wavelet method PBLH uncertainty. The shape of the covariance transform function applied to the Haar wavelet shape and the NRB profile at midday on 6 March 2023, is shown in Fig. 3c.
3.Results
3.1. Results overview
Fig. 3 illustrates the key aim of this work; the detection of the PBLH in drone and MP LiDAR vertical profiles. The profiles and PBLH retrievals are from midday on 6 March 2023. The Θ and NRB profiles are typical of those throughout the campaign, with the PBLH evident by inspection as both an increase in Θ, and decrease in NRB, ~1-km altitude. In this example, the three MP LiDAR methods agree within 100 m of each other and the drone 1.5-theta PBLH. An increase in Θ with altitude above the PBLH (Fig. 3a) indicates a stable boundary layer. To assess the atmospheric stability across the campaign, we calculate the mean Θ value in the layers 100 and 400 m thick, above the calculated 1.5 theta PBLH. Only 2% of the profiles show a Θ decrease in the 100 m above the PBLH. None show a Θ decrease on average over the 400 m above the PBLH. These results highlight the consistent stability of the boundary layer during the campaign.
The campaign average diurnal NRB profile is shown in Fig. 3b, between 0 and 1.5 km altitude. This represents the mean NRB vertical profile in each daylight hour of the day. We show campaign average results rather than daily PBLH evolution examples because the frequency of broken clouds over One Tree Island meant there were no completely clear days. Apart from some noise in the early afternoon, above 1 km, a consistent diurnal cycle emerges with backscatter increasing in magnitude and altitude throughout the morning, before decreasing in magnitude and altitude through the afternoon. Despite this, none of the MP LiDAR PBLH methods show strong variations in their diurnal cycle. No consistent increase in PBLH through the middle of the day is observed, when solar heating is strongest, indicating a lack of convective boundary layer development. This indicates that the boundary layer is well mixed and stable throughout the day. Previous boundary layer measurements in the region, at Heron Island (~30 km north-west of One Tree Island) in 2012 using radiosondes, found evidence of greater diurnal boundary layer variability (MacKellar et al. 2013) – variations in boundary layer structure therein were attributed to convection associated with the reef. The lack of PBLH diurnal variability over the campaign implies that the diurnal MP LiDAR backscatter variability in Fig. 3b is unlikely to be explained by vertical transport from the surface. Instead, the daytime aerosol enhancement may be caused by horizontal transport of aerosols into the sampling domain, possibly including aerosols regenerated from cloud droplet evaporation (Bott 1999).
The mean PBLH using the IP method is consistently higher than other MP LiDAR methods. The gradient method consistently produces the lowest mean PBLH values, whereas the wavelet method is in between. The overall campaign mean (±s.d.) PBLH values are 910 ± 200 m for the IP method, 860 ± 290 m for the wavelet method and 810 ± 260 m for the gradient method. No evidence of convective boundary layer development is observed in the mean drone PBLH values in Fig. 3b either, with the maximum PBLH at 09:00 hours (830 ± 190 m), followed by slight decreases at 12:00 hours (790 ± 170 m) and 15:00 hours (780 ± 240 m). The PBLH values here are within the range of summertime marine boundary layer heights reported at Heron Island in MacKellar et al. (2013) and McGowan et al. (2022).
3.2. Comparison of drone and MP LiDAR PBLH
Fig. 4a shows a timeseries of PBLH retrievals from the drone (data from both iMet sensors and both ascent and descent flights are shown at each sampling time) the MP LiDAR (gradient method), overlayed on the overall MP LiDAR backscatter timeseries. Data gaps, due to cloud filtering of the MP LiDAR results, are evident as white segments in the NRB timeseries and missing MP LiDAR gradient PBLH retrievals. The backscatter-derived PBLH from the gradient method is plotted as a continuous timeseries (as long as data are available), which indicates the high-frequency variability of the PBLH retrieval, and can be up to 200 m over a 2-h period. The timeseries shows frequent overlap between the MP LiDAR gradient method and the drone within the respective uncertainties. Broad temporal features are captured by each method, such as lower average PBLH values for 10–17 March than in the rest of the comparison period. Data from a weather station mounted at 10-m altitude on One Tree Island (Lufft GmbH WS800–UMB Smart Weather Sensor, data not shown) show that periods of lower PBLH correspond to low surface wind speed (typically <20 km h−1) from the northerly sector and high relative humidity (>75%). Periods of higher PBLH tend to occur with trade winds from the southerly and easterly sectors, often >20 km h−1 and relative humidity of 60–75%. These broad temporal characteristics of the timeseries agree between MP LiDAR PBLH methods.
(a) Timeseries of planetary boundary layer height (PBLH) estimates from the drone and Mini-Micropulse (MP) LiDAR (gradient method) throughout the campaign, overlayed on the MP LiDAR normalised relative backscatter (NRB) timeseries. (b), (c) and (d) Scatterplot comparisons of MP LiDAR v. drone PBLH estimates for gradient, IP and wavelet methods, respectively. Dashed lines indicate 1:1, solid lines are the linear fit to all data; all other colours in this figure correspond to measurement times 09:00, 12:00 and 15:00 hours, consistent with Fig. 3. Error bars for drone measurements are the standard deviation of the four PBLH retrievals in each timestep; error bars for MP LiDAR results are calculated as described in the Methods section.
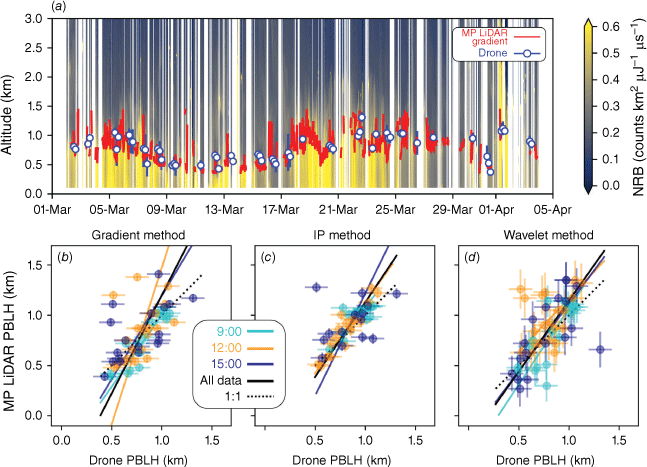
Here, we compare two distinctly different quantities as an indicator of PBLH: a thermodynamically derived measure and an aerosol backscatter-derived measure. These quantities may not necessarily be the same. Under decoupled boundary layer conditions, or in the presence of elevated aerosol pollution layers, for example, the interpretation of backscatter in relation to the thermodynamic PBLH is more complicated (Bohlmann et al. 2018; Alexander and Protat 2019). Nevertheless, Alexander and Protat (2019) and Bohlmann et al. (2018) also show that under clean marine conditions and when the boundary layer is well-mixed, the thermodynamic- and backscatter-derived PBLH will likely be similar. We use a statistical comparison of MP LiDAR PBLH methods compared to the drone 1.5-theta results to demonstrate the consistency of the similarity between the thermodynamic and backscatter-derived PBLH in the One Tree Island dataset. We used orthogonal distance regression (ODR) analysis, considering the relative uncertainties associated with the individual MP LiDAR methods and with averaging the four drone results at each sampling time. Fig. 4b–d show scatterplots with linear ODR fits for all data (black lines) and for each sampling hour (coloured lines), for the gradient, IP and wavelet methods respectively. Comparison data existed for 37 days, encompassing 111 discrete sampling times. Following the cloud filtering, 57 comparison points remain. The cloud filtering does not disproportionately remove data from any one sampling time, with each having a similar number of total comparison points: 18 for 09:00 hour, 21 for 12:00 hours and 18 for 15:00 hours. The uncertainties vary between MP LiDAR methods. The 5% uncertainty ascribed to the gradient method, ~40 m on average, is the lowest uncertainty of the three methods and just larger than the 30-m vertical resolution of the MP LiDAR. The uncertainty associated with the IP method is also low at ~6% (on average ~55 m). The uncertainty associated with the Haar wavelet method is much larger at ~18% (on average ~ 150 m).
The scatterplots show moderate scatter in each comparison. Considering the entire dataset, Pearson’s R coefficients are 0.68 for the IP method, 0.62 for the gradient method and 0.59 for the wavelet method. Considering all sampling times, R values range from 0.36 (wavelet method, 12:00 hours) to 0.92 (gradient method, 09:00 hours). The R values are consistently highest for the 09:00 hours comparison. No one MP LiDAR method has consistently higher correlation; however, the gradient and IP methods arguably show a tighter data density around the 1:1 line than the wavelet method. The gradient method’s overall R value is likely detrimentally influenced by five examples of the MP LiDAR result being much higher.
The ODR regression slopes (Fig. 4) are all greater than 1. This indicates that all MP LiDAR methods tend to locate the boundary layer lower than the drone at low altitude and higher than the drone at high altitude. For the whole data comparison, the slope is 1.9 for the gradient method, 1.5 for the IP method and 1.4 for the wavelet method. For the gradient and IP methods, the 09:00 hours comparison slope is closest to 1, with 12:00 and 15:00 hours comparison slopes being variable. The wavelet method shows the most consistent slope between sampling times, with range 1.1–1.5. Owing to the regression slopes all being >1, y-intercept values (not shown) for the ODR linear fits range are all negative. Here, we reiterate that the IP and gradient method data, apart from a few discrete poor performing examples, appear more closely clustered to the 1:1 line (Fig. 4b, c) than for the wavelet method (Fig. 4d), despite the wavelet method slopes typically being closer to 1. The higher slope values for IP and gradient methods are likely influenced these methods’ lower uncertainty compared to the wavelet method, boosting the relative uncertainty of the x-ordinate and making the slope steeper.
For the whole dataset, the NMB is −7.4% for the wavelet method, −6.5% for the IP method and only −1.1% for the gradient method. The NMB is negative for all methods and nearly all sampling times, indicating that the drone 1.5-theta PBLH value is on average lower than the MP LiDAR estimate. The generally good agreement between the drone and all MP LiDAR methods is indicated by the fact that the absolute value of the NMB for all comparisons except one (12:00 hours, wavelet method) is <10%, which means differences are typically <100 m.
4.Conclusions
This paper extends the work in Eckert et al. (2023) and Li et al. (2017) demonstrating that drones can provide a reliable method of sampling the boundary layer. Potential temperature profiles collected by the quadcopter drones were appropriate for the 1.5-theta method of determining PBLH, and in all cloud-free sampling times analysed, the PBLH found using this method was within the 1.5-km vertical sampling range. Given research interest in the complex dynamics associated with coral reefs and the marine boundary layer in the region (MacKellar et al. 2013; McGowan et al. 2022), our work highlights an important future role for drones in PBLH sampling. Drones have the substantial advantages over radiosondes of being reusable – a crucial factor in a marine national park – and being more freely able to move laterally to explore atmospheric dynamics around a reef system like Heron or One Tree Island.
The typical standard deviation of PBLH estimates from the four profiles was 14%. Determination of the PBLH using MP LiDAR at One Tree Island was limited by the frequent presence of stratiform marine clouds, with nearly 50% of the possible MP LiDAR points removed due to cloud. In cloud-free conditions, however, the three MP LiDAR PBLH retrieval methods were generally successful. Furthermore, the drone effectively measured the PBLH in fair conditions, but was limited by strong winds and rain showers.
Throughout the comparison period, the marine boundary layer was stable. Our results were consistent with the sampling domain being in clean, marine conditions, unpolluted by continental aerosols and free from consistent elevated aerosol layers above the boundary layer. This was evident from the consistent boundary layer stability and the similarity over the sampling period of the thermodynamically and backscatter-derived PBLH estimates. The wavelet method for determining PBLH from the MP LiDAR backscatter had the highest uncertainty because the entrainment zone thickness must be provided to the algorithm but is not known a priori. Although the ODR slopes for the wavelet method were more consistently close to 1 compared to the other methods, the NMB was typically larger. There was little difference between the gradient and IP methods, with each method having moderately strong correlation coefficients, steep ODR slopes, and low NMB compared to the drone results. Overall, statistical comparison of the drone PBLH values with the three MP LiDAR PBLH estimates demonstrated that the good agreement between the thermodynamically and backscatter-derived PBLH estimates in this environment were robust to MP LiDAR retrieval method, as well as sampling time and conditions.
Data availability
The raw MP LiDAR and drone potential temperature data from the One Tree Island measurement campaign used for calculating PBLH, as well as the data analysis code, are available in the Figshare repository, at DOI:10.26188/25333552, with CC BY 4.0 licensing.
Declaration of funding
This work was funded by the Reef Restoration and Adaptation Program: Cooling and Shading Subprogram. The Reef Restoration and Adaptation Program is funded by the partnership between the Australian Governments Reef Trust and the Great Barrier Reef Foundation.
Acknowledgements
We extend our deepest respect and recognition to the Gooreng Gooreng, Gurang, Bailai, and Taribelang Bunda people, traditional custodians of Great Barrier Reef Sea Country and One Tree Island. The authors also acknowledge Kim Monteforte, Stephen Childs and Mark Goolmeer who conducted most of the drone flights. R. Ryan acknowledges Adrian Doss for assistance with the all-sky camera images, and Claire Vincent for helpful discussions on boundary later meteorology.
References
Ainsworth TD, Heron SF, Ortiz JC, Mumby PJ, Grech A, Ogawa D, Eakin CM, Leggat W (2016) Climate change disables coral bleaching protection on the Great Barrier Reef. Science 352(6283), 338-342.
| Crossref | Google Scholar | PubMed |
Alexander S, Protat A (2019) Vertical profiling of aerosols with a combined Raman‐elastic backscatter LiDAR in the remote Southern Ocean marine boundary layer (43–66°S, 132–150°E). Journal of Geophysical Research: Atmospheres 124(22), 12107-12125.
| Crossref | Google Scholar |
Archer CL, Colle BA, Veron DL, Veron F, Sienkiewicz MJ (2016) On the predominance of unstable atmospheric conditions in the marine boundary layer offshore of the US northeastern coast. Journal of Geophysical Research: Atmospheres 121(15), 8869-8885.
| Crossref | Google Scholar |
Baars H, Ansmann A, Engelmann R, Althausen D (2008) Continuous monitoring of the boundary-layer top with LiDAR. Atmospheric Chemistry and Physics 8(23), 7281-7296.
| Crossref | Google Scholar |
Bohlmann S, Baars H, Radenz M, Engelmann R, Macke A (2018) Ship-borne aerosol profiling with LiDAR over the Atlantic Ocean: from pure marine conditions to complex dust–smoke mixtures. Atmospheric Chemistry and Physics 18(13), 9661-9679.
| Crossref | Google Scholar |
Bott A (1999) A numerical model of the cloud-topped planetary boundary layer: chemistry in marine stratus and the effects on aerosol particles. Atmospheric Environment 33(12), 1921-1936.
| Crossref | Google Scholar |
Brooks IM (2003) Finding boundary layer top: application of a wavelet covariance transform to LiDAR backscatter profiles. Journal of Atmospheric and Oceanic Technology 20(8), 1092-1105.
| Crossref | Google Scholar |
Campbell JR, Hlavka DL, Welton EJ, Flynn CJ, Turner DD, Spinhirne JD, Scott VS, Hwang IH (2002) Full-time, eye-safe cloud and aerosol LiDAR observation at atmospheric radiation measurement program sites: instruments and data processing. Journal of Atmospheric and Oceanic Technology 19(4), 431-442.
| Crossref | Google Scholar |
Chen Z, Schofield R, Rayner P, Zhang T, Liu C, Vincent C, Fiddes S, Ryan RG, Alroe J, Ristovski ZD (2019) Characterization of aerosols over the Great Barrier Reef: the influence of transported continental sources. Science of the Total Environment 690, 426-437.
| Crossref | Google Scholar | PubMed |
Córdoba-Jabonero C, Ansmann A, Jiménez C, Baars H, López-Cayuela M-Á, Engelmann R (2021) Experimental assessment of a micro-pulse LiDAR system in comparison with reference LiDAR measurements for aerosol optical properties retrieval. Atmospheric Measurement Techniques 14(7), 5225-5239.
| Crossref | Google Scholar |
Dang R, Yang Y, Hu X-M, Wang Z, Zhang S (2019) A review of techniques for diagnosing the atmospheric boundary layer height (ABLH) using aerosol LiDAR data. Remote Sensing 11(13), 1590.
| Crossref | Google Scholar |
de Arruda Moreira G, da Silva Lopes FJ, Guerrero-Rascado JL, Granados-Muñoz MJ, Bourayou R, Landulfo E (2014) Comparison between two algorithms based on different wavelets to obtain the Planetary Boundary Layer height. In ‘Proceedings Volume 9246, LiDAR Technologies, Techniques, and Measurements for Atmospheric Remote Sensing X’, 22–25 September 2014, Amsterdam, Netherlands. (Eds UN Singh, G Pappalardo) pp. 64–76. (SPIE Digital Library) 10.1117/12.2067352
Durre I, Vose RS, Wuertz DB (2006) Overview of the integrated global radiosonde archive. Journal of Climate 19(1), 53-68.
| Crossref | Google Scholar |
Eckert C, Monteforte KI, Harrison DP, Kelaher BP (2023) Exploring meteorological conditions and microscale temperature inversions above the Great Barrier Reef through drone-based measurements. Drones 7(12), 695.
| Crossref | Google Scholar |
Fiddes SL, Woodhouse MT, Utembe S, Schofield R, Alexander SP, Alroe J, Chambers SD, Chen Z, Cravigan L, Dunne E (2022) The contribution of coral-reef-derived dimethyl sulfide to aerosol burden over the Great Barrier Reef: a modelling study. Atmospheric Chemistry and Physics 22(4), 2419-2445.
| Crossref | Google Scholar |
Flynn CJ, Mendoza A, Zheng Y, Mathur S (2007) Novel polarization-sensitive micropulse LiDAR measurement technique. Optics Express 15(6), 2785-2790.
| Crossref | Google Scholar | PubMed |
Gamage N, Hagelberg C (1993) Detection and analysis of microfronts and associated coherent events using localized transforms. Journal of Atmospheric Sciences 50(5), 750-756.
| Crossref | Google Scholar |
Greatwood C, Richardson TS, Freer J, Thomas RM, MacKenzie AR, Brownlow R, Lowry D, Fisher RE, Nisbet EG (2017) Atmospheric sampling on Ascension Island using multirotor UAVs. Sensors 17(6), 1189.
| Crossref | Google Scholar | PubMed |
Harrison D, Baird M, Harrison L, Utembe S, Schofield R, Escobar Correa R, Mongin M, Rizwi F (2019) T14: Environmental modelling of large-scale solar radiation management. A report provided to the Australian Government by the Reef Restoration and Adaptation Program. (Australian Institute of Marine Science) Available at https://gbrrestoration.org/wp-content/uploads/2020/09/T14-Environmental-Modelling-of-Large-Scale-SRM_v3.03-3.pdf
Hayden K, Anlauf K, Hoff R, Strapp J, Bottenheim J, Wiebe H, Froude F, Martin J, Steyn D, McKendry I (1997) The vertical chemical and meteorological structure of the boundary layer in the Lower Fraser Valley during Pacific ‘93. Atmospheric Environment 31(14), 2089-2105.
| Crossref | Google Scholar |
Hennemuth B, Lammert A (2006) Determination of the atmospheric boundary layer height from radiosonde and LiDAR backscatter. Boundary-Layer Meteorology 120, 181-200.
| Crossref | Google Scholar |
Hernandez-Jaramillo DC, Harrison L, Kelaher B, Ristovski Z, Harrison DP (2023) Evaporative cooling does not prevent vertical dispersion of effervescent seawater aerosol for brightening clouds. Environmental Science & Technology 57, 20559-20570.
| Crossref | Google Scholar | PubMed |
Hernandez-Jaramillo D, Medcraft C, Braga RC, Butcherine P, Doss A, Kelaher B, Rosenfeld D, Harrison D (2024) New airborne research facility observes sensitivity of cumulus cloud microphysical properties to aerosol regime over the Great Barrier Reef. Environmental Science: Atmospheres 8, 861-871.
| Google Scholar |
Hu X-M, Sigler JM, Fuentes JD (2010) Variability of ozone in the marine boundary layer of the equatorial Pacific Ocean. Journal of Atmospheric Chemistry 66, 117-136.
| Crossref | Google Scholar |
Jones G, Curran M, Deschaseaux E, Omori Y, Tanimoto H, Swan H, Eyre B, Ivey J, McParland E, Gabric A (2018) The flux and emission of dimethylsulfide from the Great Barrier Reef region and potential influence on the climate of NE Australia. Journal of Geophysical Research: Atmospheres 123(24), 13,835-813,856.
| Crossref | Google Scholar |
Lewis JR, Welton EJ, Molod AM, Joseph E (2013) Improved boundary layer depth retrievals from MPLNET. Journal of Geophysical Research: Atmospheres 118(17), 9870-9879.
| Crossref | Google Scholar |
Li H, Yang Y, Hu XM, Huang Z, Wang G, Zhang B, Zhang T (2017) Evaluation of retrieval methods of daytime convective boundary layer height based on LiDAR data. Journal of Geophysical Research: Atmospheres 122(8), 4578-4593.
| Crossref | Google Scholar |
McGowan H, Lensky NG, Abir S, Saunders M (2022) Coral reef coupling to the atmospheric boundary layer through exchanges of heat, moisture, and momentum: case studies from tropical and desert fringing coral reefs. Frontiers in Marine Science 9, 900679.
| Crossref | Google Scholar |
MacKellar MC, McGowan HA, Phinn SR, Soderholm JS (2013) Observations of surface energy fluxes and boundary-layer structure over Heron Reef, Great Barrier Reef, Australia. Boundary-Layer Meteorology 146, 319-340.
| Crossref | Google Scholar |
Mentzel S, Nathan R, Noyes P, Brix KV, Moe SJ, Rohr JR, Verheyen J, Van den Brink PJ, Stauber J (2024) Evaluating the effects of climate change and chemical, physical, and biological stressors on nearshore coral reefs: a case study in the Great Barrier Reef, Australia. Integrated Environmental Assessment and Management 20(2), 401-418.
| Crossref | Google Scholar | PubMed |
Nielsen-Gammon JW, Powell CL, Mahoney MJ, Angevine WM, Senff C, White A, Berkowitz C, Doran C, Knupp K (2008) Multisensor estimation of mixing heights over a coastal city. Journal of Applied Meteorology and Climatology 47(1), 27-43.
| Crossref | Google Scholar |
Osibanjo O, Rappenglück B, Ahmad M, Jaimes-Palomera M, Rivera-Hernández O, Prieto-González R, Retama A (2022) Intercomparison of planetary boundary-layer height in Mexico City as retrieved by microwave radiometer, micro-pulse LiDAR and radiosondes. Atmospheric Research 271, 106088.
| Crossref | Google Scholar |
Shaw WJ, Berg LK, Debnath M, Deskos G, Draxl C, Ghate VP, Hasager CB, Kotamarthi R, Mirocha JD, Muradyan P, Pringle WJ, Turner DD, Wilczak JM (2022) Scientific challenges to characterizing the wind resource in the marine atmospheric boundary layer. Wind Energy Science 7(6), 2307-2334.
| Crossref | Google Scholar |
Skyllingstad ED, Vickers D, Mahrt L, Samelson R (2007) Effects of mesoscale sea-surface temperature fronts on the marine atmospheric boundary layer. Boundary-Layer Meteorology 123, 219-237.
| Crossref | Google Scholar |
Steyn DG, Baldi M, Hoff R (1999) The detection of mixed layer depth and entrainment zone thickness from LiDAR backscatter profiles. Journal of Atmospheric and Oceanic Technology 16(7), 953-959.
| Crossref | Google Scholar |
Stull RB (1988) ‘An introduction to boundary layer meteorology (Vol. 13).’ (Springer Science & Business Media) 10.1002/qj.49711548614
Su T, Li J, Li C, Xiang P, Lau AKH, Guo J, Yang D, Miao Y (2017) An intercomparison of long‐term planetary boundary layer heights retrieved from CALIPSO, ground‐based LiDAR, and radiosonde measurements over Hong Kong. Journal of Geophysical Research: Atmospheres 122(7), 3929-3943.
| Crossref | Google Scholar |
Sullivan PP, McWilliams JC (2010) Dynamics of winds and currents coupled to surface waves. Annual Review of Fluid Mechanics 42, 19-42.
| Crossref | Google Scholar |
Swan HB, Jones GB, Deschaseaux ES, Eyre BD (2017) Coral reef origins of atmospheric dimethylsulfide at Heron Island, southern Great Barrier Reef, Australia. Biogeosciences 14(1), 229-239.
| Crossref | Google Scholar |
Wang Z, Sassen K (2001) Cloud type and macrophysical property retrieval using multiple remote sensors. Journal of Applied Meteorology and Climatology 40(10), 1665-1682.
| Crossref | Google Scholar |
Wang Y-C, Wang S-H, Lewis JR, Chang S-C, Griffith SM (2021) Determining planetary boundary layer height by micro-pulse LiDAR with validation by UAV measurements. Aerosol and Air Quality Research 21(5), 200336.
| Crossref | Google Scholar |
Welton EJ, Campbell JR (2002) Micropulse LiDAR signals: uncertainty analysis. Journal of Atmospheric and Oceanic Technology 19(12), 2089-2094.
| Crossref | Google Scholar |
Welton EJ, Voss KJ, Gordon HR, Maring H, Smirnov A, Holben B, Schmid B, Livingston JM, Russell PB, Durkee PA (2000) Ground‐based LiDAR measurements of aerosols during ACE‐2: Instrument description, results, and comparisons with other ground‐based and airborne measurements. Tellus B 52(2), 636-651.
| Crossref | Google Scholar |
Welton EJ, Voss KJ, Quinn PK, Flatau PJ, Markowicz K, Campbell JR, Spinhirne JD, Gordon HR, Johnson JE (2002) Measurements of aerosol vertical profiles and optical properties during INDOEX 1999 using micropulse LiDARs. Journal of Geophysical Research: Atmospheres 107(D19), INX2 18-11-INX12 18-20.
| Crossref | Google Scholar |
Wood R (2012) Stratocumulus clouds. Monthly Weather Review 140(8), 2373-2423.
| Crossref | Google Scholar |
World Meteorological Organization (1966) International Meteorological Tables, WMO-No.188. TP. 94. (WMO) Available at https://library.wmo.int/viewer/59923?medianame=wmo_188e_#page=7&viewer=picture&o=download&n=0&q=

