The sensitivity of fire activity to interannual climate variability in Victoria, Australia
Sarah Harris A B C , Neville Nicholls A , Nigel Tapper A and Graham Mills AA School of Earth, Atmosphere, Environment, Monash University, Clayton, Vic., Australia.
B Fire and Emergency Management, Country Fire Authority, 8 Lakeside Drive, Burwood East, Vic. 3151, Australia.
C Corresponding author. Email: sarah.harris@cfa.vic.gov.au
Journal of Southern Hemisphere Earth Systems Science 69(1) 146-160 https://doi.org/10.1071/ES19008
Submitted: 14 December 2018 Accepted: 20 June 2019 Published: 11 June 2020
Journal Compilation © BoM 2019 Open Access CC BY-NC-ND
Abstract
Climate change is expected to have an impact on fire activity in many regions around the globe. The extent of this can only be determined by first establishing the relationship between climate and fire activity. This study relates observed changes in fire activity in Victoria to observed changes in antecedent and concurrent climate parameters – maximum temperature, rainfall and vapour pressure, using data for 1972–2014. A first-difference approach was adopted to estimate the amount by which the observed changes in the climate parameters would have altered the fire activity in the absence of other confounding effects. This study provides a method for examining the sensitivity of fire activity to changes in climate parameters without the need to consider the complex response of fuel dynamics to future climates and changes in fire regime or fire management. We used stepwise multiple-regression to determine the months whose climate parameters explained much of the variance in the total number of fires (TNF) and area burned in a fire season. The best performing fire–climate models explained almost two-thirds of the variation in year-to-year variability of fire activity. The significant explanatory ability of the fire–climate models established in this study reveals the combination of climate parameters that closely relates to the observed year-to-year changes in fire activity, and this may provide an additional valuable resource for fire-management planning. Further, we explored the role changes in climate have had on the trend in fire activity. Natural logarithm of area burned and mean fire size have not significantly increased over the study period, but the TNF has significantly increased. We find that the observed increase in maximum temperatures and decrease in rainfall account for 26% of the observed increase in TNF for the 1972–2014 period. Therefore, most of the upward trend found in fire numbers must be due to factors other than climate (i.e. changes in fire occurrence, reporting/recording, land and fire-management changes). Additionally, this study concludes that total area burned should have also increased significantly due to the observed changes in climate and that improved fire-management practices may be offsetting this expected increase in the area burned. Finally, using the relationship established in this study between fire numbers and climate parameters, we estimate that a 2°C increase in mean monthly maximum temperatures could be expected to lead to a 38% increase in fire numbers.
1 Introduction
There is a range of factors such as ignition source, weather, climate, fire history, fuel type, terrain, suppression effectiveness and fire management that influence the occurrence and size of bush fires (Bradstock et al. 2009). Of these, climate is considered a major contributing factor in seasonal to longer term patterns of bush-fire occurrence (Morehouse et al. 2006). This influence of climate on fire occurrence exists because fire–climate relationships are mediated through fuels (Bedia et al. 2015), either indirectly over a longer period by moderating fuel abundance and conditions (Meyn et al. 2007; Krawchuk and Moritz 2011) or directly over a shorter period through its effect on fire ignition and spread (Rothermel 1972; Urbieta et al. 2015). Understanding the fire–climate relationship for a region may help anticipate fire activity in the investigated area in the shorter term (seasonal) (Urbieta et al. 2015). Additionally, it may be used to explain future fire activity under a changing climate. Many studies using climate projections from global climate models, particularly through the influence of climate on fire weather, suggest that climate change is likely to increase fire frequency, severity (see Beer and Williams 1995; Stocks et al. 1998; Goldammer and Price 1998; Wotton et al. 2003; Cardosa et al. 2003; Brown et al. 2004; Flannigan et al. 2006, 2009; Lucas et al. 2007; Pitman et al. 2007; Westerling and Bryant 2008; Moritz et al. 2012; Bedel et al. 2013) and fire-season length (Jolly et al. 2015). However, a major review on the topic of climate change and fire response conducted by Flannigan et al. (2009) revealed that there is large variation in the response regionally, with some regions exhibiting a likely reduction in fire frequency and severity in future climates. Understanding the current fire–climate relationship of a fire-prone region is essential in order to assess the potential impacts that climate may exert in the future (Bedia et al. 2015). Quantifying the relationships between climate and fire activity may also improve our understanding of parameters that can be used for improving seasonal and longer term fire activity forecasts, which could result in improved planning and preparation and, therefore, more effective fire-management practices.
Fuel moisture is a critical determinant of fire activity as it controls the flammability of the fuel (Nolan et al. 2016). Unfortunately, long-term spatially coherent fuel moisture data are not currently available. Additionally, fuel structure, load and continuity are also critical variables for resulting fire behaviour (Gould and Cruz 2012) but consistent detailed long-term data sets are also lacking for these variables. Climate influences fuel moisture, continuity and load (Bedia et al. 2015), and long-term climate data sets are readily available and are, therefore, used in determining fire activity.
Many studies have tested the sensitivity of fire activity to changes in climate using a range of climate parameters, fire activity measures, averaging periods and methods. Some studies have found that the concurrent climate conditions are of most importance when estimating fire activity (e.g. Koutsias et al. 2013; Morton et al. 2013), whereas other studies have found antecedent climate to have a significant role in fire activity (e.g. Harris et al. 2008, 2014; Nicholls and Lucas 2007). Furthermore, studies have found the relationship with climate differs depending on the fire metric, such as area burned or numbers of fires (Harris et al. 2014), the size of the study area (Urbieta et al. 2015), vegetation types or bioregions (Keeley and Syphard 2016; Bradstock et al. 2014), major climate zones (Keeley and Syphard 2017) and also that the relationship may vary over time (Keeley and Syphard 2015; Higuera et al. 2015). These differences in results suggest that it is important that the fire–climate relationships are identified and applied regionally.
There are now many studies linking climate and fire and future trends for the western United States (Keeley and Syphard 2015, 2016, 2017; Abatzoglou and Williams 2016; Littell et al. 2016) and other regions globally (Pausas and Paula 2012; Koutsias et al. 2013; Turco et al. 2014; Bedia et al. 2015; Jolly et al. 2015), yet less has been done for the fire-prone state of Victoria, Australia. South-east Australia is one of the worst regions globally for socially disastrous fires (Gill et al. 2013; Gill and Cary 2012). Bush fires in the south-east Australian state of Victoria have contributed to over 67% of all bush fire–related deaths that have occurred in Australia over the last 110 years (Blanchi et al. 2014). Victoria has experienced some of the most destructive Australian fires in the last century, including Black Friday in 1939, Ash Wednesday in 1983 and more recently Black Saturday in 2009 that resulted in the loss of 173 human lives (Teague et al. 2010). A report by Hughes (2014) focusing on Victoria suggests that over the remainder of this century, the incidence and severity of bush fires is likely to significantly increase, resulting in bush-fire damage to infrastructure and loss of life, as well as increasing suppression costs. Unfortunately, this region lacks the quantitative analyses between past climate variations and fire activity to assess the role climate may have in changing fire activity. Some studies that have linked climate and fire activity include Harris et al. (2014) where relationships between antecedent and concurrent climate parameters with fire activity for the state of Victoria were identified. Bradstock et al. (2014) assessed trends in area burned with fire danger indicators for 32 bioregions of south-eastern Australia and found significant warming and drying contributed to changes in some regions. A global study by Bedia et al. (2015) using the Canadian Fire Weather Index as the climate parameter has also identified climate as a chief driver of total burned areas in eastern Australia. Additionally, there are many studies of how fire weather, not to be confused with fire activity, may change in south-east Australia in the future, including Jolly et al. (2015), Clarke et al. (2013), Pitman et al. (2007), Lucas et al. (2007), and Hennessy et al. (2005). A direct, multivariate empirical relationship between fire activity and climate parameters may potentially be the best method for assessing the effects of climate change on fire activity (Bedia et al. 2015), yet there is no multivariate model that combines observed climate variations to estimate fire activity for Victoria.
This study aims to address two research questions for the Victorian landscape:
How sensitive is fire activity to changes in interannual climate variability?
What contribution have the longer term changes in climate made to the changes in fire activity?
To address these questions, we investigate how fire activity, measured by the total number of fires (TNF), area burned and mean fire size, varies in response to a combination of antecedent and concurrent climate parameters. This is achieved using a first-difference approach to avoid the confounding influence of other factors that influence fire activity, such as long-term changes in land-management practices and by developing a model using stepwise multiple-regression to identify the climate parameters and periods with the greatest influence on fire activity for the period 1972–2014. Finally, maximum temperature, one of the parameters in the selected model for estimating the TNF, is used with a simple climate projection of an increase of 2°C in mean monthly maximum temperature to estimate what effect a trend in climate parameters might have on future fire activity in the absence of changes in other possible confounding effects, such as changes in land and fire management.
2 Study area
Victoria, located in the south-east of Australia (Fig. 1), is topographically and climatologically diverse (Bryant 2008). There are three broad climatic zones: southern and coastal areas that are relatively more temperate and moist, cool to cold alpine areas and semiarid plains to the west and northwest that are drier and warmer (Bryant 2008). Victoria is well known for its high-impact fires (Gill and Cary 2012). This is due to the combination of available fuel to burn, population residing within or on the edge of vegetated regions and the unique climate of the region. It experiences a ‘Mediterranean-like’ climate, with hot, dry summers and mild, wet winters (Lucas et al. 2007), and its topography allows hot, very dry continental air to be advected over the state ahead of the dry cold fronts that are a feature of its summertime climate. These conditions can be further exacerbated by periodic drought (Lucas et al. 2007).
|
3 Data and methods
3.1 Fire activity data
The Department of Environment, Land, Water and Planning (DELWP) is responsible for the management of fires on public land in Victoria. DELWP maintain a data set of all reported bush-fire ignitions and areas burned since 1972. This data set includes information such as start date, latitude and longitude at the point of ignition (or first reported position) for all fires reported to DELWP in Victoria. Only ignitions that were classed as ‘Good Quality’ (i.e. recorded information was consistent and within Victoria) by Phan and Kilinc (2015) were included in the analyses. All fires classed as being caused by a ‘prescribed burn’ (also known as planned burn, burning off or fuel-hazard reduction burn) were excluded to restrict the analysis to fires commonly known as ‘wildfires’ or ‘bush fires’. Of these ~50% were caused by lightning with the remainder caused by humans or categorised as unknown.
The data were sorted into the monthly number of fires for the period between July 1972 and December 2014. To analyse lag relationships between fire activity and climate parameters, the fire activity data were grouped into ‘fire seasons’. A fire season in this study was defined as the period from November to March, as 85% of the number of fires occur in this period, resulting in over 95% of the area burned. Therefore, the first fire season in this study is November 1972 to March 1973 and the last fire season is November 2013 to March 2014. There is no single fire metric that fully explains ‘fire activity’. We have selected a number of fires and total area burned each season from the data base and from these calculated the mean fire size for each fire season. The time series of area burned and mean fire season is strongly skewed by a few years having more than 100 000 ha burned. Therefore, the natural logarithms of total area burned and mean fire sizes each year were calculated to reduce the effect of skewness on the subsequent analyses. After natural logarithm transformation, the total area burned (lnTAB), mean fire size (lnMFS) and the TNF data passed a Shapiro–Wilk goodness-of-fit test (>0.05) with normal quantile–quantile (QQ) plots used to assess the distribution of the data.
Ordinary least square (OLS) regression was used to estimate the trend in TNF, lnTAB and lnMFS from 1972–73 to 2013–14. This provided the total change and the percentage change in fire activity during the study period. The calculation of trend is sensitive to the choice of start and end dates of the calculation (Clarke et al. 2013). We tested the robustness of the trend in a similar approach to Clarke et al. (2013), with a simple sensitivity test by changing the start and end dates by 1, 5 and 10 years. Robustness of the lnTAB and lnMFS trends was not further tested, as the observed trends in these measures of fire activity were not statistically significant.
3.2 Climate data
Climate data for this study were derived from the Australian Water Availability Project (AWAP) data set. The development and reliability of the AWAP data are well documented (Jones et al. 2009), and this data set has been found to be suitable for regional scale analysis (King et al. 2012). The gridded daily data include daily maximum (MaxT) and minimum (MinT) temperature, total precipitation (Rain) and vapour pressure at 0900 (VP09) and 1500 hours (VP15). The earliest date for which all five climate parameters are available is January 1971. The data have a resolution of 0.058° latitude by 0.058° longitude (~5 × 5 km2), with a positional accuracy of 0.01° (~1 km) or better and were provided by the Bureau of Meteorology.
Previous work by Harris et al. (2014) established that MinT and VP09 had a weaker relationship with fire activity than the other AWAP climate parameters, and these were, therefore, not included in the following analyses. From the gridded AWAP data set, monthly total rainfall and monthly mean MaxT and VP15 were calculated as 1-month averages and as 3-month running means for July 1972–March 2014 (to match the extent of the fire activity data set including preceding months). The climate data were spatially averaged across Victoria. Although climate varies substantially across the state of Victoria, climate anomalies tend to show considerable spatial coherence across Australia, so large-scale (state-wide) spatial averages can be useful (see Harris et al. 2016). Previous work by Harris et al. (2014) demonstrated that the months with the strongest relationship between climate parameters and fire activity existed between the July preceding the fire season and extended until February in the following year (during the fire season). Therefore, only these months were included in the analyses.
The 1- and 3-monthly climate parameters were each related to the TNF and were found to be comparable in the strengths and directions of their relationships, although the 3-monthly correlation coefficients with the fire metrics were, in most cases, stronger than those for individual months. Thus, we hereafter focus on fire response to 3-monthly patterns of climate parameters. Therefore, the 3-monthly data set extends from July (3-monthly mean VP15, MaxT and 3-monthly mean of total rain June–August) 1972 to February (3-monthly mean VP15, MaxT and 3-monthly mean of total rain January–March) 2014.
All of the 3-monthly averages of the climate variables were tested to determine if they were normally distributed using Shapiro–Wilk goodness-of-fit test. All were normally distributed except rain in December (3-month mean November–January), January (3-month mean December-February) and February (3-month mean January–March) and VP15 in January (3-month mean December–February). The independent variables in regression analyses do not need to be normally distributed; therefore, these climate parameters were still considered in the analyses. Finally, to estimate the change in each climate parameter from the start to the end of the study period (July 1972–February 2014) OLS regression was used.
3.3 Regression analysis
A first-difference approach was used to estimate the contribution of change in fire activity each fire season as a result of change in the 3-monthly climate parameters. This method removes the effects of the trends in the fire activity and climate parameter time series by calculating first differences of the parameters (i.e. year-to-year changes in each variable), hence removing issues around autocorrelation in time series data (Urbieta et al. 2015). Furthermore, this method reduces the confounding influence of long-term variations in land and fire management, with such factors appearing as noise around the relationships between the year-to-year changes in fire activity and climate parameters (Nicholls 1997). Bedia et al. (2015) explain that the main assumption behind the application of this method is that other factors affecting fire activity (e.g. land use, fire management and population growth) have much smaller year-to-year changes than climate; therefore, their influence on fire activity is minimised when using the first-difference approach. Studies that have used this approach include Nicholls (1997, 2009), Lobell and Field (2007) and studies focusing on fire using this approach include Trouet et al. (2009), Turco et al. (2014), Bedia et al. (2015), and Urbieta et al. (2015).
Regression analysis was used to determine which of the climate parameters have the strongest contribution to fire activity. A stepwise regression analysis was performed relating the year-to-year change in TNF (δTNF), year-to-year change in natural logarithm of area burned (δlnTAB) (ha) and year-to-year change in natural logarithm of mean fire size (δlnMFS) (ha) to the year-to-year changes in 3-month climate parameters (δVP15, δMaxT and δRain). The intercept was forced through the origin to remove a trend effect (similar to Nicholls 1997, 2009). To ensure no multicollinearity existed in the model, the correlation coefficients between the climate parameters included in the final fire–climate models were cross-checked with each other and none were found to have a correlation coefficient greater than 0.60. Multicollinearity was further tested in the statistical models using the variance inflation factor with a range between 1 and 1.2 indicating very little of the adjusted r-square due to collinearity (Keeley and Syphard 2017).
In a similar approach to Urbieta et al. (2015) we tested combinations of all possible climate parameters, maintaining those that were statistically significant (P < 0.05) and that added to the variance explained of the δTNF, δlnTAB and δlnMFS. Goodness of fit of the models was assessed by maximum log-likelihood explained variance (adjusted r-squared) and by examining the model residuals (plots of predicted vs standardised residuals). Finally, resulting models for δTNF, δlnTAB and δlnMFS were compared using Akaike’s information criterion (AIC) (Akaike 1974). The model satisfying statistical tests and with the minimum AIC was selected as the ‘best model’. Only the results from the best model are presented in this paper. The stepwise regression was conducted using SPSS statistics software (SPSS Inc v22.0); all other statistical tests were conducted using the Python package – Statsmodel v0.6.1 (http://statsmodels.sourceforge.net/, accessed 22 April 2020).
4 Results
4.1 Historical variability and trends
There is large interannual variability in the TNF that occur each fire season although the average number of fires has been increasing (Fig. 2). For the study period of 1972–73 to 2013–14 the mean annual number of fires is 353, with a standard deviation (SD) of 182. The maximum annual number of fires is 805 (in 1997–98) and the minimum number of fires is 65 (in 2010–11). These maximum and minimum periods in fire occurrence correspond to ENSO phases with a strong El Niño event in 1997 and a strong La Niña in 2010–11 (Bureau of Meteorology 2012). From 1972–73 to 2013–14, there is a mean increase of 330 fires during the fire season (November to March); this represents a 171% increase above the OLS calculated TNF of 192 at the start of the period of study (1972–73). Results testing different start and end fire seasons (to overcome concerns regarding OLS sensitivity to the start and end date) all reveal an increase in trend, although this ranges from an increase of 85% to an increase of 245% in TNF (see Table 1).

|

|
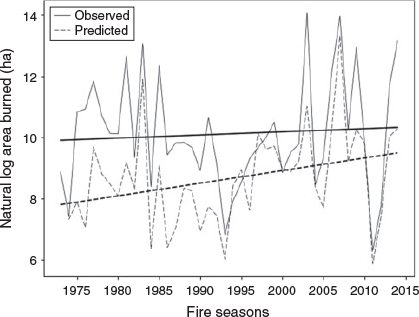
There is also large interannual variability in area burned each fire season (Fig. 3a). Fire seasons with over 100 000 ha burned include 1976–77, 1980–81, 1982–83, 1984–85, 2002–03, 2006–07, 2008–09, 2012–13 and 2013–14 with 2002–03 and 2006–07 burning over 1 000 000 ha. The seasons with the least area burned (<1000 ha burned) include 1992–93 and 2010–11. Linear trends were not analysed for area burned because the data are not normally distributed. The natural logarithm of area burned (ha) was calculated and is shown in Fig. 4. The slight upward trend of 4% in natural logarithm of area burned for the study period is not statistically significant.

|
|
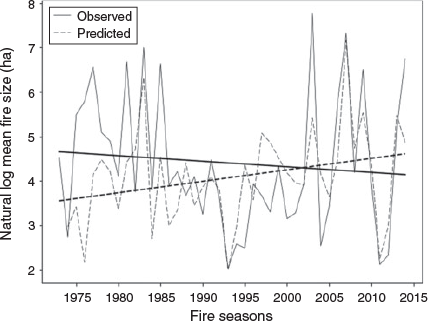
Additionally, there is also large interannual variability in mean fire size each fire season (Fig. 3b). There were 8 years that had a mean fire size over 500 ha; these include 1976–77, 1980–81, 1982–83, 1984–85, 2002–03, 2006–07, 2008–09 and 2013–14. The maximum mean fire size occurred in 2002–03 (2387 ha) and the minimum occurred in 1992–93 (7.6 ha). Linear trends for mean fire size were not analysed because the data are not normally distributed. The natural logarithm of mean fire size was calculated and is shown in Fig. 5. There is a slight downward trend of 11% for the study period although this is not statistically significant. This reduction is consistent with the substantial increase in number of fires and the only small increase in total area burned.
|
The trends and variability in climate parameters differ for the different seasons – there has been a greater change in each of the climate parameters in spring as compared with summer or winter for the study period (matching period to the fire seasons 1972–2014) (Table 2). The maximum temperature (MaxT) in spring has increased by 1.40°C compared to 0.87°C in summer and 0.50°C in winter with the greatest variability in summer (SD = 1.19°C). This study found that the vapour pressure at 1500 hours (VP15) has not only the greatest variability in summer (SD = 1.0 hPa) but also spring (SD = 1.02 hPa) and has decreased by 0.58 hPa in spring compared to a decrease of 0.20 hPa in summer and an increase of 0.02 hPa in winter. Rainfall, which has the largest variability in spring (SD = 19 mm), has decreased by 14 mm in spring, increased by 6 mm in summer and decreased by 5 mm in winter. Rainfall has the greatest percentage change over the study period amongst the climate parameters, followed by maximum temperature and finally vapour pressure. Using OLS regression, many of these trends are not statistically significant, with the exception of maximum temperatures from September to December (see Table 2). These trends agree with a study by Murphy and Timbal (2008) who found an increase in daily maximum temperature for south-east of Australia (for a different period) and a decrease in rainfall. Similarly, many of the trends found by Murphy and Timbal (2008) were not statistically significant with the exception of the annual means and the autumn period.
4.2 Fire activity and individual climate parameters
Year-to-year change in TNF (δTNF) is significantly correlated with the year-to-year change in all three climate parameters (δMaxT, δVP15 and δRain), with differing strengths for different antecedent and concurrent months (Table 3). The change in TNF in each fire season is significantly correlated with the change in precipitation for all months (3-month mean of total monthly Rain), with the two most strongly related months of precipitation being November (3-month mean October–December) (r = −0.63, n = 41, P < 0.05) and January (3-month mean December–February) (r = −0.60, n = 41, P < 0.05). The change in 1500 hours vapour pressure is significantly correlated with the change in TNF for all months and most strongly correlated in August (3-month mean July–September) (r = −0.56, n = 41, P < 0.05) and September (3-month mean August–October) (r = −0.58, n = 41, P < 0.05). The change in TNF is not significantly correlated with the change in maximum temperature in July (3-month mean June-August), August (3-month mean July–September) or September (3-month mean August–October). However, maximum temperature is strongly (and significantly) correlated in November (3-month mean October–December) (r = 0.58, n = 41, P < 0.05) and January (3-month mean December–February) (r = 0.56, n = 41, P < 0.05).
The year-to-year change in natural logarithm of area burned (ha) is significantly correlated with all climate parameters for all months with the exception of vapour pressure in February (3-month mean January–March). Overall the natural logarithm of area burned is most strongly correlated with the change in vapour pressure particularly in September, October and November (r = 0.63, 0.65 and 0.67 respectively n = 41, P < 0.05). The change in precipitation is most significantly correlated with the change in natural logarithm of area burned (ha) in November (3-month mean October–December) (r = −0.54, n = 41, P < 0.05) and December (3-month mean November–January) (r = −0.54, n = 41, P < 0.05). Finally, change in natural logarithm of area burned (ha) is most strongly correlated with maximum temperature in January (r = 0.54, n = 41, P < 0.05).
The strongest correlation between year-to-year change in natural logarithm of mean fire size (ha) and the climate parameters is with vapour pressure from September to December with the strongest correlations with vapour pressure in October and November (3-month mean) (r = −0.59 and −0.60 respectively n = 41, P < 0.05). The only months not statistically significant between natural logarithm of mean fire size and vapour pressure are January and February. Precipitation is statistically significant for all months except February and is most strongly correlated in September (r = −0.44, n = 41, P < 0.05). Maximum temperature is also statically significantly related to logarithm of mean fire size for all months except August, November and December and is most strongly related in October (3-month mean) (r = 0.40, n = 41, P < 0.05).
4.3 Fire–climate models
The regression model for change in number of fires each fire season (δTNF) is shown in Eqn 1, in natural logarithm of area burned (δlnTAB) in Eqn 2 and in natural logarithm of mean fire size (δlnMFS) in Eqn 3. The δTNF model has an adjusted r-squared of 0.66, that is the model accounts for ~two-thirds of the variability in δTNF. The δlnTAB model has an adjusted r-square of 0.61. The δlnMFS model accounts for even less than the other models with an adjusted r-square of 0.43. In our stepwise multiple linear regression analysis, we find that all included climate parameters are significant (P < 0.05).
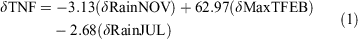
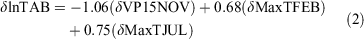
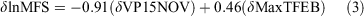
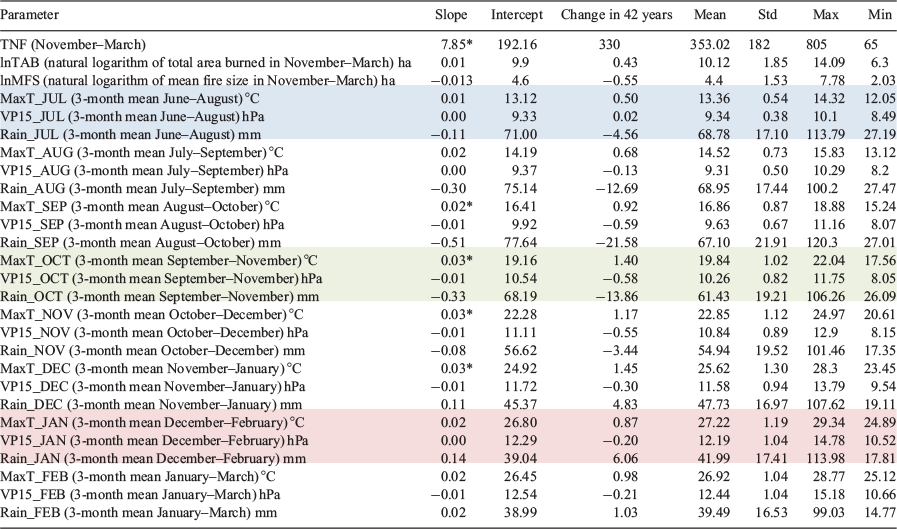
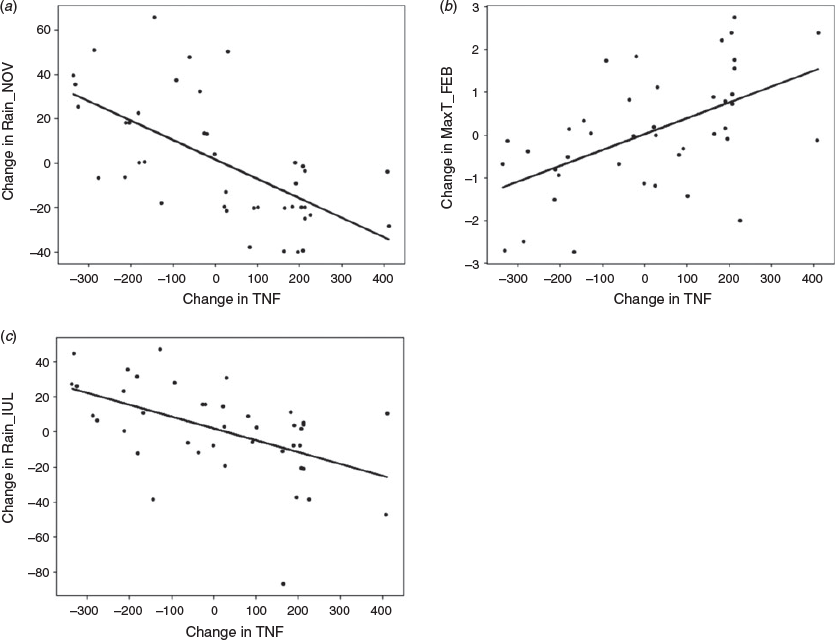
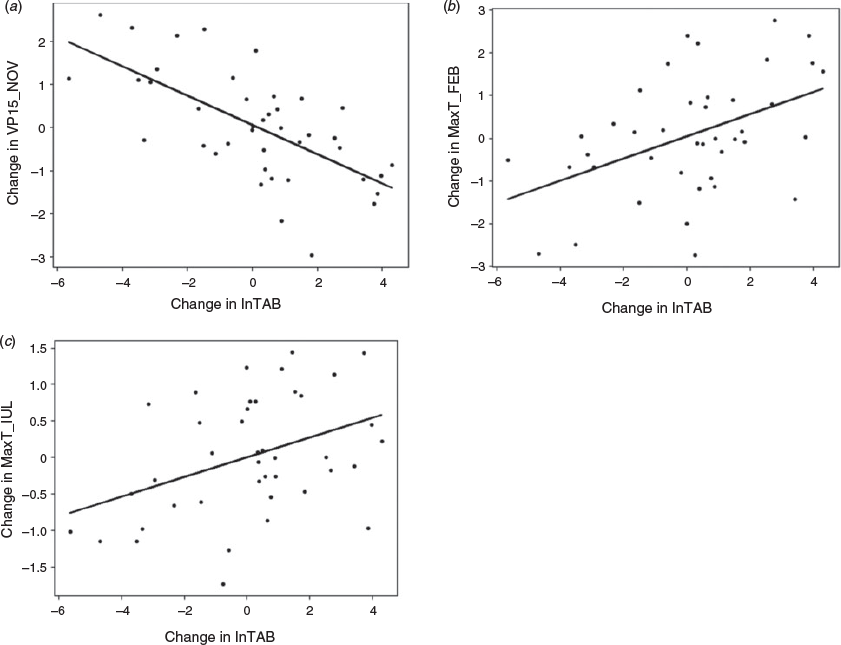
The climate parameters included in the δTNF model are the change in November rainfall (δRainNOV) (3-month mean October–December), change in February maximum temperature (δMaxTFEB) (3-month mean January–March) and change in July rainfall (δRainJUL) (3-month mean June-August) (Table 4). The climate parameters included in the δlnTAB model are the change in November vapour pressure (δVP15NOV) (3-month mean October–December), change in February maximum temperature (δMaxTFEB) (3-month mean January–March) and change in July maximum temperature (δMaxTJUL) (3-month mean June–August) (Table 5). The climate parameters included in the δlnMFS model include two parameters, both of which were included in the δlnTAB model; change in November vapour pressure (δVP15NOV) (3-month mean October–December) and change in February maximum temperature (δMaxTFEB) (3-month mean January–March) (Table 6). Scatterplots between the climate parameters included in each model with the relevant fire metric are shown in Figs 6–8. The climate parameters included in all three models indicate the importance of rainfall and dry air preceding a fire season and also rainfall and maximum temperature during the fire season. All fire metrics have the February maximum temperature included in the model and an indicator of moisture in spring (either rain or vapour pressure). However, δTNF includes rainfall from July, whereas for area burned maximum temperature in July is included. Change in natural logarithm of area burned is most strongly influenced by change in vapour pressure where there are no vapour pressure parameters included in the δTNF model; this is instead most strongly controlled by change in maximum temperature in February.
The coefficients for each of the climate parameters in Tables 4–6 indicates the mean change expected in δTNF, δlnTAB and δlnMFS respectively given a one-unit change in the value of the climate variable, if all other climate parameters in the model are fixed. For example, we could expect an increase of 63 fires in the following season and an increase of 0.68 (ha) natural logarithm of area burned for every 1°C increase in δMaxTFEB (3-month mean January–March), assuming that all other climate parameters in the model are fixed. Additionally, a decrease of 1.06 natural logarithm of area burned can be expected for every 1 hPa increase in vapour pressure in November (3-month mean October–November).
4.4 Predicting year-to-year variability in fire activity
The ability of the regression model to reproduce the variations in observed TNF is shown in Fig. 2. Using the observed TNF (of 76) in 1972–73 fire season, we then use Eqn 1 with the substituted year-to-year change in each climate parameter to calculate the following year’s TNF, then adding each year’s predicted TNF up to 2013–14. Because the first year has a low TNF and the prediction is even lower (due to a high rainfall amount), the initial predicted value is negative; this then influences the subsequent values. However, this does not influence the variability and trends in the predicted values. The regression model closely reproduces the variations in observed TNF. Figure 2 also highlights that climate is not the dominant factor in the upward trend of TNF, as the observed trend is substantially larger than that predicted from the climate variables.
A similar approach was taken to reproduce the variations in observed natural logarithm of area burned (Fig. 4). Using the observed lnTAB (of 8.87) in 1972–73 fire season we then use Eqn 2 with the substituted year-to-year change in each climate parameter to calculate the following year’s lnTAB, then adding each year’s predicted lnTAB up to 2013–14. The observed change in lnTAB over the study period is 4.3%, which is not statistically significant (P = 0.67), whereas the predicted upward trend is 25% and is statistically significant (P = 0.03). The peaks and troughs are well matched but the observed and modelled magnitude for some years varies.
The same approach was taken to reproduce the variations in observed natural logarithm of mean fire size (Fig. 5). Using the observed lnMFS (of 4.53) in 1972–73 fire season, we then use Eqn 3 with the substituted year-to-year change in each climate parameter to calculate the following year’s lnMFS, then adding each year’s predicted lnMFS up to 2013–14. The observed change in lnMFS over the study period is an 11% decrease, which is not statistically significant (P = 0.67), whereas the predicted upward trend is 30% (P = 0.07). The peaks and troughs are well matched in some years, particularly the last 10 years; however, the initial 10 years of the study period are not well predicted. This may suggest that mean fire size is more difficult to predict using these variables, although there are other factors to consider.
4.5 Trends and estimated changes in total number of fires
TNF has a significant upward trend so this was further analysed to assess the contribution climate makes to this upward trend. This analysis is not conducted for area burned or mean fire size as the observed trends were not statistically significant for these two fire activity measures. Substituting the 1972–2014 trends (listed in Table 2) in the three climate parameters (δRainNOV = −3.44 mm, δMaxTFEB = 0.98°C and δRainJUL = −4.56 mm) in Eqn 1 gives an estimate of TNF due to the climate trends. Eqn 1 gives a mean estimate of 85 additional fires due to the climate trends, that is, a 44% increase in the TNF due to climate (from the 1972 to 73 mean of TNF 192); this accounts for 26% of the total observed increase in TNF (total observed change in study period of 330 fires – see Table 2).
The separate effects of each climate parameter on the change in TNF can also be estimated from the regression results in Eqn 1 and Table 4. February maximum temperature (3-month mean January–March) resulted in the largest increase in TNF (62). This climate parameter is followed by the decrease in rainfall in July (3-month mean June-August) (12). The smaller decrease in rainfall in November (3-month mean October–December) further contributed to the increase in number of fires (11).
The individual influence of the warming in February (3-month mean January–March) maximum temperature (of 0.98°C over 42 years, P = 0.08) contributed, by itself, to 62 extra fires, which is almost 19% of the total increase observed in fire numbers during the fire season from 1972 to 2014 (total change in TNF is equal to 330). This is an increase, by itself, of 32% over the TNF occurring, on average, from the start of this period (the mean number of fires at the start of this period 192 (see Table 2)). If the relationship between the TNF and February (3-month mean January–March) maximum temperature is assumed to remain constant; for each degree Celsius increase in February (3-month mean January–March) maximum temperatures, 63 additional fires can be expected.
The best model for the δTNF fire–climate relationship established in this study was then used with a simple climate projection to estimate what effect a trend in climate parameters might have on future fire activity in the absence of changes in other possible confounding effects such as future changes in land and fire management. In this study we use a change of 2°C to estimate changes in the numbers of fires. This projection was chosen based on the results of Webb and Hennessy (2015) who presented projections of future climate parameters for different Australian cities. Webb and Hennessy (2015) estimate the annual projection in temperature change for Melbourne in 2090 ranges from a median of 1.5°C using an intermediate emissions scenario for greenhouse gases and aerosols to a median of 3°C using a high-emission scenario for greenhouse gases and aerosols. A 2°C increase in year-to-year February (3-month mean January–March) maximum temperature would lead to an additional 126 fires (i.e. an additional 38% increase in the number of fires typical of the period 1972–2014), if the relationship remains unchanged and other factors are held constant.
5 Discussion
To be able to project the impact of climate change on fire activity it is essential to determine the influence of variability and change in climate on fires in the past (Bowman et al. 2014; Moritz et al. 2014). However, attributing change in fires to climate is difficult due to the role of confounding factors that affect fire–climate relationships (Cramer et al. 2014; Urbieta et al. 2015). Urbieta et al. (2015) and Littell et al. (2009) highlight that it is important when using long-term data series for the analysis of fire–climate relationships for studies to use proper analytical techniques or to consider the role of other fire-drivers such as fuels, landscape, land use and fire management. However, relating the relative (year-to-year) changes in fires to year-to-year changes in climate parameters removes some of the confounding effects of long-term changes, thereby allowing a more accurate estimate of the effect of climate on fire activity. The results in this study indicate that 26% of the observed increase in fire activity (TNF) could be attributed to the changes in climate over the same period, holding other factors constant. Therefore, climate is not the dominant factor in the increase in TNF in Victoria. Other factors that may be influencing the increase in TNF could be changes in land and fire-management practices, a change in fire reporting methods or accuracy, frequency and area of dry lightning storms (Veraverbeke et al. 2017) or other trends in ignitions sources and possibly another climate variable not considered here. Further work should consider these and other known climate parameters related to fire activity when trying to explain the full extent of the upward trend. Nevertheless, our historical analysis confirms that climate change will increase the likelihood for further increases in Victorian fire activity, at least with number of fires, with the increase in maximum temperature playing the largest role. However longer time periods bring greater uncertainty, because climate change may significantly shift fuel properties through changes in species’ distributions and forest structure (Chen et al. 2011; Keane et al. 2013; Keeley and Syphard 2015), and any increase in fire activity may also decrease subsequent fire intensity through the reduction in fuels (Batllori et al. 2013; Keeley and Syphard 2015). As well, changes in fire and land management would also impact on fire activity. Regardless, historical relationships between fire and climate are one of the few tools we have for understanding future climate change impacts on fire regimes (McKenzie et al. 2004; Safford et al. 2012; Keeley and Syphard 2015). Predicting and understanding these changes is a critical element underpinning the future management of fire-prone and adapted landscapes.
The fire–climate relationship documented here supports models published elsewhere showing that climate affects fires, and many studies suggest this relationship is through the effect climate has on fuels through changing fuel conditions and abundance (see Keeley and Syphard 2015, 2016, 2017; Littell et al. 2009; Batllori et al. 2013; Nolan et al. 2016; Williamson et al. 2016). This study found that maximum temperature, vapour pressure and precipitation are significantly influencing the fire activity in a fire season, probably due to their effect on the fuel moisture content (drying of the fuel and therefore flammability) in the months before and during a fire season. The fire–climate models for each fire metric all include maximum temperature in summer. However, there are differences in the climate parameters that relate to the number of fires and to area burned. TNF is more strongly influenced by rainfall in the months at the beginning of the fire season, particularly November, whereas it is vapour pressure in spring and summer that influence the total area burned. These findings are consistent with Harris et al. (2014) who used similar data sets. The combination of climate parameters in both models is able to explain two-thirds of the variation in changes to fire activity. The explanation of year-to-year change in fire activity in our model is comparable to and often better than fire–climate models found elsewhere, such as those of Keeley and Syphard (2015), Higuera et al. (2015), Urbieta et al. (2015) and Keeley and Syphard (2017), although the explained variance for fires in the Mediterranean is slightly higher (Turco et al. 2014). The ability of our model using a combination of climate parameters to capture the observed peaks and troughs reveals a potentially useful tool for seasonal predictions of fire activity. The variation in year-to-year burning not explained by the model may be due to factors such as long-term drought, fire weather, human ignitions and suppression efforts (Keeley and Syphard 2017) and changes in lightning ignitions (Bradstock et al. 2014).
To improve on the relationships established in this study a number of further analyses should be conducted. For example, future work should consider separating analyses by vegetation type, which might change the relationship between fire activity and climate parameters. A study by Keeley and Syphard (2015) did analyse the fire–climate relationship separately for different vegetation types and found differences existed depending on the vegetation type. Bradstock et al. (2014) also found area burned explained by fire danger indicators varied by bioregions in south-eastern Australia, whereas a study by Urbieta et al. (2015) found that the strength of the relationship between climate parameters and fire metrics varied depending on the study area size due to vegetation, although the overall trend was the same. Keeley and Syphard (2016) point out that the inclusion of fuel structure is critical to fully capture accurate relationships with climate. Further work by Keeley and Syphard (2017) found that relationships also differed when analyses were conducted separately for each major climate division. Unfortunately, the current study was limited by a fire activity data set in which all fires could not be reliably attributed to a particular vegetation type or climate zone. In future this may be resolved when the time series of remotely sensed data increases. A more accurate and longer time series of fire activity data would also alleviate the concerns of Doerr and Santin (2016) about insufficient data to predict future fire activity.
A statistically significant upward trend in the TNF has occurred in Victoria, over the study period. However, only a slight, and not statistically significant, increase has occurred in the natural logarithm of area burned, and there has been a downward trend in the natural logarithm of mean fire size (again, not statistically significant). However, using the climate parameters in this study we predicted there should have been a significant upward trend in both area burned and mean fire size (as well as in the TNF). The finding for area burned somewhat agrees with a study by Bradstock et al. (2014) that found an increase in annual proportion of area burned only for 8 out of 32 bioregions in south-eastern Australia for 1975–2009. Other studies have also looked at trends in fire activity; for example, Earl and Simmonds (2017) found a decreasing trend using remotely-sensed active fires for 2001–15 for Victoria, and this is supported by Giglio et al. (2013) for 1998–2011 (Australia wide), whereas Dutta et al. (2016) found an increase in fire activity for 2007–13 (Australia wide). The absence of strong upward trends in area burned and mean fire size, despite the trends in climate variables which infer that both these measures of fire activity should have increased, suggests that other factors such as improved fire management have offset the likely increase from a changing climate. So Victoria has seen more fires (partly the result of changes in climate over the study period), but improved fire management or other factors appear to have acted to ensure that this increase in fire number did not lead to major increases in area burnt. It would be of considerable interest to analyse these interactions further in order to ensure the total area burnt remains lower than our model predictions.
Future work should consider other climate parameters such as a fire weather index and long-term drought indices or rainfall deficit parameters (see Urbieta et al. 2015; Bedia et al. 2015; Higuera et al. 2015; Littell et al. 2016) as these variables may be better climate predictors of fire activity. Another essential parameter to consider is fuel moisture, but without a consistent long-term data set this is difficult to consider. Additionally, recent studies by Keeley and Syphard (2015) and Higuera et al. (2015) both found the relationship between climate parameters and fire metrics differed between the first half of the 20th century and the second half, suggesting that changes in the strength of the relationship for different periods should be explored.
In this study we have used the best available fire data to explore the relationship between fire activity and climate and to estimate trends. Further work should also consider the reliability of the data set, as the relationship established will be sensitive to the quality of the data. Finally, the cause of ignition should be considered in the analyses, as trends in each cause may differ and, therefore, their relationship with climate parameters may also differ (see Collins et al. 2015 for different ignition causes resulting in different models). Nevertheless, the fire–climate relationship developed in this study may yet prove the most adequate tool for the assessment of fire risk (Bedia et al. 2015).
6 Summary and conclusion
Climate parameters in months prior to, and during, the fire season exhibit statistically significant relationships with fire activity. There is large interannual variability in total area burned and number of fires in Victoria over the last 42 years, and two-thirds of this can be explained by a combination of climate parameters. This was established using a first-difference approach and stepwise multiple regression to identify the climate parameters that best explain the variance in fire activity. The climate parameters included in the fire–climate models indicate the importance of rainfall preceding a fire season and also rainfall and maximum temperature during the fire season. However maximum temperature in January to March was the strongest explanatory variable for TNF, whereas vapour pressure in October to December was the strongest variable for area burned and for mean fire size.
The TNF during the fire season in Victoria has increased over the last 42 years. Over this same period maximum temperature has increased and vapour pressure has decreased in spring and summer prior to, and concurrent with, the fire season, along with a decrease in rainfall in spring and an increase in rainfall in summer. From the model we estimate that the observed changes in the climate parameters over the 42 years have been associated with an increase of 44% in the TNF in the fire season, accounting for 26% of the observed change for 1972–2014, with maximum temperature accounting for most of that change. Therefore, the major part of the apparent trend in TNF since 1972 has been the result of factors other than climate trends. Based on the observed relationships between climate and fire activity, we estimate that a future mean monthly maximum temperature warming of 2°C would lead to an increase in fire activity of 38% based on the fire activity observed in the period 1972–2014, holding all other variables constant.
The relationships between year-to-year changes in climate variables and the other two measures of fire activity examined here (total area burned and mean fire size) also suggest that the observed changes in climate should have led to increases in these two measures. The absence of strong increases in these two measures suggests that other factors such as improved fire management have offset the expected increase from the climate trends. A useful extension of this study would be to identify exactly what factors have contributed to this offsetting effect.
As well as providing a simple but credible method for estimating the effects of climate changes on fire activity in the past and in the future, the relationships determined in this study between climate and fire activity, combined with seasonal climate forecasts, could lead to improved seasonal and longer term forecasts of fire activity that in turn could result in more effective fire-management practices.
Acknowledgements
The authors thank the Bushfire Natural Hazards CRC for Project Management and Facilitation and the Department of Environment, Land, Water and Planning (DELWP) for funding this research. Valuable advice and feedback that considerably improved the manuscript was received from Dr Musa Kilinc (CFA) and Andy Ackland (DELWP).
References
Abatzoglou, J. T., and Williams, A. P. (2016). Impact of anthropogenic climate change on wildfire across western US forests. Proc. Natl. Acad. Sci. U.S.A. 113, 11770–11775.| Impact of anthropogenic climate change on wildfire across western US forests.Crossref | GoogleScholarGoogle Scholar |
Akaike, H. (1974). A new look at the statistical model identification. IEEE Trans. Autom. Control 19, 716–723.
| A new look at the statistical model identification.Crossref | GoogleScholarGoogle Scholar |
Batllori, E., Parisien, M. A., Krawchuk, M. A., and Moritz, M. A. (2013). Climate change-induced shifts in fire for Mediterranean ecosystems. Glob. Ecol. Beogeogr. 22, 1118–1129.
| Climate change-induced shifts in fire for Mediterranean ecosystems.Crossref | GoogleScholarGoogle Scholar |
Bedel, A. P., Mote, T. L., and Goodrick, S. L. (2013). Climate change and associated fire potential for the south-eastern United States in the 21st century. Int. J. Wildland Fire 22, 1034–1043.
| Climate change and associated fire potential for the south-eastern United States in the 21st century.Crossref | GoogleScholarGoogle Scholar |
Bedia, J., Herrera, S., Gutiérrez, J. M., Benali, A., Brands, S., Mota, B., and Moreno, J. M. (2015). Global patterns in the sensitivity of burned area to fire-weather: implications for climate change. Agric. For. Meteorol. 214–215, 369–379.
| Global patterns in the sensitivity of burned area to fire-weather: implications for climate change.Crossref | GoogleScholarGoogle Scholar |
Beer, T., and Williams, A. (1995). Estimating Australian forest fire danger under conditions of doubled carbon dioxide concentrations. Clim. Change 29, 169–188.
| Estimating Australian forest fire danger under conditions of doubled carbon dioxide concentrations.Crossref | GoogleScholarGoogle Scholar |
Blanchi, R., Leonard, J., Haynes, K., Opie, K., James, M., and de Oliveira, F. D. (2014). Environmental circumstances surrounding bushfire fatalities in Australia 1901-2011. Environ. Sci. Policy 37, 192–203.
| Environmental circumstances surrounding bushfire fatalities in Australia 1901-2011.Crossref | GoogleScholarGoogle Scholar |
Bowman, D. M. J. S., Murphy, B. P., Williamson, G. J., and Cochrane, M. A. (2014). Pyrogeographic models, feedbacks and the future of global fire regimes. Glob. Ecol. Biogeogr. 23, 821–824.
| Pyrogeographic models, feedbacks and the future of global fire regimes.Crossref | GoogleScholarGoogle Scholar |
Bradstock, R. A., Cohn, J. S., Gill, A. M., Bedward, M., and Lucas, C. (2009). Prediction of the probability of large fires in the Sydney region of south-eastern Australia using components of fire weather. Int. J. Wildland Fire 18, 932–943.
| Prediction of the probability of large fires in the Sydney region of south-eastern Australia using components of fire weather.Crossref | GoogleScholarGoogle Scholar |
Bradstock, R., Penman, T., Boer, M., Price, O., and Clarke, H. (2014). Divergent responses of fire to recent warming and drying across south-eastern Australia. Glob. Change Biol. 20, 1412–1428.
| Divergent responses of fire to recent warming and drying across south-eastern Australia.Crossref | GoogleScholarGoogle Scholar |
Brown, T. J., Hall, B. L., and Westerling, A. L. (2004). The impacts of 21st century climate change on wildland fire danger in western United States: an application perspective. Clim. Change 62, 365–388.
| The impacts of 21st century climate change on wildland fire danger in western United States: an application perspective.Crossref | GoogleScholarGoogle Scholar |
Bryant, C. (2008). Understanding bushfire: trends in deliberate vegetation fires (Victoria) Issue 27 of Australian Institute of Criminology technical and background paper series Issue 27 of Technical and background paper series. (Australian Institute of Criminology.).
Bureau of Meteorology. (2012). Record-breaking La Niña events: an analysis of the La Niña life cycle and the impacts and significance of the 2010-11 and 2011-12 La Niña events in Australia. (Commonwealth of Australia: Melbourne, Vic., Australia.)
Cardosa, M. F., Hurtt, G. C., Moore, B., Nobre, C. A., and Prins, E. M. (2003). Projecting future fire activity in Amazonia. Glob. Change Biol. 9, 656–669.
| Projecting future fire activity in Amazonia.Crossref | GoogleScholarGoogle Scholar |
Chen, I. C., Hill, J. K., Ohlemuller, R., Roy, D. B., and Thomas, C. D. (2011). Rapid range shifts of species associated with high levels of climate warming. Science 333, 1024–1026.
| Rapid range shifts of species associated with high levels of climate warming.Crossref | GoogleScholarGoogle Scholar |
Clarke, H., Lucas, C., and Smith, P. (2013). Changes in Australian Fire Weather between 1973 and 2010. Int. J. Climatol. 33, 933–991.
| Changes in Australian Fire Weather between 1973 and 2010.Crossref | GoogleScholarGoogle Scholar |
Collins, K. M., Price, O. F., and Penman, T. D. (2015). Spatial patterns of wildfire ignitions in south-eastern Australia. Int. J. Wildland Fire 24, 1098–1108.
| Spatial patterns of wildfire ignitions in south-eastern Australia.Crossref | GoogleScholarGoogle Scholar |
Cramer, W., Yohe, G., Auffhammer, M., Huggel, C., Molau, U., Faus da Silva Dias, M. A., Solow, A., Stone, D., and Tibig, L. (2014). Detection and attribution of observed impacts Climate Change 2014: Impacts, Adaptation, and Vulnerability: IPCC Working Group II Contribution to AR5 ch 18, p 94. Available at https://ipcc-wg2.gov/AR5/images/uploads/WGIIAR5-Chap18_FINAL.pdf [Verified 22 April 2020].
Doerr, S. H., and Santin, C. (2016). Global trends in wildfire and its impacts: perceptions versus realities in a changing world. Philos. Trans. R. Soc. Publ. 371, 20150345.
| Global trends in wildfire and its impacts: perceptions versus realities in a changing world.Crossref | GoogleScholarGoogle Scholar |
Dutta, R., Das, A., and Aryal, J. (2016). Big data integration shows Australian bush-fire frequency increasing significantly. R. Soc. Open Sci. 3, 150241.
| Big data integration shows Australian bush-fire frequency increasing significantly.Crossref | GoogleScholarGoogle Scholar |
Earl, N., and Simmonds, I. (2017). Variability, trends, and drivers of regional fluctuations in Australian fire activity. J. Geophys. Res.: Atmos. 122, 7445–7460.
| Variability, trends, and drivers of regional fluctuations in Australian fire activity.Crossref | GoogleScholarGoogle Scholar |
Gould, J., and Cruz, M. (2012). ‘Australian Fuel Classification: Stage II’. (Ecosystem Science and Climate Adaptations Flagship CSIRO: Australia.)
Flannigan, M. D., Amiro, B. D., Logan, K. A., Stocks, B. J., and Wotton, B. M. (2006). Forest fires and climate change in the 21st century. Mitigation Adapt. Strateg. Glob. Change 11, 847–859.
| Forest fires and climate change in the 21st century.Crossref | GoogleScholarGoogle Scholar |
Flannigan, M. D., Krawchuk, M. A., de Groot, W. J., Wotton, B. M., and, and Gowman, L. M. (2009). Implications of changing climate for global wildland fire. Int. J. Wildland Fire 18, 483–507.
| Implications of changing climate for global wildland fire.Crossref | GoogleScholarGoogle Scholar |
Giglio, L., Randerson, J. T., and van der Werf, G. R. (2013). Analysis of daily, monthly and annual burned area using the fourth-generation global fire emissions database (GFED4). J. Geophys. Res.: Biogeosci. 118, 317–328.
| Analysis of daily, monthly and annual burned area using the fourth-generation global fire emissions database (GFED4).Crossref | GoogleScholarGoogle Scholar |
Gill, A. M., and Cary, G. J. (2012). Socially disastrous landscape fires in south-eastern Australia: impacts, responses, implications. In ‘Wildfire and Community: Facilitating Preparedness and Resilience’. (Eds D. Paton and F. Pedrosa.) pp. 14–32. (Charles C. Thomas: Springfield, IL, USA.)
Gill, A. M., Stephens, S. L., and Cary, G. J. (2013). The worldwide “wildfire” problem. Ecol. Appl. 23, 438–454.
| The worldwide “wildfire” problem.Crossref | GoogleScholarGoogle Scholar |
Goldammer, J. G., and Price, C. (1998). Potential impacts of climate change on fire regimes in the tropics based on MAGICC and a GISS GCM-derived lightning model. Clim. Change 39, 273–296.
| Potential impacts of climate change on fire regimes in the tropics based on MAGICC and a GISS GCM-derived lightning model.Crossref | GoogleScholarGoogle Scholar |
Harris, S., Tapper, N., Packham, D., Orlove, B., and Nicholls, N. (2008). The relationship between the monsoonal summer rain and dry-season fire activity of northern Australia. Int. J. Wildland Fire 17, 674–684.
| The relationship between the monsoonal summer rain and dry-season fire activity of northern Australia.Crossref | GoogleScholarGoogle Scholar |
Harris, S., Nicholls, N., and Tapper, N. (2014). Forecasting fire activity in Victoria, Australia, using antecedent climate variables and ENSO indices. Int. J. Wildland Fire 23, 173–184.
| Forecasting fire activity in Victoria, Australia, using antecedent climate variables and ENSO indices.Crossref | GoogleScholarGoogle Scholar |
Harris. S., Mills, G., and Brown, T. (June 2016). Characterising fire weather for Victoria, Australia. Report to the Department of Environment, Land, Water and Planning.
Hennessy, K., Lucas, C., Nicholls, N., Bathols, J., Suppiah, R., and Ricketts, J. (2005). Climate Change impacts on fire-weather in south-east Australia. (Consultancy report. CSIRO Marine and Atmospheric Research and the Australian Government Bureau of Meteorology.)
Higuera, P. E., Abatzoglou, J. T., Littell, J. S., and Morgan, P. (2015). The changing strength and nature of fire-climate relationships in the northern Rocky Mountains, USA 1902–2008. PLoS One , .
| The changing strength and nature of fire-climate relationships in the northern Rocky Mountains, USA 1902–2008.Crossref | GoogleScholarGoogle Scholar |
Hughes, L. (2014). Be Prepared: Climate Change and the Victorian bushfire threat by Professor Lesley Hughes (Climate Council of Australia).
Jones, D. A., Wang, W., and Fawcett, R. (2009). High-quality spatial climate data-sets for Australia. Aust. Meteorol. Oceanogr. J. 58, 233–248.
| High-quality spatial climate data-sets for Australia.Crossref | GoogleScholarGoogle Scholar |
Jolly, W. M., Cochrane, M. A., Freeborn, P. H., Holden, Z. A., Brown, T. J., Williamson, G. J., and Bowman, D. M. J. S. (2015). Climate-induced variations in global wildfire danger from 1979 to 2013. Nat. Commun. 6, 7537.
| Climate-induced variations in global wildfire danger from 1979 to 2013.Crossref | GoogleScholarGoogle Scholar |
Keane, R. E., Cary, G. J., and Flannigan, M. D. (2013). Exploring the role of fire, succession, climate, and weather on landscape dynamics using comparative modelling. Ecol. Modell. 266, 172–186.
| Exploring the role of fire, succession, climate, and weather on landscape dynamics using comparative modelling.Crossref | GoogleScholarGoogle Scholar |
Keeley, J. E., and Syphard, A. D. (2015). Different fire–climate relationships on forested and non-forested landscapes in the Sierra Nevada ecoregion. Int. J. Wildland Fire 24, 27–36.
| Different fire–climate relationships on forested and non-forested landscapes in the Sierra Nevada ecoregion.Crossref | GoogleScholarGoogle Scholar |
Keeley, J. E., and Syphard, A. D. (2016). Climate change and future fire regimes: examples from California. Geosciences 6, 37.
| Climate change and future fire regimes: examples from California.Crossref | GoogleScholarGoogle Scholar |
Keeley, J. E., and Syphard, A. D. (2017). Different historical fire-climate patterns in California. Int. J. Wildland Fire 26, 253–268.
| Different historical fire-climate patterns in California.Crossref | GoogleScholarGoogle Scholar |
King, A. D., Alexander, L. V., and Donat, M. G. (2012). The efficacy of using gridded data to examine extreme rainfall characteristics: a case study for Australia. Int. J. Climatol. 33, 2376–2387.
| The efficacy of using gridded data to examine extreme rainfall characteristics: a case study for Australia.Crossref | GoogleScholarGoogle Scholar |
Koutsias, N., Xanthopoulos, G., Founda, D., Xystrakis, F., Nioti, F., Pleniou, M., Mallinis, G., and, and Arianoutsou, M. (2013.). On the relationships between forest fires and weather conditions in Greece from long-term national observations (1894–2010). Int. J. Wildland Fire 22, 493–507.
| On the relationships between forest fires and weather conditions in Greece from long-term national observations (1894–2010).Crossref | GoogleScholarGoogle Scholar |
Krawchuk, M. A., and Moritz, M. A. (2011). Constraints on global fire activity vary across a resource gradient. Ecology 92, 121–132.
| Constraints on global fire activity vary across a resource gradient.Crossref | GoogleScholarGoogle Scholar |
Littell, J. S., McKenzie, D., Peterson, D. L., and Westerling, A. L. (2009). Climate and wildfire area burned in western U.S. ecoprovinces, 1916–2003. Ecol. Appl. 19, 1003–1021.
| Climate and wildfire area burned in western U.S. ecoprovinces, 1916–2003.Crossref | GoogleScholarGoogle Scholar |
Littell, J. S., Peterson, D. L., Riley, K. L., Liu, Y., and Luce, C. H. (2016). A review of the relationships between drought and forest fire in the United States. Glob. Change Biol. 22, 2353–2369.
| A review of the relationships between drought and forest fire in the United States.Crossref | GoogleScholarGoogle Scholar |
Lobell, D. B., and Field, C. B. (2007). Global scale climate-crop yield relationships and the impacts of recent warming. Environ. Res. Lett. 2, 014002.
| Global scale climate-crop yield relationships and the impacts of recent warming.Crossref | GoogleScholarGoogle Scholar |
Lucas, C., Hennessy, K., Mills, G., and Bathols, J. (2007). Bushfire weather in Southeast Australia: Recent trends and projected climate change impacts. Consultancy report prepared for the Climatic Institute of Australia. (Bushfire CRC and Australian Bureau of Meteorology and CSIRO Marine and Atmospheric Research.)
McKenzie, D. Z., Gedalof, Z., Peterson, D. L., and Mote, P. (2004). Climatic change, wildfire and conservation. Conserv. Biol. 18, 890–902.
| Climatic change, wildfire and conservation.Crossref | GoogleScholarGoogle Scholar |
Meyn, A., White, P. S., Buhk, C., and Jentsch, A. (2007). Environmental drivers of large, infrequent wildfires: the emerging conceptual model. Progr. Phys. Geogr. 31, 287–312.
| Environmental drivers of large, infrequent wildfires: the emerging conceptual model.Crossref | GoogleScholarGoogle Scholar |
Morehouse, B. J., Christopherson, M., Crimmins, M. A., Orr, B., Overpeck, J. T., Swetnam, T., and Yool, S. (2006). Modeling Interactions among Wildland Fire, Climate and Society in the Context of Climatic Variability and Change in the Southwest US in Regional Climate Change and Variability. In ‘Impacts and Responses’. (Eds M. Ruth, K. Donaghy, P. Kirshen.) pp. 58–78. (Edward Elgar: Cheltenham, UK.)
Moritz, M. A., Batllori, E., Bradstock, R. A., Gill, A. M., Handmer, J., Hessburg, P. F., Leonard, J., McCaffrey, S., Odion, D. C., Schoennagel, T., and Syphard, A. D. (2014). Learning to coexist with wildfire. Nature 515, 58–66.
| Learning to coexist with wildfire.Crossref | GoogleScholarGoogle Scholar |
Moritz, M. A., Parisien, M. -A., Batllori, E., Krawchuk, M. A., Van Dorn, J., Ganz, D. J., and Hayhoe, K. (2012). Climate change and disruptions to global fire activity. Ecosphere 3, 1–22.
| Climate change and disruptions to global fire activity.Crossref | GoogleScholarGoogle Scholar |
Morton, D. C., Collatz, G. J., Wang, D., Randerson, J. T., Giglio, L., and Chen, Y. (2013). Satellite-based assessment of climate controls on US burned area. Biogeosciences 10, 247–260.
| Satellite-based assessment of climate controls on US burned area.Crossref | GoogleScholarGoogle Scholar |
Murphy, B. F., and Timbal, B. (2008). A review of recent climate variability and climate change in southeastern Australia. Int. J. Climatol. 28, 859–879.
| A review of recent climate variability and climate change in southeastern Australia.Crossref | GoogleScholarGoogle Scholar |
Nolan, R. H., Boer, M. M., Resco de Dios, V., Caccamo, G., and Bradstock, R. A. (2016). Large-scale dynamic transformations in fuel moisture drive wildfire activity across southeastern Australia. Geophys. Res. Lett. 43, .
| Large-scale dynamic transformations in fuel moisture drive wildfire activity across southeastern Australia.Crossref | GoogleScholarGoogle Scholar |
Nicholls, N., and Lucas, C. (2007). Interannual variations of area burnt in Tasmanian bushfires: relationships with climate and predictability. Int. J. Wildland Fire 16, 540–546.
| Interannual variations of area burnt in Tasmanian bushfires: relationships with climate and predictability.Crossref | GoogleScholarGoogle Scholar |
Nicholls, N. (2009). Estimating changes in mortality due to climate change. Clim. Change 97, 313.
| Estimating changes in mortality due to climate change.Crossref | GoogleScholarGoogle Scholar |
Nicholls, N. (1997). Increased Australian wheat yield due to recent climate trends. Lett. Nat. 387, 484–485.
| Increased Australian wheat yield due to recent climate trends.Crossref | GoogleScholarGoogle Scholar |
Pausas, J. G., and Paula, S. (2012). Fuel shapes the fire-climate relationship: evidence from Mediterranean ecosystems. Glob. Ecol. Biogeogr. 21, 1074–1082.
| Fuel shapes the fire-climate relationship: evidence from Mediterranean ecosystems.Crossref | GoogleScholarGoogle Scholar |
Phan, T., and Kilinc, M. (2015). Integrating Fire Ignition and Fire History Databases. Report to the Department of Environment, Land, Water and Planning.
Pitman, A. J., Narisma, G. T., and McAneney, J. (2007). The impact of climate change on the risk of forest and grassland fires in Australia. Clim. Change 84, 383–401.
| The impact of climate change on the risk of forest and grassland fires in Australia.Crossref | GoogleScholarGoogle Scholar |
Rothermel, R. C. (1972). A mathematical model for predicting fire spread in wildland fuels. Res. Pap. INT-115. 40 pp. (U.S. Department of Agriculture, Intermountain Forest and Range Experiment Station: Ogden, UT, USA.)
Safford, H. D., Hayward, G. D., Heller, N. E., and Wiens, J. A. (2012). Historical ecology, climate change, and resource management: can the past still inform the future? In ‘Historical Environmental Variation in Conservation and Natural Resource Management’. (Eds J. A. Wiens, G. D. Hayward, H. D. Safford, C. M. Giffen) pp. 46–62. (Wiley-Blackwell: Oxford, UK.)
Stocks, B. J., Fosberg, M. A., Lynham, T. J., Mearns, L., and Wooton, B. M. (1998). Climate change and forest fire potential in Russian and Canadian boreal forests. Clim. Change 38, 1–13.
| Climate change and forest fire potential in Russian and Canadian boreal forests.Crossref | GoogleScholarGoogle Scholar |
Teague, B., McLeod, R., and Pascoe, S. 2010. 2009 Victorian Bushfires Royal Commission: Final Report. (Parliament of Victoria: Melbourne, Vic., Australia.) Available at http://royalcommission.vic.gov.au/Commission-Reports/Final-Report.html [Verified 8 July 2019].
Trouet, V., Taylor, A. H., Carleton, A. M., and Skinner, C. N. (2009). Interannual variations in fire weather, fire extent, and synoptic-scale circulation patterns in northern California and Oregon. Theor. Appl. Climatol. 95, 349–360.
| Interannual variations in fire weather, fire extent, and synoptic-scale circulation patterns in northern California and Oregon.Crossref | GoogleScholarGoogle Scholar |
Turco, M., Llasat, M. C., von Hardenberg, J., and Provenzale, A. (2014). Climate change impacts on wildfires in a Mediterranean environment. Clim. Change 125, 369–380.
| Climate change impacts on wildfires in a Mediterranean environment.Crossref | GoogleScholarGoogle Scholar |
Urbieta, I., Zavala, G., Bedia, J., Gutiérrez, J., San Miguel-Ayanz, J., Camia, A., Keeley, J. E., and Moreno, J. M. (2015). Fire activity as a function of fire–weather seasonal severity and antecedent climate across spatial scales in southern Europe and Pacific western USA. Environ. Res. Lett. 10, 114013.
| Fire activity as a function of fire–weather seasonal severity and antecedent climate across spatial scales in southern Europe and Pacific western USA.Crossref | GoogleScholarGoogle Scholar |
Veraverbeke, S., Rogers, B. M., Goulden, M. L., Jandt, R. R., Miller, C. E., Wiggins, E. B., and Randerson, J. T. (2017). Lightning as a major driver of recent large fire years in North American boreal forests. Nat. Clim. Change 7, 529–534.
| Lightning as a major driver of recent large fire years in North American boreal forests.Crossref | GoogleScholarGoogle Scholar |
Webb, L. B., and Hennessy, K. 2015. Projections for selected Australian cities. (CSIRO and Bureau of Meteorology: Australia.) Available at http://www.climatechangeinaustralia.gov.au/media/ccia/2.1.5/cms_page_media/176/CCIA_Australian_cities_1.pdf [Verified 19 May 2016].
Westerling, A. L., and Bryant, B. P. (2008). Climate change and wildfire in California. Clim. Change 87, 231–249.
| Climate change and wildfire in California.Crossref | GoogleScholarGoogle Scholar |
Williamson, G. J., Prior, L. D., Jolly, W. M., Cochrane, M. A., Murphy, B. P., and Bowman, D. M. J. S. (2016). Measurement of inter- and intra-annual variability of fire activity at a continental scale: the Australian case. Environ. Res. Lett. 11, 035003.
| Measurement of inter- and intra-annual variability of fire activity at a continental scale: the Australian case.Crossref | GoogleScholarGoogle Scholar |
Wotton, B. M., Martell, D. L., and Logan, K. A. (2003). Climate change and people-caused fire occurrence in Ontario. Clim. Change 60, 275–295.
| Climate change and people-caused fire occurrence in Ontario.Crossref | GoogleScholarGoogle Scholar |