Occurrence and trends of historical tropical cyclone rainfall on near-coastal regions of Australia
Samuel Bell A * , Andrew Dowdy A B C , Savin Chand D and Chun-Hsu Su
A * , Andrew Dowdy A B C , Savin Chand D and Chun-Hsu Su  A
A
A
B
C
D
Abstract
Extreme rainfall driven by tropical cyclones (TCs) has profound effects on Australian coastlines at both local and regional scales. Here, we develop methods for comparing TC-driven widespread and localised rainfall on three broad coastal regions of tropical Australia (west, north and east). Trends, average recurrence intervals (ARIs) and the fractional contribution of TC rainfall are explored in three historical datasets: Australian Gridded Climate Data (AGCD), ECMWF Reanalysis (ver. 5, ERA5) and the Bureau of Meteorology Atmospheric high resolution Regional Reanalysis for Australia (ver. 1, BARRA1). Results for trends and ARIs between the different datasets are generally inconsistent and also differ between regions, partially owing to the short-term temporal records of some of the data as well as inconsistencies in extreme values between datasets. By contrast, there is a general agreement between all datasets on the fractional contribution of TC rainfall, signalling an increase in recent years. This result is considered together with the trend towards fewer TCs occurring in this region over recent decades, indicating a trend towards increased rainfall intensity per TC on average, assuming steady landfall rates. The methods developed here can be applied easily to other data types such as regional climate model experiments, facilitating a multiple lines of evidence approach that incorporates both observational-based and model-based data. This research is intended to help provide new methods and guidance for identifying trends in TC-driven extreme rainfall, relevant for enhanced planning and adaptation to the impacts of these extreme weather systems.
Keywords: AGCD, average recurrence interval, BARRA, coastal Australia, extreme rainfall, fractional contribution, intercomparison, log-normal, reanalysis, trend, tropical cyclone rainfall.
1Introduction
Extreme rainfall, especially that produced by tropical cyclones (TCs) in the northern coastal regions of Australia can pose significant flood hazard risks as well as significant challenges for water management. With anthropogenic climate change causing rising global temperatures and hence an increased water holding capacity of air, the most extreme rainfall events are expected to increase in intensity. For example, an extreme value curve of the maximum rainfall rate is expected to shift to the right by some amount, with larger increases likely for the more intense and shorter duration rainfall extremes (Masson-Delmotte et al. 2021). In this context, it could prove useful to attempt to quantify any climate trends in extreme TC-driven rainfall. This includes rainfall characteristics such as the average recurrence of the most extreme events and also the fractional contribution of TCs to extreme rainfall for different TC-prone coastal regions of Australia.
Most historical rainfall observations in Australia originate from weather stations scattered across the continent and these are usually more concentrated in coastal regions. The limited spatial coverage of rainfall observations can be improved with interpolation methods that produce gridded analysis products such as the Australian Gridded Climate Data (AGCD, Jones et al. 2009). However, uncertainties remain in the gridded data, including in the more remote regions far away from observation station locations and for complex terrain (Chubb et al. 2016).
Another medium for analysing historical rainfall is through reanalysis products. These also use modelling and interpolation of historical observations but – differing to efforts such as AGCD, sub-grid scale cloud and precipitation – are often parameterised based on larger scale variables such as wind and temperature (that can be more accurately resolved than rainfall in the coarse resolution of the reanalysis simulations). ECMWF Reanalysis (ver. 5, ERA5, Hersbach et al. 2020) and the Bureau of Meteorology (The Bureau) Atmospheric high resolution Regional Reanalysis for Australia (ver. 1, BARRA1, Su et al. 2019) are two reanalyses produced over the Australian region. There is a clear trade off here between the larger and uniform spatial coverage of the reanalysis (as compared to AGCD) and the uncertainty in simulated rainfall introduced by the parameterisation scheme used. Modern-day global climate models (GCMs) also use parameterisation schemes to determine rainfall and are sometimes used to make projections. Very fine resolution (kilometre-scale) climate models, known as regional climate models (RCMs) are another medium used to analyse rainfall (e.g. Jalowska et al. 2021). These RCMs can have an advantage over coarser GCMs of being convection permitting where the majority of deep convection processes are explicitly modelled without parameterisation. However, they can be computationally intensive (and expensive) to produce, particularly for climate-scale analysis.
As discussed above, there are numerous mediums through which rainfall trends can be analysed with a presumed preference towards model-based applications in the coming years. We propose a new method for comparing climate trends of extreme rainfall and TC contribution to extreme rainfall for near-coastal regions (we define ‘near-coastal’ as those regions designated ‘cyclonic’ by Standard AS/NZS 1170.2:2021; Standards Australia 2021) of Australia such that in the future a multiple-lines-of-evidence approach can be used across multiple rainfall datasets (i.e. including climate models as well as observations data) to increase confidence in the existence of any such trends and associated impacts. Different to previous TC rainfall studies in the Australian region (e.g. Dare et al. 2012; Chen et al. 2013; Dare 2013; Lavender and Abbs 2013) and abroad (e.g. Stansfield et al. 2020 and references within), we focus on the trends of landfalling TCs by using regions that are large enough to account for their considerable interannual variability and still provide useful localised information relevant to impact-based decision making.
Our analyses are undertaken on three datasets – AGCD and two reanalysis products (ERA5 and BARRA1) – using methods that can be practically applied to climate models, including RCMs in the future. Other datasets could have also been included; however, the primary aims of this study are to determine how BARRA1 performs against more established datasets (ERA5 and AGCD) and to establish a non-conventional method for analysing TC rainfall; with documenting trends in the data analysed forming a secondary aim. Two measures of rainfall, localised and widespread, are considered in three near-coastal regions of Australia. Trends and average recurrence intervals (ARIs) of these two rainfall measures are then determined. The determination of ARIs could prove useful to determine the hazard posed by extreme TC rainfall within a climate-oriented framework. Lastly, the fractional contribution of TCs to the widespread rainfall is determined, an important characteristic when considering Australia has experienced fewer TCs on average in recent years.
2Methods and data
2.1 Methods
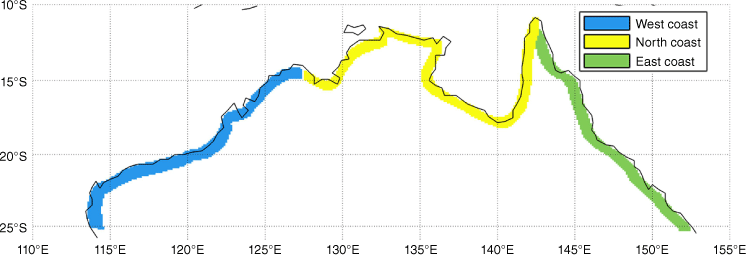
We investigate extreme rainfall occurring within 100 km inland along the tropical coastline of Australia (down to 25°S). This is divided into three regions (Fig. 1): west (114–127°E), north (127–142°E) and east (142–153°E).
For examining coastal TC rainfall trends in Australia, we use a region-based approach to measure rainfall, rather than purely considering the rainfall around individual TCs. In other words, rainfall is determined from a stationary spatial region rather than moving with a TC through its lifetime.
Explicitly:
Rainfall totals (widespread and localised) are determined each day for a region. Reanalysis totals are taken from 00:00 to 23:00 hours UTC, closely aligning with backdated AGCD data taken daily at 09:00 hours local time.
On days when there is a TC either inside or within 5° (~550 km) of a region (at 12:00 hours UTC), all rainfall on that day is considered ‘TC-related’.
This method has the distinct advantages of providing regional hazard information for the coastlines and enables comparison with non-TC rainfall extremes. However, a drawback of this method is the potential inclusion of other weather systems contributing to the TC-rainfall on some occasions, that would less likely occur using the traditional method of a radial distance of 5° around a TC to measure its rainfall contribution (e.g. Chen et al. 2013; Dare 2013; Lavender and Abbs 2013). Months where TCs generally do not form in the Australian region (May–October) are included in the analysis. The TC data are defined from The Bureau’s TC dataset (best track, as described in Section 2.2.1) and instances where TCs are flagged as undergoing extra-tropical transition in the database are retained for the TC-rainfall analysis.
In the following analyses, we consider two measures of rainfall, representing complementary aspects of extremes (i.e. localised as well as widespread extreme rainfall) as follows:
Localised maximum rainfall (mm day−1), defined using the grid cell that had the highest amount of rainfall over a 24-h period.
Widespread (or spatially averaged) rainfall (mm day−1), defined as the accumulated rainfall for every grid cell inside a region (e.g. the West coast region) over a 24-h period, divided by the total number of grid cells for that region.
The ARIs were determined for TC-induced rainfall (widespread and localised) using the peak-over-threshold method on regional daily rainfall data, where the threshold was arbitrarily chosen to produce a total average of ~2–3 peaks per year (e.g. Bell et al. 2022). The log-normal and Weibull functions best modelled the tails of our rainfall distributions in comparison to other functions (such as GEV and Gumbel; not shown). The method of maximum likelihood was used to estimate distribution parameters.
The Mann–Kendall test (Mann 1945; Kendall 1975) analyses the difference between later- and earlier-measured data to determine if there is a statistically upward or downward trend.
2.2 Data
The Bureau’s TC dataset was used to determine regional daily rainfall totals associated with TCs (i.e. occur on ‘TC days’). This dataset includes historical TCs that have affected the Australian region (90–160°E). The historical records of TCs (analysed here from the early 1900s to 2021), include TC position and time information (with a degree of uncertainty; Torn and Snyder 2012). We note that in the era preceding geostationary satellite imagery (c. 1978, Dowdy and Kuleshov 2012), TC records are likely incomplete but are likely more reliable for landfalling TCs (e.g. Callaghan and Power 2011). Nevertheless, rainfall trends in these eras are examined separately in the analysis.
ERA5 (Hersbach et al. 2020) is a global reanalysis product available at the horizontal grid spacing of 31 km. Daily precipitation values are accumulated from hourly total precipitation at each grid cell over the time period 1979–2021.
BARRA1 (Su et al. 2019) is a reasonably new reanalysis product that covers the Australian region (65°E–63°W, 20°N–60°S) and is available at a horizontal resolution of 12 km. The initial and boundary conditions are set by ERA-Interim. Daily precipitation values are accumulated from hourly total precipitation (the sum of large-scale, convective) at the surface for each grid cell over the available time period 1990 to February 2019.
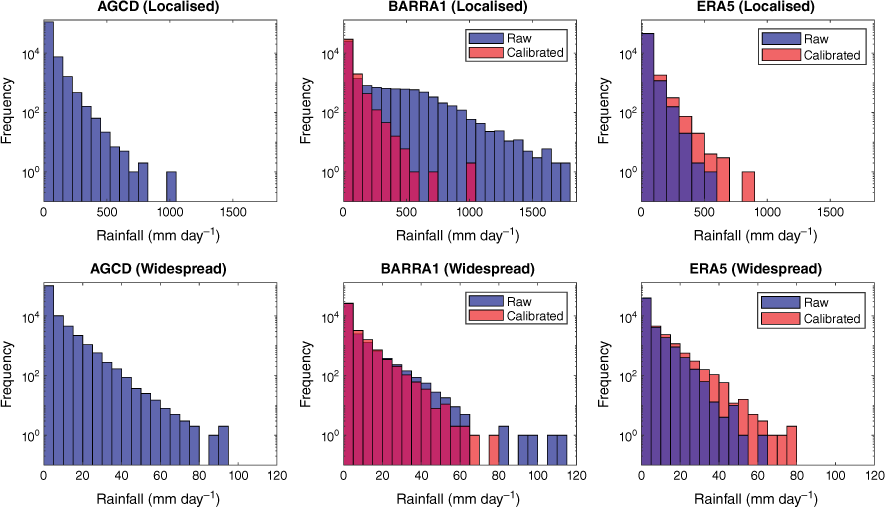
The AGCD (Jones et al. 2009) are based on a gridded climate analysis of several key variables based on site-based surface observations, aggregated and interpolated into a ~5-km grid over the Australian continent (0.05° grid spacing in both latitude and longitude). Here we use AGCD (ver. 1) daily precipitation totals to compare with precipitation in two reanalysis datasets. The ERA5 and BARRA1 rainfall data are calibrated to AGCD (Fig. 2) using a simple quantile matching approach (Bell et al. 2021) to correct inherent biases in the model data due to their differences in grid spacing.
3Results
3.1 Time series and trends
Time series of regional localised and widespread rainfall totals (mm day−1) and their relation to TCs are shown for three datasets: AGCD (Fig. 3), ERA5 (Fig. 4) and BARRA1 (Fig. 5).
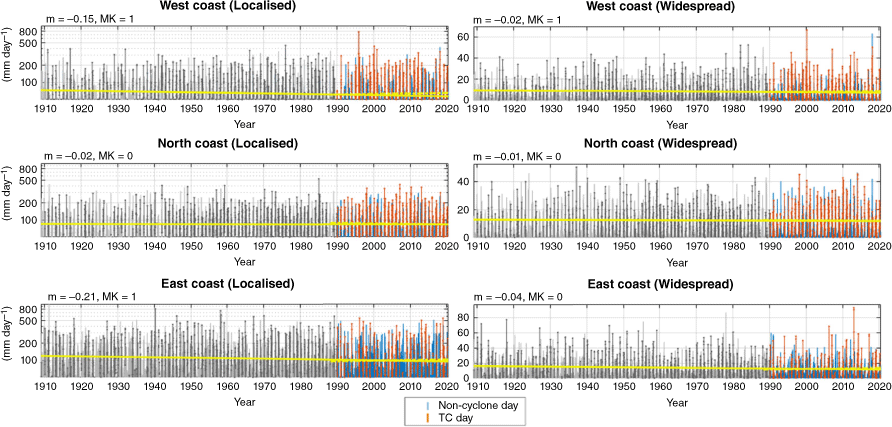
Time series and trend lines of AGCD regional daily rainfall. Localised (single grid cell) and widespread (entire region) rainfall totals either occur on ‘TC days’ or ‘non-cyclone days’ (see legend). Linear trend lines over the entire time period (yellow) and post-1990 (yellow dashed) are fitted for TC rainfall. The estimate of the gradient (m) and Mann–Kendall statistic (MK) for the full length trendlines are shown above each time series. Note that the gradients are converted to years for interpretability.
Time series and trend lines of ERA5 calibrated regional daily rainfall. Localised (single grid cell) and widespread (entire region) rainfall totals either occur on ‘TC days’ or ‘non-cyclone days’ (see legend). Linear trend lines over the entire time period (yellow) are fitted for TC rainfall. The estimate of the gradient (m) and Mann–Kendall statistic (MK) for the full length trendlines are shown above each time series. Note that the gradients are converted to years for interpretability.
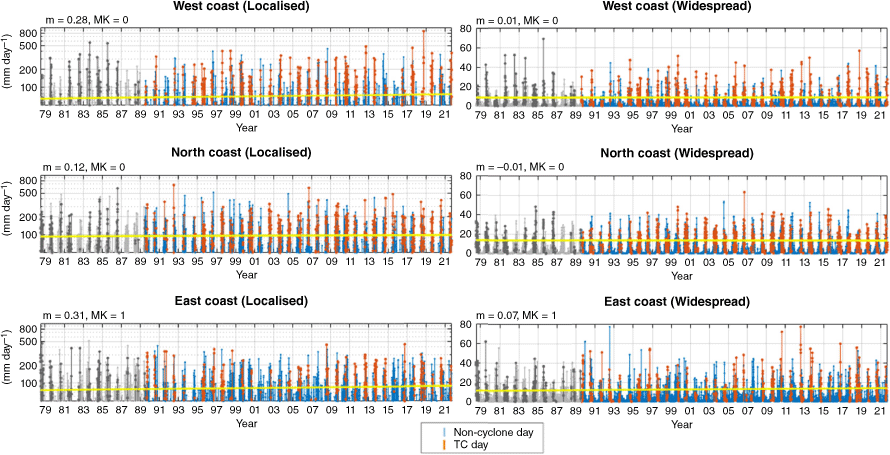
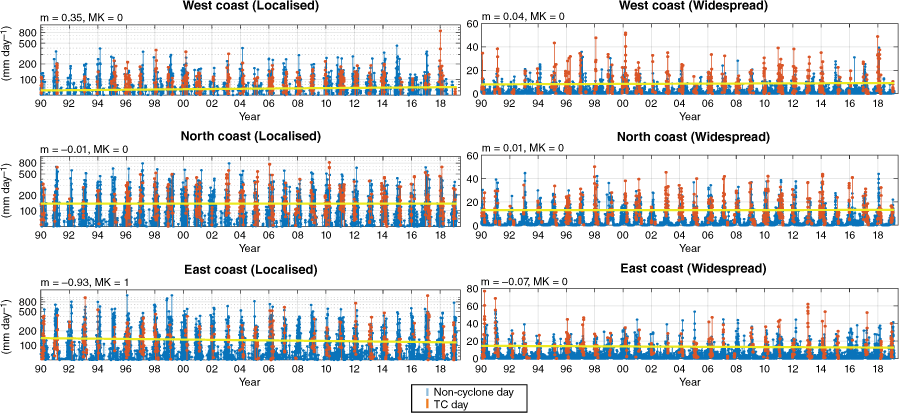
Time series and trend lines of BARRA1 calibrated regional daily rainfall. Localised (single grid cell) and widespread (entire region) rainfall totals either occur on ‘TC days’ or ‘non-cyclone days’ (see legend). Linear trend lines (yellow) are fitted for TC rainfall. The estimate of the gradient (m) and Mann–Kendall statistic (MK) for these trend lines are shown above each time series. Note that the gradients are converted to years for interpretability.
Linear trend lines are fitted over the entire length of each time series, as well as the period common to each dataset (post 1990) for widespread and local TC rainfall (Fig. 3–5). The Mann–Kendall statistic is applied with 90% confidence (two-tailed) to determine the presence of either increasing or decreasing trends. Results for trend significance are compiled for intercomparison (Table 1) and are highly variable between datasets. This includes significant trends in opposite directions for local rainfall on the east coast that may be related to fewer TCs occurring historically in this region. In fact, the only result common between datasets is that of no significant trends in either measure of rainfall for the western and northern Australian coasts since 1990, while noting that this is a reasonably short time period for assessing rainfall trends given the large interannual variability that can occur in these regions of Australia. Calibration of the reanalysis data (Fig. 2) did not change the significance of any of the Mann–Kendall test results.
| Since 1990 | Full period | ||||
|---|---|---|---|---|---|
| Local | Widespread | Local | Widespread | ||
| West coast | |||||
| AGCD | – | – | ↓ | ↓ | |
| ERA5 | – | – | – | – | |
| BARRA1 | – | – | N/A | N/A | |
| North coast | |||||
| AGCD | – | – | ↓ | – | |
| ERA5 | – | – | – | – | |
| BARRA1 | – | – | N/A | N/A | |
| East coast | |||||
| AGCD | – | – | ↓ | – | |
| ERA5 | ↑ | ↑ | ↑ | ↑ | |
| BARRA1 | ↓ | – | N/A | N/A | |
Full period denotes AGCD data since 1910 and ERA5 data since 1979. ↓, decreasing; –, none; ↑, increasing.
The trendline coefficients (m) (indicating the year-on-year size of the trends) were relatively larger for localised rainfall (compared to widespread) in AGCD and BARRA1 (top-left of Fig. 3 and 5). The opposite was true for widespread rainfall where coefficient values were relatively larger in ERA5 (top-left of Fig. 4).
Some of the significant trends can be interpreted as follows:
Since 1979, widespread daily TC rainfall on the east coast has been increasing at 0.31 mm year–1 on average (based on ERA5 reanalysis).
Since 1910, localised daily TC rainfall on the west coast has been decreasing at 0.15 mm year–1 on average (based on AGCD; notwithstanding an apparent upward trendline when beginning the trendline from 1990, Fig. 3).
Since 1990, localised daily TC rainfall on the east coast has been decreasing at 0.93 mm year–1 on average (based on BARRA1 reanalysis).
3.2 Average recurrence intervals
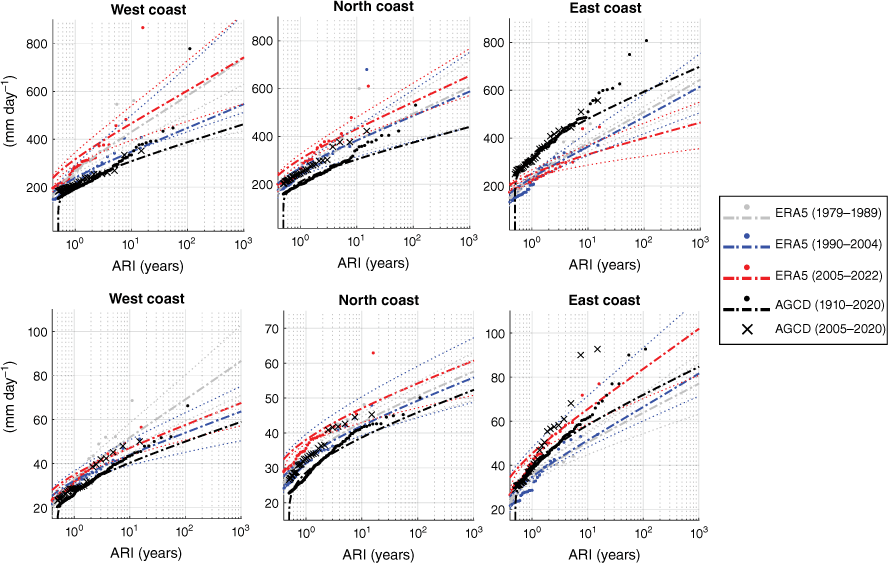
The ARIs of TC-driven localised and widespread regional rainfall totals (mm day−1) using peak-over-threshold are calculated across our three datasets with a particular focus on determining any changes in recent years (Fig. 6, 7). The ACCD data are mostly used here as a historical baseline (‘black curves’) to compare ARIs calculated over different time slices for ERA5 (Fig. 6) and BARRA1 (Fig. 7). Compared to the entire time period, the most recent epoch of AGCD data (2005–2020) contains most of the widespread extremes, while the localised extremes often occur outside of the last 15 years (comparing black crosses with black dots in Fig. 6, 7).
Average recurrence intervals (ARIs) of TC-related localised rainfall (top panel) and widespread rainfall (lower panel) for the calibrated ERA5 reanalysis as compared to AGCD. The 95% confidence intervals curves are represented by dotted lines in the appropriate colour.
As in Fig. 6 but for the BARRA1 reanalysis. Localised rainfall ARIs are in the top panel, while widespread rainfall ARIs are in the lower panel.
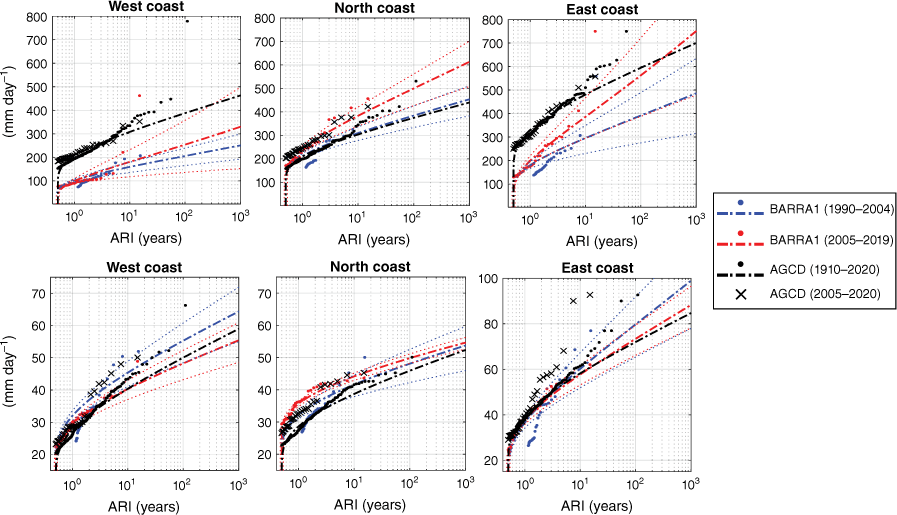
Comparing the ARIs calculated over different time slices for ERA5 and BARRA1 reveals quite variable results, although most of the curves stay within uncertainty ranges. For example, localised extremes generally increase in BARRA1 across all regions (Fig. 7 top panel). However, in ERA5, this is not the case for the east coast (Fig. 6 top-right panel), and inclusion of the earlier 1980s period (‘grey curves’) raises doubts about any conclusive climate trends occurring on the north-western coastlines.
Widespread rainfall extremes appear to increase slightly in ERA5 (Fig. 6 lower panel), but there is no obvious change, or perhaps a small decrease for opposing ends of Australian coastlines in BARRA1 (Fig. 7 lower panel).
3.3 Fractional contribution of TC rainfall
We determine the fractional contribution of TCs to widespread rainfall totals on climate timescales (includes rainfall contributions from every month of the year) in each of our three coastal regions and datasets (Table 2). Results indicate a possible increase of the fractional contribution for TCs to widespread rainfall by a small amount on north-western Australian coastlines (based on the agreement between the datasets used here) in recent years. Results for the eastern coastline are less clear. We also note the added uncertainty of limited TC data coverage preceding the 1980s, potentially leading to an underestimation of the TC contribution to AGCD rainfall during this period.
| Full period (%) | Later epoch (%) | ||
|---|---|---|---|
| West coast | |||
| AGCD | 31 | 35 | |
| ERA5 | 29 | 32 | |
| BARRA1 | 24 | 25 | |
| North coast | |||
| AGCD | 19 | 24 | |
| ERA5 | 22 | 25 | |
| BARRA1 | 19 | 20 | |
| East coast | |||
| AGCD | 18 | 17 | |
| ERA5 | 16 | 17 | |
| BARRA1 | 13 | 13 | |
‘Full period’ refers to rainfall during 1910–2020 for ACGD, 1979–2022 for ERA5 and 1990–2019 for BARRA1. ‘Later epoch’ refers to rainfall since 1990 for ACGD and since 2005 for ERA5 and BARRA1. Changes in total rainfall over these regions are negligible over climate time-scales.
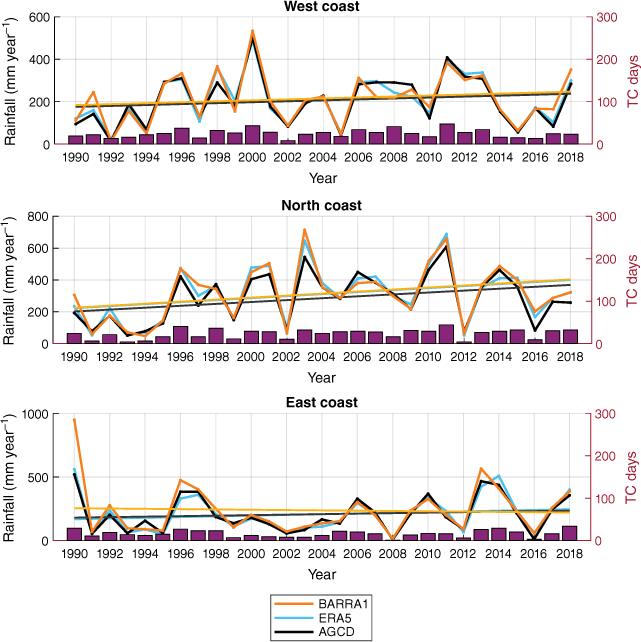
To further strengthen our conclusions pertaining to increased fractional contribution we consider annualised widespread TC rainfall totals with respect to regional TC days (Fig. 8). For the north coast region, annual rainfall counts significantly increase during 1990–2018 concurrent with significantly increasing TC days (based on the Mann–Kendall statistic, not shown). Trends for the western and eastern regions are not significant between any of the datasets or in TC days. Overall, this strengthens our conclusion of a potential increase of rainfall on average per TC, particularly for the western region.
4Discussion and conclusion
The disagreement in trends of these datasets, especially when considering daily localised rainfall, reminds us that basing conclusions from one set of data and for one time period (that can be relatively limited for extreme event sample size) on a meteorological quantity as complex as TC-rainfall is often imprudent. These complexities include noting the high interannual variability in TC occurrence and rainfall for Australia in general, making it challenging to confidently determine long-term climate change trends (e.g. Dare 2013; Lavender and Abbs 2013; Dowdy 2014; Chand et al. 2019).
Prior studies (e.g. Roca et al. 2019; Bador et al. 2020) have shown quite diverse estimates of extreme precipitation between different coarse (>50 km) reanalysis datasets and stressed the importance of careful selection when using these types of products for scientific analysis. Finer scale reanalyses (<30 km) such as BARRA1 and ERA5 may be more suitable for analyses on TC-rainfall, as increased model resolution can improve representation of high threshold events (Jermey and Renshaw 2016; Hersbach et al. 2020; Su et al. 2021).
Moreover, all reanalyses and climate analyses (such as AGCD) have inherent systematic biases. The bias comes from two parts: the inherent bias, derived from rainfall fields being increasingly smoothed out with an increasing coarser grid; and the modelling bias, which can be found in either of the two datatypes. For instance, convective parameterisation schemes can provide too much light rainfall and underdo heavy rainfall, and consistently put rainfall at the wrong locations. Quantile mapping, as applied here, can only partly address the inherent bias, and can also add its own bias to the data. Overall, there are fundamental limitations to comparing these datasets, and analyses undertaken on extreme values can be more susceptible to ambiguity than those on mean state comparisons.
BARRA1 performed as expected and did not severely deviate from the other products. We note that as the first release of a new-style product, BARRA1 can be considered quite junior compared to a product such as ERA5 that has been developed over time through a number of previous editions. BARRA1 also has more significant limitations and a shorter time period, which is to be addressed in BARRA (ver. 2.0, BARRA2, Su et al. 2022) that is expected to be released in late 2023. BARRA2 may improve certain aspects that could result in changes to the TC-rainfall recurrence and trends presented here. These improvements include the use of updated physics that can deal with single grid-cell storms that produce unrealistically high values (including rainfall) that could have had a small effect on some of the widespread rainfall values used in this paper. BARRA2 will also provide meteorological data over an extended time period back to 1979, and additionally a kilometre-scale downscaled reanalysis that does not use convection parameterisation.
In contrast to the trend analysis for TC-related rainfall, there is relatively good agreement between datasets on the fractional contribution and annualised totals of TC rainfall over the same regions. Our climatological contribution percentage values are consistent with previous studies in Australia (e.g. Dare et al. 2012; Villarini and Denniston 2015), which found higher TC contributions to total rainfall on the west compared to the east coast. Additionally, our findings indicate a trend towards an increased fractional contribution of TC rainfall (i.e. TC-related rainfall as a fraction of all rainfall). Considering this result together with the long-term climate change trend towards fewer TCs in the Australian region over recent decades (Dowdy 2014; Chand et al. 2019, 2022) suggests a trend towards more intense rainfall on average per TC, consistent with the results of Lavender and Abbs (2013). This has also been suggested from studies in other regions of the world including North America and based on a range of different study approaches (Walsh and Pittock 1998; Van Oldenborgh et al. 2017; Wang et al. 2018; Deo et al. 2021; Knutson et al. 2021).
One of the main experimental aims of this paper was to apply ARIs to TC rainfall much like they are applied to extreme wind gusts in Standard AS/NZS 1170.2:2021 (Standards Australia 2021). The development of a ‘Rainfall-type standard’ could have similar benefits as those for wind loadings, for example in identifying expected flow rates from TCs, which is important for things like pipe diameter design. However, several limitations are identified by using ARIs on this type of data, including the large disagreement between datasets and the dependence on good calibration for accurately measuring climate change trends that may be better suited to metrics other than ARIs for TC rainfall.
Another aim of this paper was to develop a method to measure the occurrence of TC rainfall on three major coastal regions of Australia that can be easily applied to climate model data and could enable simpler comparisons across different climate model experiments. We note that the penetration of TC rainfall farther inland than the regions used here perhaps poses a more serious risk regarding historical flood events (particularly with how TC rainfall overlaps with catchments) but was outside the scope of this study. It is hoped that more confidence in any such climate trends in TC rainfall can be found by applying these methods or similar to moderate-resolution and kilometre-scale (4–20 km) RCMs. The application of these methods to RCMs is likely to occur within the framework of the Australian Climate Service programme recently started in Australia, which is designed to distribute key climate-related information tailored to specific end-users.
Data availability
The ERA5 reanalysis data were downloaded from the Copernicus Climate Change Service (Hersbach et al. 2023). Best-track tropical cyclone data were downloaded from The Bureau’s website (see http://www.bom.gov.au/cyclone/tropical-cyclone-knowledge-centre/databases/). BARRA1 data are published on and accessed through NCI (https://doi.org/10.25914/6198bcb35c1c9). For data specific to this study (e.g. TC rainfall time series for different datasets), please contact Samuel Bell (samuel.bell@bom.gov.au).
Declaration of funding
This work was supported by funding from the Earth Systems and Climate Change (ESCC) Hub of the Australian Government’s National Science Program (NESP).
References
Bador M, Boé J, Terray L, Alexander LV, Baker A, Bellucci A, Haarsma R, Koenigk T, Moine M, Lohmann K, Putrasahan DA, Roberts C, Roberts M, Scoccimarro E, Schiemann R, Seddon J, Senan R, Valcke S, Vanniere B (2020) Impact of higher spatial atmospheric resolution on precipitation extremes over land in global climate models. Journal of Geophysical Research: Atmospheres 125(13),.
| Crossref | Google Scholar |
Bell SS, Chand S, Dowdy A, Ramsay H, Deo A, Su C-H, et al. (2021) Australian tropical cyclone-induced extreme coastal winds in climate datasets. Research Report 56. (Bureau of Meteorology) Available at http://www.bom.gov.au/research/publications/researchreports/BRR-056.pdf [Verified 15 August 2022]
Bell SS, Dowdy AJ, Ramsay HA, et al. (2022) Using historical tropical cyclone climate datasets to examine wind speed recurrence for coastal Australia. Scientific Reports 12, 11612.
| Crossref | Google Scholar |
Callaghan J, Power SB (2011) Variability and decline in the number of severe tropical cyclones making land-fall over eastern Australia since the late nineteenth century. Climate Dynamics 37, 647-662.
| Crossref | Google Scholar |
Chand SS, Dowdy AJ, Ramsay HA, et al. (2019) Review of tropical cyclones in the Australian region: climatology, variability, predictability, and trends. WIREs Climate Change 10, e602.
| Crossref | Google Scholar |
Chand SS, Walsh KJE, Camargo SJ, et al. (2022) Declining tropical cyclone frequency under global warming. Nature Climate Change 12, 655-661.
| Crossref | Google Scholar |
Chen Y, Ebert EE, Walsh KJE, Davidson NE (2013) Evaluation of TMPA 3B42 daily precipitation estimates of tropical cyclone rainfall over Australia. Journal of Geophysical Research Atmosphere 118, 11 966-11 978.
| Crossref | Google Scholar |
Chubb TH, Manton MJ, Siems ST, Peace AD (2016) Evaluation of the AWAP daily precipitation spatial analysis with an independent gauge network in the Snowy Mountains. Journal of Southern Hemisphere Earth Systems Science 66, 55-67.
| Crossref | Google Scholar |
Dare RA (2013) Seasonal tropical cyclone rain volumes over Australia. Journal of Climate 26, 5958-5964.
| Crossref | Google Scholar |
Dare RA, Davidson NE, McBride JL (2012) Tropical cyclone contribution to rainfall over Australia. Monthly Weather Review 140, 3606-3619.
| Crossref | Google Scholar |
Deo A, Chand SS, Ramsay HA, et al. (2021) Tropical cyclone contribution to extreme rainfall over southwest Pacific Island nations. Climate Dynamics 56, 3967-3993.
| Crossref | Google Scholar |
Dowdy AJ (2014) Long-term changes in Australian tropical cyclone numbers. Atmospheric Science Letters 15, 292-298.
| Crossref | Google Scholar |
Dowdy AJ, Kuleshov Y (2012) An analysis of TC occurrence in the Southern Hemisphere derived from a new satellite-era dataset. International Journal of Remote Sensing 23, 7382-7397.
| Crossref | Google Scholar |
Hersbach H, Bell B, Berrisford P, Hirahara S, Horányi A, Muñoz‐Sabater J, Nicolas J, Peubey C, Radu R, Schepers D, Simmons A, Soci C, Abdalla S, Abellan X, Balsamo G, Bechtold P, Biavati G, Bidlot J, Bonavita M, De Chiara G, Dahlgren P, Dee D, Diamantakis M, Dragani R, Flemming J, Forbes R, Fuentes M, Geer A, Haimberger L, Healy S, Hogan RJ, Hólm E, Janisková M, Keeley S, Laloyaux P, Lopez P, Lupu C, Radnoti G, de Rosnay P, Rozum I, Vamborg F, Villaume S, Thépaut J (2020) The ERA5 global reanalysis. Quarterly Journal of the Royal Meteorological Society 146(730), 1999-2049.
| Crossref | Google Scholar |
Hersbach H, Bell B, Berrisford P, Biavati G, Horányi A, Muñoz Sabater J, Nicolas J, Peubey C, Radu R, Rozum I, Schepers D, Simmons A, Soci C, Dee D, Thépaut J-N (2023) ‘ERA5 hourly data on single levels from 1940 to present.’ (Copernicus Climate Change Service, C3S; and Climate Data Store, CDS) 10.24381/cds.adbb2d47
Jalowska AM, Spero TL, Bowden JH (2021) Projecting changes in extreme rainfall from three tropical cyclones using the design-rainfall approach. npj Climate Atmospheric Science 4, 23.
| Crossref | Google Scholar |
Jermey PM, Renshaw RJ (2016) Precipitation representation over a two-year period in regional reanalysis. Quarterly Journal of the Royal Meteorological Society 142, 1300-1310.
| Crossref | Google Scholar |
Jones DA, Wang W, Fawcett R (2009) High-quality spatial climate data-sets for Australia. Australian Meteorological and Oceanographic Journal 58, 233-248.
| Google Scholar |
Knutson TR, Chung MV, Vecchi G, Sun J, Hsieh TL, Smith AJ (2021) Climate change is probably increasing the intensity of tropical cyclones. In ‘ScienceBrief Review’, March 2021. (Tyndall Centre for Climate Change Research, University of East Anglia: Norwich, UK) Available at https://tyndall.ac.uk/wp-content/uploads/2021/03/sciencebrief_review_cyclones_mar2021.pdf
Lavender SL, Abbs DJ (2013) Trends in Australian rainfall: contribution of tropical cyclones and closed lows. Climate Dynamics 40, 317-326.
| Crossref | Google Scholar |
Mann HB (1945) Non-parametric tests against trend. Econometrica 13, 163-171.
| Google Scholar |
Masson-Delmotte V, Zhai P, Pirani A, Connors SL, Péan C, Berger S, Caud N, Chen Y, Goldfarb L, GomisMI, Huang M, Leitzell K, Lonnoy E, Matthews JBR, Maycock TK, Waterfield T, YelekçiO, Yu R, Zhou B (Eds) (2021) Summary for policymakers. In: Climate Change 2021: the Physical Science Basis. In ‘Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change’. pp. 3–32. (Cambridge University Press: Cambridge, UK, and New York, NY, USA) 10.1017/9781009157896.001
Roca R, Alexander LV, Potter G, Bador M, Jucá R, Contractor S, Bosilovich MG, Cloché S (2019) FROGS: a daily 1° × 1° gridded precipitation database of rain gauge, satellite and reanalysis products. Earth System Science Data 11(3), 1017-1035.
| Crossref | Google Scholar |
Standards Australia (2021) Structural design actions, part 2: wind actions, AS/NZS 1170.2:2021. (Standards Australia Ltd) Available at https://store.standards.org.au/product/as-nzs-1170-2-2021
Stansfield AM, Reed KA, Zarzycki CM, Ullrich PA, Chavas DR (2020) Assessing tropical cyclones’ contribution to precipitation over the eastern United States and sensitivity to the variable-resolution domain extent. Journal of Hydrometeorology 21, 1425-1445.
| Crossref | Google Scholar |
Su C-H, Eizenberg N, Steinle P, Jakob D, Fox-Hughes P, White CJ, et al. (2019) BARRA v1.0: the Bureau of Meteorology atmospheric high-resolution regional reanalysis for Australia. Geoscientific Model Development 12, 2049-2068.
| Crossref | Google Scholar |
Su C-H, Eizenberg N, Steinle P, Jakob D, Fox-Hughes P, White CJ, Franklin C (2021) BARRA v1.0: kilometre-scale downscaling of an Australian regional atmospheric reanalysis over four midlatitude domains. Geoscientific Model Development 14, 4357-4378.
| Crossref | Google Scholar |
Su C-H, Rennie S, Dharssi I, Torrance J, Smith A, Le T, et al. (2022) BARRA2: Development of the next-generation Australian regional atmospheric reanalysis. Research Report 67. (Bureau of Meteorology) Available at http://www.bom.gov.au/research/publications/researchreports/BRR-067.pdf [Verified 4 May 2023]
Torn RD, Snyder C (2012) Uncertainty of tropical cyclone best-track information. Weather and Forecasting 27, 715-729.
| Crossref | Google Scholar |
Van Oldenborgh GJ, Van Der Wiel K, Sebastian A, Singh R, Arrighi J, Otto F, Haustein K, Li S, Vecchi G, Cullen H (2017) Attribution of extreme rainfall from Hurricane Harvey, August 2017. Environmental Research Letters 12(12), 124009.
| Crossref | Google Scholar |
Villarini G, Denniston RF (2015) Contribution of tropical cyclones to extreme rainfall in Australia. International Journal of Climatology 36(2), 1019-1025.
| Crossref | Google Scholar |
Walsh K, Pittock AB (1998) Potential changes in tropical storms, hurricanes, and extreme rainfall events as a result of climate change. Climatic Change 39, 199-213.
| Crossref | Google Scholar |
Wang SS, Zhao L, Yoon JH, Klotzbach P, Gillies RR (2018) Quantitative attribution of climate effects on Hurricane Harvey’s extreme rainfall in Texas. Environmental Research Letters 13, 054014.
| Crossref | Google Scholar |