Assessing toxicity of mining effluents: equilibrium- and kinetics-based metal speciation and algal bioassay
Yamini Gopalapillai A B , Chuni L. Chakrabarti A D and David R. S. Lean CA Ottawa-Carleton Chemistry Institute, Department of Chemistry, Carleton University, 1125 Colonel By Drive, Ottawa, ON, K1S 5B6, Canada.
B Present address: University of Guelph, Land Resource Science, 50 Stone Road East, Guelph, ON, N1G 2W1, Canada.
C Department of Biology, University of Ottawa, 30 Marie Currie Private, PO Box 450, Station A, Ottawa, ON, K1N 6N5, Canada.
D Corresponding author. Email: chuni_chakrabarti@carleton.ca
Environmental Chemistry 5(4) 307-315 https://doi.org/10.1071/EN08027
Submitted: 23 April 2008 Accepted: 15 July 2008 Published: 19 August 2008
Environmental context. The release of mining effluents exposes natural waters to excess metals and thereby threatens both human and environmental health. The present study explores the toxicity of aqueous mining effluents collected from a mining area in Sudbury (Ontario, Canada), using two different methods for determination of metal speciation, and an algal toxicity study. The results show reasonable correlation between metal speciation and the observed toxicity and suggest the importance of taking into account other factors related to water quality criteria such as nutrient concentrations, diluent water and presence of other toxic metals that can greatly influence the toxicological result.
Abstract. The present study explores the toxicity of aqueous mining and municipal effluents from the Sudbury area (Canada) using equilibrium- and kinetics-based estimates of metal speciation and chronic toxicity studies using algae (Pseudokirchneriella subcapitata). Free metal ion concentration was determined by the Ion Exchange Technique (IET) and a computer speciation code, Windermere Humic Aqueous Model (WHAM) VI. Labile metal concentration was determined using the Competing Ligand Exchange Method. In general, no correlation was found between the observed IC25 (concentration of test substance that inhibits growth of organism by 25%) and the [Ni]labile, [Ni2+]IET or [Ni2+]WHAM, probably because of contributions by other metals such as Cu and Zn being also significant. Reasonable correlation (r2 = 0.7575) was found when the observed toxicity was compared with the sum of free metal ions of Cu, Ni, and Zn predicted by WHAM. The results of the present study reveal the importance of taking into account other factors related to water quality criteria such as nutrient concentrations, diluent water, and the presence of other toxic metals, which greatly influence the toxicological result in complex, multi-metal contaminated waters.
Additional keywords: algae, bioavailability, chronic toxicity, metal speciation, mining effluents.
Introduction
Aqueous mining effluents are a persistent threat to human and environmental health.[1] A well-known example of a nickel contamination source in Canada is the nickel smelter in Sudbury (Ontario). In Canada, the new Metal Mining Effluent Regulations (MMER) require mines to assess the possibility for chronic effects of effluents via Environmental Effects Monitoring (EEM) studies and a set of laboratory-based chronic toxicity tests.[2] However, the window between the concentration where nickel is an essential nutrient to aquatic organisms[3] and where it becomes toxic requires further evaluation. This uncertainty is due to lack of convenient, sensitive methods for determination of speciation of nickel in environmental samples containing appreciable concentrations of dissolved organic matter. Most importantly, the link between geochemical speciation of nickel in aqueous mining effluents and its bioavailability and toxicity to aquatic biota is still unclear.
Metal speciation, defined as the quantitative distribution of an element between its free and complexed forms,[4,5] is influenced by the presence of ligands such as dissolved organic carbon (DOC). DOC consists mainly of humic substances (HS) (approx. 50–90% of DOC).[6] Metals complexed with HS are often less bioavailable to aquatic biota[7,8]; however, some studies have found that HS may increase uptake of metals by increasing algal membrane permeability[9] or by formation of a ternary complex between the metal, humic acid, and algal surface.[10] According to a new view of humic substances recently proposed by Sutton and Sposito,[11] they are collections of diverse, relatively low molecular mass components forming dynamic associations and stabilised by hydrophobic interactions and hydrogen bonds. These associations are capable of organising into micellar structures in suitable aqueous environments. HS–metal complexation is affected by factors such as charge, binding sites distribution, variable reaction stoichiometry and the competitive nature of the ion binding.[12]
Labile metal species may be indicators of metal bioavailability[13]; however, the free metal ion concentration is generally believed to be a better predictor of bioavailability.[6] The kinetic-control model assumes the rate of metal uptake by the organism is fast compared with the rate of diffusion of the metal species to the cell surface (i.e. the biotic ligand). As this will create a concentration gradient surrounding the cell surface, the labile metal complexes will dissociate to offset the disruption in the chemical equilibrium near the cell surface. Examples of samples under kinetic control have been illustrated previously,[14] particularly at low free metal ion concentrations for organisms with high membrane permeability and thus high metal uptake rates. The Free Ion Activity Model (FIAM) is based on thermodynamic control of metal bioavailability. This equilibrium basis assumes that the rate of metal uptake across a cell surface is comparatively slow compared with the rate of diffusion to the cell surface, and the surface-bound metal rapidly comes into pseudo-equilibrium with the metal in the bulk solution.[15] Exceptions to this assumption were found to be rare. In fact, 52 out of 59 cases conformed to the assumption[16] and validated the applicability of FIAM. Recently, the Gill Surface Interaction Model (GSIM)[17] has been combined with FIAM concepts to form the Biotic Ligand Model (BLM). This model envisages that toxicity is due to accumulation of metal at physiologically active sites such as the gill in fish. The BLM approach has already received wide acceptance and has been incorporated in the regulatory framework for copper by the US Environmental Protection Agency (EPA).[18]
The objective of the present research was to assess the toxicity of nickel-contaminated aqueous mining effluents to aquatic freshwater organisms using algal bioassays, and both equilibrium- and kinetics-based estimates of nickel speciation, which has rarely been done earlier. Free ion concentration in the Sudbury mining effluent samples was evaluated by the Ion Exchange Technique (IET),[19] and a computer speciation code, Windermere Humic Aqueous Model (WHAM) VI, and the labile metal concentration was determined by the Competing Ligand Exchange Method (CLEM). An additional objective of the present study was to test the hypothesis that BLM (WHAM VI) is a satisfactory model to predict toxicity to freshwater biota in complex natural waters containing multi-metal mixtures and dissolved organic matter.
Analytical models
Ion Exchange Technique (IET): equilibrium-based
Ion exchange theory for equilibria, kinetics and mixed systems was critically reviewed and revised in 1962 by Helfferich.[20] IET was later applied by Cantwell et al.[21] and Fortin and Campbell[22] for metal speciation in solution. IET involves a simple concept in which the ions in the sample solution exchange with ion exchangers of a strong acid cation resin, by which a relationship between the concentrations of metal adsorbed to the resin and the free metal ion can be established.[23] Gopalapillai et al.[19] have provided a detailed account of IET theory and procedure.
Competing Ligand Exchange Method (CLEM): kinetics-based
A modified version[24,25] of the kinetic model originally proposed by Olson and Shuman[26] was utilised to investigate the kinetic speciation of nickel and copper in aqueous mining and municipal effluents. Mandal et al.[27] published a comprehensive description of the model.
Experimental
Materials and reagents
All solutions were prepared with ultrapure water (resistivity 18.2 MΩ-cm), which was obtained direct from a Nanopure Diamond purification system (Barnstead International, Dubuque, IO, USA) fitted with a purifying column to remove organic matter. Standard solutions containing NiII and CuII separately were prepared by dilution of 1000 mg L–1 high-purity nickel and copper aqueous standards (Inductively Coupled Plasma grade, purchased from SCP Science, Montreal, Canada). This standard was used to prepare working standards for graphite furnace atomic absorption spectrometry (GFAAS) by serial dilution; the diluted standards were acidified to contain 1% (v/v) ultrapure nitric acid (Baseline, Seastar Chemicals, Sydney, BC, Canada) in order to prevent metal loss by adsorption on the container walls. For pH adjustments, a 0.1 M (mol L–1) sodium hydroxide solution was prepared by dissolving sodium hydroxide pellets (puriss. p.a. reagent American Chemical Society, Riedel-de Haën, Seelze, Germany) in ultrapure water, and ultrapure nitric acid (Baseline, Seastar Chemicals) was used to prepare a 1.5 M HNO3 solution. The pH of samples was measured using an Accumet 20 pH meter (Fisher, Ottawa, ON, Canada).
Containers for water samples
All sample containers were made of Teflon and were precleaned by soaking in 10% (v/v) HNO3 (AR grade) for 1 week at room temperature, followed by five rinses with ultrapure water. The containers were kept filled with ultrapure water until used.[28]
Aqueous mining and municipal effluent samples
Aqueous mining and municipal effluent samples were collected in May 2006 from several sampling sites in the Sudbury area using precleaned Teflon bottles. The samples were collected at discharge points of the treatment plants including Crean Hill Mine, Garson Mine, Whistle Mine, Copper Cliff Waste Water Treatment Plant (WWTP), Nolin Creek WWTP, and Sudbury Municipal WWTP. The samples were transported immediately to the laboratory and filtered within 48 h of collection through 0.45-μm membrane filters (AquaPrep 600 Capsules, Pall Corporation, East Hills, NY, USA) to remove particulate matter. A small subsample of the filtered sample was acidified to contain 1% (v/v) ultrapure nitric acid; the subsamples were analysed for total metal, major cation and major anion concentrations. The remaining samples were stored in acid-washed[28] Teflon containers and refrigerated (in the dark) at 4°C until the experiments. DOC levels in the samples were determined using a Shimadzu TOC analyser (Columbia, MD, USA).
Algal bioassay
Algal bioassays were performed to examine toxicity of metal species in the Sudbury aqueous mining and municipal effluents. The bioassays were performed in accordance with the Environment Canada[29] protocol for algal bioassays using the green alga, Pseudokirchneriella subcapitata (previously known as Selenastrum capricornutum). This alga was used as the test species because it is known to be one of the most sensitive species for metal toxicity testing.[30] As phosphate concentrations found in the effluents are often high, we anticipated problems due to algal growth stimulation[27] by increasing phosphate levels to four times that in the original protocol. Modifications to the above-cited protocol also included the omission of ethylenediaminetetraacetic acid (EDTA) from the test medium. EDTA was avoided in order to prevent its complexation with metals, which may mask their true toxicity. Preliminary algal growth tests with the modified medium showed normal exponential growth in the stock culture. P. subcapitata (University of Toronto Culture Collection (UTCC) strain #37) was grown axenically in 250-mL glass Erlenmeyer flasks using the Environment Canada growth medium[29] at 24 ± 2°C under continuous cool white fluorescent light at 100 mmol m–2 s–1, and on a continuous shaker at 100 rpm. The cultures were renewed weekly under sterile conditions. Purity of the stock culture was verified before each transfer by examination under a microscope. Contamination of microorganisms that cannot be detected under a microscope was verified monthly by transferring 1 mL of the algal culture onto a Petri dish containing a solid bacterial nutrient (e.g. Standard Plate Count Agar) that was incubated at 37.5°C for 48 h.
In order to derive IC25 (concentration of test substance that inhibits growth of organism by 25%), a series of eight effluent dilutions in laboratory water (ultrapure, 18 MΩ-cm resistivity) were prepared, for example 100, 80, 40, 20, 10, 5, 2, and 0% (v/v) of effluent water. Test samples were equilibrated to room temperature before experiment. The stock algal cells were washed and centrifuged following the Environment Canada protocol[29] to remove traces of EDTA and achieve the appropriate algal cell density in the test flasks. The tests were conducted in triplicate in 50-mL glass Erlenmeyer flasks covered with aerated tin foil (punched with mini holes using a micro-syringe) and incubated for 72 h at 24°C under continuous cool white fluorescent lights (100 mmol m–2 s–1), on a continuous shaker at 100 rpm. Each test flask received 10 mL of the test solution and was inoculated with 600 μL of algal suspension (500 μL nutrient spike + 100 μL of 106 cells mL–1 algal stock solution) to maintain a final algal density of 10 000 cells mL–1 and final nutrient concentrations as specified in the Environment Canada protocol,[29] with the exception of K2HPO4 (4.16 mg L–1 in growth and test medium) and EDTA (not included in the test medium). The pH of the samples was tested before and after the experiment to ensure no drastic pH changes had occurred during the course of the experiment. Each experiment included blank (diluent water) flasks in triplicate.
As growth was stimulated by addition of effluent (see results), toxicity tests were reproduced for Garson Mine effluent and Copper Cliff WWTP using Vermillion River water (receiving river) as diluent instead of laboratory (ultrapure) water. Some of the water quality parameters of the Vermillion River water include pH 6.7, conductivity 20.1 mS m–1, [DOC] 9.91 mg L–1, and hardness 1.30 mM. In order to asses the effect of water quality on metal toxicity, Ni and Cu were added in the laboratory water and the Vermillion River water independently, for concentrations ranging from 0 to 3.4 μM and 0 to 1.6 μM, respectively. Effect of addition of nutrients (phosphate, nitrate and Zn) on algal growth in the laboratory water was also studied.
After the incubation period, the test samples in flasks, with algae settled to the bottom, were resuspended with a pipette before transferring a 220-μL subsample into a well in a 96-well microplate. Algal growth was determined by measuring chlorophyll a fluorescence using a Molecular Devices Corporation SPECTRAmax GEMINI XS dual-scanning microplate spectrofluorometer (Sunnyvale, CA, USA) (excitation wavelength 465 nm, emission wavelength 685 nm). Chlorophyll a fluorescence for algae was calibrated using fluorescence of a series of diluted suspensions of Pseudokirchneriella subcapitata (from algal stock) against repeated manual cell counts with a haemocytometer (minimum of six times). To ensure reproducible measures of cell concentration during the experiments, the calibration was tested with one sample (minimum of six manual cell counts) before every experiment. The fluorescence method was previously shown to be a more accurate approach than manual cell counting.[31] Algal growth was determined from fluorescence using the established calibration curve. Percentage of growth inhibition v. log of percentage sample was plotted, and the linear section of the curve was isolated and analysed by linear regression. IC25 was calculated from the resulting regression equation for the curve and was also calculated using the software ICPIN.[32]
Quality control was assessed with copper and nickel standards to ensure that the algal cells were healthy. The test was conducted with Cu(NO3)2 (0–1.6 μM) and Ni(NO3)2 (0–3.4 μM) in laboratory water using the same algal inoculation as for the tests (10 000 cells mL–1). The last column in each microplate was a blank for the spectrofluorometer that included the diluent water and nutrient spike but no algae or metals.
The original protocol[29] suggested the use of 96-well non-treated flat-bottomed polystyrene microplates for the test incubation instead of flasks. However, preliminary tests using Nalge Nunc International (Rochester, NY, USA) non-treated flat-bottomed polystyrene microplates showed algal growth inhibition in the control microplates. The reasons for the inhibition are unknown. However, it is likely that the flat-bottomed microplates do not allow favourable suspension of the algae in the growth media. Thus, the u-bottomed microplates may have provided a more favourable chamber for healthy algal growth and should be evaluated in future studies.
Competing Ligand Exchange Method
CLEM/GFAAS was used as follows: 3 g (1% w/v) of Chelex-100 (Bio-Rad, Hercules, CA, USA) was added to 300 mL of sample in the cylindrical Teflon Reactor. The previously filtered effluent sample was filtered with an online 0.45-μm polycarbonate membrane filter to separate the Chelex resin from the filtrate. Aliquots of the filtrate were collected and the Ni and Cu concentrations were determined using GFAAS.
Predictions of Windermere Humic Aqueous Model (WHAM) VI
The computer speciation code, WHAM VI,[33] was used to determine the free metal ion concentrations of NiII, CuII, and ZnII in the effluent water samples. A detailed explanation of the WHAM VI parameters used in the present work has been provided earlier.[19]
Results and discussion
Nickel speciation
Major cation and anion concentrations and trace metal concentrations in the Sudbury effluent samples were reported previously.[19] Crean Hill Mine and Garson Mine aqueous effluents have elevated total nickel concentrations of 1.76 and 2.33 μM, respectively. Copper Cliff WWTP aqueous effluent had high copper and zinc concentrations of ~2.70 μM. A high concentration of sulfate (15.9 mM) was found in Copper Cliff WWTP and an elevated concentration of phosphate (3.37 μM) was observed in Sudbury WWTP. In addition, calcium concentrations were high in Copper Cliff WWTP (11.5 mM) and in Garson Mine effluent (6.10 mM). Such concentrations of major cations (Ca2+ or Mg2+) can increase the release of bound nickel as free Ni2+ from labile nickel complexes.[34] High concentrations of cations and anions are usually present in aqueous effluent samples as a result of effluent treatment activities before the treated effluents are released to the freshwater systems.
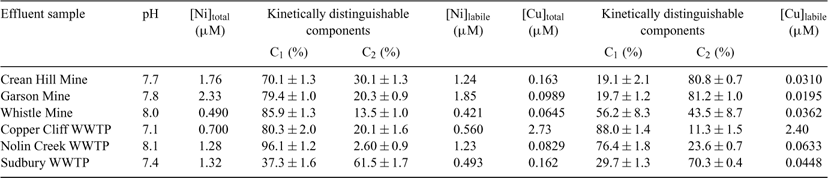
Labile nickel ([Ni]labile) and copper concentrations ([Cu]labile) were determined in the same samples by CLEM/GFAAS. [Cu]labile was also measured because copper had a significant presence in the effluent samples. The results were used to aid in the interpretation of the toxicity results discussed later in the current paper. Kinetically distinguishable components of the nickel and copper complexes in the test samples are presented in Table 1. The pH of the test samples ranged from 7.1 to 8.1. The fastest kinetically distinguishable component (C1) represents ~37–96% of the total NiII–DOC complexes and 19–88% of the total CuII –DOC complexes.
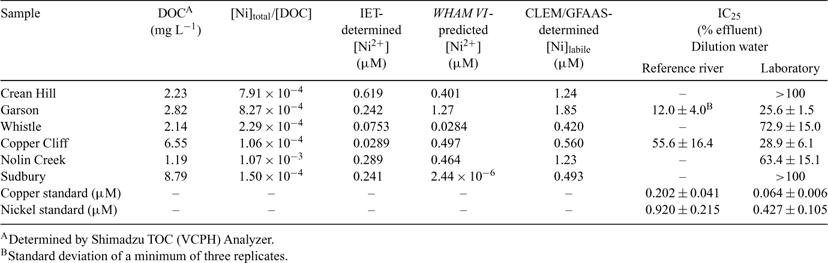
In Table 2, a comparison of nickel speciation and toxicity results is presented. Free nickel ion concentrations determined by IET ([Ni2+]IET) and those predicted by WHAM VI ([Ni2+]WHAM) have been reported previously.[19] Crean Hill Mine effluent had a Ni-to-DOC ratio of 7.91 × 10–4 and Nolin Creek WWTP aqueous effluent had a ratio of 1.07 × 10–3, which amounts to a 1.3-fold difference. [Ni2+]IET was 2.1-fold lower for Nolin Creek compared with Crean Hill; however, the [Ni2+]WHAM and the measured [Ni]labile were similar for both samples. As expected, [Ni]labile was higher than [Ni2+]IET for all samples. For WHAM VI predictions, 40% of the DOC was assumed to be active based on the best fit, and the estimates by Morel and Hering,[8] who have suggested that ~50% of DOC is found as humic substances. According to the WHAM VI predictions, Garson Mine aqueous effluent had the highest [Ni2+]WHAM (1.27 μM); however, [Ni2+]IET was much lower (0.242 μM) and less than [Ni2+]IET for Crean Hill Mine effluent (0.619 μM). The equilibrium IET is highly dependent of cationic composition of the sample. Indeed, for [Ni2+] evaluation using this technique, it is expected to take into account: ionic strength and pH, as well as contribution of other major cations. When [Ni2+]IET is much lower than [Ni2+]WHAM, such as in Garson Mine and Copper Cliff WWTP, it is interesting to note that cationic components are present in high concentrations (total major cation concentrations of 10.0 mM and 19.2 mM, respectively),[19] which could in part explain the underestimation of [Ni2+] measured by IET.
|
Interestingly, for Sudbury WWTP, [Ni2+]WHAM was excessively lower than [Ni2+]IET (approx. 105 fold). This low value may be due to errors in the measured high DOC concentration (8.79 mg L–1), which may have overestimated nickel complexation. It is also important to consider that a drawback in the WHAM modelling for real samples is that it requires an input datum for the concentration of ‘active’ DOC (i.e. the concentration of DOC that behaves like an isolated fulvic acid and is actively involved in the binding of metals).[33] This is an important parameter because it determines the number of binding sites available to the metals. WHAM VI’s underestimation of [Ni2+] in Sudbury WWTP compared with the measured [Ni2+]IET may also be due to the presence of anthropogenic organic matter, which most likely has different characteristics from the humic substances used in the calibration of WHAM. However, it is difficult to fully explain the differences between the WHAM VI predictions and the measured values of free nickel concentration because of the complexity of the samples. There are possible deficiencies, both in the wider application of such a simple model as WHAM to independent datasets, and artefacts associated with differences in analytical methods or experimental design. For all other samples, the predictions were either close to the measured values, or they slightly overestimated [Ni2+].
Fig. 1 illustrates the effect of nickel-to-DOC ratio on [Ni2+]IET and [Ni]labile (measured by CLEM/GFAAS) in the mining and municipal effluent water samples collected from the Sudbury area. Ni-to-DOC ratio was previously shown to correlate with both the release of free Ni2+ and the resulting toxicity of nickel-polluted effluent waters.[21] Fig. 1 shows that, in general, [Ni2+]IET increases with increasing nickel-to-DOC ratio. Similarly, [Ni]labile also tends to increase with increasing nickel-to-DOC ratio, although to a smaller degree. As the Ni-to-DOC ratio increases, the strong binding sites will be fully occupied (~1–10% of the total binding sites of the DOC) leaving the nickel to then bind to weak sites (~99–90% of the total binding sites of the DOC).[35] Hence, the weakly bound nickel complexes will be labile and will release free Ni2+. The results show that the Ni-to-DOC ratio correlated better with the measured [Ni2+]IET (r2 = 0.911) than with the measured labile nickel complexes(r2 = 0.784) (Fig. 1). If bioavailability can be correlated with [Ni2+], then a technique that gives [Ni2+] will be better than a technique that yields labile metal concentration in order to provide a reliable indicator for bioavailability.

|
Algal toxicity studies
The algal (Pseudokirchneriella subcapitata) yield in the control flasks with laboratory (ultrapure) water was from 3 × 105 to 5 × 105 cells mL–1 after a 72-h growth period under continuous light. However, in control flasks with the Reference River (defining the receiving water, Vermillion River, as ‘Reference River’ henceforth), the algal yield was between 1.8 × 106 and 3.5 × 106 cells mL–1. The range in control biomass can be a result of variations in lag phase (up to several hours) and inoculation at different times of the exponential growth phase. The larger algal growth in the Reference River water may be due to exposure to additional nutrients. Differences in pH, [DOC], hardness and alkalinity between river water and laboratory water may also contribute to the differences in the control algal growth and toxicity observed.
An initial algal stimulation was observed in most of the effluent samples when diluted with the laboratory water (Fig. 2), followed by inhibition with greater amounts of the test sample. Similar observations were reported by others.[27,36,37] Fig. 2a shows the algal bioassay curve for Sudbury WWTP effluent sample. The algal growth was stimulated up to 60% of the test sample composition, after which a toxic effect of the effluent is detectable. As mentioned earlier, this sample was high in DOC levels (up to 7.4-fold higher than the other effluent samples) and in phosphate levels (up to 10.7-fold higher than the other effluent samples). The high DOC contributes to its greater complexation of trace metals, which reduces toxicity. The abundance in phosphate (3.37 μM), a well-known algal nutrient, may have had the greatest effect on the stimulation in Sudbury WWTP. This shows that it is difficult to avoid stimulation effects by adjusting nutrient content in the growth media as was attempted in the current study (4-fold increase in phosphate level from 1.04 mg L–1 to 4.16 mg L–1 than that in the original Environment Canada[29] recipe).

|
Fig. 2b, c illustrates algal bioassays for the mining effluent samples: Garson Mine effluent (b) and Copper Cliff WWTP (c), diluted in the Reference River water (Vermillion River) or the laboratory water (ultrapure water). It shows that algal growth is increased when Reference River water is used. However, the overall toxic effect of the effluent sample is still observed. For Garson Mine effluent, the observed toxicity in the Reference River water was greater (IC25 12.0 ± 4.0%) than that in the laboratory water (IC25 25.6 ± 1.5%) (Table 2). For Copper Cliff WWTP, the opposite effect was observed; the observed toxicity was lower in the Reference River water (IC25 55.6 ± 16.4%) than in the laboratory water (IC25 28.9 ± 6.1%). Similarly, toxicity was reduced in the Reference River water for the standard copper and nickel tests (Table 2). In addition, the stimulation effect, as seen in the laboratory water, is observed to a lesser extent when performed in the Reference River water. These findings suggest that using the receiving water instead of the laboratory water for studying toxicity of effluents may be a better approach, because the stimulation effect will be masked by the receiving water, and a more comprehensible toxic effect can be observed.
To further investigate the effect of added nutrients, a study was conducted with added zinc, phosphate and nitrate nutrients levels over a time-period of 72 h. The results were plotted as a percentage of growth in the control water in Fig. 3. Fig. 3a shows the effect of addition of 0.153 μM (10 μg L–1), 1.53 μM (100 μg L–1) and 3.06 μM (200 μg L–1) of zinc standard to the growth media. A stimulation effect was evident for a low concentration (0.153 μM) of zinc in the initial 24 h; however, this effect was diminished by the end of the third day. At the higher concentrations (1.53 and 3.06 μM) of zinc, the growth of algae was inhibited within 24 h. This indicates that the effluent samples with excess zinc concentrations (Copper Cliff WWTP) probably cause toxicity rather than stimulation. Fig. 3b shows that the added low phosphate concentration (0.526 μM or 0.05 mg P L–1) had a significant stimulation effect by the third day. Similarly, at the higher concentration (3.16 μM or 0.30 mg P L–1), stimulation was also observed, but at a greatly lower degree. The low concentration of added nitrate (24.2 μM or 1.5 mg N L–1) had a large stimulation effect by the third day, but the effect was again lower for the higher, 484 μM (30 mg N L–1) nitrate addition. Hence, increase in the phosphate or nitrate levels tended to stimulate algal growth even though the growth media presumably contain sufficient nutrients. However, the higher levels of phosphate and nitrate (3.16 μM and 484 μM, respectively), which are similar to the highest phosphate and nitrate concentrations measured in the effluent waters, were characterised by a decreased stimulation effect compared with the lower concentrations tested. This is probably because of the added effect of toxicity at such high levels and the eventual nutrient limitation that occurs with a high population density. It is also important to note that the stimulation tests were performed in laboratory water. Hence, complexation effects would have been lower than in the effluent or the receiving waters, and the effect in the effluent waters may be quite different for the same concentrations tested.

|
With respect to speciation, a previous study from our laboratory observed that dilution of the mining effluents with the Reference River water increased the percentage of nickel released from NiII–DOC complexes as measured by both CLEM using Adsorptive Cathodic Stripping Voltammetry (CLEM/AdCSV) and CLEM/GFAAS.[38] An increase in the nickel release means more nickel is bioavailable and can cause toxicity. There is agreement with that conclusion and the results of the present study for Garson Mine effluent where greater toxicity was observed when using the Reference River water as diluent. However, this observation may be the result of discrepancies in the toxicity testing rather than the chemical speciation. In fact, the results of toxicity tests conducted in the Reference River water for Copper Cliff WWTP, standard copper and standard nickel, all contradict the above conclusion. For those samples, the use of receiving water for dilution decreased the overall algal toxicity (IC25) (Table 2). For example, the IC25 for the nickel standard increased from 0.427 to 0.920 μM (2-fold) and for Cu from 0.064 to 0.202 μM (3-fold) for the laboratory water v. Reference River water studies. This is likely due to the absence of DOC in the laboratory water and its presence in the Reference River water, which can increase complexation of metals by the DOC, and thereby reduce toxicity. Nonetheless, the numerous confounding factors in effluent water samples make it difficult to formulate more definitive conclusions.
Table 2 presents the calculated IC25 levels for the effluent water samples and the related nickel speciation data. Both Crean Hill and Sudbury WWTP had an IC25 of more than 100% effluent, indicating the absence of significant toxicity. As discussed above, the toxic effects of these samples may have been masked by the observed stimulation, especially in Sudbury WWTP samples (Fig. 2a). Garson and Copper Cliff samples showed the highest toxicity with an IC25 of 25.6 ± 1.5% and 28.9 ± 6.1%, respectively. When looking at these two samples independently, the toxicity data match with the speciation data in that Garson effluent was found to have the highest [Ni]labile (1.85 μM) and Copper Cliff had the highest [Cu]labile (2.40 μM) (Table 1). WHAM VI also predicted highest [Ni2+]WHAM (1.27 μM) for Garson (Table 2) and highest [Cu2+]WHAM (2.40 μM) for Copper Cliff WWTP (results not shown). Nolin Creek and Sudbury WWTP had very similar [Ni]total (1.28 μM and 1.32 μM, respectively). However, the difference in nickel lability in the samples (96.5% and 37.3%, respectively) and the immense stimulation effect in Sudbury WWTP most likely caused the difference in toxicity observed for the two samples (IC25 63% and >100%, respectively).
In general, the toxicity data do not correlate with [Ni2+]WHAM, [Ni2+]IET or [Ni]labile (Fig. 4a, error bars are not shown for the purpose of simplicity). This is likely because of the significant amounts of copper and zinc (up to 2.70 μM) present in some of the samples, which may also have affected the toxicity results. In fact, a weak correlation (r2 = 0.5907) was observed when the sum of [Ni]labile and [Cu]labile was plotted against the IC25 results (Fig. 4b). A plot of toxicity v. [Ni2+]WHAM plus [Cu2+]WHAM showed better correlation (r2 = 0.6378, Fig. 4c), which was further improved by inclusion of [Zn2+]WHAM (r2 = 0.7575, Fig. 4d).
Conclusions
The BLM, which is based on FIAM, has gained extensive acceptance in equilibrium-based toxicity predictions and has already been incorporated into the US EPA’s Ambient Water Quality Criteria for copper.[18] The capabilities of geochemical speciation and toxicity prediction models have greatly improved in the past decade, especially in incorporating the effect of DOC. However, more field validations are still required and the extension of the BLM to chronic toxicity effects is a challenge. The results of the present study indicate that for effluent waters, WHAM-predicted metal speciation correlated well with the observed chronic toxicity when taking into consideration the three major bioavailable metal species (Ni2+, Cu2+, Zn2+). These findings increase our confidence in the reliable application of the BLM (based on WHAM VI predictions) as a tool for predicting toxicity in multi-metal contaminated natural waters and justifies incorporation of the BLM into the regulatory framework for mining effluents. In addition, the present study shows the importance of taking into account other parameters of water quality such as diluent water and nutrient concentrations.
Acknowledgements
The authors gratefully acknowledge the financial supports of the Natural Sciences and Engineering Research Council (NSERC) of Canada and the NSERC Metals in the Human Environment – Research Network (MITHE-RN). The authors also wish to thank Dr Emmanuel Yumvihoze (University of Ottawa) for measuring phosphate levels in the samples. Y.G. received a graduate scholarship from Carleton University Emmette Dunne Fund and Ontario Graduate Scholarship in Science and Technology.
[1]
[2]
[3]
B. T. A. Muyssen ,
K. V. Brix ,
D. K. DeForest ,
C. R. Janssen ,
Nickel essentiality and homeostasis in aquatic organisms.
Environ. Rev. 2004
, 12, 113.
| Crossref | GoogleScholarGoogle Scholar |

[4]
M. W. G. de Bolster ,
Glossary of terms used in bioinorganic chemistry (IUPAC recommendations 1997).
Pure Appl. Chem. 1997
, 69, 1251.
| Crossref | GoogleScholarGoogle Scholar |

[5]
D. Templeton ,
F. Ariese ,
R. Cornelis ,
L. G. Danielson ,
H. Muntau ,
H. Van Leeuwen ,
R. Lobinski ,
Guidelines for terms related to chemical speciation and fractionation of elements: definitions, structural aspects and methodological approaches (IUPAC recommendations 2000).
Pure Appl. Chem. 2000
, 72, 1453.
| Crossref | GoogleScholarGoogle Scholar |

[6]
[7]
B. Vigneault ,
P. G. C. Campbell ,
Uptake of cadmium by freshwater green algae: effects of pH and aquatic humic substances.
J. Phycol. 2005
, 41, 55.
| Crossref | GoogleScholarGoogle Scholar |

[8]
[9]
B. Vigneault ,
A. Percot ,
M. Lafleur ,
P. G. C. Campbell ,
Permeability changes in model and phytoplankton membranes in the presence of aquatic humic substances.
Environ. Sci. Technol. 2000
, 34, 3907.
| Crossref | GoogleScholarGoogle Scholar |

[10]
C. Lamelas ,
V. I. Slaveykova ,
Comparison of Cd(II), Cu(II), and Pb(II) biouptake by green algae in the presence of humic acid.
Environ. Sci. Technol. 2007
, 41, 4172.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[11]
R. Sutton ,
G. Sposito ,
Molecular structure in soil humic substances: the new view.
Environ. Sci. Technol. 2005
, 39, 9009.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[12]
E. R. Unsworth ,
K. W. Warnken ,
H. Zhang ,
W. Davison ,
F. Black ,
J. Buffle ,
J. Cao ,
R. Cleven ,
J. Galceran ,
P. Gunkel ,
E. Kalis ,
D. Kistler ,
H. P. van Leeuwen ,
M. Martin ,
S. Noël ,
Y. Nur ,
N. Odzak ,
J. Puy ,
W. V. Riemsdijk ,
L. Sigg ,
E. Temminghoff ,
M.-L. Tercier-Waeber ,
S. Toepperwien ,
R. M. Town ,
L. Weng ,
H. Xue ,
Model predictions of metal speciation in freshwaters compared to measurements by in situ techniques.
Environ. Sci. Technol. 2006
, 40, 1942.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[13]
S. C. Apte ,
G. E. Batley ,
K. C. Bowles ,
P. L. Brown ,
N. Creighton ,
L. T. Hales ,
R. V. Hyne ,
M. Julli ,
S. J. Markich ,
F. Pablo ,
N. J. Rogers ,
J. L. Stauber ,
K. Wilde ,
A comparison of copper speciation measurements with the toxic response of three sensitive freshwater organisms.
Environ. Chem. 2005
, 2, 320.
| Crossref | GoogleScholarGoogle Scholar |

[14]
P. G. C. Campbell ,
O. Errécalde ,
C. Fortin ,
V. P. Hiriart ,
B. Vigneault ,
Metal bioavailability to phytoplankton – applicability of the Biotic Ligand Model.
Comp. Biochem. Phys. C 2002
, 133, 189.

[15]
G. E. Batley ,
S. C. Apte ,
J. L. Stauber ,
Speciation and bioavailability of trace metals in water: progress since 1982.
Aust. J. Chem. 2004
, 57, 903.
| Crossref | GoogleScholarGoogle Scholar |

[16]
[17]
G. K. Pagenkopf ,
Gill surface interaction model for trace metal toxicity to fish: role of complexation, pH, and water hardness.
Environ. Sci. Technol. 1983
, 17, 342.
| Crossref | GoogleScholarGoogle Scholar |

[18]
[19]
Y. Gopalapillai ,
I. I. Fasfous ,
J. D. Murimboh ,
T. Yapici ,
P. Chakraborty ,
C. L. Chakrabarti ,
Determination of free nickel ion concentrations using the ion exchange technique: application to aqueous mining and municipal effluents.
Aquat. Geochem. 2008
, 14, 99.
| Crossref | GoogleScholarGoogle Scholar |

[20]
[21]
F. C. Cantwell ,
J. S. Nielson ,
S. E. Hrudey ,
Free nickel ion concentration in sewage by an ion exchange column–equilibration method.
Anal. Chem. 1982
, 54, 1498.
| Crossref | GoogleScholarGoogle Scholar |

[22]
C. Fortin ,
P. G. C. Campbell ,
An ion-exchange technique for free-metal ion measurements (Cd2+, Zn2+): application to complex aqueous media.
Int. J. Environ. Anal. Chem. 1998
, 72, 173.
| Crossref | GoogleScholarGoogle Scholar |

[23]
[24]
R. Mandal ,
M. S. A. Salam ,
J. Murimboh ,
N. M. Hassan ,
C. L. Chakrabarti ,
M. H. Back ,
D. C. Gregoire ,
W. H. Schroeder ,
Effect of the competition of copper and cobalt on the lability of Ni(II)-organic ligand complexes, Part II: in freshwaters (Rideau River surface waters).
Anal. Chim. Acta 1999
, 395, 323.
| Crossref | GoogleScholarGoogle Scholar |

[25]
Y. Lu ,
C. L. Chakrabarti ,
M. H. Back ,
D. C. Gregoire ,
W. H. Schroeder ,
Kinetic studies of aluminium and zinc speciation in river water and snow.
Anal. Chim. Acta 1994
, 293, 95.
| Crossref | GoogleScholarGoogle Scholar |

[26]
D. L. Olson ,
M. S. Shuman ,
Copper dissociation from estuarine humic materials.
Geochim. Cosmochim. Acta 1985
, 49, 1371.
| Crossref | GoogleScholarGoogle Scholar |

[27]
R. Mandal ,
N. M. Hassan ,
J. Murimboh ,
C. L. Chakrabarti ,
M. H. Back ,
U. Rahayu ,
D. R. S. Lean ,
Chemical speciation and toxicity of nickel species in natural waters from the Sudbury area (Canada).
Environ. Sci. Technol. 2002
, 36, 1477.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[28]
C. L. Chakrabarti ,
Y. Lu ,
J. Cheng ,
D. C. Grégoire ,
M. H. Back ,
W. H. Schroeder ,
Studies on metal speciation in the natural environment.
Anal. Chim. Acta 1993
, 276, 47.
| Crossref | GoogleScholarGoogle Scholar |

[29]
[30]
P. Radix ,
M. Leonard ,
C. Papantoniou ,
G. Roman ,
E. Saouter ,
S. Gallotti-Schmitt ,
H. Thiebaud ,
P. Vasseur ,
Comparison of four chronic toxicity tests using algae, bacteria, and invertebrates assessed with sixteen chemicals.
Ecotoxicol. Environ. Saf. 2000
, 47, 186.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[31]
S. Winch ,
J. Ridal ,
D. Lean ,
Increased metal bioavailability following alteration of freshwater dissolved organic carbon by ultraviolet B radiation exposure.
Environ. Toxicol. 2002
, 17, 267.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[32]
[33]
E. Tipping ,
Humic ion-binding model VI: an improved description of the interactions of protons and metal ions with humic substances.
Aquat. Geochem. 1998
, 4, 3.
| Crossref | GoogleScholarGoogle Scholar |

[34]
R. Mandal ,
M. S. A. Salam ,
J. Murimboh ,
N. M. Hassan ,
C. L. Chakrabarti ,
M. H. Back ,
D. C. Gregoire ,
Competition of Ca(II) and Mg(II) with Ni(II) for binding by a well-characterized fulvic acid in model solutions.
Environ. Sci. Technol. 2000
, 34, 2201.
| Crossref | GoogleScholarGoogle Scholar |

[35]
J. Buffle ,
R. S. Altmann ,
M. Filella ,
A. Tessier ,
Complexation by natural heterogeneous compounds: site occupation distribution functions, a normalized description of metal complexation.
Geochim. Cosmochim. Acta 1990
, 54, 1535.
| Crossref | GoogleScholarGoogle Scholar |

[36]
J. L. Stauber ,
C. M. Davies ,
Use and limitations of microbial bioassays for assessing copper bioavailability in the aquatic environment.
Environ. Rev. 2000
, 8, 255.
| Crossref | GoogleScholarGoogle Scholar |

[37]
K. Hund ,
Algal growth inhibition test – feasibility and limitations for soil assessment.
Chemosphere 1997
, 35, 1069.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[38]
P. Chakraborty ,
Y. Gopalapillai ,
J. Murimboh ,
I. I. Fasfous ,
C. L. Chakrabarti ,
Kinetic speciation of nickel in mining and municipal effluents.
Anal. Bioanal. Chem. 2006
, 386, 1803.
| Crossref | GoogleScholarGoogle Scholar | PubMed |