Humic acid complexation to Zn and Cd determined with the new electroanalytical technique AGNES
Encarnació Companys A , Jaume Puy A and Josep Galceran A BA Departament de Química, Universitat de Lleida, Rovira Roure 191, E-25198 Lleida, Spain.
B Corresponding author. Email: galceran@quimica.udl.cat
Environmental Chemistry 4(5) 347-354 https://doi.org/10.1071/EN07051
Submitted: 27 July 2007 Accepted: 3 September 2007 Published: 2 November 2007
Environmental context. Humic substances are complex mixtures that play an important role in trace metal bioavailability in soils and aquatic environments. The bioavailability of a metal depends on what chemical forms, or species, it is in. We need to know how much of the metal is present as a free metal ion in solution, and how much is bound up in complexes with humic acids, for example. This work reports the complexation of Cd and Zn to humic acids by means of a simple and robust technique, AGNES (absence of gradients and Nernstian equilibrium stripping).
Abstract. AGNES (absence of gradients and Nernstian equilibrium stripping), an emerging electroanalytical technique specifically designed for the determination of the free concentration of heavy metals in aqueous solutions, is here implemented to characterise the binding of CdII and ZnII to a soil humic acid. A set of metal titration experiments were performed by adding Cd or Zn to a purified humic acid (Aldrich) at pH 4, 5, 6 and 7 and measuring the free metal concentration by AGNES. The application of a program with two potential steps along the deposition stage allows for the reduction of the deposition time in the humic titration. The polyelectrolytic effects of the macromolecular ligand were taken into account through the Donnan model. Data free of electrostatic effects were reasonably described by the NICA isotherm, which accounts for heterogeneity, considering just a monomodal distribution (because of the range of pH covered). The obtained affinity parameters indicate a similar strength for Zn and Cd binding to the purified humic acid.
Additional keywords: AGNES, bioavailability, humic acids, metal binding, speciation.
Introduction
Metal ion binding to natural organic matter has a large impact on free metal concentration, which is assumed to be directly correlated with the element uptake by organisms, in surface waters, soil solutions and groundwater.[1,2] Here we focus on the implementation of a new technique to determine free metal ion concentration as a means of studying metal ion complexation, which takes place in a variety of binding sites (e.g. carboxylic and phenolic functional groups) present in humic acid (HA). Phenomena to take into account in the interpretation of the results are: (i) the large binding site heterogeneity, (ii) the presence of electrostatic interactions, (iii) the different stoichiometry of the binding reaction for different ions and (iv) the competition effects. Models[3,4] such as WHAM (Windermere humic aqueous acid, models IV–VI) and NICA Donnan (see ref. [5] and references cited therein), which attempt to address these issues, have been developed in the last decade.
For the quantification of metal ion binding to HA, the determination of the free metal ion concentration is required. Commercial ion selective electrodes (ISEs)[6,7] have been widely used for this purpose, although their practical implementation sometimes lacks stability or reproducibility and are generally restricted to situations when the total metal concentration is above 1 × 10–6 M,[8] which is not suitable to reproduce environmental conditions.[9] Moreover, ISEs for some species (such as Zn) are not of routine use, which can be one of the reasons for the paucity of data available[10–14] on the complexation of Zn to HA. Thus, the development of alternative approaches can be helpful, especially if they can be applied with conventional equipment.
Other widely used experimental tools in complexation studies are voltammetric techniques. Among the typically claimed advantages, their low level of detection is particularly attractive and is usually achieved by stripping variants[15–18] that rely on some pre-concentration step. However, a major problem in voltammetric techniques (such as anodic stripping voltammetry, stripping chronopotentiometry or pulse polarography) is the complex interpretation of the response functions in order to determine the free metal concentration,[19] since both free metal and complex species contribute to the measured current directly or by (partial) dissociation.[20] Among other innovative techniques (see ref. [21]) to directly sense free metal concentrations, we highlight the Donnan membrane technique (DMT).[14]
Recently, we have designed[22] a new stripping technique aimed at the determination of free metal ion concentration, whose name, AGNES (absence of gradients and Nernstian equilibrium followed by stripping), indicates that the stripping step is applied when a special situation (no concentration gradients at both sides of the electrode surface and Nernstian equilibrium) has been achieved. One clear advantage of the new technique is its simple interpretation: the faradaic current is proportional to the free metal concentration. In more recent work, we have shown that AGNES can determine free Zn concentrations in simple ligand solutions (oxalate and nitrilotriacetic acid)[23] and in Mediterranean seawater samples.[24] We now aim to implement and develop the AGNES methodology to study the binding of Cd and Zn to HA, a complex and heterogeneous mixture of metal binding ligands. Cd (at relatively high concentrations) has been chosen because of the possibility to compare with a previous work of ours where an ISE was used,[20] while Zn has been chosen because of the aforementioned paucity of data and to illustrate the use of AGNES when an ISE is not available. This work highlights the usefulness of AGNES for HA–metal complexation, while further developments should tackle, among other issues, the lowering of the limit of detection. Purified Aldrich humic acid (PAHA) is titrated with each metal at a different pH and the binding data is interpreted using the NICA–Donnan approach in order to compare with affinity parameters reported in the existing literature and discuss their physical interpretation.
Theoretical background
Principles of AGNES
AGNES has been presented with great detail in previous works.[22–26] We summarise here the principles of this electroanalytical technique which consists of two stages: deposition (first stage) and stripping (second stage).
First stage
The key feature of AGNES is that by the end of the first stage a special condition (or target) is reached:
-
‘Absence of gradients’: there are no concentration profiles at either side of the electrode surface. So, the free metal concentration at the bulk is the same as at the electrode surface and we represent both of them here as cM.
-
‘Nernstian equilibrium’. The couple M0/M has reached the equilibrium that corresponds to the applied potential (E1). The Nernst equation allows one to compute the ratio of concentrations at each side of the electrode surface (which we call the preconcentration factor or ‘gain’ Y) as
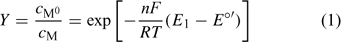
where F is the Faraday constant, R the gas constant, T the temperature and E°′ is the standard formal potential (where the activity coefficients are embedded). In the present implementation of AGNES, the preconcentration factor is determined from Epeak, the potential peak of a differential pulse polarography (DPP) experiment:[22]
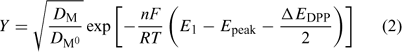
where DM and DM0 are the diffusion coefficients for the free metal ion and the reduced metal (inside the amalgam) and ΔEDPP is the pulse amplitude of the DPP experiment.
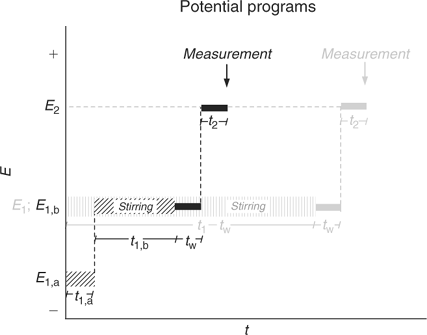
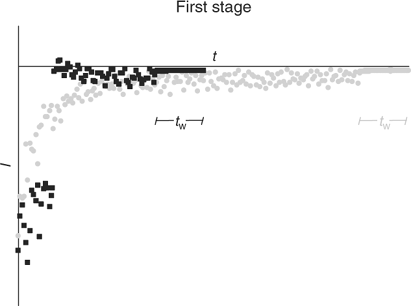
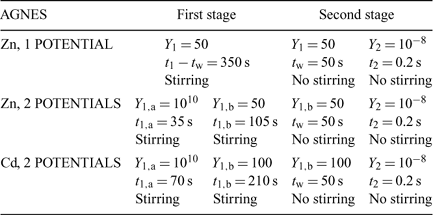
In the simplest implementation of AGNES (Fig. 1) only one potential step is applied along the deposition time t1, while stirring is on during a time t1 – tw. In order to reduce the deposition time, another potential program has been recently proposed: this consists in splitting the first stage into two different sub-stages (a potential step that corresponds to diffusion limited conditions followed by a potential step at the desired concentration gain Y, also denoted Y1,b) (see Fig. 1). This strategy has been proven to reduce the deposition time needed to reach the target situation of the first step.[23] Fig. 2 shows the output currents measured in this first step.
|
|
Second stage
The aim of the second stage is the determination of the concentration of M0 in the amalgam. For that purpose, a simple strategy consists in applying a sufficiently less negative potential (E2) to produce a stripping current under diffusion limited conditions (see Figs 1 and 3). The measured response function of AGNES is the current I at a certain time t2.
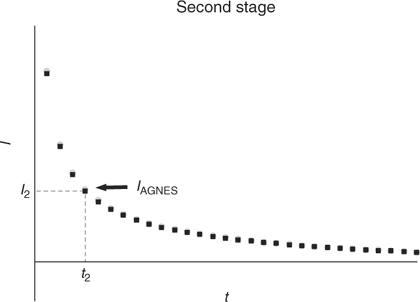
|
The proportionality factor, h
Because of the linear properties of the diffusion of M0 inside the amalgam,[22] there is a direct proportionality between the Faradaic current, If, under diffusion limited conditions for re-oxidation, at a given time, and the concentration of M0 built up inside the mercury drop in the first stage. But Eqn 1 indicates another direct proportionality between this M0 concentration and that of free M. So, regardless of processes such as electrodic adsorption (which is a well known interfering phenomenon in the system Cd–HA), complexation or hydrodynamic regimes, the following fundamental relationship between Faradaic current and free metal concentration applies:

As the measured current, I, contains other components different to the Faradaic one, there is a need to subtract a blank from the total current. The classical way to determine the blank consists in the application of the same potentials program as for the sample to a solution that contains the same matrix but without metal. The proportionality factor, h, can be obtained from a calibration with the same set-up.
Specific and non-specific binding. The NICA–Donnan model
With an aim to compare the binding results of AGNES with those previously reported in the literature, the standard NICA–Donnan model has been used to fit the binding data[27] and the retrieved parameters are discussed.
In the NICA–Donnan model, the Donnan approach[27,28] is used to account for the electrostatic effects. Since humic substances have a three-dimensional structure that may exhibit similar properties to a polyelectrolyte gel,[29–31] the humic material is considered to behave as an electrically neutral phase that has a certain volume throughout which there is a uniform, averaged, electrostatic potential known as the Donnan potential.
The variation of the Donnan volume with ionic strength, cs, for various humic substances is usually assumed to follow an empirical relationship (independent of the pH)[28,32] such as:
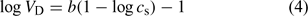
where b is an adjustable parameter.
Concentrations in the Donnan phase can be written in terms of the bulk concentrations and the Donnan potential, which is then determined from the electroneutrality condition. Once the electrostatic interactions are accounted for with the Donnan model, the plot of the amount of specifically bound metal (QM,S) v. the free metal concentration close to the binding site (i.e. in the Donnan phase, cM,D) indicates a variation of the affinity with the metal concentration. This dependence can be described using a macroscopic isotherm. In the NICA (the consistent Non-Ideal Competitive Adsorption) model this isotherm is written as:[5,33–35]
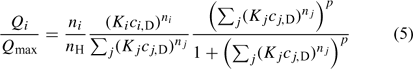
where Qi is the total amount of component i specifically bound to the HA in mol kg–1, Qmax is the number of sites in mol kg–1, Ki is the affinity parameter for species i, and ci,D and cj,D are the free concentrations of ion i and j, respectively, in the Donnan phase. The exponents ni and nj (0 < n ≤ 1) in Eqn 5 are ion-specific parameters that account for any ‘non-ideal’ behaviour and whose relationship to ion-site stoichiometry[5,35] has recently been stressed. p (0 < p ≤ 1) represents the generic or intrinsic heterogeneity of the macromolecule and is common to all components. Since both the electrostatic and the specific binding are coupled, all the parameters that correspond to both effects have been obtained after convergence of an iterative process that solves each one of these effects for a given set of parameters of the other effect. Details of the data treatment can be found in the Accessory Materials.
When a wide range of pH is considered, the HA exhibits a bimodal distribution, which is mainly a result of the phenolic- and carboxylic-type groups. The NICA model, given by Eqn 5 for the monomodal case, can be easily extended to reflect this:[33]
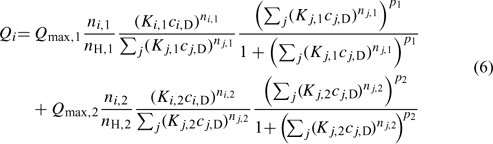
where subscripts 1 and 2 refer to the carboxylic- and phenolic-type parts of the distribution, respectively.
Experimental methods
Instrumentation and reagents
Voltammetric measurements were carried out with Eco Chemie Autolab PGSTAT30 and PGSTAT10 potentiostats attached to Metrohm 663VA Stands and were controlled from a computer by means of the GPES (Eco Chemie) software package. The working electrode was a Metrohm multimode mercury drop electrode. The smallest drop in our stand was chosen, which, according to the catalogue, corresponds to a radius around 1.41 × 10–4 m.
The auxiliary electrode was a glassy carbon electrode and the reference electrode was Ag/AgCl/3 mol L–1 KCl, encased in a 0.1 mol L–1 KNO3 jacket.
A glass combined electrode (Orion 9103) was attached to an Orion Research 720A ion analyser and introduced in the cell to control the pH. A glass jacketed cell provided by Metrohm was used in all measurements. The vessel was thermostated at 25.0°C.
HA (H1, 675-2) was purchased from Aldrich and purified by a procedure outlined elsewhere.[36,37] HA (10 g) was added to 1 L of 0.1 M HCl/0.3 M HF solution, stirred overnight and filtered (Whatman Cellulose filter). The HA residue was washed several times with 1 M HCl, neutralised, and dissolved in KOH solution to pH 9.0 under N2 atmosphere over 24 h. The remainder was then centrifuged at high speed (12 000 rpm) to remove the suspended solids, and then reprecipitated by adding 1 M HNO3 to pH 1.0 with constant stirring. After stirring for 24 h, the suspension was centrifuged at 12 000 rpm for 50 min. The precipitate was redissolved with KOH to pH 7.0 and exhaustively dialysed (molecular weight cut-off, MWCO = 12 000) against purified water until the conductivity of the dialysate remained constant. The dialysed solution (MWCO > 12 000) was then treated with a Dowex 50WX4 ion exchanger to convert the material into the acid form. The purified HA (PAHA) was stored as a concentrated solution in the dark at 4°C.
Zinc and cadmium stock solutions were prepared from Zn(NO3)2·4H2O and Cd(NO3)2·4H2O (Merck, analytical grade), respectively, and standardised by means of a complexometric endpoint titration with ethylenediaminetetraacetic acid (EDTA).[38] Potassium nitrate was used as the inert supporting electrolyte and prepared from solid KNO3 (Merck, Suprapur).
KOH and HNO3 titrisol (Merck) were added to fix the pH to the desired values. Ultrapure water (Milli-Q plus 185 System, Millipore) was employed in all the experiments. Purified water-saturated nitrogen N2(50) was used for deaeration and blanketing of solutions.
Procedure
Voltammetric titrations
For both metals, Zn and Cd, titrations at fixed values of pH (4, 5, 6 and 7) were performed. In each case the following procedure was applied:
-
A fixed volume of 0.1 M KNO3 with an initial amount of HA (0.45 g L–1) was placed into the voltammetric cell and extensively deareated.
-
The pH was then brought to the desired value by small additions of acid or base, when necessary, after which the AGNES procedures were applied.
-
The blank current, Ib, was measured in the solution that contained HA and the supporting electrolyte, and includes current components that arise from a variety of sources such as traces of contaminants or the capacitive charge. This latter component is expected to be small given that the measurement of the current is taken at a relatively long time (t2 = 0.2 s) in the stripping pulse. Except for the first additions at each pH, this blank current was practically negligible in front of the main measurement.
-
A set of additions of a standard metal solution were subsequently added to the cell, after which, the pH was measured and corrected, when necessary, and then the AGNES procedures were performed (i.e. the current I was measured at each total metal concentration).
-
Given the h value, Eqn 3, taking If = I – Ib, allows for the determination of the free metal concentration at each addition.
The h value was determined in a previous calibration experiment performed just before the titration and at the same KNO3 concentration, but without HA as follows:
-
Different volumes of a metal solution were added to an initial KNO3 solution and AGNES was applied.
-
The program VMINTEQ[39] was used to determine the free metal concentration at each addition to take into account known complexes of the studied metal ion (such as those with hydroxo or nitrate ions).
-
The average of the h values obtained at the different concentrations was subsequently used for the calculations in the titrations with HA.
AGNES parameters
DPP experiments (with the largest drop so that the planar electrode expression Eqn 2 applies) were performed with the most concentrated solutions of the calibration, in order to compute the required E1 value (for a desired Y).
Table 1 summarises the parameters applied for AGNES, which were selected taking into account previous experiments[23] where the time needed to fulfill AGNES conditions for a fixed gain Y were determined. For Zn experiments we applied a potential program of a unique potential in the first stage, but also another potential program[23] that consisted of two potential steps along the first stage (see Fig. 1 and Table 1). The potential program for the measurements of Cd applied in this work consists only in applying two potential steps in the first stage.
|
Results and discussion
Zinc binding
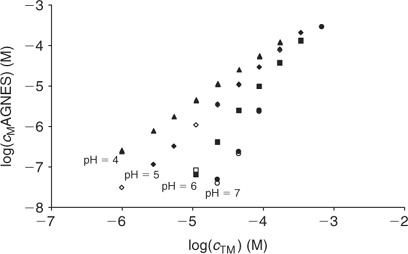
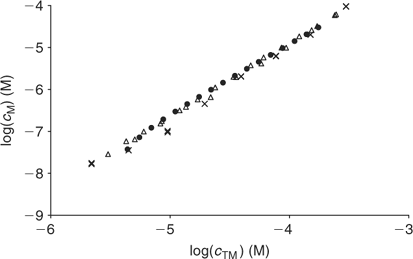
The free Zinc concentration in the presence of PAHA was measured at pH 4, 5, 6 and 7 (see Fig. 4) with two different strategies of AGNES: one and two potentials in the preconcentration stage (see Figs 1, 2 and 3). No significant differences were observed in the free metal concentrations measured using both strategies. In analogy to the case of the synthetic solutions,[23] the strategy of splitting the first stage of the simplest potential program into two sub-stages also satisfactorily reduces the deposition time. Metal is preconcentrated during t1,a seconds under diffusion limited conditions (or very close to these). In some cases, there is an ‘overshoot’: the sudden change in the current sign indicates that the new prescribed gain Y is lower than the currently already achieved concentration gain, so that the excess of Zn0 preconcentrated inside the drop is now forced to reoxidise. The duration of the second potential step is selected to be long enough for the residual current to be recovered by the end of the first stage.
|
Calibrations were performed the day previous to or following that of the titration experiment at each pH. The found proportionality factors h, were 0.120, 0.144, 0.104 and 0.109 at pH 4, 5, 6 and 7, respectively. A set of uncontrollable factors in the set-up, such as drop size, could explain the differences among them, but, as expected from the theoretical considerations of the technique, the experimental h showed no significant dependence on pH. Moreover, the proportionality factors obtained are of the same order of those reported in previous experiments for the same gain Y = 50.[23] In order to calculate the free metal concentrations for each HA titration at each pH, using Eqn 3, the corresponding h value was taken, as was considered to best reproduce the conditions of the set-up of the titration experiment.
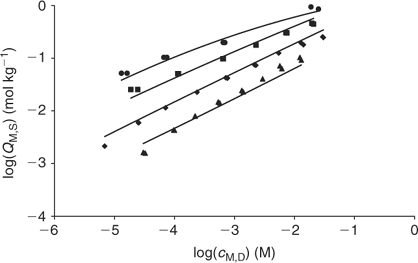
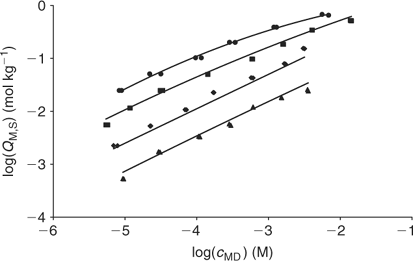
The fitting of the NICA–Donnan model to the Zn2+ binding data over the pH range and concentrations considered is reasonably good (see Table 2 and Fig. 5). The pH range considered (4 to 7) justifies the fitting of the NICA isotherm with only one kind of site (the carboxylic ones) by applying Eqn 5. Through the application of the Donnan model the total bound metal can be split into the specifically and the electrostatically bound. The average of the proportion of specifically bound zinc under the conditions used here appears to be 94% of the total bound Zn. Although the concentration of Zn in the Donnan phase is around 100 times the concentration in the bulk solution, the Donnan volume is very small (because of the relatively high ionic strength used in the experiments), so that only a very small percentage of the bound Zn is electrostatically bound. The percentage of specifically bound Zn decreases slightly with decreasing pH.
|
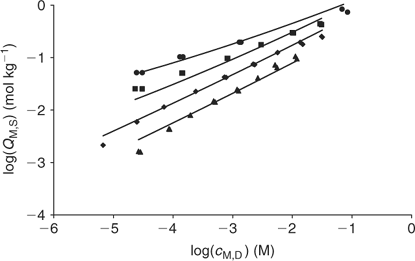
The application of the bimodal NICA model (Eqn 6) to the Zn titration data does not substantially improve the fitting with respect to the monomodal model (Eqn 5), except in avoiding some discrepancies observed at high coverages and pH 7 (compare upper curves in Figs 5 and 6) between experimental data and the expected ones computed with Eqn 5. However, because of the lack of data at higher pH, the bimodal isotherm does not lead to an accurate determination of the second type of groups (i.e. there is a large error in the retrieved parameters for the second type of sites as seen in Table 3).
|
|
Cadmium binding
The complexation of Cd with the purified HA from Aldrich has been studied with AGNES applying the technique with two different potentials in the first stage. Both the Zn–HA data reported in the previous section, and the results previously published,[23,24] show that this potential program yields correct values. Because of the time saved by this strategy, all experiments with Cd have been performed at a higher gain, Y = 100, which enables access to lower detection limits.
As observed for Zn, the Cd calibrations performed to determine the proportionality factor, h, showed no significant effect of the pH. The h values at pH 4, 5, 6 and 7 were 0.185, 0.187, 0.182 and 0.179, respectively.
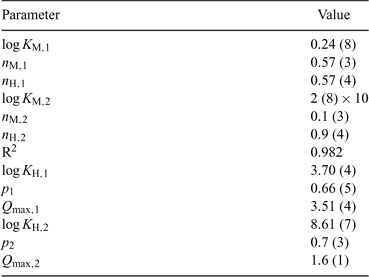
Fig. 7 compares AGNES results at pH 6 with data from a previous work[20] using the same PAHA at practically the same concentration (the initial PAHA concentration in the titration was 0.50 g L–1 in the previous work and 0.45 g L–1 in the current one). In the previous work two different electroanalytical techniques were used: potentiometry and voltammetry, and, as seen in Fig. 7, the free concentrations retrieved from both techniques are in good agreement with those obtained here with AGNES. This confirms the ability of AGNES to determine free metal concentrations, even in the presence of induced reactant adsorption as is well known for Cd–HA.
|
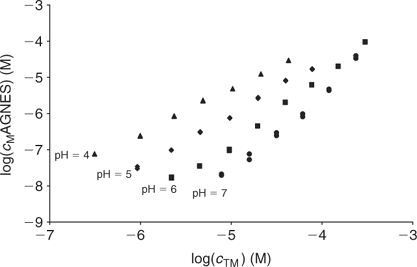
Fig. 8 plots the log cM measured by AGNES v. the total Cd added for each studied pH. These experimental bulk free concentrations have then been corrected to take into account the electrostatic effects considering the Donnan model (see Accessory Material). After this correction, the unimodal NICA isotherm fits the data well (see Table 2 and Fig. 9). The specifically bound cadmium in the conditions used here appears to be 95% of the total. It is concluded that the electrostatic binding is low as also observed for zinc.
|
|
As previously seen with Zn, the fitting (data not shown) with the bimodal distribution (Eqn 6) improves the fitting for the main discrepancies at pH 7 and high metal loading, but the retrieved parameters are not reliable.
Retrieved NICA–Donnan parameters
Many factors contribute to justifying the differences between retrieved parameters from different authors, ranging from fittings that include monomodal or bimodal distributions, the different nature (or purification process) of the humic matter, the quality of the measured free concentrations, etc., so that a reasonable comparison between different works should mainly focus on trends and relative values.
If we compare the results obtained here for Zn with those reported by Milne et al.[40] (see Table 2), which correspond to the application of the NICA–Donnan model to different sets of previously published data[10,11,14] on the binding of different kinds of HAs, we can conclude a good agreement for log KZn, nZn and nH.
Regarding Cd, the parameters obtained here (see Table 2) are in general agreement with the ones reported in previous studies.[5,40] The affinity parameter KCd that we obtain for our PAHA (log KCd = 0.62) is in between the generalised parameter reported by Milne et al.[40] (log KCd = –0.20) and the one (log KCd = 1.42) more recently reported by Koopal et al.[5] If we now consider the ion-specific parameters, there is a close similarity of our nH = 0.78 to that of Koopal et al. (nH = 0.65[5]) and the generic one (nH = 0.81, reported by Milne et al.[40]), but our nCd = 0.65 is slightly lower than those (0.82 and 0.73) of previous works.
The differences between our p values and those of the literature (see Table 2) have been traced back mainly to the proton binding fittings which, for our data, yielded a relatively low product nH × p. However, the agreement between the p values obtained here for Zn and the Cd binding (0.50 and 0.47) in independent fittings is remarkable. Notice that the parameter p characterises the heterogeneity of the ligand, i.e. the heterogeneity common to all the binding cations. The coincidence of the p parameter is, thus, consistent with its physical meaning. The proximity between the ion-specific coefficients nZn = 0.56 and nCd = 0.65 also indicates that a similar ion-heterogeneity can be attributed to both cations when binding to the PAHA.
While some authors found that Cd binds to HA stronger than Zn,[41] other authors found the opposite.[14,40] Our results indicate that HA binding to Cd is practically equal to Zn. As seen in the literature,[12] even the source of the HA can modify the relative strength of Cd and Zn binding to HA. In summary, the lack of a sufficient number of works on the Zn–HA system still hinders a definitive conclusion on this issue.
Conclusion
AGNES has, before the application of any interpretative model, been shown to be a useful and simple tool to determine complexation concentrations (from which the parameters will follow with the appropriate modelling) in systems that contain natural organic matter. Comparison with a previous work confirms that electrodic adsorption (even at the relatively high HA concentrations used) does not hinder an accurate determination of free Cd concentration with AGNES. Further work with Zn, Cd and other metals should be addressed to measure free metal concentration at lower detection limits, at a broader range of pH values and in natural media.
AGNES concentrations found here for Cd and Zn binding to PAHA can be described with the unimodal NICA–Donnan model. Because of the probed pH range (4 to 8), bimodal NICA fitting is not reliable. The modelling of the metal ion binding with the monomodal NICA–Donnan model yields parameters that are in good agreement with previously published data on humics and follow reasonable physicochemical trends. PAHA displays similar binding affinities for both Zn and Cd.
Acknowledgements
Experiments were conducted with the help of Silvia Cerdán and Anna Sedó, whose contribution is gratefully acknowledged. The authors also thank the support of this research by the Spanish Ministry of Education and Science (Projects CTQ2006-14385 and CTM2006-13583) and from the ‘Comissionat d’Universitats i Recerca de la Generalitat de Catalunya’.
Details on the practical implementation of the NICA–Donnan model and on the proton titration of PAHA are available from the authors (http://web.udl.es/usuaris/q4088428/Publications/Publicacions.html), from the corresponding author or from Environmental Chemistry.
[1]
[2]
[3]
Y. Dudal ,
F. Gerard ,
Accounting for natural organic matter in aqueous chemical equilibrium models: a review of the theories and applications.
Earth Sci. Rev. 2004
, 66, 199.
| Crossref | GoogleScholarGoogle Scholar |

[4]
[5]
L. K. Koopal ,
T. Saito ,
J. P. Pinheiro ,
W. H. van Riemsdijk ,
Ion binding to natural organic matter: General considerations and the NICA-Donnan model.
Colloid Surface A 2005
, 265, 40.
| Crossref | GoogleScholarGoogle Scholar |

[6]
P. Buhlmann ,
E. Pretsch ,
E. Bakker ,
Carrier-based ion-selective electrodes and bulk optodes. 2. Ionophores for potentiometric and optical sensors.
Chem. Rev. 1998
, 98, 1593.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[7]
E. Bakker ,
P. Buhlmann ,
E. Pretsch ,
Carrier-based ion-selective electrodes and bulk optodes. 1. General characteristics.
Chem. Rev. 1997
, 97, 3083.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[8]
N. Serrano ,
J. M. Díaz-Cruz ,
C. Arino ,
M. Esteban ,
J. Puy ,
E. Companys ,
J. Galceran ,
J. Cecilia ,
Full-wave analysis of stripping chronopotentiograms at scanned deposition potential (SSCP) as a tool for heavy metal speciation: Theoretical development and application to Cd(II)-phthalate and Cd(II)-iodide systems.
J. Electroanal. Chem. 2007
, 600, 275.
| Crossref | GoogleScholarGoogle Scholar |

[9]
R. M. Town ,
M. Filella ,
Implications of natural organic matter binding heterogeneity on understanding lead(II) complexation in aquatic systems.
Sci. Total Environ. 2002
, 300, 143.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[10]
N. S. Randhawa ,
F. E. Broadbent ,
Soil organic matter-metal complexes: 6. Stability constants of Zinc-Humic Acids complexes at different pH values.
Soil Sci. 1965
, 99, 362.

[11]
H. van Dijk ,
Cation binding of Humic Acids.
Geoderma 1971
, 5, 53.
| Crossref | GoogleScholarGoogle Scholar |

[12]
M. L. Sohn ,
M. C. Hughes ,
Metal-ion complex-formation constants of some sedimentary humic acids with Zn(II), Cu(II) and Cd(II).
Geochim. Cosmochim. Ac. 1981
, 45, 2393.
| Crossref | GoogleScholarGoogle Scholar |

[13]
T. I. Nifant’eva ,
P. Burba ,
O. Fedorova ,
V. M. Shkinev ,
B. Y. Spivakov ,
Ultrafiltration and determination of Zn- and Cu-humic substances complexes stability constants.
Talanta 2001
, 53, 1127.
| Crossref | GoogleScholarGoogle Scholar |

[14]
L. A. Oste ,
E. J. M. Temminghoff ,
T. M. Lexmond ,
W. H. van Riemsdijk ,
Measuring and Modeling zinc and cadmium binding by humic acid.
Anal. Chem. 2002
, 74, 856.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[15]
[16]
I. I. Fasfous ,
C. L. Chakrabarti ,
J. Murimboh ,
T. Yapici ,
Complexation of lead in model solutions of humic acid: Heterogeneity and effects of competition with copper, nickel, and zinc.
Environ. Chem. 2006
, 3, 276.
| Crossref | GoogleScholarGoogle Scholar |

[17]
H. P. van Leeuwen ,
R. M. Town ,
Stripping chronopotentiometry at scanned deposition potential (SSCP). Part 1. Fundamental features.
J. Electroanal. Chem. 2002
, 536, 129.
| Crossref | GoogleScholarGoogle Scholar |

[18]
M. E. Abdelsalam ,
G. Denuault ,
S. Daniele ,
Calibrationless determination of cadmium, lead and copper in rain samples by stripping voltammetry at mercury microelectrodes – Effect of natural convection on the deposition step.
Anal. Chim. Acta 2002
, 452, 65.
| Crossref | GoogleScholarGoogle Scholar |

[19]
F. Berbel ,
J. M. Díaz-Cruz ,
C. Arino ,
M. Esteban ,
F. Mas ,
J. L. Garcés ,
J. Puy ,
Voltammetric analysis of heterogeneity in metal ion binding by humics.
Environ. Sci. Technol. 2001
, 35, 1097.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[20]
E. Companys ,
J. Puy ,
M. Torrent ,
J. Galceran ,
J. Salvador ,
J. L. Garcés ,
F. Mas ,
Binding curve from normalised limiting currents of labile heterogeneous metal-macromolecular systems. The case of Cd/humic acid.
Electroanalysis 2003
, 15, 452.
| Crossref | GoogleScholarGoogle Scholar |

[21]
H. P. van Leeuwen ,
R. M. Town ,
J. Buffle ,
R. Cleven ,
W. Davison ,
J. Puy ,
W. H. van Riemsdijk ,
L. Sigg ,
Dynamic speciation analysis and Bioavailability of metals in Aquatic Systems.
Environ. Sci. Technol. 2005
, 39, 8545.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[22]
J. Galceran ,
E. Companys ,
J. Puy ,
J. Cecília ,
J. L. Garcés ,
AGNES: a new electroanalytical technique for measuring free metal ion concentration.
J. Electroanal. Chem. 2004
, 566, 95.
| Crossref | GoogleScholarGoogle Scholar |

[23]
E. Companys ,
J. Cecília ,
G. Codina ,
J. Puy ,
J. Galceran ,
Determination of the concentration of free Zn2+ with AGNES using different strategies to reduce the deposition time.
J. Electroanal. Chem. 2005
, 576, 21.
| Crossref | GoogleScholarGoogle Scholar |

[24]
J. Galceran ,
C. Huidobro ,
E. Companys ,
G. Alberti ,
AGNES: a technique for determining the concentration of free metal ions. The case of Zn(II) in coastal Mediterranean seawater.
Talanta 2007
, 71, 1795.
| Crossref | GoogleScholarGoogle Scholar |

[25]
G. Alberti ,
R. Biesuz ,
C. Huidobro ,
E. Companys ,
J. Puy ,
J. Galceran ,
A comparison between the determination of free Pb(II) by two techniques: Absence of gradients and Nernstian equilibrium stripping and Resin Titration.
Anal. Chim. Acta 2007
, 599, 41.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[26]
C. Huidobro ,
E. Companys ,
J. Puy ,
J. Galceran ,
J. P. Pinheiro ,
The use of microelectrodes with AGNES.
J. Electroanal. Chem. 2007
, 606, 134.
| Crossref | GoogleScholarGoogle Scholar |

[27]
D. G. Kinniburgh ,
C. J. Milne ,
M. F. Benedetti ,
J. P. Pinheiro ,
J. Filius ,
L. K. Koopal ,
W. H. van Riemsdijk ,
Metal-ion binding by Humic-Acid – Application of the Nica-Donnan model.
Environ. Sci. Technol. 1996
, 30, 1687.
| Crossref | GoogleScholarGoogle Scholar |

[28]
M. F. Benedetti ,
W. H. van Riemsdijk ,
L. K. Koopal ,
Humic substances considered as a heterogeneous donnan gel phase.
Environ. Sci. Technol. 1996
, 30, 1805.
| Crossref | GoogleScholarGoogle Scholar |

[29]
J. A. Marinsky ,
J. Ephraim ,
A unified physicochemical description of the protonation and metal-ion complexation equilibria of natural organic-acids (Humic and Fulvic-Acids). 1. Analysis of the influence of polyelectrolyte properties on protonation equilibria in ionic media – Fundamental-concepts.
Environ. Sci. Technol. 1986
, 20, 349.
| Crossref | GoogleScholarGoogle Scholar |

[30]
J. A. Marinsky ,
S. Gupta ,
P. Schindler ,
A unified physicochemical description of the equilibria encountered in Humic-Acid gels.
J. Colloid. Interf. Sci. 1982
, 89, 412.
| Crossref | GoogleScholarGoogle Scholar |

[31]
J. Ephraim ,
S. Alegret ,
A. Mathuthu ,
M. Bicking ,
R. L. Malcolm ,
J. A. Marinsky ,
A united physicochemical description of the protonation and metal-ion complexation equilibria of natural organic-acids (Humic and Fulvic Acids). 2. Influence of polyelectrolyte properties and functional-group heterogeneity on the protonation equilibria of Fulvic Acid.
Environ. Sci. Technol. 1986
, 20, 354.
| Crossref | GoogleScholarGoogle Scholar |

[32]
C. J. Milne ,
D. G. Kinniburgh ,
E. Tipping ,
Generic NICA-Donnan model parameters for proton binding by humic substances.
Environ. Sci. Technol. 2001
, 35, 2049.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[33]
D. G. Kinniburgh ,
W. H. van Riemsdijk ,
L. K. Koopal ,
M. Borkovec ,
M. F. Benedetti ,
M. J. Avena ,
Ion binding to natural organic matter: competition, heterogeneity, stoichiometry and thermodynamic consistency.
Colloid Surface A 1999
, 151, 147.
| Crossref | GoogleScholarGoogle Scholar |

[34]
L. K. Koopal ,
W. H. van Riemsdijk ,
D. G. Kinniburgh ,
Humic matter and contaminants. General aspects and modeling metal ion binding.
Pure Appl. Chem. 2001
, 73, 2005.
| Crossref |

[35]
W. H. van Riemsdijk ,
L. K. Koopal ,
D. G. Kinniburgh ,
M. F. Benedetti ,
L. P. Weng ,
Modeling the interactions between humics, ions, and mineral surfaces.
Environ. Sci. Technol. 2006
, 40, 7473.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[36]
[37]
E. Companys ,
J. L. Garces ,
J. Salvador ,
J. Galceran ,
J. Puy ,
F. Mas ,
Electrostatic and specific binding to macromolecular ligands. A general analytical expression for the Donnan volume.
Colloid Surface A 2007
, 306, 2.
| Crossref | GoogleScholarGoogle Scholar |

[38]
[39]
[40]
C. J. Milne ,
D. G. Kinniburgh ,
W. H. van Riemsdijk ,
E. Tipping ,
Generic NICA-Donnan model parameters for metal-ion binding by humic substances.
Environ. Sci. Technol. 2003
, 37, 958.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[41]
G. K. Brown ,
P. MacCarthy ,
J. A. Leenheer ,
Simultaneous determination of Ca, Cu, Ni, Zn and Cd binding strengths with fulvic acid fractions by Schubert’s method.
Anal. Chim. Acta 1999
, 402, 169.
| Crossref | GoogleScholarGoogle Scholar |

Accessory materials



