A perspective on time: loss frequencies, time scales and lifetimes

Additional keywords: chemical modes, eigenvalues, global warming potentials.

The description of atmospheric chemistry and composition, or other components of the Earth’s system, using a scalar with units of time or inverse time is widespread.^[1–7] These quantities are often used as metrics of the system to describe the duration or decay of a perturbation, or even the cumulative effect of an action as in ozone depletion potential or global warming potential.^[8–12] There are many different ways to derive metrics of time, and they describe different properties of the system. Here we carefully define three of those metrics: loss frequency (LF) that is typically used in the continuity equation for loss of a species, time scale (TS) that can describe the e-fold of a perturbation to the system, and lifetime (LT) that is a budgetary term derived from integrated burden and loss. We demonstrate which properties of the system they describe. Three examples are taken from atmospheric chemistry and biogeochemistry, but they are readily generalised.

The confusion in deriving quantities with units of time to describe an Earth system is widespread. For example, the quantity designated ‘lifetime’ is sometimes calculated inconsistently with respect to the total burden of the species, and often used in place of the true decay time when evaluating environmental effects in assessments.^[13,14] Local photochemical loss frequencies are not really system lifetimes, and are only one component of what determines the dynamical time scales of the system. A careful set of definitions and derivations is needed to ensure that we are reporting, publishing and comparing the same quantities. In cases where the chemical losses are much slower than the transport time scales that mix the atmosphere, the difference between lifetime and time scale is small (e.g. for CHF₃), but for those long-lived gases with chemical feedbacks this does not hold (e.g. for N₂O^[15]). In the former case the steady-state lifetime for any surface emissions is very close to the e-fold time scale for decay of a perturbation. This simplification fails for short-lived species,^[16–19] but the lifetime remains the correct integrating factor if one scales the pulse to the steady-state pattern. A correction from lifetime to perturbation lifetime is correctly applied when calculating the environmental effect of additional emissions, such as the global warming potentials for gases with chemical feedbacks like CH₄ and N₂O,^{[4,8,15,20,21]} but the time scale of those effects cannot always be represented by a simple e-fold as in most assessments.^{[13,14,22,23]} The use of metrics involving time is powerful, can be straightforward and follows directly from the different ways of defining them.

The continuity equation describing the rate of change of a species (y) at a given location (x) and time (t) can be written as:

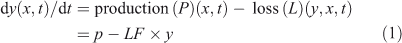
The production rate is often assumed to be independent of y and includes sources, in situ chemistry, transport and radiative terms, whereas the loss rate includes in situ chemistry, transport and other terms removing y (see Prather^[1]). The loss rate is often presumed to be a linear function of y, and hence the loss frequency (LF), with units of inverse time (i.e. year^–1), is calculated simply as LF = L/y. LF is the eigenvalue of a one-box, linear system.

For many important cases, such as the example of tropospheric O₃ presented below, the linear form of Eqn 1 is substantially incorrect. For such non-linear systems the loss frequency may change as the system evolves, nevertheless a first-order accurate description of the system comes from the Taylor expansion of Eqn 1 about the current state (y).

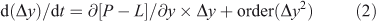
This corrected loss frequency, LF = –∂([P – L](y))/∂y, is the partial derivative of the chemical terms and is evaluated at the current state (y) and for a one-box, non-linear system describes the decay (or growth) of a perturbation (Δy).

A time scale (TS) has units of time (e.g. year) and should describe the temporal behaviour of the system or perturbations to it, in the sense of an e-folding time for some component:

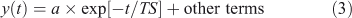
In this notation a negative time scale describes an unstable system. For a one-variable, one-box, constant-in-time, linear system, TS = 1/LF and Eqn 3 is the solution to Eqn 1.

Most systems described by Eqn 1, however, exhibit multiple time scales that couple chemistry and transport across the system. These times scales are the inverse eigenvalues of a coupled linear system, also called mode times,^{[1,20,24–27]} and the temporal behaviour of a single species usually involves multiple time scales, where ∑_j a^j = 1.

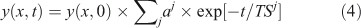
A lifetime (LT) is an integrated quantity that characterises the overall budgets or throughput of the system (e.g. emissions, losses) and has units of time (e.g. year). It is derived from the integral species (Y ≡ ∫y, kg), production (P ≡ ∫p, kg year^–1) and loss (L ≡ ∫loss = ∫LF·y, kg year^–1) over the system. The instantaneous lifetime in atmospheric chemistry is defined as the integrated system-wide burden of a constituent divided by the integrated loss of that constituent (LT ≡ Y/L, year). In effect, the inverse lifetime is the weighted average of the loss frequencies (<LF>).

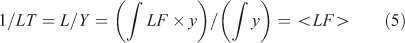
In general the lifetime is not a time scale of the system as defined in Eqns 3 and 4 but an amalgam of these time scales. An analogy would be the human lifetime: the time from birth to death contains a mix of times of growth, development and senescence, but one’s lifetime is an integral across these processes that cover very different types of activities. For the one-variable, one-box, constant-in-time, linear system, LT = TS = 1/LF.

Lifetimes can be defined for specific losses but always use the total burden. For example, if the total loss can be split among three processes, L = L^a + L^b + L^c, then the ‘a’ process lifetime, LT^a ≡ Y/L^a, and the inverse lifetimes are additive. In general, none of these are time scales of the system.

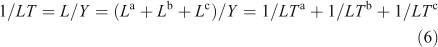
The steady-state lifetime (LT^SS) is a special case when production balances loss: i.e. dy/dt = 0 at the local scale, and P = L = Y^SS/LT^SS on the global scale. It is special also in that this lifetime represents the cumulative environmental effects of a pulse^[28]: the time integral of effects (e.g. ozone depletion, surface air quality, radiative forcing) following an emission pulse of a species exactly equals the steady-state pattern of effects from that emission pattern multiplied by the steady-state lifetime of the perturbing species for that emission pattern, assuming the perturbation and decay can be linearised. These effects generally occur over a wide range of time scales (both faster and slower) than the steady-state lifetime. This leads to the somewhat confusing result that although the system-wide Eqn 7, which is used in assessments:

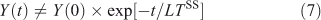
does not accurately describe the decay of a perturbation Y(0), it still gives the exact integral of such a pulse and can be related to eigenvalue time scales (see Eqn 4).

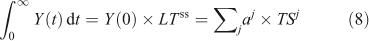
In non-linear systems, the lifetime of a perturbation (Δ) to the burden (Y) can differ from the lifetime of the burden itself, i.e. LT^Y+Δ ≠ LT^Y ≠ LT^Δ. The perturbation lifetime (LT^Δ) describes the cumulative effect of a small pulse, and it differs from the base-state lifetime if the lifetime changes with burden. To derive LT^Δ consider the losses in a perturbed system, L(Y + Δ), to be the sum of the base-state loss defined as burden over lifetime plus that from the perturbation:

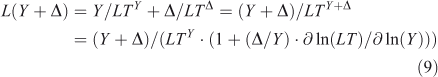
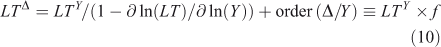
where the sensitivity of lifetime to burden is s = ∂ ln(LT)/∂ ln(Y), and the feedback factor on steady-state lifetime is f = 1/(1 – s). For atmospheric CH₄ the feedback factor is ~1.4; and for N₂O, it is ~0.92.^[4,13,29,30] The perturbation lifetime is used correctly in climate and ozone assessments as a measure of the cumulative effect of a pulse emission, but it is often mistaken for the time scale (e-fold decay) of the pulse (i.e. Eqns 7–8). Thus, if the perturbation lifetime (LT^Y × f) of CH₄ is 12 years, then a pulse of CH₄ decays with a mix of time scales both greater than and less than 12 years, but the integrated effect of such a pulse (Eqn 8) has a weighting factor of 12 years. See the example of CH₃Br and ozone depletion below. The loss frequency and time scales are inherent properties of the system, but the lifetime and its variants depend on how the system is being forced with sources.

Another quantity with units of time, the age-of-air in the stratosphere^[31,32] or troposphere,^[33] refers to the mean age (e.g. year) of an air mass since contact with some defined location (e.g. tropopause or surface). It is an integrative quantity like lifetime, only in this case the integral is over all transport paths that air could have taken since the point of last contact to reach that location. Age-of-air is traditionally defined for conserved tracers; but a photochemical age-of-air could include chemical aging of the tracer in transit; and that is what we actually calculate when simulating for example the abundance of chloroflourocarbons (CFCs) in the stratosphere. Age-of-air, like lifetime, does not describe local frequencies nor the time scales of the system. For example, the age-of-air in the upper stratosphere and mesosphere is typically 40 % or more larger that the e-fold time scale for removal of a conserved tracer from the stratosphere.^[6]

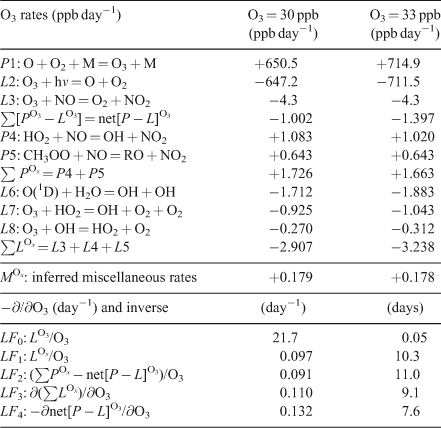
Tropospheric ozone (O₃) provides a great example of the problems in deriving loss frequencies. The photochemistry of O₃ is coupled through families of radicals (e.g. HO_x, NO_y), and the simplistic linear assumptions often used to calculate the loss frequency or time scales of O₃ are often significantly in error. Several studies have derived eigenvalues and modes for the HO_x–NO_y–O₃ chemistry from near surface to the mesosphere.^[34–37] An example of clean-air O₃ chemistry in summertime mid-latitudes at the surface is given in Table 1. Here a single 24-h day is integrated with [O₃] fixed for a reference case (O₃ = 30 ppb, 1 ppb = 1 nmol mol^–1), and 24-h average rates are reported. Here we use upper-case P and L because this is a one-box system where y = Y and p = P. Partial derivatives with respect to O₃ are calculated as finite differences with a +10 % perturbation. Initial conditions of other species are typical of an unpolluted site (see Table 1). The major production rates (P1) and loss rates (L2, L3) are large (±650 ppb day^–1) and approximately cancel. By carefully adding up all rates that directly include O₃ production or loss (e.g. rates L7, L8 and others), we calculate a net [P – L]^O₃ of –1.002 ppb day^–1. Note that to achieve three-place accuracy on the net [P – L], we must calculate the main terms (P1, L2) to an accuracy of six decimal places.

Table 1.  Tropospheric ozone linearised loss frequencies (LF)
Notes: Ozone production and loss rates (ppb day^–1) for a 24-h integration at the surface 45°N solstice. The air density M equals 2.5 × 10¹⁹ molecules cm^–3. Photodissociation rates are denoted by hν. Uses a methane-only photochemistry (no non-methane hydrocarbons) and starting conditions of O₃ = 30 ppb (1 ppb = 1 nmol mol^–1), CO = 100 ppb, CH₄ = 1700 ppb, NO_x = 24 ppt (1 ppt = 1 pmol mol^–1), N₂O₅ = 5 ppt, HNO₃ = 184 ppt, HO₂NO₂ = 275 ppt. Major production and loss rates for O₃ and O_x are shown. Other, unlisted rates for O₃ are less than 1 ppb day^–1. For O_x, the miscellaneous missing rates are inferred from the difference between O_x rates and the true [P – L]^O₃. Five different methods of evaluating the loss frequency of O₃ are shown. The partial derivatives, LF₃ and LF₄, are calculated as a finite difference using the +10 % O₃ perturbation

The O₃ loss frequency is often calculated as loss rate divided by abundance (Eqn 1), and in Table 1 we compare these estimates with the more accurate linearisation (Eqn 2). Defining an O₃ loss frequency from reactions L2 and L3 gives a large value, LF₀ = 1/(0.05 days), which is unrealistic in terms of the observed fluctuations of O₃. Recognising that rate 1 (O + O₂ + M = O₃ + M) followed by rate 2 (O₃ + hν = O + O₂) does not change O₃, the scientific community proposed that the O₃ continuity Eqn 1 be solved for the odd-oxygen (O_x) family consisting of O₃ plus both forms of atomic oxygen (ground state O(³P) and metastable O(¹D)). In the stratosphere this definition of O_x reasonably describes the time scales of the Chapman ozone mechanism.^[1] In the troposphere, the second largest loss rate L3 (O₃ + NO = NO₂ + O₂) is usually followed by photolysis and reformation of O_x (NO₂ + hν = NO + O), and hence NO₂ might also be considered as O_x. The loss frequency defined from the three largest rates of O_x loss (L6 + L7 + L8), gives a more reasonable estimate of the time scales for O₃, LF₁ = 1/(10.3 days). A parallel approach based on O_x assumes that the production of NO₂ from peroxy radicals (P^O_x = P4 + P5) is fixed, independent of O₃, and that the sum of the remaining O₃ production and loss terms represent a loss that is linear in O₃ (L^O_x = P^O_x – net[P – L]^O₃ = LF₂ × O₃). For the clean-air case in Table 1, LF₂ = 1/(11.0 days).

The concept of O_x is used today when calculating O₃ tendencies in some chemistry transport models, but including NO₂ in the O_x family adds complications in tracer transport, for example, does peroxyacetyl nitrate (PAN), which forms from and thermally decomposes to NO₂ in the boundary layer, count as O_x? In general it is difficult to account for the true [P – L] of O₃ (–1.00 ppb day^–1) using the definition of O_x. For the example here, 18 % of the net production (+0.18 ppb day^–1) occurs through small rates that are hard to identify as they depend on the ambiguous definition of O_x, particularly through the NO_x reactions.

Linearisation of L^O_x is calculated numerically by increasing O₃ from 30 to 33 ppb and gives LF₃ = 0.110 day^–1, which is significantly larger than LF₁ = 0.097 day^–1 because the abundances of HO₂ and OH increase with O₃. A full linearisation of [P – L]^O₃ (Eqn 2) gives LF₄ = 0.132 day^–1, a further increase in the loss frequency because the O_x production rate P4 decreases by 6 % for a 10 % increase in O₃.

In summary, all of the O_x-based loss frequencies can greatly underestimate the true loss frequency for an O₃ perturbation. The difference between LF₂ and LF₄, ~40 % in the clean boundary layer, becomes significant when we use this loss frequency to evaluate O₃ as a tagged tracer, such as following the stratospheric influx of O₃ to the surface^[38,39] or estimating the long-range transport of pollution. In both cases the decay of the tagged O₃ is underestimated. In the opposite sense, the use of tagged tracers for CO^[40] can overestimate the decay rate because the added CO reduces OH abundances and thus its own loss frequency. Table 1 is only an example; accurate simulation of O₃ perturbations with a chemistry transport model would require linearisation of the chemical system (tangent linear model) at each time step at each location.

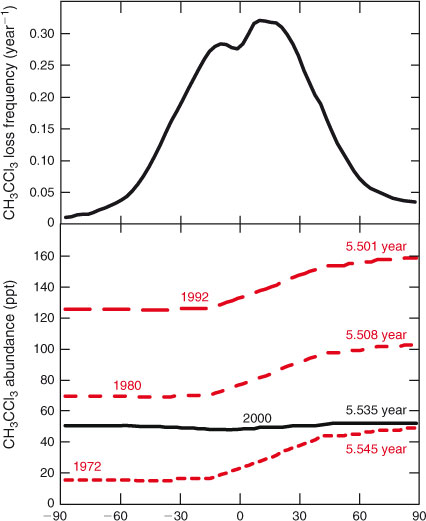
The trace gas CH₃CCl₃ (methyl chloroform, 1,1,1-trichloroethane) provides a case study in which the lifetime of the gas shifts as its atmospheric distribution evolves in response to changing emissions and atmospheric accumulation. Methyl chloroform is an industrially produced ozone-depleting halocarbon. Its abundance peaked in the early 1990s with a tropospheric mean of ~140 ppt (1 ppt = 1 pmol mol^–1) and a North Pole to South Pole gradient of ~40 ppt due to the predominant northern sources. The latitudinal distribution from four different years (1972, 1980, 1992 and 2000) are shown in Fig. 1 (bottom). For the latter three periods these are derived from observations.^[41–43] The absolute north–south gradient (ppt) is determined by the annual emissions and the rate of north–south transport. For this example we assume that it is the same from 1972 to 1992 as the mean tropospheric abundance increases. After 2000, the peak tropical loss results in a tropical depression of ~5 % in abundance that persists for the next decade as the CH₃CCl₃ decays at a near-uniform rate of ~0.18 year^–1,^[42] Over the entire period we assume that tropospheric OH remains unchanged and calculate the CH₃CCl₃ loss frequencies from the University of California–Irvine chemistry-transport model (CTM).^[44] This annual, tropospheric, zonal mean loss frequency (Fig. 1, top) ranges from 0.01 to 0.32 year^–1.

Fig. 1.  (Top) Mean tropospheric loss frequency (year^–1) of methyl chloroform (CH₃CCl₃) as a function of latitude. Annual zonal mean loss frequency of CH₄ against reaction with tropospheric OH is integrated from the surface to tropopause as calculated from Holmes et al.^[52] and multiplied by 1.66^[53] to scale to CH₃CCl₃. (bottom) Approximate tropospheric latitudinal abundances of CH₃CCl₃ (ppt) for the years 1972, 1980, 1992 and 2000. Each abundance profile is labelled with the year and the lifetime (years) against OH loss. Abundances and latitudinal patterns are based on reported observations,^[41–43] except that the 1972 and 1980 latitudinal patterns have been reconstructed here using the same absolute gradients as for 1992 and hence assume that emissions then were similar to the latter period (e.g. 500–700 Mt year^–1). Lifetimes consider only tropospheric OH loss but include the total atmospheric burden.

Combining latitudinal distribution with latitudinal loss frequency and weighting by air mass, we can calculate a lifetime against tropospheric loss for these four years. Results are given for each latitudinal profile in Fig. 1, see notes in caption. In the early years, the lifetime is largest (5.545 years) because a greater fraction of the CH₃CCl₃ burden is at high northern latitudes, whereas the loss frequency peaks in the tropics. As the total burden grows, a greater fraction is in the tropics and the lifetime drops (to 5.508 years in 1980 and 5.501 years in 1992). In the final stage, CH₃CCl₃ decays everywhere with a single e-fold, the lifetime becomes constant (5.535 years), and it is longer again because the small minimum in abundance matches the peak loss frequency in the tropics. At steady-state with the 1992 northern industrial emissions, the CH₃CCl₃ abundance would asymptote to ~175 ppt with a lifetime of 5.50 years (not shown). In the final phase, the lifetime (5.535 years) is also a time scale of the system, describing the decay of the longest lived chemical mode of the system, see discussion of CH₃Br below. Although the differences in lifetime here are small, they serve to illustrate that even with fixed chemical loss frequencies and transport (and hence fixed time scales), the lifetime depends on the distribution of the species, which is driven by the history of emissions, as noted in the supplement of Montzka et al.^[41]

Methyl bromide (CH₃Br) presents an interesting case study of loss frequencies, time scales and lifetimes because the chemistry can be treated as fully linear but the interplay of different reservoirs (stratosphere, troposphere, ocean mixed layer) creates non-intuitive results. Methyl bromide is a naturally occurring gas with oceanic sources.^[45] Its production and use in agriculture and fumigation has increased its atmospheric abundance, and the bromine radicals it releases in the stratosphere (Br_Y) cause ozone depletion. Formal treatment of the CH₃Br system identified lifetimes and time scales that were not directly recognisable from the local loss frequencies.^[46] Here, we revisit that work but collapse the 1-D chemistry diffusion problem into a three-box model with chemical model and exchange coefficients as summarised in Table 2. On the far right column of Table 2 is shown the mole fraction of CH₃Br in the three reservoirs at steady-state with troposphere-only sources (scaled to 1 ppt in the troposphere). The ocean layer is equivalent to 2.9 % of the atmosphere, based on a 100-m mixed layer and the solubility of CH₃Br.

Table 2.  Parameters defining 3-box chemical model for CH₃Br–Br_Y system
Notes: loss frequencies and exchange rates for the 3-box model chosen to match the 1-D diffusion model of Prather^[46]; 1 atm = 1.765 × 10²⁰ moles of dry air; 14.1 Tg Br ppt-atm^–1. The cases shown for troposphere-only and ocean-only emissions are scaled to 10-ppt tropospheric CH₃Br, as is the last case (C) for which the mix of troposphere and ocean emissions yields a 100 % supersaturation (neutral) ocean layer. For evolution of atmospheric and oceanic CH₃Br see Yvon-Lewis and Butler,^[45] Butler^[47] and Hu et al.^[48]

The eigenvalue decomposition of the system with six degrees of freedom is given in Table 3. Because Br_Y does not feedback on CH₃Br in this simplified system, there are only three CH₃Br eigenvalues. These three time scales of 3.2, 0.92 and 0.018 years differ substantially from the inverse loss frequencies for CH₃Br because the exchange rates between reservoirs play a key role in determining the time scales of the system. The coefficients for each time scale following a single pulse of 1 ppt CH₃Br in the troposphere are given in Table 3. The abundance of CH₃Br in the troposphere (trp) and stratosphere (str) follow three exponential decay curves

Table 3.  Eigenvalue decomposition of 3-box, 2-species system, showing coefficients (ppt) of eigenvalue time scales for 1-ppt tropospheric CH₃Br pulse

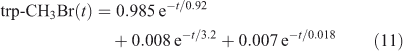
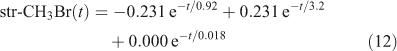
Note that trp-CH₃Br decays rapidly with 0.92 years e-fold, but then ~1 % decays with the much longer 3.2 years e-fold that is tied to the decay of str-CH₃Br. The str-CH₃Br abundance builds initially as the CH₃Br reaches the stratosphere and then decays with the single longest-lived chemical mode time for CH₃Br of 3.2 years. Stratospheric Br_Y, effectively a proxy for ozone depletion, has more complex behaviour due to the time scale for stratosphere–troposphere exchange.

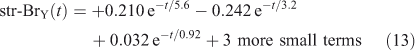
Note the str-Br_Y takes longer than str-CH₃Br to reach its peak, and then it takes much longer to decay with a time scale of 5.6 years. These are the true time scales of the system, and not readily predicted from the loss frequencies alone.

The steady-state lifetimes derived from the budgets are given in Table 4 for three different cases with tropospheric CH₃Br abundances of 10 ppt: (a) a hypothetical, troposphere-only source giving an ocean saturation level of 46 % (i.e., 4.6 ppt); (b) a hypothetical, ocean-only source giving an ocean saturation level of 177 % and (c) a mix of both sources to yield a net neutral ocean saturation of 100 %. During the peak of anthropogenic emissions in the 1990s, ocean saturation was about 85 %,^[45,47] and following mitigation the abundance dropped to ~8 ppt with average ocean saturation of 100 %.^[48] Note that this drop of 20 % in CH₃Br tropospheric abundance requires reduction of more than 50 % in tropospheric emissions. The steady-state lifetime, 1.03 years in case A and 0.50 in case B, is straightforward. In case C the combination gives an intermediate lifetime of 0.70 years. Thus we have a clear and obvious case where the lifetime depends on the source.

Table 4.  Steady-state budgets and lifetimes under different emissions scenarios

The steady-state lifetime and pattern for a tropospheric source are important numbers in that they describe exactly the integral of exposure (e.g. ppt-year) following a single tropospheric pulse.^[1,28] First, take a 1-ppt tropospheric pulse (i.e. 0.872 ppt-atm) and distribute the same burden in the steady-state pattern. This gives 0.910 ppt of CH₃Br in the troposphere (with the remainder in the stratosphere and ocean) and 0.404 ppt Br_Y in the stratosphere. Multiplying each of these by the steady-state lifetime for tropospheric sources, 1.029 years, we get 0.936 ppt-year for trp-CH₃Br and 0.416 ppt-year for str-Br_Y, which is exactly (with enough decimal places) the integral from zero to infinity of Eqns 11 and 13 respectively. It is important to note that the ozone depletion persists for more than 5 years although the lifetime of the CH₃Br source is only ~1 year. Thus the CH₃Br lifetime is the correct integrating factor for effects following the release but it fails to describe the time scales of those effects.

Loss frequency is often used as a simple scaling factor, relating the local loss rate of a species to its abundance. In general with coupled, multi-species systems, the simple linear scaling fails, but an effective loss frequency can be calculated for a perturbation to a species with a linearisation of the system (e.g. tropospheric O₃). Lifetimes, which are defined in terms of integrated budgets, depend on the method of external forcing. The lifetime of a trace gas can change even when the chemical reactivity of the atmosphere is unchanged (e.g. CH₃CCl₃). For a perturbation forced by a specific emission pattern, the product of the steady-state pattern and the lifetime are an exact integral of a pulse of that emission, including any consequent environmental effects^[28] (e.g. CH₃Br and O₃ depletion). This method of defining lifetime works even for trace gases with known chemical feedbacks or indirect effects such as N₂O, CH_4, CO and NO_x as long as one uses the perturbation lifetime.^[8,13,49,50] Even for relatively simple systems, time scales reflect the multitude of degrees of freedom (e.g. CH₃Br); however, proper diagnosis even in 3-D models can identify the correct response to perturbations.^[5,30,51] The often-made simplifying assumption – that these three metrics are the same – may be appealing if one is sure that the errors are small, but the lack of rigor may propagate to systems where much larger, unrecognised errors will occur.