Predicting availability of mineral elements to plants with the DGT technique: a review of experimental data and interpretation by modelling
Fien Degryse A C , Erik Smolders A , Hao Zhang B and William Davison BA Division of Soil and Water Management, K.U.Leuven, Kasteelpark Arenberg 20, 3001 Heverlee, Belgium.
B Department of Environmental Science, Lancaster University, Lancaster, LA1 4YQ, UK.
C Corresponding author. Email: fien.degryse@ees.kuleuven.be
Environmental Chemistry 6(3) 198-218 https://doi.org/10.1071/EN09010
Submitted: 23 January 2009 Accepted: 24 April 2009 Published: 18 June 2009
Environmental context. Total concentrations of mineral elements in soil bear little relation to their availability for plants. The DGT (diffusive gradients in thin-films) technique has been found to be a good predictor of trace metal uptake and P deficiency, though not consistently in all studies for all elements. This review examines the fundamental basis for the relation between DGT fluxes and plant uptake and assesses under which conditions this relation may break down.
Abstract. In the DGT technique, elements are accumulated on a binding gel after their diffusive transport through a hydrogel. In this paper, we explore in more detail why – and under which conditions – DGT correlates with plant uptake. The theoretical considerations are illustrated with experimental results for metal uptake and toxicity, and for phosphorus deficiency. Strong correlations between DGT and plant uptake are predicted if the diffusive transport of the element from soil to the plant roots is rate-limiting for its uptake. If uptake is not limited by diffusive transport, DGT-fluxes and plant uptake may still correlate provided that plant uptake is not saturated. However, competitive cations may affect the plant uptake under these conditions, whereas they have no effect on the DGT flux. Moreover, labile complexes are not expected to contribute to the plant uptake if diffusion is not limiting, but they are measured with DGT. Therefore, if plant uptake is not limited by diffusion, interpretation of the observed correlation in terms of the labile species measured by DGT is inappropriate.
Additional keywords: bioavailability, deficiency, DGT, metals, phosphorus, plants, soils.
Introduction
It is well established that the total concentrations of mineral elements in soil bear little relation to their availability for plants.[ 1 ] Numerous soil extraction procedures have been developed to improve the measurement of the bioavailability of these elements. These techniques have found their applications in soil fertility assessment and for risk assessment of soil contaminants that enter the food chain via plant uptake. For example, diethylenetriaminepentaacetic acid (DTPA)-extractable metal in soil is often used to assess trace element availability, as this chelator only extracts the more ‘labile’ metal forms.[ 2 ] Other measures such as the concentration in soil solution or in a weak salt extract have also been proposed as indicators of plant availability,[ 3 ] since plants access mineral elements from the soil solution. However, soil solutions may also contain ‘inert’ species that are presumably unavailable to plants.[ 4 ] Nevertheless, trace metal concentrations in plant tissues usually correlate better with soil solution concentration or CaCl2 (0.01 M)-extractable concentrations than with total concentrations in soil (e.g. refs [3,5,6]). In soil testing for phosphorus, a remarkably wide range of soil testing procedures are used such as Colwell-P,[ 7 ] Bray-P[ 8 ] and resin-P[ 9 , 10 ] methods.
Soil tests are generally developed in an empirical way. A strong correlation with uptake may suggest, but does not prove, which supply mechanisms determine the nutrient uptake by plants in soil. Moreover, soil tests have the drawback that their applicability is restricted to the conditions to which they are calibrated, i.e. they do not allow generalisation. Models of solute uptake by plants are an alternative to the empirical soil testing for predicting and unravelling factors that control plant availability. Models based on a mechanistic approach have been used to describe uptake of major nutrients such as N, P and K (e.g. the Barber–Cushman model).[ 11 ] The same type of models have also, though more rarely, been used to model uptake of micro-nutrients, such as Zn and Mn[ 12 , 13 ] or non-essential trace elements, such as Cd.[ 14 ] These models have improved our understanding of the mechanisms involved in the transfer of elements from soil to plant. However, despite their scientific use, they are not used in practice since extensive – and often unavailable – information on soil and plant characteristics is required. Also, the simulated and observed uptake does not always agree well, especially for trace elements (e.g. ref. [14]), which may be related to model shortcomings (i.e. processes not taken into account or misrepresented) or to uncertainty in the input parameters.
Quite recently, the method of DGT (diffusive gradients in fhin-films) has been promoted as a tool to predict metal bioavailability.[ 15 ] The DGT method measures the diffusive supply of elements under infinite-sink conditions. A good correlation between concentrations of metals in plants and their measurement by DGT has been observed in several studies.[ 3 , 15 – 18 ] The empirical evidence that DGT correlates with plant uptake of an element has preceded process analysis that explains why DGT should correlate with plant uptake. The reported strong correlations suggest that diffusive transport of metals to the plant roots is the rate-determining process in the metal uptake. However, uptake by plants may not be limited by diffusion if transport through the biological membrane (internalisation) is relatively slow, which may be the case if the plant has little affinity for the element or if the supply is large and the plant uptake is saturated. Under these conditions, the uptake will not be determined by the supply rate to the roots, but by the plant’s demand. Comparison of plant uptake and DGT fluxes may, therefore, provide valuable insight into which process is the rate-limiting step in plant uptake, which will allow DGT to be used as an investigative research tool.
The objectives of this paper are to review the mechanisms of mineral element availability and how they relate to diffusive fluxes measured by DGT. The theoretical basis for using DGT to mimic uptake by plants has been examined before.[ 19 , 20 ] For the mathematical details of the relevant models, we refer to these papers. Here, we focus on the concepts and illustrate how plant and DGT are affected by soil properties. We discuss under which conditions the relationship between uptake by DGT and plants may break down. Where possible, the theoretical considerations are illustrated with experimental results. We first elaborate on the mechanisms of trace element and nutrient uptake from soil before embarking on the reactions between soil and a DGT device. As will be shown, there are striking similarities between the fluxes to roots and those to the DGT. We restrict the analysis to the elements for which DGT has been tested, i.e. trace elements and phosphorus.
Speciation of trace metals and phosphorus in soil
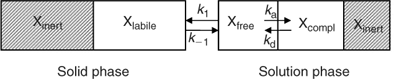
The availability of elements for uptake by plants or DGT depends on their speciation in soil. In this section, we give a general, and greatly simplified, outline of how the speciation in soil can be described (Fig. 1). In the solution phase, elements are present as free ions, as complexes with inorganic or organic ligands, or associated with mineral colloids. The free ion in solution is generally the most reactive species in terms of reaction with the solid phase. The sorption of the free ion on the solid phase is relatively fast, and is often described with a solid–liquid distribution coefficient or K d. In the remainder of the manuscript, the term K d will be used as the ratio of the concentration of element that is reversibly sorbed on the solid phase (also termed ‘labile’) to the solution concentration. Part of the element in the solid phase may be inert (non-labile) on the time-scale considered. For example the element may be present as a pure or mixed solid, in crystal lattices, or in internal pores of sorbents (e.g. oxides) after intraparticle diffusion. Of course, this binary classification in labile and non-labile solid phase pools is an oversimplification. However, a more sophisticated approach, e.g. a continuous distribution of sorption kinetics, would be impractical to deal with. Moreover, isotopic dilution studies suggest that labile and non-labile pools are reasonably distinguishable, since the isotopically exchanged metal generally changes little with isotope equilibration time, beyond a few days of equilibration.[ 21 , 22 ]
|
Modelling and conceptualising uptake by plants
Uptake fluxes and plant concentrations
The way in which uptake of elements by plants is quantified depends on the model used or on the experimental approach. Mechanistic models often quantify uptake by expressing the uptake as a root area based flux, i.e. the amount of element taken up per unit of time per unit root area (e.g. in mol cm–2 s–1), or as a root length based flux (e.g. in mol cm–1 s–1). Root surface area and root length are of course related through the root radius.[ 23 ] When uptake by plants is studied in short-term experiments in hydroponics, the uptake is usually also expressed as an uptake flux, often based on root weight (e.g. in moles per gram root fresh weight (RFW) per hour).[ 24 , 25 ] These root-weight-based fluxes can be converted into area or length-based fluxes if the specific root area (cm–2 per g RFW) or specific root length is known (cm per g RFW). However, in many experiments, uptake by plants is studied in long-term experiments. The plants are grown for several weeks in nutrient solution or in soil, and the uptake is assessed by measuring the element concentrations in the plant tissue at the end of the experiment. As a result, the uptake is usually quantified as internal concentrations in the plant or total uptake of the element (= concentration × yield).
Uptake fluxes and internal concentrations are of course related. Assuming exponential growth and that the uptake flux is constant over time, the internal plant concentration M pl (mol g–1 dry weight (DW)) is related to the uptake flux as follows[ 26 ]:
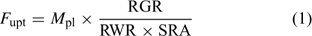
where F upt (mol cm–2 day–1) is the root-area-based uptake flux, RWR is the relative weight of the root (root weight v. total plant weight) and SRA (cm2 g–1 DW) is the specific root area. The relative growth rate, RGR (day–1), sometimes termed the growth (rate) constant, describes the exponential growth:
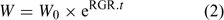
where W and W 0 are the plant weights at time t and time 0 respectively.
In this manuscript, several graphs illustrate the uptake by plants both as flux and as concentration in the (whole) plant. The uptake fluxes represent time-averaged fluxes, as uptake fluxes in soil decrease over time in case of diffusion limitations.
Free ion activity model (FIAM) and biotic ligand model (BLM)
We will first briefly discuss the ‘equilibrium models’, which assume that the transport in solution towards the site of uptake is fast compared with the actual uptake, before progressing to models that take into account possible transport limitations in the uptake. A more elaborate discussion of these equilibrium models can be found elsewhere.[ 27 , 28 ]
The FIAM relates metal toxicity and availability to the free ion activity of the metal in the surrounding solution. The FIAM was formulated to rationalise the experimentally observed relationship between free ion activity and uptake or toxicity of metals (e.g. refs [29,30]). Many studies from the literature for aquatic systems, where unicellular organisms were studied, support the FIAM, although some exceptions have been found (e.g. ref. [31]).
The FIAM has also been applied to describe metal uptake by plants from solution, but the number of studies that support the FIAM for higher plants is limited. Some studies have shown that addition of chelators to hydroponic solutions decreased the biouptake (e.g. ref. [32]), and these are often considered to be supportive of the FIAM. However, the decrease in free ion activity upon addition of chelator was probably in many cases larger than the decrease in uptake, which actually illustrates that the FIAM does not hold and that complexes partly contribute to the uptake. Studies that show exceptions to the FIAM for metal uptake by higher plants[ 33 – 39 ] are much more numerous than those that unequivocally support the FIAM. We speculate that these exceptions are in many cases a consequence of the diffusional supply of metal to the uptake site being rate-limiting, rather than the rate of internalisation (as is assumed in the FIAM). Under these conditions, labile complexes can contribute to the metal uptake by enhancing the diffusion flux (see later).
The BLM is similar to the FIAM but also takes into account the effect of competing cations. The BLM predicts the degree of metal binding – which is related to the toxicological response – at the site of action (‘biotic ligand’). The BLM has been successfully applied to predict metal toxicity for a variety of aquatic organisms and metals (e.g. refs [40,41]).
These concepts have also been used to predict metal uptake by plants from soil. The distribution of a metal between solid and liquid phases is then modelled with an equilibrium partitioning model, and the plant response (uptake or toxicity) is modelled from the solution composition using a FIAM or BLM approach.[ 42 – 46 ] These models give reasonable predictions of the uptake, but this does not prove that the ‘equilibrium’ assumptions behind the model are valid. For example, Hough et al.[ 46 ] showed that the prediction using a FIAM approach was not superior to that of a simple empirical regression model. As pointed out by the authors, the derived ‘reaction constants’ could truly represent an equilibrium condition, in which case they describe the affinity of metal and proton ions for the root sites, but they could also be fitting parameters in a transport-limited uptake process.
Taking all evidence together, the free-ion-based equilibrium models (FIAM/BLM) generally performed better for unicellular aquatic organisms and for higher plants in the toxic concentration range. For metal uptake by higher plants under non-toxic conditions, contrary to the predictions of the FIAM, complexes were often found to contribute to metal uptake.
Diffusion limitations and bias in the Michaelis constant (K M)
The FIAM and BLM assume that the diffusive transport of elements to the site of uptake is not rate-limiting, and result in an equilibrium approach in which uptake is related to the free ion activity in the bulk medium. Diffusion limitations may explain the experimentally observed deviations from the FIAM. To evaluate whether uptake is diffusion limited, the limiting diffusion flux must be compared with the plant uptake flux.[ 47 ]
Labile complexes may contribute to the diffusion flux, but this will be discussed further on. Here, we make the comparison for a solution without complexes, for which the total concentration of the element in solution, c, equals the free ion concentration, [M2+]. The limiting diffusion flux (i.e. the diffusion flux when the free ion concentration at the surface, [M2+]s, is zero) equals:
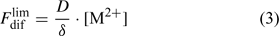
where D is the diffusion coefficient and δ is the thickness of the diffusion layer. The diffusion coefficient in water at 20°C is around 5 × 10–6 cm2 s–1 for most metals ions and for phosphate.
The plant’s demand can be described with the Michaelis–Menten equation, which relates the uptake flux F upt to the free metal concentration at the root surface, [M2+]s:
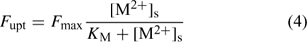
where the parameters F max and K M define the Michaelis–Menten curve. The ‘Michaelis constant’ K M equals the free ion concentration at which the uptake flux is half of the maximal uptake flux F max. A smaller value of K M denotes a higher affinity of the transporter for the element. At low activities ([M2+]s < K M), the Michaelis–Menten equation can be reduced to a linear relationship:
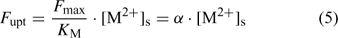
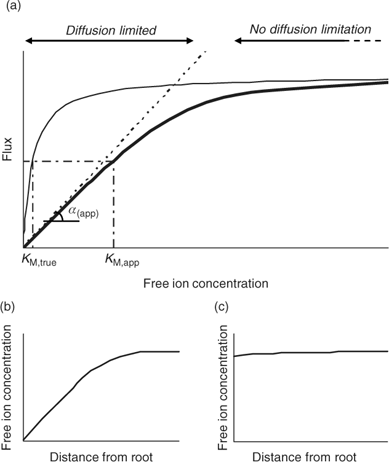
Although the root absorbing power α is strictly defined as the ratio of uptake flux and the concentration at the root surface,[ 48 ] it is in practice usually calculated as the ratio of uptake flux and concentration in the bulk solution, since the concentration at the root surface is not known. The root absorbing power is then the slope of the linear relation between uptake flux and concentration in the surrounding solution, at low concentration where plant uptake is not yet saturated (Fig. 2). If bulk concentrations and concentrations at the root surface are equal (i.e. no diffusion limitations), we obtain:
|
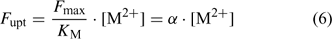
The uptake is limited by diffusion if the (limiting) diffusional flux is smaller than the plant’s demand, i.e. if F max/K M >> D/δ, which may occur at low concentrations (Fig. 2). In that case, the free ion concentration at the root surface will be much smaller than in the bulk solution, and the diffusion flux as well as the uptake flux F upt will approach the limiting diffusion flux (i.e. F upt = F dif lim). This is mathematically expressed by the Best equation,[ 49 ] which gives the steady-state solution for Michaelis–Menten uptake kinetics in combination with diffusive transport (cf. the thick line in Fig. 2a).
The Michaelis–Menten parameters are usually determined by measuring uptake at different free ion concentrations, with the assumption that bulk concentrations equal the concentrations near the root surface. However, if uptake is limited by diffusion, the derived Michaelis constant will not reflect the plant root affinity. Rather, apparent constants will be obtained that provide an indication of the diffusion limitation, as shown by combining Eqns 3 and 5:
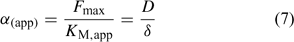
Under diffusion limitations, an increase in the diffusion flux will increase the plant uptake. For example, a decrease in the diffusion layer thickness will increase the value of α (app) and decrease the apparent Michaelis constant. Stirring indeed increased the value of α for short-term uptake of Cd by spinach in solution.[ 50 ] Based on Eqn 7 and on the data from ref. [50], we estimate a value for δ of ~500 μm in a stagnant solution and 150 μm in a stirred solution (Table 1). Literature values for α determined in solution culture are generally between 7 × 10–5 and 10–3 cm s–1 for Cd and Zn (SRA of 200 cm2 g–1 root fresh weight assumed to convert root-weight-based flux into surface-area-based flux), which corresponds to values for δ between 50 and 700 μm.[ 25 , 51 , 52 ] Also for phosphorus, solution culture experiments generally yield values for α of the same magnitude, between 8 × 10–5 and 8 × 10–4 cm s–1.[ 53 – 55 ] This strongly suggests that the Michaelis constant is biased by transport limitations and that uptake of Cd, Zn and P is limited by diffusion in the lower concentration range (c < K M,app). We found strong indications that true K M values of Cd and Zn are in the nM range, i.e. over two orders of magnitude lower than the values usually reported (F. Degryse et al., unpubl. data).

|
Barber–Cushman model
The Barber–Cushman model and other similar plant uptake models consider the diffusive supply of solutes to the plant roots. These models were initially developed to model nutrient uptake,[ 11 ] but have more recently been used to also model uptake of trace metals.[ 12 , 14 ] Here, we used the NST 3.0 model[ 13 ] to calculate uptake according to the mechanistic approach of Barber.[ 56 ]
In the Barber–Cushman model, the Michaelis–Menten equation (Eqn 4) is combined with a transport equation. This transport equation includes both mass flow and radial diffusion of the elements to the plant roots. The amount of element delivered by mass flow can be calculated from the amount of water used and the concentration of the element in solution. Table 2 gives typical plant and soil solution concentrations for essential plant nutrients, and estimated concentration factors, CF, i.e. the ratio of plant concentration to soil solution concentration. While recognising that there are large differences in soil solution concentrations between soils, this approach allows elements for which uptake is most likely not limited by diffusion to be distinguished from those for which diffusion limitations may arise. Typically, the water inflow rate v 0 is around 5 × 10–7 cm3 cm–2 s–1 or 0.04 cm day–1.[ 56 ] Mass flow should, therefore, be sufficient to supply the plant’s demand if its supply flux, given by (v 0 × c), is greater than the flux to the plant, F upt. Substituting from Eqn 1, this condition is equivalent to:
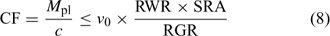
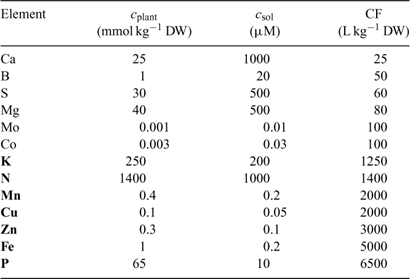
|
Using realistic values[ 26 ] for RGR (0.2 day–1), RWR (0.2 g root g–1 plant) and SRA (2000 cm2 g–1 root DW), we estimate that mass flow alone is sufficient if the concentration factor is below ~100 L kg–1 DW. Mass flow thus supplies a sufficient quantity to satisfy the plant’s demand for elements such as Mg, Ca and S (Table 2). Excess supply by mass flow over demand may even lead to these elements accumulating at the root surface, and result in a larger concentration near the root surface than in the bulk solution.[ 56 ] However, mass flow does not meet the plant’s demand for many other elements, for which the plant’s requirement (internal concentration) relative to the solution concentration is much larger. Consequently, elements such as K and P are depleted near the root surface. The resulting concentration gradient perpendicular to the root surface induces a diffusive flux of the element from the bulk solution to the root surface.
Contribution of metal complexes to metal availability
The Barber–Cushman model, that was developed for macronutrients, does not take into account solution speciation, as the speciation of macronutrients in solution is usually dominated by one ionic form (e.g. nitrate, phosphate, sulfate anions, potassium and calcium cations). The speciation of trace metals in solution is, however, more complex. They occur not only as free ions, but also as complexes with inorganic or organic ligands. For example, Cu in solution is usually mainly present as complexes with dissolved organic compounds.[ 57 ] Cadmium and zinc occur mainly as free ions in solution at low pH – unless there are elevated concentrations of inorganic ligands that may form complexes – but a considerable fraction may be complexed with dissolved organic matter at pH > 6.5.[ 57 ] Neither the original Barber–Cushman model, nor the more recent plant uptake models (e.g. NST 3.0), include the effect of labile complexes, which act as a mobile buffer. While the theoretical framework is available to incorporate this in plant uptake models,[ 58 ] the main obstacle is probably a lack of reliable data on metal speciation and lability of complexes under relevant conditions (i.e. in ‘real’ soil solutions). Determination of the metal speciation in soil solutions often poses practical challenges. First, isolation of soil solution in volumes that are large enough to carry out the speciation analysis is a laborious method, since the solution should preferably be extracted at a moisture content close to that in situ (e.g. by centrifugation). Soil extracts with dilute salts at larger liquid-to-solid ratios are easier to obtain. However, dilution of complexing ligands occurs at larger liquid-to-solid ratios, and the speciation of elements with high affinity for organic ligands (e.g. Cu) may, therefore, strongly differ between a soil extract and ‘true’ soil solution.[ 59 ] Second, determination of the metal speciation in the solution often poses analytical difficulties, especially for elements with a small free ion fraction.[ 57 ]
In solutions with labile complexes, the limiting diffusion flux is larger than in ligand-free solutions at the same free ion activity, since the labile complexes dissociate within the diffusion layer, and thus contribute to the diffusive supply. The limiting diffusive flux under these conditions is:
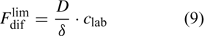
where c lab is the concentration of all labile species, i.e. the free ion as well as the complexes that dissociate fast enough to contribute to the diffusion flux. The association and dissociation rate of a complex, ML, can be quantified by first order kinetics. The first order rate constants for association (k a) and dissociation (k d) are related through the stability constant, K ML:
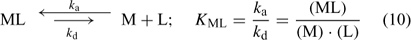
The faster a complex dissociates (large k d), the more likely it is to contribute to the diffusion flux. At the same free ion activity, the limiting diffusion flux (the diffusion flux under infinite sink conditions) increases with increasing concentrations and increasing dissociation rate constants of the complexes.
The presence of metal complexes in solution makes the application of the Barber–Cushman model more complicated. If uptake is limited by diffusion, the depletion of the free ions near the root surface will induce the dissociation of complexes. All complexes that dissociate fast enough will then contribute to the uptake (Fig. 3a). Therefore, uptake will not depend on free ion activity alone. If uptake is not limited by diffusion, only the free ion will affect the uptake, which can then be predicted by a model based on free-ion activity (e.g. BLM).
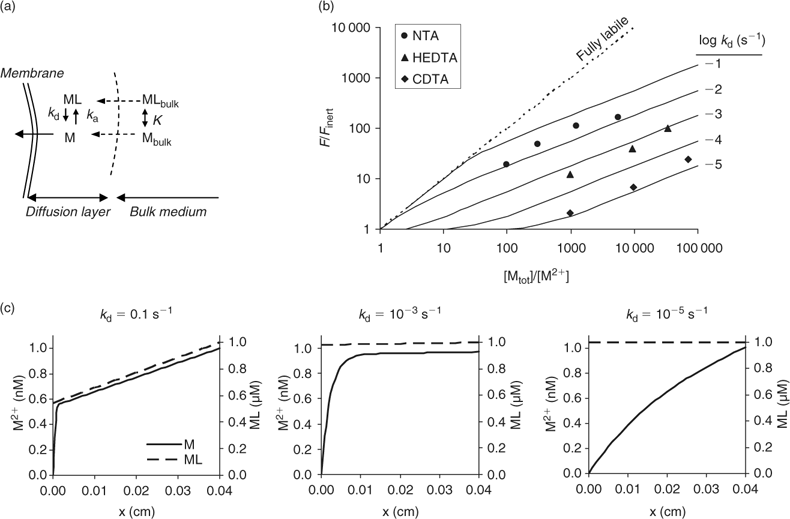
Measurements of uptake by plants in nutrient solutions have indeed demonstrated that metal complexes may contribute to metal uptake by plants.[ 33 – 39 ] Uptake of Cd by spinach in chelator-buffered solutions at constant Cd2+ concentration of 1 nM increased with increasing dissociation rate of the complex. At 1 μM of complex, the uptake in a solution with Cd–1,2-cyclohexanediaminetetraacetic acid (CDTA) (k d ~10–5 s–1) was only two-fold larger than in an unbuffered solution with the same free ion activity, while it was 100-fold larger if Cd–nitrilotriacetic acid (NTA) (k d > 0.01 s–1) was used as the complex. The observed effect of complexes agreed well with model calculations in which plant uptake was assumed to be governed by the diffusional flux (Fig. 3b).[ 50 ] The modelled concentration profiles illustrate that fast dissociating complexes contribute substantially to the uptake flux, as apparent from the large depletion in the complex near the root surface, while only a minor fraction contributes in the case of slowly dissociating complexes (Fig. 3c). Most environmentally relevant metal complexes probably dissociate relatively quickly (k d >10–3 s–1),[ 60 ] and are therefore expected to contribute considerably to plant uptake under diffusion-limited conditions.
Effect of solid-phase buffering on metal availability
If uptake is limited by diffusion, the depletion in the solution concentration disturbs the equilibrium between metals in solution and metals sorbed on the solid phase. Metals then desorb from the solid phase to restore the equilibrium. The equilibrium of an element between the (labile) sorbed pool and solution phase is often described with Freundlich parameters or with a simple K d (common unit: L kg–1) in case of linear sorption. In the NST 3.0 model,[ 13 ] the solid-phase buffering is expressed as the buffer power b, which gives the relationship between total amount of the element per volume unit of soil and the solution concentration. The buffer power is related to the K d (in case of linear sorption) as follows:
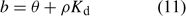
where θ is the volumetric moisture content (dimensionless) and ρ the bulk density of the soil (kg L–1). Fig. 4 illustrates the effect of solid-phase buffering in the case where uptake is diffusion limited. The depletion zone is much smaller for well-buffered solutes with high K d (e.g. phosphate, metals), because of the larger resupply from the solid phase, than for non- or weakly buffered solutes (e.g. nitrate). The larger supply from the solid phase for well buffered elements results in a larger root absorption power and larger concentration factor. At constant solution concentration, the Barber–Cushman model predicts that an increase in solid-phase buffering by a factor of 10 will increase the uptake flux (under diffusion limited conditions) by a factor of 1.3 (at low buffering) to 2.7 (at high buffering) (Fig. 4).
|
The Barber–Cushman (or NST 3.0) model assumes that there is an equilibrium between the solid phase and solution phase. However, desorption from the solid phase may be kinetically limited, in which case the effect of solid-phase buffering will be overestimated with the Barber–Cushman model.[ 19 ] The effect of slow desorption on the diffusion flux will be discussed in more detail below.
The DGT technique
The DGT technique was originally developed for measurement of trace metal concentrations in water.[ 61 ] A device typically consists of a resin-gel overlain by a hydrogel layer and filter membrane that is in contact with the solution. The resin (Chelex) has a high affinity for metal ions and acts as a zero sink, thus inducing diffusion of metals through the diffusion layer (i.e. the hydrogel and filter), before their being captured on the Chelex resin. After a set period of time t, the amount of metals (M) accumulated on the resin is measured, and the time-averaged flux can be calculated as:
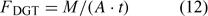
where A is the area of the exposure window. The DGT measurements are often reported as DGT-measured concentrations (c DGT).
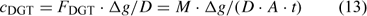
where D is the diffusion coefficient of the ion and Δg the thickness of the diffusion layer. The DGT-measured concentration is – by definition – the time-averaged concentration at the interface (between DGT device and solution) of metal species that contribute to the diffusion flux, either free ion or labile complexes. In well stirred solutions, there is minimal depletion in the solution near the interface, and the DGT-concentration, therefore, equals the bulk concentration of all (DGT-)labile species. Procedures are available to correct for non-negligible depletion in solution if necessary.[ 62 ]
If c DGT is smaller than the bulk concentration for a well stirred solution, it indicates the presence of complexes that are non-labile on the DGT timescale. The DGT technique can thus serve as a dynamic speciation tool, with the ratio of c DGT to total solution concentration allowing evaluation of the dissociation kinetics of complexes in solution, and has indeed been used for that purpose in recent years.[ 63 – 65 ] The DGT timescale depends on the thickness of the diffusion layer, and the kinetic window, which defines the measurable species, can therefore be varied, typically from 1 min to 1 h, by varying the thickness of the diffusion layer. A larger thickness of the diffusion layer allows for more dissociation – and hence larger contribution – of the complexes. Warnken et al.[ 60 ] used this approach to obtain information on the dissociation rate of metal complexes in situ in a river.
Fig. 5b shows the modelled effect of concentration and dissociation rate of complexes on the DGT flux (calculations with Matlab; same model as ref. [63]). As for diffusion-limited plant uptake (Fig. 3b), it is predicted that – at a constant free ion concentration – the flux increases with increasing concentration and increasing dissociation rate of the complex. Similar concentration profiles are predicted for diffusion-limited plant uptake (Fig. 3c) and during DGT deployment (Fig. 5c). A comparison of Figs 3c and 5c indicates, however, that more dissociation of the complexes is induced during DGT deployment than during plant uptake. This can be explained by the presence of the resin layer. The complexes diffuse into the resin layer, where dissociation of the complex is strongly promoted, since the resin acts as a zero sink. For example, Garmo et al.[ 65 ] observed that increasing the thickness of the resin layer increased the lability of lanthanide complexes, which confirms that the resin layer affects the lability of the complexes. This effect is most pronounced for strong, slowly dissociating complexes. It was indeed observed that DGT-measured and plant uptake fluxes of Cd were well correlated, but that the contribution of Cd complexes to the DGT flux was larger than the (diffusion-limited) plant uptake.[ 50 ]
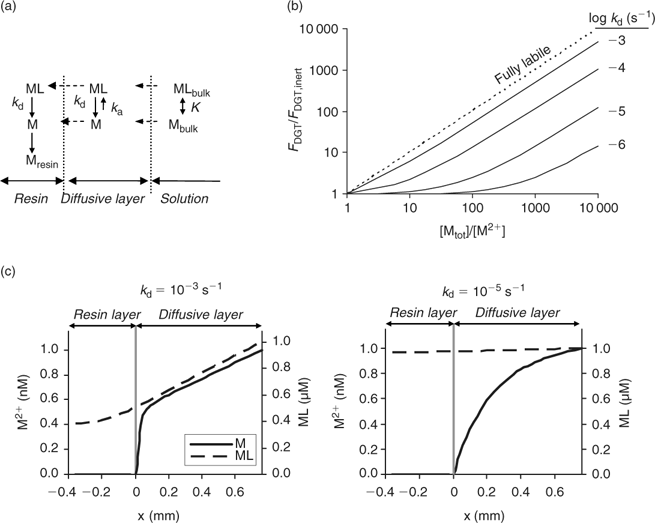
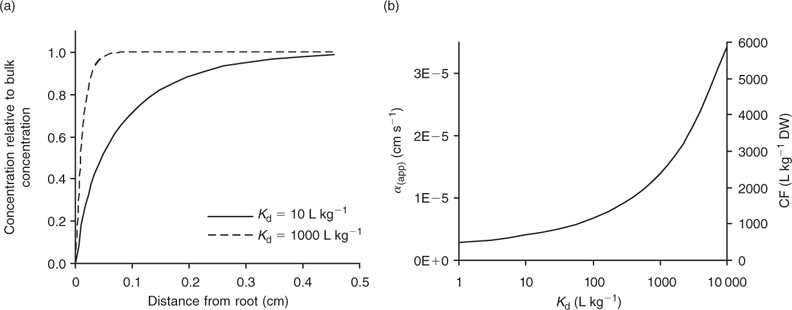
The DGT technique can also be applied to sediments and soils.[ 66 ] The device is then brought in close contact with the sediment or soil, which is usually wetted to saturation. In contrast to the situation in a stirred solution, there may be considerable depletion of the solution concentration in the soil near the interface between soil and DGT. As a result, metals will desorb from the solid phase to resupply the solution. The solution concentration near the interface will be less depleted for strongly buffered solutes than for solutes that are not well buffered, either because the solid-phase pool is small or because desorption from the solid phase is slow. The diffusive layer can extend several centimetres into the soil if there is little buffering.[ 67 ] Therefore, the DGT timescale, which is determined by the total thickness of the diffusion layer in the device and soil, can be up to several hours to days for solutes in soils with poor buffering. Harper et al.[ 68 ] developed a mathematical model (DIFS, DGT induced fluxes in sediments and soils) to describe these processes and made it available in one-dimensional (1-D) form. Later, a two-dimensional (2-D) version, which accounts for the lateral diffusion at the edges of the DGT window, became available.[ 69 ] The DIFS model allows prediction of the ratio (R) of DGT concentration to total solution concentration, given the deployment time, the solid–liquid distribution coefficient (K d) and the response time of the sorption process (T c = (k 1 + k –1)–1, see Fig. 1).[ 67 ] For a deployment time of 24 h, values of this ratio R are typically around 0.8, 0.5 and 0.25 for K d values of 1000, 100 and 10 L kg–1 respectively, when resupply is fast (T c < 1 min) (Fig. 6). Thus, at constant solution concentration, the DGT flux increases with increasing solid-phase buffering. In the K d range 10–1000 L kg–1, an increase by a factor 1.5–2.5 is predicted if the K d increases by a factor 10, which is similar to the relative increases for diffusion-limited plant uptake (Fig. 4). If desorption is slow, the depletion in the solution concentration is more pronounced and the solid-phase pool has less effect on the DGT flux (Fig. 6).
The DIFS model can also be used to estimate T c or K d from measured values of R for different deployment times. The ratio R represents the ratio of DGT concentration to in-situ soil solution concentration during the DGT deployment. In these types of studies, the soil solution should, therefore, be extracted at the same moisture content as during the DGT deployment (typically water holding capacity), for instance by centrifugation or using Rhizon samplers. The DGT technique was used in this way to estimate the K d and sorption kinetics for Cd, Zn and Ni.[ 67 , 70 , 71 ] Note the parallel with the use of the DGT technique to measure dissociation kinetics of complexes in solution (see above). The ratio of c DGT to total concentration in solution, R, has been used to estimate the dissociation rates of complexes in solution, a low R value pointing to slow dissociation kinetics. When applied to soils, that same ratio (c DGT to total soil solution concentration) is considered to be an indicator of the desorption rate of metals from the solid phase of soils, a low R value indicating slow desorption. When using the DGT technique to estimate desorption kinetics in soils, one should bear in mind the caveat that slow dissociation kinetics of complexes in solution may also lower the value of R. As the DIFS model considers all complexes in solution to be fully labile, the resupply from the solid phase will be underestimated (i.e. K d underestimated or T c overestimated) if there are non-labile complexes in solution. This is most likely for elements that strongly bind to organic acids (e.g. Cu) or that have inherently slow kinetics (e.g. Ni).[ 60 ] However, even for elements such as Cd and Zn, biased results may be obtained since part of the metals in the <0.2 μm solution phase may be non-isotopically exchangeable (which indicates that they are non-labile), especially in high pH soils.[ 4 ] Ideally, soil solution should be separated from the soil (e.g. by centrifugation) and DGT deployment should be carried out on the solution as well, to assess the DGT lability of the soluble metals separately. Obtaining soil solution in large quantities is however a tedious work.
The DGT technique has also been applied for measuring phosphorus in water, sediment[ 72 ] and in soil.[ 73 , 74 ] Ferrihydrite is then used as binding agent instead of Chelex. Ratios of c DGT to P concentration in a stirred solution were unaffected by varying pH (pH 3–9) and by increasing concentrations of chloride, sulfate and nitrate, while bicarbonate decreased c DGT, but only at very high concentrations that are unlikely to occur in soil solutions.[ 75 ] Anions are, therefore, not expected to have an interfering effect on DGT measurements of P in soils, whereas the resin method with an anion exchange membrane[ 76 ] is more subject to anionic interferences. The capacity of the Fe oxide gel is ~2.5 μg P cm–2, which corresponds to a c DGT of 450 μg L–1 for a 24 h deployment with a standard DGT device at 25°C.[ 72 , 73 ] Saturation (i.e. a non-linear response to the solution concentration) may, therefore, start to occur under these conditions for c DGT larger than ~300 μg L–1 or 10 μM. As c DGT is usually well below this value for environmental samples (soil and water), saturation should generally not be an issue. However, solution concentrations of P may be 1000 μg L–1 or higher in heavily fertilised soil,[ 77 ] in which case it is advisable to use shorter deployment times.
When relating DGT to plant uptake, DGT measurements have often been reported as ‘effective concentrations’ c E.[ 3 , 15 , 18 ] The effective concentration is the hypothetical concentration in solution that would be needed to accumulate the observed amount of metal on the resin if there were no solid-phase buffering (i.e. only diffusional supply). The effective concentration differs from c DGT with a factor that depends on the geometry of the device, deployment time and soil tortuosity. For a 24 h deployment on saturated soil with a standard DGT device (Δg = 0.93 mm), c E is ~13 times larger than c DGT, although this factor may vary slightly depending on the water holding capacity of the soil. In the remainder of this paper, we will report DGT measurements as fluxes or as c DGT. Where reference is made to studies that reported the DGT measurements as c E, a factor of 13 was used to convert c E to c DGT.
DGT as predictor of plant availability?
In the above discussion, clear parallels between DGT fluxes and diffusion-limited plant uptake have been demonstrated, e.g. the contribution of labile complexes and the effect of solid-phase buffering. DGT mimics the action of the plant under diffusion-limited conditions, and might, therefore, serve as a predictor of uptake or availability. The DGT technique accounts for processes (e.g. slow desorption (T c > minutes), contribution of complexes) that are not taken into account by other availability indicators (soil extracts) and that are usually not considered when modelling plant uptake.
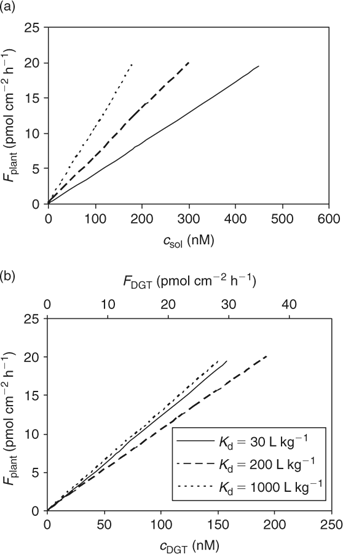
The calculated uptake by plants under diffusion-limited conditions, as a function of porewater concentration or (estimated) c DGT, for various degrees of solid-phase buffering (K d) is shown in Fig. 7. Not surprisingly, the relationships for the different degrees of buffering are closer when plant uptake flux is related to c DGT, compared with the relationship with soil solution concentration, since plant uptake and DGT fluxes are affected by the solid-phase buffering in a similar way. The lines are not completely reconciled because the relative effect of K d on plant uptake (Fig. 4) and on DGT flux (Fig. 6) is not exactly the same because of the different geometry.
|
In Fig. 7, it is predicted that the DGT-flux is about twice as large as the plant uptake flux. More generally, DGT-measured diffusion fluxes are not necessarily equal to the plant uptake fluxes for several reasons. First, the moisture content is larger during the DGT deployment (mostly performed on saturated soil) than during plant growth: a larger moisture content results in larger diffusion fluxes.[ 78 ] Second, the flux depends on the deployment time. A longer deployment time for DGT decreases the time-averaged flux and c DGT.[ 67 ] The deployment time for DGT is mostly 24 h. The uptake period during plant growth is usually several weeks, but the period during which they effectively acquire nutrients from a specific volume of soil can be much shorter, because of root growth and localised uptake along the root.[ 79 , 80 ] Third, the root geometry is different from that of the DGT device. Roots with a small radius can sustain a larger diffusion flux than thicker roots because of geometric considerations, but the effect of root radius on the (surface area based) diffusion flux is generally small. The effect of root size on uptake flux is much larger if the flux is expressed on a root weight basis,[ 56 ] as small roots have a larger specific surface area. Moreover, the presence of root hairs, which are lateral extensions of epidermal root cells, may have a large effect on the uptake of solutes if the root hairs are longer than the width of the nutrient depletion zone around the roots.[ 54 ] Root hairs are, therefore, expected have the largest effect on uptake of well buffered solutes, such as phosphate, for which the depletion zone extends a few millimetres at most. It has indeed been shown that root hairs may play an important role in the uptake of phosphate, and that some plant species respond to low P availability by growing longer and denser root hairs.[ 79 ] Finally, plants alter the soil surrounding the roots (‘rhizosphere’), which may affect the speciation of trace metals as well as of phosphate. For instance, the rhizosphere pH may be different from that in the bulk solution. These pH changes mainly depend on the cation/anion uptake ratio, which is largely related to the form of N nutrition, with ammonium supply resulting in acidification.[ 81 ] Root exudation of organic acids may also affect the speciation of mineral elements in the rhizosphere.[ 81 , 82 ] Clearly, DGT does not account for these biotic factors, and can only be used to predict differences in uptake that are related to the abiotic factors (i.e. soil properties).
We analyse below the use of DGT as a predictor of uptake, toxicity and deficiency and discuss the associated experimental evidence.
Uptake of metals
Solution
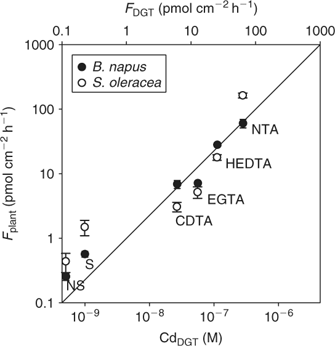
Many studies have challenged the hypothesis that uptake of metals is controlled by the free ion activity alone, as postulated by the free ion activity model. It has been frequently observed that metal complexes may also contribute to uptake of metals by plants.[ 35 , 36 , 38 , 83 ] Degryse et al.[ 50 ] measured Cd uptake by spinach in solution in the absence or presence of synthetic ligands. At constant free ion activity and constant total Cd concentration, the uptake increased with increasing dissociation rate of the complex, and correlated well with DGT-measured concentrations, which strongly suggested that Cd uptake by spinach was limited by diffusion. Similar observations were made for Cd uptake by rapeseed (Brassica napus) (Fig. 8). Although the uptake is related to the DGT measurements for both plant species, there were differences in uptake between species. In non-buffered solutions, the Cd uptake flux was larger for spinach than for rapeseed. In buffered solutions with slowly dissociating complexes, however, the uptake flux was larger for rapeseed (Fig. 8). In other words, the contribution of the slowly dissociating complexes to the uptake, relative to the contribution of the free ion, was larger for rapeseed than for spinach. A thicker diffusion layer in the apoplasm of rapeseed roots could explain the higher uptake for rapeseed in the solutions that are buffered with slowly dissociating complexes, since uptake of the free ion in the apoplast would promote the dissociation of the complexes and, therefore, their contribution to uptake. This is analogous to a thicker resin layer for DGT that enhances the contribution of slowly dissociating complexes.[ 65 ]
|
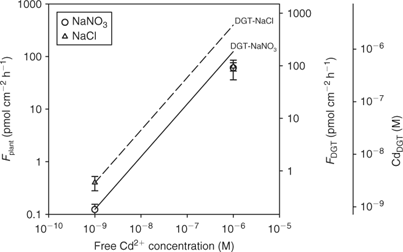
In cases where the mass flow (i.e. convective flow caused by plant water absorption) is sufficient to meet the plant’s demand, there will be no depletion of the free ion near the root surface and, therefore, no dissociation of complexes. This situation is likely to occur at high concentrations where the plant uptake saturates (Fig. 2). Therefore, the correlation between plant uptake and DGT may break down at high concentrations, as DGT also acts as a zero sink at high concentrations (unless the resin becomes saturated after prolonged deployment). Oporto et al.[ 84 ] illustrated this by assessing the effect of Cd–chloride complexes at varying Cd supply. Cadmium–chloride complexes contributed fully to the DGT flux at both low and high Cd2+ activity (Fig. 9). The short-term uptake of Cd by spinach, however, was only enhanced in the presence of chloride complexes at the low Cd2+ activity. Consequently, DGT fluxes did not correlate with plant uptake at the high Cd2+ activity.
|
No systematic comparison between DGT fluxes and plant uptake fluxes in nutrient solutions has been made for other metals. It has, however, been shown that Cu and Zn uptake in metal-ion buffered solutions, at the same free ion activity (pZn 9.2, pCu 12.2) and same total metal concentrations, follows the following order of chelating ligand used in the metal-ion buffer: NTA > hydroxyethylethylenediaminetriacetic acid (HEDTA) > ethylenediaminetetraacetic acid (EDTA) > CDTA.[ 26 ] This is the same order as the dissociation rate of their complexes with Cu and Zn[ 26 ] and the contribution of these complexes to the DGT flux (F. Degryse, unpubl. data), which indicates that there is at least a qualitative agreement between the plant uptake fluxes and the DGT fluxes of Cu and Zn at low free ion activities.
Soil
Metal bioavailability to plants in soil has rarely been studied mechanistically. The soil solution composition and speciation of the metal must be known to model uptake with a mechanistic approach, but there are practical complications involved in determining the metal speciation in a soil solution. Isolation of a soil solution in large amounts is tedious, and determining the metal speciation usually poses analytical challenges. Most of the analytical techniques suffer from insufficient sensitivity, interferences, and/or disturbance of the solution equilibrium.[ 1 ]
If uptake is limited by diffusion, one might expect that plant uptake would correlate well with DGT-measured concentrations, as DGT effectively measures a diffusion-limited flux. Several studies have correlated metal concentrations in plants to DGT-measured concentrations and other metal concentrations in soil (Table 3). In general, good correlations between metal concentrations in plant and DGT-measured concentrations were observed, with correlation coefficients above 0.8 in most cases and often above 0.9. However, a strong correlation between plant uptake and DGT fluxes does not in itself prove that plant uptake is limited by diffusion, as will be elaborated below. In most studies where such strong correlation was observed, the uptake also correlated strongly with soil solution concentrations (Table 3). This is no surprise, as DGT and soil solution concentrations measured in soils with wide-ranging properties (metal concentrations, pH, etc.) usually co-vary strongly.

|
We compare (below) modelled and (as far as available) measured uptake by DGT and plants. The comparison is most rigorous when both DGT and plant uptake are expressed as an area-based flux. Expressing uptake fluxes on a root-surface basis for plants grown in soil over an extended period of time is not straightforward, as it requires knowledge of the shoot and root concentrations as well as the relative growth rate, and the specific root area.[ 84 ] Often, this information is not available. For instance, in many studies, only the concentrations in shoots of soil grown plants are measured. However, for some elements (e.g. Cu),[ 16 ] the amount of element in the roots contributes largely to the total amount in the plants, and the uptake fluxes can, therefore, not be calculated without knowledge of root concentrations. The more common approach is to relate the metal concentrations in the plant shoot to the DGT-measured concentration (c DGT or c E).[ 3 , 15 , 17 , 18 ]
Fig. 10 shows theoretical relationships between plant uptake and soil solution concentration or DGT-measured concentrations for high affinity uptake (small (true) K M) or low affinity uptake (high K M) The plant uptake flux was calculated with NST 3.0 using the parameters given in the Figure legend.
For high affinity uptake in the low concentration range (Fig. 10a; c < K M,app), the plant’s demand (Michaelis–Menten curve) is much larger than the maximal metal supply through diffusion. Consequently, the uptake equals the limiting diffusion flux, and plant uptake fluxes increase proportionally to DGT-measured diffusion fluxes. The predicted relation between plant-uptake flux and DGT-flux agrees well with experimental results by Oporto et al.[ 84 ] who measured uptake of Cd by spinach in soil with background Cd or in Cd-amended soil, at a set of NaCl salinities. At background Cd, increasing NaCl salinity increased both the plant uptake- and the DGT-fluxes, as a result of chloride-complexation of Cd and the contribution of these labile CdCl n 2–n complexes to the diffusion flux. At high Cd levels, however, only DGT fluxes increased with increasing NaCl salinity, whereas the plant uptake fluxes levelled off and were unaffected by the NaCl salinity (Fig. 10a). These results suggest that the well documented effect of chloride salinity on Cd uptake (e.g. ref. [85]) is a result of enhanced supply of Cd2+ in the presence of the labile complexes, and not of direct uptake of the complex.
In the higher concentration range (c > K m,app), according to the Michaelis–Menten model, the plant uptake saturates, although in reality the uptake flux may still increase with increasing solution concentration. This phenomenon is described by adding a non-saturable linear component to the (saturable) Michaelis–Menten model, and has been frequently observed for Cd and Zn.[ 25 ] This (apparently) linear component in ion uptake by plants has been attributed to passive diffusion or uptake by a low-affinity system.[ 86 ] As a result, the plant uptake fluxes can show a positive correlation with the DGT fluxes, even though the uptake is not limited by diffusion (Fig. 10a). In contrast with the diffusion-limited case, the plant uptake fluxes do not increase directly proportionally with DGT fluxes, i.e. a 10-fold increase in DGT flux does not result in a 10-fold increase in plant uptake fluxes or plant concentrations. This type of relationship is indeed often observed for Zn (e.g. refs [3,17,18]). Under these conditions, it would be wrong to interpret a good correlation with the DGT measurement in terms of a contribution of labile complexes to the plant uptake, as the uptake theoretically depends only on the activity of the free ion and its competitive binding at the site of uptake if no diffusion limitations prevail. It has indeed been observed that uptake of Zn by Brassica juncea was nearly unaffected by addition of EDTA to Zn-contaminated soil (pH 6.3) at concentrations that have theoretically little effect on the free Zn activity (buffered by the solid phase), although the soluble Zn concentrations strongly increased.[ 87 ] The DGT-measured fluxes (not measured) would probably also have increased considerably, as Zn-EDTA complexes – although not fully labile – contribute significantly to the DGT-flux (F. Degryse, unpubl. data).
Uptake of Cd and Zn by plants has been rigorously studied, both in nutrient solutions and soils, but there is comparatively little information on Cu uptake. Moreover, in most soil experiments, only concentrations in shoots were measured. As Cu translocation to shoots is restricted for most plant species, plant uptake is difficult to evaluate without knowledge of the root concentrations. A few studies have compared Cu tissue concentrations with DGT-measured concentrations as well as other potential predictors (e.g. total Cu, soil solution concentration). While strong correlations between DGT and plant concentrations in a range of soils have been reported for Cu uptake by plants,[ 15 , 16 ] Nolan et al.[ 3 ] found that Cu concentrations in shoots of wheat were rather weakly correlated with the DGT-measured concentrations and were, surprisingly, better correlated with total Cu in soil. It was generally found that Cu tissue concentrations and DGT-measured concentrations do not increase in direct proportion: a 10-fold increase in DGT concentration generally corresponded to a <10-fold increase in plant concentrations (e.g. ref. [16]). This might suggest that Cu uptake is not diffusion-limited in these (mostly) contaminated soils. We hypothesise that, as for Zn, uptake is only diffusion-limited at low supply (e.g. uncontaminated soils at high pH).
If the ‘true’ root absorbing power α (F max/K M,true) for an element is low, plant uptake may be controlled by the plant’s demand even in the low concentration range, because the potential internalisation rate is smaller than the potential diffusive supply to the uptake sites (Fig. 10b). The actual uptake rate then equals the physiological demand. In the lower concentration range (c < K m), plant uptake as well as DGT-fluxes are proportional to the solution concentration. Consequently, the relation between DGT and plant uptake is similar to that for the diffusion-limited case (Fig. 10a). Comparison of the uptake flux and diffusive flux may help in making the distinction. If the actual uptake flux approaches the maximal diffusion flux, this points to diffusion limitations.[ 31 , 38 ] However, given the uncertainties in the estimate of the maximal diffusive flux to the plant (thickness of diffusive boundary layer, active surface),[ 38 ] such comparison gives at best an indication. Assessment of the contribution of labile complexes to the uptake, may give more straightforward proof whether uptake is limited by diffusion or not. If there is no diffusion limitation, labile complexes (that are not taken up) will not contribute to the plant uptake, but the uptake will be governed by the free metal ion activity and the activity of competing ions (e.g. Ca2+, Mg2+, H+; cf. BLM concept). Consequently, DGT will wrongly predict that labile complexes contribute to uptake. We did not find literature examples that support this case. However, we recently found that uptake of Ni (at 1 nM Ni2+) by spinach in nutrient solution was not enhanced by addition of labile complexes even in the low concentration range, and was markedly decreased by Mg2+ in solution (F. Degryse, unpubl. data), which suggests that, at least in nutrient solution, uptake of Ni is not limited by diffusion.
In summary, DGT and plant uptake are expected to increase proportionally if uptake is limited by diffusion (high affinity uptake, low concentration). In this case, labile complexes increase both plant uptake and DGT fluxes. This is probably the case for Cd in most soils and for Zn in the low concentration range (which corresponds to c DGT <0.5 μM; see Fig. 10a). We distinguish two cases where uptake is not limited by diffusion: at high concentrations where plant uptake levels off (Fig. 10a), or at low concentrations in the case of low affinity uptake (Fig. 10b). If uptake is governed by the plant’s demand, the effect of competitive cations, which do not affect the DGT flux, may be important, whereas labile complexes, which are measured with DGT, will not contribute to the uptake. Interpretation of the relationship between plant uptake and the DGT measurement in terms of labile complexes is then inappropriate.
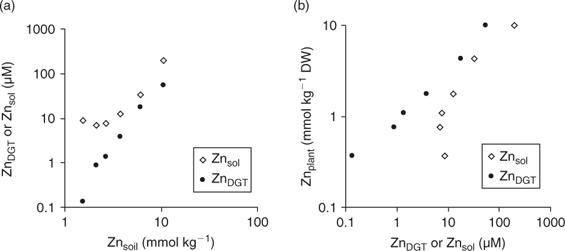
Although DGT-measured concentrations would have no added value over soil solution concentrations from a mechanistic point of view if plant uptake is not limited by diffusion, the DGT technique has several advantages, which may still make it a more suitable predictor of plant uptake, under non-diffusion limited conditions, than soil solution concentrations. First, DGT deployments are easy to perform and less time-consuming than soil solution isolation. Second, soil solutions may contain significant amounts of metal as inert colloids or complexes, especially at high pH,[ 4 ] which are unlikely to contribute to plant uptake, and bioavailability may hence be overestimated. DGT does not measure these inert complexes or metal-bearing colloids.[ 88 ] Therefore, when these inert metal species are a significant component of the soil solution, plant uptake will relate more strongly to DGT-measured concentrations than to soil solution concentrations even when diffusion-limiting conditions do not apply. Fig. 11 illustrates this for a sandy loam soil (Woburn; pH(CaCl2) = 6.4, 4.4% OC), that was amended with ZnCl2 to varying concentrations.[ 89 ] The DGT-measured concentrations increased with increasing Zn addition, whereas the soil solution concentrations at the lowest Zn doses were nearly equal to that in the unamended soil and were much larger than the DGT-measured concentration, which suggested the presence of colloidal Zn or inert Zn complexes in the soil solution (Fig. 11a). The Zn concentrations in the shoot of wheat plants, grown for 21 days on the soil, increased with increasing Zn dose, and showed a strong positive correlation with DGT-measured concentrations, but not with soil solution concentrations at the lower Zn doses (Fig. 11b), which indicates that the (presumably) colloidal Zn was unavailable to plants.
|
Metal toxicity
As discussed above, uptake is only limited by diffusion if the root absorbing power is high and in the low concentration range (c < K M,app). Under toxic conditions, uptake is most likely not diffusion limited, thus justifying the use of the BLM to predict metal toxicity. The use of the BLM requires information on the free ion activity of the metal of concern as well as the solution composition (pH, concentration of competing cations).
Zhao et al.[ 90 ] assessed Cu toxicity to plant growth in 18 soils with wide-ranging properties. The DGT-measured concentrations narrowed down the intersoil variation in EC50 values (concentration at which growth was 50% reduced) to a greater extent than Cu2+ activity or soil solution Cu. The EC50 values based on Cu2+ activity varied over five orders of magnitude and correlated negatively with pH, which indicated a protective effect of H+. The EC50 values based on soil solution Cu varied 100-fold, whereas DGT-based EC50 values varied only 10-fold, because the ratio of c DGT to soil solution concentration, R, decreased with decreasing pH. Also Zn toxicity to growth of Sorghum vulgare was reasonably well predicted by DGT for soils amended with three different Zn sources (ZnSO4 or two different Zn mine wastes).[ 91 ] The DGT-based EC10 values (reported as c E) were around 800 μM, or around 60 μM when reported as c DGT, for all three Zn sources. The CaCl2 (0.01 M) based EC10 values were even more tightly grouped for the three Zn sources at ~180 μM in the 1 : 1 CaCl2 extract, which indicates that the improvements observed using DGT cannot be simply interpreted in terms of diffusional supply. Plant growth assays with wheat in 12 soils amended with ZnCl2 to varying Zn concentrations gave similar results.[ 92 ] Growth of wheat started to decrease when c DGT was above 30 μM or the soil solution concentration was above 100 μM (Fig. 12). However, there was a considerable variation in soil solution- or DGT-based EC50 values between soils, even larger than the variation in EC50 values based on total Zn in soil (Fig. 12). This indicates that, while DGT or soil solution concentrations can reconcile differences in toxicity of Zn sources of varying solubility (e.g. Zn salt v. mine waste), they cannot completely account for the intersoil variation in Zn toxicity. We hypothesise that this is a result of the competitive (protective) effect of protons and competing cations to bind at the membrane surface, which does not affect the DGT flux, and that a BLM approach is, therefore, necessary to refine the prediction of phytotoxicity.
DGT for nutrient deficiency studies
There are at least 14 mineral elements that are essential for plant growth: the ‘macronutrients’ N, P, K, Ca, Mg and S, and the ‘micronutrients’ Fe, Mn, Zn, Cu, B, Mo, Cl and Ni. Diffusion limitations for uptake are likely to occur under nutrient deficient conditions if internalisation is fast (cf. Fig. 10a). In that case, the rapid uptake by the plant will decrease the concentration near the root surface, to induce a diffusive supply of the element to the roots. The uptake flux will be determined by the rate of this diffusive supply, and it can, therefore, be expected that DGT will be a good predictor of plant availability and might, therefore, serve as an indicator of nutrient deficiency for both cationic micronutrients (Cu, Zn, Mn, Fe), and P and Mo (measured using DGT devices with iron oxide instead of Chelex), even though DGT does not consider the biotic response to nutrient deficiency, such as increased root exudation.[ 82 ]
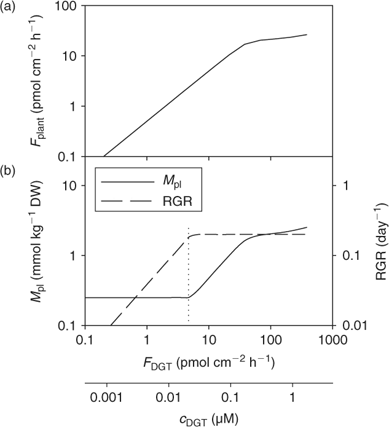
Fig. 13 illustrates the relationship between nutrient supply and plant growth (hypothetical case for Zn). The uptake flux follows an apparent Michaelis–Menten behaviour (diffusion limited at low concentration and saturation at high concentrations) and is plotted against DGT flux or c DGT. At sufficient supply, the flux is large enough to maintain the maximal relative growth rate (RGRmax), and the plant concentration will be proportional to the uptake flux (Eqn 1). However, a minimal plant concentration (M pl,crit) is required for essential elements. As a result, at low supply, the growth rate instead of the plant concentration decreases with decreasing metal supply (Fig. 13), as becomes clear when rearranging Eqn 1:
|
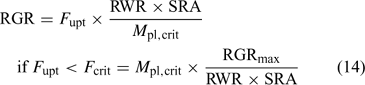
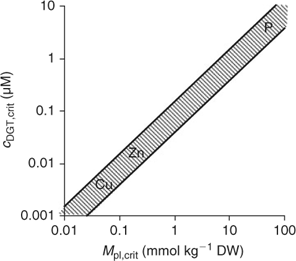
Since plant uptake fluxes and DGT fluxes are correlated under diffusion-limited conditions (cf. Fig. 7), the critical plant flux, F crit, will correspond to a critical DGT flux or DGT-measured concentration (Fig. 14). It should, therefore, be possible to define critical DGT concentrations as indicators of nutrient deficiency in soils. These critical DGT concentrations would of course be plant-species specific, since critical plant concentrations, maximal growth rate, root weight ratio and root surface area depend on the plant species and on the plant growth stage, but they would be almost independent of soil properties and could thus provide an excellent indicator of nutrient deficiency in soils. Fig. 14 gives the theoretical relationship between critical plant concentrations and critical DGT concentrations. Assuming critical plant concentrations of around 0.06 mmol Cu kg–1 DW, 0.25 mmol Zn kg–1 DW and 50 mmol P kg–1 DW,[ 93 ] we estimate critical values for c DGT of ~0.004, 0.02 and 3 μM for Cu, Zn and P, respectively.
|
Fig. 15 shows theoretical relationships between nutrient supply and plant growth for phosphorus. The plant uptake flux was calculated for different P concentrations and different realistic buffer capacities[ 94 ] (K d of 10, 100 or 1000 L kg–1) with the NST model. The RGR was calculated from the calculated uptake flux and the critical plant concentrations (Eqn 14). A maximal RGR of 0.25 day–1 was assumed. The calculated relative yield after 14 days of growth was plotted against total (labile) P concentrations in soil, soil solution concentrations or DGT-measured concentrations (estimated with the DIFS model). These theoretical curves are in good agreement with the experimental results of Pypers et al.[ 94 ] who measured P uptake and growth of pigeon pea in response to P fertilisation in soils with different P sorption characteristics. They observed a 50% yield reduction at a soil solution concentration of ~10 μM in strongly buffered soil and at ~30 μM in weakly buffered soil. The calculations show that DGT measurements indeed should narrow the difference between soils: the P concentration at which a 50% reduction in yield as a result of P deficiency was predicted differed 29-fold between scenarios (small or large K d) when expressed as total P in soil, 3.4-fold when expressed as soil solution concentration and only 1.4-fold when expressed as DGT concentration. The calculations indicate a critical c DGT, above which no growth reduction is predicted, of ~5 μM.
While the use of DGT as an indicator of deficiency has not yet been assessed for micronutrients, experimental evidence that DGT may indeed be a good predictor for P deficiency has been obtained. Menzies et al.[ 73 ] tested the yield response of tomato to the addition of P fertilizer for 24 soils in a glasshouse experiment. The DGT-measured concentration provided an excellent separation of soils on which tomato showed a yield response from the soils with no response. A critical value of 2.14 μg P per sampler was derived (24 h deployment, 0.8 mm hydrogel), which corresponds to c DGT of ~4 μM. The DGT method also well predicted responsiveness of wheat to liquid P fertilisers, with a critical c DGT of ~1.2 μM (c E ~16 μM), for a range of acidic and neutral soils.[ 74 ] Similarly, the DGT method well predicted wheat responsiveness to applied P in a growth cabinet experiment, with a critical c DGT of ~1 μM (S. Mason, R. Hamon, J. Anderson and H. Zhang, unpubl. data). The absolute value of the response (yield in the P-amended soil relative to that in the control soil) should be interpreted with some caution since these studies used a single P application rate and the maximal yield may not have been reached, but these experiments allowed responsive and non-responsive soils to be distinguished. All three studies point to a critical c DGT (below which P deficiency is expected) of 1–5 μM. These experimentally derived critical values of c DGT are in good agreement with the theoretically predicted value (Fig. 14). Comparison of these experimental studies suggests that wheat has a lower external P requirement than tomato. This was also observed by Föhse et al.[ 95 ] who found that the critical P concentration in soil solution was ~6 μM for tomato and only 1.4 μM for wheat. They explained the lower P requirement for wheat by the higher root-to-shoot ratio (cf. Eqn 14; high RWR).
Critical DGT values may not only depend on plant species, but also on growth conditions. The DGT measurements are normally performed on saturated soils. During plant growth, however, the moisture content varies, and depends strongly on the growth conditions. The moisture is in general lower under field conditions than for plants grown under laboratory conditions in a growth cabinet or glasshouse. Uptake of metals[ 96 ] or phosphorus[ 97 ] decreases with decreasing moisture content. It is, therefore, to be expected that – for the same plant species – the critical DGT concentration will be smaller for plants grown under field conditions than under laboratory conditions. To our knowledge, there is only one study that assessed the critical DGT concentration for the P deficiency of plants grown under field conditions.[ 98 ] A critical c DGT of ~3.2 μM, above which no response of wheat to P application was observed in field trials, was derived, whereas the critical c DGT for the same plant species under laboratory conditions was ~1.2 μM,[ 74 ] which supports our hypothesis of lower critical DGT concentrations for field conditions.
Conclusions
To some extent, the DGT technique mimics the action of plants if plant uptake is limited by diffusion, and might, therefore, serve as a predictor of plant uptake and availability. Several studies have observed a strong correlation between DGT-measured concentrations and metal uptake by plants, but a strong correlation does not necessarily prove that plant uptake is limited by diffusion. For example, strong correlations have been observed between DGT flux and Zn uptake by plants, even in the range where Zn uptake is most likely not limited by diffusion. Especially in the toxicity range, it is unlikely that metal uptake is limited by diffusion, and therefore, in terms of diffusional mimicry, DGT would not be expected to be a better predictor of toxicity than the soil solution concentration. However, DGT’s exclusion of (inert) colloidal species and its ease of operation may still give it an advantage over soil solution concentration as indicator of availability.
Plant uptake is likely limited by diffusion for several trace elements and for phosphorus in the low concentration range. In this case, the DGT technique is expected to perform better as a predictor of plant availability than other indicators, such as the concentration in soil solution or in a dilute salt extract. With the DGT technique, the contribution of labile complexes in solution to the diffusion flux and the buffering by the solid-phase pool is taken into account.
Apart from the pragmatic use of DGT as a predictor of plant uptake, the DGT technique may also provide additional insights into the physicochemical aspects of plant–soil interactions, and assist in obtaining experimental data to further expand models for plant uptake of mineral elements. For example, the dissociation kinetics of complexes in solution and the desorption kinetics of solid-phase species are as yet not considered in plant uptake models. While expansion of the models to include these processes is certainly feasible, obtaining reliable input parameters (desorption and dissociation rate constants) for relevant conditions will pose a greater challenge, and the DGT technique can certainly be helpful in this regard.
Glossary
-
(commonly used units in parentheses)
-
ρ, bulk density, mass of dry soil per unit (bulk) volume (kg L–1)
-
δ, thickness of the diffusion layer (cm)
-
θ, volumetric moisture content
-
α (app), (apparent) root absorbing power (cm s–1)
-
Δg, diffusive layer thickness within the DGT device (cm)
-
BLM, Biotic Ligand Model
-
c, solution concentration (μM)
-
c DGT, DGT-measured concentration = time-averaged concentration of DGT-labile species at the soil (or solution)–DGT interface (μM)
-
c E, effective concentration (μM)
-
CF, concentration factor, ratio of plant concentration to solution concentration (L kg–1)
-
D, diffusion coefficient in water (cm2 s–1)
-
f, tortuosity or impedance factor
-
FIAM, free ion activity model
-
F DGT, time-averaged DGT-measured flux (pmol cm–2 h–1)
-
F max, maximal uptake flux (pmol cm–2 h–1)
-
F upt, time-averaged plant uptake flux (pmol cm–2 h–1)
-
K d, solid–liquid distribution coefficient (L kg–1), ratio of (labile) concentration on solid phase and solution concentration
-
K M, (true) Michaelis–Menten constant (μM)
-
K M,app, apparent Michaelis–Menten constant (μM)
-
R, ratio of DGT measured concentration (c DGT) to total solution concentration
-
r, root radius (cm)
-
RGR, relative growth rate (day–1)
-
RWR, relative weight of root
-
s, solid phase concentration (mmol kg–1)
-
SRA, specific root area (cm2 g–1)
-
t, deployment time for DGT or plant uptake period (days)
-
T c, response time of adsorption–desorption process (s)

|
Acknowledgements
F. Degryse thanks the Fund for Scientific Research (FWO-Vlaanderen) for a postdoctoral fellowship.
[1]
A. L. Nolan ,
E. Lombi ,
M. J. McLaughlin ,
Metal bioaccumulation and toxicity in soils - Why bother with speciation?
Aust. J. Chem. 2003
, 56, 77.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[2]
W. L. Lindsay ,
W. A. Norvell ,
Development of a DTPA soil test for zinc, iron, manganese, and copper.
Soil Sci. Soc. Am. J. 1978
, 42, 421.
|
CAS |

[3]
A. L. Nolan ,
H. Zhang ,
M. J. McLaughlin ,
Prediction of zinc, cadmium, lead and copper bioavailability to wheat in contaminated soils using chemical speciation, diffusive gradients in thin films, extraction, and isotope dilution techniques.
J. Environ. Qual. 2005
, 34, 496.
|
CAS |
PubMed |

[4]
E. Lombi ,
R. E. Hamon ,
S. P. McGrath ,
M. J. McLaughlin ,
Lability of Cd, Cu, and Zn in polluted soils treated with lime, beringite, and red mud and identification of a non-labile colloidal fraction of metals using isotopic techniques.
Environ. Sci. Technol. 2003
, 37, 979.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[5]
E. Meers ,
R. Samson ,
F. M. G. Tack ,
A. Ruttens ,
M. Vandegehuchte ,
J. Vangronsveld ,
M. G. Verloo ,
Phytoavailability assessment of heavy metals in soils by single extractions and accumulation by Phaseolus vulgaris.
Environ. Exp. Bot. 2007
, 60, 385.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[6]
N. W. Menzies ,
M. J. Donn ,
P. M. Kopittke ,
Evaluation of extractants for estimation of the phytoavailable trace metals in soils.
Environ. Pollut. 2007
, 145, 121.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[7]
J. D. Colwell ,
The estimation of phosphorus fertilizer requirements of wheat in southern New South Wales by soil analysis.
Aust. J. Exp. Agric. 1963
, 3, 190.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[8]
R. H. Bray ,
L. H. Kurtz ,
Determination of total, organic, and available forms of phosphorus in soils.
Soil Sci. 1945
, 59, 39.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[9]
M. J. McLaughlin ,
P. A. Lancaster ,
P. G. Sale ,
N. C. Uren ,
K. I. Peverill ,
Comparison of cation/anion exchange resin methods for multi-element testing of acidic soils.
Plant Soil 1994
, 32, 229.
|
CAS |

[10]
S. Saggar ,
M. J. Hedley ,
R. E. White ,
A simplified resin membrane technique for extracting phosphorus from soils.
Fert. Res. 1990
, 24, 173.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[11]
[12]
T. Adhikari ,
R. K. Rattan ,
Modelling zinc uptake by rice crop using a Barber-Cushman approach.
Plant Soil 2000
, 227, 235.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[13]
U. S. Sadana ,
N. Claassen ,
Manganese dynamics in the rhizosphere and Mn uptake by different crops evaluated by a mechanistic model.
Plant Soil 2000
, 218, 233.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[14]
T. Sterckeman ,
J. Perriguey ,
M. Cael ,
C. Schwartz ,
J. L. Morel ,
Applying a mechanistic model to cadmium uptake by Zea mays and Thlaspi caerulescens: Consequences for the assessment of the soil quantity and capacity factors.
Plant Soil 2004
, 262, 289.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[15]
H. Zhang ,
F.-J. Zhao ,
B. Sun ,
W. Davison ,
S. P. McGrath ,
A new method to measure effective soil solution concentration predicts copper availability to plants.
Environ. Sci. Technol. 2001
, 35, 2602.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[16]
J. Song ,
F. J. Zhao ,
Y. M. Luo ,
S. P. McGrath ,
H. Zhang ,
Copper uptake by Elsholtzia splendens and Silene vulgaris and assessment of copper phytoavailability in contaminated soils.
Environ. Pollut. 2004
, 128, 307.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[17]
H. Zhang ,
E. Lombi ,
E. Smolders ,
S. McGrath ,
Kinetics of Zn release in soils and prediction of Zn concentration in plants using diffusive gradients in thin films.
Environ. Sci. Technol. 2004
, 38, 3608.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[18]
M. Koster ,
L. Reijnders ,
N. R. van Oost ,
W. G. J. M. Peijnenburg ,
Comparison of the method of diffusive gels in thin films with conventional extraction techniques for evaluating zinc accumulation in plants and isopods.
Environ. Pollut. 2005
, 133, 103.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[19]
N. Lehto ,
W. Davison ,
H. Zhang ,
W. Tych ,
Theoretical comparison of how soil processes affect uptake of metals by Diffusive Gradients in Thin-films and plants.
J. Environ. Qual. 2006
, 35, 1903.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[20]
N. Lehto ,
W. Davison ,
H. Zhang ,
W. Tych ,
Analysis of micro-nutrient behaviour in the rhizosphere using a DGT parameterised dynamic plant uptake model.
Plant Soil 2006
, 282, 227.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[21]
S. D. Young ,
H. Zhang ,
A. M. Tye ,
A. Maxted ,
C. Thums ,
I. Thornton ,
Characterizing the availability of metals in contaminated soils. I. The solid phase: sequential extraction and isotopic dilution.
Soil Use Manage. 2006
, 21, 450.
| Crossref | GoogleScholarGoogle Scholar |

[22]
R. E. Hamon ,
D. R. Parker ,
E. Lombi ,
Advances in isotopic dilution techniques in trace element research: a review of methodologies, benefits, and limitations.
Adv. Agron. 2008
, 99, 289.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[23]
G. Kirchhof ,
Measurement of root length and thickness using a hand-held computer scanner.
Field Crops Res. 1992
, 29, 79.
| Crossref | GoogleScholarGoogle Scholar |

[24]
M. M. Lasat ,
A. J. M. Baker ,
L. V. Kochkian ,
Physiological characterization of root Zn2+ absorption and translocation to shoots in Zn hyperaccumulator and nonaccumulator species of Thlaspi.
Plant Physiol. 1996
, 112, 1715.
|
CAS |
PubMed |

[25]
E. Lombi ,
F. J. Zhao ,
S. P. McGrath ,
S. D. Young ,
G. A. Sacchi ,
Physiological evidence for a high-affinity cadmium transporter highly expressed in a Thlaspi caerulescens ecotype.
New Phytol. 2001
, 149, 53.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[26]
F. Degryse ,
E. Smolders ,
D. R. Parker ,
Metal complexes increase uptake of Zn and Cu by plants: implications for uptake and deficiency studies in chelator-buffered solutions.
Plant Soil 2006
, 289, 171.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[27]
[28]
V. I. Slaveykova ,
K. J. Wilkinson ,
Predicting the bioavailability of metals and metal complexes: critical review of the biotic ligand model.
Environ. Chem. 2005
, 2, 9.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[29]
V. Zitko ,
W. V. Carson ,
W. G. Carson ,
Prediction of incipient lethal levels of copper to juvenile Atlantic salmon in the presence of humic acid by cupric electrode.
Bull. Environ. Contam. Toxicol. 1973
, 10, 265.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[30]
W. G. Sunda ,
J. A. M. Lewis ,
Effect of complexation by natural organic ligands on the toxicity of copper to a unicellular alga, Monochrysis lutheri.
Limnol. Oceanogr. 1978
, 23, 870.
|
CAS |

[31]
C. Fortin ,
P. G. C. Campbell ,
Silver uptake by the green alga Chlamydomonas reinhardtii in relation to chemical speciation: influence of chloride.
Environ. Toxicol. Chem. 2000
, 19, 2769.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[32]
P. C. DeKock ,
R. L. Mitchell ,
Uptake of chelated metals by plants.
Soil Sci. 1957
, 84, 55.
| Crossref | GoogleScholarGoogle Scholar |

[33]
V. Römheld ,
H. Marschner ,
Effect of Fe stress on utilization of Fe chelates by efficient and inefficient plant-species.
J. Plant Nutr. 1981
, 3, 551.
| Crossref | GoogleScholarGoogle Scholar |

[34]
R. T. Checkai ,
L. L. Hendrickson ,
R. B. Corey ,
P. A. Helmke ,
A method for controlling the activities of free metal, hydrogen and phosphate ions in hydroponic solutions using ion exchange and chelating resins.
Plant Soil 1987
, 99, 321.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[35]
P. F. Bell ,
R. L. Chaney ,
J. S. Angle ,
Free metal activity and total metal concentrations as indices of micronutrient availability to barley [Hordeum vulgare (L.) ‘Klages’].
Plant Soil 1991
, 130, 51.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[36]
[37]
E. Smolders ,
M. J. McLaughlin ,
Chloride increases cadmium uptake in Swiss Chard in a resin-buffered nutrient solution.
Soil Sci. Soc. Am. J. 1996
, 60, 1443.
|
CAS |

[38]
E. J. Berkelaar ,
B. A. Hale ,
Cadmium accumulation by durum wheat roots in ligand-buffered hydroponic culture: uptake of Cd-ligand complexes or enhanced diffusion?
Can. J. Bot. 2003
, 81, 755.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[39]
D. R. Parker ,
J. F. Pedler ,
Z. A. S. Ahnstrom ,
M. Resketo ,
Reevaluating the free-ion activity model of trace metal toxicity toward higher plants: experimental evidence with copper and zinc.
Environ. Toxicol. Chem. 2001
, 20, 899.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[40]
K. A. C. De Schamphelaere ,
C. R. Janssen ,
A biotic ligand model predicting acute copper toxicity for daphnia magna: the effects of calcium, magnesium, sodium, potassium, and pH.
Environ. Sci. Technol. 2002
, 36, 48.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[41]
D. G. Heijerick ,
K. A. C. De Schamphelaere ,
C. R. Janssen ,
Biotic ligand model development predicting Zn toxicity to the alga Pseudokirchneriella subcapitata: possibilities and limitations.
Comp. Biochem. Phys. C 2002
, 133, 207.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[42]
S. Thakali ,
H. E. Allen ,
D. M. Di Toro ,
A. A. Ponizovsky ,
C. P. Rooney ,
F.-J. Zhao ,
S. P. McGrath ,
P. Criel ,
et al. Terrestrial biotic ligand model. 2. Application to Ni and Cu toxicities to plants, invertebrates, and microbes in soil.
Environ. Sci. Technol. 2006
, 40, 7094.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[43]
S. Thakali ,
H. E. Allen ,
D. M. Di Toro ,
A. A. Ponizovsky ,
C. P. Rooney ,
F.-J. Zhao ,
S. P. McGrath ,
A Terrestrial Biotic Ligand Model. 1. Development and application to Cu and Ni toxicities to barley root elongation in soils.
Environ. Sci. Technol. 2006
, 40, 7085.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[44]
K. Lock ,
H. Van Eeckhout ,
K. A. C. De Schamphelaere ,
P. Criel ,
C. R. Janssen ,
Development of a biotic ligand model (BLM) predicting nickel toxicity to barley (Hordeum vulgare).
Chemosphere 2007
, 66, 1346.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[45]
K. Lock ,
K. A. C. De Schamphelaere ,
S. Becaus ,
P. Criel ,
H. Van Eeckhout ,
C. R. Janssen ,
Development and validation of a terrestrial biotic ligand model predicting the effect of cobalt on root growth of barley (Hordeum vulgare).
Environ. Pollut. 2007
, 147, 626.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[46]
R. L. Hough ,
A. M. Tye ,
N. M. J. Crout ,
S. P. McGrath ,
H. Zhang ,
S. D. Young ,
Evaluating a ‘Free Ion Activity Model’ applied to metal uptake by Lolium perenne L. grown in contaminated soils.
Plant Soil 2005
, 270, 1.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[47]
S. Jansen ,
R. Blust ,
H. P. Van Leeuwen ,
Metal speciation dynamics and bioavailability: Zn(II) and Cd(II) uptake by mussel (Mytilus edulis) and carp (Cyprinus carpio).
Environ. Sci. Technol. 2002
, 36, 2164.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[48]
P. H. Nye ,
P. B. Tinker ,
The concept of a root demand coefficient.
J. Appl. Ecol. 1969
, 6, 293.
| Crossref | GoogleScholarGoogle Scholar |

[49]
J. B. Best ,
The inference of intracellular enzymatic properties from kinetic data obtained on living cells. 1. Some kinetic considerations regarding an enzyme enclosed by a diffusion barrier.
J. Cell. Comp. Physiol. 1955
, 46, 1.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[50]
F. Degryse ,
E. Smolders ,
R. Merckx ,
Labile Cd complexes increase Cd availability to plants.
Environ. Sci. Technol. 2006
, 40, 830.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[51]
J. J. Hart ,
R. M. Welch ,
W. A. Norvell ,
L. V. Kochian ,
Transport interactions between cadmium and zinc in roots of bread and durum wheat seedlings.
Physiol. Plant. 2002
, 116, 73.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[52]
C. K. Cohen ,
T. C. Fox ,
D. F. Garvin ,
L. V. Kochian ,
The role of iron-deficiency stress response in stimulating heavy-metal transport in plants.
Plant Physiol. 1998
, 116, 1063.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[53]
J. L. Brewster ,
K. K. S. Bhat ,
P. H. Nye ,
Possibility of predicting solute uptake and plant-growth response from independently measured soil and plant characteristics. 5. Growth and phosphorus uptake of rape in soil at a range of phosphorus concentrations and a comparison of results with predictions of a simulation-model.
Plant Soil 1976
, 44, 295.
|
CAS |
| Crossref |

[54]
S. Itoh ,
S. A. Barber ,
Phosphorus uptake by six plant species as related to root hairs.
Agron. J. 1983
, 75, 457.

[55]
J. F. Loneragan ,
J. F. Ascher ,
Response of plants to phosphate concentration in solution culture. II. Rate of phosphate absorption and its relation to growth.
Soil Sci. 1967
, 103, 311.
|
CAS |
| Crossref |

[56]
[57]
A. L. Nolan ,
M. J. McLaughlin ,
S. D. Mason ,
Chemical speciation of Zn, Cd, Cu and Pb in pore waters of agricultural and contaminated soils using Donnan dialysis.
Environ. Sci. Technol. 2003
, 37, 90.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[58]
H. P. van Leeuwen ,
Metal speciation dynamics and bioavailability: inert and labile complexes.
Environ. Sci. Technol. 1999
, 33, 3743.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[59]
[60]
K. W. Warnken ,
W. Davison ,
H. Zhang ,
J. Galceran ,
J. Puy ,
In situ measurements of metal complex exchange kinetics in freshwater.
Environ. Sci. Technol. 2007
, 41, 3179.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[61]
W. Davison ,
H. Zhang ,
In situ speciation measurements of trace components in natural waters using thin-film gels.
Nature 1994
, 367, 546.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[62]
K. W. Warnken ,
H. Zhang ,
W. Davison ,
Accuracy of the Diffusive Gradients in Thin-films technique: diffusive boundary layer and effective sampling area considerations.
Anal. Chem. 2006
, 78, 3780.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[63]
M. H. Tusseau-Vuillemin ,
R. Gilbin ,
M. Taillefert ,
A dynamic numerical model to characterize labile metal complexes collected with diffusion gradient in thin films devices.
Environ. Sci. Technol. 2003
, 37, 1645.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[64]
S. Scally ,
W. Davison ,
H. Zhang ,
In situ measurements of dissociation kinetics and labilities of metal complexes in solution using DGT.
Environ. Sci. Technol. 2003
, 37, 1379.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[65]
O. A. Garmo ,
N. J. Lehto ,
H. Zhang ,
W. Davison ,
O. Royset ,
E. Steinnes ,
Dynamic aspects of DGT as demonstrated by experiments with lanthanide complexes of a multidendate ligand.
Environ. Sci. Technol. 2006
, 40, 4754.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[66]
H. Zhang ,
W. Davison ,
B. Knight ,
S. McGrath ,
In situ measurements of solution concentrations and fluxes of trace metals in soils using DGT.
Environ. Sci. Technol. 1998
, 32, 704.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[67]
H. Ernstberger ,
W. Davison ,
H. Zhang ,
A. Tye ,
S. Young ,
Measurement and dynamic modeling of trace metal mobilization in soils using DGT and DIFS.
Environ. Sci. Technol. 2002
, 36, 349.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[68]
M. P. Harper ,
W. Davison ,
H. Zhang ,
W. Tych ,
Kinetics of metal exchange between solids and solutions in sediments and soils interpreted from DGT measured fluxes.
Geochim. Cosmochim. Acta 1998
, 62, 2757.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[69]
L. Sochaczewski ,
W. Tych ,
W. Davison ,
H. Zhang ,
DGT induced fluxes in sediments and soils (2D DIFS).
Environ. Model. Softw. 2007
, 22, 14.
| Crossref | GoogleScholarGoogle Scholar |

[70]
H. Ernstberger ,
H. Zhang ,
A. Tye ,
S. Young ,
W. Davison ,
Desorption kinetics of Cd, Zn, and Ni measured in soils by DGT.
Environ. Sci. Technol. 2005
, 39, 1591.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[71]
N. J. Lehto ,
L. Sochaczewski ,
W. Davison ,
W. Tych ,
H. Zhang ,
Quantitative assessment of soil parameter (Kd and Tc) estimation using DGT measurements and the 2D DIFS model.
Chemosphere 2008
, 71, 795.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[72]
H. Zhang ,
W. Davison ,
R. Gadi ,
T. Kobayashi ,
In situ measurement of dissolved phosphorus in natural waters using DGT.
Anal. Chim. Acta 1998
, 370, 29.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[73]
N. W. Menzies ,
B. Kusomo ,
P. W. Moody ,
Assessment of P availability in heavily fertilized soils using the diffusive gradient in thin films (DGT) technique.
Plant Soil 2005
, 269, 1.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[74]
T. M. McBeath ,
M. J. McLaughlin ,
R. D. Armstrong ,
M. Bell ,
M. D. A. Bolland ,
M. K. Conyers ,
R. E. Holloway ,
S. D. Mason ,
Predicting the response of wheat (Triticum aestivum L.) to liquid and granular phosphorus fertilisers in Australian soils.
Aust. J. Soil Res. 2007
, 45, 448.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[75]
S. Mason ,
R. Hamon ,
H. Zhang ,
J. Anderson ,
Investigating chemical constraints to the measurement of phosphorus in soils using diffusive gradients in thin films (DGT) and resin methods.
Talanta 2008
, 74, 779.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[76]
B. van Raij ,
J. A. Quaggio ,
N. M. da Silva ,
Extraction of phosphorus, potassium, calcium and magnesium from soils by an ion-exchange resin procedure.
Commun. Soil Sci. Plant Anal. 1986
, 17, 547.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[77]
R. W. McDowell ,
L. M. Condron ,
Chemical nature and potential mobility of phosphorus in fertilized grassland soils.
Nutr. Cycl. Agroecosyst. 2000
, 57, 225.
| Crossref | GoogleScholarGoogle Scholar |

[78]
P. S. Hooda ,
H. Zhang ,
W. Davison ,
A. C. Edwards ,
Measuring bioavailable trace metals by diffusive gradients in thin films (DGT): soil moisture effects on its performance in soils.
Eur. J. Soil Sci. 1999
, 50, 285.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[79]
A. Jungk ,
Root hairs and the acquisition of plant nutrients from soil.
J. Plant Nutr. Soil Sci. 2001
, 164, 121.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[80]
M. A. Piñeros ,
J. E. Shaff ,
V. Kochian ,
Development, characterization, and application of a cadmium-selective microelectrode for the measurement of cadmium fluxes in roots of Thlaspi species and wheat.
Plant Physiol. 1998
, 116, 1393.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[81]
H. Marschner ,
V. Römheld ,
W. J. Horst ,
P. Martin ,
Root-induced changes in the rhizosphere: importance for the mineral nutrition of plants.
J. Plant Nutr. Soil Sc. 1986
, 149, 441.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[82]
D. L. Jones ,
Organic acids in the rhizosphere – a critical review.
Plant Soil 1998
, 205, 25.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[83]
P. M. C. Antunes ,
B. A. Hale ,
The effect of metal diffusion and supply limitations on conditional stability constants determined for durum wheat roots.
Plant Soil 2006
, 284, 229.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[84]
C. Oporto ,
E. Smolders ,
F. Degryse ,
L. Verheyen ,
C. Vandecasteele ,
DGT-measured fluxes explain the chloride-enhanced cadmium uptake by plants at low but not at high Cd supply.
Plant Soil 2009
, 318, 127.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[85]
M. J. McLaughlin ,
L. T. Palmer ,
K. G. Tiller ,
T. A. Beech ,
M. K. Smart ,
Increased soil-salinity causes elevated cadmium concentrations in field-grown potato-tubers.
J. Environ. Qual. 1994
, 23, 1013.
|
CAS |

[86]
L. V. Kochian ,
W. J. Lucas ,
Potassium transport in corn roots. 1. Resolution of kinetics into a saturable and linear component.
Plant Physiol. 1982
, 70, 1723.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[87]
L. H. Wu ,
Y. M. Luo ,
X. R. Xing ,
P. Christie ,
EDTA-enhanced phytoremediation of heavy metal contaminated soil with Indian Mustard and associated potential leaching risk.
Agric. Ecosyst. Environ. 2004
, 102, 307.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[88]
F. Degryse ,
E. Smolders ,
I. Oliver ,
H. Zhang ,
Relating soil solution Zn concentration to DGT measurements in contaminated soils.
Environ. Sci. Technol. 2003
, 37, 3958.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[89]
E. Smolders ,
J. Buekers ,
I. Oliver ,
M. J. McLaughlin ,
Soil properties affecting toxicity of zinc to soil microbial properties in laboratory-spiked and field-contaminated soils.
Environ. Toxicol. Chem. 2004
, 23, 2633.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[90]
F. J. Zhao ,
C. P. Rooney ,
H. Zhang ,
S. P. McGrath ,
Comparison of soil solution speciation and Diffusive Gradients in Thin-films measurement as an indicator of copper bioavailability to plants.
Environ. Toxicol. Chem. 2006
, 25, 733.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[91]
O. Sonmez ,
G. M. Pierzynski ,
Assessment of zinc phytoavailability by diffusive gradients in thin films (DGT).
Environ. Toxicol. Chem. 2005
, 24, 934.
| Crossref | GoogleScholarGoogle Scholar |
CAS |
PubMed |

[92]
[93]
[94]
P. Pypers ,
J. Delrue ,
J. Diels ,
E. Smolders ,
R. Merckx ,
Phosphorus intensity determines short-term P uptake by pigeon pea (Cajanus cajan L.) grown in soils with differing P buffering capacity.
Plant Soil 2006
, 284, 217.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[95]
D. Föhse ,
N. Claassen ,
A. Jungk ,
Phosphorus efficiency of plants. 1. External and internal P requirement and P uptake efficiency of different plant-species.
Plant Soil 1988
, 110, 101.
| Crossref |

[96]
W. Davison ,
P. S. Hooda ,
H. Zhang ,
A. C. Edwards ,
DGT measured fluxes as surrogates for uptake of metals by plants.
Adv. Environ. Res. 2000
, 3, 550.

[97]
Y. Q. He ,
Y. G. Zhu ,
S. E. Smith ,
F. A. Smith ,
Interactions between soil moisture content and phosphorus supply in spring wheat plants grown in pot culture.
J. Plant Nutr. 2002
, 25, 913.
| Crossref | GoogleScholarGoogle Scholar |
CAS |

[98]
[99]