Deep drainage in a Grey Vertosol under furrow-irrigated cotton

Additional keywords: cotton, deep drainage, furrow irrigation, lysimeter, Vertosol.

For much of the history of the Australian cotton industry, it was believed that deep drainage was insignificant because of the low permeability of the heavy clay soils where cotton is grown (Hearn 1998). Starting in the 1990s, concern about exactly how much drainage occurs increased, because of estimates of significant drainage under dryland cropping systems in northern New South Wales (NSW) (Ringrose-Voase et al. 2003; Paydar et al. 2005). This concern was driven by the potential for drainage to cause groundwater levels to rise, increasing the risk of salinity. Weaver et al. (2013) found that drainage water from irrigated cotton had the potential to contaminate groundwater because it can have a pH of 8.5–9.0 and electrical conductivity (EC) generally >2 dS m^–1. In addition, the industry came under pressure to improve water-use efficiency due to the scarcity of water for irrigation during periods of drought. Of particular concern was drainage under furrow irrigation, since it is the most widely used irrigation method in the cotton industry due its relatively low cost.

It is well established that clearing native vegetation in semi-arid environments increases drainage (e.g. Silburn et al. 2009). However, while Silburn et al. (2011) found that clearing native vegetation on Vertosols in southern Queensland for pasture or cropping increased drainage from near zero to 4 and 10 mm year^–1, respectively, increases under irrigated cotton are much greater. Silburn et al. (2013a) reviewed research on deep drainage under furrow irrigation and found values of 50–300 mm per season. Studies of deep drainage under irrigated cotton by Gordon (2000) and Gunawardena et al. (2011) showed similarly high values. The latter study also demonstrated that spray irrigation resulted in substantially less drainage than furrow irrigation. A thorough review of the topic is presented by Silburn et al. (2013b).

One problem is the difficulty in measuring or estimating drainage. Methods include modelling, chloride mass balance and direct measurement using lysimetry, all of which have strengths and weaknesses. Drainage can be estimated using modelling by measuring or calculating other components of the water balance (e.g. Ringrose-Voase et al. 2003). The risk is that errors in measurement or estimation of the other parts of the water balance tend to accumulate in the drainage estimate. These errors can be of the same order of magnitude as the drainage term because drainage is generally small relative to other components of the water balance. The advantage is that, once a model has been suitably tested for a region and its land uses, it is relatively easy to estimate drainage for a range of combinations of land use, soil type and climate.

The chloride mass-balance technique can be used to estimate drainage on the basis of the decrease in chloride in the soil profile, based on its concentration in applied irrigation water and rainfall and the amounts of irrigation and rainfall. Weaver et al. (2005) and Hulugalle et al. (2010) used this method to measure drainage under cotton and found seasonal drainage at 1.2 m depth of 14–83 mm, with significant differences due to tillage and crop rotation. Chloride mass balance can only provide estimates of drainage over whole seasons or longer, but is relatively cheap, thus allowing replication and measurement of different treatments or sites. A disadvantage is that it assumes water is moving as a wetting front through the soil matrix and not as bypass flow. If the latter is important in an irrigated system, the method will tend to underestimate drainage. Although Slavich and Yang (1990) propose a correction to the chloride mass-balance approach, it requires pre-knowledge of the proportion of drainage occurring as bypass flow.

Direct measurement of drainage under cotton has used lysimetry. Gordon (2000) used large, free-draining lysimeters, whereas Gunawardena et al. (2011) used the somewhat less expensive barrel lysimeter. Although lysimeters do measure drainage directly, they tend to be the most costly method, which makes it difficult to make replicate measurements in a variety of different situations. Most lysimeters are free-draining and require water to saturate the soil immediately above the lower boundary before drainage is generated. This disrupts the hydraulic gradients found in the surrounding soil and therefore the drainage rate.

Another issue with drainage in irrigated cropping is the role of bypass flow through macropores. Prendergast (1995) concluded that under flood irrigation, bypass flow accounted for drainage soon after irrigation, and that such drainage was greater the drier the soil due to the increased volume of cracks. It has often been assumed that bypass flow is inefficient at leaching salt from the root-zone (Thorburn and Rose 1990), but Prendergast (1995) found the contrary.

This paper describes the use of a drainage lysimeter following the design of Brye et al. (1999), in which the soil-water potential at the lower boundary is controlled to mimic that in the surrounding soil and thus maintain the same hydraulic gradient. It was used to measure drainage under furrow irrigation at a single site at high frequency. The lysimeter is intended to provide detailed, high-frequency data over a long period to understand drainage processes. It does so by intercepting drainage over a large area (1.58 m²) with minimal disturbance. While the cost of the facility precludes replication, it should be seen as part of a multi-faceted approach to investigating deep drainage using other, less expensive methods such as barrel lysimeters (Gunawardena et al. 2011) or chloride mass balance (Weaver et al. 2005).

The lysimeter facility is at the Australian Cotton Research Institute (ACRI) near Narrabri in northern New South Wales (30.19220°S; 149.60522°E). The lysimeter is in a long-term experiment under a plot with an irrigated cotton–wheat rotation. The experiment is described by Hulugalle et al. (2010), who also give drainage estimates for the various treatments using chloride mass balance. Cotton is generally sown in October and harvested in May. Wheat is sown immediately afterwards and harvested in November. The land is then fallow from November to October the following year. Minimum tillage is used with stubble retention and permanent beds. Cotton is fully irrigated by furrow, with alternate furrows being used for irrigation. Wheat crops generally receive only one supplementary irrigation after sowing.

The plot is 200 m long from head to tail ditch, and the lysimeter is located halfway along the plot. The plot is 24 m wide with a 4-m-wide buffer strip along one side that is managed in the same way as the plot. The lysimeter trays are located under the plot extending from 0.34 to 2.16 m from the edge of the plot adjacent to the buffer strip. The access shaft is under the buffer strip, immediately adjacent to the plot (Fig. 1 and Fig. 2).

Fig. 1.  Plan view of lysimeter trays, access shaft and other instruments. Dimensions in mm.

Fig. 2.  Vertical cross-section through the centre of the access shaft at 90° to the furrows. Dimensions in mm.

The soil is classified as a Haplic, Self-mulching, Grey Vertosol (Isbell 1996), which is grey to ~1.2 m depth and brown below this. Above 1.2 m depth, the soil is 60% clay (<2 µm), 14% silt (2–20 µm) and 25% sand (20–2000 µm). Below 1.2 m, the clay content decreases to 50% by 2 m depth with corresponding increases in silt and sand to 20% and 30%, respectively. The exchangeable sodium percentage increases with depth from <1% of cation exchange capacity at the surface to 6.5% below a depth of 1.5 m, meaning the soil below 1.5 m is mildly sodic. Measurements of hydraulic conductivity indicated a compacted layer at ~0.3–0.7 m depth. The greatest hydraulic conductivities are found in the subsoil below 1.2 m, despite the bulk density also being greatest below this depth. The soil at the site is fully described in Ringrose-Voase and Nadelko (2006).

The lysimeter design was based on the variable tension drainage lysimeter of Brye et al. (1999) as modified by Foley et al. (2003) and Pegler et al. (2003). The lysimeter consists of six adjacent trays installed at 2.1 m depth that intercept drainage at a depth of 2.1 m over an area of 1.58 m². The size of the lysimeter is of the same order of magnitude as the size of the representative elementary volume of the structure of these soils. The design has four notable features that enable accurate measurement of the drainage rate in a cracking clay soil under furrow irrigation.

First, it is a drainage lysimeter not a weighing lysimeter. In a weighing lysimeter, the soil above the trays that collect drainage has to be encased and the casing separated from the surrounding soil by a small gap so that the encased soil can be weighed. However, such a gap would prevent irrigation of the soil over the lysimeter using the furrows that run the length of the plot because water would flow from the furrow into the gap, rather than continuing along the furrow over the top of the lysimeter and then on towards the tail ditch.

Second, the collection trays are installed by tunnelling horizontally so that the overlying soil is undisturbed (Fig. 3). This is of major importance in highly structured soils such as Vertosols, in which macropores are likely to play an important role in water movement. Macropores form a highly interconnected network of dynamic surface cracks, slickensides and cylindrical pores. It is important not to disrupt this network as it could affect macropore flow. Flow through the macropore network is not necessarily vertical. Water can flow through macropores laterally into soil above the trays and can similarly flow laterally out of that soil into the surrounding soil. Thus, the trays simply intercept a cross-section of flux at 2.1 m depth.

Fig. 3.  Upper: One of six collection trays during installation, showing the horizontal tunnel, drainage and vacuum tubes and space for a second tray in front. Two other pairs of trays were later installed on either side of the tunnel shown. Lower: View into the access shaft, showing the window through which the collection trays are installed (top), the six collection tanks into which the drainage passes for measurement (left and bottom), the vacuum reservoir (bottom right) and two columns of tensiometers on either side of the installation window.

Third, the lysimeter does not have vertical walls separating the soil above the trays from the surrounding soil. Such walls would cut through the macropore network and affect its connectivity. In addition, the presence of a vertical barrier in a soil with shrink–swell properties would significantly influence the cracking pattern as the soil dries, probably by creating a crack between soil and wall.

Fourth, a vacuum is applied to the collection trays and is constantly adjusted to be equal to the soil-water potential in the surrounding soil. This ensures that the hydraulic gradient in the soil above the trays is the same as that in the surrounding soil, provided the porous material used for the top surface of the trays and the contact material between the trays and the soil are both sufficiently conductive. Matching the hydraulic gradient to that in the surrounding soil allows accurate, high-resolution measurement of the drainage rate. It is particularly important when the lysimeter has no walls, because water will be diverted away from the soil above the trays if it becomes wetter than the surrounding soil, causing drainage to be underestimated. Conversely, if it is drier, it will overestimate drainage by causing water from the surrounding soil to converge towards the lysimeter. By comparison, many weighing lysimeters have a ‘free-draining’, lower boundary that requires the soil above the collection trays to reach saturation before drainage into the trays is generated. Such designs rely on the lysimeter walls to prevent the loss of drainage into the surrounding soil.

One source of uncertainty is the effect of the tray suction on bypass flow when the matric potential at tray depth is negative. In such situations, bypass flow occurs in macropores when their local potential is close to saturation, i.e. they are not in equilibrium with the matrix. The tray suction could increase macropore flow, or alter its timing. Alternatively, the suction could impede flow by emptying macropores near the tray.

The lysimeter facility has a cylindrical access shaft of reinforced concrete with a diameter of 2 m that extends from 0.5 to 4.0 m below the ground surface (Fig. 3). Entrance is through a metal hatchway positioned so as not to interfere with the flow of irrigation water in the furrows. The floor of the shaft was thickened to 350 mm to add extra weight and make the shaft negatively buoyant.

The six lysimeter collection trays are rectangular boxes 910 mm long, 286 mm wide and 130 mm high, and are constructed from marine-grade stainless steel. The floor of each one slopes towards one corner, where a drain tube projects into a cavity below the floor and is connected to a collection tank in the access shaft. In the opposite corner, a riser tube projects through the floor and is connected to a vacuum reservoir in the access shaft. The upper surface of the trays is made of a sintered stainless-steel filter that is 1 mm thick and porous, with a nominal pore size 0.2 µm. Once saturated with water, the material can hold water against a vacuum of –28 kPa before air entry occurs. However, the maximum vacuum applied by the operating protocol was –25 kPa as a safety margin to prevent the filter from de-saturating, giving the lysimeter an operating range from saturation to –25 kPa. This means that if the soil-water potential at tray depth dries to less than –25 kPa, the lysimeter is no longer able to measure drainage. The filter material is highly transmissive. A paper-thin, fibreglass filter with a nominal pore size of 0.5 µm was placed above the steel filter to protect it. Each tray is supported by two air jacks designed to exert an upwards force equal to the overburden at that depth. The jacks are mounted on a steel bearing plate to spread the load over the floor of the tunnel in which the assembly is installed. Each tray assembly weighs ~60 kg.

The trays are arranged in a 3 by 2 array to intercept drainage from an area of 1820 by 866 mm (1.58 m²) (Fig. 1). They are positioned with their upper surface at 2.1 m depth (Fig. 2). They were installed end-to-end in pairs, with the nearest edge of the central pair 340 mm from the outside of the access shaft. The installation of each pair involved digging a 2.2-m-long horizontal tunnel away from the access shaft via a window in the access shaft wall. The tunnel for only one pair at a time was excavated to limit the tunnel width to 290 mm and reduce the risk of the tunnel ceiling collapsing. A specially designed cutting box was used for the excavation to ensure the tunnels were the correct dimensions. During excavation, the cutting box smeared the soil of the tunnel ceiling. To remove the smearing, the ceiling was dried using a heat gun, and epoxy resin was applied. A layer of foam rubber covered in fibreglass and soaked in epoxy resin was placed on a wooden board and jacked up against the ceiling. The resin was allowed to cure for 24 h before the foam rubber was gently peeled away from the ceiling, pulling a thin layer of soil with it to reveal a natural surface. In several places where the tunnel intercepted slickensides, large lumps of soil fell from the ceiling leaving it with more relief than planned. The sides and base of each tunnel were lined with a stainless steel shoring box into which the collection trays were slid, leaving a 40-mm minimum gap between the tray top and the ceiling.

A contact material was necessary to fill the gap between the upper surface of the tray and the tunnel ceiling and ensure good hydraulic contact. The material needed to be more transmissive than the soil over the operating range of the lysimeter. A coarse-grade (60G) silica flour was chosen, but required grading using a sedimentation tank to remove particles <20 µm that might block the pores in the porous upper surface of the trays. The maximum bulk density to which the contact material could be packed was 1.436 Mg m^–3. At –2 kPa, its volumetric water content was 0.423. Air entry occurred at –15 kPa, and the water content decreased to 0.207 at –28 kPa. The contact material was packed into the gap between the tray tops and tunnel ceiling ensuring that any relief in the ceiling was filled.

After installation of each pair of trays, the tunnel between the end of the nearest tray and the wall of the access shaft was back-filled with soil from the same layer that had been air-dried, crushed to <10 mm and packed to a bulk density of 1.24 Mg m^–3 (compared with an original bulk density of 1.65 Mg m^–3). Although this back-filling may affect flow near the ends of the trays nearest the access shaft, the effect is minimised because the volume of back-filled soil only extends vertically from 2.1–2.5 m depth (Fig. 2), which is below collection depth.

The drain from each tray was connected by Teflon^® tubing to its own collection tank inside the access shaft that was positioned to allow drainage to flow into the tank by gravity. The tanks hang from load cells connected to a data-logger that records their weights every 15 min. Each tank has a vacuum port connected to the same vacuum supply as the trays. The tanks can be isolated to allow them to be emptied via a tap at their base without disrupting the operation of the lysimeter.

The vacuum ports in the lysimeter trays and collection tanks are connected to a common manifold in the access shaft to which are fitted two needle-valve-regulated solenoid valves. One solenoid valve is connected to a vacuum supply reservoir mounted in the access shaft. The reservoir is kept at between –45 and –50 kPa by an automated vacuum pump. The second solenoid valve vents to atmosphere.

Two vertical arrays of tensiometers are installed 1 m either side of the trays, one under an irrigation furrow and one under a wheel furrow (Fig. 1). The ceramic tips are positioned at depths of 0.9, 1.2, 1.5, 1.8 and 2.1 m, with their shafts running into circular ports in the wall of the access shaft. The tips are positioned well away from any disturbance. The distance from the repacked soil and nearest tensiometer at 2.1 m depth is 0.63 m (Fig. 1). Measurements of soil-water potential are made every 15 min by the data-logger. A single tensiometer is installed at 1.95 m immediately above the centre of the trays and is used to check that the hydraulic potential above the trays is the same as that at the same depth in the surrounding soil, obtained by averaging the tensiometers at 1.8 and 2.1 m depth.

The tensiometers at 2.1 m are also used to control the vacuum in the trays. Every 15 min, the data-logger calculates the mean potential at 2.1 m depth and uses this as the target potential for the lysimeter trays for the following 15 min. Over this period, the data-logger measures the vacuum inside the trays and collection tanks every second with a pressure transducer. If the vacuum deviates from the target by >0.1 kPa, the data-logger opens one of the two solenoid valves to adjust the vacuum. If the mean hydraulic potential is less than –25 kPa, the data logger limits the target potential to –25 kPa to prevent air entry through the filter.

The facility is powered by a 56 Ah rechargeable battery and a 20 W solar panel. The data-logger can be interrogated via telemetry using the mobile phone network.

Two aluminium neutron-probe access tubes are installed 1.2 m up-furrow from the trays and two 1.2 m down-furrow (Fig. 1). These are used to measure soil-water content to 2.1 m at appropriate intervals. The neutron probe was calibrated using volumetric measurements of water content taken near other access tubes installed in the same field in previous years. To allow for changes to bulk density caused by shrink–swell, a logarithmic form of the regression equation was used as recommended by Graecen et al. (1981):

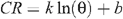
where CR is the count ratio measured by the neutron probe, θ is the volumetric water content, and k and b are regression constants. This equation can be rearranged for predicting θ:

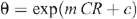
where m = 1/k and c = –b/k. The constants obtained for three layers were as follows:

where z is the depth (m).

Rainfall is recorded next to the lysimeter and other weather parameters 2 km away at the ACRI weather station.

Measuring the amount of water applied during furrow irrigation is difficult. Flumes can be used to measure over the length of the field, but are impractical to use for ongoing, as opposed to single irrigation, measurements. In addition, the amount of irrigation applied varies considerably from head to tail ditch, but using flumes over short distances, e.g. just up- and down-furrow from the lysimeter, proved ineffective due to the vagaries of flow in furrows on a cracking clay soil. For example, water would sometimes flow through a crack from a furrow next to that with the flume, where the wetting advance was faster, and cause the down-furrow flume to start flowing before the up-furrow one.

Therefore, instead of measuring the amount of irrigation applied, the amount of water that infiltrated into the soil profile was estimated for each irrigation, by measuring profile water storage (by neutron moisture meter with four replicates) shortly before (generally 1 day) and after (generally 2 days) irrigation. The quantity of irrigation infiltration was estimated from the change in profile water storage, allowing for drainage, rainfall and evapotranspiration over the period:

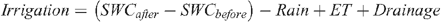
where SWC is the soil-water content from 0 to 2.1 m depth before and after irrigation; Rain is the rainfall between the two measurement days; ET is an estimate of evapotranspiration between the two measurement days using data from the ACRI weather station and a crop coefficient for the current growth stage; and Drainage is that measured by the lysimeter over the same period.

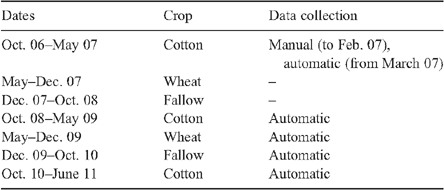
Data have been recorded by the lysimeter facility since the 2006–07 cotton season as shown in Table 1. Data were collected during three cotton crops, one wheat crop and one fallow period. However, during the 2006–07 cotton crop, measurement of drainage and soil-water potential and setting the vacuum in the lysimeter trays were performed manually while the electronic equipment was being connected to the data-logger and the data-logger was being programmed. The automatic measurement and vacuum regulation system commenced in March 2007.

Table 1.  Cropping and data collection at the ACRI lysimeter facility

Drainage measured by the lysimeter for each season is summarised in Tables 2–5, together with its EC, and inputs of rainfall and irrigation. The EC of the drainage water was measured when the collection tanks were emptied just before each irrigation and at other significant times, such as after heavy rainfall or at harvest. The EC values given are volume-weighted means over the collection period.

Table 2.  Drainage and electrical conductivity (EC) of the leachate after each irrigation during the 2006–07 cotton season as measured by variable tension lysimeter
Amounts shown are from the date of the event until the date of the next event shown on the next row. Irrigation infiltration estimated as the change in profile water content (0–2.1 m) between neutron probe measurements made before and after irrigation allowing for rainfall, approximate evapotranspiration and drainage between the two measurements

Table 3.  Drainage and electrical conductivity (EC) of the leachate after each irrigation during the 2008–09 cotton season as measured by variable tension lysimeter
Amounts shown are from the date of the event until the date of the next event shown on the next row. Irrigation infiltration estimated as the change in profile water content (0–2.1 m) between neutron probe measurements made before and after irrigation allowing for rainfall, evapotranspiration and drainage between the two measurements

Table 4.  Drainage and electrical conductivity (EC) of the leachate after each irrigation during the 2009 wheat crop and subsequent 2009–10 fallow as measured by variable tension lysimeter
Amounts shown are from the date of the event until the date of the next event shown on the next row; ‘↓’ indicates there was too little drainage for collection and analysis, so drainage was accumulated over several events. Irrigation infiltration estimated as the change in profile water content (0–2.1 m) between neutron probe measurements made before and after irrigation allowing for rainfall, evapotranspiration and drainage between the two measurements

Table 5.  Drainage and electrical conductivity (EC) of the leachate after each irrigation during the 2010–11 cotton season as measured by variable tension lysimeter
Amounts shown are from the date of the event until the date of the next event shown on the next row; ‘↓’ indicates there was too little drainage for collection and analysis, so drainage was accumulated over several events. Irrigation infiltration estimated as the change in profile water content (0–2.1 m) between neutron probe measurements made before and after irrigation allowing for rainfall, evapotranspiration and drainage between the two measurements

Drainage during the cotton season varied from 74 mm in 2006–07 to 54 mm in 2008–09 to 0.7 mm in 2010–11. Under the 2009–10 wheat–fallow, there was only 23 mm of drainage in 16 months. Moreover, the amount of drainage varied considerably between irrigation events, with most drainage occurring after irrigations early in the season. In general, total seasonal drainage increased with the total seasonal irrigation irrespective of seasonal rainfall.

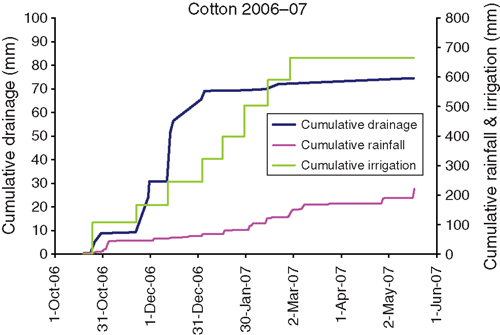
In 2006–07, only 190 mm of rain fell during the season and the first irrigation was necessary on the day after sowing (Fig. 4). In all, there were eight irrigations, more than in the other cotton seasons. Large amounts of drainage occurred after the early irrigations, in particular the second and third (Table 2), with lesser amounts after the fourth irrigation.

Fig. 4.  Cumulative drainage (left vertical axis) and cumulative rainfall and irrigation (right vertical axis) during the 2006–07 cotton season.

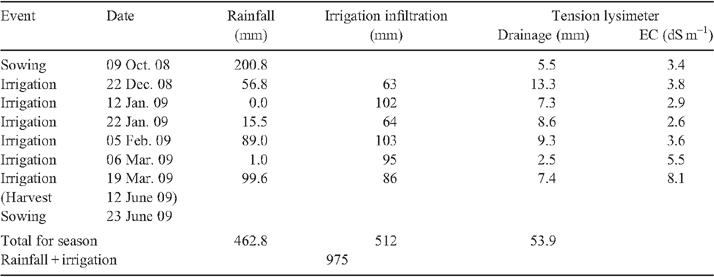
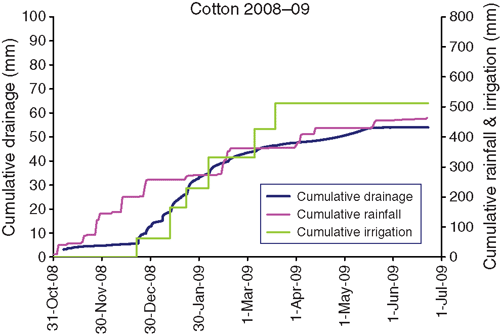
By contrast, there was 200 mm of rainfall early in the 2008–09 cotton season, and irrigation was not required until late December (Fig. 5). There were six irrigations in total. There was less drainage than in 2006–07, but the same pattern of greater drainage after the earlier irrigations than the later ones (Table 3).

Fig. 5.  Cumulative drainage (left vertical axis) and cumulative rainfall and irrigation (right vertical axis) during the 2008–09 cotton season.

The 2009 wheat crop (Table 4, Fig. 6) was sown immediately following cotton picking. The soil was dry, and two irrigations were applied to ensure germination and establishment. Dry conditions continued through the season and negligible drainage occurred. Over this period the drainage rate was <0.01 mm day^–1.

Fig. 6.  Cumulative drainage (left vertical axis) and cumulative rainfall and irrigation (right vertical axis) during the 2009 wheat season.

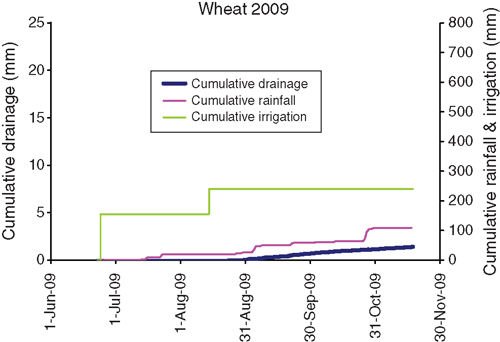
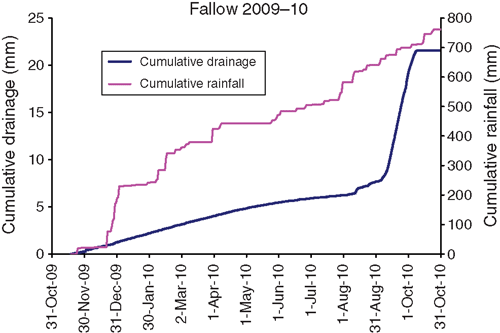
During the subsequent long fallow from November 2009 to November 2010, 170 mm of rain fell during December 2009 and was followed by a steady input of 580 mm from January to October 2010. The drainage pattern during this period (Fig. 7) was unlike those during the cotton seasons, which were characterised by sudden increases in the drainage rate after each irrigation. From November to August, there was steady drainage at ~0.03 mm day^–1. However, during late August the rate started to increase, and during September it averaged 0.38 mm day^–1.

Fig. 7.  Cumulative drainage (left vertical axis) and cumulative rainfall (right vertical axis) during the 2009–10 fallow.

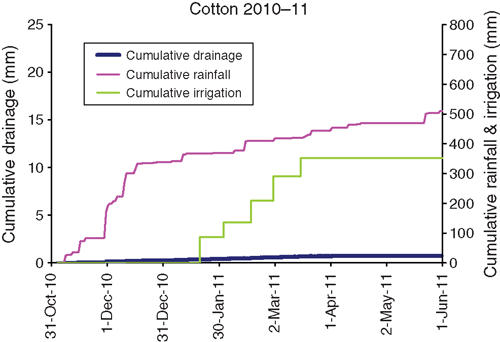
The 2010–11 season was similar to 2008–09 in having a large amount of early season rainfall; 370 mm fell between sowing and the first irrigation, which occurred in late January (Table 5, Fig. 8). Only five irrigations were necessary and there was negligible drainage. Obvious consolidation of the upper 40 cm over the lysimeter was observed visually during manual field operations and this may have contributed to the lack of drainage.

Fig. 8.  Cumulative drainage (left vertical axis) and cumulative rainfall and irrigation (right vertical axis) during the 2010–11 cotton season.

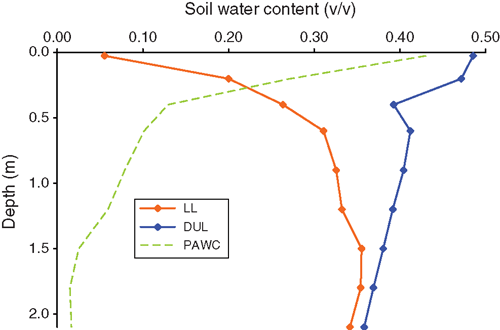
Soil-water content was measured by neutron moisture meter at intervals throughout each season. Drained upper limit (DUL) and lower limit (LL) were estimated from the results for each of the nine layers (Fig. 9), the former as the wettest water content found 2 days after an irrigation and the latter as the driest content found during a cotton crop. This LL applies only to the conditions experienced under cotton. The plant-available water content (PAWC) profile is typical of that for a Vertosol with very large PAWCs near the surface, decreasing rapidly with depth. Total PAWC to 2.1 m is 181 mm.

Fig. 9.  Drained upper limit (DUL) and lower limit for cotton (LL) for the soil profile at the ACRI lysimeter. Plant-available water capacity (PAWC) is the difference between DUL and LL.

For simplicity, soil-water content is expressed as the soil-water deficit (DUL – SWC), which shows how close each layer is to being ‘full’, irrespective of its absolute water content. The soil-water deficits over the five seasons considered are shown in Fig. 10a, c, e, and Fig. 11a, c.

Fig. 10.  Soil-water status during the 2006–07 cotton, 2008–09 cotton and 2009 wheat seasons. (a, c, e) Soil-water deficit (drained upper limit, soil-water content) for three layers measured by neutron moisture meter (four replicates). (b, d, f) Matric potential (left axis) at 1.8 and 2.1 m depth measured using tensiometers (generally two replicates) and hydraulic gradient (positive upwards) between them (right axis). Gaps in the data indicate that the soil had dried out beyond the tensiometers’ measurement range. Dates of irrigation events are shown as triangles.

Fig. 11.  Soil-water status during the 2009–10 fallow and 2010–11 cotton season. (a, c) Soil-water deficit (drained upper limit, soil water content) for three layers measured by neutron moisture meter (four replicates). (b, d) Matric potential (left axis) at 1.8 and 2.1 m depth measured using tensiometers (generally two replicates) and hydraulic gradient (positive upwards) between them (right axis). Gaps in the data indicate that the soil had dried out beyond the tensiometers’ measurement range. Dates of irrigation events are shown as triangles.

Matric potential was measured continuously during the season (except the first) at 5 depths. Results are shown only for 1.8 and 2.1 m depth in Fig. 10b, d, f, and Fig. 11b, d. Gaps in the data were caused by air entry into the tensiometers when the soil-water potential was drier than their operating range. Also shown is the hydraulic gradient between 1.8 and 2.1 m. The hydraulic gradient between two depths is the sum of the matric potential gradient and the gravitational, and is the driving force behind water movement. The gradient is calculated as:

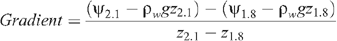
where ψ is the matric potential (kPa) at 1.8 or 2.1 m depth, z is the measurement depth (m), ρ_w is the density of water (Mg m^–3), g is the gravitational constant (9.81 m s^–2) and the gradient is expressed as kPa m^–1. Positive gradients draw water upwards and negative gradients downwards.

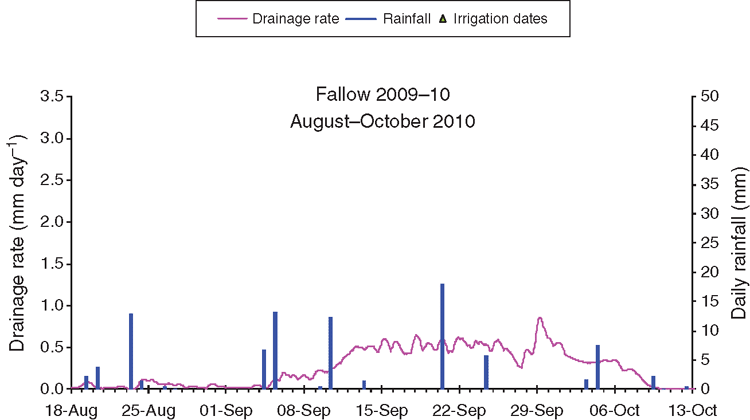
Figure 12 shows details of the high-frequency drainage measurement over 8-week periods during the 2008–09 cotton season corresponding to the intervals between irrigations. The 2006–07 season is not shown, as equipment for high-frequency measurement had not yet been installed. The 2010–11 season is not shown as there was negligible drainage. Figure 13 shows details of the drainage during an 8-week period of high flow in August–October 2010 during the 2009–10 fallow.

Fig. 12.  Mean drainage rate recorded by the lysimeter during the 2008–09 cotton season: (a) irrigations 1–3; (b) irrigations 4–6. Note: The measured drainage rate (solid line) shown after irrigation 1 (a) was affected by air-locks in the tubing between some trays and the weighing tanks causing drainage to temporarily back-up in the trays; when the air-locks were released they caused the apparent drainage peaks on, e.g. 1 and 8 January. The dotted line after 30 December attempts to correct for this by estimating a monotonic decline in the drainage rate while preserving the total volume of drainage.

Fig. 13.  Mean drainage rate recorded by the lysimeter from August to October 2009 during of the 2009–10 fallow.

The 2009–10 fallow illustrates a period of ‘normal’ soil-water behaviour, when an input of water, in this case rain, causes a wetting front to move downward through the soil, successively wetting deeper layers until it reaches tray depth and is recorded as deep drainage. Following the 2009 wheat crop, the soil was dry to depth (Fig. 11a), with the total deficit from the 0–2.1 m depth reaching 200 mm by December 2009. There was a steady input of 640 mm rain between December and August 2010 (Fig. 7), which caused wetting of the soil profile starting at the surface and gradually moving down. Figure 14b shows individual layers below 0.6 m depth wetting up successively. Figure 14b also shows that the wetting front became more diffuse as it travelled deeper, with the rate of water content change becoming slower for deeper layers. A very sharp wetting front reached 0.6 m at the end of December 2009, but did not reach 1.8 m until early August 2010.

Fig. 14.  Soil-water deficit (relative to drained upper limit) of subsoil layers from 0.6 to 2.1 m depth during (a) the 2008–09 cotton crop and (b) the 2009–10 fallow measured by neutron moisture meter.

Figure 11b shows an upwards hydraulic gradient at 2.1 m depth of about +40 kPa m^–1 at the end of August. However, there was little water movement despite the upward gradient because the hydraulic conductivity would have been very low at the matric potentials measured. The wetting front reached 1.8 m during August and the matric potential increased very suddenly to about –1 kPa. From 5 September, the downward gradient between 1.8 and 2.1 m rapidly increased and reached –135 kPa m^–1 on 20 September, causing rapid water movement into the 2.1 m layer. The matric potential at 2.1 m rose rapidly after 20 September, reaching about –2 kPa on 20 October.

The drainage rate at 2.1 m started to increase on ~5 September from the very low rates measured before then (Fig. 13b), and reached a maximum of ~0.5 mm day^–1 on ~15 September corresponding to the maximum downward hydraulic gradient. The rate started to decline from ~5 October, corresponding to the time when the potential at 2.1 m was rising most rapidly. By 11 October the rate had returned to very low levels. Overall, the wetting front took about 1 month to pass.

The pattern of drainage during the 2009–10 fallow helps to place drainage during other seasons into context and also shows that the lysimeter facility can detect and measure ‘classic’ wetting-front behaviour.

The drainage pattern measured during the cotton seasons did not exhibit this ‘classic’ behaviour. At the start of the 2006–07 cotton, the subsoil was already quite wet, with deficits of only 9 mm in both the 0.50–1.05 and 1.05–2.10 m layers (Fig. 10a). The matric potentials at 1.8 and 2.1 m were ~–15 kPa and there was a weak downward gradient (Fig. 10b). The early irrigation caused immediate further wetting of the subsoil. Because the young crop was not yet extracting water from below 0.5 m, subsequent irrigations further wet the soil below 0.5 m and the soil reached near saturation after the third irrigation. With little available storage in the subsoil, these irrigations generated significant amounts of drainage (Table 2).

After the third irrigation, the crop began to extract increasing amounts of water from 0.5–1.05 m depth, generating increasingly large deficits between later irrigations. Consequently, the amount of drainage after each irrigation fell with successive irrigations. From late March 2007, the deep subsoil at 1.8 m had dried sufficiently for the hydraulic gradient to be upwards.

The EC of the drainage fell over the first part of the season, but then increased towards the end of the season, reaching a maximum of 3.2 dS m^–1 after the last irrigation.

This season contrasts with the previous one, because the deficit below 0.5 m at the start of the season was more substantial, 44 mm (Fig. 10c, d). Irrigation was unnecessary until 22 December due to rain early in the season (Table 3, Fig. 5). However, little of this rain penetrated below 0.5 m and there was still a deficit of 28 mm below 0.5 m before the first irrigation; 13 mm of the irrigation water was stored below 0.5 m and 13 mm became drainage. The situation was repeated after subsequent irrigations, but the generation of increasing deficits below 0.5 m meant that there was less drainage. In summary, the presence of deficits below 0.5 m before all the irrigations, together with the lower number of irrigations (6 v. 8), resulted in 30% less drainage than in 2006–07, despite the greater input of water as rain and irrigation.

Throughout the season, there was an upward gradient at tray depth (Fig. 10d). Since tensiometers measure the potential of the matrix, this means that water was not draining from the profile through the soil matrix as described above for the 2009–10 fallow. Indeed, the matric potential at tray depth showed little or no response to individual irrigations despite drainage occurring. The only response was a gradual decrease in potential over the season as the subsoil dried. These observations suggest that water was not moving as a wetting front through the matrix of the soil profile but through macropores that ‘bypass’ the soil matrix. These macropores occupy a very small volume of the soil, so whether they are full or empty has negligible effect on either the soil-water content as measured by neutron moisture meter or the matric potential measured by tensiometers.

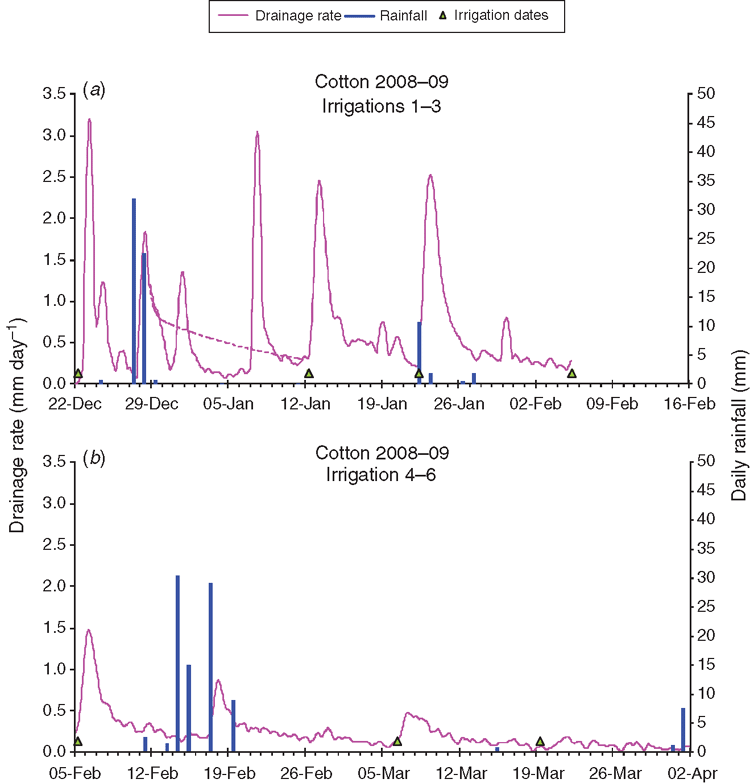
High-frequency monitoring during the 2008–09 season showed that most of the drainage occurred in short bursts shortly after irrigations 1–4 (Fig. 12). The drainage rate increased very rapidly and peaked, on average, 25 h after the irrigation front passed over the lysimeter. The rate then receded slightly more slowly than it rose, but nonetheless exponentially. The peak drainage rate was 3.2 mm day^–1 after irrigation 1 and declined to 1.5 mm day^–1 after irrigation 4. Large rainfall events in late December 2009 and mid-February 2010 also caused similar peaks. The quickness with which the peaks occurred after irrigations and their size is further evidence that water is flowing rapidly through macropores and not through the soil matrix. The peaks after irrigations 5 and 6 were much smaller (Fig. 12b).

The variability of the drainage recorded by the six trays is also evidence of the dominance of bypass flow during this cotton season. Figure 15 shows the proportion of drainage accounted for by each tray and demonstrates its considerable spatial variability over small areas—the trays covering an area of only 1.58 m² in total. The behaviour of each tray was consistent during the first four irrigations, with each delivering a similar proportion of the drainage. For example, tray 6 consistently delivered 50–55% of the total. This suggests that the large drainage rates occurring after each irrigation are due to a stable, but spatially heterogeneous, network of macropores.

Fig. 15.  Proportions of total drainage collected by each lysimeter tray in the interval after each irrigation during the 2008–09 cotton season and during the 2009–10 fallow.

After irrigations 5 and 6, the pattern of drainage collection changed, with each tray collecting more equal proportions, especially after irrigation 6. This, combined with the absence of a marked peak in the drainage rate, indicates that drainage after these events is dominated by flow through a more slowly conducting and more spatially homogeneous network of pores. Nevertheless, such flow can still be considered as bypass since there is an upward gradient and the subsoil layers still have considerable empty storage.

The proportions of flow into each tray after irrigations 5 and 6 also show an interesting similarity to those during the 2009–10 fallow, during which the data indicate that drainage was dominated by matrix flow.

An interesting feature of the drainage peaks is their long tails, with drainage continuing at low but significant rates of <0.5 mm day^–1 for weeks after the peak (Fig. 12). These rates were above those measured during the fallow period before the September 2009 wetting front, which were <0.01 mm day^–1. The drainage during these tails is still bypass flow because the hydraulic gradient was upwards throughout the season.

During the first part of the irrigation season, EC was relatively low, suggesting that the drainage had been more diluted with irrigation water that had not equilibrated with the soil matrix (Table 3). The EC rose as the drainage rate fell after irrigations 5 and 6, reaching a maximum of 8.1 dS m^–1, indicating a build-up of salt in the matrix during the season and greater equilibration between drainage flowing in macropores and the soil matrix.

The crop was sown in dry conditions shortly after cotton picking and was irrigated the day after sowing. The subsoil was very dry with a deficit of 117 mm from 0.5 to 2.1 m depth (Fig. 10e, f). After the first irrigation, this deficit absorbed 55 mm of irrigation water, which seems to have prevented any peak in drainage, unlike in the 2006–07 cotton season when irrigation immediately after sowing generated large amounts of drainage. During this period, the matric potential was between –50 and –60 kPa at 1.8 m and –40 kPa at 2.1 m, with an upward gradient all season. Almost no drainage was recorded. This may be because the potential at 2.1 m was less than –25 kPa, which is the most negative suction that can be applied to the lysimeter trays. This would have prevented water moving from the soil into the trays.

The prolonged wet period during the 2009–10 fallow (described above) wet the soil profile by the start of the 2010–11 cotton season. As with the 2006–07 cotton season, this season started with very little subsoil deficit—only 10 mm from 0.5 to 2.1 m depth (Fig. 11c). However, there was adequate rainfall for irrigation not to be required until late January, unlike in 2006–07 (Table 5, Fig. 8). By the time of the first irrigation the crop was already creating a deficit in the 0.5–1.05 m layer and negligible drainage was produced during the season. Matric potentials were close to saturation for the early part of the season and showed only a moderate decrease over the season (Fig. 11d). The gradient was weakly downward until midseason, when it became weakly upward.

The almost total absence of drainage contrasts with the earlier cotton seasons when even later irrigations generated small amounts of drainage. The deficits at 0–0.5, 0.5–1.05 and 1.05–2.1 m depths before the first irrigation were very similar to those in 2006–07, when large amounts of drainage were produced, making the 2010–11 results more puzzling. Visual observations at the site indicated consolidation of the upper 40 cm over the lysimeter, which may have prevented deep penetration of water, possibly disrupting bypass flow pathways. The consolidation was caused by lack of mechanical tillage over the lysimeter because tillage operations over the lysimeter are difficult on a regular basis and occur much less frequently than in the rest of the plot. Further evidence is the failure of irrigation to fully wet the upper 0.5 m of the profile (Fig. 11c).

Detailed measurement of deep drainage in a Vertosol under furrow irrigated cotton has shown that drainage can be significant and occurs in two forms—matrix drainage and bypass drainage. The former is the ‘normal’ form of drainage and is generally well understood and modelled. It occurs whenever the soil profile is filled to capacity by periods when water inputs exceed losses by ET. This can occur, for example, during prolonged rainy periods during a fallow, when ET is at its lowest. If irrigation occurs when the subsoil is already wet there is also potential for this type of drainage. Minimising this type of drainage requires a risk-management approach, since some drainage is inevitable and indeed desirable in order to prevent the build-up of salt. Risk management involves the whole cropping system, not just the cotton crop.

Measures to minimise the risk of matrix drainage essentially mean maintaining sufficient soil-water deficit to contain likely inputs of water through rain or irrigation. Measures can include optimising the deficit used to trigger irrigation and manipulating the crop rotation to ensure the maximum possible subsoil deficit before fallow periods or the irrigation season.

Bypass drainage occurs as rapid flow down macropores and bypasses without entering the soil matrix. The data present a complex picture of this type of drainage, in which the main pattern is that irrigations earlier in the season produce the most drainage with the drainage rate peaking at up to 3.2 mm day^–1 about 1 day after irrigation. The soil-water deficit below 0.5 m depth increases between later irrigations and this seems to mitigate the quantity of drainage generated. The very high deficit before the 2009 wheat crop appears to prevent drainage altogether. Furrow irrigation always appears to fully wet the upper 0.5 m. However, the water passing into deeper layers is relatively inefficient at wetting them, with a proportion passing out of the profile as drainage without removing the deficit. Negligible drainage during the 2010–11 cotton season is anomalous since the subsoil deficit was very low before the first irrigation, even though this occurred late in the season. If this was caused by a compacted layer, it highlights the sensitivity of bypass flow to macropore structure and the difficulties in any attempt at its prediction.

Bypass drainage is likely to be more difficult to manage because it occurs despite the presence of a subsoil deficit and even in the presence of upward hydraulic gradients. The greatest risk of bypass drainage is when early irrigation (e.g. before December) is required due to lack of rain. In this situation, the subsoil wets after the first one or two irrigations, and subsequent irrigations cause large amounts of drainage. Conversely, irrigations later in the crop, when large subsoil deficits build up between irrigations, reduce drainage to much lower levels.

Leaching salt from irrigation water that has accumulated in the soil is the reason why some drainage is necessary. Gunawardena et al. (2011) determined the leaching requirement for irrigated cotton in the northern Murray–Darling Basin as being generally <3.5% of the input water, unless low quality water is used. The results from Gunawardena et al. (2011) and this study both suggest this requirement should easily be met. However, bypass drainage is less effective at leaching than matrix drainage, and a greater leaching fraction may be required to prevent the accumulation of salt. Greater understanding is required about how rapidly salt builds up in the profile in the light of bypass drainage. Long-term modelling should be used to determine the frequency of matrix drainage and whether the frequency is sufficient to prevent salt build-up.