Comparative Study of Carbon Force Fields for the Simulation of Carbon Onions
Alireza Aghajamali A B and Amir Karton
A B and Amir Karton  A B
A B
A School of Molecular Sciences, The University of Western Australia, Perth, WA 6009, Australia.
B Corresponding authors. Email: alireza.aghajamali@uwa.edu.au; amir.karton@uwa.edu.au
Australian Journal of Chemistry 74(10) 709-714 https://doi.org/10.1071/CH21172
Submitted: 21 July 2021 Accepted: 31 August 2021 Published: 7 October 2021
Journal Compilation © CSIRO 2021 Open Access CC BY-NC-ND
Abstract
We evaluate the performance of ten common carbon force fields for the interaction energies in double and triple layered carbon onions. In particular, we consider the C20@C60, C20@C80, C20@C180, C80@C240, C60@C240 and C240@C540 double-layer carbon onions and C60@C240@C540 and C80@C240@C540 triple-layered carbon onions. We consider the following carbon force fields: Tersoff, REBO-II, AIREBO, AIREBO-M, screened versions of Tersoff and REBO-II, LCBOP-I, 2015 and 2020 versions of ReaxFF, and the machine-learning GAP force field. We show that the ReaxFF force fields give the best performance for the interaction energies of the cabon onions relative to density functional theory interaction energies obtained at the PBE0-D3/def2-TZVP level of theory. We proceed to use the ReaxFF-15 force field to explore the interaction energies in a giant ten-layered carbon onion with a C60 core and show that the interaction energy between the outer layer and the inner layers increases linearly with the number of layers in the carbon onion (with a squared correlation coefficient of R2 = 0.9996). This linear increase in the stabilization energy with each consecutive layer may have important thermodynamic consequences for describing the formation and growth of large carbon onions.
Keywords: carbon nano-onions, carbon nanomaterials, fullerenes, machine-learning force fields, empirical force fields, interaction energy.
Introduction
Carbon onions are nanoforms of carbon materials and members of the fullerene family, with quasi-spherical concentric fullerene-like shells that range from double to multi-layered structures. They are known as onion-like carbon or carbon nano-onions and were first synthesized by Iijima[1] in arc discharge experiments. The intershell distance in carbon onions is about 3.4 Å which is slightly larger than the distance between graphene layers in graphite.[2] Carbon onions are an attractive research target due to their unique thermodynamic, electronic, electrical and optical properties and the possibility of conversion into other forms of carbon.[2,3] For example, they have high electrical conductivities and improved dispersibility relative to graphene, making them promising materials for electrochemical applications. Due to their excellent capacitance retention at high current densities and improved solubility, carbon onions are ideal additives to lithium-ion batteries[4,5] and supercapacitor electrodes for high power applications.[6,7] In addition, they have potential applications in cellular imaging,[8,9] tribology, catalysis, composite materials, and electromagnetic devices.[3,10,11]
Over the past four decades, in addition to arc discharge, which is the most common approach to generating carbon onions, other synthetic methods have been employed. These include electron beam irradiation,[12–14] laser irradiation,[15] high-temperature nanometre-sized diamond annealing,[16–21] implantation of carbon ions onto metal particles[22,23] and chemical vapour deposition (CVD). It should be noted that with the exclusion of the CVD method, all the above-mentioned methods are costly due to their high-temperature processes, and they produce a limited number of carbon onions in highly condensed forms. In contrast, CVD is an effective method for generating pure carbon onions in large amounts.[24]
Atomistic simulations play an important role in modelling carbon onions. Generally, calculating the energy of a system of atoms is a prerequisite requirement for carrying out atomistic simulations. A number of density functional theory (DFT) studies have explored the formation and interaction energies in carbon onions.[25–33] However, due to the computational cost associated with DFT methods, these studies have been limited to systems with hundreds of carbons. Molecular mechanics, on the other hand, is computationally much more economical and is routinely used for calculating structural properties of nanomaterials. Molecular mechanics also provides a practical avenue for running molecular dynamics (MD) simulations which are of key importance in studying the dynamic behavior of carbon nanomaterials. For examples of force field-based MD simulations of carbon onions see:[34–41] The stability of the multi-layered carbon onions alongside the interaction energies between their layers are important in a wide range of chemical applications, such as lithium-ion batteries and supercapacitors.
In the present work we use a wide range of commonly used carbon force fields to investigate the interaction energies in a range of carbon onion structures. Namely, the double-layered C20@C60, C20@C80, C60@C180, C60@C240, C60@C240 and C240@C540 carbon onions, and C60@C240@C540 and C80@C240@C540 triple-layered carbon onions. We evaluate the performance of ten commonly used force fields developed for carbon relative to the DFT interaction energies obtained by Hashmi and Lein.[33] We then proceed to use to most reliable force field to study the stability and the interaction energies in a giant carbon onion with a C60 core (C60@C240@…@C4860@C6000).
Computational Methods
Carbon Force Fields
The first force field for carbon (Tersoff[42]) was developed in 1988 and modified the bond strengths according to the number of neighbours. It was fitted to experimental data such as lattice constant, binding energies, bulk modulus of diamond, and binding energy of graphite. The energies of carbon–carbon bond energies and simple cubic, body-centred cubic and face-centred cubic phases are fitted to DFT calculations. In 2013, to improve the description of making and breaking bonds, an environment-dependent screening function was added to the Tersoff force field, which is known as the Tersoff-S.[43]
The second generation of reactive empirical bond-ordered (REBO-II) force field,[44] an extended version of the Tersoff force field, was developed in 2002. REBO-II improves the description of short-range bonding by modifying the functional form. Its parameters are fitted to experimental data such as binding energies and lattice constants of graphite and diamond, and DFT data such as binding energies and lattice constants of simple cubic and face-centred cubic phases of carbon. In 2008, the description of the bond-making and breaking was improved by adding an environment-dependent screening function to the REBO-II force field (known as the REBO-II-S).[45]
In 2000, the adaptive intermolecular reactive empirical bond-order (AIREBO)[46] force field based on the REBO-II force field was developed, in which a Lennard-Jones term with a switching function is used to inactive the long-range terms at short distances. Another version of the AIREBO force field (named AIREBO-M) is derived by replacing the Lennard-Jones form with a Morse expression.[47] The long-range carbon bond-order potential (LCBOP-I),[48] which is generally similar to the AIREBO force field, was developed in 2003 to improve the accuracy and transferability of the model by complete reparameterization of the bond order force field.[49]
The reactive force field potential ReaxFF-15 was developed in 2015 and originally developed for hydrocarbon systems.[50] This force field was parametrized against a large dataset of DFT-D2 structures, including small fullerenes and different amorphous carbon phases. The original force field[51] was fitted to experimental data such as heats of formation and structural data for hydrocarbon compounds and crystals, and quantum chemical energy curves for bond dissociations. Recently, a reparametrization version of the ReaxFF force field[52] was developed (ReaxFF-20).[53] The force field parameters were optimized to adequately capture the flattened carbon nanotube structure and the corresponding energy values. Its parameters were trained against the PCFF-IFF force field data, which shows good agreement with DFT-D2 data.
In addition to empirical force fields, we use a machine-learning force field, which was developed recently based on the Gaussian approximation potential (GAP-20).[54] In this type of force field, kernel-based machine learning is employed instead of a classic empirical functional form and the force field is fitted to reference data computed using the optB88-vdW DFT method. In this context it should be noted that we have recently showed that the GAP-20 force field shows good performance in the prediction of the 1811 isomerization energy of C60 fullerenes.[55] Furthermore, Qian et al.[56] reported that this force field could more accurately predict the structure and formation energies for different carbon systems. They also showed that the GAP-20 is the most appropriate force field for studying thermal and mechanical properties of carbon materials.
Simulation Details
The initial fullerene geometries (C20, C60, C80, C180, C240 and C540) and the two/three shell carbon onion structures that we used in the first part of our study (i.e., C20@C60, C20@C80, C60@C180, C80@C240, C60@C240, C240@C540, C60@C240@C540, and C80@C240@C540) were taken from Hashmi and Lein.[33] The double- and triple-layered structures are shown in the right panel of Fig. 1. The initial geometries for the giant CN (N = 60 × n2 for 1 ≤ n ≤ 10) fullerenes were taken from Noël et al.[57] To generate the giant C60 core multi-shell onion structures, we followed the same procedure that used by Hashmi and Lein[37] and stacking the structures of the individual fullerenes, where each fullerene is aligned along its respective principal axes of inertia in all three possible orientations.

|

|
All calculations are performed with the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) package.[58] The geometry relaxation and the energy minimization were performed using the conjugate gradient scheme, and the convergence of energy and force are set to 1.0−6 eV and 1.0−8 eVÅ−1, respectively. The periodic boundary conditions were used in all three directions for all simulations. Note that to avoid the self-interaction of the fullerene and onion structures, we performed the simulations in a cubic box with a side length of 30 Å for double- and triple-layered onions and a 120 × 120 × 120 Å3 box for a giant onion structure. The visualizations are performed using the Open Visualization Tool (OVITO) software.[59] The interaction energy of the onion structures are calculated directly from the total energy of the carbon onion and the total energies of the inner structure(s) and outer fullerene which can be expressed as
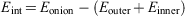
For example, for the C60@C240@C540 onion structure the interaction energy can be calculated as follows:
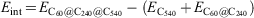
Results and Discussion
In the first part of our study we evaluate the performance of ten force field methods developed for carbon nanomaterials for the interaction energies between the layers of eight carbon onion structures. We compare the force field results with density functional theory (DFT) reference interaction energies obtained by Hashmi and Lein.[33] In particular, the DFT reference values were obtained at the RI-PBE0-D3/def2-TZVP//RI-PBE0-D3/def2-SVP level of theory. The calculated interaction energies (Eint) between the layers of the carbon onions for different force fields along with the DFT reference values are plotted in Fig. 1 and listed in Table 1. Before we discuss the force field results, we note that Hashmi and Lein[33] also obtained second-order Møller-Plesset perturbation theory (MP2) interaction energies for a subset of the smaller carbon onions and that the DFT interaction energies for C20 and C60 nested in larger fullerenes are in qualitative agreement with the MP2 interaction energies. Namely, the interaction energy decreases as the size of the carbon onion increases. We begin by examining the interaction energies of the double-layered carbon onion structures, C20@C60, C20@C80, C60@C180, C60@C240, C80@C240, C240@C540. As can be seen from Fig. 1, the general trends of most of the force fields results (except the Tersoff and REBO-II force fields) agree with the DFT trends.
For the smallest system, C20@C60, most force fields tend to significantly underestimate the repulsive interaction energy between the nested fullerenes calculated at the DFT level. The LCBOP-I (see Table 1) is the only force field which significantly overestimates the interaction energy by ~25 %. Interestingly, the GAP-20 force field is the only method that is able to reproduce the DFT interaction energy within 10 kcal mol−1. In particular, GAP-20 overestimates the DFT result by 9.3 kcal mol−1. The ReaxFF-20 force field is a close second, and underestimates the DFT result by 25.2 kcal mol−1. However, for the other force fields, i.e., Tersoff, Tersoff-S, REBO-II, REBO-II-S, AIREBO, AIREBO-M and ReaxFF-15, large underestimations are obtained (Table 1).
For the C20@C80 carbon onion, the ReaxFF-20 force field perfectly estimates the DFT interaction energy with a deviation of merely 2.8 kcal mol−1. Three force fields (i.e., Tersoff-S, AIREBO-M, and ReaxFF-15) result in reasonably good performance with deviations from the DFT interaction energies ranging between 17.7 (ReaxFF-15) and 29.7 kcal mol−1 (AIREBO-M); note that the deviations are given in absolute value. In contrast to the C20@C60 carbon onion for which the GAP-20 force field showed good performance, for the C20@C80 it results in a large deviation of 151.3 kcal mol−1. The remaining force fields show performance that is on par or worse than that of the GAP-20 force field. For the C20@C180 carbon onion, REBO-II-S force field reproduces the DFT interaction energy with a small deviation of 4.2 kcal mol−1. The second best force field is LCBOP-I which overestimates the DFT result by 19.1 kcal mol−1. In contrast to previous cases, the predicted interaction energy by the ReaxFF force fields are underestimated with the deviation of 76.7 (ReaxFF-15) and 60.8 kcal mol−1 (ReaxFF-20). In addition, similar to the C20@C80 carbon onion case, the GAP-20 force field results in a large deviation of 101.5 kcal mol−1.
Moving on to the C60@C240 carbon onion, the ReaxFF-20 force field shows the best performance with an estimated interaction energy which is 11.5 kcal mol−1 away from the DFT value. The AIREBO and ReaxFF-15 force fields are close seconds with deviation from the DFT result by 25.7 (AIREBO) and –33.6 kcal mol−1 (ReaxFF-15). The calculated Eint values of the other force fields are considerably overestimated. It should be pointed out that the interactions energy estimated by ReaxFF force fields not only agrees with the DFT calculation by Hashmi and Lein[33] but also agrees well with Stasyuk et al.[32] and Casella et al.[31] where they used different DFT functionals. Finally, we note, with the exception of the original Tersoff and REBO-II force fields, all the considered force fields show similar trends in the interaction energies to the DFT results.
The estimated interaction energy for the C80@C240 carbon onion by the ReaxFF-20 force field is close to the DFT results with a deviation of 5.3 kcal mol−1. GAP-20 is the second-best force field and underestimates the DFT result by 13.0 kcal mol−1. However, the other force fields show poor performance with large deviations ranging between 78.9 (LCBOP-I) and 144.2 kcal mol−1 (AIREBO).
The C60@C240 and C80@C240 carbon onions are the smallest systems characterized by attractive interactions between the inner and outer fullerenes at the DFT level, where the attractive interaction energy is larger in the C80@C240 carbon onion. The ReaxFF-20 force field is able to nicely capture these trends in interaction energies both qualitatively and quantitatively. The GAP-20, ReaxFF-15, and LCBOP-I force fields also result in attractive interaction energies; however, they are unable to capture their relative magnitudes.
Finally, for the largest double-layered carbon onion (C240@C540) the ReaxFF-15 force field shows good performance with a deviation of just 12.6 kcal mol−1 from the DFT Eint value. However, the other force fields tend to severely underestimate the interaction energies.
Now we examine the interaction energies of triple-layered C60@C240@C540 and C80@C240@C540 carbon onions. As can be seen from Fig. 1, these interaction energies pose a challenging target for all the force fields. The best performing force field is the ReaxFF-15 force field with deviations of over 100 kcal mol−1 from the DFT interaction energies, whilst the other force fields result in significantly larger deviations (Table 1). Nevertheless, with few exceptions (e.g. Tersoff, REBO-II, REBO-II-S, and GAP-20) the considered force fields predict considerable attractive interactions for both triple-layered carbon onions. We note that the surprising and notable deterioration in performance of the GAP-20 force field when moving from the double-layered carbon onions to the triple-layered and the giant C240@C540 carbon onions may be attributed to the fact that the machine-learning training set included much smaller fullerenes.
Overall, the above results show that the new generation of the ReaxFF force field (ReaxFF-20) is the best force field for the double-layered carbon onions, with the older version (ReaxFF-15) being a close second-best performer (with a notable exception for the C80@C240 carbon onion). Whilst for the triple-layered carbon onions the ReaxFF-15 emerges as the best performing force field. However, the other force fields can at best predict qualitative trends in the DFT interaction energies of the carbon onions. Based on these results we choose the ReaxFF-15 force field to investigate the interaction energies involved in a giant C60 core multi-shell onion structure. In order to produce a multi-layered onion structures we are using an sequence of
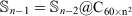
where n is the number of layers and is equal and greater than 3 (n ≥ 3), and  . For example, a fourth-layered onion structure is
. For example, a fourth-layered onion structure is  , where
, where  ; hence,
; hence,  . Table 2 contains the nine multi-layered onion structures, number of carbon atoms and calculated interaction energy for each structures.
. Table 2 contains the nine multi-layered onion structures, number of carbon atoms and calculated interaction energy for each structures.

|
Fig. 2a illustrates the cross-sectional view (1 nm slice) of the giant C60 core ten-layered ‘rainbow’ carbon onion structure that we investigate in this part of our study. Each colour represents different fullerene, and the red core structure is C60 fullerene, and the violent outer layers is C6000 fullerene. Fig. 2b shows the experimental evidence of giant carbon onion produced by electron irradiation of a polyhedral particle at a high temperature (700°C). This panel is reprinted with permission from Banhart and Ajayan.[60] During the past few decades, advancing the technology to synthesise a giant multi-layered carbon onion simulating these materials is an important area of computational nanotechnology. In this regard, in this part of our study, we investigate the interaction energy of the proposed giant multi-layered carbon onion.

|
Table 2 gives the interaction energies for all the nine multi-layered onion structures, which are calculated using the ReaxFF-15 force field. The results for all nine multi-layered carbon onions reveal that the interaction energy increases rapidly with the number of layers and subsequent size of the onion structure. For example, the interaction energy for the three-layered C60@C240@C540 onion amounts to –516.5 kcal mol−1 and it increaces up to –8117.3 kcal mol−1 for the largest carbon onion with 10 nested fullerenes. Inspection of Table 2 reveals that the increase in interaction energy with each consecutive shell (i.e.,  ) correlates linearly with the number of shells and following size of the multi-layered structure (with a squared correlation coefficient of R2 = 0.9996). This linear correlation is illustrated in Fig. 3. This linear increase in the stabilization energy with each consecutive layer may have important thermodynamic consequences for describing the formation and growth of large carbon onions.
) correlates linearly with the number of shells and following size of the multi-layered structure (with a squared correlation coefficient of R2 = 0.9996). This linear correlation is illustrated in Fig. 3. This linear increase in the stabilization energy with each consecutive layer may have important thermodynamic consequences for describing the formation and growth of large carbon onions.

|
Conclusion
We evaluate the performance of ten well-known carbon force fields for the interaction energy of six different double-layered carbon onions (C20@C60, C20@C80, C60@C180, C80@C240, C60@C240 and C240@C540) and two triple-layered onions (C60@C240@C540 and C80@C240@C540). The reference interaction energy values have been obtained at the PBE0-D3/def2-TZVP level of theory. The ReaxFF-20 force field provides the best overall performance for the double-layered carbon onions, whilst the ReaxFF-15 force field provides the best overall performance for the triple-layered carbon onions. Interestingly, both force fields outperform the recently developed carbon machine-learning force field (GAP-20) for both double- and triple-layered carbon onions. We proceed to use the ReaxFF-15 force field to explore the interaction energies in a giant ten-layered carbon onion with a C60 core and show that the interaction energy between the outer layer and the inner layers increases linearly with the number of layers in the carbon onion (with a squared correlation coefficient of R2 = 0.9996). This linear increase in the stabilization energy with each consecutive layer may have important thermodynamic consequences for describing the formation and growth of large carbon onions.
Supplementary Material
ReaxFF-15 optimized geometries for the double-layered, triple-layered, and giant carbon onions considered in the present work are available on the Journal’s website.
Data Availability Statement
The data that support this study are available in the article and accompanying online supplementary material.
Conflicts of Interest
Amir Karton is an Associate Editor of the Australian Journal of Chemistry but was blinded from the peer-review process for this paper.
Declaration of Funding
This research was funded by the Australian Research Council (Project no. FT170100373).
Acknowledgements
We gratefully acknowledge the generous allocation of computing time from the National Computational Infrastructure (NCI) National Facility, and system administration support provided by the Faculty of Science at UWA to the Linux cluster of the Karton group. AK is the recipient of an Australian Research Council (ARC) Future Fellowship (Project No. FT170100373).
References
[1] S. Iijima, J. Cryst. Growth 1980, 50, 675.| Crossref | GoogleScholarGoogle Scholar |
[2] Y. V. Butenko, L. Siller, M. R. C. Hunt, in Handbook of Nanophysics: Clusters and Fullerenes (Ed. K. D. Sattler) 2010, pp. 10–15 (CRC Press: Boca Raton, FL.)
[3] A. Krüger, Carbon Materials and Nanotechnology 2010 (Wiley: Hoboken, NJ.)
[4] Y. Wang, J. H. Zhao, S. F. Yu, R. S. Ran, H. S. Huai, K. K. Ostrikov, Y. Y. Hui, Carbon 2013, 64, 230.
| Crossref | GoogleScholarGoogle Scholar |
[5] W. Tian, H. Hu, Y. Wang, P. Li, J. Liu, J. Liu, X. Wang, X. Xu, Z. Li, Q. Zhao,
| Crossref | GoogleScholarGoogle Scholar | 29425027PubMed |
[6] E. G. Bushueva, P. S. Galkin, A. V. Okotrub, L. G. Bulusheva, N. N. Gavrilov, V. L. Kuznetsov, S. I. Moiseekov, Phys. Status Solidi, B Basic Res 2008, 245, 2296.
| Crossref | GoogleScholarGoogle Scholar |
[7] J. K. McDonough, A. I. Frolov, V. Presser, J. Niu, C. H. Miller, T. Ubieto, M. V. Fedorov, Y. Gogotsi, Carbon 2012, 50, 3298.
| Crossref | GoogleScholarGoogle Scholar |
[8] M. Ghosh, S. K. Sonkar, M. Saxena, S. Sarkar, Small 2011, 7, 3170.
| Crossref | GoogleScholarGoogle Scholar | 22012886PubMed |
[9] S. Giordani, J. Bartelmess, M. Frasconi, I. Biondi, S. Cheung, M. Grossi, D. Wu, L. Echegoyen, D. F. O’Shea, J. Mater. Chem. B Mater. Biol. Med 2014, 2, 7459.
| Crossref | GoogleScholarGoogle Scholar | 32261971PubMed |
[10] M. Zeiger, N. Jäckel, V. N. Mochalin, V. Presser, J. Mater. Chem. A Mater. Energy Sustain 2016, 4, 3172.
| Crossref | GoogleScholarGoogle Scholar |
[11] V. Georgakilas, J. A. Perman, J. Tucek, R. Zboril, Chem. Rev. 2015, 115, 4744.
| Crossref | GoogleScholarGoogle Scholar | 26012488PubMed |
[12] D. Ugarte, Nature 1992, 359, 707.
| Crossref | GoogleScholarGoogle Scholar | 11536508PubMed |
[13] B. S. Xu, S.-i. Tanaka, Nanostruct. Mater. 1995, 6, 727.
| Crossref | GoogleScholarGoogle Scholar |
[14] H. E. Troiani, A. Camacho-Bragado, V. Armendariz, J. L. Gardea Torresday, M. J. Yacaman, Chem. Mater. 2003, 15, 1029.
| Crossref | GoogleScholarGoogle Scholar |
[15] T. Gorelik, S. Urban, F. Falk, U. Kaiser, U. Glatzel, Chem. Phys. Lett. 2003, 373, 642.
| Crossref | GoogleScholarGoogle Scholar |
[16] V. L. Kuznetsov, A. L. Chuvilin, Y. V. Butenko, I. Y. Mal’kov, V. M. Titov, Chem. Phys. Lett. 1994, 222, 343.
| Crossref | GoogleScholarGoogle Scholar |
[17] V. L. Kuznetsov, A. L. Chuvilin, E. M. Moroz, V. N. Kolomiichuk, S. K. Shaikhutdinov, Y. V. Butenko, I. Y. Mal’kov, Carbon 1994, 32, 873.
| Crossref | GoogleScholarGoogle Scholar |
[18] S. Tomita, A. Burian, J. C. Dore, D. LeBolloch, M. Fujii, S. Hayashi, Carbon 2002, 40, 1469.
| Crossref | GoogleScholarGoogle Scholar |
[19] Z. Qiao, J. Li, N. Zhao, C. Shi, P. Nash, Scr. Mater. 2006, 54, 225.
| Crossref | GoogleScholarGoogle Scholar |
[20] L. G. Bulusheva, A. V. Okotrub, V. L. Kuznetsov, D. V. Vyalikh, Diamond Relat. Mater. 2007, 16, 1222.
| Crossref | GoogleScholarGoogle Scholar |
[21] J. Xiao, G. Ouyang, P. Liu, C. X. Wang, G. W. Yang, Nano Lett 2014, 14, 3645.
| Crossref | GoogleScholarGoogle Scholar | 24823241PubMed |
[22] T. Cabioc’h, J. C. Girard, M. Jaouen, M. F. Denanot, G. Hug, Europhys. Lett. 1997, 38, 471.
| Crossref | GoogleScholarGoogle Scholar |
[23] E. Thune, T. Cabioc’h, M. Jaouen, F. Bodart, Phys. Rev. B 2003, 68, 115434.
| Crossref | GoogleScholarGoogle Scholar |
[24] C. He, N. Zhao, in Handbook of Nanophysics: Clusters and Fullerenes (Ed. K. D. Sattler) 2010, pp. 1–22 (CRC Press: Boca Raton, FL.)
[25] A. De Vita, G. Galli, A. Canning, R. Car, Appl. Surf. Sci. 1996, 104–105, 297.
| Crossref | GoogleScholarGoogle Scholar |
[26] G. Kern, J. Hafner, Phys. Rev. B 1998, 58, 13167.
| Crossref | GoogleScholarGoogle Scholar |
[27] C.-Z. Wang, K. M. Ho, M. D. Shirk, P. A. Molian, Phys. Rev. Lett. 2000, 85, 4092.
| Crossref | GoogleScholarGoogle Scholar | 11056632PubMed |
[28] F. Fugaciu, H. Hermann, G. Seifert, Phys. Rev. B 1999, 60, 10711.
| Crossref | GoogleScholarGoogle Scholar |
[29] G.-D. Lee, C. Z. Wang, J. Yu, E. Yoon, K. M. Ho, Phys. Rev. Lett. 2003, 91, 265701.
| Crossref | GoogleScholarGoogle Scholar | 14754068PubMed |
[30] S. Grimme, C. Mück-Lichtenfeld, J. Antony, J. Phys. Chem. C 2007, 111, 11199.
| Crossref | GoogleScholarGoogle Scholar |
[31] G. Casella, A. Bagno, G. Saielli, Phys. Chem. Chem. Phys. 2013, 15, 18030.
| Crossref | GoogleScholarGoogle Scholar | 24061574PubMed |
[32] A. J. Stasyuk, O. A. Stasyuk, M. Solà, A. A. Voityuk, J. Phys. Chem. C 2019, 123, 16525.
| Crossref | GoogleScholarGoogle Scholar |
[33] M. A. Hashmi, M. Lein, J. Phys. Chem. C 2018, 122, 2422.
| Crossref | GoogleScholarGoogle Scholar |
[34] J. H. Los, N. Pineau, G. Chevrot, G. Vignoles, J.-M. Leyssale, Phys. Rev. B 2009, 80, 155420.
| Crossref | GoogleScholarGoogle Scholar |
[35] P. Ganesh, P. R. C. Kent, V. Mochalin, J. Appl. Phys. 2011, 110, 073506.
| Crossref | GoogleScholarGoogle Scholar |
[36] J. M. Leyssale, G. L. Vignoles, Chem. Phys. Lett. 2008, 454, 299.
| Crossref | GoogleScholarGoogle Scholar |
[37] D. W. M. Lau, D. G. McCulloch, N. A. Marks, N. R. Madsen, A. V. Rode, Phys. Rev. B 2007, 75, 233408.
| Crossref | GoogleScholarGoogle Scholar |
[38] A. Bródka, T. W. Zerda, A. Burian, Diamond Relat. Mater. 2006, 15, 1818.
| Crossref | GoogleScholarGoogle Scholar |
[39] A. Bródka, A. Burian, S. Tomita, V. Honkimäki, J. Mol. Struct. 2008, 887, 34.
| Crossref | GoogleScholarGoogle Scholar |
[40] J. L. Fogg, A. Aghajamali, J. A. Hinks, S. E. Donnelly, A. A. Shiryaev, N. A. Marks, Nucl. Instrum. Methods Phys. Res., Sect. B 2019, 453, 32.
| Crossref | GoogleScholarGoogle Scholar |
[41] A. Aghajamali, A. A. Shiryaev, N. A. Marks, Astrophys. J. 2021, 916, 85.
| Crossref | GoogleScholarGoogle Scholar |
[42] J. Tersoff, Phys. Rev. Lett. 1988, 61, 2879.
| Crossref | GoogleScholarGoogle Scholar | 10039251PubMed |
[43] L. Pastewka, A. Klemenz, P. Gumbsch, M. Moseler, Phys. Rev. B 2013, 87, 205410.
| Crossref | GoogleScholarGoogle Scholar |
[44] D. W. Brenner, O. A. Shenderova, J. A. Harrison, S. J. Stuart, B. Ni, S. B. Sinnott, J. Phys. Condens. Matter 2002, 14, 783.
| Crossref | GoogleScholarGoogle Scholar |
[45] L. Pastewka, P. Pou, R. Pérez, P. Gumbsch, M. Moseler, Phys. Rev. B 2008, 78, 161402.
| Crossref | GoogleScholarGoogle Scholar |
[46] S. J. Stuart, A. B. Tutein, J. A. Harrison, J. Chem. Phys. 2000, 112, 6472.
| Crossref | GoogleScholarGoogle Scholar |
[47] T. C. O’Connor, J. Andzelm, M. O. Robbins, J. Chem. Phys. 2015, 142, 024903.
| Crossref | GoogleScholarGoogle Scholar | 25591383PubMed |
[48] J. H. Los, L. M. Ghiringhelli, E. J. Meijer, A. Fasolino, Phys. Rev. B 2005, 72, 214102.
| Crossref | GoogleScholarGoogle Scholar |
[49] D. W. Brenner, Phys. Rev. B 1990, 42, 9458.
| Crossref | GoogleScholarGoogle Scholar |
[50] S. G. Srinivasan, A. C. T. van Duin, P. Ganesh, J. Phys. Chem. A 2015, 119, 571.
| Crossref | GoogleScholarGoogle Scholar | 25562718PubMed |
[51] A. C. T. van Duin, S. Dasgupta, F. Lorant, W. A. Goddard, J. Phys. Chem. A 2001, 105, 9396.
| Crossref | GoogleScholarGoogle Scholar |
[52] C. Ashraf, A. C. T. van Duin, J. Phys. Chem. A 2017, 121, 1051.
| Crossref | GoogleScholarGoogle Scholar | 28072539PubMed |
[53] B. Damirchi, M. Radue, K. Kanhaiya, H. Heinz, G. M. Odegard, A. C. T. van Duin, J. Phys. Chem. C 2020, 124, 20488.
| Crossref | GoogleScholarGoogle Scholar |
[54] P. Rowe, V. L. Deringer, P. Gasparotto, G. Csányi, A. Michaelides, J. Chem. Phys. 2020, 153, 034702.
| Crossref | GoogleScholarGoogle Scholar | 32716159PubMed |
[55] A. Aghajamali, A. Karton, Chem. Phys. Lett. 2021, 779, 138853.
| Crossref | GoogleScholarGoogle Scholar |
[56] C. Qian, B. McLean, D. Hedman, F. Ding, APL Mater. 2021, 9, 061102.
| Crossref | GoogleScholarGoogle Scholar |
[57] Y. Noël, M. De La Pierre, C. M. Zicovich-Wilson, R. Orlando, R. Dovesi, Phys. Chem. Chem. Phys. 2014, 16, 13390.
| Crossref | GoogleScholarGoogle Scholar | 24879509PubMed |
[58] S. Plimpton, J. Comput. Phys. 1995, 117, 1.
| Crossref | GoogleScholarGoogle Scholar |
[59] A. Stukowski, Model. Simul. Mater. Sci. Eng. 2010, 18, 015012.
| Crossref | GoogleScholarGoogle Scholar |
[60] F. Banhart, P. M. Ajayan, Adv. Mater. 1997, 9, 261.
| Crossref | GoogleScholarGoogle Scholar |


