The effect of fuel bed structure on Rothermel model performance
Zakary Campbell-Lochrie A * , Michael Gallagher B , Nicholas Skowronski C and Rory M. Hadden A
A * , Michael Gallagher B , Nicholas Skowronski C and Rory M. Hadden A
A School of Engineering, The University of Edinburgh, Edinburgh, UK.
B Northern Research Station, USDA Forest Service, New Lisbon, NJ, USA.
C Northern Research Station, USDA Forest Service, Morgantown, WV, USA.
Abstract
Fifty years after its initial publication, Rothermel’s model continues to underpin many operational fire modelling tools. Past authors have, however, suggested a possible oversensitivity of the Rothermel model to fuel depth in certain fuel types.
To evaluate Rothermel model performance based on previous observations of the effect of fuel structure on flame spread through porous fuel beds. This is informed by the consideration of the effect of fuel structure on the physical mechanisms underpinning surface flame spread.
This study uses an existing dataset of flame spread experiments in pine needle beds to evaluate the effect of fuel structure on Rothermel model predictions of spread rate and reaction intensity.
Underpredictions of spread rate occurred for compressed fuel beds, apparently driven by an underprediction of the reaction intensity.
A greater understanding of the role of fuel structure on the energy release within the fire front region is therefore required.
The current tendency for spread rate to be underestimated in the studied fuel beds in quiescent (no wind or slope) conditions requires further consideration given the widespread use of Rothermel’s model in current operational modelling tools.
Keywords: energy release, fire behaviour, fire intensity, flame spread, fuel loading, fuel structure, modelling, operational fire models, pine needle beds, reaction intensity, Rothermel.
Introduction
Fifty years after its introduction, Rothermel’s semi-empirical flame spread model (Rothermel 1972) continues to underpin many current fire modelling systems, particularly in the USA (e.g. BehavePlus (Andrews 2014), FlamMap (Finney 2006)). Present-day implementations of this surface flame spread model typically differ little from Rothermel’s original mathematical formulations except for the inclusion of a small number of modifications suggested by Albini shortly after the model’s introduction (Albini 1976) (and more recently, a recommendation that the original upper limit on wind speed influences on spread rate should not be imposed (Andrews et al. 2013)).
There are ongoing efforts throughout the wildfire research community to develop new and improved fire models. In a recent Position Statement on Climate Change (International Association of Wildland Fire 2022), the International Association of Wildland Fire (IAWF) called for further research to develop and improve modelling tools to support efforts to address the challenges and effects of climate change on wildland fires. Changes in fire management strategies, focusing on increasing prescribed burning, drive a need for improved fire behaviour models to aid in planning, training and strategy development (Hiers et al. 2020; Sample et al. 2022).
However, presently, ‘the Rothermel surface fire spread model continues to be the foundation of many research and management applications’ (Andrews 2018, p. iii). Therefore, in this intervening period, it is important that model limitations, and where possible their root causes, are identified given the potential influence of model predictions on fire and fuels management strategies. Understanding limitations in the development approach for previous operational models is particularly pressing given ongoing efforts to develop and deploy new physics-based operational models (Finney et al. 2021).
It is therefore important to understand the implications of using a model developed using a small number of fuel types to predict the effect of fuel structure on the rate of spread across a range of natural fuel types. In this study, the performance of the Rothermel model across a range of (pine needle) fuel bed structural conditions was investigated through comparison with an existing experimental dataset (Campbell-Lochrie et al. 2021).
Rothermel model sensitivity and limitations
Past evaluation of the Rothermel model has typically involved sensitivity analysis (e.g. Dell’Orfano 1996; Salvador et al. 2001; Ujjwal et al. 2021) and/or model testing and validation with fire behaviour observations from a laboratory or field environment (e.g. Barney et al. 1978; Norum 1982; Van Wagtendonk and Botti 1984; Van Wilgen et al. 1985; Van Wilgen and Wills 1988; McAlpine and Xanthopoulos 1989; Gould 1991; Masters and Engle 1994; Marsden-Smedley and Catchpole 1995; Dell’Orfano 1996; Grabner et al. 1997; Hély et al. 2001; Fernandes et al. 2002; Streeks et al. 2005; Cruz and Fernandes 2008; Athanasiou and Xanthopoulos 2010; Weise et al. 2016), with several earlier validation studies summarised in Andrews (1980) as cited in Rothermel (1983).
Fuel bed depth has been identified as one of the highest-sensitivity model parameters in several previous studies (e.g. Dell’Orfano 1996; Salvador et al. 2001; Bachmann and Allgöwer 2002). As described by Saltelli (2000), sensitivity analysis of a mathematical model not only allows the determination of ‘the factors that mostly contribute to the output variability and that require additional research to strengthen the knowledge base’ but also allows determination of whether ‘a model resembles the system or processes under study’.
There are suggestions within the existing literature that the high sensitivity of the Rothermel model to fuel depth may not accurately reflect existing fire behaviour observations and that model bias may exist because of inaccurate representation of the effects of fuel depth. However, the difficulty in characterising fuel depth, particularly in heterogeneous fuels should also be considered (Hough and Albini 1978). For example, Catchpole et al. stated that ‘in recent (as yet unpublished) experiments we have found that the Rothermel model is overly sensitive to fuel depth’ (Catchpole et al. 1993, p. 53), with additional detail subsequently provided in a later publication (Catchpole et al. 1998). Similarly, in a previous field comparison (Dell’Orfano 1996), overpredictions of spread rates were observed in Northeastern US pine-oak forests during winter fires, which was attributed to the sensitivity of BEHAVE (underpinned by the Rothermel model) to fuel bed depth and surface-to-volume ratio of 1 h fuels (corresponding to size class of <6.35 mm diameter) (overpredictions for summer fires were attributed to the model’s inability to accurately incorporate the effect of high live Fuel Moisture Contents (FMCs)).
An oversensitivity of the Rothermel model to fuel depth was also observed (Gould 1991) in comparison with observed spread rates in grassland fire experiments. Underpredictions of spread rate occurred for fuel depths less than 0.15 m but overpredictions occurred at fuel depths greater than 0.25 m. An oversensitivity to bulk density was also observed. Neither the experimentally observed nor predicted spread rates were significantly affected by the fuel loading.
In a series of field experiments (Brown 1972) (involving two fuel loadings with three different fuel depths at each loading), greater deviations were observed between predicted and observed spread rates at lower packing ratios and fuel loadings. However, the slash fuel beds in Brown’s study were highly discontinuous (large spacing between fuel elements) and flaming was observed to be sporadic for the lower fuel loading cases.
The above examples provide motivation for further investigation of the causes of model bias. Missing from many of the existing studies is the opportunity for systematic evaluation of the model performance as a function of the fuel depth. A detailed evaluation of model performance therefore requires an understanding of the interdependent effects of fuel structure parameters on the flame spread process and on model predictions.
Effects of fuel bed structure on flame spread
For a fuel bed of fixed area, the packing ratio can be altered by varying either the fuel loading or the fuel height of the fuel bed. A fuel bed of fixed fuel loading can be compressed, thereby lowering the fuel depth and increasing the packing ratio or bulk density. Alternatively, a constant packing ratio or bulk density can be maintained while the fuel loading is altered, therefore also altering the fuel depth.
The interdependent interactions of these three parameters must therefore be considered. For example, it was previously noted (Catchpole et al. 1998) that the effect of fuel loading depends on the manner in which it is altered. Catchpole et al. observed only a slight effect on spread rate when fuel depth was increased at a constant packing ratio (addition of fuel) but a reduction in spread rate when packing ratio was increased at a constant fuel depth (fuel added and compacted).
Accurate modelling of the fire behaviour as a function of the fuel structure therefore requires a greater appreciation of the physical processes responsible for variations in fire behaviour. Varying the fuel loading alters the total amount of available combustible fuel. Varying the packing ratio alters the separation distance and pore geometry between neighbouring fuel particles, thereby altering both the flow dynamics (and hence convective heat transfer and oxygen supply) and radiative heat transfer through a porous fuel bed.
Different relationships between fuel depth and spread rate have been observed in past studies. Wilson observed a positive correlation between spread rate and the square root of the fuel depth (Wilson 1990). However, in pine needle fuel beds, Anderson (Anderson 1964) observed spread rate to be independent of fuel depth for fuel beds greater than 0.0762 m in depth (with a positive relationship observed below this depth threshold). This matched previous observations from an extensive series of crib fire experiments conducted by earlier researchers at the US Forest Service during the Project Fire Model study (Byram et al. 1966). Catchpole and colleagues (including Rothermel) (Catchpole et al. 1998) have therefore outlined the need to test, over a wider range of fuel depths, the assumption within the Rothermel model that spread rate is dependent on (and proportional to) fuel depth. This is particularly important for horizontal fuel beds (e.g. litter layer) in which the fuel depth increases much less rapidly with fuel loading than in vertically oriented fuel beds such as grasses and brush. As a result, the typical range of fuel depths observed in horizontal fuel beds such as pine needle litter layers is often below the 0.0762 m threshold observed by Anderson.
Incorporation of fuel structure effects in the Rothermel model
Rothermel’s model is based on the principle of energy conservation, with the steady-state rate of spread (R) described by the ratio between the energy transferred to the unburnt fuel and the energy required for ignition. For homogeneous fuel beds, R is calculated according to Eqn 1,
As previously described (Rothermel 1972), IR is the reaction intensity, ξ is the propagating flux ratio, ϕw and ϕs are the wind and slope correction factors respectively, ρb is the oven-dry bulk density, ∈ is the effective heating number, and Qig is the heat of pre-ignition. The fuel bed structure (fuel loading, packing ratio, bulk density) affects both the numerator (energy transferred to unburnt fuel) and denominator (heat sink term).
In quiescent conditions, the energy transferred to the unburnt fuel is simply the product of the reaction intensity (IR) and the propagating flux ratio (ξ), where, as illustrated in Fig. 1, the reaction intensity describes the overall heat energy released per unit area of the fire front (in any direction) and the propagating flux describes the proportion of this energy that is actually transferred to the unburnt fuel ahead of the flame front (which ultimately sustains flame spread). The influence of wind speed and fuel bed slope can then be accounted for by inclusion of empirical coefficients (Rothermel 1972); however, these are not described in further detail here because the present study is concerned with quiescent flame spread. Both the reaction intensity and the propagating flux ratio are dependent on the fuel bed structure as described below.
Illustration of the conceptual flame spread theory underpinning the Rothermel model, for a fuel bed of depth δ and flame front depth D, with x = 0 at the leading edge of the combustion region.
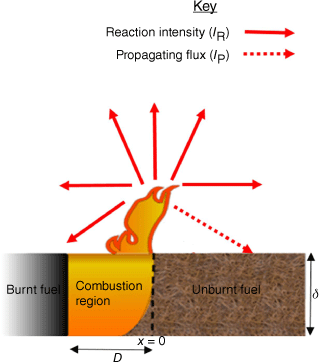
The reaction intensity (IR) is defined by Eqn 2,
where r′ is the optimum reaction velocity, wn is the net fuel loading, h is the low heat content, ηM is the moisture damping coefficient, and ηs is the mineral damping coefficient.
The reaction intensity, therefore, varies directly with the net fuel loading (and hence, if total mineral content is constant, with the oven-dry fuel loading). However, the fuel bed structure also affects the value of other parameters in the above equation. The optimum reaction velocity (r′) is a function of the packing ratio (β), and also the maximum reaction velocity , optimum packing ratio (βop) and an arbitrary variable A, as shown in Eqn 3. The latter three parameters are all functions only of the surface-to-volume ratio of the fuel elements (σ),
The optimum packing ratio attempts to describe ‘an optimum arrangement of fuel that will produce the best balance of air, fuel, and heat transfer for both maximum fire intensity and reaction velocity’ (Rothermel 1972, p. 13). The maximum reaction intensity is therefore obtained at the optimum packing ratio, i.e. .
The propagating flux ratio describes the proportion of the overall energy released in the flame front (reaction intensity) that is actually transferred to the unburnt fuel in the absence of wind or slope. The propagating flux ratio can range from zero (no transfer of heat to unburnt fuel) to one (all of heat produced in flame front transferred to unburnt fuel); however, it has been suggested that values ranging from 0.01 to 0.2 are typical (Burgan and Rothermel 1984).
Rothermel determined an empirical expression (shown in Eqn 4) for the propagating flux ratio (ξ), as a function of packing ratio (β) and surface-to-volume ratio (σ), from experimental data obtained using three fuel types (12.7 mm sticks, 6.35 mm sticks, excelsior),
The propagating flux ratio therefore varies positively with surface-to-volume ratio and packing ratio and tends towards zero as each of these parameters decreases. The effect of increased surface-to-volume ratio is greater at higher packing ratios and vice versa (Burgan and Rothermel 1984).
The heat sink term describes the energy required for ignition of the fuel. As such, if the energy transferred to the fuel remains constant, then the spread rate will vary negatively with the heat sink magnitude. The overall heat sink term is the product of the bulk density (ρb), effective heating number (∈) and heat of pre-ignition (Qig). Therefore, the magnitude of the heat sink term clearly varies positively with bulk density. The fuel bed structure does not affect the other terms but the effect of fuel element structure is incorporated within the effective heating number.
The effective heating number describes the actual proportion of a fuel element that is heated to the ignition temperature prior to the onset of flaming combustion (Burgan and Rothermel 1984; Andrews 2018). Therefore, an effective heating number of one describes a thermally thin fuel in which the entire fuel element is heated uniformly to the ignition temperature. Within the Rothermel model, the effective heating number is a function only of the surface-to-volume ratio, as shown in Eqn 5,
Rothermel defined the above equation based on a curve-fit of earlier experimental data (Frandsen 1973). However, Frandsen acknowledged that several possible curves could be fitted to the experimental data given the small number of conditions studied. This simple analysis also assumes that the effect of the thermal diffusivity of fuel elements and any moisture gradient can be considered negligible (Frandsen 1973).
The heat of pre-ignition describes the heat energy required for ignition per unit mass of fuel. An analytically determined term for cellulose was used during model development (Rothermel 1972) in which heat of pre-ignition is a function of moisture content only (with heat of pre-ignition varying positively with fuel moisture because the energy required for vaporisation increases).
This study utilised existing observations for pine needle litter beds (a typical surface fuel layer) from a previous experimental study (Campbell-Lochrie et al. 2021) in which the effects of fuel bed structure (fuel depth, fuel loading, bulk density) were evaluated in a series of laboratory-based, quiescent flame spread experiments. The fuel conditions studied represent typical field conditions for fuel loading and fuel depth for Pinus rigida Mill. litter layers in the New Jersey Pinelands National Reserve, based on available data from previous studies (e.g. Gallagher et al. 2017; Mueller et al. 2017). This dataset is particularly relevant as similar fuel bed constructions, composed of Pinus rigida needles, have been used in a number of recent studies into flame spread mechanisms and various modelling approaches (e.g. El Houssami et al. 2016; Mueller et al. 2021).
A comparison of predicted and observed spread rates across a range of fuel bed structural conditions was therefore possible allowing comparison of the predicted and actual sensitivity to the fuel structure terms of interest. However, the main aim was to identify possible physical phenomena that are insufficiently or inadequately incorporated within the semi-empirical Rothermel model and that may contribute to any model bias.
Calorimetric measurements from the flame spread experiments also allowed comparison of predicted and observed total energy release. The total energy release is an important consideration when evaluating fire behaviour and is one of three key components in the Rothermel model flame spread equation in quiescent conditions. In turn, the fuel loading and packing ratio affect the calculation of the energy release within the Rothermel model and are generally known to influence fire behaviour. In summary, the present study therefore attempts to compare and rectify existing experimental observations, our limited porous flame spread theory and the methods by which fuel structure is included within Rothermel model predictions.
Methods
A systematic experimental study of the effect of fuel bed structure on flame spread through pine needle fuel beds was previously presented in Campbell-Lochrie et al. (2021). These laboratory-based experiments were conducted in quiescent conditions (no wind or slope). The experimental series incorporated fuel beds of various fuel loadings, bulk densities and fuel bed depths. These pine needle beds are representative of typical litter layer fuels in several pine-dominated ecosystems and fall within the original intended application of the Rothermel model for largely homogeneous surface fuels contiguous to the ground. To explore the dependence on fuel depth, the performance of the Rothermel model was evaluated through comparison with observed spread rates from this experimental series.
Existing experimental dataset
Pine needle fuel beds were constructed on a flame spread table (1.5 by 0.67 m) with a vermiculite substrate and adjustable steel sidewalls. The fuel bed structure was varied by either altering the wet fuel loading (0.2–1.6 kg/m2) at a fixed fuel bed height (allowing bulk density to vary; 10–40 kg/m3) or by simultaneously varying fuel loading (0.2–1.6 kg/m2) and fuel depth (0.01–0.08 m) for a fixed bulk density.
The pine needles were dead pitch pine (Pinus rigida Mill.) or pitch-loblolly hybrid (Pinus rigida x taeda) needles collected from the Silas Little Experimental Forest in the New Jersey Pinelands National Reserve (latitude 39°54′58″N, longitude74°35′55″W). Needles were air-dried in a storage room prior to use and fuel moisture samples were collected prior to ignition of each fuel bed and oven-dried at 60°C for 24 h. The fuel properties for each pine needle species are summarised in Table 1. The fairly constant surface-to-volume ratio throughout the experimental series allows a focus on the effects of overall fuel bed structure on model performance.
| Species | Needle diametre (mm) (±s.d.) | High heat of combustion (kJ/kg) (±max./min.) | Surface-to-volume ratio (m−1) (±s.d.) | Density (kg/m3) (±s.d.) | |
|---|---|---|---|---|---|
| Pitch pine | 1.31 ± 0.15 | 19 669 ± 422 | 5063 ± 640 | 706 ± 71 | |
| Pitch-loblolly pine | 1.34 ± 0.12 | 19 672 ± 346 | 4899 ± 446 | 725 ± 33 |
The spread rate was calculated by video analysis of the flame front position over time. The combustion products were collected by a 1 MW furniture calorimeter exhaust hood and the Heat Release Rate (HRR) was calculated using oxygen consumption calorimetry, as in similar previous studies (Morandini et al. 2013). Fire intensity (as originally defined by Byram as ‘the rate of energy release, or rate of heat release, per unit time per unit length of fire front’ (Byram 1959, p. 79)) was calculated by dividing the HRR by the fire front length (0.67 m except at the lowest fuel loading of 0.2 kg/m2 where a non-linear flame front was observed). Additional experimental details and fuel properties were previously provided (Campbell-Lochrie et al. 2021).
Model implementation
In the present study, Rothermel’s original mathematical model (Rothermel 1972) was used with the later Albini modifications (Albini 1976) incorporated, and conversion to SI units using updated constants in Wilson (1980) (accounting for the listed errata added to the latter report and which are also discussed in Andrews (2018)). The mathematical flame spread model was incorporated within a MATLAB code and this implementation was verified through comparison with the SURFACE module of the BehavePlus fire modelling system (Version 6) (Andrews 2014).
The fuel beds considered in this study were homogeneous beds of dead pine needles and therefore some of Albini’s modifications (Albini 1976) (related to live fuel moisture of extinction or mixed fuel bed weighting factors) were not relevant. The modifications that were included are summarised in Table 2.
| Modified parameter | Original Rothermel | Albini modification | |
|---|---|---|---|
| Combustible dry fuel loading (W n) | |||
| Mineral damping coefficient (η s) | η s ≥ 0 | η s ≤ 1 | |
| Reaction velocity variable (A) | A = 133σ −0.7913 |
The modified combustible dry fuel loading parameter provides greater accuracy by reflecting the fact that the oven-dry fuel loading (wo) includes the mineral content. The inclusion of an upper limit of the mineral damping coefficient (ηs ≤ 1) prevents physically unrealistic estimates of ηs > 1 for effective mineral contents (Se) of less than 1.5 × 10−4. The alternative equation for the reaction velocity variable (A) prevents the occurrence of negative values for σ < 67.73, which would be physically unrealistic, as this would exceed the maximum reaction velocity.
Model inputs and assumptions
Various fuel and environmental properties are required as model inputs including six fuel properties (heat content (h), moisture content (Mf), total (ST) and effective (SE) mineral contents, fuel particle density (ρp) and surface-to-volume ratio (σ)), three fuel bed properties (oven-dry fuel loading (wo), fuel depth (δ) and moisture of extinction (Mx)), and two environmental parameters (mid-flame wind speed and slope angle (ϕ)).
In the present study, custom fuel models were defined for each fuel species and fuel bed condition, based on the actual measured fuel bed, and fuel element properties as summarised in Table 1. As the flame spread experiments considered in the present study were conducted in the absence of wind or slope, the mid-flame wind speed and angle were both assumed to equal zero. The other model inputs are summarised in Table 3 and important assumptions are discussed below.
| Parameter | Assumed value | |
|---|---|---|
| Heat content (h) | 18 608 kJ/kg | |
| Moisture content (Mf) | Measured for each fuel bed | |
| Total mineral content (ST) | 0.0555 | |
| Effective mineral content (SE) | 0.010 | |
| Fuel particle density (ρp) | Pitch pine: 706 kg/m3 | |
| Pitch-loblolly pine: 725 kg/m3 | ||
| Surface-to-volume ratio (σ) | Pitch pine: 5063 m−1 | |
| Pitch-loblolly pine: 4899 m−1 | ||
| Oven-dry fuel loading (wo) | Measured for each fuel bed | |
| Fuel depth (δ) | Measured for each fuel bed | |
| Moisture of extinction (Mx) | 30% | |
| Mid-flame wind speed | 0 km/h | |
| Slope angle (ϕ) | 0° |
The heat of combustion of both pine needle species was previously measured using bomb calorimetry (Campbell-Lochrie et al. 2021) with measured values given here in Table 1. The heat of combustion for both species varied slightly; however, this variation was within the range of experimental uncertainty. These measured values were similar to previous measurements for other pine needle species (e.g. Ovington and Heitkamp 1960; Hough 1969; Rothermel 1976) and were also similar to the generic dead fuel heat content specified in all 53 standard fuel models of 8000 BTU/lb (18 608 kJ/kg) (Burgan 1987). Therefore, this generic value was assumed for both fuel types throughout all calculations in the present study.
The moisture of extinction is the minimum moisture content at which flame spread is not sustained. This parameter is difficult to establish experimentally, particularly given the potential dependence on fuel structure. Rothermel suggested, however, that for dead fuels the moisture of extinction may vary between 0.1 and 0.4 and therefore assumed a constant value of 0.30 during the model development (Rothermel 1972). This value represents the typical fibre saturation point of wood (Byram et al. 1952; Rothermel 1972) and is similar to the range of extinction values observed or extrapolated from previous experiments (Rothermel and Anderson 1966; Anderson 1969). This constant value was also incorporated in the initial 11 fuel models (Rothermel 1972).
In the present study, the same constant moisture of extinction value (0.30) is assumed, allowing greater focus on other input parameters. In this study, as a result of air-drying the fuel, the FMC was likely significantly lower than the extinction value. The significance of the extinction value is therefore likely to be reduced, because Rothermel’s model displays increased sensitivity to this parameter for cases in which the actual FMC approaches the extinction moisture value (Burgan 1987).
Constant values of 0.0555 for the total mineral content and 0.010 for the effective mineral content were assumed throughout. These match the values assumed in the standard fuel models (Andrews 2018).
Model verification
The implementation of the Rothermel equations (with Albini modifications) in this study was verified by comparison with the SURFACE module in BehavePlus (Version 6) (Andrews 2014), which uses the Rothermel model for surface flame spread rate predictions. Custom static fuel models were used within BehavePlus to represent each of the fuel beds conditions studied in the existing experimental dataset (Campbell-Lochrie et al. 2021). These fuel beds cover a range of structural conditions with fuel loading ranging from 0.2 to 1.6 kg/m2, and fuel depths ranging from 0.01 to 0.08 m. However, the lowest fuel depth cases (10 mm) were excluded from this verification analysis as the minimum valid fuel depth in BehavePlus is 20 mm. A single fuel size class (1 h dead fuels) was specified for each fuel bed.
The fuel element density and the total and effective mineral contents are fixed constant values in BehavePlus with values of 32 lbs/ft2 (512.6 kg/m3), 0.0555 and 0.010 respectively. Therefore, for the validation study, these values were also used as model inputs in the custom MATLAB script to allow comparison of model predictions. Agreement in predicted spread rates was observed for all fuel bed conditions verifying the implementation of the model equations in this study.
Results and discussion
Rate of spread comparison
The predicted and experimentally observed Rate of Spread (RoS) for each fuel condition is shown in Table 4. The fuel structure was described in terms of fuel depth, fuel loading, packing ratio and the dimensionless parameter ασδ, which incorporates porosity (α), surface-to-volume ratio (σ) and fuel depth (δ). Similar trends between RoS and fuel structure were apparent in both the predicted and observed spread rates although absolute values varied. A positive trend between RoS and fuel loading (for a fixed bulk density with fuel depth allowed to vary) was observed for both the predicted and observed RoS. A negative trend between RoS and bulk density (for a fixed fuel loading with fuel depth allowed to vary) was also apparent in both the predicted and observed spread rates. As described in Campbell-Lochrie et al. (2021), the spread rate was previously observed to be strongly correlated with the fuel bed parameter ασδ and a positive trend was also predicted by the Rothermel model.
| Fuel type | Fuel loading (kg/m2) | δ (m) | β | ασδ | FMC (dry basis) (%) | Observed RoS (mm/min) | Predicted RoS (mm/min) | Deviation (%) | |
|---|---|---|---|---|---|---|---|---|---|
| Pitch pine | 0.2 | 0.02 | 0.014 | 100 | 10.1 ± 1.1 | 108 ± 31 | 59 | 45 | |
| 0.2 | 0.01 | 0.028 | 49 | 10.0 ± 1.2 | 114 ± 24 | 30 | 74 | ||
| 0.4 | 0.04 | 0.014 | 200 | 9.6 ± 0.8 | 144 ± 20 | 120 | 17 | ||
| 0.4 | 0.02 | 0.028 | 98 | 9.6 ± 0.6 | 126 ± 17 | 60 | 52 | ||
| 0.6 | 0.06 | 0.014 | 300 | 10.9 ± 2.1 | 180 ± 28 | 169 | 6 | ||
| 0.6 | 0.03 | 0.028 | 148 | 9.8 ± 0.7 | 132 ± 19 | 90 | 32 | ||
| 0.8 | 0.08 | 0.014 | 399 | 10.1 ± 0.5 | 210 ± 26 | 234 | −11 | ||
| 0.8 | 0.04 | 0.028 | 197 | 10.2 ± 0.7 | 162 ± 16 | 117 | 28 | ||
| 0.8 | 0.02 | 0.055 | 96 | 10.1 ± 0.9 | 126 ± 37 | 45 | 64 | ||
| 1.2 | 0.06 | 0.028 | 295 | 11.3 ± 0.3 | 174 ± 33 | 167 | 4 | ||
| 1.6 | 0.08 | 0.028 | 394 | 12.3 ± 1.7 | 246 ± 39 | 214 | 13 | ||
| Pitch-loblolly hybrid pine | 0.2 | 0.02 | 0.014 | 97 | 16.6 ± 1.9 | Unsustained | 44 | N/A | |
| 0.2 | 0.01 | 0.028 | 48 | 16.6 ± 1.9 | Unsustained | 23 | N/A | ||
| 0.4 | 0.04 | 0.014 | 194 | 15.3 ± 1.2 | 114 ± 25 | 92 | 19 | ||
| 0.4 | 0.02 | 0.028 | 96 | 15.5 ± 0.3 | 90 ± 21 | 47 | 48 | ||
| 0.6 | 0.06 | 0.014 | 290 | 15.6 ± 0.3 | 156 ± 39 | 136 | 13 | ||
| 0.6 | 0.03 | 0.028 | 144 | 17.1 ± 0.7 | 114 ± 18 | 67 | 41 | ||
| 0.8 | 0.08 | 0.014 | 387 | 15.9 ± 0.6 | 162 ± 28 | 180 | −11 | ||
| 0.8 | 0.04 | 0.028 | 191 | 15.7 ± 2.4 | 126 ± 21 | 93 | 26 | ||
| 0.8 | 0.02 | 0.055 | 93 | 16.0 ± 0.8 | 96 ± 11 | 37 | 61 |
Experimental observations from Campbell-Lochrie et al. (2021).
N/A indicates not applicable.
The deviation between the experimentally observed RoS and the RoS predicted by the Rothermel model is also shown in Table 4 for each fuel condition. The deviation is defined as the difference between observed and predicted RoS, divided by the observed RoS, and therefore represents the percentage error, with a positive value indicating an underprediction, and a negative value an overprediction.
Despite the similar trends between RoS and fuel structure, significant deviation (ranging from −11 to 74%) between predicted and observed spread was observed, with a mean deviation of 29% across all fuel conditions. For the pitch-loblolly hybrid pine needles, non-zero spread rates were predicted for the lowest fuel loading cases (0.2 kg/m2). However, experimentally, flame spread was not sustained at this fuel condition.
In general, there was a tendency for underpredictions compared with the experimentally observed RoS, as shown in Fig. 2. A similar tendency towards underprediction was also observed when comparing Rothermel spread predictions with observations in laboratory-based flame spread experiments involving ponderosa pine litter beds (McAlpine and Xanthopoulos 1989). The range of underpredictions observed by McAlpine and Xanthopoulos (15–60%) was also similar to those observed in the present study; however, there was limited variation in the fuel structures they studied (two fuel loadings were studied at a single wind speed and fuel structure was otherwise held constant).
Dependence of observed and predicted spread rate deviation on fuel loading and packing ratio for: (a) pitch pine needle fuel beds; (b) pitch-loblolly hybrid pine needle fuel beds.
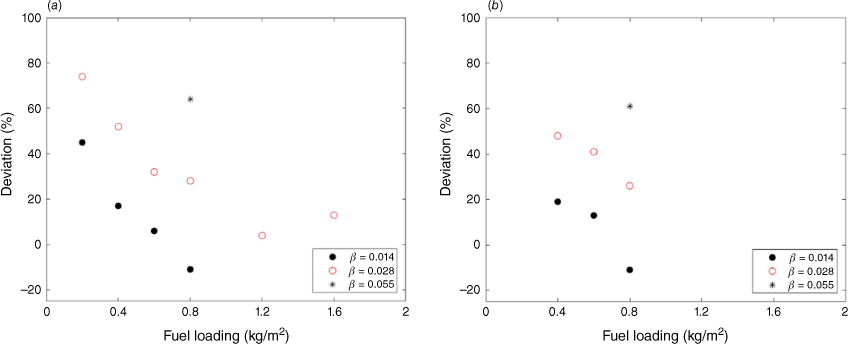
As shown in Table 4 and Fig. 2, the deviation between predicted and observed spread rates varied with the fuel structure. In Fig. 2, it is apparent that the deviation between predicted and observed spread rates varies with fuel loading and packing ratio. For fuel beds of constant fuel loading, greater deviation was observed at higher packing ratios (more compressed fuel beds) as shown in Table 4. For fuel beds of constant packing ratio, the deviation was greatest at lower fuel loadings (also shown in Table 4).
As shown in Fig. 3, significant underpredictions of spread rate (for cases in which sustained flame spread occurred experimentally) are also observed for fuel depths of 0.04 m or less. This underprediction bias supports previous suggestions of an oversensitivity of the Rothermel model to fuel depth and fuel compaction. This may therefore indicate an under-prediction of the energy released within the fire front (the reaction intensity) or of the proportion of this energy transferred to the fuel (the no-wind propagating flux).
Reaction intensity
In this study, the availability of experimental HRR measurements allows further evaluation of model predictions of energy release within the fire front (reaction intensity). The measured HRR can be converted to Byram fireline intensity, which is a commonly used descriptor in wildland fire studies (Byram 1959). The Byram fireline intensity (IB) is defined as the HRR per unit length of the fire front and therefore differs from the reaction intensity (IR), which describes the HRR per unit area of the fire front. The fireline intensity (calculated from the measured HRR) can therefore be related to the reaction intensity according to Eqn 6,
where tr is the residence time (in minutes). An equation for the residence time in uniform surface fuel beds, as a function only of fuel size (diameter (d) in inches or surface-to-volume ratio (σ) in inches−1), was previously proposed (Anderson 1969) on the basis of unpublished data and a review of existing studies (Fons et al. 1960, 1962; McCarter and Broido 1965; Woolliscroft and Law 1967), and is shown in Eqn 7,
Measurements of the surface-to-volume ratio and diameter of the fuels considered in the present study were previously obtained via random sampling (see Table 1), and therefore either form of the above equation could be used. The residence time was calculated independently using both values and the average residence time value (20 s for both fuel species) was used in Eqn 6 to relate the reaction intensity and fireline intensity. It should, however, be noted that the fuel bed properties (e.g. fuel depth, packing ratio) may also affect the residence time (Catchpole et al. 1993).
The experimentally observed reaction intensity values (based on this conversion from the measured HRR) are given in Table 5, and plotted in Fig. 4, for both species. In general, a positive linear trend between fuel loading and reaction intensity was observed, as shown in Fig. 4. Deviation from this general linear trend was observed at the lowest fuel loading in this study (0.2 kg/m2); however, the non-linear nature of the flame front at this condition (given the needle sparsity, and as observed in other similar experiments (Campbell-Lochrie et al. 2023)), should also be considered. The flame front length is therefore poorly defined at these lowest fuel loadings and conversion to a fireline intensity based on the fuel bed width may be less appropriate for these conditions.
| Fuel type | Fuel loading (kg/m2) | β | Observed IR (kW/m2) | Predicted IR (kW/m2) | Deviation (%) | |
|---|---|---|---|---|---|---|
| Pitch pine | 0.2 | 0.014 | 506 | 181 | 64 | |
| 0.2 | 0.028 | 43 | 128 | −198 | ||
| 0.4 | 0.014 | 479 | 366 | 24 | ||
| 0.4 | 0.028 | 373 | 258 | 31 | ||
| 0.6 | 0.014 | 600 | 531 | 12 | ||
| 0.6 | 0.028 | 631 | 384 | 39 | ||
| 0.8 | 0.014 | 840 | 722 | 14 | ||
| 0.8 | 0.028 | 799 | 508 | 36 | ||
| 0.8 | 0.055 | N/A | 192 | N/A | ||
| 1.2 | 0.028 | N/A | 747 | N/A | ||
| 1.6 | 0.028 | N/A | 983 | N/A | ||
| Pitch-loblolly hybrid pine | 0.2 | 0.014 | Unsustained | 162 | N/A | |
| 0.2 | 0.028 | Unsustained | 121 | N/A | ||
| 0.4 | 0.014 | 365 | 330 | 10 | ||
| 0.4 | 0.028 | 328 | 245 | 25 | ||
| 0.6 | 0.014 | 520 | 493 | 5 | ||
| 0.6 | 0.028 | 515 | 360 | 30 | ||
| 0.8 | 0.014 | 799 | 654 | 18 | ||
| 0.8 | 0.028 | 622 | 488 | 22 | ||
| 0.8 | 0.055 | 555 | 203 | 63 |
HRR measured by oxygen consumption calorimetry and converted to fireline intensity (IB).
Dependence of experimentally observed reaction intensity on fuel loading and packing ratio (β) for: (a) pitch pine; (b) pitch-loblolly hybrid pine needle beds.
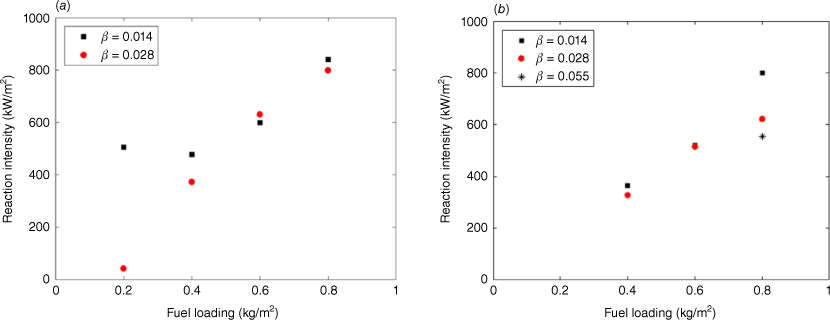
The observed trends in the experimentally observed reaction intensity are, therefore, broadly in line with the assumptions used in the model’s development. Rothermel assumed a linear trend between reaction intensity of the flame front and fuel loading (as shown in the predicted reaction intensity values presented in Table 5). Further study is required to disentangle the effects of needle sparsity and fuel loading at the lowest fuel loadings. The need for further investigation of this linear trend at lower fuel loadings has been previously highlighted (Wilson 1982).
As shown in Table 5, Rothermel model predictions of reaction intensity were typically underestimates compared with the reaction intensity calculated from the measured HRR (note that experimental HRR observations were unavailable at some fuel conditions). The tendency for underestimation is also seen in Fig. 5, where the ratio of the predicted reaction intensity to the experimentally observed reaction intensity is plotted at each fuel condition for both fuel species. A ratio of less than 1 indicates an underprediction compared with the experimentally observed reaction intensity.
Ratio of Rothermel model predictions (IR(P)) to experimental observations (IR(E)) of reaction intensity for fuel beds of: (a) different ασδ; (b) different fuel bed depths (δ). Both fuel species plotted (lowest fuel loading (0.2 kg/m2) cases omitted owing to lack of linear flame front).
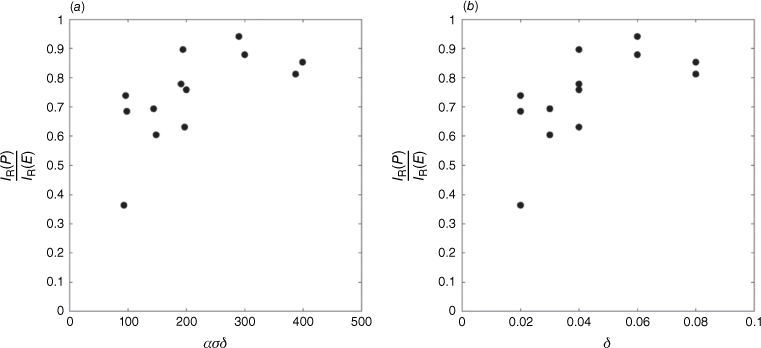
It should be noted that the experimentally measured reaction intensity is derived from the HRR, which is a global measurement of the energy release including heat released in the trailing combustion region, which can be significant (Perez-Ramirez et al. 2017). Therefore, some variation between predicted and observed reaction intensity would be expected because the Rothermel model considers energy release only in the primary fire front region. Despite this, similar values were obtained at higher fuel depths, with the ratio between predicted and observed values >0.8. However, increased divergence is observed in the same lower fuel depth range in which spread rates were also significantly underpredicted (δ ≤ 0.04 m). It therefore appears that the Rothermel model underpredicts the energy release occurring in the fire front region for these lower fuel depth cases.
Physical implications for fuel structure
Unlike empirical operational models, the Rothermel flame spread model has a physics-based, theoretical framework. This therefore allows, to a certain extent, the previously discussed reduction in model performance in low ασδ (low fuel depth or highly packed) fuel beds to be examined in the context of the underlying physical phenomena controlling the flame spread process. The experimental observations considered in this study show clear effects of fuel loading and packing ratio on the spread rate and fire behaviour. Spread rate correlates positively with fuel loading (for fixed packing ratio and variable fuel depth) and negatively with packing ratio (for fixed fuel loading and variable fuel depth). These trends are also predicted by the Rothermel model; however, deviations between observed and predicted spread rates increase for greater packing ratios at a given fuel load. This suggests that the effects of these fuel structure properties are not adequately represented in the model for this fuel type.
It appears that the energy release in the fire front (reaction intensity) is underpredicted by the Rothermel model in these more compact fuel beds. Various explanations are possible, including the lack of consideration of any packing ratio influence on other model parameters such as the moisture of extinction. However, it is also possible that the fundamental influence of the packing ratio on the energy release in the fire front is not adequately characterised for this fuel type. It was previously observed (Frandsen and Rothermel 1972) that the combustion zone depth and burning rate profile within the combustion zone vary with packing ratio but as the focus of this previous study was on the development of a novel experimental method, further systematic investigation of this trend was not pursued.
In understanding possible discrepancies, it is useful to revisit the experiments used to inform the development of empirical terms for calculation of the reaction intensity and reaction velocity (Rothermel 1972). This involved mass loss measurements during flame spread experiments in three different fuel types (12.7 mm½ inch sticks, ¼ inch 6.35 mm sticks excelsior) at various packing ratios. However, the fuel depth was held constant and therefore the fuel loading must also vary in each case, complicating efforts to separate the independent effects of fuel loading and packing ratio on the reaction velocity and reaction intensity. Indeed, it is for the same reason that Rothermel cautioned against comparison between fuels that ‘is not intended, nor can it be made because loading was not held constant.’ (Rothermel 1972, p. 17). However, no similar warning around comparisons between packing ratios is given.
This has important implications for the optimum packing ratio that is currently represented in the model as a function only of surface-to-volume ratio. This does not therefore allow for the interdependent effect of fuel loading and packing ratio on the combustion process and subsequent energy release. Issues around the optimum packing ratio are further complicated for the litter beds considered in this study given that is unclear exactly where their behaviour lies within the context of the wood cribs and excelsior fuels used in the model’s development.
This is particularly important given the lack of experimental observation of an optimum packing in excelsior fuel beds, with the selection of an optimum packing ratio instead relying on the assumption that a reaction velocity of zero occurs for cases where ‘there is no fuel to support combustion’ (Rothermel 1972, p. 16). Particularly given the complex role of fuel sparsity observed in the present study, such an assumption again requires consideration of the interdependent roles of fuel loading and packing ratio, and the effects on the underlying physical phenomena controlling flame spread (e.g. convective heat transfer, O2 supply).
Conclusions
The performance of the Rothermel flame spread model was assessed using an existing series of pine needle fuel bed experiments in which the fuel bed structure (fuel loading, packing ratio, fuel depth) was systematically varied. In general, Rothermel model predictions of spread rate were underestimates compared with the experimentally observed spread rates. Divergence between predicted and observed spread rates was greatest in fuel beds with lower fuel depths (≤0.04 m). For fuel beds of fixed fuel loading, divergence increased as the packing ratio increased (compaction of fuel bed). These observations support previous suggestions of an oversensitivity of the Rothermel model to fuel depth or fuel bed compaction. The non-conservative bias observed in model predictions at these fuel conditions is an important consideration in operational model use and highlights the need for further study of the complex effects of fuel structure on fire behaviour.
For low fuel depths, significant deviation between the predicted and experimentally observed reaction intensity was also observed. This suggests that underpredictions of energy release in the fire front are a significant contributor to underpredictions of spread rate for these shallow and/or compressed fuel beds. Further investigation of the energy release and combustion wave profile as a function of fuel structure is required to address this oversensitivity to fuel depth and compaction.
Efforts to compare experimental observations and predictions of reaction intensity highlight the importance of accurately determining the residence time; however, the effects of fuel bed structure are not adequately incorporated within existing empirical residence time formulations. Separation of the primary fire front and secondary trailing region represents an important aspect of experimental determination of residence time and is important in understanding the effect of fuel structure on the reaction intensity and subsequently the propagating flux sustaining flame spread. It is important that further work acknowledges the important influences of fuel loading and bulk density (or packing ratio) and that this is considered when applying concepts such as the optimum packing ratio.
References
Anderson HE (1969) Heat transfer and fire spread. Research Paper INT-69. (USDA Forest Service) 10.5962/bhl.title.69024
Andrews PL (2014) Current status and future needs of the BehavePlus Fire Modeling System. International Journal of Wildland Fire 23, 21-33.
| Crossref | Google Scholar |
Andrews PL, Cruz MG, Rothermel RC (2013) Examination of the wind speed limit function in the Rothermel surface fire spread model. International Journal of Wildland Fire 22, 959-969.
| Crossref | Google Scholar |
Bachmann A, Allgöwer B (2002) Uncertainty propagation in wildland fire behaviour modelling. International Journal of Geographical Information Science 16, 115-127.
| Crossref | Google Scholar |
Campbell-Lochrie Z, Walker-Ravena C, Gallagher M, Skowronski N, Mueller EV, Hadden RM (2021) Investigation of the role of bulk properties and in-bed structure in the flow regime of buoyancy-dominated flame spread in porous fuel beds. Fire Safety Journal 120, 103035.
| Crossref | Google Scholar |
Campbell-Lochrie Z, Walker-Ravena C, Gallagher M, Skowronski N, Mueller E.V., Hadden R.M. (2023) Effects of fuel bed structure on heat transfer mechanisms within and above porous fuel beds in quiescent flame spread scenarios. International Journal of Wildland Fire 32, 913-926.
| Crossref | Google Scholar |
Catchpole EA, Catchpole WR, Rothermel RC (1993) Fire behavior experiments in mixed fuel complexes. International Journal of Wildland Fire 3, 45-57.
| Crossref | Google Scholar |
Catchpole WR, Catchpole EA, Butler BW, Rothermel RC, Morris GA, Latham DJ (1998) Rate of spread of free-burning fires in woody fuels in a wind tunnel. Combustion Science and Technology 131, 1-37.
| Crossref | Google Scholar |
Cruz MG, Fernandes PM (2008) Development of fuel models for fire behaviour prediction in maritime pine (Pinus pinaster Ait.) stands. International Journal of Wildland Fire 17, 194-204.
| Crossref | Google Scholar |
El Houssami M, Thomas JC, Lamorlette A, Morvan D, Chaos M, Hadden R, Simeoni A (2016) Experimental and numerical studies characterizing the burning dynamics of wildland fuels. Combustion and Flame 168, 113-126.
| Crossref | Google Scholar |
Fernandes PM, Botelho HS, Loureiro C (2002) Models for the sustained ignition and behaviour of low-to-moderately intense fires in maritime pine stands. In ‘Forest Fire Research and Wildland Fire Safety: Proceedings of IV International Conference on Forest Fire Research 2002 Wildland Fire Safety Summit’, 18–23 November 2002, Luso, Coimbra, Portugal. (Ed. DX Viegas) p. 98. (University of Coimbra)
Frandsen WH, Rothermel RC (1972) Measuring the energy-release rate of a spreading fire. Combustion and Flame 19, 17-24.
| Crossref | Google Scholar |
Gallagher MR, Clark KL, Thomas JC, Mell WE, Hadden RM, Mueller E V, Kremens RL, El Houssami M, Filkov AI, Simeoni AA, Skowronski NS (2017) ‘New Jersey fuel treatment effects: pre-and post-burn biometric data.’ (Forest Service Research Data Archive) 10.2737/RDS-2017-0061
Grabner K, Dwyer J, Cutter B (1997) Validation of Behave Fire Behavior Predictions in Oak Savannas Using Five Fuel Models. In ‘Proceedings of the 11th Central Hardwood Forest Conference’. (Eds SG Pallardy, RA Cecich, GH Garrett, PS Johnson) Gen. Tech. Rep. NC-188. (U.S. Department of Agriculture, Forest Service, North Central Forest Experiment Station: St. Paul, MN)
Hély C, Flannigan M, Bergeron Y, McRae D (2001) Role of vegetation and weather on fire behavior in the Canadian mixedwood boreal forest using two fire behavior prediction systems. Canadian Journal of Forest Research 31, 430-441.
| Crossref | Google Scholar |
Hiers JK, O’Brien JJ, Varner JM, Butler BW, Dickinson M, Furman J, Gallagher M, Godwin D, Goodrick SL, Hood SM, Hudak A, Kobziar LN, Linn R, Loudermilk EL, McCaffrey S, Robertson K, Rowell EM, Skowronski N, Watts AC, Yedinak KM (2020) Prescribed fire science: the case for a refined research agenda. Fire Ecology 16, 11.
| Crossref | Google Scholar |
Hough WA, Albini FA (1978) Predicting fire behavior in palmetto–gallberry fuel complexes. Research Paper SE-174 44. Available at https://www.fs.usda.gov/research/treesearch/45139
International Association of Wildland Fire (2022) IAWF Position Statement on Climate Change and Wildland Fire. Available at https://www.iawfonline.org/wp-content/uploads/2021/11/IAWF-Position-statement-on-climate-change-_-FINAL.pdf
Marsden-Smedley JB, Catchpole WR (1995) Fire behaviour modelling in Tasmanian buttongrass moorlands. I. Fuel characteristics. International Journal of Wildland Fire 5, 203-214.
| Crossref | Google Scholar |
Masters RE, Engle DM (1994) Behave: Evaluated for Prescribed Fire Planning in Mountainous Oak: Shortleaf Pine Habitats. Wildlife Society Bulletin 22, 184-191.
| Google Scholar |
McAlpine RS, Xanthopoulos G (1989) Predicted vs Observed Fire Spread Rates in Ponderosa Pine Fuel Beds: A Test of American and Canadian Systems. In ‘Proceedings of the 10th Conference on Fire and Forest Meteorology’. (Eds DC MacIver, H Auld, R Whitewood) pp. 287–295. (Forestry Canada, Northern Forestry Centre, Edmonton, Alberta, Environment Canada, Ottawa, Ontario)
McCarter RJ, Broido A (1965) Radiative and convective energy from wood crib fires. Pyrodynamics 2, 65-85.
| Google Scholar |
Morandini F, Perez-Ramirez Y, Tihay V, Santoni PA, Barboni T (2013) Radiant, convective and heat release characterization of vegetation fire. International Journal of Thermal Sciences 70, 83-91.
| Crossref | Google Scholar |
Mueller EV, Skowronski N, Clark K, Gallagher M, Kremens R, Thomas JC, El Houssami M, Filkov A, Hadden RM, Mell W, Simeoni A (2017) Utilization of remote sensing techniques for the quantification of fire behavior in two pine stands. Fire Safety Journal 91, 845-854.
| Crossref | Google Scholar |
Mueller EV, Gallagher MR, Skowronski N, Hadden RM (2021) Approaches to Modeling Bed Drag in Pine Forest Litter for Wildland Fire Applications. Transport in Porous Media 138, 637-660.
| Crossref | Google Scholar |
Ovington JD, Heitkamp D (1960) The Accumulation of Energy in Forest Plantations in Britain. Journal of Ecology 48, 639-646.
| Crossref | Google Scholar |
Perez-Ramirez Y, Mell WE, Santoni PA, Tramoni JB, Bosseur F (2017) Examination of WFDS in Modeling Spreading Fires in a Furniture Calorimeter. Fire Technology 53, 1795-1832.
| Crossref | Google Scholar |
Rothermel RC (1976) ‘Forest Fires and the Chemistry of Forest Fuels.’ (Academic Press) 10.1016/b978-0-12-637750-7.50018-2
Rothermel RC (1983) How to predict the spread and intensity of forest and range fires. General Technical Report INT-GTR-143. (USDA Forest Service) 10.2737/INT-GTR-143
Salvador R, Piñol J, Tarantola S, Pla E (2001) Global sensitivity analysis and scale effects of a fire propagation model used over Mediterranean shrublands. Ecological Modelling 136, 175-189.
| Crossref | Google Scholar |
Sample M, Thode AE, Peterson C, Gallagher MR, Flatley W, Friggens M, Evans A, Loehman R, Hedwall S, Brandt L, Janowiak M, Swanston C (2022) Adaptation Strategies and Approaches for Managing Fire in a Changing Climate. Climate 10, 58.
| Crossref | Google Scholar |
Streeks TJ, Owens MK, Whisenant SG (2005) Examining fire behavior in mesquite–acacia shrublands. International Journal of Wildland Fire 14, 131-140.
| Crossref | Google Scholar |
Ujjwal KC, Aryal J, Garg S, Hilton J (2021) Global sensitivity analysis for uncertainty quantification in fire spread models. Environmental Modelling & Software 143, 105110.
| Crossref | Google Scholar |
Van Wagtendonk JW, Botti SJ (1984) Modeling Behavior of Prescribed Fires in Yosemite National Park. Journal of Forestry 82, 479-484.
| Crossref | Google Scholar |
Van Wilgen BW, Wills AJ (1988) Fire behaviour prediction in savanna vegetation. South African Journal of Wildlife Research 18, 41-46.
| Crossref | Google Scholar |
Van Wilgen BW, Le Maitre DC, Kruger FJ (1985) Fire Behaviour in South African Fynbos (Macchia) Vegetation and Predictions from Rothermel ’s Fire Model. Journal of Applied Ecology 22, 207-216.
| Crossref | Google Scholar |
Weise DR, Koo E, Zhou X, Mahalingam S, Morandini F, Balbi JH (2016) Fire spread in chaparral – A comparison of laboratory data and model predictions in burning live fuels. International Journal of Wildland Fire 25, 980-994.
| Crossref | Google Scholar |



