Fireline path optimisation in a heterogeneous forest landscape
Xu Yang A * , Emanuel Melachrinoudis A , Peter Kubat A and James MacGregor Smith BA Department of Mechanical and Industrial Engineering, Northeastern University, Boston, MA 02115, USA.
B Department of Mechanical and Industrial Engineering, University of Massachusetts, Amherst, MA 01003, USA.
International Journal of Wildland Fire 31(11) 1068-1079 https://doi.org/10.1071/WF22037
Submitted: 29 March 2022 Accepted: 13 September 2022 Published: 10 October 2022
© 2022 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of IAWF. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Background: When fighting high-intensity wildfire, firefighters may construct a defensive fireline (fuel break) away from the raging front. The path of the fireline is the key to successful fire containment. However, the study of fireline path optimisation in the literature is limited.
Aims: We aim to find the optimal path for firefighting crews to encircle and contain a growing fire in the minimum time while keeping firefighters safe.
Methods: The model considers the realistic topographic factors that affect fire behaviour and fireline production rates. The forest landscape is partitioned into small homogeneous polygons according to their burning characteristics and modelled as a complex topological network using Delaunay triangulation. An algorithm is developed to find the fireline path for firefighting crews, traversing ‘safe’ edges of a dynamic network to meet at the earliest time at which the fireline path is completed.
Key results: Various experiments were conducted leading to insights on how the algorithm can be utilised to develop more effective firefighting strategies.
Conclusions: The proposed algorithm provides an efficient way to generate the optimal fireline path.
Implications: Future work could include the stochastic and dynamic factors in the system by considering probabilistic fire propagation and fireline construction rates.
Keywords: algorithm, Delaunay triangulation network, fireline optimisation, forest fire, geographic information system (GIS), heterogeneous landscape, network optimisation, operations research in natural resources, optimal fireline path, optimal meeting path, wildfire, wildfire containment.
Introduction
Over the past few decades, costs and damage associated with wildfire suppression have increased dramatically (National Interagency Fire Center 2021). Though some wildfires can benefit wildlands and the ecosystem, fire suppression needs to be conducted if a wildland fire endangers people’s lives, property, or the environment. One of the primary goals of wildland fire suppression is to stop fires from spreading as rapidly as possible before they grow into destructive megafires and cause devastating damage. A substantial number (Calkin et al. 2005; Venn and Calkin 2011; Lee et al. 2012; Ntaimo et al. 2012; Fernandes et al. 2016; Plucinski 2019) of studies have recognised the benefit of early suppression. Wildfires can grow into mega-fires (Williams 2013) if they are not controlled at an early stage, which presents considerable difficulties for fire suppression efforts.
Wildfire containment is usually accomplished by constructing a defensive fireline around the burning perimeter to stop its further propagation. A fireline is a strip of land wide enough to mitigate chances of the fire crossing, on which any flammable materials have been removed or made fire-resistant. Two fire suppression strategies are frequently employed – direct attack and indirect attack (National Wildfire Coordinating Group 2014). Direct attack is performed right at a fire’s edge to minimise the burnt area. However, this strategy cannot be used on intense fires, where an indirect attack must be carried out by constructing a fireline that travels along a predetermined path and is set back from the fire front. In such cases, the key to effective containment is choosing the appropriate locations to allocate firefighting resources and construct firelines. Using different strategies can produce notably different containment outcomes.
Wildfire suppression is a non-trivial task owing to its complexity and uncertainty. Operations research methods have been applied to solve these complex problems with the techniques of mathematical analysis and modelling (Ntaimo et al. 2008; Minas et al. 2012; Duff and Tolhurst 2015). Common objectives that have been addressed in models include maximising the fire-related benefit, minimising the burnt area or the fire-caused loss (Donovan and Rideout 2003; Wei et al. 2011, 2018, 2021; Belval et al. 2015; Zambon et al. 2018), delaying the fire from reaching certain valuable areas (Hof et al. 2000), and fully containing the fire. The first three types of model do not intend to contain a fire. Thus, it is not required that the fireline be continually built around the fire. Rather, they decide where and in what order to construct fire barriers. In contrast, a typical assumption in fire containment models is that a fireline is constructed continually around a fire’s perimeter until the fire is contained.
In the large body of models on wildfire suppression tactics, mostlack optimisation of fireline paths. A fireline path is usually out of the scope of studies and sometimes arbitrarily defined in the literature. This can be traced as far back as the 1960s, when researchers started to consider the application of operations research methods to optimise fireline construction. Mathematical analysis models were developed to study the effectiveness of fireline construction (Albini et al. 1978; Mees 1985; Fried and Fried 1996). Jewell (1963) illustrated a simple strategy, where a straight fireline of a certain length and width was constructed some distance downwind from the fire head. The most efficient location to build the fireline was where it would be finished as soon as the fire arrived. Albini et al. (1978) assumed that two crews would construct the fireline symmetrically, starting at a point in front of the fire head and following an arbitrarily defined route. Some studies (Hu and Sun 2007; Hu and Ntaimo 2009) assumed two crews built a rectangle-shaped fireline symmetrically from the anchor point. The fire was considered contained if the length of the fireline was greater than the fire’s perimeter. HomChaudhuri and Kumar (2010) defined a fireline by a quadratic-shaped function. Each of the four crews was considered to build the fireline, starting from a point in the clockwise direction. The optimal fireline shape functions were found through the simulation–optimisation technique using a genetic algorithm.
The primary goals of the present paper are to (1) introduce the algorithm for finding the fastest meeting path for two crews in a network; (2) use the developed algorithm to find the optimal fireline path thatcontains the spreading wildfire in the minimum time safely; and (3) demonstrate how the algorithm can be used to assist anchor points through simulation optimisation. The two-crews strategy (one constructing the fireline clockwise and the other counterclockwise) is frequently used in the literature and in practical operations (Albini et al. 1978; Andrews 1986, 2009; Fried and Fried 1996, 2010; National Wildfire Coordinating Group 1996; Hu and Ntaimo 2009; Kennard 2022). Compared with a single-crew strategy, it has the advantage of being safer and more effective. In a head attack, for instance, a single crew anchors at the fire head and starts constructing a fireline. The fire behind them continues burning and may outflank the firefighters. The single crew works its way around the fire perimeter to encircle and contain the fire. If fireline construction catches the spreading fire, the fireline will encircle the fire and merge with the anchor point. In reality, owing to fatigued firefighters or running out of retardant, the fireline production rate may decrease as the crew moves closer to the fire head, where the fire spreads the fastest. This increases the chance of a fire escaping containment. However, in this study, the fireline construction rate is assumed to be constant.
In this paper, a heterogeneous forest landscape is represented as a network utilising Delaunay triangulation. It is assumed that fire will spread throughout the network. This innovative abstraction was first proposed and shown computationally efficient in Stepanov and Smith (2012). The two crews are assumed to construct the fireline, starting at a specific node (the anchor point), in opposite directions along the network edges. The fireline segments constructed by the two crews eventually merge when they meet; thus, the fire is contained. Such a meeting point is the key to the optimal fireline path, because the fastest path between the anchor point and the meeting point is the optimal fireline path for each crew. Hence, the problem of finding the optimal fireline path can be formulated as the problem of finding the optimal meeting point (OMP). The primary difficulty is that the OMP may lie on any network edges. Thus, all edges need to be examined, which can be time-consuming. This challenging problem has attracted researchers’ attention to find the OMP computationally efficiently (Xu and Jacobsen 2010; Yan et al. 2015). A shortest path based-algorithm is developed to find the OMP and the fastest fireline path for two moving crews to contain a fire in a dynamic network, i.e. some nodes and edges are eliminated over time owing to the fire spreading. Finally, various experiments are conducted, leading to insights on how the algorithm can be used to develop more effective firefighting strategies.
Solution framework
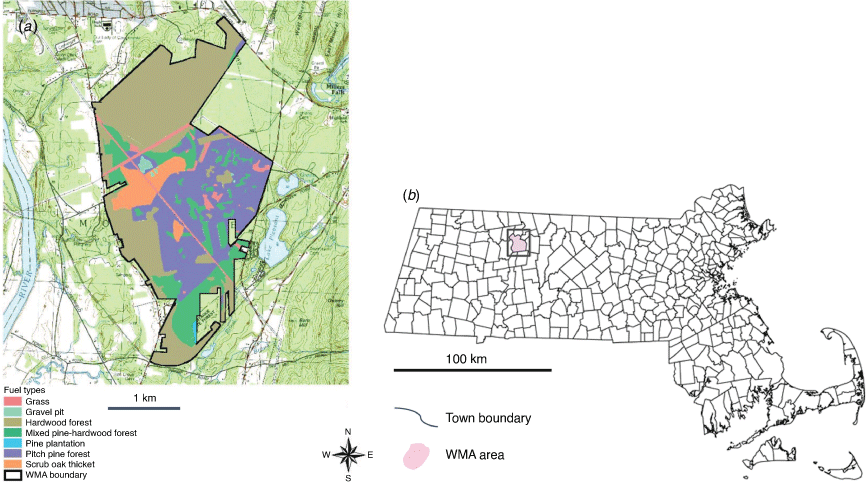
We present the procedures for developing the framework for generating the optimal fireline construction path in the following paragraphs (Fig. 1). Wildfire behaviour and fire suppression productivity are affected by fuel types, terrain (aspect and slope) and weather conditions. The study area is represented as polygon partitions using digital maps (United States Geological Survey (USGS)) of fuel distribution and terrain. For example, Fig. 2 shows the polygon layer of fuel types in a forest area of western Massachusetts (Clark and Patterson 2003), which is chosen in this research as the study area, as elaborated later in the Experimental results section. Aspect and slope are represented as Triangulated Irregular Network (TIN) triangles. These polygon data layers are overlaid and tessellated into a set of smaller homogeneous polygons, in each of which the environmental fire factors stay the same; thus, the fire propagation vectors and the fireline construction rates remain constant. The wind condition is assigned to all polygons as an attribute. This approach was initiated by Stepanov and Smith (2012). Hajian et al. (2016) extended the model by considering stochastic weather conditions. For a more detailed process, the interested reader is referred to their works.
|
One thing worth mentioning is that while constructing fireline, it is preferred to take advantage of existing fire barriers, such as bare fields, road systems and fire break corridors, because it saves time in constructing new firelines, ensures firefighters’ safe anchor points to start fireline construction or backfires, and most importantly, it provides access for firefighting operations. Some natural firebreaks, like water, swamps, cliffs and canyons, cannot be accessed by firefighters. These discrete, local-scale terrain features can be incorporated while creating homogeneous polygons by converting the maps into polygon layers using GIS (geographic information system) functionality. These polygons can be made fire-resistant or inaccessible to firefighters by appropriately adjusting the corresponding fire spread rate and fireline construction rate. In this paper, the existing fire barrier maps are represented by polygons with a slow fire spread rate and a high fireline construction rate.
The landscape was represented as a network graph G(V, E) (Fig. 1, submodel (a)) based on the constructed homogeneous polygons. The nodes V are selected at the polygons’ centroids and inside potential fireline construction locations, such as river and lake banks, trails and roads. In this research, nodes are selected every 100 m along existing fire barriers and connected with edges E defined by Delaunay triangulation (Fig. 3). The firefighters and the fires are assumed to travel over the connecting edges of the network from one node to its adjacent nodes. It is worth noting that the edges located in the polygons representing fire barriers are more likely to be chosen as the fireline paths owing to a faster construction rate – firefighters only need to enhance these fuel breaks by clearing up the highly flammable material rather than constructing them from scratch. Conversely, no edges will be selected from the polygons representing firefighters’ inaccessible sites.

|
The time it takes for the fire (firefighters) to traverse through the edge equals the edge’s length divided by the propagation rate (construction) along the edge. We refer to the National Wildfire Coordinating Group (NWCG) for production rates. Each polygon’s maximum fire propagation rate is calculated in submodel (b) using Rothermel’s surface fire spread equation (Rothermel 1972; Andrews 2018). It is then used to calculate the fire spread rates along edges that lie in the polygon. An edge that crosses multiple adjacent polygons is viewed as a set of segments. Each one is contained in a homogeneous polygon. Therefore, each segment is evaluated for fire spread rate and fireline construction rate. Then, the fire (firefighter) traversal time along the edge is calculated as the aggregation of the times to traverse all segments. The production rates can be defined by the fire incident manager based on the fire’s conditions and the availability of firefighting resources.
The fireline can only be constructed where it can be done safely. A node is considered safe if a crew can reach it some time before the fire. This time gap is defined as the Margin of Safety (MOS) (Beighley 1995; Campbell et al. 2019). Submodel (c) calculates the fire’s arrival times at nodes beforehand for use in the fireline construction modelling. As time goes by, some nodes will not be considered for the fireline as they will not be safe for firefighters to reach. In submodel (d), an algorithm is developed to determine the nodes where the fireline should be constructed in a stepwise approach. We explain this algorithm in detail in the following section.
Methodology
Imposing crews’ working directions
The algorithm generates the optimal fireline path for crews starting from the given anchor point. For the sake of argument, the anchor point v ∈ V is selected randomly on graph G(V, E). However, the algorithm can be used to find the best anchor points among candidate locations through simulation optimisation. Experiments are conducted to demonstrate this in the following section. Each crew works around one side of the fire perimeter – one crew works around the ‘left’ side, the other crew works around the ‘right’ side. They keep working until they meet, enclosing and containing the fire. Fig. 4 presents an example to illustrate the method used to impose the working direction. The black triangle represents the anchor point, and the red lightning bolt symbol represents the fire’s ignition point. A half-line (dashed blue line) is drawn from the fire ignition point, passing through the anchor point. For instance, the crew that works counterclockwise from the anchor point cannot work on any edges that cross this half line (gray edges), but only through the red edges.

|
The optimal fireline path and the optimal meeting point (OMP)
As was mentioned in the introduction, the problem of finding the optimal fireline path is the problem of finding the OMP, because given the optimal meeting point for the two crews, the fastest fireline path connecting the anchor point to the meeting point for each crew can be calculated using a shortest path algorithm such as Dijkstra’s (1959). Let x be a point on G. By points, we understand any points on G, not necessarily the nodes in V. Let ti(x) be crew i’s fastest arrival time at point x from the anchor point. The meeting time for the crews at point x is when the latest crew has arrived,  . A point x∗ ∈ G is defined as the OMP if for every point x ∈ G
. A point x∗ ∈ G is defined as the OMP if for every point x ∈ G

The meeting time at x∗,  , is the earliest possible time the two crews can meet and contain the fire.
, is the earliest possible time the two crews can meet and contain the fire.
It can be easily shown that the two crews must arrive at the OMP simultaneously from opposite directions on the edge. Intuitively, the minimum–maximum OMP in a network should be at a point x∗ where the two crews reach it simultaneously. If not, the earlier crew arriving at x∗ can continue moving toward the direction of the other crew and meet the other crew before it reaches x∗. This contradicts the optimality of x∗. Also, the two crews must reach the minimum-maximum OMP heading from different directions. If not, they can always meet at a point before arriving at x∗.
Although simple, this conclusion provides a computationally efficient way to calculate the OMP for two crews. It implies that the potential OMP candidates can simply be calculated on the edges as the opposite meeting points, and the point with the minimum meeting time Tm is the OMP. Feasible edges at which the two crews can potentially meet are evaluated for OMP candidates, i.e. heading in opposite directions, a crew should enter the edge before the other crew leaves. Take edge uv ∈ E, for instance. Let τi(u, v) be the time it takes crew i to traverse through edge uv ∈ E. Having Crew 1 traverse from node u to v, then  . Having Crew 2 proceed from node v to u, the two crews would meet if
. Having Crew 2 proceed from node v to u, the two crews would meet if  and
and  The corresponding meeting time tm can be calculated as:
The corresponding meeting time tm can be calculated as:

The algorithm for finding the optimal fireline path
The previous section demonstrated that the OMP candidates need to be evaluated on feasible edges where the two crews can potentially meet. The calculation can be time-consuming with a brute-force search in an extensive network. In the following, an efficient searching algorithm is proposed leading to results in O((E + V)logV) operations. Algorithm 1 (see Fig. 5) presents the procedures for finding the optimal (fastest yet safest) fireline path in a network graph G(V, E).
A multi-threading computation technique is used. Each thread models the fireline construction for a firefighting crew. Starting from the anchor point, each thread labels nodes with the crew’s arrival time iteratively. At each iteration, the unvisited node with the smallest label is selected as the current node and marked visited (lines 4, 5). A node and edges related to it are considered unsafe and will be eliminated if the crew cannot arrive at it some particular time earlier than the fire (lines 6, 7). This calculation is based on the assumption that the fire’s arrival times to nodes are precalculated. Every adjacent node to the current node is updated for the crew’s arrival time from it. The two crews’ meeting time on an edge is calculated using Eqn 2 if its two end nodes are marked visited in both calculation threads. The optimal meeting time is updated if it is better.
A termination condition is designed to avoid exploring all nodes in the network. A dynamic node-set frontieri is created for each thread i and is updated throughout the calculation to formulate a termination condition. A node is defined as a frontier node if it is visited and has an unvisited adjacent node. It is so called because it forms the ‘frontier’ between the visited and the unvisited nodes. At each iteration, the current node enters frontieri if it has at least one unvisited adjacent node (line 9). As the current node is visited, its adjacent nodes could lose the last unvisited neighbour, hence will be removed from frontieri (line 17). As calculation continues, the nodes with the relatively earlier crew’s arrival time leave the set, while nodes with the later crew’s arrival time enter the set. Meanwhile, the value of the best meeting time Tm decreases iteratively. A thread terminates as soon as the minimum crew arrival time in its frontier set is greater than the best meeting time generated, and the algorithm terminates when both threads end. Until the termination of both threads, all the feasible meeting edges have been considered. The OMP is the point corresponding to the best meeting time, from which the optimal fireline path for a crew can be generated by tracking back through the fastest path to the anchor point. If such a fireline path cannot be found, the fire is said to have ‘escaped’, which means that the fire cannot be fully contained with the present firefighting resources and the applied strategy.
Experimental results
Study area and required data
In this section, the GIS data provided in Stepanov and Smith (2012) areused to demonstrate the methodology. Constant wind is assigned to polygons with a speed of 20 km h−1 and a direction from southwest to northeast. The vegetation and landscape data are collected from the Montague Plain Wildfire Management Area (Clark and Patterson 2003). The property is located in western Massachusetts, extends ~3.2 by 4.8 km and encompasses approximately a 612-ha property. GIS data layers are used to generate a set of homogeneous polygons with a particular combination of fuel, slope, aspect, wind speed and direction. Nodes V are selected at points of polygon centroids and along trail paths as well because it is preferred to take advantage of trails while constructing a fireline. Edges E are generated using Delaunay triangulation based on the nodes. This example model has 2207 nodes and 5958 edges.
The fire spread time along edge segments is calculated using Rothermel’s (1972) surface fire model based on the fire environment in polygons. We use the R package of Rothermel’s surface fire to calculate the fire spread rate for a particular combination of fuel type, landscape, fuel moisture and wind conditions. The line construction rates per unit of firefighting resources in the following experiments stem from the NWCG based on the production rate for a 20-person hand-crew. The production rates are not precise but can be customised by decision-makers according to fire conditions and the availability of firefighting resources.
Before implementing the algorithm to find the fastest fireline path, we need to first reproduce the fire propagation prediction model becausethe fireline path to be determined is generated considering the fire behaviour. The methodology for developing the fire arrival path at the nodes and drawing the contour lines of the fire perimeter has been well explained in previous works (Stepanov and Smith 2012; Hajian et al. 2016). Thus, the present paper focuses on explaining the methodology of generating the fastest fireline path rather than attempting to explain it in detail. In a nutshell, the minimum fire arrival time to each node from the fire ignition point and the fire traversal path are calculated using Dijkstra’s shortest path algorithm. Then Depth Limited Dijkstra (DLD) is utilised to find the free-burning fire front points in the graph at a particular time. It is worthwhile mentioning that in this paper, the contour lines of fire perimeters (see blue line in Fig. 6) are drawn as the concave hull of the fire front points (Moreira and Santos 2007) because it turns out this method is a good balance between the convex hull and the over-fitted graph that the radial sweep method may generate. We compared the results with the ones generated by FlamMap6 (dashed line in Fig. 6), a fire simulation desktop app developed by the USDA (Finney 2006). The two results are comparable in general shape. The difference between the two results is primarily due to resolution of the models and method used in perimeter construction. It should be noted that our primary task is to evaluate fire arrival times at points of interest in order to determine whether or not fireline can be constructed safely at those locations. Plotting fire perimeters is an auxiliary feature that is used to visualise results.

|
Experimental results with different firefighting strategies
In this section, the developed algorithm is applied and tested in experiments to find the optimal fireline path with different suppression strategies. As was discussed, the firefighting resources need to arrive at a node some time before the fire reaches the node. A 15-min safe buffer is assumed to give the firefighting resources enough time to finish the construction at nodes and leave.
Optimal fireline
This section examines how the decisions about the anchor points, suppression starting time, number of firefighting resources dispatched and resource configurations affect the containment results, which are featured by the actual suppression time, containment time, total length of the fireline and final burnt area.
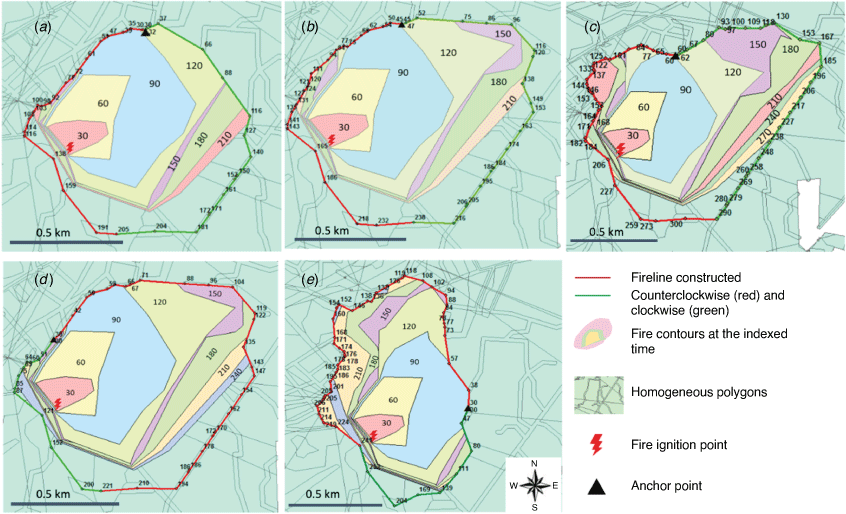
In Table 1, rows (a–f) present the results of a head attack starting from the same anchor point while varying the firefighting resources dispatched and the suppression start time. The fire ‘escapes’ with the strategy shown in rows (a) and (f), which means the algorithm cannot find a fast yet safe fireline path that encircles the fire. Hence, more resources and an earlier start time are required to contain the fire successfully. The results shown in rows (c–e) come as no surprise in that with a fixed number of resources, an earlier start on suppression results in quicker fire containment, a shorter containment duration and a smaller fire size. Correspondingly, the results of rows (c–e) are plotted on a map in Fig. 7a–c. The solid lines in red and green represent the fireline path for each firefighting crew. The numbers beside each node on the path indicate the time that the corresponding crew arrives at the node starting from the selected anchor points. The collection of overlaid polygons in different colours represents the contained fire shape for each half an hour until the fire is fully contained; time counting started when the fire ignited.

|
The decision on anchor points has a significant impact on the suppression results; under the same other conditions, head attack outperforms flank attack in terms of both containment time and final burnt area. With the same suppression starting time and quantity of resources, using a head attack contains the fire (Table 1, row (c)), whereas using a flank attack (Table 1, rows (g, j)) and a tail attack (Table 1, row (m)) fails, because the head attack stops the fire where it spreads the fastest. However, if flank attack is applied, successful containment can be achieved by reconfiguring the two crews’ firefighting resources so that more resources are sent to the crew working toward the direction of the fire head (Table 1, rows (h and k), Fig. 7d, e. It can also be seen that tail attack can hardly fully contain the fire in the presence of a strong wind (Table 1, row (m)), despite the early start of fireline construction and a fair number of resources.
In the above experiments, optimal fireline paths are generated assuming arbitrary anchor points. In the next section, experiments are conducted to find the best anchor point node in the network.
Feasible anchor points
In this section, the developed algorithm is used to examine the nodes’ feasibility as anchor points and find the optimum among them. A feasible anchor point is one from which the algorithm can find a fireline path that contains the spreading fire. In the experiment, three units of resources are assigned to each crew. Simulations are run on 419 candidate anchor point nodes that will get ignited before 210 min. This experiment illustrates the map of feasible anchor points if the suppression starts at 30, 45 or 60 min (Fig. 8a–c, respectively). The black dots represent the infeasible anchor points, whereas the green dots represent the feasible ones. The larger the size of a green dot, the earlier the fire will be contained anchoring at that node. The red dot in each figure represents the optimal node, which gives the minimum containment time among all the feasible nodes. From Fig. 8a–c, as suppression starts later, the number of green dots decreases. The choice of anchor points is crucial for effective containment because, with a fixed number of firefighting resources, the later suppression starts, the fewer feasible anchor points there will be. In summary, if the suppression begins at 30 min, there are 215 feasible anchor points, whereas at 45 and 60 min, only 137 nodes and 94 nodes, respectively, are still feasible. Later suppression starts also result in delayed containment and longer suppression periods.
Discussion and conclusion
Forest science literature contains extensive mathematical and simulation models to study various facets of wildfire management, such as firefighting resource dispatch, configuration and placement strategies. However, only a handful involve optimising the fireline construction route with an indirect attack. Indirect attack is frequently used to suppress intense fires that spread rapidly. Fire incident commanders need to decide the route to construct the fireline. This paper presents procedures toward developing a framework for generating a time-efficient fireline path.
The proposed model requires real GIS data of fire environment parameters as input to predict fire behaviour and simulate fireline construction. The fuel cover data can be found at LANDFIRE Fuel Vegetation Cover (see https://www.landfire.gov/evt.php). However, finding complete historical data for wildland fuel distribution can be challenging. The potential for broad applicability of this approach may be limited by the lack of updated fuel cover classification data, as fuel cover is dynamic owing to wildfire and managed burning. Future implementation of this methodology will benefit greatly from continued improvements in scheduled fuel cover mapping.
A network-based representation of complex forest landscapes is adopted, capturing factors that define the complex fire environment. This allows the modelling of fireline construction and fire propagation as network problems that can be solved efficiently. The proposed methodology is tailored to quickly find the best anchor points among candidate points and generate the optimal fireline path. The methodology allows the fire incident commander to select points at critical fireline construction locations. The more points and edges there are, the smoother the fireline will be. Future research should investigate the impact of point selection (density and location) on fire containment outcomes. In addition, instead of selecting points across the study area, future work can select points at identified control locations (O’Connor et al. 2017).
In this paper, a constant time is set as a safe buffer to allow a safe separate distance (SSD) (Butler and Cohen 1998; Page and Butler 2017; Campbell et al. 2022) from the fire front, i.e. a node is qualified to be selected as a fireline path if the firefighters can arrive at it at a much time earlier than the fire. This assumption is made for the sake of simplicity. In the future, efforts can be made to calculate the appropriate safe buffer at nodes by integrating models for determining the SSD based on the predicted fire spread rate, terrain and flame length at different locations. This methodology gives the flexibility to adjust the safe buffer to either increase firefighter safety or render direct attack. In order to increase firefighter safety, node qualification can be defined considering retreat feasibility. A node is considered safe if firefighters can not only complete the suppression work there safely but also safely retreat to the nearest safety zone (SZ) (Butler 2014; Campbell et al. 2017), i.e. there exists an escape path (Campbell et al. 2019) that allows them to retreat from the point to the SZ. Conversely, if a direct attack is decided on for low-intensity parts of the fire edge, such as fire flanks and tails, nodes in these regions will be assigned zero safe buffer.
The experiments demonstrate that the developed algorithm can not only generate the faster fireline path for two crews, but also assist in deciding feasible anchor points and resource configurations at various times. This paper focuses on the scenario in which the two crews start construction at the same anchor point and work in opposite directions to encircle and fully contain the fire. However, the algorithm does not require that the two crews start at the same anchor point. For example, flank attacks are normally used on moderately intense fires, in which the two crews start building the fireline at two different anchor points located on each side of the fire flank, advancing toward the fire head and eventually meeting there. The algorithm can be used to find the optimal fireline path in a flank attack.
Data availability
Data sharing is not applicable as no new data were generated or analysed during this study.
Conflicts of interest
The authors declare no conflicts of interest.
Declaration of funding
This research did not receive any specific funding.
References
Albini FA, Korovin GN, Gorovaya EH (1978) ‘Mathematical analysis of forest fire suppression.’ Research Paper INT-RP-207. (USDA Forest Service, Intermountain Forest and Range Experiment Station)Andrews PL (1986) ‘Behave: fire behavior prediction and fuel modeling system.’ Intermountain Research Station Technical Report. (USDA Forest Service: Ogden, UT)
Andrews PL (2009) ‘BehavePlus fire modeling system, version 5.0.’ Rocky Mountain Research Station Research Paper RMRS-RP-4. (USDA Forest Service: Ogden, UT)
Andrews PL (2018) ‘The Rothermel surface fire spread model and associated developments: a comprehensive explanation.’ Rocky Mountain Research Station Research Paper RMRS-GTR-371. (USDA Forest Service: Ogden, UT)
Beighley M (1995) Beyond the safety zone: Creating a margin of safety. Fire Management 55, 21–24.
Belval EJ, Wei Y, Bevers M (2015) A mixed integer program to model spatial wildfire behavior and suppression placement decisions. Canadian Journal of Forest Research 45, 384–393.
| A mixed integer program to model spatial wildfire behavior and suppression placement decisions.Crossref | GoogleScholarGoogle Scholar |
Butler BW (2014) Wildland firefighter safety zones: a review of past science and summary of future needs. International Journal of Wildland Fire 23, 295–308.
| Wildland firefighter safety zones: a review of past science and summary of future needs.Crossref | GoogleScholarGoogle Scholar |
Butler BW, Cohen JD (1998) Firefighter safety zones: a theoretical model based on radiative heating. International Journal of Wildland Fire 8, 73–77.
| Firefighter safety zones: a theoretical model based on radiative heating.Crossref | GoogleScholarGoogle Scholar |
Calkin DE, Gebert KM, Jones JG, Neilson RP (2005) Forest service large fire area burned and suppression expenditure trends, 1970–2002. Journal of Forestry 103, 179–183.
| Forest service large fire area burned and suppression expenditure trends, 1970–2002.Crossref | GoogleScholarGoogle Scholar |
Campbell MJ, Dennison PE, Butler BW (2017) Safe separation distance score: a new metric for evaluating wildland firefighter safety zones using lidar. International Journal of Geographical Information Science 31, 1448–1466.
| Safe separation distance score: a new metric for evaluating wildland firefighter safety zones using lidar.Crossref | GoogleScholarGoogle Scholar |
Campbell MJ, Page WG, Dennison PE, Butler BW (2019) Escape route index: a spatially explicit measure of wildland firefighter egress capacity. Fire 2, 40
| Escape route index: a spatially explicit measure of wildland firefighter egress capacity.Crossref | GoogleScholarGoogle Scholar |
Campbell MJ, Dennison PE, Thompson MP, Butler BW (2022) Assessing potential safety zone suitability using a new online mapping tool. Fire 5, 5
| Assessing potential safety zone suitability using a new online mapping tool.Crossref | GoogleScholarGoogle Scholar |
Clark KH, Patterson WA (2003) Fire management plan for Montague plain wildlife management area. Department of Natural Resources Conservation Technical Report. (University of Massachusetts: Amherst, MA)
Dijkstra EW (1959) A note on two problems in connexion with graphs Numerische Mathematik 1, 269–271.
| A note on two problems in connexion with graphsCrossref | GoogleScholarGoogle Scholar |
Donovan GH, Rideout DB (2003) An Integer programming model to optimize resource allocation for wildfire containment. Forest Science 49, 331–335.
| An Integer programming model to optimize resource allocation for wildfire containment.Crossref | GoogleScholarGoogle Scholar |
Duff TJ, Tolhurst KG (2015) Operational wildfire suppression modelling: a review evaluating development, state of the art and future directions. International Journal of Wildland Fire 24, 735–748.
| Operational wildfire suppression modelling: a review evaluating development, state of the art and future directions.Crossref | GoogleScholarGoogle Scholar |
Fernandes PM, Pacheco AP, Almeida R, Claro J (2016) The role of fire-suppression force in limiting the spread of extremely large forest fires in Portugal. European Journal of Forest Research 135, 253–262.
| The role of fire-suppression force in limiting the spread of extremely large forest fires in Portugal.Crossref | GoogleScholarGoogle Scholar |
Finney MA (2006) An overview of FlamMap fire modeling capabilities. In ‘Fuels management – how to measure success: conference proceedings’. (Eds LA Patricia, WB Bret) Proceedings RMRS-P-41, 213–220. (USDA Forest Service, Rocky Mountain Research Station: Fort Collins, CO)
Fried JS, Fried BD (1996) Simulating wildfire containment with realistic tactics. Forest Science 42, 267–281.
| Simulating wildfire containment with realistic tactics.Crossref | GoogleScholarGoogle Scholar |
Fried JS, Fried BD (2010) A foundation for initial attack simulation: the Fried and Fried fire containment model. Fire Management Today 70, 44–47.
Hajian M, Melachrinoudis E, Kubat P (2016) Modeling wildfire propagation with the stochastic shortest path: a fast simulation approach. Environmental Modelling & Software 82, 73–88.
| Modeling wildfire propagation with the stochastic shortest path: a fast simulation approach.Crossref | GoogleScholarGoogle Scholar |
Hof J, Omi PN, Bevers M, Laven RD (2000) A timing-oriented approach to spatial allocation of fire management effort. Forest Science 46, 442–451.
| A timing-oriented approach to spatial allocation of fire management effort.Crossref | GoogleScholarGoogle Scholar |
HomChaudhuri B, Kumar M (2010) Optimal fireline generation for wildfire fighting in uncertain and heterogeneous environment. In ‘Proceedings of the 2010 American control conference’. pp. 5638–5643. (IEEE)
| Crossref |
Hu X, Ntaimo L (2009) Integrated simulation and optimization for wildfire containment. ACM Transactions on Modeling and Computer Simulation 19, 1–29.
| Integrated simulation and optimization for wildfire containment.Crossref | GoogleScholarGoogle Scholar |
Hu X, Sun Y (2007) Agent-based modeling and simulation of wildland fire suppression. In ‘2007 Winter Simulation Conference proceedings’, Washington, DC. (IEEE)
| Crossref |
Jewell WS (1963) Forest fire problems—a progress report. Operations Research 11, 678–692.
| Forest fire problems—a progress report.Crossref | GoogleScholarGoogle Scholar |
Kennard M (2022) How do you fight a wildfire? Available at https://wildlandfirejobs.com/how-do-you-fight-a-wildfire/ [Verified 20 July 2022]
Lee Y, Fried JS, Albers HJ, Haight RG (2012) Deploying initial attack resources for wildfire suppression: Spatial coordination, budget constraints, and capacity constraints. Canadian Journal of Forest Research 43, 56–65.
| Deploying initial attack resources for wildfire suppression: Spatial coordination, budget constraints, and capacity constraints.Crossref | GoogleScholarGoogle Scholar |
Mees RM (1985) ‘Simulating initial attack with two fire containment models.’ Report P-7. (USDA Forest Service, Pacific Southwest Forest and Range Experiment Station)
Minas JP, Hearne JW, Handmer JW (2012) A review of operations research methods applicable to wildfire management. International Journal of Wildland Fire 21, 189–196.
| A review of operations research methods applicable to wildfire management.Crossref | GoogleScholarGoogle Scholar |
Moreira A, Santos MY (2007) Concave hull: a k-nearest neighbors approach for the computation of the region occupied by a set of points. In ‘Proceedings of the Second International Conference on Computer Graphics Theory and Applications’ Volume 2. (Eds J Braz, P-P Vazquez, JM Pereira) pp. 61–68.
| Crossref |
National Interagency Fire Center (2021) Federal firefighting costs (suppression only). Available at https://www.nifc.gov/fire-information/statistics/suppression-costs [Verified 20 July 2022]
National Wildfire Coordinating Group (1996) Wildland fire suppression tactics reference guide. Available at https://www.coloradofirecamp.com/suppression-tactics/how-to-attack.html [Verified 28 September 2022]
National Wildfire Coordinating Group (2014) Incident Response Pocket Guide. Available at https://www.nwcg.gov/sites/default/files/publications/pms461.pdf [Verified 20 July 2022]
Ntaimo L, Hu X, Sun Y (2008) DEVS-FIRE: Towards an Integrated Simulation Environment for Surface Wildfire Spread and Containment Simulations 84, 137–155.
| DEVS-FIRE: Towards an Integrated Simulation Environment for Surface Wildfire Spread and ContainmentCrossref | GoogleScholarGoogle Scholar |
Ntaimo L, Gallego Arrubla JA, Stripling C, Young J, Spencer T (2012) A stochastic programming standard response model for wildfire initial attack planning. Canadian Journal of Forest Research 42, 987–1001.
| A stochastic programming standard response model for wildfire initial attack planning.Crossref | GoogleScholarGoogle Scholar |
O’Connor CD, Calkin DE, Thompson MP (2017) An empirical machine learning method for predicting potential fire control locations for pre-fire planning and operational fire management. International Journal of Wildland fire 26, 587–597.
| An empirical machine learning method for predicting potential fire control locations for pre-fire planning and operational fire management.Crossref | GoogleScholarGoogle Scholar |
Page WG, Butler BW (2017) An empirically based approach to defining wildland firefighter safety and survival zone separation distances. International Journal of Wildland Fire 26, 655–667.
| An empirically based approach to defining wildland firefighter safety and survival zone separation distances.Crossref | GoogleScholarGoogle Scholar |
Plucinski MP (2019) Contain and control: wildfire suppression effectiveness at incidents and across landscapes. Current Forestry Reports 5, 20–40.
| Contain and control: wildfire suppression effectiveness at incidents and across landscapes.Crossref | GoogleScholarGoogle Scholar |
Rothermel RC (1972) ‘A mathematical model for predicting fire spread in wildland fuels.’ USDA Forest Service, Intermountain Forest and Range Experiment Station, Research Paper INT-RP-115. (Ogden, UT).
Stepanov A, Smith JM (2012) Modeling wildfire propagation with Delaunay triangulation and shortest path algorithms. European Journal of Operational Research 218, 775–788.
| Modeling wildfire propagation with Delaunay triangulation and shortest path algorithms.Crossref | GoogleScholarGoogle Scholar |
Venn TJ, Calkin DE (2011) Accommodating non-market values in evaluation of wildfire management in the United States: Challenges and opportunities. International Journal of Wildland Fire 20, 327–339.
| Accommodating non-market values in evaluation of wildfire management in the United States: Challenges and opportunities.Crossref | GoogleScholarGoogle Scholar |
Wei Y, Rideout DB, Hall TB (2011) Toward efficient management of large fires: a mixed integer programming model and two iterative approaches. Forest Science 57, 435–447.
| Toward efficient management of large fires: a mixed integer programming model and two iterative approaches.Crossref | GoogleScholarGoogle Scholar |
Wei Y, Thompson MP, Haas JR, Dillon GK, O’Connor CD (2018) Spatial optimization of operationally relevant large fire confine and point protection strategies: Model development and test cases. Canadian Journal of Forest Research 48, 480–493.
| Spatial optimization of operationally relevant large fire confine and point protection strategies: Model development and test cases.Crossref | GoogleScholarGoogle Scholar |
Wei Y, Thompson MP, Belval E, Gannon B, Calkin DE, O’Connor CD (2021) Comparing contingency fire containment strategies using simulated random scenarios. Natural Resource Modeling 34, 2295
| Comparing contingency fire containment strategies using simulated random scenarios.Crossref | GoogleScholarGoogle Scholar |
Williams J (2013) Exploring the onset of high-impact mega-fires through a forest land management prism. Forest Ecology and Management 294, 4–10.
| Exploring the onset of high-impact mega-fires through a forest land management prism.Crossref | GoogleScholarGoogle Scholar |
Xu Z, Jacobsen HA (2010) Processing proximity relations in road networks. In ‘Proceedings of the ACM SIGMOD international conference on management of data’, Indianapolis, Indiana, USA. pp. 243–254. (Association for Computing Machinery)
| Crossref |
Yan D, Zhao Z, Ng W (2015) Efficient processing of optimal meeting point queries in Euclidean space and road networks. Knowledge and Information Systems 42, 319–351.
| Efficient processing of optimal meeting point queries in Euclidean space and road networks.Crossref | GoogleScholarGoogle Scholar |
Zambon MJO, de Rezende PJ, de Souza CC (2018) Finding exact solutions for the geometric firefighter problem in practice. Computers & Operations Research 97, 72–83.
| Finding exact solutions for the geometric firefighter problem in practice.Crossref | GoogleScholarGoogle Scholar |