Reaction intensity partitioning: a new perspective of the National Fire Danger Rating System Energy Release Component
Francis M. Fujioka A B , David R. Weise B , Shyh-Chin Chen B , Seung Hee Kim A C and Menas C. Kafatos A
B , Shyh-Chin Chen B , Seung Hee Kim A C and Menas C. Kafatos A
A Center of Excellence in Earth Systems Modeling and Observations at Chapman University, Orange, CA 92866, USA.
B US Department of Agriculture, Forest Service, Riverside, CA 92507, USA.
C Corresponding author. Email: sekim@chapman.edu
International Journal of Wildland Fire 30(5) 351-364 https://doi.org/10.1071/WF20025
Submitted: 21 February 2020 Accepted: 24 February 2021 Published: 14 April 2021
Journal Compilation © IAWF 2021 Open Access CC BY
Abstract
The Rothermel fire spread model provides the scientific basis for the US National Fire Danger Rating System (NFDRS) and several other important fire management applications. This study proposes a new perspective of the model that partitions the reaction intensity function and Energy Release Component (ERC) equations as an alternative that simplifies calculations while providing more insight into the temporal variability of the energy release component of fire danger. We compare the theoretical maximum reaction intensities and corresponding ERCs across 1978, 1988 and 2016 NFDRS fuel models as they are currently computed and as they would be computed under the proposed scheme. The advantages and disadvantages of the new approach are discussed. More study is required to determine its operational implications.
Keywords: energy release, fire behaviour, fire modelling, fuel model, fuel moisture, mixed fuel bed, NFDRS 2016, Rothermel model.
Introduction
Nearly 50 years after it first appeared, the Rothermel fire spread model (Rothermel 1972) is still widely used in wildland fire danger and fire behaviour analysis and prediction in the US and elsewhere. Andrews published a comprehensive report (Andrews 2018) of the model and its applications, which Rothermel, in the foreword to the report, characterised it as a ‘complete description of not only the Rothermel model, but also the modifications and addendums that have evolved for supporting the many systems that use the model’. In the US, the initial purpose of the model was to serve as the basis for the National Fire Danger Rating System (NFDRS; Deeming et al. 1972, 1977; Bradshaw et al. 1984; Cohen and Deeming 1985; Burgan 1988), which continues to the present. The model subsequently was used to predict fire behaviour in applications such as FIRECAST (Cohen 1986), BEHAVE and BehavePlus (Andrews 1986, 2008), FARSITE (Finney 1998), HFire (Peterson et al. 2009) and FlamMap (https://iftdss.firenet.gov/firenetHelp/help/pageHelp/content/20-models/lfb/techdoc.htm).
There is a substantial difference between fire danger and fire behaviour applications, which the US National Wildfire Coordinating Group describes as follows (NWCG 2002):
‘The principal difference is that fire danger is a broad-scale assessment while fire behavior is site-specific. Fire danger ratings describe conditions that reflect the potential, over a large area, for a fire to ignite, spread and require suppression action. Fire behavior on the other hand deals with an existing fire in a given time and space.’
The spatial and temporal resolution of the Rothermel model therefore depends on how it is used. There are also separate sets of fuel models needed by the Rothermel model that differ depending on whether the application is for fire behaviour or fire danger. Andrews (2018) lists parameters for 53 fuel models used for fire behaviour (pp. 31–35), 13 from Albini (1976) and 40 from Scott and Burgan (2005); also included are 20 fuel models from the 1978 NFDRS, 20 from the revised set for the 1988 NFDRS and 5 fuel models for the 2016 NFDRS (pp. 95–97).
The principle of conservation of energy is the foundation on which the Rothermel model builds (Frandsen 1971), namely that the no-wind no-slope fire spread rate is a balance between the propagating heat energy and the heat required to bring the unburned fuel to ignition. Its development relied on empirical methods applied in a laboratory setting because the physics and chemistry that drive wildland fire were not then, and arguably are still not completely understood (Andrews 2018). FIRETEC and WRF-Fire are examples of current research models that go well beyond the Rothermel model, especially to simulate the coupling between fire and atmospheric processes (Linn et al. 2002; Coen et al. 2013; Mandel et al. 2011; Linn et al. 2020). One of the greatest challenges that models like these face before they are brought into broad application is ease of usage. FIRETEC, for example, demands extraordinary computing and new and/or scarce data sources (Furman and Linn 2018).
The present work describes a modest revision to the Rothermel model to provide further insight on fire characteristics from within the model framework. It introduces the concept of reaction intensity partitioning, which is, in a sense, a simplification of the model as it is currently being applied. It departs from the original model in the treatment of different types of live and dead fuels comprising a mixed fuel bed. The first section briefly describes the Rothermel reaction intensity function and its application for mixed fuel beds. We then introduce the reaction intensity partitioning concept (RIP), which, while modest in form, differs fundamentally in its approach to mixed fuels. This is followed by a discussion of the implications of the RIP concept related to the NFDRS Energy Release Component, and to fire behaviour modelling only to the limited extent our study allows. We conclude with some suggestions that our approach offers for operational consideration.
The reaction intensity function
The reaction intensity function is the part of the Rothermel model that expresses the principle of energy conservation, as proposed by Frandsen (1971). He conceived the mathematical problem of fire spread one-dimensionally in terms of what happens in a homogeneous fuel bed as the flaming zone propagates into unburned fuel. Combustion from the flaming zone produces a reaction intensity, expressed as Btu ft−2 min−1 (Btu, British thermal units) in US units used by the NFDRS and kJ m−2 min−1 in SI units. It is derived from the inherent fuel heat content, rate and amount of fuel consumed, and modulated by the fuel moisture and mineral contents:

where:
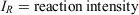
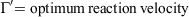
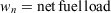
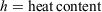
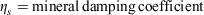
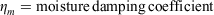
Eqn 1 applies to a single fuel type of specified fuel load, heat content, mineral content and surface area/volume ratio (σ). The latter is a critical fuel property that enters the equation through the optimum reaction velocity (Andrews 2018, p. 117).
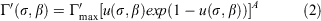
where, in both US and SI units:
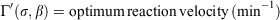
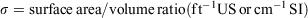
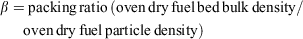
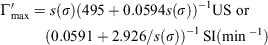
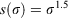
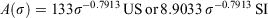
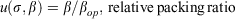

Eqn 2 is an alternative form of the optimum reaction velocity given by Wilson (1980), who converted the entire Rothermel model from US to SI units.
Note that Γ′ is largely a multiple non-linear function of σ, and is non-linear in β. The optimum packing ratio, βop, is also a non-linear function of σ. For a given σ, the reaction intensity is maximum when u, the relative packing ratio, is equal to 1, hence when β = βop. Reaction intensity is non-linear in σ and β but otherwise directly proportional to the other terms in Eqn 1. Assume, for example, specified fuel characteristics as follows:
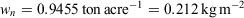
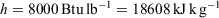
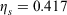
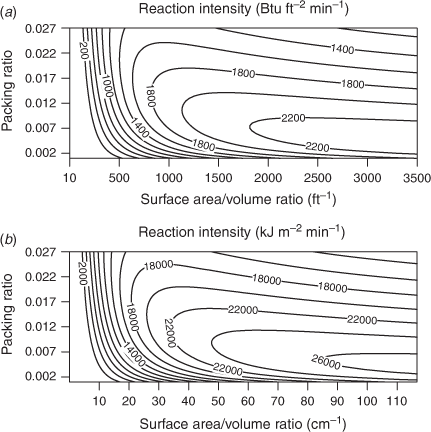
The net loading assumes an initial oven-dry fuel load of 1 ton acre−1 (0.224 kg m−2) and a total mineral content of 0.0555 ton acre−1 (0.012 kg m−2). The mineral damping coefficient is based on the effective mineral content and is the constant value used for both dead and live fuels in the NFDRS (Cohen and Deeming 1985). Setting the moisture damping coefficient to 1 assumes the fuel is moisture-free, hence maximises the reaction intensity, a special case of what Rothermel called the potential reaction velocity (Rothermel 1972, p. 11). This is a useful reference value for the given fuel conditions because when the fuel moisture content is greater than zero, the reaction velocity is simply some fraction, equal to the moisture damping coefficient, of the potential reaction velocity. When we apply these parameters to a range of σ and packing ratios that cover the 1978 NFDRS parameters, we obtain the contoured reaction intensity surface in Fig. 1.
|
The reaction intensity function for this example is highest for high σ and relatively low packing ratios, and uniformly low for low σ. σ is an important control on the heat and mass transfer through the fuel particle surface; the packing ratio similarly affects heat and air flow through the fuel bed. For a given fuel load, a change in packing ratio implies a change in fuel bed bulk density, hence a change in fuel bed depth. The relative maxima along the ridgeline decrease with decreasing σ and increasing packing ratio, apparently to an asymptotic lower limit of σ. The optimum reaction velocity gives the reaction intensity its shape while the other terms affect its amplitude.
Reaction intensity as a function of mixed fuels
Albini (1976) described the reaction intensity (Eqn 1) as a simple formula, further noting: ‘For a single size class fuel bed, the indicated calculation is simple, but the computing of weighted averages of fuel properties for beds with a mixture of fuel particle sizes gets a bit complicated’.
Because the laboratory experiments provided empirical solutions for single size class fuel beds only, mixed-class fuel beds required additional considerations. Rothermel’s approach was to determine a characteristic σ from a weighting of the individual σs in the fuel bed, i.e. surface area weighting. He used this σ to calculate the optimum reaction velocity (Eqn 2), and subsequently to calculate reaction intensity and rate of spread (Rothermel 1972, p. 26). What follows is a version of his weighting scheme preferred because it simplifies the calculations without changing the results.
Weighting schemes to determine characteristic σs for mixed fuel beds
The Rothermel model ingests fuel model data that consist of, at most, six different components categorised as either dead or live vegetation, by size within the dead category, and by herbaceous or woody type within the live category (NWCG 2002). The dead fuel components are 1-, 10-, 100- and 1000-h timelag fuels, which refer to the exponential timelag response of each to ambient weather conditions. Rothermel (1972, pp. 29 ff.) used a double subscript notation, the first to differentiate live and dead categories, the second to identify the timelag of dead fuels and type of live fuels. Without loss of generality, we adopt a single subscript notation that enumerates the six components so that the first four are the dead fuels in ascending order of their timelags, and the fifth and sixth are the herbaceous and woody live fuel types respectively. Denote surface area weights for each component by the sequence {ai}. Then
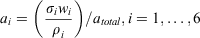
where
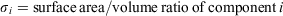
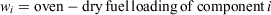
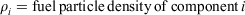
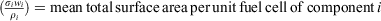 (Rothermel’s
(Rothermel’s 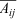 , Rothermel 1972, p. 30, eqn 53)
, Rothermel 1972, p. 30, eqn 53)

The 1000-h dead fuel component is omitted from the surface area weighting, because of its low σ value (Cohen and Deeming 1985, p. 10). The surface area weights are used to find characteristic dead, live and overall σs for the fuel model (Andrews 2018, pp. 16–18), but they are not necessary to calculate (Rothermel’s eqns 71 and 72) to determine the characteristic surface area/volume ratio for the fuel bed, 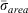 . The dead and live surface area subtotals cancel each other, leaving the component weighted mean surface areas under the summation:
. The dead and live surface area subtotals cancel each other, leaving the component weighted mean surface areas under the summation:

Note that ‘i≠4’ under the summation sign means that the 1000-h dead fuel component (the fourth in the sequence) is excluded. 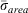 is used in computations for fire behaviour applications and for the NFDRS Spread Component and fire front residence time, i.e. the time the fire front takes to pass a given point. Andrews (2018) lists the
is used in computations for fire behaviour applications and for the NFDRS Spread Component and fire front residence time, i.e. the time the fire front takes to pass a given point. Andrews (2018) lists the 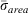 for the 53 fuel models used for fire behaviour calculations (pp. 31–35), under tabulated columns identified as ‘Characteristic SAV’ (SAV = surface-area-to-volume ratio).
for the 53 fuel models used for fire behaviour calculations (pp. 31–35), under tabulated columns identified as ‘Characteristic SAV’ (SAV = surface-area-to-volume ratio).
In contrast to 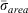 , fuel load weights {li} are used to determine a characteristic σ for the Energy Release Component (ERC), call it
, fuel load weights {li} are used to determine a characteristic σ for the Energy Release Component (ERC), call it 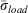 . In this case, the 1000-h fuel component is not omitted. The calculation parallels Eqn 3, with oven-dry component weights in place of surface area weights:
. In this case, the 1000-h fuel component is not omitted. The calculation parallels Eqn 3, with oven-dry component weights in place of surface area weights:
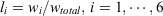
where
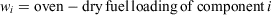
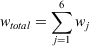
and

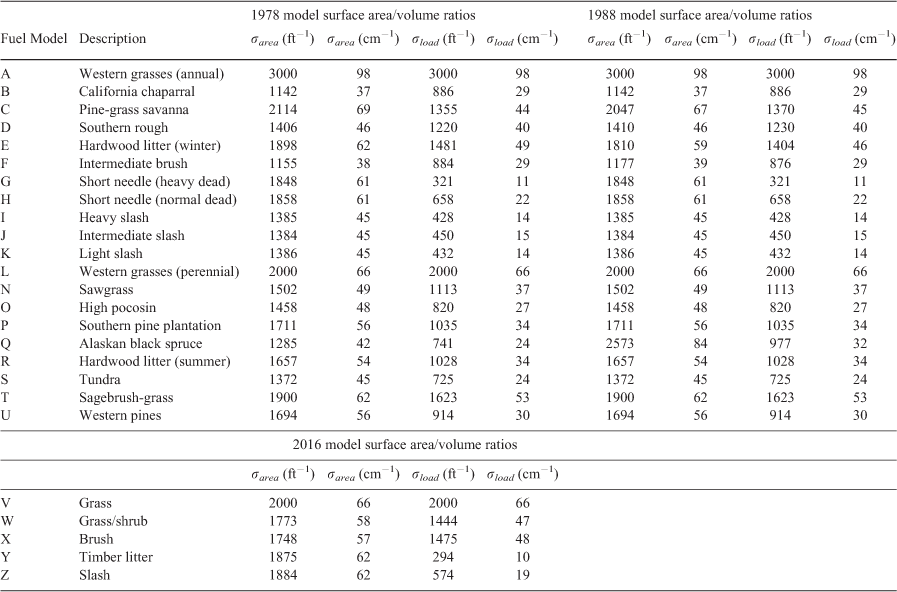
Table 1 gives  and
and 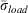 , as computed from Eqns 3 and 4, respectively, for fuel models from the 1978, 1988 and 2016 NFDRS systems.
, as computed from Eqns 3 and 4, respectively, for fuel models from the 1978, 1988 and 2016 NFDRS systems. 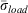 is never greater than
is never greater than 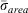 because it includes the 1000-h surface area/volume ratio.
because it includes the 1000-h surface area/volume ratio.
|
The fuel load weights are not necessarily constants. To simulate seasonal changes of fire danger, the 1978 and 1988 NFDRS incorporated dynamic transfer of live herbaceous fuel to the 1-h dead fuel load as the live herbaceous fuel moisture decreased below a specified level. The equations that describe this transfer, as given in Andrews (2018, p. 99), rewritten for the notation described above, are:
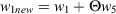
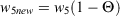
where Θ varies from 0 to 1 in proportion to the decrease below the specified level. The 2016 NFDRS also has this feature, but it ties Θ variations to the Growing Season Index (Andrews 2018). The 1988 NFDRS adds a similar option to transfer deciduous woody fuel to the 1-h dead loading as a function of live woody greenness.
To simulate longer term effects of drought, the 1988 and 2016 NFDRS include a drought load that is transferred to the dead fuel categories in proportion to their loadings relative to the total dead fuel load. The rise above 100 of the Keetch–Byram Drought Index triggers the transfer (Andrews 2018). Dynamic transfer of herbaceous fuel precedes the drought fuel load transfers. The shifts in loading between fuel components ultimately change the value of the characteristic σ, hence the reaction intensity calculated for all three NFDRS versions. σ is arguably one of the more critical fuel characteristics of the Rothermel model in both fire behaviour and fire danger applications. The fact that the range of fuel model component σ values spans three orders of magnitude (Fig. 1a) and its consequences on the reaction intensity function led to the idea of reaction intensity partitioning, described in the next section.
Reaction intensity partitioning by fuel model components
The reaction intensity equation that accounts for fuel model components indexed by i as currently implemented in the Rothermel model and its derivatives is:
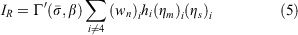
This equation expresses the reaction intensity as the sum of the intensities of the individual fuel components, where each shares a common optimum reaction velocity 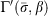 . The individual σs are replaced by the characteristic
. The individual σs are replaced by the characteristic 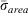 of Eqn 3 for the spread rate calculation.
of Eqn 3 for the spread rate calculation.
For our purposes, we retain the original σs, hence the individual optimum reaction velocities that depend on the σs of each fuel model component indexed by i:
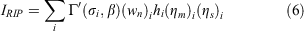
Eqns 5 and 6 both represent an overall reaction intensity as the sum of individual reaction intensities of the fuel components, except that Eqn 5 posits that a reaction velocity with a weighted mean of the individual σs is common to all fuel components. Eqn 6, on the other hand, retains each σ as uniquely representing the size class, therefore the reaction intensity of each fuel component. It represents the overall reaction intensity as the sum of partitioned single fuel fires – hence the term reaction intensity partitioning (RIP) – each burning according to its individual fuel characteristics, except that β, the packing ratio, is a function of all of the fuel loadings and bed depth. This is where RIP differs fundamentally from current practice. The experiments that gave rise to the model used only single size class fuels, hence provide no basis for either averaging σs or for reaction intensity partitioning.
Further discussion of simulating fire spread with the Rothermel model would have to consider the propagating flux, wind and slope effects, and the heat sink that consumes energy from the advancing fire. The present study does not include these factors. Instead, we now address the effects of RIP on the calculation of ERC, which is largely a function of the reaction intensity. We limit consideration to oven-dry fuels, so that ηm = 1. Moreover, the mineral damping coefficient is generally a constant across all fuel models and the heat content is a constant within a fuel model, although it may vary from one fuel model to another. Eqn 5 therefore may be rewritten as
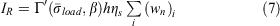
and Eqn 6 as
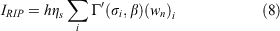
Difference between NFDRS ERC and RIP ERC
NFDRS ERC
The NFDRS ERC is a function of the reaction intensity and flaming front residence time:

where 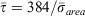 and 384 is the surface area/volume ratio (ft−1) of a fuel particle 1/8 inch (0.3 cm) in diameter.
and 384 is the surface area/volume ratio (ft−1) of a fuel particle 1/8 inch (0.3 cm) in diameter.
Because 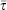 is proportional to the inverse of
is proportional to the inverse of 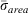 , it is proportional to the diameter of a cylindrical fuel particle, hence increases for larger fuels. This trends opposite to the reaction intensity function, as we saw in Fig. 1. Note that IERC, explained below, is different from the reaction intensity IR expressed by Eqn 7, which one might have expected in ERC on theoretical grounds. Energy release refers to heat per unit area produced by the fire front over the course of its residence time in the spatial interval from the front to the back of the flaming zone, which Andrews (2018, p. 28) gives as HA:
, it is proportional to the diameter of a cylindrical fuel particle, hence increases for larger fuels. This trends opposite to the reaction intensity function, as we saw in Fig. 1. Note that IERC, explained below, is different from the reaction intensity IR expressed by Eqn 7, which one might have expected in ERC on theoretical grounds. Energy release refers to heat per unit area produced by the fire front over the course of its residence time in the spatial interval from the front to the back of the flaming zone, which Andrews (2018, p. 28) gives as HA:

Eqn 9 renders ERC as a scaled and dimensionless HA by introducing the coefficient 0.04 with dimensions of ft2 Btu−1. Using IR from Eqn 7 in Eqn 9, but without the constant 0.04 would give an estimate of the heat release per unit area from the front passage. Instead, IERC is used to calculate the NFDRS ERC (Andrews 2018):
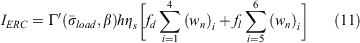
where fd and fl are the proportions of dead and live fuels, respectively, in the fuel model.
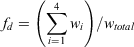
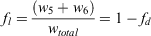
The difference between IR and IERC is in the terms under summation. Where IR includes the total net fuel load, IERC uses an average net fuel load weighted by the proportions of live and dead fuels, i.e. the bracketed expression in Eqn 11. Let 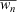 denote the average net fuel load and wntotal the total net fuel load, then
denote the average net fuel load and wntotal the total net fuel load, then 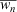 can be rewritten as:
can be rewritten as:
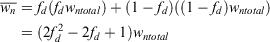
Hence, 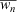 is a quadratic function of the proportion of the net dead fuel load in the fuel model. Since the average net fuel load is less than the total net fuel load when both live and dead fuels are present, we find
is a quadratic function of the proportion of the net dead fuel load in the fuel model. Since the average net fuel load is less than the total net fuel load when both live and dead fuels are present, we find
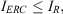
where equality is attained only for fuel models with no live fuel; although they would also be equal for a fuel model with no dead fuel, all fuel models have a non-zero 1-h dead fuel load, expressed mathematically as 0 < fd ≤ 1. When the loadings are equal, 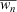 is at its minimum with respect to fd and IERC represents the reaction intensity of only half the total net fuel load.
is at its minimum with respect to fd and IERC represents the reaction intensity of only half the total net fuel load.
A loading-weighted average of the dead and live reaction intensities (Eqn 11) was not a part of the 1972 NFDRS, or the fire behaviour equivalent. The reason loading weighting was included, according to Andrews (2018, p. 109), is that ‘it produced better results with 1000-h fuels, which were added to fuel models in the 1978 NFDRS (Jack D. Cohen, Missoula Fire Sciences Laboratory, pers. comm., July 2011)’. Bradshaw et al. (1984, p. 24) reported that the developers of the 1978 NFDRS wanted the system to reflect the influence of larger fuels, particularly since 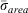 used in the spread computations omitted 1000-h fuels:
used in the spread computations omitted 1000-h fuels:
‘The approach selected to bring larger fuels into play was straightforward: use the fuel energy computations of the spread model – the reaction intensity – but base the influences of the different classes of fuel on their contribution to the total fuel load. Specifically, for the energy release component, the characteristic surface area-to-volume ratio and weighted fuel moisture of the fuel bed would be calculated using fuel class weighting factors based on loading, not surface area as in the spread component. This solution had no experimental basis.’
The last sentence in the preceding quote casts doubt on using loading for fuel class weighting factors, which will be addressed in the discussion section.
RIP ERC
Under reaction intensity partitioning, the ERC is the sum of the ERCs of each individual component in the fuel model:
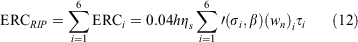
Note that the partitioning not only assigns a unique reaction intensity to each fuel component, but also a unique residence time τι, in both cases because of the dependency on σi. This implies a separation or dilation of the flaming front not addressed by the present study. As we saw in Fig. 1, the reaction intensity is very low for large fuels (small σs). Their relatively longer residence times, however, allow more heat energy to be released after the residence time of fine fuels. Each fuel component’s ERC also depends on the fuel bed mean packing ratio.
In the next section, we compare the maximum potential ERC of 1978, 1988 and 2016 NFDRS fuel models, determined first by the current method using 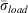 to compute reaction intensity (Eqn 11), and second by using the RIP reaction intensity (Eqn 12). The potentials are maximised by making all dynamic transfers and drought load additions of fuel loadings as appropriate for each fuel model for the most extreme dry conditions with the moisture damping coefficient equal to 1. Although ERC is derived from reaction intensity, the intercomparisons will refer to dimensionless quantities, consistent with the NFDRS ERC, but bear in mind the ERC’s theoretical relationship to heat release. This analysis is offered as a basis for comparing and contrasting the maximum potential energy resulting from the specifications of the 1978, 1988 and 2016 fuel models.
to compute reaction intensity (Eqn 11), and second by using the RIP reaction intensity (Eqn 12). The potentials are maximised by making all dynamic transfers and drought load additions of fuel loadings as appropriate for each fuel model for the most extreme dry conditions with the moisture damping coefficient equal to 1. Although ERC is derived from reaction intensity, the intercomparisons will refer to dimensionless quantities, consistent with the NFDRS ERC, but bear in mind the ERC’s theoretical relationship to heat release. This analysis is offered as a basis for comparing and contrasting the maximum potential energy resulting from the specifications of the 1978, 1988 and 2016 fuel models.
Intercomparisons of NFDRS and RIP ERCs
The NFDRS is in the process of replacing its 1978 and 1988 fuel models with 2016 NFDRS fuel models derived from the 40 fire behaviour models (Scott and Burgan 2005) by a similarity analysis to represent groupings of the 20 1978–1988 fuel models into categories of grass, grass/shrub, brush, timber, and slash (Table 2).1 Each capitalised letter in the table corresponds to the matching model named in Table 1, and the alphanumeric codes in the 2016 Fuel Model column identify the sourced reference fire behaviour models. We used the fuel model parameters listed in Andrews (2018) to compute the NFDRS ERC (Eqn 9) and RIP ERC (Eqn 12) for each of the fuel models in Table 2. The next section describes the ERC differences within and across groupings that resulted from these calculations, beginning with an intercomparison of the reaction intensities from IERC (Eqn 11) and IRIP (Eqn 8).

|
Reaction intensity intercomparisons across 2016 NFDRS fuel model groupings
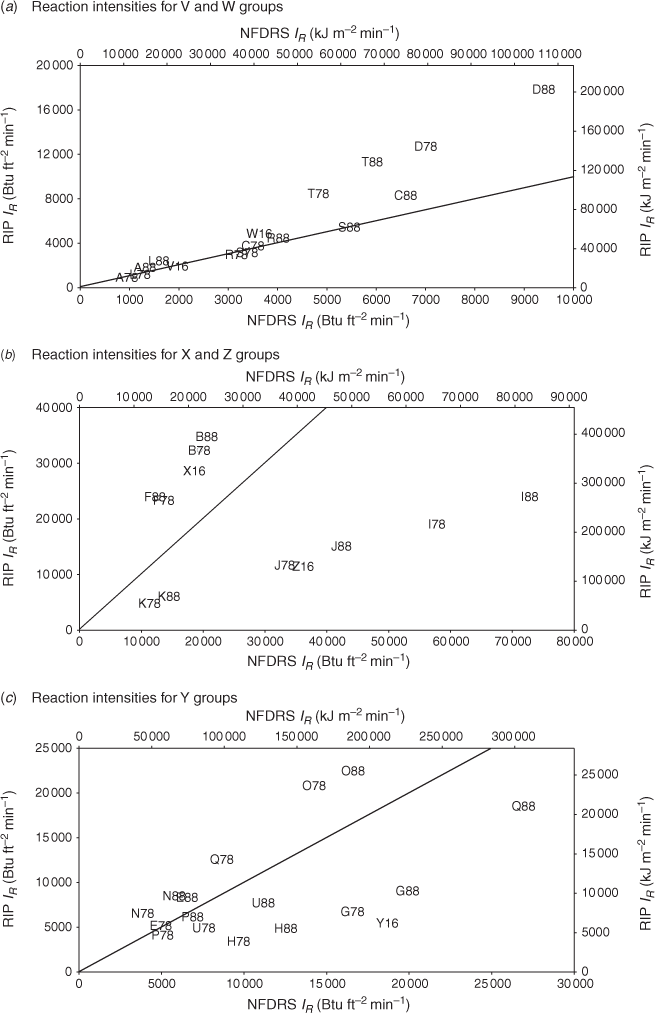
Fig. 2 shows plots of the NFDRS ERC reaction intensities computed from Eqn 11 for all NFDRS fuel models on the x-axis against the RIP reaction intensities from Eqn 8 on the y-axis. The left side of the sloping line has models for which the RIP reaction intensities are greater than the NFDRS reaction intensities, and the opposite is true for models to the right of the line. The minima for NFDRS and RIP reaction intensities are equal, but the maximum RIP intensity (model B, California chaparral) is just under half of the maximum NFDRS intensity (model I, heavy slash). Models I, J and Z represent slash fuels. Their high reaction intensities are a result of high loadings of exclusively dead fuels, including high drought load additions. The 1988 models are higher-valued than their 1978 counterparts, with the exception of model F (intermediate brush). In that case, the combination of σs and loadings lowered 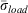 in the 1988 version and subsequently the reaction intensity. The cluster of points at the low end of reaction intensities is predominantly fine fuel models such as grass, grass/shrub and hardwood litter, which are examined in the next section. As the total fuel loadings increase, the reaction intensities increase, and the plotted points on either side of the line diverge conspicuously from each other.
in the 1988 version and subsequently the reaction intensity. The cluster of points at the low end of reaction intensities is predominantly fine fuel models such as grass, grass/shrub and hardwood litter, which are examined in the next section. As the total fuel loadings increase, the reaction intensities increase, and the plotted points on either side of the line diverge conspicuously from each other.
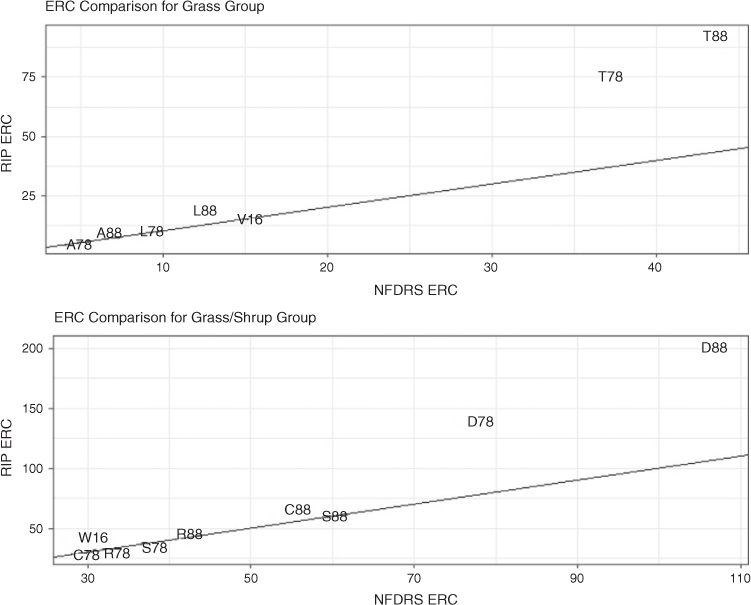
ERCs in the grass and grass/shrub groupings
The grass and grass/shrub groups occupy the low end of the ERC plane (Fig. 3), given their low loadings. The 2016 V model has ERCs similar to the Western grasses (model A) in the V group but fall short of the sagebrush–grass model (model T), especially for RIP ERCs. The range of ERCs in this group run from a minimum for annual Western grasses to a maximum for the 1988 sagebrush–grass RIP ERC. In the W group, ERCs tend higher because the loadings are greater than fuel models in the V group. Fuel model W had an NFDRS ERC that was the second lowest in the group. On average, the other models in the W group were larger by 25. The 1988 Southern rough model had the highest group NFDRS ERC, higher than the 2016 model W by 76. Its RIP ERC was nearly double that of its NFDRS ERC.
|
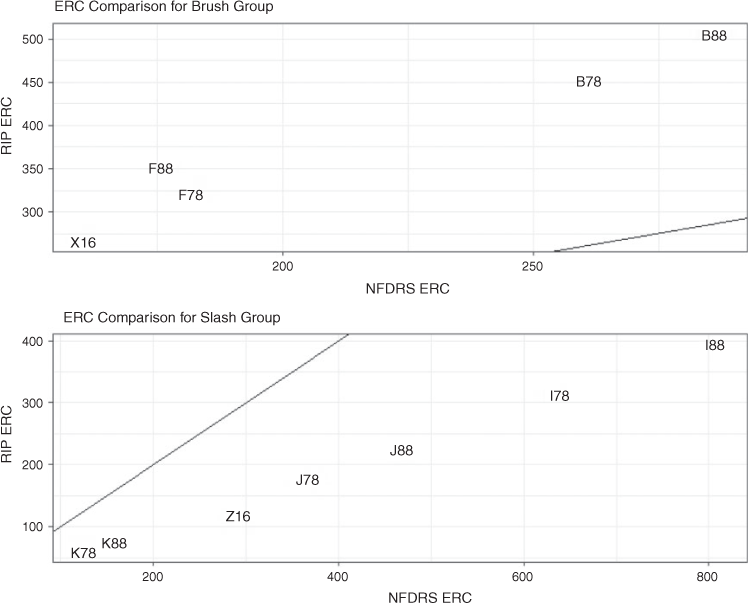
ERCs in the brush and slash groupings
The brush (X) and slash (Z) groups stand out from the rest with the largest ERCs of all groups (Fig. 4). The NFDRS ERC of the 1988 heavy slash model (model I) was highest. Within the brush group, the 2016 brush model X had the lowest NFDRS ERC. The 1988 California chaparral (model B) had a group high NFDRS ERC. Within the slash group, the heavy and exclusively dead loadings elevated the NFDRS ERCs. The 2016 slash model Z was, on average, lower than the other group members, but the light slash models (K) had the lowest group NFDRS ERCs. The 1988 heavy slash model (I) had the largest difference between the NFDRS ERC and the RIP ERC. The sloping line that defines the one-to-one ratio in the figures forms a sharp divide between the brush and slash groups indicative of the difference in the energy release calculation of NFDRS ERC and RIP. In Fig. 2, the RIP reaction intensities are up to ~150% of the NFDRS ERC reaction intensities in the brush group, while in the slash group, the NFDRS ERC reaction intensities are as high as almost 300% of the RIP reaction intensities.
|
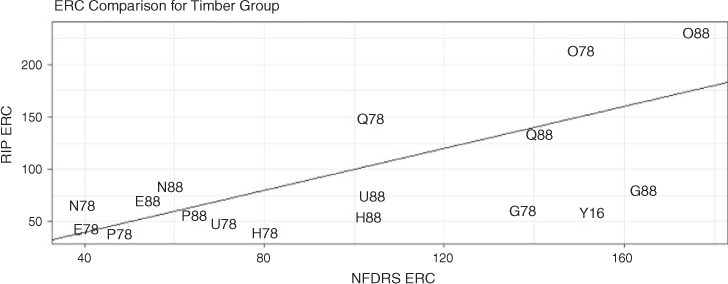
ERCs in the timber grouping
With eight members, the timber (Y) group is the largest of the five (Fig. 5). The models in this group cover the mid-range of the reaction intensity plane in Fig. 2. More models have NFDRS ERC reaction intensities that are greater than the corresponding RIP reaction intensities. The Y model in particular has a much higher NFDRS ERC reaction intensity than the RIP value, which is among the lowest in the group. Model Q (Alaskan black spruce) also stands out owing to the difference in NFDRS reaction intensity between the 1978 and 1988 versions. In this case, the  – 741 ft−1 (24 cm−1) for the 1978 and 1087 ft−1 (36 cm−1) for the 1988 versions – place both in that part of the reaction intensity function (Fig. 1) where the intensity gradient is steep for low packing ratios. A group of models clusters at the low end of reaction intensities that include hardwood litter (E), sawgrass (N), and Southern pine plantation (P).
– 741 ft−1 (24 cm−1) for the 1978 and 1087 ft−1 (36 cm−1) for the 1988 versions – place both in that part of the reaction intensity function (Fig. 1) where the intensity gradient is steep for low packing ratios. A group of models clusters at the low end of reaction intensities that include hardwood litter (E), sawgrass (N), and Southern pine plantation (P).
Unlike the preceding groups, the 2016 model Y in the timber group, timber litter, had an NFDRS ERC that was higher than most group members. Only the 1988 heavy dead short needle (G) and high pocosin (O) models had higher NFDRS ERCs. The 1978 winter hardwood litter and sawgrass models had the lowest NFDRS ERCs.
Discussion and conclusions
We said in the introduction that RIP, in a sense, simplifies the Rothermel model as it is currently applied. It does so by eliminating the requirement to calculate an average surface area/volume ratio, whether it be surface area- or loading-weighted. Instead, we use the component surface area/volume ratios as specified by the fuel model. We described the direct consequences of this model adaptation on ERC. RIP effectively passes the current ERC through a prism that separates it into its essential components, each with its own physical and temporal characteristics. The physical characteristics are given by the fuel model, but we have not covered temporal aspects, except in reference to residence times. We do so in what follows by contemplating the role played by fuel moisture in a RIP framework.
Eqn 12 gives ERCRIP for the special case when the moisture damping coefficient, ηm, is equal to 1. Generally, let
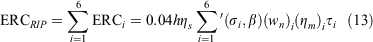
where Andrews (2018, p. 102) gives the moisture damping coefficient for component i as:
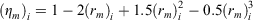
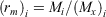
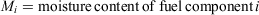
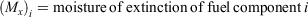
In addition to the surface area/volume ratio, net loading and residence time, each component now has its own moisture damping coefficient (ηm)i. The moisture damping coefficient varies from 0 to 1 as a function of the ratio of the fuel moisture to the moisture of extinction. Fuel moisture also varies by component in response to weather conditions and, for live fuels, the physiological plant processes that govern water content. The size and geometry of dead fuels strongly influence their moisture contents, which is why they are segregated by size and characterised by surface area/volume ratio. Their fuel moistures are also referenced by a timelag signature, i.e. 1-, 10-, 100-, and 1000-h, because they respond differently over time to weather conditions (Byram and Nelson 2015). A larger timelag indicates a slower response to weather (Bradshaw et al. 1984). Live fuel moisture estimates simulate the phenological response of herbaceous and woody vegetation as temporal changes of plant water content that are affected in part by daily to seasonal weather patterns. Estimating live fuel moisture content is a more complex issue than the simplistic approaches used in 1978 and 1988 NFDRS that may not reflect the flammability of live fuels (Jolly et al. 2014).
We conclude that the RIP method offers advantages to the current practice of computing reaction intensity and energy release for the following reasons. Instead of homogenising the fuel bed components to create a single size fuel of single loading, moisture content and residence time, the RIP perspective creates layers for each fuel component with fuel properties specified by the fuel model left intact, and with individual fuel moistures as determined by current practice. This obviously results in more information to consider, but it also offers distinct advantages, as follows:
-
There is no need to average fuel loadings, surface area/volume ratios and fuel moistures, making computations easier, and leaving specified fuel characteristics intact.
-
Temporal variability of fuel component properties is preserved.
-
Understanding the temporal complexity of fuel bed flammability is enhanced, because RIP requires tracking the fuel moisture of each component.
-
More flexibility exists to simulate the fuel bed reaction intensity characteristics.
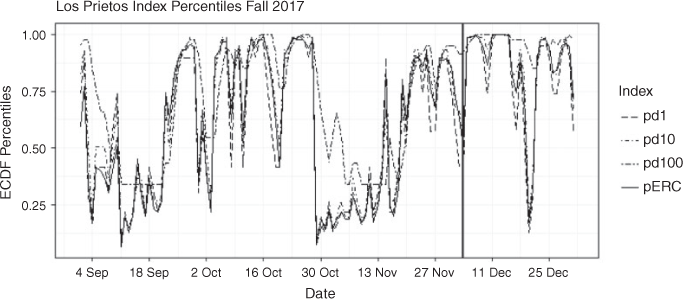
We note that the weather data that feed the NFDRS ERC almost exclusively are used to determine the fuel moistures of the various fuel components. Setting aside the dependencies of the dynamic transfer and drought load mechanisms on the Keetch–Byram Drought Index, Growing Season Index, live herbaceous fuel moisture and live woody greenness, note that the moisture damping coefficients are the only time-dependent variables in ERCRIP (Eqn 12). The {(ηm)i} carry the temporal variability of flammability of each fuel component. In effect, they quantify the dryness of each component on a scale from 0 to 1, where 0 means the fuel component is saturated and 1 means it is completely dry. We recast the moisture damping coefficients as dryness indices of the fuel components for fire danger assessment, call them d1, d10, d100, d1000, dherb and dwoody. We can plot these indices over time to track the flammability of each component as they change with weather conditions and seasonal effects. Here, we define flammability as the fractional degree to which the fuel component attains its optimum reaction velocity, 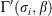 . Fig. 6 is a preliminary example from ongoing research of RIP strips for dryness of 1-, 10-, and 100-h dead fuels based on data from Los Prietos (34.53°N, 119.78°W) in the Los Padres National Forest, California, where the 1978 California chaparral fuel model (B) is used. The data cover the 2017 fall (autumn) period, when the Thomas Fire burned more than 100 000 ha in southern California, beginning on 4 December 2017. The dryness indices satisfy two attributes desired for fire danger rating (Bradshaw et al. 1984, p. 4): they are ‘physically interpretable in terms of fire occurrence and behavior,’ and they are ‘linearly related to the particular aspect of fire danger being evaluated’.
. Fig. 6 is a preliminary example from ongoing research of RIP strips for dryness of 1-, 10-, and 100-h dead fuels based on data from Los Prietos (34.53°N, 119.78°W) in the Los Padres National Forest, California, where the 1978 California chaparral fuel model (B) is used. The data cover the 2017 fall (autumn) period, when the Thomas Fire burned more than 100 000 ha in southern California, beginning on 4 December 2017. The dryness indices satisfy two attributes desired for fire danger rating (Bradshaw et al. 1984, p. 4): they are ‘physically interpretable in terms of fire occurrence and behavior,’ and they are ‘linearly related to the particular aspect of fire danger being evaluated’.
|
If the fuel loadings are kept static, the only variable terms in the RIP ERC (Eqn 13) are the moisture damping coefficients. The empirical cumulative distribution functions of the component ERCs, regardless of fuel model loadings, surface area/volume ratios, etc., then correspond to the empirical cumulative distribution functions of the dryness indices; therefore, the latter can be used to determine quantiles for ERC fire danger classes. The 1978 fuel model B used for Los Prietos is similar to a RIP model in that it is not subject to seasonal load transfers, because it does not have herbaceous fuels. The reaction intensity for ERC in this case, call it IERCB, is a version of Eqn 11 that introduces dead and live moisture damping coefficients, and a special case of the ERC reaction intensity given by Andrews (2018, p. 103):
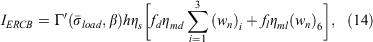
where
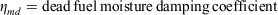
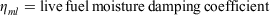
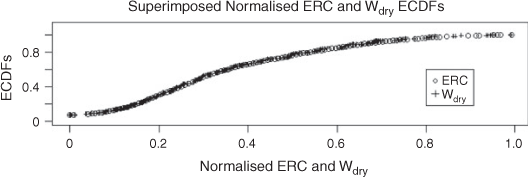
The bracketed quantity represents the load-weighted available fuel after moisture damping is taken into account, call it Wdry. After computing Wdry for the Los Prietos data, we normalised it by dividing by its maximum value, and also normalised the corresponding ERCs. When we calculated the empirical cumulative distribution functions of the normalised quantities and superimposed them, we obtained the result shown in Fig. 7. The empirical cumulative distribution functions match because Wdry completely captures the temporal variability of IERCB, hence of ERC for fuel model B.
|
The most versatile fuel model parameter is the dead fuel moisture of extinction, because it is used to calculate all of the dryness indices, including those of the live fuel components. By contrast, the live fuel moisture of extinction is a complex function of the dead fuel moisture of extinction, fuel loadings, surface area/volume ratios and dead fuel moistures (Andrews 2018, p. 101). Since the fuel components have different temporal responses to the environment, monitoring their respective dryness indices reveals the extent to which their trends are synchronised or not. We compared the daily percentiles of Los Prietos ERC and the dryness indices for fall 2017, obtained from their respective empirical cumulative distribution functions for the period 1997 to 2019. We found a good match between ERC and the 1-h dryness index time series (Fig. 8). The study of the relative impact that each fuel component has on ERC at Los Prietos is ongoing. More research is required for other fuel models at other locations.
Keeping fuel loadings static would eliminate the ability to mimic ERC enhancement due to seasonal drying by transferring live vegetation to dead categories or augmenting the latter from drought load additions as the NFDRS currently does. Alternatively under RIP, the Keetch–Byram Drought Index, Growing Season Index, or other seasonal variable of choice can be tied to the appropriate dryness index. In that case, we may be able to use the drying trend of the seasonal variable to increase the dryness index of the live herbaceous component, for example, instead of transferring live herbaceous vegetation load to the 1-h component. This may take the form of a linear response by effecting a proportional increase in the dryness index based on the drying trend of the seasonal variable, or it may be a non-linear response by effecting an increase in the moisture of extinction for live fuels. In certain respects, this alternative has an advantage over load transfers, because the latter affects ERC by more complex mathematical relationships involving 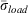 , the moisture damping coefficients and the load-weighted available fuel in the ERC reaction intensity.
, the moisture damping coefficients and the load-weighted available fuel in the ERC reaction intensity.
We return to the subject of using fuel load weighting to determine the characteristic surface/area volume ratio for ERC, which Bradshaw et al. (1984) said had no experimental basis. They did not describe exactly what problem was solved by using fuel load weighting, except to say that the influences of the different fuel components relative to the total fuel load would be reflected in the reaction intensity, hence ERC, through 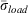 and the weighted fuel bed moisture. The NFDRS sets the surface area/volume ratio of 10-, 100-, and 1000-h fuels at 109, 30 and 8 ft−1, respectively (3.6, 1.0 and 0.26 cm−1). Including 1000-h fuel weighting to determine
and the weighted fuel bed moisture. The NFDRS sets the surface area/volume ratio of 10-, 100-, and 1000-h fuels at 109, 30 and 8 ft−1, respectively (3.6, 1.0 and 0.26 cm−1). Including 1000-h fuel weighting to determine 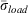 therefore lowers the average value considerably, given the low surface area/volume ratio of 1000-h fuels. This results in a lower IERC and a smaller range of variability of ERC, in spite of higher total fuel loads. Over the range of packing ratios in Fig. 1, the reaction intensities for the 1000-h and 100-h surface area/volume ratios are no greater than 1 Btu ft−2 min−1 (11 kJ m−2 min−1), and the maximum reaction intensity for 10-h is 92 Btu ft−2 min−1 (1012 kJ m2 min−1). Compare these with the maximum reaction intensity for a 1-h fuel with a surface area/volume ratio of 2000 ft−1 (67 cm−1), which is 2230 Btu ft−2 min−1 (24 530 kJ m−2 min−1).
therefore lowers the average value considerably, given the low surface area/volume ratio of 1000-h fuels. This results in a lower IERC and a smaller range of variability of ERC, in spite of higher total fuel loads. Over the range of packing ratios in Fig. 1, the reaction intensities for the 1000-h and 100-h surface area/volume ratios are no greater than 1 Btu ft−2 min−1 (11 kJ m−2 min−1), and the maximum reaction intensity for 10-h is 92 Btu ft−2 min−1 (1012 kJ m2 min−1). Compare these with the maximum reaction intensity for a 1-h fuel with a surface area/volume ratio of 2000 ft−1 (67 cm−1), which is 2230 Btu ft−2 min−1 (24 530 kJ m−2 min−1).
We also noted that using IERC (Eqn 11) instead of IR (Eqn 7) to calculate NFDRS ERC generally leads to a lower result that would underestimate the heat release per unit area (Eqn 10), because of the dead and live fuel load weighting used for IERC. On the other hand, dead and live fuel weighting does not influence the reaction intensities for the most energetic models, slash fuels, because they contain no live fuel component, and IERC = IR in that case. In fuel models with live fuels, IERC < IR because the total net fuel load is underrepresented in the former. This problem is inherited by NFDRS flame length and fireline intensity, which are functions of IERC. In fact, fireline intensity is a function of rate of spread, which in turn is a function of a different IR, resulting in two different reaction intensities for the same fuel bed. Studies have shown that the fireline intensity–flame length relationship produces better approximations for low-intensity fires, such as observed in prescribed burns in light grass and pine needle fuel beds (Byram 1959; Alexander and Cruz 2012; Weise et al. 2018).
The low reaction intensities for large fuels expose a critical weakness in the RIP approach, given the orders of magnitude difference between 1-h and larger dead fuels indicated by the reaction intensity function. This is not apparent in the NFDRS ERC because it uses 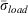 for all fuel components. Given that the largest fuel in the Rothermel report (1972) was 0.5 inch (1.3 cm), can the reaction intensity function be extrapolated to larger fuels? A preferred alternative would be to derive intensities for large fuels experimentally. In related studies, Albini and Reinhardt (1995) examined the burning rate of large woody fuels with respect to fuel properties and the fire environment. Anderson (1990) examined surface burning rate and flame lengths of stationary cribs composed of dimensional wood up to 15.24 cm (6 inches) in width. Using the total fuel surface area burn rate converted to a platform surface area burn rate of 0.0005 g cm−2 s−1, and assuming a fuel heat content of 16.5 kJ g−1 yielded a heat release rate (IR) of 4950 kJ m−2 min−1 (436 Btu ft−2 min−1), which is much smaller than the IR reported in Rothermel (1972) for cribs composed of smaller fuels.
for all fuel components. Given that the largest fuel in the Rothermel report (1972) was 0.5 inch (1.3 cm), can the reaction intensity function be extrapolated to larger fuels? A preferred alternative would be to derive intensities for large fuels experimentally. In related studies, Albini and Reinhardt (1995) examined the burning rate of large woody fuels with respect to fuel properties and the fire environment. Anderson (1990) examined surface burning rate and flame lengths of stationary cribs composed of dimensional wood up to 15.24 cm (6 inches) in width. Using the total fuel surface area burn rate converted to a platform surface area burn rate of 0.0005 g cm−2 s−1, and assuming a fuel heat content of 16.5 kJ g−1 yielded a heat release rate (IR) of 4950 kJ m−2 min−1 (436 Btu ft−2 min−1), which is much smaller than the IR reported in Rothermel (1972) for cribs composed of smaller fuels.
The intercomparisons of ERC for the NFDRS fuel models were presented to introduce the RIP concept. We offer the RIP process to simplify computations and decompose energy release into its basic components, each having its own temporal characteristics through the dryness index. We found that the dead and live load weighting factors used to calculate IERC artificially manipulate the net fuel load, which invalidates its conceptual relationship to energy release, flame length and fireline intensity.
We remarked earlier that this study did not include all the factors that make up the Rothermel spread equations. With that in mind, we are limited in extending the RIP concept to fire spread modelling. A natural extension of partitioning reaction intensity is partitioned spread. Conceptually, this takes the form of multiple flaming fronts initially propagating from the same ignition point but thereafter separating at their respective rates of spread. Without considering the factors affecting fire spread that were not covered in this study, it would be difficult to even speculate how such separation would occur. The rate of spread is strongly influenced by the surface area/volume ratio of the 1-h fuel component. Using an average surface area/volume ratio instead will generally decrease the resultant reaction intensity, hence spread rate, substantially. We suggest that in cases where simulations are underestimating the rate of spread of a fire, one can reduce the fuel models used to 1-h dead fuels exclusively, which will more than likely increase the simulated spread rate as a result of a higher reaction intensity. In effect, this isolates the simulation to the dead fine fuel layer, keeping the other fuel components in the background. More research is required to flesh out concepts implicit to RIP not covered here.
We conclude with an assessment of research related to the present study that is needed to advance its relevant science and technology objectives. First and foremost is that the reaction intensity functions originating with the Rothermel model and modified by RIP both falsely assume that the total reaction intensity of a mixed fuel bed is the sum of the component reaction intensities. Instead, the fine fuel components provide the initial source of heat energy, which the larger fuels use to ignite in turn. This requires the model to have mechanisms that describe interactions between fuel components that are conceptually and mathematically more complex. Albini et al. (1995) worked on this problem in both laboratory and field settings. The laboratory experiments were similar to Rothermel’s (1972), but fuel components of up to six different sizes were used that encompassed all four dead fuel components. The approach in effect partitioned the fuel bed. Their study concluded with encouraging results but they cited model weaknesses that required more work. This objective remains unfulfilled.
Since its debut, the Rothermel model has found roles that go far beyond its initial purpose for fire danger rating. It now serves in a highly complex coupled model framework, WRF-SFIRE, that describes atmosphere–fire interactions to simulate weather and fire feedback processes that locally affect each, and to simulate the effects of both on air quality (Mandel et al. 2011; Mandel et al. 2014). Recent large fires in the western US generated smoke that degraded air quality in the skies of New York and Washington, DC.2 This can happen when the heat energy from the fires injects smoke high enough in the atmosphere that it is carried over long distances. This requires knowledge of the time-dependent energy release over the entire actively burning area, not just the fire front. WRF-SFIRE incorporated the previously mentioned model developed by Albini and Reinhardt (1995), which they intended to determine burnout rates in large woody fuels, but in their judgement was incomplete for operational use at the time of the report. There is still a need for a model that simulates heat production from large woody fuels, whether to predict air quality effects that large fires have on distant cities, or simply to improve fire danger assessments.
None of the work we report here is ready for operational use. We cited quotes from those involved in the development of the Rothermel model and the NFDRS that recognised the pitfalls and weaknesses they faced. We believe some of their concerns are still valid and hope that we have posed questions and identified avenues of research on the reaction intensity function that eventually lead to improvements in fire danger analysis and prediction.
Conflicts of interest
The authors declare no conflicts of interest.
Declaration of funding
The lead author gratefully acknowledges funding for part of this work by the NSF-PREEVENTS ICER-1664173 grant through the Department of Geography, University of California, Santa Barbara, and the support of the Center of Excellence for Earth Systems Modelling and Observation at Chapman University, Orange, CA, and the USDA Forest Service, Pacific Southwest Research Station, Riverside, CA.
Acknowledgements
We thank the reviewers of a previous draft of the manuscript for suggestions that vastly improved the succeeding version.
References
Albini FA (1976) Estimating wildfire behavior and effects. USDA Forest Service, Intermountain Forest and Range Experiment Station, General Technical Report INT-30. (Ogden, UT) Available at http://www.fs.fed.us/rm/pubs_int/int_gtr030.pdf [Verified 19 March 2021]Albini FA, Reinhardt ED (1995) Modeling ignition and burning rate of large woody natural fuels. International Journal of Wildland Fire 5, 81–91.
| Modeling ignition and burning rate of large woody natural fuels.Crossref | GoogleScholarGoogle Scholar |
Albini FA, Brown JK, Reinhardt ED, Ottmar RD (1995) Calibration of a large fuel burnout model. International Journal of Wildland Fire 5, 173–192.
| Calibration of a large fuel burnout model.Crossref | GoogleScholarGoogle Scholar |
Alexander ME, Cruz MG (2012) Interdependencies between flame length and fireline intensity in predicting crown fire initiation and crown scorch height. International Journal of Wildland Fire 21, 95–113.
| Interdependencies between flame length and fireline intensity in predicting crown fire initiation and crown scorch height.Crossref | GoogleScholarGoogle Scholar |
Anderson HE (1990) Relationship of fuel size and spacing to combustion characteristics of laboratory fuel cribs. USDA Forest Service, Intermountain Research Station, Research Paper INT-424. (Ogden, UT). Available at https://www.fs.fed.us/rm/pubs_int/int_rp424.pdf [Verified 19 March 2021]
Andrews PL (1986) BEHAVE: Fire behavior prediction and fuel modeling system – BURN subsystem, part 1. USDA Forest Service, Intermountain Forest and Range Experiment Station, General Technical Report INT-194. (Ogden, UT).
Andrews PL (2008) BehavePlus fire modeling system, version 4.0: Variables. USDA Forest Service, Rocky Mountain Research Station, General Technical Report RMRS-GTR-213WWW. (Fort Collins, CO)
Andrews PL (2018) The Rothermel surface fire spread model and associated developments: A comprehensive explanation. USDA Forest Service, Rocky Mountain Research Station, General Technical Report RMRS-GTR-371. (Fort Collins, CO)
Bradshaw L, Deeming JE, Burgan RE, Cohen JD (1984) The 1978 National Fire-Danger Rating System: technical documentation. USDA Forest Service, Intermountain Forest and Range Experiment Station, General Technical Report INT-169. (Ogden, UT)
Burgan RE (1988) 1988 revisions to the 1978 National Fire Danger Rating System. USDA Forest Service, Southeastern Forest Experiment Station, Research Paper SE-273. (Asheville, NC)
Byram GM (1959) Combustion of forest fuels. In ‘Forest fire: control and use’. (Ed. KP Davis) pp. 61–89. (McGraw-Hill: New York)
Byram GM, Nelson RM, Jr (2015) An analysis of the drying process in forest fuel material. USDA Forest Service, Southern Research Station, e-General Technical Report SRS-200. (Asheville, NC) Available at https://www.treesearch.fs.fed.us/pubs/47925 [Verified 19 March 2021]
Coen JL, Cameron M, Michalakes J, Patton EG, Riggan PJ, Yedinak KM (2013) WRF-Fire: coupled weather–wildland fire modeling with the Weather Research and Forecasting Model. Journal of Applied Meteorology and Climatology 52, 16–38.
| WRF-Fire: coupled weather–wildland fire modeling with the Weather Research and Forecasting Model.Crossref | GoogleScholarGoogle Scholar |
Cohen JD (1986) Estimating fire behavior with FIRECAST: user’s manual. USDA Forest Service, Pacific Southwest Forest and Range Experiment Station, General Technical Report PSW-90. (Berkeley, CA) Available at http://www.fs.fed.us/psw/publications/documents/psw_gtr090/psw_gtr090.pdf [Verified 19 March 2021]
Cohen JD, Deeming JE (1985) The National Fire Danger Rating System: Basic equations. USDA Forest Service, Pacific Southwest Forest and Range Experiment Station, General Technical Report PSW-82. (Berkeley, CA)
Deeming JE, Lancaster JW, Fosberg MA, Furman RW, Schroeder MJ (1972) The National Fire-Danger Rating System. USDA Forest Service, Rocky Mountain Forest and Range Experiment Station, Research Paper RM-84. (Fort Collins, CO)
Deeming JE, Burgan RE, Cohen JD (1977) The National Fire Danger Rating System – 1978. USDA Forest Service, Intermountain Forest and Range Experiment Station, General Technical Report INT-39. (Ogden, UT)
Finney MA (1998) FARSITE: Fire Area Simulator – Model development and evaluation. USDA Forest Service, Rocky Mountain Research Station, Research Paper RMRS-RP-4. (Ogden, UT)
Frandsen WH (1971) Fire spread through porous fuels from the conservation of energy. Combustion and Flame 16, 9–16.
| Fire spread through porous fuels from the conservation of energy.Crossref | GoogleScholarGoogle Scholar |
Furman JH, Linn R (2018) What is FIRETEC (and why should I care)? Fire Management Today 76, 33–36.
Jolly WM, Hadlow AM, Huguet K (2014) De-coupling seasonal changes in water content and dry matter to predict live conifer foliar moisture content. International Journal of Wildland Fire 23, 480–489.
| De-coupling seasonal changes in water content and dry matter to predict live conifer foliar moisture content.Crossref | GoogleScholarGoogle Scholar |
Linn R, Reisner J, Colman JJ, Winterkamp J (2002) Studying wildfire behavior using FIRETEC. International Journal of Wildland Fire 11, 233–246.
| Studying wildfire behavior using FIRETEC.Crossref | GoogleScholarGoogle Scholar |
Linn RR, Goodrick SL, Brambilla S, Brown MJ, Middleton RS, O’Brien JJ, Hiers JK (2020) QUIC-fire: A fast-running simulation tool for prescribed fire planning. Environmental Modelling & Software 125, 104616
| QUIC-fire: A fast-running simulation tool for prescribed fire planning.Crossref | GoogleScholarGoogle Scholar |
Mandel J, Beezley JD, Kochanski AK (2011) Coupled atmosphere–wildland fire modeling with WRF 3.3 and SFIRE 2011. Geoscientific Model Development 4, 591–610.
| Coupled atmosphere–wildland fire modeling with WRF 3.3 and SFIRE 2011.Crossref | GoogleScholarGoogle Scholar |
Mandel J, Amram S, Beezley JD, Kelman G, Kochanski AK, Kondratenko VY, Lynn BH, Regev B, Vejmelka M (2014) Recent advances and applications of WRF-SFIRE. Natural Hazards and Earth System Sciences 14, 2829–2845.
| Recent advances and applications of WRF-SFIRE.Crossref | GoogleScholarGoogle Scholar |
National Wildfire Coordinating Group (2002) Gaining an understanding of the National Fire Danger Rating System. PMS 932. Available at https://www.nwcg.gov/sites/default/files/products/pms932.pdf [Verified 19 March 2021]
Peterson SH, Morais ME, Carlson JM, Dennison PE, Roberts DA, Moritz MA, Weise DR (2009) Using HFire for spatial modeling of fire spread in shrublands. USDA Forest Service, Pacific Southwest Research Station, Research Paper PSW-RP-259. (Albany, CA). Available at http://www.fs.fed.us/psw/publications/documents/psw_rp259/psw_rp259.pdf [Verified 19 March 2021]
Rothermel RC (1972) A mathematical model for predicting fire spread in wildland fuels. USDA Forest Service, Intermountain Forest and Range Experiment Station, Research Paper INT-115. (Ogden, Utah)
Scott JH, Burgan RE (2005) Standard fire behavior fuel models: A comprehensive set for use with Rothermel’s surface fire spread model. USDA Forest Service, Rocky Mountain Research Station, General Technical Report RMRS-GTR-153. (Fort Collins, Colorado).
Weise DR, Fletcher TH, Cole W, Mahalingam S, Zhou X, Sun L, Li J (2018) Fire behavior in chaparral: evaluating flame models with laboratory data. Combustion and Flame 191, 500–512.
| Fire behavior in chaparral: evaluating flame models with laboratory data.Crossref | GoogleScholarGoogle Scholar |
Wilson RA, Jr (1980) Reformulation of forest fire spread equations in SI units. USDA Forest Service, Intermountain Forest and Range Experiment Station, Research Note INT-292. (Ogden, UT).
1 Information from National Interagency Fire Center web page accessed on 2 September 2019 at https://gacc.nifc.gov/eacc/predictive_services/fuels_fire-danger/documents/Overview%20of%20NFDRS2016%20and%20Implementation%20and%20Evaluation.pdf
2 https://www.bbc.com/future/article/20200821-how-wildfire-pollution-may-be-harming-your-health