The effect of fuel bed height in grass fire spread: addressing the findings and recommendations of Moinuddin et al. (2018)
Miguel G. Cruz A B , Andrew L. Sullivan A and James S. Gould A
A and James S. Gould A
A CSIRO, GPO Box 1700, Canberra, ACT 2601, Australia.
B Corresponding author. Email: miguel.cruz@csiro.au
International Journal of Wildland Fire 30(3) 215-220 https://doi.org/10.1071/WF19186
Submitted: 8 November 2019 Accepted: 10 January 2020 Published: 7 February 2020
Abstract
A recent numerical simulation study by Moinuddin et al. (2018) determined that over a specific range of Froude numbers defined by them as ‘plume mode’, grass fuel height has a strong inverse effect on the rate of fire spread in grasslands. They then suggested that a relationship for effect of fuel height derived from their simulation results could be used to support fire management decision-making. The present analysis used fire spread measurement data from two outdoor experimental burning studies in grass fuels where an explicit control of fuel height was imposed to verify the realism of their results. It was found that a reduction in grass height, with or without removal of the cut fuel and regardless of the Froude number, led to a significant reduction in rate of fire spread, a result opposite to the simulations obtained by Moinuddin et al. (2018).
Additional keywords: crop fuels, fire behaviour experiments, fire mitigation, grass fuels, headfire.
Introduction
Moinuddin et al. (2018), hereafter MSM18, used simulations from a physics-based model (Mell et al. 2007) to quantify the effect of fuel height on the rate of spread of grass fires. The simulations, based on fixed environmental conditions and an artificial fuel bed resembling grass with variable height (bulk density held constant; fuel load varied proportionally with fuel height), yielded two disparate trends in fire characteristics. The authors interpreted the results as the signal of the existence of two distinct flame spread regimes, termed ‘boundary layer mode’ and ‘plume mode’, and suggested a Froude number (Fr, as calculated by Apte et al. 1991) of 0.5 as the threshold separating these spread modes. From the simulation-derived effect of grass fuel height on rate of fire spread for the so-called ‘plume mode’ (Fr <0.5), they proposed a parametric relationship between these two variables. The relationship suggested a strong and inverse effect of grass fuel height on rate of fire spread (i.e. a reduction in fuel height will result in a substantial increase in rate of fire spread). MSM18 noted that ‘…these results shed light on dependence on grass height and it is useful for fire agencies to have a correlation between RoS of the fire and grass height to assist in strategic decision-making’ (p. 811) and further suggested the broader use of physics-based model simulations to develop parametric models in support of fire management decision-making.
Although the MSM18 grass height–rate-of-spread relationship might be considered novel, it is counter-intuitive. After all, a common fire mitigation measure is to mow or cut grass to reduce the spread and intensity potential of a wildfire (e.g. NSW Rural Fire Service (RFS) 2010; Clements et al. 2019; Country Fire Authority (CFA) 2019). As they stand, the MSM18 results would necessitate a rethink of how grass fire mitigation measures should be conducted; instead of decreasing grass fuel height as a fuel hazard reduction treatment, grasses should be left in their natural state and their growth even encouraged.
In our view, it is important to comment on MSM18’s results and conclusions, namely due to their potential applied implications. At a time when computer-based modelling is suggested as a way to advance our understanding of fire behaviour and produce applied outcomes (Hoffman et al. 2018), often due to the difficulties and costs of carrying out field-based research (Alexander and Quintilio 1990), it is critical to identify incongruencies in modelling results before they become established and widely accepted (also apposite to results from field experiments and their analysis).
The objective of this comment is to verify MSM18’s simulation results through the analysis of robust empirical evidence of the effect of grass fuel bed height on the forward rate of fire spread as measured in field-scale experiments.
Methods
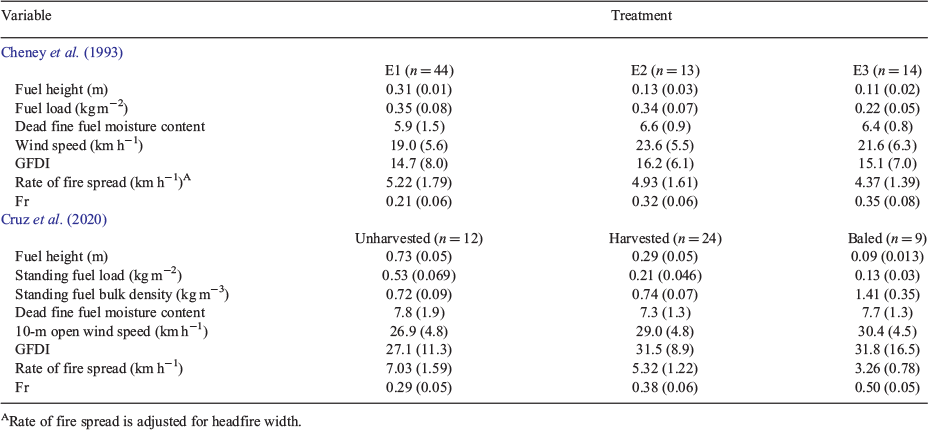
To analyse the effect of grass height in fire spread rate, we used two datasets (Cheney et al. 1993; Cruz et al. 2020) of free-spreading experimental fires where an explicit manipulation of grass fuel height has been conducted, mimicking the simulated treatment of fuels in MSM18. We used the Eriacchne spp. (locally known as kerosene grass) subset (71 experimental fires) of the CSIRO Annaburro Station study in the Northern Territory, Australia, as described by Cheney et al. (1993). This subset contained three grass states: E1 – natural undisturbed grass (control), and the result of two fuel manipulation treatments; E2 – grasses cut to 50% of their natural height and clippings left on site; and E3 – grasses cut to 50% of their natural height and the clippings removed.
We also used data from Cruz et al. (2020) fire spread experiments in a wheat crop (Triticum spp.) in Victoria, Australia, for three different fuel conditions: Harvested (control); Unharvested (treatment 1); and harvested and baled (treatment 2, hereafter termed Baled). Fires in this dataset were conducted as simultaneous paired experiments (control v. treatment) to observe the direct effect of differences in fuel structure on fire behaviour.
Fuels in both the Cheney et al. (1993) and Cruz et al. (2020) datasets were destructively sampled and reported on a per experimental fire basis. Readers wanting detailed information on the methods used for weather and fire behaviour measurements should consult the original publications.
The Apte et al. (1991) Froude number (Fr) was calculated for each fire in the Cheney et al. (1993) and Cruz et al. (2020) datasets utilising the methodology of MSM18.
For the Cheney et al. (1993) dataset, we analysed the relationship between fuel height and rate of fire spread through correlation and linear regression analysis. A Tukey’s post hoc test was used to conduct multiple comparisons of the three grass condition characteristics and associated rate of fire spread. For the Cruz et al. (2020) dataset, we conducted direct comparisons between the relevant variables through paired t-tests. Given the reduced sample size of each population, the Shapiro–Wilk test of normality was used to determine if the variables were normally distributed. Grassland Fire Danger Index (GFDI), a surrogate of fire spread potential incorporating the effect of wind speed and fuel dryness, was calculated using the Mk 3 equation given by Noble et al. (1980). All statistical analysis was conducted using the software R (R Core Team 2018).
Results
Cheney et al. (1993) dataset
Table 1 summarises the average fuel characteristics, rate of fire spread and Fr for each of the grass conditions (see also Fig. S1 available as Supplementary Material to this paper). The changes in fuel height are within the range of the simulated treatments in MSM18, with the E3 treatment most closely replicating, in the real world, the simulated treatment (i.e. a reduction in fuel height with the removal of cut fuel particles leaving fuel bed bulk density mostly constant). Fr1 in the dataset varied between 0.11 and 0.47, with lower values associated with the experiments carried out in the undisturbed grasses (E1).
|
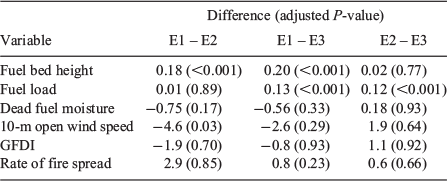
Average grass fuel height varied between 0.31 m in the control (E1) to 0.13 and 0.11 for E2 and E3. A Tukey multiple comparison test revealed significant differences in fuel height between E1 and E2 or E3 (Table 2). No significant differences were found for dead fuel moisture or GFDI. The control had the lowest 10-m open wind of the three subsets, with the difference between E1 and E2 being significant (P < 0.05; Table 2), but not significant between E1 and E3. Despite the lower average wind speed, E1 had the highest average rate of fire spread (Table 1), but the differences between the control and treatments were not significant (Table 2).
|
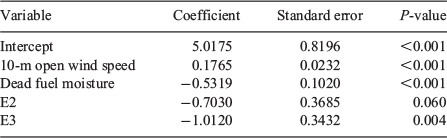
Linear regression analysis of rate of fire spread with wind speed, dead fuel moisture content and height reduction treatment as a categorical variable resulted in an adjusted R2 of 0.60 and indicated a reduction in rate of fire spread with treatment (Table 3), i.e. a reduction in fuel height resulted in a reduction in rate of fire spread. The coefficients for E2 and E3 suggest a bulk reduction in rate of fire spread of −0.7 and −1.0 km h−1, respectively, over the control. The magnitude of this reduction is notable given the mean and range in the rate of fire spread for the dataset (Fig. S1). Notably, the effect of E2 was quantified as being weakly significant (P = 0.06), whereas the effect of E3 was quantified as highly significant (P = 0.004).
|
Cruz et al. (2020) dataset
Paired burns (i.e. control v. treatment) allowed direct contrast of the effect of fuel height on rate of fire spread for two fuel configurations, i.e. Harvested v. Unharvested and Harvested v. Baled. Table 1 provides a summary of the range in fuel, weather, Fr and rate of spread data per crop condition (see also Fig. S2). Mean fuel heights varied between 0.73 m in the Unharvested condition, 0.29 m in the Harvested and 0.09 m in the Baled condition. Fuel load for standing fuels varied as: Unharvested: 0.53 kg m−2; Harvested: 0.21 kg m−2; and Baled: 0.13 kg m−2. Harvesting operations in the Harvested and Baled treatments led to the formation of a matted fuel layer on the ground. The structure of this layer did not differ between the Harvested and Baled conditions, with an average matted fuel load of 0.23 kg m−2. No matted or ground fuels were present in the Unharvested condition. Importantly, in the experimental fires the ignition interface was observed to spread in the standing fuels, with the charring and consumption of matted fuels occurring a few metres behind the leading edge of the flame front (Cruz et al. 2019). As such, despite the presence of matted fuels, the dominance of the standing fuels driving fire propagation approaches the artificial condition used by MSM18 of only standing fuels with constant bulk density. The matted fuels, when present, contributed to the overall energy release but not to the net horizontal heat flux as per Thomas et al. (1964) and thus rate of spread. All Unharvested and Harvested experiments were characterised by Fr <0.5. Fr averaged 0.5 in the Baled condition, with four fires characterised by Fr being between 0.5 and 0.58. Overall, 92% of the fires in this dataset had Fr <0.5.
Figure S2 shows the marked differences in fuel structure between the three configurations, similarities in environmental burning conditions (10-m open wind speed, fuel moisture and GFDI), and the notable differences in observed rate of fire spread. Figure 1 provides visual contrast between fires burning in the three fuel types under similar fire danger conditions. Overall, the Unharvested condition showed the highest rate of fire spread, with an average rate of spread of 7.03 km h−1 and a maximum value of 10.15 km h−1. In contrast, the Baled condition was characterised by the lowest rates of fire spread, with an average value of 3.26 km h−1 within a range of 2.36 and 4.58 km h−1.
The 10-m open wind speed, standing fuel moisture content, GFDI and rate of fire spread were found to be normally distributed according to the Shapiro–Wilk test of normality (P > 0.05). Paired t-tests for differences between control–treatment pairs found significant differences in rate of fire spread, with the Unharvested crop condition fires spreading on average 2.1 km h−1 faster than the fires in the Harvested condition (Table 4). Similar results were obtained for the comparison between the Baled and Harvested condition fires, with the fires spreading on average 2.1 km h−1 faster in the taller fuel condition. Nonetheless, this last comparison is not strictly within the Fr <0.5 flow regime of MSM18 and can be discounted from the analysis.

|
Discussion
Empirical evidence
The results of our analyses of experimental fire spread data in field conditions are clear and unequivocal. For the range of fuel bed heights typical of temperate grasslands (e.g. Sneeuwjagt and Frandsen 1977; Anderson 1982; Andrews et al. 2006) and Fr constraints used by MSM18 (Fr <0.5), a reduction in grass height, with or without removal of the cut fuel (i.e. with or without change in bulk density), led to a corresponding reduction in average rate of fire spread. This is the opposite of the results presented by MSM18, in which a strong and inverse effect was determined. Cohen et al. (2006) reasoned that increases in fuel depth allow for the extension of the flow length of potential flame contact with unburned fuel, with fuel bed depth being directly related to potential convective heat transfer for flame spread. A reduction of fuel bed height would reduce the flame potential flow length, and consequently reduce the efficiency of convective heat transfer to fuels in the path of the advancing fire.
We disagree with the statement by MSM18 that the dependence of rate of fire spread on grass height is a matter of debate. The results obtained by Cheney et al. (1993) on a broader analysis than the one presented here showed a direct and significant correlation between fuel bed height in grasslands and rate of fire spread (r = 0.23, P < 0.01). Cruz et al. (2016, 2018) failed to find such a relationship because the data in these studies originated from a variety of structurally different grasslands and autocorrelations between fuel height and fuel load or fuel height and fuel particle surface area to volume ratio masked the effect of fuel height. For example, when considering unmodified grasses, finer grasses with higher surface area to volume ratios tend to be shorter. In contrast, the high fuel load grasses in the Cruz et al. (2018) study were taller and coarser. In the Cruz et al. (2018) dataset, fuel load showed a stronger relationship with rate of fire spread (r = −0.50; P < 0.001) than fuel height and showed a reduction in the rate of fire spread for values above ~0.6 kg m−2. Given these autocorrelation issues, one should not attempt to derive a statistical secondary effect of fuel height on rate of fire spread from the datasets of Cruz et al. (2016, 2018). With the data used in the present comment, we removed any confounding effects of fuel coarseness from the analysis and thus can directly replicate the simulation assumptions in MSM18.
The effect of grass height observed in the Cheney et al. (1993) and Cruz et al. (2020) subsets of data are distinct in magnitude. This is not surprising because the observed reduction in rate of fire spread depends on other structural characteristics of the fuel bed, including the absolute reduction in fuel height and associated burning conditions, namely the wind speeds, under which the fires were conducted.
A reduction in fuel bed height while maintaining bulk density, as simulated by MSM18, results in a corresponding decrease in the fuel available for combustion. It is not easy to disentangle the effect of these two fuel characteristics on the rate of fire spread, but experimental results in grasslands (Cheney et al. 1993), forest fuels (McCaw et al. 2012) and shrublands (Anderson et al. 2015) suggest that fuel bed height has a stronger effect than fuel load. These findings are applicable when fuel loads are not limiting in regard to the formation or oxidation of gas-phase volatiles that we see as flame.
Modelling assumptions
Without a detailed forensic investigation of the physics-based model’s formulations, assumptions and settings, it is impossible to isolate any one reason as to why MSM18 obtained the results they did. However, several candidate factors may be identified from the detail provided in their paper. Foremost among these could be the representation of the fuel as a homogeneous layer (i.e. boundary fuel) and the inherent assumptions regarding the effect on drag in air flow over the fuel bed. These assumptions include that heat is released from above the fuel bed rather than within the fuel bed, and that grass blades were modelled solid cylinders (with commensurate drag coefficient) that are not malleable to bend with the wind, thus affecting roughness length (Penman and Long 1960), which might perhaps mean the drag force imposed by the fuel on the air flow over it is overstated. The result of this could be an underprediction of the dynamic forces and an overprediction of the buoyant forces at the flame front.
Concluding remarks
We commend the efforts of MSM18 to attempt to derive an understanding of the effect of fuel characteristics on fire behaviour through numerical simulations using a physics-based model. Such approaches are necessary to improve model behaviour and ultimately an understanding of fire dynamics. Nonetheless, awareness of existing empirical evidence, namely from well controlled field experiments, is key to evaluating the realism of numerical experiments and is ultimately necessary if one aims to use physics-based models to investigate still unanswered questions on the dynamic nature of wildfire propagation and particularly the response of fire to changes in fuel structure. There are several published results and datasets available from studies on grass fire propagation that were not mentioned by MSM18, in particular those from Cheney et al. (1993), a large-scale experimental study aimed at understanding the effect of grass fuel load and height on fire behaviour. There are also other relevant published data available, such as in Sneeuwjagt and Frandsen (1977) and Clark (1983), where one can investigate the effect of grass fuel bed height on rate of fire spread. Awareness of these datasets and the empirical trends would have allowed MSM18 to understand the incongruencies in their simulation results, the likely causes of it, and allow for improvements in the model understanding and future behaviour.
Often modellers aim to publish model evaluation studies where it is shown how well a model fits the real-world data. This is not difficult to achieve with fire behaviour models. Given the degrees of freedom in a physics-based model of fire behaviour, one can always fit a model to an experiment. Given the unknowns in the physical processes driving fire propagation, the uncertainty inherent in any fire quantity measurement, either indoors or outdoors, and the coarseness of existent numerical models, we believe that modellers should not attempt to evaluate or ‘validate’ a model by showing how well the model fits reality, but strive to show how models fail to replicate observed behaviour (Watts 1987). Failure drives improvement. Investigating a model’s poor or erroneous results will contribute to its improvement to a level where it may perform adequately over a broad range of conditions and, ultimately, be able to be used to contribute to successful fire management.
Conflict of interest
The authors declare that they have no conflicts of interest.
Acknowledgements
We thank Wesley Page and Marty Alexander for their comments on a draft of this manuscript.
References
Alexander ME, Quintilio D (1990) Perspectives on experimental fires in Canadian forestry research. Mathematical and Computer Modelling 13, 17–26.| Perspectives on experimental fires in Canadian forestry research.Crossref | GoogleScholarGoogle Scholar |
Anderson HE (1982) Aids to determining fuel models for estimating fire behavior. USDA Forest Service, Intermountain Forest and Range Experimental Station, General Technical Report No. INT-122. (Odgen, UT, USA)
Anderson WR, Cruz MG, Fernandes PM, McCaw L, Vega JA, Bradstock RA, Fogarty L, Gould JS, McCarthy G, Marsden-Smedley JB, Matthews S, Mattingley G, Pearce HG, van Wilgen BW (2015) A generic, empirical-based model for predicting rate of fire spread in shrublands. International Journal of Wildland Fire 24, 443–460.
| A generic, empirical-based model for predicting rate of fire spread in shrublands.Crossref | GoogleScholarGoogle Scholar |
Andrews PL, Anderson SAJ, Anderson WR (2006) Evaluation of a dynamic load transfer function using grassland curing data. In ‘Fuels management: how to measure success conference proceedings,’ 28–30 March 2006, Portland, OR, USA. (Eds PL Andrews, BW Butler) pp. 381–395. USDA Forest Service, Rocky Mountain Research Station, Proceedings RMRS-P-41. (Fort Collins, CO, USA)
Apte V, Bilger R, Green A, Quintiere J (1991) Wind-aided turbulent flame spread and burning over large-scale horizontal PMMA surfaces. Combustion and Flame 85, 169–184.
| Wind-aided turbulent flame spread and burning over large-scale horizontal PMMA surfaces.Crossref | GoogleScholarGoogle Scholar |
Cheney NP, Gould JS, Catchpole WR (1993) The influence of fuel, weather and fire shape variables on fire-spread in grasslands. International Journal of Wildland Fire 3, 31–44.
| The influence of fuel, weather and fire shape variables on fire-spread in grasslands.Crossref | GoogleScholarGoogle Scholar |
Clark RG (1983) Threshold requirements for fire spread in grassland fuels. PhD Thesis, Texas Tech University. (Lubbock, TX, USA)
Clements CB, Kochanski AK, Seto D, Davis B, Camacho C, Lareau NP, Contezac J, Restaino J, Heilman WE, Krueger SK, Butler B, Ottmar RD, Vihnanek R, Flynn J, Filippi J-B, Barboni T, Hall DE, Mandel J, Jenkins MA, O’Brien J, Hornsby B, Teske C (2019) The FireFlux II experiment: a model-guided field experiment to improve understanding of fire–atmosphere interactions and fire spread. International Journal of Wildland Fire 28, 308–326.
Cohen JD, Finney MA, Yedinak KM (2006) Active spreading crown fire characteristics: implications for modelling. In ‘Proceedings of the V International Conference on Forest Fire Research,’ 16–20 November 2006, Figueira da Foz, Coimbra, Portugal. (Ed. DX Viegas) pp. 1–12. (ADAI Press: Coimbra, Portugal)
Country Fire Authority (CFA) (2019) Grassfires – rural. (Country Fire Authority of Victoria) Available at https://www.cfa.vic.gov.au/plan-prepare/grassfires-rural [Verified 14 August 2019]
Cruz MG, Hurley R, Bessell R, Sullivan AL (2020) Fire behaviour in wheat crops – effect of fuel structure on rate of fire spread. International Journal of Wildland Fire
Cruz MG, Sullivan AS, Kidnie S, Hurley R, Nichols S (2016) The effect of grass curing and fuel structure on fire behaviour – final report. CSIRO Client Report No. EP 166414. (Canberra, ACT, Australia)
Cruz MG, Sullivan AL, Gould JS, Hurley RJ, Plucinski MP (2018) Got to burn to learn: the effect of fuel load on grassland fire behaviour and its management implications. International Journal of Wildland Fire 27, 727–741.
| Got to burn to learn: the effect of fuel load on grassland fire behaviour and its management implications.Crossref | GoogleScholarGoogle Scholar |
Cruz MG, Hurley R, Bessell R, Sullivan AL (2019) Fire behaviour in wheat crops. Final report. CSIRO Client Report No. EP 195825. (Canberra, ACT, Australia)
Hoffman C, Sieg C, Linn R, Mell W, Parsons R, Ziegler J, Hiers J (2018) Advancing the science of wildland fire dynamics using process-based models. Fire 1, 32
| Advancing the science of wildland fire dynamics using process-based models.Crossref | GoogleScholarGoogle Scholar |
McCaw WL, Gould JS, Cheney NP, Ellis PFM, Anderson WR (2012) Changes in behaviour of fire in dry eucalypt forest as fuel increases with age. Forest Ecology and Management 271, 170–181.
| Changes in behaviour of fire in dry eucalypt forest as fuel increases with age.Crossref | GoogleScholarGoogle Scholar |
Mell W, Jenkins MA, Gould JS, Cheney NP (2007) A physics-based approach to modelling grassland fires. International Journal of Wildland Fire 16, 1–22.
| A physics-based approach to modelling grassland fires.Crossref | GoogleScholarGoogle Scholar |
Moinuddin KAM, Sutherland D, Mell W (2018) Simulation study of grass fire using a physics-based model: striving towards numerical rigour and the effect of grass height on the rate of spread. International Journal of Wildland Fire 27, 800–814.
| Simulation study of grass fire using a physics-based model: striving towards numerical rigour and the effect of grass height on the rate of spread.Crossref | GoogleScholarGoogle Scholar |
Noble IR, Bary GAV, Gill AM (1980) McArthur’s fire danger meters expressed as equations. Australian Journal of Ecology 5, 201–203.
| McArthur’s fire danger meters expressed as equations.Crossref | GoogleScholarGoogle Scholar |
NSW Rural Fire Service (RFS) (2010) Grass fires. (State of New South Wales) Available at https://www.rfs.nsw.gov.au/__data/assets/pdf_file/0017/9431/Grass-Fires-Factsheet.pdf [Verified 14 August 2019]
Penman HL, Long IF (1960) Weather in wheat: an essay in micro‐meteorology. Quarterly Journal of the Royal Meteorological Society 86, 16–50.
| Weather in wheat: an essay in micro‐meteorology.Crossref | GoogleScholarGoogle Scholar |
R Core Team (2018) R: A language and environment for statistical computing. (R Foundation for Statistical Computing: Vienna, Austria) Available at https://www.R-project.org/ [Verified 13 January 2020]
Sneeuwjagt RJ, Frandsen WH (1977) Behavior of experimental grass fires vs. predictions based on Rothermel’s fire model. Canadian Journal of Forest Research 7, 357–367.
| Behavior of experimental grass fires vs. predictions based on Rothermel’s fire model.Crossref | GoogleScholarGoogle Scholar |
Thomas PH, Simms DL, Wraight HG (1964) Fire spread in wooden cribs. Joint Fire Research Organization, Fire Research Note 537. (Boreham Wood, UK)
Watts JM (1987) Editorial: validating fire models. Fire Technology 23, 93–94.
| Editorial: validating fire models.Crossref | GoogleScholarGoogle Scholar |
1 Here we used the Apte et al. (1991) Fr as calculated by MSM18 to be consistent with their analysis. We note that we do not believe that this Fr is relevant for the study of flame zone processes in free burning fires, as its calculation integrates all the energy released by a fire, in contrast to just the energy released in the forward propagating section. As a spreading fire increases in area with time, Fr naturally decreases but the dynamics driving forward fire propagation is unchanged.



