Drivers of long-distance spotting during wildfires in south-eastern Australia
Michael A. Storey A C , Owen F. Price A , Jason J. Sharples B and Ross A. Bradstock A
A C , Owen F. Price A , Jason J. Sharples B and Ross A. Bradstock A
A Centre for Environmental Risk Management of Bushfires, University of Wollongong, Wollongong, NSW 2522, Australia.
B School of Physical, Environmental and Mathematical Sciences, University of New South Wales (UNSW), Canberra, ACT 2600, Australia.
C Corresponding author. Email: mas828@uowmail.edu.au
International Journal of Wildland Fire 29(6) 459-472 https://doi.org/10.1071/WF19124
Submitted: 14 August 2019 Accepted: 20 January 2020 Published: 2 March 2020
Journal Compilation © IAWF 2020 Open Access CC BY-NC-ND
Abstract
We analysed the influence of wildfire area, topography, fuel, surface weather and upper-level weather conditions on long-distance spotting during wildfires. The analysis was based on a large dataset of 338 observations, from aircraft-acquired optical line scans, of spotting wildfires in south-east Australia between 2002 and 2018. Source fire area (a measure of fire activity) was the most important predictor of maximum spotting distance and the number of long-distance spot fires produced (i.e. >500 m from a source fire). Weather (surface and upper-level), vegetation and topographic variables had important secondary effects. Spotting distance and number of long-distance spot fires increased strongly with increasing source fire area, particularly under strong winds and in areas containing dense forest and steep slopes. General vegetation descriptors better predicted spotting compared with bark hazard and presence variables, suggesting systems that measure and map bark spotting potential need improvement. The results from this study have important implications for the development of predictive spotting and wildfire behaviour models.
Additional keywords: fire behaviour, line scan, spot fire.
Introduction
Spotting is an influential form of wildfire spread whereby firebrands (i.e. burning pieces of vegetation or other combustible materials) are blown into unburnt fuels and ignite separate new ‘spot fires’ (Koo et al. 2010; Albini et al. 2012). Wildfires can quickly ignite hundreds of spot fires (mass spotting; Sharples et al. 2016), and in some cases spot fires can ignite many kilometres downwind (long-distance spotting). This level of spotting behaviour can make wildfire spread appear chaotic and unpredictable, confounding the issuance of community warnings and increasing danger to fire crews. Containment methods can become ineffective as spotting jumps fuel breaks. Houses that are otherwise well prepared (e.g. good defensible space) can be burnt down after igniting from firebrands or nearby spot fires (Ramsay et al. 1987; Blanchi et al. 2006; Cohen and Stratton 2008). Spotting can be the dominant mechanism driving wildfire spread and asset destruction, particularly in ‘extreme’ wildfires – highly unpredictable wildfires characterised by widespread flaming areas, deep pyroconvection and high energy release that can lead to the development of pyrocumulus or pyrocumulonimbus (McRae et al. 2015; Sharples et al. 2016). Spotting is a major reason that the extreme 2009 Black Saturday wildfires in Australia (173 people killed, >2000 buildings destroyed) were so destructive (Cruz et al. 2012; Price and Bradstock 2013). It is vital that we increase our understanding of the drivers of spotting behaviour to improve our ability to prepare for, predict and safely respond to wildfires.
Spot fires can be classified based on the distance (or range) they ignite from the main wildfire (referred to here as ‘source fire’), and the degree to which they interact with the main fire. Although distance classifications vary in the literature, in general, short-distance (and medium-distance) spot fires ignite within several hundred metres and may increase overall fire spread rates through rapid coalescence with other spot fires and the source fire (Cheney and Bary 1969; Sharples et al. 2016). Long-distance spot fires ignite several hundred metres to tens of kilometres downwind, where they spread independently of the source fire. In the eucalypt-dominated forests of Australia, maximum spot fire distances of 30 to 35 km were reported during the 2009 Black Saturday wildfires (Cruz et al. 2012), 29 km during the 1965 wildfires in eastern Victoria (McArthur 1967) and up to 25 km during the 1983 Ash Wednesday wildfires in Victoria (Rawson et al. 1983). Distances of up to 19 km have also been reported from North American conifer forests (Werth et al. 2016).
Long-distance spotting stretches containment efforts over a large area. Isolated long-distance spot fires, which can often be treated as a separate wildfire, can be suppressed by fire crews if detected early and the area is accessible (e.g. nearby access tracks, suitable terrain; Rawson et al. 1983). However, suppression becomes more difficult as the number of spot fires increases; numerous spot fire ignitions will overwhelm suppression efforts by fire crews (e.g. water bombing; Plucinski and Pastor 2013), with the problem exacerbated if large numbers of both short- and long-distance spot fires are igniting (Cruz et al. 2012). Because of these issues, it is vital to understand what drives variation in spotting distances and numbers.
Current understanding delineates three sequential stages of spotting (Koo et al. 2010).
-
Firebrand generation: the number and form of firebrands generated from available fuels (e.g. bark, small branches). Trees with fibrous bark types (e.g. messmate – Eucalyptus obliqua) can generate intense spotting behaviour (Cruz et al. 2012; Ellis 2013). Trees with long bark streamers (or ribbons, e.g. ribbon gum – Eucalyptus viminalis) produce aerodynamic firebrands capable of being lofted tens of kilometres while combusting (Hall et al. 2015).
-
Firebrand transport: surface and upper-level winds, temperature and moisture, smoke plume dynamics and the aerodynamic attributes of the firebrand can influence the distance and direction of firebrand lofting and deposition (Albini et al. 2012; Ellis 2013; Hall et al. 2015; Thurston et al. 2017).
-
Ignition of fuels upon landing: If a firebrand is still smouldering or flaming, and lands in sufficiently dry combustible fuel, a spot fire can ignite and spread, subject to favourable fuel conditions (Plucinski and Anderson 2008; Ganteaume et al. 2009; Ellis 2011).
Several environmental variables are known to influence the spotting process across one or more of these stages. For example, strong winds combined with dry fuels increase fire intensity, which increases firebrand generation (more fuel burning) and plume development (stronger convection), sending more combusting firebrands greater distances, where wind can help ignite dry fuels (Koo et al. 2010). A greater understanding of the relative contribution of different variables to observed patterns of long-distance spotting is needed to develop accurate predictive models.
Several studies have focused on understanding maximum spot fire distance from a source fire (spotting distance) (McArthur 1967; Albini 1979; Noble et al. 1980; Ellis 2000; Gould et al. 2008; Koo et al. 2010; Albini et al. 2012). The general approach has been to mathematically model how far firebrands can fly and land while still combusting, often incorporating empirical models developed from laboratory testing (e.g. firebrand combustion duration while lofted in a wind tunnel; Ellis 2000). Modelled distances depend strongly on factors such as wind speed, fuel moisture, firebrand size, firebrand shape and flame height or intensity. Current spotting models are generally not suitable for more extreme fires because highly convective plumes or large aerodynamic firebrands are not accounted for (Gould et al. 2008; Albini et al. 2012; Andrews 2014). The likelihood of spot fire ignition on firebrand landing, the number of spot fires or their spatial distribution are also not generally modelled, although Martin and Hillen (2016) recently suggested a theoretical mathematical model framework for spotting distributions. Some operational fire spread simulators include components to predict spotting distribution (e.g. Phoenix Rapidfire; Tolhurst et al. 2008). However, the accuracy and consistency of such approaches in predicting long distance-spotting (including number and maximum distances) has not been tested.
Model development and validation has been hampered by a lack of empirical data on spot fire distance and numbers during actual wildfires. Spotting models have been developed with few or sometimes no observations from extreme wildfires, or by using observations only from fires of low-to-moderate intensity. Extreme wildfire observations have historically been too difficult to collect because equipment capable of recording reliable data from a safe distance had not yet been developed (Filkov et al. 2018).
However, in the last 15 to 20 years, wildfire agencies in south-east Australia have routinely deployed aircraft fitted with infrared and/or multispectral line scanning equipment to capture images of wildfires, including spotting, for operational mapping. In the present study, we have exploited these data to investigate the environmental drivers of long-distance spotting; maximum spot fire distance and the number of long-distance spot fires (‘long-distance’ is defined here as spot fires over 500 m from source fire). Specifically, we derived empirical models using line scan data to explain maximum spot fire distance and number of long-distance spot fires as a function of potential determinants (i.e. source fire area, weather, topography and fuels).
Methods
Study location and line scans
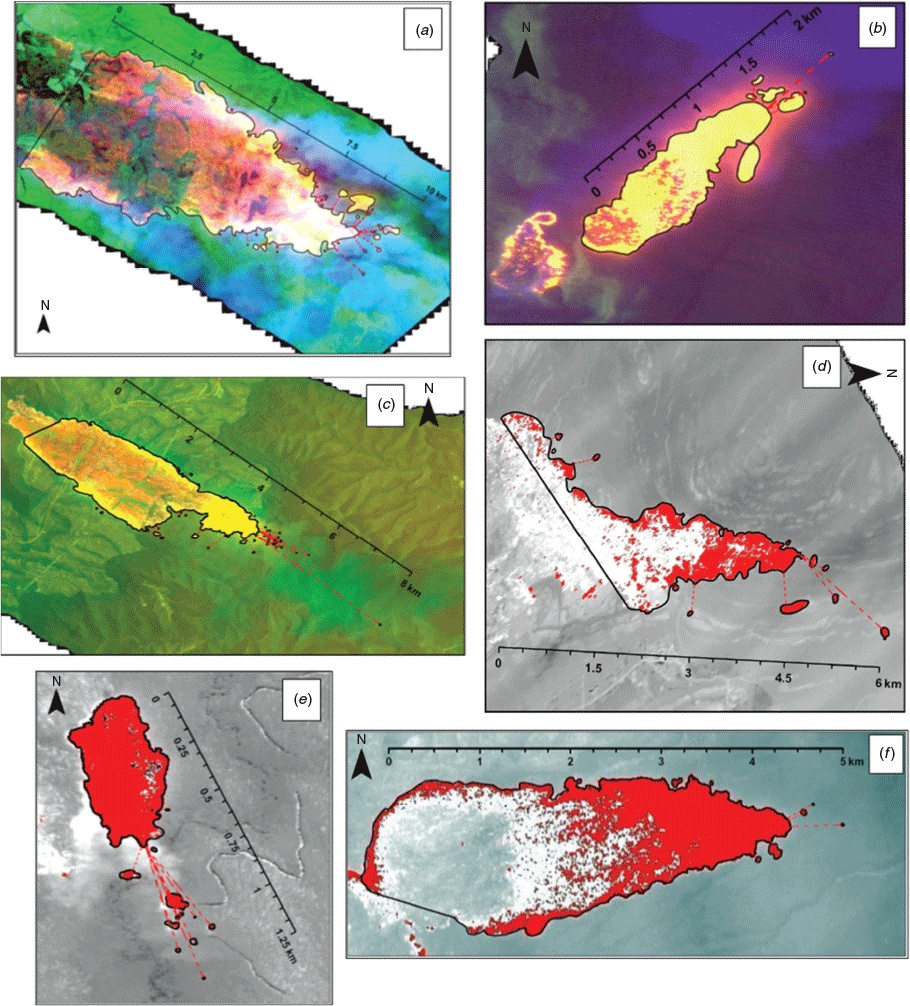
Our study focused on wildfires in south-east Australia between 4 December 2002 and 28 February 2018 (Fig. 1). Since ~2002, the New South Wales Rural Fire Service (RFS, operated by Air Affairs Australia) and the Victorian Department of Environment, Land, Water and Planning (DELWP) have regularly deployed aircraft fitted with optical line scanning equipment capable of capturing radiation emitted from wildfires in multiple spectral bands. This includes infrared, which penetrates smoke plumes (except very dense smoke plumes such as pyrocumulonimbus), to allow for an unobstructed wildfire image to be captured (Matthews 1997). The scanner builds an image of the area below by continuously scanning side-to-side as the aircraft moves forward. Images are georectified via an attitude correction system (Cook et al. 2009), with pixel size generally 5–15 m depending on the aircraft’s operating altitude. RFS uses a subset of three bands (one blue and two shortwave infrared (SWIR) at 1.6 µm and 2.2 µm) that are extracted to create images that display active fire as yellow–orange (Fig. 2, Appendix 1). DELWP creates single band images (longwave infrared (LWIR) at 8–14 µm) that are processed to highlight active fire (i.e. high LWIR pixel values) as red (Fig. 3, Appendix 1). RFS and DELWP supplied over 15 000 digital images capturing some part of a wildfire (i.e. whole or part of a wildfire, actively burning to extinguished) for the present study. The DELWP images included some wildfires in Tasmania from an interstate deployment.

|

|
Images were initially sorted into three groups: (1) spotting – actively burning wildfire with at least one spot fire (~10% of all images, retained for analysis); (2) non-spotting – active fire but zero spot fires (~50% of all images, not analysed here); and (3) no fire – images without any (or very little) active fire visible (~40% of all images, discarded). Images from the first group (i.e. spotting present) with acquisition errors (e.g. colour saturation, cloud obscured), wildfires burning towards no-fuel areas (e.g. burnt in recent days, ocean) or with no apparent head fire (i.e. flank fire only images) were also excluded. These issues affected <5% of the spotting present images. The line scan operator can adjust spectral sensitivity settings between missions depending on the fire situation. However, these settings were not recorded in the data, which may have affected spot fire detectability in some images.
There were some cases where two scans acquired within a short period (<1 h) showed the same spot fires. To ensure no spot fires were measured twice, the image that showed the longest distance downwind from the source fire was retained and the other image was excluded. Georectification errors were observed for several images (some were not georectified). To improve alignment, georeferencing to a common base image was carried out in ArcGIS ver. 10.5 (ESRI, Redlands, CA, https://www.arcgis.com/index.html).
Fire data digitisation
GIS polygons were created for sampling in ArcGIS 10.5. As calibration data and raw radiance data were not available for each image, employing an automated method to map fire area (or extract fire intensity) was not possible. Instead, visual interpretation of each image and manual drawing of source fire and spot fire polygons was carried out.
Specifically, the source fire polygon was digitised in ArcGIS by manually drawing a polygon from the actively burning head fire tip and back along the actively burning fire length of each flank, before finalising the polygon with a line joining the back end of the two flanks (Figs 2, 3, Appendix 1). A large wildfire complex could contain multiple source fires when separate individual actively burning head fires could be identified (e.g. two tongues of fire spreading along separate ridges were different source fires, see Fig. 2). Spot fires were each digitised as separate polygons, and distance to the closest point on the nearest source fire perimeter was recorded (Fig. 2, Appendix 1).
There were important limitations of the line scan data used for the present study (also see Page et al. 2019). Spot fire omission errors may have occurred when a spot fire was very small, beyond the downwind image extent, or was under extremely dense smoke or thick canopy. There is also a small chance that some spot fires may have been separate fires ignited by other means, such as previous lighting or arson. The line scans did not detect actual firebrands. Instead, they detected spot fires that were assumed to have been ignited from firebrands. This meant that the precise locations of firebrand generation could not be determined. We assumed that all spot fires were ignited by firebrands generated from the source fire polygon, but some may have been ignited by firebrands generated from other nearby spot fires. Additionally, given that each line scan image usually contained multiple spot fires of various sizes, the precise ignition time of each spot fire and exact source fire area at the time of line scan capture could not be determined. Instead, our mapping of the source fire identifies the general area of fire activity from which firebrands were likely to have been emitted, including actively burning fire edges in the line scan and the recently burning area between the active edges (e.g. Fig. 3, Appendix 1). Spot fire distances measured here are likely to be underestimates of maximum spotting distances, because the source fire would have continued to spread towards the spot fire locations in the time between spot fire ignition and line scan capture.
It should be noted that how a source fire appears in a line scan image is affected by various factors, including the sensitivity settings of the scanning equipment (selected by operator) and the equipment used (variable over time and among agencies). These influences may introduce unquantified levels of uncertainty into our manual source fire mapping. However, from our observations it appeared that pixels that are at a stage of cooling after actively burning were most likely to be affected by these issues (i.e. cooling pixel may show as actively burning yellow or cooling orange, depending on operator setting or equipment used). It also appeared that the threshold between burning and unburnt was clear for most images (although some ‘washed-out’ images were not used), making consistent fire edge mapping possible. We believe the manual and visual interpretation method employed moderated equipment and sensitivity issues because it relied on identifying the active fire edge (burnt or unburnt), and did not attempt to distinguish among pixels of different temperatures in the centre of the fire (i.e. all burning and cooling pixels between the active edges are incorporated in the source fire area).
Explanatory data
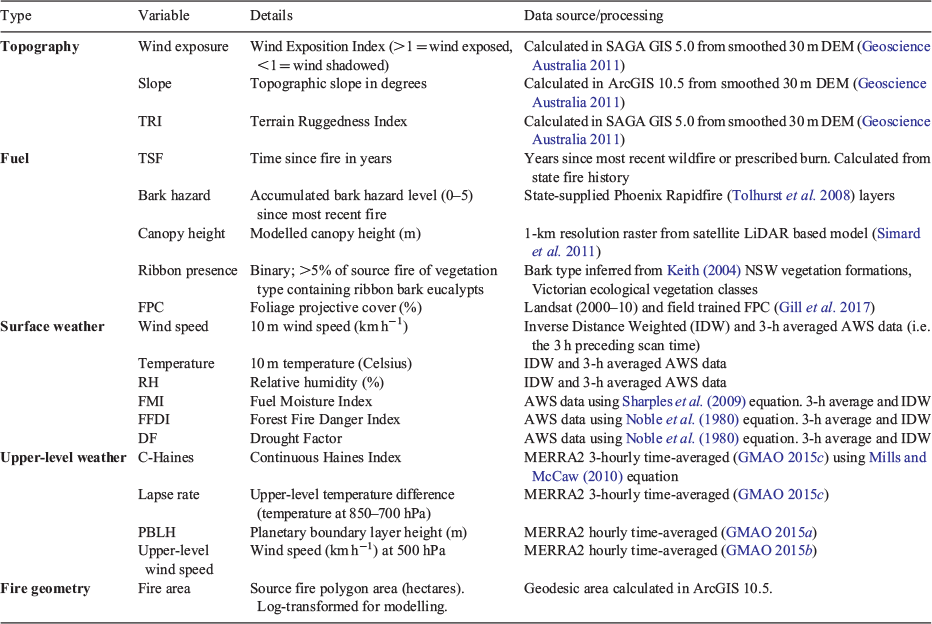
The area of the source fire polygon (hectares) was calculated as an explanatory variable, because it provided the best proxy of fire activity available from the line scan data. Other measures of fire activity that may be important to spotting, but which could not be extracted from the operational line scan data, included intensity (raw radiances not available) and rate of spread (sequential scans were not available for most fires). Raster data for other known wildfire-driving variables were processed and sampled in ArcGIS 10.5 and R ver. 3.4.3 (R Foundation for Statistical Computing, Vienna, https://cran.r-project.org/bin/windows/base/old/3.4.3/; Table 1).
|
Surface weather was assigned to each source fire using nearby Bureau of Meteorology Automatic Weather Station (AWS) data to estimate 3-hourly time-averaged (i.e. the 3 h preceding the scan time) and spatially interpolated (inverse distance weighted) values. The interpolation estimates were used because data from the nearest AWS may not have matched the fire ground weather, owing to distance and elevation differences. Time averaging also was likely to moderate errors owing to uncertainties in knowing the timing of wildfire activity (i.e. sometime preceding the scan) that produced the spot fires in a line scan. We extracted temperature, relative humidity, wind speed, Fuel Moisture Index (FMI), Forest Fire Danger Index (FFDI) and drought factor (Table 1).
FMI is an indicator of dead fuel moisture content, shown to provide information comparable to more complicated moisture indices (Sharples et al. 2009). It is defined by:
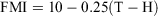
where H = relative humidity and T = dry-bulb temperature.
FFDI was calculated as in Noble et al. (1980):
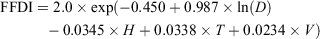
where D = drought factor, H = relative humidity, V = wind speed and T = dry-bulb temperature. Drought factor is derived from the Keetch–Byram Drought Index (Keetch and Byram 1968), with an adjustment for dead fuel moisture. FFDI, in various forms, has been the primary forest fire weather index used in south-east Australia for assessing fire ignition probability and for predicting aspects of fire behaviour since the 1960s (McArthur 1967; Noble et al. 1980).
In south-east Australia, observations of the upper-level weather conditions occur at only five stations twice per day. Instead we used the Modern-Era Retrospective Analysis for Research and Applications Version 2 (MERRA2) global atmospheric reanalysis dataset (Gelaro et al. 2017) to extract four variables that indicate tropospheric conditions conducive to extreme fire behaviour and smoke plume development (thus firebrand dispersal): Continuous Haines Index (C-Haines); lapse rate; wind speed at 500 hPa; and planetary boundary layer height. MERRA2 is produced by NASA’s Global Modelling and Assimilation Office and includes time-averaged (hourly or 3-hourly) and gridded (~0.5° resolution) datasets (accessed 31 March 2018).
Planetary boundary layer height (PBLH) was extracted for 1 h before each line scan time from hourly time-averaged MERRA2 data (GMAO 2015a). PBLH is a measure of the height of the surface mixing layer, and although plumes can burst through the PBL (e.g. strong pyroconvective plumes and pyrocumulonimbus), greater values of PBLH have been linked to development of taller smoke plumes (Potter 2012a; Di Virgilio et al. 2018; Price et al. 2018).
Wind speed at 500 hPa (~5800 m, i.e. above PBLH) from 1h before scan time was extracted from hourly time-averaged MERRA2 (GMAO 2015b). Wind speed at different heights in the troposphere can influence firebrand lofting by directly blowing firebrands downwind, or by producing a more tilted and turbulent plume with puffy updrafts capable of lofting and emitting firebrands greater distances (Thurston et al. 2017).
The mid-level C-Haines index was calculated as in Mills and McCaw (2010), using the difference between 3-hourly averaged temperature at 850 and 700 hPa (stability component) and dewpoint depression at 850 hPa (moisture component; GMAO 2015b). C-Haines is intended as an indicator of the potential for extreme fire occurrence, including development of a strong convective plume (Mills and McCaw 2010; Potter 2012a). The moisture component in C-Haines has been questioned by some authors (Potter 2018), so we calculated the stability component of C-Haines (850–700 hPa temperature difference, or lapse rate) as a separate variable for our analysis.
A digital elevation model was used to calculate three topographic raster layers: slope; Terrain Ruggedness Index; and Wind Exposition Index. Slope refers to topographic slope steepness, measured in degrees. Terrain Ruggedness Index (TRI; Conrad et al. 2015) indicates topographic heterogeneity based on elevation differences between adjacent pixels (Riley et al. 1999). Wind Exposition Index (Conrad et al. 2015) is a dimensionless index highlighting wind-exposed pixels. The calculation of Wind Exposition Index incorporates multiple wind directions, aspect relative to wind and angle to horizon (Böhner and Antonić 2009). Values >1 indicate wind-exposed pixels, and values <1 indicate wind-shadowed pixels.
Fire history and wildfire fuel maps were supplied by DELWP, RFS and the Tasmanian Fire Service. Fire history was used to calculate Time Since Fire (TSF), which is the number of years since the last wildfire or prescribed fire before the scan date. Bark hazard was extracted from state-based wildfire fuel maps used for wildfire behaviour modelling in Phoenix Rapidfire (Tolhurst et al. 2008). These maps indicate the presence of tree species likely to generate many or highly aerodynamic firebrands (e.g. ‘ribbon’ or ‘stringy’ bark eucalypts). It is based on a categorical score (0 to 5), with 5 indicating the presence of highly spot-fire-prone eucalypt species (Hines et al. 2010). The scores are also a function of time since fire, so that recently burnt areas have a low bark hazard, which increases at different rates over time depending on vegetation type.
Detailed tree species or dominant bark-type mapping did not exist for the entire study area. Instead we assigned dominant bark types (stringy, ribbon, other, non-eucalypt) to vegetation classes from state-based vegetation maps and associated descriptions of dominant and/or representative tree species. We then also calculated a binary variable of ribbon bark presence in a source fire (in at least 5% of the source fire), because ribbon bark is most associated with long-distance spotting (Hall et al. 2015). We included only the binary ribbon variable in further analysis, because an initial exploratory analysis suggested a greater explanatory power than the bark type variable.
Source fires were forest dominant (76% of samples), sparse forest or woodland dominant (18%), with some shrub (3%) and grass (3%) source fires also present. All vegetation types were included in our analysis but were described by two general vegetation variables. Canopy height was extracted from a 1-km resolution raster of modelled canopy top height per pixel produced by Simard et al. (2011), using spaceborne LiDAR (light detection and ranging) and global forest type, tree cover, elevation and climatology maps. Foliage Projective Cover (FPC) was also extracted, and was created by Gill et al. (2017) using time-series analysis and field data matching techniques to process Landsat images from 2000–10.
We considered including receiver fuel (i.e. fuel at site of spot fire ignition) variables, because these are important for understanding spot fire ignition probability (Plucinski and Anderson 2008; Viegas et al. 2014); however, receiver fuels, sampled using spot fire polygons, did not differ significantly from source fire fuels (correlations >0.8), so were not used in the modelling.
Sampling and model fitting
We used 50-m spatial point grids covering each source fire polygon to sample the fuel and topography variables. A data table was constructed, with each row consisting of an independent source fire and columns for source fire area, weather variables extracted from the source fire centre-point and summary statistics (mean, maximum) for each fuel and topographic variable (Table 1). We summarised spot fire distances to create the dependent variables for two separate generalised linear models (GLM): (1) Maximum-distance model – maximum spot fire distance from source fire; and (2) Spot-number model – number of spot fires >500 m from source fire (i.e. number of ‘long-distance’ spot fires).
Model fitting was conducted on a randomly selected training set (75% of the data), and a test set was used for model validation (the remaining 25% of the data). Model fitting was run in R 3.4.3 by testing all variable combinations and selecting the best model according to Akaike’s Information Criterion (AIC; Burnham and Anderson 2003). Highly correlated predictors (>0.7) were not included in the same models. Initial analysis and model fitting indicated: (1) maximum values for fuel and topographic variables for each source fire performed better than mean values; and (2) a significant non-linear relationship between source fire area and the dependent variables for both models. Thus, maximum fuel and topographic values, and log-transformed source fire area were used for further model fitting (no other variables were transformed for model fitting). Initial analysis for the Spot-number model indicated that application of a standard GLM for count data (e.g. Poisson) was not appropriate owing to zero inflation (i.e. many source fires had zero long-distance (>500 m) spot fires) and over-dispersion. To account for these issues a two-part Negative Binomial hurdle model was fitted for the Spot-number analysis; see Appendix 2 for details (Zeileis et al. 2008; Zuur et al. 2009).
The GLMs used (Maximum-distance, gamma with log link; Spot-number, Negative-binomial hurdle model) performed better or similarly to other methods tested (GAM and random forests), thus are reported here. Likelihood-based R2LR (Magee 1990) was calculated as an indicator of fit and likelihood-ratio tests (LR) were used to compare the best model with reduced models to indicate relative importance of each predictor variable. These were calculated for the gamma Maximum-distance model and separately for the two parts of the Spot-number hurdle model (see Appendix 2). Reduced models were a version of the best model where an individual predictor was removed (done iteratively for each predictor in the model). Root Mean Square Error (RMSE) and Mean Absolute Error (MAE) of the test set predictions of the Maximum-distance model and the Spot-number hurdle model were calculated for model validation.
From the 338 source fires digitised, 151 source fires had at least one long-distance (>500 m) spot fire and 187 had zero long-distance spot fires. Two source fires were excluded from the Spot-number modelling because less than 500 m downwind was captured in the line scan, which was insufficient to detect any long-distance spot fires.
Results
Data distribution
Maximum spot fire distances ranged from 5.0 m to 13.9 km (mean, 0.9 km; 95th percentile, 3.9 km). The mean number of spot fires per source fire (irrespective of distance) was 13. The distribution of maximum distance values appeared exponential, with a high proportion of shorter distances (Fig. 4a). Very long-distance spotting was rare; only 11 source fires had a maximum spotting distance >5 km.
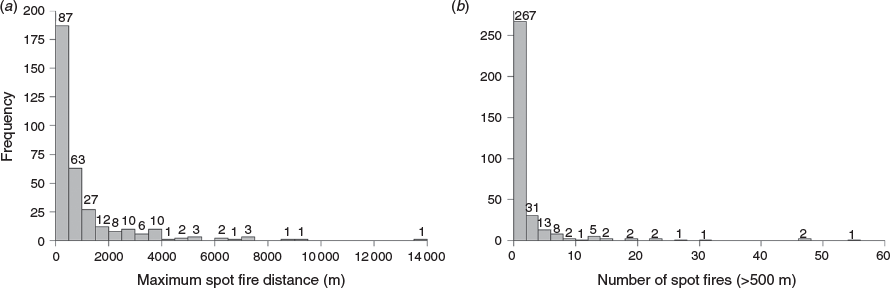
|
The number of long-distance spot fires (>500 m) for the whole dataset had an exponential distribution with zero inflation (Fig. 4b), and ranged from 0 to 55 (mean, 2.3; 95th percentile, 10.2). Although most source fires had zero long-distance spot fires (187), 116 had between one and five long-distance spot fires, and 17 source fires had at least 10 long-distance spot fires.
The source fires that spotted the longest distances were not necessarily the source fires that produced the highest numbers of long-distance spot fires. For source fires that spotted at least 5 km, the number of long-distance spot fires ranged from one to 55. Also, the three cases with the farthest maximum spotting distances produced 10 or fewer long-distance spot fires each.
Maximum-distance model
The Maximum-distance model (Table 2) produced an R2LR of 0.52. Log-transformed source fire area was the most important predictor (LR = 55.09, P < 0.001). FPC and wind speed had strong positive effects on maximum spotting distance and moderate importance (LR = 13.6, P < 0.001 and LR = 8.9, P = 0.003 respectively). Slope (LR = 4.3, P = 0.040), wind exposure (LR = 4.8, P = 0.019) and upper-level wind speed (LR = 4.2, P = 0.035) all had significant positive effects and were of similar importance.

|
RMSE was 1.2 km and MAE was 0.66 km using the Maximum-distance model to predict for the test set. Spatial autocorrelation of residuals was low (Moran’s I <0.1).
Predicted maximum spot fire distance derived from the model increased strongly with source fire area, particularly in densely forested areas with steep slopes and high wind exposure (i.e. high FPC, slope and wind exposure). In these areas, maximum spot fire distances of 4 km are predicted under strong winds and with a source fire of ~1000 ha (i.e. log source fire area = 6.9), increasing to ~8 km for a ~5000-ha source fire (Fig. 5). Short forest or sparsely forested plains (low FPC, low slope and lower wind exposure) had a much less substantial increase in predicted maximum spotting distance with source fire area under strong winds (0.4 km at ~1000 ha, 0.9 km at ~5000 ha; Fig. 5).

|
Long-distance Spot-number hurdle model
The binomial part modelled the occurrence of long-distance (>500 m) spot fires (Table 3a) and produced an R2LR of 0.39. Log-transformed source fire area and wind speed were the most important predictors (LR = 25.2, P < 0.001 and LR = 17.94, P < 0.001 respectively), both having strong positive effects. Canopy height and slope had significant positive effects (LR = 11.1, P = 0.002 and LR = 8.2, P = 0.005 respectively), whereas FMI had a negative effect on long-distance spot fire occurrence (i.e. drier fuels means higher spot fire probability), but was not significant at the 0.05 level (LR = 3.8, P = 0.057). Three supported models (i.e. within 2 AIC) were also found. These models contained identical predictors, except that FMI was replaced by another variable in each supported model (i.e. lapse rate, relative humidity and then upper-level wind speed).

|
The Negative-binomial count part modelled the number of long-distance spot fires (Table 3b) and produced an R2LR of 0.39. Log-transformed source fire area was the most important predictor (LR = 35.7, P < 0.001), having a strong positive effect. Canopy height, lapse rate and upper-level wind speed all had significant positive effects and were of similar importance (LR 4.1 to 5.6, P = 0.017 to 0.046).
RMSE of the combined Spot-number hurdle model applied to the test set was 5.35, and MAE was 1.79. Spatial autocorrelation of residuals was low (Moran’s I <0.1).
Long-distance Spot-number was predicted to rise strongly with source fire area, particularly in tall forests (high canopy height) when the air was unstable (large lapse rate) and with high upper-level wind speed (Fig. 6). Predicted long-distance spot fire number varied widely in tall forests depending on the levels of lapse rate and upper-level wind speed.

|
Discussion
Our analysis of 338 wildfire line scan observations found source fire area to be the strongest predictor of long-distance spotting. Source fire area (log-transformed), a measure of the area of fire activity, was the strongest predictor in the Maximum-distance model and in both parts of the Spot-number model (long-distance (>500 m) spot fire occurrence and long-distance spot fire number). Fuel, topography and weather had important secondary effects that significantly altered predicted spotting. These variables also likely had indirect effects on spotting via their influence on source fire area.
Fire area
Source fire area (log-transformed) had a strong effect on long-distance spotting, particularly under strong winds and in taller and/or denser forests (Figs 5, 6). Under such conditions, wildfires burn intensely and produce higher total energy release, or ‘power’ (Harris et al. 2012). These characteristics enhance the development of strong convective plumes to transport the numerous firebrands generated from the large burning area (increasing spot fire number), including large aerodynamic firebrands (increasing maximum distance) (Koo et al. 2010; Duane et al. 2015). However, source fire area did not explain all variation; there were several examples of smaller source fires producing long-distance spot fires (two source fires ~500 ha spotted >7 km, and six source fires of 50–100 ha produced at least three spot fires >500 m). There are several possible reasons for such outliers that could not be captured with the explanatory data used (e.g. specific source and/or receiver fuel arrangements, local ridge or valley arrangements, plume dynamics). Nevertheless, the findings suggest that to accurately predict spotting, models must incorporate a measure of current of area fire activity (i.e. source fire area, Appendix 1). Operational spotting predictions would require either accurate wildfire area simulations or regular monitoring of active wildfire area. Regular acquisition of multispectral line scans is ideal, but not all jurisdictions have such systems. Although not operationally tested, coarse resolution multispectral data from geostationary satellites that capture calibrated images every 10–15 min (e.g. Himawari, GOES) may be useful for extracting source fire area (or perhaps total area of actively burning pixels) for large wildfires when finer resolution data is unavailable. While they could not be measured from the data available for our study, fire intensity, rate of spread or a measure of fire power (e.g. intensity × area or perimeter; Harris et al. 2012) may also be similar or superior predictors to source fire area. Measurement of these would require access to raw radiance data with known equipment calibration settings (for intensity) and a series of sequential line scans (for rate of spread).
Weather
Wind speed was important to both Maximum-distance and long-distance Spot-number. Upper-level wind speed had weaker but still significant effects in the models. Wind at different levels can influence many aspects of wildfire behaviour, including plume development, plume turbulence and tilt, fire intensity, vorticity development, firebrand transport and ignition likelihood in receiver fuels (Koo et al. 2010; Potter 2012b; Thurston et al. 2017).
Our spatially interpolated and time-averaged surface weather estimates only provided a coarse representation of actual fire ground weather, which may be a reason why stronger effects of weather variables (e.g. temperature or FMI) were not found. There were several long-distance spotting source fires, particularly in the Great Dividing Range, that were associated with estimated mild weather. For example, the 2013 Aberfeldy fire (7.3 km max. distance, 48 long-distance spot fires, temp. 20°C, RH 43%, wind speed 18 km h−1) and the 2015 Gold Mine fire (3.5 km max. distance, 27 long-distance spot fires, temp. 24°C, RH 61%, wind speed 23 km h−1). Weather observations from closer to the fire ground would help to capture any localised differences in wind, moisture and temperature. Employing computational fluid dynamics modelling of wind flow may also help capture localised wind patterns.
The Spot-number results suggest that high upper-level wind speed, together with unstable air (high lapse rate), increases the number of long-distance spot fires, potentially because of greater convection and turbulence in plumes enhancing firebrand dispersal (Thurston et al. 2017). Although these variables indicated potential plume behaviour, further research matching observations of plume development and spot fire ignitions is needed to fully understand how plume behaviour affects long-distance spotting. There is recognition that extreme wildfires can be driven by two different processes (Rothermel 1991; Sharples et al. 2016; Tedim et al. 2018): strong surface winds (wind-driven fires) or strong pyro-convection (plume-driven fires). Although delineation is not always clear, wind-driven fires are described as long elliptical wildfires that spread rapidly as strong winds drive continuous advancement of the main front (Duane et al. 2015), with long-distance spotting usually not occurring owing to the absence of a deep convective plume. Plume-driven fires develop deep convective plumes, and potentially pyrocumulonimbus, which can loft masses of firebrands long distances (Rothermel 1991; Sharples et al. 2016; Tedim et al. 2018). There is evidence that some of the large source fires in our study that spotted long distances and in large numbers were plume-driven (e.g. Kosciuszko South 2003, possible evidence of pyrocumulonimbus in line scan, 23 spot fires over 500 m, max. distance ~4 km), and that other large source fires with less long-distance spot fires were wind-driven (e.g. State Mine 2013, more transparent and flatter smoke plume in scan, two spot fires >500 m, max. distance ~1 km). However, there was also at least one large source fire (2006 Wandoo fire in NSW) that appeared to be wind-driven (deep convective plume absent from scan, only five spot fires over 500 m), but still spotted 13.9 km. The apparently complex relationships between plume type and spotting behaviour may have caused some of the large outliers in the models, as explanatory data was not available to determine plume types.
Fuel
The significant positive effects of FPC (Maximum-distance) and canopy height (Spot-number) could result from enhancement of plume development by higher energy release rates of denser forest wildfires, and because high FPC and canopy height forests in the study area are generally associated with larger spotting-prone eucalypt species, e.g. ‘ribbon’ and ‘stringy’ bark eucalypts (Ellis 2013; Hall et al. 2015). However, these latter effects were not detected through our bark variables (i.e. bark hazard score and ribbon bark presence did not appear in the best models), although better mapping of spotting prone tree species is required to more thoroughly test the role of bark. Also, bark hazard score, based on a crude qualitative assessment used operationally in south-east Australia (Hines et al. 2010), has significant limitations and may not sufficiently delineate effects of different bark types (or amounts) on long-distance spotting (Duff et al. 2017; Cawson et al. 2018).
TSF was not a significant predictor, although a supplementary Welch’s t-test indicated a significantly (P < 0.01) lower number of long-distance spot fires (0.2 v. 2.3) for recently burnt source fires (mean TSF ≤5) compared with all other source fires (mean TSF >5). However, the low proportion of source fires with low TSF values (only 9 had a mean TSF ≤5 years) may have limited the likelihood of any potential effect to be detected in the models. Incorporating fire severity mapping into future analyses may reveal more about the effect of recent fire on spotting, as higher-severity fire may remove more bark, including upper branch bark, than lower-severity fires (Luke and McArthur 1978; McCaw et al. 2012).
Owing to limitations of the data, our measures of fuel were summarised from the entire source fire area, thus precise locations of firebrand generation within the source fire area were unknown. Data with higher spatial and temporal resolution (e.g. infrared video, frequent line scans) would be needed to identify finer resolution patterns of firebrand generation within a source fire.
Topography
Slope and wind exposure both appeared in the models. A steep slope somewhere within the source fire (i.e. source fire max. slope) increased the maximum spot fire distance and the probability of spot fire occurrence >500 m. TRI performed similarly but was highly correlated with slope (>0.9), so was not included in the same models. An area of relatively high wind exposure (e.g. exposed ridge) also increased maximum spotting distance. Slope and wind exposure may be important through interactions with wind, changing wind speed, increasing turbulence and potentially enhancing pyroconvection, leading to enhanced firebrand generation and transport.
There may be other important effects of topography not captured in our analysis. Observations that capture more information about firebrand generation and fire spread (e.g. infrared video, frequent sequential line scans) would be needed to identify specific points of enhanced firebrand generation and to investigate, for example, spotting distances and/or numbers from ridges v. valleys, or differences in spotting that stem from differences in fire spread orientation to local ridges or valleys (e.g. fire spreading across ridge v. fire spreading along a ridge). Such data and analysis may help to explain some of the outliers present in our models (e.g. smaller fires that produced long-distance spot fires).
Model accuracy
The models presented provide important empirical insights into the main drivers of long-distance spotting. However, large under- and over-predictions limit their application in operational contexts. For example, applying the Maximum-distance model (using supplementary satellite data) to predict for the large Kilmore East fire at 1500 hours on Black Saturday (7 February 2009) produces a large under-prediction (8800 ha, predicted 18.5 km, observed 30 to 35 km; Cruz et al. 2012). However, the Maximum-distance model significantly overpredicted for the State Mine fire (17 October 2013 at 1730 hours), which was part of the model training dataset (4600 ha, predicted 15.3 km, observed 1 km). The Spot-number model also had several large underpredictions, including for a 2500-ha source fire, part of the 2003 Kosciuszko South wildfire complex on 30 January 2003 (55 observed, 17 predicted). Improved measurement accuracy of our explanatory variables (e.g. local weather), high temporal resolution data capturing precise location of firebrand dispersal and addition of other explanatory variables (e.g. plume observation, fire intensity) would likely improve modelling accuracy.
Conclusions
An improved capacity to predict long-distance spotting is required if we are to better plan for and respond to wildfires. Our study provides a detailed empirical analysis of long-distance spotting from real wildfires. Source fire area was the most important predictor of long-distance spotting, although predicted distances and numbers alter significantly depending on fuel, weather and topography. However, we did not find a commonly used measure of bark spotting potential to be a significant predictor. Our results suggest that to accurately predict long-distance spotting, models must incorporate a measure of source fire area. Gathering data on spotting and plume development at wildfires over a range of intensities (including measuring intensity and frequent line scans) and improving fuel maps should be prioritised to allow for the development of reliable predictive spotting models.
Conflicts of interest
The authors declare no conflicts of interest.
Acknowledgements
Data for this research was provided by the NSW Rural Fire Service and Victorian Department of Environment, Land, Water and Planning. The provision of a PhD scholarship to Michael Storey from the Bushfire and Natural Hazards Cooperative Research Centre is gratefully acknowledged.
References
Albini FA (1979) Spot fire distance from burning trees: a predictive model. Intermountain Forest and Range Experiment Station, Forest Service, US Department of Agriculture. (Ogden, UT)Albini FA, Alexander ME, Cruz MG (2012) A mathematical model for predicting the maximum potential spotting distance from a crown fire. International Journal of Wildland Fire 21, 609–627.
| A mathematical model for predicting the maximum potential spotting distance from a crown fire.Crossref | GoogleScholarGoogle Scholar |
Andrews PL (2014) Current status and future needs of the BehavePlus Fire Modeling System. International Journal of Wildland Fire 23, 21–33.
| Current status and future needs of the BehavePlus Fire Modeling System.Crossref | GoogleScholarGoogle Scholar |
Blanchi R, Leonard JE, Leicester RH (2006) Lessons learnt from post-bushfire surveys at the urban interface in Australia. Forest Ecology and Management 234, S139
| Lessons learnt from post-bushfire surveys at the urban interface in Australia.Crossref | GoogleScholarGoogle Scholar |
Böhner J, Antonić O (2009) Land-surface parameters specific to topo-climatology. In ‘Developments in soil science’. (Eds T Hengl, HI Reuter) Vol. 33, pp. 195–226. (Elsevier: Amsterdam)
Burnham KP, Anderson DR (2003) ‘Model selection and multimodel inference: a practical information-theoretic approach second edition.’ (Springer Science & Business Media: Fort Collins, CO)
Cawson JG, Duff TJ, Swan MH, Penman TD (2018) Wildfire in wet sclerophyll forests: the interplay between disturbances and fuel dynamics. Ecosphere 9, e02211
| Wildfire in wet sclerophyll forests: the interplay between disturbances and fuel dynamics.Crossref | GoogleScholarGoogle Scholar |
Cheney N, Bary G (1969) The propagation of mass conflagrations in a standing eucalypt forest by the spotting process. In ‘Mass Fire Symposium’, 10–12 February 1969, Canberra. Vol. 1, Paper A6. (Defense Standards Laboratories: Melbourne)
Cohen JD, Stratton RD (2008) Home destruction examination: Grass Valley Fire, Lake Arrowhead, California. Missoula Fire Sciences Laboratory. (Missoula, MT)
Conrad O, Bechtel B, Bock M, Dietrich H, Fischer E, Gerlitz L, Wehberg J, Wichmann V, Böhner J (2015) System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geoscientific Model Development 8, 1991–2007.
| System for Automated Geoscientific Analyses (SAGA) v. 2.1.4.Crossref | GoogleScholarGoogle Scholar |
Cook R, Walker A, Wilkes S (2009) Airborne Fire Intelligence. In ‘Innovations in Remote Sensing and Photogrammetry’. (Eds S Jones, K Reinke) pp. 239–253. (Springer: Berlin)
Cruz MG, Sullivan AL, Gould JS, Sims NC, Bannister AJ, Hollis JJ, Hurley RJ (2012) Anatomy of a catastrophic wildfire: the Black Saturday Kilmore East fire in Victoria, Australia. Forest Ecology and Management 284, 269–285.
| Anatomy of a catastrophic wildfire: the Black Saturday Kilmore East fire in Victoria, Australia.Crossref | GoogleScholarGoogle Scholar |
Di Virgilio G, Hart MA, Jiang N (2018) Meteorological controls on atmospheric particulate pollution during hazard reduction burns. Atmospheric Chemistry and Physics 18, 6585–6599.
| Meteorological controls on atmospheric particulate pollution during hazard reduction burns.Crossref | GoogleScholarGoogle Scholar |
Duane A, Piqué M, Castellnou M, Brotons L (2015) Predictive modelling of fire occurrences from different fire spread patterns in Mediterranean landscapes. International Journal of Wildland Fire 24, 407–418.
| Predictive modelling of fire occurrences from different fire spread patterns in Mediterranean landscapes.Crossref | GoogleScholarGoogle Scholar |
Duff T, Keane R, Penman T, Tolhurst K (2017) Revisiting wildland fire fuel quantification methods: the challenge of understanding a dynamic, biotic entity. Forests 8, 351
| Revisiting wildland fire fuel quantification methods: the challenge of understanding a dynamic, biotic entity.Crossref | GoogleScholarGoogle Scholar |
Ellis PF (2000) The aerodynamic and combustion characteristics of eucalypt bark: a firebrand study. Ph.D. Thesis, Australian National University, Canberra.
Ellis PFM (2011) Fuelbed ignition potential and bark morphology explain the notoriety of the eucalypt messmate ‘stringybark’ for intense spotting. International Journal of Wildland Fire 20, 897–907.
| Fuelbed ignition potential and bark morphology explain the notoriety of the eucalypt messmate ‘stringybark’ for intense spotting.Crossref | GoogleScholarGoogle Scholar |
Ellis PFM (2013) Firebrand characteristics of the stringy bark of messmate (Eucalyptus obliqua) investigated using non-tethered samples. International Journal of Wildland Fire 22, 642–651.
| Firebrand characteristics of the stringy bark of messmate (Eucalyptus obliqua) investigated using non-tethered samples.Crossref | GoogleScholarGoogle Scholar |
Filkov A, Duff T, Penman T (2018) Improving fire behaviour data obtained from wildfires. Forests 9, 81
| Improving fire behaviour data obtained from wildfires.Crossref | GoogleScholarGoogle Scholar |
Ganteaume A, Lampin-Maillet C, Guijarro M, Hernando C, Jappiot M, Fonturbel T, Pérez-Gorostiaga P, Vega JA (2009) Spot fires: fuel bed flammability and capability of firebrands to ignite fuel beds. International Journal of Wildland Fire 18, 951–969.
| Spot fires: fuel bed flammability and capability of firebrands to ignite fuel beds.Crossref | GoogleScholarGoogle Scholar |
Gelaro R, McCarty W, Suárez MJ, Todling R, Molod A, Takacs L, Randles CA, Darmenov A, Bosilovich MG, Reichle R, Wargan K, Coy L, Cullather R, Draper C, Akella S, Buchard V, Conaty A, da Silva AM, Gu W, Kim G-K, Koster R, Lucchesi R, Merkova D, Nielsen JE, Partyka G, Pawson S, Putman W, Rienecker M, Schubert SD, Sienkiewicz M, Zhao B (2017) The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). Journal of Climate 30, 5419–5454.
| The modern-era retrospective analysis for research and applications, version 2 (MERRA-2).Crossref | GoogleScholarGoogle Scholar | 32020988PubMed |
Geoscience Australia (2011) 1 second SRTM digital elevation model. GeoScience Australia, Canberra. Available at http://data.bioregionalassessments.gov.au/dataset/9a9284b6-eb45-4a13-97d0-91bf25f1187b [Accessed 2016].
Gill T, Johansen K, Phinn S, Trevithick R, Scarth P, Armston J (2017) A method for mapping Australian woody vegetation cover by linking continental-scale field data and long-term Landsat time series. International Journal of Remote Sensing 38, 679–705.
| A method for mapping Australian woody vegetation cover by linking continental-scale field data and long-term Landsat time series.Crossref | GoogleScholarGoogle Scholar |
GMAO (2015a) MERRA-2 tavg1_2d_flx_Nx: 2d, 1-hourly, time-averaged, single-level, assimilation, surface flux diagnostics V5.12.4. Global Modeling and Assimilation Office, Greenbelt, MD. Available at https://disc.gsfc.nasa.gov/daac-bin/FTPSubset2.pl [Accessed 31 January 2018]
GMAO (2015b) MERRA-2 tavg1_2d_slv_Nx: 2d, 1-hourly, time-averaged, single-level, assimilation, single-level diagnostics V5.12.4. Global Modeling and Assimilation Office, Greenbelt, MD. Available at https://disc.gsfc.nasa.gov/daac-bin/FTPSubset2.pl [Accessed 31 January 2018]
GMAO (2015c) MERRA-2 tavg3_3d_asm_Nv: 3d, 3-hourly, time-averaged, model-level, assimilation, assimilated meteorological fields V5.12.4. Global Modeling and Assimilation Office, Greenbelt, MD. Available at https://disc.gsfc.nasa.gov/daac-bin/FTPSubset2.pl [Accessed 31 January 2018]
Gould JS, McCaw W, Cheney N, Ellis P, Knight I, Sullivan A (2008) ‘Project Vesta: fire in dry eucalypt forest: fuel structure, fuel dynamics and fire behaviour.’ (CSIRO Publishing: Canberra)
Hall J, Ellis PF, Cary GJ, Bishop G, Sullivan AL (2015) Long-distance spotting potential of bark strips of a ribbon gum (Eucalyptus viminalis). International Journal of Wildland Fire 24, 1109–1117.
| Long-distance spotting potential of bark strips of a ribbon gum (Eucalyptus viminalis).Crossref | GoogleScholarGoogle Scholar |
Harris S, Anderson W, Kilinc M, Fogarty L (2012) The relationship between fire behaviour measures and community loss: an exploratory analysis for developing a bushfire severity scale. Natural Hazards 63, 391–415.
| The relationship between fire behaviour measures and community loss: an exploratory analysis for developing a bushfire severity scale.Crossref | GoogleScholarGoogle Scholar |
Hines F, Tolhurst KG, Wilson AAG, McCarthy GJ (2010) Overall fuel hazard assessment guide: Report no. 82. Victorian Department of Sustainability and Environment. (Melbourne)
Jackson S (2017) pscl: classes and methods for R developed in the political science computational laboratory. United States Studies Centre, University of Sydney. (Sydney). Available at https://github.com/atahk/pscl/ [Verified January 2020]
Keetch JJ, Byram GM (1968) A drought index for forest fire control. USDA Forest Service Southeastern Forest Experiment Station. (Asheville, NC)
Keith D (2004) ‘Ocean shores to desert dunes: the native vegetation of New South Wales and the ACT.’ (New South Wales Government, Environment Protection Authority: Sydney)
Koo E, Pagni PJ, Weise DR, Woycheese JP (2010) Firebrands and spotting ignition in large-scale fires. International Journal of Wildland Fire 19, 818–843.
| Firebrands and spotting ignition in large-scale fires.Crossref | GoogleScholarGoogle Scholar |
Luke RH, McArthur AG (1978) ‘Bush fires in Australia.’ (Australian Government Publishing Service: Canberra)
Magee L (1990) R 2 measures based on Wald and likelihood ratio joint significance tests. The American Statistician 44, 250–253.
| R 2 measures based on Wald and likelihood ratio joint significance tests.Crossref | GoogleScholarGoogle Scholar |
Martin J, Hillen T (2016) The spotting distribution of wildfires. Applied Sciences (Basel, Switzerland) 6, 177
| The spotting distribution of wildfires.Crossref | GoogleScholarGoogle Scholar |
Matthews AG (1997) FIRESCAN: a technique for airborne infra-red mapping of wild fires. Ph.D. Thesis, Monash University, Melbourne.
McArthur AG (1967) Fire behaviour in Eucalypt forests. Department of National Development Forestry and Timber Bureau Leaflet Number 107. (Canberra)
McCaw WL, Gould JS, Phillip Cheney N, Ellis PFM, Anderson WR (2012) Changes in behaviour of fire in dry eucalypt forest as fuel increases with age. Forest Ecology and Management 271, 170–181.
| Changes in behaviour of fire in dry eucalypt forest as fuel increases with age.Crossref | GoogleScholarGoogle Scholar |
McRae R, Sharples J, Fromm M (2015) Linking local wildfire dynamics to pyroCb development. Natural Hazards and Earth System Sciences 15, 417–428.
| Linking local wildfire dynamics to pyroCb development.Crossref | GoogleScholarGoogle Scholar |
Mills GA, McCaw WL (2010) Atmospheric stability environments and fire weather in Australia: extending the Haines Index. Centre for Australian Weather and Climate Research. 1921605553. (Canberra)
Noble IR, Gill AM, Bary GAV (1980) McArthur’s fire-danger meters expressed as equations. Australian Journal of Ecology 5, 201–203.
| McArthur’s fire-danger meters expressed as equations.Crossref | GoogleScholarGoogle Scholar |
Page WG, Wagenbrenner NS, Butler BW, Blunck DL (2019) An analysis of spotting distances during the 2017 fire season in the Northern Rockies, USA. Canadian Journal of Forest Research 49, 317–325.
| An analysis of spotting distances during the 2017 fire season in the Northern Rockies, USA.Crossref | GoogleScholarGoogle Scholar |
Plucinski MP, Anderson WR (2008) Laboratory determination of factors influencing successful point ignition in the litter layer of shrubland vegetation. International Journal of Wildland Fire 17, 628–637.
| Laboratory determination of factors influencing successful point ignition in the litter layer of shrubland vegetation.Crossref | GoogleScholarGoogle Scholar |
Plucinski MP, Pastor E (2013) Criteria and methodology for evaluating aerial wildfire suppression. International Journal of Wildland Fire 22, 1144–1154.
| Criteria and methodology for evaluating aerial wildfire suppression.Crossref | GoogleScholarGoogle Scholar |
Potter BE (2012a) Atmospheric interactions with wildland fire behaviour – I. Basic surface interactions, vertical profiles and synoptic structures. International Journal of Wildland Fire 21, 779–801.
| Atmospheric interactions with wildland fire behaviour – I. Basic surface interactions, vertical profiles and synoptic structures.Crossref | GoogleScholarGoogle Scholar |
Potter BE (2012b) Atmospheric interactions with wildland fire behaviour – II. Plume and vortex dynamics. International Journal of Wildland Fire 21, 802–817.
| Atmospheric interactions with wildland fire behaviour – II. Plume and vortex dynamics.Crossref | GoogleScholarGoogle Scholar |
Potter B (2018) The Haines Index – it’s time to revise it or replace it. International Journal of Wildland Fire 27, 437–440.
| The Haines Index – it’s time to revise it or replace it.Crossref | GoogleScholarGoogle Scholar |
Price O, Bradstock R (2013) Landscape scale influences of forest area and housing density on house loss in the 2009 Victorian bushfires. PLoS One 8, e73421
| Landscape scale influences of forest area and housing density on house loss in the 2009 Victorian bushfires.Crossref | GoogleScholarGoogle Scholar | 24009753PubMed |
Price OF, Purdam PJ, Williamson GJ, Bowman DMJS (2018) Comparing the height and area of wild and prescribed fire particle plumes in south-east Australia using weather radar. International Journal of Wildland Fire 27, 525–537.
| Comparing the height and area of wild and prescribed fire particle plumes in south-east Australia using weather radar.Crossref | GoogleScholarGoogle Scholar |
Ramsay GC, McArthur NA, Dowling VP (1987) Preliminary results from an examination of house survival in the 16 February 1983 bushfires in Australia. Fire and Materials 11, 49–51.
| Preliminary results from an examination of house survival in the 16 February 1983 bushfires in Australia.Crossref | GoogleScholarGoogle Scholar |
Rawson RP, Billing PR, Duncan SF (1983) The 1982–83 forest fires in Victoria. Australian Forestry 46, 163–172.
| The 1982–83 forest fires in Victoria.Crossref | GoogleScholarGoogle Scholar |
Riley SJ, DeGloria SD, Elliot R (1999) Index that quantifies topographic heterogeneity. Intermountain Journal of Science 5, 23–27.
Rothermel RC (1991) Predicting behavior and size of crown fires in the northern Rocky Mountains. US Department of Agriculture, Forest Service, Intermountain Research Station. Research paper INT-438. (Ogden, UT)
Sharples JJ, McRae RHD, Weber RO, Gill AM (2009) A simple index for assessing fuel moisture content. Environmental Modelling & Software 24, 637–646.
| A simple index for assessing fuel moisture content.Crossref | GoogleScholarGoogle Scholar |
Sharples JJ, Cary GJ, Fox-Hughes P, Mooney S, Evans JP, Fletcher M-S, Fromm M, Grierson PF, McRae R, Baker P (2016) Natural hazards in Australia: extreme bushfire. Climatic Change 139, 85–99.
| Natural hazards in Australia: extreme bushfire.Crossref | GoogleScholarGoogle Scholar |
Simard M, Pinto N, Fisher JB, Baccini A (2011) Mapping forest canopy height globally with spaceborne LiDAR. Journal of Geophysical Research. Biogeosciences 116, G04021
Tedim F, Leone V, Amraoui M, Bouillon C, Coughlan M, Delogu G, Fernandes P, Ferreira C, McCaffrey S, McGee T, Parente J, Paton D, Pereira M, Ribeiro L, Viegas D, Xanthopoulos G (2018) Defining extreme wildfire events: difficulties, challenges, and impacts. Fire 1, 9
| Defining extreme wildfire events: difficulties, challenges, and impacts.Crossref | GoogleScholarGoogle Scholar |
Thurston W, Kepert JD, Tory KJ, Fawcett RJB (2017) The contribution of turbulent plume dynamics to long-range spotting. International Journal of Wildland Fire 26, 317–330.
| The contribution of turbulent plume dynamics to long-range spotting.Crossref | GoogleScholarGoogle Scholar |
Tolhurst K, Shields B, Chong D (2008) Phoenix: development and application of a bushfire risk management tool. Australian Journal of Emergency Management 23, 47
Viegas DX, Almeida M, Raposo J, Oliveira R, Viegas CX (2014) Ignition of Mediterranean fuel beds by several types of firebrands. Fire Technology 50, 61–77.
| Ignition of Mediterranean fuel beds by several types of firebrands.Crossref | GoogleScholarGoogle Scholar |
Werth PA, Potter BE, Alexander ME, Clements CB, Cruz MG, Finney MA, Forthofer JM, Goodrick SL, Hoffman C, Jolly WM (2016) Synthesis of knowledge of extreme fire behavior. Volume 2 for fire behavior specialists, researchers, and meteorologists. US Department of Agriculture, Forest Service, Pacific Northwest Research Station. General Technical Report PNW-GTR-891. (Portland, OR)
Zeileis A, Kleiber C, Jackman S (2008) Regression models for count data in R. Journal of Statistical Software 27, 1–25.
| Regression models for count data in R.Crossref | GoogleScholarGoogle Scholar |
Zuur AF, Ieno EN, Walker NJ, Saveliev AA, Smith GM (2009) Zero-truncated and zero-inflated models for count data. In ‘Mixed effects models and extensions in ecology with R’. (Eds AF Zuur, EN Ieno, N Walker, AA Saveliev, GM Smith) pp. 261–293. (Springer: New York, NY)
Appendix 1 Line scan and source fire examples
Appendix 2 Spot-number hurdle model details
A hurdle model consists of two parts (i.e. two individual generalised linear models; GLMs) that are combined to calculate fitted values and residuals (Zeileis et al. 2008; Zuur et al. 2009). The first part is a binomial GLM fitted to all data to model the probability of a phenomenon occurring (i.e. zero v. positive records). The second part is a count (or continuous) GLM fitted to the zero-truncated (i.e. non-zero) portion of the data to model the magnitude of the phenomenon. A hurdle model can be used to handle data with a high number of zeros and model overdispersion (Zeileis et al. 2008).
A hurdle model was used for our Spot-number model after initial application of standard GLMs produced poor results. For example, the application of a standard Poisson GLM for the number of spot fires over 500 m, for which 129 of the 250 training set source fires had zero spot fires, resulted in high overdispersion (measured using Pearson-based dispersion statistic) and unreasonably low significance values for each variable modelled (i.e. almost all variables tested produced significant P-values). Application of the hurdle model here reduced overdispersion and produced more reasonable significance values for each variable.
The Spot-number hurdle model consisted of two parts: (1) a binomial GLM modelling occurrence of at least one spot fire >500 m from its source fire; and (2) a Negative-binomial GLM with log link fitted to the zero-truncated portion of the data. A Negative-binomial GLM is suitable for modelling count data when overdispersion is present (Zeileis et al. 2008; Zuur et al. 2009). The Spot-number hurdle model selection process required two actions: (1) run Akaike Information Criterion model selection process (testing all combinations of predictors) in R for part 1 and part 2 separately and retain the best model for each part; and (2) combine each part into the hurdle model using the ‘hurdle’ function from the R pscl package (Zeileis et al. 2008; Jackson 2017) to calculate fitted values (training set) and predicted values (test set).