Where to prescribe burn: the costs and benefits of prescribed burning close to houses
Veronique Florec A B D , Michael Burton A B , David Pannell A B , Joel Kelso C and George Milne C
C and George Milne C
A School of Agriculture and Environment, University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia.
B Centre for Environmental Economics and Policy, University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia.
C Department of Computer Science and Software Engineering, University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia.
D Corresponding author. Email: veronique.florec@uwa.edu.au
International Journal of Wildland Fire 29(5) 440-458 https://doi.org/10.1071/WF18192
Submitted: 30 October 2018 Accepted: 27 March 2019 Published: 3 June 2019
Journal Compilation © IAWF 2020 Open Access CC BY-NC-ND
Abstract
Prescribed burning is used in Australia as a tool to manage fire risk and protect assets. A key challenge is deciding how to arrange the burns to generate the highest benefits to society. Studies have shown that prescribed burning in the wildland–urban interface (WUI) can reduce the risk of house loss due to wildfires, but the costs and benefits of different arrangements for prescribed burning treatments have rarely been estimated. In this study, we use three different models to explore the costs and benefits of modifying the spatial arrangement of prescribed burns on public land, using the south-west of Western Australia as a case study. We simulate two hypothetical scenarios: landscape treatments and WUI treatments. We evaluate the long-term costs and benefits of each scenario and compare the results from the three models, highlighting the management implications of each model. Results indicate that intensifying prescribed burning treatments in public land in the WUI achieves a greater reduction in damages compared with applying the majority of the treatments in rural areas. However, prescribed burning in the WUI is significantly more expensive and, despite additional benefits gained from this strategy, in most cases it is not the most economically efficient strategy.
Additional keywords: benefit-cost analysis, fire management, fuel treatment, house loss, preventative mitigation, risk, trade-off, wildland fire economics, wildland–urban interface.
Introduction
Wildfires, termed bushfires in Australia, can cause significant damage to ecosystems, life and property (Gill 2005; Bowman et al. 2009). In the last two decades, Australia has experienced some of the worst fires in its history (e.g. Canberra bushfires in January 2003, McLeod 2003; Black Saturday fires in February 2009, Teague et al. 2010). With climate change predictions showing a likely increase in the number of extreme weather days (Cary et al. 2012; Barbero et al. 2015; Jolly et al. 2015), the need for improved strategies for wildfire management and mitigation is growing.
Prescribed burning – the planned application of fire to the landscape – is one of the strategies implemented throughout Australia to reduce the intensity of bushfires and reduce the risk to people and property from damaging bushfires (Penman et al. 2011; Bentley and Penman 2017). There is a debate regarding the effectiveness of prescribed burning in reducing wildfire risk (Fernandes and Botelho 2003; Cary et al. 2009; Altangerel and Kull 2013; Gill et al. 2013) and where it should be applied to maximise its effectiveness (Stockmann et al. 2010; Penman et al. 2011). At the same time, the application of prescribed burning is becoming more difficult. With climate change, the window of opportunity presenting suitable conditions for the application of prescribed burning treatments is becoming smaller (Quinn-Davidson and Varner 2012; Jolly et al. 2015). In addition, escaped prescribed burns and issues caused by smoke emissions (e.g. health issues caused by increased levels of fine particulate matter air pollution or damage to agricultural production such as wine grapes) have resulted in resistance to the practice in certain communities (Brunson and Evans 2005; Bell and Oliveras 2006; Broome et al. 2016). Thus, there is a need to identify strategies that maximise the benefits of the practice and strike the right balance between asset protection, resource needs and potential disruptions.
The economic evaluation of prescribed burning, and more broadly the economic evaluation of fire management practices, is still a sparsely researched topic (Hesseln 2000; Fernandes and Botelho 2003; Mercer et al. 2007). Some research has been conducted to develop models for determining the optimal prescribed burning regime (e.g. Prestemon et al. 2001; Mercer et al. 2007; Mercer et al. 2008; Butry et al. 2010), or the optimal timing for applying the treatment (e.g. Jones et al. 1999). Other work has investigated the most cost-effective strategy to reduce the area burned by wildfires or to reduce the probability of houses being destroyed by fire (Omi et al. 1999; Liu et al. 2010; Stockmann et al. 2010; Penman et al. 2014).
As a general rule, fire agencies practice wildfire prevention based on values at risk and take into consideration the differences in value and importance of communities, houses, infrastructure and natural resources when planning and allocating resources for fire mitigation and suppression (Department of Fire and Emergency Services (DFES), Department of Parks and Wildlife (DPaW), Government of Western Australia 2016). However, most of the published research literature evaluating the costs and benefits of prescribed burning in different locations has used in their models the same value per hectare for all hectares in the landscape (i.e. values at risk are the same for all hectares) or has not estimated the benefits in dollar values to be able to compare them with the costs of wildfire mitigation. For instance, Prestemon et al. (2001), Mercer et al. (2007) and Butry et al. (2010) evaluated the costs and benefits of prescribed burning in Florida, but assumed that all parts of the landscape had the same value per hectare. Omi et al. (1999) and Liu et al. (2010) estimated the costs of different strategies to reduce area burned but did not estimate the benefits of reductions in wildfire area. Stockmann et al. (2010) and Penman et al. (2014) estimated the costs of different placements for prescribed burning treatments to reduce the risk of wildfires destroying houses. Their models estimated the probability of a fire reaching houses and investigated which prescribed burning strategy achieves the highest reduction in risk to houses. However, these studies did not estimate house losses in dollar values, from which to be able to infer the value for money delivered by the treatments. In the present study, we have developed a model that can simultaneously: (i) estimate the costs of prescribed burning, taking into account changes in costs with treatment size and location (i.e. distance from human habitations); (ii) use a different value per unit area rather than the same value for all hectares in the landscape; and (iii) estimate the benefits (in dollars) of changes in wildfire area and asset loss for each fuel reduction strategy to compare them with implementation costs. We compare the results of our model with the results that would be obtained from a model using a single value per hectare and a model minimising the probability of a fire reaching houses.
There are several arguments for concentrating fuel management around the wildland–urban interface (WUI). One argument is that house losses due to wildfire can be reduced when the fuel load close to houses is reduced (Bar Massada et al. 2011; Gibbons et al. 2012; Penman et al. 2015). Some authors argue that reducing the potential of home ignition by reducing fuels adjacent to houses should be the focus of land-management agencies (Cohen 1999; Cohen 2004; Stocks et al. 2004; Calkin et al. 2014). Also, when a fire is getting close to a town, firefighting resources may be more effective at protecting life and property if the intensity of the fire is reduced when the fire encounters a treated area close to the town (Underwood et al. 1985; McCaw 2013). Another argument is related to the distribution of fire ignitions. Wildfire ignition probability is generally higher close to population centres (Penman et al. 2013; Plucinski et al. 2014), so if fuel management is intensified around the WUI, these ignitions are less likely to produce damaging wildfires. However, prescribed burning close to human habitations is usually more expensive because these burns require more planning and fire agencies tend to use more resources per hectare treated to prevent the burns from escaping (Berry et al. 2006; Calkin and Gebert 2006; Hesseln et al. 2006; Penman et al. 2014).
The question addressed here is: what spatial arrangement of prescribed burning (WUI vs landscape treatments) maximises the net benefits of prescribed burning, allowing for its various benefits, costs and risks? In particular, are the benefits from concentrating prescribed burning in the WUI sufficient to justify the higher costs of doing so? We use wildfire simulation technology in combination with an economic model to evaluate different strategies for prescribed burning in the long term. We compare our model with previous models evaluating the costs and benefits of prescribed burning programs. We use the south-west forest region of Western Australia (WA) as a case study.
Methods
We used three different models to evaluate the costs and benefits of two different arrangements of prescribed burning treatments (WUI vs landscape treatments) and different amounts of area treated per year. The first model (here referred to as the ‘minimum costs plus net value change model’) is the one we developed. It is a modified version of the original cost plus net value change (C+NVC) model (Donovan and Rideout 2003), which is the most widely used model for the economic evaluation of fire management programs (Ganewatta 2008). The second and third models (here referred to as the ‘equal asset value and modified costs model’ and the ‘minimum house loss model’) are based on previous studies evaluating the costs and benefits of prescribed burning (Mercer et al. 2008; Butry et al. 2010; Stockmann et al. 2010; Penman et al. 2014). We applied the three models to a case study area in the south-west of WA and compared their results. Each model estimates the costs of the prescribed burning program according to the strategy implemented (WUI or landscape treatments) and the amount of area treated, as well as wildfire damages (in dollar values or expressed as the probability of a fire reaching houses, depending on the model used) and suppression costs. The counterfactual used for all three models is the no-prescribed-burning scenario (i.e. 0% area treated); thus the benefits of applying the different prescribed-burning strategies correspond to the reduction in damages and suppression costs achieved by the implementation of each strategy compared with doing nothing.
Prescribed burning strategies
We evaluated two prescribed-burning strategies corresponding to different spatial arrangements for the treatments:
-
One where the majority of the area treated (but not all) is located in rural areas (hereafter called ‘landscape treatments’). This strategy is similar to the strategy currently implemented by the WA Department of Biodiversity, Conservation and Attractions (DBCA) in the south-west of WA.
-
Another where the majority of the area treated (but not all) is concentrated around human habitations (hereafter called ‘WUI treatments’). Here, we implemented a similar strategy to that suggested by Burrows and McCaw (2013), where the treatments are distributed as follows:1
-
-
Zone 1: Community protection zone. Fuels are maintained at <4 years old within a 5-km radius of towns.
-
Zone 2: Bushfire modification zone. Fuels are maintained at <5 years old in areas in a 5–10-km radius of towns and between 5 and 7 years old in areas in a 10–20-km radius of towns. The purpose of this zone is to modify bushfire behaviour in order to reduce damages and increase the likelihood of suppression of the fires before they reach a town.
-
Zone 3: Biodiversity management zone. In this zone, located >20 km from towns, the goal is to maintain a diversity of fire regimes and fuel ages (through mosaic burning) where possible. Fuels are maintained at <4 years old in one-third of the area, at 4–7 years old in another third of the area, and carry older fuels in the remaining third.
-
For each strategy, we tested five different prescribed burning regimes:
-
0 ha treated per year. This is the 0% regime.
-
39 500 ha treated per year, which corresponds to 5% of the area managed by DBCA in the case study area (DBCA manages ~790 000 hectares of land in the case study area. This corresponds to 42% of the total area of the case study area). This is the 5% regime.
-
79 000 ha treated per year, which corresponds to 10% of the area managed by DBCA in the case study area. This is the 10% regime.
-
118 500 ha treated per year. This is the 15% regime.
-
158 000 ha treated per year. This is the 20% regime.
Each regime was applied over a 15-year period (with wildfires burning in each fire season) until fuels reached an ‘equilibrium’ level. All burned areas (both wildfire and prescribed fire) alter the fuel levels (risk) of the ‘equilibrium’ layer for each regime. All changes done to fuel levels for a period of 15 years (as a result of prescribed burning and wildfires) in order to reach the equilibrium are not part of the economic analysis; their only purpose is to arrive at equilibrium loads where the fuels would be at a level representative of the regime applied. The area treated per annum for both strategies (landscape and WUI treatments) is the same for any given regime (0, 5, 10, 15 or 20%), the only thing that changes between the two strategies is where the treatments are located on the landscape. The treatments were only applied on public land, selecting the patches with the oldest fuel age within each zone. Feasibility was not considered in the model, the assumption being that all areas selected for treatment could actually be treated. The risk of fire escaping and destroying high-value assets was not considered for the selection of the patches, but was indirectly accounted for in the costs of prescribed burning (higher costs for treatments located closer to human habitations).
The costs of prescribed burning change depending on where on the landscape the treatment is applied – close to or far from human habitations – and the size of the patch burned (the costs of prescribed burning are further explained in the descriptions of the models below). Table 1 shows the area treated for different treatment sizes and distances from towns for the strategy with majority landscape treatments. This strategy is similar to the strategy implemented by DBCA and was derived from historical records of the application of prescribed burning by DBCA in the case study area. Table 2 shows the area treated with intensified WUI treatments, which was derived from the three-zones strategy suggested by Burrows and McCaw (2013).

|

|
Minimum cost plus net value change model
In this model, the most efficient strategy is the one that minimises the sum of prescribed burning costs, suppression costs and damages (Donovan and Rideout 2003; Rodríguez y Silva and González-Cabán 2010). For each regime, we simulated 220 fire seasons (parameter M), each containing 110 fires (parameter K), with ignition location and weather conditions changing between fire seasons (see more details in the section Using simulation technology below). We then calculated the average suppression costs and average damage for all fire seasons simulated. Our model is formulated as follows:
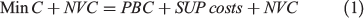
with
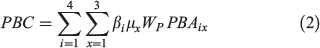
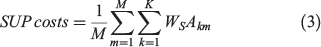
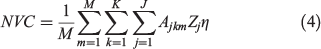
Prescribed burning costs (PBC) in Eqn (2) were calculated by multiplying the total number of hectares prescribed-burned per year PBA in treatments of size x and at distance i from the closest town, by the average cost of prescribed burning per hectare (Wp). We used two coefficients to change prescribed-burning cost per hectare depending on the size of the treatment and its location (i.e. distance from the closest town): βi varies with distance i from the closest town, and µx varies with the size x of the treatment. Table 3 shows the values used for each coefficient and resulting prescribed-burning costs per hectare, which are based on historical cost data (2003–13) provided by DBCA. Economies of scale are incorporated in the model through the coefficient µx, which diminishes as the size of the treatment gets larger. However, other likely economies of scale resulting from reductions in the overall level of fuels in the landscape, increased staff experience, or improved leverage of available resources, etc., were not possible to isolate from the DBCA costs data and consequently are not accounted for in our model. Therefore, although economies of scale are incorporated through the coefficient µx, total prescribed burning costs increase linearly because the area treated in each combination of treatment size and distance from towns increases linearly between the regimes tested. Total prescribed burning costs for each strategy are shown in Table 4 (see Supplementary material Tables S1 and S2 for details on how these costs were calculated for each strategy).

|

|
SUP costs in Eqn (3) correspond to the average suppression costs for all fire seasons simulated. We calculated suppression costs for each fire season by multiplying the average suppression cost per hectare WS by the number of hectares burned Akm by fire k (k = 1,…,K) in fire season m (m = 1,…,M), where K is the total number of fires in a fire season (110 on average) and M is the total number of fire seasons simulated for each strategy and each regime (a total of 220; see more details in the section Using simulation technology). We estimated average suppression cost per hectare (WS) at AU$1170 using DBCA suppression costs data and area burned in the case study area between 2003 and 2013.
NVC in Eqn (4) is the average net damage for all the fire seasons simulated, which depends on the number of hectares burned, the type of assets burned, and the intensity with which they burned. Ajkm is the number of hectares burned in land-use category j by fire k (k = 1,…,K) in fire season m (m = 1,…,M); Zj is the value in dollars of 1 ha of land-use category j; and η is the percentage of value destroyed depending on the level of intensity (0 ≥ η ≤ 1). We used five different land-use categories of the five most predominant land uses in the region. The values used in our economic model for each land-use category are shown in Table 5.

|
The model estimates the costs and benefits of prescribed burning at ‘equilibrium’, that is, the simulations are run on what would likely be a representative year in the future, if the prescribed burning regime tested was applied for a long period of time (i.e. at least 15 years). Therefore, prescribed burning costs, suppression costs and damages are only estimated for 1 single year, which corresponds to any year in the future after the long-term application of the regime evaluated. Our objective is to minimise the costs and damages at equilibrium, which is very different from a dynamic optimisation model. Dynamic optimisation would require the use of discounting and would likely lead to very different results. As we estimate the costs and damages for 1 single year, our approach does not call for discounting. Thus, our results should be interpreted as the average costs and damages that could be expected in any 1 year in the future following the long-term application of each regime. Estimating the costs of reaching such equilibrium is beyond the scope of the present study.2 Our model is not set up to do this type of analysis; instead, it takes 1 single representative year in the future and evaluates the costs and benefits for that year. In the following two models, all costs and damages are also estimated at equilibrium.
Equal asset value and modified costs model
Similarly to the previous model, the equal value model also aims to minimise the sum of prescribed burning costs, suppression costs and damages, but differs from the previous model in two aspects: first, it uses a single value per hectare for all hectares in the landscape (as done by Prestemon et al. 2001; Mercer et al. 2007; Butry et al. 2010). Second, per-hectare costs of prescribed burning change with the size of the treatments but they do not change with location. That is, two treatments of equal size would have the same cost regardless of how close they are to human habitations. In order to assess the effects of these model specifications and compare the results with the previous model, we have formulated it as follows:
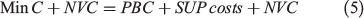
with
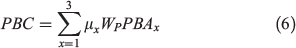
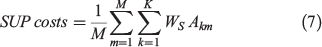
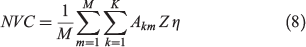
Prescribed burning costs (PBC) in Eqn (6) only change with the size of the treatment (and not with its location) and therefore only coefficient µx is used. Coefficient βi is removed from this equation. Similarly, because all hectares have the same value, the different types of land-use category j are not differentiated in this model and NVC only depends on the number of hectares burned by wildfire Akm and the value in dollars of a hectare Z. All hectares in the landscape have the same value Z = AU$8636, which is the weighted average of the values presented in Table 5. The percentage of value destroyed η according to the level of intensity is also taken into account in this model. Total prescribed burning costs for each strategy according to the specifications of this model are shown in Table 4 (see Supplementary material Tables S3 and S4 for details on how these costs were calculated).
Minimum house loss model
This model is based on the analyses conducted by Stockmann et al. (2010) and Penman et al. (2014). In the minimum house loss model, the aim is to find the prescribed burning strategy that minimises house losses due to wildfires. To make the analysis comparable with the aforementioned studies, this model minimises the probability of wildfires reaching houses and is formulated as follows:
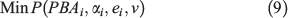
subject to
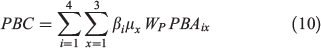
where P is the probability of a fire reaching houses, which depends on the number of ignitions  in location i (WUI or landscape), several environmental variables ei (i.e. slope, aspect and vegetation type) in location i, and fire weather v. Penman et al. (2014) treated prescribed burning costs differently, using generalised linear models (GLMs) to illustrate the relationship between the natural logarithm of cost per hectare and the natural logarithm of area (ha) treated in different locations (WUI and landscape). Thus, their model accounts for changes in per-hectare costs of prescribed burning with treatment size and location. Stockmann et al. (2010) used different per-hectare costs for wildland and home ignition zone treatments, thus accounting for changes in per-hectare costs with location, but did not account for changes in per-hectare costs with treatment size. However, in order to make the different models comparable, we have formulated total prescribed burning costs PBC in the same way as in our model. Total prescribed burning costs for each strategy with the specifications of this model are shown in Table 4.
in location i (WUI or landscape), several environmental variables ei (i.e. slope, aspect and vegetation type) in location i, and fire weather v. Penman et al. (2014) treated prescribed burning costs differently, using generalised linear models (GLMs) to illustrate the relationship between the natural logarithm of cost per hectare and the natural logarithm of area (ha) treated in different locations (WUI and landscape). Thus, their model accounts for changes in per-hectare costs of prescribed burning with treatment size and location. Stockmann et al. (2010) used different per-hectare costs for wildland and home ignition zone treatments, thus accounting for changes in per-hectare costs with location, but did not account for changes in per-hectare costs with treatment size. However, in order to make the different models comparable, we have formulated total prescribed burning costs PBC in the same way as in our model. Total prescribed burning costs for each strategy with the specifications of this model are shown in Table 4.
Study area
The study area for this analysis is one of the three management regions of DBCA in the south-west of WA, called the South-West Forest Region (SWFR) (see study area location in Fig. 1). In the area, DBCA implements a coordinated approach to prescribed burning in public land (see DBCA-managed land in Fig. 2). For other tenures (e.g. private land, unallocated crown land), there is not a single agency responsible for fuel management. Private landowners have to establish fire breaks and manage fuels on boundaries adjacent to Crown and pasture land, but generally there is no coordination between landowners to do so.

|

|
The SWFR, which has a size of ~1 880 000 ha, is characterised by a Mediterranean climate with hot dry summers and mild wet winters. The region receives between 600 and 1000 mm of rainfall annually, but rainfall is seasonal and more than 80% of annual rainfall occurs between May and October. During the peak of the fire season (December to February), mean monthly rainfall in the region averages less than 25 mm and maximum temperatures are often above 35°C (Burrows and McCaw 2013). The vegetation in the region is dry enough to burn between October and May and dry lightning is often a source of ignition between October and March (McCaw and Hanstrum 2003; Burrows and McCaw 2013).
The SWFR contains a mix of eucalyptus forests, agricultural land and human habitations (see land use in the region in Fig. 3). The forests and woodlands are dominated by three species of trees – jarrah (Eucalyptus marginata), marri (Corymbia calophylla) and karri (Eucalyptus diversicolor) – and the coastal plains are mostly covered by mallee shrublands and heathlands. The region has large WUI areas where high-value human assets are often intermixed with flammable vegetation. The population of the SWFR is ~128 000 people, concentrated primarily around two small coastal cities (Busselton and Bunbury) and several towns in the agricultural and forested areas (see Fig. 4). The region also receives ~1.6 million tourists per year (South West Development Commission n.d.). Fire management in the SWFR is complex not only because of the WUI context, but also because of the many different land uses, tenures and stakeholders, and the fact that the region is located in a biodiversity hotspot (Myers and Mittermeier 2000; Mittermeier et al. 2011), where biodiversity conservation is an important land-management objective that needs to be integrated into fire management (Burrows 2008).
Using simulation technology
To evaluate a prescribed burning strategy, we need to know what effects this strategy would have on wildfire behaviour and wildfire damages to different types of assets (houses and their contents, industrial and commercial buildings, crops, plantations, livestock, etc.). Fire simulation has been successfully used to evaluate the effects of prescribed burning on wildfire impacts (e.g. Penman et al. 2014; Collins et al. 2015), evaluate different risk management strategies (e.g. Penman et al. 2015), or obtain rapid information on potential fire spread in order to better coordinate the deployment of suppression resources (e.g. DFES 2013; Thwaites 2015). An advantage of using wildfire simulation for the economic analysis of prescribed burning is that it allows many wildfire scenarios to be tested. Used in this way, fire simulators provide information on the confidence that can be attached to the results.
We used the AUSTRALIS wildfire simulator (Johnston et al. 2008; Kelso et al. 2015) to simulate the spread of wildfires and assess the effects of the two contrasting prescribed burning strategies in a wide range of plausible wildfire scenarios in the south-west of WA. AUSTRALIS predicts the spread of a wildfire across the landscape using empirically derived fire spread models for different types of vegetation (from Noble et al. 1980; McCaw and Burrows 1989; McCaw 1997; Cheney et al. 1998; Plucinski 2003). Various types of information (weather, topography, vegetation and fuel age data) are required as inputs to the simulator to estimate the spread time between discrete areas of the landscape, called cells, and the intensity with which each cell burns. Here, a ‘cell’ is defined as a portion of the landscape that has the size of 1 ha. For each cell in the landscape, we know its physical attributes including fuel type, fuel load, slope, orientation, and the type and value of the assets it contains. We also know whether it was burned by a wildfire or not, and the intensity with which it burned. We used this information to estimate the damage caused by the fires simulated.
The baseline scenario for our analysis assumes no prescribed burning for a period of at least 15 years, with wildfires simulated in each fire season during that time, and fuel levels modified accordingly. We simulated 24 200 fires under the no-prescribed-burning scenario, varying the location of the ignition points, the time and date of ignition and the climatic parameters for the duration of the fire (i.e. temperature, relative humidity, wind speed and wind direction). We then repeated the same 24 200 simulations for each of the different regimes tested using both prescribed burning strategies. The 24 200 fires correspond to 22 different ignition patterns (each containing 110 fires, which is the average number of fires burning annually in the SWFR), simulated under 10 different weather scenarios (we used the historical weather patterns of 20 weather stations in the SWFR between 2003 and 2013). This amounts to a total of 220 fires seasons simulated for each regime. The location of the ignition points was based on a logit model applied to 10 years of ignition location data in the region (2003 to 2013).3 The times and dates of ignition were generated at random, using a normal distribution centred around January for the date, and a normal distribution centred at midday for the time. Areas prescribed-burned do not affect the logit model; they simply reduce the fuel loads in different areas. If an ignition occurs in a treated area, then it has less chances of successfully spreading and becoming a wildfire, thereby reducing the total number of wildfires. However, the initial number of ignitions remains the same for the different prescribed-burning regimes.
Suppression
The AUSTRALIS simulator does not simulate suppression per se; that is, it does not simulate the deployment of firefighting forces to suppress a fire event, or the results of their efforts on the rate of spread of the fire. Without a model for suppression or a rule for stopping the fires, the simulated fires would keep on burning until they either encounter a natural barrier or until the weather conditions lead to the self-extinction of the fire. However, this would be a poor reflection of reality, and a rule is needed to act as a proxy for suppression. We developed a stopping rule based on the time that it would take firefighting forces to reach the fire and their capacity to suppress the fire depending on the intensity of the fire front. We simulated all historical fires occurring in the SWFR between 2003 and 2013 under the same weather conditions they occurred and tested different stopping rules until the most appropriate rule was found; that is, when the total area burned and the fire size distribution were similar to the historical data. Fig. 5 shows the fire size distribution of historical and simulated fires using the same ignition point and weather conditions of the historical data. The stopping rule is different for fires occurring in average weather conditions (usually resulting in fires ≤1500 ha) and for fires occurring in more extreme weather conditions (usually resulting in fires >1500 ha). The rule that best fitted historical data is formulated as:
Stop fire spread from any cell after a delay D in seconds of:

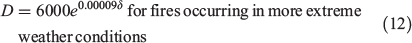
where δ is the distance from the closest town, if the intensity I is:
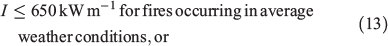
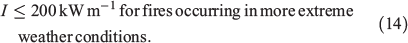
Both criteria D and I have to be met for a cell in the simulator to stop the fire spreading to neighbouring downwind cells. The underlying simulation mechanism (implemented in software) is described in detail in Johnston et al. 2008 and Kelso et al. 2015.

|
In reality, other factors such as the type of assets at risk would also affect the spread of the fire, given the difference in suppression resource deployments depending on the assets threatened by the fire. For instance, suppression efforts are higher when the fire approaches high values at risk, such as human lives and property, and fire spread within or outside the WUI is likely to be affected by this. Our suppression rule, however, does not directly account for changes in suppression strategies for fires in the WUI. This is only indirectly captured by the delay criterion D, which would be significantly smaller for fires occurring in the WUI, allowing cells of low intensity to be extinguished earlier than if the fire occurred far from the WUI. Prescribed-burned areas affect suppression effectiveness in our proxy suppression model by changing the intensity of the fire front. If the intensity is reduced when a wildfire reaches a treated area, then criterion I may be met sooner and the spread of the fire may be slowed or stopped.
Results
Minimum cost plus net value change model
The prescribed burning regime that minimises the C+NVC (i.e. the sum of prescribed burning costs, suppression costs and damages) for this model is 15% for both strategies (see Fig. 6, Table 6 and Table 7); that is, when 118 500 ha is treated per year in the SWFR. At this level, landscape treatments generate more net benefits than WUI treatments, with a difference of almost AU$9 million (AU$236 million net benefits for landscape treatments compared with AU$227 million for WUI treatments). Thus, the most economically efficient prescribed burning strategy in the SWFR is landscape treatments with a 15% regime.

|
Although the average size of area burned is relatively small in urban areas compared with other land-use categories (Table 8), damages are largely dominated by losses in urban areas, regardless of which strategy is applied (Fig. 7). This is due to the high value per hectare of the urban land-use category. Consequently, WUI treatments, which achieve a greater reduction in wildfire area in the WUI, result in greater reductions in damages compared with landscape treatments for all regimes. However, WUI treatments are considerably more expensive than landscape treatments, which results in landscape treatments generating higher net benefits for all regimes except one. Only when 5% of DBCA-managed land is treated per year (i.e. 39 500 ha) are the net benefits of WUI treatments higher than landscape treatments (see Table 6 and Table 7). In this case, net benefits are significantly higher for WUI treatments than for landscape treatments, with a difference of nearly AU$49 million (AU$212 million net benefits for WUI treatments compared with AU$163 million for landscape treatments). However, a 5% regime does not minimise the sum of costs and damages (the C+NVC). For a fire manager in the SWFR, this means that if there are restrictions on the size of area that can be treated per year and only 39 500 ha can be treated (5% regime), then WUI treatments would generate more net benefits than landscape treatments. But for the other regimes tested in our model, the opposite is true.

|

|
Fig. 6 shows that the C+NVC curve initially decreases rapidly, but flattens for both strategies when ≥10% of DBCA-managed land is treated. This suggests that there are several near-optimal options for both strategies. For a fire manager, this means that if the optimal regime (15%) cannot be implemented, a lower regime of 10% could be implemented with a relatively moderate loss in net benefits for landscape treatments (less than AU$6 million) and a minor loss in net benefits for WUI treatments (AU$0.6 million). However, for a 10% regime, landscape treatments still generate more net benefits than WUI treatments (AU$231 million compared with AU$227 million).
To test the robustness of our results, we increased and decreased all parameter values (separately) by 50%. The sensitivity analysis shows that the results for landscape treatments are quite robust (Table 9), with the optimal regime only changing when prescribed burning costs are reduced by 50%. The minimum C+NVC remains relatively stable despite the parameter changes, and only shows a more significant change when prescribed-burning costs are increased or decreased or when the assumed level of damage caused by different levels of intensity is increased or decreased. The results of WUI treatments are less robust (Table 10). The optimal regime changes when the value of urban areas is changed, as well as the value of conservation areas, prescribed burning costs, suppression costs and the level of damages caused by different levels of intensity. However, the minimum C+NVC remains reasonably stable, often close to the baseline results.

|

|
Our results suggest that in the study area, WUI treatments are less cost-effective compared with landscape treatments if the (economically) optimal level of prescribed burning is applied. However, if the management agency is restricted in terms of the size of area that can be treated (i.e. if for instance only 5% of the area managed can be prescribed-burned), then WUI treatments should be applied as they generate higher benefits for low levels of prescribed burning.
Equal asset value and modified costs model
The prescribed burning regime that minimises the sum of prescribed burning costs, suppression costs and damages for this model is 20% for both strategies (see Fig. 8, Table 11 and Table 12); that is, when 158 000 ha is treated per year in the SWFR. Using this model, the most economically efficient prescribed burning strategy in the SWFR is landscape treatments with a 20% regime. Landscape treatments generate more net benefits for all regimes except 5% (AU$509 million net benefits for landscape treatments compared with AU$613 million for WUI treatments).

|
Damages are largely dominated by losses in agriculture, plantations and nature and conservation for both strategies (Fig. 9). This is due to the large number of hectares burned in these land-use categories. Using the same value for all hectares in the landscape, losses in urban areas appear insignificant.

|
Minimum house loss model
Looking solely at the probability of a fire reaching houses, WUI treatments achieve a much more rapid reduction in risk to houses compared with landscape treatments (Fig. 10). The application of WUI treatments at a 5% regime (39 500 ha treated) results in a significant reduction in risk to houses; to achieve a similar level of risk reduction, landscape treatments need to be applied at a 15% regime, requiring the treatment of 118 500 ha. Thus, a substantially higher number of hectares needs to be treated with landscape treatments to achieve the same level of reduction in risk to houses as is obtained with WUI treatments. For high levels of prescribed burning (15% regime or higher), the reduction in risk to houses compared with doing nothing is the same for both strategies.

|
Discussion
The three models yield very different results. The minimum C+NVC suggests that the most economically efficient strategy in the SWFR is landscape treatments when applied at a 15% regime per annum, whereas the equal asset value and modified costs model suggests a 20% regime, and the minimum house loss model favours WUI treatments over landscape treatments for all regimes. Furthermore, the equal asset value and modified costs model estimates a much higher level of damages (in the order of AU$850 million for the 0% regime) compared with the minimum C+NVC model (approximately AU$200 million). This suggests that using the same value for all hectares in the landscape can lead to an overestimation of the benefits of prescribed burning. For fire managers, this highlights the importance of having good-quality information on the assets at risk in the landscape and their respective values.
The results from the minimum house loss model show that when house losses are not estimated in dollars, this can lead to the conclusion that prescribed burning in the WUI is always more effective than landscape treatments. Using only the numbers of houses destroyed or the probability of a fire reaching houses to evaluate the benefits of different arrangements of prescribed burning shows only part of the picture. This can lead fire managers to make suboptimal decisions that do not maximise the benefits to society and the environment. In contrast, when house losses are converted to dollars, the benefits of different treatment locations can be more fully appreciated and the value for money delivered by the treatments better understood.
It is clear from the three models that the absence of fuel reduction treatments in the long term would result in considerably higher damages and suppression expenditures for the South-West forest region of WA or considerably higher risk of house losses. This is consistent with the economic analyses of prescribed burning conducted in other areas, which suggest that in order to protect life, property and the environment from wildfires, a minimum level of prescribed burning has to be continuously maintained in the long term (Snider et al. 2006; Mercer et al. 2007; Liu et al. 2010; Stockmann et al. 2010; Gibson and Pannell 2014; Penman et al. 2014). The minimum C+NVC model indicates that the absence of prescribed burning for 15 years in the SWFR, with only wildfires altering fuel levels, would result in average annual suppression costs ~10 times higher than the optimal level, and average damage costs more than 20 times higher than the optimal level.
The results from all models show that increasing the rate of prescribed burning in the SWFR reduces the average area burned by wildfires and risk to structures such as housing, resulting in reduced wildfire damages and reduced suppression costs. These results are consistent with existing studies (Omi et al. 1999; Snider et al. 2006; Mercer et al. 2007). However, this happens at a decreasing rate; that is, prescribed burning exhibits diminishing marginal returns, as other studies have also demonstrated (e.g. Mercer et al. 2007; Butry et al. 2010; Bradstock et al. 2012). What previous studies have not discussed is the wide range of near-optimal options (the flattening of the C+NVC curve), even though in some studies a similar outcome can be seen (e.g. Mercer et al. 2007). Our results show that, if the optimal regime cannot be implemented, suboptimal regimes could be implemented with fairly minor losses in benefits. This information is very useful to fire managers, who can use it to make decisions on the level of investment for prescribed burning and the arrangement of the treatments with a better knowledge of the trade-offs involved.
The optimal prescribed-burning rates derived from the minimum C+NVC model and the equal asset value and modified costs model point to rates that are considerably higher than current practice in the case study area (15 and 20% respectively). A regime of 15% of DBCA-managed land prescribed-burned per year is comparable with the rate that was applied the 1960s and 1970s in the region (Department of Parks and Wildlife (DPaW) 2016). However, in today’s management context, applying such high rates may not be feasible, given the reduction in the climatic window for the application of the treatment due to climate change, past fuel accumulations and the expansion of the WUI in the region.
All models indicate that concentrating prescribed-burning treatments in the WUI results in greater reductions in damages when compared with landscape treatments (which has the majority of the area treated located in rural areas). This is mostly due to greater reductions in house losses or risk to houses, or in the case of the equal asset value and modified costs model, due to greater reductions in wildfire area (because most ignitions occur close to human habitations, prescribed burning in the WUI reduces the chances of these ignitions turning into large wildfires). Other simulation and empirical studies have shown a similar effect (Cary et al. 2009; Bradstock et al. 2012; Gibbons et al. 2012; Penman et al. 2014). However, for all regimes tested in the present study except 5%, net benefits are higher for landscape treatments than WUI treatments. Net benefits are only higher for WUI treatments when 39 500 ha is treated per year, but such a regime is a suboptimal strategy (i.e. it does not minimise the sum of costs and damages). This information is also useful to fire managers, who may be restricted on the number of hectares that can be treated per year, given the limited availability of resources, the short window of opportunity for the application of the treatments, and the potential resistance to the practice from the local population. If only 39 500 ha can be treated per year in the SWFR (a suboptimal regime), then WUI treatments would generate higher net benefits than landscape treatments. For the other regimes tested in the present study, landscape treatments are more economically efficient.
It is important to note that the results for WUI treatments are less robust and are sensitive to changes in the value of urban areas, conservation areas, prescribed burning costs, suppression costs and the level of damages caused by different levels of intensity. Thus, as new information becomes available and is integrated in this study, or if other costs and values at risk are added to our model (such as the value of life and injuries, opportunity costs, animal welfare, cultural heritage values, other costs incurred owing to the time it takes to rebuild or regrow the affected areas), the results could be considerably different. Nevertheless, with the assets we have included in our study (buildings, conservation areas, state forests, agricultural production from crops and vines, and mining), our results show that prescribed burning in public land in the WUI is significantly more expensive and, despite additional benefits gained from this strategy, in most cases it is not the most economically efficient strategy.
Our results are contingent on treatments being applied on public land only and ignore the efforts carried out by private landowners to reduce wildfire risk to their properties. Including fuel reductions on private land may significantly affect the results. However, there are very limited data available regarding what happens on private land. Improvements in this area will help fire managers make better decisions regarding the distribution of treatments across the landscape and get better value for money from prescribed-burning treatments.
Although the sum of costs and damages is generally lower for landscape treatments than for WUI treatments, society as a whole may be willing to accept higher prescribed-burning costs in exchange for lower damages in fire-prone areas. Our study only includes the reconstruction value of residential and commercial buildings in urban areas. However, other high-value human assets, particularly intangible (non-market) values such as lives lost, injuries, memorabilia, animal welfare, social disruption and mental health issues, have not been included. This is a limitation of our model. Also, we have not included the cost generated by the application of prescribed burning in terms of nuisance to the local population from smoke issues (Martin et al. 2007; Broome et al. 2016) or damage to agricultural production (e.g. prescribed-burning smoke impacts on neighbouring vineyards; McCaw 2013). If these values were included in our study, the results could show a different outcome.
Although the application of prescribed burning in the SWFR reduces the level of damages caused by wildfires, it does not eliminate the risk entirely, and even with a very high prescribed-burning regime (e.g. 20%), annual average wildfire damages can be expected to reach AU$8 million (using the minimum C+NVC model) or AU$47 million (using the equal asset value and modified costs model). Therefore, no matter how much prescribed burning is applied to the landscape, there is always a residual level of risk. This is consistent with the findings from other studies in Australia (Gill 2005; Gill and Stephens 2009; Bradstock et al. 2012) and elsewhere (Calkin et al. 2014).
Our model is sensitive to a few key parameters (prescribed burning costs, suppression costs and the level of damage caused by different levels of intensity). In order to make better decisions for prescribed burning, it is important to have improved information on prescribed-burning costs and the level of damage cause by fires of different severity. In addition, when prescribed burning is applied in the WUI, obtaining accurate information on the value of assets at risk, both human and environmental assets, becomes particularly important.
In this study, we have assumed that all the prescribed-burning treatments planned for any 1 year can be implemented within the estimated costs. But as the window of opportunity with suitable conditions to apply the treatments is shortened under the influence of climate change, increases in the area treated could become significantly more costly. Furthermore, the costs of prescribed burning correspond only to the fire management agency’s direct expenditure in prescribed burning (i.e. equipment used, staff, trucks, planning, etc.). A limitation of our model is that it does not include the potential ecological damage that the long-term application of prescribed burning could cause to certain species and changes in vegetation structure that it could produce (Parr and Andersen 2006). For instance, low and high levels of prescribed burning can cause a decline in Callitris verrucosa populations, a predominant plant in semiarid mallee shrubland communities in southern Australia that is highly sensitive to variations in fire regime (Bradstock et al. 2006). High fire frequency can significantly increase the probability of extinction of obligate seeder species of Banksia, irrespective of fire size (Bradstock et al. 1996).
Future developments of our model would include a wider range of values at risk, particularly non-market values, such as lives, injuries, social disruption and environmental values. For this, further research is needed on how non-market values are affected by bushfires in the long term (Venn and Calkin 2011; Rideout et al. 2014). Given the high number of non-market values affected by wildfires, several researchers have already emphasised the need to better integrate non-market values in economic analyses of fire management (Rideout et al. 1999; Thompson and Calkin 2011; Venn and Calkin 2011). Also, as intensifying prescribed burning in the WUI has the effect of replacing losses by increased prescribed burning costs in the SWFR, better understanding is required regarding society’s willingness to pay for reductions in wildfire damage and their willingness to accept higher prescribed-burning costs.
Conclusion
The three models yield very different results. The strategy and area treated that minimise the sum of prescribed burning costs, suppression costs and damages are different depending on the model used. However, the equal asset value and modified costs model overestimates wildfire damages and the minimum house loss model does not provide enough information to assess the value for money delivered by different arrangements of the treatments. This study shows that the minimum C+NVC model is more appropriate than the other models for the economic evaluation of prescribed-burning strategies, because it can make the trade-offs between the different options more explicit.
Intensifying prescribed burning treatments in the WUI achieves a greater reduction in damages and risk to houses compared with applying the majority of the treatments in rural areas. However, despite the additional benefits gained from WUI treatments, in most cases it is not the most economically efficient strategy. Only in limited circumstances does prescribed burning on public land in the WUI generate more net benefits than landscape treatments.
Our study also shows the value of using detailed simulation technology for the evaluation of prescribed-burning strategies in order to assist with strategic decision making for wildfire management. Simulation is the only means of conducting a large number of experiments with a wide range of prescribed-burning strategies over a sustained period and can help fire managers evaluate many different scenarios.
Conflicts of interest
The authors declare that they have no conflicts of interest.
Acknowledgements
We thank the Western Australian DBCA and Department of Fire and Emergency Services for fire history, prescribed burning costs and suppression costs data. We thank two anonymous reviewers and an associate editor for providing helpful comments and suggestions that significantly improved the manuscript. This study was funded by the Bushfire and Natural Hazards Cooperative Research Centre and the University of Western Australia.
References
AHA Viticulture (2006) Margaret River regional profile. Final report to the Grape and Wine Research & Development Corporation. (AHA Viticulture: Dunsborough, WA, Australia) Available at https://www.wineaustralia.com/getmedia/8850e859-225f-48eb-a79f-7b8c943eb542/AHA-05-03-Final-Report [Verified 23 April 2019]Altangerel K, Kull C (2013) The prescribed burning debate in Australia: conflicts and compatibilities. Journal of Environmental Planning and Management 56, 103–120.
| The prescribed burning debate in Australia: conflicts and compatibilities.Crossref | GoogleScholarGoogle Scholar |
Bar Massada A, Radeloff VC, Stewart SI (2011) Allocating fuel breaks to optimally protect structures in the wildland–urban interface. International Journal of Wildland Fire 20, 59–68.
| Allocating fuel breaks to optimally protect structures in the wildland–urban interface.Crossref | GoogleScholarGoogle Scholar |
Barbero R, Abatzoglou JT, Larkin NK, Kolden CA, Stocks B (2015) Climate change presents increased potential for very large fires in the contiguous United States. International Journal of Wildland Fire 24, 892–899.
| Climate change presents increased potential for very large fires in the contiguous United States.Crossref | GoogleScholarGoogle Scholar |
Bell T, Oliveras I (2006) Perceptions of prescribed burning in a local forest community in Victoria, Australia. Environmental Management 38, 867–878.
| Perceptions of prescribed burning in a local forest community in Victoria, Australia.Crossref | GoogleScholarGoogle Scholar | 17001507PubMed |
Bentley PD, Penman TD (2017) Is there an inherent conflict in managing fire for people and conservation? International Journal of Wildland Fire 26, 455–468.
| Is there an inherent conflict in managing fire for people and conservation?Crossref | GoogleScholarGoogle Scholar |
Berry AH, Donovan GH, Hesseln H (2006) Prescribed burning costs and the WUI: economic effects in the Pacific Northwest. Western Journal of Applied Forestry 21, 72–78.
Bowman DMJS, Balch JK, Artaxo P, Bond WJ, Carlson JM, Cochrane MA, D’Antonio CM, DeFries RS, Doyle JC, Harrison SP, Johnston FH, Keeley JE, Krawchuk MA, Kull CA, Marston JB, Moritz MA, Prentice IC, Roos CI, Scott AC, Swetnam TW, van der Werf GR, Pyne SJ (2009) Fire in the earth system. Science 324, 481–484.
| Fire in the earth system.Crossref | GoogleScholarGoogle Scholar |
Bradstock RA, Bedward M, Scott J, Keith DA (1996) Simulation of the effect of spatial and temporal variation in fire regimes on the population viability of a banksia species. Conservation Biology 10, 776–784.
| Simulation of the effect of spatial and temporal variation in fire regimes on the population viability of a banksia species.Crossref | GoogleScholarGoogle Scholar |
Bradstock RA, Bedward M, Cohn JS (2006) The modelled effects of differing fire management strategies on the conifer Callitris verrucosa within semi-arid mallee vegetation in Australia. Journal of Applied Ecology 43, 281–292.
| The modelled effects of differing fire management strategies on the conifer Callitris verrucosa within semi-arid mallee vegetation in Australia.Crossref | GoogleScholarGoogle Scholar |
Bradstock RA, Cary GJ, Davies I, Lindenmayer DB, Price OF, Williams RJ (2012) Wildfires, fuel treatment and risk mitigation in Australian eucalypt forests: insights from landscape-scale simulation. Journal of Environmental Management 105, 66–75.
| Wildfires, fuel treatment and risk mitigation in Australian eucalypt forests: insights from landscape-scale simulation.Crossref | GoogleScholarGoogle Scholar | 22531752PubMed |
Broome RA, Johnston FH, Horsley J, Morgan GG (2016) A rapid assessment of the impact of hazard reduction burning around Sydney, May 2016. The Medical Journal of Australia 205, 407–408.
| A rapid assessment of the impact of hazard reduction burning around Sydney, May 2016.Crossref | GoogleScholarGoogle Scholar | 27809737PubMed |
Brunson MW, Evans J (2005) Badly burned? Effects of an escaped prescribed burn on social acceptability of wildland fuels treatments. Journal of Forestry 103, 134–138.
Bureau of Transport Economics (2001) Economic costs of natural disasters in Australia. (Bureau of Transport Economics, Commonwealth of Australia: Canberra, ACT, Australia) Available at https://bitre.gov.au/publications/2001/files/report_103.pdf [Verified 23 April 2019]
Burrows N, McCaw L (2013) Prescribed burning in south-western Australian forests. Frontiers in Ecology and the Environment 11, e25–e34.
| Prescribed burning in south-western Australian forests.Crossref | GoogleScholarGoogle Scholar |
Burrows ND (2008) Linking fire ecology and fire management in south-west Australian forest landscapes. Forest Ecology and Management 255, 2394–2406.
| Linking fire ecology and fire management in south-west Australian forest landscapes.Crossref | GoogleScholarGoogle Scholar |
Butry DT, Prestemon JP, Abt KL, Sutphen R (2010) Economic optimisation of wildfire intervention activities. International Journal of Wildland Fire 19, 659–672.
| Economic optimisation of wildfire intervention activities.Crossref | GoogleScholarGoogle Scholar |
Calkin DE, Gebert K (2006) Modeling fuel treatment costs on forest service lands in the western United States. Western Journal of Applied Forestry 21, 217–221.
Calkin DE, Cohen JD, Finney MA, Thompson MP (2014) How risk management can prevent future wildfire disasters in the wildland–urban interface. Proceedings of the National Academy of Sciences of the United States of America 111, 746–751.
| How risk management can prevent future wildfire disasters in the wildland–urban interface.Crossref | GoogleScholarGoogle Scholar | 24344292PubMed |
Cary G, Bradstock R, Gill A, Williams RJ (2012) Global change and fire regimes in Australia. In ‘Flammable Australia: fire regimes, biodiversity and ecosystems in a changing world’. (Eds R Bradstock, MA Gill, RJ Williams) pp. 180–204. (CSIRO Publishing: Melbourne, Vic., Australia)
Cary GJ, Flannigan MD, Keane RE, Bradstock RA, Davies ID, Lenihan JM, Li C, Logan KA, Parsons RA (2009) Relative importance of fuel management, ignition management and weather for area burned: evidence from five landscape–fire–succession models. International Journal of Wildland Fire 18, 147–156.
| Relative importance of fuel management, ignition management and weather for area burned: evidence from five landscape–fire–succession models.Crossref | GoogleScholarGoogle Scholar |
Cheney N, Gould J, Catchpole W (1998) Prediction of fire spread in grasslands. International Journal of Wildland Fire 8, 1–13.
| Prediction of fire spread in grasslands.Crossref | GoogleScholarGoogle Scholar |
Cohen JD (1999) Reducing the wildland fire threat to homes: where and how much. In ‘Proceedings of the symposium on fire economics, planning, and policy: bottom lines’, 5–9 April 1999, San Diego, CA, USA. (Tech. coord. A Gonzalez-Caban) pp. 189–195. USDA Forest Service, Pacific Southwest Research Station, General Technical Report PSW-GTR-173. (Albany, CA, USA)
Cohen JD (2004) Relating flame radiation to home ignition using modeling and experimental crown fires. Canadian Journal of Forest Research 34, 1616–1626.
| Relating flame radiation to home ignition using modeling and experimental crown fires.Crossref | GoogleScholarGoogle Scholar |
Collins L, Penman TD, Price OF, Bradstock RA (2015) Adding fuel to the fire? Revegetation influences wildfire size and intensity. Journal of Environmental Management 150, 196–205.
| Adding fuel to the fire? Revegetation influences wildfire size and intensity.Crossref | GoogleScholarGoogle Scholar | 25500136PubMed |
Department of Fire and Emergency Services (DFES) (2013) Locally developed Aurora scores State awards. 24seven 2, 50–51. Available at https://www.dfes.wa.gov.au/newsandmedia/24seven/24seven/DFES-24seven-2013-Issue2.pdf [Verified 13 September 2018]
Department of Fire and Emergency Services (DFES), Department of Parks and Wildlife (DPaW), Government of Western Australia (2016) Capes Zone Response: i-zone (Inter face), o-zone (Outer zone), Operational Protocols 2013/2016. Available at https://www.amrshire.wa.gov.au/library/file/1Council/Meetings/Committees/BFAC/I%20Zone%20O%20ZoneOperational%20Protocols%202013%2014%20protocols%20V10.pdf [Verified 15 November 2017]
Department of Parks and Wildlife (DPaW) (2016) ‘Annual Report 2015–2016.’ (Government of Western Australia: Perth, WA, Australia)
Donovan GH, Rideout DB (2003) A reformulation of the cost plus net value change (C+NVC) model of wildfire economics. Forest Science 49, 318–323.
Dunford MA, Power L, Cook B (2014) National Exposure Information System (NEXIS) Building Exposure – Local Government Area (LGA). (Geoscience Australia: Canberra, ACT, Australia) Available at https://researchdata.ands.org.au/national-exposure-information-area-lga/1277833?source=suggested_datasets [Verified 23 April 2019]
Fernandes PM, Botelho HS (2003) A review of prescribed burning effectiveness in fire hazard reduction. International Journal of Wildland Fire 12, 117–128.
| A review of prescribed burning effectiveness in fire hazard reduction.Crossref | GoogleScholarGoogle Scholar |
Ganewatta G (2008) The economics of bushfire management. In ‘Community bushfire safety’. (Eds J Handmer, K Haynes) pp. 151–159. (CSIRO Publishing: Melbourne, Vic., Australia)
Gibbons P, van Bommel L, Gill AM, Cary GJ, Driscoll DA, Bradstock RA, Knight E, Moritz MA, Stephens SL, Lindenmayer DB (2012) Land management practices associated with house loss in wildfires. PLoS One 7, e29212
| Land management practices associated with house loss in wildfires.Crossref | GoogleScholarGoogle Scholar | 23227217PubMed |
Gibson FL, Pannell DJ (2014) Integrated economic assessment of fire risk management strategies: case studies in central Otago, New Zealand, and Mount Lofty Region, South Australia – final report for the Integrated Assessment of Prescribed Burning project. (Bushfire CRC: Melbourne, Vic., Australia) Available at http://www.bnhcrc.com.au/publications/biblio/14 [Verified 23 April 2019]
Gill AM (2005) Landscape fires as social disasters: an overview of the bushfire problem. Environmental Hazards 6, 65–80.
| Landscape fires as social disasters: an overview of the bushfire problem.Crossref | GoogleScholarGoogle Scholar |
Gill AM, Stephens SL (2009) Scientific and social challenges for the management of fire-prone wildland–urban interfaces. Environmental Research Letters 4, 034014
Gill AM, Stephens SL, Cary GJ (2013) The worldwide ‘wildfire’ problem. Ecological Applications 23, 438–454.
| The worldwide ‘wildfire’ problem.Crossref | GoogleScholarGoogle Scholar | 23634593PubMed |
Greene WH (2012) ‘Econometric analysis. 7th edn.’ (Prentice Hall: Upper Saddle River, NJ, USA)
Hesseln H (2000) The economics of prescribed burning: a research review. Forest Science 46, 322–334.
Hesseln H, Donovan GH, Berry AH (2006) The effect of the wildland–urban interface on prescribed burning costs in the Pacific Northwest. Western Journal of Applied Forestry 21, 72–78.
Johnston P, Kelso J, Milne GJ (2008) Efficient simulation of wildfire spread on an irregular grid. International Journal of Wildland Fire 17, 614–627.
| Efficient simulation of wildfire spread on an irregular grid.Crossref | GoogleScholarGoogle Scholar |
Jolly WM, Cochrane MA, Freeborn PH, Holden ZA, Brown TJ, Williamson GJ, Bowman DMJS (2015) Climate-induced variations in global wildfire danger from 1979 to 2013. Nature Communications 6, 7537
Jones JG, Chew JD, Zuuring HRA (1999) Applying simulation and optimization to plan fuel treatments at landscape scales. In ‘Proceedings of symposium on fire economics, planning and policy: bottom lines’, 5–9 April 1999, San Diego, CA, USA. (Tech. coord. A Gonzalez-Caban) pp. 189–195. USDA Forest Service, Pacific Southwest Research Station, General Technical Report PSW-GTR-173. (Albany, CA, USA)
Kelso JK, Mellor D, Murphy ME, Milne GJ (2015) Techniques for evaluating wildfire simulators via the simulation of historical fires using the Australis simulator. International Journal of Wildland Fire 24, 784–797.
| Techniques for evaluating wildfire simulators via the simulation of historical fires using the Australis simulator.Crossref | GoogleScholarGoogle Scholar |
Liu Z, He HS, Chang Y, Hu Y (2010) Analyzing the effectiveness of alternative fuel reductions of a forested landscape in north-eastern China. Forest Ecology and Management 259, 1255–1261.
| Analyzing the effectiveness of alternative fuel reductions of a forested landscape in north-eastern China.Crossref | GoogleScholarGoogle Scholar |
Martin WE, Brajer V, Zeller K (2007) Valuing the health effects of a prescribed fire. In ‘Wildfire risk: human perceptions and management implications’. (Eds WE Martin, C Raish, BJ Kenny) pp. 244–261. (Resources for the Future: Washington, DC, USA)
McCaw WL (1997) Predicting fire spread in Western Australian mallee-heath shrubland. PhD thesis, University College, University of New South Wales. (Sydney, NSW, Australia)
McCaw WL (2013) Managing forest fuels using prescribed fire – a perspective from southern Australia. Forest Ecology and Management 294, 217–224.
| Managing forest fuels using prescribed fire – a perspective from southern Australia.Crossref | GoogleScholarGoogle Scholar |
McCaw WL, Burrows N (1989) Fire management. In ‘The jarrah forest: a complex Mediterranean ecosystem’. (Eds B Dell, JJ Havel, N Malajczuk) pp. 317–335. (Kluwer Academic Publishers: Dordrecht, the Netherlands)
McCaw WL, Hanstrum B (2003) Fire environment of Mediterranean south-west Western Australia. In ‘Fire in ecosystems of south-west Western Australia: impacts and management’. (Eds I Abbott, N Burrows) pp. 87–106. (Backhuys Publishers: Leiden, the Netherlands)
McLeod R (2003) ‘Inquiry into the operational response to the January 2003 Bushfires in the ACT.’ (Information Planning and Services, Department of Urban Services, ACT Government: Canberra, ACT, Australia)
Mercer DE, Prestemon JP, Butry DT, Pye JM (2007) Evaluating alternative prescribed burning policies to reduce net economic damages from wildfire. American Journal of Agricultural Economics 89, 63–77.
| Evaluating alternative prescribed burning policies to reduce net economic damages from wildfire.Crossref | GoogleScholarGoogle Scholar |
Mercer DE, Haight RG, Prestemon JP (2008) Analyzing trade-offs between fuels management, suppression, and damages from wildfire. In ‘The economics of forest disturbances: wildfires, storms and invasive species’. (Eds TP Holmes, JP Prestemon, K Abt) pp. 247–272. (Springer: Dordrecht, the Netherlands)
Mittermeier RA, Turner WR, Larsen FW, Brooks TM, Gascon C (2011) Global biodiversity conservation: the critical role of hotspots. In ‘Biodiversity hotspots’. (Eds FE Zachos, JC Habel) pp. 3–22. (Springer: Dordrecht, the Netherlands)
Myers N, Mittermeier RA (2000) Biodiversity hotspots for conservation priorities. Nature 403, 853–858.
| Biodiversity hotspots for conservation priorities.Crossref | GoogleScholarGoogle Scholar | 10706275PubMed |
Noble IR, Bary GAV, Gill AM (1980) McArthur’s fire-danger meters expressed as equations. Australian Journal of Ecology 5, 201–203.
| McArthur’s fire-danger meters expressed as equations.Crossref | GoogleScholarGoogle Scholar |
Omi PN, Rideout DB, Botti SJ (1999) An analytical approach for assessing cost-effectiveness of landscape prescribed fires. In ‘Proceedings of symposium on fire economics, planning and policy: bottom lines’, 5–9 April 1999, San Diego, CA, USA. (Tech. coord. A Gonzalez-Caban) pp. 237–241. USDA Forest Service, Pacific Southwest Research Station, General Technical Report PSW-GTR-173. (Albany, CA, USA)
Parr CL, Andersen AN (2006) Patch mosaic burning for biodiversity conservation: a critique of the pyrodiversity paradigm. Conservation Biology 20, 1610–1619.
| Patch mosaic burning for biodiversity conservation: a critique of the pyrodiversity paradigm.Crossref | GoogleScholarGoogle Scholar | 17181796PubMed |
Penman TD, Christie FJ, Andersen AN, Bradstock RA, Cary GJ, Henderson MK, Price O, Tran C, Wardle GM, Williams RJ, York A (2011) Prescribed burning: how can it work to conserve the things we value? International Journal of Wildland Fire 20, 721–733.
| Prescribed burning: how can it work to conserve the things we value?Crossref | GoogleScholarGoogle Scholar |
Penman TD, Bradstock RA, Price O (2013) Modelling the determinants of ignition in the Sydney Basin, Australia: implications for future management. International Journal of Wildland Fire 22, 469–478.
| Modelling the determinants of ignition in the Sydney Basin, Australia: implications for future management.Crossref | GoogleScholarGoogle Scholar |
Penman TD, Bradstock RA, Price OF (2014) Reducing wildfire risk to urban developments: simulation of cost-effective fuel treatment solutions in south-eastern Australia. Environmental Modelling & Software 52, 166–175.
| Reducing wildfire risk to urban developments: simulation of cost-effective fuel treatment solutions in south-eastern Australia.Crossref | GoogleScholarGoogle Scholar |
Penman TD, Nicholson AE, Bradstock RA, Collins L, Penman SH, Price OF (2015) Reducing the risk of house loss due to wildfires. Environmental Modelling & Software 67, 12–25.
| Reducing the risk of house loss due to wildfires.Crossref | GoogleScholarGoogle Scholar |
Plucinski M (2003) The investigation of factors governing ignition and development of fires in heathland vegetation. PhD thesis, School of Mathematics and Statistics, Australian Defence Force Academy, University of New South Wales. (Sydney, NSW, Australia)
Plucinski MP, McCaw WL, Gould JS, Wotton BM (2014) Predicting the number of daily human-caused bushfires to assist suppression planning in south-west Western Australia. International Journal of Wildland Fire 23, 520–531.
| Predicting the number of daily human-caused bushfires to assist suppression planning in south-west Western Australia.Crossref | GoogleScholarGoogle Scholar |
Prestemon J, Mercer DE, Pye JM, Butry D, Holmes TP, Abt K (2001) Economically optimal wildfire intervention regimes. In ‘Paper presented at the American Agricultural Economics Association annual meeting’, 5–8 August 2001, Chicago, IL, USA. (Agricultural & Applied Economics Association: Milwaukee, WI, USA) Available at https://ageconsearch.umn.edu/record/20470/files/sp01pr05.pdf [Verified 12 September 2017]
Quinn-Davidson LN, Varner JM (2012) Impediments to prescribed fire across agency, landscape and manager: an example from northern California. International Journal of Wildland Fire 21, 210–218.
| Impediments to prescribed fire across agency, landscape and manager: an example from northern California.Crossref | GoogleScholarGoogle Scholar |
Rideout DB, Loomis JB, Omi PN (1999) Incorporating non-market values in fire management planning. In ‘Proceedings of symposium on fire economics, planning and policy: bottom lines’, 5–9 April 1999, San Diego, CA, USA. (Tech. coord. A Gonzalez-Caban) pp. 217–225. USDA Forest Service, Pacific Southwest Research Station, General Technical Report PSW-GTR-173. (Albany, CA, USA)
Rideout DB, Ziesler PS, Kernohan NJ (2014) Valuing fire planning alternatives in forest restoration: using derived demand to integrate economics with ecological restoration. Journal of Environmental Management 141, 190–200.
| Valuing fire planning alternatives in forest restoration: using derived demand to integrate economics with ecological restoration.Crossref | GoogleScholarGoogle Scholar | 24878985PubMed |
Rodríguez y Silva F, González-Cabán A (2010) ‘SINAMI’: a tool for the economic evaluation of forest fire management programs in Mediterranean ecosystems. International Journal of Wildland Fire 19, 927–936.
| ‘SINAMI’: a tool for the economic evaluation of forest fire management programs in Mediterranean ecosystems.Crossref | GoogleScholarGoogle Scholar |
Snider G, Daugherty PJ, Wood D (2006) The irrationality of continued fire suppression: an avoided cost analysis of fire hazard reduction treatments versus no treatment. Journal of Forestry 104, 431–437.
South West Development Commission (n.d.) Our region. Available at http://www.swdc.wa.gov.au/our-region.aspx [Verified 23 April 2019]
Stockmann KD, Burchfield J, Calkin DE, Venn TJ (2010) Guiding preventative wildland fire mitigation policy and decisions with an economic modeling system. Forest Policy and Economics 12, 147–154.
| Guiding preventative wildland fire mitigation policy and decisions with an economic modeling system.Crossref | GoogleScholarGoogle Scholar |
Stocks BJ, Alexander ME, Lanoville RA (2004) Overview of the International Crown Fire Modelling Experiment (ICFME). Canadian Journal of Forest Research 34, 1543–1547.
| Overview of the International Crown Fire Modelling Experiment (ICFME).Crossref | GoogleScholarGoogle Scholar |
Teague B, McLeod R, Pascoe S (2010) The 2009 Victoria Bushfires Royal Commission final report. (Government Printer for the State of Victoria: Melbourne, Vic., Australia) Available at http://www.royalcommission.vic.gov.au/Commission-Reports/Final-Report.html [Verified 23 April 2019]
Thompson MP, Calkin DE (2011) Uncertainty and risk in wildland fire management: a review. Journal of Environmental Management 92, 1895–1909.
| Uncertainty and risk in wildland fire management: a review.Crossref | GoogleScholarGoogle Scholar | 21489684PubMed |
Thwaites T (2015) The computer program that saved a town. Pursuit. (The University of Melbourne, Melbourne, Vic., Australia) Available at https://pursuit.unimelb.edu.au/articles/the-computer-program-that-saved-a-town [Verified 22 June 2018]
Underwood RJ, Sneeuwjagt RJ, Styles HG (1985) The contribution of prescribed burning to forest fire control in Western Australia: case studies. In ‘Symposium on fire ecology and management in Western Australian ecosystems’, May 1985 (Ed JR Ford) pp. 153–170. Western Australian Institute of Technology (WAIT), Environmental Studies Group Report No. 14. (Perth, WA, Australia)
Venn TJ, Calkin DE (2011) Accommodating non-market values in evaluation of wildfire management in the United States: challenges and opportunities. International Journal of Wildland Fire 20, 327–339.
| Accommodating non-market values in evaluation of wildfire management in the United States: challenges and opportunities.Crossref | GoogleScholarGoogle Scholar |
Wooldridge JM (2009) ‘Introductory econometrics: a modern approach. 4th edn.’ (South-Western Cengage Learning: Mason, OH, USA)
1 The strategy outlined here is slightly different to the one presented in Burrows and McCaw (2013) but it follows the same principles of zoning for community protection, bushfire modification and biodiversity management, and has similar splitting distances.
2 In order to move from a 0% regime (doing nothing) to a 10% regime and reach equilibrium for 10%, it is necessary to prescribe-burn 10% of public land every year for a number of years. The annual costs of applying this strategy for several years until equilibrium is reached are not included in our model.
3 A logistic (or logit) model is a statistical model that uses a logistic function to model the probability of an outcome (for a binary dependent variable) given a set of regressors (Greene 2012; Wooldridge 2009). Our model estimates the probability of ignition in a cell depending on its distance from roads, land use, topography and fuel loads.








