Clarifying the meaning of mantras in wildland fire behaviour modelling: reply to Cruz et al. (2017)
William Mell A G , Albert Simeoni B , Dominique Morvan C , J. Kevin Hiers D , Nicholas Skowronski E and Rory M. Hadden FA Pacific Wildland Fire Sciences Laboratory, US Forest Service, 400 N. 34th Street, Suite 201, Seattle, WA 98074, USA.
B Fire Protection Engineering Department, Worcester Polytechnic Institute, 100 Institute Road, Worcester, MA 01609, USA.
C Aix-Marseille University, CNRS, Centrale Marseille, M2P2, Marseille, France.
D Tall Timbers Research Station, 13093 Henry Beadel Drive, Tallahassee, FL 32312, USA.
E Northern Research Station, US Forest Service, 180 Canfield Street, Morgantown, WV 26505, USA.
F School of Engineering, University of Edinburgh, King’s Buildings, Mayfield Road, Edinburgh, EH9 3JL, UK.
G Corresponding author. Email: wemell@fs.fed.us
International Journal of Wildland Fire 27(11) 770-775 https://doi.org/10.1071/WF18106
Submitted: 11 July 2018 Accepted: 26 July 2018 Published: 20 August 2018
Abstract
In a recent communication, Cruz et al. (2017) called attention to several recurring statements (mantras) in the wildland fire literature regarding empirical and physical fire behaviour models. Motivated by concern that these mantras have not been fully vetted and are repeated blindly, Cruz et al. (2017) sought to verify five mantras they identify. This is a worthy goal and here we seek to extend the discussion and provide clarification to several confusing aspects of the Cruz et al. (2017) communication. In particular, their treatment of what they call physical models is inconsistent, neglects to reference current research activity focussed on combined experimentation and model development, and misses an opportunity to discuss the potential use of physical models to fire behaviour outside the scope of empirical approaches.
Additional keywords: CFD, empirical models, physics-based models.
Introduction
In a recent commentary on fire-behaviour models, Cruz et al. (2017) identify five statements, or mantras, they believe have gained ‘currency as facts – or truths’ regarding empirical and physical (sometimes called physics-based or process-based) wildland fire models. Cruz et al. (2017) are concerned that an unquestioning acceptance of the mantras will lead to poorly informed use of the models in question. They seek, therefore, ‘to discuss the validity’ of these mantras. We agree that model users should be aware of the strengths and weaknesses of a given model. However, inconsistencies between how the mantras are represented by Cruz et al. (2017), and how they appear in the literature, add confusion, rather than clarity, to a broader discussion. In some cases, the authors’ discussion of the mantras is not even consistent within their own framework. Regarding physical models, the largely negative critique is confused by inconsistent definitions, inaccuracies and falls short of understanding how model advancement in engineering science is coupled to appropriate measurements. The authors appear to favour empirical models for prediction while not recognising the capabilities of physical models, especially those based on computational fluid dynamics, for improving our understanding of the underlying physical and chemical mechanisms and their role in driving fire behaviour.
Although we appreciate the motivation and goal of Cruz et al. (2017), our intent in this response is to provide a constructive critique of Cruz et al. (2017) by clarifying the particularly confusing elements and providing viewpoints from the engineering and management perspectives. In Cruz et al. (2017), empirical (as opposed to semi-empirical) models are the subject of the first two mantras and what they call ‘physical’ models are considered in the last three mantras. These mantras are:
-
Mantra 1 (M1). Empirical models work well over the range of their original data.
-
Mantra 2 (M2). Empirical models are not appropriate for and should not be applied to conditions outside the range of the original data.
-
Mantra 3 (M3). Physical models provide insight into the mechanisms that drive wildland fire spread and other aspects of fire behaviour.
-
Mantra 4 (M4). Physical models give a better understanding of how fuel treatments modify fire behaviour.
-
Mantra 5 (M5). Physical models can be used to derive simplified models to predict fire behaviour operationally.
The discussion regarding physical models is flawed
The discussion related to the mantras for the physical models displays a limited understanding of modelling approaches that attempt to include (explicitly or implicitly) physical processes driving wildland fire. In the first paragraph of Cruz et al. (2017), the authors define a physical modelling approach as one that ‘employs a mathematical description of fundamental physical and chemical processes underpinning combustion, fluid flow and heat transfer’. We take this to mean that the processes driving fire behaviour are explicitly accounted for in ‘physical models’. Cruz et al. then use the term ‘physical model’ for both simpler models that, for example, neglect the process of convective heat transfer (in M3 and M5) and for more comprehensive physical models based on computational fluid dynamics (CFD) that explicitly account for all the recognised driving processes (in M3 and M4), including convective heat transfer.
A consequence of this inconsistent use of the term ‘physical model’ is confusion and lack of completeness. For clarity, here we place physical models into two groups: one group uses CFD, and the other does not. Both have model equations that are the result of approximations based on physically motivated assumptions. To be more precise, we use CFD-based physical models to denote comprehensive approaches that explicitly model the recognised processes driving fire behaviour. This is consistent with references cited for CFD-based models and statements made by Cruz et al.
In Cruz et al., nearly all the cited non-CFD physical models do not explicitly model convective heat transfer. Cruz et al. appear to mistakenly assume that convective heat transfer was neglected because the model developers assumed it is not relevant to fire spread, which is clearly not the case. If one reads the cited literature, it is clear that the model developers are fully aware that convective heat transfer, in some environmental conditions, will be relevant; but these are not the environmental conditions for which they derive their model. The assumption of radiation dominance in these models is not, therefore, an ‘example of our ignorance of the fundamental processes governing wildland fire behaviour’ as stated in the third paragraph of the M3 discussion.
Adding to the confusion, Cruz et al. incorrectly interpret findings in the cited literature (Anderson et al. 2010; Butler 2010) when they write (end of second paragraph of M3 discussion) ‘recent experimental evidence suggests it is convective heat transfer … that is the dominant heat transfer mechanism determining wildland fire propagation’. Anderson et al. (2010) did not measure radiation and, therefore, do not compare radiative and convective heat fluxes. Butler (2010) found that convective and radiative heat flux can be comparable in magnitude at certain times, and did not state that convective heat transfer dominates. Finney et al. (2015) do state that ‘repetitive convective heating thus appears to be the critical heat transfer mechanism causing ignition and spread of these fires’. In addition, Morandini and Silvani (2010) (a study not cited by Cruz et al. 2017) conducted five field experiments and found that, depending on the fire experiment, radiative heat transfer either dominated convective heat transfer, or they were of similar magnitude. Morandini and Silvani (2010) considered shrub fires, Butler (2010) considered full-scale crown fires, and Finney et al. (2015) considered laboratory-scale surface fire in highly uniform fuel beds. Clearly, more work is needed to determine why the findings of these experiments differ. This point is missed by Cruz et al.
The latter part of the discussion of M3 and most of the M4 discussion is focussed on the challenges facing CFD-based physical models, including the need for some empiricism and more model validation. Although our response is not comprehensive, some of Cruz et al.’s statements are notably incorrect and demonstrate a limited understanding of CFD modelling. For example, it is not possible to model buoyant flow driven by combustion while assuming (as stated by Cruz et al. in the M3 section) constant density, incompressible flow.
Significantly, what Cruz et al. (2017) do not convey is that the reason they can list challenges to CFD-based modelling is precisely because these models are well characterised, both in their modelling approach and in areas needing improvement. CFD-based fire-behaviour models are constructed from coupled numerical models, for the governing processes, that vary in their degree of maturity and proven physical fidelity. For example, the models for fluid flow (including buoyancy induced flow) and radiation are significantly more advanced and validated than models for the processes of thermal degradation and momentum drag in vegetation. Cruz et al. (2017) give an incomplete picture of the advances made and the state of activity (including new experiments) in pursuit of improvements to these models (e.g. Anand et al. 2017; Mueller 2017; Lamorlette et al. 2018).
In the last sentence of the M3 section, Cruz et al. (2017) summarise their view of CFD-based physical modelling:
Until a complete and robust understanding of the processes … we question how much is to be gained from pure modelling exercises…
This statement is problematic for several reasons. Physical models have approximations and will not be ‘complete’, but they can be useful and their failings can be characterised and addressed, making this a specious criticism. In addition, the suggestion that the developers of CFD-based physical models are in some way focussed on ‘pure modelling exercises’ displays a lack of familiarity with fire engineering science. It is fundamental to the scientific method and well established in the fire engineering community that the development of physical models requires comparison with observations and experiments (see Mell et al. 2007; Tihay et al. 2008; Mell et al. 2009; Morvan et al. 2009; Tihay et al. 2009; Hoffman et al. 2016; El Houssami et al. 2018). The necessity to have detailed comparisons between numerical results and experimental data (i.e. not just rate of spread observations) often push experimentalists to use more and more sophisticated experimental diagnostic methods in the laboratory (Marcelli et al. 2004; Morandini et al. 2005; Zhou et al. 2007; Lozano et al. 2010) and in the field (Frankman et al. 2013, Mueller et al. 2017). This list of experimental studies, using advanced diagnostics, is only a sampling, many more exist.
Mantra 2 is not representative of statements in literature
There is no acknowledgement or discussion of how the particular wording of any given mantra, which affects the mantra’s meaning, required choices by the authors. For example, consider Mantra 2 which is stated to be ‘likely the most commonly used fire behaviour modelling mantra’. In the literature cited in table 1 of Cruz et al. (2017) for M2, the following text can be found (note, Cruz et al. 2017 do not provide these excerpts):
While such models may be very successful over fuel and environmental conditions similar to those occurring in the test fires, their lack of a physical basis means that the use of such models outside of these conditions must be treated with caution. [Catchpole and de Mestre 1986]
The predicted values for the ROS [rate of spread] remain valid for conditions close to the experimental conditions which were used to gauge the parameters of the model… Unfortunately the results obtained with this type of approaches are not easily applicable for more general fire conditions. [Morvan and Larini 2001]
…but the model is only valid in the range of experiments for which it was validated. Peculiarly, the change from laboratory to field scale experiments is not supported, but involves a new calibration of the parameters. [Balbi et al. 2009]
…strictly speaking, their application to environmental conditions outside of those for which they were derived is not justified. [Mell et al. 2010]
These are only applicable to systems in which conditions are identical to those used in formulating and testing the models. [Pastor et al. 2003]
Later in the paper it is stated, regarding McArthur meters for dry eucalypt forest, that:
Nevertheless, the use of this model in landscapes with vegetation different from that of dry eucalypt forest in Australia should be done with caution. [Pastor et al. 2003]
At first glance, these quoted statements seem to be well represented by M2 of Cruz et al. (2017) However, most of the statements allow for the possibility of applying an empirical model outside its original dataset, but with appropriate caution. Thus, the wording of the Cruz et al. (2017) version of this mantra is stricter than that of the authors cited because Cruz et al. (2017) make no allowance for the possibility that an empirical model may work outside the original environmental conditions. This sets the stage for easily invalidating M2 by finding any case where an empirical model works sufficiently well outside its originating environmental conditions. This is what Cruz et al. (2017) do in their discussion of M2.
Cruz et al. (2017) go further and state that ‘empirical models are likely to be valid for far drier and windier conditions than those involved in the model development’. But this statement required sufficient measurements in the new environment to show that the original model actually worked outside its dataset. Also, there are contrary examples. The work by Fernandes (2014) had the opposite finding: an empirical model could not be successfully extended to environmental conditions outside its original dataset unless it was recalibrated using the new data.
Although many scientists would allow that an empirical model may work for environmental conditions outside its originating dataset, they would also agree that, without measurements confirming it, there is no justification for asserting that the empirical model will do so with quantifiable confidence. Caution is inherent to the process of using empirically fit models beyond their domain of inference and is taught in basic statistics (Sokal and Rohlf 1995). In essence, Cruz et al. (2017) agree with this when they state, at the end of M2, ‘evaluation should always precede the use of models within operational contexts’.
Are Mantras 3 through 5 valid?
We agree that the wording of M3 is representative of the literature and believe it to be valid. As an example, we provide a simple demonstration of how of CFD based models can provide insight into the roles of convective and radiative heat transfer. Fig. 1 shows results from a three-dimensional, time-dependent simulation (using the wildland–urban interface fire dynamics simulator (WFDS); Mell et al. 2009; Perez-Ramirez et al. 2017 have model details) of a surface fire spreading, with no ambient wind, through a 10 cm deep, 80 cm wide, 1.8 m long excelsior fuel bed. Fig. 1 shows the time histories of the gas and vegetation temperatures and the contribution of the convective (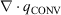 ) and radiative (
) and radiative (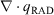 ) heat fluxes to the rate of change of the vegetation’s temperature. These quantities are plotted at two vertical locations (both at a distance of 1 m from the ignition region): z = 35 cm above the fuel bed (i.e. a location subjected to the combustion generated buoyant plume and intermittent flame) and at z = 0 cm (i.e. top of fuel bed and subjected to a relatively slower and less variable flow and radiation from a continuous fire front). Consistent with the findings of Finney et al. (2015) (see their fig. 5A), the vegetation temperature at z = 35 cm follows a ‘stair-stepped’ rise that is controlled by a varying convective heat flux (Fig. 1a, b). At z = 0 cm on top of the fuel bed (Fig. 1c, d), radiation dominates until near ignition (i.e. the temperature of the vegetation, Tveg = ~350°C at time = 36 s), at which point radiation and convection are comparable, at no point does convection exhibit the large oscillations seen at z = 35 cm. The experimental configuration of Finney et al. (2015) is a surface fire and their measurement location is similar to Figs. 1c, d (i.e. at the top of the fuel bed). Their results are similar to Figs. 1a, b because their imposed wind increases the unsteady behaviour of the flame. Simulations with WFDS give similar results with an imposed wind (not shown).
) heat fluxes to the rate of change of the vegetation’s temperature. These quantities are plotted at two vertical locations (both at a distance of 1 m from the ignition region): z = 35 cm above the fuel bed (i.e. a location subjected to the combustion generated buoyant plume and intermittent flame) and at z = 0 cm (i.e. top of fuel bed and subjected to a relatively slower and less variable flow and radiation from a continuous fire front). Consistent with the findings of Finney et al. (2015) (see their fig. 5A), the vegetation temperature at z = 35 cm follows a ‘stair-stepped’ rise that is controlled by a varying convective heat flux (Fig. 1a, b). At z = 0 cm on top of the fuel bed (Fig. 1c, d), radiation dominates until near ignition (i.e. the temperature of the vegetation, Tveg = ~350°C at time = 36 s), at which point radiation and convection are comparable, at no point does convection exhibit the large oscillations seen at z = 35 cm. The experimental configuration of Finney et al. (2015) is a surface fire and their measurement location is similar to Figs. 1c, d (i.e. at the top of the fuel bed). Their results are similar to Figs. 1a, b because their imposed wind increases the unsteady behaviour of the flame. Simulations with WFDS give similar results with an imposed wind (not shown).
Regarding M4, we believe that Cruz et al. (2017) chose a wording that is stricter than in the literature. This mantra should read: ‘physical models have the potential to give a better understanding of how fuel treatments modify fire behaviour’, which we believe is valid. It is not clear why Cruz et al. (2017) did not write M4 this way, especially because their opening sentence introducing M4 does. CFD-based models have been used to simulate the influence of the spatial heterogeneity of vegetation on fire behaviour (e.g. in addition to the references in Cruz et al. (2017): Pimont et al. 2011; Hoffman et al. 2015; Ziegler et al. 2017). The challenge is to evaluate how well these simulations represent reality, which requires well-designed experiments. This is well recognised by physical modellers and the community would be better served if Cruz et al. (2017) discussed the need for well-designed experiments to support model development and current activity. Instead, Cruz et al. (2017) present an obstructive discussion on model approximations and the lack of model validation. Also, with their emphasis that the physical models are not ready for operational use, the discussion deviates from M4. The wording of M4 does not explicitly state that it refers to either CFD based physical models (which is the only type of physical model cited) or operational objectives.
We agree with Cruz et al.’s (2017) statement in M5 that models applied to operational objectives need to be properly used and their limitations known. However, their M5 discussion suffers from another inconsistent use of the term ‘physical model’. In this section, they write:
…the physical model is an acceptable representation of the fire processes and that the only limitations for model implementation are extraneous to the modelling of the fire processes, such as numerical implementation issues and computational time demands.
This is followed by their declaration that Albini’s model (Albini 1996, 2000) is a physical model of crown fire spread. But Albini’s model does not meet the characteristics of a physical model as described above by Cruz et al. (2017). Instead, Albini’s model is a simpler approach and Butler et al. (2004) combine four existing simpler models for different components of the problem (see bottom right of p. 1590 in Butler et al. 2004). Thus, Cruz et al.’s (2017) use of Butler et al. (2004) has no relevance to M5.
Although we do not find compelling evidence that M5 appears in the references cited, we agree with the mantra in the sense that it is possible to use ROS predictions from CFD-based models to develop ‘empirical’ formulae. For example, the study of Mell et al. (2007) found good agreement of the head fire ROS determined from numerical predictions and an empirical model based on field observations. This included predictions of fireline acceleration dependent on the head-fire width. Thus, these simulations could have been the basis of an empirical model. But model developers, as a matter of course, are reluctant to provide such empirical models without sufficient characterisation of model performance, which requires a range of appropriate experiments. Examples of analysis leading to a reduced model from a more comprehensive physical model include the works of Simeoni et al. (2001), who use the approach of model reduction, and Margerit and Sero-Guillaume (2002) who use asymptotic analysis.
Management implications
From the perspective of a land manager, the changing landscapes in which wildfires and prescribed fires are managed demand a more robust toolset for understanding the processes at play. Operational tools for predicting fire behaviour lag far behind the science of fire–atmosphere interactions, and a continued reliance on empirical models becomes less ‘predictive’ as managers face increasingly novel combinations of fuels (from non-native species), weather, climate and heterogeneity across landscapes (Kraaij et al. 2018). Furthermore, by definition, empirical models cannot capture, with well-characterised confidence, the limits or extremes of observed fires (see discussion of M2). This limitation creates the need for caution, which is often not adequately relayed to the management community, when employing empirical models beyond their domain of origin. Also, managing fire in conditions for which measurements are incomplete creates an important operational decision space for the use of CFD-based approaches for understanding the potential physical mechanisms in increasingly complex contexts. Empirical modelling focuses almost exclusively on the ROS. The use of ROS as a gold standard for validation further misses a critical management need to understand complex fire–atmosphere feedbacks, multiple fireline development and canopy-induced flows on planned ignitions. There are simply too many management tactics and decisions that involve critical fire-behaviour phenomena outside the domain of empirical inference. Because managers are themselves empirical modellers, tools that operate at conditions and fire behaviour at the edge of their experience are the most critical for enhancing decision making in operational contexts.
Using CFD or other physical-modelling tools is needed for the evaluation, either retrospectively or proactively, of processes and mechanisms that generate unexpected fire behaviours. Such lessons learned for fire reconstructions has proven useful in understanding rare events (e.g. Cunningham and Reeder 2009). It is equally important for managers to understand when CFD- or other physics-based modelling tools approach the limits of their applicability. If scepticism of CFD and trust in empirical models is the ultimate point of Cruz et al. (2017), then they sadly miss the opportunities that each approach provides as managers tackle a range of operational contexts.
Conclusions
We believe that there is a need for many types of models for research and for operational purposes. We also firmly reject the assertion that because all the physical processes and their interaction driving fire behaviour are not fully understood, physical modelling should be discouraged or held suspect. History and the scientific method have shown that progress in physical modelling is made with initial simplifying approximations to be tested against well designed experiments. The idea that the two approaches (experimental and theoretical or numerical) are complementary is widely shared in the scientific community (as, notably, stated in Cruz et al. 2011).
Recurrent in Cruz et al. (2017) is the recognised need for well-designed experiments for the development and evaluation of both empirical and physical models. We heartily agree and emphasise that for physical models, especially in the field, these measurements are challenging (e.g. Mueller et al. 2017, 2018) and require careful consideration of model needs in order to adequately provide information on vegetation, wind, and fire behaviour.
Uncertainty is and will always be part of a fire manager’s risk calculations, and most managers clearly understand that models are tools. Nearly all managers are also anxiously awaiting tools that provide insight into fire behaviours not already self-evident through their own observations. The critical targeting of new approaches based on physical modelling, especially CFD based, by Cruz et al. (2017) runs the risk of undermining innovation and opportunities for managers to learn from this branch of fire research.
Conflicts of interest
The authors declare that they have no conflicts of interest.
Acknowledgements
The authors thank the Chad Hoffman, Russ Parsons, and Morgan Varner for their suggestions and comments during the development of this manuscript.
References
Albini FA (1996) Iterative solution of the radiation transport equations governing spread of fire in wildland fuel. Fizika Gorenia i Vzryva 32, 71–82.Albini FA (2000) Crown fire spread rate model RDCFZX. USDA Forest Service, Rocky Mountain Research Station, Fire Sciences Laboratory, Contract 53-0343-0-0008, Final Report. (Missoula, MT, USA)
Anand C, Shotorban B, Mahalingham S, McAllister S, Weise DR (2017) Physics-based modeling of live wildland fuel ignition experiments in the forced ignition and flame spread test apparatus. Combustion Science and Technology 189, 1551–1570.
| Physics-based modeling of live wildland fuel ignition experiments in the forced ignition and flame spread test apparatus.Crossref | GoogleScholarGoogle Scholar |
Anderson WR, Catchpole EA, Butler BW (2010) Convective heat transfer in fire spread through fine fuel beds. International Journal of Wildland Fire 19, 284–298. doi.org/10.1071/WF09021
Balbi JH, Morandini F, Silvani X, Filippi JB, Rinieri F (2009) A physical model for wildland fires. Combustion and Flame 156, 2217–2230. doi.org/10.1016/j.combustflame.2009.07.010
Butler BW (2010) Characterization of convective heating in full scale wildland fires. In ‘Proceedings of the 6th International Conference on Forest Fire Research’, 15–18 November 2010, Coimbra, Portugal. (Ed. DX Viegas) (CD-ROM) (University of Coimbra: Coimbra, Portugal).
Butler BW, Finney MA, Andrews PL, Albini FA (2004) A radiation driven model of crown fire spread. Canadian Journal of Forest Research 34, 1588–1599.
| A radiation driven model of crown fire spread.Crossref | GoogleScholarGoogle Scholar |
Catchpole EA, de Mestre N (1986) Physical models for a spreading line fire. Australian Forestry 49, 102–111.
| Physical models for a spreading line fire.Crossref | GoogleScholarGoogle Scholar |
Cruz MG, Butler BW, Viegas DX, Palheiro P (2011) Characterization of flame radiosity in shrubland fires. Combustion and Flame 158, 1970–1976.
| Characterization of flame radiosity in shrubland fires.Crossref | GoogleScholarGoogle Scholar |
Cruz MG, Alexander ME, Sullivan AL (2017) Mantras of wildland fire behaviour modelling: facts or fallacies? International Journal of Wildland Fire 26, 973–981.
| Mantras of wildland fire behaviour modelling: facts or fallacies?Crossref | GoogleScholarGoogle Scholar |
Cunningham P, Reeder MJ (2009) Severe convective storms initiated by intense wildfires: numerical simulations of pyro-convection and pyro-tornadogenesis. Geophysical Research Letters 36, L12812
| Severe convective storms initiated by intense wildfires: numerical simulations of pyro-convection and pyro-tornadogenesis.Crossref | GoogleScholarGoogle Scholar |
El Houssami M, Lamorlette A, Morvan D, Hadden RM (2018) Framework for submodel improvement in wildfire modeling. Combustion and Flame 190, 12–24.
| Framework for submodel improvement in wildfire modeling.Crossref | GoogleScholarGoogle Scholar |
Fernandes PM (2014) Upscaling the estimation of surface-fire rate of spread in maritime pine (Pinus pinaster Ait.) forest. IForest (Viterbo) 7, 123–125.
| Upscaling the estimation of surface-fire rate of spread in maritime pine (Pinus pinaster Ait.) forest.Crossref | GoogleScholarGoogle Scholar |
Finney MA, Cohen JD, Forthofer JM, McAllister SS, Gollner MJ, Gorham DJ, Saito K, Akafuah NK, Adam BA, English JD (2015) Role of buoyant flame dynamics in wildfire spread. Proceedings of the National Academy of Sciences of the United States of America 112, 9833–9838.
| Role of buoyant flame dynamics in wildfire spread.Crossref | GoogleScholarGoogle Scholar |
Frankman D, Webb BW, Butler BW, Jimenez D, Forthofer JM, Sopko P, Shannon KS, Hiers JK, Ottmar RD (2013) Measurements of convective and radiative heating in wildland fires. International Journal of Wildland Fire 22, 157–167.
| Measurements of convective and radiative heating in wildland fires.Crossref | GoogleScholarGoogle Scholar |
Hoffman CM, Linn R, Parsons R, Sieg C, Winterkamp J (2015) Modeling spatial and temporal dynamics of wind flow and potential fire behavior following a mountain pine beetle outbreak in a lodgepole pine forest. Agricultural and Forest Meteorology 204, 79–93.
| Modeling spatial and temporal dynamics of wind flow and potential fire behavior following a mountain pine beetle outbreak in a lodgepole pine forest.Crossref | GoogleScholarGoogle Scholar |
Hoffman CM, Ziegler J, Canfield J, Linn RR, Mell W, Sieg CH, Pimont F (2016) Evaluating crown fire rate of spread predictions from physics-based models. Fire Technology 52, 221–237.
| Evaluating crown fire rate of spread predictions from physics-based models.Crossref | GoogleScholarGoogle Scholar |
Kraaij T, Baard JA, Arndt J, Vhengani L, van Wilgen BW (2018) An assessment of climate, weather and fuel factors influencing a large, destructive wildfire in the Knysna region, South Africa. Fire Ecology 14, In press.
Lamorlette A, Houssami ME, Morvan D (2018) An improved non-equilibrium model for the ignition of living fuel. International Journal of Wildland Fire 27, 29–41.
| An improved non-equilibrium model for the ignition of living fuel.Crossref | GoogleScholarGoogle Scholar |
Lozano J, Tachajapong W, Weise DR, Mahalingam S, Princevac M (2010) Fluid dynamic structures in a fire environment observed in laboratory-scale experiments. Combustion Science and Technology 182, 858–878.
| Fluid dynamic structures in a fire environment observed in laboratory-scale experiments.Crossref | GoogleScholarGoogle Scholar |
Marcelli T, Santoni PA, Simeoni A, Leoni E, Porterie B (2004) Fire spread across pine needle fuel beds: characterisation of temperature and velocity distributions within the fire plume. International Journal of Wildland Fire 13, 37–48.
| Fire spread across pine needle fuel beds: characterisation of temperature and velocity distributions within the fire plume.Crossref | GoogleScholarGoogle Scholar |
Margerit J, Sero-Guillaume O (2002) Modelling forest fires. Part II: reduction to two-dimensional models and simulation of propagation. International Journal of Heat and Mass Transfer 45, 1723–1737.
| Modelling forest fires. Part II: reduction to two-dimensional models and simulation of propagation.Crossref | GoogleScholarGoogle Scholar |
Mell W, Jenkins MA, Gould J, Cheney P (2007) A physics-based approach to modelling grassland fires. International Journal of Wildland Fire 16, 1–22.
| A physics-based approach to modelling grassland fires.Crossref | GoogleScholarGoogle Scholar |
Mell W, Maranghides A, McDermott R, Manzello SL (2009) Numerical simulation and experiments of burning Douglas-fir trees. Combustion and Flame 156, 2023–2041.
| Numerical simulation and experiments of burning Douglas-fir trees.Crossref | GoogleScholarGoogle Scholar |
Mell WE, McDermott RJ, Forney GP (2010) Wildland fire behavior modeling: perspectives, new approaches and applications. In ‘Proceedings of the Third Fire Behavior and Fuels Conference’, 25–29 October 2010, Spokane, WA, USA. (Eds DD Wade, M Robinson) (CD-ROM) (International Association of Wildland Fire: Birmingham, AL, USA)
Morandini F, Silvani X (2010) Experimental investigation of the physical mechanisms governing the spread of wildfires. International Journal of Wildland Fire 19, 570–582.
| Experimental investigation of the physical mechanisms governing the spread of wildfires.Crossref | GoogleScholarGoogle Scholar |
Morandini F, Simeoni A, Santoni PA, Balbi JH (2005) A model for the spread of fire across a fuel bed incorporating the effects of wind and slope. Combustion Science and Technology 177, 1381–1418.
| A model for the spread of fire across a fuel bed incorporating the effects of wind and slope.Crossref | GoogleScholarGoogle Scholar |
Morvan D, Larini M (2001) Modeling of one dimensional fire spread in pine needles with opposing air flow. Combustion Science and Technology 164, 37–64.
| Modeling of one dimensional fire spread in pine needles with opposing air flow.Crossref | GoogleScholarGoogle Scholar |
Morvan D, Méradji S, Accary G (2009) Physical modelling of fire spread in grasslands. Fire Safety Journal 44, 50–61.
| Physical modelling of fire spread in grasslands.Crossref | GoogleScholarGoogle Scholar |
Mueller EV (2017) Examination of the underlying physics in a detailed wildland fire behavior model through field-scale experimentation. PhD dissertation University of Edinburgh. Available at http://hdl.handle.net/1842/22039 [Verified 2 August 2018]
Mueller EV, Skowronski N, Clark K, Gallagher M, Kremens R, Thomas JC, El Houssami M, Filkov A, Hadden RM, Mell W, Simeoni A (2017) Utilization of remote sensing techniques for the quantification of fire behavior in two pine stands. Fire Safety Journal 91, 845–854.
| Utilization of remote sensing techniques for the quantification of fire behavior in two pine stands.Crossref | GoogleScholarGoogle Scholar |
Mueller EV, Skowronski N, Thomas JC, Hadden RM, Mell W, Simeoni A (2018) Local measurements of wildland fire dynamics in a field-scale experiment. Combustion and Flame
| Local measurements of wildland fire dynamics in a field-scale experiment.Crossref | GoogleScholarGoogle Scholar |
Pastor E, Zarate L, Planas E, Arnaldos J (2003) Mathematical models and calculation systems for the study of wildland fire behaviour. Progress in Energy and Combustion Science 29, 139–153. doi.org/10.1016/S0360-1285(03)00017-0
Perez-Ramirez Y, Santoni PA, Tramoni JB, Bosseur F, Mell WE (2017) Examination of WFDS in modeling spreading fire in a furniture calorimeter. Fire Technology 53, 1795–1832.
| Examination of WFDS in modeling spreading fire in a furniture calorimeter.Crossref | GoogleScholarGoogle Scholar |
Pimont F, Dupuy JL, Linn RR, Dupont S (2011) Impacts of tree canopy structure on wind flows and fire propagation simulated with FIRETEC. Annals of Forest Science 68, 523
| Impacts of tree canopy structure on wind flows and fire propagation simulated with FIRETEC.Crossref | GoogleScholarGoogle Scholar |
Simeoni A, Santoni PA, Larini M, Balbi JH (2001) Proposal for theoretical contribution for improvement of semi-physical forest fire spread models thanks to a multiphase approach: application to a fire spread model across a fuel bed. Combustion Science and Technology 162, 59–83.
| Proposal for theoretical contribution for improvement of semi-physical forest fire spread models thanks to a multiphase approach: application to a fire spread model across a fuel bed.Crossref | GoogleScholarGoogle Scholar |
Sokal RR, Rohlf FJ (1995) ‘Biometry the Principle and Practices of Statistics in Biological Research’, 3rd edn. (W.H. Freeman and Company: New York, NY, USA)
Tihay V, Simeoni A, Santoni PA, Rossi L, Bertin V, Bonneau L, Garo JP, Vantelon JP (2008) On the interest of studying degradation gases for forest fuel combustion modeling. Combustion Science and Technology 180, 1637–1658.
| On the interest of studying degradation gases for forest fuel combustion modeling.Crossref | GoogleScholarGoogle Scholar |
Tihay V, Santoni PA, Simeoni A, Garo JP, Vantelon JP (2009) Skeletal and global mechanisms for the combustion of gases released by crushed forest fuels. Combustion and Flame 156, 1565–1575.
| Skeletal and global mechanisms for the combustion of gases released by crushed forest fuels.Crossref | GoogleScholarGoogle Scholar |
Zhou X, Mahalingam S, Weise D (2007) Experimental study and large eddy simulation of effect of terrain slope on marginal burning in shrub fuel beds. Proceedings of the Combustion Institute 31, 2547–2555.
| Experimental study and large eddy simulation of effect of terrain slope on marginal burning in shrub fuel beds.Crossref | GoogleScholarGoogle Scholar |
Ziegler JP, Hoffman C, Battaglia M, Mell W (2017) Spatially explicit measurements of forest structure and fire behavior following restoration treatments in dry forests. Forest Ecology and Management 386, 1–12.
| Spatially explicit measurements of forest structure and fire behavior following restoration treatments in dry forests.Crossref | GoogleScholarGoogle Scholar |


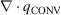 ) and radiative (
) and radiative (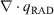 ) flux into a 2-cm3 volume of excelsior are plotted v. time. The left-side column (a and b) show these quantities at a location z = 35 cm above the fuel bed. The right-side column (c and d) are for a location at the top of the fuel bed, z = 0 cm.
) flux into a 2-cm3 volume of excelsior are plotted v. time. The left-side column (a and b) show these quantities at a location z = 35 cm above the fuel bed. The right-side column (c and d) are for a location at the top of the fuel bed, z = 0 cm.
