Wildland fire probabilities estimated from weather model-deduced monthly mean fire danger indices
Haiganoush K. Preisler A D , Shyh-Chin Chen B , Francis Fujioka B , John W. Benoit B and Anthony L. Westerling CA USDA Forest Service, Pacific Southwest Research Station, 800 Buchanan St, West Annex, Albany, CA 94710, USA.
B USDA Forest Service, Pacific Southwest Research Station, Riverside, CA 92507, USA.
C Sierra Nevada Research Institute, PO Box 2039, Merced, CA 95344, USA.
D Corresponding author. Email: hpreisler@fs.fed.us
International Journal of Wildland Fire 17(3) 305-316 https://doi.org/10.1071/WF06162
Submitted: 9 December 2006 Accepted: 11 December 2007 Published: 23 June 2008
Abstract
The National Fire Danger Rating System indices deduced from a regional simulation weather model were used to estimate probabilities and numbers of large fire events on monthly and 1-degree grid scales. The weather model simulations and forecasts are ongoing experimental products from the Experimental Climate Prediction Center at the Scripps Institution of Oceanography. The monthly average Fosberg Fire Weather Index, deduced from the weather simulation, along with the monthly average Keetch–Byram Drought Index and Energy Release Component, were found to be more strongly associated with large fire events on a monthly scale than any of the other stand-alone fire weather or danger indices. These selected indices were used in the spatially explicit probability model to estimate the number of large fire events. Historic probabilities were also estimated using spatially smoothed historic frequencies of large fire events. It was shown that the probability model using four fire danger indices outperformed the historic model, an indication that these indices have some skill. Geographical maps of the estimated monthly wildland fire probabilities, developed using a combination of four indices, were produced for each year and were found to give reasonable matches to actual fire events. This method paves a feasible way to assess the skill of climate forecast outputs, from a dynamical meteorological model, in forecasting the probability of wildland fire severity with known precision.
Additional keywords: FWI, model appraisal, mutual information, NFDRS, semi-parametric logistic regression, spline functions.
Acknowledgements
We are grateful to J. Roads of the Experimental Climate Prediction Center, University of California, San Diego, for providing model-deduced NFDRS indices. The fire histories used here were developed and updated with support from the National Oceanographic and Atmospheric Administration’s Office of Global Programs via the California Applications Program.
Brillinger DR (2004) Some data analyses using mutual information. Brazilian Journal of Probability and Statistics 18, 163–182.
Brillinger DR, Preisler HK , Benoit JW (2006) Probabilistic risk assessment for wildfires. Environmentrics 17, 623–633.
| Crossref | GoogleScholarGoogle Scholar |
Chen S-C (2001) Model mismatch between global and regional simulation. Geophysical Research Letters 29(5), 4.1–4.4.
Hoadley JL, Westrick K, Ferguson SA, Goodrick SL, Bradshaw L , Werth P (2004) The effect of model resolution in predicting meteorological parameters used in fire danger rating. Journal of Applied Meteorology 43, 1333–1347.
| Crossref | GoogleScholarGoogle Scholar |
Juang H-MH , Kanamitsu M (1994) The NMC nested regional spectral model. Monthly Weather Review 122, 3–26.
| Crossref | GoogleScholarGoogle Scholar |
Preisler HK , Westerling AL (2007) Statistical model for forecasting monthly large wildfire events in Western United States. Journal of Applied Meteorology and Climatology 46(7), 1020–1030.
| Crossref | GoogleScholarGoogle Scholar |
Roads JO, Chen S-C, Fujioka F, Kanamitsu M , Juang H-MH (1995) Global to regional fire weather forecasts. International Forest Fire News 17, 33–37.
Westerling AL, Gershunov A , Cayan DR (2003) Statistical forecasts of the 2003 western wildfire season using canonical correlation analysis. Experimental Long-Lead Forecast Bulletin 12, 1–2.
Appendix A1
The logistic regression lines used to estimate the probabilities of fire occurrence and large fire events are specified in the following equation:
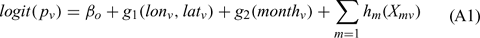
where the subscript v indicates the 1 × 1-degree by 1-month voxel; p is set to either the probability of ignition or conditional probability of large fire given ignition; (lon, lat) are the longitude and latitude of the midpoint of the grid cell; Xm are explanatory fire weather and fire danger variables. The function h is a non-parametric smoothing function (Hastie et al. 2001); g2 is a periodic spline function (for estimating month-in-year effect); and g1 is a thin plate spline function (for estimating the spatial surface as a function of lon and lat). Estimation was done with the R statistical package (R Development Core Team 2004). The procedure within the R package consists of first running the bs (basis spline) function on each of the explanatory variables, then using the outputs from the bs runs as the new explanatory variables in a simple logistic regression routine. A periodic spline function (bs.per) is used for the month variable to allow for a smooth transition between the months of December and January. For the two-dimensional spline function of (lon, lat), the thin plate spline function (ts) is used to produced the necessary variables.
The MI statistic was defined as follows: let Y indicate the occurrence of a fire (or alternatively, a large fire event) and X indicate the logit line (linear predictor) as described in Eqn A1; then the MI statistic is given by
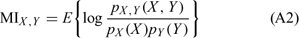
where pX,Y(X, Y), pX(X) and pY(Y) are the joint and marginal distributions of X, Y respectively. For the bivariate normal case, 1 – e–2MIX,Y is the coefficient of determination. In general, MIX,Y = 0 when X and Y are independent and MIX,Y ≤ MIZ,Y if Y is independent of X given Z (Brillinger 2004). A similar and more commonly used statistic for choosing between models is the Akaike information criterion (AIC) given by 
Although AIC and MI often give similar results, as was the case in the present study, AIC does not have the same interpretation as the MI statistic as a measure of the strength of statistical dependence.
