Effect of a controlled burn on the thermophysical properties of a dry soil using a new model of soil heat flow and a new high temperature heat flux sensor*
W. J. Massman A B and J. M. Frank AA USDA Forest Service, Rocky Mountain Research Station, 240 West Prospect, Fort Collins, CO 80526, USA.
B Corresponding author. Email: wmassman@fs.fed.us
International Journal of Wildland Fire 13(4) 427-442 https://doi.org/10.1071/WF04018
Submitted: 26 March 2004 Accepted: 17 August 2004 Published: 15 December 2004
Abstract
Some fires can be beneficial to soils but, if a fire is sufficiently intense, soil can be irreversible altered. We measured soil temperatures and heat fluxes at several soil depths before, during, and after a controlled surface burn at Manitou Experimental Forest (southern Colorado, USA) to evaluate its effects on the soil’s thermophysical properties (thermal conductivity and volumetric specific heat capacity). During the burn the soil was heated to over 400°C at a depth of 0.02 m and to almost 100°C at 0.30 m. Relatively high temperatures persisted for several hours to days even over 1 m deep into the soil. At these intensities and durations significant changes in soil chemistry, structure, and nutrient cycling are likely. However, soil thermophysical properties, estimated before and after the fire with a new model of periodic heat flow in soils, were not significantly changed between the times shortly after sensor installation (October 2001) and 1 month after the fire (February 2002). Estimates of the soil thermophysical properties derived with the new model underestimate laboratory analyses performed on soil samples obtained after the fire. Also presented in this study are some of the first soil heat flux measurements made during a surface fire. Furthermore, data and analyses of the type discussed in this study should aid modeling studies of the soil thermal pulse associated with fire. The ultimate goal of this experiment was to provide tools to assist land managers in the use of prescribed fire to benefit ecosystems and to reduce the potential for harm by examining how the soil’s physical properties and different fuel amounts, geometries, and loading densities influence soil recovery and forest regeneration after fires.
Additional keywords: fuel management; modeling periodic soil heat flow; slash; soil heat flux measurements during fires; soil thermal conductivity; soil volumetric specific heat capacity.
Badía D , Martí C (2003) Plant ash and heat intensity effects on chemical and physical properties of two contrasting soils. Arid Land Research and Management 17, 23–41.
| Crossref | GoogleScholarGoogle Scholar |
Campbell GS, Jungbauer JD, Bidlake WR , Hungerford RD (1994) Predicting the effect of temperature on soil thermal conductivity. Soil Science 158, 307–313.
Friedli HR, Radke LF , Lu JY (2001) Mercury in smoke from biomass fires. Geophysical Research Letters 28, 3223–3226.
| Crossref | GoogleScholarGoogle Scholar |
Kadoya K, Matsunaga N , Nagashima A (1985) Viscosity and thermal conductivity of dry air in the gaseous phase. Journal of Physical and Chemical Reference Data 14, 947–970.
Maqsood A, Anis-ur-Rehman M , Gul IH (2003) Chemical composition, density, specific gravity, apparent porosity, and thermal transport properties of volcanic rocks in the temperature range 253 to 333 K. Journal of Chemical and Engineering Data 48, 1310–1314.
| Crossref | GoogleScholarGoogle Scholar |
Novak MD (1986) Theoretical values of daily atmospheric and soil thermal admittances. Boundary-Layer Meteorology 34, 17–34.
| Crossref | GoogleScholarGoogle Scholar |
Rose CW (1968) Water transport in a soil with a daily temperature wave. I. Theory and experiment. Australian Journal of Soil Research 6, 31–44.
Sauer TJ, Meek DW, Ochsner TE, Harris AR , Horton R (2003) Errors in heat flux measurement by flux plates of contrasting design and thermal conductivity. Vadose Zone Journal 2, 580–588.
* This manuscript was written and prepared by U.S. Government employees on official time and therefore is in the public domain and not subject to copyright.
Appendix 1
The purpose of this appendix is to derive an analytical model of heat transfer in soils with non-uniform thermophysical properties. Although the focus here is on modeling heat flow for monotonically increasing soil thermophysical properties, the mathematical development can also be used as a template for monotonically decreasing soil thermophysical properties as well. For the sake of simplicity this discussion is cast in terms of the fundamental or 24-h periodic thermal wave. However, the results can easily be generalized to higher harmonics.
The model described here was developed to meet three specific conditions; therefore, all compromises and approximations used in deriving this model are a result of these imposed conditions. First, it must employ simple continuous analytical expressions for describing depth-dependency of periodic variations in soil temperatures, T(z, t), and heat fluxes, Gs(z, t). Second, it must permit a simple, but more general, expression for the phase difference between Gs(z, t) and T(z, t), than the more traditional π/4 (3 h) for the diel cycle. (Note here that a phase difference of 2π corresponds to the 24 h period of the diel cycle.) Third, it should not violate physical reality much more than what occurs by assuming uniform soil thermophysical properties.
The one-dimensional (non-advective) soil heat conduction equation is given as follows
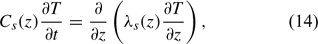
where Cs(z) is the soil volumetric specific heat capacity (J m−3 K−1), which is considered to be a function of depth z (m), λs(z) is the soil thermal conductivity (W m−1 K−1) also a function of depth, T is temperature (K), and t is time (s). Here z is taken as positive downwards with z = 0 at the soil surface and Cs(z) and λs(z) are functions of depth only and are, therefore, invariant with time and temperature. (Note here that both Cs(z) and λs(z) are, in fact, generally temperature dependent (Kay and Goit 1975; Campbell et al. 1994).)
Nerpin and Chudnovskii (1984) showed that equation (14) can be transformed into the following expression
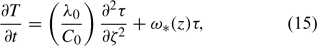
where τ is the transformed temperature (K)
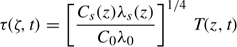
and ζ is the transformed depth (m)
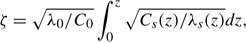
where C0 = Cs(0) and λ0 = λs(0) are the surface values of the soil thermophysical parameters and ω*(z) (s−1) is given as follows:
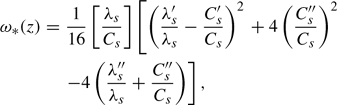
for which the prime (′) denotes differentiation with respect to z, i.e. λs′ = dλs/dz, λs″ = d2λsdz2, etc.
For periodic forcing, such as the daily 24-h cycle, and for soil thermophysical properties that are constant with depth (i.e. λs(z) ≡ λ0, Cs(z) ≡ C0, ζ ≡ z, τ(ζ,t) ≡ T(z,t), and ω*(z) ≡ 0). Equation (14) has the well-known periodic solution (e.g. van Wijk and de Vries 1963: equations (2) and (3) of the main text). However, for a soil with non-uniform thermophysical properties the solution is more complicated. Although some analytical periodic solutions exist for both equations (14) and (15) (van Wijk and Borghorst 1963; Novak 1986; Massman 1993; Karam 2000), they are piecewise continuous (e.g. van Wijk and Derksen 1963; Massman 1993; Karam 2000), which for the present purposes is extremely inconvenient. Here we present a simpler, but approximate, analytical solution to equation (15), which is continuous for all soil depths and which is a relatively simple generalization of the solution to equation (14) for uniform thermophysical properties. These solutions are, however, based on the case that the soil thermophysical properties are either monotonically increasing or decreasing functions of depth into the soil.
Consider the following two cases describing Cs(z) and λs. Case I (monotonically increasing with depth): Cs(z) = C0(2 − e−αcz) and λs(z) = λ0(2 − e−αλz), and Case II (monotonically decreasing with depth): Cs(z) = C0(1 + e−αcz) and λs(z) = λ0(1 + e−αλz)/2. For Case I Cs(z) increases monotonically from C0 at z = 0 to 2C0 at z = ∞ (similarly for λs(z)). For Case II Cs(z) = C0/2 and λs(z) = λ0/2 at z = ∞. These two cases are reasonable parameterizations, but they are not the only possibilities. Similar related functions could easily have been constructed to range over more than or less than a factor of 2.0 but, for the present discussion which is largely confined to a dry soil, the above functions are sufficient. For a dry soil Cs and λs are largely functions of the bulk density of the soil (e.g. Farouki 1986; Campbell et al. 1994; Campbell and Norman 1998) and, in general, for a dry soil Cs may vary somewhat less than a factor of two (if the bulk density, for example, varies with depth), whereas λs may vary slightly more than a factor of two. Thus the factor of 2 is a compromise.
Two other compromises are needed to make equation (15) amenable to a simple analytical solution. One is to assume that αc = αλ. This insures that ζ ≡ z. Consequently, we will drop the subscripts from α when describing the depth variation of Cs and λs. The second approximation involves ω*(z). Focusing on Case I (monotonically increasing thermophysical properties) yields the following expression for ω*(z):
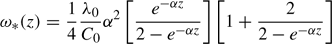
which leads to the following inequality valid for all depths:
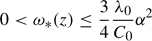
For periodic solutions the time dependency of both τ(z, t) and T(z, t) can be described by eiωt, which allows the preceding inequality to be expressed as
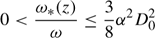
where ω = 7.272(10−5)s−1 is the frequency of the diel cycle, 
is the unit imaginary number, and 
(m) is the attenuation depth for the new model and is the analog to the attenuation depth for the uniform soil thermophysical properties model. The second approximation simply replaces ω*(z) in equation (15) by its maximum value, as given in the last inequality. Incorporating the above approximations into equation (15) yields the following solution (model) for periodic heat flow in soils with monotonically increasing thermophysical properties
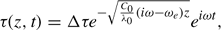
where ωe = 3α2 D02ω/8 and Δτ is the amplitude of the periodic τ-wave at the soil surface. Further algebraic manipulation yields
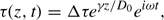
where 
. But, γ can be further simplified by assuming that ωe/ω = 3α2 D02ω/8 < 1. At this point this purely a heuristic assumption, which is justified only by the limited data presented in this study (see the Results section) and some unpublished soil data obtained at a site near where the present experiment was performed. In fact, the data presented in this study suggest that ωe/ω < 0.2 is more precise. Consequently, γ = (1 − 3α2 D02/16) + i(1 + 3α2 D02/16) appears to be a good approximation. Furthermore, if ωe/ω < 0.2 proves universally true, then γ can be further simplified to γ = 1 + i. For the soil data presented in this study, this last simplification is reasonable and will be adopted for the remainder of this work.
The resulting new model for periodic soil temperature variations is
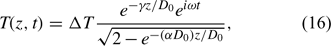
where ΔT is the surface amplitude of the diel soil temperature wave. Note here (1) that Δτ ≡ ΔT, which follows from the preceding relationship between τ(ζ, t) and T(z, t); and (2) that we have intentionally expressed the exponent in the denominator as (αD0)z/D0 because, as shown next, the product, (αD0), can be determined directly from the phase relationship between the diel soil heat flux and temperature waves.
The soil heat flux, Gs(z, t) (W m−2), is given as
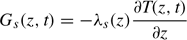
which yields
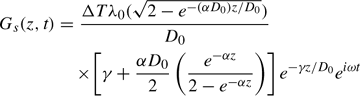
or
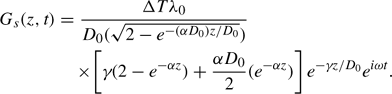
The term in the square brackets determines the phase difference between the soil heat flux wave and the temperature wave, which not surprisingly is a function of depth. Here we simplify the phase component only by replacing the terms e−α z and (2 − e−α z) with their maximum values, which is equivalent to approximating the phase term in either of these two models of Gs(z,t) by [γ + αD0/2]. With this assumption the only difference between the last two expressions for Gs(z,t) is the 
term, which is part of the numerator in the first relationship and part of the denominator in the second. Comparisons with observed profiles of heat fluxes suggested that incorporating it in the denominator produced a better model. Therefore, the second expression is the preferred model for this study. After some further complex arithmetic and using a Fourier expansion of tan−1 x about π/4, the final expression for the new soil heat flux model is
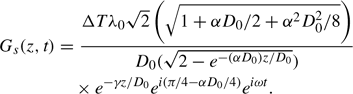
Equations (16) and (17) are the new model for periodic heat flow in a soil with monotonically increasing thermophysical parameters. They are relatively simple continuous functions, which generalize the standard (uniform thermophysical properties) model for periodic diel soil heat flow. This new model differs from the standard model primarily with the introduction of one additional parameter, α, which when combined with the attenuation depth, D0, essentially determines the phase difference between the daily soil heat flux and the temperature waves. In equation (17) this phase relation is expressed through the term ei(π/4−αD0/4) which, because α > 0 and D0 > 0, is consistent with Massman's (1993) prediction that the soil heat flux wave leads the temperature wave by less than 3 h when soil thermophysical properties increase with depth. Although not discussed here, the case for monotonically decreasing soil thermophysical properties results in a lag time that exceeds 3 h, also in agreement with Massman (1993).
