Validation of BARRA2 and comparison with MERRA-2 and ERA5 using historical wind power generation
Graham Palmer A * , Roger Dargaville A , Chun-Hsu Su
A * , Roger Dargaville A , Chun-Hsu Su  C , Changlong Wang A B , Andrew Hoadley A and Damon Honnery A
C , Changlong Wang A B , Andrew Hoadley A and Damon Honnery A
A
B
C
Abstract
Atmospheric reanalyses are a popular source of wind speed data for energy modelling but are known to exhibit biases. Such biases can have a significant impact on the validity of techno-economic energy assessments that include simulated wind power. This study assesses the Australian BARRA-R2 (Bureau of Meteorology Atmospheric Regional Reanalysis for Australia, version 2) atmospheric reanalysis, and compares it with MERRA-2 (Modern-Era Retrospective analysis for Research and Applications, V2) and ERA5 (European Centre for Medium-Range Weather Forecasts Reanalysis, fifth generation). Simulated wind power is compared with observed power from 54 wind farms across Australia using site-specific wind turbine specifications. We find that all of the reanalyses replicate wind speed patterns associated with the passage of weather systems. However, modelled power can diverge significantly from observed power at times. Assessed by bias, correlation and error, BARRA-R2 gave the best results, followed by MERRA-2, then ERA5. Annual bias can be readily corrected by wind speed scaling; however, linear scaling will not narrow the error distribution, or reduce the associated error in the frequency distribution of wind power. At the level of a wind farm, site-specific factors and microscale wind behaviour are contributing to differences between simulated and observed power. Although the performance of all the reanalyses is good at times, variability is high and site-dependent. We recommend the use of confidence intervals that reflect the degree of uncertainty in wind power simulation, and the degree of confidence required in the energy system model.
Keywords: Australia, BARRA, energy system modelling, ERA5, MERRA-2, National Electricity Market, NEM, optimisation, reanalyses, South West Interconnected System, SWIS, wind farm, wind power, wind turbines.
1.Introduction
Wind power is a critical renewable technology and will need to expand significantly to meet climate mitigation goals (International Energy Agency 2021). However, wind is highly variable, both across space and across time. At sub-daily intervals, this variability presents system-level challenges when renewable penetration is high (Pichault et al. 2021). Understanding the characteristics of the wind resource across different regions and time horizons – both short and long-term – is essential. Long-term simulation or optimisation of these systems is often conducted using energy system models. One approach, known as bottom–up or engineering modelling, uses time series power datasets (or ‘traces’) as model inputs (Wang et al. 2018), which are sometimes derived from atmospheric reanalyses such as ERA5 (ECMWF Re-Analysis, fifth generation; ECMWF, European Centre for Medium-Range Weather Forecasts) or MERRA-2 (Modern-Era Retrospective analysis for Research and Applications, V2).
Several methods are available to produce hourly wind power traces. The default method, when suitable data are available, is historical time series output from operating wind farms. The strength of these is that they integrate the various important factors, including the nature of the site-specific wind resource, the wind power technology used to convert the kinetic energy of wind into electrical energy, and the various localised complexities, such as turbulence and topography. A weakness is that these traces pertain only to those wind farms, or prospective locations within the same wind regime. Wind regimes refer to regions in which wind speed is highly correlated. In general, correlation diminishes with widening distance between locations (Huva 2014). A further weakness is that traces can be produced only for the period for which the wind farm has been operating. There may also be factors that influence reported wind power such as outages and curtailment.
Another method is synthetic traces. Their strength is that they can be produced with prescribed statistical properties for any area over any time horizon (Sturt and Strbac 2011). Once a synthetic model is built, the parameters can be readily calibrated to match known performance across regions, such as wind conditions, terrain type and turbine model. Nonetheless, synthetic wind power traces are still dependant on historical data for calibration.
A further method is applying a power curve to wind speed measured at meteorological stations (Cowin et al. 2023). Wind speed is reliably measured with high temporal resolution at many locations, potentially significantly expanding the geographic coverage of wind power traces. The main weakness is that the standard meteorological mast height of 10 m is well below that of the typical wind turbine hub height of 80 m or higher. (Australian weather stations use a standard anemometer height of 10 m. Methods of sampling wind are given in Australian Standard AS/NZS 3580.14.) Wind observations may be influenced by local topography, vegetation and buildings. Wind speed sampling at 10 m may capture broad wind patterns, but is likely to be unrepresentative of wind power at typical wind turbine hub heights, even if adjustments are made for height. Average wind speed in undisturbed flow increases with height in an approximately logarithmic manner. However, when the flow is disturbed owing to changes in the ground roughness, the wind speed changes in a more complex manner (Standards Australia 2014).
An increasingly popular method of producing wind power traces is atmospheric reanalyses. Atmospheric reanalyses combine a climate forecast model with observations that are distributed irregularly in space and time into a spatially complete gridded meteorological dataset (Rienecker et al. 2011). Reanalyses include many variables, such as temperature, atmospheric pressure and wind speed. Observations come from a wide variety of sources including land-based weather stations, buoys, radiosonde balloons and satellites. Reanalyses span the historic weather record and are widely used in climate and weather research. Reanalysis data are freely available as geographically gridded data with hourly time step.
Reanalyses report wind speed at various heights, from which wind power can be estimated. Given a wind power trace dataset spanning a full year, the annual capacity factor can be determined for that year. The popularity of reanalyses stems from their convenience, long time spans and wide coverage (Staffell and Pfenninger 2016). The most prominent global reanalyses are NASA’s MERRA-2 (Rienecker et al. 2011) and the ECMWF’s ERA5 (Hersbach et al. 2023). In addition to these global reanalyses, several regional reanalyses are produced, including the Australian Bureau of Meteorology’s BARRA (Bureau of Meteorology Atmospheric Regional Reanalysis for Australia) reanalysis (Su et al. 2019), and the updated BARRA2 reanalysis (Su et al. 2022), which is the focus of the present study.
Although widely used for wind power modelling, the most prominent global reanalyses, MERRA-2 and the newer ERA5, are known to exhibit significant bias. In a validation of MERRA-2 covering 23 countries in Europe, Staffell and Pfenninger (2016) found that a simulation without bias correction resulted in an annual capacity factor error range of −30% up to +60%. They proposed a bias correction method based on a national-level capacity factor, which improved the correlation of simulated with observed wind power to above 0.95 at a national level.
A few studies have compared the accuracy of MERRA-2 and ERA5 for simulating wind power production. Jourdier (2020) assessed both reanalyses using France as a case study. Jourdier’s study had two components – a comparison of simulated with measured wind speed at eight sites, at mast height between 55 and 100 m, and a comparison of simulated wind power with observed wind power at wind farms. They found that MERRA-2 exhibited significant biases in annual capacity factor, and that ERA5 performed better, although ERA5 underestimated wind speed and exhibited problems at certain times of the day. Olauson (2018) assessed MERRA-2 and ERA5, both for aggregated national generation for five countries (Germany, Denmark, France, Sweden and Bonneville Power Administration in north-west USA), and also for individual wind turbines in Sweden, and also concluded that ERA5 performed better. They noted that the effects of local topography on wind speed could not be discerned in either MERRA-2 or ERA5, and advised against their use for determining average wind speed at a particular site. Using national-level data, they applied a correction method that involved linearly scaling the mean wind speed from the model so that the capacity factor of the model matched the measured capacity factor for the region under investigation. Gruber et al. (2022) assessed MERRA-2 and ERA5 in four countries (US, Brazil, South Africa and New Zealand), and assessed bias correction using the Global Wind Atlas, version 2 (GWA2). They found that ERA5 performed better than MERRA-2 and that error was not improved with bias correction. The overall median correlation was 0.82 for ERA5 and 0.77 for MERRA-2, and with a larger spread of correlations for MERRA-2. However, Murcia et al. (2022) found that bias correction of ERA5 using GWA2 showed good agreement with observed country-level generation data for Europe.
In Australia, only a few studies have used the BARRA reanalysis, and only one study could be identified that has assessed its accuracy in the context of wind power.1 Cowin et al. (2023) compared the performance of BARRA-R (from the first version of BARRA) with MERRA-2 and ERA5 for offshore wind development and found a wide variance in simulated capacity factor between the reanalyses. In their study, reanalysis data were compared with weather station data at 10-m mast height.
ROAM Consulting used the forerunner of BARRA (ACCESS-A, Australia Community Climate and Earth System Simulator) to produce wind power traces for the Australian electricity system operator’s 100% renewables study in 2012 (Cutler et al. 2012). The study covered the eastern states, which form the National Electricity Market (NEM). ROAM Consulting used a generic power curve for all sites. Bias correction involved applying a scaling factor to wind speed so that the simulated capacity factor matched the known capacity factor at wind farms. The same data were recently used in an Australia renewables simulation undertaken by Rispler et al. (2022) to assess the potential role of offshore wind power in Australia’s future energy mix. A weakness of adjusting wind speed based on known wind power capacity factors after the fact is that it is unclear how accurate this adjustment will be for future wind farms. This is because the physical basis for such scaling is not well understood.
In another study covering the Australian NEM but using MERRA-2, Gilmore et al. (2022) assessed the risk of ‘energy droughts’, which are a concurrent lack of wind and solar over a given interval. Similarly to ROAM Consulting, bias correction involved applying a wind speed scaling factor to match the known capacity factor at wind farms. For new sites, a region-wide scaling factor was applied. The duration of energy droughts is a critical determinant of renewable firming and energy storage capacity. Laslett et al. (2016) also used MERRA-2 to generate synthetic time series wind power for the south west region of Western Australia.
The present study compares simulated wind power using the BARRA-R2 (Regional-scale reanalysis of BARRA, version 2) reanalysis (12- × 12-km grid) from the most recent BARRA2 suite, and compares the results with MERRA-2 (55- × 70-km grid) and ERA5 (30 × 30 km grid). These power estimates are compared with observed power at operating wind farms based on reported power from the electrical system operator for the two largest interconnected systems: the NEM and the South-West Interconnected System (SWIS). A total of 54 sites, corresponding to operational wind farms, are assessed. Data are included for 2014–2021, giving up to 8 years of data for some sites, based on data quality and availability.
Most studies assess wind power at a national or regional level, and many use generic turbine power functions. This study differs from previous studies in comparing simulated with observed power at the level of a wind farm, using site-specific turbine parameters.
Our objective is to assess the accuracy of the BARRA-R2 reanalysis for wind power modelling in Australia. It is essential to understand not only the bias in modelled wind power but also the confidence in this bias across regions where calibration data are not available. Observed wind farm power data provide the most reliable benchmark for energy system modelling and serve as a baseline reference. In addition to BARRA-R2, we evaluate the performance of MERRA-2 and ERA5, two of the most widely used reanalyses internationally. Although these reanalyses have been evaluated in other contexts, their accuracy in Australia remains less well understood. The metrics assessed include correlation, bias, power distribution and the hourly rate of change in simulated wind power. A further aim is to identify the factors influencing the accuracy of simulated wind power at the scale of a wind farm. These factors include technical aspects related to wind turbines and wind farms, as well as characteristics specific to the reanalyses.
The paper is structured as follows: Section 1 introduces the study and reviews the literature. Section 2 discusses the reanalyses, comparison methodology and analysis methodology. Section 3 presents the results and Section 4 discusses the results. Section 5 concludes the paper.
2.Data and methods
2.1. Reanalysis data
BARRA2 is the second generation of Australian reanalysis. BARRA2 covers the Australian continent and the surrounding region including parts of South-east Asia and New Zealand (Su et al. 2022). BARRA2 includes three reanalysis suites – BARRA-R2, which is a deterministic reanalysis at ~12 km or 0.11°; BARRA-RE2, which is an ensemble reanalysis at 24 km or 0.22°; and BARRA-C2, which is a convective-scale downscaled reanalysis. The boundary conditions for BARRA-R2 are given by ERA5. For this study, BARRA-R2 pre-release development data were used (https://doi.org/10.25914/1x6g-2v48). Data access was kindly provided by The Bureau of Meteorology before general release.
From MERRA-2, the hourly, time-averaged, single-level, assimilation, single-level diagnostics (M2T1NXSLV) dataset was used (see https://disc.gsfc.nasa.gov/datasets/M2T1NXSLV_5.12.4/summary). From ERA5, instantaneous2 hourly data on single levels from 1940 to the present were used (see https://cds.climate.copernicus.eu; Hersbach et al. 2023).
All reanalysis products report hourly zonal (u) and meridional (v) wind velocity at several heights above ground level. BARRA-R2 reports wind speeds at 10, 50, 100, 150, 200, 250 and 1500 m; MERRA-2 reports at 2, 10 and 50 m, and ERA5 reports at 10 and 100 m (see Table 1). For all reanalyses, wind speeds at the 10-m height were excluded because they are prone to disturbed flow.
2.2. Electricity regions
Australia has two major grids, which cover most of the population, and many minor grids covering remote and regional communities. The largest grid by population and energy is the NEM, which includes the states of South Australia, Victoria, New South Wales, Queensland and Tasmania. Annual traded energy is currently 189 TWh (Australian Energy Regulator 2023). The second largest grid by energy is the SWIS, which covers the southwest of Western Australia. Annual traded energy is currently 20 TWh (Australian Energy Market Operator 2025). The present study includes sites located within both the NEM and the SWIS. All states were included except for the Northern Territory (see Fig. 1).
2.3. Wind power data
Wind power data were taken from the respective grid operator’s publicly available Supervisory Control And Data Acquisition (SCADA) data (SCADA refers to the communications protocol used to send and receive data from the network operator’s energy management system and remote devices). The NEM SCADA dataset has 5-min temporal resolution, corresponding to the operational settlement period, whereas the SWIS dataset has 30-min resolution. Both were aggregated to hourly resolution, giving an average power per hourly time step. The timestamp of the reanalysis datasets is given as Coordinated Universal Time (UTC), whereas the NEM is given as Australian Eastern Standard Time (AEST) and the SWIS as Australian Western Standard Time (AWST). The SCADA timestamp (yyyy-mm-dd hh:mm) was adjusted to align with the reanalyses’ hourly window, where the time refers to the upcoming hour, e.g. 2021-01-01 00:00 refers to the first hour of the 2021 year.
The parameters of interest for this work are ‘availability’ and ‘scadavalue’ (generation is recorded in two tables – DISPATCHLOAD and DISPATCHUNITSCADA; ‘availability’ is a parameter in the former, ‘scadavalue’ in the latter). Where possible, the ‘availability’ parameter is used because it measures the power that is available for dispatch just before the dispatch period, ignoring curtailment. For wind generators, this describes the forecast power just before the 5-min (or 30-min for the SWIS) dispatch interval. The measure is calculated by the Australian Wind Energy Forecasting System, AWEFS (AWEFS is the electricity system operator’s wind forecasting system), taking into account current generation, the wind turbines that are available and on-site measurement of wind, or otherwise a self-forecast provided by the generator. Where the ‘availability’ is not available, the ‘scadavalue’ parameter was used. This parameter indicates the reported generation just before the dispatch interval; however, the reported output may occasionally be lower than available owing to curtailment.
An additional factor that influences the reported power is participation in the frequency control ancillary services (FCAS) market.3 Only four wind farms in Australia participate in the FCAS market, and three of these are co-located with battery energy storage systems (Bulgana, Hornsdale and Lake Bonney). The batteries have separate identification numbers, and are treated as separate entities. Musselroe is the only non-storage wind farm that participates in the FCAS market. In principle, wind farm operators will seek to supply as much power as available to maximise revenue from the energy market. However, participation in the FCAS market may involve strategic withholding of power to earn revenue from the FCAS market. Inspection of data for Musselroe does not show significant anomalies that might suggest that FCAS is a significant factor. For the purpose of this study, it is assumed that Musselroe’s FCAS participation has only a minor effect on its results.
2.4. Wind farm information
Wind farms were selected based on data availability and quality. Multiple years were included where data were available, but on a full calendar year basis only in order to ensure that seasonal aspects were included in the analysis. During commissioning, it is common for operators to stagger commissioning of turbines or to take turbines offline. At other times, non-scheduled maintenance, operational, or transmission constraint issues may affect reported generation. These years were excluded from the study.
Ideally, a study such as this would provide sample diversity with respect to geographical location, wind turbine model, turbine layout, etc. In practice, the sample set is limited to registered wind farms that have a sufficiently long period of operation to enable a clear record of operation. In addition to a strong wind resource, various planning, policy, economic and development factors influence wind farm siting, turbine selection and wind farm layout. As of August 2023, there were 88 registered wind farms in the NEM and 12 in the SWIS. Many of these have been registered in the last few years. This study includes 54 wind farms, making up 54% of the registered wind farms in the NEM and SWIS. Data are included for 2014–2021, giving up to 8 years of data for some sites. In total, 221 site-years were included in the analysis.
The location, make and model of wind turbine, hub height, ground elevation above mean sea level, rated power, commissioning year and power curve were ascertained from various sources including the electricity system operator (AEMO, Australian Energy Market Operator), the websites for the respective wind farm operators, The Wind Power website (see https://www.thewindpower.net/), the Open Energy Platform website (see https://openenergyplatform.org/), OpenStreetMap and TessaDEM digital elevation model. Where power curve data were not available, data from the closest specification model were used. The wind farms and their locations are given in Fig. 1 and Tables A1 and A2.
2.5. Wind power model
A wind power model was used to estimate wind turbine power, given wind speed, and modified by air density and a scaling factor that accounted for factors that reduced available power. For the purpose of this study, it is assumed that a wind farm behaves as a scaled-up, discrete wind turbine. Limitations of this assumption are discussed in Section 4.
The power available from a wind turbine is given by:
where Cp is a variable turbine power coefficient, ρ is the density of air, A is the swept area and U is the magnitude of the wind speed. In typical wind turbines, Cp increases from ~0.3 at the cut-in speed, up to a peak of ~0.45 at 7.5–8.5 m s−1 and decays by U−3 thereafter (see Fig. 2) (Svenningsen 2010).
Illustration of reported and simulated wind turbine power curve, and turbine power coefficient (Cp) (see Eqn 1). This example is for a GE Energy 2.5xl wind turbine model used at Mumbida wind farm.
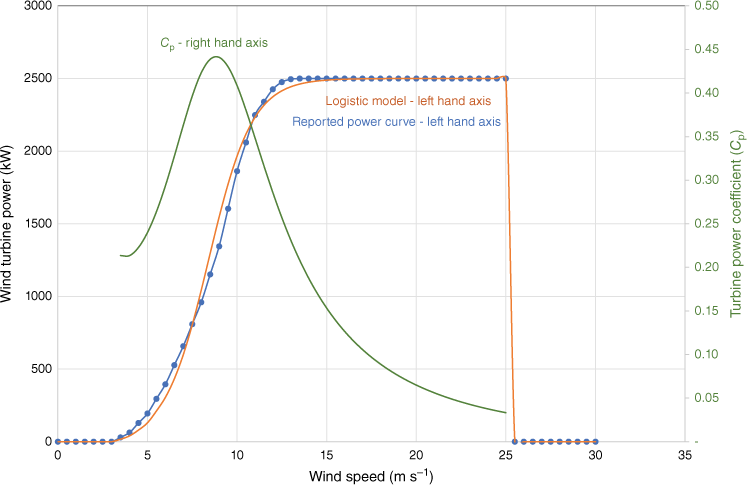
The turbine power coefficient is a function of wind speed and the aggregate of the aerodynamic, mechanical and electrical efficiency. In addition, wind turbine self-load reduces net power output. For commercial wind turbines, the various aspects of efficiency and self-load are aggregated to give a wind power curve for the specific model of wind turbine. These curves are produced by wind turbine manufacturers according to the requirements of the International Electrotechnical Commission IEC 61400-12. Wind power is reported against wind speed at discrete (piece-wise) 0.5 m s−1 wind speed intervals, normalised to the International Organization for Standardization (ISO) International Standard Atmosphere (ISA) density of 1.2250 kg m−3. A representative wind power curve is shown in Fig. 2.
For this study, the wind power curve was simulated as a continuous parametric function. The advantage of a parametric function over a piece-wise function is that the parameters can be readily adjusted over a continuous range for optimisation. A parametric function that approximately replicates the shape of wind power curves is the logistic function, of which various configurations are available (Villanueva and Feijóo 2018). The logistic function used in this work is a three-parameter type, which represents a trade-off between precision and complexity. The complete transfer function, taking into account cut-in and cut-out speeds, is given in Eqn 2.
where P(t) is the simulated wind power at time t, a is the rated power4 of the wind farm, where it is assumed that the wind farm behaves as a wind turbine, c is the wind speed scale (midpoint of the wind power curve), b is the shape of the curve and U(t) is the wind speed at time t given by the reanalysis data and calculated from the u and v wind components using the Pythagorean theorem.
Reported wind speeds at discrete heights must be modified to give estimated wind speed at the turbine hub height. For MERRA-2 (Gelaro et al. 2017) and ERA5 (Hersbach et al. 2020), the reported wind speed at 50 m (MERRA-2) and 100 m (ERA5) was modified using the log law equation (Archer and Jacobson 2003) given below.
where U(z) is the adjusted wind speed, z0 is the surface roughness length, z is the hub height and Ur is the wind speed at the reference height, zr. The surface roughness length is influenced by the vegetation type, with grasslands, croplands and pastures having the shortest lengths, whereas forests have the longest (Hahmann et al. 2020). Most of Australia’s wind farms are situated on agricultural land, including previously cleared grazing or cropping areas, some with scattered patches of woodland. Wind farms located near the coast are sometimes located in scrubland areas. To maximise wind turbine performance, wind farms require large, open spaces. Given these conditions, the surface roughness length for all wind farms was set to 0.1 m, corresponding to vegetation types with a short roughness length.
For BARRA-R2, wind speeds are reported at a range of heights enabling direct vertical interpolation. Log-interpolation was selected given the log-law relationship between height and wind speed within the surface layer of the atmospheric boundary layer. The surface layer is limited to approximately the lowest 100 m of the boundary layer.
A source of uncertainty and variability is the operational availability of wind turbines. For large wind farms, it is usual for one or more wind turbines to be unavailable owing to scheduled maintenance or unscheduled outages. The power scaling factor, e, is a heuristic that scales the rated power. It was initially set to 0.95 and adjusted by visual inspection of the time series graphs for each site so that the typical maximum simulated power was set to equal the maximum observed power of the wind farm. In practice, e will vary on an hour-by-hour basis; however, no reliable data could be found that would enable hourly calibration.
A related factor is that transmission constraints may reduce maximum power flows below the combined nameplate power of the wind turbines, or output may be curtailed in response to electrical operator instructions. By visual inspection of time series graphs, the power scaling factor appears to be a good guide under typical operating conditions.
Parameters v0 and b describe the scale and shape of the power curve, and were set by minimising the error between the continuous function and the piece-wise power curve for the specific wind turbine. The resulting parameters are given in Table A3.
Given that wind power curves are normalised to the ISO ‘Standard Atmosphere’, an adjustment was required for air density. The recommended normalisation process for wind turbines with active power control is given in IEC 61400-12 (8.1), and recommends adjusting the wind speed using Eqn 4 below, and using the adjusted wind speed to determine the normalised wind power:
where Ud is the adjusted wind speed, U is the given wind speed, ρ is the air density for the sample, ρ0 is the standard air density of 1.2250 kg m−3.
Air density was not given directly in the reanalysis data. Using available data within each of the reanalyses (see Fig. 3 for the parameters used for each reanalysis), air density ρ was calculated from barometric (total) pressure Pt, partial pressure of water vapour Pv, air temperature T and the gas constant for dry air Rd, for each hourly sample at the appropriate location, using the approximation given in Eqn 5. Partial pressure of water vapour Pv was calculated with Teten’s approximation, given in Eqn 6, where RH is relative humidity, T is temperature (°C) and Pv is pressure (kPa).
Block diagram of the validation model used for this study. Wind velocity given as zonal (u) and meridional (v) components. Wind speed adjustment uses International Electrotechnical Commission (IEC) standard for wind turbine performance reporting. BARRA-R2 labels: ta50m, air temperature at 50 m, psl, air pressure at mean sea level, hurs, near-surface relative humidity. MERRA-2 labels: T10M, air temperature at 10 m; SLP, air pressure at sea level; QV10M, specific humidity at 10 m.
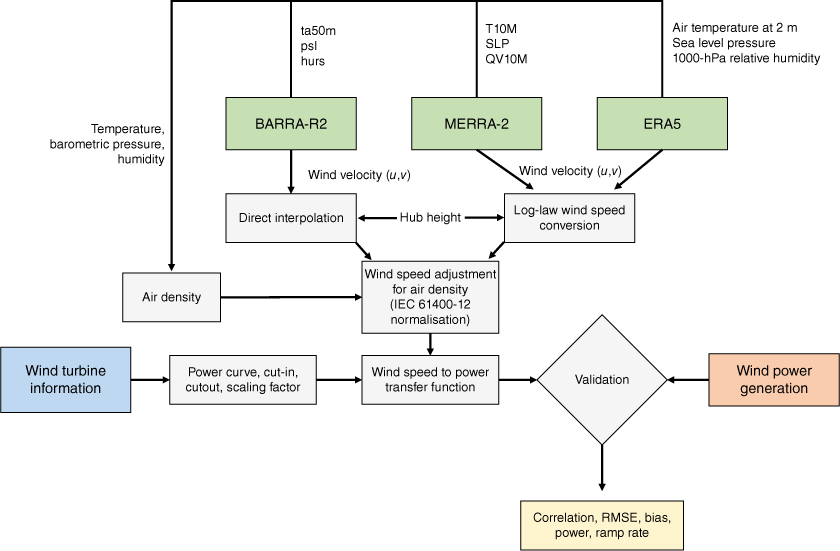
2.6. Wind turbine parameters
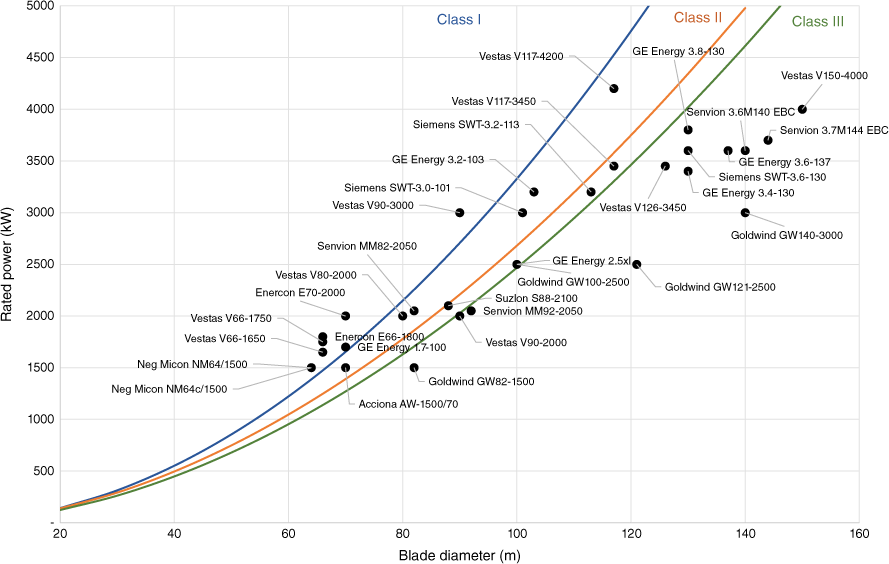
Table A3 lists the specifications for the wind turbine models used in this study. The class was determined according to the closest fit to the power law curves given in Engels et al. (2009) (see Fig. 4).
Wind turbine models with respect to blade diameter, power and wind class. Curves based on equations from Engels et al. (2009).
2.7. Validation
We followed the recommendation of Borsche et al. (2015), testing for Pearson correlation, root mean square error (RMSE) and bias. We introduced two additional tests – the error between the simulated and observed frequency distribution of power, and the similarity between the simulated and observed ramp rates. Overall, reanalyses were validated in the time domain (x-axis is time), power domain (x-axis is power) and energy domain (integral of power over time) (see Table 2 and Fig. 3). Validation was performed using five statistical parameters as follows:
Pearson correlation (R) to test for hourly correlation between observed and simulated power in the time domain. Pearson correlation is an indicator of the similarity between the temporal profile of simulated and observed generation, but not necessarily the magnitude. If the highest simulated results tend to match the highest observed results and vice versa, the correlation is high.
Bias is a measure of the capability of the simulations to reproduce the observed annual capacity factor. It is measured as the error between the simulated and observed wind power annual capacity factor. Graphical results are presented in two ways: as the natural log difference between simulated and observed so that under- and over-estimation is presented symmetrically, and as a percentage. As local land surface and topography is important, the capacity factor results are compared with the Global Wind Atlas (GWA 3.1), which produces capacity factor estimates at 250- × 250-m resolution.
RMSE, which is an indicator of the difference between observed and simulated power with respect to both the magnitude and the temporal profile. As the rated power varies across wind farms, the observed and simulated data are firstly non-dimensionalised by dividing by the rated power so that the wind farms are compared on a common basis. The resulting RMSE embeds the temporal correlation, as well as the additive and multiplicative bias relative to the wind farm capacity.
RMSE is given in Eqn 7.
where Si is simulated, Oi is observed and n is sample size.
The capability of the simulations to reproduce the observed frequency distribution of power is measured by comparing the overlap of the respective probability density functions (PDFs), described below.
The similarity between observed and simulated power of adjacent time steps (1 h) is a measure of the hourly ramp rate. Similarity is expressed as the overlap of observed and simulated hourly change histograms, described in more detail below.
| Domain | Statistical measure | |
|---|---|---|
| Time | Pearson correlation | |
| RMSE (non-dimensionalised) | ||
| Power | Power frequency distribution error | |
| Overlap of the hourly change histogram | ||
| Energy | Annual capacity factor bias |
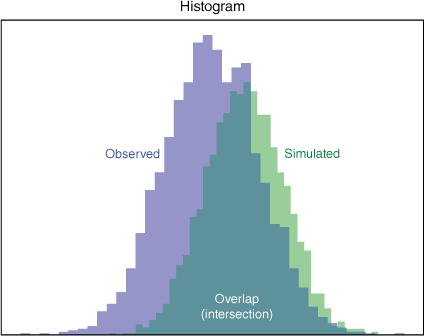
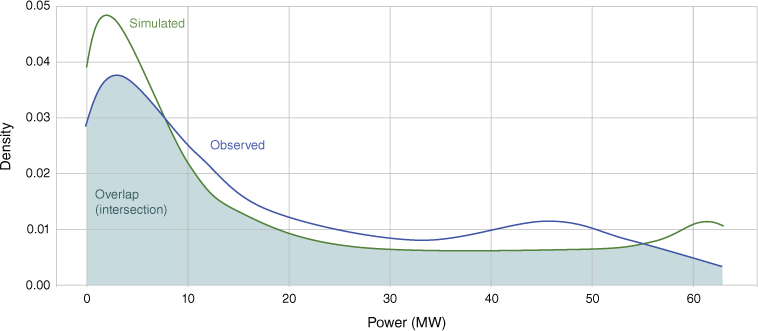
As validation in the power domain is novel in the wind reanalysis literature, it is described as follows (validation of wind speed distribution has been undertaken in the climatology literature, e.g. Hahmann et al. 2020). Probability density functions of wind power were constructed for both observed and simulated wind power. The PDFs were compared piece-wise using the intersection (overlap) equation from Cha (2007), given in Eqn 8. The overlap (0–1) of the PDFs provides a simple estimate of the similarity of the shape of the respective power distributions, and therefore the validity of the simulated wind power in the power domain (see Fig. 5 and 6).
where Op is overlap in the power domain, Mi is the frequency of values in a given bin for observed, Ni is the frequency of values in a given bin for simulated, n is number of bins.
Illustration of power frequency distribution overlap between the observed (NEM and SWIS) and simulated probability density functions (PDFs).
In addition to the power distribution, we also test for the change of power, or equivalently, hourly ramp rates. This is measured by taking the power difference between adjacent time steps and sorting into histogram bins. The observed and simulated histograms are compared as the overlap of the respective bins, also using the equation from Cha (2007), given in Eqn 9. The result is expressed as the overlap (0–1), and provides an indication of the similarity of the respective histograms.
where Oc is overlap of the change of power, Zi is the frequency of values in a given bin for observed, Wi is the frequency of values in a given bin for simulated, b is number of bins.
3.Results
In this section, we present the results, beginning with the reanalysis wind speed distributions. Following this, a snapshot of 4-day time series results is presented, illustrating representative behaviour of the simulations against the observed power. Snapshots of wind droughts are also presented, illustrating the capability of the simulations to reproduce these. Subsequently, the correlation measures are presented, which demonstrate the capabilities and weaknesses of the simulations. Bias results are presented including statistical measures that support estimation of confidence intervals. The results from the power domain are presented, which point to the ways in which the simulations differ from the observed power.
3.1. Wind speed distribution
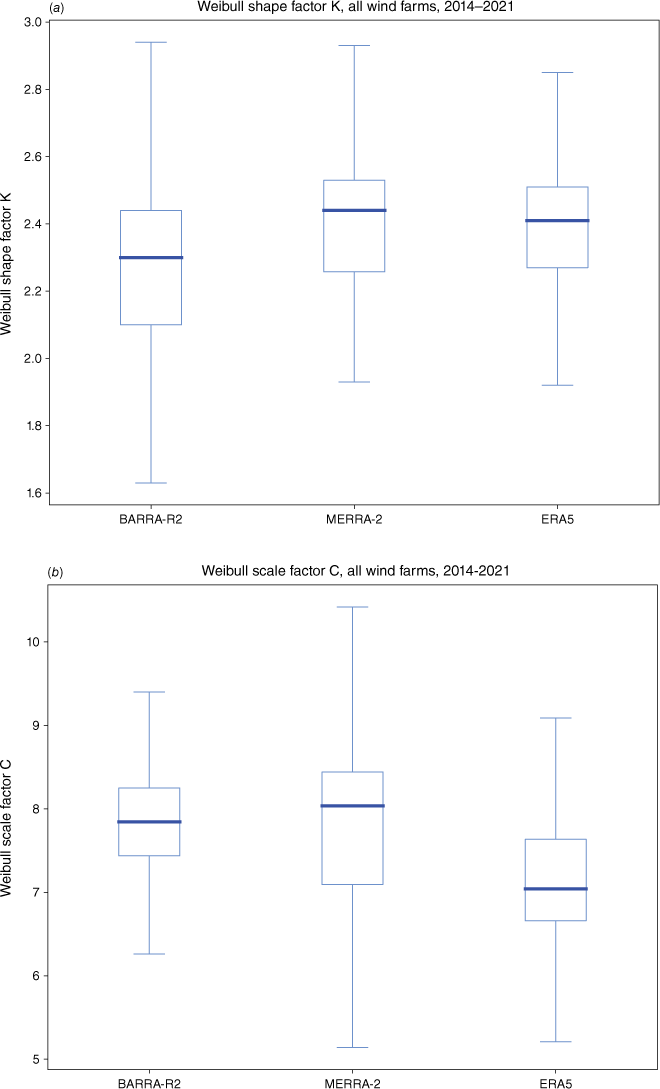
Wind energy researchers have shown that the Weibull distribution fits probability densities for wind speed quite well (Christofferson and Gillette 1987). The Weibull distribution can be described by a shape factor K and a scale factor C. In order to test whether the reanalyses were consistent with a Weibull distribution, each of the reanalyses was fitted on an annual basis using a Weibull fitting function. (The Python scipy.stats function was used, which minimises the negative log-likelihood function; see https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.weibull_min.html.)
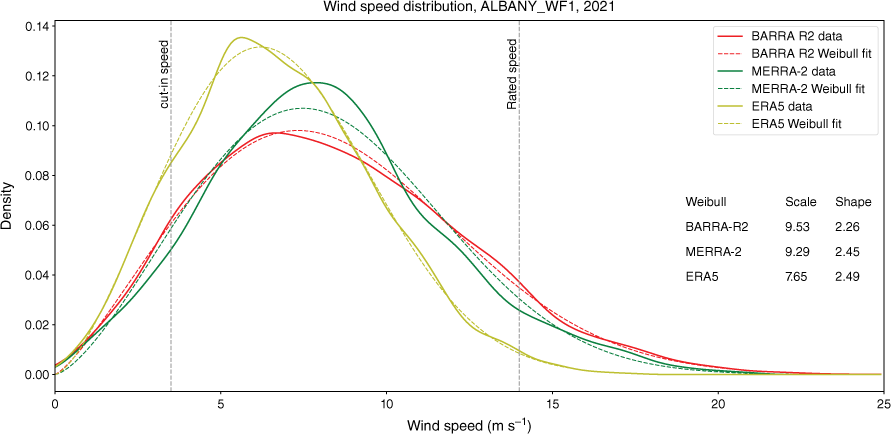
Across reanalyses and years, the shape and scale factors are broadly consistent with a Weibull distribution of shape factor of 2.1–2.5. An illustrative series of plots, showing both the distribution of wind speed and accompanying Weibull distributions with best-fit parameters are shown in Fig. 7. These visually show a good fit of the data to the Weibull distribution. The estimated Weibull shape K and a scale C factors for BARRA-R2 are given in Table A4 in the Appendix. The shape and scale parameters for the three reanalyses are shown as box and whisker plots in Fig. A1a, b. For all plots, the box extends from the lower to upper quartile values of the data (the interquartile range, IQR), with a line at the median. The upper whisker extends to the last datum less than (Q3 + 1.5 × IQR), whereas the lower whisker extends to the first datum greater than (Q1 – 1.5 × IQR).
Wind speed distribution and best-fit Weibull parameters – illustrative example for Albany, 2021. Solid lines are wind speed data. Dashed lines are Weibull plots using accompanying best-fit parameters. Also shown are the cut-in and cut-out speeds for the Enercon E66-1800 wind turbine used at the Albany wind farm.
3.2. Time series results
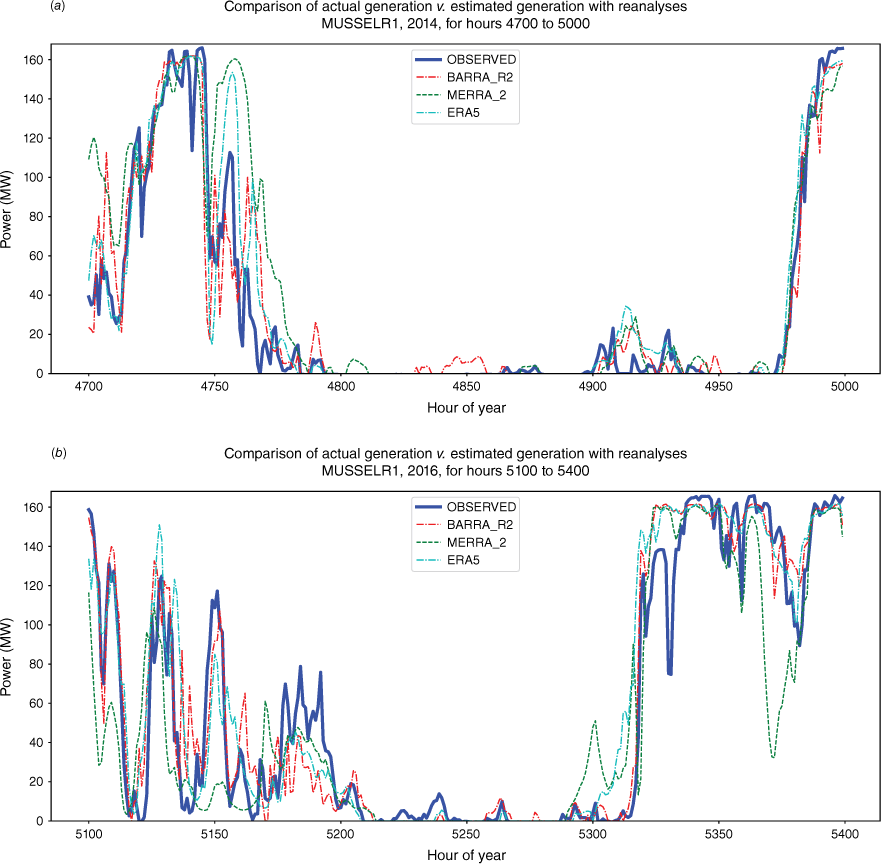
Two illustrative time series plots are shown in Fig. 8a, b. These are 4-day snapshots with hourly resolution. The choice of a 4-day time interval is intended to provide a balance between a sufficiently long time horizon to display the movement of weather patterns, without overwhelming the plot with detail. The first depicts a snapshot during which there are clear weather patterns producing high and low wind speed, while also giving good correlation at an hourly interval. The second depicts another 4-day snapshot, which also replicates weather patterns, but which demonstrates much greater variability with respect to hourly correlation. In general, all reanalyses are good at reproducing the general trends of the passage of weather systems, but the reproduction at shorter time intervals is highly variable.
Two illustrative time series plots. Thick blue line is observed power as reported by electrical system operator. Dashed lines are for simulated power using BARRA-R2, MERRA-2 and ERA5 reanalyses. Correlation and capacity factor on right side is for the 4-day snapshot. (a) Collgar 2014, 4-day snapshot for hour of year 100 to 196. (b) Albany 2018, 4-day snapshot for hour of year 200 to 296.
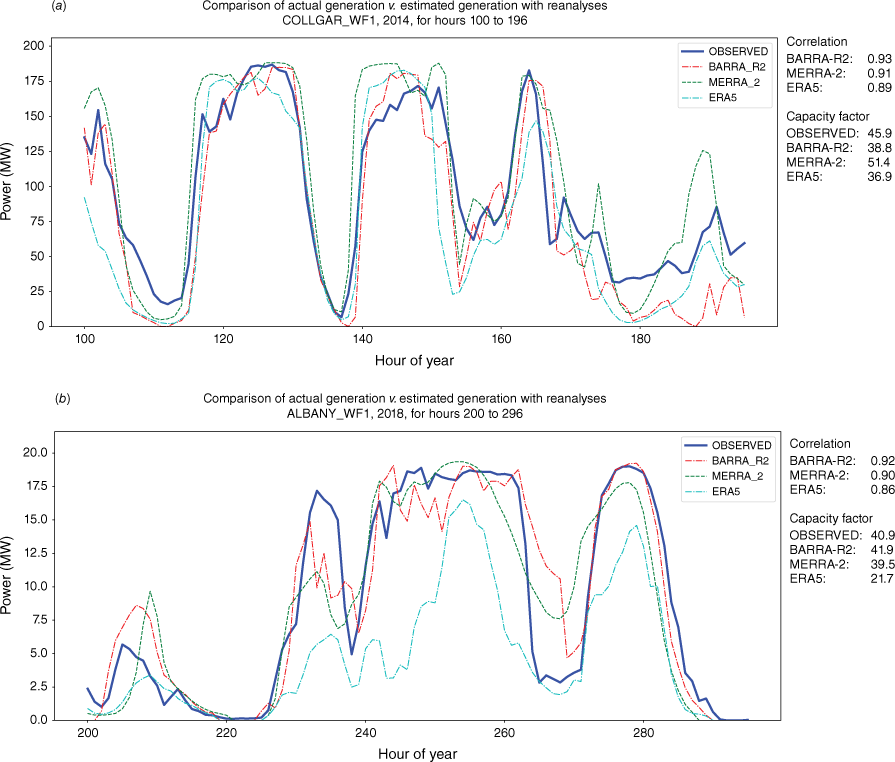
An important result is that the reanalyses are very good at reproducing extended wind lulls. Although hourly variability remains, the simulations generally show low power for most of the duration of lulls. Two representative snapshots, one depicting a 180-h lull and the other a 120-h lull, are shown in Fig. 9a, b.
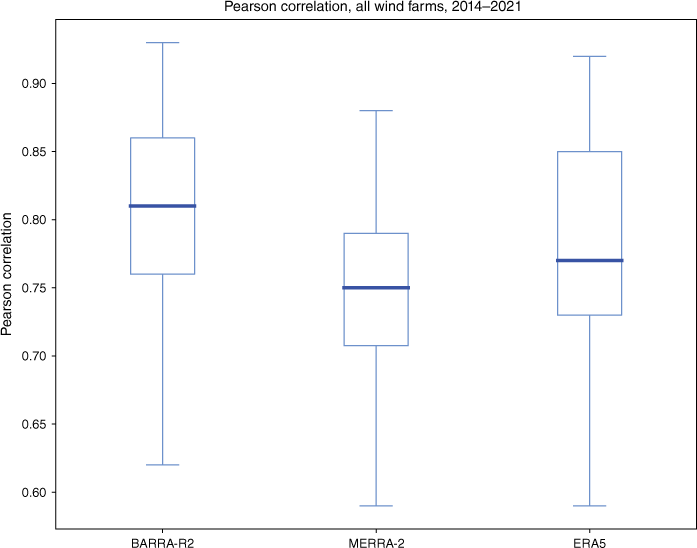
3.3. Correlation
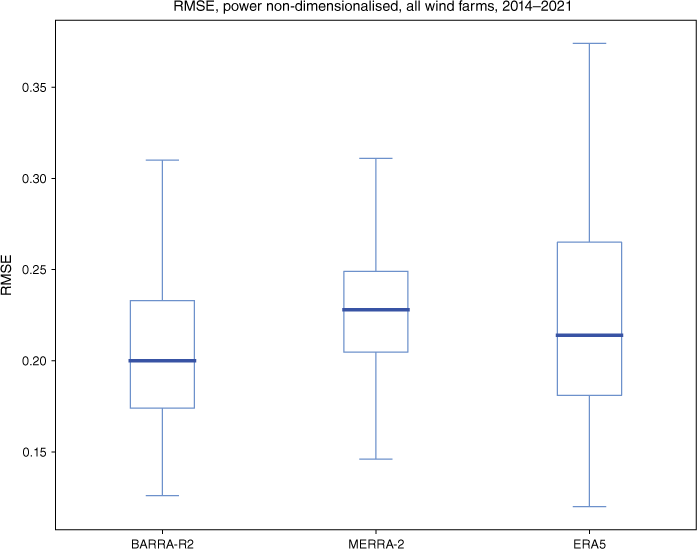
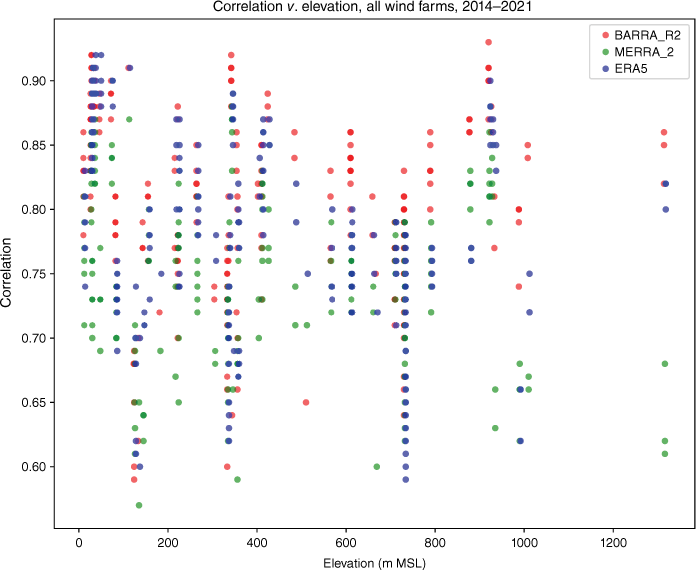
The correlation results are presented as box plots for Pearson correlation and RMSE after non-dimensionalisation (Fig. 10 and 11, Tables A5–A6). These show generally good correlation but a wide variance. Pearson correlations are also presented as scatter plots against ground elevation to test whether these parameters are predictive of correlation (see Fig. 12). However, ground elevation does not add useful information.
RMSE between modelled and observed wind power, non-dimensionalised, all wind farms, 2014–2021.
Pearson correlation v. ground elevation, all wind farms, 2014–2021. Each site–year reanalysis is one data point. The R2 for the linear trend lines is no higher than 0.11, suggesting that ground elevation is not predictive of Pearson correlation.
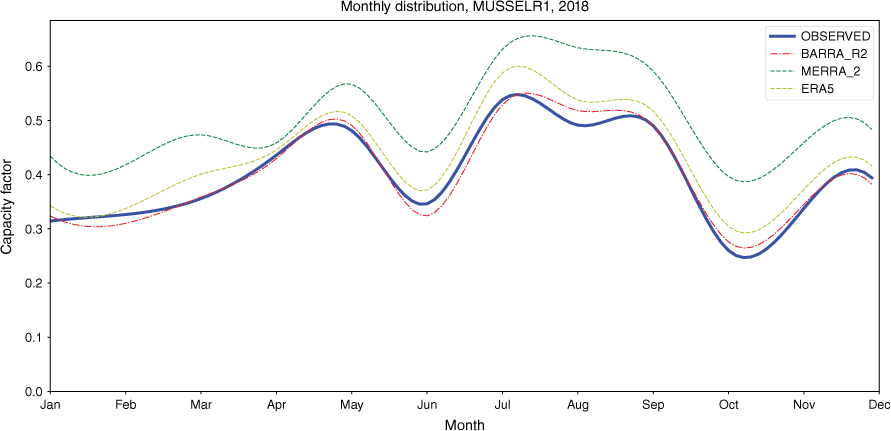
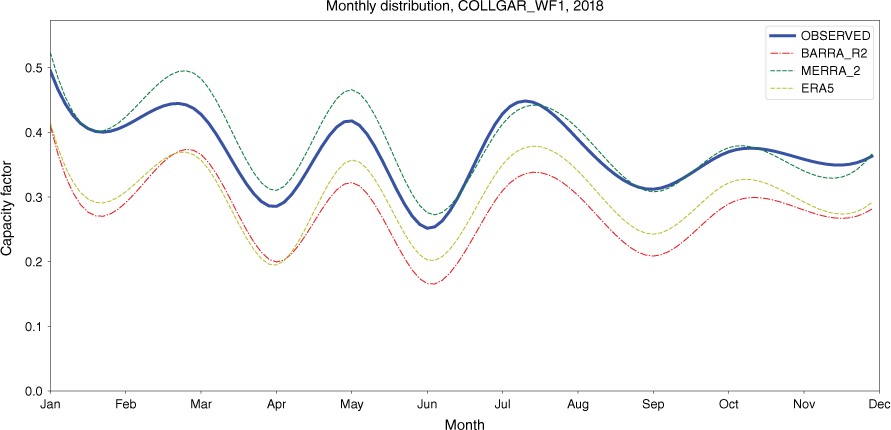
At longer time intervals, temporal aggregation appears to improve simulation quality with respect to correlation. This is demonstrated by the average monthly capacity factor graphs. Two representative sites are shown in Fig. 13 and 14. These graphs demonstrate two aspects. Firstly, the correlation between simulated and observed is high after monthly averaging. Secondly, the bias for all simulations is consistent across the year (Table 3).
Average capacity factor by month, Collgar, 2018. Bias for each reanalysis, averaged over 1 month, is similar across 1 year.
3.4. Bias
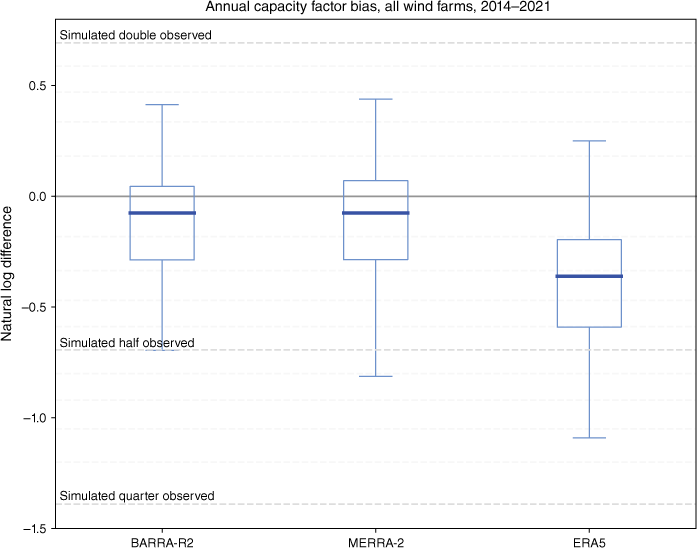
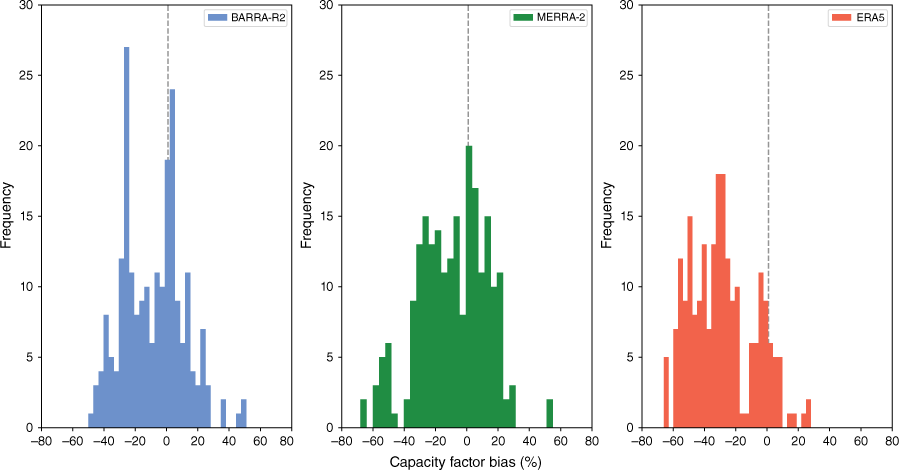
Bias is measured as the error between the simulated and observed wind power annual capacity factor. Error is plotted with box plots as the difference in natural logarithm in Fig. 15 so that over- and under-estimation bias is plotted symmetrically. Fig. 16 plots the same data on histograms, shown as percentage bias. Table 4 plots the data in tabular form. The downward bias of ERA5 is clear on both types of plots, whereas a slight downward bias is evident for BARRA-R2 and MERRA-2.
Bias between modelled and observed wind power, all wind farms, 2014–2021, shown as difference of natural logarithms. Dashed reference lines shown for simulation v. observed being double (y = 0.693), half (y = 0.693) and quarter (y = −1.386). Intermediate dashed lines for intermediate equal steps (+20, +40%, etc.).
Bias between modelled and observed wind power, all wind farms, 2014–2021, shown as percentage. Each data point is one site–year, plotted with 31 bins.
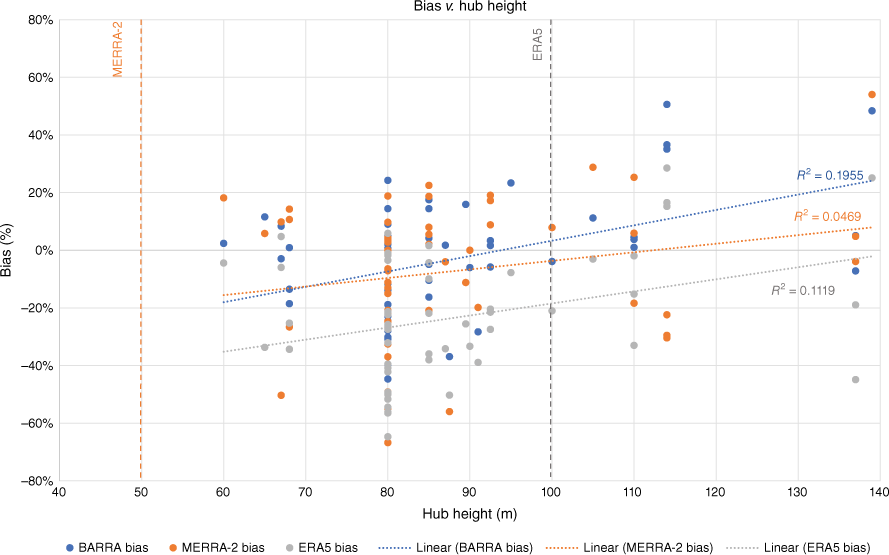
To evaluate whether bias could be attributed to log-law extrapolation (applicable to MERRA2 and ERA5), we performed a linear regression of bias against hub height across all wind farms. Results indicate a slight overestimation bias with increasing hub height for all reanalyses, including BARRA-R2, which employs direct interpolation, suggesting that log-law extrapolation was not a reliable predictor of bias. Further details are included in the Appendix.
In order to use these results to estimate confidence intervals, it would be useful to know if they are consistent with a normal distribution. To test for normality, we apply D’Agostino and Pearson’s test.5 The resulting P values are 0.21 (BARRA-R2), 0.32 (MERRA-2) and 0.01 (ERA5) (n = 221). From these, we can deduce that the ERA5 bias samples are likely not normally distributed, whereas BARRA-R2 and MERRA-2 are potentially normally distributed. For completeness, the resulting mean and standard deviation assuming normally distributed bias are given in Table 5.
| Quartile | BARRA-R2 (%) | MERRA-2 (%) | ERA5 (%) | |
|---|---|---|---|---|
| Upper | +5 | +7 | −17 | |
| Median | −7 | −7 | −30 | |
| Lower | −25 | −25 | −45 |
In energy modelling, it is standard practice to adjust for bias across a region using operating wind farms for calibration. Assuming a hypothetical site with a simulated (BARRA-R2) capacity factor of 30%, applying bias correction with ±1 s.d. (giving 68% of normally distributed data samples) would give a bias corrected capacity factor range of 21.6–33.3%.6
Such a range is much wider than would normally be assumed in energy system models.
| Statistic | BARRA-R2 (%) | MERRA-2 (%) | ERA5 (%) | |
|---|---|---|---|---|
| Mean | −8.4 | −8.9 | −28.6 | |
| Std | 19.5 | 22.1 | 20.3 |
ERA5 not normally distributed. See text.
A summary of capacity factors is given in Table A7 in the Appendix, and a summary of bias across all sites and years in Table A8 and Fig. 13.
3.5. Power domain
The power distribution graphs illustrate one way in which the simulated results differ from the observed data. The main difference is the presence, or not, of a peak at high power. All of the simulated results present as a bimodal distribution, with a peak at both low and high power. However, many of the observed samples present as a unimodal distribution, with a peak at low power only. A sample of power distributions is presented in Fig. 17a, b.
Sample of power frequency distributions for two wind farms, 2018, full year. The second (right) peak is clearly evident for Musselroe (top figure), but is flattened for Albany (bottom figure). (a) Musselroe, 2018. (b) Albany, 2018.
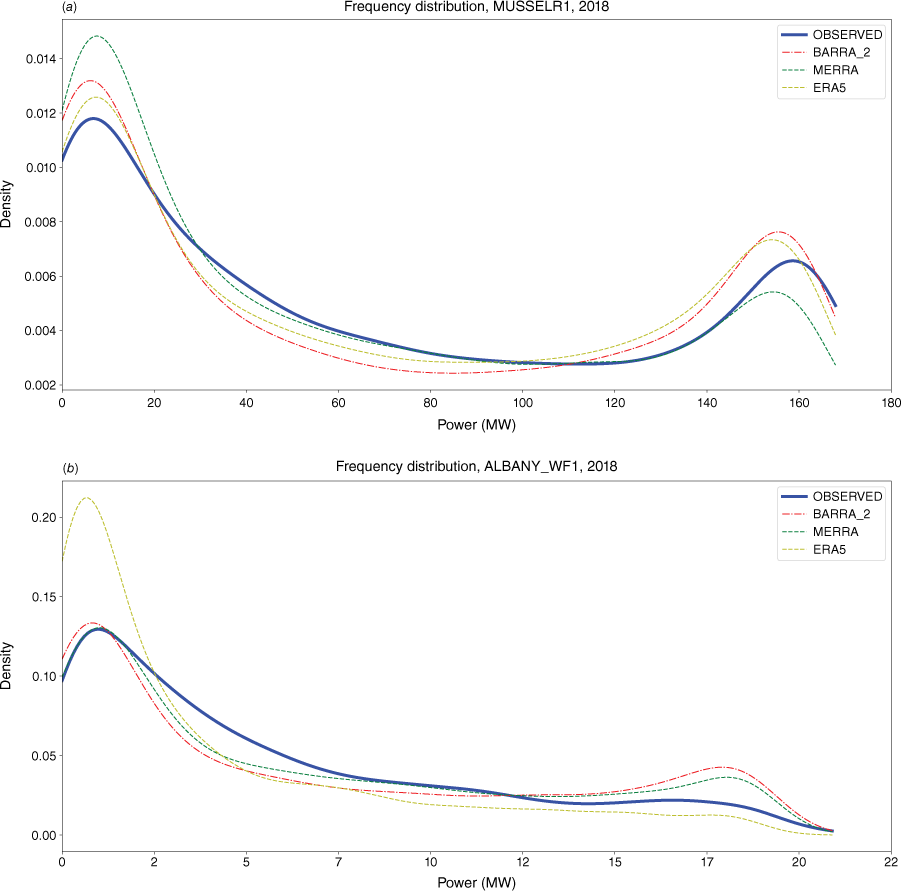
The lower peak is explained by the Weibull-like wind speed distribution of the sampled sites, which exhibits a peak towards lower wind speeds. The higher peak is explained by the extended plateau of the wind power transfer function, which essentially ‘bunches up’ the power distribution over a wide range of wind speeds.
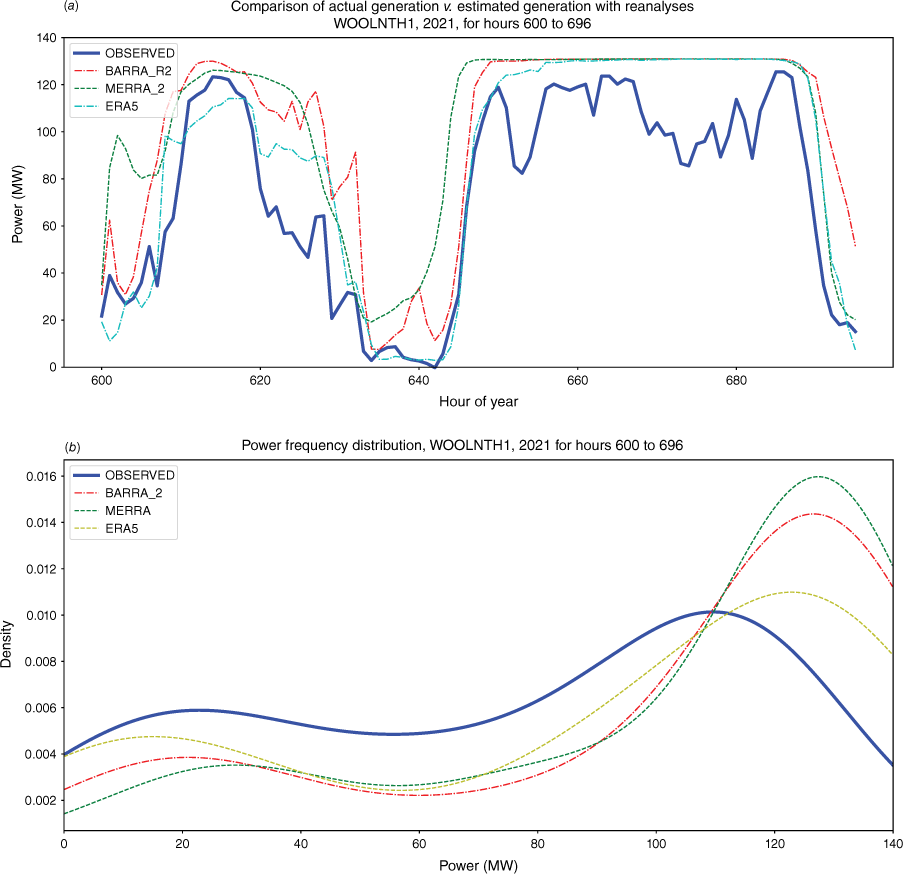
Associated with this is the tendency for the observed wind power to fluctuate towards, but rarely remain at, rated power. Fig. 18a, b illustrates this tendency. The 4-day snapshot presents a 2-day period during which all reanalyses reported high continuous wind conditions. The difference between observed and simulated is evident in Fig. 18b, which shows a distinct peak near rated power for BARRA-R2 and MERRA-2, and slightly less so for ERA5, but for the observed, the same peak is shifted downwards (lower power) and flattened.
Woolnorth 2021, 4-day snapshot for hours 600–696. (a) Time series graph showing all the reanalyses reported high wind conditions for hours 650–690, while the observed (NEM) power fluctuated towards rated power. (b) Power frequency distribution displaying the same information as the above graph, but in the power domain (x-axis is power). The full power peak is evident for the simulations. The observed peak is shifted downwards (lower power) and flattened. Graph is produced using kernel density estimation.
The difference between simulated and observed power distribution overall is shown is Fig. 19. The goodness-of-fit was estimated as the overlap of the simulated with the observed. A higher overlap indicates a better fit. The results are presented as a box plot, showing a wide variance, with similar results for BARRA-R2 and MERRA-2. ERA5 shows a wider range, extending to a lower fit.
Power frequency distribution overlap between modelled and observed wind power, all wind farms, 2014–2021.
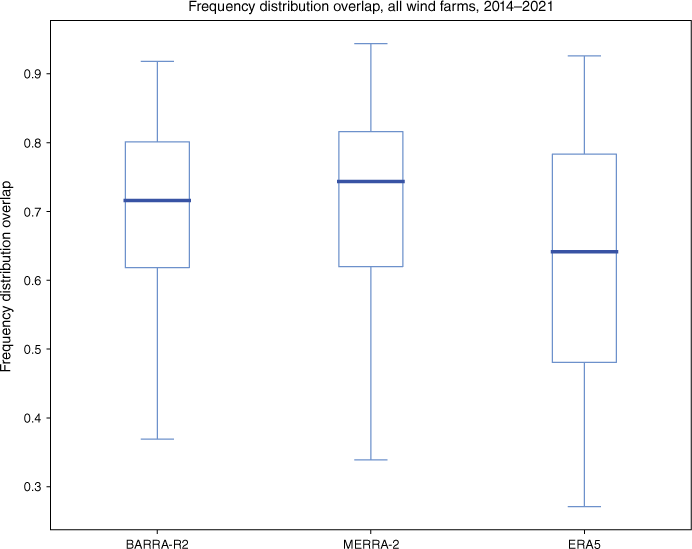
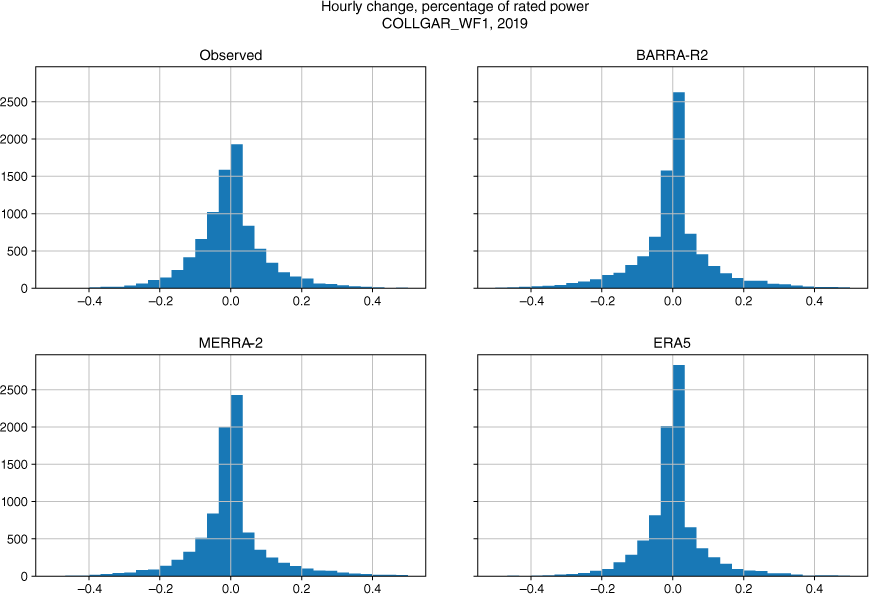
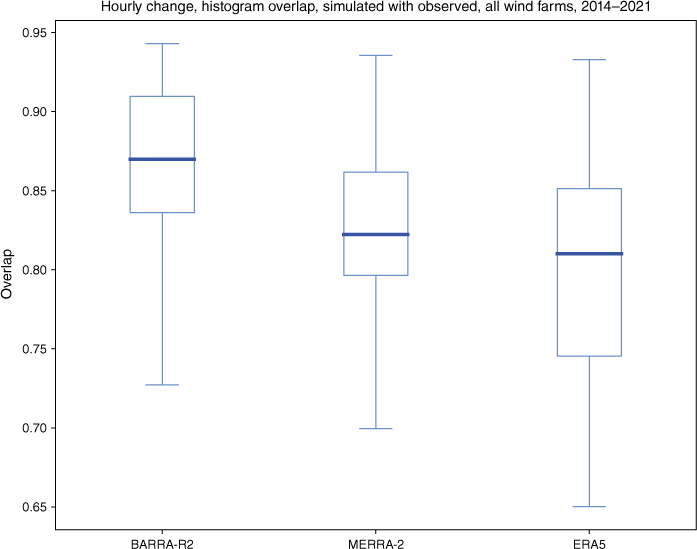
Fig. 20 is a representative set of histograms for the hourly change in power for adjacent time steps. The goodness-of-fit was also estimated as the overlap of the simulated with the observed. The performance of all the reanalyses is generally good (see Fig. 21), with the performance of BARRA-R2 the highest, followed by MERRA-2, then ERA5. In general, the simulations tend to show a peakier and narrower distribution than observed.
Hourly change (1-h ramp rate) as proportion of rated power, shown with 41 bins. Illustrative sample for Albany, 2019. The x-axis is percentage change, y-axis is number of samples; 8759 data points for 1 year.
Histogram overlap for hourly change as proportion of rated power (see sample Fig. 20), simulated with observed, all wind farms, 2014–2021. A higher overlap indicates a better fit.
3.6. Global Wind Atlas
The Global Wind Atlas (GWA 3.1; see https://globalwindatlas.info/en/about/method) is a web-based application that produces wind density and capacity factor estimates for most land areas of the world. GWA has been used for calibration of reanalysis data in some studies, e.g. Gruber et al. (2022), Nefabas et al. (2021). It uses a downscaling process on 10 years (2008–17) of ERA5, combined with a high-resolution topographical and land cover map, to produce a high-resolution wind distribution. Terrain elevation is based on the Viewfinder dataset (see http://www.viewfinderpanoramas.org/dem3.html) and land cover is based on the European Space Agency (ESA) Land Cover Climate Change Initiative version 2.0.7 (see https://data.ceda.ac.uk/neodc/esacci/land_cover/data/land_cover_maps/v2.0.7). GWA gives capacity factor for 100-m hub height at 250-m horizontal grid resolution.
Given that wind behaviour at sub-grid length scales is a significant factor, our results were compared with GWA 3.1 to determine whether higher spatial resolution surface and topography modelling could reduce bias. However, as can be seen in Table 6 of selected representative sites, the GWA capacity factor is significantly higher than the observed capacity factor for the sites in this study. In general, the GWA capacity factor estimates are very high across the Australian continent, and appear to be unrepresentative of operating wind farms. GWA provides capacity factor estimates for 100-m hub height only, thereby explaining some of the bias for sites with a hub height lower than 100 m. Although GWA offers mean wind speeds at 50, 150 and 200 m, estimating a capacity factor requires a wind speed time series, which GWA does not provide.
| Observed | BARRA-R2 | GWA 3.1 | Actual hub | ||
|---|---|---|---|---|---|
| Site | c.f.% | c.f.% | c.f.% (100-m hub) | Height (m) | |
| Badgingarra | 43.9 | 39.3 | 49–56 (Class III) | 85 | |
| Bald Hills | 37.8 | 39.4 | 49–53 (Class II) | 85 | |
| Collgar | 36.8 | 28.4 | 52–54 (Class III) | 80 | |
| Coopers Gap | 32.1 | 33.3 | 42–59 (Class III) | 110 | |
| Crookwell 2 | 34.7 | 42.8 | 40–55 (Class III) | 95 | |
| Crowlands | 35.7 | 34.3 | 43–52 (Class III) | 100 | |
| Gunning | 38.7 | 31.4 | 37–46 (Class II) | 80 | |
| Mt Millar | 28.9 | 24.2 | 35–48 (Class I) | 85 | |
| Mumbida | 38.9 | 30.0 | 46–56 (Class III) | 80 | |
| Musselroe | 37.6 | 38.4 | 49–52 (Class I) | 80 | |
| Sapphire | 33.4 | 35.1 | 39–42 (Class I) | 137 | |
| Silverton | 40.6 | 41.0 | 47–60 (Class I) | 110 | |
| Woodlawn | 33.8 | 24.6 | 43–54 (Class II) | 80 | |
| Woolnorth | 40.3 | 41.8 | 59–66 (Class I) | 80 |
Range given for 3- × 3-km region in online GWA mapping tool, centred on wind farm location. Note: GWA capacity factor given for 100-m hub height only.
4.Discussion
The two main purposes for wind power modelling using reanalysis products are for: (1) capacity factor estimation, and (2) wind power trace production for use in energy system models.
For capacity factor estimation, the critical accuracy measures are bias and bias spread. In principle, given a narrow bias spread, bias can be readily corrected using linear wind speed scaling. However, there are two limitations with wind speed scaling. The first is that the bias spread of all the reanalyses is high, giving much wider confidence intervals than would normally be required for energy system models. Unless such uncertainty is accounted for in these models, the resulting techno-economic assessments may be unreliable. For example, a simulated capacity factor of 30% using BARRA-R2 that gives a levelised cost of electricity (LCOE) of A$73 MWh–1 would translate to a range of LCOE of A$65–101 MWh–1 for a bias corrected range with ±1 s.d. (LCOE assumptions: capital expenditure, CAPEX, A$1800 kW–1; operational expenditure, OPEX, A$22.0 kW–1 year–1; 25-year project life, 8% discount rate).
The second limitation is that it is not clear what the physical basis of universal wind speed scaling is. In principle, scaling at a local level to account for topography or elevation, for example, may be justified. However, applying a universal scaling factor across an entire region would seem to be undermining the physical basis of reanalyses.
BARRA-R2 exhibited the narrowest bias spread, followed by MERRA-2, then ERA5. Both BARRA-R2 and MERRA-2 biased slightly under (median −7%), whereas ERA5 biased strongly under (median −30%). When used to provide seasonal or annual capacity factor estimates, consideration should be given to confidence intervals. The lower to upper quartiles for BARRA-R2 are −25 to +5%, for MERRA-2 are −25 to +7%, and for ERA5 are −45 to −17%. In relation to MERRA-2 and ERA5, the variance in bias from the present study is broadly consistent with results from regional studies for other regions in the world, e.g. Staffell and Pfenninger (2016); Jourdier (2020); Gruber et al. (2022).
Where possible, calibration with operating wind farms that are sited within the same wind regime (Gunn et al. 2023) should be undertaken to narrow confidence intervals. For estimation of bias confidence intervals, an assumption of normality for BARRA-R2 and MERRA-2 may be appropriate; however, ERA5 bias was found to be likely not normally distributed.
For wind power trace development, the performance at an hourly time interval is important. Critical hourly measures include correlation and rate of change. For all reanalyses, hourly correlation was highly variable. At times, there was substantial disagreement between simulated and observed wind power. Overall, BARRA-R2 exhibited the highest hourly Pearson correlation with median 0.81, followed by ERA5 at 0.76 and MERRA-2 at 0.75. These results are also reflected in RMSE, with BARRA-R2 showing the best performance. Although hourly performance is variable, the correlation for all reanalyses is very high at a monthly and seasonal time interval. Much of the noise that is apparent at short time intervals is ‘washed out’ at longer time intervals, consistent with the capability of the reanalyses to broadly replicate the passage of weather systems. This is consistent with other studies (e.g. Cannon et al. 2015; Staffell and Pfenninger 2016; Gruber et al. 2022) that found that temporal aggregation increased simulation quality.
Based on a preliminary data set, a hypothesis was that correlation was improved at those sites that are at low ground elevation. A cause that was considered was that reanalyses perform better at wind speed estimation in locations without significant topographical detail. In order to test for this, the dataset was tested for linear correlation between elevation and Pearson correlation (see Fig. 12). Although a slight correlation is visually evident on the plot, the R2 for all reanalyses for elevation was no higher than 0.11, demonstrating almost no correlation. Other factors that may be relevant include the type of land cover, vegetation and surface roughness. A related hypothesis was that reanalysis performance may improve over time. However, for those sites with several years of data, no time-dependant trend was observed.
A factor that may have possibly contributed transient errors is the passage of weather fronts. Their passage is often associated with strong winds and a shift in wind direction, and they are known to be associated with sharp increases or decreases in wind power (Pichault et al. 2021). Simmonds et al. (2012) developed a method for identifying cold fronts in the Southern Hemisphere from reanalysis data. They observed that a shift of wind direction from the southwest to the northwest quadrant co-incident with an increase in the meridional wind (v) component greater than 2 m s−1 was predictive of cold fronts. In order to investigate whether detection of frontal activity added information, the error was visually compared with wind direction changes based on 1-h up to 6-h lags. However, no discernible link was found.
Despite exhibiting variable correlation at short time intervals, all reanalyses generally capture wind droughts, defined here as region-wide continuous periods of at least 1 day of wind power output below 10% of capacity. Wind droughts that are co-incident with solar droughts represent the most critical periods from an operational and planning perspective. Owing to lower average insolation, the winter season is the most critical. The depth and duration of wind and solar energy droughts determine the capacity of dispatchable generation and/or electricity storage required to maintain system reliability (Gilmore et al. 2022). Prediction of wind droughts is therefore important from a system perspective. The confidence of wind drought simulation is high.
Analysis in the power domain revealed limitations in the use of reanalyses for wind power trace production. In order to explore these limitations, we identify two factors: (1) the wind speed distribution, and (2) the transfer function that governs the transformation of wind speed into wind turbine power. Wind speeds have been shown to be described by the Weibull distribution, which shows a peak at low wind speeds. The speed-to-power transfer function for wind turbines is typically described by a logistic function, with an extended plateau from the rated speed, up to the cut-out speed. This gives a peak near the rated power of the wind turbine. Given these two factors, the wind power distribution would be expected to exhibit two peaks – the first due to the wind speed peak at low wind speeds, and the second peak at higher power due to the extended plateau of wind power.
In all simulated results, both peaks in the frequency distribution of wind power were evident, although the magnitude of the higher peak varied across different sites. Notably, the higher peak appeared significantly less frequently than anticipated in the observed power distributions. Additionally, although the simulations often exhibited brief, continuous periods of rated power, it was rare for the observed power to sustain levels at or near rated capacity for extended durations.
This outcome is surprising, particularly in light of the wind speed-to-power transfer function. Notably, 12 out of 54 sites displayed a clearly defined higher peak, whereas the remaining sites did not. This indicates that, at high wind speeds, the modelled wind power does not accurately reflect the observed behaviour. Overall, the performance of BARRA-R2 and MERRA-2 was comparable, whereas ERA5 performed less effectively in this context.
Such behaviour may be related to factors that are important at the scale of a wind farm. One possibility may be that additional turbulence at high wind speeds reduces flow normal to the turbine blades. Associated with this is that high wind speeds are often associated with wind direction changes, requiring active turbine yaw changes. Under such dynamic conditions, wind turbines may be unable to maintain optimal yaw.
Wind turbines are optimised for a range of wind speeds, defined by the class. Approaching the cut-out speed, wind turbines are programmed to either feather to reduce the angle of attack, or to increase the angle of attack until stalling, both of which reduce lift (Burton et al. 2011). Rotor speed is typically regulated to provide a fixed tip speed to wind speed ratio. Although active control occurs in real time, dynamic wind conditions, especially changes in wind direction and turbulence, may reduce power output below that predicted based on steady-state conditions. Assuming a distribution of wind speeds across a wind farm, it is possible, during high average wind conditions as reported by hourly data, that some turbines are operating at or near their cut-out speed. A weakness of reanalyses generally is that wind speed is reported as grid cell averages for an entire geographic grid.
It is noteworthy that wind farm developers undertake detailed onsite measurement at anticipated wind turbine hub heights, often coupled with detailed flow analysis, to determine the optimum location of turbines. Such an approach suggests that variation in wind speeds at a local level is significant. The role of orography is important, owing to increases in wind speed on ridges or escarpments. Such ground surface information lies below the spatial resolution of reanalyses. Interestingly, the micro-scale spatial resolution of the GWA did not improve bias accuracy, and performed worse than uncorrected BARRA-R2 simulated results. In one study using Italy as a case study, Cavaiola et al. (2023) compared a high-resolution downscaled reanalysis based on ERA5 with a machine learning approach using coarser reanalysis wind speed, and found that the machine learning approach outperformed the downscaling approach.
The spatial distribution of wind flows across a wind farm can be partly addressed using computational fluid dynamics (CFD) tools, which enables more detailed estimation of the spatial dynamics of wind flows (Letzgus et al. 2022). However, such modelling is far more detailed and site-specific than practical for the purpose of high-level energy system modelling. Related to this is the role of wake effects, which reduce power below that expected by simulation for wind directions aligned with turbine layout. Wind turbine layout is governed by several factors, the most important of which is to maximise annual output while maintaining a minimum distance between turbines in the prevailing wind direction to prevent any excessive wake effects (Serrano Gonz´alez et al. 2014). As such, wake effects are a source of uncertainty in simulation modelling, and would be expected to lead to overestimation of annual output.
Related to changing wind conditions is the sub-hourly ramp rate. From an electrical system operational perspective, it is more critical to be able to predict ramp rates at shorter time intervals than 1 h. Additionally, ramp-downs are generally more important for system reliability than ramp-ups. Given the limitation of the 1-h time step of the reanalyses, sub-hourly ramp rates could not be determined. Nonetheless, the 1-h performance of all the reanalyses is generally good, with the performance of BARRA-R2 the highest, followed by MERRA-2, then ERA5. In general, the simulations tend to show a peakier and narrower distribution than observed.
One factor that was investigated but determined to be unimportant was the role of turbine inertia in damping the power rate of change. Large wind turbine rotors and blades possess significant inertia when rotating. Blade mass (kg) has been shown to approximate rad2.30, where rad is swept radius (m), giving 8 tonnes for a 50-m swept radius (Veers et al. 2003). The inertia time constant determines the time interval during which a turbine can supply its rated power using only the kinetic energy stored in its rotational mass. The inertia time constant of wind turbines typically ranges between 2 and 6 s (Fernández-Guillamón et al. 2019). Given that this is two orders of magnitude shorter than the temporal resolution of the reanalyses, it was deemed insignificant.
Another factor that may influence bias is the difference between operational and prescribed performance. Wind turbine vendors report the measured power curve according to the requirements of IEC 61400. This is intended to be representative of all turbines of a specific model under steady-state conditions. However, the performance of individual turbines may differ from the prescribed performance owing to several factors. These may include the maintenance schedule, the climatic conditions to which turbines are subjected and age-related degradation. In one study, Staffell and Green (2014) assessed the UK wind farm fleet and found that turbines lose 1.6 ± 0.2% of their output per year. Age-related degradation was not explicitly accounted for in the present study, although the power scaling heuristic, e, should partly account for such degradation.
5.Conclusion
Regional atmospheric reanalyses are a convenient source of wind speed data for wind power modelling. Using desktop modelling tools, reanalyses enable energy researchers or commercial developers to produce capacity factor estimates, or wind power traces, for any location within the reanalysis region. Such traces can serve as important inputs into energy system models and techno-economic assessments. However, reanalyses are known to exhibit significant biases. Such biases and their uncertainty can significantly reduce the validity of energy assessments.
Bias has been widely investigated for the most popular global reanalyses, MERRA-2 and ERA5; however, the Australian-based reanalysis suites BARRA and the newer BARRA2 have not been validated against operating wind farms.
An aim of this study was to validate simulated wind power output using BARRA2 against observed output from operating wind farms – observed wind farm output represents the most reliable baseline in regards to energy system modelling and wind power estimates. Regional-level wind speed estimates can provide high-level estimates of wind power potential; however, many factors interact in complex ways at the scale of a wind farm. Investigation at the scale of a wind farm is one way of exploring and identifying those factors.
We found that all of the reanalyses broadly replicate wind speed patterns associated with the passage of weather systems, as well as replicating seasonal patterns. A notable strength is their capability of reproducing wind droughts. At short time intervals (i.e. 6-hourly, hourly), correlation was highly variable, with at times no correlation between simulated and observed power. Bias, measured as the error between observed and simulated capacity factor, was variable across sites.
Judged by five factors – bias, bias spread, hourly correlation, RMSE and the distribution of hourly change (hourly ramp rates) – BARRA-R2 gave the best results, followed by MERRA2, then ERA5. None of the reanalyses was able to consistently reproduce the observed power distribution of wind farms.
In order to translate bias and uncertainty into cost estimates, we estimated the LCOE for a hypothetical wind farm. Using BARRA-R2 with a simulated capacity factor of 30% and a LCOE of A$72 MWh–1, translates to a cost range of A$65–101 MWh–1 after bias correction with ±1 s.d.
At the level of a wind farm, it is apparent that site-specific factors are contributing to differences between simulated and observed power. These differences are evident in the frequency distribution of wind power and the hourly ramp rates, and are likely related to micro-scale wind behaviour and wind turbine response. It is also evident that some of the difference derives from wind speed error in the reanalyses. In considering their own study, as well as similar studies employing MERRA-2 and ERA5, Staffell and Pfenninger (2016) suggested that at least some of the problem lies in the underlying reanalysis wind speed data. The results presented here similarly suggest that reanalyses can capture wind speed at scales compatible with the reanalysis resolution, but are not able to replicate wind speeds at a spatial and temporal scale that is relevant at the level of a wind farm.
The relative success of machine learning in other studies demonstrates that it is possible to calibrate reanalyses with known data (Cavaiola et al. 2023), and points to the potential for improving simulation quality. A challenge remains as how to estimate, and narrow, the confidence intervals for those sites for which calibration data are not available.
Although reanalysis performance is good at times, we recommend the use of confidence intervals that reflect the degree of uncertainty in wind power simulation, and the degree of confidence required in the energy system model.
Data availability
Input data, code and sample figures for this study are available at Monash University’s data repository (see https://figshare.com/s/ff1dba6f6020dde0049c).
Acknowledgements
The authors thank the Australian Bureau of Meteorology (The Bureau) for permission to use the BARRA2 reanalysis. Thanks to Peter Steinle from The Bureau for valuable comments and feedback. Additionally, we are grateful to the reviewers for their valuable and constructive feedback, which has greatly contributed to improving the manuscript.
Authors contributions
Graham Palmer provided conceptualisation, methodology, software, analysis, and writing and reviewing of the written text. Roger Dargaville, Changlong Wang, Andrew Hoadley and Damon Honnery contributed conceptualisation, methodology, and reviewing of the written text. Chun-Hsu Su provided methodology and reviewing of the written text.
References
Australian Energy Market Operator (2025) The Wholesale Electricity Market Fact Sheet. (AEMO) Available at https://aemo.com.au/en/learn/energy-explained/fact-sheets/the-national-electricity-market-fact-sheet
Archer CL, Jacobson MZ (2003) Spatial and temporal distributions of US winds and wind power at 80 m derived from measurements. Journal of Geophysical Research: Atmospheres 108, 4289.
| Crossref | Google Scholar |
Borsche M, Kaiser-Weiss AK, Undén P, Kaspar F (2015) Methodologies to characterize uncertainties in regional reanalyses. Advances in Science and Research 12, 207-218.
| Crossref | Google Scholar |
Burton T, Jenkins N, Sharpe D, Bossanyi E (2011) Aerodynamics of horizontal axis wind turbines. In ‘Wind Energy Handbook’. (Eds T Burton, N Jenkins, D Sharpe, E Bossanyi) pp. 39–136. (Wiley) 10.1002/9781119992714.ch3
Cannon DJ, Brayshaw DJ, Methven J, Coker PJ, Lenaghan D (2015) Using reanalysis data to quantify extreme wind power generation statistics: a 33 year case study in Great Britain. Renewable Energy 75, 767-778.
| Crossref | Google Scholar |
Cavaiola M, Tuju PE, Ferrari F, Casciaro G, Mazzino A (2023) Ensemble machine learning greatly improves ERA5 skills for wind energy applications. Energy and AI 13, 100269.
| Crossref | Google Scholar |
Cha SH (2007) Comprehensive survey on distance/similarity measures between probability density functions. International Journal of Mathematical Models and Methods in Applied Sciences 1, 300-307.
| Google Scholar |
Christofferson RD, Gillette DA (1987) A simple estimator of the shape factor of the two-parameter Weibull distribution. Journal of Climate and Applied Meteorology 26, 323-325.
| Crossref | Google Scholar |
Cowin E, Wang C, Walsh SD (2023) Assessing predictions of Australian offshore wind energy resources from reanalysis datasets. Energies 16, 3404.
| Crossref | Google Scholar |
Fernández-Guillamón A, Gómez-Lázaro E, Muljadi E, Molina-García A (2019) Power systems with high renewable energy sources: a review of inertia and frequency control strategies over time. Renewable and Sustainable Energy Reviews 115, 109369.
| Crossref | Google Scholar |
Gelaro R, McCarty W, Suárez MJ, Todling R, Molod A, Takacs L, Randles CA, Darmenov A, Bosilovich MG, Reichle R, Wargan K, Coy L, Cullather R, Draper C, Akella S, Buchard V, Conaty A, da Silva AM, Gu W, Kim GK, Koster R, Lucchesi R, Merkova D, Nielsen JE, Partyka G, Pawson S, Putman W, Rienecker M, Schubert SD, Sienkiewicz M, Zhao B (2017) The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). Journal of Climate 30, 5419-5454.
| Crossref | Google Scholar | PubMed |
Gruber K, Regner P, Wehrle S, Zeyringer M, Schmidt J (2022) Towards global validation of wind power simulations: a multi-country assessment of wind power simulation from MERRA-2 and ERA-5 reanalyses bias-corrected with the global wind atlas. Energy 238, 121520.
| Crossref | Google Scholar |
Gunn A, Dargaville R, Jakob C, Mcgregor S (2023) Spatial optimality and temporal variability in Australia’s wind resource. Environmental Research Letters 18, 114048.
| Crossref | Google Scholar |
Hahmann AN, Sile T, Witha B, Davis NN, Dörenkämper M, Ezber Y, Garciá-Bustamante E, González-Rouco JF, Navarro J, Olsen BT, Söderberg S (2020) The making of the New European Wind Atlas – part 1: model sensitivity. Geoscientific Model Development 13, 5053-5078.
| Crossref | Google Scholar |
Hersbach H, Bell B, Berrisford P, Hirahara S, Horányi A, Muñoz-Sabater J, Nicolas J, Peubey C, Radu R, Schepers D, Simmons A, Soci C, Abdalla S, Abellan X, Balsamo G, Bechtold P, Biavati G, Bidlot J, Bonavita M, De Chiara G, Dahlgren P, Dee D, Diamantakis M, Dragani R, Flemming J, Forbes R, Fuentes M, Geer A, Haimberger L, Healy S, Hogan RJ, Hólm E, Janisková M, Keeley S, Laloyaux P, Lopez P, Lupu C, Radnoti G, de Rosnay P, Rozum I, Vamborg F, Villaume S, Thépaut JN (2020) The ERA5 global reanalysis. Quarterly Journal of the Royal Meteorological Society 146, 1999-2049.
| Crossref | Google Scholar |
Hersbach H, Bell B, Berrisford P, Biavati G, Horányi A, Muñoz Sabater J, Nicolas J, Peubey, C, Radu, R, Rozum, I, Schepers, D, Simmons, A, Soci, C, Dee, D, Thépaut, JN (2023) ERA5 hourly data on single levels from 1940 to present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS) [Dataset] doi:10.24381/cds.adbb2d47
International Energy Agency (2021) Net Zero by 2050 – A Roadmap for the Global Energy Sector. Technical Report. (IEA) Available at https://www.iea.org/reports/net-zero-by-2050
Jourdier B (2020) Evaluation of ERA5, MERRA-2, COSMO-REA6, NEWA and AROME to simulate wind power production over France. Advances in Science and Research 17, 63-77.
| Crossref | Google Scholar |
Laslett D, Creagh C, Jennings P (2016) A simple hourly wind power simulation for the southwest region of Western Australia using MERRA data. Renewable Energy 96, 1003-1014.
| Crossref | Google Scholar |
Letzgus P, Guma G, Lutz T (2022) Computational fluid dynamics studies on wind turbine interactions with the turbulent local flow field influenced by complex topography and thermal stratification. Wind Energy Science 7, 1551-1573.
| Crossref | Google Scholar |
Murcia JP, Koivisto MJ, Luzia G, Olsen BT, Hahmann AN, Sørensen PE, Als M (2022) Validation of European-scale simulated wind speed and wind generation time series. Applied Energy 305, 117794.
| Crossref | Google Scholar |
Nefabas KL, Söder L, Mamo M, Olauson J (2021) Modeling of Ethiopian wind power production using ERA5 reanalysis data. Energies 14, 2573.
| Crossref | Google Scholar |
Olauson J (2018) ERA5 : The new champion of wind power modelling? Renewable Energy 126, 322-331.
| Crossref | Google Scholar |
Pichault M, Vincent C, Skidmore G, Monty J (2021) Characterisation of intra-hourly wind power ramps at the wind farm scale and associated processes. Wind Energy Science 6, 131-147.
| Crossref | Google Scholar |
Rienecker M, Suarez M, Gelaro R, Todling R, Bacmeister J, Liu E, Bosilovich M, Schubert S, Takacs L, Kim G, Bloom S (2011) MERRA: NASA’s modern-era retrospective analysis for research and applications. Journal of Climate 24, 3624-3648.
| Crossref | Google Scholar |
Rispler J, Roberts M, Bruce A (2022) A change in the air? The role of offshore wind in Australia’s transition to a 100% renewable grid. Electricity Journal 35, 107190.
| Crossref | Google Scholar |
Serrano González J, Burgos Payán M, Santos JMR, González-Longatt F (2014) A review and recent developments in the optimal wind-turbine micro-siting problem. Renewable and Sustainable Energy Reviews 30, 133-144.
| Crossref | Google Scholar |
Simmonds I, Keay K, Bye JAT (2012) Identification and climatology of Southern Hemisphere mobile fronts in a modern reanalysis. Journal of Climate 25, 1945-1962.
| Crossref | Google Scholar |
Staffell I, Green R (2014) How does wind farm performance decline with age? Renewable Energy 66, 775-786.
| Crossref | Google Scholar |
Staffell I, Pfenninger S (2016) Using bias-corrected reanalysis to simulate current and future wind power output. Energy 114, 1224-1239.
| Crossref | Google Scholar |
Sturt A, Strbac G (2011) Time series modelling of power output for large-scale wind fleets. Wind Energy 14, 953-966.
| Crossref | Google Scholar |
Su CH, Eizenberg N, Steinle P, Jakob D, Fox-Hughes P, White CJ, Rennie S, Franklin C, Dharssi I, Zhu H (2019) BARRA v1.0: the Bureau of Meteorology atmospheric high-resolution regional reanalysis for Australia. Geoscientific Model Development 12, 2049-2068.
| Crossref | Google Scholar |
Veers PS, Ashwill TD, Sutherland HJ, Laird DL, Lobitz DW, Griffin DA, Mandell JF, Mu´sial WD, Jackson K, Zuteck M, Miravete A, Tsai SW, Richmond JL (2003) Trends in the design, manufacture and evaluation of wind turbine blades. Wind Energy 6, 245-259.
| Crossref | Google Scholar |
Villanueva D, Feijóo A (2018) Comparison of logistic functions for modeling wind turbine power curves. Electric Power Systems Research 155, 281-288.
| Crossref | Google Scholar |
Wang C, Dargaville R, Jeppesen M (2018) Power system decarbonisation with Global Energy Interconnection – a case study on the economic viability of international transmission network in Australasia. Global Energy Interconnection 1, 507-519.
| Crossref | Google Scholar |
A1.Wind farms assessed
| Wind farm | Year commenced | Electricity region | Rated (MW) | Wind turbine | Hub height (m) | |
|---|---|---|---|---|---|---|
| Albany | 2001 | SWIS-WA | 21.6 | Enercon E66-1800 | 65 | |
| Ararat | 2017 | NEM-VIC | 240 | GE Energy 3.2-103 | 85 | |
| Badgingarra | 2019 | SWIS-WA | 130 | Siemens SWT-3.6-130 | 85 | |
| Bald Hills | 2015 | NEM-VIC | 106.6 | Senvion MM92-2050 | 85 | |
| Boco Rock | 2015 | NEM-NSW | 113 | GE Energy 1.7-100 | 80 | |
| Bodangora | 2019 | NEM-NSW | 113.2 | GE Energy 3.4-130 | 85 | |
| Canunda | 2005 | NEM-SA | 46 | Vestas V80-2000 | 67 | |
| Capital | 2010 | NEM-NSW | 140 | Suzlon S88-2100 | 80 | |
| Cathedral Rocks | 2007 | NEM-SA | 66 | Vestas V80-2000 | 60 | |
| Cattle Hill | 2020 | NEM-TAS | 153.6 | Goldwind GW140-3000 | 110 | |
| Challicum Hills | 2003 | NEM-VIC | 52 | Neg Micon NM64/1500 | 68 | |
| Cherry Tree | 2020 | NEM-VIC | 57.6 | Vestas V136-3450 | 91 | |
| Collgar | 2011 | SWIS-WA | 206 | Vestas V90-2000 | 80 | |
| Coopers Gap | 2020 | NEM-QLD | 452.9 | GE Energy 3.8-130 | 110 | |
| Crookwell 2 | 2018 | NEM-NSW | 96 | GE Energy 3.4-130 | 95 | |
| Crowlands | 2019 | NEM-VIC | 80 | Senvion MM92-2050 | 100 | |
| Dundonnell 1 | 2020 | NEM-VIC | 168 | Vestas V150-4000 | 114 | |
| Dundonnell 2 | 2020 | NEM-VIC | 46.2 | Vestas V150-4000 | 114 | |
| Dundonnell 3 | 2020 | NEM-VIC | 121.8 | Vestas V150-4000 | 114 | |
| Granville Harbour | 2020 | NEM-TAS | 111.6 | Vestas V126-3450 | 137 | |
| Gullen Range | 2014 | NEM-NSW | 161 | Goldwind GW100-2500 | 80 | |
| Gunning | 2011 | NEM-NSW | 46.5 | Acciona AW-1500/70 | 80 | |
| Hallett 1 Brown Hill | 2008 | NEM-SA | 94.5 | Suzlon S88-2100 | 80 | |
| Hallett 2 Hallett Hill | 2010 | NEM-SA | 71.4 | Suzlon S88-2100 | 80 | |
| Hallett 4 Nth Brown | 2010 | NEM-SA | 132.3 | Suzlon S88-2100 | 80 | |
| Hallett 5 The Bluff | 2012 | NEM-SA | 52.5 | Suzlon S88-2100 | 80 | |
| Hornsdale Stage 1 | 2017 | NEM-SA | 102.4 | Siemens SWT-3.2-113 | 92 | |
| Hornsdale Stage 2 | 2017 | NEM-SA | 102.4 | Siemens SWT-3.2-113 | 92 | |
| Hornsdale Stage 3 | 2017 | NEM-SA | 112 | Siemens SWT-3.2-113 | 92 | |
| Lake Bonney 1 | 2005 | NEM-SA | 80.5 | Vestas V66-1750 | 67 | |
| Lake Bonney 2 | 2008 | NEM-SA | 159 | Vestas V90-3000 | 80 | |
| Lake Bonney 3 | 2010 | NEM-SA | 39 | Vestas V90-3000 | 80 | |
| Lincoln Gap | 2020 | NEM-SA | 126 | Senvion 3.6M140 EBC | 110 | |
| Mount Gellibrand | 2018 | NEM-VIC | 66 | Goldwind GW82-1500 | 88 | |
| Mount Mercer | 2014 | NEM-VIC | 131.2 | Senvion MM82-2050 | 80 | |
| Mount Millar | 2006 | NEM-SA | 70 | Enercon E70-2000 | 85 | |
| Mumbida | 2013 | SWIS-WA | 55 | GE Energy 2.5xl | 80 | |
| Murra Warra stage 1 | 2020 | NEM-VIC | 225.7 | Senvion 3.7M144 EBC | 139 | |
| Musselroe | 2013 | NEM-TAS | 168 | Vestas V90-3000 | 80 | |
| Oaklands Hill | 2012 | NEM-VIC | 67.2 | Suzlon S88-2100 | 80 | |
| Salt Creek | 2018 | NEM-VIC | 54 | Vestas V126-3450 | 87 | |
| Sapphire | 2018 | NEM-NSW | 270 | Vestas V126-3450 | 137 | |
| Silverton | 2020 | NEM-NSW | 198.9 | GE Energy 3.4-130 | 110 | |
| Snowtown South | 2014 | NEM-SA | 126 | Siemens SWT-3.0-101 | 80 | |
| Snowtown Stage 2 Nth | 2014 | NEM-SA | 144 | Suzlon S88-2100 | 80 | |
| Starfish Hill | 2003 | NEM-SA | 35 | Neg Micon NM64c/1500 | 68 | |
| Taralga | 2015 | NEM-NSW | 106.8 | Vestas V90-2000 | 80 | |
| Waterloo | 2011 | NEM-SA | 131 | Vestas V90-3000 | 90 | |
| Wattle Point | 2005 | NEM-SA | 91 | Vestas V66-1650 | 68 | |
| White Rock Stage 1 | 2018 | NEM-NSW | 172.5 | Goldwind GW121-2500 | 90 | |
| Willogoleche | 2019 | NEM-SA | 119.4 | GE Energy 3.8-130 | 85 | |
| Woodlawn | 2011 | NEM-NSW | 48.3 | Suzlon S88-2100 | 80 | |
| Woolnorth | 2007 | NEM-TAS | 140 | Vestas V90-3000 | 80 | |
| Yaloak South | 2018 | NEM-VIC | 28.7 | Senvion MM92-2050 | 80 | |
| Yandin | 2021 | SWIS-WA | 211.68 | Vestas V150-4000 | 105 |
A2.Wind turbine parameters
| Wind farm | Latitude (°) | Longitude (°) | Elevation above MSL (m) | Distance to coast (km) | |
|---|---|---|---|---|---|
| Albany | −35.065 | 117.798 | 82 | 0 | |
| Ararat | −37.263 | 143.081 | 402 | 137 | |
| Badgingarra | −30.439 | 115.324 | 123 | 25 | |
| Bald Hills | −38.758 | 145.956 | 72 | 5 | |
| Boco Rock | −33.328 | 149.125 | 988 | 80 | |
| Bodangora | −32.407 | 149.041 | 484 | 217 | |
| Capital | −35.167 | 149.517 | 877 | 84 | |
| Cathedral Rocks | −34.848 | 135.593 | 124 | 0 | |
| Cattle Hill | −42.151 | 146.688 | 878 | 90 | |
| Challicum Hills | −37.395 | 143.105 | 264 | 101 | |
| Cherry Tree | −37.100 | 145.267 | 510 | 87 | |
| Collgar | −31.597 | 118.491 | 410 | 290 | |
| Coopers Gap | −26.717 | 151.449 | 667 | 160 | |
| Crookwell 2 | −34.547 | 149.589 | 926 | 125 | |
| Crowlands | −37.167 | 143.165 | 336 | 151 | |
| Dundonnell 1 | −37.863 | 142.944 | 215 | 71 | |
| Dundonnell 2 | −37.863 | 142.944 | 215 | 71 | |
| Dundonnell 3 | −37.863 | 142.944 | 215 | 71 | |
| Granville Harbour | −41.802 | 145.056 | 111 | 2 | |
| Gullen Range | −34.624 | 149.459 | 920 | 127 | |
| Gunning | −34.690 | 149.380 | 709 | 100 | |
| Hallett 1 Brown Hill | −33.328 | 138.705 | 730 | 69 | |
| Hallett 2 Hallett Hill | −33.546 | 138.761 | 730 | 69 | |
| Hornsdale Stage 1 | −33.059 | 138.538 | 610 | 47 | |
| Hornsdale Stage 2 | −33.059 | 138.538 | 610 | 47 | |
| Hornsdale Stage 3 | −33.059 | 138.538 | 610 | 47 | |
| Lake Bonney 1 | −37.760 | 140.392 | 26 | 8 | |
| Lake Bonney 2 | −37.780 | 140.406 | 26 | 8 | |
| Lake Bonney 3 | −37.820 | 140.406 | 26 | 8 | |
| Lincoln Gap | −32.546 | 137.553 | 344 | 149 | |
| Mount Gellibrand | −38.257 | 143.799 | 143 | 36 | |
| Mount Mercer | −37.847 | 143.870 | 342 | 53 | |
| Mount Millar | −33.632 | 136.685 | 356 | 20 | |
| Mumbida | −28.991 | 114.960 | 222 | 14 | |
| Murra Warra stage 1 | −36.438 | 142.246 | 133 | 205 | |
| Musselroe | −40.779 | 147.983 | 28 | 0 | |
| Oaklands Hill | −37.679 | 142.553 | 354 | 75 | |
| Salt Creek | −37.918 | 142.796 | 222 | 14 | |
| Sapphire | −29.710 | 151.446 | 1008 | 161 | |
| Silverton | −31.860 | 141.296 | 304 | 330 | |
| Snowtown South | −33.691 | 138.166 | 333 | 28 | |
| Snowtown Stage 2 Nth | −33.691 | 138.166 | 333 | 28 | |
| Starfish Hill | −35.570 | 138.140 | 155 | 0 | |
| Taralga | −34.425 | 149.860 | 933 | 93 | |
| Waterloo | −33.991 | 138.916 | 565 | 72 |
| Wind turbine model | Rated power (kW) | Cut-in speed (m s−1) | Cut-out speed (m s−1) | Power curve | Modelled class | ||
|---|---|---|---|---|---|---|---|
| vo | b | ||||||
| Acciona AW-1500/70 | 1500 | 4 | 25 | 8.383 | 0.688 | 1/2 | |
| Enercon E66-1800 | 1800 | 3.5 | 25 | 9.395 | 0.696 | 1 | |
| Enercon E70-2000 | 2000 | 2 | 25 | 9.000 | 0.818 | 1 | |
| GE Energy 1.7-100 | 1700 | 3.5 | 23 | 8.410 | 0.819 | 1 | |
| GE Energy 2.5xl | 2500 | 3.5 | 25 | 8.410 | 0.819 | 3 | |
| GE Energy 3.2-103 | 3200 | 3 | 25 | 7.719 | 0.825 | 1/2 | |
| GE Energy 3.4-130 | 3400 | 3 | 25 | 7.830 | 0.770 | 3 | |
| GE Energy 3.6-137 | 3600 | 3 | 25 | 7.830 | 0.770 | 3 | |
| GE Energy 3.8-130 | 3800 | 3 | 25 | 7.830 | 0.770 | 3 | |
| Goldwind GW100-2500 | 2500 | 2.5 | 25 | 8.538 | 0.789 | 3 | |
| Goldwind GW121-2500 | 2500 | 3 | 22 | 7.208 | 0.806 | 3 | |
| Goldwind GW140-3000 | 3000 | 2.5 | 20 | 9.100 | 0.713 | 3 | |
| Goldwind GW82-1500 | 1500 | 3.6 | 25 | 8.383 | 0.688 | 3 | |
| Neg Micon NM64/1500 | 1500 | 5 | 25 | 9.023 | 0.817 | 1 | |
| Neg Micon NM64c/1500 | 1500 | 4.5 | 25 | 9.023 | 0.817 | 1 | |
| Senvion 3.6M140 EBC | 3600 | 2.5 | 21 | 7.256 | 0.950 | 3 | |
| Senvion 3.7M144 EBC | 3700 | 2.5 | 26 | 7.256 | 0.950 | 3 | |
| Senvion MM82-2050 | 2050 | 4 | 22 | 8.589 | 0.702 | 1/2 | |
| Senvion MM92-2050 | 2050 | 3.5 | 22 | 8.212 | 0.710 | 3 | |
| Siemens SWT-3.0-101 | 3000 | 3.5 | 25 | 8.705 | 0.690 | 1/2 | |
| Siemens SWT-3.2-113 | 3200 | 2.5 | 25 | 7.719 | 0.825 | 2/3 | |
| Siemens SWT-3.6-130 | 3600 | 2.5 | 25 | 7.643 | 0.946 | 3 | |
| Suzlon S88-2100 | 2100 | 3.5 | 25 | 8.965 | 0.934 | 2 | |
| Vestas V117-3450 | 3450 | 4 | 25 | 8.718 | 0.828 | 2/3 | |
| Vestas V117-4200 | 4200 | 3 | 25 | 8.718 | 0.828 | 1/2 | |
| Vestas V126-3450 | 3450 | 4.5 | 25 | 8.250 | 0.914 | 3 | |
| Vestas V150-4000 | 4000 | 3 | 22.5 | 7.330 | 0.823 | 3 | |
| Vestas V66-1650 | 1650 | 3.5 | 25 | 9.024 | 0.963 | 1 | |
| Vestas V66-1750 | 1750 | 3.5 | 25 | 9.110 | 0.614 | 1 | |
| Vestas V80-2000 | 2000 | 3.5 | 25 | 8.980 | 0.620 | 1/2 | |
| Vestas V90-2000 | 2000 | 3.5 | 25 | 8.050 | 0.993 | 3 | |
| Vestas V90-3000 | 2000 | 3.5 | 25 | 9.100 | 0.713 | 1 | |
Rated power, cut-in speed and cut-out speed from manufacturers’ data, The Wind Power website (see https://www.thewindpower.net/) and the Open Energy Platform website (see https://openenergyplatform.org/). Power curve parameters vo and b determined from best fit between the continuous function and the piece-wise power curve for the specific wind turbine.
A3.Wind speed distribution
| Wind farm | Scale K | Shape C | |||
|---|---|---|---|---|---|
| Average | s.d. | Average | s.d. | ||
| Albany | 9.05 | 0.34 | 2.3 | 0.1 | |
| Ararat | 7.39 | 0.23 | 2.07 | 0.07 | |
| Badgingarra | 7.75 | 0.12 | 2.59 | 0.1 | |
| Bald Hills | 8.34 | 0.23 | 2.14 | 0.06 | |
| Boco Rock | 6.87 | 0.18 | 2.07 | 0.04 | |
| Bodangora | 7.07 | 0.13 | 2.31 | 0.03 | |
| Canunda | 8.02 | 0.17 | 2.4 | 0.07 | |
| Capital | 7.24 | 0.25 | 1.97 | 0.03 | |
| Cathedral Rocks | 8.36 | 0.18 | 2.41 | 0.09 | |
| Cattle Hill | 13.51 | 0.51 | 2.47 | 0.12 | |
| Challicum Hills | 7.59 | 0.22 | 2.27 | 0.07 | |
| Cherry Tree | 6.42 | 0.24 | 1.82 | 0.05 | |
| Collgar | 6.51 | 2.07 | 2.33 | 0.51 | |
| Coopers Gap | 7.54 | 0.16 | 2.69 | 0.07 | |
| Crookwell 2 | 8.5 | 0.26 | 2.29 | 0.05 | |
| Crowlands | 6.87 | 2.21 | 2.22 | 0.47 | |
| Dundonnell 1 | 7.61 | 2.49 | 2.19 | 0.46 | |
| Dundonnell 2 | 7.61 | 2.49 | 2.19 | 0.46 | |
| Dundonnell 3 | 7.61 | 2.49 | 2.19 | 0.46 | |
| Granville Harbour | 4.83 | 3.79 | 1.39 | 0.39 | |
| Gullen Range | 8.13 | 0.26 | 2.23 | 0.05 | |
| Gunning | 7.77 | 0.27 | 2.13 | 0.05 | |
| Hallett 1 Brown Hill | 7.88 | 0.2 | 2.41 | 0.08 | |
| Hallett 2 Hallett Hill | 7.88 | 0.2 | 2.41 | 0.08 | |
| Hallett 4 North Brown Hill | 7.88 | 0.2 | 2.41 | 0.08 | |
| Hallett 5 The Bluff | 7.88 | 0.2 | 2.41 | 0.08 | |
| Hornsdale Stage 1 | 7.66 | 0.18 | 2.44 | 0.07 | |
| Hornsdale Stage 2 | 7.66 | 0.18 | 2.44 | 0.07 | |
| Hornsdale Stage 3 | 7.66 | 0.18 | 2.44 | 0.07 | |
| Lake Bonney 1 | 8.02 | 0.17 | 2.4 | 0.07 | |
| Lake Bonney 2 | 8.33 | 0.17 | 2.41 | 0.07 | |
| Lake Bonney 3 | 8.33 | 0.17 | 2.41 | 0.07 | |
| Lincoln Gap | 7.38 | 0.19 | 2.17 | 0.07 | |
| Mount Emerald | 6.42 | 0.29 | 2.17 | 0.18 | |
| Mount Gellibrand | 7.46 | 0.21 | 2.07 | 0.06 | |
| Mount Mercer | 8.5 | 0.24 | 2.2 | 0.05 | |
| Mount Millar | 7.68 | 0.2 | 2.21 | 0.09 | |
| Mumbida | 7.65 | 0.13 | 2.54 | 0.09 | |
| Murra Warra stage 1 | 7.43 | 2.42 | 2.4 | 0.53 | |
| Musselroe | 9.43 | 0.46 | 1.96 | 0.08 | |
| Oaklands Hill | 7.1 | 2.3 | 2.19 | 0.45 | |
| Salt Creek | 8.11 | 0.21 | 2.35 | 0.07 | |
| Sapphire | 7.01 | 2.26 | 2.02 | 0.39 | |
| Silverton | 8.2 | 0.11 | 2.69 | 0.11 | |
| Snowtown South | 6.81 | 0.2 | 2.22 | 0.07 | |
| Snowtown Stage 2 North | 6.81 | 0.2 | 2.22 | 0.07 | |
| Starfish Hill | 7.82 | 0.24 | 2.09 | 0.06 | |
| Taralga | 6.36 | 0.24 | 1.7 | 0.05 | |
| Waterloo | 8.18 | 0.23 | 2.34 | 0.09 | |
| Wattle Point | 8.56 | 0.21 | 2.4 | 0.08 | |
| White Rock Stage 1 | 7.25 | 0.18 | 2.13 | 0.06 | |
| Willogoleche | 8.14 | 0.22 | 2.34 | 0.07 | |
| Woodlawn | 7.7 | 0.28 | 2.03 | 0.05 | |
| Woolnorth | 11.02 | 0.35 | 2.44 | 0.1 | |
| Yaloak South | 8.23 | 0.26 | 1.96 | 0.06 | |
| Yandin | 7.81 | 0.11 | 2.7 | 0.11 | |
Mean and standard deviation across 2014–2021.
A4.Pearson correlation
| Farm | Pearson correlation | |||
|---|---|---|---|---|
| BARRA-R2 | MERRA-2 | ERA5 | ||
| Albany | 0.79 | 0.72 | 0.73 | |
| Ararat | 0.82 | 0.72 | 0.82 | |
| Badgingarra | 0.68 | 0.65 | 0.7 | |
| Bald Hills | 0.89 | 0.84 | 0.9 | |
| Boco Rock | 0.78 | 0.66 | 0.65 | |
| Bodangora | 0.85 | 0.72 | 0.8 | |
| Canunda | 0.88 | 0.73 | 0.9 | |
| Capital | 0.86 | 0.82 | 0.76 | |
| Cathedral Rocks | 0.64 | 0.66 | 0.67 | |
| Challicum Hills | 0.82 | 0.76 | 0.81 | |
| Cherry Tree | 0.65 | 0.71 | 0.75 | |
| Collgar | 0.80 | 0.79 | 0.84 | |
| Coopers Gap | 0.75 | 0.60 | 0.72 | |
| Crookwell 2 | 0.87 | 0.82 | 0.86 | |
| Crowlands | 0.78 | 0.77 | 0.79 | |
| Dundonnell 1 | 0.77 | 0.67 | 0.80 | |
| Dundonnell 2 | 0.84 | 0.74 | 0.87 | |
| Dundonnell 3 | 0.83 | 0.76 | 0.85 | |
| Granville Harbour | 0.91 | 0.87 | 0.91 | |
| Gullen Range | 0.90 | 0.82 | 0.88 | |
| Gunning | 0.75 | 0.76 | 0.76 | |
| Hallett 1 Brown Hill | 0.75 | 0.72 | 0.69 | |
| Hallett 2 Hallett Hill | 0.73 | 0.70 | 0.67 | |
| Hallett 4 North Brown Hill | 0.77 | 0.72 | 0.70 | |
| Hallett 5 The Blu↵ | 0.77 | 0.77 | 0.74 | |
| Hornsdale Stage 1 | 0.81 | 0.74 | 0.75 | |
| Hornsdale Stage 2 | 0.85 | 0.74 | 0.77 | |
| Hornsdale Stage 3 | 0.84 | 0.76 | 0.78 | |
| Lake Bonney 1 | 0.86 | 0.84 | 0.88 | |
| Lake Bonney 2 | 0.86 | 0.84 | 0.88 | |
| Lake Bonney 3 | 0.83 | 0.82 | 0.85 | |
| Lincoln Gap | 0.64 | 0.66 | 0.69 | |
| Mount Gellibrand | 0.78 | 0.63 | 0.71 | |
| Mount Mercer | 0.90 | 0.86 | 0.88 | |
| Mount Millar | 0.75 | 0.74 | 0.74 | |
| Mumbida | 0.76 | 0.76 | 0.81 | |
| Murra Warra stage 1 | 0.66 | 0.61 | 0.65 | |
| Musselroe | 0.90 | 0.73 | 0.89 | |
| Oaklands Hill | 0.82 | 0.66 | 0.77 | |
| Salt Creek | 0.83 | 0.75 | 0.82 | |
| Sapphire | 0.84 | 0.66 | 0.74 | |
| Silverton | 0.74 | 0.68 | 0.77 | |
| Snowtown South | 0.70 | 0.69 | 0.70 | |
| Snowtown Stage 2 North | 0.74 | 0.71 | 0.68 | |
| Starfish Hill | 0.80 | 0.77 | 0.77 | |
| Taralga | 0.79 | 0.64 | 0.84 | |
| Waterloo | 0.79 | 0.75 | 0.76 | |
| Wattle Point | 0.82 | 0.76 | 0.79 | |
| White Rock Stage 1 | 0.84 | 0.64 | 0.81 | |
| Willogoleche | 0.80 | 0.73 | 0.76 | |
| Woodlawn | 0.83 | 0.76 | 0.75 | |
| Woolnorth | 0.89 | 0.84 | 0.9 | |
| Yaloak South | 0.88 | 0.78 | 0.86 | |
| Yandin | 0.72 | 0.69 | 0.75 | |
A5.RSME
| Farm | Root mean square error (RMSE) | |||
|---|---|---|---|---|
| BARRA-R2 | MERRA-2 | ERA5 | ||
| Albany | 0.2 | 0.21 | 0.21 | |
| Ararat | 0.18 | 0.21 | 0.15 | |
| Badgingarra | 0.28 | 0.28 | 0.27 | |
| Bald Hills | 0.16 | 0.2 | 0.15 | |
| Boco Rock | 0.24 | 0.31 | 0.34 | |
| Bodangora | 0.17 | 0.22 | 0.22 | |
| Canunda | 0.14 | 0.25 | 0.13 | |
| Capital | 0.18 | 0.2 | 0.26 | |
| Cathedral Rocks | 0.22 | 0.23 | 0.21 | |
| Challicum Hills | 0.18 | 0.2 | 0.19 | |
| Cherry Tree | 0.29 | 0.26 | 0.26 | |
| Collgar | 0.2 | 0.2 | 0.19 | |
| Coopers Gap | 0.2 | 0.23 | 0.21 | |
| Crookwell 2 | 0.18 | 0.19 | 0.16 | |
| Crowlands | 0.2 | 0.21 | 0.2 | |
| Cattle Hill | 0.43 | 0.42 | 0.41 | |
| Dundonnell 1 | 0.22 | 0.23 | 0.17 | |
| Dundonnell 2 | 0.27 | 0.23 | 0.21 | |
| Dundonnell 3 | 0.23 | 0.22 | 0.18 | |
| Granville Harbour | 0.16 | 0.19 | 0.16 | |
| Gullen Range | 0.14 | 0.2 | 0.17 | |
| Gunning | 0.23 | 0.25 | 0.26 | |
| Hallett 1 Brown Hill | 0.24 | 0.25 | 0.29 | |
| Hallett 2 Hallett Hill | 0.25 | 0.26 | 0.3 | |
| Hallett 5 The Blu↵ | 0.21 | 0.22 | 0.24 | |
| Hornsdale Stage 1 | 0.2 | 0.24 | 0.24 | |
| Hornsdale Stage 2 | 0.17 | 0.24 | 0.22 | |
| Hornsdale Stage 3 | 0.17 | 0.23 | 0.2 | |
| Lincoln Gap | 0.29 | 0.29 | 0.26 | |
| Lake Bonney 1 | 0.15 | 0.17 | 0.14 | |
| Lake Bonney 2 | 0.15 | 0.16 | 0.14 | |
| Lake Bonney 3 | 0.17 | 0.17 | 0.16 | |
| Mount Mercer | 0.14 | 0.16 | 0.17 | |
| Mount Gellibrand | 0.31 | 0.41 | 0.37 | |
| Mount Millar | 0.2 | 0.21 | 0.21 | |
| Musselroe | 0.15 | 0.24 | 0.16 | |
| Murra Warra stage 1 | 0.31 | 0.34 | 0.27 | |
| Mumbida | 0.23 | 0.22 | 0.22 | |
| Hallett 4 North Brown Hill | 0.23 | 0.25 | 0.29 | |
| Oaklands Hill | 0.18 | 0.27 | 0.22 | |
| Salt Creek | 0.19 | 0.22 | 0.21 | |
| Sapphire | 0.19 | 0.26 | 0.26 | |
| Snowtown Stage 2 North | 0.26 | 0.24 | 0.29 | |
| Snowtown South | 0.27 | 0.24 | 0.28 | |
| Starfish Hill | 0.18 | 0.2 | 0.2 | |
| Silverton | 0.23 | 0.25 | 0.21 | |
| Taralga | 0.22 | 0.32 | 0.19 | |
| Waterloo | 0.19 | 0.2 | 0.21 | |
| Willogoleche | 0.21 | 0.24 | 0.2 | |
| Woodlawn | 0.21 | 0.25 | 0.28 | |
| Woolnorth | 0.18 | 0.2 | 0.14 | |
| Wattle Point | 0.2 | 0.24 | 0.21 | |
| White Rock Stage 1 | 0.19 | 0.25 | 0.2 | |
| Yandin | 0.24 | 0.27 | 0.22 | |
A6.Capacity factor
| Farm | Capacity factor | ||||
|---|---|---|---|---|---|
| Observed | BARRA2 | MERRA-2 | ERA5 | ||
| Albany | 29.4 | 32 8 | 31.1 | 19.5 | |
| Ararat | 27.8 | 31 8 | 33.0 | 26.6 | |
| Badgingarra | 43.9 | 39 3 | 44.8 | 34.3 | |
| Bald Hills | 37.8 | 39 4 | 29.9 | 38.4 | |
| Boco Rock | 35.4 | 24 5 | 18.0 | 12.5 | |
| Bodangora | 34.7 | 33 0 | 36.6 | 21.5 | |
| Canunda | 30.2 | 29 3 | 15.0 | 28.4 | |
| Capital | 28.5 | 21 5 | 20.8 | 12.5 | |
| Cathedral Rocks | 29.2 | 29 9 | 34.5 | 27.9 | |
| Challicum Hills | 29.7 | 24 2 | 21.8 | 19.5 | |
| Cherry Tree | 35.7 | 25 6 | 28.6 | 21.8 | |
| Collgar | 36.8 | 28 4 | 38.4 | 27.1 | |
| Coopers Gap | 32.1 | 33 3 | 26.2 | 21.5 | |
| Crookwell 2 | 34.7 | 42 8 | 32.0 | 32.0 | |
| Crowlands | 35.7 | 34 3 | 38.5 | 28.2 | |
| Dundonnell 1 | 32.6 | 49 1 | 25.3 | 41.9 | |
| Dundonnell 2 | 36.8 | 49 7 | 25.6 | 42.4 | |
| Dundonnell 3 | 36.9 | 50 4 | 26.0 | 43.0 | |
| Granville Harbour | 41.7 | 38 7 | 43.7 | 33.8 | |
| Gullen Range | 33.2 | 33 4 | 24.5 | 24.1 | |
| Gunning | 38.7 | 31 4 | 26.1 | 23.4 | |
| Hallett 4 North Brown Hill | 36.6 | 26 5 | 28.5 | 18.3 | |
| Hallett 5 The Bluff | 31.1 | 26 8 | 29.1 | 18.4 | |
| Hallett Stage 1 Brown Hill | 35.9 | 26 4 | 28.4 | 18.2 | |
| Hallett Stage 2 Hallett Hill | 36.8 | 25 7 | 27.7 | 17.8 | |
| Hornsdale Stage 1 | 39.7 | 37 4 | 43.2 | 28.8 | |
| Hornsdale Stage 2 | 37.2 | 378 | 43.6 | 29.2 | |
| Hornsdale Stage 3 | 36.2 | 37 4 | 43.1 | 28.8 | |
| Lake Bonney 1 | 27.5 | 29 8 | 30.2 | 28.8 | |
| Lake Bonney 2 | 28.7 | 30 1 | 29.7 | 28.4 | |
| Lake Bonney 3 | 28.9 | 30 1 | 29.7 | 28.4 | |
| Lincoln Gap | 39.5 | 41 3 | 49.5 | 33.5 | |
| Mount Gellibrand | 49.3 | 31 1 | 21.7 | 24.5 | |
| Mount Mercer | 32.2 | 35 1 | 29.9 | 23.9 | |
| Mount Millar | 28.9 | 24 2 | 31.2 | 18.5 | |
| Mumbida | 38.9 | 30 0 | 38.9 | 26.4 | |
| Murra Warra stage 1 | 33.5 | 49 7 | 51.6 | 41.9 | |
| Musselroe | 37.6 | 38 4 | 33.4 | 39.8 | |
| Oaklands Hill | 30.1 | 26 6 | 13.6 | 17.4 | |
| Salt Creek | 34.8 | 35 4 | 33.4 | 22.9 | |
| Sapphire | 33.4 | 35 1 | 32.1 | 18.4 | |
| Silverton | 40.6 | 41 0 | 43.0 | 39.8 | |
| Snowtown South | 37.5 | 22 6 | 32.6 | 18.9 | |
| Snowtown Stage 2 North | 34.0 | 18 8 | 28.9 | 14.8 | |
| Starfish Hill | 28.8 | 24 9 | 32.9 | 18.9 | |
| Taralga | 31.9 | 23 0 | 10.6 | 25.1 | |
| Waterloo | 31.5 | 29 6 | 31.5 | 21.0 | |
| Wattle Point | 32.8 | 33 1 | 36.3 | 24.5 | |
| White Rock Stage 1 | 34.0 | 39 4 | 30.2 | 25.3 | |
| Willogoleche | 34.2 | 40 2 | 41.9 | 30.8 | |
| Woodlawn | 33.8 | 24 6 | 21.3 | 15.4 | |
| Woolnorth | 40.4 | 50 2 | 48.0 | 39.0 | |
| Yaloak South | 34.0 | 38 9 | 37.3 | 26.4 | |
| Yandin | 39.3 | 43 7 | 50.6 | 38.1 | |
| Farm | Capacity factor bias expressed as natural log difference | |||
|---|---|---|---|---|
| BARRA2 | MERRA-2 | ERA5 | ||
| Albany | 0.11 | 0.06 | −0.41 | |
| Ararat | 0.13 | 0.17 | −0.05 | |
| Badgingarra | −0.11 | 0.02 | −0.25 | |
| Bald Hills | 0.04 | −0.23 | 0.02 | |
| Boco Rock | −0.37 | −0.68 | −1.04 | |
| Bodangora | −0.05 | 0.05 | −0.48 | |
| Canunda | −0.03 | −0.70 | −0.06 | |
| Capital | −0.28 | −0.31 | −0.83 | |
| Cathedral Rocks | 0 02 | 0.17 | −0.05 | |
| Challicum Hills | −0.21 | −0.31 | −0.43 | |
| Cherry Tree | −0.33 | −0.22 | −0.50 | |
| Collgar | −0.26 | 0.04 | −0.31 | |
| Coopers Gap | 0.04 | −0.20 | −0.40 | |
| Crookwell 2 | 0.21 | −0.08 | −0.08 | |
| Crowlands | −0.03 | 0.08 | −0.23 | |
| Dundonnell 1 | 0.41 | −0.25 | 0.25 | |
| Dundonnell 2 | 0.30 | −0.36 | 0.14 | |
| Dundonnell 3 | 0.31 | −0.35 | 0.15 | |
| Granville Harbour | −0.08 | 0.04 | −0.21 | |
| Gullen Range | 0.00 | −0.30 | −0.32 | |
| Gunning | −0.21 | −0.39 | −0.50 | |
| Hallett 4 North Brown Hill | −0.32 | −0.25 | −0.70 | |
| Hallett 5 The Blu↵ | −0.15 | −0.06 | −0.52 | |
| Hallett Stage 1 Brown Hill | −0.31 | −0.23 | −0.68 | |
| Hallett Stage 2 Hallett Hill | −0.36 | −0.29 | −0.73 | |
| Hornsdale Stage 1 | −0.06 | 0.09 | −0.32 | |
| Hornsdale Stage 2 | 0.02 | 0.16 | −0.24 | |
| Hornsdale Stage 3 | 0.03 | 0.17 | −0.23 | |
| Lake Bonney 1 | 0.08 | 0.10 | 0.05 | |
| Lake Bonney 2 | 0.05 | 0.04 | −0.01 | |
| Lake Bonney 3 | 0.04 | 0.03 | −0.02 | |
| Lincoln Gap | 0.04 | 0.22 | −0.16 | |
| Mount Gellibrand | −0.46 | −0.82 | −0.70 | |
| Mount Mercer | 0.08 | −0.08 | −0.30 | |
| Mount Millar | −0.18 | 0.08 | −0.45 | |
| Mumbida | −0.26 | 0.00 | −0.39 | |
| Murra Warra stage 1 | 0 39 | 0.43 | 0.22 | |
| Musselroe | 0.02 | −0.12 | 0.06 | |
| Oaklands Hill | −0.12 | −0.80 | −0.55 | |
| Salt Creek | 0.02 | −0.04 | −0.42 | |
| Sapphire | 0.05 | −0.04 | −0.60 | |
| Silverton | 0.01 | 0.06 | −0.02 | |
| Snowtown South | −0.51 | −0.14 | −0.68 | |
| Snowtown Stage 2 North | −0.59 | −0.16 | −0.83 | |
| Starfish Hill | −0.15 | 0.13 | −0.43 | |
| Taralga | −0.33 | −1.10 | −0.24 | |
| Waterloo | −0.06 | 0.00 | −0.4 | |
| Wattle Point | 0.01 | 0.10 | −0.3 | |
| White Rock Stage 1 | 0.15 | −0.12 | −0.29 | |
| Willogoleche | 0.16 | 0.20 | −0.11 | |
| Woodlawn | −0.32 | −0.46 | −0.78 | |
| Woolnorth | 0.22 | 0.17 | −0.04 | |
| Yaloak South | 0.14 | 0.09 | −0.25 | |
| Yandin | 0.11 | 0.25 | −0.03 | |
A7.Log-law extrapolation bias
One potential source of bias in the MERRA-2 and ERA5 reanalyses is the use of log-law extrapolation, which estimates wind speeds at turbine hub heights based on a single reference height in the dataset. To conduct a preliminary investigation, we plotted and performed a linear regression on bias against hub height. The results indicate a slight overestimation bias at higher hub heights across all reanalyses, including BARRA-R2, which does not rely on log-law extrapolation. The R2 is very low, indicating a weak correlation. It should be noted that hub height is also correlated with several factors, especially rated power (higher power turbines require longer blades and taller towers), turbine age (newer turbines tend to be higher power) and the recent increased deployment of Class III turbines, which are more effective in low-wind conditions. Log-law extrapolation might explain some bias, but it is difficult to make any confident conclusions given the wide spread of data points and relatively low sample size. Further detailed analysis would be necessary to disentangle these factors (Fig. A2).
Footnotes
1 A Scopus search using (TITLE-ABS-KEY (BARRA) AND TITLE-ABS-KEY (wind) AND TITLE-ABSKEY (reanalysis)) found six articles, only one of which investigated the use of BARRA reanalysis for energy system modelling. Equivalent Scopus searches with MERRA and ERA5 found 112 and 208 that were energy system-related.
2 In ERA5, instantaneous parameters are valid at the specified time and do not represent averages. However, because they cannot represent variability on shorter time scales, such parameters tend to evolve smoothly (source: https://confluence.ecmwf.int/display/CKB/Model+grid+box+and+time+step).
3 FCAS refers to the market for ancillary services, which are used by the system operator to manage the power system safely, securely and reliably. These services maintain key technical characteristics of the system, including standards for frequency, voltage, network loading and system restart processes.
4 For each generator, AEMO publishes both a maximum capacity and a registered capacity (see https://wattclarity.com.au/articles/2022/09/analyticalchallenge-installedcapacity/).
5 D’Agostino and Pearson’s test is based on the sample kurtosis and skewness. We use Python scipy.stats.normaltest (see https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.normaltest.html).