Climate sensitivity revisited
G. P. AyersA Visiting Scientist Emeritus, Bureau of Meteorology, 700 Collins Street, Docklands, Melbourne, Vic. 3001, Australia. Email: greg.ayers@bom.gov.au
Journal of Southern Hemisphere Earth Systems Science 70(1) 151-159 https://doi.org/10.1071/ES19031
Submitted: 27 November 2018 Accepted: 20 December 2019 Published: 17 September 2020
Journal Compilation © BoM 2020 Open Access CC BY-NC-ND
Abstract
The commonly used energy balance model from Gregory et al. (2002) that underlies many published estimates of Equilibrium Climate Sensitivity (ECS) and Transient Climate Response (TCR) to anthropogenic forcing requires only four parameters for calculation of ECS and three for TCR. Both estimates require a value for the increase in global mean surface air temperature (ΔT) over a period of time, the increment in forcing driving the temperature change over that period (ΔF), and knowledge of the radiative forcing resulting from a doubling in CO2 concentration (F2×CO2). For ECS a value for the associated global heating rate (ΔQ) is also required. Each of these parameters has a best estimate available from the IPCC’s Fifth Assessment Report, but the authors did not provide best estimates for ECS and TCR within the broad uncertainty ranges quoted, 1.5–4.5 K for ECS and 1.0–2.5 K for TCR. Best estimates for ECS and TCR consistent with AR5 best estimates for ΔF and F2×CO2 are provided here. A well-known heuristic model was modified and applied to seven observation-based global temperature datasets to isolate temperature trend due to anthropogenic forcing from confounding effects of variability due to volcanism, cycles in solar irradiance and internal climate variability. The seven estimates of ECS and TCR were remarkably similar despite very large differences in time-base of the datasets analysed, yielding best estimates of 2.36 ± 0.13 K and 1.58 ± 0.09 K respectively at 95% confidence based on the AR5 best estimates for ΔF, F2×CO2 and ΔQ from Wijffels et al. (2016). The ECS and TCR best estimates here are tied to those AR5 and ΔQ best estimates, but can be simply scaled were those best estimate values to be refined in the future.
Keywords: air temperature, anthropogenic forcing, climate change, climate sensitivity, CO2 concentration, energy balance model, equilibrium climate sensitivity, global air temperature, IPCC, transient climate response.
1 Introduction
One of the more researched topics in the climate science literature is that of Equilibrium Climate Sensitivity (ECS). It figures prominently in all Intergovernmental Panel on Climate Change (IPCC) Assessment Reports, with the Fifth Assessment, AR5, defining ECS as: ‘The equilibrium climate sensitivity quantifies the response of the climate system to constant radiative forcing on multi-century time scales. It is defined as the change in global mean surface temperature at equilibrium that is caused by a doubling of the atmospheric CO2 concentration. Equilibrium climate sensitivity is likely in the range 1.5°C to 4.5°C (high confidence)’ (IPCC 2013). A major reason behind the ongoing attention given to ECS is that it has proved very difficult to quantify with certainty, as evidenced in the choice of the AR5 authors not to list a central tendency or best estimate value for ECS, but to list only the broad range of 1.5°C to 4.5°C.
The related variable TCR, or Transient Climate Response, is typically investigated in concert with ECS. As noted by Forster (2016): ‘TCR is defined as how much the world would warm after 70 years of continually increasing CO2 levels (at 1% per year)’. It is also uncertain, but has a narrower uncertainty range than ECS, as summarised in AR5: ‘The transient climate response is likely in the range of 1.0°C to 2.5°C (high confidence)’.
ECS and TCR have both been studied using a variety of methods, frequently based on analysis of climate model simulations, analysis of observational and paleo- temperature records, or a mixture of these and other approaches. One of the most widely used methods is the energy balance method from Gregory et al. (2002). For the planetary system not at steady state in response to ongoing forcing ECS is expressed as:
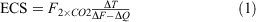
where ΔT is the change in global mean surface temperature over a period of time, ΔF is the increment in forcing driving the change in temperature, ΔQ the observed global heating rate and F2×CO2 the radiative forcing resulting from a doubling in CO2 concentration.
TCR is more simply expressed as it does not require knowledge of global heating rate, ΔQ:

A few of many recent examples from the literature that follow Gregory et al. (2002) by using Eqns 1 and 2 to underpin the diagnosis of ECS and TCR are provided by Otto et al. (2013); Schwartz et al. (2014); Lewis and Curry (2015); Marvel et al. (2016); Richardson et al. (2016) and Armour (2017), whereas Forster (2016) provides a convenient summary of ECS values from more than twenty individual studies. It is evident from all such studies that uncertainty in each of ΔT, ΔF and ΔQ contribute to the broad uncertainties quoted for ECS and TCR. Choice of timescale over which the evaluation is made has a significant bearing on uncertainty (Forster 2016). In this regard Lewis and Curry (2015) among others make the point that choice of timescale/reference period is important to minimise confounding the estimate of ΔT by exogenous factors not related to anthropogenic forcing, such as volcanism, or uncommon extremes in internal climate variability. Frankcombe et al. (2015) explore the question of how to separate forced and unforced variability in considerable detail.
The purpose of this paper is to revisit the estimation of ECS and TCR from observed global mean near-surface temperature series using an empirical analysis aimed at removing confounding effects on ΔT of exogenous factors and internal climate variability so as to return best estimate values for ECS and TCR that are independent of timescale/reference period used. The aim is to provide a central tendency or best estimate value for each variable that is consistent with the likely/high confidence ranges quoted above from the AR5 Working Group 1 report (IPCC 2013).
2 Data and methods
To deduce from observed global mean temperature series a value of ΔT attributable solely to anthropogenic forcing requires removal of the contributions to variability or trend from other exogenous forcings and internal climate variability. To do this a modified version of the widely cited empirical multiple regression analysis method developed and applied to monthly global temperature anomaly series by Lean and Rind (2008) is used. This model has been applied and modified in various ways by others (e.g. Lean and Rind 2009; Lean 2010; Foster and Rahmstorf 2011; Kopp and Lean 2011; Tung and Zhou 2013; Zhou and Tung 2013; Chylek et al. 2014; Santer et al. 2014). It was also utilised in one specific form to illustrate a point in the AR5 WG1 report (see figure 10.6 in IPCC 2013).
The original method models empirically the global temperature anomaly as a linear combination of contributions to temperature variability and trend from variations in El Niño-Southern Oscillation (ENSO), periodic cooling from volcanic eruptions that inject aerosol into the upper atmosphere (VOLC), the small ~11-year regular cycles that occur in total solar irradiance (TSI) and a trend due to net anthropogenic forcing (ANTH, representing greenhouse gas warming modified to some degree by other anthropogenic influences on forcing: short-lived aerosol precursors, aerosol and land-use change effects). Zhou and Tung (2013) and Chylek et al. (2014) found that the model fitted the global temperature anomaly time-series better when the Atlantic Multidecadal Oscillation (AMO) was added as an explanatory variable. Consistent with this Rohde et al. (2013) found that a two parameter regression fit to surface air temperature over land for the period 1753–2011 had a residual strongly resembling the long-term AMO record. Accordingly AMO was added to the model as an additional term, leading to the model used here having the final form:
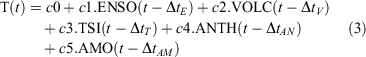
where T is the monthly air temperature anomaly, the explanatory variables are also given as anomalies (reference 1961–1990 average) and c1, c2, c3 and so on are the fitted coefficients; Δt is a time lag in months that was specified for each explanatory variable to maximise the goodness of fit. Here the optimum lags proved to be 2 months for ENSO, 5 months for VOLC and 3 months for TSI, with ANTH and AMO having zero lag. The lags were fixed at these values in all analyses undertaken.
The original model (Lean and Rind 2008) was expanded by Kopp and Lean (2011) to improve variance explained by broadening the explanatory parameter series by having the ENSO component incorporated three times, at different lags (0, 2 and 10 months), and VOLC was included twice with different lags (0 and 10 months). Use of multiple lagged series for any individual independent variable does not add any new degrees of freedom, acting only as a simple smoothing filter. The three ENSO series spanning 10 months lag can be thought of as representing a 10 month running mean but with seven of the ten component values not used. The two VOLC series similarly reflect a 10 month running mean of which only the two end values are used. The effects of these simple smoothing filters are twofold: to introduce (on average) a lag for each variable, and to some degree to filter out parameter variability at sub-10 month scale.
The purpose of the analysis here is to determine ECS and TCR at decadal to century timescales. Thus removal of short-term variability that conceptually can be thought of arising from synoptic scale ‘weather’ processes, rather than weather-averaged ‘climate’ processes, was tested as a means of removing weather ‘noise’ from the climate ‘signal’. Use of a 12 month running mean as an improvement on the multiple lag/simple smoother used by Kopp and Lean (2011) was tested in a recent application of the Lean and Rind model to analysis of lower tropospheric T data covering the warming slowdown period from 1997–2016 (Ayers 2017). The running mean acts as a simple low-pass filter applied to the T series. Comparison of the filtered T series model with the model using unfiltered monthly data showed a significant increase in goodness of fit (r2 increased from 0.71 to 0.89), with no significant change to the numerical values of the independent variable coefficients, confirming that climate ‘signal’ was not removed, just weather ‘noise’. In the present work tests were carried out using a cubic spline and LOESS (Local Polynomial Regression) smoothers as well as the simple 12 month running mean as low pass filter. There was negligible difference in results, with very similar improvements in goodness of fit obtained by each of these methods, thus the simple 12 month running mean as used previously (Ayers 2017) was used in this work.
Following Lean and Rind (2008) a relevant index was adopted for each independent variable. For ENSO the Multivariate ENSO Index (MEI) from NOAA was used. Since that index goes back only to 1871 but two of the T time series analysed here go back to 1850 the index was extended back to 1866 using the UEA Climatic Research Unit SOI (Southern Oscillation Index), and from 1866 back to 1850 was approximated by the annual average paleo-SOI reconstruction from NOAA’s National Climatic Data Center (NCDC) linearly interpolated to provide monthly values. Scaling of SOI to approximate MEI was carried out using overlapping comparison periods for 20 years from 1871. For VOLC the stratospheric aerosol optical thickness series of Sato was used. For TSI the historical annual series produced by Greg Kopp was used, linearly interpolated to monthly values. For ANTH the IPCC’s representative concentration pathways provide a well characterised estimate of historical net anthropogenic forcing up to 2005, and projected forcings under different emissions and control scenarios post-2005. As the projected pathways post-2005 do not diverge significantly until beyond 2020 (van Vuuren et al. 2011; Power et al. 2017) it makes no difference which pathway is used to describe historical forcing and the small extrapolation from 2005 to 2016: here the middle pathway, RCP4.5 was used. The final index employed in this work was the Atlantic Multidecadal Oscillation index (AMO), obtained from NOAA/ESRL back to January 1856, supplemented for the 6 years back to 1850 by the index estimated from the Hadley Centre sea surface temperature (SST) data set. As noted earlier the optimum lags for these explanatory variables, each used only once, were 2 months for ENSO, 5 months for VOLC and 3 months for TSI. The data source locations for all indices used are listed in Tables 1 and 2.

|

|
Seven available global temperature series were subjected to the empirical regression analysis. These seven series consisted of four global mean surface temperature anomaly series: the Hadley Centre’s HadCRUT4 series (Had) and the equivalent series from the Berkeley Earth project (Berk), the US National Climatic Data Center (NCDC) and from Goddard Institute of Space Science (GISS). Additional global temperature anomaly data sets analysed were the Hadley Centre’s HadAT2 radiosonde record (at 850 hPa) spanning 1958–2012, the satellite MSU/AMSU lower tropospheric temperature record from Remote Sensing Systems (RSS) beginning January 1979, and the ERA Interim 1000 hPa level global reanalysis (ERAI) from the European Centre for Medium Range Weather Forecasts, also commencing in 1979. All the data were employed as monthly means. For the analysis, all temperature series were low-pass filtered with a 12 month running mean as discussed above. Of the five explanatory variables used, none of TSI (interpolated from annual means), VOLC or ANTH exhibits significant sub-annual variability, so these variables were used without filtering. ENSO and AMO both have significant power at sub-annual frequencies, so were low-pass filtered as for the air temperature data.
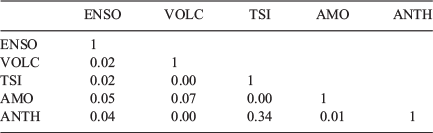
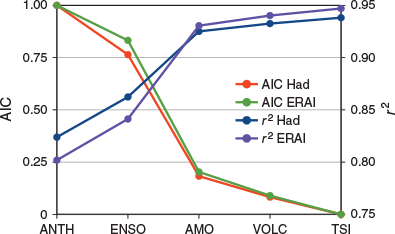
For reassurance that the empirical multiple regression model is well posed it was tested by starting solely with ANTH followed by stepwise addition of the other explanatory variables one at a time. Table 3 confirms the independence of these variables, and Fig. 1 shows the improvement (decrease) in the Akaike Information Criterion (AIC) as each variable was added, and accompanying increase in the regression’s r2 value.
|
|
3 Results
3.1 Regression model outputs
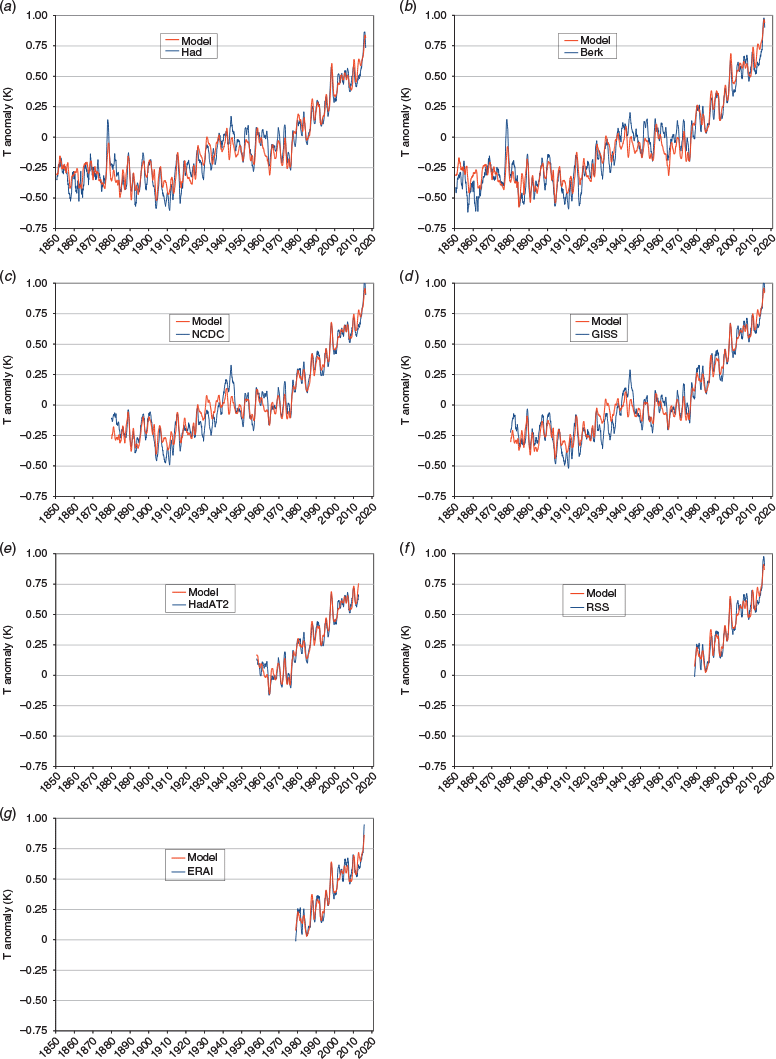
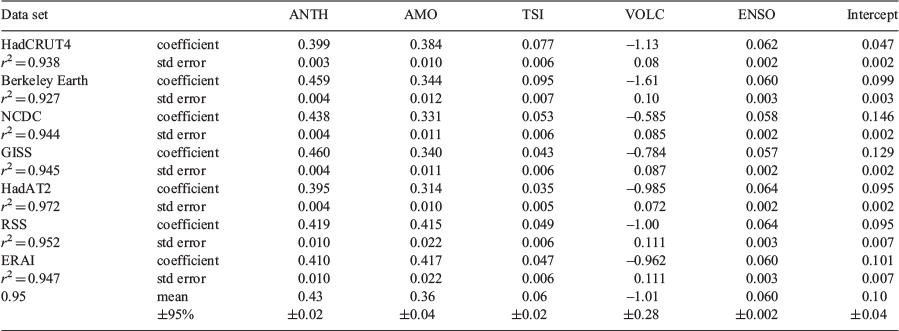
Application of the model to each of the low-pass filtered air T data series yields the regression coefficients listed in Table 4 and the graphical comparisons between the T series and resultant regression models in Fig. 2. It is evident from the table and the figure that the regression model fits the analysed T data series with a high degree of fidelity. The plots in Fig. 2 provide visual confirmation that not only the overall trend and its long-period oscillation but also the bumps and wiggles in the smoothed T records at annual to decadal scale are convincingly reproduced. This heuristic model based on just the five variables listed in Table 1, three reflecting forcing (ANTH, TSI and VOLC) and two reflecting internal climate variability (ENSO, AMO), provides a remarkably good explanation of variability and trend in all the temperature data series analysed at the annual and greater timescales that are the focus here.
|
Not only is each model a very good fit to its particular data set, but the models are highly similar. The two bottom lines in Table 4 give the mean value of each coefficient calculated from the seven regression model results and its 95% confidence interval based on those seven values. The coefficients contributing to each mean are remarkably similar despite the large variability in time base of the various data sets used, from 166 years for Had and Berk to <40 years for RSS and ERAI. The coefficients for ANTH, AMO and ENSO are particularly tightly clustered with 95% confidence intervals for these means only one tenth or less than the mean value itself. These are very consistent results, despite the different types of data analysed ranging from surface network observations, to radiosonde observations, satellite-derived/height-averaged lower troposphere observations and the 1000 hPa ERAI re-analysis product, over a wide variety of time periods.
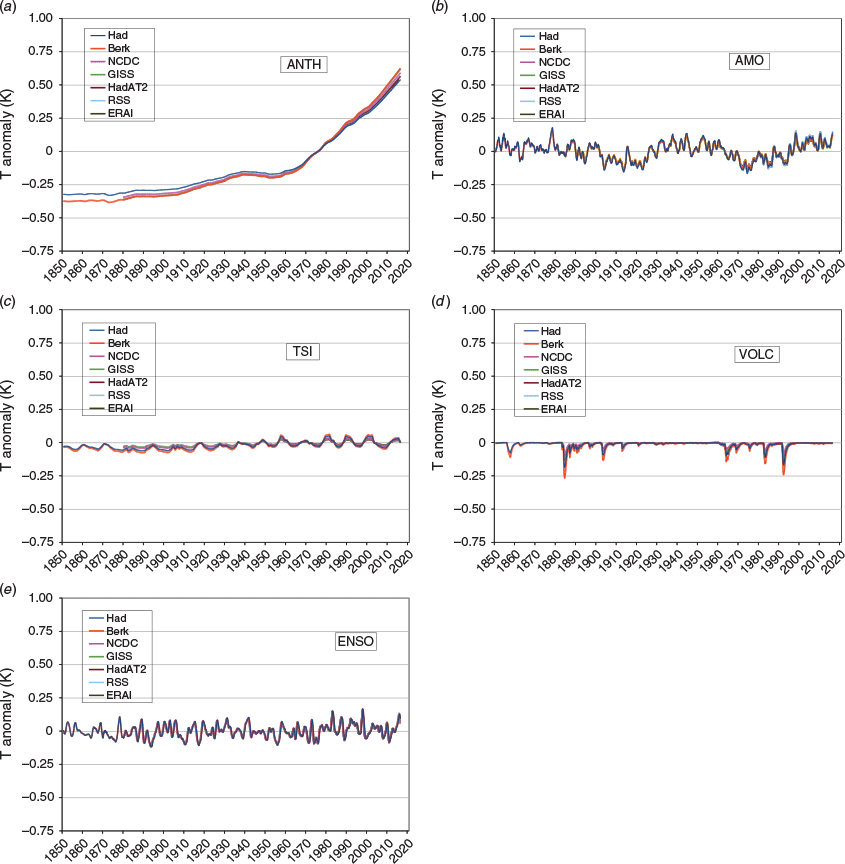
Visual confirmation of the highly consistent regression results is further provided in Fig. 3 where the individual contributions to air T from each of the five explanatory variables are over-plotted for all the analysed temperature series. As noted in the introduction, the objective here was to separate the effects on air temperature of exogenous forcings other than ANTH and of internal climate variability to enable an un-confounded estimation of ΔT caused by anthropogenic forcing, for comparison with that forcing, ΔF. The coefficients in Table 4 and the curves in Fig. 3 show that this objective has been achieved. The second objective of achieving results independent of reference timescale has also been achieved since the highly consistent regression results are independent of the very different timescales of the seven temperature series.
3.2 Estimation of TCR and ECS from observed T series
Consider first the numerically simpler of the two climate response parameters, TCR, which is estimated using Eqn 2. One feature of the heuristic regression model employed here is that for the case with RCP4.5 forcing used for ANTH it obviates the need to estimate ΔT and ΔF separately. The RCP4.5 ANTH coefficient returned by the regression is already what is required by Eqn 2, ΔT/ΔF. Moreover, because the ANTH curve for T has exactly the same time dependence as (it uses functional form of) the anthropogenic forcing curve represented by the RCP4.5 projection from 2005 added to the historical forcing estimated by the IPCC, there is no dependence at all on timeframe within any single T series regression. All that is required for estimation of TCR is multiplication of the RCP4.5 ANTH regression coefficient by F2×CO2, which is given in AR5 as 3.7 W m−2. Resultant values for TCR are given as TCR in Table 5 along with mean and 95% confidence interval calculated for the mean of the seven results.

|
Estimation of ECS from the regressions using RCP4.5 for ANTH using Eqn 1 is almost as straightforward as the TCR estimation. The required values of ΔTRCP were obtained by projecting each ΔT curve from December 2016 back to January 1850 and taking the difference.
As expected from Fig. 2a these ΔTRCP values are tightly clustered. ΔF is similarly defined as the difference between December 2016 and January 1850 values. The final number required is that for ΔQ, the global heating rate. For ΔQ in this work the update by Wijffels et al. (2016) is used. These authors provide an estimate of 0.65–0.8 W m−2, leading to use of the mid-range value of 0.725 W m−2 here for calculation of the ECSRCP values. These are all given in Table 5 along with the 95% confidence on the mean value calculated from the seven separate estimates.
4 Discussion
The objective of this work was to provide best estimates for TCR and ECS that were not provided by the AR5 assessment. Thus the focus here is not on the overall uncertainty in calculation of TCR and ECS, but solely on how to generate the most robust central estimate, within the uncertainty ranges for TCR and ECS given in AR5, 1–2.5 K for TCR and 1.5–4.5 K for ECS. Therefore in using Eqns 1 and 2 to provide consistent best estimates for ECS and TCR the values adopted for F2×CO2 and ΔF are the mean values provided and used in AR5, 3.7 W m−2 for the former, and 2.17 W m−2 for the latter. As noted earlier, the AR5 ΔF value is deduced from the AR5 historical forcing plus RCP4.5 projections post–2005 by subtraction of the January 1850 anthropogenic forcing estimate from the December 2016 anthropogenic forcing estimate.
The data analysis method developed and applied here uses the well-known and widely used energy balance method of Gregory et al. (2002) coupled with a modified version of the heuristic model of Lean and Rind (2008) to extract directly from observed global temperature records a value of ΔT/ΔF for use in Eqn 2. The RCP4.5 ANTH coefficient (ΔT/ΔF) is attributable solely to anthropogenic forcing, free from influences of internal climate variability and episodic variations in solar irradiance and volcanic aerosol forcing that the regression determines separately. Thus neither ΔT nor ΔF needed to be determined separately for the TCR calculation, as this regression method returns that ratio directly because the functional form of the time evolution of temperature is exactly the same as the time dependence of anthropogenic forcing. In taking this approach, the method has the virtue of being independent of the time base used for determining ΔT/ΔF for use in the energy balance model. This is the case not only within the analysis of a single time series but also between series, as shown by the consistency of the seven ANTH regression coefficients in Table 3.
Using Eqn 2 and AR5’s F2×CO2 of 3.7 W m−2 the best estimate for TCR from this analysis is thus a tightly constrained mean value of 1.58 ± 0.09 K from the seven air T series covering different time periods and using different observational methods (Table 5). It sits perfectly within the 1.0–2.5 K ‘high confidence’ range listed by the AR5 authors. Of course the 95% confidence interval of this mean is not the overall uncertainty in TCR, but just that for the mean derived from the seven series analysed. It reflects a remarkably small between-series variability in estimation of ΔT, because the same value of forcing (ΔF) was used in each regression so there is no between-series variability in ΔF contributing to the seven regression results for the ANTH coefficient. The limited variability stems from the ΔT values returned by the regressions, tightly clustered with mean value of 0.93 ± 0.05 K over the period January 1860 to December 2016 (Table 5). It is worth noting also that the ΔT values obtained here, calculated solely for ANTH, with other sources of variability removed, are very closely related to the Global Warming Index (GWI) of Haustein et al. (2017) and have similar values, sitting well within the +0.87 to +1.22 K 95% confidence range quoted.
Overall uncertainty range in TCR determined here therefore rests heavily on the uncertainty in ΔF, not ΔT. The best estimate for ΔF here was taken from the AR5 historical forcing estimate from 1850–2005, projected forward between 2005 and 2016 according to RCP4.5. Uncertainty in anthropogenic forcing in the AR5 assessment and in numerous papers on the literature (e.g. Gregory et al. 2002; Padilla et al. 2011; Otto et al. 2013; Lewis and Curry 2015; Richardson et al. 2016) is treated in considerable detail, is thought to be large, and has resisted attempts at reduction due largely to the ongoing uncertainty in the magnitude of direct and indirect anthropogenic aerosol forcing. In these and other studies (e.g. Marvel et al. 2016; Storelvmo et al. 2016) the variability in TCR estimates and overall uncertainty range in TCR range has not changed much from that given in AR5, quoted earlier as ranging from 1–2.5 K. The method applied here can provide no additional perspective on that issue, or on the uncertainty in F2×CO2. In this work the AR5 value of 3.7 W m−2 is used, but as an example one widely cited alternative estimate for F2×CO2, is that of due to Otto et al. (2013) having the 7% lower value 3.44 W m−2.
What this work does is provide a tightly constrained best estimate for TCR under the specific constraint of the AR5 best estimates for ΔF and F2×CO2. Should these parameters in future be determined more accurately and be different from the AR5 values used here, updating TCR is simply a matter of appropriately scaling the best estimate TCR value provided here. Scaling has been used in other studies in the exploration of climate sensitivity (e.g. Grose et al. 2017).
The result for ECS is analogous. The mean value derived from the seven observation-based T series based on RCP4.5 for ANTH is 2.36 ± 0.13 K. Like the mean TCR value the mean ECS value has low uncertainty associated with it due to the highly consistent values of ΔT produced by the seven regression analyses. Again, this represents an ECS best estimate within the constraints of the F2×CO2 and ΔF best estimates provided by AR5, to which a best estimate for ΔQ was also required. For ΔQ here the recent update of Wijffels et al. (2016) was adopted. These authors list a range of 0.65–0.8 W m−2, leading to the mid-range value of 0.725 W m−2 being used for estimation of ECS using Eqn 1 in this work.
As for TCR, the overall uncertainty range in ECS is much larger than solely for the mean value calculated under the constraint of AR5’s best estimates for F2×CO2 and ΔF, and ΔQ from Wijffels et al. (2016). Uncertainty in ΔQ adds to overall uncertainty. Nonetheless, the best estimate for ECS here, 2.36 ± 0.13 K, like TCR sits very well within the AR5 broad ‘high confidence’ range of 1.5–4.5 K that does reflect the overall uncertainties in F2×CO2, ΔF and ΔQ.
5 Conclusions
The objective here was to provide best estimates for TCR (Transient Climate Response) and ECS (Equilibrium Climate Sensitivity) consistent with the analysis and findings of the IPCC’s Fifth Assessment Report, that were not provided by that Report. The heuristic model of Lean and Rind (2008) based on multiple regression was applied here in modified form to seven observation-based global air temperatures series to extract the temperature response due to anthropogenic forcing, free from confounding effects of episodic volcanic and solar forcing, or effects of variation in two major modes of internal climate variability, AMO and ENSO. IPCC’s estimates of historical anthropogenic forcing to 2005 plus projection forward from 2005 via the RCP4.5 scenario were used to represent time evolution of net anthropogenic forcing. The seven analyses yielded a very tightly constrained set of responses to anthropogenic forcing, averaging 0.43 ± 0.02 K per W m−2. Adopting AR5’s value of 3.7 W m−2 for F2×CO2, the level of radiative forcing resulting from a doubling in CO2 concentration, leads to a mean value of 1.58 ± 0.09 K for TCR, which sits very well within the AR5 ‘high confidence’ range of 1.0–2.5 K.
The analogous calculation for ECS was performed after adopting a best estimate for global heating rate of 0.725 W m−2 from Wijffels et al. (2016), leading to a best estimate for ECS of 2.36 ± 0.13 K, likewise fully consistent with the AR5 ‘high confidence range’ of 1.5–4.5 K.
It is important to emphasise that the 95% confidence intervals shown refer to the uncertainty in the mean calculated under the constraint of having adopted the AR5 best estimate values for F2×CO2 and for anthropogenic forcing, and the Wijffels et al. (2016) central value for global heating rate: any change in those best estimate values will require a proportionate scaling of the best estimate values of 1.58 K and 2.36 K derived here, in order to update TCR and ECS.
Conflicts of interest
The author is Editor in Chief of this journal. He was blinded from the review process and had no editorial involvement with this paper, which was handled independently by other members of the Editorial Board. There are no other conflicts.
Acknowledgements
This research did not receive any specific funding.
References
Armour, K. C. (2017). Energy budget constraints on climate sensitivity in light of inconstant climate feedbacks. Nat. Clim. Change 7, 331–335.| Energy budget constraints on climate sensitivity in light of inconstant climate feedbacks.Crossref | GoogleScholarGoogle Scholar |
Ayers, G. P. (2017). Lower Tropospheric Temperatures 1978–2016: The role played by anthropogenic global warming. J. South. Hemisph. Earth Sys. Sci. 67, 2–11.
| Lower Tropospheric Temperatures 1978–2016: The role played by anthropogenic global warming.Crossref | GoogleScholarGoogle Scholar |
Chylek, P., Klett, J. D., Lesins, G., Dubey, M. K., and Hengartner, N. (2014). The Atlantic Multidecadal Oscillation as a dominant factor of oceanic influence on climate. Geophys. Res. Lett. 41, 1689–1697.
| The Atlantic Multidecadal Oscillation as a dominant factor of oceanic influence on climate.Crossref | GoogleScholarGoogle Scholar |
Forster, P. M. (2016). Inference of climate sensitivity from analysis of Earth’s energy budget. Annu. Rev. Earth Planet. Sci. 44, 85–106.
| Inference of climate sensitivity from analysis of Earth’s energy budget.Crossref | GoogleScholarGoogle Scholar |
Foster, G., and Rahmstorf, S. (2011). Global temperature evolution 1979–2010. Environ. Res. Lett. 6, 044022.
| Global temperature evolution 1979–2010.Crossref | GoogleScholarGoogle Scholar |
Frankcombe, L. M., England, M. H., Mann, M. E., and Steinman, B. A. (2015). Separating internal variability from the externally forced climate response. J. Climate 28, 8184–8202.
| Separating internal variability from the externally forced climate response.Crossref | GoogleScholarGoogle Scholar |
Gregory, J. M., Stouffer, R. J., Raper, S. C. B., Stott, P. A., and Rayner, N. A. (2002). An observationally based estimate of the climate sensitivity. J. Climate 15, 3117–3121.
| An observationally based estimate of the climate sensitivity.Crossref | GoogleScholarGoogle Scholar |
Grose, M. R., Colman, R., Bhend, J., and Moise, A. F. (2017). Limits to global and Australian temperature change this century based on expert judgment of climate sensitivity. Clim. Dyn. 48, 3325–3339.
| Limits to global and Australian temperature change this century based on expert judgment of climate sensitivity.Crossref | GoogleScholarGoogle Scholar |
Haustein, K., Allen, M. R., Forster, P. M., Otto, F. E. L., Mitchell, D. M., Matthews, H. D., and Frame, D. J. (2017). A real-time global warming index. Sci. Rep. 7, 15417.
| A real-time global warming index.Crossref | GoogleScholarGoogle Scholar | 29133863PubMed |
IPCC (2013) Climate change 2013: The physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. (Eds T. F. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S.K. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex and P.M. Midgley). Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 1535 pp.
Kopp, G., and Lean, J. L. (2011). A new, lower value of total solar irradiance: Evidence and climate significance. Geophys. Res. Lett. 38, L01706.
| A new, lower value of total solar irradiance: Evidence and climate significance.Crossref | GoogleScholarGoogle Scholar |
Lean, J. L. (2010). Cycles and trends in solar irradiance and climate. WIREs Clim. Change 1, 111–122.
| Cycles and trends in solar irradiance and climate.Crossref | GoogleScholarGoogle Scholar |
Lean, J. L., and Rind, D. H. (2008). How natural and anthropogenic influences alter global and regional surface temperatures: 1889 to 2006. Geophys. Res. Lett. 35, L18701.
| How natural and anthropogenic influences alter global and regional surface temperatures: 1889 to 2006.Crossref | GoogleScholarGoogle Scholar |
Lean, J. L., and Rind, D. H. (2009). How will Earth’s surface temperature change in future decades? Geophys. Res. Lett. 36, L15708.
| How will Earth’s surface temperature change in future decades?Crossref | GoogleScholarGoogle Scholar |
Lewis, N., and Curry, J. A. (2015). The implications for climate sensitivity of AR5 forcing and heat uptake estimates. Clim. Dyn. 45, 1009–1023.
| The implications for climate sensitivity of AR5 forcing and heat uptake estimates.Crossref | GoogleScholarGoogle Scholar |
Marvel, K., Schmidt, G. A., Miller, R. L., and Nazarenko, L. S. (2016). Implications for climate sensitivity from the response to individual forcings. Nat. Clim. Change 6, 386–389.
| Implications for climate sensitivity from the response to individual forcings.Crossref | GoogleScholarGoogle Scholar |
Otto, A., Otto, F. E., Allen, M. R., Boucher, O., Church, J., Hegerl, G., Forster, P. M., Gillett, N. P., Gregory, J., Johnson, G. C., and Knutti, R. (2013). Energy budget constraints on climate response. Nat. Geosci. 6, 415–416.
| Energy budget constraints on climate response.Crossref | GoogleScholarGoogle Scholar |
Padilla, L. E., Vallis, G. K., and Rowley, C. W. (2011). Probabilistic estimates of transient climate sensitivity subject to uncertainty in forcing and natural variability. J. Climate 24, 5521–5537.
| Probabilistic estimates of transient climate sensitivity subject to uncertainty in forcing and natural variability.Crossref | GoogleScholarGoogle Scholar |
Power, S., Delage, F., Wang, G., Smith, I., and Kociuba, G. (2017). Apparent limitations in the ability of CMIP5 climate models to simulate recent multi-decadal change in surface temperature: implications for global temperature projections. Clim. Dyn. 49, 53–69.
| Apparent limitations in the ability of CMIP5 climate models to simulate recent multi-decadal change in surface temperature: implications for global temperature projections.Crossref | GoogleScholarGoogle Scholar |
Richardson, M., Cowtan, K., Hawkins, E., and Stolpe, M. B. (2016). Reconciled climate response estimates from climate models and the energy budget of Earth. Nat. Clim. Change 6, 931–935.
| Reconciled climate response estimates from climate models and the energy budget of Earth.Crossref | GoogleScholarGoogle Scholar |
Rohde, R., Muller., R. A., Jacobsen, R., Muller, E., Perlmutter, S., et al. (2013). A New Estimate of the Average Earth Surface Land Temperature Spanning 1753 to 2011. Geoinfor. Geostat.: An Overview 1, 1000101.
| A New Estimate of the Average Earth Surface Land Temperature Spanning 1753 to 2011.Crossref | GoogleScholarGoogle Scholar |
Santer, B. D., Bonfils, C., Painter, J. F., Zelinka, M. D., Mears, C., Solomon, S., Schmidt, G. A., Fyfe, J. C., Cole, J. N., Nazarenko, L., and Taylor, K. E. (2014). Volcanic contribution to decadal changes in tropospheric temperature. Nat. Geosci. 7, 85–189.
| Volcanic contribution to decadal changes in tropospheric temperature.Crossref | GoogleScholarGoogle Scholar |
Schwartz, S. E., Charlson, R. J., Kahn, R., and Rodhe, H. (2014). Earth’s climate sensitivity: apparent inconsistencies in recent assessments. Earth’s Future 2, 601–605.
| Earth’s climate sensitivity: apparent inconsistencies in recent assessments.Crossref | GoogleScholarGoogle Scholar |
Storelvmo, T., Leirvik, T., Lohmann, U., Phillips, P. C., and Wild, M. (2016). Disentangling greenhouse warming and aerosol cooling to reveal Earth’s climate sensitivity. Nat. Geosci. 9, 286–289.
| Disentangling greenhouse warming and aerosol cooling to reveal Earth’s climate sensitivity.Crossref | GoogleScholarGoogle Scholar |
Tung, K.-K., and Zhou, J. (2013). Using data to attribute episodes of warming and cooling in instrumental records. PNAS 110, 2058–2063.
| Using data to attribute episodes of warming and cooling in instrumental records.Crossref | GoogleScholarGoogle Scholar | 23345448PubMed |
van Vuuren, D. P., Edmonds, J., Kainuma, M., et al. (2011). The representative concentration pathways: an overview. Clim. Change 109, 5.
| The representative concentration pathways: an overview.Crossref | GoogleScholarGoogle Scholar |
Wijffels, S., Roemmich, D., Monselesan, D., Church, J., and Gilson, J. (2016). Ocean temperatures chronicle the ongoing warming of Earth. Nat. Clim. Change 6, 116.
| Ocean temperatures chronicle the ongoing warming of Earth.Crossref | GoogleScholarGoogle Scholar |
Zhou, J., and Tung, K.-K. (2013). Deducing multidecadal anthropogenic global warming trends using multiple regression analysis. J. Atmos. Sci. 70, 3–8.
| Deducing multidecadal anthropogenic global warming trends using multiple regression analysis.Crossref | GoogleScholarGoogle Scholar |