Phosphorus buffering determines how soil properties and rainfall influence wheat (Triticum aestivum) yield response to phosphorus fertiliser
Craig A. Scanlan A B C * , Raj Malik D , Gustavo Boitt B E , Mark Gherardi F , James Easton E and Zed Rengel B
A B C * , Raj Malik D , Gustavo Boitt B E , Mark Gherardi F , James Easton E and Zed Rengel B
A
B
C
D
E
F
Abstract
Current decision support systems (DSS) for phosphorus (P) fertiliser were developed using data from historical cropping systems. An understanding of how soil properties and rainfall influence wheat (Triticum aestivum) response to P fertiliser in current systems is required to optimise P management.
The aims of this study were to: (1) assess the soil properties that have the greatest influence on relative yield; (2) examine how rainfall conditions influence relative yield; and (3) examine whether there were interactive effects between rainfall and soil properties on relative yield.
Forty P rate-response field experiments were completed in Western Australia. Regression tree modelling, soil test calibration curves and the sliding window approach were used to examine relationships between soil properties or rainfall and relative yield.
Phosphorus buffering index (PBI) was important for determining the factors that influence relative yield. For sites with PBI 0–10 cm <56 (n = 30), regression tree modelling showed rainfall before sowing and soil pHCa were important factors (R2 = 0.59). For sites where PBI >56 (n = 10), relative yield was closely related to plant-available P at 0–10 cm and the r-value for the calibration curve was 0.95.
Rainfall and soil pHCa influence wheat response to P where PBI <56 is attributed to an accumulation of soil P after decades of fertiliser applications and the availability of stored soil P to crops.
Pre-sowing rainfall should be included in DSS so that grain producers can make informed, tactical decisions about P fertiliser applications for wheat at sowing.
Keywords: Colwell P, DGT-P, fertiliser, PBI, phosphorus, rainfall, soil analysis, wheat.
Introduction
Decisions about phosphorus (P) fertiliser application in crop production need to meet multiple objectives. A P fertiliser strategy needs to be designed that: (1) maximises the economic benefit from P application; (2) builds, maintains, or draws down the soil P resource as required; and (3) minimises the potential for negative environmental effects. In some cases, a single strategy will meet all these objectives, while in others the decision maker needs to assess the payoffs between different strategies. Decision support systems (DSS) play an important role in enabling decision makers to identify the optimal strategy for a particular scenario.
Decisions about fertiliser P rate, placement and product for application in grain production are typically guided by DSS. The foundation for most DSS for P fertiliser application is soil testing. It is used to assess the P supply status of the soil and, in combination with empirically-derived models, to predict yield response to P fertiliser application (Jordan-Meille et al. 2012). The predicted yield response is used to identify an economically optimum rate based on grain and fertiliser prices. The DSS tend to be empirical rather than mechanistic and are calibrated with regionally relevant field experiments (e.g. Kuchenbuch and Buczko 2011; Bell et al. 2013; Conyers et al. 2020). These empirical models are well suited to the environments they have been derived from. However, the practical value of these models may decline over time as the cropping systems they are being applied to diverge from the cropping systems they were derived from. The grain-producing region of Western Australia (WA) is an example of where current conditions for P management differ from those when current DSS were developed several decades ago.
Current grain production systems in WA differ from those practised 20 to 60 years ago when the majority of the research on P management in grain production was done (Bell et al. 2013). In that period, there have been significant changes to crop production systems in this region. For example, near-complete long-term adoption of no-tillage sowing systems that band P fertiliser below the seed (Bolland and Brennan 2006; Llewellyn and Ouzman 2019), a shift away from leguminous crops and pastures to more intensive production of wheat (Triticum aestivum), canola (Brassica napus), and barley (Hordeum vulgare) (Seymour et al. 2012; Harries et al. 2021) and a shift towards earlier sowing (Flohr et al. 2018). In addition, there has been an increase in the diversity of soil types and environments used for grain production in comparison to those included in the historical research.
The aim of this study was to gain a comprehensive understanding of how soil properties and rainfall influence wheat yield response to P fertiliser in current cropping systems. For this study, a series of field experiments was conducted throughout the grain-producing region of WA to capture a diversity of the factors mentioned above. The objectives of this study were to: (1) assess the soil and site properties that have the greatest influence on relative yield; (2) examine how rainfall conditions influence relative yield; and (3) examine whether there were interactive effects between rainfall and soil properties on relative yield.
Materials and methods
Field experiments
Forty P rate-response field experiments were completed with the same experimental design. The design included five rates of P fertiliser: 0, 5, 10, 20, and 40 kg P ha−1 (referred to as P0, P5, P10, P20, and P40, respectively) drilled at about 3 cm below the seed as mono-ammonium phosphate (MAP). The field experiments were arranged in randomised complete block design with three or four replicates. The rate of nitrogen (N) applied as urea at sowing was adjusted for each P rate to ensure all plots received 20 kg N ha−1 as fertiliser at sowing. The appropriate amounts of urea (46% N) and MAP were drilled below the seed at sowing together with 35 kg ha−1 potassium sulfate (15 kg potassium (K) ha−1, 6 kg sulfur (S) ha−1).
Agronomic management of the field experiments was consistent with current cropping systems in WA. Wheat (Triticum aestivum L.) cv. Scepter, a commonly grown variety in WA (Shackley et al. 2021), was sown at all sites. Experiments were sown with plot seeders fitted with no-till tines and press wheels. The experiments were sown in fields used for long-term no-till crop production, where the preceding crops were wheat (16 experiments), canola (Brassica napus L.) (13 experiments), barley (Hordeum vulgare L.) (three experiments), lupin (Lupinus angustifolius) (three experiments), pasture (three experiments), and oats (Avena sativa) (two experiments). Only one crop per year is grown in this region. Weed control was achieved by applying mixtures of knockdown and pre-emergent herbicides immediately before sowing (e.g. Harries et al. 2020) and selective herbicides post-sowing as required. The median and interquartile range for sowing date was 18 May, and 11−27 May, respectively, which fall within the window used for sowing wheat by grain producers in WA (Fletcher et al. 2016; Harries et al. 2020). Post-sowing N was surface-applied as urea or urea-ammonium-nitrate at a rate appropriate for each site based on assessments of yield potential and soil N supply. The median and interquartile range for total N application was 72 kg N ha−1 and 62 to 96 kg N ha−1, respectively, similar to the rates regularly applied to cereals in WA (Planfarm 2021). The size of plots sown differed slightly between the two providers managing the experiments. Half of the experiments were sown by CSBP Field Research (https://csbpfertilisers.com/advice/research-and-agronomy/field-research) and plots were 15 m long and 1.89 m wide, at 0.27 m row spacing, and half were sown by Summit Field Research (https://www.summitfertz.com.au/research-agronomy) and were 10 m long and 2.25 m wide at 0.22-m row spacing.
Soil measurements
Soil at the sites were classified according to the Australian Soil Classification (ASC) (Isbell R.F. and the National Committee on Soil and Terrain 2021). The ASC soil orders at the field experiment sites were Tenosols (15 sites), Chromosols (11 sites), Kandosols (11 sites), Calcarosols (two sites), and Kurosols (one site). For a brief description of the soil orders, see Supplementary Table S1.
Soil samples were collected from 0–5, 5–10, 10–15, 15–20, 20–30, 30–40, and 40–60 cm depth by combining five cores at each depth from plots with no fertiliser added in each replicate. Soil samples were dried at 50°C in a forced draught oven and sieved (<2 mm) for soil physical or chemical measurements.
Soil chemical properties were analysed according to Rayment and Lyons (2011). Soil pH (CaCl2) (Method 4A1), Colwell extractable P (Method 9B), P buffering index (PBI) (Method 912C), Colwell extractable K (Method 18A1), KCl-40-extractable S (Method 10D1), oxalate-extractable iron (Ox-Fe) and aluminium (Ox-Al) (Method 13A1), electrical conductivity (EC) (Method 3A1), and organic carbon (OC) (Method 6A1) were measured. Plant-available P using the diffusive gradient in thin films method (DGT-P) (Mason et al. 2010) was also measured.
Particle size analysis of the fine earth fraction (<2 mm) was measured using the pipette method (Indorante et al. 1990). Soil texture was determined using the soil texture wizard package in R (Moeys 2018). Particle size distribution for gravel (≥2 mm) was measured using FAO size classifications (Jahn et al. 2006).
Rainfall measurement
Rainfall data were recorded for each site. At each site, a logging pluviometer (ICT International, Armidale, NSW, Australia) was installed immediately after sowing, and daily rainfall was calculated from each recorded 0.2 mm tip and its associated time period. Complete annual rainfall data for each site were created by merging observed rainfall and the interpolated data from the nearest rainfall station in the SILO database (Jeffrey et al. 2001).
Data transformation and statistical analysis
Data transformation, analysis and visualisation was done in R (R Core Team 2021). Imputation of left-censored values was done using Iterative Robust Model-based Imputation (Kowarik and Templ 2016). Left censored values are those below the reporting threshold for the laboratory used. The threshold used, and percent of samples in the soil data below this were: Colwell P (2 mg kg−1, 4%); Colwell K (15 mg kg−1, 2%); and DGT-P (4 μg L−1, 10%). All the left-censored data were from soil samples below 10 cm depth. Linear and quadratic models were fitted to grouped data with lmList function (Bates et al. 2015). The arcsine-log calibration curve (ALCC) was fitted using the soiltestcorr package (Correndo et al. 2023). Figures were produced using the ggplot2 and ggthemes packages (Wickham 2016; Arnold et al. 2021) in R.
Relative yield (RY) was calculated for each site using the mean values of grain yield for the P treatments. Analysis of variance and comparison of treatment means using least significant difference (5%) showed grain yield was lower at P40 than P20 at five of the 40 sites. To avoid a reduction in yield at P40 compared to P20 leading to an over-estimate of relative yield, the maximum yield from the P treatments was used to calculate RY (%):
Mean values for soil chemical or physical properties were calculated to assess the relationships between crop response and soil test data from different depth intervals (e.g. simulated sampling depths of 0–5, 0–10, 0–20 cm). The depth-weighted mean was calculated based on the depth of the sampling intervals (e.g. Sharpley 2003). The values for soil chemical properties were not adjusted for soil gravel content.
Description of the database
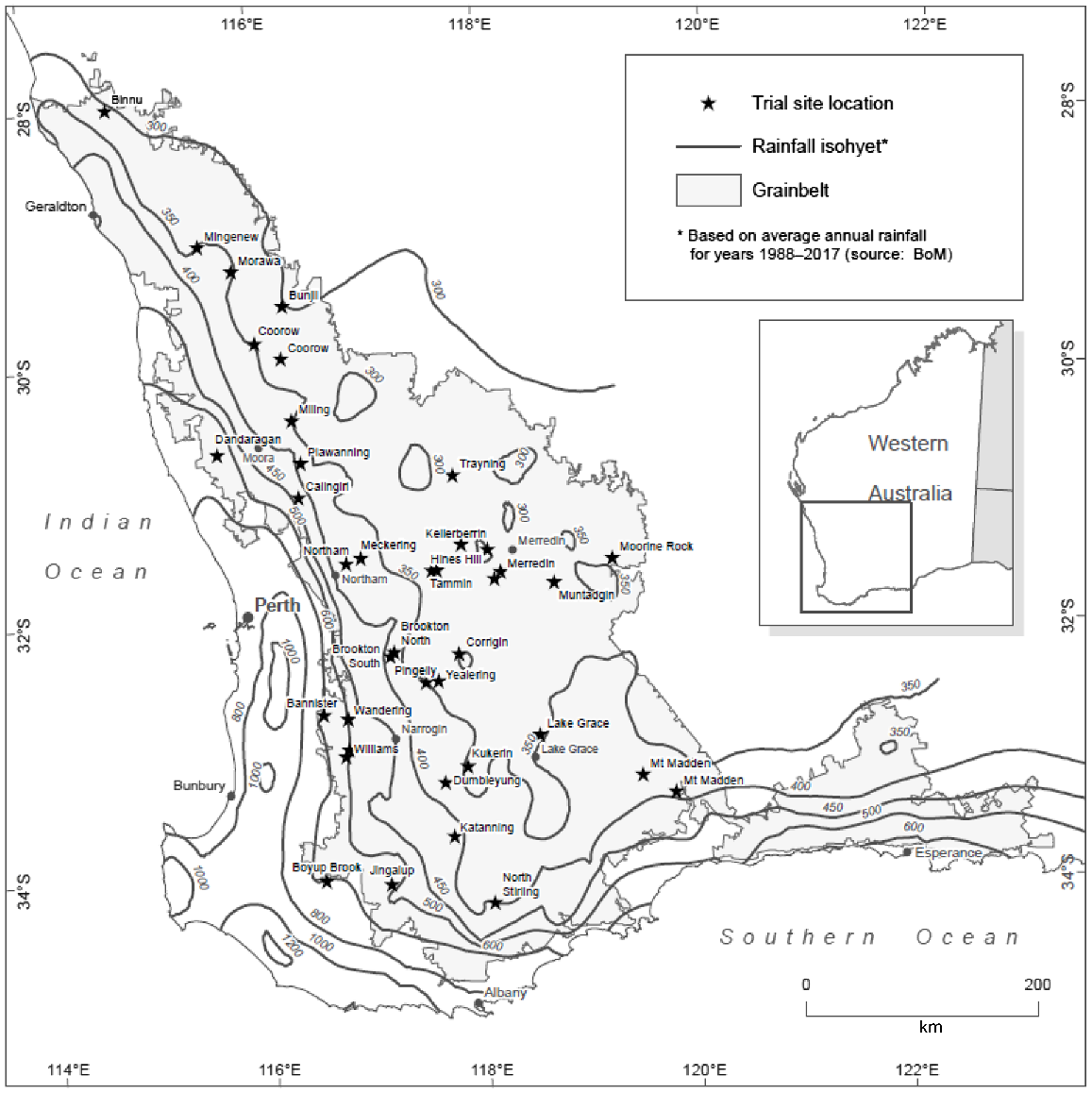
The geographical distribution of the field experiments is in Fig. 1. The sites provided a good geographical representation of the agroecological zones in WA. Median growing season rainfall for the experiment sites across 4 years was 223 mm, and the range was 135 to 496 mm (Fig. S1). The sites also captured the north-south gradient in mean annual temperature (ranging from 15 to 21°C) that is typical for this region (Harries et al. 2021). Summary statistics for site mean grain yield, RY and the absolute yield response (max grain yield – grain yield at P0) are in Fig. S1.
Geographical distribution of the field experiments in the grain-producing region of Western Australia (shaded grey) from 2018 to 2021. Rainfall isohyets are in mm per year, based on rainfall observations from 1988 to 2017 (BoM, Bureau of Meteorology). Trial sites are labelled based on the closest town.
Summary statistics for selected soil properties are in Fig. S2. Median clay content increased as soil depth increased; from 9 to 22% at 0–5 cm and 40–60 cm, respectively. Similarly, median gravel content increased with soil depth, from 4% at 0–5 cm to 20% of soil weight at 40–60 cm. Most of the soil profiles were acidic, with a depth-profile typical for subsurface acidity induced by crop production; pHCa at 10–20 cm was lower than the soil above and below this depth (e.g. Tang and Rengel 2003). Median soil pHCa at 0–5, 10–15, and 40–60 cm was 5.6, 4.9, and 5.7, respectively.
The distribution of PBI values for 0–10 cm in this study was positively skewed, with 38% of values in the Moody (2007) ‘very very low’ category of 15–35. The experimental sites used in this study were representative of the PBI values that occur in this region; the frequency distribution of PBI values is like that from a large-scale survey (Weaver and Wong 2011) of 109,000 samples from 0 to 10 cm in the grain-producing region of WA (Fig. S3). The PBI showed an increasing trend with depth, whereas Ox-Al was more uniformly distributed with depth. The OC, Colwell P and DGT-P were stratified, with the highest values in the surface 10 cm (Fig. S2).
Our preliminary analysis showed that relative yield was not related to sowing date, total nitrogen fertiliser applied (kg N ha−1) and preceding crop, and these variables were not included in the data analysis reported here. Relationships between these variables are in Fig. S4.
Approach to statistical analysis
The steps taken to address our research objectives are described in detail below. In some cases, the results from one step in our analysis was used to guide the analysis in the following step.
Objective 1. Assessment of soil properties that had the greatest influence on relative yield
Investigating whether soil chemical profiles differ between sites clustered by relative yield. Relative yield was separated into three groups with univariate clustering (Wang and Song 2011) to examine whether differences in the soil properties down the profile could be detected between RY groups. A preliminary clustering of RY did not reveal an optimum number, so RY was clustered into three groups (low, medium and high) with mean values of 61, 77, and 91%, respectively. Differences in soil properties for the three RY groups were assessed at each soil depth using analysis of variance (ANOVA) in R.
Investigating interactions between soil properties on relative yield. The interactive effects of soil properties on RY were assessed using regression trees with the Rpart package (Therneau and Atkinson 2019a; 2019b) in R, and trees were pruned to minimise cross-validation error. The regression tree analysis was done at four levels of soil data complexity:
-
all soil chemical and physical data measured for each layer (162 input variables);
-
all soil chemical and physical data measured for 0–10 cm, plus the Australian Soil Classification soil order (24 input variables); and
-
all soil chemical and physical data for 10 cm increments to 40 cm depth, plus the 40–60 cm data (116 input variables).
-
Investigating soil test calibration curves.
-
A quadratic model was fitted to all RY vs soil property data, and the R2 value from the model fitting was used as a criterion to identify soil properties that may be suitable for predicting relative yield.
-
Relationships between soil properties and RY (soil test calibration curve) were analysed using the arcsine-loc calibration curve (ALCC) method (Dyson and Conyers 2013; Correndo et al. 2017) with the soiltestcorr package (Correndo et al. 2023) in R. The ALCC method quantifies the relationship between the transformed soil test and RY data using Pearson’s correlation coefficient (r-value) and calculates the soil test level required for a specified RY target (90% used here). Bootstrapping (n = 1000) was used to provide a more robust estimate of r-value and critical soil test value (CSTV) than would be obtained through calculating a single value only, to allow comparison between calibration curves. The 0.05 and 0.95 quantiles were calculated from the bootstrap samples to provide the 90% confidence intervals (CI), and the 0.5 quantile (median) for these parameters. The r-value was also calculated for different P buffering index (PBI) classes that have been identified for Australian soils (Moody 2007). The use of the ALCC method allowed comparison to previous work relating soil Colwell P to RY (Bell et al. 2013; Conyers et al. 2020). A minimum of eight data points was required to fit the ALCC model (Bolster et al. 2023) when the data were separated into groups based on PBI ranges.
-
The range of PBI values where Colwell P and DGT-P provided the best fit to RY data was assessed for each sampling depth. This analysis was like the sliding window approach (described below) where the range of PBI 0–10 cm values included in a window was varied, and the soil test calibration curve was assessed for each PBI-based window. The array of values used for PBI ranges were calculated as the mid-points of the array of PBI 0–10 cm values from the 40 sites, rounded to the nearest whole number. The lower and upper limits of the PBI range were calculated by rounding the lowest and highest PBI 0–10 cm value down, and up, respectively. For each sampling depth (0–5 cm to 0–60 cm) and PBI 0–10 cm range, the median r value and 90% CI was calculated for the soil test calibration curve where there were at least eight observations. An ascending range (lower value fixed at PBI = 9) and descending PBI range (upper value fixed at PBI = 396) were assessed for Colwell P and DGT-P.
-
Objective 2. Investigation of how climatic conditions influence yield response to P fertiliser
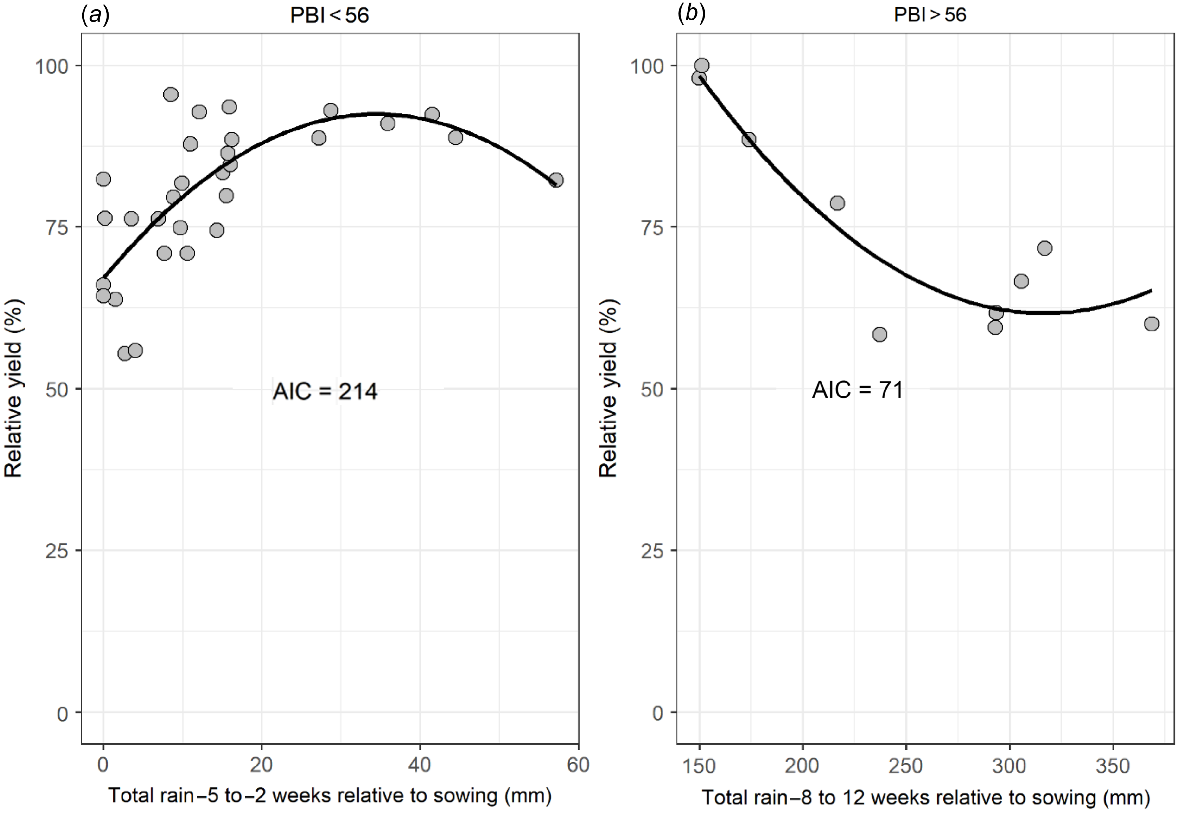
The effect of rainfall on the yield response to P fertiliser was assessed using the sliding window approach (Bailey and van de Pol 2016). The purpose of this approach is to examine whether there are climatic conditions within time-based windows that relate to an observed response. In this study, we analysed relative yield in relation to the total rainfall within time-based windows using a function written in R. The opening time for the windows ranged from −20 weeks to 19 weeks relative to sowing, and the closing time ranged from the opening time from +1 week to 20 weeks after sowing. For example, for the opening time of −2 weeks relative to sowing, windows closing from −1 week to 20 weeks relative to sowing were assessed. The sliding window analysis included fitting linear and quadratic models to all RY-rainfall data, or groups of data based on the PBI threshold identified above (PBI 0–10 cm <56 (PBI <56), PBI 0–10 cm >56 (PBI >56)) for each time-based window. Akaike information criterion (AIC) was used to compare different model fits because it accounts for goodness of fit and the number of model parameters. The model with the lowest AIC is the preferred model.
Objective 3. Examine whether there were interactive effects between rainfall and soil properties on relative yield
Interactive effects between rainfall and soil properties on relative yield were assessed using regression tree modelling. The modelling was done after the analysis described in Objective 2 was completed, where a systematic relationship between rainfall before sowing and relative yield was identified for sites with PBI was <56.
Results
Objective 1. Assessment of the soil and site properties that had the greatest influence on relative yield
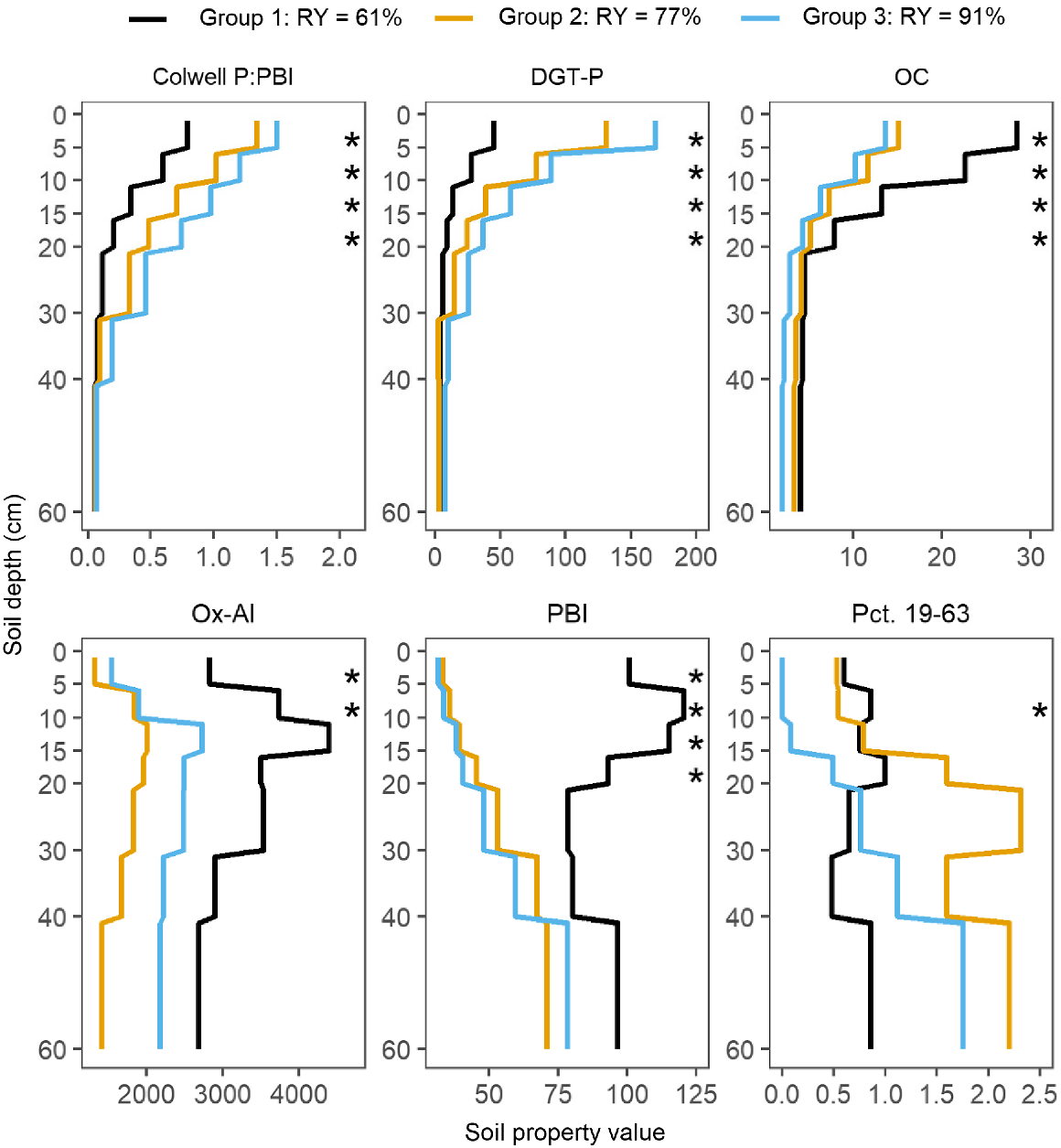
ANOVA of soil properties at each depth revealed that differences between RY groups mostly occurred in the surface 20 cm (Fig. 2). The lowest RY group (Group 1) was associated with the highest PBI, Ox-Al and OC values, the lowest DGT-P and the ratio Colwell P:PBI. The only instance where soil properties for RY Groups 2 and 3 differed was for percent gravel in 19–63 mm fraction at 5 to 10 cm; it was lower in RY group 3 (0%) than Groups 1 and 2 (0.85 and 0.54%, respectively).
Soil chemical profiles for relative yield clusters. Depths where soil properties differed significantly (P < 0.05) between relative yield groups within a depth layer are marked with *. PBI, phosphorus buffering index; Ox-Al, oxalate-extractable Al (mg kg−1); OC, organic carbon (g kg−1). Units for Colwell P and DGT-P are mg kg−1 and μg L−1, respectively. Pct. 19–63, percent gravel (19–63 mm) of whole soil by weight.
Overall, the regression tree models based on soil data provided a poor fit to the RY data (not shown). The best prediction of RY was a regression tree using soil Data Sets 2 (soil data from 0 to 10 cm only) and 3 (soil data in 10 cm increments); R2 was 0.42 for both. The inclusion of data below 10 cm depth in soil Data Set 3 did not influence the regression tree; the trees were the same for soil Data Sets 2 and 3. There was only one split in these trees; where DGT-P 0–10 cm was <36 μg L−1, mean RY was 64%, whereas at DGT-P 0–10 cm values ≥36 μg L−1, mean RY was 83%. The regression trees did not show evidence of interactions between soil chemical or physical properties influencing RY.
An examination of the relationships between RY and soil chemical or physical properties showed closer relationships between soil properties from combined depths than the individual depths. A quadratic model was fitted to all combinations of soil depth and soil property data (not shown here). The better model fits were observed for soil data 0–10 cm for DGT-P, OC or Ox-Extr. Al and relative yield with R2 ranging from 0.19 to 0.22. However, RY was not closely related to any single soil property, so we focussed on combinations of PBI and measurements of plant-available P (Colwell P, DGT-P).
To investigate whether PBI influenced the relationships between RY and Colwell P or DGT-P, the data were analysed based on PBI classes developed for Australian soils by Moody (2007) using the ALCC approach. Our initial analysis (data not shown) indicated insufficient data points (<8) in some of these PBI classes to fit a calibration curve, so the six PBI classes proposed by Moody (2007) were aggregated into two classes; i.e. 0–35 (n = 22) and >35 (n = 18). The median r-values (and 90% CI) for the calibration curve for Colwell P were low for the whole data set (r=−0.07, −0.35–0.2), PBI 0–35 (r = 0.02, −0.39–0.41), and PBI >35 (r=−0.11, −0.43–0.26). The r-values for the calibration curve for DGT-P was highest for PBI >35 (r = 0.63, 0.52–0.83), followed by the whole data set (r = 0.45, 0.23–0.63) and PBI 0–35 (r = 0.34, −0.10–0.68). The PBI classes presented by Moody (2007) were for a national data set and may not be optimal for WA soils; therefore, we investigated how the r-values changed for different PBI ranges.
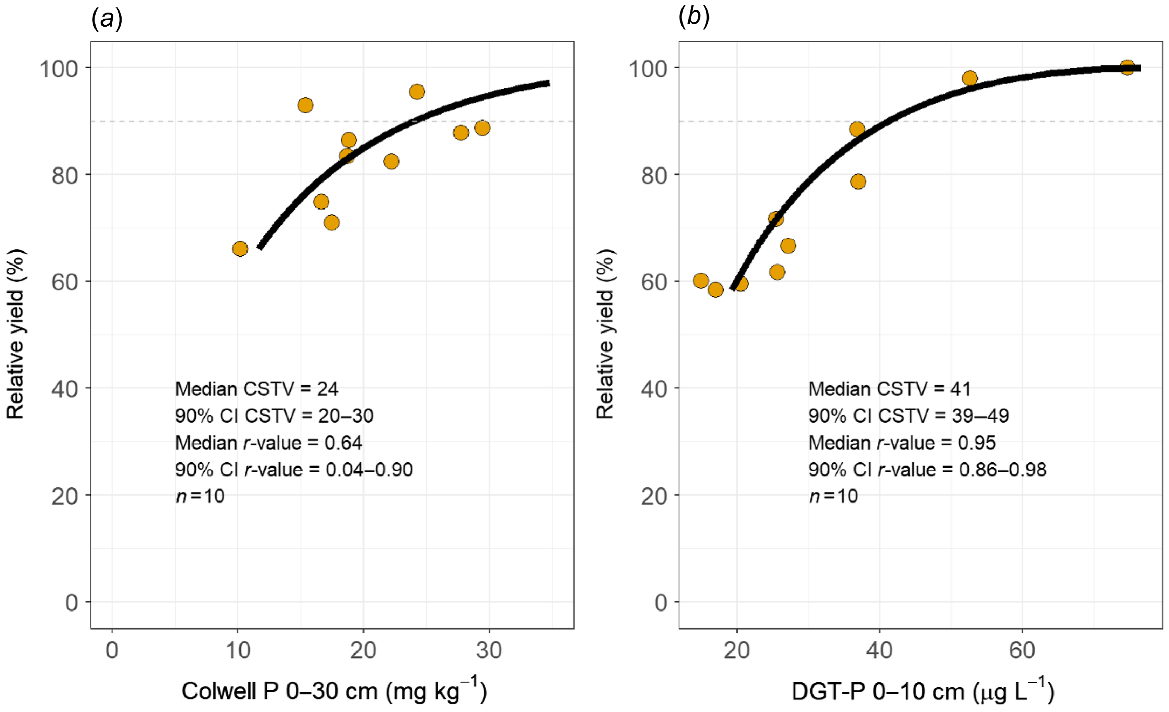
Overall, the goodness of fit for soil test calibration curves was best for DGT-P at the high end of the range of PBI values observed in this study (Figs S5 and S6). For DGT-P, the best calibration was for a sampling depth of 0–10 cm and PBI range 56–396, and the median r-value was 0.95 (90% CI was 0.86–0.98) (Fig. 3). There were seven other combinations of sampling depth and PBI range with a median r-value >0.9, but all had PBI 0–10 cm greater than 56 and sampling depth within 30 cm depth. The goodness of fit of the calibration curve for DGT-P decreased as the range of PBI values increased; for 0–10 cm sampling depth and PBI range 45–396, median r-value was 0.83 (0.65–0.97), and PBI range 40–396 the median r-value was 0.72 (0.48–0.95) and this trend continued as the lower limit of the range of PBI decreased further (Fig. S6). The 90% CI for r-value for a lower limit for PBI of 37 or below did not overlap with that for PBI 56–396. In this dataset, there appears to be a threshold of PBI 56 for DGT-P; relative yield at sites with a PBI below this threshold were not as closely related to DGT-P as those above. The best calibration curve for Colwell P was for a sampling depth of 0–30 cm and a PBI range 9–17 (n = 10), and the median r-value was 0.64 (0.04–0.9) (Fig. 3). There were several calibration curves for Colwell P that had similar r-values as the best calibration curve, but all were for a narrow range of PBI (e.g. 9–17, 9–18 or 9–19) but included a wide range of sampling depths (from 0–20 cm to 0–60 cm). In comparison to DGT-P, the 90% CI for r-values was wider for Colwell P that for DGT-P. Based on the overlap of the 90% CI for r-values for Colwell P for different sampling depths and PBI ranges, we could not clearly identify a best sampling strategy for Colwell P. It is worth noting that the best calibration curves for DGT-P and Colwell P only accounted for 20 sites, and that RY was not closely related to Colwell P or DGT-P at the other 20 sites.
Soil test calibration curves with highest r values identified for Colwell P (a) and DGT-P (b) from the analysis of soil test calibration curves for differing PBI ranges and soil sampling depth. The highest r-value for DGT-P was found for a sampling depth of 0–10 cm and PBI 0–10 cm range 56 to 396. The highest r-value for Colwell P was for a sampling depth of 0–30 cm and PBI 0–10 cm range 9 to 17. The r-values and critical soil test value (CSTV) (for 90% relative yield) were calculated using the arcsine-log calibration curve method. The median and 90% confidence interval (CI) for the calculated parameters are for the bootstrap samples done for these calibration curves.
Objective 2. Investigation of how climatic conditions influence yield response to P fertiliser
The sliding window approach did identify relationships between rainfall and RY, but only when the sites were analysed using the PBI groups identified above. The quadratic models provided a better fit than the linear models, and was used to identify time-based windows with the closest relationship between rainfall and RY. For sites where PBI <56, the best fit was for the window from −5 weeks to −2 weeks relative to sowing (Fig. 4a). For PBI >56, the best fit was for the window from −8 weeks to 12 weeks relative to sowing (Fig. 4b). A matrix plot of AIC values for different combinations of opening and closing times (Fig. S7) shows the best model fits for PBI <56 were for time-based windows that opened in the weeks just before or after sowing, providing some evidence that timing of rainfall is important for RY. Using a threshold of delta AIC ≤5, there were six windows with a similar model fit to the RY-rainfall data from −5 weeks to −2 weeks; the opening values ranged from −5 weeks to −7 weeks, and the closing values ranged from −1 week to 8 weeks relative to sowing (Fig. S7a). For PBI >56, the best fit was for the window from −8 weeks to 12 weeks relative to sowing (Fig. 4b), and there were 25 windows with a similar model fit as weeks from −8 weeks to 12 weeks; the opening values ranged from −13 week to 0 week, and closing values ranged from 3 weeks to 13 weeks relative to sowing (Fig. S7b). For PBI >56, the effect of timing of rainfall was not apparent.
Objective 3. Examine whether there were interactive effects between rainfall, soil properties and relative yield
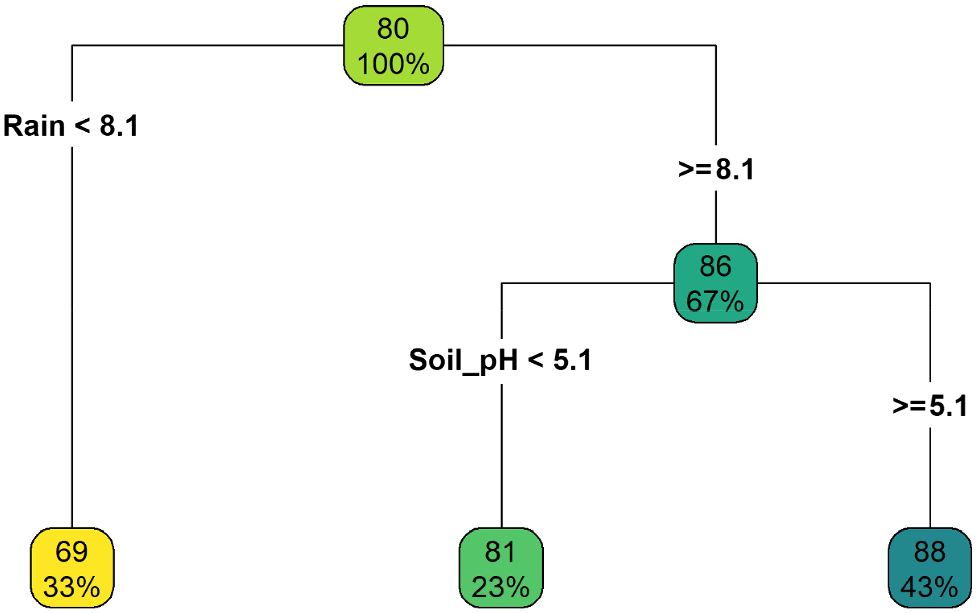
The data for the window from −5 weeks to −2 weeks relative to sowing were analysed further to examine whether soil properties influenced the RY–rainfall relationship. Because our regression tree analysis showed soil properties at 0–10 cm were the most important for predicting RY, we used the data for this depth only. Regression tree analysis was done to examine whether there were interactions between soil properties at 0–10 cm and rainfall from −5 weeks to −2 weeks relative to sowing. The first split was rainfall and the second was pHCa, and the resulting R2 was 0.59 (Fig. 5). There was no relationship between rain in this window and Colwell P 0–10 cm, or Colwell P 0–30 cm (data not shown).
Regression tree for relative yield, based on rain in a time-based window from −5 weeks to −2 weeks relative to sowing for sites where phosphorus buffering index 0–10 cm was <56, and on soil properties 0–10 cm. Values in coloured boxes are the mean values for relative yield and the percentage of observations that fall within that node.
Our analysis of rain, soil and relative yield data for the window from −8 weeks to 12 weeks relative to sowing for the PBI >56 data showed a relationship between rain in this window and DGT-P. The DGT-P decreased from approximately from 50 to 10 μg L−1 as rain during this period increased from 150 mm to 350 mm (data not shown). However, it is unlikely that this is a causal relationship because the window closed from 2 to 3 months after the soil sampling was done, meaning that some, or all the rain occurred after DGT-P was measured.
Discussion
Our analysis of soil, site and climate data has provided a valuable advance in our understanding of the factors influencing relative yield for wheat in current cropping systems in WA. In this study, the governing factor for effects of soil properties and rainfall on wheat response to P fertiliser was PBI. Where PBI was above 56, we identified a soil test calibration curve for DGT-P, and below this threshold, yield response was influenced by rainfall prior to sowing and soil pHCa. The use of a novel approach (sliding window) in agronomic research has allowed the effect of rainfall prior to sowing to be detected. The partitioning of the responses into two groups based on PBI is attributed to the inherent differences in soil properties.
Objective 1. Assessment of the soil properties that had the greatest influence on relative yield
The PBI threshold we identified for determining whether rainfall and soil pHCa, or DGT-P should be used to predict yield response to P ought to be viewed as an indicator, rather than a precise cut-off point. The PBI threshold of 56 was determined empirically by a search for the soil test calibration curve with the highest r-values over a range of soil sampling depths and PBI values in the current study. However, previous work in WA does support the use of a PBI threshold similar to the one we identified; the analysis of soil test calibration data for Colwell P showed that calibration curves above and below a threshold PBI of 55 differed (Neuhaus et al. 2018).
The calibration curve we identified for DGT-P is close to those derived in previous work. The DGT-P value at 90% RY for wheat trials conducted between 1968 and 2008 was 34 μg L−1 (n = 131) for soils other than Calcarosols (Speirs et al. 2013). In the high-rainfall zone of south-east Australia, the DGT-P value at 90% RY for wheat in trials 2015–2018 was 25 μg L−1 (n = 12) (McCaskill et al. 2020). It was 41 μg L−1 in the current study but was derived from 10 sites only (out of 40 included in this study). The critical level for DGT-P from the current study was derived from a data set only slightly above the minimum recommended (n = 8) to derive a calibration curve (Dyson and Conyers 2013). A collation and analysis of a larger set of P response data from current cropping systems from sites with a range of soil P buffering levels, paired with measurements of soil P forms, is required to develop DSS capacity using DGT-P.
Objective 2. Investigation of how climatic conditions influence relative yield
The influence of rainfall prior to sowing on RY detected in this study has been observed previously. In a time of sowing x P rate study in South Australia (Mason and McDonald 2021), RY showed a similar relationship with April rainfall for the first time of sowing (26 April−2 May) to that identified here; there was a threshold of about 15 mm after which RY was higher. However, this relationship was not apparent for the second or third time of sowing, indicating that time of sowing influences crop response to P fertiliser via the relative timing of soil P supply and crop P demand (Conyers et al. 2020; Gherardi et al. 2022). Testing for an interaction between time of sowing and rainfall distribution on RY could not be done in this study since there was only one time of sowing at each site. A better understanding of the interaction between time of sowing (a key management decision for WA grain producers (Fletcher et al. 2016)) and rainfall prior to sowing on relative yield for P is needed to inform tactical P fertiliser decisions at sowing.
The impact of rainfall prior to sowing on relative yield is attributed to a combination of factors. The threshold of 8 mm rainfall in a 4-week period may be linked to a minimum water content for mineralisation of organic phosphorus, or improved germination and early growth. Soil carbon mineralisation was detected at gravimetric soil water content as low as 7% in a silt loam after a 1-week incubation (Qiu et al. 2022); however, this threshold has not been examined in sandy soils. Rainfall prior to sowing may also have an additive effect with rainfall around sowing and crop emergence, leading to higher soil water content and faster emergence (e.g. Rinaldi et al. 2005), better early vigour and greater uptake of soil P (McBeath et al. 2012). However, some caution needs to be applied to the use of the rainfall threshold identified in the regression tree analysis. The mean predictive error for monthly rainfall in the SILO database is in the range of 0–5 mm (Jeffrey et al. 2001), about half of the amount of the identified threshold.
Objective 3. Examine whether there were interactive effects between rainfall and soil properties on yield response to P fertiliser
We did not detect a relationship between Colwell P and RY in the current study, but we did detect an effect of rainfall and soil pHCa. Our inference is that for soils with a history of P build-up through crop fertilisation, the factors that influence the availability of the existing soil P have a greater influence on crop access to soil P than available soil P levels per se.
How do the outcomes of this study relate to the current knowledge?
The outcomes of the current study differ from previous work in WA, which is attributed to a build-up of soil P in soils with ‘extremely low’ to ‘very low’ PBI. Most fields used for crop production in WA have had a positive P balance for decades; surveys of farmer practice have shown that the mean P balance for crops was 2 kg P ha−1 year−1 (NLWRA 2001; Harries et al. 2021). Long-term positive P balances have led to a build-up of soil P (Weaver and Wong 2011). Soil test calibration curves for Colwell P for P response trials completed in WA from 1958 to 994 (187 trials, r-value = 0.65) and from 1995 to 2011 (107 trials, r-value = 0.57) (Bell et al. 2013) were independent of PBI values, whereas in the current study, we obtained them only for soils with PBI (0–30 cm) values of 9–17. The difference in the capacity to identify a soil test calibration curve for Colwell P may be related to the range of Colwell P levels measured. In the study by Bell et al. (2013), a significant proportion of samples had a Colwell P (0–10 cm) value values of <10 mg kg−1, whereas in the current study, the lowest Colwell P (0–10 cm) was 14 mg kg−1. It may also be due to the over-estimation of plant available P using the Colwell method, due to the extraction of non-labile P (Mason et al. 2013), which is of greater significance in the current compared to the historical work due to the accumulation of soil P precipitated to Al, Ca or Fe in soils used for cropping (McLaughlin et al. 2011).
Outlook
The influence of rainfall prior to sowing detected in this study and sowing date in recent work on wheat yield response to P requires a reassessment of how DSS are structured. At present, DSS used for P fertilisation in Australia are structed around the Mitscherlich equation (e.g. Bowden and Bennett 1974), using site details to parameterise the asymptote (rainfall-limited yield) and the yield with nil P applied (rainfall-limited yield × RY). Rainfall in the period before sowing and growing season rainfall varies greatly from year to year in rainfed cropping systems. Future modelling efforts need to be able to account for the variability in rainfall and management factors such as sowing date on yield response to P fertiliser to inform tactical decision making.
Long-term positive P balances and the resulting build-up of soil P introduces another objective into P fertiliser decisions; managing environmental risk. Phosphorus runoff was detected in WA where grain and livestock production were the dominant land uses, with the source of the P runoff attributed to areas where Colwell P was above critical levels (Sharma et al. 2021). Runoff and leaching losses have not been characterised for the grain-producing region in WA, and this knowledge gap needs to be addressed to link to environmental risk indices (e.g. Weaver et al. 2023) that can be incorporated into P fertiliser decisions for crop production.
The presence of ironstone gravels in the landscapes used for grain production in WA (Holmes et al. 2021) has been a source of concern for P management (e.g. Weaver et al. 2022). In some soil types, ironstone gravel can account for 50–60% of soil weight (e.g. Scanlan et al. 2018), potentially reducing the supply of plant-available P. Previous field research in WA has discarded the gravel fraction when preparing soil samples for chemical analysis so it has not been possible to examine how gravel content influences yield response to P fertiliser (Bell et al. 2013; Weaver et al. 2022). In this study, we did not detect a consistent effect of gravel content on crop response to P fertiliser. However, for future work, the inclusion of detailed measurements of gravel content is still justified because of the extent of soils with gravel present; 15% of soils in the 14 M ha used for grain production in WA have a layer of ferric nodules (ironstone gravel) within the top 15 cm of soil (Geographic Information Services 2016; Holmes et al. 2021).
While the current study has provided valuable advances in our understanding of P response in current farming systems, the relatively small size of the data set poses some limitations. Previous studies have utilised data sets of several hundreds to thousands of trial years (Kuchenbuch and Buczko 2011; Bell et al. 2013). It is possible that some important interactions have not been detected in the current study because of insufficient data, or missing measurements, to capture them, for example a wide range of sowing dates; alternatively, the statistical methods used here could not detect subtle interactions. A larger data set would allow more sophisticated statistical techniques to be used to develop models that could form the basis of DSS (Correndo et al. 2021) and allow a more rigorous analysis using the sliding window approach (Van de Pol et al. 2016).
Conclusion
The build-up of soil P in WA cropping soils requires a re-evaluation of DSS for P fertiliser in crop production. Historically, a combination of Colwell P and PBI has been used as the basis for DSS for P fertiliser decisions. However, this combination of soil properties did not relate to the yield responses observed in the current study. Instead, the yield responses observed were related to rainfall and soil pHCa (PBI 0–10 cm <56) or DGT-P at (PBI 0–10 cm >56). At PBI <56, the wheat yield response to P was influenced by rainfall and soil pHCa (factors that determine the availability of soil P over time) rather than by a point-in-time measure of potentially plant-available P, which may be attributed to accumulated soil P. The influence of rainfall requires its inclusion into DSS to allow farmers to account for the effect of rainfall before sowing and make informed, tactical decisions about P fertiliser applications. The accumulation of soil P also requires that DSS include environmental risk indices.
Data availability
The data that support this study will be shared upon reasonable request to the corresponding author.
Conflicts of interest
Zed Rengel is the Editor-in-Chief of Crop and Pasture Science. To mitigate this potential conflict of interest he did not have editor-level access to this paper during peer review. The authors did not have any other conflicts of interest.
Declaration of funding
This research was funded by the GRDC project ‘Increasing profit from N, P and K fertiliser inputs into the evolving cropping sequences in the Western Region’ (UMU1801-006RTX, UWA1801-002RTX).
Acknowledgements
We thank staff at CSBP (Ryan Guthrie and Nichola Cassidy) and Summit (Saritha Marais, Jack Pages-Oliver, and Harley Royce) for managing the field experiments. We also thank staff at DPIRD; Gavin Sarre, Zac Way, and Pete Gray, and to Joel Andrew (MapIQ) for completing the plant and soil sampling and sample preparation for analysis. Thank you to Dr Shahab Pathan (DPIRD) for completing the soil classifications and to Phil Goulding (DPIRD) for producing Fig. 1.
References
Arnold JB, Daroczi G, Werth B (2021) ggthemes: extra themes, scales and geoms for “ggplot2”. R package version 4. Available at https://github.com/jrnold/ggthemes
Bailey LD, van de Pol M (2016) climwin: an R toolbox for climate window analysis. PLoS ONE 11(12), e0167980.
| Crossref | Google Scholar |
Bates D, Mächler M, Bolker B, Walker S (2015) Fitting linear mixed-effects models using lme4. Journal of Statistical Software 67, 1-48.
| Crossref | Google Scholar |
Bell R, Reuter D, Scott B, Sparrow L, Strong W, Chen W (2013) Soil phosphorus-crop response calibration relationships and criteria for winter cereal crops grown in Australia. Crop & Pasture Science 64(5), 480-498.
| Crossref | Google Scholar |
Bolland MDA, Brennan RF (2006) Phosphorus, copper and zinc requirements of no-till wheat crops and methods of collecting soil samples for soil testing. Australian Journal of Experimental Agriculture 46(8), 1051-1059.
| Crossref | Google Scholar |
Bolster CH, Correndo AA, Pearce AW, Spargo JT, Slaton NA, Osmond DL (2023) A spreadsheet for determining critical soil test values using the modified arcsine-log calibration curve. Soil Science Society of America Journal 87(1), 182-189.
| Crossref | Google Scholar |
Conyers M, Bell R, Bell M (2020) Factors influencing the soil-test calibration for Colwell P and wheat under winter-dominant rainfall. Crop & Pasture Science 71(2), 113-118.
| Crossref | Google Scholar |
Correndo AA, Salvagiotti F, García FO, Gutiérrez-Boem FH (2017) A modification of the arcsine–log calibration curve for analysing soil test value–relative yield relationships. Crop & Pasture Science 68(3), 297-304.
| Crossref | Google Scholar |
Correndo AA, Tremblay N, Coulter JA, Ruiz-Diaz D, Franzen D, Nafziger E, Prasad V, Rosso LHM, Steinke K, Du J, Messina CD, Ciampitti IA (2021) Unraveling uncertainty drivers of the maize yield response to nitrogen: a Bayesian and machine learning approach. Agricultural and Forest Meteorology 311, 108668.
| Crossref | Google Scholar |
Correndo AA, Pearce A, Bolster CH, Spargo JT, Osmond D, Ciampitti IA (2023) The soiltestcorr R package: an accessible framework for reproducible correlation analysis of crop yield and soil test data. SoftwareX 21, 101275.
| Crossref | Google Scholar |
Dyson CB, Conyers MK (2013) Methodology for online biometric analysis of soil test-crop response datasets. Crop & Pasture Science 64(5), 435-441.
| Crossref | Google Scholar |
Fletcher A, Lawes R, Weeks C (2016) Crop area increases drive earlier and dry sowing in Western Australia: implications for farming systems. Crop & Pasture Science 67(12), 1268-1280.
| Crossref | Google Scholar |
Flohr BM, Hunt JR, Kirkegaard JA, Evans JR, Trevaskis B, Zwart A, Swan A, Fletcher AL, Rheinheimer B (2018) Fast winter wheat phenology can stabilise flowering date and maximise grain yield in semi-arid Mediterranean and temperate environments. Field Crops Research 223, 12-25.
| Crossref | Google Scholar |
Geographic Information Services (2016) Potentially arable areas in the Western Australian wheatbelt. Department of Primary Industries and Regional Development, Western Australia, Perth. Available at https://library.dpird.wa.gov.au/gis_maps/20/
Harries M, Flower KC, Scanlan CA, Rose MT, Renton M (2020) Interactions between crop sequences, weed populations and herbicide use in Western Australian broadacre farms: findings of a six-year survey. Crop & Pasture Science 71(5), 491-505.
| Crossref | Google Scholar |
Harries M, Flower KC, Scanlan CA (2021) Sustainability of nutrient management in grain production systems of south-west Australia. Crop & Pasture Science 72(3), 197-212.
| Crossref | Google Scholar |
Holmes KW, Griffin EA, van Gool D (2021) Digital soil mapping of coarse fragments in southwest Australia: targeting simple features yields detailed maps. Geoderma 404, 115282.
| Crossref | Google Scholar |
Indorante SJ, Hammer RD, Koenig PG, Follmer LR (1990) Particle-size analysis by a modified pipette procedure. Soil Science Society of America Journal 54(2), 560-563.
| Crossref | Google Scholar |
Jeffrey SJ, Carter JO, Moodie KB, Beswick AR (2001) Using spatial interpolation to construct a comprehensive archive of Australian climate data. Environmental Modelling & Software 16(4), 309-330.
| Crossref | Google Scholar |
Jordan-Meille L, Rubæk GH, Ehlert PAI, Genot EV, Hofman G, Goulding K, Recknagel J, Provolo G, Barraclough P (2012) An overview of fertilizer-P recommendations in Europe: soil testing, calibration and fertilizer recommendations. Soil Use and Management 28(4), 419-435.
| Google Scholar |
Kowarik A, Templ M (2016) Imputation with the R Package VIM. Journal of Statistical Software 74(7), 1-16.
| Crossref | Google Scholar |
Kuchenbuch RO, Buczko U (2011) Re-visiting potassium- and phosphate-fertilizer responses in field experiments and soil-test interpretations by means of data mining. Journal of Plant Nutrition and Soil Science 174(2), 171-185.
| Crossref | Google Scholar |
Mason S, McDonald G (2021) Time of sowing influences wheat responses to applied phosphorus in alkaline calcareous soils in a temperate climate. Crop & Pasture Science 72(11), 861-873.
| Crossref | Google Scholar |
Mason S, McNeill A, McLaughlin MJ, Zhang H (2010) Prediction of wheat response to an application of phosphorus under field conditions using diffusive gradients in thin-films (DGT) and extraction methods. Plant and Soil 337, 243-258.
| Crossref | Google Scholar |
Mason SD, McLaughlin MJ, Johnston C, McNeill A (2013) Soil test measures of available P (Colwell, resin and DGT) compared with plant P uptake using isotope dilution. Plant and Soil 373, 711-722.
| Crossref | Google Scholar |
McBeath TM, McLaughlin MJ, Kirby JK, Armstrong RD (2012) The effect of soil water status on fertiliser, topsoil and subsoil phosphorus utilisation by wheat. Plant and Soil 358, 337-348.
| Crossref | Google Scholar |
McCaskill MR, Riffkin P, Pearce A, Christy B, Norton R, Speirs A, Clough A, Midwood J, Merry A, Suraweera D, Partington D (2020) Soil-test critical values for wheat (Triticum aestivum) and canola (Brassica napus) in the high-rainfall cropping zone of southern Australia. Crop & Pasture Science 71(12), 959-975.
| Crossref | Google Scholar |
McLaughlin MJ, McBeath TM, Smernik R, Stacey SP, Ajiboye B, Guppy C (2011) The chemical nature of P accumulation in agricultural soils—implications for fertiliser management and design: an Australian perspective. Plant and Soil 349, 69-87.
| Crossref | Google Scholar |
Moody PW (2007) Interpretation of a single-point P buffering index for adjusting critical levels of the Colwell soil P test. Soil Research 45(1), 55-62.
| Crossref | Google Scholar |
Qiu W, Curtin D, Hu W, Beare M (2022) Sensitivity of organic matter mineralisation to water availability: role of solute diffusivity and the ‘Birch effect’. Soil Research 61(1), 9-19.
| Crossref | Google Scholar |
Rinaldi M, Paolo ED, Richter GM, Payne RW (2005) Modelling the effect of soil moisture on germination and emergence of wheat and sugar beet with the minimum number of parameters. Annals of Applied Biology 147(1), 69-80.
| Crossref | Google Scholar |
Scanlan CA, Rahmani H, Bowles R, Bennamoun M (2018) Three-dimensional scanning for measurement of bulk density in gravelly soils. Soil Use and Management 34(3), 380-387.
| Crossref | Google Scholar |
Seymour M, Kirkegaard JA, Peoples MB, White PF, French RJ (2012) Break-crop benefits to wheat in Western Australia – insights from over three decades of research. Crop & Pasture Science 63(1), 1-16.
| Crossref | Google Scholar |
Sharma R, Wong MTF, Weaver DM, Bell RW, Ding X, Wang K (2021) Runoff and leaching of dissolved phosphorus in streams from a rainfed mixed cropping and grazing catchment under a Mediterranean climate in Australia. Science of The Total Environment 771, 145371.
| Crossref | Google Scholar | PubMed |
Sharpley A (2003) Soil mixing to decrease surface stratification of phosphorus in manured soils. Journal of Environmental Quality 32(4), 1375-1384.
| Crossref | Google Scholar | PubMed |
Speirs SD, Scott BJ, Moody PW, Mason SD (2013) Soil phosphorus tests II: a comparison of soil test–crop response relationships for different soil tests and wheat. Crop & Pasture Science 64(5), 469-479.
| Crossref | Google Scholar |
Therneau T, Atkinson B (2019a) rpart: recursive partitioning and regression trees. Available at https://CRAN.R-project.org/package=rpart
Therneau TM, Atkinson EJ (2019b) An introduction to recursive partitioning using the RPART routines. CRAN. Available at cran.r-project.org/
Van de Pol M, Bailey LD, McLean N, Rijsdijk L, Lawson CR, Brouwer L (2016) Identifying the best climatic predictors in ecology and evolution. Methods in Ecology and Evolution 7(10), 1246-1257.
| Crossref | Google Scholar |
Wang H, Song M (2011) Ckmeans.1d.dp: Optimal k-means clustering in one dimension by dynamic programming. The R Journal 3(2), 29-33.
| Crossref | Google Scholar | PubMed |
Weaver DM, Wong MTF (2011) Scope to improve phosphorus (P) management and balance efficiency of crop and pasture soils with contrasting P status and buffering indices. Plant and Soil 349, 37-54.
| Crossref | Google Scholar |
Weaver D, Summers R, Schweizer S, Leopold M, Scanlan C (2022) Valuable phosphorus retained by ironstone gravels can be measured as bicarbonate extractable P. Geoderma 418, 115862.
| Crossref | Google Scholar |
Weaver D, Summers R, Neuhaus A (2023) Agronomic soil tests can be used to estimate dissolved reactive phosphorus loss. Soil Research 61(7), 627-646.
| Crossref | Google Scholar |