Structure, Thermal Behaviour, and Energetic Properties of 4-Amino-1,2,4-triazole Dinitroguanidine Salt
Xinghui Jin A , Bingcheng Hu A B , Huanqing Jia A , Zuliang Liu A and Chunxu Lu AA School of Chemical Engineering, Nanjing University of Science and Technology, Nanjing, Jiangsu, 210094, China.
B Corresponding author. Email: hubingcheng210094@163.com
Australian Journal of Chemistry 67(2) 277-282 https://doi.org/10.1071/CH13426
Submitted: 20 August 2013 Accepted: 4 October 2013 Published: 7 November 2013
Abstract
A novel nitrogen-rich energetic compound 4-amino-1,2,4-triazole dinitroguanidine salt (4-ATDNG) was synthesized and fully characterized. Its crystal, thermal behaviour, and detonation properties were investigated by X-ray diffraction, thermogravimetry-derivative thermogravimetry-differential scanning calorimetry (TG-DTG-DSC) coupling system, and the Kamlet–Jacobs equation. In view of the obtained values such as the critical temperature of thermal explosion (Tb, 186.36°C), entropy of activation (ΔS≠, 60.22 J mol–1 k–1), enthalpy of activation (ΔH≠, 143.24 kJ mol–1), free energy of activation (ΔG≠, 116.34 kJ mol–1), detonation pressure (P, 29.78 GPa), detonation velocity (V, 8.28 km s–1), and impact sensitivity (h50 = 135 cm), it is proposed that 4-ATDNG possesses excellent thermal stability and has the potential to be a useful energetic material in the future.
Introduction
During the last few decades, considerable effort has been focussed on the development of nitrogen-rich high-energy-density materials (HEDMs) with high performance and decreased sensitivity as well as environmental compatibility.[1–5] Unfortunately, energetic compounds usually exhibit poorer thermal stability and high sensitivity to impact, friction, thermal shock, and electrostatic discharge. One possible approach to solve this problem is to introduce strong hydrogen bonds (especially the hydrogen bonds between –NH2 and –NO2 groups) in the crystal structure. The inter- and intra-molecular hydrogen-bonding networks between –NH2 and –NO2 groups may contribute to higher density, higher thermal stability, and lower sensitivity in an energetic compound.
One of the hottest topics in the field of HEDM is organic nitrogen-rich energetic salts. The energetic salts often possess advantages over their atomically similar non-ionic analogues, as these salts tend to exhibit lower vapour pressures and higher thermal stability.[6–8] Through suitable combination of different energetic cations and anions, the properties of energetic salts may be readily improved and optimized. So far, many organic nitrogen-rich energetic salts with excellent properties have been prepared from various energetic cations or anions derived from imidazole,[9,10] triazole,[11] and tetrazole.[12,13]
Dinitroguanidine,[14] which has inter- and intra-molecular hydrogen-bonding networks between the –NH2 and –NO2 groups, has received much attention for its excellent energetic properties and high density.[15] A considerable number of studies have also demonstrated that R–NHNO2 normally can act as a moderately strong acid, and that the stability of these compounds can be dramatically increased by transformation of the –NHNO2 moiety into –[NNO2]– to form a salt.[16] However, the high enthalpy of formation of an energetic material is directly attributable to the large number of inherently energetic N–N and C–N bonds. Not surprisingly, 4-amino-1,2,4-triazole consists of this type of structure with an excellent energetic performance and a rather high calculated enthalpy of formation of +318 kJ mol–1.[17] Herein, a novel nitrogen-rich energetic material 4-amino-1,2,4-triazole dinitroguanidine salt (4-ATDNG, Scheme 1) was designed. Its crystal structure, thermal behaviour, and calculated detonation properties were investigated to give a better understanding of its physical and chemical properties.

|
Materials and Methods
Experimental Section
4-Amino-1,2,4-triazole was prepared according to Sanz et al.[18] Dinitroguanidine was prepared according to Astrat’yev et al.[14]
The 4-ATDNG salt was prepared as follows: to a vigorously stirred solution of dinitroguanidine (1.49 g, 0.01 mol) in methanol (15 mL) was added dropwise a solution of 4-amino-1,2,4-triazole (0.84 g, 0.01 mol) in methanol (15 mL). A precipitate of 4-ATDNG was formed immediately during the process. The suspension was stirred at 40°C for 30 min and cooled to room temperature. Then, the insoluble solid was filtered and washed with cool methanol several times. Recrystallization (water/methanol) of this material afforded the 4-ATDNG (1.93 g, 82.8 %) as white needles, mp 147–149°C. νmax/cm–1 3344, 3249, 3106, 2857, 2706, 1620, 1384, 1221, 734. δC ([D6]DMSO, 125 MHz) 144.57, 163.01. m/z (ESI) 147.9 [M – H]–, 85.1 [M + H]+. Anal. Calc. for C3H7O4N9: C 15.45, H 3.00, N 54.08; found C 15.38, H 3.11, N 53.89 %.
Experimental Equipment and Conditions
Crystallographic data (excluding structure factors) for the structure in this paper have been deposited with the Cambridge Crystallographic Data Centre (CCDC), 12 Union Road, Cambridge CB2 1EZ, UK. Copies of the data can be obtained free of charge on quoting the depository number CCDC-935171 (fax: + 44 1223 336033; email: deposit@ccdc.cam.ac.uk, http://www.ccdc.cam.ac.uk, accessed 10 October 2013).
A BrukerAvance III 500 MHz spectrometer was used for 13C NMR spectra of 4-ATDNG; IR spectra were obtained on a Thermo Nicolet IS10 IR instrument; electrospray ionization mass spectrometry (ESI-MS) results were obtained on a Finnigan TSQ Quantum mass spectrometer and elemental analysis was carried out on a Perkin–Elmer PE-2400. Thermogravimetry-derivative thermogravimetry-differential scanning calorimetry (TG-DTG-DSC) curves were obtained on a Netzsch STA 409 PC/PG coupling system with an initial mass of 5 mg placed in alumina crucibles (argon atmosphere with a flow rate of 30 mL min–1). Further, thermal behaviour at different heating rates of 5, 10, 15, and 20 K min–1 was also examined to investigate the main pyrolysis dynamics of 4-ATDNG.
Results and Discussion
Crystal Structure
Single crystals suitable for X-ray measurements were obtained by slow evaporation of an aqueous methanol solution of 4-ATDNG. A white crystal with dimensions 0.27 × 0.18 × 0.16 mm was chosen for X-ray determination. The data were collected with a Bruker Smart Apex II CCD X-ray diffractometer using graphite-monochromated Mo-Kα radiation (λ = 0.071073 nm). The structure was solved by direct methods (SHELXTL-97) and refined by full-matrix-block least-squares methods on F2 with anisotropic thermal parameters for all non-hydrogen atoms. Crystal data and refinement results are summarized in Table 1.

|
The molecular structure and the three-dimensional packing diagram of the 4-ATDNG crystal are illustrated in Fig. 1 and Fig. 2 respectively. The analytical results indicate that the molecular structure of 4-ATDNG is made up of one 4-amino-1,2,4-triazole cation and one dinitroguanidine anion. The cation and anion are distributed in different planes, and the whole molecule presents an almost perpendicular conformation.

|

|
Table 2 shows selected bond lengths, bond angles, and dihedral angles. It can be seen that the C–N bond lengths range from 1.2973 to 1.3727 Å whereas the N–N bond lengths range from 1.3397 to 1.4041 Å. Obviously, all the C–N or N–N bond lengths are between normal C–N, N–N bond lengths (1.47 and 1.45 Å respectively) and normal C=N, N=N bond lengths (1.28 and 1.25 Å respectively). This indicates that the bonds in the 4-amino-1,2,4-triazole cation and the dinitroguanidine anion tend to be average and form a large conjugated system that promotes the stability of the crystal.

|
Thermal Behaviour
The TG-DTG-DSC curves of 4-ATDNG with an initial temperature of 40°C up to 800°C at a heating rate of 15 K min–1 are shown in Fig. 3. From the figure, two steps are obviously seen in the TG curve, which reveals that the decomposition reaction is a two-stage process: the first stage starts from 160 to 230°C with 80 % weight loss and is followed by the second stage, which starts at 650°C and ends at 750°C with ~20 % weight loss. Correspondingly, there is an evident sharp peak at ~200°C and a faint peak at ~720°C in the DTG curve. This also demonstrates that the decomposition reaction is a two-stage process. The DSC curve shows an evident endothermic peak (147.5°C) and a sharp exothermic peak (204.8°C), which correspond to the melting and decomposition of 4-ATDNG respectively. The exothermic process occurred immediately after the melting of 4-ATDNG, with a measured decomposition enthalpy of 1440 J g–1.

|
Non-isothermal Decomposition Kinetics
Two thermal analysis kinetic methods were jointly employed to calculate the relative kinetic parameters such as activation energy (Ea), pre-exponential constant (A), entropy of activation (ΔS≠), enthalpy of activation (ΔH≠), and free energy of activation (ΔG≠). The methods are expressed as follows.
Kissinger Equation (Differential Method)[19]
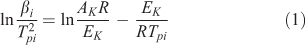
where βi is the heating rate; EK is the activation energy calculated by the Kissinger method; AK is the pre-exponential factor (A) calculated by Kissinger’s method; Tpi is the maximum peak temperature, which can be obtained from the DSC curves; and R is the gas constant. Then, a straight line was obtained by plotting ln(βi/Tpi2) v. the reciprocal of the temperature (T–1). The slope of the line is equal to –EK/R and the intercept of the line is equal to ln(AR)/EK. Thus, the activation energy calculated by the Kissinger method, EK, and the pre-exponential factor A can calculated from the slope and intercept of the plot respectively.
Ozawa–Flynn–Wall Equation (Integral Methods)[20]
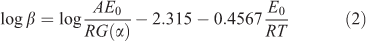
where α is conversion ratio; G(α) is the mechanism function for the thermal decomposition; E0 is apparent activation energy; A is the pre-exponential factor; T is the peak temperature; R is the gas constant and β is the heating rate. This isoconversional method allows evaluation of the dependence of the activation energy on the degree of conversion without the knowledge of the explicit form of G(α).[21] At the peak temperature, the degree of conversion (α) at different heating rates would be at a constant value.[22] Therefore, using Doyle’s approximation,[23] Eqn 2 was simplified and rewritten by Flynn–Wall–Ozawa as:
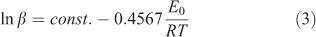
Then, another straight line was obtained by plotting ln β v. the reciprocal of the temperature (T–1). The activation energy and pre-exponential factor can easily be calculated based on the slope and intercept of the plot respectively as described above.
According to the equations, non-isothermal studies at the different heating rates of 5, 10, 15, and 20 K min–1 were carried out to obtain the relative kinetic parameters. The data β, Tpi, and the kinetic parameters obtained from the Kissinger and Ozawa methods are summarized in Table 3.

|
From Table 3, it is obvious that the values of Tpi of the exothermic peak shifted to higher temperatures as the heating rate increased. The values of E calculated from the Kissinger method (EK) agree well with that obtained by Ozawa’s method (E0), though the value of EK is slightly higher than that of E0. Besides, both of the linear correlation coefficients are very close to 1 and thus it is predicted that the result is credible. However, the apparent activation energy of 4-ATDNG is relatively low and this is consistent with the fact that 4-ATDNG easily decomposes when the temperature is above 150°C.
Based on the calculated kinetic parameters (Ea and A), other thermodynamic parameters such as the entropy of activation (ΔS≠), the enthalpy of activation (ΔH≠), and the free energy of activation (ΔG≠) could be calculated using Eqns 4–6[24,25] respectively.
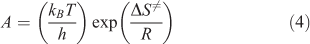

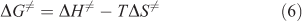
where T = Tp0, the peak temperature (Tpi) corresponding to β → 0; Ea = EK, calculated by Kissinger’s method; A = AK, calculated by Kissinger’s method; kB, the Boltzmann constant, 1.3807 × 10–23 J K–1; and h, the Plank constant, 6.626 × 10–34 J s–1.
According to the equations described above, in order to get the values of ΔS≠, ΔH≠, and ΔG≠, the value of Tp0 must be known. Then the next important task is to calculate the value of Tp0, which can be calculated from Eqn 7.[26]
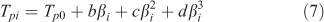
where b, c, and d are coefficients. By plugging the different heating rates (β) of 5, 10, 15, and 20 K min–1, and the corresponding peak temperature (Tpi) into Eqn 7, the value of Tp0 was calculated as 446.75 K. Based on Eqns 4–7, the values of ΔS≠, ΔH≠, and ΔG≠ could be easily extracted as 60.22 J mol–1 K–1, 143.24 kJ mol–1, and 116.34 kJ mol–1 respectively.
Critical Ignition Temperature
The critical temperature of thermal explosion (Tb), which can be defined as the lowest temperature to which a specific charge may be heated without undergoing thermal runaway,[27,28] is another important parameter for evaluating the thermal stability of energetic materials. This parameter is necessary to ensure safe storage and process operations involving explosives, propellants, and pyrotechnics. The value of Tb of 186.36°C can be calculated from the following equation:[29,30]
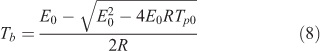
where E0 is the apparent activation energy obtained by Ozawa’s method; R is the gas constant; and Tp0 is the peak temperature corresponding to β → 0, 446.75 K.
Detonation Properties
Computations were performed with the Gaussian 03 suite of programs.[31] The geometric optimization of the structures was based on single-crystal structures, where available, and frequency analyses were carried out using the B3-LYP functional with the 6-31+G(d,p) basis set,[32,33] and single-energy points were calculated at the MP2(full)/6-311++G(d,p) level. All of the optimized structures were characterized to be true local energy minima on the potential energy surface without imaginary frequencies.
Detonation properties, such as detonation velocity (D) and detonation pressure (P), are the most important targets in screening energetic materials and many empirical methods have been applied to estimate these properties. Numerous studies have proved the Kamlet–Jacobs[34] equations to be the most reliable approach among the empirical methods:
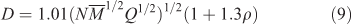
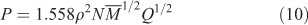
where the terms in Eqns 9 and 10 are defined as follows: D, detonation velocity (km s–1); P, detonation pressure (GPa); N, moles of detonation gases per gram explosive;  , the average molecular weight of these gases; Q, heat of detonation (cal g–1); and ρ, the loaded density of explosives (g cm–3).
, the average molecular weight of these gases; Q, heat of detonation (cal g–1); and ρ, the loaded density of explosives (g cm–3).
According to the Kamlet–Jacobs equations, the values of N,  , and Q, which could be obtained using the equations summarized in Table 4, should be calculated first to estimate the values of D and P.
, and Q, which could be obtained using the equations summarized in Table 4, should be calculated first to estimate the values of D and P.

|
Then the next important task is to determine the enthalpy of formation ( ) of the energetic salt. According to the Born–Haber energy cycle (Fig. 4), the enthalpy of formation of a salt can be simplified as the following equation (Eqn 11):
) of the energetic salt. According to the Born–Haber energy cycle (Fig. 4), the enthalpy of formation of a salt can be simplified as the following equation (Eqn 11):
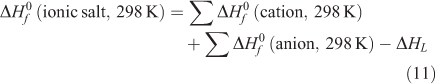
where  is the lattice energy of the salt.
is the lattice energy of the salt.

|
The value of  can be predicted by the formula suggested by Jenkins et al.:[35]
can be predicted by the formula suggested by Jenkins et al.:[35]
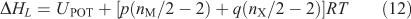
where UPOT is the lattice potential energy and nM and nX depend on the nature of the ions Mp+ and Xq–, respectively, and are equal to three for mono-atomic ions, five for linear polyatomic ions, and six for non-linear polyatomic ions. The equation for the lattice potential energy UPOT has the following form:
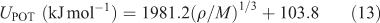
where ρ is the density (g cm–3), M is the chemical formula mass of the ionic material (g mol–1), and the coefficients γ (1982.1 kJ mol–1 cm) and δ (103.8 kJ mol–1) are assigned literature values.[35]
The enthalpy of formation ( ) of the cations and anions is computed using the method of isodesmic reactions (Scheme 2[36]). The energies of the parent ions in the isodesmic reactions were calculated from protonation reactions (Scheme 3; enthalpy of formation of H+ is 1530 kJ mol–1).[37,38] The enthalpy of the isodesmic reaction (
) of the cations and anions is computed using the method of isodesmic reactions (Scheme 2[36]). The energies of the parent ions in the isodesmic reactions were calculated from protonation reactions (Scheme 3; enthalpy of formation of H+ is 1530 kJ mol–1).[37,38] The enthalpy of the isodesmic reaction ( ) is obtained by combining the MP2/6-311++G** energy difference for the reaction, the zero-point energies (B3-LYP/6-31+G**), and other thermal factors(B3-LYP/6-31+G**). Thus, the enthalpy of formation of the cations, anions, and the salt being investigated can be extracted readily according to Eqns 11–13.
) is obtained by combining the MP2/6-311++G** energy difference for the reaction, the zero-point energies (B3-LYP/6-31+G**), and other thermal factors(B3-LYP/6-31+G**). Thus, the enthalpy of formation of the cations, anions, and the salt being investigated can be extracted readily according to Eqns 11–13.

|

|
Further, the impact sensitivity of an energetic material is essential, because it is an important index to guarantee safety for storage or use. Keshavarz et al.[39] proposed that the impact sensitivity (h50) of CaHbNcOd explosives can most appropriately be expressed as their elemental composition and some structural parameter. The impact sensitivity calculated by Eqn 14 shows an excellent correlation with the measured values and has been widely used in investigating the impact sensitivity of new energetic materials. The simplified formula is written in the following form:
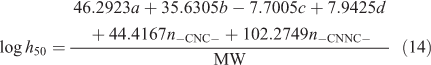
where a, b, c, and d stand for the number of C, H, N, and O atoms in the explosive molecule respectively; n–CNC– and n–CNNC– stand for the number of –CNC– and –CNNC– in the molecule respectively; and MW stands for the molecular weight.
Based on the equations and theories described above, the values of enthalpy of formation, detonation velocity, detonation pressure, and impact sensitivity of 4-ATDNG were calculated as 349.65 kJ mol–1, 8.28 km s–1, 29.78 GPa, and 135 cm respectively. This indicates that 4-ATDNG has superior detonation properties and can be considered as a potential energetic material.
Conclusions
-
4-Amino-1,2,4-triazole dinitroguanidium salt (4-ATDNG) as a novel organic nitrogen-rich energetic salt was synthesized and structurally characterized by single-crystal X-ray diffraction. It is crystallized in a monoclinic system, space group P21/C.
-
The thermal behaviour of 4-ATDNG presents two processes of weight loss and a single sharp exothermic peak at ~204.8°C. The critical temperature of thermal explosion is 186.36°C.
-
The Eas calculated via the Kissinger and Ozawa methods are 146.95 and 145.98 kJ mol–1. Some other thermodynamic parameters such as ΔS≠, ΔH≠, and G≠ were also calculated as 60.22 J mol–1 k–1, 143.24 kJ mol–1, and 116.34 kJ mol–1 respectively.
-
The calculated values of detonation velocity (D = 8.28 km s–1), detonation pressure (P = 29.78 GPa), and impact sensitivity (h50 = 135 cm) reflect that 4-ATDNG has superior detonation properties and can be considered as a potential energetic material.
Supplementary Material
Crystallographic data of 4-amino-1,2,4-triazole dinitroguanidine (4-ATDNG) are available on the Journal's website.
Acknowledgements
This study was supported by the National Natural Science Foundation of China and the China Academy of Engineering Physics (Grant No. 11076017) and the National Defence Advanced Research Projects (Grant No. J-KY-2012–1317).
References
[1] M. H. V. Huynh, M. A. Hiskey, D. E. Chavez, D. L. Naud, R. D. Gilardi, J. Am. Chem. Soc. 2005, 127, 12537.| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXpt1WisLw%3D&md5=ca05760d4efeb4876eac3a5ff2e579ccCAS |
[2] M. H. Keshavarz, J. Hazard. Mater. 2007, 141, 536.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXis1Gjtrw%3D&md5=33cdfcd0789cbfe74a34e66ac609c950CAS | 16959409PubMed |
[3] D. E. Chavez, M. A. Hiskey, J. Energ. Mater. 1999, 17, 357.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1MXntFequrs%3D&md5=aa4d6e3ec5027db347133add33b7b901CAS |
[4] D. E. Chavez, D. Parrish, D. N. Preston, I. W. Mares, Propellants Explos. Pyrotech. 2012, 37, 647.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC38Xht1emtbzL&md5=8859dd5ed5d45f1217869bd3dcc0f1abCAS |
[5] R. Wang, H. Xu, Y. Guo, R. Sa, J. M. Shreeve, J. Am. Chem. Soc. 2010, 132, 11904.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXpvVaru7c%3D&md5=dc67c5cc75e5ec85c4e4e7ece81b72aeCAS | 20690685PubMed |
[6] A. R. Katritzky, S. Singh, K. Kirichenko, J. D. Holbrey, M. Smiglak, W. M. Reichert, R. D. Rogers, Chem. Commun. 2005, 868.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXht1Kqs78%3D&md5=83dcb3ea0cd7e24f67fbab997fa30ac0CAS |
[7] H. X. Gao, C. F. Ye, O. D. Gupta, J. C. Xiao, M. A. Hiskey, B. Twamley, J. M. Shreeve, Chem. Eur. J. 2007, 13, 3853.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXlsl2isb8%3D&md5=356a549aa1a33acfa16f25cc0c4067baCAS |
[8] R. P. Singh, R. D. Verma, D. T. Meshri, J. M. Shreeve, Angew. Chem. 2006, 118, 3664.
| Crossref | GoogleScholarGoogle Scholar |
[9] C. B. Jones, R. Haiges, T. Schroer, K. O. Christe, Angew. Chem. 2006, 118, 5103.
| Crossref | GoogleScholarGoogle Scholar |
[10] A. R. Katritzky, S. Singh, K. Kirichenko, M. Smiglak, J. D. Holbrey, W. M. Reichert, S. K. Spear, R. D. Rogers, Chem. Eur. J. 2006, 12, 4630.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XmtVaitbs%3D&md5=97f81e0977d2accc7706fed8d492ee8aCAS | 16586524PubMed |
[11] G. W. Drake, T. W. Hawkins, L. A. Hall, J. A. Boatz, A. J. Brand, Propellants Explos. Pyrotech. 2005, 30, 329.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXht1amu7nI&md5=cfcedfb14cbcce73a39f15b694aa8e92CAS |
[12] K. Karaghiosoff, T. M. Klapötke, P. Mayer, H. Piotrowski, K. Polborn, R. L. Willer, J. J. Weigand, J. Org. Chem. 2006, 71, 1295.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XoslKitg%3D%3D&md5=15e5c0cf732e55e38b0f444ef0079c4eCAS | 16468775PubMed |
[13] Y. H. Joo, B. Twamley, S. Garg, J. M. Shreeve, Angew. Chem. 2008, 120, 6236.
| Crossref | GoogleScholarGoogle Scholar |
[14] A. A. Astrat’yev, D. V. Dashko, L. L. Kuznetsov, Russ. J. Org. Chem. 2003, 39, 501.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXnvFWhtbk%3D&md5=cf1d747534504258148c02f4472dc1a0CAS |
[15] A. D. Vasiliev, A. M. Astachov, M. S. Molokeev, L. A. Kruglyakova, R. S. Stepanov, Acta Crystallogr. C 2003, 59, o550.
| Crossref | GoogleScholarGoogle Scholar | 14532667PubMed |
[16] T. Altenburg, T. M. Klapötke, A. Penger, J. Stierstorfer, Z. Anorg. Allg. Chem. 2010, 636, 463.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXktlSjs70%3D&md5=32e13664ae852601407f541dd4a1a689CAS |
[17] C. F. Ye, J. C. Xiao, B. Twamley, J. M. Shreeve, Chem. Commun. 2005, 2750.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXksFejsLw%3D&md5=8f56d96fe025c1dfe6e80db56ddc802aCAS |
[18] D. Sanz, M. Pérez-Torralba, S. H. Alarcón, R. M. Claramunt, C. Foces-Foces, J. Elguero, J. Org. Chem. 2002, 67, 1462.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38Xps1aiug%3D%3D&md5=58c08c37f486a82b9531abc80761a506CAS | 11871874PubMed |
[19] H. E. Kissinger, Anal. Chem. 1957, 29, 1702.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG1cXivVequw%3D%3D&md5=eea37720fe8cb85b3c40d56909b20740CAS |
[20] T. Ozawa, Bull. Chem. Soc. Jpn. 1965, 38, 1881.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF28XjtVyisQ%3D%3D&md5=92e3311c2ba5a37370e55b0737c27c14CAS |
[21] J. M. Salla, J. M. Morancho, A. Cadenato, X. Ramis, J. Therm. Anal. Calorim. 2003, 72, 719.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXltVWhsbw%3D&md5=052463123cfa15293f47cdcff1e3e32fCAS |
[22] J. H. Yi, F. Q. Zhao, S. Y. Xu, L. Y. Zhang, H. X. Gao, R. Z. Hu, J. Hazard. Mater. 2009, 165, 853.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXks12lurc%3D&md5=11c1345a153fa105c9b7c32d34eb8927CAS | 19059712PubMed |
[23] C. D. Doyle, J. Appl. Polym. Sci. 1961, 5, 285.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF38XkvFOrtg%3D%3D&md5=3fe2194ad016d89164b0aed34053d81aCAS |
[24] J. M. Criado, L. A. Perez-Maqueda, P. E. Sanchez-Jimenez, J. Therm. Anal. Calorim. 2005, 82, 671.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XjsFCqtA%3D%3D&md5=f8efa0076a07c13985f8c715bc4c6f94CAS |
[25] R. Z. Hu, S. P. Chen, S. L. Gao, F. Q. Zhao, Y. Luo, H. X. Gao, Q. Z. Shi, H. A. Zhao, P. Yao, J. Li, J. Hazard. Mater. 2005, 117, 103.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXisFOk&md5=7ab77306209ff1f9dd2f3df5b4fea3deCAS |
[26] K. Z. Xu, H. Zhang, P. Liu, J. Huang, Y. H. Ren, B. Z. Wang, F. Q. Zhao, Propellants Explos. Pyrotech. 2012, 37, 653.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC38XhtVGnu7nK&md5=a13ff125633ae79a52f29db92fedf7d2CAS |
[27] R. N. Rogers, J. L. Janney, M. H. Ebinger, Thermochim. Acta 1982, 59, 287.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL3sXit12hug%3D%3D&md5=b6979f16048b7e6a3cfc738fb27c4b83CAS |
[28] J. M. Pickard, Thermochim. Acta 2002, 392–393, 37.
| Crossref | GoogleScholarGoogle Scholar |
[29] T. Zhang, R. Hu, Y. Xie, F. Li, Thermochim. Acta 1994, 244, 171.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2cXmvVeisLs%3D&md5=cc355fec694341592397634e9e6a9d48CAS |
[30] M. Najafi, A. K. Samangani, Propellants Explos. Pyrotech. 2011, 36, 487.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXhsFKksrvM&md5=a21512be6f7c535514a4f0bcf21716dbCAS |
[31] M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, J. A. Pople, Gaussian 03 2003 (Gaussian Inc.: Pittsburgh, PA).
[32] C. Lee, W. Yang, R. G. Parr, Phys. Rev. B 1988, 37, 785.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL1cXktFWrtbw%3D&md5=5be02d73b432a9ccf155dbb749241880CAS |
[33] Z. Dega-Szafran, A. Katrusiak, M. Szafran, Aust. J. Chem. 2013, 66, 836.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3sXhtFCqsr%2FM&md5=00669e516c9ea8922493210a94ee1d50CAS |
[34] M. J. Kamlet, S. J. Jacobs, J. Chem. Phys. 1968, 48, 23.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF1cXntVOrtQ%3D%3D&md5=c74efc1d0979935af40eb69b9c446866CAS |
[35] H. D. B. Jenkins, D. Tudeal, L. Glasser, Inorg. Chem. 2002, 41, 2364.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38Xis1CitrY%3D&md5=b47a1bc1c52c66bc2833070d2a4d6f40CAS |
[36] Y. G. Huang, Y. Q. Zhang, J. M. Shreeve, Chem. Eur. J. 2011, 17, 1538.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXhtFKrur8%3D&md5=2ad3773efda94eb24f34f685547bfb1dCAS |
[37] Z. Zeng, H. X. Gao, B. Twamley, J. M. Shreeve, J. Mater. Chem. 2007, 17, 3819..
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXhtVWktbfI&md5=f92f51caa6df9f419f459c5aeed1856dCAS |
[38] M. W. Schmidt, M. S. Gordon, J. A. Boatz, J. Phys. Chem. A 2005, 109, 7285.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXmsVymsbo%3D&md5=ebfe69a586d73af40ef34b538db64740CAS | 16834094PubMed |
[39] M. H. Keshavarz, H. R. Pouretedal, A. Semnani, J. Hazard. Mater. 2007, 141, 803.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXis1Gjtbo%3D&md5=171aac4ed64641a8b40bf836c515881dCAS | 16956725PubMed |


